 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Size-related variability of oxygen consumption rates in individual human hepatic cells†
Ermes
Botte‡
 ab,
Yuan
Cui‡
ab,
Yuan
Cui‡
 cd,
Chiara
Magliaro
ab,
Maria
Tenje
cd,
Chiara
Magliaro
ab,
Maria
Tenje
 d,
Klaus
Koren
e,
Andrea
Rinaldo
fg,
Roman
Stocker
d,
Klaus
Koren
e,
Andrea
Rinaldo
fg,
Roman
Stocker
 h,
Lars
Behrendt§
*c and
Arti
Ahluwalia§
*ab
h,
Lars
Behrendt§
*c and
Arti
Ahluwalia§
*ab
aResearch Centre “E. Piaggio”, University of Pisa, Pisa, Italy. E-mail: arti.ahluwalia@unipi.it; Tel: +39 0502217062
bDepartment of Information Engineering, University of Pisa, Pisa, Italy
cDepartment of Organismal Biology, Science for Life Laboratory, Uppsala University, Uppsala, Sweden. E-mail: lars.behrendt@scilifelab.uu.se; Tel: +46 184712591
dDepartment of Materials Science and Engineering, Science for Life Laboratory, Uppsala University, Uppsala, Sweden
eAarhus University Centre for Water Technology, Department of Biology, Aahrus University, 8000 Aarhus, Denmark
fLaboratory of Ecohydrology ECHO/IIE/ENAC, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland
gDepartment of Civil, Environmental and Architectural Engineering, University of Padova, Padova, Italy
hInstitute for Environmental Engineering, Department of Civil, Environmental and Geomatic Engineering, ETH Zurich, Zurich, Switzerland
First published on 26th July 2024
Abstract
Accurate descriptions of the variability in single-cell oxygen consumption and its size-dependency are key to establishing more robust tissue models. By combining microfabricated devices with multiparameter identification algorithms, we demonstrate that single human hepatocytes exhibit an oxygen level-dependent consumption rate and that their maximal oxygen consumption rate is significantly lower than that of typical hepatic cell cultures. Moreover, we found that clusters of two or more cells competing for a limited oxygen supply reduced their maximal consumption rate, highlighting their ability to adapt to local resource availability and the presence of nearby cells. We used our approach to characterize the covariance of size and oxygen consumption rate within a cell population, showing that size matters, since oxygen metabolism covaries lognormally with cell size. Our study paves the way for linking the metabolic activity of single human hepatocytes to their tissue- or organ-level metabolism and describing its size-related variability through scaling laws.
Introduction
Biological variability (i.e., the fluctuation of physiological traits among individuals of the same population, also referred to as biological noise) is ubiquitous and can impact phenomena such as metabolic scaling and resilience to environmental perturbations.1,2 Often, variability is not confined to one parameter but instead is characterized by an interplay between multiple variables within an organism or ecosystem. For instance, it has been suggested that the covariance between the size and metabolism of individuals influences the ability of organisms to react to external stimuli (e.g., toxins or drugs) and may explain patterns in homeostatic control.1,3,4 Joint variations between physiological parameters can also impact the susceptibility of organisms to diseases and affect their overall health.5 Biological variability has been extensively investigated at the molecular level (transcription and expression), but less so at cellular and organismal levels. Investigating single cells, instead of tissues or organs, offers the opportunity to characterize variability between individuals to infer dynamics occurring at higher scales of complexity. Single cells also provide a suitable testbed to determine intrinsic size-related variability and its role in metabolic scaling, which has been highlighted as a criterion for translating biological parameters from micro-scale in vitro systems to in vivo contexts.1,6,7As oxygen (O2) is at the heart of aerobic metabolism,8,9 several studies have measured O2 consumption in individual mammalian cells.10–13 However, the accuracy, reproducibility, and throughput of O2 measurements at this scale remain challenging. Mammalian cells possess the ability to modulate their O2 consumption according to its availability, a process that, in turn, is influenced by numerous factors (e.g., height of culture medium and cell density).14,15 However, many studies assume that cells possess a constant (zero-order) consumption rate which depends only on cell phenotype. The O2 consumption rate (Rcell, in mol s−1) of a single cell as a function of the surrounding O2 concentration (c, in mol m−3) is typically represented by the Michaelis–Menten (MM) model16–18via two parameters: the maximal consumption rate (sOCR, in mol s−1) and the MM constant (kM, in mol m−3).
 | (1) |
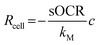 . Hence, a cell with a low kM value consumes O2 maximally even at low concentrations, whereas a cell with a high kM has a low O2 uptake efficiency (i.e., O2 levels must be high to achieve near-maximal consumption rates).
. Hence, a cell with a low kM value consumes O2 maximally even at low concentrations, whereas a cell with a high kM has a low O2 uptake efficiency (i.e., O2 levels must be high to achieve near-maximal consumption rates).
Despite the widespread application of eqn (1) in predicting how cells adapt to ambient O2, MM parameters for mammalian cells have rarely been reported. Some studies have investigated cell cultures either as 2-dimensional (2D) monolayers or 3-dimensional (3D) constructs (herein referred to as aggregates, independent of dimensionality), but to date MM parameters for individual mammalian cells have not been measured. Here we present a systematic approach to conduct single-cell measurements of O2 consumption as described by the MM model. Our primary objective was to estimate the MM parameters (i.e., sOCR and kM) and explore their size-related variability in a human hepatic cell line, HepG2.19 Using custom glass microwell devices coated with luminescent O2-sensitive optode materials,20,21 we isolated single cells or clusters of a few cells (from two to seven units confined in the same microwell but not necessarily adjacent, unlike in 2D or 3D aggregates) under precisely controlled experimental conditions. Automated fluorescence microscopy was used to perform time-series imaging of the wells to extract cell sizes and O2 concentration profiles from individual wells. A multiparameter identification procedure22 was applied to determine MM parameters from these profiles. Through this approach, we were able to estimate single-cell size and MM parameters for O2 consumption as a joint probability distribution and so describe their correlated variability.
This quantitative description of single-cell O2 consumption allows probing the biophysical basis of cooperative metabolic dynamics, which are only detectable at higher levels of organization. Furthermore, the identification and characterisation of the covariation of size and O2 consumption parameters for single cells can help in understanding how these dynamics are linked to behaviours that emerge in tissues and organs. It also provides a means for investigating the origins of allometric scaling between size and metabolic rates of whole organisms, a subject of long and wide-ranging debate.3
Materials and methods
Microwell devices for single-cell isolation and oxygen sensing
The microwell array consists of a standard borosilicate glass slide with geometrically arranged microwells (100 columns × 250 rows, n = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 microwells) fabricated via standard UV lithography and dry etching techniques. It was custom-built to allow the isolation of single cells or small clusters of cells in each microwell (see the schematic in Fig. 1 and S2†). The microfabrication procedure for this device is summarised in the ESI† (Fig. S1), and Table S1† reports relevant technical features of the dry etching process and geometric specifications of the array customized to match the size of human hepatic cells and to minimize optical and diffusional crosstalk between microwells.
000 microwells) fabricated via standard UV lithography and dry etching techniques. It was custom-built to allow the isolation of single cells or small clusters of cells in each microwell (see the schematic in Fig. 1 and S2†). The microfabrication procedure for this device is summarised in the ESI† (Fig. S1), and Table S1† reports relevant technical features of the dry etching process and geometric specifications of the array customized to match the size of human hepatic cells and to minimize optical and diffusional crosstalk between microwells.
Optode sensor composition, deposition and calibration
Calibration was performed introducing gases at five different levels of O2 saturation by combining compressed air and nitrogen (N2) through a gas mixer set up (Red-y smart series mass flow meters, Voegtlin GmbH, Muttenz, Switzerland). This system enabled modulation of the partial pressures of the mixture components by tuning the flow rate from their sources. The stability of air saturation within the sealed chamber was verified by monitoring it with a calibrated optical microsensor (OXR250, Pyroscience GmbH, Aachen, Germany). Images of single microwells were acquired with a 40× objective. All other imaging parameters were set as listed in Table 1 for monitoring cellular O2 consumption. A simplified form of the two-site model (eqn (2))27–29 was then fitted to collected datapoints in order to derive average calibration parameters for the specific array – i.e., the Stern–Volmer (SV) constant24 of the primary site for O2 quenching on the dye (kSV, expressed in 1/% air sat.) and the fractional contribution (f) of such primary site to the red-to-green ratio in totally anoxic conditions (R0, measured by exposing the device to pure N2).
 | (2) |
| Parameter | Numerical value |
|---|---|
| a To achieve optimal saturation of the sensing dye, the intensity of the excitation light was coherently adjusted for each round of calibration and subsequent experiment. | |
| Magnification | 10× |
| Large image size (n × m) | 6 × 6 |
| Time scale (tend) | 1 h |
| Time resolution (Δt) | 20 s |
| Excitation light wavelength | 396 nm |
| Excitation light intensity | 20% of maximum intensitya |
| Excitation duration | 50 ms |
Calibration curves were also estimated in liquid phase (i.e., cell culture medium) and compared to those obtained for corresponding microwell arrays using gases (data not shown). No significant differences emerged between liquid phase and gas phase calibrations, and hence we routinely relied on the more convenient gas calibration prior to each experiment. Further, we ensured that optode bleaching was negligible in the timeframe of our single-cell O2 consumption tests (see ESI3† for details). Finally, experiments were conducted to determine the extent of optical crosstalk between microwells and to define inter-well distance and cell occupancy to minimize it (see ESI4† for details).
Single-cell oxygen measurements
After optode calibration, the central area of the microwell array was overlaid with a thick poly-dimethyl-siloxane (PDMS) frame into which 500 μL of cell suspension in DMEM was pipetted. This allowed control of the seeding density and ensured that cells were confined to the region where the optode coating was determined to be homogeneous. Experiments were performed with different seeding densities, ranging from 2 × 103 cells per mL up to 106 cells per mL. The former resulted in an optimal trade-off between an acceptable number of microwells containing single cells and minimal lateral O2 diffusion between neighbouring microwells. Following cell seeding, the device was incubated overnight to allow cell adhesion to the microwells (Fig. 2C).
Following each experiment, 30 μL of trypan blue dye (0.4% w/v solution, Sigma-Aldrich) was gently pipetted through the gap between the microwell array and the coverslip. Trypan blue was left to diffuse over the array for about 10 min, then a brightfield large image was acquired setting the same scanning pathway as used during experiments. This procedure enabled identifying Ncell in each microwell and estimating cell size (i.e., the projected area) using ImageJ.32
 | (3) |
| R = ρcellRcell | (4) |
Given that cell and microwell sizes are comparable, and assuming that O2 consumption is uniform in the cell volume – and hence in the well domain – the cell density can be expressed as ρcell = Ncell/Vwell (with Vwell indicating the microwell volume, Table S1†).
As the heavy mineral oil layer is considered impermeable to O2, there is no flux at the oil/air boundary, likewise at the microwell walls or – given the homogeneity of consumption in the volume – within the domain. These assumptions imply that the O2 concentration field in the microwell depends only on time (c(x, y, z, t) = c(t)), and the governing equation can be simplified as  . In these conditions, a suitable duration for monitoring O2 consumption to hypoxia within each microwell was estimated based on the characteristic reaction time, τr:
. In these conditions, a suitable duration for monitoring O2 consumption to hypoxia within each microwell was estimated based on the characteristic reaction time, τr:
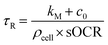 | (5) |
| Parameter | Numerical value | Description |
|---|---|---|
| c 0 | 0.2 mol m−3 (ref. 18) | Initial condition of O2 saturated-culture medium |
| sOCR | [10−18; 10−16] mol s−1 per cell (deduced from ref. 18 and 35) | Initial range of parametric sweep |
| k M | [10−3; 10−1] mol m−3 (deduced from ref. 17, 18 and 35) | Initial range of parametric sweep |
| Aggregate type | sOCR (×10−18 mol s−1 per cell) | k M (×10−3 mol m−3) | Reference |
|---|---|---|---|
| Isolated single cell | 13.35 ± 10.05 | 76.40 ± 52.60 | This study |
| Cell-laden hydrogel (3D) | 69.00 ± 0.15 | 6.20 ± 0.06 | 15 |
| Cell monolayer (2D) | 43.85 ± 27.41 | 23.50 ± 2.20 | 22 |
| Cell-laden spheroid (3D) | 78.07 ± 11.45 | 3.78 ± 1.52 | 22 |
| Cell-loaded hollow fibers (bioartificial liver) | 13.00 ± 5.89 | NA | 34 |
| Cell monolayer (2D) | 55.00 ± 9.85 | NA | 33 |
| Cell-laden hydrogel (3D) | 24.00 ± 7.13 | NA | 36 |
| Microcarrier (3D) | 75.00 ± 18.68 | NA | 37 |
Kinetic parameter identification
Experimentally measured O2 concentration profiles constituted the input datasets for the multiparameter identification algorithm reported in.22 Briefly, values of sOCR and kM were estimated comparing the O2 dynamics measured in each microwell containing cells to those predicted in silico by modelling the system according to eqn (3) and (4). A model governed by the dimensionless form of eqn (3) was iteratively solved for each specific microwell, taking Ncell from the trypan blue-stained image and parameters listed in Table 2 into account. | (6) |
In eqn (6), γ = c/c0 and T = t/τR are the non-dimensional concentration and time, respectively. Considering eqn (5), the dimensionless equation implemented for simulating O2 consumption in the well is the following:
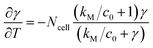 | (7) |
Statistical analysis and software
Numerical values of consumption parameters identified for microwells as a function of Ncell were compared by means of a non-parametric Kruskal–Wallis test and pairwise post hoc Dunn's multiple comparisons. Non-linear correlation (i.e., non-parametric Spearman coefficient) of sOCR and kM with respect to Ncell as well as with each other was also tested. Overall statistical differences between the MM parameters estimated here and typical literature values were assessed for both sOCR and kM using a non-parametric Wilcoxon signed-rank test. Furthermore, the joint distribution of single-cell size and sOCR was tested for both normality and lognormality via the Henze–Zirkler multivariate normality test performed on the original and log-transformed dataset, respectively.Image processing, simulation of O2 transport and consumption and multiparameter identification were implemented in Matlab (R2021b), while GraphPad Prism (version 7, GraphPad Software, California USA) was used to perform all statistical analyses.
Results
Using glass microwell devices (Fig. 2A) sealed via heavy mineral oil in conjunction with O2 sensitive optode chemistry (Fig. 2B) we measured a total of 1080 microwells across five independent experiments. Of these, 227 microwells (∼21%) contained at least one hepatic cell whose O2 consumption dynamics (Fig. 3A) could be recorded without interference from neighbouring wells (see ESI,† section ESI4). The distribution of the number of cells per well (or occupation, Ncell) is reported in Fig. 3B. Notably, in more than half of the cases in which cells were present in a microwell (i.e., 119 measurements, ∼11% of all investigated microwells), a single cell was probed (Fig. 2C), while a maximum of seven cells per well was recognized only once. | ||
| Fig. 3 MM kinetic parameters in isolated hepatic cells determined through a multiparameter identification procedure. (A) O2 concentration profiles measured in a microwell array. (B) Occupation (Ncell) frequency of cells in microwells. (C) Relative frequency of sOCR in occupied microwells. (D) Correlation between the number of cells per microwell and the corresponding sOCR value (r = −1 with p = 0.0028), over all occupied microwells. The black dashed curve is a weighted fit of results (one phase exponential decay, R2 = 0.9722). Pairwise statistical differences computed using Dunn's post hoc multiple comparisons are also reported (* p < 0.05, ** p < 0.005). (E) Relative frequency of kM in occupied microwells (expressed in logarithmic scale). (F) No correlation was observed between kM and the number of cells per well (r = −0.8286 with p = 0.0583). The vertical dark green dashed lines in (C) and (E) denote median literature values of sOCR and kM,15,18,22,33,34 respectively (see Table 3 for a complete list of reported values), while the solid black line in (E) indicates the O2 saturation level in water (c0). In (D) and (F), data are reported as median ± range. | ||
Oxygen consumption kinetics and number of cells per well
O2 profiles determined from individual or multiple cells were used to compute sOCR and kM through a multiparameter identification algorithm.22 Both MM parameters are reported as overall probability distributions (Fig. 3C and E) and as a function of Ncell (Fig. 3D and F). A Kruskal–Wallis test highlighted significant differences among sOCR values determined for microwells containing different numbers of cells (p < 0.0001). Specifically, we found that sOCR decreases with increasing Ncell (Fig. 3D, Spearman coefficient r = −1 with p = 0.0028); this suggests that cells adjust their sOCR in the presence of neighbouring cells sharing the same microenvironment. Notably, although our sOCR values are similar to previous estimates for hepatocytes cultured in a hollow fibre bioartificial liver,34 they are significantly lower (median sOCR = 1.1 × 10−17 mol s−1 per cell) than most of those reported in the literature for hepatocyte monolayers or 3D aggregates (median sOCR = 5.5 × 10−17 mol s−1 per cell, Wilcoxon test, p < 0.0001, Fig. 3C).6,15,18,22,33,36,37Our measurements of kM show a wide distribution, covering three orders of magnitude (Fig. 3E), with a significantly higher median (5.1 × 10−2 mol m−3) compared to values previously reported for 2D and 3D hepatic constructs (6.2 × 10−3 mol m−3 – Wilcoxon test, p < 0.0001).15,22 Approximately 34% of the measured kM values are comparable to or even higher than the O2 saturation level in water (c0 = 0.21 mol m−3), suggesting that, once isolated, about a third of the cells do not approach their maximal consumption rate but instead follow first order kinetics. Due to the large variability of kM, neither a significant correlation with Ncell (Spearman coefficient r = −0.8286 with p = 0.0583) nor statistical differences among its medians for different Ncell values (Kruskal–Wallis test, p = 0.2075) were detected (Fig. 3F).
To help distinguish mutual dependencies of sOCR and kM, MM parameters for all microwells investigated are presented in a scatter plot (Fig. 4A). Data points referring to microwells populated by the same number of cells are clustered along the sOCR axis, while no noticeable separation among groups of points corresponding to different values of Ncell with respect to kM is observed. A correlation analysis suggests that the two MM parameters depend on each other (Spearman coefficient r = 0.5864 with p < 0.0001), albeit less significantly than in previous observations for 2D and 3D aggregates of hepatic cells (e.g., r = 0.7857, ref. 22). For comparison, bulk values for the two kinetic parameters, averaged over several cells as reported in the literature,6,15,18,22,33,34,36,37 are also indicated in Fig. 4A and listed in Table 3.
 | ||
| Fig. 4 Mutual dependency of MM parameters and the size-related variability of O2 consumption in single human hepatic cells. (A) Scatter plot of measured sOCR and kM values. The Spearman coefficient indicates that the two parameters are weakly correlated (r = 0.5864). Each data point is denoted by a marker having shape and colour which depend on the corresponding value of Ncell for that data point. The green plus15 and the dark blue cross22 are median bulk values from the literature (see Table 3). Black vertical lines indicate sOCR values from previous studies assuming zero-order kinetics for O2 consumption (dotted: ref. 36, solid: ref. 37, dashed: ref. 34). Note that kM values are reported in logarithmic scale. (B) Joint distribution of single-cell size (i.e., projected area) and O2 metabolism (i.e., sOCR), expressed as relative frequency of occurrence. | ||
Joint measurements of single-cell size and metabolism
Immediately after each experiment, HepG2 cells were stained with Trypan Blue, which allowed determining single-cell sizes from projected cell areas. From this data, we estimated the joint distribution of single-cell size and sOCR (Fig. 4B). The Henze–Zirkler test (α = 0.05) demonstrated that the sample can be described by a lognormal joint probability density function (p = 0.0633). Further confirmation of lognormality was provided by independent optical measurements of dry mass of individual HepG2 cells – performed by means of quantitative phase imaging – which also displayed a marginal distribution with a lognormal shape (see ESI6†).Discussion
Here we report on the characterization of O2 metabolism in single human hepatic cells through an integrated in vitro–in silico approach. One or a few cells were seeded in microfabricated microwells coated with O2-sensitive optodes and sealed from ambient air, enabling the precise measurement of O2 consumption over time. These data were then exploited in a multiparameter identification algorithm22 to characterize the cellular O2 consumption kinetics according to the MM model (eqn (1)). As shown in Fig. 3C and Table 3, we demonstrate that isolated HepG2 cells have lower sOCR values compared to previously reported ones for 2D or 3D aggregates of the same cell type in comparable environmental conditions (except for ref. 34), including those obtained in our previous studies.15,22 Interestingly, the sensing principle (i.e., fluorescence quenching) exploited in ref. 15 and 22 is the same as that of the optodes used here, while the other data in Table 3 refer to O2 concentration measurements performed using commercial electrochemical sensors (e.g., Clark-type electrodes). This suggests that cells change their O2 consumption when isolated as individuals or in clusters of a few cells, reducing their maximal consumption rate (i.e., sOCR). Furthermore, the decrease in sOCR with increasing microwell occupancy (Ncell) shows that changes in metabolism occur as a function of both the local O2 concentration – as per the MM equation – and the presence of neighbouring cells (Fig. 3D) – manifested as a reduction in sOCR. This behaviour mirrors observations on hepatocytes in 2D and 3D aggregates and could be interpreted as an effect of cooperation between individual cells which are not aggregated but coexist in a microenvironment where a limited resource is shared. However, contrary to our previous observations for hepatic cells in 2D and 3D, the adaptive behaviour – that is the modulation as a function of the number of neighboring cells, if any – in isolated cells appears not to affect the O2 uptake efficiency, since kM is not dependent on Ncell (Fig. 3F).In fact, the correlation between the two parameters is weak (Fig. 4A) and less significant than in 2D or 3D aggregates.22
It is worth noting that the identification of kM is influenced by the ability of the microwell system to effectively achieve hypoxic steady-state conditions. Thus, although the optodes are highly sensitive at low O2 concentrations (see ESI2†), even slight variations of stationary O2 levels can influence the estimation of kM and widen its dispersion. Indeed, precisely characterizing kM is a well-known challenge due to the sensitivity of estimated values to experimental conditions,22,38,39 which might ultimately mask potential trends. Nonetheless, the estimates of sOCR reported here are statistically robust and not impacted by the uncertainty in kM, as shown in Fig. 3D.
In ref. 22 we showed that the MM parameters can be combined to define an uptake coefficient – a measure of the surrounding area per unit time in which a cell is able to perceive and consume O2 – which can be related to a proximity index – PI, expressing the extent of cell packing within the aggregate.22 The uptake coefficient increases to a saturating threshold along with PI in cell aggregates. In the microwells, in the limit PI → 0 for a single cell, while it is of the order of magnitude of 10−3 μm−1 for cell clusters (see SM7 for the analytical details), leading to uptake coefficients coherent with the values of sOCR and kM we report here (Fig. 3, Table 3). This suggests that the lower values of sOCR with respect to cell aggregates are a consequence of limited packing and inter-individual interaction (i.e., aggregation) in microwells.
Together with our previous findings,22 this study lays the foundations toward a refinement of the current formulation of the MM model, involving the mutual dependency of sOCR and kM through the extent of cell packing (i.e., PI). This might be beneficial for predicting O2 metabolism in in vitro liver systems and consequently promote the design of tissue models with enhanced resemblance to their in vivo counterpart. Furthermore, these results may help in the mechanistic explanation of liver zonation40 and provide useful insights for the development of novel and more effective therapeutic treatments for hepatic diseases.
The throughput of our approach also allowed us to measure the correlated variability of cell size and maximal O2 consumption rate (i.e., sOCR) and describe their joint frequency distribution (Fig. 4B). This outcome successfully overcomes the challenge of jointly investigating individual size and metabolism, a hurdle previously encountered by our group and others.3 Although further experiments are required to fully capture the covariance between single-cell size and O2 consumption,1 our study provides the first size-metabolic rate distribution based on joint experimental datasets reported so far. Notably, our analysis demonstrates that the sample is extracted from a population characterized by a lognormal multivariate function. Lognormally-distributed marginal probabilities have been commonly observed for organismal sizes,41 but they have not been explicitly reported for metabolic rates. Their covariation demonstrates that size is a determinant of O2 consumption in single cells. The lognormality suggests that most cells are relatively small and typically associated with low values of sOCR, while larger cells are less frequent and unlikely to consume O2 rapidly. This result is also supported by previous experimental investigations on eukaryotic cells,42–44 highlighting that there exists an optimal range of sizes which allows for optimized single-cell metabolic activity. This implies that – although the mitochondrial count per cell has been reported to increase linearly with size44 – the largest individuals within a cell population are less efficient from a functional point of view and hence rarely observable.
Characterizing the covariance of single-cell size and metabolic parameters – as achieved here – is crucial to comprehensively describe the O2 consumption dynamics of human hepatocytes in isolation. It also paves the way to link these dynamics to the tissue or organ levels and to interpret behaviours emerging at higher scales such as cooperation or size-related (allometric) scaling. A direct application of this work is the development of engineered cellular systems capable of recapitulating the heterogeneity of single-cell metabolic phenotypes. This may enhance precision medicine approaches, drug development strategies or (eco)toxicological assessments. Besides the biomedical field, the proposed methodology is also of general interest as it provides a powerful framework for systematically characterizing O2 metabolism and its size-related fluctuations in other single-cell scenarios, ranging from the photosynthetic activity of marine microorganisms to the evaluation of the impact of chemicals or environmental stressors on single-cell respiration.
Data availability
All the data supporting this manuscript, the source code of the multi-parameter identification algorithm and scripts for statistical analysis are available upon reasonable request to the corresponding authors.Author contributions
Conceptualization: AA, LB, AR, RS. Methodology: EB, YC, CM, MT, KK, LB, AA. Investigation: EB, YC. Visualization: EB, YC. Supervision: AA, LB, CM. Writing – original draft: EB. Writing – review & editing: All authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work leading to these results has received funding from the Swiss National Science Foundation, through Project SINERGIA 2019 572 CRSII5_186422/1. The authors acknowledge Myfab Uppsala for providing facilities and experimental support required to fabricate the microwells. Myfab is funded by the Swedish Research Council (2019 – 00207) as national research infrastructure. LB was supported by grants from the Swedish Research Council (2019-04401), the Science for Life Laboratory and the Carl Trygger Foundation (CTS 20:214). The Novo-Nordisk Foundation Exploratory Interdisciplinary Synergy Programme (NNF22OC0079370) also supported LB and KK. EB also acknowledges the European Union for his post-doctoral fellowship, funded by the Next Generation EU project CN00000013 ‘Centro Nazionale 1’ HPC, Big Data and Quantum Computing (CN1, PNRR, Spoke 6: Multiscale modelling and engineering applications).References
- E. Botte, F. Biagini, C. Magliaro, A. Rinaldo, A. Maritan and A. Ahluwalia, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2025211118 CrossRef CAS PubMed.
- R. Frankham, Biol. Conserv., 2005, 126, 131–140 CrossRef.
- S. Zaoli, A. Giometto, E. Marañón, S. Escrig, A. Meibom, A. Ahluwalia, R. Stocker, A. Maritan and A. Rinaldo, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 17323–17329 CrossRef CAS PubMed.
- S. K. Jung, L. M. Kauri, W. J. Qian and R. T. Kennedy, J. Biol. Chem., 2000, 275, 6642–6650 CrossRef CAS PubMed.
- Y. F. Lu, D. B. Goldstein, M. Angrist and G. Cavalleri, Cold Spring Harb. Perspect. Med., 2014, 4, 1–12 Search PubMed.
- A. Ahluwalia, Sci. Rep., 2017, 7, 1–7 CrossRef PubMed.
- C. Magliaro, A. Rinaldo and A. Ahluwalia, Sci. Rep., 2019, 9, 1–8 CrossRef CAS PubMed.
- S. Rose, The chemistry of life, Penguin Books, 4th edn, 1999 Search PubMed.
- E. Roussakis, Z. Li, A. J. Nichols and C. L. Evans, Angew. Chem., Int. Ed., 2015, 54, 8340–8362 CrossRef CAS PubMed.
- T. W. Molter, S. C. McQuaide, M. T. Suchorolski, T. J. Strovas, L. W. Burgess, D. R. Meldrum and M. E. Lidstrom, Sens. Actuators, B, 2009, 135, 678 CrossRef CAS PubMed.
- A. Hu, R. Qiu, Z. Wu, B. C. Rothwell, N. F. Kirkby, M. J. Merchant, X. Chen, L. Xiong, J. Wu, J. R. Etzkorn, W.-C. Wu, Z. Tian, P. Kim, S.-H. Jang, D. R. Meldrum, A. K.-Y. Jen and B. A. Parviz, J. Micromech. Microeng., 2010, 20, 095017 CrossRef.
- L. Kelbauskas, H. Glenn, C. Anderson, J. Messner, K. B. Lee, G. Song, J. Houkal, F. Su, L. Zhang, Y. Tian, H. Wang, K. Bussey, R. H. Johnson and D. R. Meldrum, Sci. Rep., 2017, 7, 1–13 CrossRef PubMed.
- F. J. Hartmann, D. Mrdjen, E. McCaffrey, D. R. Glass, N. F. Greenwald, A. Bharadwaj, Z. Khair, S. G. S. Verberk, A. Baranski, R. Baskar, W. Graf, D. Van Valen, J. Van den Bossche, M. Angelo and S. C. Bendall, Nat. Biotechnol., 2021, 39, 186–197 CrossRef CAS PubMed.
- C. J. Peniche Silva, G. Liebsch, R. J. Meier, M. S. Gutbrod, E. R. Balmayor and M. van Griensven, Front. Bioeng. Biotechnol., 2020, 8, 1–12 CrossRef PubMed.
- C. Magliaro, G. Mattei, F. Iacoangeli, A. Corti, V. Piemonte and A. Ahluwalia, Front. Bioeng. Biotechnol., 2019, 7, 251 CrossRef PubMed.
- L. Michaelis and M. Menten, Biochemistry, 1913, 49, 333–369 CAS.
- J. W. Allen and S. N. Bhatia, Biotechnol. Bioeng., 2003, 82, 253–262 CrossRef CAS PubMed.
- G. Mattei, S. Giusti and A. Ahluwalia, Processes, 2014, 2, 548–569 CrossRef.
- M. M. Adeva-Andany, N. Pérez-Felpete, C. Fernández-Fernández, C. Donapetry-García and C. Pazos-García, Biosci. Rep., 2016, 36, 416 CrossRef PubMed.
- T. Merl and K. Koren, Environ. Int., 2020, 144, 106080 CrossRef CAS PubMed.
- S. Scilipoti, K. Koren, N. Risgaard-Petersen, A. Schramm and L. P. Nielsen, Sci. Adv., 2021, 7, 1–6 Search PubMed.
- E. Botte, P. Mancini, C. Magliaro and A. Ahluwalia, APL Bioeng., 2023, 7, 036111 CrossRef CAS PubMed.
- R. Ramamoorthy, P. K. Dutta and S. A. Akbar, J. Mater. Sci., 2003, 38, 4271–4282 CrossRef CAS.
- M. Quaranta, S. M. Borisov and I. Klimant, Bioanal. Rev., 2012, 4, 115 CrossRef PubMed.
- K. Koren, S. M. Borisov and I. Klimant, Sens. Actuators, B, 2012, 169, 173–181 CrossRef CAS PubMed.
- R. I. Dmitriev, A. V. Kondrashina, K. Koren, I. Klimant, A. V. Zhdanov, J. M. P. Pakan, K. W. McDermott and D. B. Papkovsky, Biomater. Sci., 2014, 2, 853–866 RSC.
- E. R. Carraway, J. N. Demas, B. A. DeGraff and J. R. Bacon, Anal. Chem., 1991, 63, 337–342 CrossRef CAS.
- M. D. Hays, D. K. Ryan and S. Pennell, Anal. Chem., 2004, 76, 848–854 CrossRef CAS PubMed.
- Y. L. Lo, C. S. Chu, J. P. Yur and Y. C. Chang, Sens. Actuators, B, 2008, 131, 479–488 CrossRef CAS.
- Y. M. Stokes, Mol. Reprod. Dev., 2009, 76, 1178–1187 CrossRef CAS PubMed.
- E. Berger, C. Magliaro, N. Paczia, A. S. Monzel, P. Antony, C. L. Linster, S. Bolognin, A. Ahluwalia and J. C. Schwamborn, Lab Chip, 2018, 18, 3172–3183 RSC.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- B. A. Wagner, S. Venkataraman and G. R. Buettner, Free Radical Biol. Med., 2011, 51, 700–712 CrossRef CAS PubMed.
- J. F. Patzer, Artif. Organs, 2004, 28, 83–98 CrossRef PubMed.
- G. Mattei, C. Magliaro, S. Giusti, S. D. Ramachandran, S. Heinz, J. Braspenning and A. Ahluwalia, PLoS One, 2017, 12, e0173206 CrossRef PubMed.
- S. L. Nyberg, R. P. Remmel, H. J. Mann, M. V. Peshwa, W. S. Hu and F. B. Cerra, Ann. Surg., 1994, 220, 59 CAS.
- M. D. Smith, A. D. Smirthwaite, D. E. Cairns, R. B. Cousins and J. D. Gaylor, Int. J. Artif. Organs, 1996, 19, 36–44 CrossRef CAS PubMed.
- K. C. J. Van Rees, N. Z. J. For. Sci., 1994, 24, 226–233 CAS.
- S. Gattu, C. L. Crihfield and L. A. Holland, Anal. Chem., 2017, 89, 929–936 CrossRef CAS PubMed.
- R. Manco and S. Itzkovitz, J. Hepatol., 2021, 74, 466–468 CrossRef CAS PubMed.
- A. Giometto, F. Altermatt, F. Carrara, A. Maritan and A. Rinaldo, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4646–4650 CrossRef CAS PubMed.
- S. Son, A. Tzur, Y. Weng, P. Jorgensen, J. Kim, M. W. Kirschner and S. R. Manalis, Nat. Methods, 2012, 9, 910–912 CrossRef CAS PubMed.
- A. Tzur, R. Kafri, V. S. LeBleu, G. Lahav and M. W. Kirschner, Science, 2009, 325, 167–171 CrossRef CAS PubMed.
- T. P. Miettinen and M. Björklund, Dev. Cell, 2016, 39, 370–382 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lc00204k |
| ‡ Shared first authorship. |
| § Shared senior authorship. |
| This journal is © The Royal Society of Chemistry 2024 |


