High-precision Sm isotope analysis by thermal ionisation mass spectrometry for large meteorite samples (>1 g)

Abstract

This study presents a new procedure for high-precision Sm isotope analysis by thermal ionisation mass spectrometry (TIMS) for geological samples. A four-step chemical separation scheme results in sharp separation of Sm and Nd from the same sample aliquot. The first step utilises anion exchange resin to remove Fe from the sample solution. Two different liquid–liquid extraction resins are then used to isolate rare-earth elements (TRU-Spec) and purify Sm from Nd (DGA). Fractionation occurs on the DGA resin due to the nuclear field shift effect, but this is negligible if yields greater than 70% are achieved. Different analytical setups were tested to ascertain their ionisation efficiencies on TIMS. The effect of activators composed of Pt and Ta was tested on single Re filaments but the conventional double Re filament assembly provided efficient ionisation and more stable ion beams. The determination of nucleosynthetic isotope variations requires high precision for all Sm isotope ratios. We aimed to improve the precision on the scarce ¹⁴⁴Sm isotope (3% of all Sm). Static, multistatic and dynamic methods were tested. Isotope ratios were normalised to both ¹⁴⁷Sm/¹⁵²Sm and ¹⁵²Sm/¹⁴⁸Sm for comparison. The dynamic methods failed to provide better precision on ratios involving ¹⁴⁴Sm, whereas the multistatic method yielded improved precisions between 13 and 22 ppm (twice the standard deviation, 2 SD) on the ¹⁴⁴Sm/¹⁵²Sm ratio. Synthetic standards have variable Sm isotope compositions, thus requiring systematic and precise characterisation against terrestrial samples. Analyses conducted using this new procedure yielded high-precision values which were consistent with literature data for an array of terrestrial rock standards and the meteorite Allende.

---

1. Introduction

The lanthanides belong to the rare-earth elements (REE) and hold key information regarding the formation and evolution of geological materials. Among them, Sm and Nd are particularly well-known for their radioactive decay systems, the long-lived ¹⁴⁷Sm that decays to ¹⁴³Nd (t_1/2 = 106 Ga)¹ and the short-lived ¹⁴⁶Sm that decays to ¹⁴²Nd (t_1/2 = 103 Ma).² The ¹⁴⁷Sm–¹⁴³Nd system has been widely applied as a geochronometer (e.g. ref. 3), and to the study of large-scale silicate differentiation and continental growth (e.g. ref. 4), tracing of mantle heterogeneities (e.g. ref. 5), surface erosion (e.g. ref. 6) and ocean cycling (e.g. ref. 7). The extinct ¹⁴⁶Sm–¹⁴²Nd chronometer provides information on the early silicate differentiation of planetesimals, Mars, and the Moon (e.g. ref. 8–10). In addition, this chronometer has been used to probe silicate differentiation during the Hadean epoch on Earth (e.g. ref. 11). Samarium isotope compositions are useful to several fields of fundamental and applied research, despite not being directly needed for the determination of radiogenic isotope studies. Mass-independent variations in Sm isotope compositions of planetary materials can be of nucleosynthetic origin. This provides valuable information pertaining to protoplanetary disc dynamics (e.g. ref. 12). Samarium isotopes are produced by nucleosynthetic processes in stars. The slow and rapid neutron capture produce all Sm isotopes (s- and r-process)¹³ except for ¹⁴⁴Sm which is synthesised by photodisintegration of larger nuclei (p-processes).¹⁴ The isotope ¹⁴⁴Sm is particularly useful because it is one of the few p-nuclides, which displays nucleosynthetic heterogeneities in meteorites (e.g. ref. 12 and 15). In addition, ¹⁴⁹Sm is a sensitive epithermal neutron capture dosimeter in extraterrestrial rocks exposed to galactic cosmic rays in space because this isotope has a particularly high neutron capture cross-section.¹⁶ Finally, the nuclear industry utilises Sm in control rods and to monitor the origin of uranium ores and nuclear fuels due to the production of Sm by β-decay of fission products (e.g. ref. 17). In summary, Sm isotope data are widely used in many applications. Here, we focus on cosmochemical applications, in particular high-precision measurements of ¹⁴⁴Sm. These Sm isotope analyses require large amounts of sample, because meteorites are depleted in REE. The specific analytical requirements of these meteorite analyses are not addressed in current methods of chemical separation and mass spectrometric measurements.

Elements belonging to the lanthanides show very similar chemical behaviours and vary only slightly in their ionic radii from La (Z = 57) to Lu (Z = 71). For this reason, they are particularly difficult to separate from one another, which complicates the accurate determination of their isotope composition because they form isobaric interferences on each other's masses. Most separation protocols currently used for meteorites (e.g. ref. 18) utilise cation exchange resin (AG50W) in a hydrochloric acid (HCl) medium to isolate REE from other elements following the original procedures of Edge and Ahrens.¹⁹ However, applying these protocols to large (>1 g) sample masses would require copious volumes of resin and concentrated acids (e.g. ref. 20). Extraction chromatography resins are an alternative because they are more selective and thus larger samples can thus be processed (e.g. ref. 21). Concerning the isolation of individual REE, there are currently two preferred protocols used. The first uses cation exchange resin (AG50W) with a mobile phase of α-hydroxyisobutyric acid (HIBA or 2-methyllactic acid – 2MLA).^22–24 This protocol was applied to geological materials by Eugster et al.²⁵ and is still in use today (e.g. ref. 26). Secondly, a protocol using di-(2-ethylhexyl)-orthophosphoric acid (HDEHP, currently commercialised as LN-Spec resin) liquid–liquid separation with HCl was concurrently developed to the cation resin method^27,28 and later adapted for geological materials.⁵ The LN-Spec resin is currently the most widely used resin for Nd separation. The first separation method (cation exchange resin and HIBA/2MLA) is very effective but challenging to set up because the columns must be pressurised. The second method (LN-Spec) has the advantage of an easier setup and is therefore the most widely used for Nd separation. Nonetheless, mass-independent fractionation can be induced by the nuclear field shift effect (NFSE) during the separation procedure (e.g. ref. 29). Alternative protocols using N,N,N′,N′-tetraoctyl-1,5-diglycoamide as extractant (DGA resin) for REE separation have recently been developed (e.g. ref. 21 and 30).

Samarium isotopes are measured using both thermal-ionisation (TIMS) and inductively coupled plasma mass spectrometers (MC-ICP-MS). Only limited analytical development, not focussed on the analysis of meteorites, has been carried out (e.g. ref. 31–35). For nuclear applications, TIMS measurements are usually performed using total evaporation methods to obtain the isotope composition without using mass bias corrections (e.g. ref. 31). Geological applications do not use total evaporation methods and correct for instrumental mass fractionation using the ¹⁴⁷Sm/¹⁵²Sm ratio. Although current methods are well-suited for measuring larger Sm isotope variations related to fission products or irradiation by galactic cosmic rays (e.g. ref. 32), they do not provide a precision high enough to resolve variations in ¹⁴⁴Sm (3.08% of all Sm isotopes).³⁶ Cosmochemical studies report mass-bias corrected ¹⁴⁴Sm/¹⁵²Sm ratios (or other normalisations) with variable precisions from 20 to 75 ppm for sample loads of 100–300 ng Sm (e.g. ref. 37–40). Variable reproducibility between different measurement sessions on this ratio is observed and this impairs precise determination of the p-process contribution to Sm in meteoritic samples which requires reproducibility on the ¹⁴⁴Sm/¹⁵²Sm ratio below 30 ppm.

Our study aims to improve Sm isotope analyses for samples with low Sm concentrations which require large amounts of material to be processed. We present a new procedure for the chemical separation of Sm and Nd, combining several published protocols with adjustments.^21,30,41 We also tested several methods to improve the precision of Sm isotope measurements by TIMS.

2. Experimental

2.1. Materials and reagents

2.1.1. Chemicals and column specifications. Ultrapure water with a resistivity above 18.2 MΩ cm was used for this study. Hydrochloric (HCl) and nitric (HNO₃) acids were purified by double distillation and hydrofluoric acid (HF) by single distillation in PFA Savillex DST-100 systems.

Anion-exchange resin AG1-X8 (Biorad) with a particle size of 200–400 mesh was utilised as well as TRU-Spec (Triskem) and DGA (Triskem) resins both with particle sizes of 50–100 μm. The AG1-X8 resin was batch-cleaned using HCl and HNO₃ at various molarities. Twenty millilitres of AG1-X8 resin were placed in a Biorad Econo-Pac column with a diameter of ca. 15 mm, resulting in a resin bed height of ca. 115 mm. The resin was then cleaned on the column using 10 resin volumes (RV) of 6 M HCl, 25 RV of 0.1 M HCl, 10 RV of 1 M HF, 25 RV of 3 M HNO₃ and 5 RV of 7 M HNO₃; the resin was equilibrated with 5 RV 0.05 M HCl before use. The TRU-Spec and DGA resins were also cleaned in a 20 mL Biorad Econo-Pac column. The TRU-Spec resin was treated with 10 RV of 1 M HNO₃, 10 RV of 3 M HCl and 10 RV of 0.05 M HCl. The cleaning procedure for the DGA resin involved 10 RV of 3 M HCl and 25 RV of 0.05 M HCl. Custom-made shrink-fit PTFE columns with an internal diameter of 8.5 mm were filled with 2 mL of TRU-Spec resin, translating into a resin bed height of 35 mm. Two types of columns were prepared with the DGA resin. Biorad Poly-Prep columns were filled with 1 mL of DGA resin for Sm and Nd separation and shrink-fit PTFE columns with an internal diameter of 4.5 mm and a resin bed height of 72 mm (aspect ratio height/diameter of 16) were filled with 1 mL of DGA resin. Polypropylene frits were placed at the bottom and top of the resin bed for all columns, except for the 20 mL AG1-X8 columns which had only a bottom frit due to resin expansion.

2.1.2. Filament and activator specifications. The filaments used for TIMS analyses consisted of Re ribbons with thicknesses of 1.0, 1.2 and 1.6 mil (25.4, 30.5 and 40.6 μm, respectively) and were supplied by HCross. The purity of Re was 99.95% for 1.0 and 1.6 mil filaments, whereas 1.2 mil filaments contained zone-refined 99.998% Re. Filaments made of Ir (99.95%) with a thickness of 1 mil were supplied by HCross. All filaments were outgassed under vacuum using a custom-built device at ETH Zürich.

Three types of activators were used. We tested the addition of a 0.1 M phosphoric acid (H₃PO₄) solution. Moreover, an activator solution of hexachloroplatinic acid hydrate (H₂PtCl₆·xH₂O) was prepared following a previous protocol⁴² with a pure Pt wire (99.998%) from HCross. Finally, a Ta activator generally used for Sr isotope measurements was also tested. This activator contained tantalum oxide hydrate TaO₅·xH₂O in a mixture of HF–HNO₃–H₃PO₄.⁴³

2.1.3. Synthetic Sm standards. Four synthetic Sm standards were analysed. A Sm ICP-MS solution from Sigma Aldrich, called Sm ICP ETH hereafter, was measured in every session. We also characterised the Sm reference material SRM 3147a from the National Institute of Standards and Technology (NIST), a solution made from pure Sm produced by Ames National laboratory (AMES Rennes Sm) and a Sm ICP-MS solution from Inorganic Ventures (Sm ICP LMV).

2.2. Samples and sample preparation

A suite of terrestrial rock standards was processed to validate the newly developed analytical procedure because meteorites are precious samples and large amounts (>1 g) are required for high-precision Sm and Nd isotope measurements. The samples (BCR-2, BHVO-2, BIR-1, DNC-1, W2a, BE-N and UB-N) are widely used rock standards provided by the United States Geological Survey (USGS) and the Service d’Analyse des Roches et des Minéraux (SARM), France. They are mafic rocks except for the ultramafic sample UB-N. While the mafic standards are suitable as proxy for basaltic achondrites, the serpentinite UB-N has a chemical composition close to ultramafic achondrites. Moreover, the REE are depleted to a similar degree in UB-N and chondrites. UB-N is depleted in Fe compared to chondrites but its high matrix to REE ratio renders it an ideal terrestrial proxy for chondrites once the Fe has been removed by the first column. In addition, the carbonaceous chondrite Allende (CV3), supplied by the Museum of Natural History of the Smithsonian Institution (USA), was also processed for validation of the method. The samples were dissolved in PFA beakers using a mixture of HF and HNO₃ in the proportions 3 : 1 on a hotplate for 5 days. The solutions were then dried and taken up in concentrated HNO₃. Several uptake and dry–down cycles with concentrated HNO₃, aqua regia and 6 M HCl were applied to break down fluorides for samples with masses > 500 mg.

2.3. Chemical separation of Sm and Nd

The chemical procedure to isolate Sm and Nd from the sample matrix consisted of four steps. The protocol presented here allowed the separation of multiple elements of interest from the same sample dissolution which is vital as chondrites are precious, highly heterogeneous, and our methods are destructive. Although this procedure is time consuming, it maximises the information recovered from each fragment of chondrite and improves comparability of data for different isotope systems. As a first step, Fe was separated from the matrix using columns filled with 20 mL of anion-exchange resin AG1-X8 following the protocol of Frossard et al.²⁰ (Table 1). The second step separated the matrix elements from REE using TRU-Spec resin and is adapted from Pin and Gannoun.²¹ The Sm separation from Nd (step 3, Table 1) was performed using 1 mL of DGA resin in a Biorad Poly-prep column. The purification of the Sm and Nd fractions were performed with DGA resin in high aspect ratio columns using various molarities of HCl (Table 1). The protocols for the separations using DGA resin are inspired by the protocol of Chu et al.³⁰ Up to two grams of chondrite sample can be processed with our new procedure.

Table 1 Detailed chemical procedure

Step	Acid	Volume	Elements eluted
Step 1: Fe removal – 20 mL of AG1–X8 resin (200–400 mesh)
Conditioning	6 M HCl–0.05 M HF	80	—
Loading	6 M HCl–0.05 M HF	15	Major elements, Sr, Rb, Ba, Pb, Th, Cr, V, Ni, REE, HFSE, W
Elution of matrix	6 M HCl–0.05 M HF	65	Major elements, Sr, Rb, Ba, Pb, Th, Cr, V, Ni, REE, HFSE, W
Elution of Fe	1 M HF	28	Fe, Mo, U, W, Cu, Ga
Cleaning	6 M HCl	120	—
Cleaning	1 M HF	50	—
Cleaning	3 M HNO3	50	—
Step 2: REE separation – 2 mL of TRU-Spec resin (50–100 μm)
Conditioning	1 M HNO3–0.245 M HF	10	—
Loading	1 M HNO3–0.245 M HF	15	Major elements, Sr, Rb, Ba, Pb, Cr, V, Ni, HFSE, Mo, W, Dy, Er, Lu
Elution of matrix	1 M HNO3–0.245 M HF	10	Major elements, Sr, Rb, Ba, Pb, Cr, V, Ni, HFSE, Mo, W, Dy, Er, Lu
Elution of Nd and Sm	3 M HCl	5	Nd, Sm, La, Ce, Pr, Eu, Gd
Cleaning	0.1 M HCl–0.3 M HF	20	—
Cleaning	0.05 M HCl	20	—
Step 3: Nd and Sm separation – 1 mL of DGA resin (50–100 μm)
Conditioning	3 M HNO3	10	—
Loading	3 M HNO3	1	Major elements, Sr, Rb, Ba, Cr, V, Ni, HFSE
Elution of matrix	3 M HNO3	14	Major elements, Sr, Rb, Ba, Cr, V, Ni, HFSE
Elution of LREE	3 M HCl	25	La, Ce, Pr
Elution of Nd	1.5 M HCl	5	Nd
Elution of Sm	1.25 M HCl	8	Sm, Eu
Cleaning	0.05 M HCl	300	—
Step 4: Nd purification (repeated twice) – 1 mL of DGA resin (50–100 μm)
Conditioning	2 M HCl	5	—
Loading	2 M HCl	0.5	La, Ce, Pr
Elution of LREE	2 M HCl	3.5	La, Ce, Pr
Elution of Nd	2 M HCl	4	Nd
Cleaning	0.05 M HCl	20	—
Step 5: Sm purification (repeated twice) – 1 mL of DGA resin (50–100 μm)
Conditioning	1 M HCl	5	—
Loading	1 M HCl	0.5	La, Ce, Pr, Nd
Elution of LREE	1 M HCl	3	La, Ce, Pr, Nd
Elution of Sm	1 M HCl	4	Sm
Cleaning	0.05 M HCl	35	—

---

2.3.1. Detailed procedures for matrix removal.
2.3.1.1 First step: Fe removal with 20 mL of AG1-X8 resin. Anion resin was adopted as a first step because Fe³⁺ present in the sample solution has a high partition coefficient on this resin with 6 M HCl. Such a column is required because Fe elutes with the REE on the TRU-Spec resin, and it can also overload the subsequent column with TRU-Spec resin if large (>1 g) meteorite sample are processed. To circumvent this issue, the method of Pin and Gannoun²¹ reduces Fe³⁺ to Fe²⁺ with ascorbic acid before direct loading of the sample solution onto the TRU-Spec column. However, the use of ascorbic acid complicates multiple element separations because it remains in the matrix fraction which contains many elements of cosmochemical interest.

In our procedure, the sample was taken up in 15 mL of 6 M HCl–0.05 M HF and loaded onto the first column filled with 20 mL of AG1-X8 resin which had been conditioned with 4 RV of the same acid (Table 1). Most elements were not retained on the resin, including REE and high field strength elements (HFSE), and were collected with a total of 85 mL of 6 M HCl–0.05 M HF, including the loading step. Iron was then eluted with 28 mL of 1 M HF. The resin was further cleaned with 50 mL of 3 M HNO₃ to remove the remaining Mo and Fe and then with 100 mL of 6 M HCl, 50 mL of 1 M HF and 100 mL of 3 M HNO₃.

2.3.1.2 Second step: matrix removal with 2 mL of TRU-Spec resin. The matrix solution was dried, taken up in 5 mL of 3 M HNO₃ and heated at 110 °C for 12 hours. The solution was subsequently diluted with 9.844 mL of H₂O and 156 μL of 23.5 M HF to achieve a solution of 1 M HNO₃–0.245 M HF. As soon as HF was added to the sample, the solution was centrifuged and loaded onto the TRU-Spec column. A swift loading is needed to avoid the formation of fluorides in the sample solution. The matrix elements were further eluted with 10 mL of the same solution (Fig. 1). Heavy REE (HREE) were stripped with the matrix, whereas light REE (LREE) and Sm remained on the column and were then eluted in 5 mL of 3 M HCl. The residue was oxidised twice with ca. 360 μL of aqua regia after evaporation to remove organics from the resin.

Fig. 1 Elution curves for step 2 using TRU-Spec resin to separate LREE from matrix elements. A basalt (RU0701) from the Réunion Island in the Indian Ocean⁴⁴ was used for the calibration. Matrix elements and high-field strength elements were removed during the loading and rinsing steps in 1 M HNO₃–0.245 M HF. Neodymium and samarium were stripped off the column using 3 M HCl. Most of the Gd and heavier REE were eluted in the first step of the procedure.

2.3.2. Detailed procedures for Nd and Sm purification using the DGA resin.
2.3.2.1 Third step: Sm and Nd separation with 1 mL of DGA resin. At this stage, the matrix was nearly completely removed, but a small fraction remained because of the large masses of the processed samples. The third step further separated matrix elements and Sm from Nd based on Chu et al.³⁰ A Biorad Poly-prep column filled with 1 mL of DGA resin was used for this purpose. The sample was loaded in 1 mL of 3 M HNO₃, and the matrix was stripped from the column with 14 mL of the same acid before switching to 3 M HCl to elute LREE in 25 mL, followed by 5 mL of 1.5 M HCl to elute Nd and then 8 mL of 1.25 M HCl to elute Sm (Fig. 2A). Again, the residue was dried down and oxidised twice with ca. 120 μL of aqua regia to remove organics.

Fig. 2 Elution curves of the Sm and Nd purification steps using the DGA resin. (A) Sm and Nd were separated from one another while removing major elements remaining after the TRU-Spec column. This column provided a first order separation of interfering REE from Nd and Sm. The Gd peak below Pr is a PrO interference. All Gd is eluted in the last step with 0.05 M HCl. This calibration was performed with the reference material basalt BCR-2. (B) Neodymium was purified using a high aspect ratio column and 2 M HCl. (C) Samarium was purified using column with the same geometry as for the Nd purification and 1 M HCl. The calibrations for the Sm and Nd purification steps were performed with synthetic solutions containing La, Ce, Pr, Nd, Sm, Eu, and Gd.

2.3.2.2 Fourth and fifth steps: Sm and Nd purification with 1 mL of DGA resin. The Sm and Nd cuts were separated from remaining REE using high aspect ratio columns. The Nd cut was loaded in 0.5 mL of 2 M HCl and LREE were eluted with 3.5 mL of the same acid (step 4, Table 1). Neodymium was subsequently collected with 4 mL of 2 M HCl (Fig. 2B). A similar protocol using 1 M HCl was adapted to purify Sm (step 5, Table 1). The Sm cut was loaded in 0.5 mL of 1 M HCl and LREE were rinsed with 3 mL of 1 M HCl. Samarium was stripped from the column in 5 mL of 1 M HCl (Fig. 2C). These two purification procedures were repeated twice to remove all isobaric interference species.

An additional protocol was developed for terrestrial samples to separate Nd and Sm using the high aspect ratio columns filled with DGA resin. It was used for most terrestrial standards with the exception of UB-N, BE-N and BHVO-2 #2 and #3. For this protocol, the sample was loaded in 0.5 mL of 3 M HCl and LREE were eluted with 3.5 mL of 2 M HCl. Neodymium was then collected with 4 mL of 2 M HCl and Sm in 6 mL of 1.1 M HCl. However, this protocol was not well suited for large sample masses in which some matrix elements remained in the residue after the second column.

The final purified Sm and Nd cuts were processed through a column filled with 0.5 mL of Prefilter resin (Triskem) without drying (i.e. the solution straight from the fourth step) to remove the organics from the DGA resin. As a last step, the residues were treated twice with ca. 120 μL aqua regia und taken up in 2 M HCl before loading on the filament for TIMS analyses.

2.4. Trace element measurements

The column calibrations and yields were obtained using a Thermo Scientific Element XR sector field inductively coupled plasma mass spectrometer (SF-ICP-MS) at ETH Zürich. The concentrations were externally calibrated with multi-element solutions at 0.1 ppb, 1 ppb and 10 ppb. The yields reported in the following section were calculated for each column using volumetric dilutions. The analytical errors associated are estimated around 5 to 10%.

2.5. Mass spectrometry

2.5.1. Loading procedure. The filaments were loaded using different techniques. The purified Sm and Nd samples were taken up in 1 μL 3 M HCl and synthetic standards were loaded from 3 M HCl solutions of various Sm and Nd concentrations. Neodymium was loaded with the addition of a 0.1 M H₃PO₄ activator, whereas Sm was placed onto the filament with and without H₃PO₄. About 0.3–0.5 μL of 0.1 M H₃PO₄ was deposited on the filament and dried at 0.8 A. Once dried, the sample was added on top of it and dried at the same current. If H₃PO₄ was not used, the sample was directly placed onto the filament and dried at 0.8 A. Finally, the current of the filament was increased slowly until it emitted a dull red colour for one second after which the current was quickly decreased to zero. The Pt and Ta activators were added in various amounts before or after the sample in the same way as H₃PO₄. Between 200 and 300 ng of synthetic Sm standards were placed onto the filaments, whereas 160 to 370 ng of Sm were used for rock standards. The amount of Nd loaded onto the filaments was between 780 and 1000 ng.

2.5.2. Analyses of the Sm and Nd isotope compositions. Measurements of Sm and Nd isotope compositions were carried out using a Thermo Scientific Triton TIMS at ETH Zürich. All Faraday cup detectors were connected to 10¹¹ Ω amplifiers. A cold trap filled with liquid nitrogen improved the vacuum in the source, which was typically below 7 × 10⁻⁸ mbar. The filament heating procedure for a thickness of 1.2 mil was as follows. (i) The ionisation filament was heated at a rate of 250 mA min⁻¹ up to 4000 mA. (ii) The ionisation and evaporation filaments were then concurrently heated at a rate of 50 mA min⁻¹ up to 4400 mA and 100 mA min⁻¹ up to 1200 mA, respectively. (iii) The analyser gate was opened to check the intensity of the Sm ion beam. The evaporation filament was then heated at successively decreasing rates of 50 down to 5 mA min⁻¹ until the signal of ¹⁴⁸Sm reaches 3 × 10⁻¹¹ A. During this ramp up the source lenses voltages were adjusted to focus the beam. (iv) Once the signal was stable, source lenses parameters were adjusted, and peaks were centred. Finally, the acquisition was started. The entire heating procedure lasted approximately 45 minutes.

The method of Garçon et al.²⁹ was applied for Nd isotope analyses. It consists of multi-dynamic measurements of the Nd isotope ratios using 4-step cycles, or acquisition lines. For Sm, four methods were tested: (i) a static method, (ii) a multistatic method with two lines, (iii) a multidynamic method with 2 lines and (iv) a multidynamic method with 3 lines. The cup configurations are presented in Table 2. For all methods, each cycle corresponds to a single integration of 8.389 seconds and an idle time of 4 seconds. Amplifier gains were measured at the start of every day of analysis, or before each analysis. Baselines are measured before every block with a 60 seconds integration time. Peaks were centred and the ion beam focussed every 3 blocks. The duration of the analyses was ∼3 hours on average and varied depending on the behaviour of the signal. The typical ¹⁴⁸Sm intensity for 300 ng of Sm was 3 to 4 × 10⁻¹¹ A. The method was aborted if the signal was too low (<1 × 10⁻¹¹ A for ¹⁴⁸Sm) or the ¹⁴⁷Sm/¹⁵²Sm was below 0.5610. The number of cycles thus varies depending on the emission of the sample but is typically around 800, 400, 300 and 170 cycles for the static, multistatic, multidynamic 2 lines and multidynamic 3 lines methods, respectively. An analytical session is defined by measurements without modification of the cup configuration: 9 sessions over 2 years are reported.

Table 2 Configuration of the methods for Sm isotope analyses

Detectors	L4	L3	L2	L1	Ax	H1	H2	H3	H4	Zoom optics		Peak centre	Focus
										Focus (V)	Dispersion (V)
Static
Line 1	144	146	147	148	149	150	152	154	156	0	0	149	149
Multistatic 2 lines
Line 1	144	146	147	148	149	150	152	154	156	0	0	149	149
Line 2	142	144	145	146	147	148	150	152	154			147
Dynamic 2 lines
Line 1	142	144	145	146	147	148	150	152	154	0	0	147	147
Line 2	146	148	149	150	151	152	154	156	158	3.5	−16	152
Multidynamic 3 lines
Line 1	144	146	147	148	149	150	152	154	156	0	0	149	149
Line 2	142	144	145	146	147	148	150	152	154	2	8	147
Line 3	146	148	149	150	151	152	154	156	158	−2	−8	152

---

2.5.3. Data processing for Sm isotope analyses. The data processing was carried out using raw intensities measured in each collector corrected for background noise (baseline) and relative gains by the Thermo Evaluation software. For all methods, the currents of each Sm isotope mass were corrected for Nd and Gd interferences using the natural abundances of Nd and Gd determined by Quemet et al.⁴⁵ and Meija et al.,⁴⁶ respectively. The static method and the first line of the multidynamic 3 line method used ¹⁴⁶Nd and ¹⁵⁶Gd for interference correction, whereas other lines used ¹⁴²Nd, which is more abundant than ¹⁴⁶Nd. Some lines of the multistatic, and the dynamic methods do not include any Gd isotopes (Table 2). For these, the ¹⁵⁶Gd intensity was extrapolated from the intensities of adjacent lines. For the multistatic method, Nd interferences were corrected solely using ¹⁴²Nd measured in line 2. The isotope ratios derived from intensities corrected for interferences were normalised to fixed ratios using the exponential law to correct for instrumental mass fractionation. Two normalisations were used: the ¹⁴⁷Sm/¹⁵²Sm ratio of 0.56081 (ref. 37) and the ¹⁵²Sm/¹⁴⁸Sm ratio of 2.37689 obtained using the natural Sm isotope abundances reported by Meija et al.⁴⁶

Table 3 summarises the different methods and the obtained isotope ratios. In the multistatic method, the ratios measured in the two lines at every cycle were averaged and then all the cycles were averaged to obtain the final ratio. Ratios involving ¹⁴⁹Sm (measured only in line 1) are only calculated using one line in static mode. In the dynamic acquisition methods, most ratios are measured in several lines. Averages of these ratios at every cycle are calculated to return multistatic ratios.

Table 3 Summary of the ratios obtained using the various methods

Methods	Static	Multistatic 2 lines		Dynamic 2 lines			Dynamic 3 lines
Ratios	Static	Multistatic	Static	Dynamic	Multistatic	Static	Dynamic	Multistatic	Static
Normalisation to ^147 Sm/ ^152 Sm
^144Sm/^152Sm	✓	✓	✓
^148Sm/^152Sm	✓	✓	✓
^149Sm/^152Sm	✓		✓ L1
^150Sm/^152Sm	✓	✓	✓
^154Sm/^152Sm	✓	✓	✓
Normalisation to ^152 Sm/ ^148 Sm
^144Sm/^148Sm	✓	✓	✓	✓		✓ L1	✓	✓	✓
^147Sm/^148Sm	✓	✓	✓			✓ L1		✓	✓ L1–L2
^149Sm/^148Sm	✓		✓ L1			✓ L2		✓	✓ L1–L3
^150Sm/^148Sm	✓	✓	✓		✓	✓		✓	✓
^154Sm/^148Sm	✓	✓	✓		✓	✓		✓	✓

---

Dynamic methods were evaluated to increase the accuracy on the ¹⁴⁴Sm/¹⁴⁸Sm ratio and thus only this ratio was calculated dynamically. The dynamic ratio was obtained by correcting the ¹⁴⁴Sm/¹⁴⁸Sm ratio of one line using the normalisation ratio ¹⁵²Sm/¹⁴⁸Sm of adjacent lines, with the two ratios measured in the same collectors. The normalisation to ¹⁵²Sm/¹⁴⁸Sm is ideal for dynamic mode because of the 4-mass unit difference between ¹⁵²Sm and ¹⁴⁸Sm as well as ¹⁴⁴Sm and ¹⁴⁸Sm. In contrast, the normalisation using the ¹⁴⁷Sm/¹⁵²Sm ratio cannot be easily used to produce a dynamic ratio because of the collector configuration. The dynamic ratios were also corrected for time-drift of the instrumental fractionation which is relatively linear in TIMS. The normalisation ratio ¹⁵²Sm/¹⁴⁸Sm was recalculated for the acquisition time of the ¹⁴⁴Sm/¹⁴⁸Sm ratio by extrapolation using the 10 closest cycles following the method of Garçon et al.²⁹

To summarise, the 1-line acquisition method returns static ratios the multistatic method returns multistatic ratios and a static ratio involving ¹⁴⁹Sm, and the dynamic methods return static ratios, multistatic ratios and a dynamic ratio involving ¹⁴⁴Sm.

Results are presented either as raw ratios or as deviations from the standard value measured in the same session in parts per million (ppm), otherwise known as μ-values. Two types of errors are reported. The internal error for each measurement is defined as twice the standard error on all cycles. The external precision, or reproducibility, is twice the standard deviation defined by standards analysed in a same session.

3. Results and discussion

3.1. Analytical procedure

3.1.1. Matrix removal. The first step of our analytical procedure (Table 1) removed Fe, although some remained at trace levels in the fraction that also contains the REE (elution in 6 M HCl– 0.05 M HF). This Fe removal is essential because in step 2 (TRU-Spec resin) the presence of trivalent Fe can result in a poor separation of the REE from the matrix. These first two columns allow for a quick Sm and Nd separation from almost all the matrix elements including heavy REE, in particular compared to protocols involving cation exchange resin. For example, Frossard et al.²⁰ used 20 mL of AG50W-X8 resin for REE separation. However, in this procedure only up to ∼800 mg of digested chondrite powder can be loaded on this column before the resin is overloaded (i.e. exceeding the capacity of the resin by ∼30%), despite the removal of Fe. Larger samples need splitting which doubles the amount of resin, reagents, and time used for this part of the procedure in order to recover enough Sm for a measurement. The TRU-Spec column also has the advantage to remove most heavy REE and 80% of Gd, which is an isobaric interference for Sm. Yields of step 1 were above 95% for REE including the Allende chondrite sample, whereas the yields for step 2 were always > 70% with most samples >90%.

3.1.2. Sm and Nd separation using the DGA resin. Separation of the REE from one another was achieved by utilising the DGA resin (step 3–5; Table 1). This procedure circumvents the Ce separation with an oxidation step in bromate (e.g. ref. 29 and 47), which is a hazardous, possibly carcinogenic substance. Step 3 of the procedure removed the traces of matrix left after the TRU-Spec column and provided a good separation of Sm from Nd. Yields were 70 to 100% for both Sm and Nd. The purification of Sm and Nd (step 4 and 5) carried out using the high aspect ratio DGA columns also returned near perfect yields of 90 to 100%. They were repeated twice to ensure complete removal of the interfering species. Nevertheless, minute amounts of Nd and Gd were found in the Sm cut after purification. Larger amounts of Eu, up to Eu/Sm ratios of 2 × 10⁻², were also present but did not affect the accuracy of the measurements. The ¹⁴⁶Nd/¹⁵²Sm and ¹⁵⁶Gd/¹⁵²Sm ratios of all samples reported in this study and measured during Sm isotope analyses on the TIMS were below 2 × 10⁻⁵, except for BCR-2 that displayed a ¹⁴⁶Nd/¹⁵²Sm ratio of 1.5 × 10⁻⁴.

The Nd purification procedure also efficiently removed the LREE including Pr which is notoriously difficult to separate from Nd using the LN-Spec resin. Interferences of Ce on Nd analyses were typically low with ¹⁴⁰Ce/¹⁴⁴Nd ratios <4 × 10⁻⁵, except for BIR-1 #2 which had a ¹⁴⁰Ce/¹⁴⁴Nd ratio of 1.5 × 10⁻⁴. Samarium was virtually absent in the Nd cuts. Praseodymium was present at trace levels with ¹⁴¹Pr/¹⁴⁴Nd ratios below 5 × 10⁻⁵, whereas ¹⁴¹Pr/¹⁴⁴Nd ratios up to 3 × 10⁻¹ were reported for LN-Spec separation protocols.²⁹ Our procedure was very efficient for LREE-depleted samples, but not optimal for LREE-enriched samples for which a Ce-oxidation step with bromate solutions removes Ce interferences more effectively. Total procedural yields (step 1–5) were overall 70 to 100% for terrestrial standards and the chondrite Allende. The total procedural blanks were below 73 pg for Sm and below 80 pg for Nd, negligible compared to the amounts of Sm (160–370 ng) and Nd (780–1000 ng) processed in the samples.

3.1.3. Mass-independent fractionation during the chemical separation. Incomplete element recovery during the chemical separation can induce isotope fractionation that can affect the accuracy of high-precision analyses. Procedures using ion exchange resin are less prone to induce mass-independent isotope fractionation of the isotope composition compared to liquid–liquid extraction chromatography resins that contain organic compounds (e.g. ref. 29). The NFSE can occur during the separation of elements with the DGA and TRU-Spec resins. Such fractionation should be limited in step 2 because it is a stick/non-stick procedure in which REE are collected in a large cut to avoid incomplete recovery of the sample. The Nd and Sm separations using the DGA resin are more prone to incomplete yields that in turn could lead to fractionated isotope compositions. To assess the acceptable range of yields, single standard solutions of Sm and Nd were processed through the DGA column (step 4 and 5). Specific cuts of the Sm and Nd elution were collected (Fig. 3) and analysed on the TIMS (Tables 4 and 5). The Sm and Nd peaks were narrow and most of the analyte eluted into two cuts, while the others contained <10% (Fig. 3). The Sm and Nd isotope compositions of the cuts generally correlated with the amount eluted. The largest fractions showed little, mostly unresolved, deviations from the reference composition. However, small fractions at the start and the tail of the peak were significantly fractionated, with μ¹⁴⁴Sm down to −86 ppm. The deviations from the standard composition were consistent with the NFSE (Fig. 3). Mass balance calculations showed that Sm yields above 95%, excluding start and the tail of the peak, do not result in fractionated isotope composition within the analytical uncertainty. Results for two aliquots of the synthetic Sm ICP ETH standard processed through the entire column chemistry with a yield above 98% returned Sm isotope compositions undistinguishable from unprocessed Sm ICP ETH standard (Table 4).

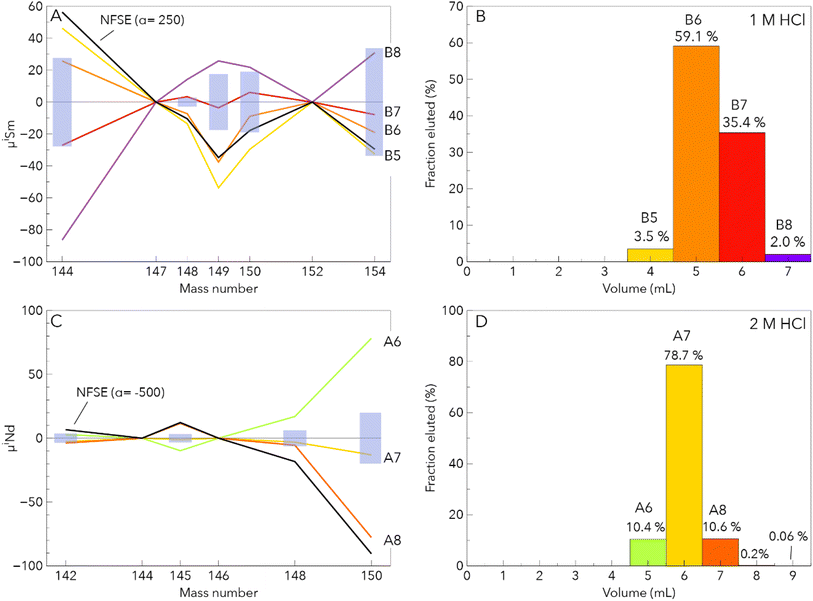Fig. 3 Fractionation of the Sm and Nd isotope composition during column separation. (A) Sm isotope composition patterns of column cuts. These compositions are very similar to the theoretical calculation of the NFSE. (B) The corresponding elution histogram. (C and D) depict the same as in panel (A) and (B), respectively, for Nd. The cuts reflecting the tail of the Nd peak were not analysed for their Nd isotope composition because of this low Nd content. NFSE corresponds to nuclear field shift effect. The latter was calculated using the equations of Fujii et al.⁴⁸, the atomic masses of Wang et al.⁴⁹ and the root mean square nuclear charge radii of Angeli and Marinova⁵⁰ and a coefficient α. The blue rectangles correspond to the reproducibility determined in the same session of analysis.

Table 4 Sm isotope composition of synthetic Sm standards, processed synthetic standards, terrestrial rock standards, the chondrite Allende and column cuts normalised to ¹⁴⁷Sm/¹⁵²Sm = 0.56081 and the Sm ICP ETH standard solution. Errors are twice the standard error (2 SE), except for averages of the synthetic and rock standards where errors are the reproducibility (2 SD). The different dissolutions are numbered “#n” and aliquots from the same dissolution are lettered (e.g. #1a)

Sample	Mass (ng)	Method	μ ^144Sm	±	μ ^148Sm	±	μ ^149Sm	±	μ ^150Sm	±	μ ^154Sm	±
Synthetic standards
Sm ICP ETH (n = 36)	200–300	Multistatic	0	15.9	0	10.0	0	11.2	0	9.2	0	9.4
NIST SRM 3147a (n = 14)	300	Multistatic	−29.6	21.8	8.7	4.0	17.8	12.3	12.8	8.1	11.5	5.9
Sm ICP LMV (n = 9)	300	Multistatic	−39.3	19.0	4.9	10.6	17.2	8.1	10.1	7.1	13.7	7.7
AMES Rennes Sm (n = 7)	300	Static	−130.2	12.7	13.2	3.1	52.6	15.3	49.5	12.7	37.8	20.5
Processed standards
Sm ICP ETH #1	300	Multistatic	−1.9	8.5	−3.2	4.4	8.1	4.9	−1.4	4.8	−3.9	3.9
Sm ICP ETH #2	300	Multistatic	2.2	6.2	8.6	2.8	9.6	3.6	10.2	3.3	0.7	2.8
Rock standards
BCR-2	180	Static	−19.0	9.8	−0.3	4.1	17.5	3.7	−10.3	4.6	−19.3	4.1
BHVO-2 #1	220	Static	2.9	8.8	2.2	3.7	1.5	3.1	−0.1	4.1	−1.0	3.4
DNC-1	220	Static	−18.9	11.0	−1.7	4.5	22.8	4.0	17.2	5.2	6.0	4.6
W-2a	160	Static	4.6	15.2	−0.1	5.1	15.6	4.7	6.9	5.7	24.7	5.2
BIR-1 #1	370	Static	−21.0	6.1	1.0	2.7	2.6	2.5	10.0	3.0	5.3	2.9
BIR-1 #2	360	Static	−9.3	7.6	−0.2	3.3	−9.3	3.0	4.1	3.9	−16.2	3.6
UB-N	220	Multistatic	−18.2	8.6	10.3	3.9	25.6	4.7	20.9	4.3	8.7	3.7
BE-N #1a	300	Multistatic	−17.5	6.7	2.8	3.4	16.3	4.1	4.1	3.7	11.8	3.3
BE-N #1b	300	Multistatic	−13.1	8.3	5.7	3.6	26.2	4.4	11.2	4.0	14.1	3.6
BE-N #1c	300	Multistatic	−12.5	4.4	6.7	2.1	5.5	2.5	3.9	2.2	11.1	2.0
BE-N #2a	300	Multistatic	−29.4	8.0	−1.0	3.7	11.1	4.4	4.1	3.9	9.8	3.1
BE-N #2b	300	Multistatic	−30.1	5.8	8.1	2.4	15.6	3.2	15.2	3.2	2.8	2.5
BE-N #2c	300	Multistatic	−35.1	9.8	7.0	4.1	18.9	5.2	−2.5	5.0	9.4	3.4
BE-N #2d	300	Multistatic	−30.0	5.2	4.6	2.5	14.7	3.0	10.4	2.9	10.4	2.5
BHVO-2 #2a	300	Multistatic	−9.4	7.3	10.3	3.5	12.9	4.2	12.5	3.6	13.7	3.2
BHVO-2 #2b	300	Multistatic	−21.4	14.2	11.4	5.4	27.7	7.6	14.4	7.5	0.4	6.7
BHVO-2 #2c	300	Multistatic	−19.5	5.9	1.1	2.8	14.0	3.5	5.9	3.0	11.8	2.6
BHVO-2 #3	300	Multistatic	−21.8	6.0	−1.2	2.6	18.3	3.6	2.2	3.0	13.2	2.5
Average rock standards		Multistatic	−21.8	16.9	5.0	8.5	16.5	12.7	7.4	11.3	9.9	8.8
Allende (CV3)	250	Multistatic	−165.4	4.4	−0.9	2.2	−37.0	3.1	89.7	2.5	12.3	2.3
Column cuts
B5	180	Static	46.3	9.1	−13.5	3.8	−53.7	3.3	−29.6	2.8	−32.5	2.3
B6	300	Static	25.8	5.4	−7.2	2.6	−37.6	2.2	−8.8	4.3	−19	3.5
B7	300	Static	−27	5.4	3.4	2.4	−3.6	2.1	6.1	2.7	−7.9	2.3
B8	110	Static	−86.4	21.1	14.2	7.1	25.8	7	21.9	8.3	31	7.6

---

Table 5 Nd isotope composition of terrestrial standards, the chondrite Allende and column cuts normalised to ¹⁴⁶Nd/¹⁴⁴Nd = 0.7219 and to the JNdi-1 standard of each session. Two separate dissolutions of BIR-1 were analysed. ε¹⁴³Nd_CHUR are calculated using ¹⁴³Nd/¹⁴⁴Nd ratios normalised the JNdi-1 value of Garçon et al.²⁹ and to the Chondritic Uniform Reservoir (CHUR) value of Bouvier et al.⁵¹ equal to 0.512630. Errors are twice the standard error (2SE), except for averages of the synthetic and rock standards where errors are the reproducibility (2SD)

Sample	Mass (ng)	Session	μ ^142Nd	±	ε ^143NdCHUR	±	μ ^145Nd	±	μ ^148Nd	±	μ ^150Nd	±
BCR-2	900	#1	−2.8	2.7	−0.19	0.02	3.4	2.0	1.3	4.4	4.6	11.3
BHVO-2	950	#1	−0.3	1.8	6.66	0.02	1.2	1.5	0.5	3.5	−1.3	8.3
DNC-1	1000	#1	−0.2	1.9	−3.50	0.02	2.4	1.5	1.0	3.4	3.8	8.2
W-2a	780	#1	0.0	2.2	−2.40	0.02	0.5	1.4	2.4	3.2	1.2	6.8
BIR-1 #1	900	#1	−1.9	1.8	8.67	0.02	0.1	1.4	8.2	3.0	1.9	7.7
BIR-1 #2	900	#1	2.9	2.0	8.73	0.02	1.7	1.6	0.9	3.6	−0.2	8.2
BE-N	1000	#2	−3.2	1.9	4.57	0.02	−1.7	1.5	1.4	3.4	−3.7	8.4
UB-N	800	#2	−0.5	1.8	5.64	0.02	0.3	1.5	−4.6	3.1	−8.8	8.0
Allende	850	#2	−30.1	2.2	−1.68	0.03	4.4	1.6	6.5	3.8	11.7	8.2
Average rock standards			−0.7	3.9	—	—	1.0	3.1	1.4	7.0	−0.3	8.7
Column cuts
A6	530	#2	3.3	1.9	—	—	−9.0	1.6	16.7	3.5	77.8	8.7
A7	1000	#2	−1.1	1.5	—	—	−0.1	1.2	−2.4	3.0	−12.2	6.2
A8	540	#2	−2.6	3.5	—	—	12.3	2.5	−6.2	5.7	−85.2	12.6
JNdi-1 session #1	1000	n = 5	0.0	5.0	0.00	0.03	0.0	3.1	0.0	5.6	0.0	14.7
JNdi-1 session #2	800–1000	n = 16	0.0	3.7	0.00	0.05	0.0	3.3	0.0	6.1	0.0	19.8

---

3.2. The role of activators and filaments in the ionisation of Sm

To evaluate the influence of activators and filaments in the ionisation of Sm, different (i) activators, (ii) filament thickness and (iii) filament material were investigated.

(i) Metals with high work function deposited on the filament can increase ionisation yields. For example, the addition of a Ta₂O₅ activator (also called TaF₅) developed by Birck and Allègre⁴³ is routinely used for Sr isotope analysis and was also applied to measure small amounts (<20 ng) of Nd and Sm.⁵² Moreover, Louis-Jean et al.⁴² developed a Pt activator that promotes high ionisation yields. The amount of Sm loaded for these two studies were below 20 ng and despite the high ionisation yields the ¹⁴⁴Sm/¹⁵²Sm ratios were not precise enough for meteorite research. Therefore, we carried out tests using 200 to 300 ng of Sm together with variable amounts of Ta and Pt-based activators loaded on a single Re filament setup. Phosphoric acid was also investigated as an activator in the more common double-filament setup.

(ii) Three different thicknesses of the filaments (1.0 mil, 1.2 mil and 1.6 mil) were tested to evaluate the effects on how to control the ion beam as efficiently as possible.

(iii) Finally, Ir ionisation filaments were also used, but these tests were not successful. Despite a much higher work function of 5.70 ± 0.02 eV,⁵³ a stable signal of more than 1 × 10⁻¹¹ A of Sm⁺ ions could not be sustained for an analysis before melting of the filament because the melting point of Ir (2446 °C) is much lower than that of Re (3185 °C).

The ratio of detected ions to the atoms loaded allows comparison of the different loading methods. The detected ions were calculated using the average ¹⁵²Sm intensity and the duration of the runs. The term “efficiency” is used hereafter to describe this parameter because not all ions produced are detected. The efficiency does not correspond solely to the ionisation yield but also includes the transmission of the ions through the instrument.⁵⁴ Moreover, the measurements presented here were not acquired in total evaporation mode contrary to the study of Louis-Jean et al.⁴² Therefore, the efficiency reported in our experiments do not represent the true yield and constitute a lower limit. Nevertheless, comparison between the different runs is possible because they were acquired in a consistent manner and correspond to the exploitable range for accurate analyses using intensity and fractionation criteria.

The average efficiencies of Sm standards loaded with Ta₂O₅ and Pt activators on single Re filaments were 0.09% (n = 8) and 0.13% (n = 5), respectively, and were substantially lower than that of the conventional double filament method that had a mean efficiency of 0.25% (n = 98) for the Sm ICP ETH standard (Fig. 4). The efficiency appeared to decrease with the amount of Pt or Ta loaded on the filament. In addition to the low efficiency, the Ta₂PO₅ and Pt activators produced unstable beams. This prompted Louis-Jean et al.⁴² to use a total evaporation method. In conclusion, the two activators tested are not well-suited for the analysis of more than 200 ng of Sm for which the double filament setup in general produces more stable and long-lasting ion beams. The enhancement of the efficiency reported for Ta₂PO₅ and Pt activators may therefore only be valid for small amounts of Sm below a few tens of nanograms. The addition of H₃PO₄ does not improve the ionisation efficiency and thus is not recommended.

Fig. 4 Efficiency (see definition in the main text) for analyses of the Sm ICP ETH standard with various parameters highlighted. The colours correspond to different activators used and the shape the filament thickness or setup. The filaments were all made of Re. The black outlines represent standards measured without activators. The blue outline represent standards to which H₃PO₄ was added during loading. The diamonds represent single filament setups with a Pt activator (yellow) or a TaO₅ activator (red). Other shapes represent double filament setups for which the thickness of the ionisation filament was tested (square for 1.0 mil, triangle for 1.2 mil and circle for 1.6 mil).

The thickness of the Re filaments did not significantly change the efficiency (Fig. 4). The three filament thicknesses are statistically very similar with averages and first and third quartiles agreeing within 0.04%. In practice, thin 1.0 mil filaments produced more unstable ion beams, and the filament must be heated with caution as 1.0 mil filaments tend to melt at lower temperature than the thicker ones. Thick 1.6 mil filaments produced more stable beams but high currents up to 5.5 A on the ionisation filament were needed to achieve optimal conditions. We observed that these high currents can induce instability of the ion beam and focus parameters. Therefore, filaments with an intermediate thickness of 1.2 mil are favoured for Sm isotope analysis.

3.3. Comparison of static, multi-static and dynamic methods

The different methods were compared using the ¹⁵²Sm/¹⁴⁸Sm normalisation scheme (Table 6 and ESI†). This ratio was chosen, because the more common normalisation relative to ¹⁴⁷Sm/¹⁵²Sm only allows for the comparison of the static and the multistatic methods. Fig. S1† shows the data acquired for the Sm ICP ETH standard over the course of this study with all the methods using the normalisation to ¹⁵²Sm/¹⁴⁸Sm. Dynamic methods theoretically reduce the effect of relative cup efficiencies and gains (e.g. ref. 55 and 56), whereas multistatic methods have been found to be return better reproducibility than static methods, and multidynamic methods in some instances (e.g. ref. 57–59). In general, our data acquired with the multistatic and dynamic methods perform better than the static method for most ratios with improvement in session reproducibility up to a factor 4 for the ¹⁵⁴Sm/¹⁴⁸Sm ratio. The ¹⁴⁷Sm/¹⁴⁸Sm ratio obtained with the multistatic method is significantly less precise than those calculated using the static and dynamic methods. The ¹⁴⁴Sm/¹⁴⁸Sm ratio of the dynamic methods were not more precise than those of the other methods with session reproducibilities between 28 and 40 ppm (Table 6). They were similar or larger than with the static and multistatic methods (below 30 ppm). A cup change occurred in the middle of our study and drastically improved the precision of the ¹⁵⁴Sm/¹⁴⁸Sm ratios. The reproducibility reached 6.3 ppm to 9.2 ppm for the multistatic method compared to 20.1 ppm before the cup change. The variation in the external precisions with different cup configurations highlights the importance of the state of the cups and amplifiers in producing high-precision isotope ratios corroborating studies on other elements (e.g. ref. 58 and 60).

Table 6 Sm isotope composition of the Sm ICP ETH standard using the different methods with both normalisation schemes

Normalisation to ^147Sm/^152Sm = 0.56081
Method	Session	^144Sm/^152Sm	2SD	2RSD (ppm)	^148Sm/^152Sm	2SD	2RSD (ppm)	^149Sm/^152Sm	2SD	2RSD (ppm)	^150Sm/^152Sm	2SD	2RSD (ppm)	^154Sm/^152Sm	2SD	2RSD (ppm)
Static	#1	0.114980	0.000002	21.1	0.420425	0.000002	5.1	0.516845	0.000006	10.7	0.275986	0.000003	11.0	0.850782	0.000027	31.5
Static	#3	0.114980	0.000002	19.4	0.420425	0.000002	5.0	0.516843	0.000007	13.4	0.275986	0.000003	12.3	0.850777	0.000027	31.6
Static	#4	0.114981	0.000003	27.7	0.420423	0.000001	2.8	0.516835	0.000009	17.5	0.275984	0.000005	19.0	0.850766	0.000029	33.7
Static	#5	0.114980	0.000002	19.0	0.420423	0.000003	6.7	0.516835	0.000014	26.4	0.275985	0.000003	11.3	0.850766	0.000027	31.4
2 lines multisatic	#4	0.114981	0.000002	19.9	0.420431	0.000004	9.1	0.516829	0.000010	19.3	0.275989	0.000002	5.7	0.850782	0.000015	18.2
2 lines multistatic	#6	0.114975	0.000002	21.5	0.420428	0.000006	15.3	0.516876	0.000007	13.0	0.275987	0.000004	13.1	0.850792	0.000004	5.0
2 lines multistatic	#7	0.114973	0.000002	16.4	0.420421	0.000005	12.3	0.516882	0.000004	8.3	0.275987	0.000003	11.0	0.850793	0.000004	4.2
2 lines multistatic	#8	0.114975	0.000001	13.0	0.420420	0.000004	8.7	0.516881	0.000003	6.7	0.275987	0.000001	5.2	0.850794	0.000004	4.6
2 lines multistatic	#9	0.114974	0.000002	13.5	0.420420	0.000003	6.7	0.516882	0.000002	4.1	0.275986	0.000002	8.8	0.850791	0.000007	8.4

---

Normalisation to ^152Sm/^148Sm = 2.37689
Method	Session	^144Sm/^148Sm	2SD	2RSD (ppm)	^147Sm/^148Sm	2SD	2RSD (ppm)	^149Sm/^148Sm	2SD	2RSD (ppm)	^150Sm/^148Sm	2SD	2RSD (ppm)	^154Sm/^148Sm	2SD	2RSD (ppm)
Static	#1	0.273681	0.000007	26.3	1.334147	0.000009	6.4	1.229122	0.000012	9.9	0.656214	0.000006	8.9	2.021525	0.000066	32.5
Static	#3	0.273680	0.000006	22.1	1.334147	0.000008	6.3	1.229118	0.000015	12.0	0.656215	0.000008	12.3	2.021515	0.000064	31.7
Static	#4	0.273685	0.000009	32.1	1.334156	0.000005	3.5	1.229103	0.000020	16.3	0.656213	0.000012	18.7	2.021482	0.000068	33.8
Static	#5	0.273684	0.000008	27.8	1.334155	0.000011	8.5	1.229102	0.000027	22.0	0.656214	0.000007	10.0	2.021482	0.000069	34.2
2 lines multistatic	#4	0.273675	0.000004	13.5	1.334124	0.000015	11.4	1.229095	0.000026	20.9	0.656218	0.000004	5.8	2.021538	0.000041	20.1
2 lines multistatic	#6	0.273664	0.000012	42.3	1.334138	0.000026	19.4	1.229174	0.000017	14.1	0.656215	0.000004	6.8	2.021554	0.000014	6.9
2 lines multistatic	#7	0.273670	0.000005	16.9	1.334164	0.000021	15.4	1.229197	0.000011	8.8	0.656221	0.000005	7.3	2.021542	0.000017	8.4
2 lines multistatic	#8	0.273675	0.000004	15.7	1.334166	0.000015	11.0	1.229195	0.000010	8.3	0.656220	0.000006	9.3	2.021542	0.000013	6.3
2 lines multistatic	#9	0.273674	0.000006	22.9	1.334167	0.000013	9.6	1.229197	0.000007	6.0	0.656221	0.000006	9.8	2.021536	0.000019	9.2
2 lines dynamic	#2	0.273655	0.000008	28.4	1.334090	0.000013	9.8	1.229115	0.000017	14.1	0.656211	0.000005	7.1	2.021590	0.000017	8.6
3 Lines dynamic	#1	0.273659	0.000011	40.4	1.334124	0.000008	5.8	1.229112	0.000014	11.1	0.656216	0.000004	6.5	2.021566	0.000016	7.9

---

The conventional normalisation to ¹⁴⁷Sm/¹⁵²Sm is preferred because it yields better reproducibilities for most isotope ratios. Data acquired with the static and multistatic methods normalised to ¹⁴⁷Sm/¹⁵²Sm are compared in Fig. S2.† All ratios were more precise using the multistatic method, with the exception of the ¹⁴⁸Sm/¹⁵²Sm. The reproducibility on the ¹⁴⁴Sm/¹⁵²Sm ratio ranged from 19 to 28 ppm for the static method compared 13 to 22 ppm for the multistatic method measured for the Sm ICP ETH standard (Fig. 5). The data produced with the static and multistatic methods have been very consistent over 2 years of measurements. In comparison, ¹⁴⁴Sm/¹⁵²Sm data from the literature are much more variable between sessions. The multistatic method developed in this study consistently provides the best session reproducibilities for ¹⁴⁴Sm/¹⁵²Sm ratios (13 to 22 ppm) and ¹⁵⁴Sm/¹⁵²Sm (4.2 to 8.5 ppm, after cup change) (Table 6).

Fig. 5 Comparison of the relative standard deviation or RSD (i.e. external precision) obtained by different studies for the ratio ¹⁴⁴Sm/¹⁵²Sm. Studies with several sessions reported variable precisions. Procedures outlined in this study provided consistently precise ¹⁴⁴Sm/¹⁵²Sm ratios throughout all sessions. Note that different amounts of Sm were measured by all studies but were often not specified. For those mentioned, it ranged from 100 to 500 ng. In this study we used Sm loads on the filaments of 200 ng (n = 12) and 300 ng (n = 86).

3.4. Errors induced by interference corrections

The Sm isotope composition is particularly prone to large interference corrections from Nd, and Gd. Errors are introduced because the interference correction calculation for instrumental fractionation assumes identical mass fractionation of Nd, Gd and Sm during evaporation. This is not the case because of the difference in evaporation temperature of these elements and therefore their exponential fractionation factor β (e.g. ref. 61) may not be the same. The isobaric interference of ¹⁴⁴Nd on ¹⁴⁴Sm is particularly challenging because of the small abundance of ¹⁴⁴Sm. In comparison, Gd is less problematic because of the very small abundances of the interfering isotopes ¹⁵²Gd and ¹⁵⁴Gd of 0.2% and 2.18%, respectively. Nonetheless, all Sm isotope ratios are affected by the Gd interference because of the normalisation relative to ¹⁵²Sm, which suffers from the isobaric interference of ¹⁵²Gd.

3.4.1. Monte Carlo approach for error propagations. We investigated the effect of an inaccurate interference correction due to variations in the Nd and Gd isotope ratios using a Monte Carlo simulation. In this model, the Nd and Gd isotope ratios were set to vary for fractionation factors β of +0.5 and −0.5 following the approach of Garçon et al.²⁹ This range likely overestimates the actual variation of the isotope ratios and provides a maximal limit. In addition, we propagated the analytical errors related to the instrument noise (random errors) in the simulation because the relative contribution of ¹⁴⁴Nd on ¹⁴⁴Sm is so large that the analytical error on the measured ¹⁴⁶Nd intensity may decrease the precision of the correction. In other words, with a very low Nd content (<0.01 mV), the ¹⁴⁶Nd signal is very noisy and errors on the correction based on the measured intensity will be larger than at higher ¹⁴⁶Nd signals. The two main sources of random errors are (i) the electronic noise of the amplifiers (Johnson–Nyquist noise) and (ii) the counting statistics. The theoretical values of these error sources are minimal values and do not account for the noise from other parts of the electronic systems. We incorporated errors calculated for the Johnson–Nyquist noise and counting statistics using the equations of Luu et al.⁶² in our Monte Carlo simulation to quantify the effect on the interference corrections. Calculations were performed using the parameters of the static method, namely one line and correction of the interference using ¹⁴⁶Nd for the interference correction, and the average intensity of ¹⁵²Sm (4.97 × 10⁻¹¹ A) and number of cycles (717) for all runs on Sm standards with that method (Fig. 5).

The results of the Monte Carlo simulation showed that the error induced by inaccurate correction of the Gd interference was below the external precisions for ¹⁵⁶Gd/¹⁵²Sm ratios up to 1 × 10⁻³ whereas the highest ¹⁵⁶Gd/¹⁵²Sm ratio in the processed samples was 8 × 10⁻⁴. In contrast, the impact of Nd was much larger so that, e.g., the nominal Nd interference correction for ¹⁴⁴Sm/¹⁵²Sm reached more than 100 ppm with ¹⁴⁶Nd/¹⁵²Sm ratios around 1 × 10⁻⁵. Error propagation within the Monte Carlo simulation showed that the effect of random errors (counting statistics and Johnson–Nyquist noise) on the measurement of ¹⁴⁶Nd were the principal error source compared to inaccurate mass-fractionation correction of Nd for ¹⁴⁶Nd/¹⁵²Sm ratios up to 0.7 × 10⁻⁶ (Fig. 6). Nearly all samples are below this threshold ratio. The maximal error induced by counting statistics and Johnson–Nyquist noise ranged from 1.2 to 3.2 ppm for ¹⁴⁶Nd/¹⁵²Sm ratios between 1 × 10⁻⁴ and 1 × 10⁻⁶, respectively, which, corresponds to that of the samples processed in this study. Since the Nd interference corrections for the other Sm isotope ratios were much lower, the propagated errors were negligible.

Fig. 6 Maximum error on isotope ratios induced by imprecise interference correction. The dashed lines correspond to the maximum error calculated solely with variable fractionation factors for Nd (−0.5 < β < 0.5). The continuous lines correspond to the maximum error for which the counting statistics and Johnson–Nyquist noise (JN + CS) were also considered.

Limits for the Nd and Gd interferences are estimated from this simulation for the ¹⁴⁴Sm/¹⁵²Sm and ¹⁵⁴Sm/¹⁵²Sm ratios, respectively, for which the interference correction is larger than the reproducibility, considering a difference in fractionation factor between Sm and interferents of −0.5 to 0.5. Considering the best session reproducibility on ¹⁴⁴Sm/¹⁵²Sm of 13 ppm, the threshold of the Nd interference corresponds to a ¹⁴⁶Nd/¹⁵²Sm ratio of about 3.5 × 10⁻⁵ (Fig. 6). Similarly, a threshold of 1.0 × 10⁻³ is determined for the ¹⁵⁶Gd/¹⁵²Sm ratio, corresponding to an error of about 4 ppm on the ¹⁵⁴Sm/¹⁵²Sm ratio for the best external precision. Both limits are considered conservative because the actual difference in fractionation factors β of Nd, Sm and Gd is unknown and likely much lower than the value of 1 used in the simulation.²⁹

3.5. Synthetic Sm standards

Four different synthetic standards, Sm ICP ETH, NIST SRM 3147a, AMES Sm Rennes and Sm ICP LMV were analysed. They substantially differ in their Sm isotope composition (Table 4 and Fig. 7). The differences reach 130 ppm for the ¹⁴⁴Sm/¹⁵²Sm ratio between Sm ICP ETH and AMES Rennes Sm. The deviations of the Sm isotope compositions among the synthetic standards match the NFSE, except for the AMES Rennes Sm (Fig. 7). The Sm isotope composition defined by standard rocks (Table 4) is in relatively good agreement with the Sm isotope composition of NIST SRM 3147a. However, NIST SRM 3147a behaved differently on the filament, it emitted at higher currents on the filament and had a different mass bias range compared to other standards and samples. This could induce variations in the Sm isotope composition after mass bias correction using an exponential law (e.g. ref. 29 and 59). This behaviour renders this standard potentially inadequate for TIMS analyses although no such offset in the Sm isotope composition was observed in our data.

Fig. 7 Diagram comparing μ¹⁴⁴Sm and μ¹⁴⁸Sm compositions of all synthetic and terrestrial rock standards measured during this study, normalised to the Sm ICP ETH standard measured during the corresponding session. The column cuts (white circles) measured individually aligned along the NFSE trend. All standards, except AMES Rennes Sm were broadly aligned on this trend. Terrestrial rock standards plot next to the composition of NIST SRM 3147a.

3.6. Sm isotope composition of terrestrial rock standards and Allende

The seven processed rock standards provide an estimate of the terrestrial Sm isotope composition. The yields for rock standards and the meteorite Allende were >70% for Sm and Nd, yields higher than 90% for most samples. Little mass-independent fractionation was therefore expected. The basaltic rock standards W-2a and BHVO-2 measured using the static method both display significantly different μ¹⁴⁴Sm compositions (Table 4 and Fig. 8). Their isotope composition does not correspond to the NFSE because μ¹⁴⁴Sm and μ¹⁴⁹Sm should have opposite signs and a ratio of about 3 to 2 (Table 4). The reason for this difference is unclear and may be related to domain mixing on the filament previously observed for Nd (e.g. ref. 63 and 64). The average terrestrial composition measured with the multistatic method and normalised to the Sm ICP ETH standard was μ¹⁴⁴Sm = −21.8 ± 16.9, μ¹⁴⁸Sm = 5.0 ± 8.5, μ¹⁴⁹Sm = 16.5 ± 12.7, μ¹⁵⁰Sm = 7.4 ± 11.3, μ¹⁵⁴Sm = 9.9 ± 8.8. The similar external precisions between the rock standards and the synthetic standard measurements demonstrates that our analytical procedure is robust.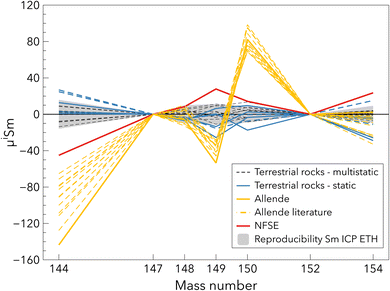

Fig. 8 Sm isotope composition of terrestrial rock standards and the chondrite Allende from this study and the literature,^12,37,38 corrected for mass fractionation using the ¹⁴⁷Sm/¹⁵²Sm ratio of 0.56081. All data were normalised to the average value of the terrestrial rock standards. Two rock standards, BHVO-2 and W-2a, measured with the static method are reported in dashed lines and display different μ¹⁴⁴Sm compositions. The grey area corresponds to the long-term reproducibility on Sm ICP ETH (Table 4).

The Allende chondrite slightly differs from the composition measured in different studies^12,37,38 for the μ¹⁴⁴Sm and μ¹⁴⁹Sm (Fig. 8), assuming the synthetic standards these studies used have a terrestrial composition, which is true within the errors reported. This offset is likely not related to an analytical artefact because the total procedural yield of this sample is 84%, similar to some rock standards. The Sm isotope ratios that are the most affected by the NFSE are μ¹⁴⁴Sm, μ¹⁴⁹Sm and μ¹⁵⁴Sm. The deviations produced by the NFSE are similar for μ¹⁴⁹Sm and μ¹⁵⁴Sm and larger and opposite sign for μ¹⁴⁴Sm. The difference in Sm isotope composition of Allende between the literature and this study are not consistent with the NFSE trend (Table 4 and Fig. 8). The reason for the difference in the Sm isotope composition of Allende may instead originate from sample heterogeneity because CV chondrites contain Ca-, Al-rich inclusions that are enriched in Sm and display negative μ¹⁴⁴Sm from −210 ± 49 to −336 ± 61.^18,38,39,65 This leads to substantial heterogeneity in μ¹⁴⁴Sm isotope compositions of CM chondrites for instance, ranging from −93 ± 22 to −51 ± 33.^12,37 Stracke et al.⁶⁶ estimated that producing a powder of Allende, which is homogeneous within 5% for trace element compositions, requires about 50 g of material. Moreover, powder prepared from a 4 kg sample of Allende has been found to be heterogeneous for REE.⁶⁷

3.7. Nd isotope composition of terrestrial rock standards

A large set of terrestrial standards were processed through our chemical procedure and measured using a 4-line dynamic method. Some standards (DNC-1 and W2-a) were characterised for the first time at high-precision for all Nd isotope ratios. These data provide a reference value for the ¹⁴³Nd/¹⁴⁴Nd ratio of these rock standards at a precision below 5 ppm. The ¹⁴³Nd/¹⁴⁴Nd data for the rock reference materials agree within error with those reported in the literature (Table 5). The remaining Nd isotope ratios were undistinguishable from the JNdi-1 synthetic standard, highlighting the performance of our chemical separation (Table 5). The terrestrial standards yielded an average composition of μ¹⁴²Nd = −0.7 ± 3.9; μ¹⁴⁵Nd = 1.0 ± 3.1; μ¹⁴⁸Nd = 1.4 ± 7.0; μ¹⁵⁰Nd = −0.3 ± 8.7.

4. Conclusion

This study reports an analytical procedure for high precision Sm isotope analyses on large meteorite samples (>1 g) using TIMS. The chemical separation procedure involves five steps to isolate both Sm and Nd. The first step, employing anion resin, removes Fe before the second step using TRU-Spec resin that separates REE from the matrix. The third step (DGA resin) separates Sm from Nd, while the last steps, also using DGA resin, further purifies these cuts. This method was tested on a variety of terrestrial standards for which Sm and Nd were recovered with yields above 70%. Procedural blanks were below 80 pg and are negligible compared to the amount of Sm and Nd processed (generally ca. 300 ng and 800 ng, respectively). In addition to the new chemical separation procedure, we investigated ways to improve the precision for Sm isotope analyses on TIMS. The use of activators made of Pt, Ta and H₃PO₄ proved to have a detrimental effect on the ionisation efficiency for loads of 200 to 300 ng Sm. The double Re filament assembly without activator provided the best efficiency. Various measurement methods were tested including static, multistatic and dynamic modes. Despite their theoretical potential in reducing errors, the dynamic methods yielded lower external precisions compared to static and multistatic methods. The multistatic method with 2 lines achieves the most precise ¹⁴⁴Sm/¹⁵²Sm ratios with external precisions of 13 to 22 ppm. Interference corrections on ¹⁴⁴Sm/¹⁵²Sm ratios are necessary but introduce non-negligible errors because of instrumental noise and inaccurate correction of the instrumental mass bias. Nevertheless, the successful purification of Sm by our new protocol mitigates their influence on the results. The four synthetic Sm standards show distinct isotope compositions. Comparison of the Sm isotope composition of these standards and seven terrestrial rock standards show the importance of characterising synthetic standards for precise ¹⁴⁴Sm/¹⁵²Sm isotope ratio determination. The external precision of our method allows for the characterisation of nucleosynthetic variations of Sm isotopes in meteorites and the exploration of the p-process nuclide ¹⁴⁴Sm. Our new analytical procedure can also be applied to other materials e.g., in environmental and nuclear applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank Colin Maden, Manuela Fehr and Corey Archer for providing technical support on the TIMS, the clean lab and the ICP-MS as well as members of the group for helping us in keeping the best working conditions in the lab. Discussions with Claudine Israel, Brad Peters, Colin Maden and Mattias Ek contributed to the development of this work. Brad Peters provided sample RU0701 and the NIST SRM 3147a synthetic standard that were used in this study. We also thank Catherine Chauvel and Maud Boyet for providing AMES Rennes Sm and Sm ICP LMV standards, respectively. We also thank Maud Boyet and the National Museum of Natural History of the Smithsonian Institution in Washington D.C., United States of America, for providing the Allende chondrite (USNM3529). This work has been supported by the Swiss Science Foundation (project 200021_208079) and ETH Zürich. We also thank two anonymous reviewers for their comments that helped improving the manuscript.

References

1. I. M. Villa, N. E. Holden, A. Possolo, R. B. Ickert, D. B. Hibbert and P. R. Renne, Geochim. Cosmochim. Acta, 2020, 285, 70–77.
2. F. Meissner, W.-D. Schmidt-Ott and L. Ziegeler, Z. Phys. At. Nucl., 1987, 327, 171–174.
3. K. Notsu, H. Mabuchi, O. Yoshioka and M. Ozima, Geochem. J., 1973, 7, 51–54.
4. C. J. Allègre and D. Ben Othman, Nature, 1980, 286, 335–342.
5. P. Richard, N. Shimizu and C. J. Allègre, Earth Planet. Sci. Lett., 1976, 31, 269–278.
6. S. L. Goldstein, R. K. O'Nions and P. J. Hamilton, Earth Planet. Sci. Lett., 1984, 70, 221–236.
7. D. J. Piepgras, G. J. Wasserburg and E. J. Dasch, Earth Planet. Sci. Lett., 1979, 45, 223–236.
8. K. Notsu, H. Mabuchi, O. Yoshioka, J. Matsuda and M. Ozima, Earth Planet. Sci. Lett., 1973, 19, 29–36.
9. G. W. Lugmair, N. B. Scheinin and K. Marti, Proc. Lunar Sci. Conf. 6th, 1975, pp. 1419–1429.
10. C. L. Jr. Harper, L. E. Nyquist, B. Bansal, H. Wiesman and C.-Y. Shih, Science, 1995, 267, 213–217.
11. G. Caro, B. Bourdon, J.-L. Birck and S. Moorbath, Nature, 2003, 423, 428–432.
12. R. Andreasen and M. Sharma, Science, 2006, 314, 806–809.
13. S. Bisterzo, C. Travaglio, R. Gallino, M. Wiescher and F. Käppeler, Astrophys. J., 2014, 787, 10.
14. M. Arnould and S. Goriely, Phys. Rep., 2003, 384, 1–84.
15. L. Qin and R. W. Carlson, Geochem. J., 2016, 50, 43–65.
16. G. P. Russ, D. S. Burnett, R. E. Lingenfelter and G. J. Wasserburg, Earth Planet. Sci. Lett., 1971, 13, 53–60.
17. H. Hidaka and F. Gauthier-Lafaye, Geochim. Cosmochim. Acta, 2001, 65, 941–949.
18. A. Bouvier and M. Boyet, Nature, 2016, 537, 399–402.
19. R. A. Edge and L. H. Ahrens, Anal. Chim. Acta, 1962, 26, 355–362.
20. P. Frossard, C. Israel, A. Bouvier and M. Boyet, Science, 2022, 377, 1529–1532.
21. C. Pin and A. Gannoun, J. Anal. At. Spectrom., 2019, 34, 2136–2146.
22. G. R. Choppin and R. J. Silva, J. Inorg. Nucl. Chem., 1956, 3, 153–154.
23. K. Wolfsberg, Anal. Chem., 1962, 34, 518–521.
24. D. L. Massart and J. Hoste, Anal. Chim. Acta, 1963, 28, 378–382.
25. O. Eugster, F. Tera, D. S. Burnett and G. J. Wasserburg, J. Geophys. Res., 1970, 75, 2753–2768.
26. E. Hyung and F. L. H. Tissot, J. Anal. At. Spectrom., 2021, 36, 1946–1959.
27. D. F. Peppard, G. W. Mason, J. L. Maier and W. J. Driscoll, J. Inorg. Nucl. Chem., 1957, 4, 334–343.
28. T. B. Pierce and P. F. Peck, Nature, 1962, 194, 84.
29. M. Garçon, M. Boyet, R. W. Carlson, M. F. Horan, D. Auclair and T. D. Mock, Chem. Geol., 2018, 476, 493–514.
30. Z.-Y. Chu, M.-J. Wang, C.-F. Li, Y.-H. Yang, J.-J. Xu, W. Wang and J.-H. Guo, J. Anal. At. Spectrom., 2019, 34, 2053–2060.
31. J. C. Dubois, G. Retali and J. Cesario, Int. J. Mass Spectrom. Ion Processes, 1992, 120, 163–177.
32. H. Hidaka, M. Ebihara and M. Shima, Anal. Chem., 1995, 67, 1437–1441.
33. H. Isnard, R. Brennetot, C. Caussignac, N. Caussignac and F. Chartier, Int. J. Mass Spectrom., 2005, 246, 66–73.
34. S. Wakaki and T. Tanaka, Int. J. Mass Spectrom., 2016, 407, 22–28.
35. J.-H. Bai, M. Lin, S.-X. Zhong, Y.-N. Deng, L. Zhang, K. Luo, H. Wu, J.-L. Ma and G.-J. Wei, J. Anal. At. Spectrom., 2023, 38, 629–637.
36. T.-L. Chang, M.-T. Zhao, W.-J. Li, J. Wang and Q.-Y. Qian, Int. J. Mass Spectrom., 2002, 218, 167–172.
37. R. W. Carlson, M. Boyet and M. Horan, Science, 2007, 316, 1175–1178.
38. C. Burkhardt, L. E. Borg, G. A. Brennecka, Q. R. Shollenberger, N. Dauphas and T. Kleine, Nature, 2016, 537, 394–398.
39. Q. R. Shollenberger, L. E. Borg, J. Render, S. Ebert, A. Bischoff, S. S. Russell and G. A. Brennecka, Geochim. Cosmochim. Acta, 2018, 228, 62–80.
40. Q. R. Shollenberger, L. E. Borg, E. C. Ramon, M. A. Sharp and G. A. Brennecka, Talanta, 2021, 221, 121431.
41. D. Wang and R. W. Carlson, J. Anal. At. Spectrom., 2022, 37, 185–193.
42. J. Louis-Jean, J. D. Inglis, S. Hanson, A. Pollington, D. Meininger, S. Reilly and R. Steiner, J. Radioanal. Nucl. Chem., 2021, 327, 317–327.
43. J. L. Birck and C. J. Allegre, Earth Planet. Sci. Lett., 1978, 39, 37–51.
44. B. J. Peters, A. Shahar, R. W. Carlson, J. M. D. Day and T. D. Mock, Geochim. Cosmochim. Acta, 2019, 245, 59–78.
45. A. Quemet, M. Angenieux and A. Ruas, J. Anal. At. Spectrom., 2021, 36, 1758–1767.
46. J. Meija, T. B. Coplen, M. Berglund, W. A. Brand, P. De Bièvre, M. Gröning, N. E. Holden, J. Irrgeher, R. D. Loss, T. Walczyk and T. Prohaska, Pure Appl. Chem., 2016, 88, 293–306.
47. N. S. Saji, D. Wielandt, C. Paton and M. Bizzarro, J. Anal. At. Spectrom., 2016, 31, 1490–1504.
48. T. Fujii, F. Moynier and F. Albarède, Earth Planet. Sci. Lett., 2006, 247, 1–9.
49. M. Wang, G. Audi, A. H. Wapstra, F. G. Kondev, M. MacCormick, X. Xu and B. Pfeiffer, Chin. Phys. C, 2012, 36, 1603–2014.
50. I. Angeli and K. P. Marinova, At. Data Nucl. Data Tables, 2013, 99, 69–95.
51. A. Bouvier, J. D. Vervoort and P. J. Patchett, Earth Planet. Sci. Lett., 2008, 273, 48–57.
52. Z. Chu, F. Chen, Y. Yang and J. Guo, J. Anal. At. Spectrom., 2009, 24, 1534.
53. M. Kaack and D. Fick, Surf. Sci., 1995, 342, 111–118.
54. J. L. Birck, Geostand. Geoanal. Res., 2001, 25, 253–259.
55. A. S. G. Roth, E. E. Scherer, C. Maden, K. Mezger and B. Bourdon, Chem. Geol., 2014, 386, 238–248.
56. T. Henshall, D. L. Cook, M. Garçon and M. Schönbächler, Chem. Geol., 2018, 482, 113–120.
57. A. Trinquier, J.-L. Birck and C. J. Allègre, J. Anal. At. Spectrom., 2008, 23, 1565.
58. R. Fukai, T. Yokoyama and S. Kagami, Int. J. Mass Spectrom., 2017, 414, 1–7.
59. Y. Di, E. Krestianinov, S. Zink and Y. Amelin, Chem. Geol., 2021, 582, 120411.
60. Y. Di, Z. Li and Y. Amelin, J. Anal. At. Spectrom., 2021, 36, 1489–1502.
61. R. W. Carlson, in Treatise on Geochemistry, 2014, pp. 337–354.
62. T.-H. Luu, R. C. Hin, C. D. Coath and T. Elliott, Earth Planet. Sci. Lett., 2019, 522, 166–175.
63. D. Upadhyay, E. E. Scherer and K. Mezger, J. Anal. At. Spectrom., 2008, 23, 561.
64. R. Andreasen and M. Sharma, Int. J. Mass Spectrom., 2009, 285, 49–57.
65. G. A. Brennecka, L. E. Borg and M. Wadhwa, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17241–17246.
66. A. Stracke, H. Palme, M. Gellissen, C. Münker, T. Kleine, K. Birbaum, D. Günther, B. Bourdon and J. Zipfel, Geochim. Cosmochim. Acta, 2012, 85, 114–141.
67. T. Tanaka, N. Nakamura and A. Masuda, Geochem. J., 1976, 10, 111–114.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1: comparison of the Sm isotope composition of the methods tested in this study. The Sm isotope compositions of the Sm ICP ETH standard are normalised to the fixed ¹⁵²Sm/¹⁴⁸Sm ratio of 2.37689. Fig. S2: comparison of the Sm isotope composition of the methods tested in this study. The Sm isotope compositions of the Sm ICP ETH standard are normalised to the fixed ¹⁴⁷Sm/¹⁵²Sm ratio of 0.56081. Supplementary tables S1–S7 are provided in a spreadsheet. Tables S1 and S2 contain Sm isotope compositions normalised to the ¹⁴⁷Sm/¹⁵²Sm ratio measured with the static and multistatic methods, respectively. Tables S3, S4, S5 and S6 contain Sm isotope compositions normalised to the ¹⁵²Sm/¹⁴⁸Sm ratio measured withthe static, multistatic, dynamic 2 lines and dynamic 3 lines methods, respectively. Table S7 contains Nd isotopecompositions normalised to the ¹⁴⁶Nd/¹⁴⁴Nd ratio. See DOI: https://doi.org/10.1039/d4ja00301b

---