Open Access Article
Open Access ArticleK3Mo2O5.6F3.4 and K3V2O3.3F5.7 – exploring transition metal cation valence and anion distribution in oxyfluorides†
Fabian
Zimmerhofer
a,
Eric
Wolf
a,
Baris
Öcal
b,
Selina
Olthof
b,
Maximilian Kai
Reimann
c,
Rainer
Pöttgen
 c and
Hubert
Huppertz
c and
Hubert
Huppertz
 *a
*a
aDepartment of General, Inorganic and Theoretical Chemistry, Innrain 80-82, A-6020 Innsbruck, Austria. E-mail: Hubert.Huppertz@uibk.ac.at; Web: https://www.uibk.ac.at/en/aatc/ag-huppertz/
bUniversity of Cologne, Institute of Physical Chemistry, Greinstraße 4-6, 50939 Köln, Germany
cUniversität Münster, Institut für Anorganische und Analytische Chemie, Corrensstraße 30, 48149 Münster, Germany
First published on 2nd February 2024
Abstract
Oxyfluorides come in many different structures and are highly adaptable in composition, not least because of their mixed-anionic nature. Slight changes, unless specifically looked for, can easily go unnoticed. In this paper, we present two oxyfluorides, K3Mo2O5.6F3.4 and K3V2O3.3F5.7, synthesized under high-pressure/high-temperature conditions, and demonstrate the importance of careful analysis of composition, oxidation state and O/F anion distribution for an accurate description of oxyfluorides. Their crystal structures were determined by single-crystal X-ray diffraction and the transition metal cation valences analyzed by X-ray photoelectron spectroscopy (XPS). The O/F anion ratio was calculated using the principle of charge neutrality and the local distribution within the crystallographic framework was studied using bond valence (BV) and charge distribution (CHARDI) calculations. Madelung Part of Lattice Energy (MAPLE) calculations and magnetic measurements provide insight into phase stability and corroborate the mixed-valent nature of the compounds.
Introduction
In contrast to their parent compounds, oxides and fluorides, oxyfluorides are a comparatively young and scarcely investigated substance class. Very rare in nature, often unstable and difficult to synthesize, they have been flying under the radar of popular research for a long time. It was only recently that oxyfluorides have started to attract more scientific interest due to their potential use in nonlinear optical materials,1 batteries,2,3 transparent glass ceramics,4 solar cells5,6 and deep-red emitting Mn4+-activated phosphor materials,7 to name but a few.What ultimately determines the properties of a new compound and its usefulness in the above applications is its crystal structure. Oxyfluorides are known for their structural diversity, due in no small part to their mixed-anionic nature.8,9 Oxygen and fluorine as anions are similar enough to share sites within the same crystallographic framework, yet different enough to have a substantial impact on the local atomic environments and, as a consequence, the optical and electronic properties of the compound in question. An excellent way of probing the boundaries of what is structurally possible are high-pressure/high-temperature experiments, as they allow us to subject samples to extreme conditions and force them to adopt structures that they would not otherwise adopt.
A handful of oxyfluorides of the general formula A3M2X9 (A = alkali metal, M = transition metal and X = O, F) have already been reported in the literature. Most of them crystallize in the structure type Cs3Cr2Cl9,10 likely limited in terms of structural variety by the size of the caesium cation: Cs3V2O2F7,11 Cs3V2O4F5,12 Cs3Mo2O6F3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 as well as the exchange variant Cs3V1.5Mo0.5O3F6.12 As for potassium variants, three representatives containing only pentavalent transition metal cations have been reported before: K3V2O4F5,14–16 K3Mo2O4F5
13 as well as the exchange variant Cs3V1.5Mo0.5O3F6.12 As for potassium variants, three representatives containing only pentavalent transition metal cations have been reported before: K3V2O4F5,14–16 K3Mo2O4F5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 and K3Nb2O4F5.18 The structure of K3V2O4F5 has never been elucidated in detail, and two different datasets are available for K3Mo2O4F5: a powder diffraction file (PDF) entry from 1983 and a complete structure determination from 2012.19 K3Nb2O4F5 is the only other known A3M2X9 representative containing potassium and was first reported by our group early last year.18 While quite similar to K3V2O4F5 and K3Mo2O4F5 at first glance, the oxyfluorides reported in the present investigation were synthesized under high-pressure/high-temperature conditions and crystallize in a different structure type, namely Ba2RbFe2F9.20 Another common point of contention in oxyfluorides is the oxidation state of the transition metal cations. This paper is the first report on A3M2X9 type oxyfluorides that includes modern XPS techniques to quantitatively and reliably determine the oxidation states of the transition metal cations and, in turn, O/F ratios. Hereinafter, we explore the complex interplay between these two aspects and investigate their influence on local atomic environments through a detailed study of two new oxyfluorides K3Mo2O5.6F3.4 and K3V2O3.3F5.7.
17 and K3Nb2O4F5.18 The structure of K3V2O4F5 has never been elucidated in detail, and two different datasets are available for K3Mo2O4F5: a powder diffraction file (PDF) entry from 1983 and a complete structure determination from 2012.19 K3Nb2O4F5 is the only other known A3M2X9 representative containing potassium and was first reported by our group early last year.18 While quite similar to K3V2O4F5 and K3Mo2O4F5 at first glance, the oxyfluorides reported in the present investigation were synthesized under high-pressure/high-temperature conditions and crystallize in a different structure type, namely Ba2RbFe2F9.20 Another common point of contention in oxyfluorides is the oxidation state of the transition metal cations. This paper is the first report on A3M2X9 type oxyfluorides that includes modern XPS techniques to quantitatively and reliably determine the oxidation states of the transition metal cations and, in turn, O/F ratios. Hereinafter, we explore the complex interplay between these two aspects and investigate their influence on local atomic environments through a detailed study of two new oxyfluorides K3Mo2O5.6F3.4 and K3V2O3.3F5.7.
Results and discussion
K3Mo2O5.6F3.4 and K3V2O3.3F5.7 were synthesized under high-pressure/high-temperature conditions at 8.0 GPa and 900 °C using a mixture of either KF and MoO3 or KHF2 and V2O5. The V variant can also be synthesized utilizing certain blends of V2O5 and VO2. For a detailed description of the synthetic procedure, refer to the Experimental section. Transition metal cation oxidation states and their respective concentrations were determined by X-ray photoelectron spectroscopy (see section XPS measurements). The O/F ratio was subsequently calculated on the basis of charge neutrality, resulting in the final compositions K3Mo2O5.6F3.4 and K3V2O3.3F5.7.The crystal structures of K3V2O3.3F5.7 and K3Mo2O5.6F3.4
K3V2O3.3F5.7 crystallizes in the rhombohedral space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 166) with the cell parameters a = 5.7442(1), c = 21.0484(6) Å, V = 601.46(2) Å3 and Z = 3 at T = 300(2) K. Except for the position of the transition metal cations within their octahedral coordination sphere, K3Mo2O5.6F3.4 crystallizes isotypically to K3V2O3.3F5.7. In accordance with the size difference between Mo6+ and V4+/5+, its cell parameters are slightly larger with a = 5.7983(1), c = 21.1801(5) Å and V = 616.68(2) Å3. Details on the single-crystal data and structure refinement process are presented in Table 1. Atomic coordinates, Wyckoff positions as well as equivalent isotropic displacement parameters are included in Table 2 (V) and Table 4 (Mo). Anisotropic displacement parameters can be found in Table 3 (V) and Table 5 (Mo), a comparison of the basic crystal structure parameters and interatomic distances is shown in Table 6.
m (no. 166) with the cell parameters a = 5.7442(1), c = 21.0484(6) Å, V = 601.46(2) Å3 and Z = 3 at T = 300(2) K. Except for the position of the transition metal cations within their octahedral coordination sphere, K3Mo2O5.6F3.4 crystallizes isotypically to K3V2O3.3F5.7. In accordance with the size difference between Mo6+ and V4+/5+, its cell parameters are slightly larger with a = 5.7983(1), c = 21.1801(5) Å and V = 616.68(2) Å3. Details on the single-crystal data and structure refinement process are presented in Table 1. Atomic coordinates, Wyckoff positions as well as equivalent isotropic displacement parameters are included in Table 2 (V) and Table 4 (Mo). Anisotropic displacement parameters can be found in Table 3 (V) and Table 5 (Mo), a comparison of the basic crystal structure parameters and interatomic distances is shown in Table 6.
| Empirical formula | K3V2O3.3F5.7 | K3Mo2O5.6F3.4 |
| Molar mass/g mol−1 | 380.27 | 463.35 |
| Crystal system | Rhombohedral | Rhombohedral |
| Space group |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 166) m (no. 166) |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 166) m (no. 166) |
| Powder data | ||
| Powder diffractometer | STOE Stadi P | STOE Stadi P |
| Radiation; wavelength λ/pm | MoKα1; 70.93 | MoKα1; 70.93 |
| Temperature/K | 295(2) | 295(2) |
| a/Å | 5.7390(2) | 5.7830(1) |
| c/Å | 21.0414(6) | 21.1892(6) |
| V/Å3 | 600.17(3) | 613.69(3) |
| Single-crystal data | ||
| Single-crystal diffractometer | Bruker D8 Quest Kappa | Bruker D8 Quest Kappa |
| Radiation; wavelength λ/pm | MoKα; 71.073 | MoKα; 71.073 |
| a/Å | 5.7442(1) | 5.7983(1) |
| c/Å | 21.0484(6) | 21.1801(5) |
| V/Å3 | 601.46(2) | 616.68(2) |
| Formula units per cell Z | 3 | 3 |
| Calculated density/g cm−3 | 3.15 | 3.74 |
| Crystal size/mm3 | 0.05 × 0.04 × 0.02 | 0.02 × 0.02 × 0.02 |
| Temperature/K | 300(2) | 300(2) |
| Absorption coefficient/mm−1 | 4.0 | 4.6 |
| F(000)/e | 546.4 | 641.4 |
| 2θ range/deg | 5.8–75.0 | 5.8–65.0 |
| Range in hkl | −10 ≤ h ≤ 10 | −10 ≤ h ≤ 10 |
| −10 ≤ k ≤ 10 | −10 ≤ k ≤ 10 | |
| −39 ≤ l ≤ 39 | −39 ≤ l ≤ 39 | |
| Total no. of reflections | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 117 117 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 993 993 |
| Independent reflections | 439 | 314 |
| R int | 0.0338 | 0.0350 |
| Reflections with I ≥ 2σ(I) | 385 | 291 |
| Data; parameters | 439; 23 | 314; 28 |
| Absorption correction | Multiscan | Multiscan |
| Final R1; wR2 [I > 2σ(I)] | 0.0271; 0.0622 | 0.0416; 0.1535 |
| Final R1; wR2 (all data) | 0.0310; 0.0655 | 0.0435; 0.1589 |
| Goodness-of-fit on F2 | 1.014 | 1.019 |
| Largest diff. peak; hole/e Å−3 | 0.96; −0.97 | 1.25; −0.79 |
| Atom | Wyckoff position | x | y | z | U eq | s.o.f. |
|---|---|---|---|---|---|---|
| V1 | 6c | 0 | 0 | 0.39708(2) | 0.0235(2) | 0.975 |
| V2 | 6c | 0 | 0 | 0.4814(8) | 0.021(3) | 0.025 |
| K1 | 3a | 0 | 0 | 0 | 0.0218(2) | 1 |
| K2 | 6c | 0 | 0 | 0.20694(3) | 0.0274(2) | 1 |
| O1 | 18h | 0.4883(2) | −x | 0.23110(5) | 0.0221(2) | 0.55 |
| F1 | 18h | 0.4883(2) | −x | 0.23110(5) | 0.0221(2) | 0.45 |
| F2 | 9e | ½ | 0 | 0 | 0.0569(7) | 1 |
| Atom | U 11 | U 22 | U 33 | U 23 | U 13 | U 12 |
|---|---|---|---|---|---|---|
| V1 | 0.0260(2) | U 11 | 0.0185(2) | 0 | 0 | 0.01300(9) |
| V2 | 0.024(5) | U 11 | 0.015(5) | 0 | 0 | 0.012(2) |
| K1 | 0.0212(2) | U 11 | 0.0229(3) | 0 | 0 | 0.0106(2) |
| K2 | 0.0253(2) | U 11 | 0.0316(3) | 0 | 0 | 0.0126(2) |
| O1|F1 | 0.0245(4) | U 11 | 0.0211(4) | −0.0016(2) | 0.0016(2) | 0.0152(4) |
| F2 | 0.0514(8) | 0.104(2) | 0.0331(8) | 0.035(2) | 0.0175(5) | 0.052(2) |
| Atom | Wyckoff position | x | y | z | U eq | s.o.f. |
|---|---|---|---|---|---|---|
| Mo1 | 36i | 0.004(2) | 0.046(2) | 0.39116(4) | 0.021(2) | 0.16 |
| Mo2 | 3b | 0 | 0 | ½ | 0.036(2) | 0.08 |
| K1 | 3a | 0 | 0 | 0 | 0.0336(6) | 1 |
| K2 | 6c | 0 | 0 | 0.20564(9) | 0.0327(5) | 1 |
| O1 | 18h | 0.4889(2) | −x | 0.2306(2) | 0.0224(6) | 0.933 |
| F1 | 18h | 0.4889(2) | −x | 0.2306(2) | 0.0224(6) | 0.066 |
| F2 | 9e | ½ | 0 | 0 | 0.047(2) | 1 |
| Atom | U 11 | U 22 | U 33 | U 23 | U 13 | U 12 |
|---|---|---|---|---|---|---|
| Mo1 | 0.015(3) | 0.021(2) | 0.0262(6) | 0.0007(4) | 0.006(2) | 0.010(2) |
| Mo2 | 0.022(2) | U 11 | 0.063(7) | 0 | 0 | 0.011(2) |
| K1 | 0.0351(7) | U 11 | 0.031(2) | 0 | 0 | 0.0176(4) |
| K2 | 0.0312(6) | U 11 | 0.0359(9) | 0 | 0 | 0.0156(3) |
| O1|F1 | 0.0244(9) | U 11 | 0.025(2) | −0.0021(4) | 0.0021(4) | 0.0171(8) |
| F2 | 0.047(2) | 0.070(3) | 0.033(2) | 0.021(2) | 0.0104(9) | 0.035(2) |
| Parameters | K3V2O3.3F5.7 | K3Mo2O5.6F3.4 | K3Nb2O4F5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 18 |
|---|---|---|---|
| Eff. ionic radius (Mn+)/Å for CN = 6 | 0.68 (V5+), 0.72 (V4+) | 0.75 (Mo6+), 0.79 (Mo4+) | 0.78 (Nb5+) |
| a/Å | 5.7442(1) | 5.7983(1) | 5.799(2) |
| c/Å | 21.0484(6) | 21.1801(5) | 21.371(4) |
| V/Å3 | 601.46(2) | 616.68(2) | 622.4(4) |
| Atoms | A1 = O|F, A2 = F | A1 = O|F, A2 = F | A1 = O|F, A2 = O |
|---|---|---|---|
| M1 occupancy | 97.5% | 92.0% | 100% |
| M1–A1/Å | 1.741(2) 3× | 1.66(2) | 1.816(2) |
| 1.83(2) | 2.007(2) 2× | ||
| 2.034(5) | |||
| M1–A1 average/Å | 1.741 | 1.84 | 1.943 |
| M1–A2/Å | 2.1331(3) 3× | 1.895(4) | 1.9338(8) 2× |
| 2.106(5) | 2.125(2) | ||
| 2.253(9) | |||
| M1–A2 average/Å | 2.1331 | 2.085 | 1.998 |
| M2 occupancy | 2.5% | 8.0% | Not occupied |
| M2–A1/Å | 1.819(9) 3× | 2.068(2) 6× | |
| 2.33(2) 3× | |||
| M2–A1 average/Å | 2.07 | 2.068 | |
| K1–A1/Å | 2.789(2) 6× | 2.814(2) 6× | 2.823(2) 6× |
| K1–A2/Å | 2.8721(2) 6× | 2.8991(2) 6× | 2.900(2) 6× |
| K2–A1/Å | 2.830(2) 3× | 2.818(3) 3× | 2.743(2) 3× |
| 2.9191(2) 6× | 2.9492(5) 6× | 2.966(2) 6× | |
| K2–A1 average/Å | 2.889 | 2.905 | 2.892 |
| K2–A2/Å | 3.1348(5) 3× | 3.181(2) 3× | 3.2813(8) 3× |
The crystal structure of the title compounds can be described with cubic close packings of atoms. The anionic network atoms form distorted cubic close packed arrangements together with potassium atoms, while the transition metal cations occupy a total of 1/6th of the octahedral voids. As there is an additional shift after every three layers, the cubic close packing is not continuous. A detailed description of the packing of atoms can be found in our previous publication for K3Nb2O4F5, which also crystallizes in the Ba2RbFe2F9 structure type.18
Fundamentally, the crystal structures consist of corner sharing [VA6]n− or [MoA6]n− octahedra (M1) forming wavelike layers in the ab plane (Fig. 1). A second set of slightly elongated octahedra (M2, signified by lighter colors in Fig. 1) acts as bridges between those layers along c. The occupancy of the larger octahedral voids is quite minor at 2.5% for V and 8% for Mo, as they are generally too large to accommodate V4+/5+ (rV4+ = 0.72 Å, rV5+ = 0.68 Å) or Mo6+ (rMo6+ = 0.73 Å) cations. The greater degree of occupancy in the Mo variant can be attributed to the incorporation of Mo4+, which possesses the perfect size to occupy these octahedral voids (rMo4+ = 0.79 Å). The amount of Mo4+ present within K3Mo2O5.6F3.4 was determined by XPS and correlates directly with the occupancy of the M2 octahedral voids in between the main layers (see section XPS measurements). The main M1 octahedral voids are under-occupied in both compounds (to a large extent in K3Mo2O5.6F3.4, but only slightly in K3V2O3.3F5.7), so the sum of the occupancies over both crystallographic M positions was constrained to 1. The anion distribution within the title compounds was determined using BV and CHARDI calculations in conjunction with crystallographic data (see section BV, CHARDI and MAPLE calculations). Both compounds likely contain one mixed position occupied by both O and F and one discrete position occupied solely by F. Interestingly, the situation is reversed in K3Nb2O4F5 with only oxygen present at the discrete site. While this disparity might seem unintuitive at first glance, it is a direct result of the transition metal cation's position within the octahedron. The degree and direction of deflection from the “ideal” central position plays a crucial role in determining which crystallographic sites are suitable for an anion of a given charge and size.
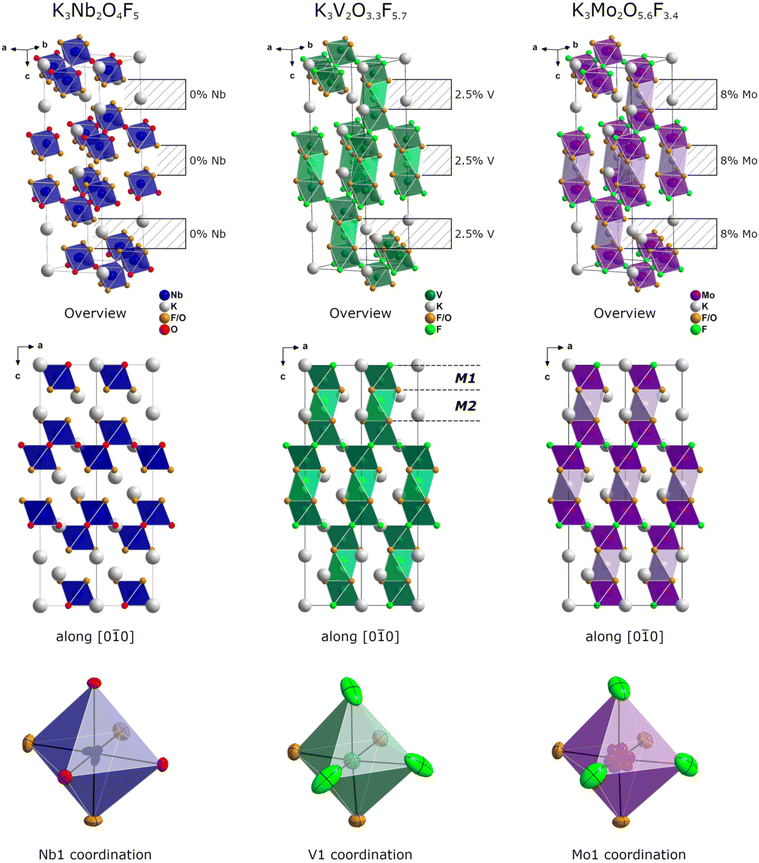 | ||
| Fig. 1 Comparison of the crystal structures of the previously reported oxyfluoride K3Nb2O4F5,18 and its two siblings K3V2O3.3F5.7 and K3Mo2O5.6F3.4. An octahedral void, which remains empty in K3Nb2O4F5 and Ba2RbFe2F9,20 the compound that gives the structure type its name, is occupied to varying degrees in the title compounds. The exact positions of the transition metal cations also vary from compound to compound depending on the occupancy of the anion site. All possible positions are depicted, but of course only one can be occupied per octahedron. | ||
The potassium atoms are coordinated either in a near-perfect cuboctahedral or a distorted anticuboctahedral manner (Fig. 2). The bond lengths are quite similar when comparing the two variants, scaling ever so slightly with the size of the transition metal cation. In K3Nb2O4F5, the position of the K2 atoms is somewhat shifted, moving closer to the mixed positions and further away from the oxygen positions. In general, one would expect the opposite to be the case due to the more covalent nature of M–O bonds compared to M–F bonds. This specific discrepancy is most likely a result of the, on average, shorter M1–A2 (M = Nb, V, Mo and A2 = O, F) bond lengths in K3Nb2O4F5 compared to its V- and Mo-based counterparts (Table 6).
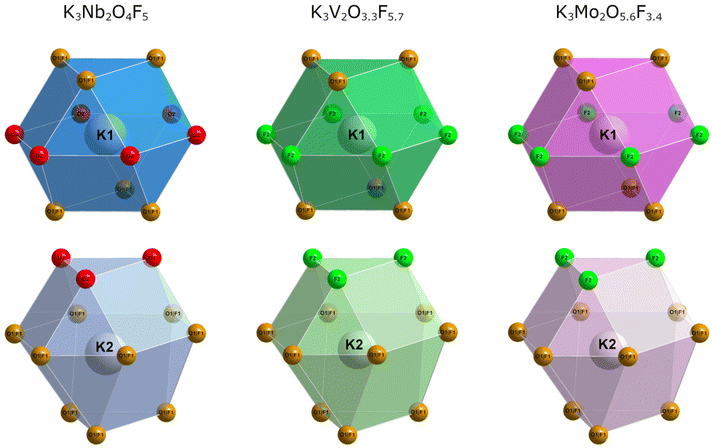 | ||
| Fig. 2 Cuboctahedral coordination sphere of K1 and anticuboctahedral coordination sphere of K2 in K3Nb2O4F5 (left), K3V2O3.3F5.7 (middle) and K3Mo2O5.6F3.4 (right). | ||
Powder X-ray diffraction
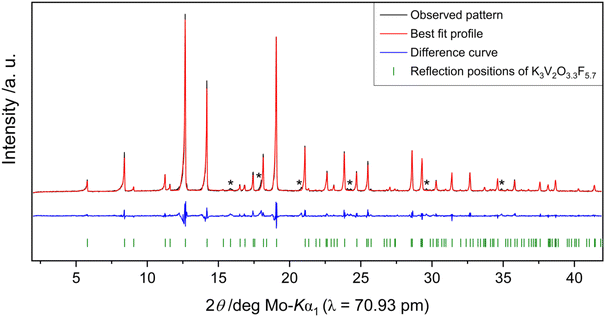
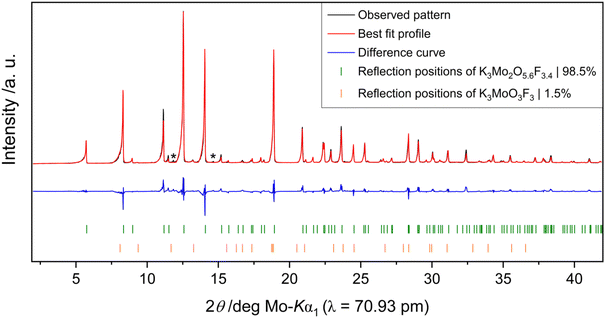
Rietveld refinements on powder diffraction measurements of product mixtures 1 (vanadium) and 2 (molybdenum) reveal that both K3V2O3.3F5.7 and K3Mo2O5.6F3.4 can be synthesized in high purity. In addition to the bulk target phase, product mixture 1 contains small quantities of an unknown by-product (Fig. 3). Product mixture 2 is composed of approximately 98.5(1) wt% K3Mo2O5.6F3.4 and 1.5(1) wt% K3MoO3F3 as well as trace amounts of a third unidentified phase (Fig. 4).BV, CHARDI and MAPLE calculations
Theoretical oxidation states of atoms within inorganic compounds can be calculated using mathematical concepts such as BV (bond valence)21–24 and CHARDI (charge distribution).25–27 These calculations allow for an evaluation of specific crystallographic positions based on their local environment and may offer valuable information in cases where certain distinctions are difficult or impossible to make using only crystallographic data. For the title compounds, these calculations first hinted at the presence of V4+ in K3V2O3.3F5.7 and allowed for a clear assignment of fluorine and oxygen to its two anion positions. Both methods are based on Pauling's well-known concept of bond length/bond strength combined with Hoppe's theory of effective coordination numbers.28–30 While BV relies on the use of empirically determined parameters for its calculations,31–33 CHARDI adopts a Madelung-type (point-charge) description of ionic crystal structures using only real observed distances, eliminating the need for pre-determined parameters altogether.34Bond valence sums (BVSs) for both compounds were calculated for all possible bonding scenarios and subsequently weighted according to their probability of occurrence. Mixed as well as incomplete occupancies were treated by multiplying the bond valence contribution with the occupancy for all affected bonds. CHARDI values were calculated using the program CHARDI2015 developed by Nespolo and Guillot.35 At only 2.5%, occupancy of the V2 site was too low to allow for an accurate prediction of its oxidation state, so it had to be removed for the calculation of CHARDI values.
The calculation results deliver a clear picture regarding the anion distribution in both K3V2O3.3F5.7 and K3Mo2O5.6F3.4. Large differences in metal–anion bond lengths typically make identification of the nature of the anion straightforward. In K3V2O3.3F5.7, V1 is deflected along a special axis towards the mixed positions, simplifying the process of distinction even more so (Table 7). In K3Mo2O5.6F3.4, the deflection of the Mo atom is more nuanced, resulting in a total of six possible positions within a single octahedron. Although this makes the assignment of anions to specific positions somewhat more difficult and leaves more room for interpretation, the differences in bond lengths to A1 and A2 are still large enough on average to allow a reasonable distinction (Table 8). Anisotropic displacement parameters also support the assignment (see Fig. 1, Tables 3 and 5).
| V1 | V2 | K1 | K2 | O1|F1 | F2 | |
|---|---|---|---|---|---|---|
| ∑V | +4.34 | +3.19 | +1.42 | +1.13 | −1.54 | −0.91 |
| ∑Q | +4.65 | — | +1.00 | +1.00 | −1.55 | −1.00 |
| Average | +4.50 | — | +1.21 | +1.07 | −1.55 | −0.96 |
| Theoretical value | +4.65 | +4.00 | +1.00 | +1.00 | −1.55 | −1.00 |
| Mo1 | Mo2 | K1 | K2 | O1|F1 | F2 | |
|---|---|---|---|---|---|---|
| ∑V | +5.39 | +3.82 | +1.44 | +1.22 | −1.86 | −1.28 |
| ∑Q | +5.94 | +3.96 | +0.99 | +0.99 | −1.96 | −1.02 |
| Average | +5.67 | +3.89 | +1.22 | +1.11 | −1.91 | −1.15 |
| Theoretical value | +6.00 | +4.00 | +1.00 | +1.00 | −1.94 | −1.00 |
Regarding cation charges, an average calculated charge of +4.50 for V1 was the first indication that +5 might not be the sole oxidation state of V as we had originally assumed (due to the use of V2O5 as a starting material). This finding prompted further investigations by magnetic measurements, which indicated a distribution of approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for V4+
1 for V4+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V5+ (see section magnetic measurements on K3V2O3.3F5.7) as well as a quantitative determination of the distribution by XPS (see section XPS measurements), suggesting an average charge of +4.65 for the V atoms. While CHARDI makes good predictions across the board, the BV method seems to have some difficulty accurately predicting the charges for positions Mo1 and K1 (both variants) in particular, underestimating the former and overestimating the latter.
V5+ (see section magnetic measurements on K3V2O3.3F5.7) as well as a quantitative determination of the distribution by XPS (see section XPS measurements), suggesting an average charge of +4.65 for the V atoms. While CHARDI makes good predictions across the board, the BV method seems to have some difficulty accurately predicting the charges for positions Mo1 and K1 (both variants) in particular, underestimating the former and overestimating the latter.
In accordance with the increase in octahedron size, the charges for V2 and Mo2 are calculated to be significantly lower at +3.19 and +3.89, respectively, outlining the inadequacy of the larger M2 octahedral void as a host for V4+/5+ and Mo6+. While the residual electron density at that position is quite minor in K3V2O3.3F5.7 at ≈2.3 e Å−3 (equating to ≈2.5% V), it is substantial in K3Mo2O5.6F3.4 at ≈9.8 e Å−3 (equating to ≈8% Mo). In contrast, K3Nb2O4F5, which shares all the main structural features with the two oxyfluorides presented here, but exhibits a different anion distribution and deflection of the transition metal cation, shows essentially no residual electron density at that position.18 The main M1 octahedral void in K3V2O3.3F5.7 can host both V5+ (rV5+ = 0.68 Å) and V4+ (rV4+ = 0.72 Å), making it so only very few atoms find their way into the larger, less adequate M2 octahedral void in between the main layers. For K3Mo2O5.6F3.4, the size difference between the two available transition metal cations is more pronounced (rMo6+ = 0.73 Å, rMo4+ = 0.79 Å), rendering one octahedral void much more suitable for a cation of a given charge than the other.
The Madelung Part of Lattice Energy (MAPLE) of a new compound can be used to validate the proposed structure model by comparing the calculated value to the sum of MAPLE values of the simple (most often binary) components.36–38 For fluorido- and oxidometalates, a difference between those two values of less than 1% indicates a plausible structure model.39 The values of the target compounds as well as all theoretical components were calculated using the program MAPLE V4 developed by Hübenthal.40 Due to a limitation of the program, the heavily under-occupied M2 octahedral sites could not be considered in the calculations. Instead, occupancy of the main M1 sites was increased to 1 to compensate for the missing transition metal cations and achieve charge neutrality. Because both V4+ as well as V5+ are located at the same crystallographic position in K3V2O3.3F5.7, the exact composition could be used for the calculation. The sum of all theoretical components could, however, only be calculated to K3V2O3F6, as the complexity of the real composition could not be matched using simple binary and ternary components. Oxygen and fluorine are similar enough to still yield a difference in the MAPLE values of only 0.81%, indicating a plausible structure model (Table 9).
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), VO2F (R
m), VO2F (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) and KVOF3 (C2/m) according to the equation: 2KF + VO2F + KVOF3 → K3V2O3F6. Due to the complex sum formula of the target phase, the O/F ratio does not match exactly
c) and KVOF3 (C2/m) according to the equation: 2KF + VO2F + KVOF3 → K3V2O3F6. Due to the complex sum formula of the target phase, the O/F ratio does not match exactly
In the case of K3Mo2O5.6F3.4, consideration of the “real” sum formula would have necessitated a reduction of the main Mo atoms’ charge from +6 to +5.8. Since we suspect the vast majority of Mo4+ to be situated at the M2 octahedral site, this reduced charge model does not represent reality, as a difference in the MAPLE values of 6.22% further emphasizes. To compensate for that, a second calculation was carried out using the sum formula K3Mo2O6F3, essentially ignoring the existence of the approximately 8% Mo4+ present within the compound. This special treatment leads to a difference in the MAPLE values of 0.44%, indicating a sensible structure solution in the absence of Mo4+ (Table 10). The small amount of Mo6+ reduced to Mo4+ during synthesis can easily be hosted by the much larger M2 octahedral void, as evidenced by BV and CHARDI calculations.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and MoO3 (Pbnm) according to the equation: 3KF + 2MoO3 → K3Mo2O6F3
m) and MoO3 (Pbnm) according to the equation: 3KF + 2MoO3 → K3Mo2O6F3
The two sets of calculations for the title compounds further reinforce some of our experimental observations. The V variant is only stable when vanadium is present in both oxidation states +5 and +4 simultaneously. Any attempts at synthesis of the target phase using only V4+ lead to the formation of K2VOF4 instead. Blends of V2O5 and VO2 can, however, be used to synthesize samples of equal purity, as long as the V4+ concentration does not exceed 35%. Beyond that critical point, K2VOF4 is formed as a side phase proportional to the amount of excess V4+. This suggests either that the V4+ content is variable within a certain window of approx. 35–58% due to percentage-based in situ reduction of V5+, or more likely that the reduction is conditional and ceases at approx. 35% to facilitate the formation of the new phase. V2O5 has been reported to go through a sequence of transformations from its original state via VO2 to V2O3 upon heating to 600 °C in a vacuum.41 While obviously influenced by the extreme synthesis conditions in our case, we suspect that this process is likely cut short by the formation of the title phase, limiting the thermal decomposition of V2O5.
For the Mo-based compound, we measured several single crystals and found varying amounts of Mo located at the larger M2 octahedral site ranging from 5–8%. With MAPLE calculations predicting a perfectly stable structure for K3Mo2O6F3 without the presence of any Mo4+ or occupancy of the M2 site, we do not believe the reduction of Mo6+ to play a major role in the formation of the new compound. Instead, we suspect that a small but varying amount of MoO3 naturally decomposes to MoO2 and O2 at high temperatures,42 leading to the incorporation of Mo4+ into the M2 octahedral void, which happens to be perfectly sized to host a cation of this nature.
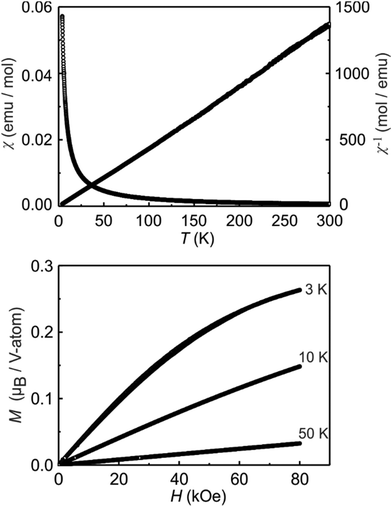
Magnetic measurements on K3V2O3.3F5.7
The K3V2O3.3F5.7 sample behaves like a Curie–Weiss paramagnet above 50 K (Fig. 5, top). Fitting of the 10 kOe measurement according to a modified Curie–Weiss law reveals an experimental magnetic moment of 0.95(1)μB V atom−1. The Weiss constant is ΘP = 3.3(1) K and the temperature independent contribution χ0 = −0.003(1) × 10−5 emu mol−1. For the ionic formula splitting 3K+ 2 V4+ 2O2− 7F− with solely tetravalent vanadium (d1 system) one would expect an effective magnetic moment of 1.73μB per V4+ ion.47 The simultaneous presence of both fluorine and oxygen, distributed over the same crystallographic sites, does, however, provide a lot of leeway in terms of possible oxidation states for vanadium. Considering a composition of 3K+ V4+ V5+ 3O2− 6F− with half of the vanadium atoms in the pentavalent state, only half the moment is expected to occur. We can thus conclude, that the sample most likely contains a distribution of domains of compositions K3V4+2−xV5+xO2+xF7−x with x around 1. Mixed-valence vanadate compounds have previously been reported to possess magnetic moments corresponding to non-integer numbers of electrons.48–50The recorded magnetization isotherms are shown at the bottom of Fig. 5. For the 10 and 50 K isotherms, we observe linear increases as expected for paramagnetic materials. The 3 K magnetization isotherm shows a continuous, field-induced increase of the magnetization with the highest magnetization of only 0.26(1)μB V atom−1 at 3 K and 80 kOe. Thus, much higher field strengths are necessary for full parallel spin alignment. The low value of the magnetization is also an indication of the low proportion of V4+ in the studied sample.
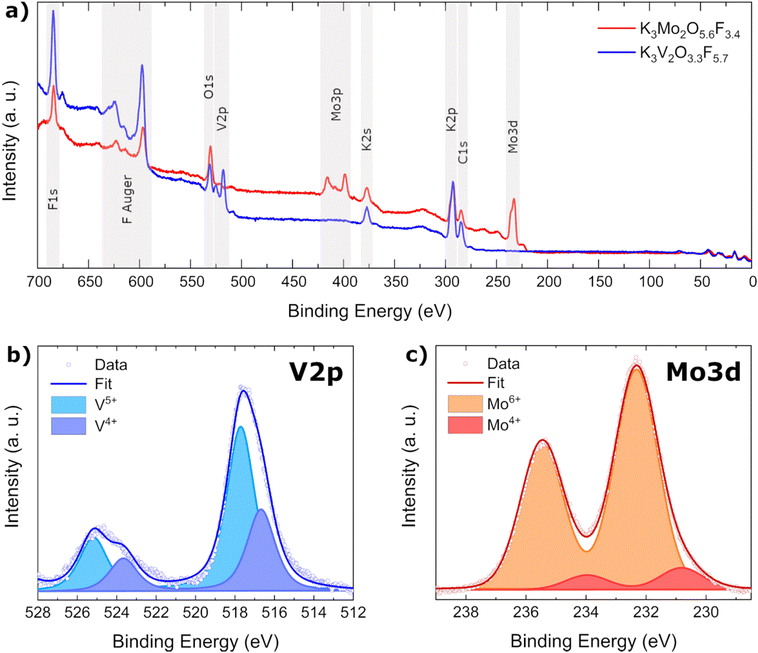
XPS measurements
As BV calculations as well as magnetic measurements indicated the simultaneous presence of multiple oxidation states in K3V2O3.3F5.7, XPS measurements were carried out on both title compounds to be able to experimentally determine the oxidation states as well as their relative concentration. Initial survey spectra of K3V2O3.3F5.7 and K3Mo2O5.6F3.4 confirmed the presence of all expected elements along with adventitious carbon (Fig. 6a).In order to distinguish between individual oxidation states of Mo and V atoms, their respective 3d (Mo) and 2p (V) core level peaks were measured and the data fitted with Voigt profiles to calculate the atomic ratios from the integrated areas (Fig. 6b and c). For details on the fitting procedure, refer to the Experimental section. As indicated by our previous investigations, vanadium is present in two different oxidation states, namely V5+ and V4+ in a ratio of approximately 1.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Molybdenum also exhibits two different oxidation states: Mo6+ and Mo4+. The highly charged Mo6+ cation is heavily favored, with a ratio of 10
1. Molybdenum also exhibits two different oxidation states: Mo6+ and Mo4+. The highly charged Mo6+ cation is heavily favored, with a ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The amount of Mo4+ determined by XPS (approx. 9%) is directly proportional to the occupancy of the larger M2 octahedral void in K3Mo2O5.6F3.4 (approx. 8%).
1. The amount of Mo4+ determined by XPS (approx. 9%) is directly proportional to the occupancy of the larger M2 octahedral void in K3Mo2O5.6F3.4 (approx. 8%).
Having determined concentrations and charges of the cations, it is possible to calculate the amount of oxygen and fluorine present in each compound using the principle of charge neutrality: K3Mo1.86+Mo0.24+O5.6F3.4 and K3V1.35+V0.74+O3.3F5.7.
Conclusion
Oxyfluorides exhibit an incredible degree of compositional adaptability due to their mixed-anionic nature. Even seemingly straightforward synthetic routes can lead to unexpectedly complex products. When both oxygen and fluorine are present as anions, it may no longer be easy to derive cation oxidation states. Similarly, it can be difficult to predict exactly how certain starting materials will behave under a given set of reaction conditions, especially extreme ones. Partial oxidation or reduction of suitable cations during synthesis can alter local atomic environments and influence the distribution of O/F anions in the final product. In some cases, such as with K3V2O3.3F5.7, mixed valence is crucial for phase stability. In other cases, such as with K3Mo2O5.6F3.4, cations of different oxidation states can be accommodated in different ways and to varying degrees. The exact influence of cation oxidation state and O/F anion distribution on compound formation and stability is complex and not easily predicted. To accurately describe oxyfluorides and understand their nuances, it is important to consider how the two interact with and influence each other.Experimental section
Synthetic procedure
Both K3V2O3.3F5.7 and K3Mo2O5.6F3.4 were synthesized under high-pressure/high-temperature conditions employing a special multianvil setup for a uniaxial 1000 t frame press (Max Voggenreiter GmbH, Mainleus, Germany). The starting mixtures were prepared in a glovebox (MBraun Inertgas-System GmbH, Garching, Germany) under argon atmosphere by simple weighing and thorough homogenization in an agate mortar. 50.00 mg (0.6402 mmol) KHF2 (Alfa Aesar, 99+% metals basis) and 33.27 mg (0.1829 mmol) V2O5 (Merck, extra pure) in a stoichiometric ratio of 3.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 served as the starting materials for the synthesis of K3V2O3.3F5.7. Alternatively, a mixture of V2O5 and VO2 (Alfa Aesar, 99% metals basis) may be used, provided that the concentration of tetravalent vanadium does not exceed 35%. In the case of K3Mo2O5.6F3.4, a stoichiometric (3
1 served as the starting materials for the synthesis of K3V2O3.3F5.7. Alternatively, a mixture of V2O5 and VO2 (Alfa Aesar, 99% metals basis) may be used, provided that the concentration of tetravalent vanadium does not exceed 35%. In the case of K3Mo2O5.6F3.4, a stoichiometric (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) mixture of 30.00 mg (0.5164 mmol) KF (Fluka, >99.0%) and 49.55 mg (0.3443 mmol) MoO3 (Merck, >99.5%) proved to yield the purest product. The resulting powders were subsequently transferred into a platinum capsule (99.95%, Ögussa, Vienna, Austria), which was, in turn, placed inside a boron nitride crucible (Henze Boron Nitride Products AG, Lauben, Germany). In the next step, the crucible was inserted into a ZrO2 sleeve, whose inside is coated with graphite. The graphite acts as a resistive heating element with the ZrO2 being responsible for keeping the heat inside the reaction chamber. Molybdenum platelets on either side of the cylindrical construction enable conductivity from the graphite oven to the outside. The construction was then inserted into the pressure medium – an octahedron consisting of MgO doped with 5% Cr2O3. The octahedral assembly was further surrounded by eight tungsten carbide cubes (Hawedia, Marklkofen, Germany) with truncated corners and held together by six glass fiber reinforced plastic panels. The experimental setup was completed upon placement of the cube into a Walker-type module alongside six steel anvils to allow for a quasi-hydrostatic compression of the sample using a uniaxial (vertical) hydraulic press. More detailed descriptions of various multianvil assemblies can be retrieved from the literature.51–54
2) mixture of 30.00 mg (0.5164 mmol) KF (Fluka, >99.0%) and 49.55 mg (0.3443 mmol) MoO3 (Merck, >99.5%) proved to yield the purest product. The resulting powders were subsequently transferred into a platinum capsule (99.95%, Ögussa, Vienna, Austria), which was, in turn, placed inside a boron nitride crucible (Henze Boron Nitride Products AG, Lauben, Germany). In the next step, the crucible was inserted into a ZrO2 sleeve, whose inside is coated with graphite. The graphite acts as a resistive heating element with the ZrO2 being responsible for keeping the heat inside the reaction chamber. Molybdenum platelets on either side of the cylindrical construction enable conductivity from the graphite oven to the outside. The construction was then inserted into the pressure medium – an octahedron consisting of MgO doped with 5% Cr2O3. The octahedral assembly was further surrounded by eight tungsten carbide cubes (Hawedia, Marklkofen, Germany) with truncated corners and held together by six glass fiber reinforced plastic panels. The experimental setup was completed upon placement of the cube into a Walker-type module alongside six steel anvils to allow for a quasi-hydrostatic compression of the sample using a uniaxial (vertical) hydraulic press. More detailed descriptions of various multianvil assemblies can be retrieved from the literature.51–54
The reaction conditions for the syntheses of the title compounds are identical. First, the starting materials were compressed to 8.0 GPa in 215 min followed by an increase in temperature to 900 °C. The temperature was held constant for an additional 30 min before it was reduced to 350 °C in 60 min. At that point the reaction was quenched, reaching room temperature in a matter of minutes. To complete the experiment, the pressure acting on the assembly was gradually reduced to atmospheric pressure over a period of 900 min. The octahedral assembly was removed from the experimental setup and transferred into a glovebox. The platinum capsule holding the sample was then recovered, separated from other assembly materials and opened to reveal a dark green (K3V2O3.3F5.7) or deep red (K3Mo2O5.6F3.4) polycrystalline sample (Fig. 7).
Single-crystal X-ray diffraction
A glovebox-stored sample of each title compound was transferred onto a microscope slide and covered with perfluoropolyalkylether to prevent oxidation and/or hydrolysis during the selection of suitable single crystals under a polarization microscope outside of the glovebox. Each crystal was subsequently mounted onto a Bruker D8 Quest single-crystal diffractometer (Bruker, Billerica, USA) equipped with a Photon III C14 detector system. Measurements were carried out at an ambient temperature of 300(2) K using MoKα radiation (λ = 71.073 pm) generated by an Incoatec Microfocus X-ray tube (Incoatec, Geesthacht, Germany) in conjunction with a multilayer monochromator.Diffraction data was collected with the program APEX V2021.4-0.55 Data reduction, integration and unit cell refinement were carried out in SAINT-V 8.40B.56 A multi-scan absorption correction was applied to the intensity data using the software SADABS-2016/2.57 Initially, space groups R3 (no. 146) and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (no. 148) were considered for structure solution. An ADDSYM58,59 check in PLATON60 indicated the presence of higher symmetry, suggesting space group R
(no. 148) were considered for structure solution. An ADDSYM58,59 check in PLATON60 indicated the presence of higher symmetry, suggesting space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 166) instead. Using the structure refinement and analysis program OLEX2,61 the structure was solved in the proposed space group R
m (no. 166) instead. Using the structure refinement and analysis program OLEX2,61 the structure was solved in the proposed space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 166) using SHELXTL-2018/2
m (no. 166) using SHELXTL-2018/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62 and refined with the OLEX2.REFINE63 refinement package employing Gauss–Newton minimization. The datasets used for refinement were restricted to angles below 75° for K3V2O3.3F5.7 and 65° for K3Mo2O5.6F3.4 to account for limited diffraction intensity at larger angles due to comparatively small crystal size (especially in the case of K3Mo2O5.6F3.4). Atomic coordinates were standardized using the PLATON subroutine STRUCTURE TIDY64 to allow for effortless comparison between the two title compounds and other related structures. All visual representations of the crystal structures were created with DIAMOND 4.6.8.65
62 and refined with the OLEX2.REFINE63 refinement package employing Gauss–Newton minimization. The datasets used for refinement were restricted to angles below 75° for K3V2O3.3F5.7 and 65° for K3Mo2O5.6F3.4 to account for limited diffraction intensity at larger angles due to comparatively small crystal size (especially in the case of K3Mo2O5.6F3.4). Atomic coordinates were standardized using the PLATON subroutine STRUCTURE TIDY64 to allow for effortless comparison between the two title compounds and other related structures. All visual representations of the crystal structures were created with DIAMOND 4.6.8.65
Powder X-ray diffraction
Powder diffractograms of high-purity K3V2O3.3F5.7 and K3Mo2O5.6F3.4 were recorded on a STOE STADI P diffractometer (STOE & CIE GmbH, Darmstadt, Germany) operating in Debye-Scherrer transmission geometry. To prevent reactions with oxygen and/or air moisture, the samples were finely ground and sealed inside soda-lime glass capillaries prior to removal from the glovebox. Ge(111)-monochromatized MoKα1 radiation (λ = 70.93 pm) diffracted by the sample was recorded on a DECTRIS MYTHEN2 DCS4 detector system. The measurement was carried out at an ambient temperature of 295(2) K across a 2θ range of 2.0–42.0° with a step size of 0.015°. Rietveld refinements of the recorded diffractograms were performed using the software package DIFFRACplus-Topas 4.2 (Bruker AXS, Karlsruhe, Germany).66XPS measurements
For XPS measurements, finely ground powders of both title compounds were applied as a thin layer to a conductive adhesive tape using a fine brush. The tape was then stuck onto the sample holders and transferred to an ultra-high vacuum system. Measurements were performed using a non-monochromatic MgKα source (VG) with an excitation energy of 1253.6 eV. The emitted photoelectrons were detected by a hemispherical analyzer (Specs, Phoibos 100) at pass energies of 90 eV for the survey scans and 20 eV for the detailed scans. Due to the inherently low conductivity of powdered samples, a charge induced shift of all binding energies by 5.5 eV (K3V2O3.3F5.7) and 5.07 eV (K3Mo2O5.6F3.4) was observed. This was corrected during data processing by shifting the 1s core level peak of adventitious carbon to 284.7 eV and adjusting the rest of the dataset accordingly. To determine the oxidation state and relative concentration of the individual V and Mo atoms, the core level peaks of Mo3d and V2p were fitted using the software XPSPEAK 4.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 using Voigt profiles and assuming a Shirley background. To distinguish between oxidation states of vanadium, O1s core level peaks were used as a reference point.68 The obtained fit has a full width at half maximum (FWHM) of 1.88 eV with a Lorentzian/Gaussian ratio of 23%. The spin–orbit splitting of the peaks is 7.58 and 7.30 eV for V4+ and V5+, respectively. The Mo3d core level doublet was fitted with a FWHM of 1.7 eV, a Lorentzian/Gaussian ratio of 11% and a spin–orbit splitting of 3.15 eV.
67 using Voigt profiles and assuming a Shirley background. To distinguish between oxidation states of vanadium, O1s core level peaks were used as a reference point.68 The obtained fit has a full width at half maximum (FWHM) of 1.88 eV with a Lorentzian/Gaussian ratio of 23%. The spin–orbit splitting of the peaks is 7.58 and 7.30 eV for V4+ and V5+, respectively. The Mo3d core level doublet was fitted with a FWHM of 1.7 eV, a Lorentzian/Gaussian ratio of 11% and a spin–orbit splitting of 3.15 eV.
Magnetic measurements
The sample with the initial composition K3V2O3.3F5.7 was pure on the level of X-ray powder diffraction and ground to a fine powder. It was filled into a polypropylene capsule for investigation, using the Vibrating Sample Magnetometer (VSM) option of a Physical Property Measurement System (PPMS) by Quantum Design. The capsule was inserted into a brass sample holder, which was attached to the sample holder rod of the VSM. The sample was then investigated in a temperature range from 2.5 to 300 K through measurements of M(T,H) with applied fields up to 80 kOe. Fitting and plotting of the data was performed with OriginPro 2016G69 and graphical editing with the program CorelDRAW2017.70Author contributions
Conceptualization, single-crystal structure solution, powder X-ray diffraction, BV, CHARDI, MAPLE calculations and original draft by FZ. Synthetic work by EW and FZ. BÖ and SO carried out the XPS analysis and contributed to the drafting of the corresponding section. MKR and RP carried out the magnetic measurements and provided a complete first draft of this section. HH supervised and guided this project, in addition to providing the necessary laboratory equipment and tools. The manuscript was reviewed and edited by all authors.Data availability
Deposition Numbers 2320478 and 2320483† contain the supplementary crystallographic data for K3V2O3.3F5.7 and K3Mo2O5.6F3.4, respectively.Conflicts of interest
The authors declare no competing interests related to this article.Acknowledgements
The authors would like to thank Assoc.-Prof. Dr Gunter Heymann and Asst.-Prof. Dr Klaus Wurst for the collection of the single-crystal X-ray data and their input regarding the structure refinement process.References
- S. Bai, D. Wang, H. Liu and Y. Wang, Recent advances of oxyfluorides for nonlinear optical applications, Inorg. Chem. Front., 2021, 8, 1637–1654 RSC
.
- R. J. Clément, Z. Lun and G. Ceder, Cation-disordered rocksalt transition metal oxides and oxyfluorides for high energy lithium-ion cathodes, Energy Environ. Sci., 2020, 13, 345–373 RSC
.
- D. Deng, Transition metal oxyfluorides for next-generation rechargeable batteries, ChemNanoMat, 2017, 3, 146–159 CrossRef CAS
.
- P. P. Fedorov, A. A. Luginina and A. I. Popov, Transparent oxyfluoride glass ceramics, J. Fluorine Chem., 2015, 172, 22–50 CrossRef CAS
.
- H.-C. Wang, J. Schmidt, S. Botti and M. A. L. Marques, A high-throughput study of oxynitride, oxyfluoride and nitrofluoride perovskites, J. Mater. Chem. A, 2021, 9, 8501–8513 RSC
.
- W. Fu, C. Zhang, Z. Li, J. Xia and Y. Ping, Luminescence of Cr3+/Yb 3+ co-doped oxyfluoride silicate glasses for crystalline silicon solar cell down-conversion devices, Ceram. Int., 2020, 46, 15054–15060 CrossRef CAS
.
- S. Adachi, Review—Mn4+-activated red and deep red-emitting phosphors, ECS J. Solid State Sci. Technol., 2020, 9, 16001 CrossRef CAS
.
- M. Leblanc, V. Maisonneuve and A. Tressaud, Crystal chemistry and selected physical properties of inorganic fluorides and oxide-fluorides, Chem. Rev., 2015, 115, 1191–1254 CrossRef CAS PubMed
.
- Y. Tsujimoto, K. Yamaura and E. Takayama-Muromachi, Oxyfluoride chemistry of layered perovskite compounds, Appl. Sci., 2012, 2, 206–219 CrossRef CAS
.
- G. J. Wessel and D. J. W. Ijdo, The crystal structure of Cs3Cr2Cl9, Acta Crystallogr., 1957, 10, 466–468 CrossRef CAS
.
- K. Waltersson, The crystal structure of Cs3V2O2F7, Cryst. Struct. Commun., 1978, 7, 507–511 CAS
.
- R. Mattes and H. Förster, Structural and spectroscopic studies of Cs3V2O4F5 and of isostructural phases in the Cs3Mo2O6F3-Cs3V2O2F7 and Cs3Mo2O6F3-Cs3V2O4F5 systems, J. Less-Common Met., 1982, 87, 237–247 CrossRef CAS
.
- R. Mattes, K. Mennemann, N. Jäckel, H. Rieskamp and H.-J. Brockmeyer, Structure and properties of the fluorine-rich oxofluoromolybdates Cs3[Mo2O6F3], (NH4)3[Mo2O2F9] and (NH4)2[MoOF5], J. Less-Common Met., 1980, 76, 199–212 CrossRef CAS
.
- R. L. Davidovich, V. I. Sergienko and L. M. Murzakhanova, Alkali metal oxofluorovanadates, Zh. Neorg. Khim., 1968, 12, 3186–3191 Search PubMed
.
- R. L. Davidovich, V. I. Sergienko and L. M. Murzakhanova, Complex vanadium fluorides in metal fluoride-vanadium pentoxide-hydrofluoric acid-water systems, Izv. Sib. Otd. Akad. Nauk SSSR, Ser. Khim. Nauk, 1968, 1, 58–61 Search PubMed
.
- Y. Y. Kharitonov and Y. A. Buslaev, Infrared absorption spectra of oxofluorides of some metals, Izv. Akad. Nauk SSSR, Ser. Khim., 1964, 5, 808–814 Search PubMed
.
- M. C. Chakravorti and A. K. Bera, Binuclear oxofluorocomplexes of molybdenum(V), Transition Met. Chem. (Dordrecht, Neth.), 1983, 2, 83–86 CrossRef
.
- F. Zimmerhofer, M. Seibald, C. Stoll, D. Baumann, K. Wurst and H. Huppertz, Crystal structure, characterization, and luminescence properties of Mn4+–doped K3Nb2O4F5, Eur. J. Inorg. Chem., 2023, e202200714 CrossRef CAS
.
- D. W. Aldous and P. Lightfoot, New structural units in molybdenum oxyfluoride chemistry, J. Fluorine Chem., 2012, 144, 108–113 CrossRef CAS
.
- E. Herdtweck, S. Kummer and D. Babel, Cation-deficient perovskites Ba2A(I)M2(II)F9 (M(II) = Fe, Co, Ni, Zn) and their hexagonal layer structure, Eur. J. Solid State Inorg. Chem., 1991, 28, 959–969 CAS
.
- I. D. Brown, Bond valences—a simple structural model for inorganic chemistry, Chem. Soc. Rev., 1978, 7, 359–376 RSC
.
- I. D. Brown, Bond valence as an aid to understanding the stereochemistry of O and F complexes of Sn(II), Sb(III), Te(IV), I(V) and Xe(VI), J. Solid State Chem., 1974, 11, 214–233 CrossRef CAS
.
- I. D. Brown and R. D. Shannon, Empirical bond-strength–bond-length curves for oxides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1973, 29, 266–282 CrossRef CAS
.
- G. Donnay and R. Allmann, How to recognize O2−, OH− and H2O in crystal structures determined by x-rays, Am. Mineral., 1970, 55(5–6), 1003–1015 CAS
.
- J.-G. Eon and M. Nespolo, Charge distribution as a tool to investigate structural details. III. Extension to description in terms of anion-centred polyhedra, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 34–47 CrossRef CAS PubMed
.
- M. Nespolo, G. Ferraris and H. Ohashi, Charge distribution as a tool to investigate structural details: meaning and application to pyroxenes, Acta Crystallogr., Sect. B: Struct. Sci., 1999, 55, 902–916 CrossRef PubMed
.
- R. Hoppe, S. Voigt, H. Glaum, J. Kissel, H. P. Müller and K. Bernet, A new route to charge distributions in ionic solids, J. Less-Common Met., 1989, 156, 105–122 CrossRef CAS
.
- R. Hoppe, Effective coordination numbers (ECoN) and mean fictive ionic radii (MEFIR), Z. Kristallogr., 1979, 150, 23–52 CrossRef CAS
.
- L. Pauling, The principles determining the structure of complex ionic crystals, J. Am. Chem. Soc., 1929, 51, 1010–1026 CrossRef CAS
.
-
L. Pauling, The Nature of the Chemical Bond: An Introduction to Modern Structural Chemistry, Cornell University Press, Ithaca, New York, 3rd edn, 1960 Search PubMed
.
- O. C. Gagné and F. C. Hawthorne, Comprehensive derivation of bond-valence parameters for ion pairs involving oxygen, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 562–578 CrossRef
.
- N. E. Brese and M. O'Keeffe, Bond-valence parameters for solids, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 192–197 CrossRef
.
- I. D. Brown and D. Altermatt, Bond-valence parameters obtained from a systematic analysis of the Inorganic Crystal Structure Database, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244–247 CrossRef
.
- M. Nespolo, Charge distribution as a tool to investigate structural details. IV. A new route to heteroligand polyhedra, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 51–66 CrossRef CAS
.
- M. Nespolo and B. Guillot, CHARDI2015: charge distribution analysis of non-molecular structures, J. Appl. Crystallogr., 2016, 49, 317–321 CrossRef CAS
.
- R. Hoppe, Madelung Constants, Angew. Chem., Int. Ed. Engl., 1966, 5, 95–106 CrossRef CAS
.
- R. Hoppe, The coordination number– an “inorganic chameleon”, Angew. Chem., Int. Ed. Engl., 1970, 9, 25–34 CrossRef CAS
.
- R. Hoppe, On the Madelung Part of Lattice Energy, Z. Naturforsch., A: Phys. Sci., 1995, 50, 555–567 CrossRef CAS
.
- R. Hoppe, Recent progress in oxo- and fluorometalate chemistry, Angew. Chem., Int. Ed. Engl., 1981, 20, 63–87 CrossRef
.
-
R. Hübenthal, MAPLE v4, University of Gießen, Germany, 1993 Search PubMed
.
- D. S. Su and R. Schlögl, Thermal decomposition of divanadium pentoxide V2O5: towards a nanocrystalline V2O3 phase, Catal. Lett., 2002, 83, 115–119 CrossRef CAS
.
- Y. Qing, K. Yang, Y. Chen, J. Zhu, Y. Li, C. Chen, Q. Li, B. Sun and J. He, Thermal stability, optical and electrical properties of substoichiometric molybdenum oxide, Materials, 2023, 16, 2841 CrossRef CAS PubMed
.
- E. Broch, I. Oftedal and A. Pabst, Neubestimmung der Gitterkonstanten von KF, CsCl und BaF2, Z. Phys. Chem., Abt. B, 1929, 3, 209–214 CAS
.
- J. C. Pérez-Flores, R. Villamor, D. Ávila-Brande, J. M. Gallardo Amores, E. Morán, A. Kuhn and F. García-Alvarado, VO2F: a new transition metal oxyfluoride with high specific capacity for Li ion
batteries, J. Mater. Chem. A, 2015, 3, 20508–20515 RSC
.
- F. H. Aidoudi, C. Black, K. S. A. Arachchige, A. M. Z. Slawin, R. E. Morris and P. Lightfoot, Structural diversity in hybrid vanadium(IV) oxyfluorides based on a common building block, Dalton Trans., 2014, 43, 568–575 RSC
.
- H. Sitepu, Texture and structural refinement using neutron diffraction data from molybdite (MoO3) and calcite (CaCO3) powders and a Ni-rich Ni50.7Ti49.30 alloy, Powder Diffr., 2009, 24, 315–326 CrossRef CAS
.
-
H. Lueken, Magnetochemie, Teubner, Stuttgart, 1999 Search PubMed
.
- P. Sandineni, H. Yaghoobnejad Asl, W. Zhang, P. S. Halasyamani, K. Ghosh and A. Choudhury, Interplay between oxo and fluoro in vanadium oxyfluorides for centrosymmetric and non-centrosymmetric structure formation, Molecules, 2021, 26, 603 CrossRef CAS PubMed
.
- M. D. Donakowski, R. Gautier, H. Lu, T. T. Tran, J. R. Cantwell, P. S. Halasyamani and K. R. Poeppelmeier, Syntheses of two vanadium oxide-fluoride materials that differ in phase matchability, Inorg. Chem., 2015, 54, 765–772 CrossRef CAS PubMed
.
- S. Das, A. Niazi, Y. Mudryk, V. K. Pecharsky and D. C. Johnston, Magnetic, thermal, and transport properties of the mixed-valent vanadium oxides LuV4O8 and YV4O8, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 104432 CrossRef
.
-
H. Huppertz, G. Heymann, U. Schwarz and M. R. Schwarz, in Handbook of Solid State Chemistry, Wiley-VCH, Weinheim, Germany, 2017, pp. 23–48 Search PubMed
.
- H. Huppertz, Multianvil high-pressure/high-temperature synthesis in solid state chemistry, Z. Kristallogr., 2004, 219, 330–338 CAS
.
- D. Walker, Lubrication, gasketing, and precision in multianvil experiments, Am. Mineral., 1991, 76, 1092–1100 Search PubMed
.
- D. Walker, M. A. Carpenter and C. M. Hitch, Some simplifications to multianvil devices for high pressure experiments, Am. Mineral., 1990, 75, 1020–1028 Search PubMed
.
-
Apex4, Bruker AXS Inc., Madison, Wisconsin, USA, 2021 Search PubMed
.
-
SAINT-V (version 8.40B), Bruker AXS Inc., Madison, Wisconsin, USA, 2021 Search PubMed
.
-
G. M. Sheldrick, SADABS (version 2016/2), University of Göttingen, Germany, 2016 Search PubMed
.
- Y. Le Page, MISSYM 1.1 – a flexible new release, J. Appl. Crystallogr., 1988, 21, 983–984 CrossRef
.
- Y. Le Page, Computer derivation of the symmetry elements implied in a structure description, J. Appl. Crystallogr., 1987, 20, 264–269 CrossRef CAS
.
- A. L. Spek, Structure validation in chemical crystallography, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155 CrossRef CAS PubMed
.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS
.
- G. M. Sheldrick, SHELXT - integrated space-group and crystal-structure determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed
.
- L. J. Bourhis, O. V. Dolomanov, R. J. Gildea, J. A. K. Howard and H. Puschmann, The anatomy of a comprehensive constrained, restrained refinement program for the modern computing environment - Olex2 dissected, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 59–75 CrossRef CAS PubMed
.
- L. M. Gelato and E. Parthé, STRUCTURE TIDY – a computer program to standardize crystal structure data, J. Appl. Crystallogr., 1987, 20, 139–143 CrossRef
.
-
H. Putz and K. Brandenburg GbR, Diamond - Crystal and Molecular Structure Visualization, Crystal Impact, Kreuzherrenstr. 120, 53227 Bonn, Germany Search PubMed
.
- A. A. Coelho, TOPAS and TOPAS-Academic: an optimization program integrating computer algebra and crystallographic objects written in C++, J. Appl. Crystallogr., 2018, 51, 210–218 CrossRef CAS
.
-
R. W. M. Kwok, XPSPEAK 4.1
.
- Y. X. Guo, C. W. Zou, Y. F. Liu, Y. Q. Xu, X. L. Wang, J. Y. Yu, Z. Y. Yang, F. Zhang and R. Zhou, Facile preparation of vanadium oxide thin films on sapphire(0001) by sol–gel method, J. Sol-Gel Sci. Technol., 2014, 70, 40–46 CrossRef CAS
.
-
OriginPro 2016G, OriginLab Corp., 2016 Search PubMed
.
-
CorelDRAW Graphics Suite 2017, Corel Corporation, 2017 Search PubMed
.
Footnote |
| † CCDC 2320478 and 2320483. For crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt00064a |
| This journal is © The Royal Society of Chemistry 2024 |