Solvent modulation of the morphology of homochiral gadolinium coordination polymers and its impact on circularly polarized luminescence

Abstract

Studying the effect of morphology on the circularly polarized luminescence (CPL) of chiral molecular materials is important for the development of CPL-active materials for applications. Herein, we report that the morphology of Gd(NO₃)₃/R-,S-AnempH₂ [AnempH₂ = (1-anthrylethylamino)methylphosphonic acid] assemblies can be controlled by solvent modulation to form spiral bundles Gd(R-,S-AnempH)₃·2H₂O (R-,S-1), crystals Gd(R-,S-AnempH)₃·2H₂O (R-,S-2) and spindle-shaped particles Gd(R-,S-AnempH)₃·3H₂O·0.5DMF (R-,S-3) with similar chain structures. Interestingly, R-,S-1 are CPL active and show the highest value of dissymmetric factor among the three pairs of enantiomers (|g_lum| = 2.1 × 10^–3), which is 2.8 times larger than that of R-,S-2, while R-,S-3 are CPL inactive with |g_lum| ≈ 0. This work provides a new route to control the morphology of chiral coordination polymers and improve their CPL performance.

---

Introduction

Controlling the morphology of molecular materials may have a profound influence on their physical or chemical properties.^1,2 Typical examples are metal–organic frameworks (MOFs) that show morphology-dependent catalytic performance due to their different expressing crystal faces.³ Studying the effect of morphology on the optical properties of chiral molecular materials, such as the circularly polarized luminescence (CPL), is another interesting issue that is important for the development of CPL-active materials for applications.⁴ CPL is a unique chiroptical property of chiral luminescent systems, and its application requires CPL emission with high quantum yield and a large dissymmetry factor, which is defined as g_lum = 2(I_L − I_R)/(I_L + I_R), where I_L and I_R refer to the intensities of left- and right-handed circularly polarized emissions. Over the past decade, significant progress has been witnessed in exploring new chiral materials with high CPL performance including organic molecules,⁵ polymers,⁶ and discrete metal–organic complexes.^7,8 However, challenges still remain in improving the luminescence dissymmetry factor. It was found that assembling chiral organic or metal–organic molecules into helical aggregates can facilitate exciton coupling mechanisms that are known to strengthen chiroptical responses.⁹ Nevertheless, the formation of helical aggregates of small molecules is often difficult to control and the mechanism is inconclusive because of the presence of complicated non-covalent intermolecular interactions. In addition, investigations of the morphology effect on the CPL properties of chiral coordination polymers are still scarce.¹⁰

Chiral coordination polymers (CPs) composed of metal ions or cluster nodes and organic linkers commonly feature good crystallinity in the solid state.¹¹ The assembly of chiral CPs in both crystalline and helical forms can provide an opportunity for understanding the chirality transcription and amplification from molecular to macroscopic scales.¹² In particular, the morphology of chiral one-dimensional (1D) CPs is the result of its intrachain structure and interchain interactions,¹³ as well as the external conditions such as solvents, additives, pH and temperature.¹⁴ Our previous work has demonstrated that the morphology of Ln³⁺/R-,S-pempH₂ (Ln = Tb, Gd; pempH₂ = (1-phenylethylamino)methylphosphonic acids) assemblies can be controlled by pH and anions, forming block-like or rod-like crystals or superhelices.^11a,15 We envision that the introduction of large aromatic components hanging from the chains will not only enhance interchain interactions, but will also change the stacking pattern of the chains, thereby altering the morphology of the assemblies under certain experimental conditions. Furthermore, the large aromatic components may bring interesting optical properties.

In this work, we employed R-,S-(1-anthrylethylamino)methylphosphonic acids (R-,S-AnempH₂) as ligands, and performed a systematic investigation on the self-assembly of Gd(NO₃)₃/R-,S-AnempH₂ in different solvents (Scheme 1). R-,S-AnempH₂ was chosen due to their similarity in coordination modes to R-pempH₂ and, in addition, the anthryl group with extended conjugated aromatic rings has the potential to provide abundant π–π and C–H⋯π interactions, steric hindrance, and rich photoluminescence properties.¹⁶ We found that the morphology of the assemblies varied with solvents. In the presence of a small amount of water, spiral bundles of Gd(R-,S-AnempH)₃·2H₂O (R-,S-1) were obtained at 90 vol% NPA/DMF, while crystals of Gd(R-,S-AnempH)₃·2H₂O (R-,S-2), and spindle-like shaped particles of Gd(R-,S-AnempH)₃·3H₂O·0.5DMF (R-,S-3) were obtained at 70 vol% and 0 vol% NPA/DMF (NPA = n-propanol), respectively. Interestingly, R-,S-1 are CPL active and show the highest value of dissymmetric factor (|g_lum| = 2.1 × 10^–3) among the three pairs of enantiomers compared to R-,S-2 (|g_lum| = 7.5 × 10^–4) and R-,S-3 (|g_lum| ≈ 0). The results indicate that the helical alignment of chiral CPs at the macroscopic level is conducive to the enhancement of |g_lum|. This work provides a new route to control the morphology of chiral CPs and improve their CPL performance.

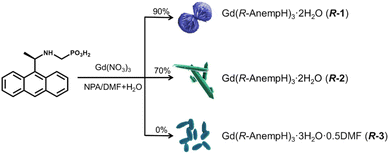Scheme 1 Synthetic routes of R-1, R-2 and R-3 in a mixture of NPA/DMF (total volume of 5 mL) and 0.5 mL of water. The percentages (0%, 70%, and 90%) refer to the proportion of NPA in NPA/DMF.

Experimental

Materials and methods

All starting materials were of analytical reagent grade and used as received without further purification. Elemental analyses for C, N and H were determined with a PerkinElmer 240C elemental analyzer. Fourier infrared spectra were measured as KBr pellets on a Bruker Tensor 27 spectrometer in the range of 400–4000 cm⁻¹. Thermogravimetric analysis (TGA) was performed on a Mettler-Toledo TGA/DSC instrument in the range of 300–600 °C under a nitrogen flow at a heating rate of 5 °C min⁻¹. Powder X-ray diffraction (PXRD) data were recorded on a Bruker D8 ADVANCE X-ray powder diffractometer (Cu-Kα) at room temperature. The morphologies of products were characterized on a scanning electron microscope (SHIMADZU, SSX-550 and S-4800) at an acceleration voltage of 5 kV. TEM measurements were performed on JEM-2100. UV-vis spectra were measured on a Shimadzu UV-3600 spectrometer. Electronic circular dichroism (ECD) spectra were recorded on a JASCO J-810 spectrophotometer at room temperature. The linear dichroism (LD) effect was checked by recording the ECD and LD spectra on a JASCO J-1700 CD spectrometer at room temperature. Circularly polarized luminescence measurements were conducted on a JASCO CPL-300 spectrometer in the solid state at room temperature (scanning rate: 20 nm min⁻¹, scanning mode: continuous, excitation slit width: 3000 μm, monitoring slit width: 3000 μm, response time: 16 seconds, and single accumulation). In order to eliminate the effect of linear dichroism on CPL, we carried out the CPL measurements by manually operated rotation of a sample by 180° and then averaged the data. The steady fluorescence spectra were obtained using a PerkinElmer LS55 spectrophotometer. Time-resolved fluorescence measurements and quantum yields were carried out on an Edinburgh FLS980. The ¹H NMR spectra were recorded on a BRUKER AVANCE III 400 MHz spectrometer at room temperature.

Synthesis of R-,S-AnempH₂

A mixture of R-1-(anthracene-9-yl)ethan-1-amine (2.21 g, 10 mmol) and (CH₂O)_n (0.33 g, 11 mmol) in 30 mL of toluene was stirred at 80 °C for 1 h. Then HPO(OEt)₂ (1.52 g, 11 mmol) was added and the reaction was kept at 80 °C for 6 h. After the removal of solvents, the product was purified by column chromatography and R-diethyl(1-(anthracene-9-yl)ethylamino)methyl-phosphonate (R-AnempEt₂) was obtained as a pale yellow oil (Scheme S1†). Yield: 6.48 g (87.3%). ¹H NMR (400 MHz, DMSO-d₆): δ = 9.34 (s, 1H), 8.53 (s, 2H), 8.08 (dd, J = 5.8, 4.0 Hz, 2H), 7.50 (dd, J = 6.5, 3.1 Hz, 4H), 5.51 (q, J = 6.7 Hz, 1H), 4.02–3.79 (m, 4H), 2.92 (dd, J = 14.4, 10.1 Hz, 1H), 2.56 (d, J = 14.7 Hz, 1H), 1.67 (d, J = 6.8 Hz, 3H), 1.13 (dt, J = 21.4, 7.0 Hz, 6H) (Fig. S1†).

The oil product (R-AnempEt₂) (6.48 g, 17.47 mmol) was mixed with 13.2 mL (100 mmol) of Me₃SiBr and 13.2 mL of CH₂Cl₂ and the mixture was stirred at room temperature for 24 h. After the removal of solvent, Me₃SiBr was quenched with 10 mL of methanol. Then 200 mL of deionized water was added and the mixture was stirred for 6 h. White powder of R-(1-anthrylethylamino)methylphosphonic acids (R-AnempH₂) was collected by suction filtration and washed with water. Yield: 5.30 g (96.4%). ¹H NMR (400 MHz, DMSO-d₆): δ = 8.95 (s, 1H), 8.69 (s, 1H), 8.52 (s, 1H), 8.14 (d, J = 9.5 Hz, 2H), 7.53 (d, J = 7.4 Hz, 4H), 5.94 (q, J = 6.6 Hz, 1H), 2.74 (t, J = 13.2 Hz, 1H), 2.42 (t, J = 13.3 Hz, 1H), 1.88 (d, J = 6.8 Hz, 3H) (Fig. S1†).

S-AnempH₂ was synthesized similarly except that S-1-(anthracene-9-yl)ethan-1-amine was used as the reaction precursor. ¹H NMR (400 MHz, DMSO-d₆): δ = 8.94 (s, 1H), 8.69 (s, 1H), 8.52 (s, 1H), 8.20–8.09 (m, 2H), 7.60–7.46 (m, 4H), 5.96 (dd, J = 13.4, 6.4 Hz, 1H), 2.75 (t, J = 13.1 Hz, 1H), 2.42 (t, J = 13.3 Hz, 1H), 1.88 (d, J = 6.8 Hz, 3H). The PXRD and IR spectra of the R- and S-isomers are identical (Fig. S2 and S3†).

Synthesis of spiral bundles R-,S-[Gd(AnempH)₃]·2H₂O (R-,S-1)

A mixture of R-AnpempH₂ (15.85 mg, 0.05 mmol), 0.5 mL of DMF and 4.5 mL of NPA (90 vol% NPA/DMF) was stirred for 10 min at room temperature. Then, 0.1667 mL of 0.1 M Gd(NO₃)₃ (0.01667 mmol) and additional water (total volume of water 0.5 mL) was added and stirred for 30 minutes. A glass bottle containing the reaction mixture was kept in a 15 mL Teflon-lined stainless steel autoclave and heated at 100 °C for 1 day. The ginger powder R-1 was collected by suction filtration and washed with water. Yield: 50.2% (9.4 mg), based on Gd(NO₃)₃. Elemental analysis (%) calculated for R-1: C, 53.87; H, 4.87; N, 3.70; found: C, 53.69; H, 4.99; N, 3.77. S-1 was obtained following a similar procedure except for using S-AnempH₂. Yield: 53% (10.0 mg), based on Gd(NO₃)₃. Elemental analysis (%) calculated for S-1: C, 53.87; H, 4.87; N, 3.70; found: C, 53.94; H, 4.91; N, 3.72.

Synthesis of crystals R-,S-[Gd(AnempH)₃]·2H₂O (R-,S-2)

R-2 and S-2 were obtained following a similar procedure to R-1 and S-1, respectively, except for using 1.5 mL of DMF and 3.5 mL of NPA (70 vol% NPA/DMF). Yield: 43% (8.1 mg), based on Gd(NO₃)₃. Elemental analysis (%) calculated for R-2: C, 53.87; H, 4.87; N, 3.70; found: C, 53.71; H, 5.11; N, 3.80. For S-2, yield: 48% (9.1 mg), based on Gd(NO₃)₃. Elemental analysis (%) calculated for S-2: C, 53.87; H, 4.87; N, 3.70; found: C, 53.95; H, 5.04; N, 3.77.

Synthesis of R-,S-[Gd(AnempH)₃]·3H₂O·0.5DMF (R-,S-3)

R-3 and S-3 were obtained following a similar procedure to R-1 and S-1, respectively, except for using 5.0 mL of DMF and 0.0 mL of NPA (0 vol% NPA/DMF). Yield: 35% (6.9 mg), based on Gd(NO₃)₃. Elemental analysis (%) calculated for R-3: C, 52.91; H, 5.08; N, 4.11; found: C, 53.63; H, 4.89; N, 4.47. For S-3, yield: 40% (7.9 mg), based on Gd(NO₃)₃. Elemental analysis (%) calculated for S-3: C, 52.91; H, 5.08; N, 4.11; found: C, 52.70; H, 5.18; N, 4.40. Found: C, 52.67; H, 4.96; N, 4.24.

Results and discussion

Synthesis and characterization

Gd(NO₃)₃ and R-AnempH₂ (molar ratio of 1 : 3) in a mixture of NPA/DMF (total volume of 5 mL with different proportions) and 0.5 mL of deionized water were reacted solvothermally at 100 °C for 24 h. Scanning electron microscope (SEM) images showed that the resulting solid products were nanoparticles in 100 vol% NPA/DMF, left-handed (M) spiral bundles in 90 vol% NPA/DMF, crystals with regular shapes in 80–40 vol% NPA/DMF, and spindle-shaped particles at 20–0 vol% NPA/DMF (Fig. S4†). Interestingly, the infrared (IR) spectra of products with different morphologies are almost the same except for the relative intensity of the peak at 1683 cm⁻¹ (Fig. S5†). The powder X-ray diffraction (PXRD) patterns are identical except for the 100 vol% NPA/DMF product (Fig. S6†). The intensity of the diffraction maxima of the latter is very low, suggesting that the product is amorphous. The results indicate that all products possess similar structures, but may differ slightly in the solvent molecules. Therefore, we chose the products obtained in 90 vol% NPA/DMF (spiral bundles, named R-1), 70 vol% NPA/DMF (crystals, named R-2), and 0 vol% NPA/DMF (spindle-shaped particles, named R-3) for further characterization, and their SEM images are shown in Fig. 1 and S7.† It is worth mentioning that the presence of a small amount of water is essential to the formation of spiral bundles of R-1. Without it, only spherical particles without chiral morphology were generated. Notably, spiral bundles can also be obtained in 90 vol% NPA/DMF plus 1.0–1.5 mL of H₂O, and their PXRD patterns are identical to that of R-1 (Fig. S8 and S9†).

Fig. 1 SEM images of the Gd(NO₃)₃/R-,S-AnempH₂ assemblies obtained in a mixture of NPA/DMF (total volume of 5 mL) and 0.5 mL of water. (a and b) 90 vol% NPA/DMF (R-1, S-1), (c) 70 vol% NPA/DMF (R-2), and (d) 0 vol% NPA/DMF (R-3).

The energy dispersive X-ray spectroscopy (EDS) analyses revealed that the atomic ratio of Gd : P is ca. 1 : 3 in R-1, R-2 and R-3 (Fig. S10–S12†). Combining the results of thermogravimetric (TG) (Fig. S13†) and elemental analyses (Table S1†), the molecular formulae are proposed to be Gd(R-AnempH)₃·2H₂O for R-1 and R-2, and Gd(R-AnempH)₃·3H₂O·0.5DMF for R-3. The existence of lattice DMF in R-3 is supported by the significantly enhanced intensity of the peak at 1683 cm⁻¹ (Fig. 2a), which is attributed to the stretching vibration of C=O from DMF.

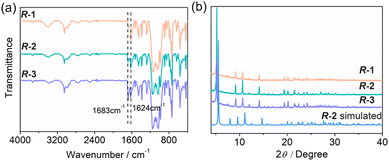Fig. 2 (a) IR spectra and (b) PXRD patterns of R-1, R-2, and R-3. The simulated pattern of R-2 is given for comparison.

When R-AnempH₂ was replaced by S-AnempH₂, we obtained S-1, S-2, and S-3 under similar solvothermal reaction conditions. The enantiomeric nature of the R- and S-isomers is confirmed by their identical IR spectra (Fig. S14†), PXRD patterns (Fig. S15†), and electronic circular dichroism (ECD) spectra with opposite Cotton effect signals in the solid state (see below). Notably, S-1 has a morphology of spiral bundles with right-handedness (P), which is opposite to R-1, manifesting that the macroscopic chirality is related to the intrinsic chirality of the building blocks (Fig. 1a and b). Similar reactions using ligands with different R-AnempH₂/S-AnempH₂ ratios have also been tested (Fig. S16†). When the enantiomeric excess (ee) value was higher than 60%, M-type helical bundles were found. Decreasing the ee to 20% resulted in a mixture of irregular M-type bundles and crystal clusters. As the ee value reached 0%, the product was a mixture of crystals and bundles without chiral morphology. As expected, further changing the ee to −20%, −60%, and −100% led to the formation of products with similar morphologies but opposite handedness to those at 20%, 60%, and 100% ee. All these products exhibited identical IR spectra and PXRD patterns (Fig. S17 and S18†). However, the ECD spectra displayed mirror profiles for the ±20%, ±60% and ±100% products, while the ee 0% product was ECD silent (Fig. S19†). Obviously, the chiral structures were in good compliance with “majority rule”.

To gain insight into the structural information for these materials, we tried to solve the crystal structure of R-2 by single crystal structural analysis but failed. Only Gd and a few P and O atoms can be located from the difference Fourier maps. A reasonable structure of R-2 was obtained through Material Studio simulation.¹⁷ As shown in Fig. 2b and S20, the simulated PXRD pattern matches well with the experimental pattern, except for a slight shift of the peaks to the right. The calculated cell parameters are: space group P3, a = 18.40 Å, c = 15.38 Å, and V = 4509.52 ų. The cell volume is smaller than that obtained by a Pawley fit of the experimental PXRD pattern of R-2 using TOPAS 5.0 ¹⁸ (4764.21 ų) (Fig. S21†), which is sensible because we did not consider the solvent molecules in the calculation, resulting in a shrunken unit cell volume.

Structural simulation revealed that R-2 crystallizes in trigonal system, chiral space group P3. The asymmetric unit contains 4/3 Gd³⁺ and four R-AnempH⁻. Each of the four crystallographically distinct Gd atoms sits in a special position with an occupation of 0.333. One of the four Gd atoms (Gd1) is nine-coordinated and the other three (Gd2, Gd3, and Gd4) are six-coordinated (Gd–O: 2.192–2.537 Å) (Tables S2 and S3†). The adjacent Gd atoms (Gd1–Gd2, Gd2–Gd3, and Gd1–Gd4) are triply bridged by three μ₃-O(P) atoms, forming a linear tetramer of {Gd₄O₉}. The equivalent tetramers are further bridged by three O–P–O units between Gd3 and Gd4 atoms, forming an infinite neutral chain running along the c-axis (Fig. 3a). Within the chain, there exist hydrogen bond interactions among the phosphonate and amino groups (Table S4†). The interchain interactions could be dominated by van der Waals contacts, but C–H⋯π interactions are also present (Fig. 3b and Table S5†). Based on the structural analysis, the correct formula of R-2 is Gd₄(R-AnempH)₁₂·8H₂O, where the number of lattice water molecules is determined by the elemental and thermal analyses. For the sake of comparison, the formula of R-2 can be simplified as Gd(R-AnempH)₃·2H₂O.

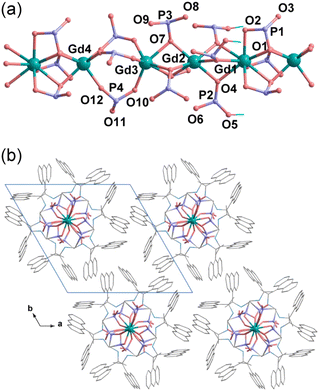Fig. 3 Simulated structure of R-2: (a) the chain structure and (b) the packing diagram. Solvent molecules were not considered in the calculation.

The PXRD patterns of R-1 and R-3 are also consistent with the simulated one of R-2 (Fig. 2), indicating that they are isomorphous phases with high crystallinity. To compare their cell parameters, we indexed the diffraction peaks using TOPAS 5.0.¹⁸ The derived parameters are: space group P3, a = 18.85 Å, c = 15.82 Å, and V = 4870.24 ų for R-1; space group P3, a = 18.86 Å, c = 15.29 Å, V = 4764.21 ų for R-2; space group P3, a = 18.87 Å, c = 15.80 Å, and V = 4872.6 ų for R-3 (Fig. S21†). Obviously, the cell volumes of R-1 spiral bundles and R-3 spindle-shaped particles are larger than those of R-2 crystals. Thus, we can conclude that R-1 and R-3 possess a chain structure similar to R-2, but the stacking of the chains is looser than that in R-2.

It is worth mentioning that the Gd(NO₃)₃/R-AnempH₂ assembly forms a chiral spiral bundle R-1 in 90 vol% NPA/DMF with the presence of a small amount of water, while the Gd(NO₃)₃/R-pempH₂ assembly we reported previously forms a superhelix Gd(R-pempH)₃·2H₂O (R-P).^14b Noting that the latter was obtained under hydrothermal conditions with pH = 3.6–4.2 at 120 °C, we performed similar hydrothermal reactions of Gd(NO₃)₃ and R-AnempH₂ but obtained flower-like nanoplates at pH = 4.0–6.0 (Fig. S22†). This fact suggests that the formation of R-1 spiral bundles rather than superhelices is determined to a large extent by its intrinsic chain structure and interchain interactions.

Since the structures of R-1 spiral bundles and R-P superhelices are closely related to their crystalline counterparts R-2 and Gd(R-pempH)₃·1.5H₂O, respectively, comparing the latter two crystal structures will help us understand why the morphologies of R-1 and R-P can be so different. As shown in Fig. 3, R-2 has several structural features distinct from Gd(R-pempH)₃·1.5H₂O: (1) The Gd atoms in the R-2 chain are bridged by three μ₃-O(P) to form a linear {Gd₄O₉} tetramer, which is then bridged by three O–P–O units to form a linear chain. In contrast, Gd atoms in Gd(R-pempH)₃·1.5H₂O are bridged by two μ₃-O(P) and one O–P–O units to form a uniformly distributed spiral chain. (2) The interchain interactions also differ. Although van der Waals interactions are dominant in both cases, C–H⋯π interactions are found in R-2 but not in Gd(R-pempH)₃·1.5H₂O (Scheme 2 and Fig. S23†). The interchain distance in R-2 (15.40 Å) is shorter than that in Gd(R-pempH)₃·1.5H₂O (15.76 Å). The structural differences can be related to the different ligands used in the two compounds. The anthryl group on the ligand R-AnempH₂ in R-2 has a larger steric hindrance and a more extended conjugated aromatic ring than the phenyl group on the ligand R-pempH₂ in Gd(R-pempH)₃·1.5H₂O, which causes stronger interchain interactions in R-2. We speculate that it is the linear chain and the relatively strong interchain interactions that promote the ordered stacking of chains, resulting in the formation of spiral bundles of R-1, rather than superhelices.

Scheme 2 The interchain interactions in R-2 (left) and Gd(R-pempH)₃·1.5H₂O (right).

Formation mechanism of the spiral bundles of R-1

Since the spiral bundle can be considered as an arrangement of needle-like crystals twisted clockwise or counter-clockwise, the question arises as to when the twisting occurs and what is the driving force for the twisting? To gain insight into the formation mechanism of R-1 spiral bundles, we monitored the solid products after the solvothermal reaction of Gd(NO₃)₃ and R-AnempH₂ in 90 vol% NPA/DMF (total volume of 5 mL) and 0.5 mL of H₂O at 100 °C for different periods of time (Fig. 4). Before 100 min, the solution of the reaction mixture was clear and the solid product could not be separated by centrifugation (16 500 r min⁻¹). At 100 min, a trace of precipitation was obtained by centrifugation (16 500 r min⁻¹), and the SEM result exhibited shuttle-shaped particles, the widths and lengths of which were ca. 3 μm and 9 μm, respectively (Fig. S24†). Notably, there is a slight clockwise twist in the centre of the particles. The twist became more significant and spiral bundles with left-handedness were clearly formed after 2 h of reaction. Further elongation of the reaction time led to the growth of spiral bundles in both length and thickness. The EDS analyses showed that the solid products obtained at 100 min, 110 min and 24 h possessed similar Gd : P atomic ratios of ca. 1 : 3 and the elements Gd, P were uniformly distributed throughout the region (Fig. S25†), indicating that the nodes and ends of the spiral bundle have similar compositions. The IR and PXRD patterns confirmed that the solid products obtained after reactions of 100 min to 24 h are the same as those for R-1 (Fig. S26 and S27†). The results demonstrate the formation of R-1 spiral bundles at 100 min of reaction and the subsequent growth of spiral bundles at extended reaction times. But what happened when the reaction time was less than 100 min?

Fig. 4 SEM images of the self-assembled products of Gd(NO₃)₃/R-AnempH₂ in 90 vol% NPA/DMF + H₂O at 100 °C for different periods of reaction time.

Since it was difficult to separate the solid products by centrifugation at less than 100 min of reaction, we examined the solution phase by ECD, SEM and TEM spectroscopy. The ECD spectra of the reaction solutions from 0 min to 90 min and even 2 h were almost identical, showing Cotton effects (−, +, −) at about 260, 268 and 350 nm, respectively (Fig. S28†). These spectra are similar to those of the ligand R-AnempH₂, but the signals have a slight red-shift that can be attributed to the coordination of the ligand with the Gd³⁺ ion. The SEM images showed that nanoparticles 10–80 nm in size formed at 30 min of reaction and reached over 100 nm with aggregation at 40–90 min of reaction (Fig. S29†). From the TEM images, we also observed the formation of 10–20 nm nanoparticles at 30 min of reaction and ca. 100 nm nanoparticles at 60 min. Interestingly, at 90 min of reaction, the nanoparticles not only grew further but also underwent aggregation to form short chains (Fig. S30†). The PXRD measurements revealed that the residues after solvent evaporation of the 60 min and 90 min reaction solutions were a mixture of R-1 and an unrecognized phase, while the 100 min product was a pure phase of R-1 (Fig. S31†). The disappearance of the unrecognized phase at 100 min of reaction indicates that R-1 is thermodynamically more stable than this unrecognized phase.

Based on the above results, we propose the formation mechanism of spiral bundles R-1 as below. First, Gd(NO₃)₃/R-AnempH₂ self-assembles into chiral nanoparticles. Then, the chiral nanoparticles grow and aggregate to form linear aggregates. Finally, the linear aggregates grow further in the longitudinal and transverse directions to form chiral bundle-like aggregates. Thus, the twisted growth of bundle aggregates may originate from the misalignment of chiral nanoparticles during the aggregation process. This misalignment may be influenced by the solvent. Indeed, the same reactions in 90 vol% CH₃OH (or EtOH)/DMF + H₂O resulted in spherical particles or crystalline clusters, whereas the reaction in 90 vol% NBA/DMF + H₂O (NBA = n-butanol) led to crystals (Fig. S32–S34†). Interestingly, spiral bundles of R-1 were also observed in 70–80 vol% EtOH/DMF + H₂O, but not in 20–100 vol% MeOH (or NBA)/DMF + H₂O solvents (Fig. S35–S37†). Obviously, solvent plays an important role in triggering this twisted stacking process. Apart from the solvent, a suitable Gd³⁺/R-AnempH₂ molar ratio (1 : 3), temperature (70–100 °C), and anion of gadolinium salt (NO₃⁻) are also essential for the formation of spiral bundles of R-1 (Fig. S38–S46†).

Optical properties

To examine the influence of morphology on the optical properties, we first investigated their UV-vis and ECD spectra in the solid state. The UV-vis absorption spectra were translated from the diffuse reflectance spectra using the Kubelka–Munk function: F(R) = (1 − R²)/2/R. As shown in Fig. 5a, R-1, R-2 and R-3 display similar UV-vis spectra with strong broad absorption bands appearing in the range of 200–490 nm, attributed to the π–π* transition of anthryl groups. Compared to the pure ligand which shows absorptions at 205–420 nm (Fig. S47†), the bands for R-1, R-2 and R-3 are broader and red-shifted due to the coordination of the ligand with the Gd³⁺ ions (Fig. S48†). The ECD spectra of the three phases are also similar. R-1 showed (−, +, −) patterns at 225, 290, and 393 nm, while R-2 and R-3 showed similar (−, +, −) patterns at 225, 283, and 390 nm, respectively (Fig. 5b and Fig. S49†). The linear dichroism (LD) effect in the solid state ECD spectra was less than 0.004 [dOD] (Fig. S50†), indicating that the observed ECD spectra are real. Notably, the relative intensities of the ECD signals at ca. 290 and 393 nm varied with the samples in the sequence R-1 > R-3 > R-2. The maximum values of g_abs are 3.38 × 10^–3 (R-1), 2.18 × 10⁻³ (R-2), and 2.35 × 10⁻³ (R-3) near 310 nm, respectively (Fig. S51 and Table S7†). Considering that R-1 and R-2 possess the same molecular composition and similar structures, the enhanced ECD signals in R-1 are related to its morphology, where the chirality is transferred and amplified from the molecular to the macroscopic level. The ECD spectra of the S-isomers show a mirror image relationship to the R-isomers, corroborating the enantiomeric nature of these compounds at the molecular level (Fig. S48–S51†).

Fig. 5 (a) UV-vis spectra; (b) ECD spectra; (c) emission spectra; (d) fluorescence decay curve and the fitting line (red line); (e) CPL spectra; and (f) g_lum spectra of R-, S-1 spiral bundles, R-, S-2 crystals, and R-, S-3 spindle-shaped particles.

We then recorded the steady photoluminescence (PL) spectra of the three compounds. All exhibited a broad emission band peaking at 484 nm (Fig. 5c and S52†). The average lifetimes (τ_av) are 3.28, 5.06, 5.47 ns for R-1, R-2 and R-3, respectively, indicating that the emission originates from the ligand (Fig. 5d, S53 and Tables S8, S9†). The quantum yields (QY) are 0.88%, 1.30%, and 2.41% for R-1, R-2 and R-3, respectively (Table S9†). The low quantum yields are ascribed to the aggregation-caused quenching (ACQ) effect.¹⁹ The S-isomers showed similar PL spectra, lifetimes and QY values to their R-counterparts as expected (Fig. S52, S54 and Table S9†). Impressively, the circularly polarized luminescence spectra are quite different for the three phases. As shown in Fig. 5e and f, R-1 is CPL active and shows the highest value of dissymmetric factor (|g_lum| = 2.1 × 10⁻³) among the three samples. In contrast, R-3 is CPL inactive with |g_lum| ≈ 0. Although R-2 is CPL active, its dissymmetric factor (|g_lum| = 7.5 × 10^–4) is much lower than that of R-1. The results demonstrate that the amplification of chirality from the molecular to the macroscopic level in R-1 has a significant effect on enhancing the CPL activity and increasing the |g_lum| value of the material.

Conclusions

We systematically investigated the solvent effect on the morphology of Gd(NO₃)₃/R-,S-AnempH₂ assemblies and obtained three materials with different morphologies, namely spiral bundles R,S-1, crystals R-2 and spindle-shaped particles R-3. The formation of the spiral bundle R-1 may be related to the misalignment of initially formed chiral nanoparticles during the aggregation process. Importantly, the morphology has a sizable effect on the performance of CPL. R-1 shows the highest value of g_lum (|g_lum| = 2.1 × 10^–3), compared with R-2 (|g_lum| = −7.5 × 10^–4) and R-3 (|g_lum| ≈ 0). The significance of this work is twofold: (i) it provides a rare example to understand the formation mechanism of spiral bundles of coordination polymers and (ii) it shows a clear relationship between the morphology and asymmetric factors based on structurally identical molecular materials. This work provides a new route to control the morphology of chiral CPs and improve their CPL performance.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (21731003, 92356303).

References

1. (a) L. Feng, K.-Y. Wang, J. Powell and H.-C. Zhou, Matter, 2019, 1, 801–824; (b) G. Cai, P. Yan, L. Zhang, H.-C. Zhou and H.-L. Jiang, Chem. Rev., 2021, 121, 12278–12326.
2. (a) K. Suresh, D. Aulakh, J. Purewal, D. J. Siegel, M. Veenstra and A. J. Matzger, J. Am. Chem. Soc., 2021, 143, 10727–10734; (b) Y. Lv, Z. Xiong, Y. Yao, A. Ren, S. Xiang, Y. S. Zhao and Z. Zhang, Chem. – Eur. J., 2021, 27, 3297–3301; (c) X. Wen, Y. Luo, Y. Deng, X. Zeng, Y. Tian, J. He and X. Hou, Nanoscale, 2023, 15, 11582–11591.
3. (a) X. Shi, X. Lian, D. Yang, X. Hu, J. Zhang and X.-H. Bu, Dalton Trans., 2021, 50, 17953–17959; (b) J. Wan, D. Liu, H. Xiao, H. Rong, S. Guan, F. Xie, D. Wang and Y. Li, Chem. Commun., 2020, 56, 4316–4319; (c) C. Hu, Y. Hu, A. Zhu, M. Li, J. Wei, Y. Zhang and W. Xie, Chem. – Eur. J., 2022, 28, e202200138.
4. (a) W. Chen, K. Ma, P. Duan, G. Ouyang, X. Zhu, L. Zhang and M. Liu, Nanoscale, 2020, 12, 19497–19515; (b) X. Tang, X. Liao, X. Cai, J. Wu, X. Wu, Q. Zhang, Y. Yan, S. Zheng, H. Jiang, J. Fan, S. Cai, W. Zhang and Y. Liu, Angew. Chem., Int. Ed., 2023, 62, e202216310; (c) J. Kumar, T. Nakashima, H. Tsumatori and T. Kawai, J. Phys. Chem. Lett., 2014, 5, 316–321.
5. (a) T. Zhao, J. Han, P. Duan and M. Liu, Acc. Chem. Res., 2020, 53, 1279–1292; (b) J. L. Greenfield, J. Wade, J. R. Brandt, X. Shi, T. J. Penfoldd and M. J. Fuchter, Chem. Sci., 2021, 12, 8589–8602; (c) C. Liu, J.-C. Yang, J. W. Y. Lam, H.-T. Feng and B. Z. Tang, Chem. Sci., 2022, 13, 611–632; (d) S. Felder, M.-L. Delcourt, D. Contant, R. Rodríguez, L. Favereau, J. Crassous, L. Micouin and E. Benedetti, J. Mater. Chem. C, 2023, 11, 2053–2062; (e) X.-J. Liao, D. Pu, L. Yuan, J. Tong, S. Xing, Z.-L. Tu, J.-L. Zuo, W.-H. Zheng and Y.-X. Zheng, Angew. Chem., Int. Ed., 2023, 62, e202217045.
6. S.-Y. Li, L. Xu, R.-T. Gao, Z. Chen, N. Liu and Z.-Q. Wu, J. Mater. Chem. C, 2023, 11, 1242–1250.
7. (a) O. G. Willis, F. Zinna and L. Di Bari, Angew. Chem., Int. Ed., 2023, 62, e202302358; (b) Z.-L. Gong, Z.-Q. Li and Y.-W. Zhong, Aggregate, 2022, 3, e177; (c) X.-Y. Luo and M. Pan, Coord. Chem. Rev., 2022, 468, 214640; (d) L. Song, Y. Zhou, T. Gao, P. Yan and H. Li, Acta Chim. Sin., 2021, 79, 1042–1048.
8. (a) Y. Okayasu, K. Wakabayashi and J. Yuasa, Inorg. Chem., 2022, 61, 15108–15115; (b) J. Song, H. Xiao, L. Fang, L. Qu, X. Zhou, Z.-X. Xu, C. Yang and H. Xiang, J. Am. Chem. Soc., 2022, 144, 2233–2244; (c) X.-H. Ma, J. Li, P. Luo, J.-H. Hu, Z. Han, X.-Y. Dong, G. Xie and S.-Q. Zang, Nat. Commun., 2023, 14, 4121; (d) K. Dhbaibi, M. Grasser, H. Douib, V. Dorcet, O. Cador, N. Vanthuyne, F. Riobé, O. Maury, S. Guy, A. Bensalah-Ledoux, B. Baguenard, G. L. J. A. Rikken, C. Train, B. Le Guennic, M. Atzori, F. Pointillart and J. Crassous, Angew. Chem., Int. Ed., 2023, 62, e202215558.
9. (a) J. Kumar, T. Nakashima and T. Kawai, J. Phys. Chem. Lett., 2015, 6, 3445–3452; (b) M. Li, S. Nizar, S. Saha, A. Thomas, S. Azzini, T. W. Ebbesen and C. Genet, Angew. Chem., Int. Ed., 2023, 62, e202212724; (c) G.-G. Weng, K. Xu, T. Hou, X.-D. Huang, M.-F. Qin, S.-S. Bao and L.-M. Zheng, Inorg. Chem., 2023, 62, 21044–21052.
10. O. El-Zubir, P. R. Martinez, G. Dura, C. Doherty, F. Cucinotta, L. E. Mackenzie, R. Pal, B. R. Horrocks and A. Houlton, Dalton Trans., 2023, 52, 5545–5551.
11. (a) G.-G. Weng and L.-M. Zheng, Sci. China: Chem., 2020, 63, 619–636; (b) H. M. Tay, N. Kyratzis, S. Thoonen, S. A. Boer, D. R. Turner and C. Hua, Coord. Chem. Rev., 2021, 435, 213763; (c) W. Gong, Z. Chen, J. Dong, Y. Liu and Y. Cui, Chem. Rev., 2022, 122, 9078–9144; (d) L. A. Hall, D. M. D'Alessandro and G. Lakhwani, Chem. Soc. Rev., 2023, 52, 3567–3590.
12. (a) J. Huang, H.-M. Ding, Y. Xu, D. Zeng, H. Zhu, D.-M. Zang, S.-S. Bao, Y.-Q. Ma and L.-M. Zheng, Nat. Commun., 2017, 8, 2131; (b) G.-G. Weng, B.-K. Hong, S.-S. Bao, Y. Wen, L.-Q. Wu, X.-D. Huang, J.-G. Jia, G.-H. Wen, S.-H. Li, L. Peng and L.-M. Zheng, Chem. Sci., 2021, 12, 12619–12630.
13. Y. Xu, Y.-S. Yu, X.-D. Huang, S.-S. Bao, H.-M. Ding, Y.-Q. Ma and L.-M. Zheng, Inorg. Chem., 2018, 57, 12143–12154.
14. (a) J.-G. Jia, C.-C. Zhao, Y.-F. Wei, Z.-M. Zhai, S.-S. Bao, A. J. Jacobson, J. Ma and L.-M. Zheng, J. Am. Chem. Soc., 2023, 145, 23948–23962; (b) C.-Y. Wang, J.-G. Jia, G.-G. Weng, M.-F. Qin, K. Xu and L.-M. Zheng, Chem. Sci., 2023, 14, 10892–10901; (c) G.-G. Weng, X.-D. Huang, R. Hu, S.-S. Bao, Q. Zou, G.-H. Wen, Y.-Q. Zhang and L.-M. Zheng, Chem. – Asian J., 2021, 16, 2648–2658.
15. (a) L.-Q. Wu, Y. Xu, T. Hou, J.-G. Jia, X.-D. Huang, G.-G. Weng, S.-S. Bao and L.-M. Zheng, Chem. – Eur. J., 2021, 27, 16722–16734; (b) T. Hou, L. Q. Wu, Y. Xu, S.-S. Bao and L.-M. Zheng, Molecules, 2023, 28, 163.
16. (a) M. Menelaou, F. Ouharrou, L. Rodríguez, O. Roubeau, S. J. Teat and N. Aliaga-Alcalde, Chem. – Eur. J., 2012, 18, 11545–11549; (b) X.-F. Ma, Y. Guo, X.-D. Huang, G.-H. Wen, S.-S. Bao, Y.-Q. Zhang and L.-M. Zheng, Dalton Trans., 2022, 51, 12026–12030.
17. Materials Studio, version 7.0, Accelrys Inc., San Diego, 2013.
18. TOPAS, version 5.0, Bruker AXS Inc., Madison, WI, 2014.
19. Y. Hong, J. W. Y. Lam and B. Z. Tang, Chem. Soc. Rev., 2011, 40, 5361–5388.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dt03735e

---