Open Access Article
Open Access ArticleTuning the electronic properties of asymmetric YZrCOF MXene for water splitting applications: an ab initio study†
Mounir
Ould-Mohamed
*a,
Tarik
Ouahrani
 *bc,
Chewki
Ougherb
d,
Ruth
Franco
d and
Daniel
Errandonea
*bc,
Chewki
Ougherb
d,
Ruth
Franco
d and
Daniel
Errandonea
 *e
*e
aLPTHIRM, Département de physique, Faculté des sciences, Université Saâd DAHLAB-Blida 1, B.P. 270 Route de Soumâa, 09000 Blida, Algeria. E-mail: ouldmohamedmounir79@gmail.com
bÉcole supérieure en sciences appliquées, ESSA-Tlemcen, BB 165 RP Bel Horizon, Tlemcen 13000, Algeria. E-mail: tarik_ouahrani@yahoo.fr
cLaboratoire de Physique Théorique, Université de Tlemcen, BP 119, 13000, Algeria. E-mail: tarik_ouahrani@yahoo.fr
d(MALTA) Consolider Team and Departamento de Química Física y Analítica, Universidad de Oviedo, E-33006 Oviedo, Spain
eDepartamento de Física Aplicada - Instituto de Ciencia de Materiales, Matter at High Pressure (MALTA) Consolider Team, Universidad de Valencia, Edificio de Investigación, C/Dr. Moliner 50, Burjassot, 46100, Valencia, Spain. E-mail: daniel.errandonea@uv.es
First published on 6th February 2024
Abstract
Identifying and evaluating novel and extremely stable materials for catalysis is one of the major challenges that mankind faces today to rapidly reduce the dependence on fossil fuels. To contribute to achieving this goal, we have evaluated within the density-functional framework the properties of a new two-dimensional MXene structure, the asymmetric MXene YZrCOF monolayer. Phonon dispersion calculations at 0 K and 300 K indicate that the studied material is dynamically stable. The calculations also indicate that the material has a rigid crystal structure with a wide band gap, a strong potential difference, and a band-gap alignment that favors the production of both H2 and O2 molecules from water splitting. We also report the outcome of the strain effect on the electrical and photocatalytic characteristics of the studied material. We will demonstrate that even under a large strain, the YZrCOF monolayer is stable and useful for photocatalytic applications.
1. Introduction
At present, the global energy crisis and pollution are major challenges faced by society. The dependence on fossil fuels and overuse of natural resources have led to an alarming increase in greenhouse gas emissions and environmental degradation. The development of technologies capable of producing renewable energy with low or harmless emissions has become a crucial task for modern societies. One alternative to overcome this issue is the use of green energy, for instance, green hydrogen, as an alternative to fossil fuels. In fact, green hydrogen is a clean and versatile energy source that could be produced from renewable resources. For instance, through water electrolysis using solar energy. Hydrogen can be employed to produce electricity and in the transportation and industrial sectors, offering a sustainable alternative to fossil fuels and therefore contributing to lowering greenhouse gas emissions.1 Additionally, hydrogen can be stored and used to stabilize electrical grids, enhancing the reliability of energy systems. Thus, the development of materials tailored to improve the efficiency of green hydrogen production is currently a hot topic. One efficient mechanism to achieve this goal is the hydrogen evolution reaction (HER), which offers a potential solution for allowing excess renewable energy to be stored as hydrogen.2 This mechanism is part of the photo-catalytic water-splitting reaction. The challenge resides in the search for materials optimized for such are action. Due to their properties, a wide range of two-dimensional (2D) materials have recently been intensively explored as photo-catalysts for water splitting.3 In contrast to bulk photo-catalysts, 2D photo-catalysts offer various benefits, including a larger specific surface area for efficient photo-catalytic reactions, high photon absorption in the visible light spectrum, and reduced exciton recombination rates. In theory, an ideal photo-catalyst needs to meet some characteristics to allow its availability for the water-splitting process. First of all, it must possess a band gap equal to or larger than 1.23 eV. The origin of this value is the difference between the redox potentials of H+/H2 and H2O/O2. Second, the band-edge alignment of the photo-catalyst needs to span both the reduction and oxidation potentials of water.4 Additionally, the material should have both a large light absorbance and a large quantum efficiency.5 Finally, the material should be stable mechanically, dynamically, and thermally.To guarantee an efficient water-splitting mechanism and produce both H2 and O2 molecules, the material used as a catalyst must allow external control of the internal electric fields using photo-excited charge carriers. Among the 2D photo-catalysts, 2D Janus structures, due to the presence of a vertical intrinsic electric field (EF), have shown the capability to accelerate the inhibition of the recombination of excitons and ensure photo-catalysis efficiency. In addition, the non-symmetric structure of Janus material breaks the conventional limitation of 1.23 eV for the band gap of the photo-catalyst.6 These properties, especially the broken out-of-plane symmetry and ferroelectricity, lead to an enlarged light absorption, even in the infrared region.7 The investigation of 2D Janus structures (compounds with a biphasic or asymmetric structures),8–12 including transition-metal dichalcogenides, such as Ga2SeTe, Ga2STe, and Ga2SSe monolayers,13,14 showed that due to their unique structural characteristics, a built-in electric field results from the difference in the electrostatic potential between the two surfaces of the 2D materials. Thanks to this characteristic, the solar to hydrogen conversion efficiency of Janus Pd4S3Se3 reaches up to 30.1% overcoming the theoretical efficiency limit, 18%, of popular 2D MoS2.15 Inspired by these promising capabilities of 2D Janus materials, we study here the properties of a related material, a monolayer of YZrCOF, a MXene with a hexagonal asymmetric crystal structure. This structure is a special derivative of the 2D MXene of well-known 3D MAX structures of ternary carbides and notrodes.16 The structure of 3D YZrCOF is mainly labeled as asymmetric MXene (aMXene). The asymmetry of the structure is important because MXene has an unusually high dipole perpendicular to the 2D plane, which would favor its competitive advantages as an outstanding molecular monolayer.16 Using density-functional theory (DFT), we have methodically examined the structural stability, mechanical, dynamical, and electrical properties, and photo-catalytic water-splitting capabilities of the YZrCOF aMXene monolayer. It will be shown here that mechanical strain may have a positive effect on the electrical and structural characteristics of YZrCOF, which may then have an effect on the efficiency of the material for photocatalysis. The enhancement of the photo-catalytic efficiency is mostly caused by the strong electronegativity difference that is formed between the F and O sides of the structure under investigation, which enhances the vertical asymmetry of the structure. The electronegativity difference will induce an intrinsic electric field, which will affect the capacity of the material capacity to produce charge carriers, absorb light, and take part in redox processes, thus affecting thus, photo-catalysis. The goal of our contribution is to screen the potential of YZrCOF as a new material with improved efficiency for a range of applications.
2. Computational methodology
In this study, the Quantum Espresso (QE) package17–19 has been employed for performing first-principles calculations, utilizing the projector-augmented wave pseudo-potential. The revised Perdew–Burke–Ernzerhof for solids (PBEsol) within the generalized-gradient approximation (GGA) has been used to describe the exchange-correlation functional. The kinetic cut-off energy for the plane-wave basis has been fixed at 680 eV. The energy convergence has been set to 8 × 10−9 eV. The Brillouin zone sampling has been performed by employing 8 × 8 × 2 and 30 × 30 × 2 Monkhorst-Pack grid meshes20 for relaxation calculations and electronic structure calculations, respectively. To simulate weak interactions, we have included the van der Waals (vdW) interaction using the DFT-D2 correction developed by Grimme.21 In addition, a large vacuum space of 28 Å along the z-direction has been used to eliminate any interaction between neighboring slabs. The atomic positions in the unit cell and the lattice parameters have been relaxed using the variable-cell command of the QE package, employing the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm.22–25 The relaxation process has been performed until the forces on each atom converged and reached a magnitude lower than 0.005 eV au−1. A 2 × 2 × 1 super-cell and the small displacement technique, implemented in the PHONOPY code26 interfaced to the Quantum Espresso package, have been used to obtain the phonon dispersion curves. Ab initio molecular-dynamics (AIMD) simulations have been performed on a 3 × 3 × 1 super-cell using the Nosé-Hoover thermostat approach at 300 and 700 K, with a time step of 0.5 ps.27–29 The dynamical behavior of atoms and electrons over time is the main emphasis of AIMD. By incorporating the dynamics of atoms at finite temperatures, it enables the simulation of temperature effects. The elastic constants have been finally determined using the energy-strain method.30 We have used the ALAMODE code31 to simulate how temperature affects the phonon dispersion curve. The code can handle temperature effects by incorporating temperature-dependent atomic displacements and calculates the anharmonic spectra by fitting the force constants up to the 4th order. It extracts the force constants that describe the response of a crystal lattice to small atomic displacements. Here, we employ a displacement of 0.08 Å for a 2 × 2 × 1 supercell containing 20 atoms. We have gotten, respectively, 25 harmonic, 104, and 316 anharmonic displacements after computing the forces acting on atoms. We used an 8 × 8 × 4 reciprocal space k-mesh, using a 4 × 4 × 2 interpolating mesh for the self-consistent phonon calculations (SCPH)32 procedure to assess the phonon dispersion curve at a finite temperature. The least-squares method was used for fitting the force constants from the displacement forces datasets.Given that PBEsol approach often tends to underestimate electronic band-gap energy, to calculate the band structure we have also used the Heyd–Scuseria–Ernzerhof hybrid functional (HSE06) functional,33 which is renowned for its accuracy in band-gap predictions. For this approach, we have set the mixing value to 0.25. The electronic band structure using HSE06 has been determined through a Wannier interpolation,34 using the Wannier package version 3.1.035 interfaced with QE For practical purposes, we converged the Wannierization parameters by determining a suitable energy window for the construction of the maximally localized Wannier functions (MLWFs) and taking a converged grid band. The task also includes the determination of the projected windows for disentanglement, and the correct Wannier grid size. The convergence tests and related plots are shown in Fig. S1–S3 of the ESI.†
3. Results and discussion
3.1. Structural stability of the YZrCOF monolayer
The investigated monolayer has a hexagonal crystal structure described by the space group P3m1 (no. 156), instead of P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (no. 164) like most of MXenes. It consists of five layers of atoms stacked in the Y–Zr–C–O–F sequence. Given the fact that the mirror symmetry is broken in the monolayer, the point group corresponding to this structure is C3v. The fact that in the investigated structure the two surfaces are composed of different atoms potentially enriches its functionality. The crystal structure is displayed in Fig. 1. The calculations reveal that the optimized lattice constant for the YZrCOF monolayer is a = 3.408 Å and the optimized thickness of the monolayer is d = 4.516 Å. The optimized atomic coordinates within the layer are (2/3, 1/3, 0.214) for F, (1/3, 2/3, 0.258) for Zr, (0, 0, 0.4816) for C, (2/3, 1/3, 0.8321) for Y, and (1/3, 2/3, 1) for O. The calculated bond lengths are summarized in Table 1. We can observe that the difference in bond distances enhances the electronegativity difference between the top and bottom elements of the layer, which leads to an asymmetric dipole distribution. This fact results in a “colossal vertical electric field”. This finding agrees well with the values of parameters reported in the aNANt material database.36 Our results are comparable to those of successfully synthesized aMXene structures.37,38
m1 (no. 164) like most of MXenes. It consists of five layers of atoms stacked in the Y–Zr–C–O–F sequence. Given the fact that the mirror symmetry is broken in the monolayer, the point group corresponding to this structure is C3v. The fact that in the investigated structure the two surfaces are composed of different atoms potentially enriches its functionality. The crystal structure is displayed in Fig. 1. The calculations reveal that the optimized lattice constant for the YZrCOF monolayer is a = 3.408 Å and the optimized thickness of the monolayer is d = 4.516 Å. The optimized atomic coordinates within the layer are (2/3, 1/3, 0.214) for F, (1/3, 2/3, 0.258) for Zr, (0, 0, 0.4816) for C, (2/3, 1/3, 0.8321) for Y, and (1/3, 2/3, 1) for O. The calculated bond lengths are summarized in Table 1. We can observe that the difference in bond distances enhances the electronegativity difference between the top and bottom elements of the layer, which leads to an asymmetric dipole distribution. This fact results in a “colossal vertical electric field”. This finding agrees well with the values of parameters reported in the aNANt material database.36 Our results are comparable to those of successfully synthesized aMXene structures.37,38
| d Y–O | d Y–C | d Y–Zr | d Zr–F | d Zr–C |
|---|---|---|---|---|
| 2.12 | 2.69 | 3.44 | 2.34 | 2.20 |
Next, the dynamical stability of the YZrCOF monolayer has been studied by examining the phonon dispersion, which is displayed in Fig. 2a. The absence of any imaginary branch along the high-symmetry k-point path in the first Brillouinzone indicates that the YZrCOF monolayer is dynamically stable. The phonon dispersion consists of a total of fifteen vibrational phonon modes, comprising three low-frequency acoustic modes and twelve high-frequency optical modes. Additionally, the analysis of the phonon density of states (PHDOS), reported in Fig. 2b, reveals that the phonon branches in the lower frequency range primarily originated from both Y and Zr atoms. Whereas, the intermediate vibration frequencies are predominantly contributed by Zr and F atoms. The plot also shows that the high-frequency vibration is mainly contributed by the lighter atoms, specifically the O and C atoms.
Based on a symmetry analysis, the modes at the Γ point of the Brillouin zone can be categorized into the following irreducible representations: Γoptic = 4A1 + 4E and Γacoustic = A1 + 2E resulting in 12 optical modes and three acoustic modes. Table 2 summarizes the calculated wavenumbers for each mode with the respective assignments. It should be noted that all modes E are doubly degenerated. Unfortunately, no previous experimental results are available to compare with. However, we can note that the values of the optical modes are comparable with those of synthesized MoSSe and WSSe.39 Commonly, for two-dimensional layered structures, the acoustic modes correspond to rigid translations of the monolayer (E mode) and a flexural response (A mode). They have a linear dependence in the q-space near the Γ point. This involves an atomic movement within the plane. In Fig. 3, we report the atomic movements associated with each of the optical modes. The A modes involve out-of-plane vibrations, and the E modes involve movements of the atoms in a direction parallel to the surface of the monolayer. The A mode with a wavenumber of 193.9 cm−1 involves movements of O, Zr, and F atoms in the opposite direction than Y and C atoms, being the movement of O atoms the one with the smallest magnitude. The A mode, having a wavenumber of 377.2 cm−1 involves basically a stretching vibration of the Zr–F bond. The A mode with wavenumber 460.6 cm−1 involves movements of Y and C atoms in opposite directions, and the A mode with wavenumber 632.1 cm−1 involves movements of F and O atoms in opposite directions. On the other hand, the E mode with wavenumber 103.1 cm−1 involves mainly movements of C and Y atoms in one direction along a direction parallel to the surface and Zr, F, and O atoms in the opposite direction than C and Y. The E mode with wavenumber 168.4 cm−1 involves basically a bending vibration of the Zr–F bond. The E mode with wavenumber 479.7 cm−1 involves movements of C and O atoms in opposite directions, and the E mode with wavenumber 505.9 cm−1 involves basically a bending vibration of the Y–O bonds.
| Mode | ω (cm−1) |
|---|---|
| A1 | 193.9 |
| A1 | 377.2 |
| A1 | 460.6 |
| A1 | 632.1 |
| E | 103.1 |
| E | 168.4 |
| E | 479.7 |
| E | 505.9 |
Temperature changes may also affect the thermodynamics of the water-splitting process. By influencing the viscosity of the electrolyte, temperature can improve the mass transfer of reactants and products to and from the electrode surface. Retaining high reaction rates requires efficient mass transfer. But, in rare circumstances, a temperature rise may alter the equilibrium position of the reaction in a way that additionally favors the creation of hydrogen. A high temperature could also have negative consequences, such as accelerated corrosion or alterations to the stability and structure of catalyst materials. Because the hydrogen evolution reaction operates at high temperatures for a variety of applications, such as electrolysis for hydrogen production or fuel cell operation, it is also crucial to analyze the temperature dependence on the crystal structure. To perform this analysis, we have also carried out AIMD simulations on a 3 × 3 × 1 super-cell of the YZrCOF structure. They have been carried out at 300 K and at 700 K. The results are shown in Fig. 4a and b. In the simulations, the evolution of temperature and total energy as a function of time is periodic, and no evidence of structural transitions or instabilities under the change of temperature is detected. This means that the YZrCOF monolayer could quite likely be synthesized in the laboratory under ambient conditions, and it is also stable at high temperatures. However, we note large temperature fluctuations at 700 K. To be sure that simulations do not involve the melting of the investigated structure or a phase transition between different crystal structures, we have plotted in the ESI† a sequence of the simulated structure for a different time step of the AIMD simulations (see Fig. S4 in the ESI†). No indication of a structural change was found for the two temperatures considered. This indicates the thermal stability of the YZrCOF monolayer.
Self-consistent phonon calculations (SCPH) at different temperatures have been also calculated. The results are plotted in Fig. 5. According to this plot, it is evident that the YZrCOF monolayer is dynamically stable at 300 K; but, at 700 K, a slight instability starts to develop (see Fig. S5 in the ESI†). Although the structure might likely be impacted by extremely high temperatures, however, these conditions are not necessary for the application of this structure for water splitting.
 | ||
| Fig. 5 Anharmonic phonon dispersion curves of the YZrCOF monolayer as a function of temperature. The black, blue, and orange lines correspond to temperatures equal to 0, 300, and 700 K, respectively. | ||
An important piece of information about the YZrCOF monolayer is the characterization of the effect of strain on the electronic properties and the related photo-catalytic attributes. To understand it, it is mandatory to analyze the response of the studied structure to strain via the calculations of elastic components. This will allow us to select the appropriate strains to be applied in the next sections to improve photocatalytic properties. To calculate the elastic constants of the YZrCOF monolayer, small external strains ε around the equilibrium position were applied. The strain energy per unit area can be expressed as follows:30
 | (1) |
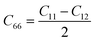 . This means that the mechanical stability of YZrCOF requires only the calculation of two independent constants, C11 and C12. The obtained values are presented in Table 3. The calculated values satisfy the Born–Huang criteria of stability (C11 > 0, C112 − C122 > 0)40,41 supporting the mechanical stability of the investigated structure.
. This means that the mechanical stability of YZrCOF requires only the calculation of two independent constants, C11 and C12. The obtained values are presented in Table 3. The calculated values satisfy the Born–Huang criteria of stability (C11 > 0, C112 − C122 > 0)40,41 supporting the mechanical stability of the investigated structure.
| C 11 | C 12 | C 66 |
|---|---|---|
| 205.03 | 67.48 | 68.78 |
| K | Y 2D | ν | G |
|---|---|---|---|
| 136.23 | 182.82 | 0.33 | 68.78 |
It can be seen in Table 3 that the calculated value of C11 for the YZrCOF monolayer (205.032 N m−1) is notably larger than the value of C12 (67.482 N m−1). This observation indicates that axial compression exerts higher forces compared to shear and tensile deformation. This is a typical characteristic of 2D materials, as reported for 2D MoSSe, MoSeTe, MoSTe, and ZBrCl,42,43 or typical MXene monolayers.44 Based on the obtained elastic constants, we have also determined the in-plane Young's modulus (Y2D), 2D shear modulus (G), 2D bulk modulus (K), and Poisson ratio (ν) as follows:45 , G = C66,
, G = C66,  , and
, and  . Table 3 lists all these mechanical parameters. The obtained values are comparable to those reported for available 2D materials.42–44
. Table 3 lists all these mechanical parameters. The obtained values are comparable to those reported for available 2D materials.42–44
3.2. Electronic structure and band gap alignment
A thorough investigation of the electronic properties is imperative to check the possibility of using the YZrCOF monolayer effectively in electronic and photocatalytic applications. For it, the band structure, the density of states, and the related band-gap energy are calculated. In addition to the PBESol functional; the HSE0633 functional has been also employed. The calculated band structures are shown in Fig. 6. This plot shows that the studied compound is a semiconducting material with a quasi-indirect band gap at the K–Γ direction, with band-gap energies of 3.59 eV for the HSE functional and 2.61 eV for PBEsol. The PBEsol value agrees well with the value reported in the aNant database, which was calculated using a similar approach.36 However, the value of the band gap obtained using HSE06, 3.59 eV, should be considered as the most realistic value for comparison with future experiments. Fig. 7 illustrates the calculated projected electronic density of states (PDOS) for the YZrCOF monolayer, providing a more comprehensive analysis of its orbital nature and electronic properties.46,47 The analysis of the PDOS reveals that the electronic states near the Fermi level of the YZrCOF monolayer are mainly contributed by the Y-4d, Zr-4d, C-2p, O-2p, and F-2p orbitals, with a small contribution of Y-5p states. However, the conduction band is mainly contributed by Y-4d and Zr-4d, with a small contribution from 2p-C orbitals, while the contributions from the F and O atoms are relatively insignificant. | ||
| Fig. 6 Band structure of the YZrCOF monolayer calculated using the (a) PBEsol and (b) HSE06 functional. The band structure calculated with HSE06 is interpolated by disentangled bands along the path through the Brillouin zone using maximally localized Wannier functions (MLWFs). For more information see the ESI.† | ||
Certain characteristics should be met by the ideal photo-catalyst. First of all, its band-gap energy (Eg) ought to be higher than 1.23 eV. Furthermore, at pH = 0/7, the valence band maximum (VBM) position should be lower than the water oxidation potential (−5.67 eV vs. vacuum). On the other hand, the conduction band maximum (CBM) position should be higher than the standard redox potential (−4.44 eV vs. vacuum). It is noteworthy to mention that the relative positions of the CBM and VBM concerning the normal hydrogen electrode (NHE) potential, specifically about the standard reduction potential H+/H2 and the oxidation potential O2/H2O, are 0 eV and 1.23 eV, respectively.48 The energy edges of the conduction band ECBM and valence band EVBM for YZrCOF are determined using the following formula concerning NHE:
| EVBM = χ − Ee + 0.5Eg | (2) |
| ECBM = EVBM − Eg | (3) |
| χ = (χ(Y)χ(Zr)χ(C)χ(O)χ(F))1/5 | (4) |
We rationalized the band-edge alignment to uncover the capabilities of using the YZrCOF aMXene monolayer for photo-catalytic water splitting. The results are displayed in Fig. 8 depicting the band alignments of the oxidation and reduction potentials for water splitting concerning the band CBM levels contain both the oxidation potential of O2/H2O and the reduction potential of H+/H2 at pH = 0, respectively.50 This confirms that the studied monolayer can facilitate O2 evolution and the hydrogen evolution reaction (HER) in both acidic and alkaline solutions. The intrinsic electric field created by the YZrCOF aMXene's violation of symmetry and vertically asymmetrical structure causes this tendency to occur on the two distinct surfaces. This trend could be predicted by the calculation of the electrostatic potential curve, which is shown in Fig. 9. The mechanical difference between the Y–O and Zr–F bonds that comprise the two sides of the aMXene is what causes the strong difference of potential. This fact leads to an intrinsic electric field, which has a direction from the O surface to the F surface. The oxygen reaction will therefore occur on the F layer, and the hydrogen reaction will occur on the O layer due to the photo-generated electrons and holes moving in opposing directions in the electric field. This separation is critical for the prolonged lifetime of the photo-catalytic device. The distinct vacuum level differences ΔΦ are both gathered in Table 4. Because of the significant difference in vacuum levels, it appears that electrons on the F surface can escape more easily than those on the O surface. In experiments, the potential difference, also known as voltage, is a key component in the electrolysis process, which is the process of water splitting.
| E PBEsolg (eV) | E HSE06g (eV) | Φ 1 (eV) | Φ 2 (eV) | ΔΦ (eV) |
|---|---|---|---|---|
| 2.62 | 3.59 | 4.19 | 5.31 | 1.11 |
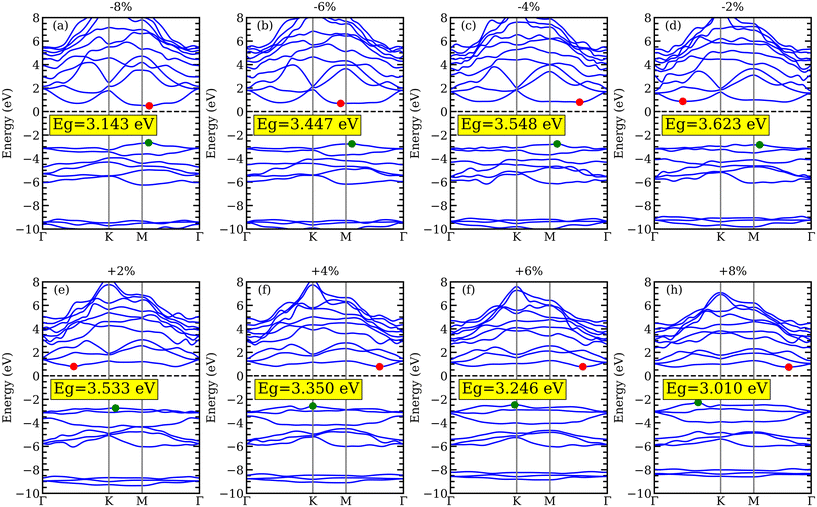
 is the definition of the biaxial strain, where as and a0 are the lattice constants of the strained and unstrained aMXene YZrCOF monolayer, respectively. The positive and negative marks, respectively, represent compressive and tensile strains. To investigate the effect of strain on the band-gap energy, YZrCOF is first deformed with biaxial strain in the range of −8% to +8% with an increment of 2%. Fig. 10a shows how the band-gap energy changes as the biaxial strain increases. It is evident that the band-gap energy monotonically grows when the compressive strain changes from −8% to 0%, and monotonically drops when the strain changes from 0% to 8%. It is also evident that the material under study maintains the indirect band gap under strain within the −6% to +8% range. The calculated band structures under different strains, which are show on in Fig. 11, consistently show that when compressive strain is present, the valence-band maximum is located at the M point of the Brillouin zone, and when tensile strain is present, it is located at the K point. Under tensile tension (apart from −8%), the conduction-band minimum is situated between the Γ and K points; under compressive strain, it is situated between the Γ and M points. A semiconductor–metal transition cannot be induced by the applied stresses. It is clear that the band-edge positions of the YZrCOF monolayer still match the requirements of photo-catalysis for water splitting at pH = 0 within the strain range of −8% to +8% (Fig. 10b).
is the definition of the biaxial strain, where as and a0 are the lattice constants of the strained and unstrained aMXene YZrCOF monolayer, respectively. The positive and negative marks, respectively, represent compressive and tensile strains. To investigate the effect of strain on the band-gap energy, YZrCOF is first deformed with biaxial strain in the range of −8% to +8% with an increment of 2%. Fig. 10a shows how the band-gap energy changes as the biaxial strain increases. It is evident that the band-gap energy monotonically grows when the compressive strain changes from −8% to 0%, and monotonically drops when the strain changes from 0% to 8%. It is also evident that the material under study maintains the indirect band gap under strain within the −6% to +8% range. The calculated band structures under different strains, which are show on in Fig. 11, consistently show that when compressive strain is present, the valence-band maximum is located at the M point of the Brillouin zone, and when tensile strain is present, it is located at the K point. Under tensile tension (apart from −8%), the conduction-band minimum is situated between the Γ and K points; under compressive strain, it is situated between the Γ and M points. A semiconductor–metal transition cannot be induced by the applied stresses. It is clear that the band-edge positions of the YZrCOF monolayer still match the requirements of photo-catalysis for water splitting at pH = 0 within the strain range of −8% to +8% (Fig. 10b).
4. Conclusions
In summary, using density-functional theory, we have examined the stability and underlying electrical and photo-catalytic characteristics of the unstrained and strained aMXene YZrCOF monolayer. We have found that the non-centrosymmetric structure of aMXene YZrCOF is dynamically, thermally, and mechanically stable. We have showed that the YZrCOF monolayer has comparable properties to Janus materials, providing further feasible options for the reduction of water. Two different exchange-correlation functionals have been used to study the electronic characteristics: PBEsol and HSE06/Wannier90 functionals. Both techniques showed that the material has an indirect band gap optimized for the photo-catalysis of hydrogen and oxygen. Furthermore, it has been demonstrated that the positions of the conduction-band minimum and valence-band maximum favor water oxidation and redox potentials. The ability of the studied structure to produce a significant intrinsic electric field between the two different surfaces of the material is demonstrated by the considerable vacuum level differences that arise from the calculation of electrostatic potential. This phenomenon could encourage different photosynthesized states at the valence band and conduction band levels of the band structure. In addition, we have investigated how strain affects the crystal structure and electronic properties. We have found that the band-gap energy of the material can be easily tuned by the application of strain, which may be an extra benefit for photocatalysis because it allows the modification of the binding energy in the conduction-band minium position, optimizing the material to meet the requirements of catalytic applications. A significant degree of compressive and tensile strain can be applied without damaging the suitability of YZrCOF for photo-catalysis applications.Author contributions
Mounir Ould Mohamed: conceptualization, investigation, writing – original draft – DFT calculations; Tarik Ouahrani: analysis, writing-review & editing. Chewki Ougherb: DFT calculations. Ruth Franco: review & editing; Daniel Errandonea: analysis and discussion, writing-review & editing.Data availability
All relevant data are available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
D. E. thanks the financial support from the Spanish Ministerio de Ciencia e Innovación (https://doi.org/10.13039/501100011033) under Projects PID2019-106383GB-41, PID2022-138076NB-C41, RED2018-102612-T, and RED2022-134388-T. D. E. also acknowledges the financial support of Generalitat Valenciana, through grants PROMETEO CIPROM/2021/075-GREENMAT and MFA/2022/007. This study forms part of the Advanced Materials program and is supported by MCIN with funding from the European Union Next Generation EU (PRTR-C17.I1) and by the Generalitat Valenciana. R. F. acknowledges the financial support from Spanish MCIU under projects 22-PID2021-122585NB-C21, and from Principado de Asturias (FICYT) and FEDER under project AYUD/2021/51036 are gratefully acknowledged. Wethank the MALTA-Consolider supercomputing center for computer facilities.References
- J. Clemens and C. Cuhls, Greenhouse gas emissions from mechanical and biological waste treatment of municipal waste, Environ. Technol., 2003, 24, 745–754, DOI:10.1080/09593330309385611.
- A. Fujishima and K. Honda, Electrochemical photolysis of water at a semiconductor electrode, Nature, 1972, 238, 37–38, DOI:10.1038/238037a0.
- A. K. Singh, K. Mathew, H. L. Zhuang and R. G. Hennig, Computational screening of 2D materials for photo-catalysis, J. Phys. Chem. Lett., 2015, 6, 1087–1098, DOI:10.1021/jz502646d.
- H. Chen, C. Tan, K. Zhang, W. Zhao, X. Tian and Y. Huang, Enhanced photocatalytic performance of ZnO monolayer for water splitting via biaxial strain and external electric field, Appl. Surf. Sci., 2019, 481, 1064–1071, DOI:10.1016/j.apsusc.2019.03.105.
- K. Maeda and K. Domen, Photo-catalytic Water Splitting: Recent Progress and Future Challenges, J. Phys. Chem. Lett., 2010, 1(18), 2655–2661, DOI:10.1021/jz1007966.
- C. F. Fu, J. Sun, Q. Luo, X. Li, W. Hu and J. Yang, Intrinsic Electric Fields in Two-dimensional Materials Boost the Solar-to-Hydrogen Efficiency for photo-catalytic Water Splitting, Nano Lett., 2018, 18(10), 6312–6317, DOI:10.1021/acs.nanolett.8b02561.
- X. Li, Z. Li and J. Yang, Proposed Photosynthesis Method for Producing Hydrogen from Dissociated Water Molecules Using Incident Near-Infrared Light, Phys. Rev. Lett., 2014, 112, 018301, DOI:10.1103/PhysRevLett.112.018301.
- X. Deng, W. Zhang, X. Zhou, Z. Wang, J. Tang, L. Hu, Y. Feng, K. Wu and C. Yang, InSe based Janus V-III-IV-V monolayers as water-splitting photo-catalysts: Role of vacuum level difference, Int. J. Hydrogen Energy, 2021, 46(71), 35271–35279, DOI:10.1016/j.ijhydene.2021.08.068.
- A. Bouheddadj, A. Daouli, T. Ouahrani, R. M. Boufatah and M. Badawi, Unveiling the electronic properties of the Janus HfSSe monolayer and its partially oxygenated counterparts from ab initio calculations, Mater. Chem. Phys., 2022, 289, 126489, DOI:10.1016/j.matchemphys.2022.126489.
- J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy, L. Shi and J. Lou, Janus monolayer transition-metal dichalcogenides, ACS Nano, 2017, 11(8), 8192–8198, DOI:10.1021/acsnano.7b03186.
- H. Yang, P. Zhao, Y. Ma, X. Lv, B. Huang and Y. Dai, Janus single-layer group-III monochalcogenides: a promising visible-light photo-catalyst, J. Phys. D: Appl. Phys., 2019, 52, 455303, DOI:10.1088/1361-6463/ab37d1.
- M. Sun and U. Schwingenschlögl, B2P6: a two-dimensional anisotropic Janus material with potential in photo-catalytic water splitting and metal-ion batteries, Chem. Mater., 2020, 32(11), 4795–4800, DOI:10.1021/acs.chemmater.0c01536.
- L. Hu and D. Wei, Janus Group-III Chalcogenide Monolayers and Derivative Type-II Heterojunctions as Water- Splitting photo-catalysts with Strong Visible-Light Absorbance, J. Phys. Chem. C, 2018, 122(49), 27795–27802, DOI:10.1021/acs.jpcc.8b0657.
- V. V. Thanh, D. V. Truong and N. T. Hung, Janus γ-GeSSe Monolayer as a High-Performance Material for photo-catalysis and Thermoelectricity, ACS Appl. Energy Mater., 2023, 6, 910–919, DOI:10.1021/acsaem.2c03316.
- Y. Luo, M. Sun, J. Yu and U. Schwingenschlögl, Pd4S3Se3, Pd4S3Te3, and Pd4Se3Te3: Candidate Two-Dimensional Janus Materials for photo-catalytic Water Splitting, Chem. Mater., 2021, 33, 4128–4134, DOI:10.1021/acs.chemmater.1c00812.
- C. Ougherb, T. Ouahrani, M. Badawi and Á. Morales-García, Effect of the sulfur termination on the properties of Hf2CO2 MXene Phys, Chem. Chem. Phys., 2022, 24(12), 7243–7252, 10.1039/D2CP00288D.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502, DOI:10.1088/0953-8984/21/39/395502.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncre, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901, DOI:10.1088/1361-648X/aa8f79.
- P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. de Gironcoli, P. Delugas, F. F. Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, Quantum ESPRESSO toward the exascale, J. Chem. Phys., 2020, 152(15), 154105, DOI:10.1063/5.0005082.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192, DOI:10.1103/PhysRevB.13.5188.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799, DOI:10.1002/jcc.20495.
- C. G. Broyden, The Convergence of a Class of Double-rank Minimization Algorithms 1. General Considerations, IMA J. Appl. Math., 1970, 6(1), 76–90, DOI:10.1093/imamat/6.1.76.
- R. Fletcher, A new approach to variable metric algorithms, Comput. J., 1970, 13(3), 317–322, DOI:10.1093/comjnl/13.3.317.
- D. Goldfarb, A family of variable-metric methods derived by variational means, Math. Comput., 1970, 24, 23–26, DOI:10.2307/2004873.
- D. F. Shanno, Conditioning of quasi-Newton methods for function minimization, Math. Comput., 1970, 24, 647–656, DOI:10.2307/2004840.
- T. Atsushi and T. Isao, First principles of phonon calculations in materials science, Scr. Mater., 2015, 105, 1–5, DOI:10.1016/j.scriptamat.2015.07.021.
- G. J. Martyna, M. L. Klein and M. Tuckerman, Nose-Hoover chains: the canonical ensemble via continuous dynamics, J. Chem. Phys., 1992, 97, 2635, DOI:10.1063/1.463940.
- S. Nose, A molecular dynamics method for simulations in the canonical ensemble, Mol. Phys., 1984, 52, 255, DOI:10.1080/00268978400101201.
- S. Nose, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511, DOI:10.1063/1.447334.
- Y. Z. Abdullahi, T. L. Yoon and T. L. Lim, Elastic and electronic properties of C2N monolayer: first-principles calculation, Mater. Res. Express, 2019, 6, 025601, DOI:10.1088/2053-1591/aae9ca.
- T. Tadano, Y. Gohda and S. Tsuneyuki, Anharmonic force constants extracted from first-principles molecular dynamics: applications to heat transfer simulations, J. Phys.: Condens. Matter, 2014, 26, 225402, DOI:10.1088/0953-8984/26/22/225402.
- T. Tadano and S. Tsuneyuki, Self-consistent phonon calculations of lattice dynamical properties in cubic SrTiO3 with first-principles anharmonic force constants, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 054301, DOI:10.1103/PhysRevB.92.054301.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215, DOI:10.1063/1.1564060.
- N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Maximally localized wannier functions: Theory and applications, Rev. Mod. Phys., 2012, 84, 1419, DOI:10.1103/RevModPhys.84.1419.
- G. Pizzi, V. Vitale, R. Arita, S. Blügel, F. Freimuth, G. Géranton, M. Gibertini, D. Gresch, C. Johnson, T. Koretsune, J. Ibañez-Azpiroz, H. Lee, J. M. Lihm, D. Marchand, A. Marrazzo, Y. Mokrousov, J. I. Mustafa, Y. Nohara, Y. Nomura, L. Paulatto, S. Poncé, T. Ponweiser, J. Qiao, F. Thöle, S. S. Tsirkin, M. Wierzbowska, N. Marzari, D. Vanderbilt, I. Souza, A. A. Mostofi and J. R. Yates, Wannier90 as a community code: new features and applications, J. Phys.: Condens. Matter, 2020, 32, 165902, DOI:10.1088/1361-648X/ab51ff.
- aNANt: A functional materials database (https://anant.mrc.iisc.ac.in).
- B. Li, H. Guo, Y. Wang, W. Zhang, Q. Zhang, L. Chen, X. Fan, W. Zhang, Y. Li and W. Lau, Asymmetric MXene/monolayer transition metal dichalcogenide heterostructures for functional applications, npj Comput. Mater., 2019, 5, 16, DOI:10.1038/s41524-019-0155-6.
- Z. M. Wong, T. Deng, W. Shi, G. Wu, T. L. Tan and S.-W. Yang, High-performance photocatalytic and thermoelectric two-dimensional asymmetrically ordered Janus-like MXene alloys, Mater. Adv., 2020, 1, 1176, 10.1039/D0MA00391C.
- M. M. Petric, M. Kremser, M. Barbone, Y. Qin, Y. Sayyad, Y. Shen, S. Tongay, J. J. Finley, A. R. Botello-Méndez and K. Müller, Raman spectrum of Janus transition metal dichalcogenide monolayers WSSe and MoSSe, Phys. Rev. B, 2021, 103, 035414, DOI:10.1103/PhysRevB.103.035414.
- M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Clarendon, Oxford, 1954 Search PubMed.
- T. Ouahrani and R. M. Boufatah, Understanding the Semiconducting-to-Metallic Transition in the CF2Si Monolayer under Shear Tensile Strain, Crystals, 2022, 12, 1476, DOI:10.3390/cryst12101476.
- M. Xiong, Z.-Y. Chen, C.-E. Hu, Y. Cheng and H.-Y. Geng, First-principles study of strain effect on elastic and optical properties and lattice thermal conductivity of Janus ZrBrCl monolayer, Mater. Today Commun., 2021, 26, 101995, DOI:10.1016/j.mtcomm.2020.101995.
- L. Dong, J. Lou and V. B. Shenoy, Large In-Plane and Vertical Piezoelectricity in Janus Transition Metal Dichalchogenides, ACS Nano, 2017, 11(8), 8242–8248, DOI:10.1021/acsnano.7b03313.
- A. Lipatov, H. Lu, M. Alhabeb, B. Anasori, A. Gruverman, Y. Gogotsi and A. Sinitsky, Elastic properties of 2D Ti3C2Tx MXene monolayers and bilayers, Sci. Adv., 2018, 4, 10394, DOI:10.1126/sciadv.aat0491.
- M. Faghihnasiri, A. Ahmadi, S. A. Golpayegan, S. G. Sharifabadi and A. Ramazani, A First-Principles Study of Nonlinear Elastic Behavior and Anisotropic Electronic Properties of Two-Dimensional HfS2, Nanomaterials, 2020, 10, 446, DOI:10.3390/nano10030446.
- T. N. Do, N. N. Hieu, N. A. Poklonski, N. T. T. Binh, C. Q. Nguyencd and N. D. Hien, Computational insights into structural, electronic, and optical properties of Janus GeSO monolayer, RSC Adv., 2021, 11, 28381–28387, 10.1039/D1RA05424D.
- T. Ouahrani, R. Khenata, B. Lasri, A. H. Reshak, A. Bouhemadou and S. Bin-Omran, First and second harmonic generation of the XAl2Se4 (X = Zn, Cd, Hg) defect chalcopyrite compounds, Phys. B: Condens. Matter, 2012, 407, 3760–3766, DOI:10.1016/j.physb.2012.05.057.
- H. T. T. Nguyen, T. V. Vu, N. T. T. Binh, D. M. Hoat, N. V. Hieu, N. T. T. Anh, C. V. Nguyen, H. V. Phuc, H. R. Jappor, M. M. Obeid and N. N. Hieu, Strain-tunable electronic and optical properties of monolayer GeSe: Promising for photo-catalytic water splitting applications, Chem. Phys., 2020, 529, 110543, DOI:10.1016/j.chemphys.2019.110543.
- B. Rerbal and T. Ouahrani, Enhancement of optoelectronic properties of layered MgInSe compound under uniaxial strain, an ab initio study, Eur. Phys. J. B, 2021, 94, 185, DOI:10.1140/epjb/s10051-021-00188-7.
- A. Bouheddadj, A. Daouli, T. Ouahrani, R. M. Boufatah and M. Badawi, Unveiling the electronic properties of the Janus HfSSe monolayer and its partially oxygenated counterparts from ab initio calculations, Mater. Chem. Phys., 2022, 289, 126489, DOI:10.1016/j.matchemphys.2022.126489.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dt04027e |
| This journal is © The Royal Society of Chemistry 2024 |