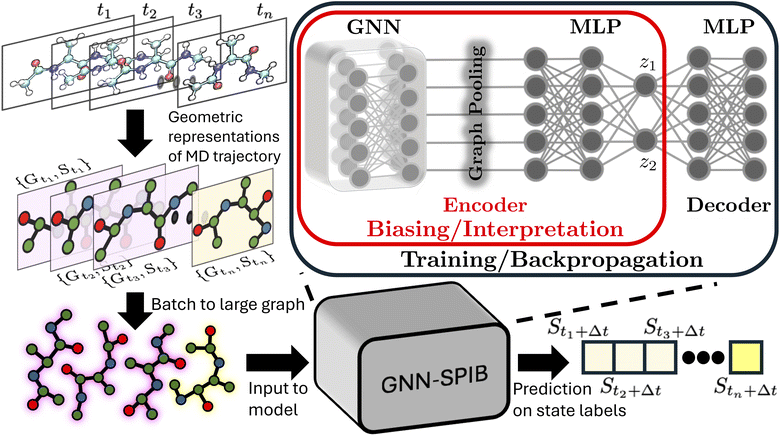
Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A graph neural network-state predictive information bottleneck (GNN-SPIB) approach for learning molecular thermodynamics and kinetics†
Ziyue
Zou
a,
Dedi
Wang
bc and
Pratyush
Tiwary
 *acd
*acd
aDepartment of Chemistry and Biochemistry, University of Maryland, College Park 20742, USA. E-mail: ptiwary@umd.edu
bBiophysics Program, University of Maryland, College Park 20742, USA
cInstitute for Physical Science and Technology, University of Maryland, College Park 20742, USA
dUniversity of Maryland Institute for Health Computing, Bethesda 20852, USA
First published on 28th November 2024
Abstract
Molecular dynamics simulations offer detailed insights into atomic motions but face timescale limitations. Enhanced sampling methods have addressed these challenges but even with machine learning, they often rely on pre-selected expert-based features. In this work, we present a Graph Neural Network-State Predictive Information Bottleneck (GNN-SPIB) framework, which combines graph neural networks and the state predictive information bottleneck to automatically learn low-dimensional representations directly from atomic coordinates. Tested on three benchmark systems, our approach predicts essential structural, thermodynamic and kinetic information for slow processes, demonstrating robustness across diverse systems. The method shows promise for complex systems, enabling effective enhanced sampling without requiring pre-defined reaction coordinates or input features.
1 Introduction
Molecular dynamics (MD) simulations are widely used in computational research, offering detailed spatial and temporal resolution of atomic motions. However, standard MD faces a timescale challenge, as processes of practical interest can take months or years of computer time to simulate. To tackle this, enhanced sampling methods have been developed, but most of these approaches require collective variables (CVs) to effectively capture key system information.1 These CVs are typically based on physical insights or experimental data, yet constructing them becomes challenging when transitions are unknown or difficult to sample.In recent years, machine learning methods have been introduced for this purpose, enabling an automated representation learning framework that can enable CV discovery and enhanced sampling.1–15 However, many of these approaches still require hand-crafted expert-based features as input for the ML model. To overcome this limitation, in this work, we build upon the State Predictive Information Bottleneck (SPIB) method,16,17 enabling it to learn directly from atomic coordinates instead of relying on hand-crafted expert-based features. SPIB, a variant of the reweighted autoencoded variational Bayes for enhanced sampling (RAVE) method,18 is a machine learning technique for dimensionality reduction under a semi-supervised framework. Its structure is based on a time-lagged variational autoencoder where the encoder learns a low-dimensional representation by approximating the posterior distribution of the latent variables given the input features at time t. Unlike in a traditional autoencoder where the decoder focuses on reconstructing the input, the SPIB decoder is trained to predict the state labels in the future t + Δt from the latent variables.
The performance of the original SPIB approach is significantly influenced by two key factors. First is the quality of the sampled trajectory, which ideally should include back-and-forth transitions between target metastable states. This requirement is difficult to meet in complex systems with transitions occurring on long timescales, where alternative approaches like using collections of short MD trajectories initiated at initial and final states can be considered.19–21
The second challenge, which we focus on in this manuscript, is that the input variables for the SPIB model are typically derived from prior knowledge of the system, such as expert-based metrics like root mean square deviation (RMSD),22 radius of gyration (Rg), coordination number,23 and Steinhardt order parameters.24 However, these hand-crafted variables often lack transferability across systems, necessitating parameter tuning to construct effective CVs.25
To address this challenge, efforts have been made to construct ML-based CVs from elementary variables like pairwise distances,26–30 yielding valuable insights. However, as noted in ref. 28 and 29, the stability of these methods deteriorates when the input dimension exceeds 100 when biasing, making them less suitable for many-body systems or large biomolecules. Additionally, this approach does not resolve symmetry issues common, for instance, in materials science. Although pairwise distances are invariant to translation and rotation, the learned latent variables in typical neural networks are not permutation-invariant, meaning reordering input features can alter the CV value for the same configuration. While symmetry functions can be introduced to enforce invariance, this is often time-consuming.25,31,32 Moreover, ML methods with multilayer perceptrons (MLPs) lack transferability to systems of different sizes, whereas GNNs can accommodate systems of varying sizes.
Graph neural networks (GNNs) have recently gained attention because of their effectiveness in constructing representations across various applications, particularly in materials science, due to their inherent permutation invariance.7,17,33–44 In this work, we extend the SPIB framework by incorporating a GNN head with different graph convolutional layers. This specifically addresses the limitations of the original SPIB algorithm which needed physical-inspired hand-crafted input variables, while here a meaningful representation is learned on the fly with invariant pairwise distance variables. This enables us to apply the same framework with similar architectures across diverse systems without relying on system-specific expert knowledge, making it more broadly applicable. We tested our enhanced method on three representative model systems using our machine-learned CVs, which we call GNN-SPIB CVs. The systems are the Lennard-Jones 7 cluster, where permutation symmetry is crucial, and alanine dipeptide and tetrapeptide, where high-order representations such as torsion angles are typically required. With straightforward graph construction and basic features, our approach successfully learns meaningful and useful representations across all systems, using three representative graph layers to show the flexibility of our proposed framework. Additionally, the latent variables derived from our method provided thermodynamic and kinetic estimates comparable to those obtained using metadynamics-based methods that bias physically inspired expert-based CVs. This demonstrates the robustness and adaptability of our approach in overcoming previous challenges.
2 Methods
In this section, we provide an overview of the different techniques we use to learn latent geometric representations and assess their quality through enhanced sampling. Details of the enhanced sampling methods,45–47 model system setups, neural network training protocols, and definition of the expert-based collective variables are provided in the ESI.†2.1 State predictive information bottleneck
The state predictive information bottleneck (SPIB) developed by Wang and Tiwary16 is a variant of the Reweighted Autoencoded Variational Bayes for Enhanced sampling (RAVE) method.48 RAVE allows one to learn a meaningful representation with a variational autoencoder (VAE) framework from biased or unbiased data in the form of a time-series Ytn, comprising generally of several expert-selected features as a function of time. Building on this theme, SPIB was introduced as a more interpretable and robust model within the RAVE family, designed to learn a meaningful low-dimensional representation that accounts for the metastable states of most molecular systems, where the system spends extended periods undergoing fluctuations. Instead of predicting the details of these fluctuations Y within the states, it is then more crucial to predict which metastable state S the system will be in after a time delay Δt. To reflect this, the objective function, in SPIB, aims to predict future state labels Stn+Δt:
in SPIB, aims to predict future state labels Stn+Δt: | (1) |
 is the mutual information between variables x and y; z is the low-dimensional latent representation; and Stn+Δt is the state label after a time delay Δt. β is a tunable hyperparameter which controls regularization versus prediction, while tuning the time delay Δt controls the extent of temporal coarse-graining of the dynamics as learned by SPIB. After an initial trial assignment of states which can be very approximate, SPIB learns both the number of metastable states and their locations in the high-dimensional feature space Y. The number of metastable states generally reduces as a function of the time delay Δt. Introducing this metastability based prediction task makes SPIB latent space physically meaningful as now they correspond to the slow degrees of freedom, making the learned representation more interpretable. This approach has been successfully applied to enhancing sampling of transitions in complex systems28,49 and to approximating the 50% committor surface between metastable states.21,50
is the mutual information between variables x and y; z is the low-dimensional latent representation; and Stn+Δt is the state label after a time delay Δt. β is a tunable hyperparameter which controls regularization versus prediction, while tuning the time delay Δt controls the extent of temporal coarse-graining of the dynamics as learned by SPIB. After an initial trial assignment of states which can be very approximate, SPIB learns both the number of metastable states and their locations in the high-dimensional feature space Y. The number of metastable states generally reduces as a function of the time delay Δt. Introducing this metastability based prediction task makes SPIB latent space physically meaningful as now they correspond to the slow degrees of freedom, making the learned representation more interpretable. This approach has been successfully applied to enhancing sampling of transitions in complex systems28,49 and to approximating the 50% committor surface between metastable states.21,50
2.2 Graph and graph neural network
Graph data, denoted as G(V, E), consist of a set of nodes V and edges E, each carrying specific geometric information. Typically, three key components define this graph structure, which we summarize here for the sake of completeness:(1) Node features (Xi): each node i ∈ V is associated with a feature vector Xi, which encapsulates the intrinsic properties or characteristics of the node.
(2) Edge indices (i, j): the relationships between nodes are represented by edge indices (i, j) in an adjacency matrix aij ∈ {0, 1}, defining the neighborhood structure and indicating direct connections between nodes.
(3) Edge features (Lij): these describe the nature of the connection between nodes i and j, capturing attributes like weight, distance, or type.
In order to make meaningful predictions with inputs in graph objects, a special type of neural network, known as a graph neural network (GNN), is needed. Given the complexity of typical graph data, layers in the GNN are designed and trained with care. Within each graph layer, message-passing can break into three sequential steps:
(1) At layer l, message m between node i and each neighbor  , defined by the adjacency matrix, is computed via a message function (eqn (2)). The embedding h0 = X at layer l = 0 will be updated via each message passing operation.
, defined by the adjacency matrix, is computed via a message function (eqn (2)). The embedding h0 = X at layer l = 0 will be updated via each message passing operation.
| mijl = msg{hil, hjl, Lij} | (2) |
(2) This information from neighbors is then combined via an aggregate function (eqn (3)), which can be as simple as summation and averaging.
| mil = agg{mijl} | (3) |
(3) Lastly, the collected information from step 2 is integrated into the node features through an update function (eqn (4)):51
| hil+1 = upd{hil, mil} | (4) |
Note that preserving the permutation-invariant property in GNNs requires careful design of the above operations. In this work, we ensured that our models maintain this property by including invariant input features and allowing invariant operation during message passing in graph layers.
2.3 Graph-based SPIB
As introduced above, low-dimensional representations learned by an SPIB model are capable of learning the number of metastable states and their locations and capturing the slow processes that govern transitions between them. These joint capabilities differentiate SPIB from other dimensionality reduction schemes. However, SPIB still needs a dictionary of features Y which can collectively, in high dimensions, demarcate different metastable states. Defining these variables can be challenging when studying complex systems, as they often rely on prior system knowledge. Using poorly distinguishable input variables may degrade the performance of enhanced sampling methods that use SPIB-trained variables. To fully automate the representation learning in SPIB and eliminate the need for expert-defined input variables, we integrate a graph neural network head into the existing SPIB model.Integrated together, the architecture is summarized in Fig. 1, and we refer to it as GNN-SPIB. While it is overall akin to the original SPIB framework,16 the input trajectory is now a graph comprising geometric representations of the simulation cell at each time frame, whereas in SPIB, the input comprised expert-based features. Following the same notation, we denote the input graph as Gtn at time frame tn, and therefore the loss function in eqn (1) is rewritten as:
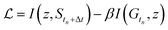 | (5) |
Additionally, the high-dimensional nature of graph data provides a better description of the simulation cell than expert-based features. In this work, SPIB and graph models were developed with Pytorch52 and Pytorch geometric53 packages, respectively. Given the diversity of graph layers, we do not want to limit ourselves to certain graph layers or GNN architecture, and therefore, we selected three representative graph message passing layers when studying the three model systems to present the general applicability of our proposed framework. We believe that the selection of graph message passing layers can be rather flexible given the fact that the basic principle, message-passing operation is permutational-invariance, is enforced in most of these graph layers. The only design parameter here that requires care is that informative graph layers are always at a higher computational cost which may largely slow down enhancing sampling methods.
Workarounds similar to ours have been used in other representation learning methods. The closest related method is the variational approach for Markov processes (VAMP) net, a machine learning architecture that constructs a Markov state model (MSM) and optimizes the VAMP-2 score derived from the single value decomposition of the corresponding Koopman operator.54 In VAMPnet, MD configuration coordinates are used as input to the machine learning model. To address symmetry issues, alignment of configurations is necessary, which is common in computational studies of biological systems but less applicable to materials science. As an alternative, a graph representation was introduced into the standard VAMPnet architecture.44,55,56 All GNN layers chosen in this work are E(3)-invariant GNNs, while a more data-efficient equivariant GNN representation learning scheme was introduced recently in ref. 44.
3 Results and discussion
We evaluate the ability of the GNN-SPIB low-dimensional latent representations to enhance sampling for three model systems. For all three systems, we perform well-tempered metadynamics (WTmetadD) (see the ESI† for a detailed introduction to this method) to quantify the quality of calculated free energy and infrequent metadynamics (imetaD) (see the ESI† for details about this method) to calculate kinetics. The three systems are Lennard-Jones 7 (LJ7, in Sec. 3.1), alanine dipeptide (Sec. 3.2) and alanine tetrapeptide (Sec. 3.3). As a general pipeline for the three systems, we first train the models with data collected from short MD simulations at higher temperatures in which all targeted metastable states are visited but their sampling is incorrect/unconverged especially for the lower temperature of interest. We then perform WTmetaD simulations biasing along the GNN-SPIB latent variables, compute the free energy difference between states, and compare with results from much longer unbiased MD simulations and WTmetaD simulations biasing conventional expert-based CVs. After thermodynamic measurements with WTmetaD, we also collect kinetic information with imetaD simulations.3.1 Lennard-Jones 7
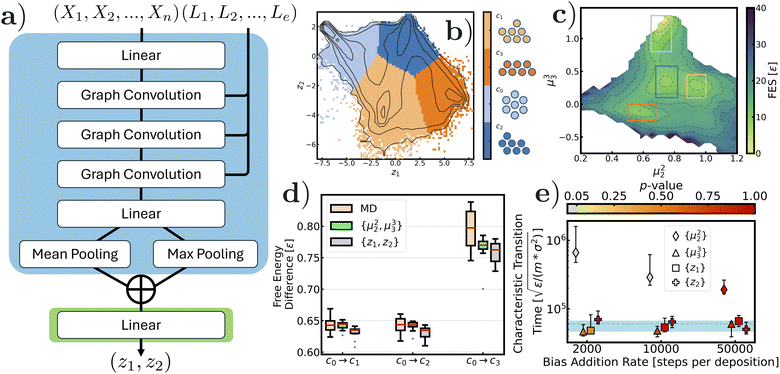
As suggested by its name, Lennard-Jones 7 (LJ7) consists of a cluster of 7 Lennard-Jones particles in 2-d. It is considered one of the simplest model systems for colloidal rearrangements, where translational-, rotational-, and permutational-symmetry problems are encountered, with metastable states. The free energy landscape and state-to-state dynamics of LJ7 are well-studied, making it an excellent model system for benchmarking enhanced sampling methods of rare events.57Fig. 2 summarizes the results when biasing along the 2-dimensional GNN-SPIB latent variables, z1 and z2. The input graphs come from snapshots of a trajectory of 1 × 107 steps at a temperature of kBT = 0.2∈. These are composed of identical node attributes {Xn} = {1, 1⋯1} and pair distance edge features {Le}. The graph convolution layers, which are considered as one of the simplest graph layers, are directly adopted from ref. 58 and graph embeddings are pooled with mean and max operators (see Fig. 2a in blue). The hidden embedding of graph layers is then fed into the SPIB model (Fig. 2a in green; we have provided detailed information about the training process in the ESI†) for extrapolating dynamic information. Fig. 2b shows the SPIB converged state labels as colored regions where we observe four distinct, local minima corresponding to the four well known structures for the LJ-7 system. In particular, these 4 configurations are c0 (hexagon), c1 (capped parallelogram 1), c2 (capped parallelogram 2), and c3 (trapezoid) (see schematics next to Fig. 2b and the colorbar). Given the fact that the predicted state labels are correctly assigned to 4 distinct energy minima in GNN-SPIB latent space, we believe that the trained model is able to classify the configuration of the LJ7 cluster when providing the corresponding geometric representation in nodes and edges, and therefore, the encoded latent representation from GNN-SPIB can be used as a biasing variable in metadynamics simulations.
To verify this, WTmetaD simulations were performed at kBT = 0.1∈ biasing the 2-d reaction coordinates, z1 and z2, and the resulting free energy surfaces are shown in (Fig. 2c). For better evaluation of the sampling quality, we projected the free energy surface onto the more meaningful space comprising the second and third moments of the coordination numbers, introduced previously in ref. 59. These expert-based CVs have been used previously to study this system60 and thus provide a good way to test the quality of samples generated from biasing along the GNN-SPIB, which is physically less meaningful. Four distinct local minima were sampled, which is a strong indicator of good sampling quality for this system. To further evaluate the quality of the sampling, we tabulated the free energy differences between the sampled configurations and the initial state, c0. As a benchmark, we performed an additional 10 independent, unbiased long MD simulations, 10 WTmetaD simulations biasing the conventional CV set {μ22, μ33}, and 10 WTmetaD simulations biasing the machine-learned 2D CV {z1, z2}. The MD simulations lasted for 1 × 109 steps, and the WTmetaD simulations lasted for 1 × 108 steps. Inspection of Fig. 2d reveals that WTmetaD simulations using GNN-SPIB CV produce results comparable to those using the expert-crafted moments of coordination number CVs (refer to the ESI† for numerical values). Notably, no information about the coordination was directly provided as input to the model and only the pairwise distances of neighboring nodes were used. We further evaluate the GNN-SPIB against conventional CVs by computing their correlation coefficients. The results (see the ESI†) show that both z1 and z2 have a stronger correlation to μ33 than to μ22.
As an even more demanding test, we ascertained the quality of the GNN-SPIB CV in obtaining accurate kinetics through imetaD calculations. In this task, we performed kinetic measurements by estimating the transition time of the slowest transition from initial state c0 to c3 using the imetaD method at kBT = 0.1∈. We performed these 1-d imetaD simulations separately biasing the GNN-SPIB z1 and z2. We benchmarked on characteristic transition time from reference unbiased MD simulations (dashed line with shaded errors in Fig. 3e). We also provide results of 1-d imetaD simulations using expert-based CVs μ22 and μ33. In particular, since the 1-d projection along μ33 suggests that the states c0 and c3 are well-separated, we expect μ33 to be a better expert-based CV for biasing relative to μ22 as it fails to distinguish c0 from c3. Using the imetaD method, the characteristic transition time remained robust and accurate under various bias addition frequencies when μ33, z1, and z2 variables were used. Specifically, we obtained transition times of 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 829 (95% confidence interval (CI): [46
829 (95% confidence interval (CI): [46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 282,73
282,73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 303]) and 64
303]) and 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 (95% CI: [52
504 (95% CI: [52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 986,77
986,77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 703])
703])  when biasing along the GNN-SPIB z1 and z2, respectively, with bias added every 1 × 104 steps. For reference, the transition time from long unbiased MD for the c0 → c3 transition was estimated to be 60
when biasing along the GNN-SPIB z1 and z2, respectively, with bias added every 1 × 104 steps. For reference, the transition time from long unbiased MD for the c0 → c3 transition was estimated to be 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630.31 (95% CI [46
630.31 (95% CI [46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 945, 66
945, 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 598])
598])  . The numerical values of 95% CI and the p-values of all performed simulations are provided in the ESI.† However, when μ22 was used in imetaD simulations, the characteristic transition time was off by at least one order of magnitude compared to the benchmark value, with a p-value less than 0.05 (markers in grey in Fig. 2e). In summary, the thermodynamic and kinetic evidence suggests that either of our GNN-SPIB CVs shows results comparable to conventional expert-based CVs when used in enhanced sampling.
. The numerical values of 95% CI and the p-values of all performed simulations are provided in the ESI.† However, when μ22 was used in imetaD simulations, the characteristic transition time was off by at least one order of magnitude compared to the benchmark value, with a p-value less than 0.05 (markers in grey in Fig. 2e). In summary, the thermodynamic and kinetic evidence suggests that either of our GNN-SPIB CVs shows results comparable to conventional expert-based CVs when used in enhanced sampling.
 | ||
| Fig. 3 Summary of WTmetaD simulation results for the alanine dipeptide system: (a) representation of the alanine dipeptide molecule61 with definition to expert-based CVs, ϕ and ψ. Graph representation is constructed with only heavy atoms and atomic labels are followed through the assigned node index to graphs; (b) a schematic of how the reaction coordinate, {z1, z2}, is computed with node {Vn} and edge {Le} features; (c) state label predictions in different colors from the model decoder with contour lines separated by 3 kJ mol−1; (d) reweighted free energy surface biasing the machine learned RC at 300 K using {ϕ, ψ} projection with conformer definitions in boxes; (e) free energy differences with the state defined in (d) under different sampling schemes; and (f) kinetic measurements of the transition from (C7eq, C5) to C7ax at 300 K with imetaD simulation. Dashed line in cyan is the benchmark MD simulation and marker points are results from imetaD using different RCs. The shaded region and error bars are the 95% confidence intervals. p-values from the K–S test for imetaD simulations are reflected by the colors and when the p-value is less than 0.05 (in grey), the result is unreliable. | ||
3.2 Alanine dipeptide
While the rearrangement of the LJ7 cluster is considered a simple model of colloidal system dynamics, the alanine dipeptide molecule serves as a popular toy model for biomolecular conformational changes. Here, we focus on transitions in a vacuum between three conformers: C5, C7eq, and C7ax. The set of expert-based CVs commonly used in enhanced sampling methods for this system includes the dihedral angles ϕ and ψ (Fig. 3a).27,62 In our model, unlike the previous example, the three elements carbon, nitrogen and oxygen in alanine dipeptide are one-hot encoded in their node features. Once again, we leverage the computational efficiency of using inter-atomic distances as edge features, similar to the LJ7 model. Although conformational changes in biomolecules like alanine dipeptide are generally described by high-order representations such as torsion angles, lower-dimensional descriptors for enhanced sampling methods can be learned through machine learning-based dimensionality reduction on inter-atomic distances.26,27,63,64 To increase the expressiveness of the model, we applied a basis function to slice the edge features (refer to the ESI† for details on this operation).43The overall architecture remains the same as in the study of the LJ7 cluster, but we replaced the graph convolution layers with more informative graph attention network (GAT) convolution layers, to show the robustness of our proposed framework. We have provided information about the training process and the hyperparameters used in the ESI.65† However, this does not necessarily mean that the graph convolutional layer, which was adopted in the LJ7 system, is not applicable here. We trained another GNN-SPIB with the exact architecture shown in (Fig. 2a) on alanine dipeptide data and the results showing the model's ability in distinguishing all metastable states are presented in the ESI.† Three distinct minima are shown when projected onto the learned latent space with input data sampled at T = 400 K (Fig. 3c), and the reweighted free energy surface in the ϕ, ψ space from WTmetaD simulations using the z1 and z2 variables is shown in Fig. 3d, where all targeted states are well-sampled. The free energy differences between individual conformers were tabulated and benchmarked with brute-force MD simulations and WTmetaD simulations using ϕ, ψ dihedrals (see Fig. 3e). The results are in good agreement, with discrepancies of less than 1 kJ mol−1. The numerical values of the free energy difference are reported in the ESI.† In addition, we see a strong correlation of z1 with ϕ and ψ variables and only a moderate correlation of z2 with these two torsion angles (see the ESI† for the scatter plot).
We then move to the more challenging validation of kinetics through enhanced sampling. The evaluation metric of kinetics focused on the slowest transition, C7eq → C7ax, in alanine dipeptide, and the results are summarized in Fig. 3f. The characteristic transition time was estimated to be 3.340 (95% CI [2.857, 4.259]) μs, which is in accordance with ref. 66. The values in Fig. 3f suggest that both the 1-d expert-based CV ϕ and our GNN-SPIB CV {z1, z2} are effective at the obtained accurate reweighted kinetics (see the ESI† for complete reports on kinetics measurements). ψ alone is known to be a poor CV for this system,66 which is reflected in the inaccurate kinetics when biasing along ψ irrespective of the frequency of bias deposition. Notably, unlike the LJ7 case, we directly performed imetaD simulations on the 2-d CV set, as 1-d imetaD simulations biasing either z1 or z2 did not yield good estimations of transition times. This is unsurprising, as the GNN-SPIB latent variables were set and trained in 2-d, and thus the complete information of this complex conformational change was likely not captured by z1 or z2 alone. At a 50 ns−1 bias addition rate (i.e. 1 Gaussian deposition every 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps), the estimated transition time is 4.424 (95% CI [3.662, 5.384]) μs, which is in agreement with that estimated in MD simulations (see all estimated values at different deposition rates in the ESI†).
000 steps), the estimated transition time is 4.424 (95% CI [3.662, 5.384]) μs, which is in agreement with that estimated in MD simulations (see all estimated values at different deposition rates in the ESI†).
We further evaluated the attention coefficients from the GAT layers, which reflect how information is exchanged during message passing, providing insights into the system (see the ESI† for complete attention matrices). In the first graph attention convolution layer, long-range interactions describing global molecular orientations, such as Cw1–Cw2 and N1–N2 distances, drew the model's attention. In contrast, local arrangements (e.g., O1–N1 and N1–Cβ distances) had high attention weights in the second graph attention layer (see Fig. 3a for atom labels). This suggests that, without high-order representations of the conformation, transitions between conformers are decoded sequentially from far to near using pairwise distances. Additionally, edges with large attention weights are those connected to the N1 atom, which is used to define the torsion angle ϕ, indicating the importance of the ϕ angle over the ψ angle.
3.3 Alanine tetrapeptide
For our third and final example, we study conformational changes in a much more complicated model system, namely alanine tetrapeptide in a vacuum. For this system, there exist at least 8 metastable states in total. For these states, we follow the notations from ref. 67, numbering these states as in ref. 67 as si, i = 1⋯8. In particular, to capture the intricacies of alanine tetrapeptide conformational changes, six dihedral angles are considered important: ϕ1, ϕ2, ϕ3, ψ1, ψ2, and ψ3 (see Fig. 4b for their definitions). Using a similar workflow as before, the alanine tetrapeptide molecule is first converted into graph objects, i.e., all hydrogens are removed and C, N, and O atoms are retained during the graph construction. The nodes in the graph are set to be fully connected, and edge features are defined as interatomic distances. We adopted a skip connection scheme that allows information from all graph layers to flow to the pooling operator, thereby improving the model's expressiveness in capturing features from all metastable states. Additionally, as shown in Fig. 4a, we considered all three typical pooling operations: mean, max, and sum in this example. | ||
| Fig. 4 Summary of WTmetaD simulation results in the alanine tetrapeptide system: (a) a schematic of reaction coordinate construction with a combination of embeddings of each graph convolution layers via skip connections before graph-level pooling operations; (b) representation of the alanine tetrapeptide molecule61 with definitions of characteristic dihedral angles, ϕ1, ϕ2, ϕ3, ψ1, ψ2, and ψ3 and only heavy atoms are involved during graph construction; (c) the learned latent variable space {z1, z2} with state labels predicted by the model on training data and the free energy surface with contours separated by 2 kJ mol−1; (d) reweighted free energy surface of WTmetaD simulations using 2-d {z1, z2} variables at 350 K projected onto {ϕ1, ϕ2, ϕ3} space; (e) tabulated free energy differences between all conformers from brute force MD simulations, WTmetaD simulations biasing {ϕ1, ϕ2, ϕ3}, and WTmetaD simulations biasing {z1, z2}; and (f) characteristic transition times of s1 → s7 measured by imetaD simulations using different variables at 400 K. Dashed line in cyan is the benchmark MD simulation and marker points are results from imetaD using different RCs. The shaded region and error bars are the 95% confidence intervals. p-values from the K–S test for imetaD simulations are reflected by the colors and when the p-value is greater than 0.05, the estimation is reliable. | ||
Once again, the graph layers were switched and chosen to be an expressive Gaussian Mixture model (see the ESI† for details about the model).68 Similarly, we trained a GNN-SPIB with the architecture shown in (Fig. 2a) to present the generalizability of our approach, and the results (see the ESI†) suggest that the model is able to identify metastable states in alanine tetrapeptide. Our input training data are from a 1 μs-long MD simulation at 400 K, where s6 is barely sampled. These input training data are projected onto the trained latent space {z1, z2} in Fig. 4c. As shown by the color coding, the model successfully learned 7 out of 8 metastable states, though the states s6 and s7 remain indistinguishable from each other. This is due to the lack of samples from s6 during training. Nevertheless, performing WTmetaD simulations using {z1, z2} for 200 ns at a lower temperature of 350 K drives the system to visit all 8 metastable states for alanine tetrapeptide. To demonstrate the quality of our sampling, we project the trajectory onto the {ϕ1, ϕ2, ϕ3} space and label all target states in Fig. 4d. The free energy differences between all 8 states are computed and shown in a box plot (Fig. 4e), along with two benchmark methods: standard long MD simulations and 3-d WTmetaD simulations using {ϕ1, ϕ2, ϕ3} variables. The free energy differences converge to well-defined values, aligning with those from the benchmark methods (Fig. 4e) (see the ESI† for details). From evaluating the correlation between machine learned variables and conventional variables, we find that z1 and z2 show correlations with only a few torsion angles such as ϕ3 and ψ2. This suggests that our machine learning model learned different descriptors of conformational changes in the system compared to conventional knowledge-based variable – torsion angles, such discrepencies have been detailed investigated in ref. 69.
While performing 3-d biasing along {ϕ1, ϕ2, ϕ3} space reveals accurate kinetic measurements, imetaD simulations using {ψ1, ψ2, ψ3} performed poorly by largely overestimating the transition time under various biasing paces. Values estimated by imetaD simulations biasing the 2-d GNN-SPIB {z1, z2} variables were in agreement with benchmark values and this variable remained robust to frequent biasing deposition rates. As summarized in the subplot of Fig. 4f, we estimated the characteristic transition time from the unfolded substate s1 to the folded substate s7 at 400 K. The timescale was estimated to be 489 (95% CI [409, 612]) ns using reference unbiased MD simulations. Values estimated by imetaD simulations biasing the 2-d GNN-SPIB {z1, z2} variables were 460 (95% CI [378, 618]) ns with a 500 ns−1 deposition rate (i.e. 1 Gaussian deposition every 1000 steps), in agreement with the benchmark values and remained robust to frequent bias deposition rates (see the ESI† for details). Finally, while performing 3-d biasing along the {ϕ1, ϕ2, ϕ3} space reveals accurate kinetic measurements, imetaD simulations using {ψ1, ψ2, ψ3} performed poorly, significantly overestimating the transition time under various biasing paces. This reflects how one set of expert-based CVs can significantly differ from another in the quality of sampling.
4 Conclusion
While enhanced sampling methods have significantly extended the capabilities of molecular dynamics simulations, identifying optimal coordinates remains an ongoing challenge. Even methods using machine learning, while somewhat automating the process, still rely on expert-based features to be pre-selected. In this work, we introduced a hybrid framework combining graph neural networks and the state predictive information bottleneck, named the GNN-SPIB approach, to automatically learn low-dimensional representations of complex systems, further removing this limitation. This approach allows the model to learn configurations via graph layers while capturing system dynamics through the past-future information bottleneck.We demonstrated the effectiveness of our method on three benchmark systems: the Lennard-Jones 7 cluster, alanine dipeptide, and alanine tetrapeptide. Each system presents distinct challenges in learning meaningful representations, such as the need for permutation invariance in the Lennard-Jones cluster or high-order variables like angles for peptide systems. By applying three representative graph message-passing layers, we showcased the robustness and flexibility of the proposed framework. Importantly, our results are not confined to specific graph layers or architectures, underscoring the generalizability of this approach across diverse systems.
Biasing these GNN-SPIB in WTmetaD simulations yielded results comparable to those obtained using conventional CVs both for the calculation of free energy surfaces and kinetic transition times. Given the simplicity of the input features, specifically pairwise distances, we believe that this method holds promise for complex systems where optimal reaction coordinates for enhanced sampling methods are not known a priori. The major computational cost of the current method remains to be backpropagating low-dimensional representations to high-dimensional atomic coordinates, which can be properly accelerated with GPU-support44 and/or by optimizing the design of current models with an optimal number of training parameters. Like other variants in the RAVE family, our learned reaction coordinates can be iteratively improved with better sampling, particularly for complex systems, as noted in ref. 29. Future work could expand this approach by incorporating high-order representations such as angles or spherical harmonics.51 Additionally, the input data for model training need not be limited to simulations; static data from metastable states, as demonstrated in previous studies, can also lead to meaningful latent representations.17,19–21
Data availability
The codes used for reproducing the simulations are available at PLUMED-NEST https://www.plumed-nest.org/eggs/24/020/.Author contributions
Z. Z., D. W., and P. T. designed research; Z. Z. and D. W. developed algorithms; Z. Z. performed research and analyzed data; Z. Z. wrote the initial draft; and Z. Z., D. W., and P. T. revised the paper.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This research was entirely supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, CPIMS Program, under Award DE-SC0021009. Z. Z. thanks Zachary Smith and Suemin Lee for help in graph neural nets and infrequent metadynamics simulations. The authors thank Eric Beyerle, Bodhi P. Vani, Shams Mehdi, Akashnathan Aranganathan, and Venkata Adury for fruitful discussions. The authors also thank Bodhi P. Vani, Zachary Smith, Vanessa J. Meraz, and Suemin Lee for proofreading the manuscript. P.T. is an investigator at the University of Maryland-Institute for Health Computing, which is supported by funding from Montgomery County, Maryland, and The University of Maryland Strategic Partnership: MPowering the State, a formal collaboration between the University of Maryland, College Park, and the University of Maryland, Baltimore. We are also grateful to NSF ACCESS Bridges2 (project CHE180053) and the University of Maryland Zaratan High-Performance Computing cluster for enabling the work performed in this study.References
- S. Mehdi, Z. Smith, L. Herron, Z. Zou and P. Tiwary, Enhanced Sampling with Machine Learning, Annu. Rev. Phys. Chem., 2024, 75, 38382572 CrossRef PubMed.
- F. Noé, A. Tkatchenko, K.-R. Müller and C. Clementi, Machine learning for molecular simulation, Annu. Rev. Phys. Chem., 2020, 71, 361–390 CrossRef PubMed.
- M. Chen, Collective variable-based enhanced sampling and machine learning, Eur. Phys. J. B, 2021, 94, 1–17 CrossRef.
- S. Sarupria, S. W. Hall and J. Rogal, Machine learning for molecular simulations of crystal nucleation and growth, MRS Bull., 2022, 47, 949–957 CrossRef CAS.
- E. R. Beyerle, Z. Zou and P. Tiwary, Recent advances in describing and driving crystal nucleation using machine learning and artificial intelligence, Curr. Opin. Solid State Mater. Sci., 2023, 27, 101093 CrossRef CAS.
- H. Jung, R. Covino, A. Arjun, C. Leitold, C. Dellago, P. G. Bolhuis and G. Hummer, Machine-guided path sampling to discover mechanisms of molecular self-organization, Nat. Comput. Sci., 2023, 1–12 CAS.
- F. M. Dietrich, X. R. Advincula, G. Gobbo, M. A. Bellucci and M. Salvalaglio, Machine Learning Nucleation Collective Variables with Graph Neural Networks, J. Chem. Theory Comput., 2024, 20, 1600–1611 CrossRef CAS.
- N. S. M. Herringer, S. Dasetty, D. Gandhi, J. Lee and A. L. Ferguson, Permutationally Invariant Networks for Enhanced Sampling (PINES): Discovery of Multimolecular and Solvent-Inclusive Collective Variables, J. Chem. Theory Comput., 2024, 20, 178–198 CrossRef CAS.
- O. Elishav, R. Podgaetsky, O. Meikler and B. Hirshberg, Collective Variables for Conformational Polymorphism in Molecular Crystals, J. Phys. Chem. Lett., 2023, 14, 971–976 CrossRef CAS.
- W. Zhang and C. Schütte, Understanding recent deep-learning techniques for identifying collective variables of molecular dynamics, PAMM, 2023, 23, e202300189 CrossRef.
- E. Prašnikar, M. Ljubič, A. Perdih and J. Borišek, Machine learning heralding a new development phase in molecular dynamics simulations, Artif. Intell. Rev., 2024, 57, 102 CrossRef.
- L. Müllender, A. Rizzi, M. Parrinello, P. Carloni and D. Mandelli, Effective data-driven collective variables for free energy calculations from metadynamics of paths, PNAS Nexus, 2024, 3, pgae159 CrossRef.
- A. Majumder and J. E. Straub, Machine Learning Derived Collective Variables for the Study of Protein Homodimerization in Membrane, J. Chem. Theory Comput., 2024, 20, 5774–5783 CrossRef CAS PubMed.
- A. France-Lanord, H. Vroylandt, M. Salanne, B. Rotenberg, A. M. Saitta and F. Pietrucci, Data-Driven Path Collective Variables, J. Chem. Theory Comput., 2024, 20, 3069–3084 CrossRef CAS.
- S.-K. Lee, S.-T. Tsai and S. C. Glotzer, Classification of complex local environments in systems of particle shapes through shape symmetry-encoded data augmentation, J. Chem. Phys., 2024, 160, 154102 CrossRef CAS PubMed.
- D. Wang and P. Tiwary, State predictive information bottleneck, J. Chem. Phys., 2021, 154, 134111 CrossRef CAS.
- Z. Zou and P. Tiwary, Enhanced Sampling of Crystal Nucleation with Graph Representation Learnt Variables, J. Phys. Chem. B, 2024, 128, 3037–3045 CrossRef CAS.
- Y. Wang, J. M. L. Ribeiro and P. Tiwary, Past–future information bottleneck for sampling molecular reaction coordinate simultaneously with thermodynamics and kinetics, Nat. Commun., 2019, 10, 1–8 CrossRef.
- B. P. Vani, A. Aranganathan, D. Wang and P. Tiwary, AlphaFold2-RAVE: From Sequence to Boltzmann Ranking, J. Chem. Theory Comput., 2023, 19, 4351–4354 CrossRef CAS PubMed.
- B. P. Vani, A. Aranganathan and P. Tiwary, Exploring Kinase Asp-Phe-Gly (DFG) Loop Conformational Stability with AlphaFold2-RAVE, J. Chem. Inf. Model., 2024, 64, 2789–2797 CrossRef CAS.
- X. Gu, A. Aranganathan and P. Tiwary, Empowering AlphaFold2 for protein conformation selective drug discovery with AlphaFold2-RAVE, eLife, 2024, 13, RP99702 CrossRef PubMed.
- S. K. Kearsley, On the orthogonal transformation used for structural comparisons, Acta Crystallogr., Sect. A, 1989, 45, 208–210 CrossRef.
- S.-T. Tsai, Z. Smith and P. Tiwary, Reaction coordinates and rate constants for liquid droplet nucleation: Quantifying the interplay between driving force and memory, J. Chem. Phys., 2019, 151, 154106 CrossRef.
- P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Bond-orientational order in liquids and glasses, Phys. Rev. B:Condens. Matter Mater. Phys., 1983, 28, 784 CrossRef CAS.
- P. Geiger and C. Dellago, Neural networks for local structure detection in polymorphic systems, J. Chem. Phys., 2013, 139, 164105 CrossRef PubMed.
- J. Rydzewski and O. Valsson, Multiscale Reweighted Stochastic Embedding: Deep Learning of Collective Variables for Enhanced Sampling, J. Phys. Chem. A, 2021, 125, 6286–6302 CrossRef CAS PubMed.
- L. Bonati, V. Rizzi and M. Parrinello, Data-Driven Collective Variables for Enhanced Sampling, J. Phys. Chem. Lett., 2020, 11, 2998–3004 CrossRef CAS.
- S. Mehdi, D. Wang, S. Pant and P. Tiwary, Accelerating All-Atom Simulations and Gaining Mechanistic Understanding of Biophysical Systems through State Predictive Information Bottleneck, J. Chem. Theory Comput., 2022, 18, 3231–3238 CrossRef CAS PubMed.
- S. Lee, D. Wang, M. A. Seeliger and P. Tiwary, Calculating Protein–Ligand Residence Times through State Predictive Information Bottleneck Based Enhanced Sampling, J. Chem. Theory Comput., 2024, 20, 6341–6349 CrossRef CAS.
- D. Wang and P. Tiwary, Augmenting Human Expertise in Weighted Ensemble Simulations through Deep Learning based Information Bottleneck, J. Chem. Theory Comput., 2024 DOI:10.1021/acs.jctc.4c00919.
- J. Behler and M. Parrinello, Generalized neural-network representation of high-dimensional potential-energy surfaces, Phys. Rev. Lett., 2007, 98, 146401 CrossRef.
- J. Rogal, E. Schneider and M. E. Tuckerman, Neural-Network-Based Path Collective Variables for Enhanced Sampling of Phase Transformations, Phys. Rev. Lett., 2019, 123, 245701 CrossRef CAS PubMed.
- D. Kuroshima, M. Kilgour, M. E. Tuckerman and J. Rogal, Machine Learning Classification of Local Environments in Molecular Crystals, J. Chem. Theory Comput., 2024, 20(14), 6197–6206 CrossRef CAS PubMed.
- M. Sipka, A. Erlebach and L. Grajciar, Constructing Collective Variables Using Invariant Learned Representations, J. Chem. Theory Comput., 2023, 19, 887–901 CrossRef CAS.
- R. S. DeFever, C. Targonski, S. W. Hall, M. C. Smith and S. Sarupria, A generalized deep learning approach for local structure identification in molecular simulations, Chem. Sci., 2019, 10, 7503–7515 RSC.
- A. Moradzadeh, H. Oliaei and N. R. Aluru, Topology-Based Phase Identification of Bulk, Interface, and Confined Water Using an Edge-Conditioned Convolutional Graph Neural Network, J. Phys. Chem. C, 2023, 127, 2612–2621 CrossRef CAS.
- S. Banik, D. Dhabal, H. Chan, S. Manna, M. Cherukara, V. Molinero and S. K. Sankaranarayanan, CEGANN: Crystal Edge Graph Attention Neural Network for multiscale classification of materials environment, npj Comput. Mater., 2023, 9, 23 CrossRef.
- Q. Kim, J.-H. Ko, S. Kim and W. Jhe, GCIceNet: a graph convolutional network for accurate classification of water phases, Phys. Chem. Chem. Phys., 2020, 22, 26340–26350 RSC.
- M. Fulford, M. Salvalaglio and C. Molteni, DeepIce: A deep neural network approach to identify ice and water molecules, J. Chem. Inf. Model., 2019, 59, 2141–2149 CrossRef CAS.
- T. Xie and J. C. Grossman, Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- P. B. Jørgensen, K. W. Jacobsen and M. N. Schmidt, Neural message passing with edge updates for predicting properties of molecules and materials, arXiv, 2018, preprint, arXiv:1806.03146, DOI:10.48550/arXiv.1806.03146.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Neural message passing for quantum chemistry, International conference on machine learning, 2017, pp. 1263–1272 Search PubMed.
- K. Schütt, P.-J. Kindermans, H. E. Sauceda Felix, S. Chmiela, A. Tkatchenko and K.-R. Müller, Schnet: A continuous-filter convolutional neural network for modeling quantum interactions, Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, ed. I. Guyon, U. von Luxburg, S. Bengio, H. M. Wallach, R. Fergus, S. V. N. Vishwanathan and R. Garnett, Long Beach, CA, USA, December 4–9, 2017, 30, pp. 991–1001 Search PubMed.
- J. Zhang, L. Bonati, E. Trizio, O. Zhang, Y. Kang, T. Hou and M. Parrinello, Descriptors-free Collective Variables From Geometric Graph Neural Networks, arXiv, 2024, preprint, arXiv:2409.07339, DOI:10.48550/arXiv.2409.07339.
- O. Valsson, P. Tiwary and M. Parrinello, Enhancing important fluctuations: Rare events and metadynamics from a conceptual viewpoint, Annu. Rev. Phys. Chem., 2016, 67, 159–184 CrossRef CAS PubMed.
- A. Laio and M. Parrinello, Escaping free-energy minima, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS.
- P. Tiwary and M. Parrinello, From metadynamics to dynamics, Phys. Rev. Lett., 2013, 111, 230602 CrossRef PubMed.
- J. M. L. Ribeiro, P. Bravo, Y. Wang and P. Tiwary, Reweighted autoencoded variational Bayes for enhanced sampling (RAVE), J. Chem. Phys., 2018, 149, 072301 CrossRef.
- N. D. Pomarici, S. Mehdi, P. K. Quoika, S. Lee, J. R. Loeffler, K. R. Liedl, P. Tiwary and M. L. Fernández-Quintero, Learning high-dimensional reaction coordinates of fast-folding proteins using State Predictive information bottleneck and Bias Exchange Metadynamics, bioRxiv, 2023, preprint, DOI:10.1101/2023.07.24.550401.
- D. Wang, R. Zhao, J. D. Weeks and P. Tiwary, Influence of Long-Range Forces on the Transition States and Dynamics of NaCl Ion-Pair Dissociation in Water, J. Phys. Chem. B, 2022, 126, 545–551 CrossRef CAS.
- A. Duval, S. V. Mathis, C. K. Joshi, V. Schmidt, S. Miret, F. D. Malliaros, T. Cohen, P. Liò, Y. Bengio and M. Bronstein, A Hitchhiker's Guide to Geometric GNNs for 3D Atomic SystemsarXiv, 2024, preprint, arXiv:2312.07511, DOI:10.48550/arXiv.2312.07511.
- A. Paszke, et al., PyTorch: An Imperative Style, High-Performance Deep Learning Library, arXiv, 2019, preprint, arXiv:1912.01703, DOI:10.48550/arXiv.1912.01703.
- M. Fey and J. E. Lenssen, Fast Graph Representation Learning with PyTorch Geometric, arXiv, 2019, preprint, arXiv:1903.02428, DOI:10.48550/arXiv.1903.02428.
- A. Mardt, L. Pasquali, H. Wu and F. Noé, VAMPnets for deep learning of molecular kinetics, Nat. Commun., 2018, 9, 1–11 CrossRef.
- M. Ghorbani, S. Prasad, J. B. Klauda and B. R. Brooks, GraphVAMPNet, using graph neural networks and variational approach to Markov processes for dynamical modeling of biomolecules, J. Chem. Phys., 2022, 156, 184103 CrossRef CAS PubMed.
- B. Liu, M. Xue, Y. Qiu, K. A. Konovalov, M. S. O'Connor and X. Huang, GraphVAMPnets for uncovering slow collective variables of self-assembly dynamics, J. Chem. Phys., 2023, 159, 094901 CrossRef CAS PubMed.
- P. Schwerdtfeger and D. J. Wales, 100 Years of the Lennard-Jones Potential, J. Chem. Theory Comput., 2024, 20, 3379–3405 CrossRef CAS.
- V. G. Satorras, E. Hoogeboom and M. Welling, E(n) Equivariant Graph Neural Networks, arXiv, 2021, preprint, arXiv:2102.09844, DOI:10.48550/arXiv.2102.09844.
- G. A. Tribello, M. Ceriotti and M. Parrinello, A self-learning algorithm for biased molecular dynamics, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 17509–17514 CrossRef CAS.
- L. Evans, M. K. Cameron and P. Tiwary, Computing committors in collective variables via Mahalanobis diffusion maps, Appl. Comput. Harmon. Anal., 2023, 64, 62–101 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- P. G. Bolhuis, C. Dellago and D. Chandler, Reaction coordinates of biomolecular isomerization, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 5877–5882 CrossRef CAS PubMed.
- T. Fröhlking, L. Bonati, V. Rizzi and F. L. Gervasio, Deep learning path-like collective variable for enhanced sampling molecular dynamics, J. Chem. Phys., 2024, 160, 174109 CrossRef.
- P. Kang, E. Trizio and M. Parrinello, Computing the committor with the committor to study the transition state ensemble, Nat. Comput. Sci., 2024, 4, 451–460 CrossRef.
- S. Brody, U. Alon and E. Yahav, How Attentive are Graph Attention Networks?, International Conference on Learning Representations, 2022, https://openreview.net/forum?id=F72ximsx7C1 Search PubMed.
- O. Blumer, S. Reuveni and B. Hirshberg, Combining stochastic resetting with Metadynamics to speed-up molecular dynamics simulations, Nat. Commun., 2024, 15, 240 CrossRef CAS.
- S.-T. Tsai, Z. Smith and P. Tiwary, SGOOP-d: Estimating Kinetic Distances and Reaction Coordinate Dimensionality for Rare Event Systems from Biased/Unbiased Simulations, J. Chem. Theory Comput., 2021, 17, 6757–6765 CrossRef CAS PubMed.
- F. Monti, D. Boscaini, J. Masci, E. Rodolà, J. Svoboda and M. M. Bronstein, Geometric deep learning on graphs and manifolds using mixture model CNNs, 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017, pp. 5425–5434 Search PubMed.
- D. Errington, C. Schneider, C. Bouysset and F. A. Dreyer, Assessing interaction recovery of predicted protein-ligand poses, arXiv, 2024, preprint, arXiv:2409.20227, DOI:10.48550/arXiv.2409.20227.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00315b |
| This journal is © The Royal Society of Chemistry 2025 |