Open Access Article
Open Access ArticleElectrostatic embedding machine learning for ground and excited state molecular dynamics of solvated molecules†
Patrizia
Mazzeo
 *,
Edoardo
Cignoni
*,
Edoardo
Cignoni
 ,
Amanda
Arcidiacono
,
Amanda
Arcidiacono
 ,
Lorenzo
Cupellini
,
Lorenzo
Cupellini
 * and
Benedetta
Mennucci
* and
Benedetta
Mennucci

Dipartimento di Chimica e Chimica Industriale, Università di Pisa, Via G. Moruzzi 13, 56124 Pisa, Italy. E-mail: patrizia.mazzeo@phd.unipi.it; lorenzo.cupellini@unipi.it
First published on 11th October 2024
Abstract
The application of quantum mechanics (QM)/molecular mechanics (MM) models for studying dynamics in complex systems is nowadays well established. However, their significant limitation is the high computational cost, which restricts their use for larger systems and long-timescale processes. We propose a machine-learning (ML) based approach to study the dynamics of solvated molecules on the ground- and excited-state potential energy surfaces. Our ML model is trained on QM/MM calculations and is designed to predict energies and forces within an electrostatic embedding framework. We built a socket-based interface of our machinery with AMBER to run ML/MM molecular dynamics simulations. As an application, we investigated the excited-state intramolecular proton transfer of 3-hydroxyflavone in two different solvents: methanol and methylcyclohexane. Our ML/MM simulations accurately distinguished between the two solvents, effectively reproducing the solvent effects on proton transfer dynamics.
1 Introduction
In the last few decades, advances in hardware and software, as well as algorithmic improvements,1–4 have expanded the applicability of multiscale approaches combining a quantum mechanical (QM) treatment with a molecular mechanics (MM) model. The resulting QM/MM methods are nowadays successfully used to study the properties and processes of complex systems.5–8A critical issue of QM/MM methodologies is related to their computational cost especially when applied to dynamics. At present, QM/MM molecular dynamics (MD) simulations allow processes to be studied on the order of 10–100 picoseconds,3,7 while purely classical models are needed to study longer timescales. Several efforts are being made in order to speed up QM/MM MD simulations, for example by using enhanced sampling,9–11 and by making smart guesses of the solution of the QM problem by using the trajectory information.12–16
A possible strategy to significantly enhance the applicability of QM/MM methods to ground- and excited-state dynamics is to introduce surrogate machine learning (ML) models. In recent years, in fact, ML methods have proven to be a viable solution to obtain energies and properties with QM accuracy at a much reduced computational cost.17,18 From the beginning, ML methods have been coupled with MD engines, allowing the simulation of systems over timescales inaccessible to pure QM simulations.19–24 In addition, several efforts have been devoted to properly couple the ML description with a classical description of the environment. Some authors have used ML to obtain more accurate implicit solvent models.25,26 When ML is applied to the modelling of an MM environment, some works focus on some sort of mechanical embedding27–29 scheme, where ML potentials substitute the MM force field for part of the simulation. More recently, several models tackled the challenges of a more rigorous electrostatic embedding level.30–37 These models attempt at reproducing the effects of electrostatic embedding QM/MM approaches, where the properties of the QM part are modified by the MM charges. Within deep learning potentials, some authors have directly included the electrostatic fields from the MM environment into existing neural network architecture.30–32 Others focused on predicting atomic charges and polarizabilities for the ML part, which are then allowed to interact with the MM environment.33,35 A similar strategy is used by Grassano et al.36 to correct a purely mechanical embedding ML/MM with the polarization of the ML part. Another strategy is to divide the system into more than two regions and treat their interaction at different levels of theory.38,39
ML potentials are usually trained to describe the ground state of molecules,40–42 even though works have appeared where ML is used to tackle the additional challenges of excited states.43–48 However, to the best of our knowledge, electrostatic ML/MM models to describe excited-state dynamics in solvated systems have not been developed.
In this work, we develop ML models to describe the dynamics of solvated molecules in their ground and excited states, taking into account the environment within an electrostatic embedding scheme. In the context of ML simulations in condensed-phase systems, we aimed to reproduce the environment effects by including electrostatic interactions with MM charges and the polarization of the QM region due to the surrounding environment.
Our work represents the first application of the ML/MM method with electrostatic embedding in excited-state dynamic simulations. We exploit the expressiveness of kernel methods such as Gaussian process regression to construct a model that can describe a molecule in different solvents using relatively small training sets. The model is implemented in JAX49 in an open-source package called GPX,50 and interfaced to the Sander program of the AmberTools51 suite to perform ML/MM molecular dynamics via the Python script  .52 The ML/MM MD is orders of magnitude faster than the corresponding QM/MM implementation, allowing simulation of the dynamics over larger timescales with QM accuracy.
.52 The ML/MM MD is orders of magnitude faster than the corresponding QM/MM implementation, allowing simulation of the dynamics over larger timescales with QM accuracy.
This machinery is applied to 3-hydroxyflavone (3HF), a model system to study excited-state intramolecular proton transfer (ESIPT). The ESIPT reaction in 3HF allows for the interconversion between the normal (N) and the tautomeric (T) forms (Fig. 1), both exhibiting different fluorescent properties. Experiments have shown that steady state fluorescence and time-resolved properties have a strong dependence on the solvent.53–56 Furthermore, experimental and computational studies indicated that the ESIPT reaction is characterized by a fast component (tens of femtoseconds) and a slow component (around 10 picoseconds).10,57–60 The slow component is present exclusively in hydrogen-bonding solvents57,59 and is due to the breaking of hydrogen bonds between the 3HF and the solvent.59 Clearly, describing such a drastic solvent dependence requires including the electrostatics of the environment in a QM/MM (or ML/MM) embedding. We show that our ML/MM MD simulations reproduce the fast and slow components of the ESIPT process when 3HF is solvated with methylcyclohexane (MCH) and methanol (MeOH). This is achieved with as few as 1000 training points and few hours of training time, making our model an attractive strategy for ML/MM ground- and excited-state MD simulations.
2 Methods
2.1 Machine learning models
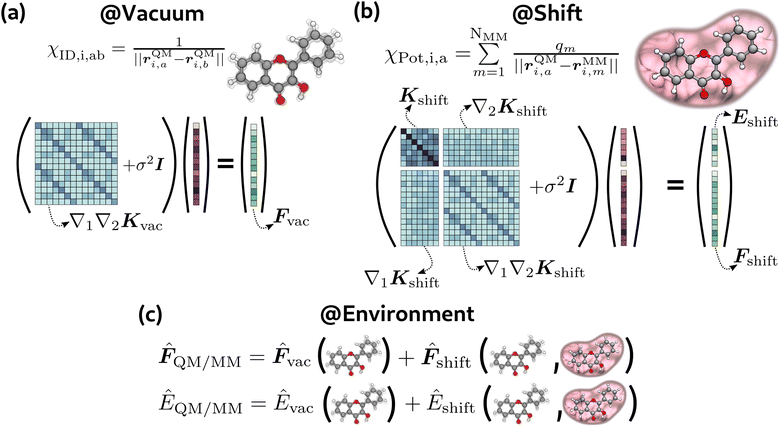
In this section we discuss the ML strategy we adopted to predict QM/MM quantities. Specifically, our focus in this work is on predicting QM/MM energies and gradients in the electrostatic embedding framework. This approach was applied to obtain these quantities for both the ground state (GS) and excited state (ES).Our model is built on some χ = χ(R) descriptor of the R geometry of the system, encoding both the QM and the MM part, and some parameters Θ. A QM/MM property (force or energy) is then given as the function
 | (1) |
The QM/MM energy can be written as a sum of contributions
| EQM/MM = EvacQM + EintQM-MM + EpolQM = EvacQM + Eshift |
Similarly to ref. 34, 37 and 61, we implemented a hierarchical model for both forces and energies. In this model, the QM-MM interaction is predicted as the environment shift to be added to the vacuum prediction.
 | (2) |
Both predictions are made with Gaussian process regression (GPR). The primary consideration is to maintain the integral/derivative relationship between energies and forces to ensure energy conservation throughout the simulation. Within GPR, this can be done by solving the following linear system:22,62
 | (3) |
In this compact notation, ∇ represents the derivative with respect to the coordinates of the system. The subscripts in ∇1 and ∇2 indicate that the derivative is performed on the first and the second argument of the kernel, respectively. In eqn (3), the upper left block is the kernel matrix
| Kij = K(χ(Ri),χ(Rj)) | (4) |
 | (5) |
The lower left block indicates the element-wise derivative of the first argument of the kernel matrix with respect to the coordinates of the system:
 | (6) |
The lower right block is the Hessian of the kernel, which can be written as follows:
 | (7) |
 | (8) |
 | (9) |
 | (10) |
The kernel function we used for taking into account the internal geometry changes belongs to the class of Materns, ν = 2.5:
 | (11) |
| dij = ‖χID,i − χID,j‖. | (12) |
For the vacuum model (see Fig. 2(a)), following the approach of the GDML models,40,41 we found that it was sufficient to solve only part of the general system in eqn (3). In particular, we trained this model only on forces, solving the following problem:
| (∇QM1∇QM2Kvac + σvac2I)αvac = −Fvac | (13) |
| Kvac(χi,χj) = Kinternal(χID,i,χID,j) | (14) |
We employed this approach for both GS and ES vacuum models, where Fvac in eqn (13) represents forces for the QM part calculated in a vacuum for the ground state and the first excited state, respectively. From the model described above, the prediction of forces on a χ* test point is achieved through a linear combination of Hessian kernel evaluations with the training points:
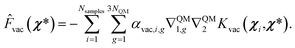 | (15) |
The prediction of energies is then obtained as the integral of the previous expression
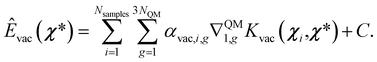 | (16) |
Notice that since this prediction requires an integral, this energy is defined up to a constant C, which can be defined as:41,64
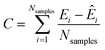 | (17) |
2.2 Environment model
The environment model (eqn (2), see also Fig. 2(c)) consists of the sum of vacuum prediction and the environment shift, which takes into account the QM-MM interaction. The latter depends both on internal changes of the molecular geometry and the effect of the environment. The effect of the environment was taken into account using the electrostatic potential generated by MM atoms on QM positions: | (18) |
| Kdirect(χPot,i,χPot,j) = χPot,iT·χPot,j. | (19) |
Contrary to the vacuum model, the environment shift model needed to train on both energies and forces (eqn (3), see also Fig. 2(b)) to obtain low errors. We attribute this different behaviour to the amount of information contained in the χID and χPot descriptors. Indeed, while χID is a complete descriptor of the molecular geometry, the potential χPot contains a trace over the MM atoms and is evaluated on the QM atoms only, so it is intrinsically approximate. For this model, we imposed an equal regularization for energies and forces (σe = σf). In this case, the targets are energies and forces for both the ground and the first excited state, computed as the difference between the QM/MM calculation and the vacuum:
 | (20) |
Also in this case we trained two models, for GS and ES respectively. We put both the direct environment effect and the influence of internal geometry in the covariance matrix:
| Kshift(χi,χj) = Kdirect(χPot,i,χPot,j)·Kinternal(χID,i,χID,j). | (21) |
This is possible due to the versatility of GPR, which allows the use of any symmetric and positive semi-definite function as a kernel, e.g. the Hadamard product of two symmetric and positive semi-definite functions.
Note that we train only on shift forces acting on QM atoms, but the QM-MM interaction contributes to the forces on both QM and MM atoms. This means that during the prediction phase, the derivative with respect to the first argument of the kernel will always pertain to QM positions, as it corresponds to the training points. On the other hand, the derivative with respect to the test point geometry will vary: it will be with respect to the QM coordinates for the QM/MM force contribution to QM atoms (![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) QMshift) and with respect to the MM coordinates for the QM/MM force contribution to MM atoms (
QMshift) and with respect to the MM coordinates for the QM/MM force contribution to MM atoms (![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) MMshift):
MMshift):
 | (22) |
 | (23) |
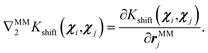 | (24) |
The energy (Êshift) is predicted following eqn (9). More detailed expressions of the derivatives in eqn (22) and (23) are provided in the ESI.† Our environment shift model essentially learns the relationship between QM/MM energy and force shifts and the electrostatic potential used as a descriptor. Since changing the solvent alters the MM charges and, consequently, the potential, our shift model should, in principle, be able to extrapolate to any solvent, despite being trained on a specific one.
The separation of our QM/MM prediction into a vacuum component and a shift component gives us greater control over each model. It also makes our environment shift model compatible with any existing model for the vacuum. Additionally, the environment shift model depends only on the coordinates of the system (both QM and MM) and the MM charges. These quantities are readily available in any MD engine capable of performing QM/MM simulations.
3 Coupling with molecular dynamics
In order to perform ML/MM molecular dynamics, we have built an interface with Sander, the CPU simulation engine of the AmberTools MD suite,51 which already provides an infrastructure to perform QM/MM simulations with external programs.65 Our interface allows for any model exposed to Python to be used in MD. In our case, our models are implemented using the GPX program50 (see Fig. 3). Sander deals with the trajectory propagation, and computes energies and forces for the classical (MM) subsystem and dispersion and repulsion ML-MM interactions. It receives from the Python server the total energies and forces for the ML part and the ML–MM component for MM atoms, which are then added to the MM forces computed by Sander.65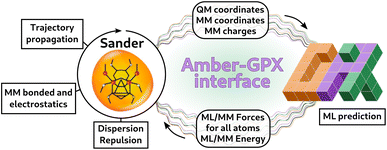 | ||
Fig. 3 Scheme representing the Amber-GPX interface via the  program.52 At each step of the dynamics, Sander computes the MM energies and forces, and the ML–MM dispersion and repulsion interaction. Coordinates and charges are sent to the Python server, and are used by GPX models to predict the energies and forces of the ML part, as well as the MM forces coming from the ML–MM interaction. This information is sent back to Sander, which performs one step of the trajectory. program.52 At each step of the dynamics, Sander computes the MM energies and forces, and the ML–MM dispersion and repulsion interaction. Coordinates and charges are sent to the Python server, and are used by GPX models to predict the energies and forces of the ML part, as well as the MM forces coming from the ML–MM interaction. This information is sent back to Sander, which performs one step of the trajectory. | ||
The communication between Python and Sander is based on a TCP socket, in which a Python server ( 52) is executed at the start of the MD and kept running during the whole simulation. Avoiding the Python initialization at each step has the advantage of saving the time needed to import all the necessary packages. In addition, since our models are implemented in JAX49via the GPX50 packages and are thus JIT-compiled, having a single instance of Python running for the whole simulation means that the JAX functions are compiled only at the first step, with significant gains in performance during the MD. The Python server communicates with a Sander client through a Socket implementation in Fortran (
52) is executed at the start of the MD and kept running during the whole simulation. Avoiding the Python initialization at each step has the advantage of saving the time needed to import all the necessary packages. In addition, since our models are implemented in JAX49via the GPX50 packages and are thus JIT-compiled, having a single instance of Python running for the whole simulation means that the JAX functions are compiled only at the first step, with significant gains in performance during the MD. The Python server communicates with a Sander client through a Socket implementation in Fortran ( 66) which allows exchanging data between Python and Sander without writing and reading on disk. Avoiding input/output (IO) operations on disk allows for a much faster exchange of information, at the price of recompiling Sander with the Fortran-based socket. We also provide the option to leave Sander untouched, and perform the communication between Python and Sander using disk IO operations, in a similar way to the implementation in the
66) which allows exchanging data between Python and Sander without writing and reading on disk. Avoiding input/output (IO) operations on disk allows for a much faster exchange of information, at the price of recompiling Sander with the Fortran-based socket. We also provide the option to leave Sander untouched, and perform the communication between Python and Sander using disk IO operations, in a similar way to the implementation in the  35 code. Throughout this paper, we present ML/MM MD results obtained with the faster, in-memory data exchange mode.
35 code. Throughout this paper, we present ML/MM MD results obtained with the faster, in-memory data exchange mode.
4 Computational details
4.1 Machine learning scores
For the validation of our models, we show the root mean squared error (RMSE) and the mean absolute error (MAE), defined as follows: | (25) |
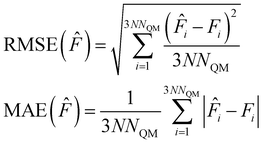 | (26) |
In eqn (25) and (26), N is the number of test points and NQM is the number of QM atoms.
4.2 Dataset generation with active learning
The geometries for the dataset were derived from an ab initio umbrella sampling (US) simulation of 3HF in MeOH conducted in a previous study.10 We implemented an active learning procedure based on an initial GPR model trained on energy data. We used a starting training set of 200 geometries, on which we fitted the GPR model. Then, we iteratively extracted 200 additional geometries with the highest predicted uncertainty at each step and fitted a GPR model on the enlarged dataset. The procedure was continued until an RMSE error on the energy below chemical accuracy was reached, for a total of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 training points (see Fig. S1 in the ESI†). We randomly split this dataset in the training (80%) and test sets (20%). The higher amount of information (3 × NQM per sample) contained in the training on forces allowed us to use a number of training points which is far below 10
000 training points (see Fig. S1 in the ESI†). We randomly split this dataset in the training (80%) and test sets (20%). The higher amount of information (3 × NQM per sample) contained in the training on forces allowed us to use a number of training points which is far below 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, obtaining errors under the chemical accuracy for both energies and forces with 1000 samples, which were chosen among the initial 8000 training points.
000, obtaining errors under the chemical accuracy for both energies and forces with 1000 samples, which were chosen among the initial 8000 training points.
Since the aim was to simulate a reactive process, the training was constructed including all significant geometries that the molecule can assume during time evolution. The most difficult part to be described is the transition state (TS), where the moving proton is in the middle between the two oxygen atoms. Because of that, the training set was divided in three parts, corresponding to the two minima (N and T forms) and the region surrounding the TS. For both vacuum and environment models, the actual training set comprises 500 geometries among the two 3HF forms and 500 geometries near the TS, selected using the farthest point sampling (FPS)67 approach. This approach allows us to obtain configurations as distant as possible from each other.
The prediction of excited-state energies and forces presents the additional challenge of dealing with the mixing between different states. We followed the same procedure described above in terms of building the 1000-point training set, and we trained two models: one including only the excitations with pure HOMO–LUMO transitions and the other selecting geometries among the whole dataset, allowing for mixing with other states. While both models performed similarly on the test sets, we observed differences in their performance during simulation tests. In particular the mixed-state model was more prone to simulation crushes. Therefore, we present the results obtained with the pure HOMO–LUMO transition model.
The target for the vacuum models is simply 3HF forces in a vacuum (see Fig. 2(a)). For the environment shift model, the targets are the differences between QM/MM energies and forces and the respective vacuum quantity (see Fig. 2(b)), i.e., the environment shift model requires two sets of calculations for each geometry. Following the same approach of the US simulation, all the calculations were performed at the ωB97XD level (TD-ωB97XD for the excited state). The basis set was customized in order to have an accurate description of the proton transfer, so we used 6-31G(d,p) for the moving proton and the two oxygen atoms involved in the bond breaking and formation and 6-31G for all the others. All calculations were run on Gaussian16.68
4.3 Training of ML models
All our models were implemented and trained using our Python package GPX.50 The inverse distance and electrostatic potential descriptors, and the FPS algorithm are implemented in the Python package Moldex.69 Both packages were implemented in JAX49 and are available on GitHub under the GNU LGPL agreement.Concerning the performance of our GPX package, we trained our models on a single computer node AMD EPYC 7282 running@2.8 GHz using 32 threads. By exploiting an analytic solver, GPX took 6.5 min for the training on forces and 8.1 min for the training on energies and forces with 1000 training points (average time between GS and ES models).
Since we imposed equal regularization for energies and forces in eqn (3), we have two hyperparameters to optimize for both vacuum and environment models: λ of the Matern kernel and σ of regularization. Hyperparameter optimization for each model was conducted using grid search (λ = [5, 10, 15, 20], σ = [10−5, 10−4, 10−3]) and four-fold cross-validation (CV). The total training time, including CV for hyperparameter optimization, was 4.29 h. For all the models, CV produced very small values of the σ hyperparameter (10−5), making them more prone to overfitting. Indeed, during initial MD simulation tests, we encountered instabilities in our environment shift models, leading to the breaking of the system. We utilized these failed trajectories as additional test cases to further validate our models, but we did not include them in the training set. This process revealed the need to increase the regularization strength to accurately describe geometries outside the training set. Raising the σ parameter from 10−5 to 10−3 caused slightly larger errors on the test set, but significantly improved the robustness of our environment shift models. Therefore, for both GS and ES shift models we set σ = 10−3 and used again cross-validation to find the optimal value of λ. These last models are the ones we show in the Results section and that we used for production simulations. We included the learning curves for all models in the ESI (Fig. S2†).
4.4 Generation of the test set
We validated our models on geometries of 3HF in both MeOH and MCH solvents. The MeOH test set comprises 1000 geometries extracted from the test set mentioned in the Dataset generation section. For generating geometries of MCH, we performed two 2.5 ps long NVE simulations (GS and ES) using our ML/MM machinery. From each trajectory, we extracted 500 geometries as the MCH test set. On these geometries, we performed reference calculations at the same level of theory as the MeOH dataset.4.5 Molecular dynamics simulations
We started from the classical MD simulations of 3HF in the two solvents of interests (MeOH and MCH), which were performed in a previous work.10 For each solvent, we extracted 25 starting points and, following the same protocol of ref. 10, we used the “droplet model” approach, in which we selected droplets containing the solute and solvent molecules within 30 Å from it (Fig. 4). To avoid the solvent evaporation, we applied a harmonic potential pointing towards the geometrical center of 3HF to all atoms beyond a certain threshold. More details on how the harmonic constant has been determined can be found in ref. 10. This harmonic restraint was imposed using the open-source, community-developed PLUMED library,70 version 2.9.71 All the simulations were performed using a modified version of Amber interfaced with GPX and with PLUMED. The instructions to recompile the AmberTools with the provided files can be found in the available on GitHub.52 We performed a 10 ps long NVT ML/MM simulation on the ground state with the Langevin thermostat to keep the temperature at 300 K. This equilibration is necessary to relax the system after the discontinuity in the potential energy surface that appears when we move from classical simulations to the ML/MM ones, as is common practice in QM/MM molecular dynamics.10,16,72 From these ground-state trajectories we extracted coordinates and velocities every 2.5 ps, for a total of 100 starting points for both solvents. We then ran the excited-state ML/MM production simulations in the NVE ensemble. We did not impose any cutoff on the electrostatics, both for MM–MM interactions and ML–MM ones. This means that all the MM atoms are taken into account and are used for the ML/MM prediction at each step of the simulation.
available on GitHub.52 We performed a 10 ps long NVT ML/MM simulation on the ground state with the Langevin thermostat to keep the temperature at 300 K. This equilibration is necessary to relax the system after the discontinuity in the potential energy surface that appears when we move from classical simulations to the ML/MM ones, as is common practice in QM/MM molecular dynamics.10,16,72 From these ground-state trajectories we extracted coordinates and velocities every 2.5 ps, for a total of 100 starting points for both solvents. We then ran the excited-state ML/MM production simulations in the NVE ensemble. We did not impose any cutoff on the electrostatics, both for MM–MM interactions and ML–MM ones. This means that all the MM atoms are taken into account and are used for the ML/MM prediction at each step of the simulation.
5 Results and discussion
5.1 ML models for forces and energies
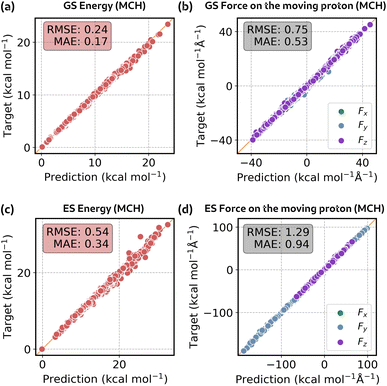
As previously mentioned, we trained four models: a vacuum model and an environment shift model for both GS and ES. Since all the geometries in the training set were extracted from simulations in MeOH, at first we validated our models on a test set consisting of 1000 3HF geometries in MeOH. In Fig. 5, we report the correlation curves for the energy and the force on the proton that moves during proton transfer. Plots of the total force for all QM atoms can be found in Section S2 of the ESI.†In Table 1 we report the errors on the MeOH test set for all the models. GS and ES models have similar errors, indicating that, in the absence of mixing with other states, learning the excited state is not more difficult than learning the ground state. For the vacuum model, the error in energies is generally below 0.1 kcal mol−1 and the error in forces is below 0.5 kcal mol−1 Å−1. Notably, these very low errors in energy are achieved despite the model being trained solely on forces. Moving to the shift model, we can observe a decrease in the error in forces with respect to the vacuum, likely due to the lower absolute value of shift forces. Conversely, the error in energies increases despite the lower absolute value of environment shift energy. We attribute this behaviour to the fact that, as previously mentioned, the environment shift model contains only a trace of the MM atoms, while the energy depends equally on QM and MM atoms. However, the combined prediction gives an error well below the chemical accuracy (environment model, Table 1). We also reported a plot of the errors in energy and forces along the reaction coordinate in Fig. S15 in the ESI.†
| @Vacuum | @Shift | @Environment | |||||
|---|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | ||
| GS | Energy | 0.067 | 0.051 | 0.267 | 0.214 | 0.273 | 0.217 |
| Force | 0.433 | 0.280 | 0.143 | 0.100 | 0.458 | 0.307 | |
| ES | Energy | 0.066 | 0.050 | 0.265 | 0.215 | 0.272 | 0.218 |
| Force | 0.473 | 0.291 | 0.184 | 0.125 | 0.497 | 0.321 | |
5.2 Extrapolation to methylcyclohexane
As already mentioned, the environment shift model should be able to extrapolate to any solvent. Our interest was to study this reaction in the same solvents used in ab initio simulations in ref. 10; therefore, we validated our models trained on MeOH samples also for 3HF in MCH.The performance of our models is reported in Table 2 and Fig. 6. Plots of the force for all QM atoms can be found in Section S2 of the ESI.† When examining the @shift column of Table 2, we can conclude that the model is capable of describing the environment effect in MCH. The environment shift model errors in MCH are significantly lower than the ones in MeOH because MCH provides a minimal environmental contribution to energies and forces, resulting in reduced error.
| @Vacuum | @Shift | @Environment | |||||
|---|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | ||
| GS | Energy | 0.221 | 0.157 | 0.091 | 0.074 | 0.240 | 0.171 |
| Force | 0.890 | 0.606 | 0.062 | 0.043 | 0.891 | 0.607 | |
| ES | Energy | 0.509 | 0.316 | 0.121 | 0.100 | 0.537 | 0.337 |
| Force | 1.612 | 1.033 | 0.070 | 0.048 | 1.612 | 1.034 | |
A larger error is present for the vacuum model. This dissimilarity can be attributed to the different way in which MeOH and MCH test sets are generated, since for MeOH we used geometries extracted from the same ab initio trajectory of the training set, whereas the MCH test set consists of completely new geometries extracted from an ML/MM simulation (see Section 4.4). The larger error on the full prediction in the environment reflects the larger error on the vacuum model.
5.3 Performance analysis
In this section we report the analysis of the timings for our ML/MM simulations. These values refer to an MD simulation in MCH of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 531 atoms in total. The latter was conducted on a single computer node AMD EPYC 7282 running@2.8 GHz using 32 threads, exploiting MPI-compiled versions of Amber and PLUMED.
531 atoms in total. The latter was conducted on a single computer node AMD EPYC 7282 running@2.8 GHz using 32 threads, exploiting MPI-compiled versions of Amber and PLUMED.
Fig. 7 shows the approximate timings for each significant part.
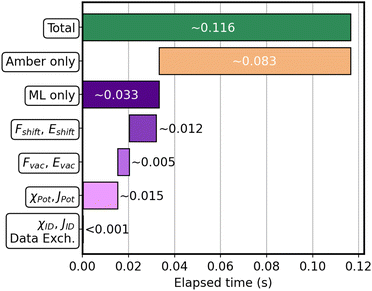 | ||
| Fig. 7 Graphical representation of the average time required for each operation at each step of the simulation. | ||
The bar-plot highlights that 70% of the time is employed by Amber, which evaluates the MM-only classical energies and forces, and computes the van der Waals interactions with the 3HF. Concerning the ML part, we can say that the remaining 30% is almost equally divided between the computation of the descriptor and Jacobian for the MM part, χPot and JPot, and the predictions of the vacuum and shift contributions. The calculation of the ID descriptor χID and Jacobian JID, as well as the data exchange between Sander and the Python server, takes negligible time (more details are provided in Table S1 in the ESI†).
5.4 Validation of ML/MM dynamics and comparison with QM/MM
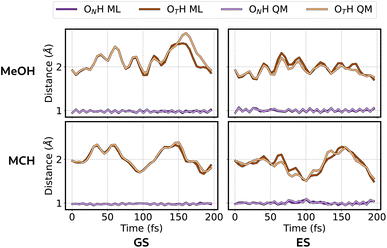
Test errors alone may not be sufficient to guarantee the stability and accuracy of simulations.73,74 For this reason, we validate our ML/MM simulations first by direct comparison with QM/MM simulations. Starting from a specific phase space point extracted from the equilibration, we ran both an ML/MM simulation and a QM/MM simulation at the same QM level used for the training set to compare the results. The QM/MM simulation was conducted using the interface between Gaussian16 and Sander. The plots in Fig. 8 show reaction coordinates for the proton transfer in all four cases. ON indicates the protonated oxygen atom when 3HF is in its N form, and OT indicates the oxygen protonated in the T form. For GS trajectories, the ML/MM simulations closely match the reference ones for the first 100 fs. After this period, despite some differences starting to arise, the oscillation amplitudes remain consistent. This divergence is expected, as the ML prediction errors accumulate over time causing the trajectories to diverge. This error is slightly more pronounced for the ES case. Although we cannot achieve a perfect match between ML/MM and QM/MM, we are still sampling the correct region of the phase space with the correct oscillation. In Fig. S16 in the ESI† we reported the same comparison for the dihedral angle which involves the ON and OT atoms.In terms of computational efficiency on similar hardware, reference QM/MM simulations achieve a performance of approximately 1.0 ps per day for ground-state simulations. In contrast, using our ML/MM strategy, we achieve a significantly higher performance of 200 ps per day. For excited-state simulations, the advantage is even more pronounced. Here, our ML/MM approach maintains the same high performance as ground-state simulations. In contrast, traditional TD-DFT simulations typically achieve a performance of only 0.1 ps per day.
This significant improvement in performance allows us to conduct simulations more rapidly and efficiently, which is particularly beneficial for studying complex processes such as excited-state dynamics.
Finally, to show the stability of our ML/MM potential for longer dynamics, we plot in Fig. S17 of the ESI† the results of a 1 ns long ML/MM simulation of the ES in MeOH in the NVE ensemble. Within this timescale we did not observe drifts in the total energy or sudden spikes in the force, which demonstrates the stability of our simulations.
5.5 Simulation of ESIPT in MeOH and MCH
After validating all the models, we initiated our production ES ML/MM simulations to study the ESIPT reaction of 3HF in MeOH and MCH. As detailed in the Computational details section, we conducted 10 ps long trajectories, 100 per solvent. This approach allowed us to explore both the ultrafast and the slow components of the ESIPT reaction, which would be unfeasible with standard ab initio simulations due to their high computational cost.In Fig. 9 we plotted the reaction coordinates (OTH and ONH) for the proton transfer over the simulation time for a representative MeOH trajectory. The moment in which the two lines cross identifies the proton transfer. Grey lines in Fig. 9 show all the other MeOH trajectories, which display PT at different times.
The cumulative results of our simulations in both solvents are reported in Fig. 10. This plot illustrates the fraction of trajectories that undergo PT over the simulation time. We can confirm that our model effectively captures the differences between the two solvents. The plot shows that the ultra-fast component is observed in both solvents, but with lower probability in MeOH. On the other hand, the slow component is present only in MeOH, due to the presence of hydrogen bonds, which must be broken before the proton transfer can happen. This is the reason why all trajectories exhibit the ESIPT within approximately 3 ps for MCH. Conversely, for MeOH, not all trajectories reached the T form even after 10 ps of simulation. This is in agreement with the experimental observation that fluorescence emanates only from the T form in non-hydrogen-bonding solvents and from both N and T forms in hydrogen-bonding ones.53 Within the statistical uncertainty, this plot is comparable to the one obtained with ab initio simulations,10 even though a direct comparison is not possible due to the different approach for what concerns the environment description (electrostatic embedding vs. polarizable embedding) and the statistical accuracy (fewer trajectories were run in ref. 10).
In Table 3, we present the results of a multi-exponential fitting of the curves shown in Fig. 10. The fitted curves are depicted in Fig. S18 of the ESI.† We achieved a good fit using a combination of two exponential functions for MCH and three for MeOH. For both solvents, we found an ultrafast component of the order of 150 fs and a slower one of 1.0 ps. The presence of an ultrafast component is in agreement with transient absorption experiments,57,59 although in experiments this component seems even faster than in our simulations. A 1.6 ps component was also measured in ref. 59, which we connect with the 1.0 ps component found in simulations.
| τ 1 ps (a1) | τ 2 ps (a2) | τ 3 ps (a3) | |
|---|---|---|---|
| MCH | 0.15 (0.50) | 1.0 (0.50) | |
| MeOH | 0.18 (0.04) | 1.0 (0.23) | 16.0 (0.73) |
The slow component (∼10 ps) was observed only for MeOH, which is consistent with experimental measurements,57,59 as the authors could attribute the ∼10 ps component measured in MCH to hydrogen-bonding impurities in the solution.
Overall, our simulations well reproduce the qualitative difference between MeOH and MCH solvents in the PT timescale and extent. The ultrafast components indicate that PT is almost barrierless in MCH, as well as in part of the MeOH configurations.10 Our timescales are slightly slower than experiments for this component, which we can tentatively attribute to missing nuclear quantum effects in the proton transfer coordinate.
6 Conclusions
We have presented a strategy to predict QM/MM energies and forces within the electrostatic embedding framework for the ground and the excited state of solvated molecules. Our approach is based on a hierarchical prediction, in which the QM/MM contribution is reproduced as the sum of a vacuum term and an environment shift contribution. Despite this requiring two sets of calculations for each sample (one in a vacuum and one in the environment), two such separated models are easier to tune and are independent. In principle, our model for the environment can be coupled to any model that predicts energies and forces in a vacuum. Our models were trained on geometries extracted from reference ab initio simulations in solvent, which still represent an expensive step. Simpler methods are needed to generate training datasets for solvated molecules without sacrificing simulation accuracy. Further work in our group will be devoted to overcoming this limitation.For the training of our models we rely on GPR in the gradient domain (learning only forces or both energies and forces). This approach is beneficial because it provides 3 × NQM forces from a single sample, allowing us to train with a relatively small dataset. With only 2 × Nsample calculations (one in a vacuum and one in the environment) one can run numerous trajectories over extended timescales. This approach can thus significantly enhance ground-state simulations, but it has an even greater effect on excited-state simulations, which are considerably more computationally demanding. Training a model for excited states is very delicate, as strong mixing can significantly impact learning, sometimes necessitating the use of diabatization procedures.37,48,75 However, for excited states with low mixing, learning based on geometries that exhibit a pure HOMO–LUMO transition makes training for the excited state as straightforward as for the ground state.
We also built a machinery which is able to connect the GPX software with Amber to perform ML/MM simulations. The core of this interface is a Python script ( ), which receives coordinates and charges from Sander and returns forces and energies. This server is not specific to GPX, allowing any ML model to be implemented and used for simulations. This socket-based data exchange is crucial as it eliminates the overhead associated with reading and writing files, significantly reducing the cost of the simulation.
), which receives coordinates and charges from Sander and returns forces and energies. This server is not specific to GPX, allowing any ML model to be implemented and used for simulations. This socket-based data exchange is crucial as it eliminates the overhead associated with reading and writing files, significantly reducing the cost of the simulation.
Our strategy was applied to the study of excited-state intramolecular proton transfer (ESIPT) of 3-hydroxyflavone in two solvents: methanol as a polar protic solvent and methylcyclohexane as an apolar and aprotic one. The use of ML can overcome the main limitations of ab initio approaches. By running 100 trajectories per solvent, we significantly increased the statistical accuracy of our descriptions. Furthermore, we were able to investigate both the ultra-fast and the slow components of the ESIPT reaction using standard simulations, whereas the latter required enhanced sampling techniques for ab initio simulations.10 Our simulations could reproduce with good accuracy the experimentally determined ESIPT time constants in both solvents. Importantly, our environment models proved able to extrapolate to a different solvent than the one used in the training. On the other hand, these models are specific for the molecule in the QM part. In fact, both the inverse distance descriptor and the electrostatic potential on QM atoms encode the QM molecule “globally”. However, we note that training our models requires only a relatively small number (1000) of training points, and the training time for a molecule like 3-hydroxyflavone is of few hours for both GS and ES. This makes us confident that a similar protocol could be applied to diverse and more complex systems.
Data availability
The ML models used for this article, including vacuum and environment models for the ground and the first excited state of 3-hydroxyflavone, and two examples of input files for simulations in methanol and methylcyclohexane are available in a zenodo repository at https://doi.org/10.5281/zenodo.13739507.Author contributions
P. M., E. C., L. C. and B. M. conceived and designed the study. P. M., E. C. and A. A. developed the code. P. M. trained the ML models, ran ML/MM simulations, and analyzed the data. L. C. and E. C. oversaw the ML training and simulations. P. M., E. C., L. C. and B. M. wrote the paper. All authors read and approved the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. A., L. C. and B. M. acknowledge financial support from the Italian MUR through the PRIN 2022 grant 2022N8PBLM (PhotoControl). L. C. and B. M. also acknowledge financial support from ICSC-Centro Nazionale di Ricerca in high-performance computing, big data, and quantum computing, funded by the European Union-NextGenerationEU-PNRR, Missione 4 Componente 2 Investimento 1.4. L. C. and B. M. acknowledge financial support from the University of Pisa through project PRA_2022_34.Notes and references
- L. Lagardère, L.-H. Jolly, F. Lipparini, F. Aviat, B. Stamm, Z. F. Jing, M. Harger, H. Torabifard, G. A. Cisneros and M. J. Schnieders, et al. , Chem. Sci., 2018, 9, 956–972 RSC.
- V. W. D. Cruzeiro, M. Manathunga, K. M. Merz Jr and A. W. Goötz, J. Chem. Inf. Model., 2021, 61, 2109–2115 CrossRef CAS PubMed.
- B. Raghavan, M. Paulikat, K. Ahmad, L. Callea, A. Rizzi, E. Ippoliti, D. Mandelli, L. Bonati, M. De Vivo and P. Carloni, J. Chem. Inf. Model., 2023, 63, 3647–3658 CrossRef CAS PubMed.
- G. Rossetti and D. Mandelli, Curr. Opin. Struct. Biol., 2024, 86, 102814 CrossRef PubMed.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
- U. N. Morzan, D. J. Alonso de Armiño, N. O. Foglia, F. Ramírez, M. C. González Lebrero, D. A. Scherlis and D. A. Estrin, Chem. Rev., 2018, 118, 4071–4113 CrossRef CAS PubMed.
- E. Brunk and U. Rothlisberger, Chem. Rev., 2015, 115, 6217–6263 CrossRef CAS PubMed.
- S. F. Sousa, A. J. Ribeiro, R. P. Neves, N. F. Brás, N. M. Cerqueira, P. A. Fernandes and M. J. Ramos, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1281 Search PubMed.
- N. Gillet, M. Elstner and T. Kubař, J. Chem. Phys., 2018, 149, 1–10 CrossRef PubMed.
- M. Nottoli, M. Bondanza, F. Lipparini and B. Mennucci, J. Chem. Phys., 2021, 154, 184107 CrossRef CAS PubMed.
- D. Ray, S. Das and U. Raucci, J. Chem. Inf. Model., 2024, 64, 3953–3958 CrossRef CAS PubMed.
- J. M. Herbert and M. Head-Gordon, Phys. Chem. Chem. Phys., 2005, 7, 3269–3275 RSC.
- P. Tangney, J. Chem. Phys., 2006, 124, 1–14 CrossRef PubMed.
- A. M. Niklasson, Phys. Rev. Lett., 2008, 100, 123004 CrossRef PubMed.
- F. Pes, É. Polack, P. Mazzeo, G. Dusson, B. Stamm and F. Lipparini, J. Phys. Chem. Lett., 2023, 14, 9720–9726 CrossRef CAS PubMed.
- P. Mazzeo, S. Hashem, F. Lipparini, L. Cupellini and B. Mennucci, J. Phys. Chem. Lett., 2023, 14, 1222–1229 CrossRef CAS PubMed.
- B. Huang and O. A. Von Lilienfeld, Chem. Rev., 2021, 121, 10001–10036 CrossRef CAS PubMed.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K. R. Müller, Chem. Rev., 2021, 121, 10142–10186 CrossRef CAS PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577–606 Search PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- Y.-F. Hou, F. Ge and P. O. Dral, J. Chem. Theory Comput., 2023, 19, 2369–2379 CrossRef CAS PubMed.
- Y. Tao, T. J. Giese, Ş. Ekesan, J. Zeng, B. Aradi, B. Hourahine, H. M. Aktulga, A. W. Götz, K. M. Merz and D. M. York, J. Chem. Phys., 2024, 160, 224104 CrossRef CAS PubMed.
- H. Zhang, V. Juraskova and F. Duarte, Nat. Commun., 2024, 15, 6114 CrossRef CAS PubMed.
- Y. Chen, A. Krämer, N. E. Charron, B. E. Husic, C. Clementi and F. Noé, J. Chem. Phys., 2021, 155, 084101 CrossRef CAS PubMed.
- S. Yao, R. Van, X. Pan, J. H. Park, Y. Mao, J. Pu, Y. Mei and Y. Shao, RSC Adv., 2023, 13, 4565–4577 RSC.
- S.-L. J. Lahey and C. N. Rowley, Chem. Sci., 2020, 11, 2362–2368 RSC.
- J. W. Vant, S.-L. J. Lahey, K. Jana, M. Shekhar, D. Sarkar, B. H. Munk, U. Kleinekathoöfer, S. Mittal, C. Rowley and A. Singharoy, J. Chem. Inf. Model., 2020, 60, 2591–2604 CrossRef CAS PubMed.
- R. Galvelis, A. Varela-Rial, S. Doerr, R. Fino, P. Eastman, T. E. Markland, J. D. Chodera and G. D. Fabritiis, J. Chem. Inf. Model., 2023, 63, 5701–5708 CrossRef CAS PubMed.
- X. Pan, J. Yang, R. Van, E. Epifanovsky, J. Ho, J. Huang, J. Pu, Y. Mei, K. Nam and Y. Shao, J. Chem. Theory Comput., 2021, 17, 5745–5758 CrossRef CAS PubMed.
- L. Böselt, M. Thürlemann and S. Riniker, J. Chem. Theory Comput., 2021, 17, 2641–2658 CrossRef PubMed.
- M. Gastegger, K. T. Schütt and K.-R. Müller, Chem. Sci., 2021, 12, 11473–11483 RSC.
- K. Zinovjev, J. Chem. Theory Comput., 2023, 19, 1888–1897 CrossRef CAS PubMed.
- E. Cignoni, L. Cupellini and B. Mennucci, J. Chem. Theory Comput., 2023, 19, 965–977 CrossRef CAS PubMed.
- K. Zinovjev, L. Hedges, R. M. Andreu, C. Woods, I. Tuñón and M. W. van der Kamp, J. Chem. Theory Comput., 2024, 20, 4514–4522 CrossRef CAS PubMed.
- J. S. Grassano, I. Pickering, A. E. Roitberg, M. C. G. Lebrero, D. A. Estrin and J. A. Semelak, J. Chem. Inf. Model., 2024, 64, 4047–4058 CrossRef CAS PubMed.
- A. Arcidiacono, E. Cignoni, P. Mazzeo, L. Cupellini and B. Mennucci, J. Phys. Chem. A, 2024, 128, 3646–3658 CrossRef CAS PubMed.
- B. Lier, P. Poliak, P. Marquetand, J. Westermayr and C. Oostenbrink, J. Phys. Chem. Lett., 2022, 13, 3812–3818 CrossRef CAS PubMed.
- L. Wang, C. Salguero, S. A. Lopez and J. Li, Chem, 2024, 10, 2295–2310 Search PubMed.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Sci. Adv., 2017, 3, e1603015 CrossRef PubMed.
- S. Chmiela, H. E. Sauceda, I. Poltavsky, K. R. Müller and A. Tkatchenko, Comput. Phys. Commun., 2019, 240, 38–45 CrossRef CAS.
- S. Raghunathan and S. A. K. Nakirikanti, Mach. Learn.: Sci. Technol., 2023, 4, 035006 Search PubMed.
- R. Ramakrishnan, M. Hartmann, E. Tapavicza and O. A. Von Lilienfeld, J. Chem. Phys., 2015, 143, 1–8 CrossRef PubMed.
- W.-K. Chen, X.-Y. Liu, W.-H. Fang, P. O. Dral and G. Cui, J. Phys. Chem. Lett., 2018, 9, 6702–6708 CrossRef CAS PubMed.
- J. Westermayr, M. Gastegger and P. Marquetand, J. Phys. Chem. Lett., 2020, 11, 3828–3834 CrossRef CAS PubMed.
- J. Westermayr and R. J. Maurer, Chem. Sci., 2021, 12, 10755–10764 RSC.
- E. Cignoni, D. Suman, J. Nigam, L. Cupellini, B. Mennucci and M. Ceriotti, ACS Cent. Sci., 2024, 10, 637–648 CrossRef CAS PubMed.
- S. Axelrod, E. Shakhnovich and R. Gómez-Bombarelli, Nat. Commun., 2022, 13(13), 1–11 Search PubMed.
- J. Bradbury, R. Frostig, P. Hawkins, M. J. Johnson, C. Leary, D. Maclaurin, G. Necula, A. Paszke, J. VanderPlas, S. Wanderman-Milne and Q. Zhang, JAX: compostable transformations of Python+NumPy programs, 2018, http://github.com/google/jax, accessed July 26, 2024.
- E. Cignoni, P. Mazzeo, A. Arcidiacono, L. Cupellini and B. Mennucci, GPX: Gaussian Process Regression in JAX, 2023, https://github.com/Molecolab-Pisa/GPX, accessed July 26, 2024.
- D. A. Case, H. M. Aktulga, K. Belfon, D. S. Cerutti, G. A. Cisneros, V. W. D. Cruzeiro, N. Forouzesh, T. J. Giese, A. W. Götz and H. Gohlke, et al. , J. Chem. Inf. Model., 2023, 63, 6183–6191 CrossRef CAS PubMed.
- P. Mazzeo, E. Cignoni, L. Cupellini and B. Mennucci, ML-server, 2024, https://github.com/Molecolab-Pisa/ML-server, accessed September 10, 2024.
- P. K. Sengupta and M. Kasha, Chem. Phys. Lett., 1979, 68, 382–385 CrossRef CAS.
- D. McMorrow and M. Kasha, J. Phys. Chem., 1984, 88, 2235–2243 CrossRef CAS.
- S. Protti and A. Mezzetti, J. Mol. Liq., 2015, 205, 110–114 CrossRef CAS.
- T. Kumpulainen, B. Lang, A. Rosspeintner and E. Vauthey, Chem. Rev., 2017, 117, 10826–10939 CrossRef CAS PubMed.
- B. J. Schwartz, L. A. Peteanu and C. B. Harris, J. Phys. Chem., 1992, 96, 3591–3598 CrossRef CAS.
- S. M. Ormson, D. Legourrierec, R. G. Brown and P. Foggi, J. Chem. Soc. Chem. Commun., 1995, 2133–2134 RSC.
- S. Ameer-Beg, S. M. Ormson, R. G. Brown, P. Matousek, M. Towrie, E. T. Nibbering, P. Foggi and F. V. Neuwahl, J. Phys. Chem. A, 2001, 105, 3709–3718 CrossRef CAS.
- K. Chevalier, M. M. Wolf, A. Funk, M. Andres, M. Gerhards and R. Diller, Phys. Chem. Chem. Phys., 2012, 14, 15007–15020 RSC.
- E. Cignoni, L. Cupellini and B. Mennucci, J. Phys.: Condens. Matter, 2022, 34, 304004 CrossRef CAS PubMed.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Chem. Rev., 2021, 121, 10073–10141 CrossRef CAS PubMed.
- M. Pinheiro, F. Ge, N. Ferré, P. O. Dral and M. Barbatti, Chem. Sci., 2021, 12, 14396–14413 RSC.
- S. Chmiela, H. E. Sauceda, A. Tkatchenko and K.-R. Müller, in Accurate Molecular Dynamics Enabled by Efficient Physically Constrained Machine Learning Approaches, ed. K. T. Schütt, S. Chmiela, O. A. von Lilienfeld, A. Tkatchenko, K. Tsuda and K.-R. Müller, Springer International Publishing, Cham, 2020, pp. 129–154 Search PubMed.
- A. W. Götz, M. A. Clark and R. C. Walker, J. Comput. Chem., 2014, 35, 95–108 CrossRef PubMed.
- B. F. Garcia, F2Py Sockets, 2018, https://github.com/b-fg/f2py-sockets/, accessed July 26, 2024.
- D. S. Hochbaum and D. B. Shmoys, Math. Oper. Res., 1985, 10, 180–184 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- A. Arcidiacono, P. Mazzeo, E. Cignoni, L. Cupellini and B. Mennucci, moldex: molecular descriptors in JAX, 2023, https://github.com/Molecolab-Pisa/moldex, accessed July 26, 2024.
- M. Bonomi, G. Bussi, C. Camilloni, G. A. Tribello, P. Banáš, A. Barducci, M. Bernetti, P. G. Bolhuis, S. Bottaro, D. Branduardi, R. Capelli, P. Carloni, M. Ceriotti, A. Cesari, H. Chen, W. Chen, F. Colizzi, S. De, M. D. L. Pierre, D. Donadio, V. Drobot, B. Ensing, A. L. Ferguson, M. Filizola, J. S. Fraser, H. Fu, P. Gasparotto, F. L. Gervasio, F. Giberti, A. Gil-Ley, T. Giorgino, G. T. Heller, G. M. Hocky, M. Iannuzzi, M. Invernizzi, K. E. Jelfs, A. Jussupow, E. Kirilin, A. Laio, V. Limongelli, K. Lindorff-Larsen, T. Löhr, F. Marinelli, L. Martin-Samos, M. Masetti, R. Meyer, A. Michaelides, C. Molteni, T. Morishita, M. Nava, C. Paissoni, E. Papaleo, M. Parrinello, J. Pfaendtner, P. Piaggi, G. M. Piccini, A. Pietropaolo, F. Pietrucci, S. Pipolo, D. Provasi, D. Quigley, P. Raiteri, S. Raniolo, J. Rydzewski, M. Salvalaglio, G. C. Sosso, V. Spiwok, J. Šponer, D. W. Swenson, P. Tiwary, O. Valsson, M. Vendruscolo, G. A. Voth and A. White, Nat. Methods, 2019, 16(8), 670–673 CrossRef PubMed.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- M. Nottoli, B. Mennucci and F. Lipparini, Phys. Chem. Chem. Phys., 2020, 22, 19532–19541 RSC.
- Y. Zuo, C. Chen, X. Li, Z. Deng, Y. Chen, J. Behler, G. Csányi, A. V. Shapeev, A. P. Thompson, M. A. Wood and S. P. Ong, J. Phys. Chem. A, 2020, 124, 731–745 CrossRef CAS PubMed.
- X. Fu, Z. Wu, W. Wang, T. Xie, S. Keten, R. Gomez-Bombarelli and T. Jaakkola, 2023.
- J. Westermayr and P. Marquetand, Chem. Rev., 2021, 121, 9873–9926 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Derivatives of kernels; learning curves; full force plots; errors along the reaction coordinate; comparison between ML/MM and QM/MM trajectories; trajectory stability; timings; fitting of the PT curves. See DOI: https://doi.org/10.1039/d4dd00295d |
| This journal is © The Royal Society of Chemistry 2024 |