Open Access Article
Open Access ArticleEmbedding material graphs using the electron-ion potential: application to material fracture†
Sherif Abdulkader
Tawfik‡
 *ab,
Tri Minh
Nguyen‡
*ab,
Tri Minh
Nguyen‡
 a,
Salvy P.
Russo
a,
Salvy P.
Russo
 c,
Truyen
Tran
c,
Truyen
Tran
 a,
Sunil
Gupta
a,
Sunil
Gupta
 a and
Svetha
Venkatesh
a and
Svetha
Venkatesh
 a
a
aApplied Artificial Intelligence Institute, Deakin University, Geelong, Victoria 3216, Australia. E-mail: s.abbas@deakin.edu.au; tri.nguyen1@deakin.edu.au; svetha.venkatesh@deakin.edu.au; sunil.gupta@deakin.edu.au
bARC Centre of Excellence in Exciton Science, Deakin University, Geelong, Victoria 3216, Australia
cARC Centre of Excellence in Exciton Science, School of Science, RMIT University, Melbourne 3000, Australia
First published on 8th November 2024
Abstract
At the heart of the flourishing field of machine learning potentials are graph neural networks, where deep learning is interwoven with physics-informed machine learning (PIML) architectures. Various PIML models, upon training with density functional theory (DFT) material structure–property datasets, have achieved unprecedented prediction accuracy for a range of molecular and material properties. A critical component in the learned graph representation of crystal structures in PIMLs is how the various fragments of the structure's graph are embedded in a neural network. Several of the state-of-art PIML models apply spherical harmonic functions. Such functions are based on the assumption that DFT computes the Coulomb potential of atom–atom interactions. However, DFT does not directly compute such potentials, but integrates the electron–atom potentials. We introduce the direct integration of the external potential (DIEP) methods which more faithfully reflects that actual computational workflow in DFT. DIEP integrates the external (electron–atom) potential and uses these quantities to embed the structure graph into a deep learning model. We demonstrate the enhanced accuracy of the DIEP model in predicting the energies of pristine and defective materials. By training DIEP to predict the potential energy surface, we show the ability of the model in predicting the onset of fracture of pristine and defective carbon nanotubes.
1 Introduction
In the last few years, machine learning (ML) potential models have been amassing an unprecedented number of contributions from interdisciplinary research teams worldwide. The capabilities of these models rapidly expanded into various material science applications, promising a future where highly accurate quantum material science computations can be performed at the cost of classical molecular dynamics, if not at a lower cost. The accuracy and generalisability of the models have been empowered by two key factors: the emergence of graph neutral network (GNN)1 models that superseded standard ML models in accuracy and complexity,2 and the abundance of a massive amount of quantum mechanically-computed material data in online databases. Over the last few years, the online databases, such as Materials Project (MP),3 JARVIS,4 AFLOW,5 Open Quantum Mechanical Database (OQMD),6 and others, have availed more than 3 million DFT-computed structures, and have been part of a standard benchmarking workflow for new ML models. GNNs have further been improved by the introduction of physical laws within the fabric of the neural network, establishing what is commonly known as physics-informed machine learning (PIML) models, as was demonstrated in DimeNet,7 its derivative M3GNET8 and MACE9 for property prediction and structure discovery. These models have explicitly incorporated physics-based representations for the atomic structure by transforming doublets (atom–atom pairs) using a radial basis function (RBF), and triplets (groups of three atoms within a sphere of a given radius) using spherical harmonics. The utilization of spherical harmonics stemmed from the analytical structure of the wave function, which is the solution of the Schrödinger equation that DFT aims to approximate. Trained on over 133k samples, the M3GNET achieved a mean absolute error (MAE) of 20 meV per atom for predicting the formation energy (Ef) of the test set samples. However, as will be shown in this work, the model struggles with the prediction of the properties of defective crystals, and in predicting the onset of carbon nanotube fracture.We propose a novel physics-informed ML framework for accurate prediction of both pristine and imperfect crystal materials. Called DIEP, it directly integrates the external potential of a structure, and it was implemented on the codebase of M3GNET. This direct integration is a critical correction to the physics in M3GNET, and we show its value in discerning the impact of material defects. In particular, DIEP is able to more accurately predict the total energy per atom of a defective system, as well as the structural changes that result from the presence of a defect in a material. We demonstrate these two merits of the DIEP model by conducting two learning tasks using datasets of crystalline systems: in task 1, we train the models to predict the total energy per atom and demonstrate the accuracy of DIEP in predicting the total energy per atom for 6 classes of material imperfections, which are displayed in Fig. 1. We further interrogate the models on common defects of diamond, and show that the accuracy of DIEP exceeds that of the trained M3GNET model in most of the test cases. In task 2, we train a potential model that predicts both the energy per atom and the atomic forces, which amount to the prediction of the potential energy surface (PES). We show the ability of DIEP in (1) reproducing the ground state crystal structure of a number of binary materials, and (2) in computing the fracture strain of a large carbon nanotube structure due to the presence of carbon vacancy defects, while the M3GNET model does not predict rupture of the CNT at excessive elongation strains.
2 Improving the physics
The PIML in M3GNET is based on embedding the graph nodes (including the atom–atom pairs, or bonds, and the three-atom structures, or triplets) into the neural network through a layer that calculates DFT-related properties, as was initially proposed in the DimeNET model. The DFT-related properties assume that the atoms in the structure are directly coupled by a Coulomb potential in a simplified Schrödinger equation, and embed the nodes by using the solutions of that equation as functions of the bonds and triplets in the structure. However, the direct atom–atom interaction emulated by the M3GNET is in fact neglected in typical DFT calculations. This is because, based on the Born–Oppenheimer approximation, the positions of atoms are treated as fixed. In this work, we introduce an alternative PIML approach that is based on the numerical integration of the external potential which is directly relevant to DFT. We embed the graph nodes using an integration layer, in which the atom–electron potential, rather than the atom–atom potential, is computed. Computing an integration for atom–electron interaction is advantageous because the atom–electron interaction uniquely determines the ground state DFT electron density ρ(r) (a direct implication of the Honenberg–Kohn theorem10), where ρ(r) is the function that enables the determination of the ground state total energy. Our method computes a simplified form for this term for the graph's bonds and triplets on a two-dimensional mesh, and passes these atom–electron interaction messages into the GNN.The total DFT energy is calculated by summing the kinetic energy T[ρ(r)], atom–electron energy (or external energy) Eext[ρ(r)], the Hartree energy EH[ρ(r)], and the exchange correlation energy EXC[ρ(r)], which are all functionals of the electron density ρ(r):
| ET[ρ(r)] = T[ρ(r)] + Eext[ρ(r)] + EH[ρ(r)] + EXC[ρ(r)] | (1) |
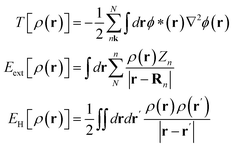 | (2) |
where
 is the complex conjugate of ϕi(r), the minimization problem is solved by applying the variational principle to ET with respect to the orbital functions ϕi(r). This yields the Kohn–Sham equations,
is the complex conjugate of ϕi(r), the minimization problem is solved by applying the variational principle to ET with respect to the orbital functions ϕi(r). This yields the Kohn–Sham equations,| HKSϕi(r) = Eiϕi(r) | (3) |
 | (4) |
In a GNN, structural data are generated for the input structure into a graph object with nodes and edges. For a given structure, nodes can represent information about atoms at the nodes' spacial positions Ri, and edges can represent the bonds between the atoms. The structure of the graph, as well as the count of nodes and edges, is different for each structure. In a GNN, the NN learns the graph connection between each node and the neighboring nodes iteratively. Following the extraction of bonds and triplets from the graphical representation of the input crystal structure, which is routinely performed by common GNN-based packages, DIEP performs the following standardization transformation on bonds and triplets, which is depicted in Fig. 2:
• for a bond between atoms with atomic numbers Zi and Zj, positions Ri and Rj, the line joining the points Ri and Rj is transformed into the line joining the two points 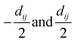 , where dij is the distance between Ri and Rj;
, where dij is the distance between Ri and Rj;
• for a triplet involving three atoms with atomic numbers Zi, Zj and Zk, positions Ri, Rj and Rk, the triangle Ri—Rj—Rk is transformed to Ra—Rb—Rc such that Ra—Rb is the longest side, followed by Rb—Rc then Ra—Rc.
For a transformed bond, identifying either atoms as Zi or Zj is the same, whereas for a triplet, we set the identities of the atoms in the transformed triangle based on the intersection between the identities of the atom pairs in the bonds of the triangle. This transformation ensures that the transformed structure is invariant to permutation of the identities of atoms.
Both the transformed bond and triangle are then centred within a two-dimensional grid where the x- and y axes range from −L to +L (in units of Å), with step size Δl. The transformation of the triangle Ri—Rj—Rk ensures that any three atoms at positions Ri, Rj and Rk will have a unique value for Eijk.
The 2D grid in DIEP is a simplification for the actual 3D grid in which the external potential is integrated; it is only a 2D “slice” of the 3D box. The points on the mesh represent the coordinates r of the electronic density function ρ(r). The representation of a triplet as a triangle on a mesh is an explicit incorporation of three-body interactions that combines the properties of the atoms (atomic numbers Zi) with their positions in a natural way, rather than embedding the triplet using bond angles that are separated from the atomic numbers as in M3GNET.
To embed a transformed bond, we compute the following terms, which are based on the external energy term Eext[ρ(r)] in eqn (3):
 | (5) |
 | (6) |
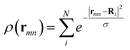 | (7) |
While this charge density representation is not representative for a large number of bonds, particularly in charge transfer situations where one of the atom loses a significant portion of its charge density (such as in the case of transition metals), it is still a reasonable assumption for the broad variety of bonds, as well as being computationally efficient. An improvement to the charge density representation would either use parametrised expressions such the one in ref. 11 or to express the charge density as a sum of gaussians with learnable parameters. Those learnable parameters would then be tuned as part of the entire training cycles of the DIEP model. Even though these trained 2D fragment charge densities will not be as complete as the densities that are obtained from models trained on actual densities, such as ref. 12–14 they would be expected to model the densities of their respective fragments. Exploring alternative strategies to represent ρ(r) is currently in progress.
Following the computation of the quantities Eij,mn and Eijk,mn, these quantities are then used to embed the bonds ij and triplets ijk into the neural network. This by performing the following numerical integration across the grid:
 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157 in the M3GNET model. Hence, an improvement in the DIEP model is not due to introducing additional learnable parameters. The DIEP hyperparameters include: the resolution of the grid (the values of L and Δl), the choice of using the external potential or external energy terms, whether to use the entire grid points or to use the summation of terms, and the value of σ in the exponential formula for ρ(r).
157 in the M3GNET model. Hence, an improvement in the DIEP model is not due to introducing additional learnable parameters. The DIEP hyperparameters include: the resolution of the grid (the values of L and Δl), the choice of using the external potential or external energy terms, whether to use the entire grid points or to use the summation of terms, and the value of σ in the exponential formula for ρ(r).
Next, To examine the predictive power of DIEP compared with M3GNET, we perform two training tasks. In the first task, we train DIEP and M3GNET models on a subset of stable materials from MP, and then challenge the generalisability the two models on deformed materials which are described in Fig. 5. In the second task, we train the M3GNET and DIEP models on a dataset of structural optimisation trajectories (the MPF.2021.2.8 dataset used in ref. 8) and compare the accuracy of predicting the total energy per atom and the atomic forces.
3 Results and discussion
3.1 Prediction of the energy of defective materials
• Random strains: for a sample of unit cells with a maximum of 4 atoms, a uniaxial strain is applied, where we randomly pic a strain value from the set of percentage strain values ±1%, ±2%, ±3%, ±4% and ±5% along the a lattice direction. For another sample of unit cells with a maximum of 4 atoms, we applied random triaxial strains, where we randomly pic a strain value from the set of percentage strain values ±1%, ±2%, ±3%, ±4% and ±5% along each of the axial directions.
• Single-site defects: for a sample of unit cells with a maximum of 4 atoms, a point defect is created in 2 × 2 × 1 supercells by either removing an atom, or substituting an atom with another, such that the two atoms are in the same group of the periodic table. This ensures the same number of valence electrons in the unit cell and avoid the complexity of dealing with potentially charged defects.
• Swapping of atomic positions: this disorder naturally occurs in high entropy alloys, where the distribution of the atoms within the lattice structure is rather stochastic.15
• Multi-site defects: a permutation of multiple vacancies is created in a supercell. In some cases, the permutations do not result in significant changes in the total energy. In this case, this class of deformations examines the false positives: whether the ML model will overestimate the energy cost of a small geometric change.
• Interstitial defects: hydrogen atoms are introduced into interstitial sites of metals and perovskites.
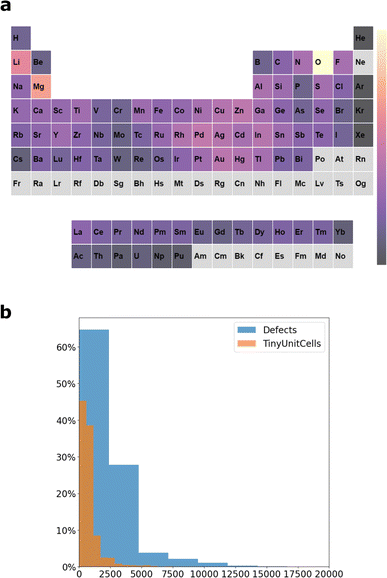
To examine the ability of DIEP and M3GNET in predicting the energies of the above defects, we first train both models on a sample of pristine materials from MP with up to 10 atoms in the unit cell, TinyUnitCells (version 1). The composition of this dataset is: 10k materials with up to 4 atoms per unit cell, 1k with 5 or 6 atoms per unit cell, and 1k materials with 7–10 atoms per unit cell. The representation of each of the elements in TinyUnitCells is displayed in Fig. 3a. There are 88 elements represented in the dataset (out of 89 elements that are represented in MP), the most frequently occurring elements are O, Li and Mg. The large representation of O in TinyUnitCells is similar to the case of the larger dataset MPF.2021.2.8.8
| Deformation | Dataset size | DIEP MAE (meV per atom) | M3GNET MAE (meV per atom) | |
|---|---|---|---|---|
| Strains | Triaxial | 404 | 90 | 94 |
| Optimised uniaxial | 929 | 59 | 65 | |
| Unoptimised uniaxial | 943 | 61 | 66 | |
| Single-site defects | Vacancies | 213 | 78 | 79 |
| Substitutions | 196 | 108 | 120 | |
| Atomic swaps | PtPdIrRh | 257 | 41 | 55 |
| CoCrFeNi | 263 | 90 | 45 | |
| FeNi | 123 | 328 | 287 | |
| PtIr | 268 | 41 | 43 | |
| Multi-vacancy swaps | LiCoO2 | 53 | 53 | 112 |
| LiAlO2 | 53 | 96 | 11 | |
| LiFePO4 | 70 | 195 | 231 | |
| Single interstitial H defect | Metals | 246 | 97 | 90 |
| Perovskites | 141 | 91 | 101 | |
| Multiple interstitial H defects | Zn | 18 | 48 | 103 |
| Ni | 14 | 24 | 35 | |
| Fe | 10 | 136 | 180 | |
| Pt | 10 | 56 | 144 |
DIEP outperforms M3GNET in predicting the energies of strained unit cells, whether the strain is triaxial, uniaxial optimised or uniaxial unoptimised, as shown in Table 1. We further examine the optimised uniaxial strained structures by observing the errors obtained for the strains ±1%, ±2%, ±3%, ±4%, and ±5%. The MAE for the DIEP model for each group of strains gradually increase with strain, as expected: 37 meV per atom, 45 meV per atom, 56 meV per atom, 68 meV per atom and 94 meV per atom. Except for the ±4% strain, these errors are consistently lower than those obtained using the trained M3GNET model: 44 meV per atom, 53 meV per atom, 62 meV per atom, 67 meV per atom and 101 meV per atom.
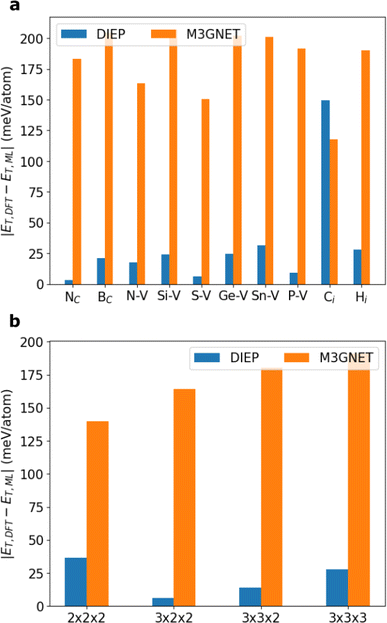
For single-site defects, DIEP is only 7 meV per atom better than M3GNET. Both models can accurately predict substitutional defects, where an atom is replaced by another atom that is one row above or below it in the periodic table (such as F replaced with Cl). They both struggle to predict the energy of substitutional defects where a small atom is substituted with a larger one that is 2 or more rows lower in the periodic table. For example, the DFT-calculated total energy per atom for BN ( ) with a N atom substituted with Bi is −7.90 eV per atom, but DIEP predicted a value of −9.87 eV per atom and M3GNET predicted −9.74 eV per atom. Vacancy defects are generally accurately predicted.
) with a N atom substituted with Bi is −7.90 eV per atom, but DIEP predicted a value of −9.87 eV per atom and M3GNET predicted −9.74 eV per atom. Vacancy defects are generally accurately predicted.
For alloy structures with swapped atomic positions, atomic swapping leads to mild changes in the total energy per atom in the PtPdIrRh, CoCrFeNi and PtIr alloy systems, and significant changes in the FeNi alloy system. The range of energies (difference between the highest and lowest values) in these alloy systems is 44 meV per atom, 73 meV per atom, 21 meV per atom and 354 meV per atom, respectively. Such spread in the data affected the predictive accuracy of both models. We also examine the swapping of multiple vacancy sites in the cathode materials LiCoO2 and LiFePO4, and LiAlO2, a cathode coating material. Lithium diffusion is key to the function of these materials, and it involves the presence of various defect configurations at any instance of time. We swap 3 defect sites in LiCoO2, 4 in LiFePO4 and 3 in LiAlO2. The structures for these defects were obtained by enumerating all the possible symmetrically unique combination of defects using the python library  . Swapping of defects in these materials caused very small changes in the total energy per atom: the energies vary within a range of 40 meV per atom. In all three cases, both methods were able to reflect the small variance in energies, with DIEP performing better than M3GNET in 2 of the 3 cases.
. Swapping of defects in these materials caused very small changes in the total energy per atom: the energies vary within a range of 40 meV per atom. In all three cases, both methods were able to reflect the small variance in energies, with DIEP performing better than M3GNET in 2 of the 3 cases.
Next, we consider H interstitial defects. An extra H is inserted into a crystal void of metallic structures and perovskites using the  function from the
function from the  class in the
class in the  python package. The presence of interstitial H in metals is one of the key causes of their embrittlement,16 and occurs during the diffusion of hydrogen in perovskites en route of water splitting. Predicting the energy of a single interstitial atom in both metals and perovskites was challenging for DIEP and M3GNET. For metals, the highest errors were due to H interstitial defects in crystal with triclinic symmetry (MAE for DIEP is 110 meV per atom, for M3GNET is 160 meV per atom). While DIEP is more accurate than M3GNET in predicting the energies of cubic and triclinic crystals, M3GNET surpassed the accuracy of DIEP for monoclinic (DIEP: 86 meV per atom, M3GNET: 80 meV per atom), orthorhombic (DIEP: 99 meV per atom, M3GNET: 92 meV per atom), trigonal (DIEP: 105 meV per atoms, M3GNET 73 meV per atom) and tetragonal (DIEP: 101 meV per atom, M3GNET: 86 meV per atoms) crystals. Adding more interstitial H atoms in a selection of metals (Fe, Pt, Ni and Zn) improved the accuracy of the DIEP model, as shown in the bottom of Table 1.
python package. The presence of interstitial H in metals is one of the key causes of their embrittlement,16 and occurs during the diffusion of hydrogen in perovskites en route of water splitting. Predicting the energy of a single interstitial atom in both metals and perovskites was challenging for DIEP and M3GNET. For metals, the highest errors were due to H interstitial defects in crystal with triclinic symmetry (MAE for DIEP is 110 meV per atom, for M3GNET is 160 meV per atom). While DIEP is more accurate than M3GNET in predicting the energies of cubic and triclinic crystals, M3GNET surpassed the accuracy of DIEP for monoclinic (DIEP: 86 meV per atom, M3GNET: 80 meV per atom), orthorhombic (DIEP: 99 meV per atom, M3GNET: 92 meV per atom), trigonal (DIEP: 105 meV per atoms, M3GNET 73 meV per atom) and tetragonal (DIEP: 101 meV per atom, M3GNET: 86 meV per atoms) crystals. Adding more interstitial H atoms in a selection of metals (Fe, Pt, Ni and Zn) improved the accuracy of the DIEP model, as shown in the bottom of Table 1.
Further, we examine the impact of dilution on the quality of the predictions. Defect dilution means that a single defect is created in increasingly large supercells. Here we focus on the single carbon vacancy defect. Fig. 5b displays the prediction error for the defect, starting with the defect in a 2 × 2 × 2 diamond supercell, up to 3 × 3 × 3. The MAE of the prediction of both M3GNET and DIEP reduces as the defect becomes more dilute, with DIEP highly surpassing the accuracy of M3GNET at all defect concentrations considered.
3.2 Prediction of the potential energy surface
Training an ML model to predict the potential energy surface (PES)27 requires the ability of the model to predict the potential energy as well as the atomic force vectors. The equivalence between the negative of the neural network's gradients with respect to the atomic coordinates and the forces on those atoms along those coordinates, is a natural connection between neural learning and the PES that was observed by Behler and Parrinello28 in their early work on neural network regression of material properties. To train the models, we use the MPF.2021.2.8 dataset which includes the total energy per atom, atomic forces and lattice stresses for nearly 188k structures. We applied the same network architecture as that used for M3GNET training. For the network parameters lmax and nmax, we test the following combination of values to find the combination (lmax, nmax) that will yield the lowest validation error for the total energy per atom: (2, 1), (2, 2) and (3, 3). We applied a training-validation-test partitioning of 90%, 5%, 5% and only included structures with atomic forces within the range −10 and 10 eV Å−1, following the procedure in ref. 29. We label the PES trained model DIEP-PES, and compare its performance against the M3GNET-PES model released as part of the python library (
python library ( ).8 We train the DIEP-PES model by optimising the total energy per atom and the atomic forces, without optimising the lattice stress. The combination (lmax, nmaxthat gave the lowest validation MAE for the total energy per atom was (3, 3), where the validation set error is 41 meV per atom. For the test set, the DIEP-PES models achieves a total energy per atom MAE of 61 meV per atom and a force MAE of 73 meV Å−1. The total energy per atom MAE for DIEP-PES is higher than that of the M3GNET-PES (which is 34 meV per atom) whereas the force MAE of the DIEP-PES is close to that of the M3GNET-PES (70 meV Å−1).
).8 We train the DIEP-PES model by optimising the total energy per atom and the atomic forces, without optimising the lattice stress. The combination (lmax, nmaxthat gave the lowest validation MAE for the total energy per atom was (3, 3), where the validation set error is 41 meV per atom. For the test set, the DIEP-PES models achieves a total energy per atom MAE of 61 meV per atom and a force MAE of 73 meV Å−1. The total energy per atom MAE for DIEP-PES is higher than that of the M3GNET-PES (which is 34 meV per atom) whereas the force MAE of the DIEP-PES is close to that of the M3GNET-PES (70 meV Å−1).
To assess the computation cost for running a PES calculation, we performed a single-point calculation with both DIEP-PES and M3GNET-PES on each structure of the entire MP database (155k structures). The average execution time of DIEP-PES on 1 GPU processor is 5.3 milliseconds per atom, while that of M3GNET-PES is 5.5 milliseconds per atom. We further examined the computational cost comparison by performing single-point calculations with DIEP-PES, M3GNET-PES and DFT (using VASP) for a random selection of 96 structures from the MP database where the number of atoms exceeds 30 atoms. The mean number of atoms in the set is 59 atoms. The DIEP-PES on 1 GPU processor consumed 1.4 milliseconds per atom, M3GNET-PES 1.3 milliseconds per atom, while the DFT calculation on 96 CPU cores consumed 18.1 seconds per atom. This shows that the computational complexities of the two methods are very close, and that the computational performance of the ML methods exceeds that of DFT by 3 orders of magnitude.
The computational performance per atom improves with larger number of atoms. To see how the structure size influences the computational performance, we perform a single-point calculation on a supercell of diamond with size N × 1 × 1 where N takes values from 1 to 100. The number of atoms at N = 1 is 8. The result is displayed in Fig. 6, showing that the computational scaling behaviours of both DIEP-PES and M3GNET-PES are very close.
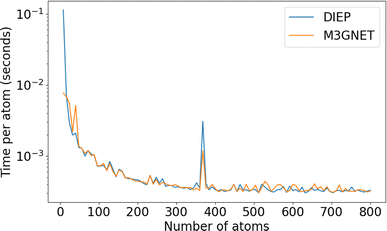 | ||
| Fig. 6 The scaling behaviour of DIEP-PES and M3GNET-PES: the computational time per atom as the size of the system increases. | ||
 python package which wraps the genetic library in
python package which wraps the genetic library in  . We compare the number of compounds that we successfully re-discovered by DIEP-PES against those re-discovered by M3GNET. We display the results in Table 2.
. We compare the number of compounds that we successfully re-discovered by DIEP-PES against those re-discovered by M3GNET. We display the results in Table 2.
| MP ID | Formula | DIEP-PES | M3GNET-PES |
|---|---|---|---|
| mp-24208 | CrH2 | ||
| mp-784631 | CrNi2 | ||
| mp-182 | SrGa2 | 0.01 | |
| mp-24728 | VH2 | ||
| mp-2732 | PRh2 | ||
| mp-11237 | ScAg | 0.00 | 0.04 |
| mp-1018138 | VI2 | ||
| mp-1000 | BaTe | 0.00 | 0.00 |
| mp-1169 | ScCu | 0.00 | 0.01 |
| mp-2516 | YZn | 0.00 | 0.00 |
| mp-1441 | CsO2 | ||
| mp-1883 | SnTe | 0.00 | |
| mp-1008626 | VTe2 | ||
| mp-2221 | Zr2Ag | ||
| mp-2697 | SrO2 | 0.01 | |
| mp-2857 | ScN | 0.02 | 0.01 |
| mp-23251 | KBr | 0.00 | 0.00 |
| mp-987 | ZnCu | 0.00 | 0.00 |
| mp-2658 | AlFe | 0.00 | 0.00 |
| mp-28013 | MnI2 | 0.29 | |
| mp-1207380 | ZrIn | 0.00 | 0.00 |
We examine the ability of DIEP-PES to re-discover the stable crystal structure for a number of binary compounds with an energy above hull of zero eV per atom. We utilise the  class which is a wrapper for the genetic algorithm code within the
class which is a wrapper for the genetic algorithm code within the  python library. We limit the genetic optimisation process to an initial population of 20 structures, and 5 evolutions where 20 candidate structures are generated every evolution. The genetic algorithm uses the total DFT energy as the fitness function. The following genetic evolution operators are allowed: cut and splice pairing,30 soft mutation31 and strain mutation,32 with probabilities of 0.4, 0.3 and 0.3, respectively. To compare between the optimised structures, we calculate the root mean square distance between two structures using the
python library. We limit the genetic optimisation process to an initial population of 20 structures, and 5 evolutions where 20 candidate structures are generated every evolution. The genetic algorithm uses the total DFT energy as the fitness function. The following genetic evolution operators are allowed: cut and splice pairing,30 soft mutation31 and strain mutation,32 with probabilities of 0.4, 0.3 and 0.3, respectively. To compare between the optimised structures, we calculate the root mean square distance between two structures using the  method in the
method in the  python library. The results are displayed in Table 2. The DIEP-PES was able to score more hits than M3GNET-PES: the DIEP-PES optimiser re-discovered the equilibrium structure of 12 out of 22 structures, whereas M3GNET-PES re-discovered 10 structures.
python library. The results are displayed in Table 2. The DIEP-PES was able to score more hits than M3GNET-PES: the DIEP-PES optimiser re-discovered the equilibrium structure of 12 out of 22 structures, whereas M3GNET-PES re-discovered 10 structures.
4 Conclusion
The ability to accurately predict the total energy is critical for the determination of the thermodynamic properties of materials. Our work improved the accuracy of predicting this quantity for materials with and without defects by introducing the direct integration of the external potential (DIEP) method. In principle, DIEP partially reflects the computations that take place during the electronic structure optimisation step in density functional theory, and therefore more faithfully introduces “physics” in a physics-informed machine learning process. We demonstrated the enhanced accuracy of DIEP in predicting the total energy per atom for several datasets: a 12k dataset of pristine materials, and datasets that represent 6 classes of material imperfections. In addition, we established the ability of DIEP in predicting the potential energy surface for materials (total energies and forces) by performing structure optimisation and molecular dynamics tasks, in particular reproducing the maximum strain of a carbon nanotube structure. Enriched with its unique physical insight, DIEP is therefore suited for high-throughput screening procedures for accelerating material discovery.5 Methods
5.1 DFT calculations
DFT calculations are performed using VASP 5.4.4.37 The generalized gradient approximation (GGA) of Perdew, Burke and Ernzerfof (PBE),38 The energy cut-off for the plane wave basis set is 520 eV, and the energy tolerance is 10−6 eV to ensure the accuracy of the calculations. In the structural energy minimization, the internal coordinates are allowed to relax until all of the forces are less than 0.01 eV Å−1. For magnetic structures, the initial magnetic moments are set using the default VASP values.Code availability
DIEP was implemented on the codebase of Matgl and is available here: https://github.com/sheriftawfikabbas/diep. The code that was used to generate the deformed structures is available as part of the package: https://github.com/sheriftawfikabbas/oganesson.
package: https://github.com/sheriftawfikabbas/oganesson.
Data availability
The VASP POSCAR files for the materials in TinyUnitCells and all of the defects examined in the work, the trained DIEP and M3GNET models are available here: https://github.com/sheriftawfikabbas/materialsalchemist.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by computational resources provided by the Australian Government through NCI and Pawsey under the National Computational Merit Allocation Scheme. S. A. T and S. R acknowledge computational resources that were received through the Australian Research Council funded Center of Excellence in Exciton Science (CE170100026).References
- I. I. Baskin, V. A. Palyulin and N. S. Zefirov, J. Chem. Inf. Comput. Sci., 1997, 37, 715–721 CrossRef CAS.
- X. Zhang, L. Wang, J. Helwig, Y. Luo, C. Fu, Y. Xie, M. Liu, Y. Lin, Z. Xu, K. Yan, K. Adams, M. Weiler, X. Li, T. Fu, Y. Wang, H. Yu, Y. Xie, X. Fu, A. Strasser, S. Xu, Y. Liu, Y. Du, A. Saxton, H. Ling, H. Lawrence, H. Stärk, S. Gui, C. Edwards, N. Gao, A. Ladera, T. Wu, E. F. Hofgard, A. M. Tehrani, R. Wang, A. Daigavane, J. Kurtin, Q. Huang, T. Phung, M. Xu, C. K. Joshi, S. V. Mathis, K. Azizzadenesheli, A. Fang, A. Aspuru-Guzik, M. Bronstein, M. Zitnik, A. Anandkumar, S. Ermon, P. Liò, R. Yu, S. Günnemann, J. Leskovec, H. Ji, J. Sun, R. Barzilay, T. Jaakkola, C. W. Coley, X. Qian, T. Smidt and S. Ji, Artificial Intelligence for Science in Quantum, Atomistic, and Continuum Systems, arXiv, 2023, preprint, arXiv:2307.08423, DOI:10.48550/arXiv.2307.08423.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- K. Choudhary, K. F. Garrity, A. C. E. Reid, B. DeCost, A. J. Biacchi, A. R. Hight Walker, Z. Trautt, J. Hattrick-Simpers, A. G. Kusne, A. Centrone, A. Davydov, J. Jiang, R. Pachter, G. Cheon, E. Reed, A. Agrawal, X. Qian, V. Sharma, H. Zhuang, S. V. Kalinin, B. G. Sumpter, G. Pilania, P. Acar, S. Mandal, K. Haule, D. Vanderbilt, K. Rabe and F. Tavazza, npj Comput. Mater., 2020, 6, 173 CrossRef.
- S. Curtarolo, W. Setyawan, G. L. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang, O. Levy, M. J. Mehl, H. T. Stokes, D. O. Demchenko and D. Morgan, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 15010 CrossRef CAS.
- J. Gasteiger, J. Groß and S. Günnemann, Directional Message Passing for Molecular Graphs, arXiv, 2022, preprint, arXiv:2003.03123, DOI:10.48550/arXiv.2003.03123.
- C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718–728 CrossRef PubMed.
- I. Batatia, D. P. Kovács, G. N. C. Simm, C. Ortner and G. Csányi, MACE: Higher Order Equivariant Message Passing Neural Networks for Fast and Accurate Force Fields, arXiv, 2023, preprint, arXiv:2206.07697, DOI:10.48550/arXiv.2206.07697.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- B. Cuevas-Zuviría and L. F. Pacios, J. Chem. Inf. Model., 2020, 60, 3831–3842 CrossRef PubMed.
- E. M. Sunshine, M. Shuaibi, Z. W. Ulissi and J. R. Kitchin, J. Phys. Chem. C, 2023, 127, 23459–23466 CrossRef CAS.
- S. Gong, T. Xie, T. Zhu, S. Wang, E. R. Fadel, Y. Li and J. C. Grossman, Phys. Rev. B, 2019, 100, 184103 CrossRef CAS.
- P. B. Jørgensen and A. Bhowmik, DeepDFT: Neural Message Passing Network for Accurate Charge Density Prediction, arXiv, 2020, preprint, arXiv:2011.03346, DOI:10.48550/arXiv.2011.03346.
- T. A. Batchelor, J. K. Pedersen, S. H. Winther, I. E. Castelli, K. W. Jacobsen and J. Rossmeisl, Joule, 2019, 3, 834–845 CrossRef CAS.
- S. Lynch, in Stress Corrosion Cracking, Elsevier, 2011, pp. 90–130 Search PubMed.
- L. Rondin, J.-P. Tetienne, T. Hingant, J.-F. Roch, P. Maletinsky and V. Jacques, Rep. Prog. Phys., 2014, 77, 056503 CrossRef CAS PubMed.
- G. Thiering and A. Gali, Phys. Rev. B, 2016, 94, 125202 CrossRef.
- T. Iwasaki, F. Ishibashi, Y. Miyamoto, Y. Doi, S. Kobayashi, T. Miyazaki, K. Tahara, K. D. Jahnke, L. J. Rogers, B. Naydenov, F. Jelezko, S. Yamasaki, S. Nagamachi, T. Inubushi, N. Mizuochi and M. Hatano, Sci. Rep., 2015, 5, 12882 CrossRef CAS PubMed.
- T. Iwasaki, Y. Miyamoto, T. Taniguchi, P. Siyushev, M. H. Metsch, F. Jelezko and M. Hatano, Phys. Rev. Lett., 2017, 119, 253601 CrossRef PubMed.
- A. M. Flatae, S. Lagomarsino, F. Sledz, N. Soltani, S. S. Nicley, K. Haenen, R. Rechenberg, M. F. Becker, S. Sciortino, N. Gelli, L. Giuntini, F. Taccetti and M. Agio, Diamond Relat. Mater., 2020, 105, 107797 CrossRef CAS.
- J. M. Baker, J. A. Van Wyk, J. P. Goss and P. R. Briddon, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235203 CrossRef.
- A. Mainwood, J. Phys. C: Solid State Phys., 1979, 12, 2543–2549 CrossRef CAS.
- R. Kalish, Diamond Relat. Mater., 2001, 10, 1749–1755 CrossRef CAS.
- J. P. Goss, R. Jones, M. I. Heggie, C. P. Ewels, P. R. Briddon and S. Öberg, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 115207 CrossRef.
- C. Weigel, D. Peak, J. W. Corbett, G. D. Watkins and R. P. Messmer, Phys. Rev. B: Solid State, 1973, 8, 2906–2915 CrossRef.
- J. Simons, P. Joergensen, H. Taylor and J. Ozment, J. Phys. Chem., 1983, 87, 2745–2753 CrossRef CAS.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- J. Qi, T. W. Ko, B. C. Wood, T. A. Pham and S. P. Ong, npj Comput. Mater., 2024, 10, 43 CrossRef.
- L. B. Vilhelmsen and B. Hammer, Phys. Rev. Lett., 2012, 108, 126101 CrossRef PubMed.
- A. O. Lyakhov, A. R. Oganov and M. Valle, Comput. Phys. Commun., 2010, 181, 1623–1632 CrossRef CAS.
- C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713–720 CrossRef CAS.
- L. Yang, I. Greenfeld and H. D. Wagner, Sci. Adv., 2016, 2, e1500969 CrossRef PubMed.
- D. Troya, S. L. Mielke and G. C. Schatz, Chem. Phys. Lett., 2003, 382, 133–141 CrossRef CAS.
- Q. Zhao, M. B. Nardelli and J. Bernholc, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 144105 CrossRef.
- S. L. Mielke, D. Troya, S. Zhang, J.-L. Li, S. Xiao, R. Car, R. S. Ruoff, G. C. Schatz and T. Belytschko, Chem. Phys. Lett., 2004, 390, 413–420 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: The data points for Table 1 are available in the Supplementary Information file. The structures in the sheets of the Excel file are available in the structure repository https://github.com/sheriftawfikabbas/materialsalchemist. See DOI: https://doi.org/10.1039/d4dd00246f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |