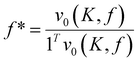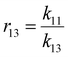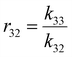Multi-objective synthesis optimization and kinetics of a sustainable terpolymer

Abstract

The properties of polymers are primarily influenced by their monomer constituents, functional groups, and their mode of linkages. Copolymers, synthesized from multiple monomers, offer unique material properties compared to their homopolymers. Optimizing the synthesis of terpolymers is a complex and labor-intensive task due to variations in monomer reactivity and their compositional shifts throughout the polymerization process. The present work focuses on synthesizing a new terpolymer from styrene, myrcene, and dibutyl itaconate (DBI) monomers with the goal of achieving a high glass transition temperature (T_g) in the resulting terpolymer. While the copolymerization of pairwise combinations of styrene, myrcene, and DBI have been previously investigated, the terpolymerization of all three at once remains unexplored. Terpolymers with monomers like styrene would provide high glass transition temperatures as the resultant polymers exhibit a rigid glassy state at ambient temperatures. Conversely, minimizing styrene incorporation also reduces reliance on petrochemical-derived monomer sources for terpolymer synthesis, thus enhancing the sustainability of terpolymer usage. To balance the objectives of maximizing T_g while minimizing styrene incorporation, we employ multi-objective Bayesian optimization to efficiently sample in a design space comprising 5 experimental parameters. We perform two iterations of optimization for a total of 89 terpolymers, reporting terpolymers with a T_g above ambient temperature while retaining less than 50% styrene incorporation. This underscores the potential for exploring and utilizing renewable monomers such as myrcene and DBI, to foster sustainability in polymer synthesis. Additionally, the dataset enables the calculation of ternary reactivity ratios using a system of ordinary differential equations based on the terminal model, providing valuable insights into the reactivity of monomers in complex ternary systems compared to binary copolymer systems. This approach reveals the nuanced kinetics of terpolymerization, further informing the synthesis of polymers with desired properties.

---

Introduction

Polymers, due to their versatile mechanical and physical properties, play an indispensable role in everyday life with applications in numerous industries and products. These properties can be attributed to the polymer's molecular weight distribution (MWD),^1,2 as well as the identity of the monomers that make up the final polymer,³ among other factors.⁴ Terpolymerization, which involves the simultaneous polymerization of three monomers, has commercial significance due to its potential to create polymers with unique properties absent in their corresponding homopolymers, allowing for greater customization of polymer properties.⁵ One example is acrylonitrile–butadiene–styrene (ABS), a tough material used for consumer products made through injection molding.^6,7 In comparison to its homopolymer polystyrene, ABS is opaque, exhibits good impact strength, and improved chemical resistance. The properties of ABS can also be tailored with the ratio of the three monomers⁸ based on specific requirements.

However, the traditional production of terpolymers and synthetic polymers relies heavily on petroleum-based monomers derived from fossil fuels,⁹ leading to environmental concerns such as greenhouse gas emissions¹⁰ and the depletion of non-renewable resources.¹¹ Therefore, there is a pressing need to explore alternative sources of monomers used in polymer synthesis that are renewable, ideally possessing similar properties to their petroleum-based counterparts. One such avenue includes research into sustainable polymers¹² which exhibit reduced environmental impact throughout their life cycles.¹³ By utilizing monomers obtained from renewable resources such as bio-based materials,¹⁴ polymers with reduced reliance on fossil fuels can be developed that contribute to a more circular economy.¹⁵ A polymer that has a high percentage of its carbon content derived from natural or biobased sources generally has a higher sustainability footprint than those with lower biobased carbon content. Therefore, we set a threshold of 50% of carbon from natural sources to identify materials that contribute to sustainability by reducing dependence on fossil fuels and lowering carbon footprints. This aligns with the guidelines set forth by the International Organization for Standardization (ISO) regarding the utilization of natural or bio-derived products across various applications.¹⁶ Consequently, the development of sustainable polymers has become increasingly imperative in today's world.¹⁷

Tremendous efforts have been taken for the synthesis of sustainable or green polymers in the literature.^12,18–20 A sustainable poly(DBI-co-butadiene) elastomer was synthesized^21avia environmentally benign emulsion polymerization methods. The resulting copolymers showed very high molecular weight (M_n, 236 kDa to 392 kDa) and mechanical properties as good as the synthetic rubber although they possess T_g of −42 to −72 °C. Copolymerization of myrcene and styrene for the synthesis of terpene-based renewable polymers under cationic polymerization conditions in aqueous medium was reported.^21b The resulting copolymers exhibit high molecular weights (M_n, 60 to 120 kDa) and glass transition temperatures (T_g, −43 to 15 °C). Sarkar and Bhowmick also reported the synthesis of Myr–DBI copolymers which have shown potential as substitutes for synthetic elastomers, exhibiting a range of sub-ambient glass T_g between −60.3 °C to −33.5 °C, depending on the weight percent of myrcene.²² Myrcene is a naturally occurring terpene found in plants such as thyme and lemongrass,²³ while DBI can be produced by the fermentation of raw corn starch,²⁴ resulting in a fully bioderived myrcene–DBI copolymer. These efforts mark an important step towards the replacement of petroleum-based polymers with sustainable alternatives. However, the lower T_g restricts the copolymer's use across a broader range of applications. To enhance the practical utility of this polymer, we propose incorporating styrene as a third monomer. This modification is expected to elevate the T_g of the resulting terpolymer to the ambient range enabling further applications of the terpolymer in its glassy state. We posit that the presence of rigid phenyl side chains in the styrene monomer would increase the T_g of the terpolymer.^25,26 Although styrene is not derived from renewable sources, its global production exceeds 30 million tons per year,²⁷ making it an easily accessible monomer. To maintain the sustainability profile of the final terpolymer, we aim to limit the incorporation of styrene while still seeking to elevate the T_g of the terpolymer. Additionally, in an effort to further enhance the sustainability footprint of the terpolymer synthetic process, we carry out the terpolymerization reaction in a solvent-free manner, circumventing the use of hazardous and toxic chemicals as solvents.

With this goal in mind, we looked to optimize the synthesis of styrene–myrcene–DBI terpolymers with maximal T_g and minimal styrene incorporation utilizing machine learning (ML) methods with the experimental data collected from one-pot radical terpolymerization reactions. To achieve this, we varied not only the molar ratio of the three monomers in the reaction feed, but also explored different AIBN (azobisisobutyronitrile) radical initiator molar ratios, reaction temperatures, and reaction durations, as shown in the reaction scheme in Fig. 1 below.

Fig. 1 Reaction scheme for the terpolymerization of styrene, myrcene and DBI. Styrene, myrcene and DBI will undergo terpolymerization in the presence of the AIBN radical initiator to form the styrene–myrcene–DBI terpolymer. The input parameters of the reaction include the feed molar ratios of the three monomers, ranging from 5 mol% to 95 mol% individually. The feed molar ratios of the three monomers must add to 100%. The AIBN molar ratio against the total amount of monomer ranges from 0.01 mol% to 5 mol%, the reaction temperature ranges from 60 °C to 80 °C, while the reaction time ranges from 1 hour to 8 hours. n, x and y subscripts in the terpolymer structure stands for the fraction of monomer incorporation in the synthesized terpolymer.

These experimental parameters can be adjusted to explore different combinations and their effects on the terpolymer properties. Although six input experimental parameters are listed, only five input parameters are independent due to the linear dependence²⁸ between the feed molar ratios of styrene, myrcene, and DBI. As previously mentioned, we focus on maximizing the T_g and minimizing styrene incorporation of the final terpolymer. These terpolymer attributes are then measured offline by differential scanning calorimetry (DSC) and ¹H NMR, respectively.

Uniformly grid sampling across the 5-dimensional input parameter space would be extremely labour and resource-intensive. Therefore, we employ Bayesian Optimization (BO),²⁹ which is a sample-efficient optimizer using the predictive capabilities of a surrogate model to suggest the next experiment(s) to perform, by which the model is updated on the new observations. This process is iterated until the desired optimization objective is attained. In a bi-objective optimization problem, both objectives must be balanced, where the optimal set of non-dominated solutions (meaning there are no other solutions which are as good or better in both objectives) is denoted as the Pareto Front (PF). Hypervolume (HV) is an important performance metric which considers the space covered by optimal solutions, bounded by a reference point. To perform BO in this context, a multi-objective BO algorithm must be used.

In this work, we used the Gaussian Process^29–31 (GP) regressor as the surrogate model. GPs are Gaussian distributions over functions and serve as probabilistic ML models that can capture uncertainties associated with the black-box function. This is implemented in BoTorch³² with a Matern5/2 kernel,³³ with independent models for each objective (T_g and styrene incorporation). We opted to use q-Noisy Expected Hypervolume Improvement (qNEHVI) acquisition function which is a state-of-the-art strategy for multi-objective optimization, and is also proven to be robust in handling observation noise.^34,35 The qNEHVI acquisition function estimates the expected improvement of the HV of a suggested sample as predicted by the surrogate model.

To ensure a fixed sum of 100% ratio between styrene, myrcene and DBI, we used Sobol sampling to provide a discrete set of samples that are then normalized to sum to 1. This constrained sample set is evaluated on the qNEHVI acquisition and ranked for highest acquisition value to be evaluated next, similar to the pre-repair optimization reported by Low and Mekki-Berrada.³⁶ The workflow and optimization process are shown in Fig. 2 below.

Fig. 2 Workflow for Bayesian optimization and terpolymer discovery. A random initialization using Sobol sampling is first conducted. The terpolymer synthesis process involves a one pot terpolymerization of styrene, myrcene and DBI under the suggested input experimental conditions. Subsequently, T_g is determined via DSC, while the molar ratio of styrene incorporated is determined via¹H NMR. This process generates a dataset of the input experimental conditions, with T_g and styrene incorporation, used to train the GP surrogate model. Based on the trained surrogate model, the qNEHVI acquisition function quantifies which input conditions result in the highest expected improvement of HV. The most promising samples will be experimentally validated, and this optimization cycle is repeated twice.

The optimization campaign is initialized with 55 input conditions with styrene concentration restricted to between 5–50%, suggested from Sobol sampling³⁷ to ensure good coverage of the targeted design space. After synthesis, the T_g and styrene incorporation of the terpolymer were determined to form the dataset of experimental input and output conditions for training surrogate models. Thereafter, two iterations of BO, consisting of 20 samples and 14 samples respectively, were performed. We opted to evaluate a smaller batch size for the second iteration due to the observed saturation of the Pareto Front (PF), as well as experimental throughput limitations. In total, 89 terpolymer samples were synthesized at the end of the optimization campaign. All relevant data, including the detailed experimental procedure, T_g and styrene incorporation of all terpolymer samples are included in the ESI.†

Results and discussion

Before commencing the optimization campaign, we initially synthesized the terpolymer from styrene, myrcene, and DBI to confirm its formation. An equimolar feed ratio of all three monomers was subjected to a reaction conditions and stirred at 80 °C for 4 hours in the presence of AIBN. Samples were collected every 30 minutes to monitor the depletion of individual monomers. As illustrated in Fig. 3a, the monomers were steadily consumed, resulting in an overall monomer conversion of approximately 55%. The reaction mixture was gradually added dropwise to methanol for the precipitation of the terpolymer and analysed. Gel permeation chromatography (GPC, Fig. 3b) plot displayed unimodal and symmetrical traces at a shorter retention time of 15.9 min. The formation of polymers with number average molecular weight (M_n) 14 150 Da and polydispersity index (M_w/M_n) of 1.8 indicated the formation of higher molecular weight compounds. The incorporation of styrene, myrcene and DBI was confirmed by analysing ¹H NMR of the precipitated polymer. The broad peaks observed at 7.2 ppm, 5.0 ppm and 4.0 ppm are respectively assigned to the protons of styrene, myrcene and DBI. The peak area integration of these peaks indicated that styrene, myrcene and DBI are incorporated in the resultant terpolymer in the ratio of 27.4 : 36.3 : 36.3 (Fig. S1, ESI†). This ratio is different from the equimolar feed ratio due to the difference in the reactivity ratios (cf., Table 1) amongst the different monomers in the reaction mixture. The two-dimensional Heteronuclear Single Quantum Coherence (HSQC) and Heteronuclear Multiple Bond Correlation (HMBC) spectra of the terpolymer displayed the ¹H–¹³C correlations among monomers confirms the terpolymer formation from all three monomers. The detailed information on the terpolymer synthesis and spectral assignments are presented in the ESI.† The synthesized terpolymer exhibits a T_g value of −17.5 °C, which is significantly different from pairwise combinations of equimolar amounts of styrene, myrcene, and DBI as well as their homopolymers (cf. ESI†). The above comprehensive data validates the synthesis of a terpolymer comprising styrene, myrcene, and DBI monomers.

Fig. 3 (a) Reactivity profile of styrene, myrcene and DBI in the formation of terpolymer. The unreacted monomer was quantified by NMR and plotted against reaction time. (b) GPC of the terpolymer synthesized from an equimolar feed concentration ratio of styrene, myrcene and DBI.

The objective space presented in Fig. 4a to c illustrates the trade-off between T_g and negative styrene incorporation in the final terpolymer. The observed negative correlation between T_g and styrene incorporation supports our initial hypothesis that the addition of styrene would elevate the T_g of the final terpolymer due to presence of rigid phenyl side chains. Overall, the optimization process yielded terpolymers with T_g ranging from −53.4 °C to 45.9 °C with corresponding styrene incorporation ranging from 0.9 mol% to 84.7 mol%. Fig. 4d reports an increasing realized HV across batches, indicating iterative improvements for every subsequent batch of synthesized terpolymers. Consequently, the optimization process resulted in the dense distribution of the 89 terpolymers across the entire T_g temperature range and styrene incorporation range. With reference to the input experimental conditions of these 89 terpolymers, we report the complete range of T_g and styrene incorporation by which scientists can tailor for desired properties.

Fig. 4 Objective space of the experimental outputs. (a–c) Objective space plots of the T_g against negative styrene incorporation show a negative correlation between them. Terpolymers with styrene incorporation of less than 50 mol% are highlighted with faint orange. Batch 1 (blue dots) consists of experimental data that were the result of random initialization by the BO algorithm. Batches 2 (green dots) and 3 (orange dots) were shown to be pushing the PF towards the north-east, meaning that we were able to simultaneously maximize T_g and minimize styrene incorporation. Within the region of the objective space with styrene incorporation less than 50 mol%, the highest T_g obtained was 24.6 °C. (d) A bar chart showing the evolution of the cumulative realized HV across batches, where the cumulative HV increases as the optimization campaign proceeds across batches.

When restricting the styrene incorporation to below 50 mol%, myrcene and DBI become the primary constituents of the final terpolymer, significantly enhancing its sustainability profile. The highest T_g reported with this constraint is 24.6 °C, which falls within the ambient range with an incorporation of 47.7%, 23.2% and 29.2% of styrene, myrcene and DBI respectively. (cf. Table S9, sample TP88, ESI†). This represents a significant improvement over a pure myrcene-DBI equally incorporated copolymer that exhibit T_g of −45.6 °C,¹⁷ while still maintaining a reasonable styrene incorporation. Detailed information on the BO implementation and code can be found in the ESI† and GitHub repositories.

Having reached a point of diminishing returns in the optimization process, we concluded the Bayesian Optimization (BO) after two iterations. This decision was based on the observed saturation of the Pareto Front (PF), indicating that further improvements in the optimization objectives were unlikely given the current experimental workflow. Following the conclusion of this optimization phase, we proceeded to analyse the data generated during the campaign, exploring relationships between various molecular parameters and glass transition temperatures, as detailed in the ESI.† In addition to this, we turned our attention to a deeper analysis of the monomer reactivities within the Sty–Myr–DBI ternary system.

The optimization campaign yielded 89 data points containing information on the final monomer mole fractions in the feed (f) as well as the final monomer mole fractions in the terpolymer (F). Using these data points, one can calculate the ternary reactivity ratios r_ij by setting up a system of Ordinary Differential Equations (ODEs). In this analysis, we modelled the terpolymerization via the terminal model,⁵ which treats the chemical reactivity of the propagating chain as dependent only on the identity of the monomer unit at the growing end, and the monomer that it will react with. Therefore, in a ternary system, chemical equations describing the propagation can be written down in the general form:

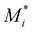where is the propagating chain ending in monomer M_i, M_j is the monomer subscripted by j, k_ij is the rate constant for the propagating chain ending in M_i adding to M_j. For a ternary system, i and j can take the values of 1, 2 or 3, representing styrene, myrcene and DBI respectively. To set up the rate equation for the ternary system, a system of ODEs which relates the rates of monomer disappearance, or the rate of monomer incorporation into the terpolymer can be written down in matrix form as follow:
where M = [M₁, M₂, M₃] denotes the vector of monomer concentrations, denotes the vector of concentrations of chains terminating in M₁, M₂ and M₃, respectively. K∈R^{3 × 3} denotes the rate constant matrix which is assumed to be invertible and diagonalizable, and ∘ denotes the element-wise product (Hadamard product). The above equation involving vectors M and M* can be normalized to give the monomer mole fraction vectors 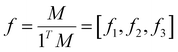and the fraction of chains terminating in monomers , where 1^T is the vector of all 1's and the elements in f and f* both sum to 1, to give the following equation:

Via the steady-state approximation, we can set , leading to the equation:

(K^Tf*)∘f − (Kf)∘f* = 0

which can be rewritten to the following:

(D_fK^T − D_Kf)f* = 0

where D_f and D_Kf represent the diagonal matrices having the elements of vectors f and Kf on their main diagonals and 0 everywhere else, respectively. Since K is assumed to be invertible and diagonalizable, the matrix (D_fK^T − D_Kf) has a one-dimensional null-space. We can denote the basis of the null space by the vector v₀(K,f). Then f* can be represented as with the following equation:

Then we can define the relationship between F and f as the following:

Given F and f from the experiments, we can solve for K by establishing a loss function which is minimized through the L-BFGS⁴¹ optimization method as follow:

where λ is a hyperparameter set to a large number (100) so that K₁₁ is set close to 1 so as to eliminate degeneracies. The absolute value of the elements in K calculated through this process would not be the actual rate constants of the propagating reaction in general. However, one can nonetheless calculate r_ij by taking the ratio of k_ii and k_ij. Detailed information on the theory of setting up the system of ODEs, mathematical formulation, the code used to optimize the loss function, usage of fitted K and f to assess F predictions can be found in the ESI† and GitHub repositories.

After optimization, we obtain the rate constant matrix and subsequently, the ternary reactivity ratios r_ij as follow:

Table 1 shows the summary of the ternary reactivity ratios rounded to 3 decimal places, along with the binary reactivity ratio values obtained from the literature for comparison. While binary and ternary reactivity ratios are not interchangeable,⁴² binary reactivity ratios provide a good basis of comparison in assessing the magnitude of the ternary reactivity ratios. In general, all ternary reactivity ratios are of similar magnitude when compared to their binary reactivity ratio counterparts, except for r₃₂ – the ternary reactivity ratio between DBI and myrcene. This implies that in a binary system of myrcene and DBI, the propagating chain terminating in DBI prefers to add to a DBI monomer as compared to a myrcene monomer, while in a ternary system of styrene, myrcene and DBI, the propagating chain terminating in DBI prefers to add to a myrcene monomer as compared to a DBI monomer, in the presence of the styrene. This stands out as an outlier warranting further investigation which could be the subject of a further study. It is important to also note that the calculated ternary reactivity ratios could be influenced by experimental noise, which should be considered when interpreting the data. In the context of this study, the ternary reactivity ratios derived in the styrene–myrcene–DBI ternary system serves as useful information for polymer chemists who looking to study similar ternary systems.

Table 1 Summary of the ternary reactivity ratios. In the first column, the formula to calculate the ternary reactivity ratios are shown. In the second column, the values of the ternary reactivity ratios, rounded to 3 decimal places are presented. In the last column, the literature values of binary reactivity ratios are included for comparison. Index 1 stands for styrene, index 2 stands for myrcene, index 3 stands for DBI

Ternary reactivity ratios (rij)	Value (3 d.p.)	Literature values of binary reactivity ratios
	0.542	0.27 (ref. 38), 0.25 (ref. 39)
	0.557	0.59 (ref. 40)
	2.031	1.36 (ref. 38), 1.88 (ref. 39)
	0.445	0.795 (ref. 22)
	0.080	0.14 (ref. 40)
	0.042	1.528 (ref. 22)

---

Conclusion

In conclusion, we have implemented multi-objective BO in the discovery of styrene–myrcene–DBI terpolymers, for maximizing T_g while minimizing styrene incorporation, demonstrating a framework for the design and synthesis of terpolymers with tailored properties. We report synthesized terpolymers with a wide range of glass transition temperature from −53.4 °C to 45.9 °C, and styrene incorporation varying from 0.9 mol% to 84.7 mol%. Notably, we were able to produce terpolymers with a styrene incorporation below 50 mol% with a glass transition temperature (T_g) of 24.6 °C. While this falls within the ambient temperature range, we did not achieve T_g exceeding 50 °C for wider applications. This limitation arises from the intrinsic physical properties of the monomers and their linkages, which are beyond the control of any optimization process. To overcome this challenge, it is necessary to expand the chemical search space beyond styrene, myrcene and DBI to other monomer systems and potentially leverage information from molecular simulations effectively. The 89 terpolymer samples also allowed for the calculation of ternary reactivity ratios, which would be useful information for the study of related terpolymer systems. Our platform shows that multi-objective optimization is an efficient way to drive sustainable polymer synthesis towards desired target properties, while simultaneously providing rich data to understand reaction kinetics.

Data availability

The data and software that support the findings of this study are openly available as follows: terpolymer NMR, DSC and GPC Data: https://github.com/TanJinDa-94/April-2024-Terpolymer, Bayesian optimization: https://github.com/andrelowky/Styrene-Terpolymer-Optimization, ternary reactivity ratio calculation: https://github.com/LiQianxiao/Generalized-Mayo-Lewis-Calculator.

Author contributions

The authors confirm their contribution to the paper as follows: J. D. T., A. K. Y. L., Y. F. L., S. K., B. R., and K. H. conceived the idea and designed the experiments. J. D. T., S. T. R. Y. and B. R. carried out the experiments and analysed the NMR data. A. K. Y. L. wrote the code for Bayesian Optimization; S. Y. T. and W. Z. collected and analysed the DSC and GPC data respectively, Q. L. developed the theory and wrote the code for the ternary reactivity ratio determination, J. D. T., A. K. Y. L., B. R., S. K. and K. H. wrote the manuscript. All authors reviewed the results and approved the final version of the manuscript.

Conflicts of interest

K. H. declare no competing non-financial interests but the following competing financial interests: he owns equity in a start-up focused on using high-throughput and machine learning for materials.

Acknowledgements

K. H. and B. R. acknowledge funding from the Materials Generative Design and Testing Framework (MAT-GDT) Program at A*STAR, provided through the AME Programmatic Fund (Grant No. M24N4b0034). K. H. acknowledges the National Research Foundation's Competitive Research Programme (NRF-CRP) in Singapore (Grant No. NRF-CRP25-2020-0002). BR thanks the Horizontal Technology Coordinating Office of A*STAR for seed funding under project No. C231218004.

References

1. D. T. Gentekos, R. J. Sifri and B. P. Fors, Controlling Polymer Properties through the Shape of the Molecular-Weight Distribution, Nat. Rev. Mater., 2019, 4(12), 761–774,  DOI:10.1038/s41578-019-0138-8.
2. R. W. Nunes, J. R. Martin and J. F. Johnson, Influence of Molecular Weight and Molecular Weight Distribution on Mechanical Properties of Polymers, Polym. Eng. Sci., 1982, 22(4), 205–228,  DOI:10.1002/pen.760220402.
3. G. Natta, Properties of Isotactic, Atactic, and Stereoblock Homopolymers, Random and Block Copolymers of α-Olefins, J. Polym. Sci., 1959, 34(127), 531–549,  DOI:10.1002/pol.1959.1203412738.
4. A. Bhattacharya and B. N. Misra, Grafting: A Versatile Means to Modify Polymers: Techniques, Factors and Applications, Prog. Polym. Sci., 2004, 29(8), 767–814,  DOI:10.1016/J.PROGPOLYMSCI.2004.05.002.
5. G. Odian, Principles of Polymerization, John Wiley & Sons, Ltd, 4th edn, 2004.
6. R. J. Young and P. A. Lovell, Introduction to Polymers, Taylor and Francis Ltd, 2011.
7. J. Sreedharan and A. K. Jeevanantham, Analysis of Shrinkages in ABS Injection Molding Parts for Automobile Applications, in Materials Today: Proceedings, Elsevier, 2018, vol. 5, pp. 12744–12749,  DOI:10.1016/j.matpr.2018.02.258.
8. E. N. Peters, Plastics: Thermoplastics, Thermosets, and Elastomers, in Handbook of Materials Selection, John Wiley & Sons, Ltd, 2007, pp. 335–355,  DOI:10.1002/9780470172551.ch11.
9. C. Vilela, A. F. Sousa, A. C. Fonseca, A. C. Serra, J. F. J. Coelho, C. S. R. Freire and A. J. D. Silvestre, The Quest for Sustainable Polyesters – Insights into the Future, Polym. Chem., 2014, 5(9), 3119–3141,  10.1039/C3PY01213A.
10. F. Bauer, T. D. Nielsen, L. J. Nilsson, E. Palm, K. Ericsson, A. Fråne and J. Cullen, Plastics and Climate Change Breaking Carbon Lock-Ins through Three Mitigation Pathways, One Earth, 2022, 5(4), 361–376,  DOI:10.1016/j.oneear.2022.03.007.
11. G. Z. Papageorgiou, Thinking Green: Sustainable Polymers from Renewable Resources, Polymers, 2018, 10(9), 952–956,  DOI:10.3390/polym10090952.
12. S. A. Miller, Sustainable Polymers: Opportunities for the next Decade, ACS Macro Lett., 2013, 2(6), 550–554,  DOI:10.1021/mz400207g.
13. Y. Zhu, C. Romain and C. K. Williams, Sustainable Polymers from Renewable Resources, Nature, 2016, 540(7633), 354–362,  DOI:10.1038/nature21001.
14. S. Thakur, J. Chaudhary, P. Singh, W. F. Alsanie, S. A. Grammatikos and V. K. Thakur, Synthesis of Bio-Based Monomers and Polymers Using Microbes for a Sustainable Bioeconomy, Bioresour. Technol., 2022, 344, 126156,  DOI:10.1016/j.biortech.2021.126156.
15. S. Torres-Giner, Sustainable Polymer Technologies for a Circular Economy, Appl. Sci., 2023, 13(10), 5864,  DOI:10.3390/APP13105864.
16. ISO, ISO 16128-1:2016, https://www.iso.org/standard/62503.html, accessed 2024-06-05.
17. D. K. Schneiderman and M. A. Hillmyer, 50th Anniversary Perspective: There Is a Great Future in Sustainable Polymers, Macromolecules, 2017, 50(10), 3733–3749,  DOI:10.1021/acs.macromol.7b00293.
18. P. B. V. Scholten, C. Detrembleur and M. A. R. Meier, Plant-Based Nonactivated Olefins: A New Class of Renewable Monomers for Controlled Radical Polymerization, ACS Sustain. Chem. Eng., 2019, 7(2), 2751–2762,  DOI:10.1021/acssuschemeng.8b05926.
19. D. Tang, C. W. Macosko and M. A. Hillmyer, Thermoplastic Polyurethane Elastomers from Bio-Based Poly(δ-Decalactone) Diols, Polym. Chem., 2014, 5(9), 3231–3237,  10.1039/C3PY01120H.
20. K. Yao and C. Tang, Controlled Polymerization of Next-Generation Renewable Monomers and Beyond, Macromolecules, 2013, 46(5), 1689–1712,  DOI:10.1021/ma3019574.
21. (a) X. Zhou, H. Ji, G.-H. Hu, R. Wang and L. Zhang, A Solvent-Less Green Synthetic Route toward a Sustainable Bio-Based Elastomer: Design, Synthesis, and Characterization of Poly(Dibutyl Itaconate-Co-Butadiene), Polym. Chem., 2019, 10(45), 6131–6144,  10.1039/C9PY01393H; (b) M. I. Hulnik, I. V. Vasilenko, A. V. Radchenko, F. Peruch, F. Ganachaudc and S. V. Kostjuk, Polym. Chem., 2018, 9, 5690–5700,  10.1039/C8PY01378K.
22. P. Sarkar and A. K. Bhowmick, Green Approach toward Sustainable Polymer: Synthesis and Characterization of Poly(Myrcene-Co-Dibutyl Itaconate), ACS Sustain. Chem. Eng., 2016, 4(4), 2129–2141,  DOI:10.1021/acssuschemeng.5b01591.
23. A. Behr and L. Johnen, Myrcene as a Natural Base Chemical in Sustainable Chemistry: A Critical Review, ChemSusChem, 2009, 2(12), 1072–1095,  DOI:10.1002/CSSC.200900186.
24. K. Yahiro, S. Shibata, S. R. Jia, Y. Park and M. Okabe, Efficient Itaconic Acid Production from Raw Corn Starch, J. Ferment. Bioeng., 1997, 84(4), 375–377,  DOI:10.1016/S0922-338X(97)89265-3.
25. J. Dudowicz, K. F. Freed and J. F. Douglas, The Glass Transition Temperature of Polymer Melts, J. Phys. Chem. B, 2005, 109(45), 21285–21292,  DOI:10.1021/jp0523266.
26. R. Xie, A. R. Weisen, Y. Lee, M. A. Aplan, A. M. Fenton, A. E. Masucci, F. Kempe, M. Sommer, C. W. Pester, R. H. Colby and E. D. Gomez, Glass Transition Temperature from the Chemical Structure of Conjugated Polymers, Nat. Commun., 2020, 11(1), 1–8,  DOI:10.1038/s41467-020-14656-8.
27. S. Fedotov, V. I. Uvarov, M. V. Tsodikov, S. Paul, P. Simon, M. Marinova and F. Dumeignil, Production of Styrene by Dehydrogenation of Ethylbenzene on a [Re, W]/γ-Al2O3 (K, Ce)/α-Al2O3 Porous Ceramic Catalytic Converter, Chem. Eng. Process., 2021, 160, 108265,  DOI:10.1016/j.cep.2020.108265.
28. G. Strang, Introduction to Linear Algebra, Wellesley-Cambridge Press, 5th edn, 2015.
29. R. Garnett, Bayesian Optimisation, Cambridge University Press, 2023.
30. P. I. Frazier, A Tutorial on Bayesian Optimization, arXiv, 2018, preprint, arXiv:1807.02811,  DOI:10.48550/arXiv.1807.02811.
31. Y.-F. Lim, C. K. Ng, U. S. Vaitesswar and K. Hippalgaonkar, Extrapolative Bayesian Optimization with Gaussian Process and Neural Network Ensemble Surrogate Models, Adv. Intell. Syst, 2021, 2100101,  DOI:10.1002/aisy.202100101.
32. M. Balandat, B. Karrer, D. R. Jiang, S. Daulton, B. Letham, A. G. Wilson and E. Bakshy, BoTorch: A Framework for Efficient Monte-Carlo Bayesian Optimization, arXiv, 2024, preprint, arXiv:1910.06403,  DOI:10.48550/arXiv.1910.06403.
33. M. G. Genton, Classes of Kernels for Machine Learning: A Statistics Perspective, J. Mach. Learn. Res, 2002, 2, 299–312.
34. S. Daulton, M. Balandat and E. Bakshy, Parallel Bayesian Optimization of Multiple Noisy Objectives with Expected Hypervolume Improvement, In 35th Conference on Neural Information Processing Systems (NeurIPS 2021), 2021, vol. 3, pp. 2187–2200.
35. A. K. Y. Low, E. Vissol-Gaudin, Y.-F. Lim and K. Hippalgaonkar, Mapping Pareto Fronts for Efficient Multi-Objective Materials Discovery, J. Mater. Inf., 2023, 3(11), 1–21,  DOI:10.20517/jmi.2023.02.
36. A. K. Y. Low, F. Mekki-Berrada, A. Gupta, A. Ostudin, J. Xie, E. Vissol-Gaudin, Y.-F. Lim, Q. Li, Y. S. Ong, S. A. Khan and K. Hippalgaonkar, Evolution-Guided Bayesian Optimization for Constrained Multi-Objective Optimization in Self-Driving Labs, npj Comput. Mater., 2024, 10(1), 1–11,  DOI:10.1038/s41524-024-01274-x.
37. I. M. Sobol, Uniformly Distributed Sequences with an Additional Uniform Property, USSR Comput. Math. & Math. Phys., 1976, 16(5), 236–242,  DOI:10.1016/0041-5553(76)90154-3.
38. D. L. Trumbo, Free Radical Copolymerization Behavior of Myrcene, Polym. Bull., 1993, 31(6), 629–636,  DOI:10.1007/BF00300120.
39. A. Métafiot, Y. Kanawati, J.-F. Gérard, B. Defoort and M. Marić, Synthesis of β-Myrcene-Based Polymers and Styrene Block and Statistical Copolymers by SG1 Nitroxide-Mediated Controlled Radical Polymerization, Macromolecules, 2017, 50(8), 3101–3120,  DOI:10.1021/acs.macromol.6b02675.
40. T. Sato, N. Morita, H. Tanaka and T. Ota, Solvent Effect on the Radical Polymerization of Di-n-Butyl Itaconate, J. Polym. Sci., Part A: Polym. Chem., 1989, 27(8), 2497–2508,  DOI:10.1002/pola.1989.080270802.
41. D. C. Liu and J. Nocedal, On the Limited Memory BFGS Method for Large Scale Optimization, Math. Program., 1989, 45(1), 503–528,  DOI:10.1007/BF01589116.
42. A. J. Scott and A. Penlidis, Binary vs. Ternary Reactivity Ratios: Appropriate Estimation Procedures with Terpolymerization Data, Eur. Polym. J., 2018, 105, 442–450,  DOI:10.1016/j.eurpolymj.2018.06.021.

---

Footnotes

† Electronic supplementary information (ESI) available: experimental details and tables of collated terpolymer data. The ESI contains the following sections: (1) GitHub repositories, (2) experimental methods, (3) terpolymer data. See DOI: https://doi.org/10.1039/d4dd00233d

‡ Authors contributed equally.

---