Discrete and mixed-variable experimental design with surrogate-based approach

Abstract

Experimental design plays an important role in efficiently acquiring informative data for system characterization and deriving robust conclusions under resource limitations. Recent advancements in high-throughput experimentation coupled with machine learning have notably improved experimental procedures. While Bayesian optimization (BO) has undeniably revolutionized the landscape of optimization in experimental design, especially in the chemical domain, it is important to recognize the role of other surrogate-based approaches in conventional chemistry optimization problems. This is particularly relevant for chemical problems involving mixed-variable design space with mixed-variable physical constraints, where conventional BO approaches struggle to obtain feasible samples during the acquisition step while maintaining exploration capability. In this paper, we demonstrate that integrating mixed-integer optimization strategies is one way to address these challenges effectively. Specifically, we propose the utilization of mixed-integer surrogates and acquisition functions–methods that offer inherent compatibility with problems with discrete and mixed-variable design space. This work focuses on piecewise affine surrogate-based optimization (PWAS), a surrogate model capable of handling medium-sized mixed-variable problems (up to around 100 variables after encoding) subject to known linear constraints. We demonstrate the effectiveness of this approach in optimizing experimental planning through three case studies. By benchmarking PWAS against state-of-the-art optimization algorithms, including genetic algorithms and BO variants, we offer insights into the practical applicability of mixed-integer surrogates, with emphasis on problems subject to known discrete/mixed-variable linear constraints.

---

1. Introduction

Experimental design includes five main steps¹ as depicted in Fig. 1: (i) define the objective of the experiments, for instance, for a chemical reaction, the objective can be maximizing the yield of a desired product; (ii) select the relevant variables and their corresponding ranges. The variables may include independent, dependent, and control variables; (iii) plan the experiments, for which different strategies can be employed; (iv) conduct the experiments; and (v) analyze the data obtained from the experiments. Performing chemical and physical experiments is often expensive in terms of the required time, resources, and human labor. Therefore, it is important to plan experiments efficiently to gather pertinent data with a small number of required experiments.

Fig. 1 General steps of experimental design.

Traditional experimental planning methods, such as full factorial designs, fractional factorial designs, and mixture design,^2,3 often involve testing a set of selected conditions exhaustively on a predefined or a trial-and-error scheme, which can be time-consuming, resource-intensive, and impractical for complex systems.⁴ For example, the extended time frame associated with translating material discoveries into market-ready products, exceeding 20 years on average, presents a significant challenge for the timely implementation of novel technologies in industrial applications.^5,6 Moreover, traditional methods rely heavily on expert knowledge, which introduces bias into an already complex design space. To address these challenges, different approaches have been studied and developed over the years to optimize the experimental planning process.

For example, recent developments in high-throughput experimentation (HTE)^7,8 have significantly broadened the scope of experimental capabilities, allowing for the collection of several thousand data points within a constrained set of conditions in a reasonable time frame. The process of HTE implies a substantial enhancement in the efficiency and scale of data acquisition compared to traditional experimental methods.⁹ Yet, deciding on the constrained set of conditions to test remains challenging. One proposed solution is to integrate machine learning methods with HTE to efficiently navigate the search space.¹⁰

Generalized subset designs and model-driven approaches such as model-based design of experiments (MBDoEs) have emerged as an answer to the shortcomings of the traditional factorial design of experiments. Generalized subset design involves efficiently selecting representative subsets from a large pool of experimental points by employing combinatorial structures like orthogonal arrays and Latin squares. These subsets are transformed into symmetrical/hypercube representations, where optimal design planes are generated and later reverted to the original experimental space.¹¹ Generalized subset designs are robust but cannot be adaptively updated with information gained and, therefore, can be inefficient when the design space is large. On the other hand, MBDoE aims to fit a reasonably well-performing semi-empirical or empirical model with a small number of information-rich samples.^12–14 The parameters of the model can be estimated by different optimality criteria. For example, the commonly used D-optimal design¹⁵ can be used to select samples to estimate the parameters by maximizing the determinant of the information matrix. One limitation of MBDoE is its restricted exploration capability,⁴ and the need for the system to be well understood for an accurate model to be derived. Additionally, MBDoE primarily relies on predefined experimental designs, which may inadvertently overlook certain regions of the experimental space. This limitation can impede the discovery of patterns or relationships within the data. For example, MBDoE may fail to consider the impact of unconventional temperatures or unique solvents if these factors are not incorporated into the initial model assumptions, thereby potentially missing out on superior reaction conditions that could significantly improve the yield of a target product.

Recently, more flexible and adaptive data-driven approaches, such as Bayesian optimization (BO) methods,^16–20 have been proposed as a solution, making it possible to adjust the experimental planning dynamically based on accumulated information. For instance, different surrogate-based optimization methods^21–23 have been developed over the years. By incorporating Bayesian principles, the experimental space can be navigated more effectively, allowing for more comprehensive exploration and a better chance of uncovering hidden insights that might be overlooked by conventional DoE approaches. This emphasizes the importance of considering alternative approaches, particularly those with enhanced exploration capabilities, to ensure a more thorough and insightful understanding of the underlying phenomena. Prior works have extensively explored surrogate modeling techniques such as Gaussian processes,²⁴ radial basis functions,^25,26 and neural networks^27,28 to approximate the underlying correlations between the design variables and the desired outcomes.

While BO-based and other surrogate-based approaches have been successfully employed in many applications, including material discoveries,^29–35 chemical synthesis,^4,32,36 and engineering design,^32,37–42 their effectiveness is limited when addressing optimization problems with mixed-variable domains. These domains encompass data structures characterized by a combination of continuous, integer, and categorical variables, and are frequently encountered in real-world chemical problems. As implemented in the current BoTorch⁴³ package (v-0.11.3), a common method employed by BO approaches to handle mixed-integer/mixed-variable cases involves iterating through all potential integer/categorical values in an outer loop while optimizing the continuous variables. This process becomes cumbersome and impractical with an increasing number of integer/categorical variables.^4,43 To avoid exhaustive enumeration, Daulton et al.⁴⁴ proposed a probabilistic reparameterization (PR) approach. In this method, discrete variables are sampled from a probability distribution that is parameterized by continuous variables. This allows for more efficient optimization of mixed-variable problems by optimizing over the continuous reparameterization rather than the discrete space directly.

The presence of discrete or mixed-variable constraints further complicates the optimization process. Constraints can be known or unknown a priori; in this paper, we limit the scope to problems with known constraints. Various BO methods have been developed for constrained problems in continuous spaces. For example, known constraints can be specified upfront to define the feasible region, which is then used to define an indicator function for feasibility. The indicator function can then be coupled with the acquisition strategies, such as expected improvement, to guide the search toward feasible samples.⁴⁵ Also, polytope sampling⁴⁶ strategies can be used to generate initial feasible samples. However, these methods were originally designed for continuous and smooth constraint landscapes, making them less effective and often inefficient when applied to discrete or mixed-variable constrained problems, particularly when dealing with a large number of constraints.

To address the challenges posed by constrained mixed-integer spaces in experimental planning, in this work, we propose a different framework – the use of mixed-integer surrogates and acquisition functions, for which we adopt the recently developed optimization package, piecewise affine surrogate-based optimization⁴⁷ (PWAS). PWAS is selected as it is tailored to address linearly-constrained discrete and mixed-variable domains enabling direct incorporation of discrete/categorical decision variables in the optimization process, which provides a more realistic representation of the problem. Additionally, PWAS can handle mixed-variable linear equality/inequality constraints, which are commonly encountered in physical and chemical systems, ensuring the proposal of feasible solutions throughout the design procedure.

The paper is organized as follows. In Section 2, we discuss the general problem formulation of the experimental planning optimization problem, focusing on problems with discrete and mixed-variable design space. In Section 3, we review existing optimization methods for the target problem. Following that, in Section 4, we lay out the overall steps of PWAS, which we proposed to employ to address experimental planning optimization with mixed-variable domains. We then discuss the implementation and performance of PWAS through three case studies: Suzuki–Miyaura cross-coupling, crossed barrel, and reacting solvent design in Section 5. Conclusion and future research directions are summarized in Section 6.

2. Problem description

In this paper, we focus on solving experimental planning optimization problems with discrete and mixed-variable domains which can be subject to linear equality and inequality constraints.

The general mathematical formulation of the targeted problem is:

X*∈ arg min f(X), (1)

where X = [x; y; Z] consists of the continuous variable x ∈ [Doublestruck R]^n_c, integer variable y ∈ [Doublestruck Z]^n_int, and categorical variable Z = [Z¹,…,Z^n_d], with n_i classes in each categorical variable Zⁱ, i = 1, …, n_d. We assume both x and y are bounded, i.e., [small script l]_x ≤ x ≤ u_x and [small script l]_y ≤ y ≤ u_y, and n_i is finite, for i = 1, …, n_d. In (1), f is the objective function that maps the optimization vector X to a scalar value in [Doublestruck R]. Here, we assume an analytic expression of f is not available, and the outcome of f(X₁) can only be measured/recorded post-experimentation/simulation at X = X₁. X may subject to known linear equality/inequality constraints. And the goal is to find the X* that minimizes f.

3. Examples of existing solution strategies

Optimization of systems involving discrete and mixed variables presents unique challenges due to the combinatorial nature of discrete variables and possible discontinuities and sharp transitions of the objective function introduced by mixed variables. Previous studies have proposed methodologies to address this challenge, for example, one can integrate surrogate models into these optimization frameworks, which has shown promise in improving convergence rates and solution quality.^22,48–50 Specifically, several optimization algorithms have been developed within the BO framework.^43,51–55 Besides that, different genetic algorithms^56,57 have been studied due to its inherent ability to handle problems in discrete and mixed-variable domains. In the following, we provide an overview of approaches implemented in several established optimization libraries on discrete and mixed-variable problems: Genetic^56,57 (evolutionary algorithm), hyperopt⁵⁸ (BO with tree-structured parzen estimator (TPE)), BoTorch⁴³ (BO with Gaussian Process (GP)), and EDBO⁴(BO with GP specialized for reaction). We consider random search as a baseline.

• Random search: aamples are drawn uniformly at random within the search domain without any encoding for categorical variables or optimization steps.

• Genetic: different genetic algorithm implementations are available.^{56,57,59–65} In this paper, we consider the evolutionary algorithm implemented in the distributed evolutionary algorithm in python (DEAP) package.^56,57 DEAP handles categorical variables by label encoding them. The solving process involves two phases – an initial sampling and an iterative sampling phase. It first initiates samples randomly within the search domain. Iterative samples are then generated through crossover, mutation, or a combination of both, depending on whether the randomly generated probabilities for the execution of crossover or mutation exceed the default threshold. Evolutionary algorithms often balance exploitation and exploration through crossover and mutation, without explicitly utilizing the input–output correlations. Therefore, when the design space is large, it may require a large number of experiments or simulations to attain desired outcomes, making it not suitable for expensive-to-evaluate problems.⁶⁶ To address this issue, different surrogate-assisted evolutionary algorithms have been proposed.^67,68 Nevertheless, surrogate model selection and relevant parameter tuning remain challenging.⁶⁸ Moreover, incorporating constraints within the framework can be non-trivial.⁶⁹

• Hyperopt:⁵⁸ hyperopt, utilizing the TPE algorithm, offers a framework specifically designed to facilitate the application of Bayesian optimization for hyperparameter selection.⁷⁰ TPE inherently handles categorical variables, eliminating the need for explicit encoding. The solving process comprises two phases: initial sampling and active learning. During the initial sampling phase, samples are randomly drawn from the design space. In the active-learning phase, TPE operates by optimizing a loss function over a tree-structured configuration space. In handling categorical (discrete) variables, it employs the estimation of distribution (EDA) approach, where candidate points are sampled according to binomial distributions.⁷¹ As for the continuous variables, the covariance matrix adaptation – evolution strategy (CMA-ES, gradient-free)⁷² is utilized. TPE is computationally cheap and simple compared to many other algorithms within the BO framework.⁵⁸ However, incorporating a relatively large number of constraints is challenging, and is not currently implemented.^58,73 Watanabe and Hutter⁷³ attempted to address this challenge by integrating the acquisition function of constrained BO by Gardner et al.⁷⁴ However, the proposed approach considers the probability of constraint improvement and still allows infeasible samples,^73,74 which may be selected and tested in simulations but can not be queried for real experiments. It is also worth mentioning that this approach is proposed to address problems with unknown constraints.

• BoTorch:⁴³ this package implements BO based on GPs. In this framework, categorical variables are one-hot encoded, and users can select different kernels. For instance, for fully-categorical design space, the hamming distance kernel is commonly used. For mixed-integer cases within the reaction optimization domain, it is recommended to use Matérn 5/2 kernel for both continuous and integer (discrete) variables.^4,22 Similar to other BO-based approaches, the solving process includes two stages – the initial and active-learning stages. During the initial sampling stage, samples are randomly chosen from the search domain. During the active-learning stage, the next sample to evaluate is determined by optimizing the acquisition function (e.g., expected improvement). We also note that, for mixed-integer cases, BoTorch finds the next point to test by iterating through all possible integer values in an outer loop and optimizing the remaining continuous variables while keeping the integer value fixed. Subsequently, it selects the integer value that returns the best evaluation on the acquisition function. This step can cause the computational time to increase significantly, especially when the number of integer (discrete) variables increases and/or the number of possible options for these variables increases. Alternative approach that utilize PR was proposed and implemented in⁴⁴ to address this issue, but has not yet been merged into the main BoTorch repository. Additionally, constraint handling for mixed-integer cases has not been implemented⁴³ as conventional approaches, such as trust regions, cannot be trivially integrated with the current framework.

• EDBO:⁴ this package also implements BO based on GPs, where it considers three descriptors to encode the categorical variables, which are density functional theory (DFT),⁷⁵ mordred,⁷⁶ and one-hot encoding. Here, continuous descriptors such as DFT and mordred are used to encode categorical variables so that GP with kernels that are designed for continuous design spaces can also be used/tested.

Different from BoTorch, EDBO pre-trains the GP model with data from the literature for the following two reactions: Suzuki–Miyaura reaction,⁷⁷ consisting of 3696 reactions in the dataset, and the Buchwald–Hartwig reaction, whose training dataset consists of 3960 unique reactions.⁷⁵ While EDBO, similar to other BO methods such as BoTorch, improves with additional training samples and can suggest optimal solutions even with poorly trained surrogate models,⁷⁸ its key advantage lies in its pre-training phase. This pre-training makes EDBO highly efficient, particularly for optimizing reaction conditions when the target reactions share similar features with the training datasets.

Since the target problems often only involve categorical variables with finite options, the workflow of EDBO involves pre-generating all the possible combinations. The solving process involves an initial-sampling and an active-learning stage. Samples are randomly selected from the pre-generated combinations during initial sampling. While in the active learning stage, rather than searching within defined bounds, it exhaustively enumerates the entire domain, selecting the point with the lowest acquisition function evaluation. For mixed-integer cases, continuous variables first need to be discretized. The enumeration procedure in the acquisition step can become computationally expensive as the number of discretization steps increases, highlighting the trade-off between computational time and achieving a better representation of the original domain. Regarding constraint handling, there is currently no implementation integrated into EDBO.

In addition to the method discussed, we also evaluated Gryffin,¹⁹ a technique known for its recent advances in optimization problems with continuous and categorical design space. Gryffin proposed a new technique to select categorical variables based on expert knowledge. While Gryffin was included in the initial comparison, its performance in our specific case studies did not yield significant improvements over the other methods. Therefore, the detailed results and performance metrics for Gryffin are provided in the ESI (see Section 1† therein) for completeness. In summary, different methods have been proposed to handle discrete and mixed-variable problems, and several approaches have been tailored for experimental planning problems in chemistry domain. Nevertheless, limited approaches have been proposed to explicitly handle known discrete and mixed-variable constraints to ensure feasible query. And to the best of our knowledge, no such approach has been implemented for discrete and mixed-variable constrained experimental planning problems.

4. Proposed solution strategy

In this paper, we suggest using surrogates and acquisition functions suited for mixed-integer spaces. Specifically, we adopt PWAS to address the target mixed-variable problem (1). In this section, we provide a recapitulation of PWAS⁴⁷ and its benefits in these problem instances. PWAS is chosen due to its ability to handle both categorical and mixed variables, and to incorporate explicit linear constraints directly, which allows for a more realistic representation of the problem. The key steps of the PWAS are illustrated in Fig. 2. For a comprehensive description of the algorithm and its numerical properties, the reader is referred to the paper.⁴⁷

Fig. 2 The flowchart of PWAS.

Before going into the explanation of the algorithm, let us outline how samples are processed. The optimization variables are first pre-processed before feeding into PWAS. Specifically, continuous variables are scaled to [−1, 1]. As for integer variables, two strategies are implemented. If the number of combinations of integer variables is smaller than a predefined minimum, PWAS treats these integer variables as if they are categorical; otherwise, each integer variable is assigned with an auxiliary continuous variable scaled to [−1, 1]. The auxiliary continuous variables will later be used to fit the surrogate, while the original integer variables are kept to formulate the constraints (if present) to ensure feasibility. The integer variables and the auxiliary continuous variables are correlated by the scaling parameters. Regarding categorical variables, PWAS handles them by one-hot binary encoding, i.e., Zⁱ is encoded into the subvector [z_1+dⁱ⁻¹ … z_dⁱ]^T ∈ {0,1}^n_i ∀i = 1, …, n_d, where We combine all encoded categorical variables and denote them in one vector z ∈ {0,1}^dnd, with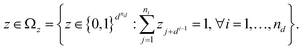

Like many surrogate-based approaches, the solution process of PWAS unfolds in two phases: the initial sampling phase and the active-learning phase (see Fig. 2). Due to the nature of our target problems, where experiments and simulations are expensive to run, we assume to operate under a fixed computational budget, i.e., only N_max experiments/simulations are allowed. During the initial sampling phase, PWAS draws N_init samples from the feasible domain. Different strategies for initial sampling are applied based on the specifics of the problem.⁴⁷ Since there is limited or no information about the current problem during the initial sampling stage, static DoE approaches, i.e., space-filling approaches, can be a good starting point, especially when no complex constraint is involved. However, we also stress that using static DoE approaches initially does not restrict the exploration capability of PWAS in the active-learning stage, which will be the case for normal DoE approaches. In general, when only box constraints are present, the Latin hypercube sampling (LHS) method is employed.⁷⁹ In cases where linear equality and/or inequality constraints exist alongside integer and/or categorical variables, the algorithm initially employs LHS and then discards any infeasible samples. Should the number of feasible samples generated be insufficient, two strategies are used: (1) if there exist only continuous variable, polytope sampler, specifically, the double description method⁸⁰ is implemented; (2) if there exist integer/categorical variables, a method involving solving mixed-integer linear programming (MILP) problems sequentially is implemented. These MILP problems utilize the exploration functions discussed later in this section as their objective functions, ensuring adherence to given constraints, and thereby obtaining feasible samples. This strategy is particularly useful when constraints are hard to fulfill by random sampling.

After obtaining the initial list of samples to test, experimentation or simulation is conducted to obtain their respective evaluations. These are then used to build a surrogate model. In PWAS, we use PARC⁸¹ to fit piecewise affine surrogates. The general procedures of PARC are illustrated in Fig. 3. PARC is a block descent algorithm, where it first groups samples in K_init clusters. Clusters containing fewer samples than a predefined minimum threshold are discarded, resulting in K_updated remaining clusters. We then fit piecewise affine (PWA) separation functions among these clusters to form K_updated partitions of the design space. Within each partition, a PWA surrogate function is fitted to make predictions. We conducted a comparative study to evaluate the effectiveness of the PWA surrogate function on a set of benchmark functions. The results indicate that PWA can provide better fitting to the underlying function compared to GP with RBF, Matérn, and linear kernels, particularly when the number of training samples is limited or when the problem involves discontinuous or sharp transitions caused by categorical variables. Full details and analysis can be found in the ESI, Section 2.†

Fig. 3 The flowchart of PARC.

A cost function comprising separability and predictability indexes is then calculated, which balances between the enhancement of separability among different partitions and the improvement of predictability within each partition. PARC terminates when either the difference in the value of the cost function between two consecutive evaluations falls below a predefined tolerance, or the number of iterations surpasses a predetermined maximum limit. Otherwise, PARC reassigns samples to K_updated clusters based on the newly fitted PWA separation functions and then iterates the procedure until termination criteria are met.

In the active-learning phase, at each iteration, we query a new sample and refine the surrogate function by re-partitioning and re-fitting the surrogates using PARC, incorporating both existing and newly acquired samples. As merely minimizing the surrogate may overlook the global optimum, PWAS sums the surrogate function, f̂(X), with a distance-based exploration function, E(X), i.e., a(X) = f̂(X) − θ_EE(X), where a(X) represents an acquisition function that balances between the exploitation of the PWA surrogates, and the exploration of the design space. Here, E(X) is a pure exploration term that quantifies the distance between X and existing samples X₁, …, X_N, which is independent of function evaluations. A user-defined trade-off parameter, denoted as θ_E, is introduced with a default setting of 0.5. This default value has been validated across a variety of benchmarks to ensure optimal performance.⁴⁷ In PWAS, two types of exploration methods, which can be directly reformulated as mixed-integer problems, are considered: a max-box approach for continuous and integer variables, and the hamming distance method for binary encoded categorical variables. These exploration functions are selected as they can be reformulated as MILPs. Therefore, the acquisition function can be minimized with a standard MILP solver to determine the next sample for testing, with the option to directly incorporate linear constraints, if present. Subsequently, a new experiment or simulation is selected and evaluated to assess the objective function value. This iterative process continues until reaching the maximum number of iterations (N_max).

5. Case studies

In this section, we assess the applicability and effectiveness of PWAS for practical experimental planning problems through three case studies: (i) reaction optimization of Suzuki–Miyaura cross-coupling (fully categorical), (ii) crossed-barrel design (mixed-integer), and (iii) optimal solvent design for Menshutkin reaction (mixed integer and categorical with linear constraints). The case studies are chosen to exhibit a range of complexities, varying in problem size, numerical difficulty, types of variables, and the presence/absence of design constraints. To demonstrate the relative performance of PWAS, optimization results are compared with those from commonly used methods, specifically the ones discussed in Section 3.

All the case studies are solved on an Intel i7-8550U 1.8 GHz CPU laptop with 24 GB of RAM, with all the results available in the GitHub repository at https://github.com/MolChemML/ExpDesign.

5.1 Suzuki–Miyaura cross-coupling

5.1.1 Problem description. The first case study focused on optimizing the reaction conditions for Suzuki–Miyaura cross-coupling.^82,83 This reaction is pivotal in medicinal chemistry and materials chemistry, serving as a fundamental process for forming carbon–carbon bonds in the synthesis of various pharmaceuticals and polymers.^82–85 A reaction scheme for the investigated Suzuki–Miyaura coupling is shown in Fig. 4, illustrating the coupling of a boronic acid derivative and an aryl halide facilitated by a palladium complex catalyst, a ligand, a base, and a solvent.^4,22,77 Here, all optimization variables are categorical and the number of possible options for each optimization variable is summarized in Table 1. The full Cartesian product space consists of 3696 unique reactions. The study looks into the relationship among these categorical variables, and aims to identify optimal combinatorial sets of precursors that can maximize the yield of the desired product within a small number of experiments, and therefore reduce the resources and time required.

Fig. 4 Suzuki–Miyaura cross-coupling reaction. The variables—boronic acid derivative (Y), aryl halide (X), ligand, base, and solvent—highlighted in blue represent the experimental design space. All other reaction conditions are fixed and noted in black.

Table 1 Reaction design space (fully categorical) for the Suzuki–Miyaura cross-coupling reaction.^4,22,77

Optimization variables	# Options
Aryl halide (X)	4
Boronic acid derivative (Y)	3
Base	7
Ligand	11
Solvent	4
Total # of possible combinations	3696

---

We employ PWAS to solve the optimization problem and benchmark its performance against established optimization libraries: genetic, hyperopt, BoTorch, and EDBO. Additionally, we consider the results obtained from random search as the baseline. The characteristics of the approaches used in these libraries have been discussed in Section 3. We note that random search, genetic (with DEAP v-1.4.1), hyperopt (v-0.2.7), and BoTorch(v-0.6.6) have been interfaced in the Olympus²² package; therefore, we use the algorithmic structure implemented in the package for benchmark tests with their default parameter values. A customized forked version tailored for our testing is also available on GitHub at https://github.com/mjzhu-p/olympus (Branch “pwas_comp”). Regarding EDBO, categorical variables, namely, distinct chemical entities, are one-hot-encoded and the default setting is used with minor changes to the original package to allow customized input for the number of initial samples (see the changes in the forked version at https://github.com/mjzhu-p/edbo/tree/pwas_comp). As for PWAS, the default setting⁴⁷ is used, i.e., the number of initial partitions (K_init) is set to 10, with the trade-off parameter between exploitation and exploration (θ_E) set to be 0.5. And the categorical variables are one-hot encoded. We note that this study specifically focused on using the one-hot-encoded reaction representation, in line with the original benchmark problem. While more advanced encoding methods, such as differential reaction fingerprints,⁸⁶ and the integration of expert knowledge to narrow down the design space⁸⁷ have been shown to influence optimization performance and offer promising search strategy, our objective was to maintain consistency with the benchmark to ensure comparability with previous methods. For readers interested in advanced encoding techniques, we refer to the work of Ranković et al.⁸⁸

For each optimization method, we conduct 30 repetitions for statistical analysis. Given that the goal of our study is to assess the performance of the algorithms on case studies where only a small number of experiments/simulations can be done due to time and resource constraints, we cap the maximum number of experiments at 50 within each repetition.

5.1.2 Results and discussion. The performance comparisons of different methods on Suzuki–Miyaura cross-coupling reaction optimization are shown in Fig. 5. Fig. 5a illustrates the highest yield achieved (%) so far at different iterations. Since the numerical values of the yields are very close, especially as the number of iterations increases, a zoomed-in panel of the last five iterations is shown for better visualization. In Fig. 5b, the corresponding ranks of the yields at different iterations are presented. These ranks are derived from the known yields of all possible combinations (3696 in total).⁷⁷

Fig. 5 A comparison of the performance of PWAS and the benchmark methods on Suzuki–Miyaura cross-coupling reaction optimization. For each method, the solid line represents the mean value, and the filled area comprises the 95% confidence interval, i.e., mean ± 1.96 std. (a) Best yield achieved (%) so far at different iterations. (b) Best yield rank achieved so far at different iterations.

While EDBO achieves the highest yield after 50 iterations, PWAS demonstrates competitive performance, surpassing all other tested methods in its ability to identify optimal reaction conditions that maximize the reaction yield. It is important to note that EDBO is expected to outperform other methods in this case study, given that the GP model used in EDBO was pre-trained using the entire Suzuki–Miyaura reaction dataset (3696 reactions; see also in Section 3).⁴ In contrast, PWAS showed the similar results without requiring the pre-training step, highlighting its capacity to perform effectively with minimal prior data. To provide a clear demonstration of the efficiency of each method, we present a boxplot in Fig. 6. This visualization represents the number of iterations required by each method to achieve a top-20 ranked yield. Each data point on the plot represents the outcome of one specific run, and the statistics presented are derived from 30 repetitions to ensure robustness. On average, both PWAS and EDBO require significantly fewer iterations to attain a top-20 ranked yield when compared to other methods. This suggests their superior efficiency and potential time and resource savings in practical applications. Overall, the comparable performance of PWAS with EDBO demonstrated in the case study shows the ability of mixed-integer surrogates to more efficiently optimize the parameter space with no prior knowledge of the system, which has major implications for situations where prior data (literature or otherwise) is not available or difficult/expensive to obtain—a very common scenario in the chemical sciences.

Fig. 6 Number of iterations each method takes in each run to obtain the first top-20 ranked yield. The results for 30 repetitions are summarized in the boxplot. Each dot represents one run of the repetitions. The diamond-shaped points are the ones classified as outliers by the boxplot.

5.2 Crossed barrel

5.2.1 Problem description. The second case study explores the optimization of the design of a crossed barrel (see Fig. 7) for improved mechanical properties.^22,38 Specifically, we aim to maximize its toughness while not exceeding a specified force threshold. Here, toughness corresponds to the amount of energy a component can withstand before experiencing failure.³⁸ Components with a crossed-barrel structure are used to protect more fragile parts within a design while not passing on harmful reactionary forces.³⁸ For instance, these structures can shield sensitive instrumentation or electronics from mechanical vibrations or impacts.

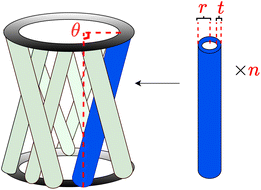Fig. 7 Schematic representation of a crossed-barrel design,³⁸ illustrating the optimization variables, where θ is twist angle of the columns (degree), r is outer radius of the columns (mm), n is the number of hollow columns, and t is thickness of the hollow columns (mm).

As depicted in Fig. 7, a crossed barrel has n hollow columns with outer radius r and thickness t, twisted at an angle θ. Here, n, r, t and θ are the design variables we want to optimize, whose data types (discrete/continuous) and domains are outlined in Table 2. Due to the involvement of continuous variables (n, r, t), exhaustively enumerating all possible combinations is impractical. Hence, an emulator, as recommended by Hickman et al.,²² is utilized to simulate the process and therefore make it possible to sample over the whole feasible domain. The emulator was modeled as Bayesian neural nets (BNN)²² and trained on over 2500 HTE data points collected by Gongora et al.,³⁸ where the weights and biases are modelled woith a normal distribution. We note that the trained emulator serves the purpose of method comparisons in this case study. Nevertheless, the accuracy of the trained model can be improved if more data could be provided.

Table 2 Optimization variables for the crossed-barrel design.^22,38

Optimization variables	Type	Domain
Number of hollow columns (n)	Integer	[6, 12]
Twist angle of the columns (θ) [degree]	Continuous	[0.0, 200.0]
Outer radius of the columns (r) [mm]	Continuous	[1.5, 2.5]
Thickness of the hollow columns (t) [mm]	Continuous	[0.7, 1.4]

---

The challenges of this case study involve balancing trade-offs between conflicting mechanical properties, such as strength (the ability to resist an applied force without being damaged) and ductility (the ability to stretch without breaking), and incorporating mixed-integer design choices. This case study is selected due to the mixed-integer nature of the problem and the availability of an adequate number of HTE experimental data to train an emulator.^22,38 Similar procedures can be followed to design chemical-related units, e.g., chemical reactors, if data acquisition is possible via experiments or high-fidelity simulations.

We solve this optimization problem with the same set of methods employed in the Suzuki–Miyaura cross-coupling case study, using the packages interfaced in the Olymnpus package for random search, genetic, hyperopt, and BoTorch. As discussed in Section 3, the method implemented in EDBO package requires a pre-defined discrete search space, meaning that the continuous variables, θ, r, and t, need to be discretized. Here, we consider three discretization schemes for the search domain, evenly divided and spaced by: 100, 10, and 10 points (EDBO_1); 10, 10, and 10 points (EDBO_2); and 10, 5, and 5 points (EDBO_3), respectively. These configurations yield 70 000, 7,000, and 1750 possible combinations to form the search domain. As for PWAS, two strategies are used to handle integer variables as detailed in the pre-processing step in Section 4, and the same values introduced in 5.1 are used for K_init and θ_E. Similarly to the Suzuki–Miyaura cross-coupling case study, we run 30 repetitions for statistical analysis. Within each run, we include 10 initial experiments and then allow a maximum of 50 iterations.

5.2.2 Results and discussion. The optimization outcomes are summarized in Fig. 8, 9, and Table 3. In achieving the best objective function values within a specified budget, EDBO_1 outperforms all other methods, while PWAS is comparable with that of hyperopt (see Fig. 8) and EDBO_2 (see Fig. 9). However, the effectiveness of EDBO varies depending on the number of discretization steps considered. As evidenced in Fig. 9, the performance of EDBO improves with an increase in discretization steps, showing that only EDBO_1 outperforms PWAS. Although the differences in objective function values obtained by EDBOs and PWAS are marginal, the number of discretization steps required to achieve a particular quality of solution is unknown and there is no systematic method of determining appropriate value. Furthermore, the increase in the number of discretization steps can result in higher computational cost, particularly with a higher number of continuous variables. This is reflected in Table 3, where the CPU time for EDBO and BoTorch are significantly higher than that of other methods. Despite that, we acknowledge that the time required for actual experiments or simulations outweighs the computational overhead in many cases. Therefore, the difference in CPU time may not always be significant. Nevertheless, there are some scenarios where computational efficiency becomes critical, such as in applications requiring rapid feedback loops, including flow chemistry.^89,90 Additionally, selecting an appropriate discretization scheme that guarantees improved performance a priori may not be straightforward, particularly when the number of continuous variables and their ranges grow. Evolutionary-assisted surrogate-based methods such as the one proposed in Low et al.⁷⁸ may be used to alleviate the computational burden.

Fig. 8 Best toughness achieved so far at different iterations for the designed structure at different iterations for crossed barrel design. Results are summarized over 30 repetitions. For each method, the solid line represents the mean value, and the filled area comprises the 95% confidence interval, i.e., mean ± 1.96 std.

Table 3 CPU time (seconds) required by different methods for one run of the optimization for the crossed barrel design. Statistics were obtained from 30 random runs

	Random	Genetic	Hyperopt	BoTorch	PWAS	EDBO_1	EDBO_2	EDBO_3
Average	1.85	1.77	2.80	398.68	35.36	272.54	227.54	212.92
Std	0.44	0.35	0.71	260.71	2.00	67.61	2.52	20.38

---

Fig. 9 Best toughness achieved so far at different iterations for the designed structure at different iterations with EDBO method with different discretization steps for crossed barrel design. The trajectory of PWAS is also shown for comparison.

5.3 Solvent design

5.3.1 Problem description. In the third case study, we consider the design of solvents for enhanced kinetics of a Menschutkin reaction (see Fig. 10), following the computer-aided molecular design (CAMD) formulation of Gui et al.¹³ Choosing an appropriate solvent is crucial for liquid-phase reactions, as it can reduce the Gibbs free energy barrier (see Fig. 10) and therefore promote fast reaction kinetics. The aim of optimization is to determine the optimal molecular structure of the solvent that maximizes the reaction rate constant k [L mol⁻¹ s⁻¹], for which we define the objective function as f(X) = −ln k. We note that (1) is formulated as a minimization problem, thereby maximizing ln k is equivalent to minimizing −ln k. Here, ln k is used, which is a common practice when developing data-driven models and comparing with experimental data,¹³ because k can significantly differ across different solvents, sometimes by orders of magnitude.

Fig. 10 The Menschutkin reaction of phenacyl bromide and pyridine. In the illustration, solvent 2 is preferred which lowers the free energy compared to Solvent 1.^13,91

A set of 46 functional groups were selected as molecular building blocks. The solvent was represented by integer variables to indicate the number of each functional group present in the solvent molecule. To ensure that only chemically feasible combinations of functional groups are generated during the optimization process and to limit the size of the solvent, a set of chemical feasibility and complexity constraints was imposed. For instance, constraints were used to ensure the octet rule.¹² Since the solvent designed must be in the liquid phase at reaction conditions, the normal melting point (T_m) and the boiling point (T_b) of the solvent were added as design constraints. Two physical properties, namely, flash point (T_fp) and octanol/water partition coefficient (K_ow), as well as the oral rat median lethal dose (LD₅₀) of the solvent were constrained to reduce health, safety, and environmental impact. In total, the problem consists of 115 linear inequality and 5 linear equality constraints, where one auxiliary categorical and 7 binary variables were introduced to formulate the constraints. The types of design variables and the property prediction model used are summarized in Tables 4 and 5. For a comprehensive description of the mathematical formulation used, the reader is referred to Gui et al.¹³ and Section 2.3 therein.

Table 4 Optimization variables and problem size for the solvent design¹³

Description	Notes
Number of functional group types	46 (integer)
Number of auxiliary variables introduced for chemical feasibility	1 (categorical) and 7 (binary)
Number of inequality/equality design constraints	115 (linear)/5 (linear)

---

Table 5 Property constraints for the solvent design^a

Physical property	Bounds
a The property prediction method of Hukkerikar et al.^92 is used for Tb, Tm, Tfp, and Kow, and Hukkerikar et al.^93 is used to predict LD50
T m (K)	[10^−5, 298.15]
T b (K)	[323.15, 10^5]
T fp (K)	[252, 10^5]
log Kow	[10^−5, 3]
−log LD50 (mol kg^−1)	[10^−5, 3]

---

5.3.2 Surrogate model for the rate constant. As discussed in Section 3, the methods examined in the previous two case studies cannot explicitly handle mixed integer/categorical constraints. While post hoc screening of infeasible solutions obtained from an unconstrained optimization may appear as a potential approach, the large number of constraints often renders such post-optimization exclusion computationally expensive and potentially inefficient in achieving convergence. Thus, direct comparisons with such methods are not practical. Instead, we benchmark our optimization results against those obtained using DoE-QM-CAMD¹³—a CAMD framework tailored to incorporate quantum-mechanical (QM) calculations of rate constant and computational experimental design into the molecular design process.

In the following, we provide an overview of the DoE-QM-CAMD¹³ method. DoE-QM-CAMD employed a multiparameter solvatochromic equation^94,95 to correlate solvent properties and the logarithm of the rate constant:

ln k = c₀ + c_AA + c_BB + c_SS + c_δδ + c_Hδ_H², (2)

where A, B, S, δ, and δ_H² are the Abraham's overall hydrogen-bond acidity, Abraham's overall hydrogen-bond basicity, dipolarity/polarisability, and Hildebrand solubility parameter, respectively, of the solvent, and c₀, c_A, c_B, c_S, c_δ, and c_H are the coefficients that need to be estimated via multiple linear regression (MLR). Estimating the parameters in the MLR model with high accuracy can be challenging because only a small number of experiments can often be conducted, restricting its predictive capacity. To address this challenge, DoE-QM-CAMD first selects an information-rich set of (computer) experiments using the D-optimality criterion. These initial experiments, which are observed to cover a wider range of solvent properties, are then used to train an initial MLR model. Subsequently, to refine the MLR model and enhance its predictability around the optimal solvent region, iterative optimization is undertaken to identify the best solvent (i.e., the one that gives the highest reaction rate) based on the current MLR model. Should a new solvent be identified, the MLR model undergoes re-fitting with the updated experimental set that consists of the newly identified optimal solvent and the solvents in the original set. The iterative process terminates when the best solvent, determined by optimizing the MLR model, has been sampled previously. Upon convergence of the MLR model, the top 10 solvents are determined by re-initializing and optimizing the problem, wherein integer cuts are added to exclude previously identified solutions. We note that the active-learning-like iterative process of DoE-QM-CAMD after the initial experiments relies solely on the newly fitted MLR model with limited capabilities for exploration. Also, as a grey box algorithm, it can propagate the biases.

In contrast, PWAS, similar to most surrogate-based optimization strategies,^29,96,97 solves the problem by employing an active-learning technique with exploration capability. It systematically identifies optimal solvents for examination, effectively balancing the trade-off between exploring new possibilities for model improvement and exploiting known knowledge of reaction kinetics. As opposed to DoE-QM-CAMD, which assumes linear relationship between the expert-derived solvent properties and ln k, PWAS adopts PWA surrogates to represent the correlations between the functional groups within the designed solvent and ln k, where the relationship between solvent properties and ln k are learned implicitly. As discussed in Section 4, PWAS leverages PARC⁸¹ to fit the surrogates, where PARC first clusters samples in K_init initial partitions. The initial partitions are then optimized by balancing between enhancing separability, which relies on similarities among different solvents (in this context, functional groups), and improving the predictability of the surrogate function within each partition, in this case, the input–output correlations. Here, the output (ln k) correlates with the properties of the designed solvent and therefore can be implicitly learned during surrogate fitting, offering insights not available when solely considering individual functional groups.

Consistent with previous case studies, default parameters are utilized when solving the problem with PWAS, including a maximum of 50 experiments, with an initial set of 10 samples. It is important to highlight that the complete QM reaction constant data were generated by exhaustively enumerating all 326 feasible solvents within the defined design space,⁹⁸ enabling the sampling of new solvents without the need for additional calculations and providing the true rank of the solvents.

5.3.3 Results and discussion.
5.3.3.1 Comparison between PWAS and DoE-QM-CAMD. In the following, we compare the performance of PWAS and DoE-QM-CAMD based on the top 10 solvents identified by PWAS and DoE-QM-CAMD, for which we compare their rank alignment with QM calculated values. As shown in Tables 6 and 7, respectively, the top 10 solvents identified by PWAS are consistent with the true rank, in contrast to ranks of the optimal solvents obtained from DoE-QM-CAMD, which show a large deviation. Also, we observe that the predicted values based on PWAS are more accurate to the QM calculated values compared to those of DoE-QM-CAMD (the mean squared errors for the top-10 ranked solvents with QM are 2.4 × 10⁻⁴ log units for PWAS and 0.46 log units for DoE-QM-CAMD). These observations can be attributed to the inherent nature of PWAS and DoE-QM-CAMD. The MLR model utilized within the DoE-QM-CAMD method primarily serves as a predictive tool across the design space. As previously noted, it generates predictions for the top-ranked samples post-generation of the MLR model, which may not align well with the experimental results. In contrast, PWAS operates as an optimization mechanism, focusing on refining the predictive model within the design space where promising solvent candidates exist—those that yield high reaction rates, while also exploring uncovered design space to prevent from being stuck in the local optimum. It achieves this by iteratively proposing new samples for evaluation through active learning, where an acquisition function that trades off between exploitation (finding the solvents with a high reaction rate) and exploration (covering unexplored design space) is minimized. As a result, it is not surprising that PWAS performs better in terms of the rank alignment and predictability around the optimal region.

Table 6 The top 10 ranked solvents identified by PWAS for the solvent design case study^a

Rank	Chemical formula	ln k
		QM	Pred
a k [L mol^−1 s^−1]: rate constant for the Menschutkin reaction, QM: ln k obtained from quantum-mechanical calculation, pred: ln k predicted by the PWAS surrogate.
1	CH3NHCHO	−5.92	−5.92
2	OHCH2NO2	−6.46	−6.49
3	CH2OHCH2NO2	−6.72	−6.69
4	(CH3)2SO	−6.82	−6.82
5	(CH2)2OHCH2NO2	−6.93	−6.93
6	CH3CHOHCH2NO2	−6.96	−6.97
7	CH2=COHCH2NO2	−6.98	−6.97
8	CH=CHOHCH2NO2	−7.00	−6.98
9	(CH2)3OHCH2NO2	−7.10	−7.10
10	CHCH2=CHOHCH2NO2	−7.11	−7.11

---

Table 7 The top 10 ranked solvents identified by DoE-QM-CAMD for the solvent design case study^a

Rank	Chemical formula	ln k
		QM	Pred
a k [L mol^−1 s^−1]: rate constant for the Menschutkin reaction, QM: ln k obtained from quantum-mechanical calculation, pred: ln k predicted by the DoE-QM-CAMD surrogate, i.e., the multiparameter solvatochromic eqn (2)
1	CH2OHCH2NO2	−6.72	−5.50
2	(CH3)2SO	−6.82	−5.59
3	CH2OHCH2NO2	−6.72	−6.28
4	CH2=COHCH2NO2	−6.98	−6.66
5	(CH2)2OHCH2NO2	−6.93	−6.74
6	CH3CHOHCH2NO2	−6.96	−6.87
7	(CH3)2COHCH2NO2	−7.23	−6.91
8	CH=CHOHCH2NO2	−7.00	−6.92
9	CH2CH2=COHCH2NO2	−7.15	−6.97
10	CH3NHCHO	−5.92	−7.00

---

5.3.3.2 Analysis of algorithmic exploitation and exploration capabilities. To further analyze the exploitation and exploration capabilities of PWAS, we examine the solvents determined by PWAS. Specifically, we aim to show that PWAS can exploit the surrogate to implicitly learn the preferred solvent properties that lead to a high reaction rate, and can explore the design space to obtain a set of solvents with diverse structures and chemical properties.

Before examining specific solvents, we first perform a sensitivity analysis using partial dependence plot (PDP) and individual conditional expectation (ICE) plots to investigate the relative influence of solvent properties on the reaction rate constant, which we will then use to assess PWAS's exploitation and exploration capability. Seven representative descriptors considered are refractive index at 298 K (n²), Abraham's overall hydrogen-bond acidity (A), Abraham's overall hydrogen-bond basicity (B), dielectric constant at 298 K (ε), microscopic surface tension at 298 K (γ), aromaticity, and halogenticity, which are used in a successful quantum mechanical continuum solvation model.⁹⁹ The descriptors of all feasible solvents are calculated using the group contribution method of Sheldon et al.¹⁰⁰ As can be seen in Fig. 11, the fluctuation in PDPs is most pronounced for ε, while the fluctuation in ICEs is most significant for three properties, namely, n², B, and ε, indicating their strong marginal effect on predicting ln k. This finding aligns with the established results for S_N2 reactions. As reported in the literature,^101–103 solvent effects on reaction kinetics stem from the fact that the solvent–solute interactions stabilize the reactant(s) and the transition state to different extents. In general, when the transition state is (partially) ionic by nature and the reactants are neutral, a solvent with larger dielectric constant, indicating greater polarity, or those with stronger hydrogen bond basicity, meaning they are more potent hydrogen bond acceptors, can lower the free energy of the transition state more than that lowered for the reactants, thereby reducing the overall free energy barrier. It is also known that non-basic, polar aprotic solvents are preferred as they do not solvate the nucleophile strongly, making it more reactive and available for the reaction. Regarding the refractive index, although it does not directly reflect the polarity of solvents, it can greatly affect the solvation of reactants and the overall environment. Besides the dominant solvent descriptors, from Fig. 11, we can see that the relationship between the reaction rate and the solvent properties is not strictly linear. Additionally, there are dependencies among different properties, explaining why the MLR model (2) integrated into the DoE-QM-CAMD approach demonstrates inconsistent performance across the entire design space. While the MLR model could be improved by incorporating second-order terms and interaction terms, as discussed by Gui et al.,⁹⁸ deciding which terms to include often resorts to a trial-and-error approach, which can be time-consuming and potentially hard to justify. In contrast, PWAS provides a systematic approach to decompose the solvent design space based on their similarity related to rate constants, making it possible to capture the nonlinear relationship between the solvent properties and the reaction rate without making prior assumptions on the functional form, which we demonstrate in the following.

Fig. 11 Partial dependence plots (PDP) and individual conditional expectation (ICE) plots utilized to assess the influence of diverse solvent properties on the reaction rate across all feasible solvents. n²: refractive index at 298 K, B: Abraham's overall hydrogen-bond basicity, ε: dielectric constant at 298 K, A: Abraham's overall hydrogen-bond acidity, γ: the macroscopic surface tension at 298 K. Solvent properties are calculated based on the property prediction method of Sheldon et al.^98,100 Note: each gray line represents the relevant changes of the descriptor for one feasible solvent.

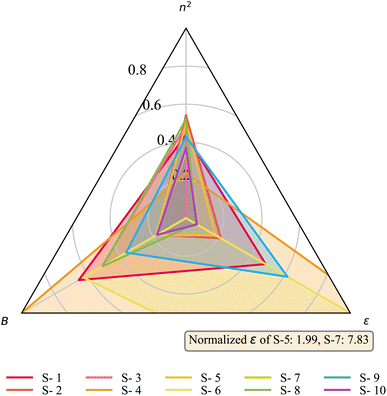
Focusing on the most significant solvent descriptors, n², B, and ε, three radar charts are plotted in Fig. 12 and 13, showing the relevant properties of the initial, first-10 active-learning, and last-10 active learning samples. To facilitate comparison, all features are normalized to a range between 0 and 1 using min–max normalization, except for the dielectric constant. Since the dielectric constants of two solvents are significantly higher than the others, the dielectric constant is normalized relative to the remaining solvents, resulting in values of these two solvents exceeding 1. Besides the radar charts, we also depict the structures of the solvents and their categorization based on the constituent functional groups in Fig. 14. Fig. 14a arranges the solvents in the sequence of optimization steps, distinguishing the initial and subsequent active-learning samples with a black line in, while Fig. 14b arranges the solvents into partitions, with orange lines denoting partition boundaries.

Fig. 12 Radar chart of the three selected features of the first 10 initial samples. n²: refractive index at 298 K, B: Abraham's overall hydrogen-bond basicity, ε: dielectric constant at 298 K. All features were normalized to a range between 0 and 1 using min–max normalization, except for the dielectric constant. Since the dielectric constants of S-5 and S-7 were significantly higher than those of the others, the dielectric constant was normalized relative to the remaining solvents. With the relative normalized dielectric constants of S-5 and S-7 denoted in the figure.

Fig. 13 Radar chart of the three selected features for the first-10 (a) and last-10 (b) active learning samples. n²: refractive index at 298 K, B: Abraham's overall hydrogen-bond basicity, ε: dielectric constant at 298 K. All features are normalized to a range between 0 and 1. (a) The first-10 active-learning samples. (b) The last-10 active-learning samples.

Fig. 14 Solvents identified by PWAS in 50 iterations, whose structures are depicted in functional group representations. (a) In sequential iteration order, with a black line separating the initial and active-learning samples; (b) grouped in partitions, with orange lines representing the boundary of the partitions (in total 10 partitions).

By examining Fig. 12–14, it can be observed that PWAS explores diverse solvent structures, covering large ranges of solvent properties, during the initial sample step, and then gradually converges toward clear patterns while maintaining an exploratory nature. These results demonstrate the effectiveness of PWAS at finding a diverse and promising set of solvents over the constrained mixed-integer and categorical domain. One major advantage of PWAS is that it allows one not only to group solvents with similar functional groups into the same partition, but also to place solvents with similar chemical properties into the same partition through the PARC mechanism. These similar findings across the functional group- and property-based design spaces highlight the adeptness of PWAS in identifying key implicit relationships, demonstrating its capability to effectively discern and utilize the links between functional groups and the ensuing solvent properties.

5.3.3.3 Preferred solvent properties. We further investigate the implicitly learned solvent properties to gain some chemical insights to derive general conclusions on the preferred solvent properties that can result in a high reaction rate for the Menschutkin reaction. In Fig. 15, we plot each solvent in relative-rank order, with x and y axis indicating n² and log  ε, respectively. B is represented by the size of each bubble whose scales are shown in the legend. The relative ranks are indicated using a colorbar, with the top-10 and last-10 ranked solvents also denoted with texts for clarity. Upon examination of Fig. 15, it seems that the dielectric constant emerges as the predominant factor influencing reaction kinetics. This finding aligns with the established results for the Menschutkin reaction, where polar aprotic solvents are typically favored.^101,102 Also, in scenarios where differences in dielectric constants are small, a higher refractive index tends to correlate with higher reaction rates. Among the top-ranked solvents, there exists a notable uniformity in basicity levels, while no clear trend can be observed for basicity across all identified solvents, which is also consistent with the PDP plot for B (see Fig. 11).

Fig. 15 Bubble chart of solvent properties of the solvents identified by PWAS. n²: refractive index at 298 K, ε: dielectric constant at 298 K. Abraham's overall hydrogen-bond basicity is represented by the size of each bubble, with the relevant bubble size scale shown in the legend. The relative ranks of each solvent are indicated using a color bar, with the top-10 and last-10 ranked solvents also denoted with texts for clarity.

In summary, we compared the effectiveness of two approaches for the solvent design case: PWAS and DoE-QM-CAMD. Our findings reveal the strengths in each method: the DoE-QM-CAMD approach, utilizing a MLR model, demonstrates more robust predictive capabilities across the entire design space; while, PWAS, employing PWA surrogates, can better predict reaction rates in proximity to optimal regions, which is important for our optimization objective. Furthermore, PWAS can learn correlations between solvent properties and reaction rates and offer valuable insights.

6. Conclusion

In this work, we have shown the effectiveness of mixed-integer surrogates, specifically piecewise affine surrogate-based optimization, with emphasis on problem subject to known discrete and mixed-variable constraints.

For the first two case studies, we compared the performances of PWAS with Random Search and four state-of-the-art methods representing varying optimization strategies, including an evolutionary method, and three methods within the BO framework. Compared to the established methods, PWAS achieved comparable or superior performance in terms of the number of experiments required to achieve satisfactory performance.

In the final case study, the complexity of the solvent design problem, with 10 linear equalities and 115 inequalities, limited the applicability of the benchmark methods. These methods struggle to incorporate a large number of constraints while guaranteeing feasible experimental suggestions. In contrast, PWAS offers a distinct advantage by directly incorporating these constraints within its formulation during the acquisition step. This capability is particularly relevant in chemical optimization problems, where a large number of constraints are often essential to define a feasible and well-defined design space. These constraints ensure that proposed solutions are both synthetically achievable and safe for experimentation. Therefore, the results obtained from PWAS were compared with a recently proposed DoE-QM-CAMD approach.¹³ The comparison highlighted the effectiveness of PWAS in systematically exploring the mixed-integer solvent design space. This is mainly attributed to its ability to implicitly learn underlying correlations within the data and effectively consider uncertain design space, ultimately identifying high-performing solvents. This level of analysis is particularly beneficial in the field of chemistry, as it provides a deeper understanding of the fundamental principles governing the underlying process.

In conclusion, while BO has undeniably revolutionized the landscape of optimization in experimental planning, especially in the chemical domain, it is important to recognize the potential of other surrogate-based approaches within conventional chemistry optimization problems. This is particularly relevant given the inherent complexity of many chemical problems, which are often characterized by mixed variables and a relatively large number of constraints, making it challenging for many widely adopted BO methods to obtain feasible samples during the acquisition step while still maintaining exploration capability. Nevertheless, BO as a general framework is highly adaptable and can incorporate various strategies to overcome these challenges. Here, we demonstrated that integrating mixed-integer optimization strategies can be an effective way.

Future work could be directed to extend the capabilities of PWAS to handle nonlinear constraints, thereby enhancing its applicability across a wider range of problem domains, particularly those present in the physical world. Additionally, it is useful to investigate the adoption of acquisition strategies in PWAS to existing BO methods, especially the ones with tree-based kernels, to address the target problems.

Data availability

The code and data used to produce all results in this work can be accessed at https://github.com/MolChemML/ExpDesign.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the anonymous reviewers and the editors for the valuable feedback to improve the quality of the work. The authors thank Tom Savage and Friedrich Hastedt for helping proofread the manuscript. AMM is supported by the Eric and Wendy Schmidt AI in Science Postdoctoral Fellowship, a Schmidt Sciences program.

Notes and references

1. R. Leardi, Anal. Chim. Acta, 2009, 652, 161–172.
2. D. C. Montgomery, Design and Analysis of Experiments, John Wiley & Sons, 2017.
3. G. E. Box, W. H. Hunter, S. Hunter, et al., Statistics for Experimenters, John Wiley and SonsNew York, 1978, vol. 664.
4. B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. M. Alvarado, J. M. Janey, R. P. Adams and A. G. Doyle, Nature, 2021, 590, 89–96.
5. National Science and Technology Council (US), Materials Genome Initiative for Global Competitiveness, Executive Office of the President, National Science and Technology Council (US), 2011.
6. A. M. Mroz, V. Posligua, A. Tarzia, E. H. Wolpert and K. E. Jelfs, J. Am. Chem. Soc., 2022, 144, 18730–18743.
7. J. A. Selekman, J. Qiu, K. Tran, J. Stevens, V. Rosso, E. Simmons, Y. Xiao and J. Janey, Annu. Rev. Chem. Biomol. Eng., 2017, 8, 525–547.
8. L. Buglioni, F. Raymenants, A. Slattery, S. D. Zondag and T. Noël, Chem. Rev., 2021, 122, 2752–2906.
9. S. M. Mennen, C. Alhambra, C. L. Allen, M. Barberis, S. Berritt, T. A. Brandt, A. D. Campbell, J. Castañón, A. H. Cherney and M. Christensen, et al. , Org. Process Res. Dev., 2019, 23, 1213–1242.
10. N. S. Eyke, B. A. Koscher and K. F. Jensen, Trends Chem., 2021, 3, 120–132.
11. I. Surowiec, L. Vikstrom, G. Hector, E. Johansson, C. Vikstrom and J. Trygg, Anal. Chem., 2017, 89, 6491–6497.
12. G. Franceschini and S. Macchietto, Chem. Eng. Sci., 2008, 63, 4846–4872.
13. L. Gui, Y. Yu, T. O. Oliyide, E. Siougkrou, A. Armstrong, A. Galindo, F. B. Sayyed, S. P. Kolis and C. S. Adjiman, Comput. Chem. Eng., 2023, 177, 108345.
14. C. J. Taylor, A. Pomberger, K. C. Felton, R. Grainger, M. Barecka, T. W. Chamberlain, R. A. Bourne, C. N. Johnson and A. A. Lapkin, Chem. Rev., 2023, 123, 3089–3126.
15. P. F. de Aguiar, B. Bourguignon, M. Khots, D. Massart and R. Phan-Than-Luu, Chemom. Intell. Lab. Syst., 1995, 30, 199–210.
16. H. J. Kushner, J. Mathemat. Anal. Appl., 1962, 5, 150–167.
17. H. J. Kushner, J. Basic Eng., 1964, 86, 97–106.
18. F. Hase, L. M. Roch, C. Kreisbeck and A. Aspuru-Guzik, ACS Central Sci., 2018, 4, 1134–1145.
19. F. Häse, M. Aldeghi, R. J. Hickman, L. M. Roch and A. Aspuru-Guzik, Appl. Phys. Rev., 2021, 8, 031406.
20. D. Van De Berg, T. Savage, P. Petsagkourakis, D. Zhang, N. Shah and E. A. del Rio-Chanona, Chem. Eng. Sci., 2022, 248, 117135.
21. L. M. Rios and N. V. Sahinidis, J. Global Optim., 2013, 56, 1247–1293.
22. R. Hickman, P. Parakh, A. Cheng, Q. Ai, J. Schrier, M. Aldeghi and A. Aspuru-Guzik, ChemRxiv, 2023 DOI:10.26434/chemrxiv-2023-74w8d.
23. R. H. Myers, D. C. Montgomery and C. M. Anderson-Cook, Response Surface Methodology: Process and Product Optimization Using Designed Experiments, John Wiley & Sons, 2016.
24. C. E. Rasmussen, C. K. Williams, et al., Gaussian Processes for Machine Learning, Springer, 2006, vol. 1.
25. H.-M. Gutmann, J. Global Optim., 2001, 19, 201–227.
26. A. Bemporad, Comput. Optim. Appl., 2020, 77, 571–595.
27. J. Snoek, O. Rippel, K. Swersky, R. Kiros, N. Satish, N. Sundaram, M. Patwary, M. Prabhat and R. Adams, International Conference on Machine Learning, 2015, pp. 2171–2180.
28. J. T. Springenberg, A. Klein, S. Falkner and F. Hutter, Advances in Neural Information Processing Systems 29: Annual Conference on Neural Information Processing Systems 2016, Barcelona, 5-10 December 2016, 2016, pp. 4141–4149.
29. P. I. Frazier and J. Wang, Information Science for Materials Discovery and Design, 2016, pp. 45–75.
30. T. Ueno, T. D. Rhone, Z. Hou, T. Mizoguchi and K. Tsuda, Mater. Discovery, 2016, 4, 18–21.
31. Y. Zhang, D. W. Apley and W. Chen, Sci. Rep., 2020, 10, 4924.
32. E. Stach, B. DeCost, A. G. Kusne, J. Hattrick-Simpers, K. A. Brown, K. G. Reyes, J. Schrier, S. Billinge, T. Buonassisi and I. Foster, et al. , Matter, 2021, 4, 2702–2726.
33. S. Greenhill, S. Rana, S. Gupta, P. Vellanki and S. Venkatesh, IEEE Access, 2020, 8, 13937–13948.
34. R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D.-G. Ha and T. Wu, et al. , Nat. Mater., 2016, 15, 1120–1127.
35. T. Lookman, P. V. Balachandran, D. Xue, J. Hogden and J. Theiler, Curr. Opin. Solid State Mater. Sci., 2017, 21, 121–128.
36. R.-R. Griffiths and J. M. Hernández-Lobato, Chem. Sci., 2020, 11, 577–586.
37. I. G. Osio and C. H. Amon, Res. Eng. Des., 1996, 8, 189–206.
38. A. E. Gongora, B. Xu, W. Perry, C. Okoye, P. Riley, K. G. Reyes, E. F. Morgan and K. A. Brown, Sci. Adv., 2020, 6, eaaz1708.
39. L. Guillemard, N. Kaplaneris, L. Ackermann and M. J. Johansson, Nat. Rev. Chem, 2021, 5, 522–545.
40. M. Zhu, D. Piga and A. Bemporad, IEEE Trans. Control Syst. Technol., 2021, 30, 2176–2187.
41. E. A. del Rio Chanona, P. Petsagkourakis, E. Bradford, J. A. Graciano and B. Chachuat, Comput. Chem. Eng., 2021, 147, 107249.
42. T. Savage, N. Basha, J. McDonough, O. K. Matar and E. A. del Rio Chanona, Comput. Chem. Eng., 2023, 179, 108410.
43. M. Balandat, B. Karrer, D. Jiang, S. Daulton, B. Letham, A. G. Wilson and E. Bakshy, Adv. Neural Inform. Process. Syst., 2020, 33, 21524–21538.
44. S. Daulton, X. Wan, D. Eriksson, M. Balandat, M. A. Osborne and E. Bakshy, Adv.Neural Inform. Process. Syst., 2022, 35, 12760–12774.
45. J. Gardner, M. Kusner, Z. Xu, K. Weinberger and J. Cunningham, ICML, 2014, pp. 937–945.
46. Y. Chen, R. Dwivedi, M. J. Wainwright and B. Yu, J. Mach. Learn. Res., 2018, 19, 1–86.
47. M. Zhu and A. Bemporad, arXiv, 2023, preprint, arXiv:2302.04686,  DOI:10.48550/arXiv.2302.04686.
48. N. Ploskas and N. V. Sahinidis, J. Global Optim., 2022, 1–30.
49. C. Audet, E. Hallé-Hannan and S. Le Digabel, Operat. Res. Forum, 2023, 4 DOI:10.1007/s43069-022-00180-6.
50. K. Dreczkowski, A. Grosnit and H. B. Ammar, arXiv, 2023, preprint, arXiv:2306.09803,  DOI:10.48550/arXiv.2306.09803.
51. R.-R. Griffiths, L. Klarner, H. B. Moss, A. Ravuri, S. Truong, B. Rankovic, Y. Du, A. Jamasb, J. Schwartz, A. Tripp, G. Kell, A. Bourached, A. Chan, J. Moss, C. Guo, A. A. Lee, P. Schwaller and J. Tang, Adv. Neural Inform. Process. Syst., 2024, 36.
52. J. P. Folch, R. M. Lee, B. Shafei, D. Walz, C. Tsay, M. van der Wilk and R. Misener, Comput. Chem. Eng., 2023, 172, 108194.
53. C. Fare, P. Fenner, M. Benatan, A. Varsi and E. O. Pyzer-Knapp, NPJ Comput. Mater., 2022, 8, 257.
54. A. Thebelt, J. Kronqvist, M. Mistry, R. M. Lee, N. Sudermann-Merx and R. Misener, Comput. Chem. Eng., 2021, 151, 107343.
55. A. Thebelt, C. Tsay, R. Lee, N. Sudermann-Merx, D. Walz, B. Shafei and R. Misener, Adv. Neural Inform. Process. Syst., 2022, 35, 37401–37415.
56. F.-A. Fortin, F.-M. De Rainville, M.-A. G. Gardner, M. Parizeau and C. Gagné, J. Mach. Learn. Res., 2012, 13, 2171–2175.
57. F.-M. De Rainville, F.-A. Fortin, M.-A. Gardner, M. Parizeau and C. Gagné, Proceedings of the 14th Annual Conference Companion on Genetic and Evolutionary Computation, 2012, pp. 85–92.
58. J. Bergstra, D. Yamins and D. Cox, International Conference on Machine Learning, 2013, pp. 115–123.
59. K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, IEEE Trans. Evol. Comput., 2002, 6, 182–197.
60. A. F. Gad, Multimedia Tools Appl., 2023, 1–14.
61. D. Giacomelli, GeneticSharp, https://https://github.com/giacomelli/GeneticSharp, 2017.
62. M. Halford, EAOPT: Evolutionary Optimization Library for Go (Genetic Algorithm, Particle Swarm Optimization, Eifferential Evolution), https://github.com/MaxHalford/eaopt, 2016.
63. A. Tripp, mol_ga: Simple, Lightweight Package for Genetic Algorithms on Molecules, https://github.com/AustinT/mol_ga, 2023.
64. J. H. Jensen, Chem.l Sci., 2019, 10, 3567–3572.
65. N. Brown, M. Fiscato, M. H. Segler and A. C. Vaucher, J. Chem. Inform. Model., 2019, 59, 1096–1108.
66. K. Hussain, M. N. Mohd Salleh, S. Cheng and Y. Shi, Artif. Intell. Rev., 2019, 52, 2191–2233.
67. Y. Jin, Swarm Evol. Comput., 2011, 1, 61–70.
68. L. Pan, C. He, Y. Tian, H. Wang, X. Zhang and Y. Jin, IEEE Trans. Evol. Comput., 2018, 23, 74–88.
69. C. A. C. Coello, Proceedings of the Genetic and Evolutionary Computation Conference Companion, 2022, pp. 1310–1333.
70. J. Bergstra, R. Bardenet, Y. Bengio and B. Kégl, Adv. Neural Inform. Process. Syst., 2011, 2546–2554.
71. P. Larrañaga and J. A. Lozano, Estimation of Distribution Algorithms: A New Tool for Evolutionary Computation, Springer Science & Business Media, 2001, vol. 2.
72. N. Hansen, Towards a New Evolutionary Computation: Advances in the Estimation of Distribution Algorithms, 2006, pp. 75–102.
73. S. Watanabe and F. Hutter, Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, 2023, pp. 4371–4379.
74. M. A. Gelbart, J. Snoek and R. P. Adams, 30th Conference on Uncertainty in Artificial Intelligence, UAI 2014, 2014, pp. 250–259.
75. D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Science, 2018, 360, 186–190.
76. H. Moriwaki, Y.-S. Tian, N. Kawashita and T. Takagi, J. Cheminform., 2018, 10, 1–14.
77. D. Perera, J. W. Tucker, S. Brahmbhatt, C. J. Helal, A. Chong, W. Farrell, P. Richardson and N. W. Sach, Science, 2018, 359, 429–434.
78. A. K. Low, F. Mekki-Berrada, A. Gupta, A. Ostudin, J. Xie, E. Vissol-Gaudin, Y.-F. Lim, Q. Li, Y. S. Ong and S. A. Khan, et al. , NPJ Comput. Mater., 2024, 10, 104.
79. M. D. McKay, R. J. Beckman and W. J. Conover, Technometrics, 1979, 21, 239–245.
80. T. S. Motzkin, H. Raiffa, G. L. Thompson and R. M. Thrall, Contribut. Theory of Games, 1953, 2, 51–73.
81. A. Bemporad, IEEE Trans. Automatic Control, 2023, 68, 3194–3209.
82. N. Miyaura, K. Yamada and A. Suzuki, Tetrahedron Lett., 1979, 20, 3437–3440.
83. N. Miyaura and A. Suzuki, Chem. Rev., 1995, 95, 2457–2483.
84. T. E. Barder, S. D. Walker, J. R. Martinelli and S. L. Buchwald, J. Am. Chem. Soc., 2005, 127, 4685–4696.
85. A. J. Lennox and G. C. Lloyd-Jones, Chem. Soc. Rev., 2014, 43, 412–443.
86. D. Probst, P. Schwaller and J.-L. Reymond, Digital Discovery, 2022, 1, 91–97.
87. J. Y. Wang, J. M. Stevens, S. K. Kariofillis, M.-J. Tom, D. L. Golden, J. Li, J. E. Tabora, M. Parasram, B. J. Shields and D. N. Primer, et al. , Nature, 2024, 626, 1025–1033.
88. B. Ranković, R.-R. Griffiths, H. B. Moss and P. Schwaller, Digital Discovery, 2024, 3, 654–666.
89. M. B. Plutschack, B. Pieber, K. Gilmore and P. H. Seeberger, Chem. Rev., 2017, 117, 11796–11893.
90. B. J. Reizman and K. F. Jensen, Acc. Chem. Res., 2016, 49, 1786–1796.
91. H. Struebing, Z. Ganase, P. G. Karamertzanis, E. Siougkrou, P. Haycock, P. M. Piccione, A. Armstrong, A. Galindo and C. S. Adjiman, Nat. Chem., 2013, 5, 952–957.
92. A. S. Hukkerikar, S. Kalakul, B. Sarup, D. M. Young, G. Sin and R. Gani, J. Chem. Inform. Model., 2012, 52, 2823–2839.
93. A. S. Hukkerikar, B. Sarup, A. Ten Kate, J. Abildskov, G. Sin and R. Gani, Fluid Phase Equilib., 2012, 321, 25–43.
94. M. J. Kamlet, J. L. Abboud and R. Taft, J. Am. Chem. Soc., 1977, 99, 6027–6038.
95. M. H. Abraham, R. M. Doherty, M. J. Kamlet, J. M. Harris and R. W. Taft, J. Chem. Soc. Perkin Trans. 2, 1987, 913–920.
96. D. R. Jones, M. Schonlau and W. J. Welch, J. Global Optim., 1998, 13, 455–492.
97. A. I. Forrester and A. J. Keane, Progr. Aerospace Sci., 2009, 45, 50–79.
98. L. Gui, A. Armstrong, A. Galindo, F. B. Sayyed, S. P. Kolis and C. Adjiman, Mol. Syst. Des. Eng., 2024 10.1039/D4ME00074A.
99. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
100. T. Sheldon, C. Adjiman and J. Cordiner, Fluid Phase Equilib., 2005, 231, 27–37.
101. C. Reichardt and T. Welton, Solvents and Solvent Effects in Organic Chemistry, John Wiley & Sons, 2011.
102. J. Sherwood, H. L. Parker, K. Moonen, T. J. Farmer and A. J. Hunt, Green Chem., 2016, 18, 3990–3996.
103. H. T. Turan, S. Brickel and M. Meuwly, J. Phys. Chem. B, 2022, 126, 1951–1961.

---

Footnote

† Electronic supplementary information (ESI) available: GitHub Repository. See DOI: https://doi.org/10.1039/d4dd00113c

---