Auto-VTNA: an automatic VTNA platform for determination of global rate laws

Abstract

The ability and desire to collect kinetic data has greatly increased in recent years, requiring more automated and quantitative methods for analysis. In this work, an automated program (Auto-VTNA) is developed, to simplify the kinetic analysis workflow. Auto-VTNA allows all the reaction orders to be determined concurrently, expediting the process of kinetic analysis. Auto-VTNA performs well on noisy or sparse data sets and can handle complex reactions involving multiple reaction orders. Quantitative error analysis and facile visualisation allows users to numerically justify and robustly present their findings. Auto-VTNA can be used through a free graphical user interface (GUI), requiring no coding or expert kinetic model input from the user, and can be customised and built on if required.

---

Introduction

The study of chemical kinetics supports our mechanistic understanding of chemical reactions and is crucial for the development of safe and efficient synthetic procedures on scale.^1–5 Chemical kinetics is also utilised extensively to understand and optimise the behaviour of reaction systems, particularly complex catalytic reactions.^5–10 The global rate law is a mathematical expression that correlates the rate of a reaction with the concentration of each reaction species, with the general form:

Rate = k_obs[A]^m[B]ⁿ[C]^p (1)

where [A], [B], and [C] = the molar concentrations of the reacting components (reactants, catalyst, products); k_obs = observed rate constant; and m, n and p = the orders of the reaction with respect to each reaction component.

A global rate law can be constructed empirically from experimental data, without explicit considerations of the reaction mechanism or mass transfer effects.^11,12 Traditionally, kinetic experiments include “flooding”^13,14 or the initial rates method.^15,16 While these methods are generally easy to analyse (as the data can be linearised), the results must be treated with caution, as they are either performed under non-synthetically relevant conditions,^4,17 or cannot detect changes in reaction orders associated with more complex mechanisms, such as catalyst deactivation or product inhibition.^18,19

In the past few decades, modern advances in process analytical tools and computing power have greatly accelerated the development of data-rich kinetic experiments under synthetically relevant conditions. In the late 1990's, Blackmond pioneered the development of Reaction Progress Kinetic Analysis (RPKA),²⁰ which greatly streamlines the determination of rate laws from a series of “same excess” and “different excess” experiments.^21–23 The experimental data can be manipulated in an electronic spreadsheet to obtain overlays between rate vs. concentration plots to obtain individual reactant order. Later, a “time adjusted” concentration vs. time plot method was developed,⁷ followed by the Time Normalization Analysis (TNA) method for determining catalyst order, further expanding the suite of visual kinetic analysis tools.²⁴ Later in the same year, this was further extended to all reacting species as “Variable Time Normalization Analysis” (VTNA).²⁵ One of the most attractive features of these visual kinetic analysis tools is that reaction orders can be derived without the need for bespoke software or significant complex mathematical calculations, hence making them more accessible to the synthetic chemistry community than previously available kinetic tools.^26–29

In the last few years, the widespread popularity of Python as a general programming language has greatly accelerated the automation of machine-readable tasks.^30–33 Recently, Hein and co-workers have developed a Python package “Kinalite”, a simple API for performing VTNA.^34–36 Kinalite requires kinetic data from each experiment to be imported as individual csv files, containing time–concentration data of different reaction species. The user selects a reaction species and two relevant experimental data to determine the reaction order automatically. For multiple species, or for more than two data series, this process must be performed sequentially, determining one species order at a time. The package presents the result as a plot of ‘errors’ associated with different order values for a specific reaction species, demonstrating the best order value. These individually calculated orders can be combined to yield the global rate law. By removing the need for visual inspection, Kinalite removes human bias. However, other challenges remain, such as:

(1) Analysing more than two experiments at a given time.

(2) Determining the order of multiple or all reaction species concurrently.

(3) Robustly quantifying error in the reaction orders computed.

In this work, the development of a new and more robust Python package to perform VTNA is described, which can elucidate the reaction orders of several species simultaneously. As well as enabling significant time saving, an unlimited number of initial concentrations can be altered between experiments by computationally assessing the overlay across a wide range of order value combinations. This presents a novel way of carrying out “different excess” experiments which improves the amount of kinetic information obtained per run.

Method

The Auto-VTNA program offers the following features:

(1) Manual and automatic VTNA in a more time efficient manner.

(2) VTNA with several normalised reaction species.

(3) Visualisation of overlay score across different reaction orders.

(4) Quantification of overlap and error.

(5) Improved accessibility.

Each of these features will be presented below as a ‘unique selling point’ (USP) of the package, followed by a Results and discussion, where the application of Auto-VTNA is showcased with several examples.

USP1: automatic VTNA in Python

Traditionally, VTNA involves normalising the time axis of concentration time data with respect to a particular reaction species, whose initial concentration varies across different experiments. Several reaction orders are entered in a spreadsheet by trial-and-error, until the order giving the best visual overlay of the concentration profiles is identified. Concentration profiles linearise if the time axis is normalised with respect to every reaction component raised to its correct order.^10,37,38 However, most examples of VTNA involve overlay of non-linear monotonically increasing or decreasing product or reactant concentration profiles (Fig. 1).^39–42

Fig. 1 VTNA overlay plots from literature with the reported order values giving concentration profile overlay.^39–42

To develop a robust automated method, a Python script was developed to emulate the manual VTNA routine which calculates the transformed time axis for a chosen reaction species and corresponding order value(s) using a selected subset of the kinetic data, tested on selected literature examples (see ESI Appendix SA2‡).²⁵ Subsequently, a robust automatic method of assessing the overlay of reaction progress profiles was developed, removing the need for manual visual inspection. This method involves fitting all profiles to a common flexible function and utilising a goodness-of-fit score (e.g. RMSE), as an ‘overlay score’, to quantify the degree of overlay.

In order to process non-linear fitting, a 5^th degree monotonic polynomial fitting, a statistical method with several scientific applications,^43–45 was selected as the default method. Although a more computationally efficient non-monotonically constrained polynomial fitting can be selected that is circa. 10 times faster, there is an increased risk of overfitting effects for reaction profiles with few datapoints. Additionally, Auto-VTNA allows linear fitting, which is particularly useful when reaction profiles linearise upon complete normalisation of the time axis, and can evaluate the k_obs of the global rate law (see ESI, Section S6.2‡).

The ‘overlay score’ of Auto-VTNA, based on total fitting to a flexible function, is different from that employed in Kinalite, which relies on the difference in y-axis values of datapoints when sorted by transformed time value (‘error’) (see ESI, Section S2.2‡). This ‘error’ measure can in some cases yield incorrect order values that do not reflect optimal concentration profile overlay, especially if the density of the two compared data series is different.³⁶ In contrast, Auto-VTNA reliably yields the order value(s) that maximise concentration profile overlay as judged by visual inspection on all tested examples (see ESI, Section S6.3‡), thus successfully automating the visual part of VTNA.

Upon establishing a robust method for computationally assessing the degree of concentration profile overlay, an algorithm was developed to perform automatic VTNA and embedded into a Python package named “Auto-VTNA”.

USP2: VTNA with several normalised reaction species

Unlike previous methods, Auto-VTNA can be used to identify the order values which optimise concentration profile overlay for several reaction species in the same calculation. The basic workflow is demonstrated in Fig. 2. Firstly, a mesh with a selected number of order values within a specified range is defined, e.g. from −1.5 to 2.5 (step 1). Secondly, a list of every combination of reaction order values for each normalised species is created (step 2). For each combination of orders, the time axis is normalised, and the transformed concentration profiles fitted to obtain the overlay score (step 3 and 4). This reveals the optimal order combination around which a new collection of order value combinations is generated to increase the precision with which the optimal reaction orders are determined (steps 5 and 6). This procedure is repeated a selected number of times to increase precision without an unacceptably high processing time (see ESI, Section S7‡).

Fig. 2 Flowchart illustrating the basic workflow of the Auto-VTNA algorithm including the inputs required for the algorithm and the iterative steps the algorithm progresses through to return the overlay score of all reaction order combinations trialled as well as the order values that gave the best overlay score.

Traditional “different excess” experiments only alter the initial concentration of one reaction species at a time. Auto-VTNA can simultaneously determine the reaction orders of several reaction species efficiently. This reduces researcher analysis time and facilitates more efficient “different excess” experiments, where the initial concentrations of several reaction species are altered between experiments at the same time. Potentially, such an experimental method could reduce the number of experiments required to determine all reaction species orders in a complex reaction mixture. However, the penalty on accuracy of determined orders with reduction in the number of experiments should be considered and could be assessed through Auto-VTNA.

USP3: visualising the results of automatic VTNA

Conventionally, VTNA results are presented by comparing “bad” with “optimal” overlays (Fig. 3a). In contrast, Auto-VTNA offers a more detailed visualisation of how changing order values affects overlay (Fig. 3b). As the degree of reaction profile overlay is calculated for a range of different order values, a plot of overlay score against order value(s) can be produced. Thus, researchers utilising this method can justify the optimal reaction order in a quantifiable manner. As a general guide, the value of the optimal overlay score (when set to RMSE) can be classified as excellent (<0.03), good (0.03–0.08), reasonable (0.08–0.15) or poor (>0.015).

Fig. 3 Different representations of VTNA results: (a) Overlay plots for simulated data involving the catalytic conversion of reactants A + B → P, including catalyst decomposition.²⁵ (b) Plot showing the overlay scores (RMSE of 5^th degree monotonic polynomial fits) against the reaction order in catalyst obtained using Auto-VTNA. (c) Corresponding “error plot” obtained using Kinalite.

Through its “error” metric, Kinalite can also produce a rudimentary overlay score (Fig. 3c and ESI Section S2.2‡), which produces almost the same order assignment as Auto-VTNA for the simulated kinetic data in Fig. 3a. However, its reduced reliability becomes evident from the erratic curve produced, particularly at negative order values.³⁶

When utilising Auto-VTNA to determine the orders of two species, the correlation between the overlay score and the combinations of order values can be visualised by a contour plot (Fig. 4, central plot). If the algorithm is set to obtain the reaction orders of three or more species, overlay scores can be tabulated for a selected number of order value combinations. However, in this case, the results are challenging to visualise due to the higher dimensionality of the data. Alternatively, if a reaction order in a species is already known, this can be inputted as a fixed value, if desired. The algorithm then calculates the overlay score as a function of the remaining species. This lowers the dimensionality of the results obtained so that they can be visualised by a graph or contour plot.

Fig. 4 VTNA overlay plots generated using kinetic data on the aza-Michael reaction between methyl itaconate (1) and piperidine (2).⁴⁶ The overlay plots are generated by right-clicking on the contour plot.

The graphs and contour plots generated by Auto-VTNA (Fig. 3 and 4, respectively), allow individual overlay plots to be produced in an interactive manner through mouse clicks (Fig. 4). By left-clicking on the graph or contour plot, a traditional overlay plot is generated, whereas right-clicks show the plot with normalised y axis, the fitted function, and the overlay score of the click order value(s). This allows the operator to interrogate the overlay score landscape obtained by Auto-VTNA and verify that the calculated reaction order(s) give optimal concentration profile overlay.

USP4: error analysis

Certainty in a set of order values can also be assessed through automatic calculation of the range in which the overlay score for a set of order values is no greater than 15% (by default) from the optimal overlay score. For example, the assigned order of 0.94 shown in Fig. 5b has a 15% overlay score interval of (0.912, 0.987) whereas the corresponding interval for Fig. 5a is (0.937, 1.084) in 1 and (0.973, 1.059) in 2. Noisier kinetic data will give wider intervals, whereas kinetic datasets with good variation in initial concentrations and high signal-to-noise ratio will give narrower intervals, indicating greater certainty in the calculated order values (see ESI, Section S8.2‡). The range of order value combinations within this cut-off can be represented by an orange line if the order in only one species is calculated (Fig. 5a) or visualised as blue dots in a contour plot (Fig. 5b).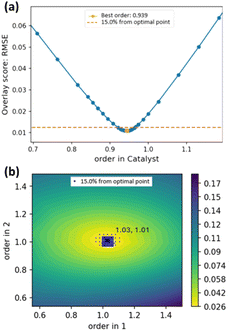

Fig. 5 (a) Overlay score vs. order in catalyst for simulated kinetic data.²⁵ (b) Contour plot illustrating the degree of concentration profile overlay across different reaction order values in 1 and 2 for data on the aza-Michael addition in EtOH (Scheme 1).²⁷ The blue dots illustrate the order combination values with overlay scores within 15% of the optimal point at (1.03, 1.02).

The absolute optimal overlay score can also provide valuable information about the reaction under study. High optimal RMSE overlay scores reflect effects that can lower the confidence in the global reaction order afforded by VTNA, such as noisy kinetic data, incorrectly cropped data, or insufficient data point density for accurate numerical integration, as well as more complex reaction mechanisms giving changing order values, e.g. catalyst deactivation. To improve the utility of absolute overlay score values, it is necessary to limit the influence of factors other than the degree of concentration profile overlay. For example, to prevent the concentration scale from influencing goodness-of-fit values, Auto-VTNA normalises the y-axis prior to generating the overlay score. Moreover, the effect of over- and under-fitting on the overlay score is limited by employing a flexible 5^th or 7^th degree monotonic polynomial fit (see ESI, Section S6‡). Lastly, to facilitate the comparison of optimal overlay scores obtained with different datasets, RMSE has been set as the default goodness-of-fit measure.

USP5: improved accessibility

Last but not least, an open-source graphical user interface (GUI) named “Auto-VTNA Calculator” was developed using PySimpleGUI (Fig. 6).⁴⁷ This provides access to the benefits of Auto-VTNA without requiring knowledge of Python coding. Upon uploading kinetic data as an Excel file or multiple csv files, dropdown menus allow the experiments, reaction species for time axis normalisation, and the output species to be selected for VTNA or Auto-VTNA analysis. Calculation and data visualisation features can be adjusted in settings menus, and the results from automatic VTNA can be saved as an Excel or csv file. A “Crop Data” feature can be used to streamline the modification of the input data to investigate the impact on reaction order values, for example, to remove outliers, or to truncate excess data points recorded after reaction completion. The fitting function can also easily be modified and the monotonic constraint removed if the inputted kinetic data requires. By clicking “show + info”, the user can also view the overlay score intervals of each reaction species for a selected% from the optimal overlay score (see ESI, Section S5‡). In comparison to Kinalite, which can be accessed via a website, we provide Auto-VTNA as an open source executable file. This facilitates handling of more complex calculations, implementation into automated systems, and further development to add to Auto-VTNA. A tutorial video has also been created to improve accessibility.

Fig. 6 The graphical user interface of the Auto-VTNA Calculator.

Results and discussion

The reliability and functionality of Auto-VTNA were evaluated by the analysis of kinetic data previously reported in literature and comparing the results. The first selected example was the aza-Michael addition of piperidine 2 to dimethyl itaconate 1 (Scheme 1) reported by Clark et al.^27,46 Interestingly, the order of the reaction was reported to change in different solvents: the reaction order in the piperidine was found to be 1 in ethanol, 2 in DMSO, 2 in THF, but 1.6 in IPA.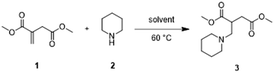

Scheme 1 Aza-Micheal addition of piperidine 2 to dimethyl itaconate 1.⁴⁶

Utilising the Auto-VTNA Calculator with default settings (5^th degree monotonic fitting with an RMSE overlay score), reaction orders in 1 and 2 were identified for the ethanol, IPA, THF, and DMSO datasets (Table 1) within 3 minutes. Generally, the Auto-VTNA derived order values match the orders reported within 0.1 and gave equal or better concentration profile overlay than that obtained using reported orders (see ESI, Fig. SA38‡). An exception is the reaction in DMSO, for which the computed reaction orders of 0.77 and 1.86 deviated more significantly from the reported order values of 1 and 2. This is attributed to the sparsity of kinetic data obtained from the reaction DMSO (3 experiments with 4 time points each), which leads to a greater influence of random errors and inaccurate numerical integration. The results from each calculation can be represented as contour plots (Fig. 7), showing well-defined overlay score minima around the best order values, in particular for the ethanol dataset (Fig. 7a).

Table 1 Comparison of reported and reanalysed reaction orders for the aza-Michael reaction of dimethyl itaconate 1 and piperidine 2

Solvent	Reported value	Auto-VTNA
EtOH	[1]^1[2]^1	[1]^1.03[2]^1.01
IPA	[1]^1[2]^1.6	[1]^1.00[2]^1.66
DMSO	[1]^1[2]^2	[1]^0.77[2]^1.93
THF	[1]^1[2]^2	[1]^0.94[2]^1.86

---

Fig. 7 Contour plots for the aza-Michael reaction of dimethyl itaconate 1 and piperidine 2 in (a) ethanol; (b) IPA; (c) THF; and (d) DMSO illustrating the degree of concentration profile overlay as the RMSE of the total fit against the reaction order in dimethyl itaconate 1 and piperidine 2.

Overall, this example illustrates that Auto-VTNA reliably computes order values based on optimal concentration profile overlay that match reported orders obtained by visual inspection. It also emphasises the importance of a suitable quality and quantity of kinetic data for application of any kinetic analysis technique.

Automatic determination of rate equations using Auto-VTNA

Following from this, Auto-VTNA was applied to kinetic data from a further 23 selected publications,^{6,9,10,39–42,48–63} including stoichiometric and catalytic reactions (Table 2, entries 1–14) containing up to 6 reaction species (reactants, reagents, catalyst, and additives).

Table 2 Reaction systems for which kinetic data was available in the literature with reported order values derived via conventional VTNA as well as reaction order values calculated by automatic sequential and total VTNA using Auto-VTNA. The order values in the sequential VTNA column were calculated using a 5^th degree monotonic polynomial apart from the orders in 6, 33, 34, 39, 40 and 49 which were calculated using a 7^th degree monotonic polynomial (see ESI, Sections S6.3 and S6.4). The order values in the total VTNA column were calculated in one calculation using an ordinary 5^th degree polynomial using the quick algorithm settings (see ESI, Section S7). The RMSE overlay scores at the reported and calculated order values are also shown to illustrate that the calculated order values are more precise than the reported values

Entry	Reaction system	Reported orders	Calculated orders		Total VTNA overlay score with
			Sequential VTNA	Total VTNA	Reported orders	Total Auto-VTNA orders
1^56		[4]^1[5]^1[6]^1[7]^0[8]^1	[4]^1.00[5]^1.13[6]^0.82[7]^−0.03[8]^1.04	[4]^1.00[5]^1.04[6]^1.02[7]^−0.02[8]^1.01	0.0379	0.0378
2^48		[11]^1[12]^1[13]^−0.5	[11]^0.85[12]^0.92[13]^−0.48	[11]^0.94[12]^0.99[13]^−0.49	0.0174	0.0143
3^52		[14]^0.9[12]^1.0[15]^1.0[16]^0	[14]^0.85[12]^1.04[15]^1.07[16]^0.09	[14]^0.95[12]^1.02[15]^1.06[16]^0.04	0.0178	0.0162
4^63		[18]^1[19]^1[20]^1	[18]^1.06[19]^0.98[20]^1.02	[18]^1.00[19]^0.95[20]^0.91	0.0356	0.0338
5^57		[22]^0.85[23]^−0.6[24]^0.9	[22]^0.95[23]^−0.58[24]^0.94	[22]^0.90[23]^−0.58[24]^0.94	0.0729	0.0590
6^54		[27]^1[28]^1[29]^1	[27]^0.91[28]^0.97[29]^0.90	[27]^0.92[28]^0.97[29]^0.96	0.0308	0.0231
7^53		[31]^1.5[32]^1[33]^0.15	[31]^1.59[32]^0.89[33]^0.15	[31]^1.51[32]^1.18[33]^0.20	0.0114	0.0055
8^6		[34]^−1[35]^1[36]^1	[34]^−1.10[35]^1.05[36]^1.14	[34]^−1.07[35]^1.05[36]^1.12	0.1157	0.0537
9^6		[34]^−1[35]^1[36]^1	[34]^−0.43[35]^1.60[36]^1.08	[34]^−0.44[35]^0.99[36]^1.19	0.3911	0.2866
10^62		[38]^1[39]^1[40]^1	[38]^1.04[39]^0.97[40]^0.83	[38]^1.10[39]^0.95[40]^0.83	0.0557	0.0455
11^10		[42]^1[43]^0.75[44]^1[45]^0.5[46]^0[47]^1	[42]^1.05[43]^0.77[44]^1.02[45]^0.36[46]^0.04[47]^0.94	[42]^1.07[43]^0.60[44]^1.02[45]^0.30[46]^−0.04[47]^0.99	0.1163	0.1015
12^56		[49]^0[50]^0.9[51]^1.1[52]^1	[49]^0.11[50]^0.79[51]^1.24[52]^0.91	[49]^−0.03[50]^0.62[51]^1.26[52]^0.86	0.1250	0.0912
13^50		[54]^1[55]^0[56]^0[57]^1	[54]^0.85[55]^0.13[56]^−0.07[57]^0.95	[54]^0.76[55]^0.10[56]^−0.10[57]^1.07	0.0618	0.0359
14^61		[60]^1[61]^1[62]^1	[60]^0.74[61]^0.96[62]^0.96	[60]^0.71[61]^0.95[62]^0.86	0.1412	0.1013
15^41		[64]^0[65]^1[66]^1	[64]^0.32[65]^1.02[66]^0.98	[64]^0.53[65]^0.92[66]^0.79	0.1231	0.1102
16^51		[68]^2.05[69]^0.78[70]^−0.03[71]^0.20[23]^0.02	[68]^0.97[69]^0.60[70]^0.11[71]^0.18[23]^0.10	[68]^1.05[69]^0.62[70]^−0.04[71]^0.18[23]^0.03	0.1275	0.0230

---

The current approach to VTNA experimentation involves performing a “standard” reaction, under synthetically relevant conditions, followed by “different excess” experiments, where only the initial concentration of each reaction species is altered. This experiment design we define as “sequential VTNA”, as the orders are obtained for one reaction species at a time by identifying the order that makes the standard and relevant different excess profiles overlay. Pleasingly, we found that Auto-VTNA could identify the order values giving optimal overlay in all cases using sequential VTNA. A monotonic polynomial degree of 5 was sufficient in most instances to avoid inaccurate order values due to underfitting. However, for concentration profiles exhibiting significant curvature, a 7^th degree polynomial was necessary to ensure convergence to the optimal overlay order value (see ESI, Section S6.4‡).

In “total-VTNA”, all experiments are combined and normalised with respect to every species for which an order has been obtained via sequential VTNA. If every species contributing to the rate has been normalised, linearisation occurs so that the observed rate constant can be derived.^{8,10,48,50–53,63} However, despite previous VTNA methods supporting total-VTNA, such methods have been utilised only occasionally to derive reaction orders.^51,56 As Auto-VTNA significantly reduced the time and effort to determine the reaction orders of an unlimited number of reaction species rapidly through one single calculation, it facilitates a simultaneous total-VTNA approach. Researchers can vary multiple initial concentration at a time, increasing the information content per reaction run, and lowering the signal to noise ratio for the total VTNA calculation. This change from sequential to total VTNA is analogous to the improvement offered by design of experiments (DoE) over one-factor-at-the-time (OFAT) approaches for reaction optimisation in terms of accuracy and speed.⁶⁴

Currently, there are few reported kinetic studies with different excess experiments in which more than one initial concentration is varied at a time.^46,56 Nonetheless, as long as the concentration profiles of every reaction species have been measured or can be inferred from the product profiles, total VTNA can also be applied to ordinary VTNA datasets. This was performed for kinetic data obtained from 17 publications.^{6,10,40,41,48–57,61–63} Two of these publications were omitted as sequential VTNA had revealed that reaction orders change with the initial concentrations of reactants.^39,49 Kinetic data from the remaining 15 publications was re-analysed by Auto-VTNA sequentially and by automatic total VTNA (Table 2).

For entries 1–8 of Table 2, Auto-VTNA for both sequential and total VTNA yielded order values in close agreement with the reported values. The 15% overlay score intervals for the optimal order values were also moderate for these datasets (see ESI, Fig. S47‡). For entries 9–14 of Table 2, the order values obtained by automatic total VTNA deviate more significantly from the reported values. However, the calculated order values demonstrate closer overlay than the reported values, as evidenced by their superior overlay scores. This supports the claim that Auto-VTNA yields the order values that maximise concentration profile overlay without human bias. This allows calculated order values and a measure of error (15% overlay score intervals) to be reported alongside rounded order values, even if the latter is believed to be the “true” order (see ESI, Section S8‡). Entry 15 of Table 2 produced broad order intervals both in sequential and total VTNA, suggesting that more experiments may be needed to confirm the true order, particularly in the pyrrolidine substrate (see ESI, Fig. SA34‡). Entry 16 of Table 2 yielded order values in close agreement with those reported, with the exception of the order in the alkyne which was found to be 1.05 rather than 2.05 (see ESI, Fig. SA35 and SA36‡).

Case studies

Kinetic data on the cyclopropanation of styrene with dirhodium tetracarboxylate catalysts recorded by Wei et al.⁶ was re-analysed to obtain orders consistent with the reported values, although with a catalyst order of 1.12 (15% overlay score interval: 1.09–1.16) rather than 1.0 which could indicate catalyst inhibition (Fig. 8 and Table 2, entry 8).⁶ This Auto-VTNA result suggests further experiments should be performed to investigate this potential catalyst inhibition. The same excess run was included in the calculation to further improve reaction order accuracy, illustrating the power of varying more than one initial concentration per run. Auto-VTNA was also applied to the analogous kinetic dataset recorded by Wei et al. in dimethylcarbonate (Table 2, entry 9) which was found to be less consistent.⁶ We hypothesised that by including all experiments indiscriminately, the noise caused by poorly controlled factors such as water concentration would cancel out to reveal the true orders. While the calculated order in diazo compound matched the reported value of 1, the order in styrene was lower than initially reported, suggesting that styrene inhibition is less severe in dimethylcarbonate. The order in catalyst was again found to be greater than the reported value of 1 (see ESI, Fig. SA22‡).

Fig. 8 VTNA overlay plots illustrating the degree of concentration profile overlay achieved by total VTNA using: (a) the reported order values; (b) and those calculated using Auto-VTNA.⁶ Every colour refers to a different experiment.

A kinetic study by Lancaster et al. on a catalytic asymmetric alkene bromoesterification reaction (Table 2, entry 1) is a good demonstrator of the power of automatic total VTNA for elucidating rate equations for catalytic reaction systems (Fig. 9a). Using Auto-VTNA the analysis could be expanded to include same excess and product doping experiments, revealing an order of −0.75 in the amide by-product and an order of 0 in the desired product (Fig. 9b). The linearisation achieved by also normalising the time axis with respect to the inhibitory by-product indicates that the complete rate equation has been elucidated.

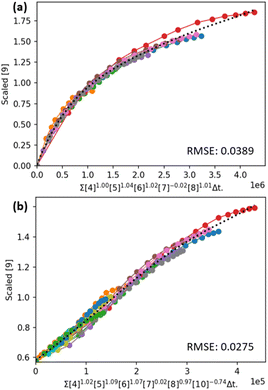Fig. 9 VTNA overlay plots obtained utilising Auto-VTNA for the catalytic asymmetric alkene bromoesterification reaction reported by Lancaster et al.⁵⁵ analysed for: (a) all reactants and catalyst, with the relevant different excess experiments; and (b) all species present in the reaction including product, by-product, and internal standard, with both different excess, same excess and product addition experiments.

In the final example, Auto-VTNA was applied to analyse product concentration profiles for kinetic data by Newton et al. for the Heck reaction between iodobenzene and methyl acrylate catalysed by varying amounts of Pd(OAc)₂,⁹ where it was reported that the catalyst order is dependent on catalyst loading, due to the presence of more than one active catalyst species and different catalyst deactivation rates. Investigation utilising Auto-VTNA emulated the reported results: for low catalyst loading experiments (30, 50, 100, and 200 ppm), a catalyst order of 1.73 was identified, close to the reported value of 1.7; while a lower catalyst order of 0.87 was obtained for higher catalyst loadings (200, 400, 600, 800, and 1000), similar to the reported value of 0.9. The concentration profiles with high catalyst loadings exhibited a wider interval of reaction order values with overlay scores only 15% above the minimum (0.79 to 0.94 vs. 1.70 to 1.77) as well as a higher overlay score at the optimal catalyst order (0.041 vs. 0.023) (Fig. 10).

Fig. 10 Graphs illustrating overlay score versus order in catalyst and VTNA overlay plots with catalyst order values found to maximise concentration profile overlay for kinetic data on a Heck reaction reported by Newton et al.⁹ for (a) and (b) low catalyst loadings; and (c) and (d) high catalyst loadings.

To investigate whether the reported catalyst order step change at 200 ppm is supported by Auto-VTNA, order values were calculated for pairs of experiments with consecutive catalyst loadings (Fig. 11). Indeed, a step change is observed at 200 ppm in catalyst order value, although the catalyst order obtained from the 600 and 800 ppm experiments appears to be an outlier. The equivalent plots for order values obtained from groups of 3 or 4 experiments with consecutive catalyst loadings also indicate a step change from high to low catalyst orders, although less pronounced as the mid-range order values are obtained from concentration profiles from both the high and low catalyst loading domains (see ESI, Fig. SA40–SA42‡). This demonstrates the power of Auto-VTNA to quickly and accurately provide kinetic analysis with robust quantified justification.

Fig. 11 Calculated reaction orders in catalyst for pairs of reaction profiles with consecutively higher loadings of Pd(OAc)₂ from the kinetic data collected by Newton et al. on a Heck reaction with low catalyst loadings.⁹ Open circles and dashed lines represent visual VTNA performed in the original work by Newton et al. on four “low catalyst loadings” and five “high catalyst loadings”.

Best practice

To aid standard reporting of Auto-VTNA results, we recommend that calculated order values should be quoted to two decimal places with the range of order values which fall within 15% of the minimum overlay score also quoted. This reporting represents an “error bar” for the result. If then desired a rounded order value can be suggested with greater confidence if it falls within this error range. As Auto-VTNA becomes more widely used, we encourage others to develop more detailed statistical methods for assessing uncertainty in orders based on the data produced by Auto-VTNA. Overlay plots, minimum overlay score, or overlay score vs. order plots should also supplement these reported values and can be interpreted as discussed in USP 4 (for more detail see ESI, Section S8‡).

Conclusions

In summary, a robust method has been developed to automate VTNA. This mode of analysis simplifies data handling and enables automatic identification of the reaction order values giving concentration profile overlay for “different excess” experiments. Auto-VTNA utilises a robust method for computationally assessing the degree of concentration profile overlay through a monotonic polynomial fitting procedure. To minimise processing time, the algorithm iteratively tests reaction order combinations, honing in on the optimal reaction order values. The results from Auto-VTNA can then be visualised as a graph or contour plot for 1 and 2 normalised reaction species respectively, providing an efficient justification of the reported reaction order values. Furthermore, Auto-VTNA can improve the assessment of error ranges in assigned order values via overlay score intervals. The absolute overlay score can be used as an indicator of the uncertainty in the assigned orders.

Auto-VTNA was tested on kinetic data obtained from literature to demonstrate the key features and advantages. The ability to compute several reaction orders, utilising kinetic data obtained from multiple experiments, (total-VTNA) is especially highlighted. The application of the method in a Heck reaction that involves changes in the catalyst order at different catalyst loadings was also demonstrated.

Last but not least, a graphical user interface has been constructed and made freely available, as well as the underlying code, to facilitate the use of Auto-VTNA by researchers. The program has been optimised for efficiency of use and does not require coding experience. It includes several features, such as removal of selected datapoints, kinetic data visualisation, and interactive representation of Auto-VTNA results. We hope that this work will encourage wider adoption of VTNA by researchers and enable the justification of assigned reaction order values in a more informative and efficient manner.

Data availability

The code for the Auto-VTNA Python package and the executable file for the Auto-VTNA Calculator GUI can be found at https://github.com/ddalland/Auto-VTNA. All data used in this work is from published papers as referenced throughout.

Author contributions

DD and LS conceptualised the ideas within this work. DD developed the code, sourced the data, and analysed the data. LS and KKH offered advice during the work and mentorship to DD. DD wrote the original draft. Subsequent revisions of the manuscript were performed by all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are thankful to BASF SE and the EPSRC Centre of Doctoral Training in Next Generation Synthesis & Reaction Technology [‘rEaCt’, EP/S023232/1] for financial support. We thank the following for providing the kinetic data required for testing and validating Auto-VTNA: Prof. Jason Hein (University of British Columbia), Prof. Clement Mazet (Université de Genève), Dr Helena Lundberg (KTH Royal Institute of Technology), Ben Lancaster (Imperial College London), Prof. T. V. Rajan Babu (The Ohio State University) and Dr James Herbort (Merck), Prof. R. Tom Baker (University of Ottawa), Dr Matt Elsby (Yale University), Dr Rylan Lundgren (University of Alberta), Prof. Ian Tonks (University of Bristol), and Prof. Paul Chirik (Princeton University). We are also grateful to those researchers who made their kinetic data readily available from the ESI‡ of their publication.

Notes and references

1. A. Kossoy and Y. Akhmethshin, Identification of Kinetic Models for the Assessment of Reaction Hazards, Process Saf. Prog., 2006, 25, 326–330.
2. S. Wagschal, D. Broggini, T. D. C. Cao, P. Schleiss, K. Paun, J. Steiner, A. L. Merk, J. Harsdorf, W. Fiedler, S. Schirling, S. Hock, T. Strittmatter, J. Dijkmans, I. Vervest, T. Van Hoegaerden, B. Egle, M. P. Mower, Z. Liu, Z. Cao, X. He, L. Chen, L. Qin, H. Tan, J. Yan, N. L. Cunière, C. S. Wei, V. Vuyyuru, R. Ayothiraman, S. Rangaswamy, M. Jaleel, R. Vaidyanathan, M. D. Eastgate, R. Klep, C. Benhaïm, I. Vogels, K. Peeters and S. Lemaire, Toward the Development of a Manufacturing Process for Milvexian: Scale-Up Synthesis of the Side Chain, Org. Process Res. Dev., 2023, 27, 680–691.
3. K. Wang, L. Han, J. Mustakis, B. Li, J. Magano, D. B. Damon, A. Dion, M. T. Maloney, R. Post and R. Li, Kinetic and Data-Driven Reaction Analysis for Pharmaceutical Process Development, Ind. Eng. Chem. Res., 2020, 59, 2409–2421.
4. V. Farina, How to Develop Organometallic Catalytic Reactions in the Pharmaceutical Industry, Org. Process Res. Dev., 2023, 27, 831–846.
5. L. Schrecker, J. Dickhaut, C. Holtze, P. Staehle, M. Vranceanu, K. Hellgardt and K. K. Hii, Discovery of unexpectedly complex reaction pathways for the Knorr pyrazole synthesis via transient flow, React. Chem. Eng., 2023, 8, 41–46.
6. B. Wei, J. C. Sharland, P. Lin, S. M. Wilkerson-Hill, F. A. Fullilove, S. McKinnon, D. G. Blackmond and H. M. L. Davies, In Situ Kinetic Studies of Rh(II)-Catalyzed Asymmetric Cyclopropanation with Low Catalyst Loadings, ACS Catal., 2020, 10, 1161–1170.
7. R. D. Baxter, D. Sale, K. M. Engle, J. Q. Yu and D. G. Blackmond, Mechanistic rationalization of unusual kinetics in Pd-catalyzed C-H olefination, J. Am. Chem. Soc., 2012, 134, 4600–4606.
8. D. C. Braddock, B. C. Rowley, P. D. Lickiss, S. J. Fussell, R. Qamar, D. Pugh, H. S. Rzepa and A. J. P. White, On the Use of Triarylsilanols as Catalysts for Direct Amidation of Carboxylic Acids, J. Org. Chem., 2023, 88, 9853–9869.
9. O. J. Newton, K. Hellgardt, J. Richardson and K. K. M. Hii, Homeopathic’ palladium catalysis? The observation of distinct kinetic regimes in a ligandless Heck reaction at (ultra-)low catalyst loadings, J. Catal., 2023, 424, 29–38.
10. J. I. Higham and J. A. Bull, Amine-Catalyzed Copper-Mediated C-H Sulfonylation of Benzaldehydes via a Transient Imine Directing Group, Angew. Chem., Int. Ed., 2022, 61, e202202933.
11. M. Á. de Carvalho Servia, I. O. Sandoval, D. Zhang, K. Hellgardt, K. K. M. Hii and A. del Rio Chanona, Automated Kinetic Model Discovery – A Methodological Framework, Comput.-Aided Chem. Eng., 2023, 52, 33–38.
12. V. A. C. Saltão, J. W. Thybaut, L. Pirro, F. G. Freire and P. S. F. Mendes, Automation of Data-Driven Rate Equation Screening for Heterogeneously Catalyzed Reactions, Ind. Eng. Chem. Res., 2022, 61, 13841–13853.
13. B. G. Cox, in Modern Liquid Phase Kinetics, Oxford University Press, Oxford, 1994, p. 27.
14. E. C. Brigham and G. J. Meyer, Ostwald isolation to determine the reaction order for TiO 2(e-)|S+↔ TiO2|S charge recombination at sensitized TiO2 interfaces, J. Phys. Chem. C, 2014, 118, 7886–7893.
15. S. Zhang, J. Zhang and H. Zou, C(sp3)-H oxygenation via alkoxypalladium(ii) species: an update for the mechanism, Chem. Sci., 2022, 13, 1298–1306.
16. J. H. Espenson, O. Pestovsky, P. Huston and S. Staudt, Organometallic Catalysis in Aqueous Solution: Oxygen Transfer to Bromide, J. Am. Chem. Soc., 1994, 116(7), 2869–2877.
17. I. W. Ashworth, L. Frodsham, P. Moore and T. O. Ronson, Evidence of Rate Limiting Proton Transfer in an SNAr Aminolysis in Acetonitrile under Synthetically Relevant Conditions, J. Org. Chem., 2022, 87, 2111–2119.
18. M. C. Deem, I. Cai, J. S. Derasp, P. L. Prieto, Y. Sato, J. Liu, A. J. Kukor and J. E. Hein, Best Practices for the Collection of Robust Time Course Reaction Profiles for Kinetic Studies, ACS Catal., 2023, 13(2), 1418–1430.
19. C. Alamillo-Ferrer, G. Hutchinson and J. Burés, Mechanistic interpretation of orders in catalyst greater than one, Nat. Rev. Chem, 2023, 7, 26–34.
20. D. G. Blackmond, Reaction progress kinetic analysis: a powerful methodology for mechanistic studies of complex catalytic reactions, Angew. Chem., Int. Ed., 2005, 44, 4302–4320.
21. M. J. Ardolino and J. P. Morken, Congested C-C bonds by Pd-catalyzed enantioselective allyl-allyl cross-coupling, a mechanism-guided solution, J. Am. Chem. Soc., 2014, 136, 7092–7100.
22. H. Xue, D. Jiang, H. Jiang, C. W. Kee, H. Hirao, T. Nishimura, M. W. Wong and C. H. Tan, Mechanistic Insights into Bicyclic Guanidine-Catalyzed Reactions from Microscopic and Macroscopic Perspectives, J. Org. Chem., 2015, 80(11), 5745–5752.
23. S. P. Mathew, M. Klussmann, H. Iwamura, D. H. Wells, A. Armstrong and D. G. Blackmond, A mechanistic rationalization of unusual kinetic behavior in proline-mediated C-O and C-N bond-forming reactions, Chem. Commun., 2006, 4291–4293.
24. J. Burés, A Simple Graphical Method to Determine the Order in Catalyst, Angew. Chem., Int. Ed., 2016, 128, 2068–2071.
25. J. Burés, Variable Time Normalization Analysis: General Graphical Elucidation of Reaction Orders from Concentration Profiles, Angew. Chem., Int. Ed., 2016, 55, 16084–16087.
26. G. Durin, A. Fontaine, J. Berthet, E. Nicolas, P. Thuéry and T. Cantat, Metal-Free Catalytic Hydrogenolysis of Silyl Triflates and Halides into Hydrosilanes, Angew. Chem., Int. Ed., 2022, 134, 1–5.
27. D. M. Day, T. J. Farmer, J. Granelli, J. H. Lofthouse, J. Lynch, C. R. McElroy, J. Sherwood, S. Shimizu and J. H. Clark, Reaction Optimization for Greener Chemistry with a Comprehensive Spreadsheet Tool, Molecules, 2022, 27, 1–12.
28. M. Scott, A. Sud, E. Boess and M. Klussmann, Reaction progress kinetic analysis of a copper-catalyzed aerobic oxidative coupling reaction with N-phenyl tetrahydroisoquinoline, J. Org. Chem., 2014, 79, 12033–12040.
29. S. B. Kedia and M. B. Mitchell, Reaction progress analysis: powerful tool for understanding suzuki-miyaura reaction and control of polychlorobiphenyl impurity, Org. Process Res. Dev., 2009, 13, 420–428.
30. F. V. Ryzhkov, Y. E. Ryzhkova and M. N. Elinson, Python in Chemistry: Physicochemical Tools, Processes, 2023, 11(10), 2897.
31. C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Reaction mechanism generator: automatic construction of chemical kinetic mechanisms, Comput. Phys. Commun., 2016, 203, 212–225.
32. B. M. Matysiak, D. Thomas and L. Cronin, Reaction Kinetics using a Chemputable Framework for Data Collection and Analysis, Angew. Chem., Int. Ed., 2024, 63, e2023152.
33. M. Á. de Carvalho Servia, I. O. Sandoval, K. K. M. Hii, K. Hellgardt, D. Zhang and E. Antonio del Rio Chanona, The automated discovery of kinetic rate models – methodological frameworks, Digital Discovery, 2024, 3, 954–968.
34. S. Clark, Kinalite Example, https://gitlab.com/heingroup/kinalite_example/-/blob/master/main.py.
35. S. Clark, Kinalite 0.0.6, https://pypi.org/project/kinalite/.
36. F. Bork, S. Clark, P. Burland, D. Sale and J. Hein, Kinalite A User-Friendly Online Tool for Automated Variable Time Normalization Analysis (VTNA), chemRxiv, 2024, preprint,  DOI:10.26434/chemrxiv-2024-m15pr.
37. C. D. T. Nielsen and J. Burés, Visual kinetic analysis, Chem. Sci., 2019, 10, 348–353.
38. J. Xia, T. Hirai, S. Katayama, H. Nagae, W. Zhang and K. Mashima, Mechanistic Study of Ni and Cu Dual Catalyst for Asymmetric C-C Bond Formation; Asymmetric Coupling of 1,3-Dienes with C-nucleophiles to Construct Vicinal Stereocenters, ACS Catal., 2021, 11, 6643–6655.
39. G. Tran, W. Shao and C. Mazet, Ni-Catalyzed Enantioselective Intermolecular Hydroamination of Branched 1,3-Dienes Using Primary Aliphatic Amines, J. Am. Chem. Soc., 2019, 141, 14814–14822.
40. Z. W. Davis-Gilbert, X. Wen, J. D. Goodpaster and I. A. Tonks, Mechanism of Ti-Catalyzed Oxidative Nitrene Transfer in [2 + 2 + 1] Pyrrole Synthesis from Alkynes and Azobenzene, J. Am. Chem. Soc., 2018, 140, 7267–7281.
41. D. Antermite, A. J. P. White, L. Casarrubios and J. A. Bull, On the Mechanism and Selectivity of Palladium-Catalyzed C(sp3)-H Arylation of Pyrrolidines and Piperidines at Unactivated C4 Positions: Discovery of an Improved Dimethylaminoquinoline Amide Directing Group, ACS Catal., 2023, 13, 9597–9615.
42. T. P. Pabst, J. V. Obligacion, É. Rochette, I. Pappas and P. J. Chirik, Cobalt-Catalyzed Borylation of Fluorinated Arenes: Thermodynamic Control of C(sp2)-H Oxidative Addition Results in ortho-to-Fluorine Selectivity, J. Am. Chem. Soc., 2019, 141, 15378–15389.
43. K. Murray, S. Müller and B. A. Turlach, Revisiting fitting monotone polynomials to data, Comput. Stat., 2013, 28, 1989–2005.
44. J. J. Bon, K. Murray and B. A. Turlach, Fitting monotone polynomials in mixed effects models, Stat. Comput., 2019, 29, 79–98.
45. D. Schmitz, Polyfit, https://polyfit.readthedocs.io/en/latest/, accessed 13 October 2023.
46. D. M. Day, T. J. Farmer, J. Sherwood and J. H. Clark, An experimental investigation into the kinetics and mechanism of the aza-Michael additions of dimethyl itaconate, Tetrahedron, 2022, 121, 132921.
47. PySimpleGUI User Interfaces For Humans, https://www.pysimplegui.org/en/latest/, accessed 5 January 2024.
48. A. Matviitsuk, M. D. Greenhalgh, D. B. Antúnez, A. M. Z. Slawin and A. D. Smith, Aryloxide-Facilitated Catalyst Turnover in Enantioselective α,β-Unsaturated Acyl Ammonium Catalysis, Angew. Chem., Int. Ed., 2017, 129, 12450–12455.
49. C. Margarita, P. Villo, H. Tuñon, O. Dalla-Santa, D. Camaj, R. Carlsson, M. Lill, A. Ramström and H. Lundberg, Zirconium-catalysed direct substitution of alcohols: enhancing the selectivity by kinetic analysis, Catal. Sci. Technol., 2021, 11, 7420–7430.
50. Y. Nishii, M. Ikeda, Y. Hayashi, S. Kawauchi and M. Miura, Triptycenyl Sulfide: A Practical and Active Catalyst for Electrophilic Aromatic Halogenation Using N-Halosuccinimides, J. Am. Chem. Soc., 2020, 142, 1621–1629.
51. C. Pfeffer, N. Wannenmacher, W. Frey and R. Peters, Stereo- and regioselective dimerization of alkynes to enynes by bimetallic syn-carbopalladation, ACS Catal., 2021, 11, 5496–5505.
52. S. M. Smith, M. D. Greenhalgh, T. Feoktistova, D. M. Walden, J. E. Taylor, D. B. Cordes, A. M. Z. Slawin, P. H. Y. Cheong and A. D. Smith, Scope, Limitations and Mechanistic Analysis of the HyperBTM-Catalyzed Acylative Kinetic Resolution of Tertiary Heterocyclic Alcohols, Eur. J. Org Chem., 2022, e202101111.
53. S. Aikonen, M. Muuronen, T. Wirtanen, S. Heikkinen, J. Musgreave, J. Burés and J. Helaja, Gold(I)-Catalyzed 1,3-O-Transposition of Ynones: Mechanism and Catalytic Acceleration with Electron-Rich Aldehydes, ACS Catal., 2018, 8, 960–967.
54. M. R. Elsby, M. Son, C. Oh, J. Martin, M. H. Baik and R. T. Baker, Mechanistic Study of Metal-Ligand Cooperativity in Mn(II)-Catalyzed Hydroborations: Hemilabile SNS Ligand Enables Metal Hydride-Free Reaction Pathway, ACS Catal., 2021, 11, 9043–9051.
55. D. C. Braddock, B. M. J. Lancaster, C. J. Tighe and A. J. P. White, Surmounting Byproduct Inhibition in an Intermolecular Catalytic Asymmetric Alkene Bromoesterification Reaction as Revealed by Kinetic Profiling, J. Org. Chem., 2023, 88, 8904–8914.
56. J. H. Herbort, R. F. Lalisse, C. M. Hadad and T. V. Rajanbabu, Cationic Co(I) Catalysts for Regiodivergent Hydroalkenylation of 1,6-Enynes: An Uncommon cis-β-C-H Activation Leads to Z-Selective Coupling of Acrylates, ACS Catal., 2021, 11, 9605–9617.
57. E. Antico, M. Leutzsch, N. Wessel, T. Weyhermüller, C. Werlé and W. Leitner, Selective oxidation of silanes into silanols with water using [MnBr(CO)5] as a precatalyst, Chem. Sci., 2022, 14, 54–60.
58. T. C. Malig, D. Yu and J. E. Hein, A Revised Mechanism for the Kinugasa Reaction, J. Am. Chem. Soc., 2018, 140, 9167–9173.
59. C. J. C. Cooze, W. McNutt, M. D. Schoetz, B. Sosunovych, S. Grigoryan and R. J. Lundgren, Diastereo-, Enantio-, and Z-Selective α,δ-Difunctionalization of Electron-Deficient Dienes Initiated by Rh-Catalyzed Conjugate Addition, J. Am. Chem. Soc., 2021, 143, 10770–10777.
60. I. Smajlagic, B. White, O. Azeez, M. Pilkington and T. Dudding, Organocatalysis Linked to Charge-Enhanced Acidity with Superelectrophilic Traits, ACS Catal., 2022, 12, 1128–1138.
61. S. D. Mendoza, M. Rombola, Y. Tao, S. J. Zuend, R. Götz, M. J. McLaughlin and S. E. Reisman, Expanding the Chiral Monoterpene Pool: Enantioselective Diels-Alder Reactions of α-Acyloxy Enones, Org. Lett., 2022, 24, 3802–3806.
62. P. St. Onge, S. I. Khan, A. Cook and S. G. Newman, Reductive Cleavage of C(sp2)-CF3 Bonds in Trifluoromethylpyridines, Org. Lett., 2023, 25, 1030–1034.
63. C. McLaughlin, A. M. Z. Slawin and A. D. Smith, Base-free Enantioselective C(1)-Ammonium Enolate Catalysis Exploiting Aryloxides: A Synthetic and Mechanistic Study, Angew. Chem., Int. Ed., 2019, 131, 15255–15263.
64. V. Czitrom, One-factor-at-a-Time versus Designed Experiments, Am. Statistician, 1999, 53, 126–131.

---

Footnotes

† For any use of Auto-VTNA, the seminal paper by Búres should also be cited along with this paper.²⁵

‡ Electronic supplementary information (ESI) available: Range of interests and levels of detail for Auto-VTNA from those wishing to use the Auto-VTNA GUI to those developing their own software in this research space. Sections include details on: the theory of VTNA; choices in the development of Auto-VTNA; algorithmic efficiency analysis; best practice for the reporting of order values and interpreting overlay scores; a user guide to the Auto-VTNA code; a user guide to the Auto-VTNA Calculator GUI; appendices including overlay graphs of all reactions in Table 2, more complex examples, and simulated data. A tutorial video for the Auto-VTNA Calculator GUI is also available, linked from https://github.com/ddalland/Auto-VTNA. See DOI: https://doi.org/10.1039/d4dd00111g

---