Open Access Article
Open Access ArticleOM-Diff: inverse-design of organometallic catalysts with guided equivariant denoising diffusion†
François
Cornet
 a,
Bardi
Benediktsson
a,
Bardi
Benediktsson
 b,
Bjarke
Hastrup
b,
Mikkel N.
Schmidt
b,
Bjarke
Hastrup
b,
Mikkel N.
Schmidt
 a and
Arghya
Bhowmik
a and
Arghya
Bhowmik
 *b
*b
aDepartment of Applied Mathematics and Computer Science, Technical University of Denmark, Kgs. Lyngby 2800, Denmark. E-mail: frjc@dtu.dk
bDepartment of Energy Conversion and Storage, Technical University of Denmark, Kgs. Lyngby 2800, Denmark. E-mail: arbh@dtu.dk
First published on 23rd July 2024
Abstract
Organometallic complexes are ubiquitous in numerous technological applications, and in particular in homogeneous catalysis. Optimization of such complexes for specific applications is challenging due to the large variety of possible metal–ligand combinations and ligand–ligand interactions. Here we present OM-Diff, an inverse-design framework based on a diffusion generative model for in silico design of such complexes. Due to the importance of the spatial structure of a catalyst, the model operates on all-atom (including H) representations in 3D space. To handle the symmetries inherent to that data representation, OM-Diff combines an equivariant diffusion model with an equivariant property predictor. The diffusion model generates ligands conditioned on a specified metal-center, while the property predictor guides the generation towards novel complexes with desired properties. We demonstrate the potential of OM-Diff by designing optimized catalysts for a family of cross-coupling reactions, and validating a selection of novel proposed compounds with DFT calculations.
1 Introduction
Organometallic complexes are ubiquitous in numerous application areas such as energy, medicine, functional materials, sensors, or optical devices. They are designed for therapeutics as metallodrugs,1 can be used to form specialty polymers,2 to make organic light emitting materials,3 as photovoltaic materials,4 are used in batteries5 or as sensors.6 Importantly, organometallics are also widely used in catalytic processes, in particular in homogeneous catalysis, and are crucial for many industrial chemical reactions, such as hydrogenation,7 hydroformylation,8 olefin metathesis,9 or cross-coupling reactions (e.g., Suzuki,10 Heck,11 and Stille12 reactions). In silico catalyst design is a grand chemical challenge,13,14 and the combination of machine learning (ML) and quantum chemistry (QC) methods is an appealing strategy for such endeavor.15Augmenting conventional high-throughput screening workflows with machine learned predictive models16 is a common approach. Comprehensive overviews of the role of ML predictive models in the computational discovery of organometallic complexes can be found in the review of Kulik et al.,17 and in the perspective of Aspuru-Guzik et al.18 for the specific case of homogeneous catalysis. In general, the usual workflow consists of an initial training phase on a moderately-sized database of representative examples,19–25 followed by a screening campaign on a large virtual library containing similar compounds.26,27 The screening library is usually constructed based on the chemical intuition of the practitioner, e.g. by combinatorial enumeration of pre-defined building blocks,26,27 or via systematical functionalization of a starting scaffold.28 ML models offer fast property evaluation while preserving an accuracy nearly identical to that of the reference method.
A more recent paradigm29 attempts to move beyond chemical intuition and systematical enumeration by using generative models to learn the distribution of the chemical space of interest in a data-driven way.30 Novel complexes that share aggregate properties with the training data can in turn be generated by sampling from the model. When combined with predictive modelling, generative models open the door to the inverse-design of materials and molecules with optimised properties, i.e. goal-directed generation.31 Homogeneous catalysts are molecular in nature, and numerous generative models for molecules have been proposed in the literature.32 Existing models mainly differ by the data representation and the generative paradigm they employ. Strings33,34 and molecular graphs are the most extensively used representations. On these geometry-free representations, common approaches include Generative Adversarial Networks (GAN),35,36 auto-regressive models,37,38 Variational Auto-Encoders (VAE),39–42 or Reinforcement Learning.43–45 Genetic Algorithms (GA)46,47 are a notable exception that does not involve learning but instead evolves a population of candidates via a set of predefined operations. Due to the importance of spatial information in molecular properties, another line of work has focused on the generation of 3D structures, as point clouds48,49 or voxels.50 Instead of relying on external software51–53 to map the generated geometry-free descriptors to possible conformations, these models28,48–50,54,55 directly output structures in 3D space. Among the different generative paradigms, diffusion models56,57 on point clouds48 have emerged as particularly promising. Their expressivity, resulting from a series of (simple) transformations with shared parameters that map the prior distribution to the data distribution, combined with the possibility of leveraging architectural advances in neural network force fields58 are supposedly two reasons behind this success. Since the introduction of the equivariant diffusion model for molecules,48 multiple further developments have been done to tackle various related problems such as conformer generation,59,60 transition-state generation,61,62 linker design,63 structure-based design,64 target-aware design,65 or molecular docking.66 For the specific task of molecular inverse-design, conditional diffusion48 and guidance67 constitute the two principal approaches, and in particular guidance was recently demonstrated to be practically effective.68 The success of diffusion models at inverse-design has not been limited to point cloud representations, but also to image representations encoding microstructures69 and zeolites.70
1.1 Contributions
In this work, we introduce OM-Diff, a generic inverse-design framework for generating organometallic complexes with optimized properties. Given the importance of geometry in catalytic activity, our framework operates on 3D atomistic structures. At its core, OM-Diff implements an equivariant diffusion model generating ligands conditioned on a fixed geometric description of the center. To perform inverse-design, an auxiliary equivariant property predictor steers the generative process of the diffusion model towards properties of interest via a guidance mechanism. Compared to a property-conditional generative model, guidance limits the amount of expensive task-specific labeled data required (e.g. energy barriers for a particular reaction) to what is needed for obtaining a surrogate model of satisfactory accuracy, and enables unconditional training over large relevant databases.21–23 To demonstrate the potential of OM-Diff, we inverse-design organometallic catalysts for a family of cross-coupling reactions.26 The corresponding workflow is depicted in Fig. 1.We summarize our contributions as follows:
• We propose OM-Diff, a framework that implements a 3D equivariant diffusion generative model, specifically designed for organometallic complexes, combined with an equivariant property predictor to perform regressor-guidance, and sample novel complexes with targeted properties;
• We analyze several key design choices needed to attain a practical performance level, such as treating the center as contextual information, and varying the expressivity of the denoising neural network architecture;
• For the specific problem of optimizing a critical step in a family of cross-coupling reactions, we close the loop by validating a selection of generated complexes using DFT calculations, and identify several novel compounds of potential interest.
1.2 Related work
Existing generative models that have been successfully applied to catalyst optimization are based on geometry-free representations. Most notably, GA71–74 have proven very effective when coupled with a reliable and reasonably cheap fitness function. A VAE operating on SMILES42 has also shown promises. While concurrent work75 similarly leverages an equivariant diffusion model to perform scaffold-conditioned ligand design for organometallic complexes, OM-Diff constitutes, to the best of our knowledge, the first76 complete inverse-design framework based on equivariant diffusion for organometallic catalysts. Methodologically, OM-Diff bears similarities with previous work in different application areas. The 3D-conditioning mechanism employed in OM-Diff resembles that introduced in DiffSBDD64 and in DiffLinker,63 where an equivariant diffusion model also generates ligands conditioned on a fixed geometric context. In terms of inverse-design, the closest framework in the literature is GauDi,68 where property-conditioned generation is performed similarly using the guidance mechanism proposed by Bao et al.67 Compared to GauDi, OM-Diff is conditioned on the 3D geometry of the center, operates on all-atom representations instead of coarse-grained graphs of fragments, and targets a different chemical space (organic molecules vs. organometallic complexes). In summary, the combination of the 3D conditioning on the center, the guidance mechanism and target application is what delineates OM-Diff from previous work.2 Methods
2.1 Problem statement
The goal of OM-Diff is to inverse-design novel organometallic complexes, that we refer to as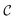 , with desired properties, that we denote y. We frame this task as a conditional sampling problem, where we aim to sample from the conditional distribution
, with desired properties, that we denote y. We frame this task as a conditional sampling problem, where we aim to sample from the conditional distribution  . We approximate the conditional distribution,
. We approximate the conditional distribution, 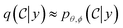 , by combining an unconditional diffusion model,
, by combining an unconditional diffusion model, 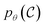 , with a property predictor
, with a property predictor 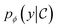 .
.
2.2 Outline
In Section 2.3, we introduce how organometallic complexes are represented in practice, i.e. the data representation that the different models operate on. In Section 2.4, we present the unconditional generative model. Using the unconditional generative model and an auxiliary property predictor, we present in Section 2.5 the guidance procedure for performing conditional sampling. Finally in Section 2.6, we present details about the surrogate model used to screen the complexes sampled from the generative model.
are represented in practice, i.e. the data representation that the different models operate on. In Section 2.4, we present the unconditional generative model. Using the unconditional generative model and an auxiliary property predictor, we present in Section 2.5 the guidance procedure for performing conditional sampling. Finally in Section 2.6, we present details about the surrogate model used to screen the complexes sampled from the generative model.
2.3 Data representation
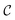 , by two distinct subsets: one with the atoms belonging to the center, denoted
, by two distinct subsets: one with the atoms belonging to the center, denoted  , and the other with the atoms belonging to the ligands, denoted
, and the other with the atoms belonging to the ligands, denoted  . Formally, we write
. Formally, we write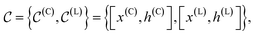 | (1) |
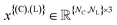 represents the atomic coordinates, and
represents the atomic coordinates, and 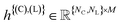 the atom types.
the atom types.
Modelling metal center and ligands separately is motivated by two factors. On one hand, the geometry of the region around the center often has to follow strict (known) rules, and is thereby often fixed. For instance, the square planar geometry is prevalent for transition metal complexes with d8 configuration. This is known and should therefore not be learnt by the model. On the other hand, when generating novel catalysts one wants to have full control over the center in order, for example, to enforce the central atom to be an earth-abundant transition metal. Depending on the problem under study, the positions (x(C)), and/or the compositions (h(C)), or possibly parts thereof, can therefore be fixed and viewed as a form of context around which the ligands should be built.
In our experiments in Section 3, we consider a simple case where only the metal center is fixed and only one coordination pattern is present in the training data. However, the formulation in eqn (1) entails more complicated cases such as centers featuring different coordination patterns, or scaffold-based design where some of the ligands can be also be considered part of the center subset.
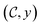 . In our experiments, we specifically consider a case where the target property corresponds to the binding energy of a specific reaction.
. In our experiments, we specifically consider a case where the target property corresponds to the binding energy of a specific reaction.
2.4 Diffusion model for organometallic catalysts
In our framework, the objective of the generative model is to learn an unconditional distribution over organometallic complexes,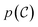 , from which we can readily sample novel complexes. In practice, we implement a tailored extension of the equivariant diffusion model for atomistic point clouds (EDM).48
, from which we can readily sample novel complexes. In practice, we implement a tailored extension of the equivariant diffusion model for atomistic point clouds (EDM).48
Diffusion models56,57 are generative models that include two distinct processes: (1) a fixed diffusion process that iteratively corrupts data points (atomistic structures) towards a known prior distribution (i.e. white noise) through additive noise, and (2) a generative denoising process optimised to reverse the diffusion process. Starting from complete noise, the trained denoising process produces realistic atomistic point clouds through iterative denoising.
 that are increasingly noisy versions of an initial atomistic structure
that are increasingly noisy versions of an initial atomistic structure  ,
, | (2) |
As  is fixed, and transitions are Gaussian, each step is defined as
is fixed, and transitions are Gaussian, each step is defined as
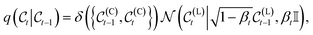 | (3) |
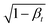 , and (2) being summed with Gaussian noise of variance βt.
, and (2) being summed with Gaussian noise of variance βt.
For large enough T, the terminal distribution of the ligand features (i.e. positions and atom types) becomes data-independent,  . Due to the formulation of the diffusion process in eqn (2) and (3), i.e. Markovianity and Gaussian transitions, any time marginal, or said otherwise distribution of any
. Due to the formulation of the diffusion process in eqn (2) and (3), i.e. Markovianity and Gaussian transitions, any time marginal, or said otherwise distribution of any  given
given 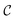 , can be derived analytically as
, can be derived analytically as
 | (4) |
 , and σt is a function of the noise schedule
, and σt is a function of the noise schedule 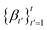 up to time t. This implies that any noisy version of
up to time t. This implies that any noisy version of  ,
, 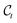 , can then be obtained without the need of going through the whole chain defined in eqn (2),
, can then be obtained without the need of going through the whole chain defined in eqn (2), | (5) |
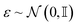 . This formulation reveals particularly useful for learning the generative denoising process.
. This formulation reveals particularly useful for learning the generative denoising process.
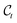 into
into 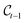 . In what follows, we simplify notations by omitting the Dirac distribution for the center. With access to
. In what follows, we simplify notations by omitting the Dirac distribution for the center. With access to  , the true denoising process is another normal distribution that writes
, the true denoising process is another normal distribution that writes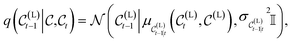 | (6) |
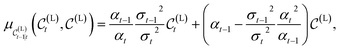 | (7) |
 | (8) |
While the variance of the true denoising process in eqn (8) only depends on the (known) time schedule, the mean in eqn (7) involves  that is unknown at sampling time, as it is what we seek to generate. We therefore learn an approximation to
that is unknown at sampling time, as it is what we seek to generate. We therefore learn an approximation to 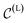 . Using eqn (5), we can rewrite
. Using eqn (5), we can rewrite  , such that
, such that  can now be determined given its current noisy version
can now be determined given its current noisy version  , and the noise ε. The latter is not known but can be approximated using a denoising neural network εθ trained to map
, and the noise ε. The latter is not known but can be approximated using a denoising neural network εθ trained to map  to ε. We can then parameterise our generative model using εθ, as
to ε. We can then parameterise our generative model using εθ, as
 | (9) |
 | (10) |
 by its approximation
by its approximation  in eqn (7). We note that, in addition to
in eqn (7). We note that, in addition to 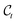 , the denoising neural network εθ is also provided with the time step t to facilitate the learning of a time-dependent function.
, the denoising neural network εθ is also provided with the time step t to facilitate the learning of a time-dependent function.
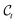 , obtained using eqn (5), and is tasked with predicting the (unscaled) noise ε that was sampled to obtain the corrupted structures, its training objective follows naturally. The parameters of εθ are optimized by the so-called simplified loss objective,77
, obtained using eqn (5), and is tasked with predicting the (unscaled) noise ε that was sampled to obtain the corrupted structures, its training objective follows naturally. The parameters of εθ are optimized by the so-called simplified loss objective,77 | (11) |
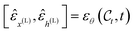 denotes the output of the denoising neural network, and
denotes the output of the denoising neural network, and  is the noise sampled to form
is the noise sampled to form 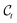 according to eqn (5).
according to eqn (5).
εθ([Rxx + tx,h],t) = [Rx![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) x(L), x(L),![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) h(L)] h(L)] | (12) |
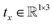 denotes any vector, and
denotes any vector, and  denotes any orthogonal (rotation/reflection) matrix.
denotes any orthogonal (rotation/reflection) matrix.
![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) h(L), while the final vectorial states are aggregated in a single vector
h(L), while the final vectorial states are aggregated in a single vector ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) x(L). More details about the neural network architecture are given in Section S1.2.†
x(L). More details about the neural network architecture are given in Section S1.2.†
 should be invariant under rigid transformations. In other words, all possible orientations of a given complex should have the same probability of being sampled. Rotation invariance is ensured by the combination of the rotation-equivariant architecture of εθ, and the isotropic Gaussian prior and transition distributions.59 Translation invariance can be ensured by the translation-invariant architecture of εθ, and by having a prior and transition distributions over atomistic positions with fixed center of mass,
should be invariant under rigid transformations. In other words, all possible orientations of a given complex should have the same probability of being sampled. Rotation invariance is ensured by the combination of the rotation-equivariant architecture of εθ, and the isotropic Gaussian prior and transition distributions.59 Translation invariance can be ensured by the translation-invariant architecture of εθ, and by having a prior and transition distributions over atomistic positions with fixed center of mass, 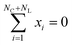 . Alternatively, translation invariance can be ensured by keeping the position of the metal center fixed, which is what we do.
. Alternatively, translation invariance can be ensured by keeping the position of the metal center fixed, which is what we do.
 – possibly composed of multiple atoms, by drawing it from an empirical distribution over centers;‡ (2) we then sample the number of remaining atoms that will compose the ligands given the center,
– possibly composed of multiple atoms, by drawing it from an empirical distribution over centers;‡ (2) we then sample the number of remaining atoms that will compose the ligands given the center,  ; (3) we sample the initial positions and atom types of the ligand atoms,
; (3) we sample the initial positions and atom types of the ligand atoms,  ; (4) we finally employ the trained denoising neural network εθ, and execute the standard ancestral sampling procedure by iteratively applying eqn (9).
; (4) we finally employ the trained denoising neural network εθ, and execute the standard ancestral sampling procedure by iteratively applying eqn (9).
2.5 Regressor guidance
So far, we have introduced the necessary tools for learning a generative model from which novel atomistic structures can be sampled unconditionally. When performing inverse-design, we are interested in being able to sample novel atomistic structures with optimised properties, i.e. sample from . In this section, we present a procedure, named regressor-guidance, for performing conditional sampling using a pretrained unconditional generative model presented in Section 2.4 combined with an auxiliary property predictor.
. In this section, we present a procedure, named regressor-guidance, for performing conditional sampling using a pretrained unconditional generative model presented in Section 2.4 combined with an auxiliary property predictor.
 | (13) |
 is the unconditional denoising process from eqn (9), and
is the unconditional denoising process from eqn (9), and  is a conditional distribution over properties induced by a property predictor yϕ. Here, we define
is a conditional distribution over properties induced by a property predictor yϕ. Here, we define 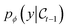 in terms of an energy function,
in terms of an energy function,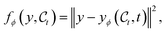 | (14) |
 . This formula is also similar to that of loss-guided diffusion (LGD),83 with a loss function that includes a learnt component, i.e. yϕ. The conditional denoising process from eqn (13) writes as a corrected version of the unconditional denoising process defined in eqn (9),
. This formula is also similar to that of loss-guided diffusion (LGD),83 with a loss function that includes a learnt component, i.e. yϕ. The conditional denoising process from eqn (13) writes as a corrected version of the unconditional denoising process defined in eqn (9), | (15) |
 | (16) |
The correction is obtained by evaluating the gradient of fϕ with respect to the mean predicted by the unconditional model. In practice, sampling from the conditional distribution amounts to first evaluating the mean of the unconditional distribution, then evaluating the energy function in eqn (14) using the estimated mean, and finally computing the correction expressed as the gradient of eqn (14) with respect to  .
.
 , given
, given  a noisy version thereof. This implies that yϕ should be trained on noisy structures obtained with the same diffusion process as that of the generative model. In practice, the prediction task becomes very difficult when t → T, as the input structures are close to pure noise. To limit the negative influence of the noisiest structures on the learning process, a solution is to resort to a robust objective function such as the Huber loss
a noisy version thereof. This implies that yϕ should be trained on noisy structures obtained with the same diffusion process as that of the generative model. In practice, the prediction task becomes very difficult when t → T, as the input structures are close to pure noise. To limit the negative influence of the noisiest structures on the learning process, a solution is to resort to a robust objective function such as the Huber loss | (17) |
 denotes the model prediction.
denotes the model prediction.
 . We consequently parameterise the property predictor yϕ in eqn (14) with a neural network, that features an encoder similar to that of the denoising neural network εθ, i.e. that maintains and updates a set of scalar and vectorial states for each atom. The encoder is followed by a readout layer that aggregates the final scalar states into a sole complex-level state using an attention mechanism. That aggregated state is in turn passed to a fully-connected neural network outputting the predicted value of y.
. We consequently parameterise the property predictor yϕ in eqn (14) with a neural network, that features an encoder similar to that of the denoising neural network εθ, i.e. that maintains and updates a set of scalar and vectorial states for each atom. The encoder is followed by a readout layer that aggregates the final scalar states into a sole complex-level state using an attention mechanism. That aggregated state is in turn passed to a fully-connected neural network outputting the predicted value of y.
 | (18) |
Open-ended target conditioning can also be achieved by altering eqn (14). An instance of suitable energy function can be  , where s = 1 in the case of a minimization and s = −1 in the case of a maximization.
, where s = 1 in the case of a minimization and s = −1 in the case of a maximization.
2.6 Screening surrogate
Once samples have been generated, it is not feasible to evaluate all of them using DFT calculations. We therefore employ a surrogate model for screening the generated samples, before running further calculations with DFT on the most promising candidates. The screening surrogate shares the same architecture as the time-conditioned regressor presented in Section 2.5, but without time input. We are interested in having a surrogate that behaves well over the whole property space, and avoids very large errors, as those could lead to missed candidates, or unfruitful expensive DFT calculations. We consequently train the screening surrogate with a loss function that penalizes large errors more. In particular, we resort to the reverse Huber loss84 which, compared to eqn (17), apply the L2-norm to outliers.3 Experiments and results
As a test bench for OM-Diff, we choose the inverse-design of organometallic catalysts for cross-coupling reactions. This family of reactions constitutes an interesting case study for OM-Diff for two reasons: (1) its practical relevance, and (2) the compelling literature showing that relevant catalysts can be searched through optimization of a binding energy that acts as a proxy for the actual catalytic activity.853.1 Practical relevance
As mentioned in the Introduction, cross-coupling reactions are important in several fields. They are crucial in the synthesis of various organic molecules, as they enable facile formation of carbon–carbon (C–C) and carbon–heteroatom (C–N, C–O, C–S, etc.) bonds. Examples of applications of the compounds synthesized by cross-coupling include active pharmaceutical ingredients,86 organic semiconductors,87 and conductive polymers.88 Cross-coupling reactions can be made to be environmentally friendly, as it is possible to utilize catalytic systems that minimize waste and avoid the use of toxic reagents. Furthermore, the Suzuki cross-coupling reaction enables the formation of carbon–carbon bonds by coupling olefins with organoboron compounds under mild conditions. This method is popular due environmental friendliness, using less toxic and more stable reagents, thereby aligning with principles of green chemistry. The importance of the Suzuki cross-coupling reaction is perhaps best demonstrated by the fact that it led to the inventors to receive the 2010 Nobel prize in chemistry.89,903.2 Volcano plots
The Suzuki reaction is part of a larger family of cross-coupling reactions (Suzuki, Kumada, Negishi, Stille and Hiyama)91,92 – whose cycle is generically represented in Fig. 2a, where the leaving group is usually a halide (represented by an X in Fig. 2a). The five reactions differ by the nature of the cross-coupling partner (represented by Y in Fig. 2a). As Corminboeuf et al.26,85 proposed, the rate limiting step of these reactions can be described with volcano plots. Although not common in homogeneous catalysis, volcano plots have proved to be very useful in heterogeneous catalysis. Volcano plots for the cross-coupling reactions under study have been shown to be similar,92 differing only by the width of the plateau region. The Hiyama reaction has widest plateau region spanning [−82.2, 2.0] kcal mol−1, while the region of interest for the Suzuki reaction is only between −32.1 and −23.0 kcal mol−1. The other reactions have a plateau region lying in between that of the two aforementioned reactions. As a consequence, catalysts that bind too strongly or too weakly for the Suzuki reaction might still be efficient for other cross-coupling reaction variants. Using volcano plots, the reaction energy of the oxidative addition process, highlighted in blue in Fig. 2a, can be used as a descriptor to estimate catalytic activity.26,92 This approximation allows for faster screening of candidates, since the whole catalytic cycle does not need to be explored. All possible catalyst candidates should sit on the volcano plateau, or near the top.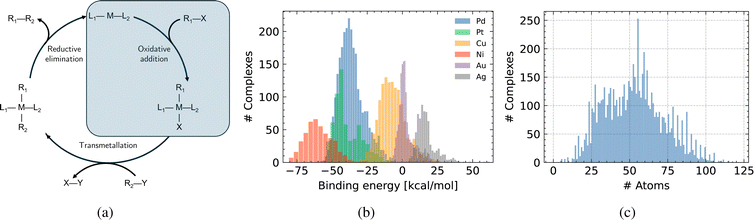 | ||
| Fig. 2 (a) Reaction under study in this work—the model generates L1–M–L2 and optimises the reaction energy of the oxidative addition. (b) Distribution of binding energy in the considered dataset.26 (c) Distribution of number of atoms in the considered dataset.26 On average complexes are composed of 53 atoms. | ||
3.3 Dataset
We perform our experiments using the DFT-level subset of the C–C cross-coupling database.26 In the database, each catalyst is an inorganic complex made of a metal center that binds to two ligands, as L1–M–L2 with M ∈ {Ni, Pd, Pt, Cu, Ag, Au}. The ligands L1 and L2 can either be identical or different. In addition to the aforementioned DFT-level subset, the database also contains geometries of all the possible combinations of metals and ligands at the MMFF-level of theory,93 that is, 6 metal centers with 91 distinct ligands. This makes for a total of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 116 possible combinations. However, in the database, optimized geometries and the corresponding oxidative addition binding energies were computed with DFT for around 7000 complexes. Those complexes cover the 6 different metal centers, and 72 unique ligands (all depicted in Fig. S16 and S17†). Pd is the only metal present with all possible ligands, while the other metals are only combined with a limited number thereof. An overview of the metal–ligand combinations present in the data is provided in Fig. S15.† Although DFT relaxed geometries and binding energies are available for around 7000 complexes, the diversity of the data is limited because only 72 ligands, or building blocks, were used. The binding energies are for the oxidative addition reaction of the substrate with the transition metal, depicted in blue in Fig. 2a. The corresponding distribution across the dataset is illustrated in Fig. 2b.
116 possible combinations. However, in the database, optimized geometries and the corresponding oxidative addition binding energies were computed with DFT for around 7000 complexes. Those complexes cover the 6 different metal centers, and 72 unique ligands (all depicted in Fig. S16 and S17†). Pd is the only metal present with all possible ligands, while the other metals are only combined with a limited number thereof. An overview of the metal–ligand combinations present in the data is provided in Fig. S15.† Although DFT relaxed geometries and binding energies are available for around 7000 complexes, the diversity of the data is limited because only 72 ligands, or building blocks, were used. The binding energies are for the oxidative addition reaction of the substrate with the transition metal, depicted in blue in Fig. 2a. The corresponding distribution across the dataset is illustrated in Fig. 2b.
 ) for Pt complexes. The parameters for the 3-21G basis set were downloaded from the basis set exchange.104 We used the original D3 dispersion correction105 (ORCA keyword
) for Pt complexes. The parameters for the 3-21G basis set were downloaded from the basis set exchange.104 We used the original D3 dispersion correction105 (ORCA keyword  ), as per the original protocol.26 The RIJCOSX approximation106,107 was used to speed up Coulomb and Exchange integrals, with the automatic generation of an auxiliary basis set108 (ORCA keyword
), as per the original protocol.26 The RIJCOSX approximation106,107 was used to speed up Coulomb and Exchange integrals, with the automatic generation of an auxiliary basis set108 (ORCA keyword  ) for calculations that used the 3-21G basis set, and the def2/J auxiliary basis set109 (ORCA keyword
) for calculations that used the 3-21G basis set, and the def2/J auxiliary basis set109 (ORCA keyword  ) for the def2 family of basis sets. For energy evaluations, we performed single point calculations using the Ahlrichs def2 triple-ζ basis set103 (ORCA keyword
) for the def2 family of basis sets. For energy evaluations, we performed single point calculations using the Ahlrichs def2 triple-ζ basis set103 (ORCA keyword 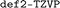 ).
).
3.4 Unconditional generation
We first test the ability of OM-Diff to perform effective unconditional generation of organometallic complexes. This constitutes a prerequisite for effective conditional generation, and is also a valid inverse-design procedure when combined with screening. We evaluate and compare the ability of different ablated versions of OM-Diff to learn the unconditional data distribution. We specifically study two aspects of the generative diffusion model: (1) the modelling of the central region as context around which the model is tasked to build the ligands, and (2) the expressiveness of the neural network architecture.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samples, where the number of atoms is drawn from the empirical distribution displayed in Fig. 2c. Firstly, we evaluate the properties of the generated samples in terms of structural metrics: validity, uniqueness and novelty. Secondly, we compare the samples with the empirical data distribution in terms of the geometry around the metal center M, the binding energy as estimated by a surrogate model, and the composition. For the geometric metrics, we also include metrics computed on the force-field-level subset26 to get an idea of the advantage yielded by a generation in 3D. In Fig. 6b, we additionally compare the distribution of the strain energy at xTB-level110 of the generated compounds, i.e. energy difference between generated structure and xTB-optimised structure. Additional details about the evaluation procedure and the different baselines are provided in Section S2,† where we additionally report the error of the diffusion variants on a held-out set as a function of the noise level Fig. S1.†
000 samples, where the number of atoms is drawn from the empirical distribution displayed in Fig. 2c. Firstly, we evaluate the properties of the generated samples in terms of structural metrics: validity, uniqueness and novelty. Secondly, we compare the samples with the empirical data distribution in terms of the geometry around the metal center M, the binding energy as estimated by a surrogate model, and the composition. For the geometric metrics, we also include metrics computed on the force-field-level subset26 to get an idea of the advantage yielded by a generation in 3D. In Fig. 6b, we additionally compare the distribution of the strain energy at xTB-level110 of the generated compounds, i.e. energy difference between generated structure and xTB-optimised structure. Additional details about the evaluation procedure and the different baselines are provided in Section S2,† where we additionally report the error of the diffusion variants on a held-out set as a function of the noise level Fig. S1.†
| Fixed | Improved εθ | Structural metrics [%] (↑) | Distance to empirical distribution (↓) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Center-proximal geom. | Binding energy [kcal mol−1] | Generated atom types [TV] | |||||||||
| Valid | Valid and unique | Valid, unique and novel | Length [Å], WL1,2–M | Angle [rad], WL1–M–L2 | W ΔE | Center, TVM | Non-center, TVnon-M | Center-proximal, TVprox | |||
| a The TVM is virtually 0 for models that sample directly from the empirical distribution. | |||||||||||
| OM-Diff | ✗ | ✗ | 8.9 | 7.9 | 4.8 | 0.256 | 0.0113 | 0.0044 | 0.347 | 1.036 | 0.079 |
| ✓ | ✗ | 19.6 | 16.4 | 7.5 | 0.165 | 0.0084 | 0.0044 | ≅0.0 | 0.482 | 0.029 | |
| ✗ | ✓ | 18.9 | 17.6 | 11.1 | 0.203 | 0.0089 | 0.0040 | 0.388 | 1.005 | 0.041 | |
| ✓ | ✓ | 28.2 | 23.9 | 11.8 | 0.147 | 0.0079 | 0.0036 | ≅0.0 | 0.593 | 0.019 | |
| Merck molecular force field | — | — | — | 0.814 | 0.0257 | — | — | — | — | ||
 | ||
| Fig. 3 Distribution of (a) metal-centers, (b) non-metal elements, and (c) molecular weight in unconditional sampling. | ||
We hypothesize that the observed improvement is due to a simplified classification task. When inspecting Fig. S1,† we see lower losses on εh and h, especially for larger noise levels. In Table S2,† we can also see that chemical validity is improved, i.e. fixing the center can make up for a less expressive backbone in terms of validity.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 generated. The two proposed modifications yield a substantial improvement, allowing a better modelling of the chemical space under study. With nearly 3000 valid structures out of 10
000 generated. The two proposed modifications yield a substantial improvement, allowing a better modelling of the chemical space under study. With nearly 3000 valid structures out of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, this corresponds to over threefold improved efficiency of valid sample generation. In Fig. 4a, we display validity as a function of the size of the generated complexes. As expected, larger complexes tend to be more difficult to generate than smaller ones. As a molecule is deemed invalid if e.g. the valence of any of its atoms is not respected, validity at complex-level decreases quickly with complex size, even if the atomwise validity is kept constant. In Fig. 4a, we can clearly see that the full OM-Diff is the only variant of the model able to generate larger valid complexes.
000, this corresponds to over threefold improved efficiency of valid sample generation. In Fig. 4a, we display validity as a function of the size of the generated complexes. As expected, larger complexes tend to be more difficult to generate than smaller ones. As a molecule is deemed invalid if e.g. the valence of any of its atoms is not respected, validity at complex-level decreases quickly with complex size, even if the atomwise validity is kept constant. In Fig. 4a, we can clearly see that the full OM-Diff is the only variant of the model able to generate larger valid complexes.
In Table S2,† we provide more details regarding the validity results. We observe that already 50% of the generated structures are deemed invalid due to abnormal pairwise distances, i.e. isolated or clashing atoms. Among the structures passing the distance check, only around 60% can be properly parsed by  ,51i.e. the bonding structure can be inferred without charge and the resulting object contains exactly two fragments corresponding to L1 and L2. This highlights the most recurring failure modes that were observed: disconnected/clashing atoms, and missing protons leading to charged complexes. While an appropriate post-processing procedure, e.g. removing the disconnected fragments or fixing valences, could further increase the effective validity, modelling the bonding information112,113 could help solve connectivity and valence issues at the source.
,51i.e. the bonding structure can be inferred without charge and the resulting object contains exactly two fragments corresponding to L1 and L2. This highlights the most recurring failure modes that were observed: disconnected/clashing atoms, and missing protons leading to charged complexes. While an appropriate post-processing procedure, e.g. removing the disconnected fragments or fixing valences, could further increase the effective validity, modelling the bonding information112,113 could help solve connectivity and valence issues at the source.
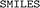 strings and limiting the comparison based on
strings and limiting the comparison based on 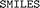 description. Two identical
description. Two identical  strings can actually have been obtained from (slightly) different geometries. Novelty is also observed to remain constant as the number of generated complexes is increased. Interestingly, while OM-Diff clearly yields more valid (and unique) complexes, it is on par in terms of novelty with the variant where the metal-center is not modelled as context. Finally, when looking closer at non-unique complexes, we observe that it is mostly non-novel complexes (i.e. present in the training data) that are generated multiple times. However, the model is also able to generate novel compounds multiple times. In Fig. S3,† we show the number of novel ligands generated as a function of the number of generated complexes. We can see that it steadily increases with the number of complexes generated.
strings can actually have been obtained from (slightly) different geometries. Novelty is also observed to remain constant as the number of generated complexes is increased. Interestingly, while OM-Diff clearly yields more valid (and unique) complexes, it is on par in terms of novelty with the variant where the metal-center is not modelled as context. Finally, when looking closer at non-unique complexes, we observe that it is mostly non-novel complexes (i.e. present in the training data) that are generated multiple times. However, the model is also able to generate novel compounds multiple times. In Fig. S3,† we show the number of novel ligands generated as a function of the number of generated complexes. We can see that it steadily increases with the number of complexes generated.
 is similar to ligand
is similar to ligand  with an extra F atom.
with an extra F atom.
 | ||
| Fig. 6 Cumulative distribution of (a) predictive uncertainty, as estimated by an ensemble of 10 surrogates, evaluated on the samples generated by the different variants of the generative diffusion model; (b) strain energy per atom as estimated by xTB.110 | ||
3.5 Performance of the surrogate models
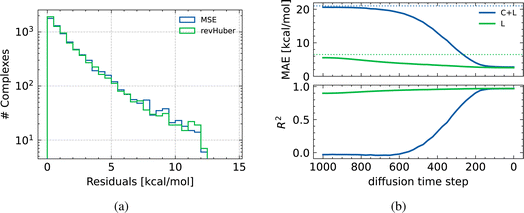
As illustrated in Fig. 1, our framework heavily relies on surrogates trained to approximate DFT-level binding energies. Such models are involved at two different steps: (1) to steer the conditional generation, and (2) to screen and filter final samples prior to DFT computations. It is therefore crucial to evaluate the accuracy of the different surrogates across the chemical space of interest. The range of the binding energy across the dataset, is around 120 kcal mol−1. Following previous work, we consider a model useful if its error is within 5% of that range, i.e. around 5 kcal mol−1. A dummy model that outputs the conditional mean of the dataset gets an average root-mean-squared error of around 8.3 kcal mol−1. To evaluate errors, we perform a stratified 10-fold cross-validation, where folds were designed to keep the proportion of metal centers approximately equal across folds, and to cover the property range uniformly. We compare against two baselines: one based on SLATM,26 and another that trains a neural network surrogate in the latent space of a VAE.42| MAE [kcal mol−1] (↓) | RMSE [kcal mol−1] (↓) | Q95 AE [kcal mol−1] (↓) | Max AE [kcal mol−1] (↓) | R 2 [—] (↑) | |
|---|---|---|---|---|---|
| μ M | 6.49 | 8.50 | — | 41.71 ± 12.38 | — |
| SLATM26 | 2.61 | — | — | — | — |
| String + MLP42 | 2.42 | 3.85 | — | 26.02 | 0.974 |
| Ours (MSE) | 2.14 ± 0.08 | 3.50 ± 0.33 | 6.98 ± 0.31 | 32.09 ± 16.95 | 0.978 ± 0.004 |
| Ours (revHuber) | 2.04 ± 0.08 | 3.42 ± 0.29 | 6.92 ± 0.45 | 32.36 ± 16.37 | 0.979 ± 0.004 |
 ) or not (variant
) or not (variant  ). In terms of error, models tend to behave similarly to dummy regressors – respectively mean predictor and conditional mean predictors (represented by the dotted horizontal lines), as structures are getting noisier. The intuition is that making meaningful predictions from (or close to) pure noise is difficult. Both types of models reach a similar accuracy for lower levels of noise. Initially, the error of model
). In terms of error, models tend to behave similarly to dummy regressors – respectively mean predictor and conditional mean predictors (represented by the dotted horizontal lines), as structures are getting noisier. The intuition is that making meaningful predictions from (or close to) pure noise is difficult. Both types of models reach a similar accuracy for lower levels of noise. Initially, the error of model  is significantly larger than that of
is significantly larger than that of  as the model cannot guess what metal center the complex is going to feature. From Fig. 2b, we know that the metal center has a determinant influence on the binding energy.
as the model cannot guess what metal center the complex is going to feature. From Fig. 2b, we know that the metal center has a determinant influence on the binding energy.
3.6 Conditional generation and inverse-design
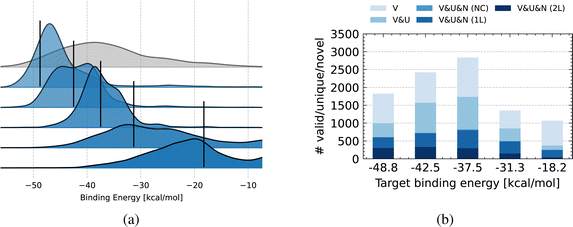
In this section, we study the ability of OM-Diff to generate novel optimized organometallic complexes, that can effectively catalyze cross-coupling reactions.For each metal center, we choose the target values to be the following percentiles of the training data distribution: [0.05, 0.25, 0.50, 0.75, 0.95]. This is to make sure that the surrogate predictions remain somewhat reliable, as we cannot afford DFT calculations for all generated compounds. For each pair metal center – target value, we sample 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 compounds, evaluate their binding energy using the surrogate model, and finally display the corresponding distribution. As an example in Fig. 8a, we show the conditional distributions obtained for Pd, while the same plots for the other metal centers are provided in Fig. S13.† We can observe that for target values above the median, the conditional distributions tend to become more spread out. We hypothesize that this is due to the fact that the unconditional distribution, shown in grey in the back of Fig. 8a, is not symmetric around its median, and usually that target values above the median are more sparsely distributed. Nonetheless, we can effectively steer the conditional distribution. We also expect that the conditional distributions can be made sharper by upscaling the contribution of the guidance term in eqn (16), at the cost of a lower validity and uniqueness.
000 compounds, evaluate their binding energy using the surrogate model, and finally display the corresponding distribution. As an example in Fig. 8a, we show the conditional distributions obtained for Pd, while the same plots for the other metal centers are provided in Fig. S13.† We can observe that for target values above the median, the conditional distributions tend to become more spread out. We hypothesize that this is due to the fact that the unconditional distribution, shown in grey in the back of Fig. 8a, is not symmetric around its median, and usually that target values above the median are more sparsely distributed. Nonetheless, we can effectively steer the conditional distribution. We also expect that the conditional distributions can be made sharper by upscaling the contribution of the guidance term in eqn (16), at the cost of a lower validity and uniqueness.
As for property controllability, metrics such as validity, uniqueness and novelty are impacted by the target value as seen in Fig. 8b for Pd complexes, and in Fig. S14† for the other metal centers. For parts of the property space that are less well covered by training data, the different metrics tend to drop. Specifically, when targeting the 0.95 percentile, the conditional distribution tends to spread out, and (abnormally) high binding energies are predicted by the model. While the binding energy of these samples is probably mistakenly estimated by the surrogate, we observe that the conditional generative model is still able to produce novel complexes, namely around 250.
As previously, we generate 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 complexes for Pd and Pt. After checking for validity and uniqueness, we only keep novel complexes. We additionally discard the ones with an estimated binding energy that does not fall within the range of interest. Of the remaining samples, we randomly keep 5 compounds for each metal center. For these compounds, we recompute the binding energies using DFT, employing the protocol described in Section 3.3. The novel catalysts are displayed in the two upper rows of Fig. 9, along with their binding energy estimated by the surrogate and calculated using DFT. For the Pd complexes, displayed in the top row, 4 out of 5 fall in the range of interest, and within 2 kcal mol−1 of the energy calculated with DFT. For the Pt complexes, all 5 complexes fall in the range of interest and within 2.5 kcal mol−1 of DFT. These slight discrepancies between DFT and surrogate predictions are in accordance with the errors reported Fig. S11,† where the estimated MAE in that region of the property space is shown to be around 2−3 kcal mol−1.
000 complexes for Pd and Pt. After checking for validity and uniqueness, we only keep novel complexes. We additionally discard the ones with an estimated binding energy that does not fall within the range of interest. Of the remaining samples, we randomly keep 5 compounds for each metal center. For these compounds, we recompute the binding energies using DFT, employing the protocol described in Section 3.3. The novel catalysts are displayed in the two upper rows of Fig. 9, along with their binding energy estimated by the surrogate and calculated using DFT. For the Pd complexes, displayed in the top row, 4 out of 5 fall in the range of interest, and within 2 kcal mol−1 of the energy calculated with DFT. For the Pt complexes, all 5 complexes fall in the range of interest and within 2.5 kcal mol−1 of DFT. These slight discrepancies between DFT and surrogate predictions are in accordance with the errors reported Fig. S11,† where the estimated MAE in that region of the property space is shown to be around 2−3 kcal mol−1.
 | ||
| Fig. 9 Overview of the novel complexes validated with DFT. (Top row) Pd complexes, (middle row) Pt complexes, and (bottom row) Cu complexes. All binding energies are expressed in kcal mol−1. | ||
Interestingly, we note that although the training dataset contains various ligand types, eight out of ten Pd/Pt complexes contain phosphine-type ligands, that are σ-donors and π-acceptors. Furthermore, four out of five Pd-complexes contain a CO ligand, a σ-donor and π-acceptor. These ligand properties are known to be important for cross-coupling reactions. Although the model does not explicitly learn the electronic structure properties, its choice of ligands can nonetheless be rationalized.
The inaccuracy of the screening surrogate is not the only explanation to the unsuccessful conditional generation for the initial target of −27.55 kcal mol−1. The time-conditioned surrogate is also inaccurate in that region of the property space due to lack of training data, and thereby likely to drive the generation process towards complexes with erroneous binding energies. Finally, as the generative model has only seen a handful of complexes in that part of the property space, we can imagine that it is not extremely good at modelling the distribution in that particular area.
4 Discussion and conclusion
We have introduced OM-Diff, a framework for inverse-designing organometallic complexes for target applications. The framework is based on a guided equivariant denoising diffusion model specifically tailored for the generation of organometallic complexes with targeted properties. Instead of directly learning a property-conditional generative model, which would require large volume of computationally expensive data, OM-Diff decouples the structure generative section from the conditional guidance towards coveted property, allowing the use of larger molecular databases for training, and requiring only a limited set of task-specific labeled data for accurate model performance. To inverse-design organometallic catalysts for reactions of interest with OM-Diff, one needs to establish (1) the chemical space of the complexes that catalyze the reaction and (2) the mechanism of the catalyzed reaction along with the rate-determining step.While OM-Diff is in principle a generic framework for inverse-designing homogeneous catalysts, the demonstration of its potential was limited to the inverse-design of catalyst candidates for a family of cross-coupling reactions, where the considered chemical space had restricted variety and only featured one coordination pattern. In that context, we first showed that the increased expressivity of the denoising neural network combined with a proper modelling of the metal center enables effective unconditional generation of novel complexes. Second, we showed that the model offered controllability, and that sampling could effectively be steered across the property space, while maintaining novelty in the sampled complexes. For the specific case of the Suzuki reaction, we further validated a handful of optimized complexes with DFT calculations. We could successfully generate promising Pd- and Pt-based complexes, and the compounds were shown to have a binding energy (for the activity determining step) within the range of interest. For Cu complexes, we could not generate complexes in the range of interest, highlighting the limitations of the proposed approach in parts of the property space sparsely represented in the training data. However, when the target value was around a less extreme percentile of the property distribution, novel complexes featuring the prompted binding energy (or close to) could successfully be generated. This is promising and indicates that our framework could effectively be integrated in an active learning setup towards real discovery, where the training data is progressively extended towards properties of interest.
As illustrated in the Experimental section, goal-directed generation is attainable but remains a difficult endeavor for models trained offline, with a static dataset. Other methods, based on GA or RL, are known to perform well in settings where they can query the function to be optimized. A hybrid method that uses an offline pretrained diffusion model, and that then further gets optimised online through RL or in an active learning setup is an interesting avenue for future work. As samples with attractive properties often lie at the boundaries of the training data, such candidates can be evaluated with the QM method of choices, added to the training data, and the surrogate retrained on the augmented dataset. An iterative framework,114 where data is gathered continuously, is also a promising avenue that would allow the generative model to progressively move towards regions of interest that were not well covered in the initial dataset.
We envision a significant scope for future work in both application areas and methodological development. While the framework was shown to work in a rather small data regime and with limited variety in the training data, pre-training on a relevant database,113e.g. the TMQM database,23 before fine-tuning it in the chemical space of interest might allow for more valid, and novel molecules that lie beyond the neighborhood of the property-labeled training data. For practical relevance, validity and novelty are necessary but not sufficient, and an in silico inverse-design framework should also suggest compounds that are amenable to synthesis.31 In OM-Diff, the generation is steered towards promising parts of the chemical space based on a chemical target function, regardless of the potential validity and synthesizability. To address the limited effective validity of the generated complexes, a possible avenue would be to only consider heavy atoms in the generative process, and adding an hydrogenation post-processing step. This would also make the training and sampling faster by reducing the size of generated point clouds. Another related approach would consist in grouping atoms together, i.e. representing fragments as coarse-grained nodes.68 Such procedure would require to define (1) a mapping transforming all-atom structures to coarse-grained representations, and (2) a post-processing step replacing the group nodes in the generated structures by their actual composition. The latter would additionally require to decide on the orientation and/or attachment point if multiple possibilities exist.115 A third approach could leverage the guidance setup described from Section 2.5, where a target function could be designed to include the feedback of a classifier trained to distinguish between valid and invalid compounds. Similarly the feedback of a surrogate trained to estimate synthesizability could be leveraged to favour the generation of easily synthesizable complexes. Another relevant direction for future work is multi-property conditioning. The scheme introduced in eqn (18) could for instance be leverage to inverse-design catalysts for more complex reactions, where high catalytic activity requires optimal binding energy in multiple reaction steps. Other methodological improvements in OM-Diff could include modelling of atom and bond types as categorical variables112,113 (instead of the continuous relaxation used in this work) and predicting the denoised structures directly, as it has been shown to work better for atomistic data.113 Regarding the conditional sampling procedure, finding a better way to combine the feedback from the generative model and the guide would be useful as well. As seen in Fig. S12,† the time-conditioned property predictor is equivalent to a random guess on the early phases of the denoising process. If the surrogate provides uncertainty, this could also be leveraged to bias the generation, either to avoid uncertain regions or, in an active learning setting, to explore uncertain areas. Finally, while we have demonstrated the applicability of OM-Diff on the basis of generation of all ligands from scratch (i.e. where the center is composed of one atom), the formulation introduced in Section 2.4 is more general, and naturally extends to problems where the context is composed of multiple atoms, for instance in cases where the catalyst is designed based on a handful of scaffolds,116 or in a functionalization setting.28
Data availability
Along with this paper, we release a code repository, that can be accessed at https://github.com/frcnt/om-diff, allowing other researchers to build upon our work.Author contributions
F. C., M. N. S. and A. B. conceived the research idea. F. C. developed the code with help from B. H., ran the experiments, analyzed the results, and wrote the original draft based on inputs from all authors. B. B. performed validation with DFT calculations. M. N. S. and A. B. supervised the research. All authors discussed, commented on, and revised the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the Independent Research Fund Denmark with project DELIGHT (Grant No. 0217-00326B), TeraBatt project (Grant No. 2035-00232B) and ADANA project (Grant No. 3164-00297B).References
- P. Zhang and P. J. Sadler, Advances in the design of organometallic anticancer complexes, J. Organomet. Chem., 2017, 839, 5–14 CrossRef CAS.
- K. A. Williams, A. J. Boydston and C. W. Bielawski, Main-chain organometallic polymers: synthetic strategies, applications, and perspectives, Chem. Soc. Rev., 2007, 36(5), 729–744 RSC.
- J. Kalinowski, V. Fattori, M. Cocchi and J. A. G. Williams, Light-emitting devices based on organometallic platinum complexes as emitters, Coord. Chem. Rev., 2011, 255(21–22), 2401–2425 CrossRef CAS.
- W.-Y. Wong and C.-L. Ho, Organometallic photovoltaics: a new and versatile approach for harvesting solar energy using conjugated polymetallaynes, Acc. Chem. Res., 2010, 43(9), 1246–1256 CrossRef CAS PubMed.
- D.-Y. Wang, R. Liu, W. Guo, G. Li and Y. Fu, Recent advances of organometallic complexes for rechargeable batteries, Coord. Chem. Rev., 2021, 429, 213650 CrossRef CAS.
- J. W. Steed, Coordination and organometallic compounds as anion receptors and sensors, Chem. Soc. Rev., 2009, 38(2), 506–519 RSC.
- M. D. Jones, R. Raja, J. M. Thomas, B. F. G. Johnson, D. W. Lewis, J. Rouzaud and K. D. M. Harris, Enhancing the enantioselectivity of novel homogeneous organometallic hydrogenation catalysts, Angew. Chem., Int. Ed., 2003, 42(36), 4326–4331 CrossRef CAS PubMed.
- J. Pospech, I. Fleischer, R. Franke, S. Buchholz and M. Beller, Alternative metals for homogeneous catalyzed hydroformylation reactions, Angew. Chem., Int. Ed., 2013, 52(10), 2852–2872 CrossRef CAS PubMed.
- T. M. Trnka and R. H. Grubbs, The development of L2X2Ru
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHR olefin metathesis catalysts: an organometallic success story, Acc. Chem. Res., 2001, 34(1), 18–29 CrossRef CAS PubMed.
CHR olefin metathesis catalysts: an organometallic success story, Acc. Chem. Res., 2001, 34(1), 18–29 CrossRef CAS PubMed. - Z. Xi, X. Zhang, W. Chen, S. Fu and D. Wang, Synthesis and structural characterization of nickel(II) complexes supported by pyridine-functionalized N-heterocyclic carbene ligands and their catalytic activities for Suzuki coupling, Organometallics, 2007, 26(26), 6636–6642 CrossRef CAS.
- A. Kumar, G. K. Rao, S. Kumar and A. K. Singh, Formation and role of palladium chalcogenide and other species in Suzuki–Miyaura and heck C–C coupling reactions catalyzed with palladium(II) complexes of organochalcogen ligands: realities and speculations, Organometallics, 2014, 33(12), 2921–2943 CrossRef CAS.
- P. Espinet and A. M. Echavarren, The mechanisms of the Stille reaction, Angew. Chem., Int. Ed., 2004, 43(36), 4704–4734 CrossRef CAS PubMed.
- J. G. Freeze, H. R. Kelly and V. S. Batista, Search for catalysts by inverse design: artificial intelligence, mountain climbers, and alchemists, Chem. Rev., 2019, 119(11), 6595–6612 CrossRef CAS PubMed.
- M. Foscato and V. R. Jensen, Automated in silico design of homogeneous catalysts, ACS Catal., 2020, 10(3), 2354–2377 CrossRef CAS.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Inverse molecular design using machine learning: Generative models for matter engineering, Science, 2018, 361(6400), 360–365 CrossRef CAS PubMed.
- C. Duan, A. Nandy and H. J. Kulik, Machine learning for the discovery, design, and engineering of materials, Annu. Rev. Chem. Biomol. Eng., 2022, 13(1), 405–429 CrossRef CAS PubMed.
- A. Nandy, C. Duan, M. G. Taylor, F. Liu, A. H. Steeves and H. J. Kulik, Computational discovery of transition-metal complexes: from high-throughput screening to machine learning, Chem. Rev., 2021, 121(16), 9927–10000 CrossRef CAS PubMed.
- G. dos P. Gomes, R. Pollice and A. Aspuru-Guzik, Navigating through the maze of homogeneous catalyst design with machine learning, Trends Chem., 2021, 3(2), 96–110 CrossRef.
- J. Hachmann, R. Olivares-Amaya, S. Atahan-Evrenk, C. Amador-Bedolla, R. S. Sánchez-Carrera, A. Gold-Parker, L. Vogt, A. M. Brockway and A. Aspuru-Guzik, The harvard clean energy project: large-scale computational screening and design of organic photovoltaics on the world community grid, J. Phys. Chem. Lett., 2011, 2(17), 2241–2251 CrossRef CAS.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho and W. Hu, et al., Open catalyst 2020 (OC20) dataset and community challenges, ACS Catal., 2021, 11(10), 6059–6072 CrossRef CAS.
- J. J. Irwin and B. K. Shoichet, Zinc – a free database of commercially available compounds for virtual screening, J. Chem. Inf. Model., 2005, 45(1), 177–182 CrossRef CAS PubMed.
- M. Nakata and T. Shimazaki, PubChemQC project: a large-scale first-principles electronic structure database for data-driven chemistry, J. Chem. Inf. Model., 2017, 57(6), 1300–1308 CrossRef CAS PubMed.
- D. Balcells and B. B. Skjelstad, tmQM dataset—quantum geometries and properties of 86k transition metal complexes, J. Chem. Inf. Model., 2020, 60(12), 6135–6146 CrossRef CAS PubMed.
- T. Gensch, G. dos P. Gomes, P. Friederich, E. Peters, T. Gaudin, R. Pollice, K. Jorner, A. K. Nigam, M. Lindner-D’Addario and M. S. Sigman, et al., A comprehensive discovery platform for organophosphorus ligands for catalysis, J. Am. Chem. Soc., 2022, 144(3), 1205–1217 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The cambridge structural database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72(2), 171–179 CrossRef CAS PubMed.
- B. Meyer, B. Sawatlon, S. Heinen, O. A. Von Lilienfeld and C. Corminboeuf, Machine learning meets volcano plots: computational discovery of cross-coupling catalysts, Chem. Sci., 2018, 9(35), 7069–7077 RSC.
- P. Friederich, G. dos P. Gomes, R. De Bin, A. Aspuru-Guzik and D. Balcells, Machine learning dihydrogen activation in the chemical space surrounding Vaska's complex, Chem. Sci., 2020, 11(18), 4584–4601 RSC.
- A. V. Kalikadien, E. A. Pidko and V. Sinha, ChemSpaX: exploration of chemical space by automated functionalization of molecular scaffold, Digital Discovery, 2022, 1(1), 8–25 RSC.
- D. M. Anstine and O. Isayev, Generative models as an emerging paradigm in the chemical sciences, J. Am. Chem. Soc., 2023, 145(16), 8736–8750 CrossRef CAS PubMed.
- S. Kang and K. Cho, Conditional molecular design with deep generative models, J. Chem. Inf. Model., 2018, 59(1), 43–52 CrossRef PubMed.
- W. Gao and C. W. Coley, The synthesizability of molecules proposed by generative models, J. Chem. Inf. Model., 2020, 60(12), 5714–5723 CrossRef CAS PubMed.
- C. Bilodeau, W. Jin, T. Jaakkola, R. Barzilay and K. F. Jensen, Generative models for molecular discovery: Recent advances and challenges, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(5), e1608 Search PubMed.
- M. Krenn, F. Häse, A. K. Nigam, P. Friederich and A. Aspuru-Guzik, Self-referencing embedded strings (selfies): A 100% robust molecular string representation, Mach. Learn.: Sci. Technol., 2020, 1(4), 045024 Search PubMed.
- D. Weininger, Smiles, a chemical language and information system. 1. introduction to methodology and encoding rules, J. Chem. Inf. Comput. Sci., 1988, 28(1), 31–36 CrossRef CAS.
- G. Lima Guimaraes, B. Sanchez-Lengeling, C. Outeiral, P. L. C. Farias and A. Aspuru-Guzik, Objective-reinforced generative adversarial networks (organ) for sequence generation models, arXiv, 2017, preprint, arXiv:1705.10843, DOI:10.48550/arXiv.1705.10843.
- N. De Cao and T. Kipf, MolGAN: An implicit generative model for small molecular graphs, arXiv, 2018, preprint arXiv:1805.11973, DOI:10.48550/arXiv.1805.11973.
- J. You, R. Ying, X. Ren, W. Hamilton, and J. Leskovec, GraphRNN: Generating realistic graphs with deep auto-regressive models, in International Conference on Machine Learning, PMLR, 2018, pp. 5708–5717 Search PubMed.
- C. Shi, M. Xu, Z. Zhu, W. Zhang, M. Zhang and J. Tang, GraphAF: a flow-based autoregressive model for molecular graph generation, in International Conference on Learning Representations, 2020 Search PubMed.
- M. J. Kusner, B. Paige and J. Miguel Hernández-Lobato, Grammar variational autoencoder, in International Conference on Machine Learning, PMLR, 2017, pp. 1945–1954 Search PubMed.
- W. Jin, R. Barzilay and T. Jaakkola, Junction tree variational autoencoder for molecular graph generation, in International Conference on Machine Learning, PMLR, 2018, pp. 2323–2332 Search PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, Automatic chemical design using a data-driven continuous representation of molecules, ACS Cent. Sci., 2018, 4(2), 268–276 CrossRef PubMed.
- O. Schilter, A. Vaucher, P. Schwaller and T. Laino, Designing catalysts with deep generative models and computational data. A case study for Suzuki cross coupling reactions, Digital Discovery, 2023, 2(3), 728–735 RSC.
- M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, Molecular de novo design through deep reinforcement learning, J. Cheminf., 2017, 9, 1–14 Search PubMed.
- J. You, B. Liu, Z. Ying, V. Pande and J. Leskovec, Graph convolutional policy network for goal-directed molecular graph generation, Proceedings of the 32nd International Conference on Neural Information Processing Systems, 2018, pp. 6412–6422 Search PubMed.
- E. Bengio, M. Jain, M. Korablyov, D. Precup and Y. Bengio, Flow network based generative models for non-iterative diverse candidate generation, Adv. Neural Inf. Process. Syst., 2021, 34, 27381–27394 Search PubMed.
- J. H. Jensen, A graph-based genetic algorithm and generative model/Monte Carlo tree search for the exploration of chemical space, Chem. Sci., 2019, 10(12), 3567–3572 RSC.
- A. K. Nigam, R. Pollice, M. Krenn, G. dos P. Gomes and A. Aspuru-Guzik, Beyond generative models: superfast traversal, optimization, novelty, exploration and discovery (stoned) algorithm for molecules using selfies, Chem. Sci., 2021, 12(20), 7079–7090 RSC.
- E. Hoogeboom, V. Garcia Satorras, C. Vignac and M. Welling, Equivariant diffusion for molecule generation in 3D, in International Conference on Machine Learning, PMLR, 2022, pp. 8867–8887 Search PubMed.
- N. Gebauer, M. Gastegger and K. Schütt, Symmetry-adapted generation of 3d point sets for the targeted discovery of molecules, Adv. Neural Inf. Process. Syst., 2019, 32, 7566–7578 Search PubMed.
- M. Ragoza, T. Masuda and D. R. Koes, Generating 3d molecules conditional on receptor binding sites with deep generative models, Chem. Sci., 2022, 13(9), 2701–2713 RSC.
- G. Landrum, et al., RDKit: A software suite for cheminformatics, computational chemistry, and predictive modeling, ed. G. Landrum, 2013, vol. 8, p. , p. 31 Search PubMed.
- E. I. Ioannidis, T. Z. H. Gani and H. J. Kulik, molSimplify: A toolkit for automating discovery in inorganic chemistry, 2016 Search PubMed.
- M. G. Taylor, D. J. Burrill, J. Janssen, E. R. Batista, D. Perez and P. Yang, Architector for high-throughput cross-periodic table 3d complex building, Nat. Commun., 2023, 14(1), 2786 CrossRef CAS PubMed.
- M. Foscato, G. Occhipinti, V. Venkatraman, B. K. Alsberg and V. R. Jensen, Automated design of realistic organometallic molecules from fragments, J. Chem. Inf. Model., 2014, 54(3), 767–780 CrossRef CAS PubMed.
- N. W. A. Gebauer, M. Gastegger, S. S. P. Hessmann, K.-R. Müller and K. T. Schütt, Inverse design of 3d molecular structures with conditional generative neural networks, Nat. Commun., 2022, 13(1), 973 CrossRef CAS PubMed.
- J. Sohl-Dickstein, E. Weiss, N. Maheswaranathan and S. Ganguli, Deep unsupervised learning using nonequilibrium thermodynamics, in International Conference on Machine Learning, PMLR, 2015, pp. 2256–2265 Search PubMed.
- J. Ho, A. Jain and P. Abbeel, Denoising diffusion probabilistic models, Adv. Neural Inf. Process. Syst., 2020, 33, 6840–6851 Search PubMed.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schuett, A. Tkatchenko and K.-R. Mueller, Machine learning force fields, Chem. Rev., 2021, 121(16), 10142–10186 CrossRef CAS PubMed.
- M. Xu, L. Yu, Y. Song, C. Shi, S. Ermon and J. Tang, GeoDiff: A geometric diffusion model for molecular conformation generation, in International Conference on Learning Representations, 2021 Search PubMed.
- B. Jing, G. Corso, J. Chang, R. Barzilay and T. Jaakkola, Torsional diffusion for molecular conformer generation, Adv. Neural Inf. Process. Syst., 2022, 35, 24240–24253 Search PubMed.
- C. Duan, Y. Du, H. Jia and H. J. Kulik, Accurate transition state generation with an object-aware equivariant elementary reaction diffusion model, Nat. Comput. Sci., 2023, 3(12), 1045–1055 CrossRef PubMed.
- S. Kim, J. Woo and W. Y. Kim, Diffusion-based generative AI for exploring transition states from 2D molecular graphs, Nat. Commun., 2024, 15(1), 341 CrossRef CAS PubMed.
- I. Igashov, H. Stärk, C. Vignac, A. Schneuing, V. Garcia Satorras, P. Frossard, M. Welling, M. Bronstein and B. Correia, Equivariant 3D-conditional diffusion model for molecular linker design, Nat. Mach. Intell., 2024, 1–11 Search PubMed.
- A. Schneuing, Y. Du, C. Harris, A. Jamasb, I. Igashov, W. Du, T. Blundell, P. Lió, C. Gomes, M. Welling, et al., Structure-based drug design with equivariant diffusion models, arXiv, 2022, preprint, arXiv:2210.13695, DOI:10.48550/arXiv.2210.13695.
- J. Guan, W. W. Qian, X. Peng, Y. Su, J. Peng and J. Ma. 3D equivariant diffusion for target-aware molecule generation and affinity prediction, in The Eleventh International Conference on Learning Representations, 2022 Search PubMed.
- G. Corso, B. Jing, R. Barzilay, T. Jaakkola, et al., DiffDock: Diffusion steps, twists, and turns for molecular docking, in International Conference on Learning Representations (ICLR 2023), 2023 Search PubMed.
- F. Bao, M. Zhao, Z. Hao, P. Li, C. Li and J. Zhu, Equivariant energy-guided sde for inverse molecular design, in The Eleventh International Conference on Learning Representations, 2022 Search PubMed.
- T. Weiss, E. Mayo Yanes, S. Chakraborty, L. Cosmo, A. M. Bronstein and R. Gershoni-Poranne, Guided diffusion for inverse molecular design, Nat. Comput. Sci., 2023, 3(10), 873–882 CrossRef PubMed.
- N. N. Vlassis and W. C. Sun, Denoising diffusion algorithm for inverse design of microstructures with fine-tuned nonlinear material properties, Comput. Methods Appl. Mech. Eng., 2023, 413, 116126 CrossRef.
- J. Park, A. P. S. Gill, S. M. Moosavi and J. Kim, Inverse design of porous materials: a diffusion model approach, J. Mater. Chem. A, 2024, 12, 6507–6514 RSC.
- R. Laplaza, S. Gallarati and C. Corminboeuf, Genetic optimization of homogeneous catalysts, Chem.: Methods, 2022, 2(6), e202100107 CAS.
- J. Seumer, J. K. S. Hansen, M. B. Nielsen and J. H. Jensen, Computational evolution of new catalysts for the Morita–Baylis–Hillman reaction, Angew. Chem., Int. Ed., 2023, 62(18), e202218565 CrossRef CAS PubMed.
- M. Strandgaard, J. Seumer, B. Benediktsson, A. Bhowmik, T. Vegge and J. H. Jensen, Genetic algorithm-based re-optimization of the Schrock catalyst for dinitrogen fixation, PeerJ Phys. Chem., 2023, 5, e30 CrossRef.
- J. Seumer and J. H. Jensen, Beyond predefined ligand libraries: A genetic algorithm approach for de novo discovery of catalysts for the Suzuki coupling reactions, ChemRxiv, 2024, preprint, DOI:10.26434/chemrxiv-2024-9xh38-v2.
- H. Jin and K. M. Merz Jr, LigandDiff: de novo ligand design for 3D transition metal complexes with diffusion models, J. Chem. Theory Comput., 2024, 20, 4377–4384 CrossRef CAS PubMed.
- F. R. J. Cornet, B. Benediktsson, B. Hastrup, A. Bhowmik and M. N. Schmidt, Inverse-design of organometallic catalysts with guided equivariant diffusion, in AI for Accelerated Materials Design-NeurIPS 2023 Workshop, 2023 Search PubMed.
- D. Kingma, T. Salimans, B. Poole and J. Ho, Variational diffusion models, Adv. Neural Inf. Process. Syst., 2021, 34, 21696–21707 Search PubMed.
- V. Garcia Satorras, E. Hoogeboom and M. Welling, E(n) equivariant graph neural networks, in International Conference on Machine Learning, PMLR, 2021, pp. 9323–9332 Search PubMed.
- K. Schütt, O. Unke and M. Gastegger, Equivariant message passing for the prediction of tensorial properties and molecular spectra, in International Conference on Machine Learning, PMLR, 2021, pp. 9377–9388 Search PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Neural message passing for quantum chemistry, in International Conference on Machine Learning, PMLR, 2017, pp. 1263–1272 Search PubMed.
- C. K. Joshi, C. Bodnar, S. V. Mathis, T. Cohen and P. Lio, On the Expressive Power of Geometric Graph Neural Networks, 2023, https://openreview.net/forum?id=Rkxj1GXn9_ Search PubMed.
- P. Dhariwal and A. Nichol, Diffusion models beat gans on image synthesis, Adv. Neural Inf. Process. Syst., 2021, 34, 8780–8794 Search PubMed.
- J. Song, Q. Zhang, H. Yin, M. Mardani, M.-Y. Liu, J. Kautz, Y. Chen and A. Vahdat, Loss-guided diffusion models for plug-and-play controllable generation, in International Conference on Machine Learning, PMLR, 2023, pp. 32483–32498 Search PubMed.
- S. Lambert-Lacroix and L. Zwald, The adaptive BerHu penalty in robust regression, J. Nonparametric Statistics, 2016, 28(3), 487–514 CrossRef.
- R. Laplaza, S. Das, M. D. Wodrich and C. Corminboeuf, Constructing and interpreting volcano plots and activity maps to navigate homogeneous catalyst landscapes, Nat. Protoc., 2022, 17(11), 2550–2569 CrossRef CAS PubMed.
- M. J. Buskes and M.-J. Blanco, Impact of cross-coupling reactions in drug discovery and development, Molecules, 2020, 25(15), 3493 CrossRef CAS PubMed.
- A. Marrocchi, A. Facchetti, D. Lanari, C. Petrucci and L. Vaccaro, Current methodologies for a sustainable approach to π-conjugated organic semiconductors, Energy Environ. Sci., 2016, 9(3), 763–786 RSC.
- K. Jiang, L. Zhang, Y. Zhao, J. Lin and M. Chen, Palladium-catalyzed cross-coupling polymerization: A new access to cross-conjugated polymers with modifiable structure and tunable optical/conductive properties, Macromolecules, 2018, 51(23), 9662–9668 CrossRef CAS.
- A. Suzuki, Cross-coupling reactions of organoboranes: an easy way to construct C–C bonds (nobel lecture), Angew. Chem., Int. Ed., 2011, 30(50), 6722–6737 CrossRef PubMed.
- N. Miyaura and A. Suzuki, Palladium-catalyzed cross-coupling reactions of organoboron compounds, Chem. Rev., 1995, 95(7), 2457–2483 CrossRef CAS.
- M. Busch, M. D. Wodrich and C. Corminboeuf, A generalized picture of C–C cross-coupling, ACS Catal., 2017, 7(9), 5643–5653 CrossRef CAS.
- B. Sawatlon, M. D. Wodrich, B. Meyer, A. Fabrizio and C. Corminboeuf, Data mining the C–C cross-coupling genome, ChemCatChem, 2019, 11(16), 4096–4107 CrossRef CAS.
- T. A. Halgren, Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94, J. Comput. Chem., 1996, 17(5–6), 490–519 CrossRef CAS.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(1), 73–78 CAS.
- F. Neese, Software update: The ORCA program system—version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(5), e1606 Search PubMed.
- A. D. Beck, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98(7), 5648–5656 CrossRef.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38(6), 3098 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle–Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785 CrossRef CAS PubMed.
- J. S. Binkley, J. A. Pople and W. J. Hehre, Self-consistent molecular orbital methods. 21. Small split-valence basis sets for first-row elements, J. Am. Chem. Soc., 1980, 102(3), 939–947 CrossRef CAS.
- W. J. Pietro, M. M. Francl, W. J. Hehre, D. J. DeFrees, J. A. Pople and J. S. Binkley, Self-consistent molecular orbital methods. 24. supplemented small split-valence basis sets for second-row elements, J. Am. Chem. Soc., 1982, 104(19), 5039–5048 CrossRef CAS.
- K. D. Dobbs and W. J. Hehre, Molecular orbital theory of the properties of inorganic and organometallic compounds 5. Extended basis sets for first-row transition metals, J. Comput. Chem., 1987, 8(6), 861–879 CrossRef CAS.
- K. D. Dobbs and W. J. Hehre, Molecular orbital theory of the properties of inorganic and organometallic compounds. 6. Extended basis sets for second-row transition metals, J. Comput. Chem., 1987, 8(6), 880–893 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305 RSC.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, New basis set exchange: An open, up-to-date resource for the molecular sciences community, J. Chem. Inf. Model., 2019, 59(11), 4814–4820 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange, Chem. Phys., 2009, 356(1–3), 98–109 CrossRef CAS.
- R. Izsák and F. Neese, An overlap fitted chain of spheres exchange method, J. Chem. Phys., 2011, 135(14), 144105 CrossRef PubMed.
- G. L. Stoychev, A. A. Auer and F. Neese, Automatic generation of auxiliary basis sets, J. Chem. Theory Comput., 2017, 13(2), 554–562 CrossRef CAS PubMed.
- F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8(9), 1057–1065 RSC.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—an accurate and broadly parametrized self-consistent tight-binding quantum chemical method with multipole electrostatics and density-dependent dispersion contributions, J. Chem. Theory Comput., 2019, 15(3), 1652–1671 CrossRef CAS PubMed.
- A. Morehead and J. Cheng, Geometry-complete diffusion for 3D molecule generation, in ICLR 2023 – Machine Learning for Drug Discovery Workshop, 2023 Search PubMed.
- C. Vignac, N. Osman, L. Toni and P. Frossard, MiDi: Mixed graph and 3D denoising diffusion for molecule generation, in Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Springer, 2023, pp. 560–576 Search PubMed.
- T. Le, J. Cremer, F. Noe, D.-A. Clevert and K. T. Schütt, Navigating the design space of equivariant diffusion-based generative models for de novo 3D molecule generation, in The Twelfth International Conference on Learning Representations, 2024 Search PubMed.
- J. Westermayr, J. Gilkes, R. Barrett and R. J. Maurer, High-throughput property-driven generative design of functional organic molecules, Nat. Comput. Sci., 2023, 3(2), 139–148 CrossRef CAS PubMed.
- X. Fu, T. Xie, A. S. Rosen, T. S. Jaakkola and J. A. Smith, MOFDiff: Coarse-grained diffusion for metal-organic framework design, in The Twelfth International Conference on Learning Representations, 2024 Search PubMed.
- A. M. Krieger, V. Sinha, A. V. Kalikadien and E. A. Pidko, Metal-ligand cooperative activation of HX (X = H, Br, OR) bond on Mn based pincer complexes, Z. Anorg. Allg. Chem., 2021, 647(14), 1486–1494 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00099d |
‡ In the simplest case, this is simply a distribution over a single metal center – as further in this paper. The proposed framework is however not limited to such simple case. Depending on the problem under study, one could for instance sample the metal first, and then sample the coordination pattern conditioned on the metal, leading to a set 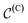 made of multiple atoms. made of multiple atoms. |
| This journal is © The Royal Society of Chemistry 2024 |