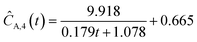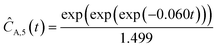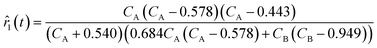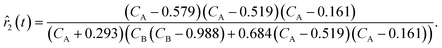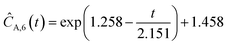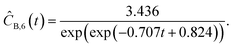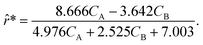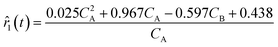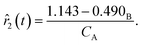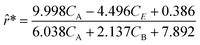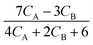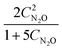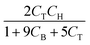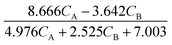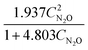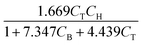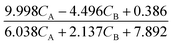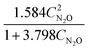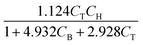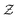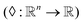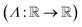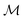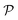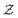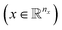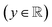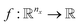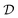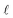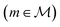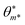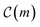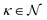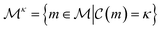The automated discovery of kinetic rate models – methodological frameworks†
Received
23rd October 2023
, Accepted 22nd March 2024
First published on 27th March 2024
Abstract
The industrialization of catalytic processes requires reliable kinetic models for their design, optimization and control. Mechanistic models require significant domain knowledge, while data-driven and hybrid models lack interpretability. Automated knowledge discovery methods, such as ALAMO (Automated Learning of Algebraic Models for Optimization), SINDy (Sparse Identification of Nonlinear Dynamics), and genetic programming, have gained popularity but suffer from limitations such as needing model structure assumptions, exhibiting poor scalability, and displaying sensitivity to noise. To overcome these challenges, we propose two methodological frameworks, ADoK-S and ADoK-W (Automated Discovery of Kinetic rate models using a Strong/Weak formulation of symbolic regression), for the automated generation of catalytic kinetic models using a robust criterion for model selection. We leverage genetic programming for model generation and a sequential optimization routine for model refinement. The frameworks are tested against three case studies of increasing complexity, demonstrating their ability to retrieve the underlying kinetic rate model with limited noisy data from the catalytic systems, showcasing their potential for chemical reaction engineering applications.
1 Introduction
Mathematical models are logical representations of complex phenomena, widely used in diverse fields such as physics,1,2 medicine,3,4 and chemical reaction engineering.5,6 They allow researchers to distill complicated phenomena into quantitative expressions, which is essential in investigating the kinetics of a chemical system and in turn, essential in the development of industrial processes.
Models play a critical role in science and engineering, but how they are constructed remains a fundamental question. There are three classical paradigms for constructing models: mechanistic, data-driven, and hybrid modeling. Mechanistic models are derived from fundamental laws (e.g., conservation equations),7,8 and have advantages such as interpretability, extrapolatory properties, and physical meaning. However, constructing mechanistic models is time-consuming and requires domain expertise. In addition, the nonlinearity of these models can result in increased experimental effort for parameter estimation. Despite these challenges, mechanistic models are still widely established in industry and developed in research.9–11
Data-driven models can be constructed quickly using only data, unlike mechanistic models that require knowledge about the system. The structure of data-driven models is flexible and can be promptly adapted to different variables or processes. They are faster to evaluate than mechanistic models,12 making them useful in real-time simulation,13–16 optimization,17–20 and soft sensor development.21–23 However, since no physical knowledge is used, their extrapolatory abilities are often limited, and their performance depends on the quantity and quality of data available, which might classify their usage in certain scenarios as unsafe.
Hybrid models aim to combine the advantages of both mechanistic and data-driven modeling. These models have a mechanistic backbone and a data-driven component that improves the fit. There are two main approaches to hybrid modeling: parallel and sequential. The parallel approach uses the data-driven block to describe the model-data mismatch, while the sequential approach uses it to describe parameters of the mechanistic backbone. With either approach, hybrid models retain the extrapolation capabilities of a mechanistic model and the flexibility and ease of construction of a data-driven model.24–26
Hybrid modeling offers an elegant solution to the limitations of mechanistic and data-driven modeling, albeit not the only one. Another effective approach is to use state-of-the-art statistical and machine learning methods to automatically generate and select symbolic models using existing data. This strategy, also known as automated knowledge discovery or symbolic regression, maintains the benefits of mechanistic models while eliminating some of their drawbacks, such as the need for background knowledge and time-consuming construction.27 The methodology presented in this work follows this paradigm.
Various methods have been proposed to solve the general symbolic regression problem, including ALAMO,28 SINDy,29 and genetic programming.30 More specifically, the application of these methods to reaction kinetics have featured in a plethora of articles showing great potential and results, to name a few: Taylor et al.,31 Neumann et al.,32 Forster et al.,33 Iba,34 Nobile et al.,35 Datta et al.,36 Sugimoto et al.37 and Cornforth et al.38 However, these automated knowledge discovery frameworks face several challenges that limit their real-world applicability. Firstly, they often require structural assumptions of the underlying data-generating model, particularly non-evolutionary strategies that require a design matrix (i.e., a model library). Not assuming model forms/structures facilitates a broader and more effective exploration of model space, essential for accurately capturing the dynamic nature of chemical reactions. Such flexibility is particularly advantageous in an era focused on data-driven research and big data, enhancing both the precision and discovery potential of our models in chemical kinetics. Secondly, they may display poor scalability with respect to the number of state variables available, especially non-evolutionary strategies. Thirdly, they lack a motivated and rigorous model selection routine, and their choice of model selection routine may not be transparent or tested. Lastly, for the discovery of non-linear dynamics, they may be sensitive to noisy data when rate measurements are not directly accessible.
In this section, we introduced the importance of mathematical modeling within chemical engineering, the challenges of classical modeling paradigms, and the shortcomings of modern automated knowledge discovery methodologies. This work aims to build and benchmark two generalizable and robust methodological frameworks that integrate a rigorous model selection routine for the automated discovery of kinetic rate models. The proposed methodologies introduce two noteworthy innovations in the field of kinetic model discovery for catalytic systems. Firstly, it presents a unique approach that combines genetic programming with parameter estimation and information criteria to discover optimal state-space models for accurate rate approximation in the strong formulation. This approach contrasts with conventional methodologies where an arbitrary polynomial is typically chosen for interpolation and rate measurement estimation.33 Additionally, the paper pioneers the application of the weak formulation of symbolic regression in genetic programming, a method that, to our knowledge, has not previously been utilized or implemented in this field. These innovations underscore the significant advancements we are contributing to the subject area.
The rest of the paper is organized as follows: in Section 2 our proposed methods are motivated and described in detail; in Section 3 we introduce three case studies that are used to analyze the performance of the proposed methodological frameworks; in Section 4 the results of the study are presented and amply discussed along with the shortcomings of the proposed methodologies; and in Section 5 the key findings are presented with a brief outlook on future research.
2 Methodological frameworks
We begin by briefly describing our methodologies, ADoK-S and ADoK-W (Automated Discovery of Kinetic models using a Strong/Weak formulation of symbolic regression). Both frameworks are composed of three main steps: (I) a genetic programming (GP) algorithm to facilitate candidate model generation, (II) a sequential optimization algorithm for estimating parameters of promising models, (III) and a reasoned and transparent model selection routine using the Akaike information criterion (AIC).‡ We decided to utilize an information criterion instead of a data-splitting approach for model selection because it allows us to utilize the entire available data set for model construction, whilst still having a robust and reliable way to test the proposed models. This approach is particularly beneficial in a low-data setting, as it maximizes the information utilized for discovering adequate kinetic models.
ADoK-S employs the conventional implementation of symbolic regression, or the strong formulation. This approach necessitates rate measurements for deriving rate models. However, these measurements are not experimentally accessible and need to be estimated. Following the delineated three-step procedure, ADoK-S identifies optimal concentration profiles, which describe the temporal evolution of the observed species concentrations. These profiles are then numerically differentiated to estimate the rate measurements of the reactive system. Upon rate approximation, the same three steps are carried out to discover the kinetic rate models best suited to these rates. The resultant rate model is then integrated and compared to the original concentration data.
Our GP approach for rate estimation demonstrated superior performance compared to most state-of-the-art methods outlined in Van Breugel et al.39 The detailed account of the results is presented in the ‘ESI†‘. It was outperformed marginally by one method, even without the utilization of the full potential to integrate prior knowledge through mathematical constraints in our approach. We hypothesize that the inclusion of such constraints in our method would further enhance the accuracy of our rate estimations, solidifying the GP approach as a highly competitive tool in the field of estimation of derivatives. However, this lies outside the scope of the current work.
In contrast, ADoK-W operates on the weak formulation of symbolic regression. This model proposal strategy bypasses rate estimation and constructs rate models directly from the measured concentration data. It does so by implementing the three-step process, but instead, the genetic programming algorithm contains an integration step. Consequently, the optimal rate model can be integrated and compared to the original concentration data in the same way as ADoK-S. It is important to note that the time series kinetic data required to execute ADoK-S and ADoK-W can be obtained from transient experiments (i.e., measuring the evolution of the concentration of species as a function of reaction time in a batch reactor) or from steady-state experiments (i.e., measuring the concentration of species as a function of residence time in a plug-flow reactor).
Both methodologies provide a closed-loop approach if the model output is not satisfactory, either due to violations of prior knowledge (e.g., the exclusion of a species' concentration from a suggested kinetic model despite the user's belief that it should influence the reaction rate) or inadequate model fitting (e.g., the non-linearities of the kinetic data not being well-captured by the proposed model). The modeler can choose to execute an optimum experiment tailored for the discovery task – determined by model-based design of experiments (MBDoE) – which can then be concatenated with the initial data set. With the new experimental data, the methodologies can be iterated and the subsequent model output examined. In a practical setting, this discriminatory experiment could also be used to validate the accuracy of models proposed in previous iterations instead of fully relying on the AIC. The number of iterations can be as many as the modeler requires or until the experimental budget is spent. Fig. 1 provides a visual representation of the workflow of both ADoK-S and ADoK-W, highlighting the most important steps and the differences between each methodology. A more detailed version is provided in Fig. 2 and 3.
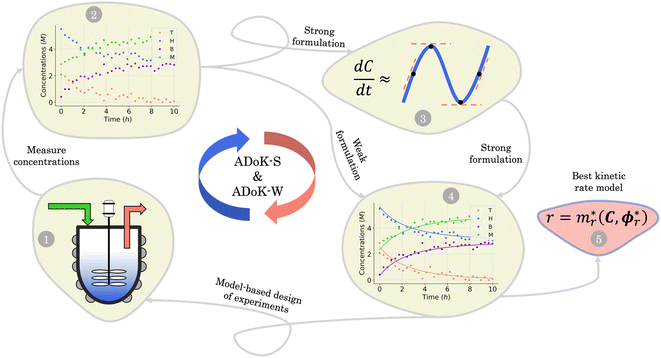 |
| | Fig. 1 Flowchart representation of the ADoK-S and ADoK-W methodologies. While ADoK-S requires numerical differentiation of concentration profiles to estimate rate measurements, ADoK-W leverages an embedded integration step that enables the direct rate model extraction from concentration data. In cases of unsatisfactory model outputs, both methodologies accommodate iterative refinement using optimum experiments (determined by MBDoE) until desired accuracy or experimental budget constraints are met. | |
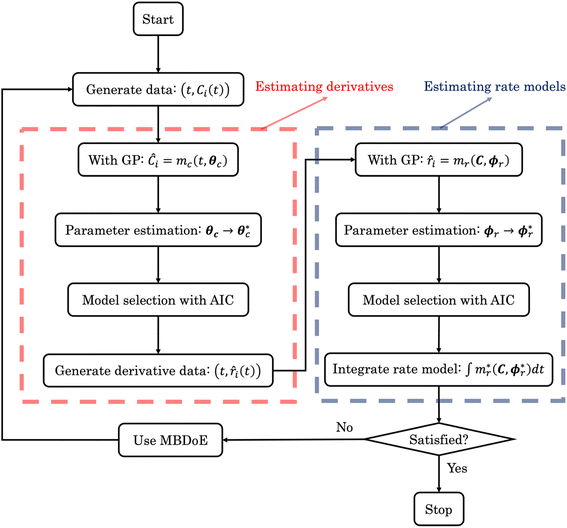 |
| | Fig. 2 The flowchart of ADoK-S (Automated Discovery of Kinetics using a Strong formulation of symbolic regression); the red and blue dashed boxes represent the steps where rate measurements and rate models are estimated, respectively. | |
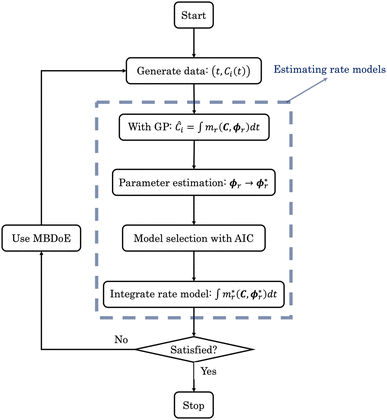 |
| | Fig. 3 The flowchart of ADoK-W (Automated Discovery of Kinetics using a Weak formulation of symbolic regression); the blue dashed box represent the steps where rate models are estimated. | |
In developing our methodology, we consciously chose a GP-based approach, despite its potential deviation from mass-action laws, in favor of automated alternatives that require proposing putative chemical reactions first. This decision is grounded in several critical advantages. Firstly, our approach bypasses the need for assumptions about reaction families or extensive computations of thermodynamic properties, both of which can be prohibitive due to either their absence or computational intensity. Secondly, a central aim of our research is to enable the extraction of vital kinetic information in scenarios where prior knowledge of the system is minimal or non-existent. Our methodology is specifically tailored to excel in such contexts. Thirdly, our approach is not rigidly fixed; it is designed to incorporate prior knowledge when available, using mathematical constraints to align with physical phenomena (although this was outside the scope of this research paper). In essence, our methodology can handle cases with limited prior information, while simultaneously maintaining the flexibility to effectively utilize available knowledge, making it a robust and versatile tool in the field of chemical kinetics.
Here we also set the necessary mathematical notation to describe our methods precisely. We start from the standard symbolic regression formulation,40 to later introduce the weak and strong variations of our framework.
The set 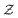 is the union of an arbitrary number of constants Γ and a fixed number of variables
is the union of an arbitrary number of constants Γ and a fixed number of variables 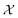 . The operator set
. The operator set 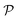 is the union of arithmetic operations
is the union of arithmetic operations 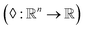 and a finite set of special one-dimensional functions
and a finite set of special one-dimensional functions 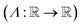 . The model search space
. The model search space 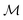 is the space of possible expressions to be reached by iterative function composition of the operator set
is the space of possible expressions to be reached by iterative function composition of the operator set 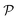 over the set
over the set 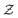 .
.
The variables can be represented as state vectors 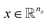 . A data point is a pair of specific states x and the associated target value
. A data point is a pair of specific states x and the associated target value 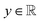 of an unknown function
of an unknown function 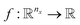 : y = f(x). The data set
: y = f(x). The data set 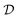 consists of nt data points:
consists of nt data points: 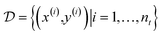 . To quantify the discrepancy between the predictions and the target values, we can leverage any adequate positive measure function
. To quantify the discrepancy between the predictions and the target values, we can leverage any adequate positive measure function 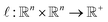 .
.
A symbolic model 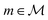 has a finite set of parameters θm whose dimension dm depends on the model. We denote the prediction of a model under specific parameter values in functional form as m(·∣θm). We use ŷm to denote the prediction of a value coming from a proposed model m (i.e., ŷm = m(·∣θm)). For our purposes, it is important to decouple the model generation step from the parameter optimization for each model. An optimal model m* is defined as
has a finite set of parameters θm whose dimension dm depends on the model. We denote the prediction of a model under specific parameter values in functional form as m(·∣θm). We use ŷm to denote the prediction of a value coming from a proposed model m (i.e., ŷm = m(·∣θm)). For our purposes, it is important to decouple the model generation step from the parameter optimization for each model. An optimal model m* is defined as
| | 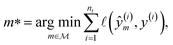 | (1) |
and its optimal parameters are such that
| | 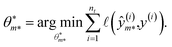 | (2) |
In dynamical systems, the state variables are a function of time, 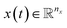 , and represent the evolution of the real dynamical system within a fixed time interval Δt = [t0, tf]. The dynamics are defined by the rates of change
, and represent the evolution of the real dynamical system within a fixed time interval Δt = [t0, tf]. The dynamics are defined by the rates of change 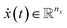 and the initial condition x0 = x(t = t0).
and the initial condition x0 = x(t = t0).
For our kinetic rate models, we assume that the nt sampling times are set within the fixed time interval, t(i) ∈ Δt. The concentration measurements C at each time point t(i) are samples of the real evolution of the system C(i) ≈ x(t(i)), while the rate estimates r are an approximation to the rate of change r(i) ≈ ẋ(t(i)).
Here the available data set 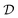 is formed by ordered pairs of time and state measurements
is formed by ordered pairs of time and state measurements 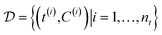 . As before, we use a hat to denote the prediction of either states Ĉm or rates
. As before, we use a hat to denote the prediction of either states Ĉm or rates ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) m coming from a proposed model m. The output of the models with specific parameters θm are denoted as Ĉm(·∣θm) and
m coming from a proposed model m. The output of the models with specific parameters θm are denoted as Ĉm(·∣θm) and ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) m(·∣θm), respectively.
m(·∣θm), respectively.
The complexity of a model is denoted as 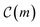 .§ We distinguish between families of expressions with different levels of complexity
.§ We distinguish between families of expressions with different levels of complexity 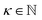 as
as 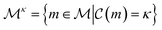 .
.
2.1 Introduction to ADoK-S
For ADoK-S, the objective is to find the model m that best maps the states to the rates:| | ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) m(t∣θm) = m(x(t)∣θm). m(t∣θm) = m(x(t)∣θm). | (3) |
For this to be done directly, an estimation of the rates of change r(i) must be derived from the available concentration measurements C(i). To solve this, our approach forms an intermediate symbolic model η such that η(t(i)) ≈ C(i) following the standard symbolic regression procedure, described in (1) and (2), with our model selection process described in Section 2.3.
Since this model is differentiable, its derivatives provide an approximation to the desired rates: ![[small eta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14f.gif) (t(i)) ≈ r(i). With these estimated values available, the optimization problem can be written as follows. The outer level optimizes over model proposals for a fixed level of complexity κ,
(t(i)) ≈ r(i). With these estimated values available, the optimization problem can be written as follows. The outer level optimizes over model proposals for a fixed level of complexity κ,
| | 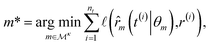 | (4) |
while the inner level optimizes over the best model's parameters,
| | 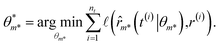 | (5) |
In eqn (4) and (5), 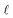 represents the residual sum of squares (RSS). The whole process of this approach is showcased in Fig. 2. The ADoK-S formulation is designed with the versatility to handle complex chemical reaction scenarios, including those involving multiple reactions occurring in parallel or in sequence. However, in this work, we have focused in applying ADoK-S to single-reaction systems. For multi-reaction systems, the approach with ADoK-S differs significantly. Instead of deriving a single, unified model that describes the kinetic rates of all species, ADoK-S needs to create individual models for each reactant and product. This necessity arises because, in multi-reaction systems, the reaction rates for each chemical species do not share a direct relationship via stoichiometric coefficients. An example on the application of ADoK-S to multi-reaction systems can be found in the ‘ESI†‘.
represents the residual sum of squares (RSS). The whole process of this approach is showcased in Fig. 2. The ADoK-S formulation is designed with the versatility to handle complex chemical reaction scenarios, including those involving multiple reactions occurring in parallel or in sequence. However, in this work, we have focused in applying ADoK-S to single-reaction systems. For multi-reaction systems, the approach with ADoK-S differs significantly. Instead of deriving a single, unified model that describes the kinetic rates of all species, ADoK-S needs to create individual models for each reactant and product. This necessity arises because, in multi-reaction systems, the reaction rates for each chemical species do not share a direct relationship via stoichiometric coefficients. An example on the application of ADoK-S to multi-reaction systems can be found in the ‘ESI†‘.
2.2 Introduction to ADoK-W
For ADoK-W, we aim to find the model m that best maps state variables to the differential equation system that define the state dynamics to then predict the concentration evolution:| | 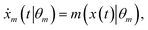 | (6a) |
| | 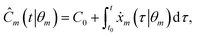 | (6b) |
where the initial condition C0 is the first concentration measurement. For this formulation, the outer level optimizes over model proposals for a specific complexity level κ as well,| | 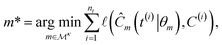 | (7) |
while the inner level optimizes over the parameters of the best model,
| | 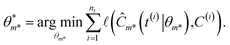 | (8) |
In eqn (7) and (8), 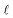 represents the RSS. The whole process of this variation is depicted in Fig. 3. ADoK-W differs from ADoK-S in that it is not suitable for use in multi-reaction systems. This limitation arises from the inherent characteristics of the weak formulation approach, where the equations that form the ODE system that describes the chemical reactions are coupled and cannot be separated into individual components. Consequently, to address this, one would necessitate the proposal and simultaneous evolution of multiple, interconnected symbolic expressions. However, achieving this simultaneous evolution of coupled models effectively remains an open challenge within the research community.
represents the RSS. The whole process of this variation is depicted in Fig. 3. ADoK-W differs from ADoK-S in that it is not suitable for use in multi-reaction systems. This limitation arises from the inherent characteristics of the weak formulation approach, where the equations that form the ODE system that describes the chemical reactions are coupled and cannot be separated into individual components. Consequently, to address this, one would necessitate the proposal and simultaneous evolution of multiple, interconnected symbolic expressions. However, achieving this simultaneous evolution of coupled models effectively remains an open challenge within the research community.
2.3 Model selection
Given a model m with parameters θm of dimension dm, the Akaike information criterion is defined as| | 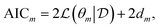 | (9) |
where 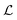 represents specifically the negative log-likelihood (NLL). Given two competing models, m1 and m2, the preferred model would be the one with the lowest AIC value calculated by eqn (9). The choice of AIC for model selection within the ADoK-S and ADoK-W framework is motivated in detail in the ‘Appendix’.
represents specifically the negative log-likelihood (NLL). Given two competing models, m1 and m2, the preferred model would be the one with the lowest AIC value calculated by eqn (9). The choice of AIC for model selection within the ADoK-S and ADoK-W framework is motivated in detail in the ‘Appendix’.
2.4 Model-based design of experiments
It is possible that the data set used for the regression is not enough to provide an adequate model proposal. For this scenario, and under the assumption that the experimental budget is not fully spent, it is possible to leverage the implicit insights in the optimized models to extract an informative proposal for a new experiment. For this purpose, we may search for an initial condition which maximizes the discrepancy between state predictions ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) (t) of the best two proposed models, η and μ, using the available data set. This MBDoE approach was developed in ref. 42:
(t) of the best two proposed models, η and μ, using the available data set. This MBDoE approach was developed in ref. 42:| | 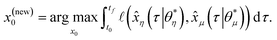 | (10) |
In eqn (10),  represents the RSS. Starting from the proposed initial condition, an experiment can be carried out to obtain a new batch of data points to be added to the original data set. Finally, the whole process of model proposal and selection can be redone with the enhanced data set, closing the loop between informative experiments and optimal models.
represents the RSS. Starting from the proposed initial condition, an experiment can be carried out to obtain a new batch of data points to be added to the original data set. Finally, the whole process of model proposal and selection can be redone with the enhanced data set, closing the loop between informative experiments and optimal models.
3 Catalytic kinetic case studies
To assess the efficacy of our methodologies, we undertook an analysis of three case studies of catalytic reactions drawn from the literature: the hydrodealkylation of toluene,43 the decomposition of nitrous oxide,44 and a theoretical isomerization reaction.45 For conciseness, our discussion focuses primarily on the most complex example – the hydrodealkylation of toluene.
In this study, the selection of catalytic kinetic case studies was carefully considered, primarily to represent different levels of complexity. This choice serves to highlight the adaptability and effectiveness of our proposed framework across a wide range of complexities. Within each specified complexity level, we chose different types of reactions to demonstrate the framework's flexibility in addressing a diverse array of applications, and to ensure that the chosen case studies reflect scenarios commonly encountered in chemical engineering. Additionally, the types of kinetic models represented in these studies are widely found, underscoring the practical applicability of our framework. By choosing these particular examples, we aim to establish that our framework is not just theoretically sound but also capable of addressing typical, real-world challenges faced in the field of chemical engineering.
3.1 The hydrodealkylation of toluene
The hydrodealkylation of toluene reaction can be represented by eqn (11) while eqn (12) provides a description of the reaction rate,43 where the kinetic parameters were defined as: kA = 2 M−1 h−1, KB = 9 M−1 and KC = 5 M−1.| | | C6H5CH3 +H2 ⇌ C6H6 + CH4 | (11) |
| | 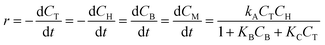 | (12) |
In eqn (12), T, H, B, and M correspond to toluene, hydrogen gas, benzene and methane, respectively. In eqn (12), kA denotes the specific rate constants, whilst KB and KC represent the adsorption constants for benzene and toluene respectively. Starting from eqn (12), an in silico data set is established wherein Δt = [0, 10] h and nt = 30. This data set is composed of five different experiments, each ran at different initial conditions (in molar units: (CT(t = 0), CH(t = 0), CB(t = 0), CM(t = 0)) ∈ {(1, 8, 2, 3), (5, 8, 0, 0.5), (5, 3, 0, 0.5), (1, 3, 0, 3), (1, 8, 2, 0.5)}); these experiments were randomly picked from a 2k factorial design.46
For all experiments, the system is assumed to be both isochoric and isothermal, and Gaussian noise is added to the in silico measurements to simulate a realistic chemical system. The added noise had zero mean and a standard deviation of 0.2 for T, H, B, M. This noise addition allows the approximation of the response of a real system. The generated data set for the second and fourth experiments are presented in (Fig. 4a and e). The data set, providing 150 datapoints, has a realistic size for kinetic studies,31,47,48 especially considering recent advancements in high-throughput setups.
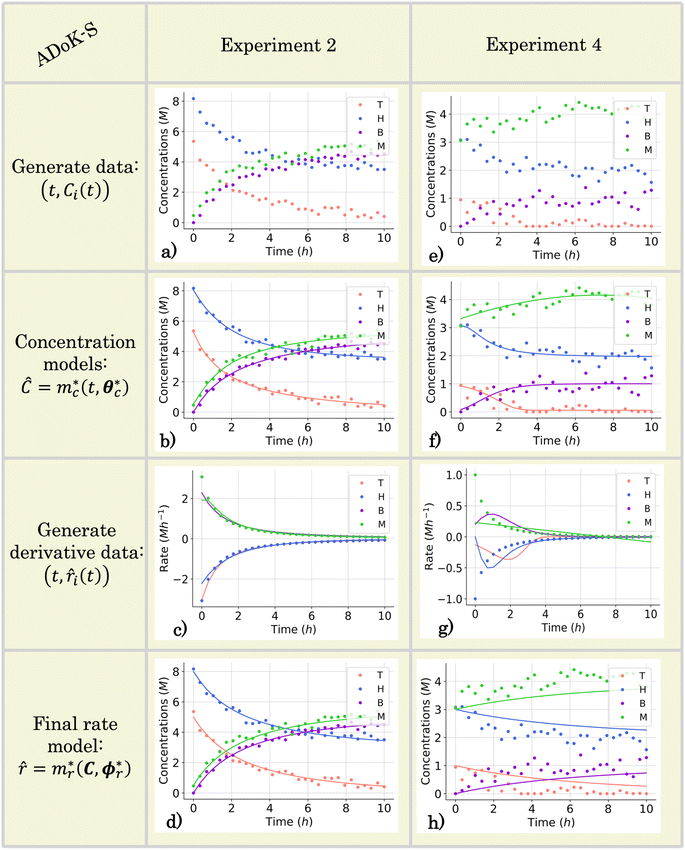 |
| | Fig. 4 The conditions for the second and fourth computational experiment are (CT,0, CH,0, CB,0, CM,0) ∈ (5, 8, 0, 0.5), (1, 3, 0, 3) M, respectively, where T, H, B, M denote toluene, hydrogen, benzene and methane, respectively. (a) and (e) The measured concentration data for the second and fourth experiments which are used in the execution of ADoK-S for the hydrodealkylation of toluene. (b) and (f) The concentration profiles selected by AIC that model the dynamic trajectories of the observable species' concentrations in the second and fourth experiments as a function of time. These models are used to approximate the rate measurements. (c) and (g) Numerical derivatives of the selected concentration profiles and the true rate measurements (which realistically are inaccessible). (d) and (h) Response of the selected rate model after the first iteration of the ADoK-S with the initial set of experiments for the second and fourth experiments. | |
3.2 The decomposition of nitrous oxide
The decomposition of nitrous oxide can be represented by eqn (13) while eqn (14) provides a description of the reaction rate,44 where the kinetic parameters were defined as: kA = 2 M−1 h−1 and kB = 5 M−1.| | 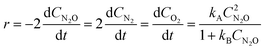 | (14) |
In eqn (14), kA and kB denote specific rate constants. Starting from eqn (14), an in silico data set is established wherein Δt = [0, 10] h and nt = 30. This data set is composed of five different experiments, each ran at different initial conditions (in molar units: (CN2O(t = 0), CN2(t = 0), CO2(t = 0)) ∈ {(5,0,0), (10,0,0), (5,2,0), (5,0,3), (0,2,3)}); these experiments were randomly picked from a 2k factorial design.46
For all experiments, the system is assumed to be both isochoric and isothermal, and Gaussian noise is added to the in silico measurements to simulate a realistic chemical system. The added noise had zero mean and a standard deviation of 0.2 for N2O, N2 and O2. This noise addition allows the approximation of the response of a real system.
3.3 The theoretical isomerization reaction
The isomerization reaction can be represented by eqn (15) while eqn (16) provides a description of the reaction rate,45 where the kinetic parameters were defined as: kA = 7 M h−2, kB = 3 M h−2, kC = 4 h−1, kD = 2 h−1 and kE = 6 M h−1.| | 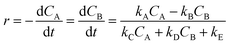 | (16) |
In eqn (16), kA, kB, kC, kD and kE denote specific rate constants. Starting from eqn (16), an in silico data set is established wherein Δt = [0, 10] h and nt = 30. This data set is composed of five different experiments, each ran at different initial conditions (in molar units: (CA(t = 0), CB(t = 0)) ∈ {(2, 0), (10, 0), (2, 2), (10, 2), (10, 1)}); these experiments were randomly picked from a 3k factorial design.49
For all experiments, the system is assumed to be both isochoric and isothermal, and Gaussian noise is added to the in silico measurements to simulate a realistic chemical system. The added noise had zero mean and a standard deviation of 0.2 for A and B. This noise addition allows the approximation of the response of a real system.
4 Results and discussions
4.1 ADoK-S performance – the hydrodealkylation of toluene
As outlined in Fig. 2, the first stage in deriving kinetic models from dynamic concentration trajectories in ADoK-S is proposing concentration profile models. This necessitates the application of a GP algorithm (in ADoK-S we use the implementation from Cranmer41), featuring the following expression construction rules: 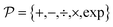 and
and 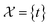 , where t denotes the time variable. This selection is considered reasonable based on our physical understanding of kinetic modeling – a clear route of injecting expert knowledge into the symbolic search.
, where t denotes the time variable. This selection is considered reasonable based on our physical understanding of kinetic modeling – a clear route of injecting expert knowledge into the symbolic search.
It is important to note that at times, the solution to the fundamental ordinary differential equation (ODE) system, delineating the kinetics of the reactive system, may not exist as a closed-form expression. In these cases, any proposed concentration model given any construction rules will be flawed. Nonetheless, in all tested cases, the chosen construction rules have evidenced their capability to successfully approximate the behavior of the concentration trajectories, and more importantly, the rate measurements, regardless of the existence of a closed-form expression.
Fig. 4b and c demonstrate ADoK-S′ ability to approximate the concentration profile as well as the rate measurements of a reactive system. However, Fig. 4f and g shows the opposite, where the ADoK-S seems to capture the appropriate behavior of the dynamic evolution of the concentrations, but provides poor rate approximations. This is because multiple models can closely fit the same concentration data yet yield significantly different gradients, which may lead to poor rate prediction and suboptimal model discovery. These results further motivate the development of ADoK-W and incentivize its use in complicated case studies despite its longer computational time.
In this particular case study, we construct four concentration models for each experiment – specifically, (ĈT,i, ĈH,i, ĈB,i, ĈM,i) for i ∈ [1, 2, …, 5], where i denotes the experiment number. It is important to underscore that the development of each of these models is an autonomous process. Some might contend that this methodology could result in models that violate essential physical principles such as the conservation of mass. However, it is argued that the primary objective at this initial phase is to approximate the system's rate measurements accurately, thereby facilitating the creation of precise kinetic models. Therefore, in this context, a certain level of physical inconsistency might be tolerable.
This section focuses on the results from the second experiment, as the same methodology has been employed across all other experiments. The GP algorithm proposes model structures for the concentrations of T, H, B and M for each complexity level, which is capped by the user. We present below the proposed concentration profiles for T in the second experiment. Here pi represents the ith parameter that can be estimated from the time-dependent concentration data set for a specific model. Further, Ĉi denotes the ith proposed concentration model of species T in the second experiment by ADoK-S.
| | 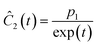 | (17b) |
| | 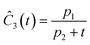 | (17c) |
| | 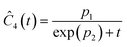 | (17d) |
| | 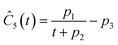 | (17e) |
| | 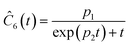 | (17f) |
| | 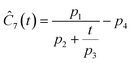 | (17g) |
After the generation of the concentration model structures, the next step involves parameter estimation. This is aimed at finding the optimal values that minimize the error between the response of the concentration models and the measured concentrations.
With parameter values determined, both the negative log-likelihood (NLL) function and the Akaike information criterion (AIC) (eqn (9)) are computed for each model to enable the model selection process. From the proposed models, m7 is the chosen model to approximate the rate of consumption measurements for the second experiment for species T.
Fig. 4b and f presents the concentration models developed, optimized, and selected through ADoK-S for all species in the second and fourth experiment. Following the selection of concentration models, the generation rates (for products) and consumption rates (for reactants) are estimated via numerical differentiation of these models. Fig. 4c and g showcases these estimated rates over time, in comparison with the rate measurements from the real system ẋ(t), generally inaccessible in practice. As mentioned, the methodology excels in the rate estimation for experiment two, but struggles in doing so for experiment four. The early equilibrium (∼2 hours), combined with high additive noise, renders experiment four less kinetically informative, making it challenging for frameworks like ADoK-S to extract meaningful insights and approximate rate measurements.
In alignment with the flowchart presented in Fig. 2, the next stage of ADoK-S employs the same GP algorithm (used to derive concentration profiles) to propose rate models. This procedure unfolds iteratively, refining populations of rate models with the aim to satisfy eqn (4). The rules for constructing expressions are 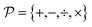 and
and  , a selection based on our prior understanding of kinetic models – yet another route to inject expert knowledge into the methodology, since the choices of the sets
, a selection based on our prior understanding of kinetic models – yet another route to inject expert knowledge into the methodology, since the choices of the sets 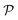 and
and 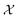 have a significant impact on the breadth of the search space that the GP algorithm explores. In our specific scenario, the reaction rate is influenced solely by the concentrations of the species being measured, as the computational experiments are conducted under constant temperature and volume conditions. It is important to note, however, that while CM does not directly affect the reaction rate, its potential influence cannot be ruled out a priori based on the available kinetic data. Therefore, it is necessary to include CM in the set
have a significant impact on the breadth of the search space that the GP algorithm explores. In our specific scenario, the reaction rate is influenced solely by the concentrations of the species being measured, as the computational experiments are conducted under constant temperature and volume conditions. It is important to note, however, that while CM does not directly affect the reaction rate, its potential influence cannot be ruled out a priori based on the available kinetic data. Therefore, it is necessary to include CM in the set 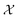 . Additionally, drawing on our experience, we can substantially narrow down the possible operators to the ones we have selected. For instance, we are confident that trigonometric operators will not be a part of the rate model governing the reaction kinetics.
. Additionally, drawing on our experience, we can substantially narrow down the possible operators to the ones we have selected. For instance, we are confident that trigonometric operators will not be a part of the rate model governing the reaction kinetics.
Based on these construction rules, the GP algorithm suggests 13 rate model structures; for the sake of brevity, we present a select few:
| | ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 1 = k1 1 = k1 | (18a) |
| | ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2 = k1CT 2 = k1CT | (18b) |
| | ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 3 = k1CTCH 3 = k1CTCH | (18c) |
| | ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 4 = k1CH − k2CT 4 = k1CH − k2CT | (18d) |
| | ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 5 = k1CTCH − k2CT 5 = k1CTCH − k2CT | (18e) |
| | 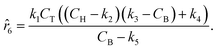 | (18f) |
The parameters ki for i ∈ [1, 2, …, 5] of the dynamical models are estimated from the concentration data, a process known as dynamic parameter estimation. The parameter estimation problem is solved by satisfying eqn (5), utilizing the ABC and LBFGS optimization algorithms to identify the optimal solution. Upon computing the NLL and AIC values for all proposed models, the selected model is ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 3, and its response is presented in Fig. 4d and h.
3, and its response is presented in Fig. 4d and h.
None of the equations shown in eqn (18a), including ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 3, match the data-generating rate model shown in eqn (12). Additionally, as displayed in (Fig. 4h), the model's response is with the concentration data from the fourth experiment as the non-linearities of the profile are not (visually) well-captured. Therefore, ADoK-S must undergo another iteration using MBDoE. For the MBDoE, the top two models yielded by ADoK-S, namely
3, match the data-generating rate model shown in eqn (12). Additionally, as displayed in (Fig. 4h), the model's response is with the concentration data from the fourth experiment as the non-linearities of the profile are not (visually) well-captured. Therefore, ADoK-S must undergo another iteration using MBDoE. For the MBDoE, the top two models yielded by ADoK-S, namely ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 3 and
3 and ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 5, are used to propose a discriminatory experiment by solving eqn (10).
5, are used to propose a discriminatory experiment by solving eqn (10).
The MBDoE procedure suggests running a sixth experiment with initial conditions (CT,0, CH,0, CB,0, CM,0) = (1.948, 7.503, 1.232, 2.504) M. The new experiment undergoes the same sequence of operations as the initial five: generate, optimize, and select the best concentration models to approximate the rates. Once the rates of the new experiment are computed, they are concatenated with the prior approximations, and new rate models are accordingly generated, optimized, and selected. For the sake of brevity, the proposed concentration and rate models are not presented here, but the best (![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 1) and second-best (
1) and second-best (![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2) kinetic models chosen by ADoK-S following the addition of the extra experiment are presented below:
2) kinetic models chosen by ADoK-S following the addition of the extra experiment are presented below:
| | 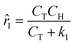 | (19a) |
| | ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2 = k1CT(−k2CB2 + k3CB + k4CH − CT + k5) + k6. 2 = k1CT(−k2CB2 + k3CB + k4CH − CT + k5) + k6. | (19b) |
Although the predictions of the new model improved compared to the initially selected rate model, the model's response is still not satisfactory due to some non-linearities being clearly not captured. As such, ADoK-S undergoes one more iteration where the MBDoE procedure suggests running a seventh experiment with initial conditions (CT,0, CH,0, CB,0, CM,0) = (2.560, 5.654, 0.341, 2.337) M. The kinetic model selected by ADoK-S after the seventh experiment, denoted as r*, is presented below:
| | 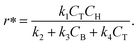 | (20) |
As demonstrated, after two iterations of ADoK-S, the methodology is able to uncover a structurally identical kinetic model (eqn (20)) to the data-generating one (eqn (12)), leading to the termination of the methodology.
4.2 ADoK-W performance – the hydrodealkylation of toluene
As exposed in Section 4.1, ADoK-S demonstrates limitation in approximating rate measurements for complex systems under conditions fraught with noise, as anticipated by.50 This motivates the desirability of circumventing rate estimations for knowledge discovery where possible.
The theoretical shortcomings of ADoK-S, when combined with its suboptimal performance in discerning the ground-truth model underpinning hydrodealkylation of toluene, sparked the creation of ADoK-W. ADoK-W, exploiting the weak formulation of symbolic regression, mitigates the need for rate approximations in proposing rate models. This novel design allows ADoK-W to suggest rate models directly from concentration data, as opposed to limiting model proposals to direct input–output mappings. This innovation lies in incorporating an integration step within the genetic programming algorithm tasked with model proposal.
Nonetheless, beyond this variation, ADoK-W operates in identical fashion to ADoK-S. Initially, models are formulated using genetic programming. The most optimal models in each complexity category are optimized by solving a parameter estimation problem. From the refined model set, the one with the lowest AIC value is selected. Should the modeler find the algorithm output unsatisfactory (and the experimental budget allows), additional experiments guided by MBDoE can be conducted, the measurements concatenated to the previous data set, and another iteration of the ADoK-W algorithm may be executed.
The rules established for rate model construction for ADoK-S remain consistent in the execution of ADoK-W. By solving eqn (7) at different complexity levels, the genetic programming algorithm formulated six rate models, presented below:
| | ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 1 = k1 1 = k1 | (21a) |
| | ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2 = k1CT 2 = k1CT | (21b) |
| | ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 3 = k1CTCH 3 = k1CTCH | (21c) |
| | 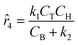 | (21d) |
| | 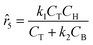 | (21e) |
| | 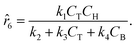 | (21f) |
Following the framework delineated in Fig. 3, upon the proposition of the best rate models, these models are refined by identifying the parameters that satisfy eqn (8). Following optimization, AIC values are computed, and the model with the lowest value is chosen. For this case study, the selected model, r6, coincides exactly with the ground-truth model in eqn (12) without any MBDoE iterations of the methodology. Fig. 5 shows the measured concentration data and the response of the selected kinetic model by ADoK-W for the second and fourth experiments. Comparing it with Fig. 4, we can clearly see how the non-linearities of the fourth experiment are captured after a single iteration, unlike what we see after the first iteration of ADoK-S. Unlike ADoK-S, ADoK-W does not need to estimate rate measurements, which guarantees that there is no source of approximation errors that may affect the effectiveness of the methodology. In this case study, this is apparent in ADoK-W finding the underlying data-generating model after a single iteration, whereas ADoK-S required three iteration to match the same results.
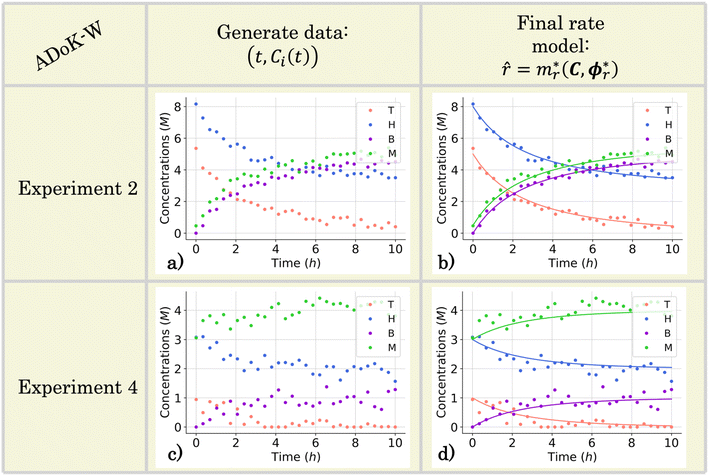 |
| | Fig. 5 The conditions for the second and fourth computational experiment are (CT,0, CH,0, CB,0, CM,0) ∈ (5, 8, 0, 0.5), (1, 3, 0, 3) M, respectively, where T, H, B, M denote toluene, hydrogen, benzene and methane, respectively. (a) and (c) The measured concentration data for the second and fourth experiments which are used in the execution of ADoK-W for the hydrodealkylation of toluene. (b) and (d) Response of the selected rate model after the first and only iteration of the ADoK-W for the second and fourth experiments. | |
4.3 ADoK-S performance – the decomposition of nitrous oxide
Starting with five initial experiments, as delineated in Section 3.2, ADoK-S generated, optimized and selected the presented concentration profiles for each species and experiment. Below, Ĉi,j is the model that describes the dynamic evolution of the concentration of species i during experiment j:| | 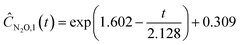 | (22a) |
| | 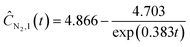 | (22b) |
| | 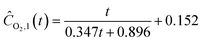 | (22c) |
| | 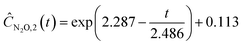 | (22d) |
| | 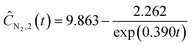 | (22e) |
| | ĈO2,2(t) = t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(exp(−0.094t)) − t exp(exp(−0.094t)) − t | (22f) |
| | | ĈN2O,3(t) = exp(1.520 − 0.418t) + 0.199 | (22g) |
| | ĈN2,3(t) = 6.970−5.032![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−0.385t) exp(−0.385t) | (22h) |
| | 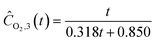 | (22i) |
| | | ĈN2O,4(t) = exp(1.533 − 0.380t) + 0.187 | (22j) |
| | ĈN2,4(t) = 1.560t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−0.122t) exp(−0.122t) | (22k) |
| | | ĈO2,4(t) = 5.343 − exp(1.741 − exp(0.270t)) | (22l) |
Approximations of the rates were calculated by numerically differentiating the concentration profiles. These estimates, in turn, are used to generate rate models. The best two models, based on the AIC ranking, are presented below:
| | 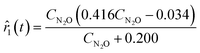 | (23a) |
| | ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2(t) = 0.061 − 0.404CN2O. 2(t) = 0.061 − 0.404CN2O. | (23b) |
Due to unsatisfactory predictions from the top-performing rate model, these two rate models were used to suggest a new experiment with MBDoE. The proposed experiment is (CN2O(t = 0), CN2(t = 0), CO2(t = 0)) = (0.000, 1.641, 1.095) M. For the sixth experiment, ADoK-S generated, optimized and selected the presented concentration profiles.
By approximating the rate measurements from the sixth experiment and concatenating the estimates to the previous data set, ADoK-S uncovers the structure and similar parameters to the data-generating rate model:
| | 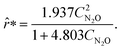 | (25) |
4.4 ADoK-W performance – the decomposition of nitrous oxide
Starting from the initial five experiments, ADoK-W generated and optimized a plethora of rate models, outputting the best two models (based on AIC ranking) presented below:| | 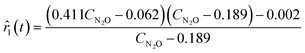 | (26a) |
| | ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2(t) = 0.411CN2O − 0.068. 2(t) = 0.411CN2O − 0.068. | (26b) |
Due to unsatisfactory predictions from the top-performing rate model, these two rate models were used to suggest a new experiment with MBDoE. The proposed experiment is (CN2O(t = 0), CN2(t = 0), CO2(t = 0)) = (0.189, 0.913, 0.926) M. After concatenating the measurements collected from the sixth experiment, ADoK-W was still unable to uncover the data-generating model. Instead, the methodology output the following models as the best and second-best models according to the AIC ranking:
| | 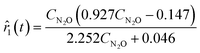 | (27a) |
| | ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2(t) = 0.414CN2O − 0.074. 2(t) = 0.414CN2O − 0.074. | (27b) |
With these two rate models, a new experiment was suggested using MBDoE. The proposed experiment is (CN2O(t = 0), CN2(t = 0), CO2(t = 0)) = (0.000,1.641,1.095) M. After concatenating the measurements collected from the seventh experiment, ADoK-S uncovers the structure and similar parameters to the data-generating rate model:
| | 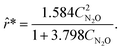 | (28) |
In this case study, ADoK-W performed worse than ADoK-S by needing one more iteration to reach the same results. Circumventing rate approximations is a significant benefit in ADoK-W, albeit not without a price. Adding the integration step within the model generation stage of the framework increases its computation time: within the same time budget, ADoK-S can evaluate more models than ADoK-W. As such, we may conclude that having a lower function-evaluation budget than ADoK-S caused ADoK-W to show a worse performance in this case study.
4.5 ADoK-S performance – the theoretical isomerization reaction
Starting with five initial experiments, as delineated in Section 3.3, ADoK-S generated, optimized and selected the presented concentration profiles for each species and experiment. Below, Ĉi,j is the model that describes the dynamic evolution of the concentration of species i during experiment j:| | | ĈA,1(t) = exp(1.470 − exp(0.642t)) + 0.634 | (29a) |
| | 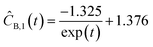 | (29b) |
| | | ĈA,2(t) = 0.075t2 − 1.375t + 9.981 | (29c) |
| | ĈB,2(t) = t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−0.084t + 0.399) exp(−0.084t + 0.399) | (29d) |
| | | ĈA,3(t) = exp(−0.615t) + 1.213 | (29e) |
| | | ĈB,3(t) = exp(1.040 − exp(−1.189 − t)) | (29f) |
| | 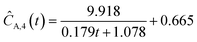 | (29g) |
| | | ĈB,4(t) = −0.055t2 + 1.128t + 2.087 | (29h) |
| | 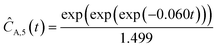 | (29i) |
| | | ĈB,5(t) = 0.608t + 2.069. | (29j) |
Approximations of the rates were calculated by numerically differentiating the concentration profiles. These estimates, in turn, are used to generate rate models. The best two models, based on the AIC ranking, are presented below:
| | 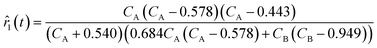 | (30a) |
| | 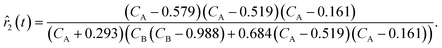 | (30b) |
Due to unsatisfactory predictions from the top-performing rate model, these two rate models were used to suggest a new experiment with MBDoE. The proposed experiment is (CA(t = 0), CB(t = 0)) = (4.926, 0.000) M. For the sixth experiment, ADoK-S generated, optimized and selected the presented concentration profiles.
| | 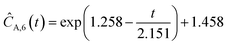 | (31a) |
| | 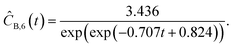 | (31b) |
By approximating the rate measurements from the sixth experiment and concatenating the estimates to the previous data set, ADoK-S uncovers the structure and similar parameters to the data-generating rate model:
| | 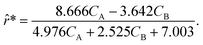 | (32) |
4.6 ADoK-W performance – the theoretical isomerization reaction
Starting from the initial five experiments, ADoK-W generated and optimized a plethora of rate models, outputting the best two models (based on AIC ranking) presented below:| | 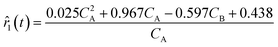 | (33a) |
| | 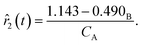 | (33b) |
With these two rate models, a new experiment was suggested using MBDoE. The proposed experiment is (CA(t = 0), CB(t = 0)) = (7.319, 2.000) M. After concatenating the measurements collected from the sixth experiment, ADoK-W managed to nearly rediscover the data-generating kinetic rate model; the model selected having an extra parameter in the numerator. Nevertheless, it is argued that the extra kinetic parameter is considerably smaller than the rest, which would inevitably lead to its deletion upon further investigation or model reduction.
| | 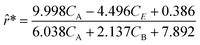 | (34) |
In this case study, ADoK-W performed as well as ADoK-S by needing the same iterations to reach the data-generating kinetic model. Similarly to the conclusions presented in the decomposition of nitrous oxide, having a lower function–evaluation budget than ADoK-S can offset the benefits presented from not having to approximate rate measurements. In this case study, this manifested itself by ADoK-S and ADoK-W having the same performance.
5 Conclusions
In this work, we introduce two data-driven frameworks, ADoK-S and ADoK-W, which tackle the symbolic regression problem to discover kinetic rate models from noisy concentration measurements. Using a genetic programming algorithm coupled with parameter estimation and an information criterion, these methods generate, refine, and select models without undue restrictions. An information criterion is preferred over a traditional data-splitting procedure for model selection because it enables the utilization of the full data set in building models while still providing a solid method for model validation. This strategy is especially advantageous in scenarios with limited data, as it ensures that all available information is leveraged to identify suitable models. Unlike black-box and hybrid models that may obscure interpretability, or traditional mechanistic models that could be time and resource intensive to construct, our methods offer a transparent and efficient process for interpretable model development.
While ADoK-S necessitates rate measurements to propose rate models, in line with a strong formulation, ADoK-W bypasses this need, directly creating rate models from concentration data, a characteristic of a weak formulation. In the case study of hydrodealkylation of toluene, both methods successfully identified the underlying rate model of the reaction.
However, due to errors in rate approximations and system complexity, ADoK-S required two extra iterations to discover the ground-truth kinetic model. On the other hand, ADoK-W found the data-generating model using solely the initial five experiments, showing better performance in complex spaces, albeit without ‘free lunch’. Where ADoK-S can propose rate models within minutes, ADoK-W requires hours to do the same.
The results from the case studies highlight the potential of using automated knowledge discovery methods in kinetic model development in reaction engineering and catalysis. The summarized results are presented in Table 1. While we demonstrated this potential with minimal prior knowledge, the long computation times hint at the need for integrating physical constraints, like the law of conservation of mass and equilibrium behavior, to reduce the search space and improve computational efficiency.
Table 1 The summarized results of the performance of ADoK-S and ADoK-S against all three case studies explored
|
|
Hypothetical isomerization reaction |
Decomposition of nitrous oxide |
Hydrodealkylation of toluene |
| Number of iterations – ADoK-S |
2 |
2 |
3 |
| Number of iterations – ADoK-W |
2 |
3 |
1 |
| Data-generating kinetic model |
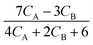
|
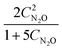
|
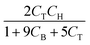
|
| Rate model uncovered – ADoK-S |
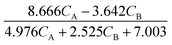
|
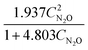
|
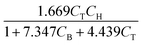
|
| Rate model uncovered – ADoK-W |
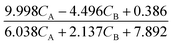
|
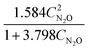
|
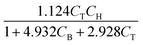
|
It is important to mention that the success of any data-driven approach, including the ones presented here, depends heavily on the data used. The data assumptions made in this case study may not always hold true. For fast reactions or reactions with different species, the sampling rate and assuming that all species can be measured might be unrealistic. The assumption of perfect device calibration and no systematic errors, although optimistic, may not always be an accurate representation of real experimental setups.
Lastly, while ADoK-S and ADoK-W have been designed for discovering kinetic models of catalytic systems, they can be extended without major modifications to explore the dynamics of non-reactive systems. This broadens their potential applications to other fields and disciplines.
Nomenclature
|
Γ
| Set of arbitrary number of constants |
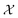
| Set of a fixed number of variables |
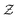
| Set of the union of an arbitrary number of constants and a fixed number of variables |
| ⋄ | Set of arithmetic operations  |
|
Λ
| Set of special one-dimensional functions 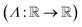 |
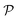
| Set of the union of arithmetic operations and a finite set of special one-dimensional functions |
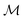
| Model search space reachable by function composition of the operator set 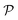 over the set over the set 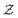 |
|
n
x
| Dimensions of state vectors |
|
x
| State vectors 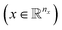 |
|
y
| Target value 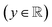 |
|
f
| Unknown function that maps state vectors to target values (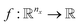 : y = f(x)) : y = f(x)) |
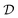
| Data set |
|
n
t
| Sampling times |
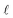
| A positive measure function that quantifies the discrepancy between the predictions and the target values |
|
m
| A symbolic model 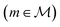 |
|
θ
m
| A finite set of parameters that parameterize a model m |
|
d
m
| The dimensions of model m |
|
m(·∣θm) | The prediction of a model under specific parameter values in functional form |
|
ŷ
m
| The prediction of a value coming from a proposed model m (i.e., ŷm = m(·∣θm)) |
|
m* | An optimal model |
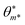
| The optimal set of parameters of an optimal model m* |
| Δt | A fixed time interval |
|
ẋ(t) | The rates of change of the state vectors |
|
x
0
| Initial conditions of a dynamic system (x0 = x(t = t0) |
|
C
| Concentration measurements: samples of the real evolution of a dynamic system |
|
r
| Rate estimates: approximations of the rate of change (r(i) ≈ ẋ(t(i))) |
|
Ĉ
m
| Prediction of the concentrations made by model m |
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) m
m
| Prediction of the rates of change made by model m |
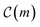
| Complexity of a model |
|
κ
| Level of complexity of a model set (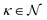 as as 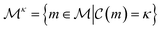 ) ) |
![[small eta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14f.gif) (t) (t) | Derivatives of a concentration model which provides an approximation to the rates of change (![[small eta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14f.gif) (t(i) ≈ r(i)) (t(i) ≈ r(i)) |
|
C
0
| Initial condition: first concentration measurement |
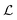
| The negative log-likelihood function 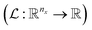 |
|
k
| The kinetic parameters of a kinetic rate model |
|
p
| The parameters of a concentration model |
Data availability
The code used to produce all results and graphs shown in this work can be accessed at https://github.com/MACServia/auto_discov_kin_rate_models.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by the Engineering and Physical Sciences Research Council (EPSRC) funding grant EP/S023232/1.
References
- C. Song, T. Koren, P. Wang and A. L. Barabási, Modelling the scaling properties of human mobility, Nat. Phys., 2010, 6(10), 818–823 Search PubMed.
- D. Brockmann, L. Hufnagel and T. Geisel, The scaling laws of human travel, Nature, 2006, 439(7075), 462–465 CrossRef CAS PubMed.
- L. C. Franssen, T. Lorenzi, A. E. F. Burgess and M. A. J. Chaplain, A Mathematical Framework for Modelling the Metastatic Spread of Cancer, Bull. Math. Biol., 2019, 81(6), 1965–2010 CrossRef CAS PubMed.
- D. H. Margarit and L. Romanelli, A mathematical model of absorbing Markov chains to understand the routes of metastasis, Biomathematics, 2016, 5(1), 1607281 Search PubMed.
- N. S. Schbib, M. A. García, C. E. Gígola and A. F. Errazu, Kinetics of Front-End Acetylene Hydrogenation in Ethylene Production, Ind. Eng. Chem. Res., 1996, 35(5), 1496–1505 CrossRef CAS.
- G. C. Battiston, L. Dalloro and G. R. Tauszik, Performance and aging of catalysts for the selective hydrogenation of acetylene: a micropilot-plant study, Appl. Catal., 1982, 2(1–2), 1–17 CAS.
- R. E. Baker, J. M. Peña, J. Jayamohan and A. Jérusalem, Mechanistic models versus machine learning, a fight worth fighting for the biological community?, Biol. Lett., 2018, 14(5), 20170660 CrossRef PubMed.
- K. V. Gernaey, A Perspective on PSE in Fermentation Process Development and Operation, Comput.-Aided Chem. Eng., 2015, 123–130 CAS.
- I. Jimenez del Val, J. M. Nagy and C. Kontoravdi, A dynamic mathematical model for monoclonal antibody N-linked glycosylation and nucleotide sugar donor transport within a maturing Golgi apparatus, Biotechnol. Prog., 2011, 27(6), 1730–1743 CrossRef CAS PubMed.
- P. M. Jedrzejewski, I. J. Jimenez del Val, A. Constantinou, A. Dell, S. M. Haslam and K. M. Polizzi,
et al., Towards Controlling the Glycoform: A Model Framework Linking Extracellular Metabolites to Antibody Glycosylation, Int. J. Mol. Sci., 2014, 15(3), 4492–4522 CrossRef PubMed.
- R. T. Giessmann, N. Krausch, F. Kaspar, M. N. Cruz Bournazou, A. Wagner and P. Neubauer,
et al., Dynamic Modelling of Phosphorolytic Cleavage Catalyzed by Pyrimidine-Nucleoside Phosphorylase, Processes, 2019, 7(6), 380 CrossRef CAS.
- H. R. S. Anna, A. G. Barreto, F. W. Tavares and M. B. de Souza, Machine learning model and optimization of a PSA unit for methane-nitrogen separation, Comput. Chem. Eng., 2017, 104, 377–391 CrossRef.
- D. Zhang, E. A. del Rio-Chanona, P. Petsagkourakis and J. Wagner, Hybrid physics-based and data-driven modeling for bioprocess online simulation and optimization, Biotechnol. Bioeng., 2019, 116(11), 2919–2930 CrossRef CAS PubMed.
- E. A. del Rio-Chanona, X. Cong, E. Bradford, D. Zhang and K. Jing, Review of advanced physical and data-driven models for dynamic bioprocess simulation: case study of algae–bacteria consortium wastewater treatment, Biotechnol. Bioeng., 2018, 116(2), 342–353 CrossRef PubMed.
- S. Y. Park, C. H. Park, D. H. Choi, J. K. Hong and D. Y. Lee, Bioprocess digital twins of mammalian cell culture for advanced biomanufacturing, Curr. Opin. Chem. Eng., 2021, 33, 100702 CrossRef.
-
Y. Sun, W. Nathan-Roberts, T. D. Pham, E. Otte and U. Aickelin, Multi-fidelity Gaussian Process for Biomanufacturing Process Modeling with Small Data, arXiv, 2022, preprint, arXiv:221114493, DOI:10.48550/arXiv.2211.14493.
- P. Petsagkourakis, I. O. Sandoval, E. Bradford, D. Zhang and E. A. del Rio-Chanona, Reinforcement learning for batch bioprocess optimization, Comput. Chem. Eng., 2020, 133, 106649 CrossRef CAS.
- E. A. del Rio-Chanona, J. L. Wagner, H. Ali, F. Fiorelli, D. Zhang and K. Hellgardt, Deep learning-based surrogate modeling and optimization for microalgal biofuel production and
photobioreactor design, AIChE J., 2018, 65(3), 915–923 CrossRef.
- G. Wu, M. Á. de Carvalho Servia and M. Mowbray, Distributional reinforcement learning for inventory management in multi-echelon supply chains, Digital Chemical Engineering, 2023, 6, 100073 CrossRef.
- P. Natarajan, R. Moghadam and S. Jagannathan, Online deep neural network-based feedback control of a Lutein bioprocess, J. Process Control, 2021, 98, 41–51 CrossRef CAS.
- M. Mowbray, H. Kay, S. Kay, P. C. Caetano, A. Hicks and C. Mendoza,
et al., Probabilistic machine learning based soft-sensors for product quality prediction in batch processes, Chemom. Intell. Lab. Syst., 2022, 228, 104616 CrossRef CAS.
- S. Kay, H. Kay, M. Mowbray, A. Lane, C. Mendoza and P. Martin,
et al., Integrating Autoencoder and Heteroscedastic Noise Neural Networks for the Batch Process Soft-Sensor Design, Ind. Eng. Chem. Res., 2022, 61(36), 13559–13569 CrossRef CAS PubMed.
- P. Kadlec, B. Gabrys and S. Strandt, Data-driven Soft Sensors in the process industry, Comput. Chem. Eng., 2009, 33(4), 795–814 CrossRef CAS.
- F. Vega-Ramon, X. Zhu, T. R. Savage, P. Petsagkourakis, K. Jing and D. Zhang, Kinetic and hybrid modeling for yeast astaxanthin production under uncertainty, Biotechnol. Bioeng., 2021, 118(12), 4854–4866 CrossRef CAS PubMed.
- M. R. Mowbray, C. Wu, A. W. Rogers, E. A. del Rio-Chanona and D. Zhang, A reinforcement learning-based hybrid modeling framework for bioprocess kinetics identification, Biotechnol. Bioeng., 2022, 120(1), 154–168 CrossRef PubMed.
- D. Zhang, T. R. Savage and B. A. Cho, Combining model structure identification and hybrid modelling for photo-production process predictive simulation and optimisation, Biotechnol. Bioeng., 2020, 117(11), 3356–3367 CrossRef CAS PubMed.
- C. Haider, F. O. de Franca, B. Burlacu and G. Kronberger, Shape-constrained multi-objective genetic programming for symbolic regression, Appl. Soft Comput., 2023, 132, 109855 CrossRef.
- Z. T. Wilson and N. V. Sahinidis, The ALAMO approach to machine learning, Comput. Chem. Eng., 2017, 106, 785–795 CrossRef.
- S. L. Brunton, J. L. Proctor and J. N. Kutz, Discovering governing equations from data by sparse identification of nonlinear dynamical systems, Proc. Natl. Acad. Sci. U.S.A., 2016, 113(15), 3932–3937 CrossRef CAS PubMed.
- J. R. Koza, Genetic programming as a means for programming computers by natural selection, Comput. Stat., 1994, 4(2), 87–112 Search PubMed.
- C. J. Taylor, M. Booth, J. A. Manson, M. J. Willis, G. Clemens and B. A. Taylor,
et al., Rapid, automated determination of reaction models and kinetic parameters, J. Chem. Eng., 2021, 413, 127017 CrossRef CAS.
- P. Neumann, L. Cao, D. Russo, V. S. Vassiliadis and A. A. Lapkin, A new formulation for symbolic regression to identify physico-chemical laws from experimental data, J. Chem. Eng., 2020, 387, 123412 CrossRef CAS.
- T. Forster, D. Vázquez, M. N. Cruz-Bournazou, A. Butté and G. Guillén-Gosálbez, Modeling of bioprocesses via MINLP-based symbolic regression of S-system formalisms, Comput. Chem. Eng., 2023, 170, 108108 CrossRef CAS.
- H. Iba, Inference of differential equation models by genetic programming, Inf. Sci., 2008, 178(23), 4453–4468 CrossRef . Including Special Section: Genetic and Evolutionary Computing..
-
M. S. Nobile, D. Besozzi, P. Cazzaniga, D. Pescini and G. Mauri, Reverse engineering of kinetic reaction networks by means of Cartesian Genetic Programming and Particle Swarm Optimization, in 2013 IEEE Congress on Evolutionary Computation, 2013, pp. 1594–601 Search PubMed.
- S. Datta, V. A. Dev and M. R. Eden, Developing non-linear rate constant QSPR using decision trees and multi-gene genetic programming, Comput. Chem. Eng., 2019, 127, 150–157 CrossRef CAS.
- M. Sugimoto, S. Kikuchi and M. Tomita, Reverse engineering of biochemical equations from time-course data by means of genetic programming, BioSystems, 2005, 80(2), 155–164 CrossRef CAS PubMed.
- T. W. Cornforth and H. Lipson, Inference of hidden variables in systems of differential equations with genetic programming, Genet. Program. Evolvable Mach., 2012, 14(2), 155–190 CrossRef.
- F. V. Van Breugel, J. N. Kutz and B. W. Brunton, Numerical Differentiation of Noisy Data: A Unifying Multi-Objective Optimization Framework, IEEE Access, 2020, 8, 196865–196877, DOI:10.1109/access.2020.3034077.
-
M. Virgolin and S. P. Pissis, Symbolic Regression is NP-hard, Trans. Mach. Learn Res., 2022, 2835–8856, Available from: https://openreview.net/forum?id=LTiaPxqe2e Search PubMed.
-
M. Cranmer, Interpretable Machine Learning for Science with PySR and Symbolic Regression, arXiv, 2023, preprint, arXiv:2305.01582, DOI:10.48550/arXiv.2305.01582.
- W. G. Hunter and A. M. Reiner, Designs for Discriminating Between Two Rival Models, Technometrics, 1965, 7(3), 307–323 CrossRef.
-
H. S. Fogler, Elements of chemical reaction engineering, Prentice Hall, Philadelphia, PA, 5th edn 2016 Search PubMed.
-
O. Levenspiel, Chemical Reaction Engineering, John Wiley & Sons, Nashville, TN, 3rd edn, 1998 Search PubMed.
-
G. B. Marin, G. S. Yablonsky and D. Constales, Kinetics of chemical reactions: decoding complexity, John Wiley & Sons, 2019 Search PubMed.
-
R. Mee, A comprehensive guide to factorial two-level experimentation, Springer Science & Business Media, 2009 Search PubMed.
- L. Schrecker, J. Dickhaut, C. Holtze, P. Staehle, M. Vranceanu and K. Hellgardt,
et al., Discovery of unexpectedly complex reaction pathways for the Knorr pyrazole synthesis via transient flow, React. Chem. Eng., 2023, 8(1), 41–46 RSC.
- C. Waldron, A. Pankajakshan, M. Quaglio, E. Cao, F. Galvanin and A. Gavriilidis, Model-based design of transient flow experiments for the identification of kinetic parameters, React. Chem. Eng., 2020, 5, 112–123 RSC.
- J. K. Telford, A brief introduction to design of experiments, Johns Hopkins APL Tech. Dig., 2007, 27(3), 224–232 Search PubMed.
- D. Bertsimas and W. Gurnee, Learning sparse nonlinear dynamics via mixed-integer optimization, Nonlinear Dyn., 2023, 111(7), 6585–6604 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: (1) A detailed evaluation of various model selection criteria, leading to the adoption of AIC for both ADoK-S and ADoK-W; (2) an analytical discussion leading to the utilization of the two top-performing models from ADoK-S or ADoK-W in MBDoE, as opposed to using Gaussian process state space models and other naive parametric models; (3) a benchmarking study comparing state-of-the-art derivative approximation methods against our GP-based approach; (4) the performance of ADoK-S on an additional multi-reaction case study. See DOI: https://doi.org/10.1039/d3dd00212h |
| ‡ Selection of AIC among other criteria is explained in the ‘Appendix’. |
| § Here we use the number of nodes in an expression tree as the complexity of a symbolic expression.41 |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Ilya Orson
Sandoval
a,
Ilya Orson
Sandoval
 a,
King Kuok (Mimi)
Hii
a,
King Kuok (Mimi)
Hii
 b,
Klaus
Hellgardt
b,
Klaus
Hellgardt
 a,
Dongda
Zhang
a,
Dongda
Zhang
 *c and
Ehecatl
Antonio del Rio Chanona
*c and
Ehecatl
Antonio del Rio Chanona
 *a
*a

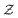 is the union of an arbitrary number of constants Γ and a fixed number of variables
is the union of an arbitrary number of constants Γ and a fixed number of variables 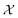 . The operator set
. The operator set 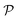 is the union of arithmetic operations
is the union of arithmetic operations 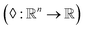 and a finite set of special one-dimensional functions
and a finite set of special one-dimensional functions 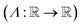 . The model search space
. The model search space 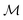 is the space of possible expressions to be reached by iterative function composition of the operator set
is the space of possible expressions to be reached by iterative function composition of the operator set 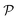 over the set
over the set 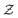 .
.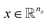 . A data point is a pair of specific states x and the associated target value
. A data point is a pair of specific states x and the associated target value 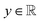 of an unknown function
of an unknown function 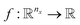 : y = f(x). The data set
: y = f(x). The data set 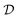 consists of nt data points:
consists of nt data points: 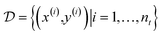 . To quantify the discrepancy between the predictions and the target values, we can leverage any adequate positive measure function
. To quantify the discrepancy between the predictions and the target values, we can leverage any adequate positive measure function 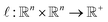 .
.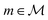 has a finite set of parameters θm whose dimension dm depends on the model. We denote the prediction of a model under specific parameter values in functional form as m(·∣θm). We use ŷm to denote the prediction of a value coming from a proposed model m (i.e., ŷm = m(·∣θm)). For our purposes, it is important to decouple the model generation step from the parameter optimization for each model. An optimal model m* is defined as
has a finite set of parameters θm whose dimension dm depends on the model. We denote the prediction of a model under specific parameter values in functional form as m(·∣θm). We use ŷm to denote the prediction of a value coming from a proposed model m (i.e., ŷm = m(·∣θm)). For our purposes, it is important to decouple the model generation step from the parameter optimization for each model. An optimal model m* is defined as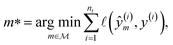
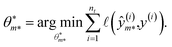
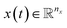 , and represent the evolution of the real dynamical system within a fixed time interval Δt = [t0, tf]. The dynamics are defined by the rates of change
, and represent the evolution of the real dynamical system within a fixed time interval Δt = [t0, tf]. The dynamics are defined by the rates of change 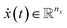 and the initial condition x0 = x(t = t0).
and the initial condition x0 = x(t = t0).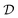 is formed by ordered pairs of time and state measurements
is formed by ordered pairs of time and state measurements 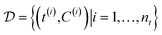 . As before, we use a hat to denote the prediction of either states Ĉm or rates
. As before, we use a hat to denote the prediction of either states Ĉm or rates ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) m coming from a proposed model m. The output of the models with specific parameters θm are denoted as Ĉm(·∣θm) and
m coming from a proposed model m. The output of the models with specific parameters θm are denoted as Ĉm(·∣θm) and ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) m(·∣θm), respectively.
m(·∣θm), respectively.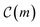 .§ We distinguish between families of expressions with different levels of complexity
.§ We distinguish between families of expressions with different levels of complexity 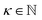 as
as 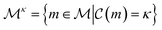 .
.![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) m(t∣θm) = m(x(t)∣θm).
m(t∣θm) = m(x(t)∣θm).![[small eta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e14f.gif) (t(i)) ≈ r(i). With these estimated values available, the optimization problem can be written as follows. The outer level optimizes over model proposals for a fixed level of complexity κ,
(t(i)) ≈ r(i). With these estimated values available, the optimization problem can be written as follows. The outer level optimizes over model proposals for a fixed level of complexity κ,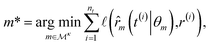
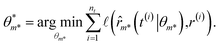
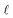 represents the residual sum of squares (RSS). The whole process of this approach is showcased in Fig. 2. The ADoK-S formulation is designed with the versatility to handle complex chemical reaction scenarios, including those involving multiple reactions occurring in parallel or in sequence. However, in this work, we have focused in applying ADoK-S to single-reaction systems. For multi-reaction systems, the approach with ADoK-S differs significantly. Instead of deriving a single, unified model that describes the kinetic rates of all species, ADoK-S needs to create individual models for each reactant and product. This necessity arises because, in multi-reaction systems, the reaction rates for each chemical species do not share a direct relationship via stoichiometric coefficients. An example on the application of ADoK-S to multi-reaction systems can be found in the ‘ESI†‘.
represents the residual sum of squares (RSS). The whole process of this approach is showcased in Fig. 2. The ADoK-S formulation is designed with the versatility to handle complex chemical reaction scenarios, including those involving multiple reactions occurring in parallel or in sequence. However, in this work, we have focused in applying ADoK-S to single-reaction systems. For multi-reaction systems, the approach with ADoK-S differs significantly. Instead of deriving a single, unified model that describes the kinetic rates of all species, ADoK-S needs to create individual models for each reactant and product. This necessity arises because, in multi-reaction systems, the reaction rates for each chemical species do not share a direct relationship via stoichiometric coefficients. An example on the application of ADoK-S to multi-reaction systems can be found in the ‘ESI†‘.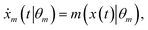
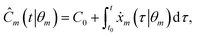
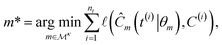
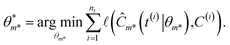
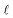 represents the RSS. The whole process of this variation is depicted in Fig. 3. ADoK-W differs from ADoK-S in that it is not suitable for use in multi-reaction systems. This limitation arises from the inherent characteristics of the weak formulation approach, where the equations that form the ODE system that describes the chemical reactions are coupled and cannot be separated into individual components. Consequently, to address this, one would necessitate the proposal and simultaneous evolution of multiple, interconnected symbolic expressions. However, achieving this simultaneous evolution of coupled models effectively remains an open challenge within the research community.
represents the RSS. The whole process of this variation is depicted in Fig. 3. ADoK-W differs from ADoK-S in that it is not suitable for use in multi-reaction systems. This limitation arises from the inherent characteristics of the weak formulation approach, where the equations that form the ODE system that describes the chemical reactions are coupled and cannot be separated into individual components. Consequently, to address this, one would necessitate the proposal and simultaneous evolution of multiple, interconnected symbolic expressions. However, achieving this simultaneous evolution of coupled models effectively remains an open challenge within the research community.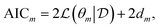
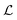 represents specifically the negative log-likelihood (NLL). Given two competing models, m1 and m2, the preferred model would be the one with the lowest AIC value calculated by eqn (9). The choice of AIC for model selection within the ADoK-S and ADoK-W framework is motivated in detail in the ‘Appendix’.
represents specifically the negative log-likelihood (NLL). Given two competing models, m1 and m2, the preferred model would be the one with the lowest AIC value calculated by eqn (9). The choice of AIC for model selection within the ADoK-S and ADoK-W framework is motivated in detail in the ‘Appendix’.
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) (t) of the best two proposed models, η and μ, using the available data set. This MBDoE approach was developed in ref. 42:
(t) of the best two proposed models, η and μ, using the available data set. This MBDoE approach was developed in ref. 42:
 represents the RSS. Starting from the proposed initial condition, an experiment can be carried out to obtain a new batch of data points to be added to the original data set. Finally, the whole process of model proposal and selection can be redone with the enhanced data set, closing the loop between informative experiments and optimal models.
represents the RSS. Starting from the proposed initial condition, an experiment can be carried out to obtain a new batch of data points to be added to the original data set. Finally, the whole process of model proposal and selection can be redone with the enhanced data set, closing the loop between informative experiments and optimal models.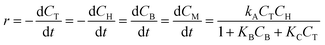
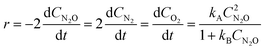
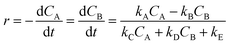
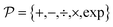 and
and  , where t denotes the time variable. This selection is considered reasonable based on our physical understanding of kinetic modeling – a clear route of injecting expert knowledge into the symbolic search.
, where t denotes the time variable. This selection is considered reasonable based on our physical understanding of kinetic modeling – a clear route of injecting expert knowledge into the symbolic search.
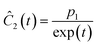
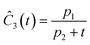
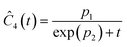
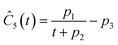
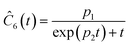
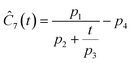
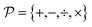 and
and  , a selection based on our prior understanding of kinetic models – yet another route to inject expert knowledge into the methodology, since the choices of the sets
, a selection based on our prior understanding of kinetic models – yet another route to inject expert knowledge into the methodology, since the choices of the sets  and
and  have a significant impact on the breadth of the search space that the GP algorithm explores. In our specific scenario, the reaction rate is influenced solely by the concentrations of the species being measured, as the computational experiments are conducted under constant temperature and volume conditions. It is important to note, however, that while CM does not directly affect the reaction rate, its potential influence cannot be ruled out a priori based on the available kinetic data. Therefore, it is necessary to include CM in the set
have a significant impact on the breadth of the search space that the GP algorithm explores. In our specific scenario, the reaction rate is influenced solely by the concentrations of the species being measured, as the computational experiments are conducted under constant temperature and volume conditions. It is important to note, however, that while CM does not directly affect the reaction rate, its potential influence cannot be ruled out a priori based on the available kinetic data. Therefore, it is necessary to include CM in the set 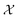 . Additionally, drawing on our experience, we can substantially narrow down the possible operators to the ones we have selected. For instance, we are confident that trigonometric operators will not be a part of the rate model governing the reaction kinetics.
. Additionally, drawing on our experience, we can substantially narrow down the possible operators to the ones we have selected. For instance, we are confident that trigonometric operators will not be a part of the rate model governing the reaction kinetics.![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 1 = k1
1 = k1![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2 = k1CT
2 = k1CT![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 3 = k1CTCH
3 = k1CTCH![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 4 = k1CH − k2CT
4 = k1CH − k2CT![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 5 = k1CTCH − k2CT
5 = k1CTCH − k2CT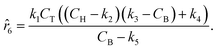
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 3, and its response is presented in Fig. 4d and h.
3, and its response is presented in Fig. 4d and h.![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 3, match the data-generating rate model shown in eqn (12). Additionally, as displayed in (Fig. 4h), the model's response is with the concentration data from the fourth experiment as the non-linearities of the profile are not (visually) well-captured. Therefore, ADoK-S must undergo another iteration using MBDoE. For the MBDoE, the top two models yielded by ADoK-S, namely
3, match the data-generating rate model shown in eqn (12). Additionally, as displayed in (Fig. 4h), the model's response is with the concentration data from the fourth experiment as the non-linearities of the profile are not (visually) well-captured. Therefore, ADoK-S must undergo another iteration using MBDoE. For the MBDoE, the top two models yielded by ADoK-S, namely ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 3 and
3 and ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 5, are used to propose a discriminatory experiment by solving eqn (10).
5, are used to propose a discriminatory experiment by solving eqn (10).![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 1) and second-best (
1) and second-best (![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2) kinetic models chosen by ADoK-S following the addition of the extra experiment are presented below:
2) kinetic models chosen by ADoK-S following the addition of the extra experiment are presented below: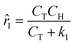
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2 = k1CT(−k2CB2 + k3CB + k4CH − CT + k5) + k6.
2 = k1CT(−k2CB2 + k3CB + k4CH − CT + k5) + k6.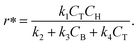
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 1 = k1
1 = k1![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2 = k1CT
2 = k1CT![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 3 = k1CTCH
3 = k1CTCH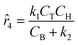
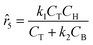
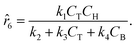
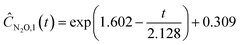
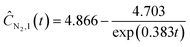
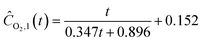
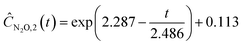
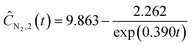
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(exp(−0.094t)) − t
exp(exp(−0.094t)) − t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−0.385t)
exp(−0.385t)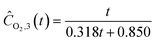
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−0.122t)
exp(−0.122t)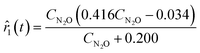
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2(t) = 0.061 − 0.404CN2O.
2(t) = 0.061 − 0.404CN2O.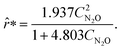
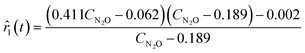
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2(t) = 0.411CN2O − 0.068.
2(t) = 0.411CN2O − 0.068.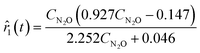
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2(t) = 0.414CN2O − 0.074.
2(t) = 0.414CN2O − 0.074.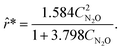
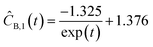
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−0.084t + 0.399)
exp(−0.084t + 0.399)