Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Divide-and-conquer potentials enable scalable and accurate predictions of forces and energies in atomistic systems
Claudio
Zeni
*ab,
Andrea
Anelli
cd,
Aldo
Glielmo
 be,
Stefano
de Gironcoli
b and
Kevin
Rossi
be,
Stefano
de Gironcoli
b and
Kevin
Rossi
 *df
*df
aMicrosoft Research, Cambridge, UK. E-mail: claudiozeni@microsoft.com
bPhysics Area, International School for Advanced Studies, Trieste, Italy
cRoche, Pharma Research and Early Development, Therapeutic Modalities, Roche Innovation Center Basel, F. Hoffmann-La Roche Ltd, Grenzacherstrasse 124, 4070, Basel, Switzerland
dInstitute of Materials, Ecole Polytechnique Fédérale de Lausanne, Lausanne, Switzerland
eBank of Italy, Italy
fDepartment of Materials Science and Engineering, Delft University of Technology, 2628 CD, Delft, The Netherlands. E-mail: K.R.rossi@tudelft.nl
First published on 15th November 2023
Abstract
In committee of experts strategies, small datasets are extracted from a larger one and utilised for the training of multiple models. These models' predictions are then carefully weighted so as to obtain estimates which are dominated by the model(s) that are most informed in each domain of the data manifold. Here, we show how this divide-and-conquer philosophy provides an avenue in the making of machine learning potentials for atomistic systems, which is general across systems of different natures and efficiently scalable by construction. We benchmark this approach on various datasets and demonstrate that divide-and-conquer linear potentials are more accurate than their single model counterparts, while incurring little to no extra computational cost.
1 Introduction
Machine learning potentials (MLPs) provide a platform for computationally efficient and linear-scaling atomistic modelling, which (approximately) retains the same accuracy as the ab initio reference method employed to generate training data. The technological relevance of this tool has made a tangible impact in advancing fundamental and/or applied studies across condensed matter, physical chemistry, chemical physics, and soft matter.1–6Consequently, a large number of strategies have been developed towards the making of fast-and-accurate MLPs. These include linear7–9 or kernel10,11 methods leveraging a fixed atom-density representation and deep learning approaches where representations are learned by means of non-linear feed-forward,12 convolutions, attention mechanisms, or message-passing operations.13,14 In particular, the latter paradigm recently demonstrated state of the art accuracy and robustness in realistic tests.15–20
In spite of their lower accuracy, linear models remain attractive since they are computationally fast both in the training- and in the prediction-stage. It is however a matter of debate whether their flexibility can capture the full complexity of interatomic interactions in systems with non-trivial phase diagrams, possibly also presenting very different electronic structure features across their phase space.
This question also holds, to a certain extent, for any non-specialized MLP, regardless of whether it exploits linear or non-linear approaches. While MLPs are often transferable,21–23 reports in the literature show that specifically tailored training sets yield models that are more accurate in predicting the properties of atomistic configurations mostly similar to the ones in the training set.24–27
In this manuscript, we discuss the development and application of a divide-and-conquer (DC) strategy28,29 to fit accurate linear MLPs. The latter consists in training a committee of expert models, where each expert is trained on a small, independent, and pre-selected subset of the full training set. The predictions of the specialized members are then combined so that contributions of the model(s) more likely to be accurate are dominant.
Previous reports in the literature also hinted at the benefit of breaking down the problem of fitting a general model for atomistic systems, across large and complex training sets. Deringer et al.30 fine-tuned the regularisation coefficients associated with different training-points to construct an accurate model leveraging a SOAP representation and a Gaussian Process regressor. Mazouin et al.31 and Lemm et al.32 demonstrated that the learning of HOMO–LUMO gaps in QM9 molecules is facilitated when training on subsets that discriminate conformers which present a ring, a chain, or other characteristic motifs. Cheng et al.33,34 showed that a clustering scheme exploiting chemo-informatics features by-passes the need for human intervention in the discrimination of molecules with different chemistries. They further observed that a regression + unsupervised clustering protocol provides optimal accuracy, transferability, and learning efficiency when applied to the learning of molecular energy in a dataset of thermalized drug-like molecules. Goldsmith et al.35 showed how sub-group discovery enables the unravelling of specific structure–property relationships within sub-populations of a large material property database. In the domain of coarse grained force-fields, a surface-hopping scheme – where different regions of the conformational space induce the use of different coarse Hamiltonians – has also been successfully developed by Bereau and Rudzinski.36
By testing on community benchmarks, we find that DC linear models consistently outperform their single linear model counterparts regardless of the chemistry of the system considered. This conclusion holds both for the case of small benchmark datasets37 (around 300 global configurations each, comprising bulk cells, surfaces, vacancies, and thermal equilibrium MD runs) as well as for a larger and more complex one30 (around 5000 global configurations comprising liquid, amorphous, polymorphic crystals, and layered structures of bulk phosphorus). The accuracy gain is particularly significant when linear potentials are built under the constraint of modelling low body-order interatomic interactions. The proposed DC approach thus paves the way to a scalable and efficient strategy to enhance the accuracy of fast linear models.
2 Divide-and-conquer learning
The workflow envisioned for DC MLP training, exploitation, and refinement is illustrated in Fig. 1. First we gather a representative set of configurations in a database and associate features with each of them according to a given representation (leftmost in Fig. 1). In a successive step, we cluster the database into M subsets (second panel in Fig. 1) and then train a model for each subset m (third panel in Fig. 1). The force and energy predictions from each model are finally combined to produce a new point's estimate (rightmost panel of Fig. 1).To formalise the DC strategy, we write the relationship between the potential energy E(S) of a system S and the machine learning (ML) function that aims at predicting the latter, under the assumption that it can be decomposed into single atomic energy contributions ε defined for interactions within a cut-off distance, as follows:
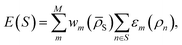 | (1) |
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) S) is the weight of the prediction from model m for system S. The choice of basing the cluster assignment on a global structural metric aims at developing models specialised in the physics of each target phase. In particular, wm(
S) is the weight of the prediction from model m for system S. The choice of basing the cluster assignment on a global structural metric aims at developing models specialised in the physics of each target phase. In particular, wm(![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) S) is here a written function of the average of all local atomic environment descriptors in S:
S) is here a written function of the average of all local atomic environment descriptors in S: 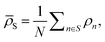 where N is the number of atoms in S. By definition, the force fi acting on atom i is found by differentiating the total energy of the system w.r.t. the position of atom i itself and reads
where N is the number of atoms in S. By definition, the force fi acting on atom i is found by differentiating the total energy of the system w.r.t. the position of atom i itself and reads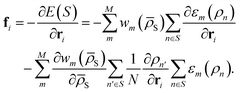 | (2) |
2.1 DC training and prediction
The supervised learning of forces and energy in each expert model of a DC MLP takes place via ridge regression. In the latter framework the target property Y is fitted as a function of the features Q times a weight W.| Y = WQ | (3) |
| Yd = [Ed, f1x, f1y, f1z,…, fSx, fSy, fSz], | (4) |
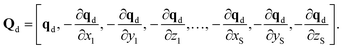 | (5) |
The computational cost of a force-energy prediction with ridge regression is associated with the calculation of the descriptor Q for the structure d and the single matrix product WQ. For the case of a divide and conquer potential comprising M members, the latter step has a cost which is paid M-times, while the computational cost of the former step remains the same. Nevertheless, we note that the dominating term is, in both cases, the calculation of the descriptor Q. The computational cost of performing M matrix products in DC potentials is, therefore, effectively negligible. The linear potential weights W are found analytically by solving a matrix-inversion problem
| W = (QTQ + λI)−1QTY, | (6) |
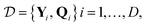 labels the training set data and λ is the ridge parameter.
labels the training set data and λ is the ridge parameter.
2.2 DC weight calculation
DC potentials possess two main additional degrees of freedom with respect to other linear MLPs: the choice of the clustering scheme and of the weight assignment algorithm. Here we discuss a possible choice of model weight assignment linked to the use of k-nearest neighbours as a clustering algorithm. Within this approach, we first cluster the training data set via a k-nearest neighbours scheme. We then write wm(![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) S) as a function of the distance between
S) as a function of the distance between ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) S and the centroid of each cluster μm, weighted by the standard deviation of each cluster σm and by the square root of the number of training structures belonging to each cluster γm. We apply a softmax function so that the sum of weights over all models m is 1. The final equation for the assignment of model weights therefore reads
S and the centroid of each cluster μm, weighted by the standard deviation of each cluster σm and by the square root of the number of training structures belonging to each cluster γm. We apply a softmax function so that the sum of weights over all models m is 1. The final equation for the assignment of model weights therefore reads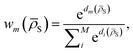 | (7) |
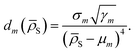 | (8) |
We empirically find that using a fourth power in the denominator of eqn (8) yields smooth transitions between clusters, while not reducing the accuracy of potentials.
The choice of the number of expert models, M, is a key variable in a DC strategy, which may also lead to overfitting. In practice, we treat M as an additional model hyper-parameter and select the value which maximises the following score:
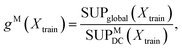 | (9) |
Another free parameter in the DC MLP fit is the regularization term of each expert model. In principle this hyper-parameter could be optimized for each specialized model. In practice we observe negligible gain and employ the same regularization term for each expert model, during each case study.
While the current implementation performs the evaluation of wm according to a distance criterion, we do not exclude that other approaches, e.g., supervised ones, could provide room for improvements in accuracy. Similarly, we do not exclude that more sophisticated approaches to combine the predictions of the different expert models could further enhance the performance of a DC MLP.
To conclude, we note a parallelism between our DC approach and the one inherent to linear decision trees (where linear models are fitted to the data in each leaf of a decision tree), with the caveat that continuity in our predictions is ensured by the DC model weighting scheme (eqn (1)). By the same token, we highlight that eqn (1) could be also interpreted as a perceptron model. In this view, wm acts as an activation function, which depends on the global structure of the system, while the single-atom contributions are calculated using linear ML units. Furthermore, we observe that one could also consider the DC weight evaluation as a classification step, through which a most suitable linear model (among a set of available one) is selected, given a certain test point.
3 Results
The method section introduced the DC framework in a general form, i.e., without referring to a specific representation of the local atomic environment. In this section, we instead discuss its specific application for the case of an atomic cluster expansion (ACE) representation, which is computed using a custom-made Python interface to the ACE.jl package.9,38 The choice of this representation stems from its success in enabling linear regression of forces and energies across systems with diverse and complex chemistries.39–413.1 Zuo et al. Benchmark
To benchmark the accuracy of the proposed DC approach we first refer to the Li, Mo, Ge, Si, Ni, and Cu dataset by Zuo et al.37 This database collects DFT PBE energies and forces for ground state crystalline bulk structures, strained crystals, low Miller index surfaces, crystalline bulk configurations and vacancy diffusion sampled over finite temperature ab initio MD for six different mono-elemental systems (Cu, Ni, Li, Mo, Si, and Ge). Configurations are randomly separated, according to a 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 split, into a training and testing set.
10 split, into a training and testing set.
To build linear and DC linear models, we represent local atomic environments up to the cut-off radii indicated by Zuo et al.37 (Mo = 5.2 Å, Si = 4.7 Å, Ge = 5.1 Å, Cu = 3.9 Å, Ni = 4.0 Å, and Li = 5.1 Å) and employ a fixed total radial and angular basis set expansion order Nmax + Lmax = 12 for the ACE descriptors. We fix force and energy regularisations at 10−6, while the number of specialised models is optimized for each dataset according to the criterion of eqn (9) and is MMo = 7, MSi = 2, MGe = 3, MCu = 5, MNi = 6, and MLi = 2.
In the left panel of Fig. 2 we report MAEs on energy predictions with a 2-, 3-, or 4-body descriptor (top to bottom graphs). In the right panel of Fig. 2 we present the same information but for the force MAEs. We observe that DC models consistently outperform the accuracy of linear ones. The accuracy gain is marginal (few percent) in the case of systems which were already accurately predicted by the linear model, i.e., Cu, Ni, and Li. The improvement is instead quite sizeable for the two other systems, namely, Mo and Ge. The case of force-and-energy predictions in Si is the only one where a balanced competition between the two approaches is observed: the linear model is slightly more accurate in energy predictions, while the DC model displays a better performance in force predictions.
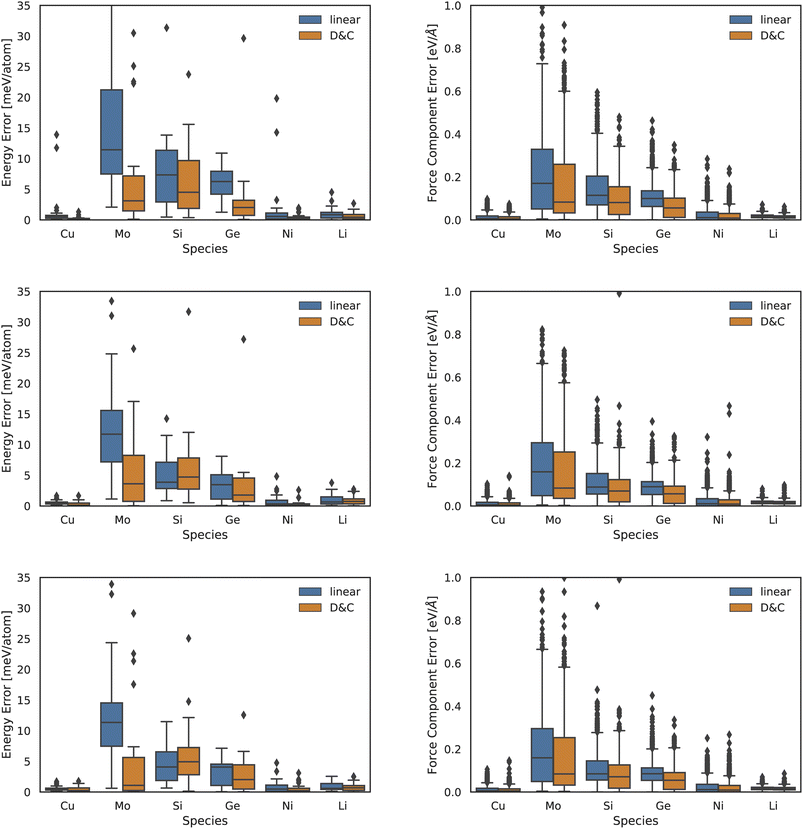 | ||
| Fig. 2 Box plot for test error on atomic energies (left column) and forces (right column) yielded using linear models (blue) and DC models (orange) for the Zuo et al.37 dataset. The first row refers to 2-body ACE descriptors, the second row to 3-body and the fourth row to 4-body ones. | ||
An analysis of the DC accuracy, as a function of the chosen interaction body-order, shows that more significant (relative) accuracy gains take place at lower body-orders. We note that low body-order MLPs are also the fastest to compute and, in turn, DC approaches provide a promising route in the deployment of low-resource, accurate, and interpretable MLPs.
Additionally, the proposed DC approach provides a relative improvement which is larger for energy predictions than for force predictions. We rationalize this trend in light of the fact that we cluster data points according to global features. This, in turn, is likely to facilitate the learning of global properties, such as the system total energy. While not explored in the present manuscript, we note that the DC approach could be modified so as to cluster data based on local atomic features rather than on summary statistics of those quantities.
3.2 P dataset
To showcase the application of DC potentials in a richer dataset, we consider the multi-phase phosphorus dataset gathered by Deringer et al.30 to chart the phase diagram of P. The database comprises 4798 configurations whose energy has been calculated at the DFT + MBD level. Configurations in the database appear in many different phases, namely, network and molecular liquid P, white P, Hittordf P, rhombohedral P, tubular parallel fibrous P, black bulk P, black bilayer P, black monolayer P, and black P ribbons. For consistency with the discussion regarding the Zuo et al.37 dataset, we split available data into a training and a testing set. Model hyperparameters are optimized during training, i.e., solely utilising training data.We fit a linear and a linear DC potential using the ACE representation with a radial cut-off of 5 Å, a maximum basis set size of 12, and considering correlations up to the 5-body order. A regularisation parameter of 10−7 is used for both the linear and the DC model fits. The DC potential fitting finds an optimal number of M = 6 clusters, following the approach detailed in eqn (9).
In Fig. 3, we report the distribution of errors incurred in energy (left panels) and force (right panels) prediction for the linear (top panels) and DC models (lower panels). A parity plot in the inset shows the relationship between true and predicted values. We observe that, also in the case of a more complex benchmark, the DC accuracy is consistently higher than the linear model's one. In particular, the accuracy gain is, again, mostly observed in the energy fitting (LP MAE = 0.128 eV per atom vs. DC MAE = 0.060 eV per atom), while forces improve by a thinner margin (LP MAE = 0.250 eV Å−1vs. DC MAE = 0.238 eV Å−1). Crucially, the partitioning of the fitting into smaller models has the largest effect on the tails of the force and energy error distributions, which are less populated for the DC models.
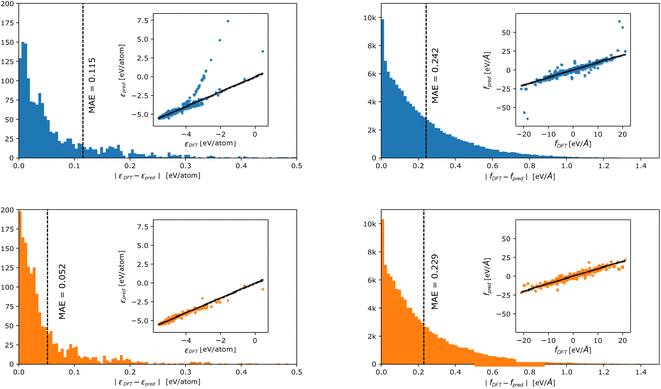 | ||
| Fig. 3 Error distribution in energy (left panels) and forces (right panels) prediction for the phosporus dataset by Deringer et al.30 incurred by a linear (blue – upper panel) and a DC (orange – lower panel) model. The inset shows parity plots between true and predicted values. Points are colour coded according to the density (yellow = high density and blue = low density) in that region. | ||
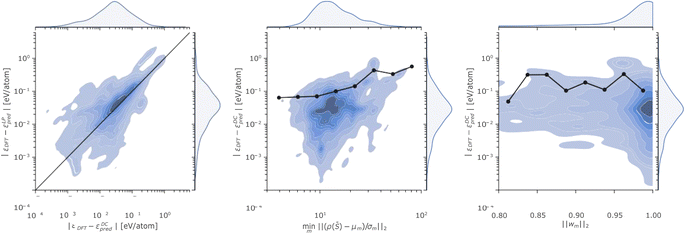
The complexity of the P database and the remarkable errors incurred by the linear and the DC models in certain regions of the phase space motivate a more detailed discussion. To this end, we analyse in Fig. 4 the relationship between the energy errors incurred by the linear and the DC models for each test structure in the P database, the minimum distance of each test point from the DC cluster centroids, and the L2 norm of the DC model weights.
The Fig. 4 left panel shows the kernel density estimate of the distribution of the (DC and LP) errors, where the straight line is a guide to the eye indicating equal accuracy between the predictions of the linear and DC potentials. All the points lying above (below) the line correspond to a configuration where the DC energy prediction is more (less) accurate than the one of the linear model. The plot thus highlights, from an additional perspective, how the DC model accuracy is more accurate than the linear one, for the majority of the test points.
The Fig. 4 central panel illustrates the relationship between the error incurred in energy prediction on the phosphorus dataset by the DC model and the minimum scaled distance of ρ(![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ) from cluster centroids. A (positive) correlation between the two quantities emerges when looking at the behaviour of the 90-th percentile of the atomic energy error incurred by the DC model as a function of the minimum distance from cluster centroids (black line and dots). We deduce that the (scaled) minimum distance from cluster centroids minm‖(ρ(
) from cluster centroids. A (positive) correlation between the two quantities emerges when looking at the behaviour of the 90-th percentile of the atomic energy error incurred by the DC model as a function of the minimum distance from cluster centroids (black line and dots). We deduce that the (scaled) minimum distance from cluster centroids minm‖(ρ(![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ) − μm)/σm‖2 can provide an upper bound to the error incurred on energy predictions, as structures whose representations are far from every model centroid are also likely to be out of the training distribution. This finding is in line with previous observations25 about the interplay between linear model error and the degree to which a test point lies in a well-sampled region of the representation space.
) − μm)/σm‖2 can provide an upper bound to the error incurred on energy predictions, as structures whose representations are far from every model centroid are also likely to be out of the training distribution. This finding is in line with previous observations25 about the interplay between linear model error and the degree to which a test point lies in a well-sampled region of the representation space.
Fig. 4 right panel displays DC errors as a function of the L2 norm of the DC weights. The latter is generally close to 1, suggesting that for each prediction only a single expert model largely contributes to the overall DC model outcome. While good accuracies are witnessed when a single model is found to dominate the predictions within the DC potential, significant errors may nonetheless be registered even when a (presumed) expert model dominates the committee prediction. We rationalize this observation in terms of the possible detrimental effect of the soft-max regularization of the DC weights (eqn (7) and (8)) on the correlation between DC error and distance from the closest cluster centroid, as the single closest model will be chosen with high certainty even in cases where the structure is far from every DC model centroid.
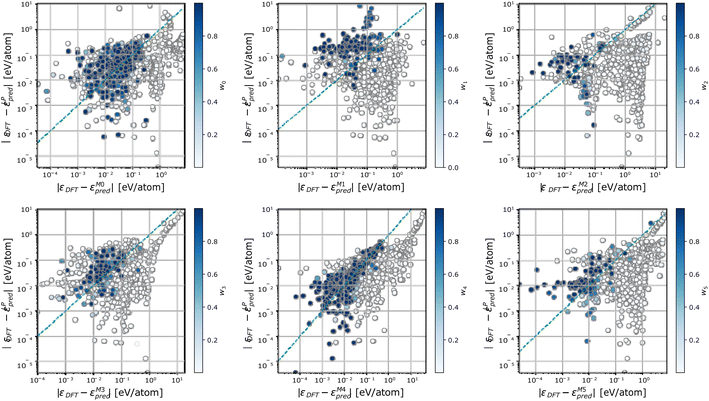
To further characterize the working mechanisms of a DC model, we report in Fig. 5 the error incurred by each member m in the DC model, against the error incurred by a linear model trained on the full dataset, and colour-code points S according to the weight wm(![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) S) of the expert model m in the overall DC prediction. Fig. 5 shows that sizeable changes in the prediction error take place when different sets of training configurations are considered. In particular, each expert model offers accurate predictions, which are on average superior to the one of the linear model trained on the full dataset, in specific regions of the phase space. These correspond to points where the expert model's relative contribution to the DC prediction is sizeable (i.e., above 0.5). Significantly, there exist configurations for which neither the expert models nor the full linear model are truly equipped to provide an accurate prediction. On these occasions, a single expert model may be elected as the most specialized one in offering a given prediction; this behaviour follows from the geometric criterion elicited in eqn (7) and (8).
S) of the expert model m in the overall DC prediction. Fig. 5 shows that sizeable changes in the prediction error take place when different sets of training configurations are considered. In particular, each expert model offers accurate predictions, which are on average superior to the one of the linear model trained on the full dataset, in specific regions of the phase space. These correspond to points where the expert model's relative contribution to the DC prediction is sizeable (i.e., above 0.5). Significantly, there exist configurations for which neither the expert models nor the full linear model are truly equipped to provide an accurate prediction. On these occasions, a single expert model may be elected as the most specialized one in offering a given prediction; this behaviour follows from the geometric criterion elicited in eqn (7) and (8).
From the analysis of Fig. 4 and 5, we conclude that the functional form in eqn (1) provides a grounded route to weight the predictions of expert models, so as to elect the most accurate ones as the most significant in the DC prediction. Nevertheless, the DC approach offers no guarantee of improvement in the robustness of predictions in regions of the phase space, which have not been densely sampled during the construction of the training set.
4 Outlook
4.1 DC uncertainty estimate
The ability to endow force and energy prediction with an uncertainty estimate represents a key feature of machine learning potentials and machine learning for atomistic systems.42–44 In this work we have shown that the distance from the centroid of the expert model clusters provides information on the likelihood of incurring large errors. This is in fair agreement with previous observations of distance metrics for uncertainty quantifications25,43 Future studies could explore the definition of rigorous frameworks for directly estimating the DC prediction uncertainty. This estimate could leverage sub-sampling approaches, in the spirit of committee methods, with the challenge of devising the correct uncertainty (re)calibration procedure.Alternative approaches could otherwise leverage the DC weights' estimate stage to further introduce anomaly detection or one-class classification and readily detect datapoints for which a model trained on the available dataset is more likely to provide unfaithful predictions.
4.2 Data efficient learning
The success of ML models applied to materials modelling has also largely benefited from two simple yet extremely effective approaches, namely, Δ-learning45,46 and active learning.47–49 We speculate that a DC strategy can be readily and effectively integrated with the above two approaches.As with all linear and kernel-based methods, the re-training of a DC ensemble of potentials can be performed analytically and computationally efficiently, without performing costly gradient-based optimisation of parameters. Moreover, since potentials within the DC approach are localized in the space of descriptors, only models for which new incoming data is relevant need to be updated during the active learning loop, thus further reducing the computational resources required.
By the same token, the proposed DC strategy can be further naturally evolved to support Δ-learning45,46 schemes. In the assumption that a fairly accurate and largely transferable force-field (see, e.g., ref. 50 and 51) or MLP (see e.g., ref. 17, 26, 52 and 53) exists, we then envision a strategy where the latter is used as a baseline, and a number of expert model corrections, whose learning is efficient by virtue of transfer learning,26 may act on the general model to further improve its accuracy.
One could also write a DC correction to an existing baseline energy model as
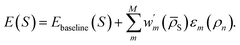 | (10) |
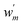 labels weights that respect
labels weights that respect 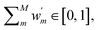 depending on whether the suggested DC correction shall or shall not be trusted (whereas
depending on whether the suggested DC correction shall or shall not be trusted (whereas 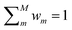 for eqn (7)). This approach finds a parallelism with the one formulated by Imbalzano et al.,54 which employed the prediction uncertainty, evaluated through an ensemble model, to weight the Δ-ML correction of a baseline model.
for eqn (7)). This approach finds a parallelism with the one formulated by Imbalzano et al.,54 which employed the prediction uncertainty, evaluated through an ensemble model, to weight the Δ-ML correction of a baseline model.
5 Conclusion
In this manuscript, we discussed in detail the application of a divide-and-conquer (DC) approach to the development of fast-and-accurate machine learning potentials (MLPs). DC MLPs leverage small partitions of a larger database – here automatically identified via a clustering algorithm – to train multiple expert models on restricted regions of the phase space, whose predictions are weighted according to a geometric distance criterion from the test data points at inference time. By benchmarking the accuracy of the proposed method on both restricted and larger datasets for materials with different chemistries, we showcase that DC potentials are more accurate than linear potentials exploiting the same representation.While the accuracy of DC MLPs leveraging linear models may not be on par with models exploiting learned representations, DC models display a substantial accuracy gain, in exchange for a negligible computational burden, against linear potentials. This result makes them an attractive tool when speed and efficiency in training and prediction are key figures of merit.
At a speculative level, we discuss how the DC approach could be extended to integrate uncertainty estimates and efficiently integrated into Δ-learning and active-learning strategies.
By showing that a committee of experts strategy can be successfully leveraged for MLP development, our work opens a new avenue for the design of accurate and scalable ML models for materials.
Data availability
The package for training ridge regression potentials is freely available under the Apache 2.0 license at https://github.com/ClaudioZeni/Castle, and a copy of the repository accessed on 07/10/2023 is stored at 10.5281/zenodo.8416687. The Zuo et al.37 materials dataset is freely available in the data directory at https://github.com/materialsvirtuallab/mlearn, and was accessed on date 20/01/2022. The Deringer et al.30 P dataset is freely available in the data directory at https://zenodo.org/record/4003703#.YyiMOKTMJmM, and was accessed on date 05/03/2022.Conflicts of interest
The views and opinions expressed in this paper are those of the authors and do not necessarily reflect the official policy or position of Banca d’Italia.Acknowledgements
CZ, AG, and SdG gratefully acknowledge support by the European Union's Horizon 2020 research and innovation program (Grant No. 824143, MaX ‘MAterials design at the eXascale’ Centre of Excellence). KR acknowledges funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Marie Curie Individual Fellowship Grant agreement No. 890414). The authors thank Alessandro Laio, Federico Grasselli, Felix Musil, Austin Zadoks, and Martin Uhrin for useful discussion.References
- G. C. Sosso, G. Miceli, S. Caravati, J. Behler and M. Bernasconi, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 174103 CrossRef
.
- N. Artrith and A. Urban, Comput. Mater. Sci., 2016, 114, 135–150 CrossRef CAS
.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC
.
- C. Zeni, K. Rossi, A. Glielmo and F. Baletto, Adv. Phys.: X, 2019, 4, 1654919 CAS
.
- J. Westermayr, M. Gastegger, D. Vörös, L. Panzenboeck, F. Joerg, L. González and P. Marquetand, Nat. Chem., 2022, 14, 914–919 CrossRef CAS PubMed
.
- V. L. Deringer, N. Bernstein, G. Csányi, C. Ben Mahmoud, M. Ceriotti, M. Wilson, D. A. Drabold and S. R. Elliott, Nature, 2021, 589, 59–64 CrossRef CAS PubMed
.
- A. P. Thompson, L. P. Swiler, C. R. Trott, S. M. Foiles and G. J. Tucker, J. Comput. Phys., 2015, 285, 316–330 CrossRef CAS
.
- A. V. Shapeev, Multiscale Model. Simul., 2016, 14, 1153–1173 CrossRef
.
- R. Drautz, Phys. Rev. B, 2019, 99, 014104 CrossRef CAS
.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef
.
- A. Glielmo, C. Zeni and A. De Vita, Phys. Rev. B, 2018, 97, 184307 CrossRef CAS
.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed
.
- K. Schütt, H. Sauceda, P. Kindermans, A. Tkatchenko and K. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef
.
- J. P. Mailoa, M. Kornbluth, S. Batzner, G. Samsonidze, S. T. Lam, J. Vandermause, C. Ablitt, N. Molinari and B. Kozinsky, Nat. Mach. Intell., 2019, 1, 471–479 CrossRef
.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 1–11 Search PubMed
.
-
I. Batatia, D. P. Kovács, G. N. Simm, C. Ortner and G. Csányi, Advances in Neural Information Processing Systems, ed. S. Koyejo, S. Mohamed, A. Agarwal, D. Belgrave, K. Cho and A. Oh, Curran Associates, Inc., 2022, vol. 35 Search PubMed
.
-
J. Gasteiger, F. Becker and S. Günnemann, Advances in Neural Information Processing Systems, 2021, pp. 6790–6802 Search PubMed
.
-
Y. Liu, L. Wang, M. Liu, Y. Lin, X. Zhang, B. Oztekin and S. Ji, International Conference on Learning Representations, 2022 Search PubMed
.
-
C. Ying, T. Cai, S. Luo, S. Zheng, G. Ke, D. He, Y. Shen and T.-Y. Liu, Thirty-Fifth Conference on Neural Information Processing Systems, 2021 Search PubMed
.
- Y. Shi, S. Zheng, G. Ke, Y. Shen, J. You, J. He, S. Luo, C. Liu, D. He and T.-Y. Liu, arXiv, 2022, preprint, arXiv:2203.04810, DOI:10.48550/arXiv.2203.04810.
- B. Monserrat, J. G. Brandenburg, E. A. Engel and B. Cheng, Nat. Commun., 2020, 11, 5757 CrossRef CAS PubMed
.
- C. Schran, F. Brieuc and D. Marx, J. Chem. Phys., 2021, 154, 051101 CrossRef CAS PubMed
.
- P. Rowe, V. L. Deringer, P. Gasparotto, G. Csányi and A. Michaelides, J. Chem. Phys., 2020, 153, 034702 CrossRef CAS PubMed
.
- C. Zeni, K. Rossi, A. Glielmo, Á. Fekete, N. Gaston, F. Baletto and A. De Vita, J. Chem. Phys., 2018, 148, 241739 CrossRef
.
- C. Zeni, A. Anelli, A. Glielmo and K. Rossi, Phys. Rev. B, 2022, 105, 165141 CrossRef CAS
.
- A. Kolluru, N. Shoghi, M. Shuaibi, S. Goyal, A. Das, C. L. Zitnick and Z. Ulissi, J. Chem. Phys., 2022, 156, 184702 CrossRef CAS
.
- S. Chong, F. Grasselli, C. Mahmoud, J. Morrow, V. Deringer and M. Ceriotti, J. Chem. Theory Comput., 2023 DOI:10.1021/acs.jctc.3c00704
.
-
G. Brassard and P. Bratley, Fundamentals of algorithmics, 1995 Search PubMed
.
-
A. Glielmo, C. Zeni, A. Fekete and A. De Vita, Building Nonparametric n-Body Force Fields Using Gaussian Process Regression, Springer, 2020 Search PubMed
.
- V. L. Deringer, M. A. Caro and G. Csányi, Nat. Commun., 2020, 11, 5461 CrossRef CAS
.
- B. Mazouin, A. A. Schöpfer and O. A. von Lilienfeld, Mater. Adv., 2022, 3, 8306–8316 RSC
.
- D. Lemm, G. F. von Rudorff and O. A. von Lilienfeld, arXiv, 2022, preprint, arXiv:2205.05633, DOI:10.48550/arXiv.2205.05633.
- L. Cheng, N. B. Kovachki, M. Welborn and T. F. Miller, J. Chem. Theory Comput., 2019, 15, 6668–6677 CrossRef CAS PubMed
.
- L. Cheng, J. Sun and T. F. Miller III, J. Chem. Theory Comput., 2022, 18(8), 4826–4835 CrossRef CAS PubMed
.
- B. R. Goldsmith, M. Boley, J. Vreeken, M. Scheffler and L. M. Ghiringhelli, Phys. Rev. B, 2017, 19, 013031 Search PubMed
.
- T. Bereau and J. F. Rudzinski, Phys. Rev. Lett., 2018, 121, 256002 CrossRef CAS PubMed
.
- Y. Zuo, C. Chen, X. Li, Z. Deng, Y. Chen, J. Behler, G. Csányi, A. V. Shapeev, A. P. Thompson, M. A. Wood and S. P. Ong, J. Phys. Chem. A, 2020, 124, 731–745 CrossRef CAS
.
- G. Dusson, M. Bachmayr, G. Csanyi, R. Drautz, S. Etter, C. van der Oord and C. Ortner, J. Comput. Phys., 2022, 110946 CrossRef CAS
.
- A. Bochkarev, Y. Lysogorskiy, S. Menon, M. Qamar, M. Mrovec and R. Drautz, Phys. Rev. Mater., 2022, 6, 013804 CrossRef CAS
.
- Y. Lysogorskiy, C. van der Oord, A. Bochkarev, S. Menon, M. Rinaldi, T. Hammerschmidt, M. Mrovec, A. Thompson, G. Csányi, C. Ortner and R. Drautz, npj Comput. Mater., 2021, 7, 97 CrossRef CAS
.
- C. Zeni, K. Rossi, A. Glielmo and S. De Gironcoli, J. Chem. Phys., 2021, 154, 224112 CrossRef CAS PubMed
.
- A. A. Peterson, R. Christensen and A. Khorshidi, Phys. Chem. Chem. Phys., 2017, 19, 10978–10985 RSC
.
- J. P. Janet, C. Duan, T. Yang, A. Nandy and H. J. Kulik, Chem. Sci., 2019, 10, 7913–7922 RSC
.
- K. Tran, W. Neiswanger, Y. Junwoong, Q. Zhang, E. Xing and Z. W. Ulissi, Machine Learning: Science and Technology, 2020, 1, 025006 Search PubMed
.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS
.
- K. Rossi, V. Jurásková, R. Wischert, L. Garel, C. Corminbœuf and M. Ceriotti, J. Chem. Theory Comput., 2020, 16, 5139–5149 CrossRef CAS PubMed
.
- G. Csányi, T. Albaret, M. C. Payne and A. De Vita, Phys. Rev. Lett., 2004, 93, 175503 CrossRef
.
- J. Vandermause, S. B. Torrisi, S. Batzner, Y. Xie, L. Sun, A. M. Kolpak and B. Kozinsky, npj Comput. Mater., 2020, 6, 20 CrossRef
.
- M. Shuaibi, S. Sivakumar, R. Q. Chen and Z. W. Ulissi, Machine Learning: Science and Technology, 2021, 2, 025007 Search PubMed
.
- A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef
.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed
.
- W. Ye, H. Zheng, C. Chen and S. Ong, Scr. Mater., 2022, 218, 114803 CrossRef CAS
.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. Bartel and G. Ceder, Nat. Mach. Intell., 2023, 5, 1031–1041 CrossRef
.
- G. Imbalzano, Y. Zhuang, V. Kapil, K. Rossi, E. A. Engel, F. Grasselli and M. Ceriotti, J. Chem. Phys., 2021, 154, 074102 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2024 |