Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
De novo generated combinatorial library design†
Simon Viet
Johansson
 *ab,
Morteza
Haghir Chehreghani
*ab,
Morteza
Haghir Chehreghani
 b,
Ola
Engkvist
b,
Ola
Engkvist
 ab and
Alexander
Schliep
ab and
Alexander
Schliep
 bc
bc
aMolecular AI, Discovery Sciences, R&D, AstraZeneca, Gothenburg, Sweden. E-mail: simon.johansson@astrazeneca.com
bDepartment of Computer Science and Engineering, University of Gothenburg, Chalmers University of Technology, Gothenburg, Sweden
cFaculty of Health Sciences, Brandenburg University of Technology Cottbus-Senftenberg, Cottbus, Germany
First published on 27th November 2023
Abstract
Artificial intelligence (AI) contributes new methods for designing compounds in drug discovery, ranging from de novo design models suggesting new molecular structures or optimizing existing leads to predictive models evaluating their toxicological properties. However, a limiting factor for the effectiveness of AI methods in drug discovery is the lack of access to high-quality data sets leading to a focus on approaches optimizing data generation. Combinatorial library design is a popular approach for bioactivity testing as a large number of molecules can be synthesized from a limited number of building blocks. We propose a framework for designing combinatorial libraries using a molecular generative model to generate building blocks de novo, followed by using k-determinantal point processes and Gibbs sampling to optimize a selection from the generated blocks. We explore optimization of biological activity, Quantitative Estimate of Drug-likeness (QED) and diversity and the trade-offs between them, both in single-objective and in multi-objective library design settings. Using retrosynthesis models to estimate building block availability, the proposed framework is able to explore the prospective benefit from expanding a stock of available building blocks by synthesis or by purchasing the preferred building blocks before designing a library. In simulation experiments with building block collections from all available commercial vendors near-optimal libraries could be found without synthesis of additional building blocks; in other simulation experiments we showed that even one synthesis step to increase the number of available building blocks could improve library designs when starting with an in-house building block collection of reasonable size.
Introduction
AI and AI-assisted tools have seen rapidly increased popularity in cheminformatics over the past decade. In drug discovery, these tools have impacted bioactivity prediction,1,2de novo molecular design,3–8 synthesis prediction9–15 and molecular property prediction.16–20 In turn, the demand for high-quality data has increased beyond the extent of existing data sources21 and there is a need to facilitate a larger number of informative experiments to generate data in a standardized format. Combinatorial chemistry is a popular method for producing large collections of compounds, motivated by material efficiency and more sustainable chemistry22,23 since synthesis of 100 molecules using two building blocks per synthesis could in the worst case require 200 different building blocks, whereas a library of the same size using combinatorial chemistry would use 20 in a 10 × 10 design. Combinatorial chemistry gained traction first in peptide chemistry24–27 and oligonucleotides.28–32 It was later applied for the synthesis of proteins,33 oligomers,34,35 oligosaccharides,36,37 small molecule chemistry38,39 and materials discovery.40Library design has traditionally aimed to optimize the selection of molecules for either molecular diversity41–43 or molecular properties like high activity towards a target or low lipophilicity, i.e. a focused library design.44–48 A diverse library design provides a larger coverage of the chemical space and is often viewed as more ‘informative’, since similar molecules hypothetically would have redundancy in the information gained.41,49 Focused libraries on the other hand might aim to optimize a selected lead compound50,51 by lowering the structural diversity and exploring similar structures to the lead compound to improve a specific property.
There are several methods for producing combinatorial libraries with different throughput, ranging from parallel synthesis robotically generating libraries of size ∼103, to DNA-encoded chemical libraries (DECLs) enabling synthesis up to size 109.52–55 The limitations of the DECLs are a restriction on the type of building blocks that can be attached to a DNA tag and the possibility of the encoding oligonucleotide affecting the binding affinity of the building block.55 Hence, it is primarily used in hit identification but recently also hit confirmation,56 while lower throughput methods are used during lead optimization.
Following the generation of a library, screening methods are employed to search the produced chemical space for desired interactions with the drug target.
Traditional High-throughput screening (HTS) has the capability to physically test approximately 106 compounds. Consequently, virtual compound libraries became the focus as the computational resources became large enough to store their chemical structures.23,57,58 The virtual library CH/PMUNK59 consists of 95 million compounds by enumerating products using common reactions from combinatorial chemistry. The virtual library REAL60 has over 6 × 109 molecules for virtual screening that obey Lipinski's rule of 5.61 The GDB-17 library of small molecules enumerated by Ruddigkeit et al.62 contains 160 billion virtual compounds with up to 17 heavy atoms. The ChemSpace Atlas63 is a collection of 4 × 104 Generative Topographic Maps64 which accommodate up to 5 × 108 compounds. The ZINC library65 is a readily updated free database for which the latest collection contains “1.4 billion compounds, 1.3 billion of which are purchasable”.
A problem with virtual libraries is that the hits produced can require specific synthesis expertise to produce the compounds with real chemistry. As such, compound suppliers offer “synthesis on demand” building blocks of which the largest is MADE,66 a catalogue of 770 million building blocks that can be ordered and made with “over 76% success rate”.
Generative models for de novo design offer an alternative to virtual screening or HTS, by instead generating focused selections with a smaller size.3,67 Generally, the binding affinity of a small molecule to a drug target is decided by a scaffold, a common structure for the library design, with variations in building blocks attached to the scaffold to accommodate for other desired molecular properties.68 Several deep learning models have been proposed to generate chemical libraries in a focused manner, in particular decorating a scaffold69 by suggesting which building blocks to attach to this scaffold. The Mol-GPT model showed capability to both optimize a lead, as well as decorate a scaffold.70 STRIFE emphasized pharmacophore information to decorate and optimize proteins.71 Domenico et al. adapted the REINVENT3 architecture to create focused libraries towards inhibiting NA, AChE and SARS-CoV-2.72 LibINVENT73 uses reinforcement learning to generate reaction-constrained decorations to input scaffolds. We will not cover generative models that are not designed to be applied to library design here, but refer others whom have addressed recent developments.74–76 These methods can generate building blocks for combinatorial library design, but do not inherently offer an optimized combinatorial selection. Given a limited experimental budget, there is motivation to develop workflows for optimizing combinatorial design for novel de novo generated building blocks.
Methods that simultaneously optimize both diversity and molecular properties of a library have been used in several previous studies, using for example simulated annealing77 (SA) or genetic algorithms (GA).78–80 These approaches provide optimization over lists of provided building blocks, or virtual libraries but cannot determine whether novel generated building blocks can be acquired or if they are only hypothetical structures impossible to synthesize in practice. As such, a design made by these models on de novo generated building blocks is limited by the “synthesis on demand” success rate. More recently, multi-objective optimization (MOO) has been approached in the chemical discovery field mostly using methods based on pareto ranking (PR).81,82 These methods do not need a weighing between different objectives, instead they keep all solutions that are non-dominated, i.e., have at least one dimension where the solution is optimal, thereby making a model of the pareto front. The most common optimization algorithms using PR are the genetic algorithms NSGA-II83 (for two to three objectives) and NSGA-III84 (for higher dimensions). However, the former is limited in scalability to large solution spaces when including diversity as it requires computation of all pair-wise distances, and the latter alleviates this by computing diversity in relation to fixed reference points that are forced to be included in the selection. This works well for feature-based diversity, such as physiochemical properties, but provides no guarantees to improving the structural diversity, as this measure is defined on the selection as a whole and not in relation to individual members of the selection.
A model that has proven to perform well for modelling the trade-off between quality and diversity is the Determinantal Point Process (DPP).85–87 DPPs are probabilistic models that have been argued to represent repulsion between items.88 They are used in other application areas for text summarization,87 pose estimation86 and diverse image selection,85 but have not yet been investigated for library design. While common methods for selecting diversity are maximizing the sum of pairwise distances41,80 or minimizing average pairwise similarity,79 the determinant of the similarities captures the interaction between multiple molecules simultaneously.89 Additionally, the max-sum or min-average methods scale in time complexity quadratically with the number of building blocks in the optimization space. While the DPP has a cubic scaling, it is instead dependent on the size of the sampled library rather than the number of options.
We propose a library optimization workflow for de novo generated building blocks in a combinatorial fashion applying recombination.90,91 Using LibINVENT,73 we generate and filter building blocks that can attach to an example scaffold using specified reactions. These building blocks can be both novel or previously existing in eMolecules,92 a platform aggregating in-stock commercial building blocks from “over 140 suppliers”. We then use the Computer Aided Synthesis Prediction (CASP) tool AiZynthFinder13 to evaluate all generated building blocks and query their availability in the eMolecules building block platform, or estimate the number of reaction steps needed to synthesize them using template-based retrosynthesis prediction.9,10 We simultaneously explore and optimize the library selection for Quantitative Estimate of Drug-likeness (QED),93 Quantitative Structure–Activity Relationship (QSAR)1,67,94,95 and structural diversity (measured by the similarity in the compounds' extended connectivity fingerprint (ECFP) representation)96 using Gibbs sampling,97 conditioned on a constant size, thus sampling from a determinantal point process of constant size k (k-DPP).98 The workflow is model-agnostic and can be applied to any list of building blocks and any CASP tool that break down the building blocks into stock-available precursors. We apply this workflow to optimize a library from all available building blocks from eMolecules, as well as compare them to libraries including generated building blocks available from varying number of synthesis reaction steps. We also simulate an in-house building block store by optimizing over a subset of the available building blocks and explore the differences in optimized libraries between using available building blocks and commercially available building blocks.
The main contributions of this framework are as follows. We
• extend combinatorial library design to score de novo designed building blocks,
• propose the use of DPPs, in particular k-DPPs, to sample libraries that optimize the trade-off between quality and diversity, and
• estimate the difference in score between libraries using available building blocks and total pool of generated reactants, and estimate the potential gain from expanding the available building blocks.
Methods
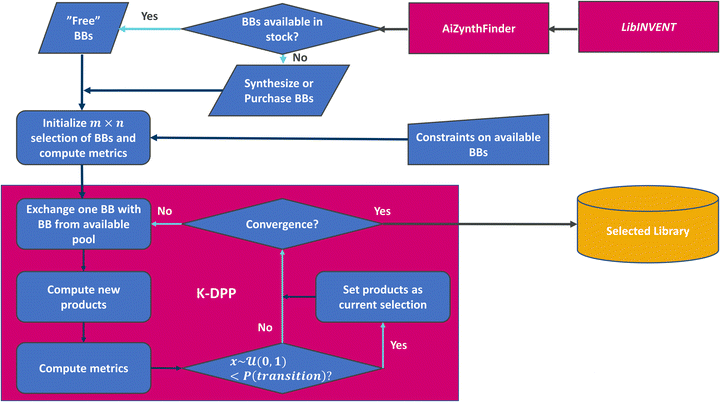
The framework (see Fig. 1) consists of the generation of building blocks, followed by use of retrosynthesis prediction models to query if the building blocks are available in a defined stock data set, or estimate if they could be produced from this stock through synthesis. While the implementation here [https://github.com/SeemonJ/combinatorial-library-design-dpp] is specifically made to work with the open source versions of LibINVENT99 and AiZynthfinder,100 the framework itself can be adapted to work with any metrics.Application example
The scaffold displayed in Fig. 2 is adapted from the original LibINVENT publication.73 The scaffold was chosen for its' suitability as a scaffold towards the Dopamine Receptor D2 (DRD2) target. Furthermore, it has two attachment points, which allows us to study the combinatorial design. Finally, the attachment points allows for two of the more common reactions in pharmaceutical chemistry, Buchwald–Hartwig101 for the left attachment point and primary amide coupling102 for the right. We will refer to these reactions as BH and AC respectively in following.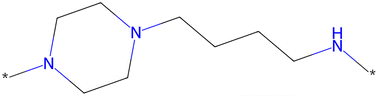 | ||
| Fig. 2 Scaffold used as input for the generation of building blocks. This figure is adapted from ref. 1. | ||
Target activity model
The QSAR model is a random forest model103 built using Scikit-learn 0.21.3 (ref. 104) with 50 trees, other settings were left as default settings. The choice of number of trees was lowered to favour computational speed without observing a drop in classification accuracy on the test set. The QSAR model was trained rather than using the model from the original LibINVENT experiments to experiment with different thresholds for bioactivity, which changed the labels of some training data points. The training data used is all dopamine receptor D2 (DRD2) data available in ExcapeDB,105 a chemogenomics database comprised of active data from assays from Chembl,106 PubChem107 and inactive compounds from PubChem screening data. The activity data for the active compounds are listed with their pXC50 data irrespective of the conducted measurement [IC50, XC50, EC50, AC50, Ki, Kd, Potency],108 and we used a threshold for active/inactive pXC50 of 6. Entries with SMILES109 strings that could not be parsed by RDKit110 were removed. With these definitions for activity, the data set had 6304 active compounds and 344![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905 inactive compounds. The compounds were represented by the extended connectivity fingerprint with 2048 bits and radius 3 (ECFP6), computed using the RDKit morgan algorithm.96,111 The model was trained using a random 80%/20% training/test data split, with 4974 active compounds in the training set (out of 280
905 inactive compounds. The compounds were represented by the extended connectivity fingerprint with 2048 bits and radius 3 (ECFP6), computed using the RDKit morgan algorithm.96,111 The model was trained using a random 80%/20% training/test data split, with 4974 active compounds in the training set (out of 280![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 967, 1.77% actives), and 1330 active compounds in the test set (out of 70
967, 1.77% actives), and 1330 active compounds in the test set (out of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 242, 1.89%). The model, as well as the script to generate the model, is provided in the repository. The data is imbalanced with most of training points labelled as inactive compounds, resulting in AUC-ROC score of 0.995 by having a bias towards predicting most input as negative. The model is trained for binary classification to predict the product label, and the metric used to evaluate a compound is the classification probability of having the “active” label. This model was used both as part of the LibINVENT reinforcement learning run and during Library selection.
242, 1.89%). The model, as well as the script to generate the model, is provided in the repository. The data is imbalanced with most of training points labelled as inactive compounds, resulting in AUC-ROC score of 0.995 by having a bias towards predicting most input as negative. The model is trained for binary classification to predict the product label, and the metric used to evaluate a compound is the classification probability of having the “active” label. This model was used both as part of the LibINVENT reinforcement learning run and during Library selection.
Building block generation using LibINVENT
The building blocks were generated using the pre-trained prior model of LibINVENT.99 The reinforcement learning was run for 1000 epochs with a batch size of 128 and a learning rate of 5 × 10−6. The default diversity filter, which penalizes previously sampled building blocks, and the custom alerts for non-druglike groups were included during training. Reaction filters for the BH and AC reactions were applied, which penalize building blocks that do not match the reaction SMARTS.112A total of 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 991 unique molecules (82%) were generated, of which 94
991 unique molecules (82%) were generated, of which 94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 808 (74%) matched the reaction filters. All molecules for which QSAR model assigned a probability of being active lower than 0.8 were removed in post-processing to reduce the optimization space. This yielded 45
808 (74%) matched the reaction filters. All molecules for which QSAR model assigned a probability of being active lower than 0.8 were removed in post-processing to reduce the optimization space. This yielded 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 928 remaining products, from which the building blocks were extracted. 32
928 remaining products, from which the building blocks were extracted. 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 159 unique carboxylic acids and 2084 unique aromatic halides were identified, corresponding to AC and BH reactions, respectively. The runtime was approximately 2 hours using a Nvidia 2080Ti. The output building blocks as a function of the training is provided in ESI Fig. S.1.†
159 unique carboxylic acids and 2084 unique aromatic halides were identified, corresponding to AC and BH reactions, respectively. The runtime was approximately 2 hours using a Nvidia 2080Ti. The output building blocks as a function of the training is provided in ESI Fig. S.1.†
Building block availability
The public version of AiZynthFinder100 was used to check which building blocks were available directly ‘in stock’, and which building blocks would require synthesis to be available. The baseline stock consists of purchasable building blocks from eMolecules,92 and consists of approximately 1.5 million building blocks (including 227k carboxylic acids and 444k aromatic halides). AiZynthFinder was set to a maximum search time of 5 minutes, and maximum 10 reaction steps for identifying a synthetic route. AiZynthFinder was run in batches across multiple CPU's of varying models as performing the analysis on ∼34k building blocks for up to 5 minutes each would, in the worst case, require ∼2800 CPU hours, in the scenario that no building blocks were available directly in stock. This analysis was performed both for the baseline stock and for five limited availability subsets, used to simulate internal stock. The limited availability subsets were sampled uniformly without replacement from the baseline stock and were chosen to be 3% of the size of the baseline size (∼45k building blocks).The parameters chosen both for generative modelling and retrosynthesis let both models run for a longer time, 1000 epochs compared to 100 during generation and 5 minutes instead of 2 for retrosynthesis evaluation, than previous uses of the same architectures.13,73 This yields more output building blocks and solves more routes than previous use in demonstrated studies, and potentially include LibINVENT output that could be a result of over-exploiting the QSAR model. This was done intentionally to increase the size of the search space and provide a larger diversity of building blocks with respect to quality properties to showcase the effect of the different strategies.
Determinantal point processes
In library design, diversity is often computed between compounds through the matrix of pairwise distances. When optimizing the library, the most common approaches maximize the sum of distances, maximize the minimum distance, or maximize the average distance to the nearest neighbour.41,79,80 This captures the distance between a pair of two molecules well, but does not capture the relationships between multiple molecules simultaneously.89Discrete DPPs are probability distributions first used by Odile to model fermions,113 and have been increasingly popular within machine learning for capturing the trade-off between diversity and quality.85 Let L ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n×n be a positive semi-definite (PSD) matrix. A discrete DPP with kernel L is a probability distribution μ: 2[n] →
n×n be a positive semi-definite (PSD) matrix. A discrete DPP with kernel L is a probability distribution μ: 2[n] → ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) +defined by
+defined by
| μ(S) ∝ Det(LS), ∀S ⊆ [n]. | (1) |
Kulesza and Taskar85 demonstrate that the quality of terms can be incorporated into DPPs by decomposing the kernel into
| Li,j = qiϕiTϕjqj, | (2) |
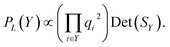 | (3) |
We denote by SY the symmetric matrix of pairwise Tanimoto similarities, and the diversity thus defined as the determinant of SY. Note that this measure is inherently hard to compare between two sets of different sizes. Furthermore, the similarity matrix consists of values in [0, 1] on the off-diagonal elements, and diagonal elements of 1, resulting in a determinant with values in [0, 1]. This will for larger kernels, i.e., larger library selections, result in determinants that approach 0 at a rapid pace. For numerical stability, we use the logarithm of the determinant (denoted by log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Det) as the measure for diversity. Two examples of (non-combinatorial) building block selections can be found in ESI Fig. S.2. and S.3.† They illustrate selections that minimize diversity and maximize diversity, respectively. The selections were made using an offline greedy selection algorithm,85,115 similar to the algorithm proposed by Nakamura et al.89
Det) as the measure for diversity. Two examples of (non-combinatorial) building block selections can be found in ESI Fig. S.2. and S.3.† They illustrate selections that minimize diversity and maximize diversity, respectively. The selections were made using an offline greedy selection algorithm,85,115 similar to the algorithm proposed by Nakamura et al.89
Sampling process
Commonly in data summarization problems, a submodular utility function is defined as the objective for optimization.89,116–119 The family of submodular functions are useful for computational methods as it can be shown that greedy solutions possess good theoretical guarantees, and in practice often perform better than the theoretical guarantees. For DPPs, the greedy solution is to start at one item, i.e. molecule, and at each point select the item which maximizes the current determinant of the kernel until the desired number of items is reached. This method however, requires a full computation of all pairwise similarities for all possible products. Evaluating the determinant of all possible products at once may introduce practical problems, since the naive implementation of determinant calculations are O(n3). This naïve implementation is used in most libraries. Due to parallelization in smaller blocks of submatrices across multiple threads, it is possible to compute determinants of matrices with n > 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in minutes. For the sampled number of possible products, n = 32
000 in minutes. For the sampled number of possible products, n = 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 159 × 2084 = 67
159 × 2084 = 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 019
019![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 356, it is computationally infeasible to compute n − k determinants for selecting item (k + 1), especially for designing larger libraries. Recent research in usage of DPP has primarily been focused on the algorithmic efficiency while keeping a close-to-greedy performance in selecting diverse items.118,120–123 For scenarios such as ours, the only selections of relevance are sets of fixed size, such as the same sizes as screening plates, i.e., 96, 384 or 1536 for parallel library synthesis, or other fixed sizes determined by a project demand. k-DPPs are an extension of general DPPs that are conditioned to selected sets of size exactly k. Gharan and Rezaei123 introduced a computationally efficient method for sampling k-DPPs using a Gibbs sampling scheme shown to have fast mixing properties. Here, the proposal distribution samples suggestions only from exchange operations between one element and one non-element of the current k-set. This ensures that the size of selection always remains constant. Moreover, at time step t during sampling, it requires only computation of the transition probability
356, it is computationally infeasible to compute n − k determinants for selecting item (k + 1), especially for designing larger libraries. Recent research in usage of DPP has primarily been focused on the algorithmic efficiency while keeping a close-to-greedy performance in selecting diverse items.118,120–123 For scenarios such as ours, the only selections of relevance are sets of fixed size, such as the same sizes as screening plates, i.e., 96, 384 or 1536 for parallel library synthesis, or other fixed sizes determined by a project demand. k-DPPs are an extension of general DPPs that are conditioned to selected sets of size exactly k. Gharan and Rezaei123 introduced a computationally efficient method for sampling k-DPPs using a Gibbs sampling scheme shown to have fast mixing properties. Here, the proposal distribution samples suggestions only from exchange operations between one element and one non-element of the current k-set. This ensures that the size of selection always remains constant. Moreover, at time step t during sampling, it requires only computation of the transition probability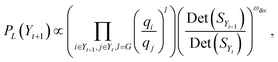 | (4) |
Since the pairwise similarity values of SX are all in [0, 1], the determinants may become too small for double precision with relevant choices of k. For numerical stability, the logarithm of the right hand side of eqn (3) is used in step 7. The logarithm of the determinant become negative, where a greater value represents a more diverse set. In the numerical experiments we let m = 12, n = 8, corresponding to the generated building blocks of carboxylic acids and aromatic halides respectively, and used k = 96 as it is a common plate size.
The acceptance ratio, α controls the probability to accept solutions that are worse than the current selection, in order to “escape” a local maximum. For these experiments, the change between two neighbouring solutions, i.e., differing only by one building block, will typically be low and as such, the transition probabilities are very high. A low α is needed for a faster model convergence. We chose to conduct experiments for α = 0 such that we only accept strict improvements (hill climbing, which is a greedy search). An extensive exploration of α was considered out of scope for this study. The selections of the model for different optimization strategies were examined, see Table 1. To explore the mixing time, the termination criteria were set as a patience parameter, sampling the distribution until 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samples were drawn without finding a better solution. We compare the results against the average result of 100 random selections and the top 96 cherry-picked compounds by QSAR values from the LibINVENT run.
000 samples were drawn without finding a better solution. We compare the results against the average result of 100 random selections and the top 96 cherry-picked compounds by QSAR values from the LibINVENT run.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Det is the logarithm of determinant of the kernel matrix, or matrix of all pairwise Tanimoto similarities in the current selection, and a measure of diversity. A value closer to 0 is more diverse. Random selection is the average values of 100 combinations selected for each reaction step availability. For each optimization strategy, we show the results of stock-available building blocks (0 reaction steps) and building blocks up to 4 reaction steps away
Det is the logarithm of determinant of the kernel matrix, or matrix of all pairwise Tanimoto similarities in the current selection, and a measure of diversity. A value closer to 0 is more diverse. Random selection is the average values of 100 combinations selected for each reaction step availability. For each optimization strategy, we show the results of stock-available building blocks (0 reaction steps) and building blocks up to 4 reaction steps away
| Selection strategy | N reaction steps | Avg QSAR (SD) | Avg QED (SD) | Avg log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Det (SD) Det (SD) |
|---|---|---|---|---|
| QSAR | 0 | 0.993 (0.000482) | 0.370 (0.0184) | −206.8 (7.07) |
| 1 | 1.000 (0.0) | 0.281 (0.0299) | −192.9 (7.87) | |
| 2 | 1.000 (0.0) | 0.278 (0.0249) | −195.9 (7.27) | |
| 3 | 1.000 (0.000104) | 0.281 (0.0281) | −193.1 (10.4) | |
| 4 | 1.000 (0.000133) | 0.277 (0.0385) | −192.1 (6.00) | |
| QED | 0 | 0.676 (0.0100) | 0.785 (0.00105) | −155.9 (3.62) |
| 1 | 0.677 (0.0126) | 0.782 (0.00122) | −154.4 (2.23) | |
| 2 | 0.685 (0.0114) | 0.781 (0.00221) | −155.5 (5.11) | |
| 3 | 0.682 (0.0122) | 0.782 (0.00173) | −153.5 (2.47) | |
| 4 | 0.675 (0.0124) | 0.781 (0.00189) | −155.1 (3.58) | |
| Diversity | 0 | 0.698 (0.00939) | 0.244 (0.0155) | −101.3 (0.239) |
| 1 | 0.699 (0.0115) | 0.138 (0.00704) | −95.88 (0.474) | |
| 2 | 0.688 (0.00741) | 0.110 (0.0105) | −94.12 (0.256) | |
| 3 | 0.687 (0.0122) | 0.103 (0.00766) | −94.13 (0.574) | |
| 4 | 0.686 (0.00947) | 0.099 (0.00717) | −93.65 (0.266) | |
| Simultaneous optimization | 0 | 0.852 (0.00676) | 0.703 (0.00620) | −126.8 (0.995) |
| 1 | 0.848 (0.00980) | 0.701 (0.00651) | −126.8 (1.45) | |
| 2 | 0.845 (0.00498) | 0.704 (0.00540) | −127.3 (1.02) | |
| 3 | 0.843 (0.0102) | 0.699 (0.00570) | −126.2 (1.47) | |
| 4 | 0.851 (0.00690) | 0.699 (0.00956) | −127.2 (2.00) | |
| Random selection | 0 | 0.765 (0.0230) | 0.354 (0.0361) | −128.3 (4.26) |
| 1 | 0.781 (0.0223) | 0.231 (0.0314) | −126.7 (4.57) | |
| 2 | 0.778 (0.0214) | 0.213 (0.0294) | −125.6 (3.88) | |
| 3 | 0.779 (0.0219) | 0.215 (0.0297) | −126.3 (4.97) | |
| 4 | 0.781 (0.0227) | 0.213 (0.0315) | −125.9 (4.419) | |
| LibINVENT top 96 | — | 1.000 | 0.43 | −88.44 |
Results
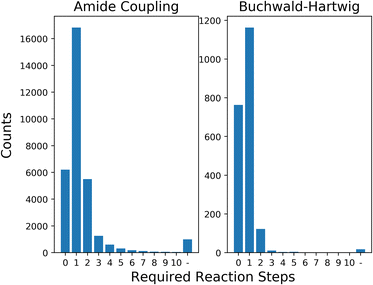
In this section, we first show the results of processing the generated building blocks from LibINVENT through AiZynthFinder, to give a measure of the selection space for the framework. We then present the average results of each optimization strategy for different levels of availability related to required number of reaction steps. Next we show optimization results for a simulated scenario of limited stock building block availability. Finally, we discuss the computational performance of the model when scaling up to larger selection space.The 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 159 unique carboxylic acids and 2084 unique aromatic halides generated through LibINVENT were analysed using AiZynthFinder. The retrosynthetic prediction found that 88.7% of the generated carboxylic acids and 98.3% of the aromatic halides could be synthesized within 2 steps of reactions from the base eMolecules stock. Of the building blocks, 6203 carboxylic acids (19.3% of the generated building blocks) and 763 aromatic halides (36.6%) were directly available in stock; i.e., required no synthesis. The full distribution of reaction availability can be seen in Fig. 3.
159 unique carboxylic acids and 2084 unique aromatic halides generated through LibINVENT were analysed using AiZynthFinder. The retrosynthetic prediction found that 88.7% of the generated carboxylic acids and 98.3% of the aromatic halides could be synthesized within 2 steps of reactions from the base eMolecules stock. Of the building blocks, 6203 carboxylic acids (19.3% of the generated building blocks) and 763 aromatic halides (36.6%) were directly available in stock; i.e., required no synthesis. The full distribution of reaction availability can be seen in Fig. 3.
The compound selection was performed on the criteria of only QSAR, only QED, only diversity and all the metrics simultaneously with equal weight. For the rest of this section, we will refer to the strategy of optimizing the metrics simultaneously with Simultaneous Optimization (SO). The single-objective strategies were performed by setting the weights ωk in Algorithm 1 for the ignored metrics to 0. This was performed for building blocks available from 0 to 4 reaction steps, as extending the search to the remaining compounds added few additional options (see Fig. 3). At each step, the new building blocks were added to the existing pool of available blocks to model the marginal gain for the chemist to perform synthesis for acquisition of new building blocks. We repeated 10 runs for each level of reaction step for Algorithm 1 from different randomized initializations. The full distribution of QSAR and QED values by combination of the considered building blocks from reaction steps 0–4 can be seen in ESI Fig. S.4.†
The results for single-objective search, cf.Table 1, show that the average QSAR values while optimizing for the other objectives tended to stay between 0.6 and 0.7, indicating that an arbitrary re-combination of building blocks from LibINVENT compounds of high QSAR values does not always result in a product that also has a high QSAR value.
Expanding the search to building blocks available by 1–4 reaction steps resulted in samples of slightly lower diversity as average QSAR value went from very close to 1.0 to selections that had each compound with a value of exactly 1.0. Optimizing for diversity maintained the average QSAR value in the observed selections. The results of SO did not improve as the number of available building blocks increased. This indicates that the set of purchasable building blocks that is already available covers optimal solutions given our scoring parameters. For the single-objective optimization strategies, the QED value tended to decrease as the size of the search space increased. A possible explanation could be that the building blocks corresponding to several steps of reactions are more complex, which tend to have a negative effect on the QED value.93 The difference between the selections from baseline available building blocks and selections of building blocks one reaction step away represent the largest change in QED score, while further expansions of the building block availability resulted in much smaller or no changes for all metrics. This observation is likely explained by the distribution of building blocks we previously observed in Fig. 3; one reaction step represents a change from a space of 6203 × 763 products to a space of 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 034 × 1926, almost ten times larger. The next reaction steps increase the size of the product space relative to the previous step by 31.7% and 4.9%, respectively. The sampling process thus selects building blocks from a pool that is very similar between these three selections, and as such the distributions are similar.
034 × 1926, almost ten times larger. The next reaction steps increase the size of the product space relative to the previous step by 31.7% and 4.9%, respectively. The sampling process thus selects building blocks from a pool that is very similar between these three selections, and as such the distributions are similar.
The top 96 compounds by predicted activity generated by LibINVENT had an average QSAR value of 1.0 and average QED of 0.43. While these compounds are more diverse than any selection found in our combinatorial selection, they achieve this by breaking the combinatorial constraint. The selection had 96 different carboxylic acids and 3 different aromatic halides. 95 carboxylic were evaluated by AiZynthfinder to be synthesizable, in at most four reaction steps. The 3 aromatic halides were all available directly in stock.
To compare these results against random selection, we sampled 100 combinatorial selections of size 12 × 8, where each building block for the respective AC and BH reactions was sampled with equal probability. This was repeated for building block availability from each level of reaction steps up to 4 reaction steps from the stock. The random selections consistently had worse QSAR values and QED values than SO, while having diversity values that were not noticeably different from the optimized selections. The average QED value among the random selections is <0.25, which is significantly lower than the average of an “attractive drug”.93 In addition, the average QSAR value is lower than 0.8, which means many products in the selection are not very likely to be bioactive. This validates the need for optimizing these selections.
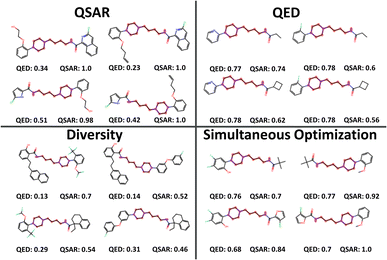
The selected products of the single-objective optimizations as well as the SO were also compared visually. Fig. 4 shows a small sample of 2 × 2 combinatorial examples from the different selections for visual clarity. The single-objective selections leave plenty of room for improvement. QED-optimized and diversity-optimized selections both have QSAR values around 0.7, but while the QED-optimized compounds are small, the diversity optimized compounds promote larger building blocks with several rings and side chains. QSAR-optimized selections have the lowest diversity and cover a range of low QED-scores, favouring building blocks with 1–2 rings each and are generally too large still for being druglike. It is likely that the QSAR score of 1.0 indicates that LibINVENT finds exactly which bits in the fingerprint representation that exploit the QSAR model. SO yielded a balanced selection of smaller building blocks that still yielded a high average QSAR value of ∼0.848.
To provide a reference frame for the diversity in relation to the log determinant, we conducted two experiments for “cherry-picking” molecules among the products at each level of building block availability, using both random selection and the RDKit MaxMin Picker. In the first experiment we filter all products to be in the same ranges as the SO selections in terms of QSAR ∈ [0.6–1.0] and QED ∈ [0.54–0.82] and sampled 100 samples using both methods. The results of this procedure can be found in Table 2.
| N reaction steps | Selection strategy | Avg QSAR (SD) | Avg QED (SD) | Avg log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Det (SD) Det (SD) |
|---|---|---|---|---|
| 0 | MaxMin | 0.729 (0.00377) | 0.570 (0.00258) | −37.29 (0.1784) |
| Random | 0.740 (0.00747) | 0.606 (0.00563) | −53.59 (1.650) | |
| 1 | MaxMin | 0.712 (0.00381) | 0.563 (0.00198) | −30.95 (0.103) |
| Random | 0.745 (0.00732) | 0.598 (0.00461) | −45.7 (0.838) | |
| 2 | MaxMin | 0.712 (0.0455) | 0.562 (0.00184) | −30.55 (0.105) |
| Random | 0.744 (0.00739) | 0.599 (0.00470) | −45.64 (0.931) | |
| 3 | MaxMin | 0.712 (0.00445) | 0.563 (0.00192) | −30.462 (0.107) |
| Random | 0.744 (0.00700) | 0.598 (0.00485) | −45.466 (0.837) | |
| 4 | MaxMin | 0.712 (0.00411) | 0.562 (0.00221) | −30.4 (0.123) |
| Random | 0.744 (0.00668) | 0.598 (0.00495) | −45.39 (0.933) |
The MaxMin picker also illustrate the competing objectives, as optimizing diversity without considering the QSAR and QED results in average values that are close to the minimum possible QED value according to the filter, while the QSAR tends to be slightly below the median (0.76) of the distribution. Another observation is that the diversity noticeably increases as reaction steps increase from step 0 to 1, but do not change significantly for subsequent steps. This was mirrored by the DPP optimization when targeting diversity. A second experiment was thus conducted where we filtered the minimum ranges to match the SO mean values, QSAR ∈ [0.84–1.0] and QED ∈ [0.7–0.82], to explore how diverse selections can be with similar values to our selections. These results are displayed in Table 3. During this study, we confirmed that the set of purchasable building blocks covered most of the highest scoring products. The number of products passing the filter that could be made from in-stock eMolecules building blocks were 1822, while 1 reaction step only increased this number to 1947. From the building blocks available in 1 reaction step to 4, this number only increases to 1984, meaning that 91% of the highest quality products were available using in-stock products. This small change is also reflected in the minor changes to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Det, which shows a small increase in diversity for the larger pools of products.
Det, which shows a small increase in diversity for the larger pools of products.
| N reaction steps | Selection strategy | Avg QSAR (SD) | Avg QED (SD) | Avg log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Det (SD) Det (SD) |
|---|---|---|---|---|
| 0 | MaxMin | 0.850 (0.00125) | 0.717 (0.00105) | −46.99 (0.298) |
| Random | 0.866 (0.00309) | 0.725 (0.00210) | −72.62 (2.397) | |
| 1 | MaxMin | 0.850 (0.00124) | 0.716 (0.000990) | −46.20 (0.338) |
| Random | 0.866 (0.00357) | 0.724 (0.00185) | −72.01 (2.080) | |
| 2 | MaxMin | 0.850 (0.00121) | 0.719 (0.000871) | −46.18 (0.308) |
| Random | 0.865 (0.00378) | 0.724 (0.00178) | −71.80 (2.303) | |
| 3 | MaxMin | 0.850 (0.00114) | 0.716 (0.00188) | −46.03 (0.314) |
| Random | 0.865 (0.00355) | 0.723 (0.00188) | −71.66 (1.871) | |
| 4 | MaxMin | 0.850 (0.00121) | 0.715 (0.000864) | −46.02 (0.291) |
| Random | 0.866 (0.00350) | 0.724 (0.00198) | −71.82 (1.931) |
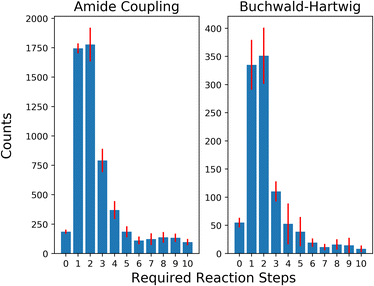
To evaluate the selection strategies in a more practically relevant setting, we restricted our building block stock availability to a subset of 3% of the original size (∼45k building blocks) simulating an approximate availability of building blocks available for a pharmaceutical company. The distribution of solved retrosynthesis routes for the building block subsets are shown in Fig. 5. The unsolved routes on average were 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 with a standard deviation of 526.6 and 1072 with a standard deviation of 132.9 for AC and BH reactions, respectively. It is noteworthy that the proportion of building blocks added per reaction step relative to the current available size is larger for these limited availability subsets, i.e., as 1745 and 385 building blocks are added for AC and BH after one reaction, compared to 16
504 with a standard deviation of 526.6 and 1072 with a standard deviation of 132.9 for AC and BH reactions, respectively. It is noteworthy that the proportion of building blocks added per reaction step relative to the current available size is larger for these limited availability subsets, i.e., as 1745 and 385 building blocks are added for AC and BH after one reaction, compared to 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 and 1163 building blocks added for the full stock. The general trend continues as the selection space is expanded to more reaction steps and in the first four reaction steps almost half of the total number of aromatic halides and more than half of the carboxylic acids become available.
831 and 1163 building blocks added for the full stock. The general trend continues as the selection space is expanded to more reaction steps and in the first four reaction steps almost half of the total number of aromatic halides and more than half of the carboxylic acids become available.
The same four selection strategies were used for building blocks available from 0 to 4 reaction steps with ten starting randomized initializations each. Here, the selection from stock-available (zero reaction steps), seen in Table 4, shows that the highest achievable values are drastically lower than after acquiring more building blocks by synthesis. For this smaller space the algorithm is likely to result in the same optimum for the given stock with multiple initializations.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Det is the logarithm of determinant of the kernel matrix, or matrix of all pairwise Tanimoto similarities in the current selection, and a measure of diversity. A value closer to 0 is more diverse. Random selection is the average values of 100 combinations selected for each reaction step availability. For each optimization strategy, we show the results of stock-available building blocks (0 reaction steps) and building blocks up to 4 reaction steps away
Det is the logarithm of determinant of the kernel matrix, or matrix of all pairwise Tanimoto similarities in the current selection, and a measure of diversity. A value closer to 0 is more diverse. Random selection is the average values of 100 combinations selected for each reaction step availability. For each optimization strategy, we show the results of stock-available building blocks (0 reaction steps) and building blocks up to 4 reaction steps away
| Selection strategy | N reaction steps | Avg QSAR | Avg QED | Avg log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Det Det |
|---|---|---|---|---|
| QSAR | 0 | 0.909 (0.0108) | 0.373 (0.0408) | −152.3 (7.32) |
| 1 | 0.984 (0.00718) | 0.386 (0.0493) | −189.5 (13.5) | |
| 2 | 0.992 (0.00534) | 0.349 (0.0340) | −196.3 (9.80) | |
| 3 | 0.992 (0.00533) | 0.341 (0.0290) | −195.4 (10.8) | |
| 4 | 0.993 (0.00464) | 0.335 (0.0331) | −196.9 (11.9) | |
| QED | 0 | 0.734 (0.0188) | 0.701 (0.00638) | −143.2 (2.24) |
| 1 | 0.685 (0.0152) | 0.775 (0.00234) | −151.4 (3.08) | |
| 2 | 0.691 (0.00809) | 0.781 (0.00334) | −155.1 (3.27) | |
| 3 | 0.687 (0.0117) | 0.782 (0.00256) | −155.2 (2.96) | |
| 4 | 0.686 (0.0133) | 0.772 (0.00231) | −155.3 (3.22) | |
| Diversity | 0 | 0.722 (0.0127) | 0.305 (0.0205) | −108.3 (0.796) |
| 1 | 0.704 (0.0133) | 0.237 (0.288) | −102.7 (0.759) | |
| 2 | 0.707 (0.0153) | 0.200 (0.0174) | −100.8 (0.783) | |
| 3 | 0.708 (0.0124) | 0.186 (0.0168) | −100.3 (0.860) | |
| 4 | 0.716 (0.0421) | 0.187 (0.0241) | −101.8 (12.6) | |
| Simultaneous optimization | 0 | 0.789 (0.0182) | 0.650 (0.00599) | −127.9 (2.33) |
| 1 | 0.836 (0.00652) | 0.700 (0.00709) | −127.1 (1.08) | |
| 2 | 0.842 (0.00771) | 0.700 (0.00718) | −126.2 (1.24) | |
| 3 | 0.846 (0.00742) | 0.703 (0.00705) | −127.2 (1.19) | |
| 4 | 0.846 (0.00722) | 0.703 (0.00793) | −127.3 (1.18) | |
| Random selection | 0 | 0.758 (0.0210) | 0.382 (0.0391) | −128.8 (3.90) |
| 1 | 0.767 (0.0240) | 0.365 (0.0488) | −131.2 (4.44) | |
| 2 | 0.770 (0.0250) | 0.330 (0.0458) | −129.8 (4.60) | |
| 3 | 0.776 (0.0231) | 0.304 (0.0414) | −130.1 (4.63) | |
| 4 | 0.772 (0.0235) | 0.312 (0.0424) | −129.4 (4.35) |
The results show that optimized selections approach their respective values from the full eMolecules availability already after extending the selection space to building blocks available within one reaction, and that the stock-available selections score similar in average QSAR and diversity to the random selection of previous experiment. The standard deviations for each sample are in the same range as for the previous experiments, and occasionally, such as for the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Det during the diversity selection strategy, significantly higher. This is expected since there is variation in both available building blocks in addition to the variation across repeat samples due to initialization. There are smaller improvements in selections with building blocks available within two reaction steps and no improvements with further reactions. We can draw parallels with the distribution of available building blocks in Fig. 4 to the distribution of the previous experiment, and note that the improvements occur when a relatively large number of new building blocks are added to the selection space. When the relative expansion of the space is low the probability of finding a new improved solution is also low.
Det during the diversity selection strategy, significantly higher. This is expected since there is variation in both available building blocks in addition to the variation across repeat samples due to initialization. There are smaller improvements in selections with building blocks available within two reaction steps and no improvements with further reactions. We can draw parallels with the distribution of available building blocks in Fig. 4 to the distribution of the previous experiment, and note that the improvements occur when a relatively large number of new building blocks are added to the selection space. When the relative expansion of the space is low the probability of finding a new improved solution is also low.
Unlike the previous experiment, however, the QED score remains at a similar level or, in some cases, improves as the number of reaction steps increase. It is likely that the number of added building blocks through reactions that are “too large”, e.g., heavier than 500 Da. We base this hypothesis on analysing the average number of heavy atoms in the building blocks as a function of reaction steps, which correlate with molecule weight. The average number of heavy atoms for the different number of reaction steps are shown for both cases in Table 5.
| Building block | In stock | 1 reaction step | 2 reaction steps | 3 reaction steps | 4 reaction steps |
|---|---|---|---|---|---|
| AC, full | 14.34 | 18.52 | 20.54 | 21.87 | 22.11 |
| AC, 3% subset | 14.09 | 14.20 | 14.66 | 16.49 | 17.42 |
| BH, full | 12.23 | 17.27 | 20.58 | 22.91 | 20.67 |
| BH, 3% subset | 11.86 | 12.76 | 14.26 | 15.97 | 16.59 |
For both the full datasets and the subsets, we compared the simultaneous optimization strategy against random selection, using the Kullback–Leibler divergence124 to measure how difficult it is to pass a selection as sampled from the random distribution as one sampled from the simultaneous optimization. The results are shown in Table 6. This show that the distributions are distinctly different from each other.
| Kullback–Leibler divergence, KL(A, B) | ||
|---|---|---|
| N reaction steps | Dataset | A = simultaneous optimization |
| B = random | ||
| 0 | Full | 79.04 |
| 1 | 138.9 | |
| 2 | 188.8 | |
| 3 | 162.3 | |
| 4 | 168.6 | |
| 0 | 3% subset | 32.20 |
| 1 | 48.57 | |
| 2 | 65.68 | |
| 3 | 79.60 | |
| 4 | 77.64 | |
The methodology of comparing the optimization results between two different stocks of availability might be useful to estimate the prospective gain from synthesizing new building blocks compared to buying available compounds or simply using the current stock by comparing the optimization results with different selection spaces. This can assist the decision-maker in designing efficient libraries in a combinatorial manner. The number of building blocks estimated to be available through synthesis shows a substantial/relevant increase in search space as the number of reaction steps increases. In practice, only stock-available building blocks or building blocks that can be synthesized in one reaction step will often be used. Alternatively, one could introduce a constraint on the total number of reaction steps used for the selected library, which could be accounted for using e.g., reaction sampling.
Computational time
During selection, we opted for relatively small selection dimensions to limit the computational time to less than ten hours per run, since we performed 12 optimizations, for 10 splits and 5 different building block availabilities, for a total of 600 selections. The observed runs would perform for approximately 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–100
000–100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samples depending on selection space, initialization and number of metrics, which could take between 20 minutes and 4 hours on a single CPU with the QSAR model being the biggest bottleneck. However, since the evaluation of a random forest model is linear in the number of new products between two samples (12 or 8 depending on the exchanged building block) and determinant calculations have the time complexity of O(k3) with total number of products, the method will eventually be limited by evaluations of diversity rather than QSAR. This appears feasible with size 1536 as here n = products2 = (u × v)2. The termination criterion for 10
000 samples depending on selection space, initialization and number of metrics, which could take between 20 minutes and 4 hours on a single CPU with the QSAR model being the biggest bottleneck. However, since the evaluation of a random forest model is linear in the number of new products between two samples (12 or 8 depending on the exchanged building block) and determinant calculations have the time complexity of O(k3) with total number of products, the method will eventually be limited by evaluations of diversity rather than QSAR. This appears feasible with size 1536 as here n = products2 = (u × v)2. The termination criterion for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samples without improvement was chosen after initial experimentation. For larger library dimensions, it is possible that more samples are more suitable to find convergence. The increase in number of building blocks to choose results in more decision variables to determine for an optimal solution. Additionally, larger dimensions generally mean the marginal change of exchanging one building block on the average values in the selection is smaller, which implies the acceptance ratio becomes closer to 1. On an Intel Xeon W-2125 CPU @ 4.00 GHz machine with 8 threads the 12 × 8 configuration required approximately 0.11 s for the QSAR computations compared to 0.04 s for computing diversity for each sample, while a 48 × 32 configuration required 0.14 s for the QSAR and 4.0 s for computing the diversity. A full exhaustive search was never considered even for the smallest subsets as e.g., the size of the average 3% subset at stock-availability in a 12 × 8 configuration results in ∼2 × 1027 different possible combinations. For the same reasons, hyperparameter optimization of acceptance ratio α and score weights ω was not performed, as this scaffold is hypothetical and that a marginally better selection would not lead to generalizable guidelines for these parameters.
000 samples without improvement was chosen after initial experimentation. For larger library dimensions, it is possible that more samples are more suitable to find convergence. The increase in number of building blocks to choose results in more decision variables to determine for an optimal solution. Additionally, larger dimensions generally mean the marginal change of exchanging one building block on the average values in the selection is smaller, which implies the acceptance ratio becomes closer to 1. On an Intel Xeon W-2125 CPU @ 4.00 GHz machine with 8 threads the 12 × 8 configuration required approximately 0.11 s for the QSAR computations compared to 0.04 s for computing diversity for each sample, while a 48 × 32 configuration required 0.14 s for the QSAR and 4.0 s for computing the diversity. A full exhaustive search was never considered even for the smallest subsets as e.g., the size of the average 3% subset at stock-availability in a 12 × 8 configuration results in ∼2 × 1027 different possible combinations. For the same reasons, hyperparameter optimization of acceptance ratio α and score weights ω was not performed, as this scaffold is hypothetical and that a marginally better selection would not lead to generalizable guidelines for these parameters.
Conclusions
We present a framework for combinatorial library design evaluated using available public data and open source software to allow reproducibility. The framework can be controlled by specifying both importance of different evaluation metrics and the acceptance ratio α. An extensive exploration of the latter parameter was not performed in this study due to the computational costs. Our experimental results show that it is possible to perform the multi-objective optimization towards both quality and diversity for our example library. The results show that our framework can navigate the search space around combinatorial library design and find selections of high (>0.8) QSAR values while retaining good (>0.7) QED values and high diversity. The trade-offs between the different objectives were investigated and it was found that the multi-objective optimization maintained a QED relatively close to the maximum possible while optimizing QSAR and diversity. Building blocks that were selected at random showed on average low (<0.25) QED values and lower QSAR value (∼0.78) than the quality-focused optimization strategies. Our experiments indicate that the set of all available purchasable building blocks require minimal extra synthesis to reach the highest observed scores, while simulated scenarios of limited stock greatly benefit—to comparable score levels—from single-step synthesis of building blocks. The former conclusion is supported by a full evaluation of all possible products in the space, where we found that the set highest scoring compounds (QSAR > 0.84 and QED > 0.7 at the same time) had 91% of the products accessible using only in-stock building blocks. The latter scenario might be useful in practise in a larger company with a sizable building block store. It might be faster and cheaper to synthesize the needed building blocks for the combinatorial library design in one step compared to purchasing additional building blocks. It was also shown that synthesizing building blocks in more than one step was not attractive given the size of the internal building block store. For an institution with a very small internal building block store, it might be favourable to synthesize the needed building blocks for the libraries in more than one step.Data availability
The code for this paper can be found at https://github.com/SeemonJ/combinatorial-library-design-dpp.Author contributions
SVJ jointly with MHC, OE and AS conceptualized the approach and developed the methodology. SVJ performed the data curation, formal analysis, and investigation, implemented the software, and performed validation, and visualization; he also wrote the original draft. MHC, OE and AS supervised and administered the project. All authors reviewed and edited the submitted manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors would like to thank Dr Samuel Genheden for help with AiZynthFinder and discussions regarding building blocks, Dr Thierry Kogej for discussions on filtering stock files for building block types and different entry formats. The authors also thank Mr Hampus Gummesson Svensson for scientific discussions and for reviewing this manuscript. Additionally, the authors want to thank the Molecular AI department at AstraZeneca and the Department of Computer Science and Engineering at Chalmers for many discussions and support. Finally, the authors thank the Knut and Alice Wallenberg foundation and the WASP program for financial support.Notes and references
- E. N. Muratov, J. Bajorath, R. P. Sheridan, I. V. Tetko, D. Filimonov, V. Poroikov, T. I. Oprea, I. I. Baskin, A. Varnek, A. Roitberg, O. Isayev, S. Curtalolo, D. Fourches, Y. Cohen, A. Aspuru-Guzik, D. A. Winkler, D. Agrafiotis, A. Cherkasov and A. Tropsha, Chem. Soc. Rev., 2020, 49, 3525–3564 RSC.
- M. Dablander, T. Hanser, R. Lambiotte and G. M. Morris, J. Cheminf., 2023, 15, 47 Search PubMed.
- M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, J. Cheminf., 2017, 9, 48 Search PubMed.
- O. Prykhodko, S. V. Johansson, P. C. Kotsias, J. Arús-Pous, E. J. Bjerrum, O. Engkvist and H. Chen, J. Cheminf., 2019, 11, 74 Search PubMed.
- R. Mercado, T. Rastemo, E. Lindelöf, G. Klambauer, O. Engkvist, H. Chen and E. J. Bjerrum, Mach. Learn.: Sci. Technol., 2020, 2 Search PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- M. H. S. Segler, T. Kogej, C. Tyrchan and M. P. Waller, ACS Cent. Sci., 2018, 4, 120–131 CrossRef PubMed.
- S. R. Atance, J. V. Diez, O. Engkvist, S. Olsson and R. Mercado, J. Chem. Inf. Model., 2022, 62, 4863–4872 CrossRef PubMed.
- M. H. S. Segler and M. P. Waller, Chem.–Eur. J., 2017, 23, 5966–5971 CrossRef PubMed.
- M. H. S. Segler, M. Preuss and M. P. Waller, Nature, 2018, 555, 604–610 CrossRef PubMed.
- C. W. Coley, R. Barzilay, T. S. Jaakkola, W. H. Green and K. F. Jensen, ACS Cent. Sci., 2017, 3, 434–443 CrossRef PubMed.
- H. Gao, T. J. Struble, C. W. Coley, Y. Wang, W. H. Green and K. F. Jensen, ACS Cent. Sci., 2018, 4, 1465–1476 CrossRef PubMed.
- S. Genheden, A. Thakkar, V. Chadimová, J.-L. Reymond, O. Engkvist and E. Bjerrum, J. Cheminf., 2020, 12, 70 Search PubMed.
- A. M. Westerlund, S. Manohar Koki, S. Kancharla, A. Tibo, L. Saigiridharan, R. Mercado and S. Genheden, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2023-685jv.
- I. Levin, M. Liu, C. A. Voigt and C. W. Coley, Nat. Commun., 2022, 13, 7747 CrossRef PubMed.
- M. Garcia de Lomana, F. Svensson, A. Volkamer, M. Mathea and J. Kirchmair, Digital Discovery, 2022, 1, 158–172 RSC.
- S. Hamzic, R. Lewis, S. Desrayaud, C. Soylu, M. Fortunato, G. Gerebtzoff and R. Rodríguez-Pérez, J. Chem. Inf. Model., 2022, 62, 3180–3190 CrossRef CAS PubMed.
- M. Withnall, E. Lindelöf, O. Engkvist and H. Chen, J. Cheminf., 2020, 12, 1 CAS.
- F. H. Vermeire, Y. Chung and W. H. Green, J. Am. Chem. Soc., 2022, 144, 10785–10797 CrossRef CAS PubMed.
- J. Born, G. Markert, N. Janakarajan, T. B. Kimber, A. Volkamer, M. R. Martínez and M. Manica, Digital Discovery, 2023, 2, 674–691 RSC.
- S. Johansson, A. Thakkar, T. Kogej, E. Bjerrum, S. Genheden, T. Bastys, C. Kannas, A. Schliep, H. Chen and O. Engkvist, Drug Discovery Today: Technol., 2019, 32–33, 65–72 CrossRef PubMed.
- K. H. Bleicher, H.-J. Böhm, K. Müller and A. I. Alanine, Nat. Rev. Drug Discovery, 2003, 2, 369–378 CrossRef CAS PubMed.
- T. Kodadek, Chem. Commun., 2011, 47, 9757–9763 RSC.
- H. M. Geysen, R. H. Meloen and S. J. Barteling, Proc. Natl. Acad. Sci. U. S. A., 1984, 81, 3998–4002 CrossRef CAS PubMed.
- J. K. Scott and G. P. Smith, Science, 1990, 249, 386–390 CrossRef PubMed.
- R. A. Houghten, C. Pinilla, S. E. Blondelle, J. R. Appel, C. T. Dooley and J. H. Cuervo, Nature, 1991, 354, 84–86 CrossRef PubMed.
- K. S. Lam, S. E. Salmon, E. M. Hersh, V. J. Hruby, W. M. Kazmierski and R. J. Knapp, Nature, 1991, 354, 82–84 CrossRef PubMed.
- A. R. Oliphant, A. L. Nussbaum and K. Struhl, Gene, 1986, 44, 177–183 CrossRef PubMed.
- M. S. Horwitz and L. A. Loeb, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 7405–7409 CrossRef PubMed.
- G. F. Joyce, Gene, 1989, 82, 83–87 CrossRef PubMed.
- C. Tuerk and L. Gold, Science, 1990, 249, 505–510 CrossRef PubMed.
- A. D. Ellington and J. W. Szostak, Nature, 1990, 346, 818–822 CrossRef PubMed.
- C. F. Barbas, J. D. Bain, D. M. Hoekstra and R. A. Lerner, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 4457–4461 CrossRef PubMed.
- R. J. Simon, R. S. Kania, R. N. Zuckermann, V. D. Huebner, D. A. Jewell, S. Banville, S. Ng, L. Wang, S. Rosenberg and C. K. Marlowe, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 9367–9371 CrossRef PubMed.
- C. Y. Cho, E. J. Moran, S. R. Cherry, J. C. Stephans, S. P. A. Fodor, C. L. Adams, A. Sundaram, J. W. Jacobs and P. G. Schultz, Science, 1993, 261, 1303–1305 CrossRef PubMed.
- S. J. Danishefsky, K. F. McClure, J. T. Randolph and R. B. Ruggeri, Science, 1993, 260, 1307–1309 CrossRef PubMed.
- O. Kanie, F. Barresi, Y. Ding, J. Labbe, A. Otter, L. S. Forsberg, B. Ernst and O. Hindsgaul, Angew. Chem., Int. Ed. Engl., 1996, 34, 2720–2722 CrossRef.
- B. Bunin, M. Plunkett and J. Ellman, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 4708–4712 CrossRef PubMed.
- J. A. Ellman, Acc. Chem. Res., 1996, 29, 132–143 CrossRef.
- X. D. Xiang, X. Sun, G. Briceño, Y. Lou, K.-A. Wang, H. Chang, W. G. Wallace-Freedman, S.-W. Chen and P. G. Schultz, Science, 1995, 268, 1738–1740 CrossRef PubMed.
- R. Pascual, J. I. Borrell and J. Teixidó, Mol. Diversity, 2003, 6, 121–133 CrossRef PubMed.
- E. A. Jamois, M. Hassan and M. Waldman, J. Chem. Inf. Comput. Sci., 2000, 40, 63–70 CrossRef PubMed.
- B. R. Beno and J. S. Mason, Drug Discovery Today, 2001, 6, 251–258 CrossRef PubMed.
- D. C. Spellmeyer and P. D. J. Grootenhuis, in Annual Reports in Medicinal Chemistry, ed. A. M. Doherty, Academic Press, 1999, vol. 34, pp. 287–296 Search PubMed.
- F. L. Stahura, L. Xue, J. W. Godden and J. Bajorath, J. Mol. Graphics Modell., 1999, 17, 1–52 CrossRef PubMed.
- D. K. Agrafiotis and V. S. Lobanov, J. Chem. Inf. Comput. Sci., 2000, 40, 1030–1038 CrossRef PubMed.
- R. P. Sheridan, S. G. SanFeliciano and S. K. Kearsley, J. Mol. Graphics Modell., 2000, 18, 320–334 CrossRef PubMed.
- E. A. Jamois, C. T. Lin and M. Waldman, J. Mol. Graphics Modell., 2003, 22, 141–149 CrossRef PubMed.
- Concepts and applications of molecular similarity, ed. M. A. Johnson and G. M. Maggiora, John Wiley & Sons, Nashville, TN, 1990 Search PubMed.
- S. D. Pickett, I. M. McLay and D. E. Clark, J. Chem. Inf. Comput. Sci., 2000, 40, 263–272 CrossRef PubMed.
- E. Jacoby, B. Wroblowski, C. Buyck, J.-M. Neefs, C. Meyer, M. D. Cummings and H. van Vlijmen, Mol. Inf., 2018, 37, 1700119 CrossRef PubMed.
- R. Liu, X. Li and K. S. Lam, Curr. Opin. Chem. Biol., 2017, 38, 117–126 CrossRef.
- V. Kunig, M. Potowski, A. Gohla and A. Brunschweiger, Biol. Chem., 2018, 399, 691–710 CrossRef PubMed.
- R. M. Franzini, D. Neri and J. Scheuermann, Acc. Chem. Res., 2014, 47, 1247–1255 CrossRef PubMed.
- Y. Shi, Y.-r. Wu, J.-q. Yu, W.-n. Zhang and C.-l. Zhuang, RSC Adv., 2021, 11, 2359–2376 RSC.
- B. Xia, G. J. Franklin, X. Lu, K. L. Bedard, L. C. Grady, J. D. Summerfield, E. X. Shi, B. W. King, K. E. Lind, C. Chiu, E. Watts, V. Bodmer, X. Bai and L. A. Marcaurelle, ACS Med. Chem. Lett., 2021, 12, 1166–1172 CrossRef PubMed.
- N. van Hilten, F. Chevillard and P. Kolb, J. Chem. Inf. Model., 2019, 59, 644–651 CrossRef PubMed.
- W. P. Walters, J. Med. Chem., 2019, 62, 1116–1124 CrossRef PubMed.
- L. Humbeck, S. Weigang, T. Schäfer, P. Mutzel and O. Koch, ChemMedChem, 2018, 13, 532–539 CrossRef PubMed.
- Enamine, REAL Building Blocks, https://enamine.net/compound-collections/real-compounds/real-database, accessed 2023-04-12 Search PubMed.
- C. A. Lipinski, F. Lombardo, B. W. Dominy and P. J. Feeney, Adv. Drug Delivery Rev., 2001, 46, 3–26 CrossRef PubMed.
- L. Ruddigkeit, R. van Deursen, L. C. Blum and J.-L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864–2875 CrossRef PubMed.
- Y. Zabolotna, F. Bonachera, D. Horvath, A. Lin, G. Marcou, O. Klimchuk and A. Varnek, J. Chem. Inf. Model., 2022, 62, 4537–4548 CrossRef PubMed.
- C. M. Bishop, M. Svensén and C. K. I. Williams, Neural Comput., 1998, 10, 215–234 CrossRef.
- J. J. Irwin, K. G. Tang, J. Young, C. Dandarchuluun, B. R. Wong, M. Khurelbaatar, Y. S. Moroz, J. Mayfield and R. A. Sayle, J. Chem. Inf. Model., 2020, 60, 6065–6073 CrossRef PubMed.
- Enamine, MADE Building Blocks, https://enamine.net/building-blocks/made-building-blocks, accessed 2023-04-12 Search PubMed.
- P. Schneider, W. P. Walters, A. T. Plowright, N. Sieroka, J. Listgarten, R. A. Goodnow, J. Fisher, J. M. Jansen, J. S. Duca, T. S. Rush, M. Zentgraf, J. E. Hill, E. Krutoholow, M. Kohler, J. Blaney, K. Funatsu, C. Luebkemann and G. Schneider, Nat. Rev. Drug Discovery, 2020, 19, 353–364 CrossRef PubMed.
- S. R. Langdon, P. Ertl and N. Brown, Mol. Inf., 2010, 29, 366–385 CrossRef PubMed.
- J. Arús-Pous, A. Patronov, E. J. Bjerrum, C. Tyrchan, J.-L. Reymond, H. Chen and O. Engkvist, J. Cheminf., 2020, 12, 38 Search PubMed.
- V. Bagal, R. Aggarwal, P. K. Vinod and U. D. Priyakumar, J. Chem. Inf. Model., 2022, 62, 2064–2076 CrossRef PubMed.
- T. E. Hadfield, F. Imrie, A. Merritt, K. Birchall and C. M. Deane, J. Chem. Inf. Model., 2022, 62, 2280–2292 CrossRef PubMed.
- A. Domenico, G. Nicola, T. Daniela, C. Fulvio, A. Nicola and N. Orazio, J. Chem. Inf. Model., 2020, 60, 4582–4593 CrossRef PubMed.
- V. Fialková, J. Zhao, K. Papadopoulos, O. Engkvist, E. J. Bjerrum, T. Kogej and A. Patronov, J. Chem. Inf. Model., 2022, 62, 2046–2063 CrossRef PubMed.
- J. P. Janet, L. Mervin and O. Engkvist, Curr. Opin. Struct. Biol., 2023, 80, 102575 CrossRef PubMed.
- C. Bilodeau, W. Jin, T. Jaakkola, R. Barzilay and K. F. Jensen, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1608 Search PubMed.
- M. Thomas, A. Boardman, M. Garcia-Ortegon, H. Yang, C. de Graaf and A. Bender, in Artificial Intelligence in Drug Design, ed. A. Heifetz, Springer US, New York, NY, 2022, pp. 1–59, DOI:10.1007/978-1-0716-1787-8_1.
- D. K. Agrafiotis, Mol. Diversity, 2000, 5, 209–230 CrossRef PubMed.
- V. J. Gillet, W. Khatib, P. Willett, P. J. Fleming and D. V. S. Green, J. Chem. Inf. Comput. Sci., 2002, 42, 375–385 CrossRef PubMed.
- H. Chen, U. Börjesson, O. Engkvist, T. Kogej, M. A. Svensson, N. Blomberg, D. Weigelt, J. N. Burrows and T. Lange, J. Chem. Inf. Model., 2009, 49, 603–614 CrossRef CAS PubMed.
- T. Meinl, C. Ostermann and M. R. Berthold, J. Chem. Inf. Model., 2011, 51, 237–247 CrossRef CAS PubMed.
- J. C. Fromer and C. W. Coley, Patterns, 2023, 4, 100678 CrossRef CAS PubMed.
- S. Luukkonen, H. W. van den Maagdenberg, M. T. M. Emmerich and G. J. P. van Westen, Curr. Opin. Struct. Biol., 2023, 79, 102537 CrossRef PubMed.
- K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, IEEE Trans. Evol. Comput., 2002, 6, 182–197 CrossRef.
- K. Deb and H. Jain, IEEE Trans. Evol. Comput., 2014, 18, 577–601 Search PubMed.
- A. Kulesza and B. Taskar, Found. Trends Mach. Learn., 2012, 5, 123–286 CrossRef.
- A. Kulesza and B. Taskar, presented in part at the Advances in Neural Information Processing Systems, 2010 Search PubMed.
- J. Gillenwater, A. Kulesza and B. Taskar, presented in part at the Proceedings of the 2012 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning, 2012 Search PubMed.
- N. Miyoshi and T. Shirai, Adv. Appl. Probab., 2014, 46, 832–845 CrossRef.
- T. Nakamura, S. Sakaue, K. Fujii, Y. Harabuchi, S. Maeda and S. Iwata, Sci. Rep., 2022, 12, 1124 CrossRef CAS PubMed.
- D. Sydow, P. Schmiel, J. Mortier and A. Volkamer, J. Chem. Inf. Model., 2020, 60, 6081–6094 CrossRef CAS.
- G. V. Andrianov, W. J. Gabriel Ong, I. Serebriiskii and J. Karanicolas, J. Chem. Inf. Model., 2021, 61, 5967–5987 CrossRef CAS PubMed.
- Emolecules, https://downloads.emolecules.com/free/, accessed 28-02-2023.
- G. R. Bickerton, G. V. Paolini, J. Besnard, S. Muresan and A. L. Hopkins, Nat. Chem., 2012, 4, 90 CrossRef CAS PubMed.
- J. Gasteiger, ChemPhysChem, 2020, 21, 2233–2242 CrossRef CAS PubMed.
- C. Hansch, P. P. Maloney, T. Fujita and R. M. Muir, Nature, 1962, 194, 178–180 CrossRef CAS.
- M. Hassan, R. D. Brown, S. Varma-O’brien and D. Rogers, Mol. Diversity, 2006, 10(3), 283–299 CrossRef CAS PubMed.
- S. Geman and D. Geman, IEEE Trans. Pattern Anal. Mach. Intell., 1984, PAMI-6, 721–741 Search PubMed.
- A. Kulesza and B. Taskar, presented in part at the Proceedings of the 28th International Conference on International Conference on Machine Learning, 2011 Search PubMed.
- V. Fialková, J. Zhao, K. Papadopoulos, O. Engkvist, E. J. Bjerrum, T. Kogej and A. Patronov, Implementation of the Lib-INVENT Decorator model, https://github.com/MolecularAI/Lib-INVENT, accessed 28-02-2023 Search PubMed.
- S. Genheden, A. Thakkar, V. Chadimová, J.-L. Reymond, O. Engkvist and E. Bjerrum, AiZynthFinder, https://github.com/MolecularAI/aizynthfinder, accessed 28-02-2023 Search PubMed.
- M. B. Smith and J. March, March's Advanced Organic Chemistry : Reactions, Mechanisms, and Structure, John Wiley & Sons, Somerset, 7th edn, 2013, pp. 751–755 Search PubMed.
- B. Mahjour, Y. Shen, W. Liu and T. Cernak, Nature, 2020, 580, 71–75 CrossRef CAS.
- T. K. Ho, Random decision forests, Proceedings of 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 1995, vol. 1, pp. 278–282 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- J. Sun, N. Jeliazkova, V. Chupakhin, J.-F. Golib-Dzib, O. Engkvist, L. Carlsson, J. Wegner, H. Ceulemans, I. Georgiev, V. Jeliazkov, N. Kochev, T. J. Ashby and H. Chen, J. Cheminf., 2017, 9, 17 Search PubMed.
- A. Gaulton, L. J. Bellis, A. P. Bento, J. Chambers, M. Davies, A. Hersey, Y. Light, S. McGlinchey, D. Michalovich, B. Al-Lazikani and J. P. Overington, Nucleic Acids Res., 2012, 40, D1100–D1107 CrossRef CAS PubMed.
- S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen, B. Yu, L. Zaslavsky, J. Zhang and E. E. Bolton, Nucleic Acids Res., 2023, 51, D1373–D1380 CrossRef PubMed.
- A. P. Bento, A. Gaulton, A. Hersey, L. J. Bellis, J. Chambers, M. Davies, F. A. Krüger, Y. Light, L. Mak, S. McGlinchey, M. Nowotka, G. Papadatos, R. Santos and J. P. Overington, Nucleic Acids Res., 2014, 42, D1083–1090 CrossRef CAS PubMed.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- G. Landrum, RDKit: Open-source cheminformatics, accessed 2023-10-15, DOI:10.5281/zenodo.7415128.
- H. L. Morgan, J. Chem. Doc., 1965, 5, 107–113 CrossRef CAS.
- Daylight, SMARTS – A Language for Molecular Patterns, https://www.daylight.com/dayhtml/doc/theory/theory.smarts.html, accessed 2023-02-28, 2023 Search PubMed.
- O. Macchi, Adv. Appl. Probab., 1975, 7, 83–122 CrossRef.
- T. T. Tanimoto, An Elementary Mathematical Theory of Classification and Prediction, International Business Machines Corporation, 1958 Search PubMed.
- A. Bhaskara, A. Karbasi, S. Lattanzi and M. Zadimoghaddam, Online MAP inference of determinantal point processes, NIPS'20: Proceedings of the 34th International Conference on Neural Information Processing Systems, 2020, vol. 288, pp. 3419–3429 Search PubMed.
- A. Norouzi-Fard, A. Bazzi, M. E. Halabi, I. Bogunovic, Y.-P. Hsieh and V. Cevher, Advances in Neural Information Processing Systems 29 (NIPS 2016), 2016 Search PubMed.
- A. Badanidiyuru, B. Mirzasoleiman, A. Karbasi and A. Krause, Streaming Submodular Maximization: Massive Data Summarization on the Fly, Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 2014, pp. 671–680 Search PubMed.
- J. Gillenwater, A. Kulesza, Z. Mariet and S. Vassilvitskii, Maximizing Induced Cardinality under a Determinantal Point Process, Proceedings of the 32nd International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 2018, pp. 6911–6920 Search PubMed.
- T. Wang, J.-Y. Zhu, A. Torralba and A. A. Efros, Dataset Distillation, arXiv, 2018, preprint, arXiv.1811.10959, DOI:10.48550/arXiv.1811.10959.
- P. Liu, A. Soni, E. Y. Kang, Y. Wang and M. Parsana, Diversity on the Go! Streaming Determinantal Point Processes under a Maximum Induced Cardinality Objective, in Proceedings of the Web Conference 2021 (WWW '21), Association for Computing Machinery, New York, NY, USA, 2021, pp. 1363–1372 Search PubMed.
- M. Wilhelm, A. Ramanathan, A. Bonomo, S. Jain, E. H. Chi and J. Gillenwater, Practical Diversified Recommendations on YouTube with Determinantal Point Processes, in Proceedings of the 27th ACM International Conference on Information and Knowledge Management (CIKM '18), Association for Computing Machinery, New York, NY, USA, 2018, pp. 2165–2173 Search PubMed.
- J. Gillenwater, A. Kulesza, Z. Mariet and S. Vassilvtiskii, A Tree-Based Method for Fast Repeated Sampling of Determinantal Point Processes, in Proceedings of the 36th International Conference on Machine Learning, Proceedings of Machine Learning Research, 2019, vol. 97, pp. 2260–2268, available from https://proceedings.mlr.press/v97/gillenwater19a.html Search PubMed.
- A. Rezaei and S. O. Gharan, A Polynomial Time MCMC Method for Sampling from Continuous Determinantal Point Processes, in Proceedings of the 36th International Conference on Machine Learning, Proceedings of Machine Learning Research, 2019, vol. 97, pp. 5438–5447, available from https://proceedings.mlr.press/v97/rezaei19a.html Search PubMed.
- S. Kullback and R. A. Leibler, Ann. Math. Stat., 1951, 22, 79–86 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00095h |
| This journal is © The Royal Society of Chemistry 2024 |