Non-steady state validation of kinetic models for ethylene epoxidation over silver catalysts†
Received
12th January 2024
, Accepted 6th May 2024
First published on 6th May 2024
Abstract
Kinetic modelling has been key to developing a mechanistic understanding of the epoxidation of ethylene to ethylene oxide over silver catalysts. However, models of varying active site and mechanistic complexity have all been able to recreate steady state activity and selectivity, leading to ambiguity about the exact mechanism and nature of the active site. Herein, we validate three leading kinetic models for ethylene epoxidation over metallic silver catalysts by numerically recreating non-steady state temporal analysis of products experiments. We find all of the models are able to very generally recreate the trends observed in the pulse experiments, but that only a two-site model modified to mimic the presence of a subsurface oxygen reservoir is able to accurately recreate the trends observed in a state-altering experiment over oxidised silver. Specific to this model is the inclusion of a electrophilic oxygen species adsorbed on top of the surface oxide which acts as the active site for the selective oxidation of ethylene. This work exemplifies that while simplified single-site models for ethylene epoxidation are useful tools for broad screening, more complex models are required to capture the precise activity of the catalyst.
1. Introduction
Heterogeneous catalytic processes are the driving force of the chemical industry, but their current use is unsustainable due to environmental, economic, and societal pressures. Despite the significance of these reactions, industrial innovation has typically outpaced our fundamental understanding, limiting catalyst development. One such reaction where our application far outstrips our understanding is the catalytic oxidation of ethylene to ethylene oxide (EO) using silver catalysts. With its global market value being 54 billion U.S. dollars in 2022, EO is one of the world's top chemicals.1 However, despite this widespread use in industry, the underlying reaction mechanism remains poorly understood.2
The net reactions for ethylene epoxidation, ethylene combustion, and EO combustion are as follows:
| |  | (1) |
| | | C2H4 + 3O2 → 2CO2 + 2H2O | (2) |
| |  | (3) |
Many studies have sought to resolve the reaction mechanism of ethylene epoxidation over metallic silver by coupling steady-state activity measurements with kinetic modelling,3–5 resulting in a variety of conflicting models. This has led to an open debate not only on the reaction mechanism, but also on the identity of the active site for this reaction.2,6–10 For ethylene epoxidation over silver there are three popular microkinetic models: the Linic–Barteau (LB) model was developed using Density Functional Theory (DFT) and surface science experiments to generate a simple 4-step, single site microkinetic model that was able to recreate the apparent activation energy of EO production.3 The Huš–Hellman (HH) model used DFT to generate an 11-step, single site microkinetic model that was validated by comparing kinetic Monte Carlo simulations to experimentally measured turnover frequencies and selectivities.4 Finally, the Stegelmann–Stoltze (SS) model used a combination of DFT and surface science to generate a 17-step, two-site microkinetic model that was able to recreate experimental turnover frequencies and selectivities across a wide range of conditions.5,11 As these models are validated against steady-state experiments, the number of activity or selectivity controlling reaction steps collapses down to a small (or single) number,12 which limits kinetic insight and can be the cause of the degeneracy seen in the models. Further, if we are to move beyond broad screening of reaction conditions to resolving the precise refinements required to increase catalytic activity and selectivity, more accurate models are required. Therefore, an external method of validating existing kinetic models against independent data recorded under different reaction conditions can provide insight into the broad applicability of these models, which, in turn, will help identify the reaction mechanism.
Non-steady-state techniques such as Temporal Analysis of Products13,14 (TAP) bypass the steady-state limitations, providing precisely resolved kinetic information and allowing more complex kinetic features to be evolved during the experiment. Previous experiments studying the epoxidation of ethylene over a metallic silver powder have been examined using TAP,15 providing some mechanistic insight, but no kinetic modelling of the TAP experiments was performed. The microkinetic modelling of TAP experiments is well-established16–18 but is seldom utilised for multi-step reactions due to the significant computational cost of the numerical simulations. Herein, we have developed a purpose-built TAP simulation package, SimTAP, that can rapidly simulate complex multi-step reaction networks. For the first time, we are able to precisely recreate entire TAP experiments, affording simulation of hundreds of pulses, and allowing the catalyst surface to evolve dynamically during the simulation as it would during the experiments.
In this work we have validated the LB, HH, and SS kinetic models against a series of TAP experiments performed over a metallic silver catalyst.15 We find that all the models were able to qualitatively recreate a single-pulse and one of the pump-probe TAP experiments over a metallic silver surface, with the HH model being the most accurate. However, more complex oxidation-titration experiments where the metallic silver catalyst is oxidised by pulsing O2 and then subsequentially reduced by pulsing ethylene were poorly reproduced. By adjusting the HH model to approximate the role of lateral interactions, we found that it was able to partially recreate the observed trends in the production of EO, but not CO2. We have found that by modifying the SS model to stop the decomposition of the oxide, and with slight changes to the physical characteristics of the TAP experiment, the qualitative trends in EO and CO2 production were reproduced. We find that while single-site models are applicable for broad screening of general catalytic activity, more complex models involving lateral interactions or multiple active sites are required to precisely recreate the observed activity and selectivity trends.
2. Materials and methods
2.1 TAP simulations
The modelling of TAP experiments has been described extensively in the literature,13,16,19–21 but it is repeated here for clarity. The TAP reactor is partitioned into zones, with the typical setup consisting of three zones that contain inert packing, catalyst, and inert packing respectively,20 but TAP reactors consisting of a single catalyst zone are also utilised.15 The transport of a reversibly adsorbing gas A through a zone during a TAP experiment is described using the following system of differential equations:| |  | (4) |
where εb is the void fraction of the reactor, CA is the concentration of species A (mols cm−3), t is the time (s), DeA is the effective Knudsen diffusivity of gas A (cm2 s−1), z is the axial coordinate of the reactor (cm), SV is the surface area of catalyst per volume of catalyst (cm2 cm−3), ka is the adsorption rate constant (cm3 mols−1 s), θ* is the concentration of free sites (mols cm−2), kd is the desorption rate constant (s−1), and θA is the concentration of adsorbed A (mols cm−2). The surface species are modelled using a mean-field microkinetic model, which for a reversibly adsorbing species would be:| |  | (5) |
For noninteracting cases (such as in the inert zones) the terms ka and kd can be set to zero leaving:| |  | (6) |
For a gas being pulsed into the reactor the initial condition is defined as:where δ(z, 0) represents a delta function introduced into the reactor at a time t = 0. After introducing the pulse into the microreactor, the pulse valve is closed, and so the boundary at the reactor exit can be defined as:| |  | (8) |
As the exit of the microreactor is attached to a vacuum, the exit condition is defined as:where L is the total length of the reactor (cm). Finally, the flux of gas leaving the reactor, which is recorded during the experiment, is defined as:| |  | (10) |
where FA is the flux of gas A leaving the reactor (mols cm−3 s). For simple cases where the kinetics can be approximated to first-order, or where there are no kinetics (diffusion only) generalised analytical solutions exist for any number of zones and configurations.19,22 For more complex kinetics (e.g., second order), such as those used in this paper, the TAP experiment must be numerically simulated. To numerically simulate the TAP experiment, the series of partial differential equations must be converted to a series of ordinary differential equations using a finite-element method which can then be evaluated using standard ODE solvers. An excellent description of how the method of lines can be applied to this series of equations is described in the previous literature.16
To perform the numerical simulation of the various TAP experiments outlined in this paper, a generalised TAP simulation package (SimTAP) was developed in the MATLAB environment. Similar to the previously published Python package TAPSolver18 and the FORTRAN code TAPFIT,23 SimTAP reads in a user generated input file describing the simulation parameters (e.g., kinetic model, kinetics, temperature, reactor length, simulation time) and numerically simulates the corresponding TAP experiment. Using the method of lines,16 the series of partial differential equations are transformed to a series of ordinary differential equations and numerically integrated using MATLAB's in-built ODE15s solver. Differing from the previous packages (TAPSolver, TAPFIT) which primarily focus on the fitting and analysis of experimental data, the SimTAP package is highly optimised to simulate complex multi-step TAP experiments. When performing a single pulse experiment, the initial concentration of surface species and size of the pulse are set using the input file. When performing multi-pulse experiments, during which both gas and surface species build up, the SimTAP package takes the exit condition from the previous pulse simulation and uses it as the initial condition for the next pulse simulation, with another pulse generated by addition of a delta function. The initial concentrations of gas and surface species during a multi-pulse experiment are set using:
| | | CN+1A(z, 0) = CNA(z, tmax) + δ(z, 0) | (11) |
| | | θN+1A(z, 0) = θNA(z, tmax) | (12) |
where
N is the current pulse number and
tmax is the total simulation time. For pump-probe experiments, the simulation time (
tmax) is set to the duration of the “pump” pulse, and the simulation is repeated with a new inlet species as the “probe” pulse. The SimTAP package has broad applications beyond ethylene epoxidation in the validation of microkinetic models for use in transient experiments. However, the current version of the package that is included alongside this work is a beta version, and as such, should be rigorously tested before applied to more complex models than those utilised in this work.
2.2 Adaptation of kinetic models
To adapt the kinetic models for use in the TAP simulations, the activation energies and pre-exponential factors were adjusted to obtain consistent units as required by SimTAP. The activation energies for each step were converted to units of kJ mol−1, and the pre-exponential factors were converted to s−1 for first order reactions, cm2 s−1 for second order surface reactions, and cm3 s−1 for adsorption steps. The three microkinetic models and adjusted Arrhenius parameters at 570 K are shown in Table 1 and are summarised graphically in Fig. 1.
Table 1 Kinetic model steps, pre-exponential factors (A), and activation energies (Ea) for the Linic–Barteau (LB),3 Huš–Hellman (HH),4 and Stegelmann–Stoltze (SS)5 models at 570 K. Pre-exponential factors (A) are shown for a temperature of 570 K and have been scaled. Pre-exponential factors are listed in units of s−1 for first order steps, cm2 s−1 for second order surface steps, and cm3 s−1 for second order adsorption steps. In the HH model, steps 3 reverse and 4 reverse were estimated as slow second order surface steps, while steps 5 forward and 5 reverse were estimated as fast second order surface steps. OME represents the oxametallacycle intermediate. In the HH model steps 2 forward and 4 forward and in the SS model steps 3 forward, 10 forward, and 14 forward were considered pseudo-second order. Steps 10 reverse and 14 reverse in the SS model were turned off in the simulations by setting their pre-exponential factors to zero due to their large activation energies
| Linic–Barteau3 |
| Number |
|
Step |
|
A
fwd
|
E
a,fwd (kJ mol−1) |
A
rev
|
E
a,rev (kJ mol−1) |
| Metallic silver sites are denoted by *. Surface oxide sites are denoted by /O*. Species adsorbed on metallic silver and surface oxide sites are denoted by X* and X/O*, respectively. |
| 1 |
O2 + 2* |
⇌ |
2O* |
2.8 × 10−13 |
72.4 |
4.0 × 10−2 |
135.1 |
| 2 |
C2H4 + * |
⇌ |
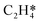
|
5.6 × 10−14 |
0.0 |
1.0 × 1013 |
33.5 |
| 3 |
O* +  |
⇌ |
C2H4O* + * |
2.0 × 10−4 |
62.3 |
1.0 × 10−2 |
100.4 |
| 4 |
C2H4O* |
⇌ |
C2H4O + * |
4.0 × 1013 |
66.9 |
4.5 × 10−12 |
46.0 |
| Huš–Hellman4 |
| Number |
|
Step |
|
A
fwd
|
E
a,fwd (kJ mol−1) |
A
rev
|
E
a,rev (kJ mol−1) |
| 1 |
C2H4 + * |
⇌ |
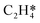
|
1.6 × 10−11 |
0.0 |
1.0 × 1015 |
7.7 |
| 2 |
O2 + 2* |
⇌ |

|
1.5 × 10−11 |
0.0 |
1.0 × 1015 |
18.3 |
| 3 |

|
⇌ |
2O* |
1.0 × 1013 |
80.1 |
1.0 × 10−7 |
126.4 |
| 4 |
O2 + 2* |
⇌ |
2O* |
1.5 × 10−11 |
61.8 |
1.0 × 10−7 |
126.4 |
| 5 |
 + O* + O* |
⇌ |
OME* + * |
1.0 × 10−2 |
45.4 |
1.0 × 10−2 |
63.7 |
| 6 |
C2H4 + O* |
⇌ |
OME* |
1.6 × 10−11 |
28.9 |
1.0 × 1015 |
63.7 |
| 7 |
OME* |
⇌ |
C2H4O* |
1.0 × 1013 |
71.4 |
1.0 × 1013 |
93.6 |
| 8 |
OME* |
⇌ |
CH3CHO* |
1.0 × 1013 |
65.6 |
1.0 × 1013 |
189.1 |
| 9 |
C2H4O* |
⇌ |
C2H4O + * |
1.0 × 1015 |
9.6 |
1.3 × 10−11 |
0.0 |
| 10 |
CH3CHO* |
⇌ |
CH3CHO + * |
1.0 × 1015 |
3.9 |
1.3 × 10−11 |
0.0 |
| Stegelmann–Stoltze5 |
| Number |
|
Step |
|
A
fwd
|
E
a,fwd (kJ mol−1) |
A
rev
|
E
a,rev (kJ mol−1) |
| 1 |
O2 + * |
⇌ |

|
1.4 × 10−14 |
5.7 |
1.1 × 1012 |
47.3 |
| 2 |
 + * + * |
⇌ |
2O* |
4.0 × 10−3 |
75.0 |
8.0 × 10−1 |
157.5 |
| 3 |
O2 + 2O* |
⇌ |
2O/O* |
1.0 × 10−12 |
20.0 |
1.3 × 100 |
96.9 |
| 4 |
C2H4 + O* |
⇌ |
C2H4/O* |
3.7 × 10−12 |
0.0 |
2.2 × 1011 |
37.1 |
| 5 |
C2H4/O* + O/O* |
⇌ |
OME* + O* |
9.0 × 10−1 |
112.0 |
5.3 × 10−1 |
183.3 |
| 6 |
C2H4O + O* |
⇌ |
C2H4O/O* |
9.9 × 10−12 |
0.0 |
4.8 × 1012 |
39.1 |
| 7 |
OME* |
⇌ |
C2H4O/O* |
1.1 × 1013 |
95.0 |
2.1 × 1012 |
93.5 |
| 8 |
OME* |
⇌ |
CH3CHO/O* |
9.0 × 1012 |
95.0 |
4.5 × 1010 |
204.3 |
| 9 |
CH3CHO/O* |
⇌ |
CH3CHO + O* |
2.9 × 1013 |
41.9 |
1.3 × 10−10 |
4.4 |
| 10 |
CH3CHO/O* + 6O* |
⇌ |
 + 4OH* + * + 4OH* + * |
2.0 × 105 |
11.0 |
— |
— |
| 11 |
C2H4 + * |
⇌ |

|
3.7 × 10−12 |
0.0 |
2.2 × 1011 |
30.1 |
| 12 |
C2H4/O* + O* |
⇌ |
C2CHOH/O* + * |
4.0 × 10−4 |
32.0 |
3.1 × 10−1 |
42.8 |
| 13 |
CH2CHOH/O* + O* |
⇌ |
CH2CHO/O* + OH* |
2.6 × 10−2 |
86.0 |
1.3 × 10−6 |
106.1 |
| 14 |
CH2CHO/O* + 5O* |
⇌ |
 + 3OH* + * + 3OH* + * |
1.0 × 105 |
0.0 |
— |
— |
| 15 |
2OH* |
⇌ |
H2O* + O* |
1.4 × 10−5 |
65.6 |
1.0 × 10−4 |
50.0 |
| 16 |

|
⇌ |
CO2 + * |
3.6 × 1014 |
38.9 |
5.1 × 10−12 |
0.0 |
| 17 |
H2O* |
⇌ |
H2O + * |
5.9 × 1014 |
46.6 |
7.1 × 10−11 |
0.0 |
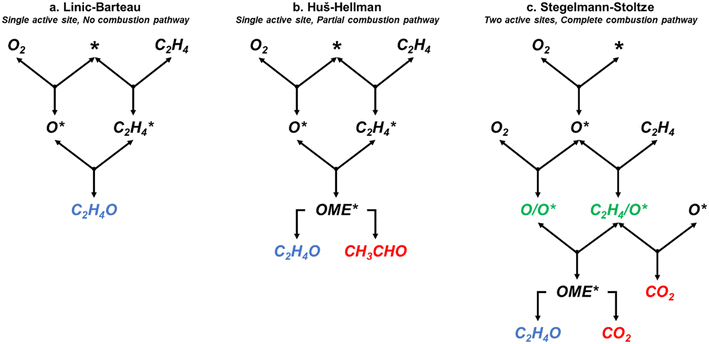 |
| | Fig. 1 Simplified representations of the (a) Linic–Barteau,3 (b) Huš–Hellman,4 and (c) Stegelmann–Stoltze reaction networks.5 * indicates empty metallic site. X* indicating an adsorbed species. OME denotes the oxametallacycle intermediate. /O* indicates a species adsorbed on an oxide site. | |
The three models have varying characteristics and levels of complexity. The LB model includes four reversible steps and a single active site. It assumes the formation of EO occurs through an oxametallacycle (OME) intermediate that is not explicitly modelled, and does not include a combustion pathway (Fig. 1a).3 The HH model includes 11 reversible steps and has a single active site which forms an explicitly modelled OME intermediate that can either form EO or decomposes to acetaldehyde (Fig. 1b). As acetaldehyde would rapidly decompose to CO2 under the experimental conditions,24 it was assumed to be qualitatively analogous to CO2 production for comparison purposes. The SS model includes 17 reversible steps, two of which (10 reverse and 14 reverse) have very high activation barriers and were removed by setting their pre-exponential factors to zero to speed up the simulations. The SS model contains two active sites; in addition to the metallic silver site (*) it includes a surface oxide active site, denoted by /O*. In this model it is the reaction between C2H4 adsorbed at an oxide site (C2H4/O*) and a electrophilic oxygen species adsorbed on top of a surface oxide (O/O*) that forms the OME intermediate (Fig. 1c). This model also includes a full combustion pathway of the OME intermediate and adsorbed C2H4 resulting in the production of CO2 and H2O.5
For the LB and SS models, the pre-exponential factors provided were adjusted as follows for implementation in SimTAP. For first order surface and desorption steps no adjustment was necessary because the factors were already reported in s−1. For second order surface steps the pre-exponential factors were adjusted by dividing the reported values by the catalyst site density to achieve units of cm2 s−1. For adsorption steps, the initial sticking coefficient was calculating using the following equation:5
| |  | (13) |
where
s0 is the calculated initial sticking rate,
k is the reported rate constant for adsorption (s
−1),
P is the thermodynamic reference pressure (Pa),
d is the density of sites (sites per m
2),
m is mass of the gas molecule (kg),
kB is the Boltzmann constant, and
T is temperature (K) at which the pre-exponential factors were calculated at in each respective model. For the LB model,
P was 101
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
325 Pa,
d was 1 × 10
19 sites per m
2 (approximated as the surface site density in the original TAP study
15), and
T was 298 K. For the SS model,
P was 1 × 10
5 Pa,
d was 6.9 × 10
18 sites per m
2, and
T was 500 K.
Pre-exponential factors for adsorption steps were subsequently calculated in units of cm3s−1 using the following equation:25
| |  | (14) |
where
ka is the pre-exponential factor for adsorption (m
3 s
−1),
σ is the surface site density (sites per m
2) in the experimental setup,
R is the ideal gas constant,
T is experiment temperature (K), and
M is molecular weight (kg mol
−1). In the LB and SS models, parameters were reported for temperatures of 298 K and 500 K respectively. Pre-exponential factors for adsorption steps were scaled to accommodate for temperature differences across the experiments, however, we assumed temperature scaling to not be significant under the simulation conditions for other parameters.
For the HH model the activation energies were taken from those calculated on the Ag(111) surface because it is the most stable facet and most common in untreated catalysts. The Ag(111) surface was also found to show the best agreement with bulk experimental data.4 The HH model did not provide pre-exponential factors, so those values were approximated using transition state theory.26 Pre-exponential factors were estimated to be 1 × 1013 s−1 for first order surface steps, 1 × 10−2 cm2 s−1 for fast second order surface reaction steps (i.e., the formation/decomposition of OME*), 1 × 10−7 cm2 s−1 for slow second order surface reaction steps (i.e., decomposition of surface oxygen species), and 1 × 1015 s−1 for first order desorption steps. For adsorption steps, pre-exponential factors were estimated and scaled using eqn (14). The initial sticking rate (s0) was assumed to be 1 for all gases. Further, the oxygen diffusion step from the original HH model is not included as it is not relevant for a mean-field simulation.
2.3 Implementation of reactor and experimental parameters
Reactor parameters were set to match those reported in the original TAP study.15 The microreactor was 1.25 cm long with a diameter of 0.64 cm. The catalyst was 500 mg of silver powder with an estimated active site density of 1 × 1015 sites per cm2. The catalyst surface area was 800 cm2 g−1. We estimated a standard value of 0.4 for voidage in the silver catalyst zone. The diffusivity of Ar through the reactor at 298 K was estimated to be 35 cm2 s−1, based on the reported time of maximum intensity of Ar at 570 K in the original study (Fig. 2).15 The pulse size was 1 × 1017 molecules per pulse unless otherwise noted. These parameters were kept consistent across all models and simulations.
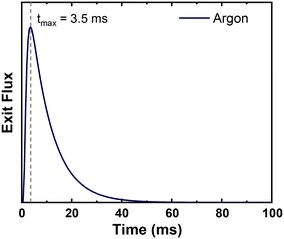 |
| | Fig. 2 Simulated pulse of Ar through the TAP microreactor with the time of maximum intensity overlayed. The maximum intensity matches that reported experimentally of 3.5 ms.15 | |
3. Results
A total of four TAP experiments were implemented in SimTAP to validate the models. One single-pulse, two pump-probe, and one multi-pulse oxidation-titration experiment. Simulations of these four experiments utilised the physical parameters exactly as reported in the ethylene oxidation TAP study15 and the kinetic parameters as adapted from the three microkinetic models.3–5 In the experiments, deuterated ethylene was used due to the overlapping masses of EO and CO2, however in the simulation this is not required. Any kinetic isotope effect that arises from deuterated ethylene is considered negligible for the purposes of comparison.
3.1 Single-pulse experiments
In the single-pulse TAP experiment, O2 and ethylene were pulsed together in a one-to-one ratio (1 × 1017 molecules of each gas per pulse) over the clean (metallic) silver catalyst at temperatures ranging from 483–570 K (Fig. 3) to probe the temperature dependence of the EO reaction over metallic silver. The products were measured for a total of 200 ms from the initiation of the O2 and ethylene pulse. Four main features were observed in the experiment: first, the conversion of ethylene was recorded to be ∼1% at 570 K. Second, increasing the temperature increased the amount of EO produced (Fig. 3a). Third, increasing the temperature increased the amount of CO2 produced. Finally, the time of peak EO production was observed to occur earlier with increasing temperature, with time of peak production ranging from 5.8 ms at 483 K to 4.6 ms at 570 K (Fig. 3h).
 |
| | Fig. 3 (a and b) Experimental and (c–g) simulated exit flux curves for the single-pulse experiment where ethylene and O2 were pulsed over the clean catalyst at varying temperatures from 483–570 K. (h) Experimental and simulated time of maximum ethylene oxide production (tmax) as a function of temperature. All three simulated models show qualitative agreement with the experimentally measured results. Experimental data was adapted from ref. 15. | |
In the simulations, the conversion of ethylene at 570 K was calculated to be 0.04% for the LB model, 77.9% for the HH model, and 20.9% for the SS model, showing poor quantitative agreement with the experimentally measured 1% conversion. This is expected as kinetic models are typically validated against experimental turnover frequencies on a logarithmic scale, as such, only qualitative comparisons will be made from here on out. All three models recreate the trend of increasing EO production with increasing temperature (Fig. 3c, e and g). Additionally, all three models show relatively consistent EO response shapes across the different temperatures, although the shape of the EO responses in the LB model were noticeably broader than those measured experimentally. This demonstrates that all three models are able to recreate the temperature dependence of the reaction over metallic silver, which is not surprising given that they are validated against steady-state data recorded at varying temperatures. The CO2 and acetaldehyde pulse responses for the SS (Fig. 3d) and HH (Fig. 3f) models respectively also matched the experimental trend of increased production with increasing temperature. However, both the SS and HH model simulations were not able to recreate the significant broadening observed in the CO2 response shape at lower temperatures. Some minor broadening was seen in the SS responses at lower temperatures, but not comparable to the amount seen experimentally. Given the significant complexity of combustion pathways, it is expected that the rate of CO2 production cannot be described by a simple second order reaction as is utilised in the models (Table 1) and indicates that further refinement of these pathways may be necessary. As the LB model does not include a combustion pathway, no comparison could be made. All three models showed a negative slope when time of maximum intensity of EO as a function of temperature was graphed, however, the time values were consistently higher in the simulated results. In summary, the single-pulse experiments show that all three models are able to generally predict the behaviour observed in the TAP experiments.
Another comparison of interest would be the selectivity trends as a function of temperature. Although the selectivity is not reported in the original study, the relative selectivity can be approximated using the integrated peak areas for EO and CO2 responses and normalising them to the values calculated at 483 K. The reported CO2 response curves from the original study did not return the baseline, and so were extrapolated using a previously established method27 (Fig. S1†) to accurately determine the CO2 integrated peak area. The relative selectivities for the experiments, SS, and HH models were calculated using integrated peak areas of EO/(EO + CO2) (Fig. S2†). Interestingly, counter to what would be expected under steady-state conditions,2,6,11 as the temperature was increased an increase in relative selectivity was observed both experimentally and in the HH model, whereas the SS model showed the expected decrease in selectivity. The increase in selectivity is not unexpected for the HH model, as the original study observed a similar increase in EO selectivity in the kinetic Monte Carlo simulations over the Ag(111) surface.4 However, why the experimentally measured responses see this increase in selectivity is not clear. We would that this analysis of the experimental responses is rudimentary at best given the limited information available in the original publication, and as such, we feel that any comparison should not be over-interpreted.
3.2 Pump-probe experiments
Two pump-probe experiments were performed over the metallic silver catalyst. In the first experiment, a pulse of O2 was applied to a cleaned catalyst surface (the “pump”), and then after a time delay of 210 ms, ethylene was pulsed (the “probe”) at varying ratios of O2 to ethylene at a temperature of 523 K. The amount of ethylene was kept constant at 1 × 1017 molecules per pulse, and the amount of O2 was varied to maintain ratios of 5, 1, and 0.5 parts O2 to 1 part ethylene. By varying the size of the oxygen pump response, different coverages of oxygen on the surface are attained, allowing the relationship between EO production and surface oxygen coverage to be probed. However, the absolute coverage of the surface oxygen species remains sufficiently low such that during the experiment the silver remains metallic. The experimental results showed an approximately linear increase in EO production with increasing O2 to ethylene ratio (Fig. 4a).15
 |
| | Fig. 4 (a and b) Experimental and (c–h) simulated ethylene oxide responses and yields for pump-probe experiments with varied oxygen to ethylene ratios at 523 K. The experimental results showed increased ethylene oxide production with increasing oxygen to ethylene ratio15 with the simulated results showing similar general trends, but the HH model is the only one to have a concave type relationship with increasing O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C2H4 ratio. Experimental data was adapted from ref. 15. C2H4 ratio. Experimental data was adapted from ref. 15. | |
The simulated results for all three models all recreated the trend of increasing EO production with increased O2 to ethylene ratio (Fig. 4b–d). The LB and SS model simulated results showed poor qualitative agreement, as the difference in the amount of EO produced between ratios 1 and 5 was significantly higher in the models than in the experiment, showing an almost exponential increase in EO production with increasing surface coverage. In comparison, the HH model showed better qualitative agreement with the experimental results, showing a more linear relationship in EO production with increasing surface coverage. This demonstrates that over metallic surfaces, a single-site model is sufficient to capture the relationship between ethylene oxide production and surface oxide coverage, and that the coverage dependence of the two-site model may not be correct over a metallic surface.
In the second pump-probe experiment, the ratio of O2 to ethylene was held constant at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and the time interval between the pump and probe pulse was varied at a temperature of 523 K. The time intervals used were 20, 50, 72, 117, and 425 ms. As the surface oxide is expected to decompose as a function of time, this experiment probes the rate of surface oxygen decomposition as a function of time and the relationship between surface oxide coverage and EO production simultaneously. Further, similar to the previous experiment, the absolute coverage of the surface oxide is sufficiently low that the catalyst remains metallic. Experimentally it was found that the peak EO production was at a 117 ms interval (Fig. 5a and b), almost double the amount measured at a 20 ms interval. A small drop in EO production was also recorded at an interval of 425 ms, but EO was still produced at higher yields than at time delays of less than the peak at 117 ms. This experiment indicated that the relationship between surface oxide coverage and EO production was more complex than a simple linear relationship, and the lifetime of the surface oxide is longer than the ∼400 ms probed.
1, and the time interval between the pump and probe pulse was varied at a temperature of 523 K. The time intervals used were 20, 50, 72, 117, and 425 ms. As the surface oxide is expected to decompose as a function of time, this experiment probes the rate of surface oxygen decomposition as a function of time and the relationship between surface oxide coverage and EO production simultaneously. Further, similar to the previous experiment, the absolute coverage of the surface oxide is sufficiently low that the catalyst remains metallic. Experimentally it was found that the peak EO production was at a 117 ms interval (Fig. 5a and b), almost double the amount measured at a 20 ms interval. A small drop in EO production was also recorded at an interval of 425 ms, but EO was still produced at higher yields than at time delays of less than the peak at 117 ms. This experiment indicated that the relationship between surface oxide coverage and EO production was more complex than a simple linear relationship, and the lifetime of the surface oxide is longer than the ∼400 ms probed.
 |
| | Fig. 5 (a and b) Experimental and (c–h) simulated ethylene oxide exit flux and ethylene oxide yield for pump-probe experiments with varied time interval between oxygen and ethylene pulses at 523 K. Pump-probe time intervals were 20 ms (A), 50 ms (B), 72 ms (C), 117 ms (D), and 425 ms (E). The experimental results showed peak ethylene oxide production at 117 ms. (c and d) The SS model simulations showed peak ethylene oxide production at the shortest time interval, 20 ms, and subsequent decrease in production as the time interval between the two pulses increased. In both the HH and LB simulated results, ethylene oxide production was consistent across the varying time delays. Experimental data was adapted from ref. 15. | |
None of the models were found to recreate the experimentally observed trend. The SS model showed peak production of EO in the shortest time delay of 20 ms, with rapidly decreasing production with increasing time delay and almost no production of EO recorded at a delay of 425 ms (Fig. 5c and d). This demonstrates that in the SS model the decomposition of the surface oxygen species is much faster than observed in the experiments. Both the HH (Fig. 5e and f) and the LB (Fig. 5g and h) models showed consistent EO production across all delays measured, which is closer to the experimental result, but do not show the peak production at 117 ms interval. A small increase in EO production was seen in the LB model simulation when increasing the delay from 20 to 50 ms, but this effect was much smaller than that measured experimentally. This shows that while the single-site models generally provide a better fit than the two-site models, they overpredict the stability of the surface oxide species and cannot recreate the complex relationship with surface oxide coverage and EO production observed experimentally.
3.3 Multi-pulse experiments
In the oxidation-titration multi-pulse experiment the catalyst surface was first oxidised by applying 200 pulses of O2 and then the surface oxygen species were titrated off using pulses of ethylene.15 This experiment provides insight into the activity and selectivity for EO production across the full range of surface oxide coverages, ranging from completely oxidised to completely reduced silver. Both the oxidation and titration were performed at 547 K. It was found in the experiment that EO production increased after the first few pulses, peaked, then decreased with increasing pulse number (Fig. 6a). Conversely, CO2 production peaked in the first pulse and decayed with increasing pulse number (Fig. 6b). This result indicated that a partially reduced surface is most active and selective for ethylene oxide production.
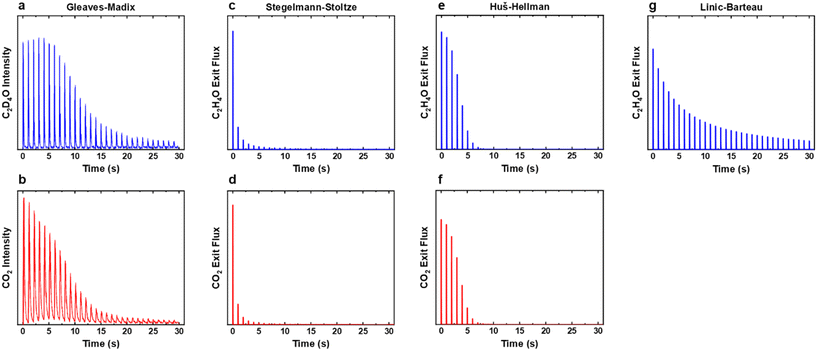 |
| | Fig. 6 (a and b) Experimental and (c–g) simulated ethylene oxide and combustion product exit fluxes for the titration experiment where ethylene was pulsed over the oxidised silver surface at 547 K. The HH model was run with 60% decreased surface area as the conversion of ethylene was 100% during the unmodified experiment. None of the models were found to recreate the experimentally observed trends. Experimental data was adapted from ref. 15. | |
None of the models were found to precisely recreate the experimentally observed trends in EO and CO2 production during the titration step. The SS model (Fig. 6c and d) showed EO and CO2 production in the first few pulses, but production of both rapidly declined to zero afterwards, showing again that the rate of decomposition of the surface oxide is too fast. The HH model (Fig. 6e and f) was run with a 60% decreased surface area as the conversion was constant at 100% for the first few pulses, obscuring the trends. After the first pulse there was then a rapid decrease in production of the two products, however the selectivity to EO remained consistent throughout, with the CO2 responses matching the trend of the EO responses. The LB model (Fig. 5g) showed a gradual decline in EO production during the simulation; however, peak production was observed in the first pulse and the results did not display an increase and decrease in production as observed experimentally. Similarly, it appears that the single-site models are able to generally recreate the trends in activity observed experimentally, even at high surface oxide coverages, but the finer kinetic features observed in the experiment are not recreated.
4. Discussion
The simulations of the TAP experiments using the SS, HH, and LB models all failed to produce quantitative agreement with the experiments, but some experimental trends were recreated qualitatively (Table 2). In the single-pulse state defining experiments over metallic silver, the simulated production of EO and CO2 followed the general trends of increasing with increasing temperature, but the simulations did not replicate the broadening of the CO2 response seen at lower temperatures (Fig. 3). Similarly, for the pump-probe experiments at varying O2 to ethylene ratios, an increase in EO production was recorded with increasing O2 to ethylene ratio, and the three models qualitatively recreated this trend (Fig. 4), with the HH model matching most closely. However, when the ratio of O2 to ethylene was fixed and the time delay was varied, a maximum of EO production was recorded at a delay time of 117 ms, whereas in the SS model the maxima was at the shortest time interval, and the HH and LB models showed no change with varying time delay (Fig. 5). Finally, for the multi-pulse oxidation-titration experiment it was observed that the peak EO production does not occur in the first pulse but a few pulses in, with a gradual decline in production afterwards. None of the models recreated this trend in the simulations (Fig. 6). It would appear that the LB and HH single-site models are most generally accurate for EO production, but do not properly capture the finer kinetic features observed as a function of surface oxide coverage, and struggle to reproduce the EO selectivity. The two-site model generally is limited by the rapid decomposition of the surface oxide. From the TAP experiments we identify the key feature being that the peak EO production was not in the first pulse during the multi-pulse ethylene titration, as other TAP-like experiments at atmospheric pressure have also observed this feature.28
Table 2 Summary of the simulated results and which models qualitatively reproduced trends observed in the experiments. ✓ indicates experimental trend was recreated, ∼ indicates experimental trend was partially recreated, x indicates experimental trend was not recreated
| Model |
Single-pulse (ΔT) |
Pump-probe |
Multi-pulse |
| C2H4 conversion |
C2H4O production |
CO2 production |
Ratio |
Time interval |
C2H4O production |
CO2 production |
| SS |
x |
✓ |
∼ |
∼ |
x |
x |
x |
| HH |
x |
✓ |
∼ |
✓ |
x |
x |
x |
| LB |
x |
✓ |
x |
∼ |
x |
x |
x |
During the multi-pulse titration experiments, the surface coverage of O* is very high after the O2 treatment, meaning that lateral interactions between O* and other adsorbates become relevant. The HH model identified that significant lateral interactions between O* and O*, OME*, and 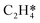 were present.4 In an attempt to understand the role that lateral interactions play in the calculated activity and selectivity, the multi-pulse titration experiment was recreated where the rate constants were re-calculated based on the coverage of O* after each pulse. The initial coverage was set to 0.4, as this was when the adsorption energy of O* becomes positive over the Ag(111) surface.4 The pairwise interactions between O* and C2H4 were found to be −9.65 kJ mol−1 (0.1 eV) and O* and OME* being 28.94 kJ mol−1 (0.3 eV) which were calculated in the original study by adsorbing the two species next to each other on an Ag(111) slab and the adsorption energies calculated relative to the isolated species. Further details are available in the original publication.4 To approximate lateral interactions, the pairwise interaction between the adsorbates was assumed be a maximum at a coverage of 1, with a linear dependence on coverage, which has been shown to be generally correct for transition metal surfaces,29 but it should be mentioned that reality is often more complex, with nonlinear scaling reported for EO formation recent studies.30 Step 1 was modified such that:
were present.4 In an attempt to understand the role that lateral interactions play in the calculated activity and selectivity, the multi-pulse titration experiment was recreated where the rate constants were re-calculated based on the coverage of O* after each pulse. The initial coverage was set to 0.4, as this was when the adsorption energy of O* becomes positive over the Ag(111) surface.4 The pairwise interactions between O* and C2H4 were found to be −9.65 kJ mol−1 (0.1 eV) and O* and OME* being 28.94 kJ mol−1 (0.3 eV) which were calculated in the original study by adsorbing the two species next to each other on an Ag(111) slab and the adsorption energies calculated relative to the isolated species. Further details are available in the original publication.4 To approximate lateral interactions, the pairwise interaction between the adsorbates was assumed be a maximum at a coverage of 1, with a linear dependence on coverage, which has been shown to be generally correct for transition metal surfaces,29 but it should be mentioned that reality is often more complex, with nonlinear scaling reported for EO formation recent studies.30 Step 1 was modified such that:
| | 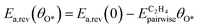 | (15) |
where
Ea,rev(
θO*) is the calculated activation barrier,
Ea,rev(0) is the activation barrier at zero coverage,
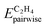
is the pairwise interaction between O* and the adsorbate, and
θO* is the coverage of O*. Step 5 was modified using the following expression:
| | | Ea,fwd(θO*) = Ea,fwd(0) + EOMEpairwiseθO* | (16) |
| |  | (17) |
With step 6
fwd, 7
rev, and 8
rev also modified using
eqn (16). The coverages and rate constants for the first 10 pulses are shown in
Table 3.
Table 3 Calculated coverage dependent activation energies for the first 10 pulses of the multi-pulse titration simulation for steps 1, 5, 6, 7 and 8 in the HH model4 with lateral interactions. All other parameters were kept consistent with the original experiment
| Pulse |
Coverage |
E
a (kJ mol−1) |
| 1fwd |
5fwd |
5rev |
6fwd |
7rev |
8rev |
|
—
|
0
|
7.72 |
45.35 |
63.68 |
28.95 |
93.59 |
189.11 |
| 1 |
0.40 |
11.58 |
56.93 |
59.82 |
40.53 |
105.17 |
200.69 |
| 2 |
0.35 |
11.12 |
55.55 |
60.28 |
39.15 |
103.79 |
199.31 |
| 3 |
0.30 |
10.61 |
54.03 |
60.79 |
37.63 |
102.27 |
197.79 |
| 4 |
0.24 |
10.07 |
52.41 |
61.33 |
36.01 |
100.65 |
196.17 |
| 5 |
0.18 |
9.50 |
50.70 |
61.90 |
34.30 |
98.94 |
194.46 |
| 6 |
0.12 |
8.92 |
48.96 |
62.48 |
32.56 |
97.20 |
192.72 |
| 7 |
0.07 |
8.38 |
47.33 |
63.02 |
30.93 |
95.57 |
191.09 |
| 8 |
0.02 |
7.96 |
46.07 |
63.44 |
29.67 |
94.31 |
189.83 |
| 9 |
0.00 |
7.76 |
45.49 |
63.63 |
29.09 |
93.73 |
189.25 |
| 10 |
0.00 |
7.72 |
45.37 |
63.67 |
28.97 |
93.61 |
189.13 |
With the inclusion of lateral interactions in the HH model, the trend of increasing ethylene oxide production for the first few pulses is observed (Fig. 7) with the maximum ethylene oxide production occurring on pulse 5. The exact same trend is observed in the CO2 (acetaldehyde) responses. While this is closer to the experimental response when lateral interactions are not included (Fig. 6), it still does not completely recreate the experimentally observed trends where the CO2 production peaks in the first pulse and then declines with increasing pulse number. This means that the model is recreating the activity for EO production as a function of pulse number but is not recreating the selectivity to EO correctly. This could be down to the fact that the model only simulates acetaldehyde production, rather than CO2, and perhaps the rate limiting step for CO2 production is after the formation of acetaldehyde. However, it is important to note that atmospheric pressure pulsed flow experiments observed a similar trend of constant selectivity.28 Further, this incorporation of lateral interactions in this model is flawed, as they are based on pairwise interactions from kinetic Monte Carlo simulations and the TAP simulations use a mean field assumption. This demonstrates that single-site models, when accounting for lateral interactions, can replicate more complex kinetic features observed during the experiments, which can explain this models broad predictability for EO production across a wide range of materials.30 However, further refinement of the combustion pathway is required in order to precisely recreate the selectivity trends as a function of surface oxygen coverage. As to why the lateral interactions cause this initial increase in both EO and CO2 production, we find that it is a combination of the increased stabilisation of  and decreased stabilisation of OME* as a function of oxygen surface coverage. At high coverages, the increased stabilisation of the
and decreased stabilisation of OME* as a function of oxygen surface coverage. At high coverages, the increased stabilisation of the  increases its lifetime on the surface, which makes it more likely to react with O* to form OME*. However, as the OME* intermediate is destabilised, based on linear scaling relationships, the reaction to form OME* would become less favourable. As such, the maximum production rate of C2H4O and CO2 is not at a maximum oxygen coverage, but it was simulated to be at an oxygen coverage of approximately 0.18 (see Fig. 7 and 8).
increases its lifetime on the surface, which makes it more likely to react with O* to form OME*. However, as the OME* intermediate is destabilised, based on linear scaling relationships, the reaction to form OME* would become less favourable. As such, the maximum production rate of C2H4O and CO2 is not at a maximum oxygen coverage, but it was simulated to be at an oxygen coverage of approximately 0.18 (see Fig. 7 and 8).
 |
| | Fig. 7 Simulated (a) ethylene oxide and (b) CO2 exit flux for the multi-pulse titration experiment over oxidised silver using the HH model with lateral interactions included. All other parameters were kept consistent with the original experiment. Peak ethylene oxide production was observed in pulse 5, with a rapid decrease in production observed afterwards. The same trend was observed in the CO2 (acetaldehyde) flux. | |
 |
| | Fig. 8 Equilibrium constants for step 1 and step 5 from the HH model with lateral interactions included (see Tables 1 and 3) with the dashed red line indicating where peak production of EO and CO2 occurs during the titration simulation (see Fig. 7). At higher coverages, the  species is stabilised by the pairwise interactions with O*, whereas the OME* intermediate is destabilised. This has an overall effect where the rate of formation of the OME* intermediate (which forms EO and CO2) reaches a maximum at an intermediate coverage. species is stabilised by the pairwise interactions with O*, whereas the OME* intermediate is destabilised. This has an overall effect where the rate of formation of the OME* intermediate (which forms EO and CO2) reaches a maximum at an intermediate coverage. | |
For the SS model, based on the pump-probe with varied time interval and the multi-pulse titration simulations, the most significant error is related to the lifetime of the surface oxygen species. The rapid loss in EO production with increasing time (and pulse number) indicates that the surface oxygen species are desorbing quickly in this model. From the TAP experiments the half-life for the active oxygen species was estimated to be ∼5 minutes at 523 K,15 whereas in the pump-probe experiment with varying time intervals (Fig. 5), the lifetime of the surface oxygen species in the SS model is significantly shorter as the production of EO is almost zero by 425 ms. In further work utilising the SS model, a type of subsurface oxygen was included.11 However, it was found that this subsurface oxygen was not relevant to simulations under steady state conditions. These steps allow for the development of an “oxygen reservoir” below the surface that can supply oxygen to the surface, extending the lifetime of the active oxide species.
| | | Osurface + *subsurface ⇌ Osubsurface + *surface | (18) |
where * indicates a metallic silver site. However, these steps could not be included in the SS model used in this work as the kinetic parameters were not reported and attempts to incorporate these steps with estimates were unsuccessful and generated unstable simulation results.
Without including the extra steps in the model, one such method to recreate an oxygen reservoir is to run the simulations with the oxygen desorption steps (Table 1, steps 1 reverse and 3 reverse) in the SS model turned off to remove oxygen decomposition. For the single-pulse experiments (Fig. 3 and 9a and b) the removal of the oxygen desorption pathway had the effect of broadening the ethylene oxide responses, such that they were closer to the experimentally measured values (Fig. S3†), and there was significantly more CO2 production at lower temperatures, but the general trends remained the same. For the ratio pump-probe experiments (Fig. 4 and 9c and d) the trend was consistent both with and without oxygen desorption. For the time interval pump-probe experiments (Fig. 5 and 9e and f), as would be expected, with the oxygen desorption pathways turned off, the production of EO was found to be time-independent.
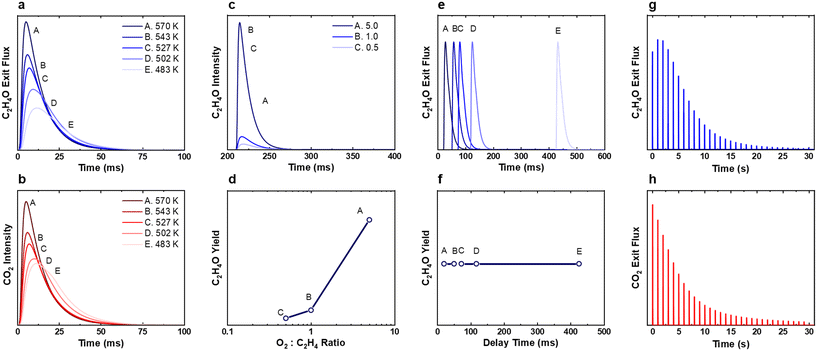 |
| | Fig. 9 Simulated (a and b) single pulse, (c and d) ratio pump-probe, (e and f) time interval pump-probe, (g and h) titration experiments with adjustments made to the Stegelmann–Stoltze (SS) modelwhere the oxygen desorption steps (1 reverse and 3 reverse) were turned off. For the titration experiment, the pulse size was reduced to 1 × 1016 molecules to better visualise the trend. All other parameters were kept consistent with the original experiment. In the titration experiment, the peak ethylene oxide production was observed later than the first pulse, while peak production of CO2 was observed in the first pulse. These trends qualitatively match those observed in the experimental data (see Fig. 4a and b). | |
For the titration experiments, if the oxygen decomposition steps are turned off during the 200 simulated pulses of O2, the coverage of oxygen rapidly saturates and generates an unrealistic surface. As such, the oxygen decomposition steps were only switched off during the C2H4 pulsing. This allows for the initial condition for the C2H4 pulsing to be the same, while extending the lifetime of the oxygen species, similar to as if there was a reservoir of subsurface oxygen refilling the surface. We believe this is a sufficient approximation as the total time for the ethylene titration (30 seconds) is significantly lower than the experimentally measured half-life for the active oxygen species of 5 minutes.15 When this was coupled with decreasing the pulse size by an order of magnitude (1016 molecules per pulse), we found that the SS model was able to recreate the experimental trend of peak EO production not being in the first pulse (Fig. 9a). For all simulations, the adjustment of the pulse size simply extends the number of pulses where EO and CO2 are produced in the titration experiments without effecting the overall trends and was utilised to more clearly depict the trends observed. Additionally, peak production of CO2 was observed in the first pulse in this simulation with production gradually decreasing throughout the experiment. Under these modified conditions we find the SS model provides an excellent recreation of the experiment (Fig. 6a and b and 9). No empirical observation between the absolute or relative coverages of oxygen could be correlated to this increase in selectivity. To fully resolve which specific steps facilitate this initial increase in EO selectivity a degree of selectivity (and rate) control analysis would be required. Unfortunately, given the significant computational expense of these simulations this analysis is not currently feasible, but could be performed in future work by using machine learning enhanced numerical methods to speed up the simulations.31
Based on the simulation results, the SS model best recreates the experimental data as measured by Gleaves and Madix, indicating that the underlying reaction network and rate constants have some validity. However, the surface oxygen species appear to be less stable than those measured experimentally. It would appear that for the less complex LB and HH models, the single site model is sufficient to recreate some of the features observed in the experiments, particularly with the inclusion of lateral interactions. However, for the SS model it would appear the inclusion of the second “electrophilic oxygen” active site (O/O*)5 where oxygen is adsorbed on top of the surface oxide (/O*) which reacts with ethylene to make the oxametallacycle alongside a subsurface oxygen reservoir is important for recreating some of the finer features observed during the multi-pulse experiment. Given the likelihood of multiple active phases existing on the catalyst surface during ethylene epoxidation,9 having multiple active sites in a model is important. The broad applicability of this model far outside of its original training dataset indicates that the proposed mechanism is a good candidate for ethylene epoxidation over metallic silver. However, the lifetime of the oxygen species and the lack of quantitative agreement between the model and the experiment would indicate that some of the kinetic coefficients are poorly scaled.
5. Conclusions
Simulations of the four experiments using the LB, HH, and SS models showed none of the models were able quantitatively recreate any of the observed experimental trends in EO production and ethylene combustion. Some qualitative agreement was found (Table 2), but none of the models recreated the experimentally observed trend of peak EO production and selectivity not being in the first pulse during the multi-pulse titration experiments over oxidised silver. By modifying the single-site HH model to include lateral interactions between adsorbates the trend in EO production was recreated, but the model was not able to recreate the trend in EO selectivity seen in the TAP experiments,15 but matched that of atmospheric pressure pulsed flow experiments.28 We find that the oxygen decomposition pathway in the SS model is incorrectly accounted for, leading to rapid decomposition of surface oxide species. We have related this to the omission of steps relating to a subsurface oxygen reservoir. With modifications to pulse size and the kinetics for oxygen decomposition set to zero, the SS model was the only of the three able to recreate both the production and selectivity to EO recorded during the multi-pulse titration experiments. The simulations suggest that the broad applicability of the SS model with its two active sites is a good candidate for the reaction mechanism for ethylene epoxidation over metallic silver, however some further refinement of the kinetic coefficients is desirable. Further, as the surface of silver is most likely oxidised under reaction conditions9 some inclusion of a subsurface oxygen species is also recommended.
The general applicability of the single-site models means that their use for materials and reaction condition screening is still valid, but if we are to push beyond wide-ranging screening to more precise refinement of reaction conditions, more complex models are required. This work reinforces that even though the “ground truth” of ethylene epoxidation is very complicated, simpler, single site models can still recreate the majority of the trends in catalytic activity. Given the broad predictability of the HH model when lateral interactions are included,30 and that the epoxidation of ethylene can occur on multiple different sites simultaneously,9 it is most likely that all of these models contain some core truth within them. However, the identity of the active site is still an open topic.10,32 Therefore, further transient experiments of ethylene epoxidation alongside more extensive screening of microkinetic models involving different active sites are required to identify the true reaction mechanism.
The original TAP experiments15 that these simulations were designed to recreate were performed using an outdated methodology. In modern TAP setups the reactor is typically packed using a thin-layer of catalyst between two inert zones rather than filling the entire microreactor with catalyst.20 Further, the precise diffusional characteristics of modern TAP systems means that the models are more applicable.13,21 Future work replicating these experiments in a more modern TAP reactor would be highly desirable, and further exploration of varying reaction conditions and temperatures could provide a framework for generating updated simulation parameters. More broadly, this approach of numerically recreating TAP experiments to validate kinetic models outside of their initial validation conditions can be generally applied to other heterogeneous catalytic systems.
Author contributions
Lilliana Brandao: investigation, validation, data curation, writing – original draft. Christian Reece: conceptualisation, methodology, software, writing – review & editing, supervision, funding acquisition. L. B. generated the SimTAP input files and performed the simulations and the data analysis. C. R. wrote the SimTAP code and guided the research. All authors participated in frequent discussions and contributed significantly to writing the manuscript.
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
C. R. gratefully acknowledges the Rowland Fellowship through the Rowland Institute at Harvard. C. R. and L. B. both acknowledge funding from the Program for Research in Science and Engineering (PRISE) summer programme. The computations in this paper were run on the FASRC Cannon cluster supported by the FAS Division of Science Research Computing Group at Harvard University.
References
- AgileIntel Research (ChemIntel360), Market value of ethylene oxide worldwide from 2015 to 2022, with a forecast for 2023 to 2030, https://www.statista.com/statistics/1244434/global-market-value-ethylene-oxide/, (accessed August 2, 2023).
- T. Pu, H. Tian, M. E. Ford, S. Rangarajan and I. E. Wachs, ACS Catal., 2019, 10727–10750 CrossRef CAS.
- S. Linic and M. A. Barteau, J. Catal., 2003, 214, 200–212 CrossRef CAS.
- M. Huš and A. Hellman, ACS Catal., 2019, 9, 1183–1196 CrossRef.
- C. Stegelmann, N. C. Schiødt, C. T. Campbell and P. Stoltze, J. Catal., 2004, 221, 630–649 CrossRef CAS.
- T. Pu, A. Setiawan, B. Mosevitzky Lis, M. Zhu, M. E. Ford, S. Rangarajan and I. E. Wachs, ACS Catal., 2022, 12, 4375–4381 CrossRef CAS.
- T. E. Jones, R. Wyrwich, S. Böcklein, E. A. Carbonio, M. T. Greiner, A. Y. Klyushin, W. Moritz, A. Locatelli, T. O. Menteş, M. A. Niño, A. Knop-Gericke, R. Schlögl, S. Günther, J. Wintterlin and S. Piccinin, ACS Catal., 2018, 8, 3844–3852 CrossRef CAS.
- J. R. Lockemeyer and T. L. Lohr, ChemCatChem, 2023, 15, e202201511 CrossRef CAS.
- J.-X. Liu, S. Lu, S.-B. Ann and S. Linic, ACS Catal., 2023, 13, 8955–8962 CrossRef CAS.
- T. Pu, A. Setiawan, A. C. Foucher, M. Guo, J.-M. Jehng, M. Zhu, M. E. Ford, E. A. Stach, S. Rangarajan and I. E. Wachs, ACS Catal., 2024, 14, 406–417 CrossRef CAS PubMed.
- C. Stegelmann and P. Stoltze, J. Catal., 2004, 226, 129–137 CrossRef CAS.
- C. T. Campbell, ACS Catal., 2017, 7, 2770–2779 CrossRef CAS.
- J. T. Gleaves, G. S. Yablonskii, P. Phanawadee and Y. Schuurman, Appl. Catal., A, 1997, 160, 55–88 CrossRef CAS.
- K. Morgan, N. Maguire, R. Fushimi, J. T. Gleaves, A. Goguet, M. P. Harold, E. V. Kondratenko, U. Menon, Y. Schuurman and G. S. Yablonsky, Catal. Sci. Technol., 2017, 7, 2416–2439 RSC.
- J. T. Gleaves, A. G. Sault, R. J. Madix and J. R. Ebner, J. Catal., 1990, 121, 202–218 CrossRef CAS.
-
R. Roelant, PhD thesis, Universitiet Ghent, 2011 Search PubMed.
- C. Reece, E. A. Redekop, S. Karakalos, C. M. Friend and R. J. Madix, Nat. Catal., 2018, 1, 852–859 CrossRef CAS.
- A. Yonge, M. R. Kunz, R. Batchu, Z. Fang, T. Issac, R. Fushimi and A. J. Medford, Chem. Eng. J., 2021, 420, 129377 CrossRef CAS.
- D. Constales, G. S. Yablonsky, G. B. Marin and J. T. Gleaves, Chem. Eng. Sci., 2001, 56, 133–149 CrossRef CAS.
- S. O. Shekhtman, G. S. Yablonsky, S. Chen and J. T. Gleaves, Chem. Eng. Sci., 1999, 54, 4371–4378 CrossRef CAS.
- L. Brandão, E. A. High, T.-S. Kim and C. Reece, Chem. Eng. J., 2023, 478, 147489 CrossRef.
- D. Constales, G. S. Yablonsky, G. B. Marin and J. T. Gleaves, Chem. Eng. Sci., 2004, 59, 3725–3736 CrossRef CAS.
- E. A. Redekop, G. S. Yablonsky, D. Constales, P. A. Ramachandran, J. T. Gleaves and G. B. Marin, Chem. Eng. Sci., 2014, 110, 20–30 CrossRef CAS.
- A. C. Lukaski and M. A. Barteau, Catal. Lett., 2009, 128, 9–17 CrossRef CAS.
- Y. Schuurman, Catal. Today, 2007, 121, 187–196 CrossRef CAS.
-
J. A. Dumesic, D. F. Rudd, L. M. Aparicio, J. E. Rekoske and A. A. Treviño, The microkinetics of heterogeneous catalysis, American Chemical Society, 1993 Search PubMed.
- K. Morgan, A. Goguet, C. Hardacre, E. V. Kondratenko, C. McManus and S. O. Shekhtman, Catal. Sci. Technol., 2014, 4, 3665–3671 RSC.
- L. Scharfenberg and R. Horn, Chem. Ing. Tech., 2017, 89, 1350–1359 CrossRef CAS.
- P. Majumdar and J. Greeley, Phys. Rev. Mater., 2018, 2, 045801 CrossRef CAS.
- M. Huš, M. Grilc, J. Teržan, S. Gyergyek, B. Likozar and A. Hellman, Angew. Chem., Int. Ed., 2023, 62, e202305804 CrossRef PubMed.
-
W. Bradley, G. S. Gusmão, A. J. Medford and F. Boukouvala, in Computer Aided Chemical Engineering, ed. Y. Yamashita and M. Kano, Elsevier, 2022, vol. 49, pp. 1741–1746 Search PubMed.
- D. Chen, L. Chen, Q.-C. Zhao, Z.-X. Yang, C. Shang and Z.-P. Liu, Nat. Catal., 2024, 1–10 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Included alongside this manuscript is a beta version of the MATLAB code SimTAP that was developed as part of this work, and the SimTAP input files for each experiment are also included. Please note that some simulations take a significant time to run. See DOI: https://doi.org/10.1039/d4cy00052h |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Christian
Reece
and
Christian
Reece
 *
*







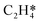

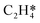


 + O*
+ O*
 + *
+ * + 4OH* + *
+ 4OH* + *
 + 3OH* + *
+ 3OH* + *


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 Pa, d was 1 × 1019 sites per m2 (approximated as the surface site density in the original TAP study15), and T was 298 K. For the SS model, P was 1 × 105 Pa, d was 6.9 × 1018 sites per m2, and T was 500 K.
325 Pa, d was 1 × 1019 sites per m2 (approximated as the surface site density in the original TAP study15), and T was 298 K. For the SS model, P was 1 × 105 Pa, d was 6.9 × 1018 sites per m2, and T was 500 K.




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C2H4 ratio. Experimental data was adapted from ref. 15.
C2H4 ratio. Experimental data was adapted from ref. 15.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and the time interval between the pump and probe pulse was varied at a temperature of 523 K. The time intervals used were 20, 50, 72, 117, and 425 ms. As the surface oxide is expected to decompose as a function of time, this experiment probes the rate of surface oxygen decomposition as a function of time and the relationship between surface oxide coverage and EO production simultaneously. Further, similar to the previous experiment, the absolute coverage of the surface oxide is sufficiently low that the catalyst remains metallic. Experimentally it was found that the peak EO production was at a 117 ms interval (Fig. 5a and b), almost double the amount measured at a 20 ms interval. A small drop in EO production was also recorded at an interval of 425 ms, but EO was still produced at higher yields than at time delays of less than the peak at 117 ms. This experiment indicated that the relationship between surface oxide coverage and EO production was more complex than a simple linear relationship, and the lifetime of the surface oxide is longer than the ∼400 ms probed.
1, and the time interval between the pump and probe pulse was varied at a temperature of 523 K. The time intervals used were 20, 50, 72, 117, and 425 ms. As the surface oxide is expected to decompose as a function of time, this experiment probes the rate of surface oxygen decomposition as a function of time and the relationship between surface oxide coverage and EO production simultaneously. Further, similar to the previous experiment, the absolute coverage of the surface oxide is sufficiently low that the catalyst remains metallic. Experimentally it was found that the peak EO production was at a 117 ms interval (Fig. 5a and b), almost double the amount measured at a 20 ms interval. A small drop in EO production was also recorded at an interval of 425 ms, but EO was still produced at higher yields than at time delays of less than the peak at 117 ms. This experiment indicated that the relationship between surface oxide coverage and EO production was more complex than a simple linear relationship, and the lifetime of the surface oxide is longer than the ∼400 ms probed.

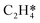 were present.4 In an attempt to understand the role that lateral interactions play in the calculated activity and selectivity, the multi-pulse titration experiment was recreated where the rate constants were re-calculated based on the coverage of O* after each pulse. The initial coverage was set to 0.4, as this was when the adsorption energy of O* becomes positive over the Ag(111) surface.4 The pairwise interactions between O* and C2H4 were found to be −9.65 kJ mol−1 (0.1 eV) and O* and OME* being 28.94 kJ mol−1 (0.3 eV) which were calculated in the original study by adsorbing the two species next to each other on an Ag(111) slab and the adsorption energies calculated relative to the isolated species. Further details are available in the original publication.4 To approximate lateral interactions, the pairwise interaction between the adsorbates was assumed be a maximum at a coverage of 1, with a linear dependence on coverage, which has been shown to be generally correct for transition metal surfaces,29 but it should be mentioned that reality is often more complex, with nonlinear scaling reported for EO formation recent studies.30 Step 1 was modified such that:
were present.4 In an attempt to understand the role that lateral interactions play in the calculated activity and selectivity, the multi-pulse titration experiment was recreated where the rate constants were re-calculated based on the coverage of O* after each pulse. The initial coverage was set to 0.4, as this was when the adsorption energy of O* becomes positive over the Ag(111) surface.4 The pairwise interactions between O* and C2H4 were found to be −9.65 kJ mol−1 (0.1 eV) and O* and OME* being 28.94 kJ mol−1 (0.3 eV) which were calculated in the original study by adsorbing the two species next to each other on an Ag(111) slab and the adsorption energies calculated relative to the isolated species. Further details are available in the original publication.4 To approximate lateral interactions, the pairwise interaction between the adsorbates was assumed be a maximum at a coverage of 1, with a linear dependence on coverage, which has been shown to be generally correct for transition metal surfaces,29 but it should be mentioned that reality is often more complex, with nonlinear scaling reported for EO formation recent studies.30 Step 1 was modified such that: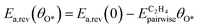
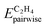 is the pairwise interaction between O* and the adsorbate, and θO* is the coverage of O*. Step 5 was modified using the following expression:
is the pairwise interaction between O* and the adsorbate, and θO* is the coverage of O*. Step 5 was modified using the following expression:
 and decreased stabilisation of OME* as a function of oxygen surface coverage. At high coverages, the increased stabilisation of the
and decreased stabilisation of OME* as a function of oxygen surface coverage. At high coverages, the increased stabilisation of the  increases its lifetime on the surface, which makes it more likely to react with O* to form OME*. However, as the OME* intermediate is destabilised, based on linear scaling relationships, the reaction to form OME* would become less favourable. As such, the maximum production rate of C2H4O and CO2 is not at a maximum oxygen coverage, but it was simulated to be at an oxygen coverage of approximately 0.18 (see Fig. 7 and 8).
increases its lifetime on the surface, which makes it more likely to react with O* to form OME*. However, as the OME* intermediate is destabilised, based on linear scaling relationships, the reaction to form OME* would become less favourable. As such, the maximum production rate of C2H4O and CO2 is not at a maximum oxygen coverage, but it was simulated to be at an oxygen coverage of approximately 0.18 (see Fig. 7 and 8).
 species is stabilised by the pairwise interactions with O*, whereas the OME* intermediate is destabilised. This has an overall effect where the rate of formation of the OME* intermediate (which forms EO and CO2) reaches a maximum at an intermediate coverage.
species is stabilised by the pairwise interactions with O*, whereas the OME* intermediate is destabilised. This has an overall effect where the rate of formation of the OME* intermediate (which forms EO and CO2) reaches a maximum at an intermediate coverage.

