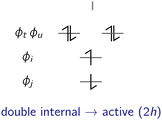Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Elucidation of the exchange interaction in photoexcited three-spin systems – a second-order perturbational approach
Michael
Franz
 a,
Frank
Neese
*b and
Sabine
Richert
a,
Frank
Neese
*b and
Sabine
Richert
 *a
*a
aInstitute of Physical Chemistry, University of Freiburg, Albertstraße 21, 79104 Freiburg, Germany. E-mail: sabine.richert@physchem.uni-freiburg.de
bMax-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, 45470 Mülheim an der Ruhr, Germany. E-mail: neese@kofo.mpg.de
First published on 10th September 2024
Abstract
Photogenerated three-spin systems show great potential for applications in the field of molecular spintronics. In these systems, the exchange interaction in the electronically excited state dictates their magnetic properties. To design such molecules for specific applications, it is thus important to understand how the sign and magnitude of the exchange interaction can be controlled. For this purpose, we developed a perturbational approach, based on previous work by the groups of de Loth and Malrieu, that allows for the direct calculation of the exchange interaction and its individual contributions up to the second order and implemented it within the ORCA program package. Within this manuscript, we present the derivation of the individual second-order contributions, provide an overview of the implementation of the code and illustrate its performance. We show that, using this perturbational approach in combination with state-averaged orbitals from minimal active space calculations, accurate values for the exchange interaction can be computed for organic nitroxides. Further, we demonstrate that the weight of the ionic determinants in the orbital optimisation of the CASSCF procedure is crucial for the computation of accurate exchange couplings. In the case of photoexcited chromophore–radical systems, we find that the dynamic spin polarisation effect constitutes the most important contribution to the exchange interaction, whereby the sign of this contribution determines the sign of the exchange interaction.
1 Introduction
Photoexcited organic multi-spin systems prove to be highly promising candidates for applications in the field of molecular spintronics.1–3 This research area aims to utilise the magnetic moment in molecular systems specifically for information processing and data storage.4 A noteworthy advantage of photogenerated organic multi-spin systems is their capability to be activated externally through light excitation, facilitating external control over their functionality.5–10 Moreover, their excited states are distinguished by spin coherence times that have the potential to exceed those of any metal-containing analogues, thereby enabling functionality close to room temperature.11,12A prominent example for such organic multi-spin systems are chromophore–radical systems, which typically comprise a chromophore (such as perylene or anthracene) covalently bound to a radical moiety (such as a nitroxide). Chromophore and radical may either be linked directly or via a molecular bridge (for example, a phenyl group), which makes these compounds structurally highly modifiable and provides the opportunity to tailor these structures to specific applications.1,13–15 In the simplest case, such systems represent three-spin systems in their excited state, which will be the focus of this manuscript.
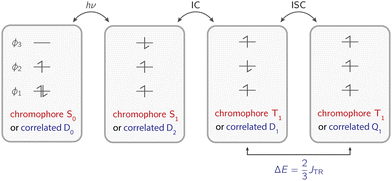
The photophysical mechanism underlying the generation of a three-spin system is illustrated in Fig. 1. The chromophore undergoes light excitation from its ground state S0 to an excited singlet state S1. Among other possible concurrent processes (electron transfer, excitation energy transfer, internal conversion, fluorescence), the excited singlet state transitions to a triplet state T1via intersystem crossing. Due to the coupling between the chromophore singlet and the radical doublet states, this transition is partially allowed and the process is then referred to as enhanced intersystem crossing (EISC). The resulting coupled triplet–doublet system can manifest either as a doublet-coupled system or a quartet-coupled system, depending on the energetic gap and arrangement dictated by the exchange interaction JTR between the chromophore triplet state and the radical doublet state.5,16–18
Since the phenomenological exchange interaction JTR dictates the magnetic properties of these systems,1,5 the motivation is to determine the factors that determine its magnitude and sign and how these factors can be influenced by structural modifications.
Especially for exchange interactions arising from the electronically excited state, it can be difficult to determine an exact value through experimental methods, such as transient continuous wave electron paramagnetic resonance spectroscopy (trEPR).1,19 Theoretical methods are particularly advantageous in this case, as they allow for the direct calculation or extraction of exchange interactions. Additionally, the exchange interaction can be analysed in detail, enabling a systematic correlation with structural factors.20,21
An important step in this direction was the pioneering work of de Loth et al.,22 where second-order perturbation theory was used to identify the classes of determinants in the first-order interacting space (FOIS) that significantly contribute to the exchange interaction. The most crucial aspect of this work was the demonstration that only a small portion of the FOIS is necessary for the calculation of the exchange interaction, as proven theoretically in an earlier work by Malrieu et al.23 Building on these early works, a variational method was developed by Miralles et al., that incorporates only those determinants into the CI space, which have an influence on excitation energies. This is the so-called difference-dedicated configuration interaction method (DDCI),24,25 which generally provides the most accurate results for the exchange interaction. However, such a high-level method is only practical for relatively small systems as the DDCI space increases as NCASN3, where N is the number of basis functions and NCAS is the dimension of the active space.21 Perturbational approaches based on CASSCF zeroth-order wavefunctions, such as the n-electron valence state perturbation theory method (NEVPT2)26–28 by Angeli et al. or the complete active space perturbation theory method (CASPT2)29 by Andersson et al., offer viable alternatives as they can also be applied to larger systems. Especially the NEVPT2 method has the great advantage of being intruder-state free. However, when using either of these two methods, the individual contributions of two different effects, namely the dynamic spin polarisation effect and the dynamic charge polarisation effect, cannot be extracted.21 The relevance of being able to resolve these two contributions prompted us to implement a “difference-dedicated perturbation theory” method based on the work of de Loth et al., which allows (i) the calculation of the individual contributions of the dynamic spin and charge polarisation effects, and, when combined with SA-CASSCF orbitals, (ii) the calculation of accurate exchange interactions for systems of medium to large size, where DDCI calculations are unfeasible.
2 Exchange interactions in three-spin systems
The exchange interaction is typically described using the Heisenberg–Dirac–van-Vleck Hamiltonian:30–32 | (1) |
| E(S − 1) − E(S) = JS. | (2) |
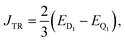 | (3) |
Now, we assume that the states D1 and Q1 can be approximately represented by the following wavefunctions:
 | (4) |
 | (5) |
 | (6) |
 | (7) |
Substituting these into eqn (3), we obtain:
 | (8) |
To determine which (structural) factors affect the phenomenological exchange interaction JTR, an analysis must be conducted to identify the factors influencing the individual exchange interactions. As noticed by Malrieu, et al.,23 the individual exchange interactions can be rationalised using a perturbative approach, analogous to the perturbation of the energy difference between a triplet and a singlet state of the same electronic configuration. This procedure was first used by de Loth, et al. to calculate the singlet–triplet splitting in the cupric acetate hydrate dimer22 and led to a series of papers also using this technique for the calculation of the singlet–triplet splitting.36–39
Here, we will use this approach to calculate JTR directly as the sum of two individual exchange couplings Jij. To this end, we will derive a modified variant of the previously published method, which will allow us to manipulate the accuracy of the calculated Jij by performing state-averaged CASSCF calculations.
3 Derivation of the second-order contributions to the exchange interaction
3.1 Difference dedicated perturbation theory versus difference dedicated configuration interaction
We will illustrate the principles of our approach by first discussing the well-known case of two interacting S = 1/2 systems.The discussion starts with the definition of the model space:
![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) 0 = {|ϕt 0 = {|ϕt![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) u〉, |ϕu u〉, |ϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) t〉}, t〉}, | (9) |
It is important to note, that, in the above Slater determinants, the internal and virtual orbitals ϕi,…,ϕj and ϕa,…,ϕb were ignored for simplicity. For the further discussion, we define the general orbital indices to be p,q, the internal orbital indices to be i,j, the active (magnetic) orbital indices to be t,u,v and the virtual orbital indices to be a,b.
We assume the molecular orbitals ϕt and ϕu to be of a localised nature. Thus the references space consists of the two neutral Ms = 0 determinants. This is the same reference space as in the DDCI2 method40 (difference-dedicated configuration interaction with two degrees of freedom) and is an excellent starting point for developing the treatment of exchange couplings. The arguments are based on perturbation theory, which is valid when the ionic contributions in the respective wavefunctions play only a small (but still decisive) role.33,41–50 In the DDCI2 method, parts are picked from the first-order-interacting space (FOIS) and ordered according to their “degrees of freedom”. A degree of freedom in this context is either a hole in the doubly occupied orbital space or a particle in the virtual orbital space. The DDCI2 method is rooted in the original and pioneering work of de Loth et al. who used perturbation theory to demonstrate which parts of the FOIS contribute in which way to the final exchange couplings.22 In DDCI2, these FOIS functions and their interaction with the reference determinants are treated variationally, which gives the method increased robustness but also leads to elevated computational cost due to the iterative nature of the configuration interaction problem and the necessity to store integrals and several copies of the wavefunction amplitudes.
An alternative method, where perturbation theory is carried through not only conceptually but also numerically is a continuation of the work of de Loth et al. In this work we will refer to it as “difference-dedicated perturbation theory” (DDPT2). The acronym emphasizes that the treatment is based on the same subspace of the FOIS as the original DDCI2 method but that perturbation theory is used for the numerical evaluation of the exchange coupling constants.
3.2 Elaboration of the DDPT equations
The full Hamiltonian Ĥ is defined as: | (10) |
 accounts for the two-electron interactions. The eigenfunctions of the electronic Hamiltonian Ĥ in the aforementioned model space are a triplet wavefunction and a singlet wavefunction:
accounts for the two-electron interactions. The eigenfunctions of the electronic Hamiltonian Ĥ in the aforementioned model space are a triplet wavefunction and a singlet wavefunction: | (11) |
 | (12) |
| ΔES→T = ES − ET = Jtu = 2Ktu. | (13) |
 | (14) |
![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) =
= ![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) 0 +
0 + ![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) r, where
r, where ![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) r includes all excited state determinants. The matrix elements of the Fock-type operator are given by:
r includes all excited state determinants. The matrix elements of the Fock-type operator are given by:| Fpq = Finactivepq + Factivepq, | (15) |
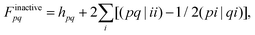 | (16) |
 | (17) |
 | (18) |
| DItu = 〈I|Êtu|I〉, | (19) |
 , where ↠and â are creation and annihilation operators. σ denotes the spin quantum number. We choose Ĥ(0) to be the CASSCF Fock-type operator since this implies, that the state-averaging procedure will allow us to influence the extent of the magnetic orbitals ϕt and ϕu, which should have a significant impact on the exchange coupling.53
, where ↠and â are creation and annihilation operators. σ denotes the spin quantum number. We choose Ĥ(0) to be the CASSCF Fock-type operator since this implies, that the state-averaging procedure will allow us to influence the extent of the magnetic orbitals ϕt and ϕu, which should have a significant impact on the exchange coupling.53
The perturbation ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) is then defined to be the difference between the full electronic Hamiltonian and the zeroth-order Hamiltonian:
is then defined to be the difference between the full electronic Hamiltonian and the zeroth-order Hamiltonian:
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) = Ĥ − Ĥ(0). = Ĥ − Ĥ(0). | (20) |
The second-order corrections are defined as follows:
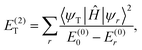 | (21) |
 | (22) |
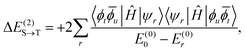 | (23) |
| ΔES→T = 2(Ktu + ΔK(2)tu) = 2Kefftu. | (24) |
The derived second-order expression assumes that the excited determinants |ψr〉 couple simultaneously with both reference determinants |ϕt![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) u〉 and |ϕu
u〉 and |ϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) t〉, leading to a significant reduction of the space of excited determinants. As a consequence, a considerable amount of computation time can be saved.22
t〉, leading to a significant reduction of the space of excited determinants. As a consequence, a considerable amount of computation time can be saved.22
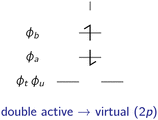
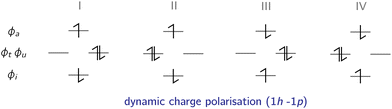
In the following, the excited determinants |ψr〉 will be classified and the corresponding corrections to the exchange integral ΔK(2)tu will be derived. The possible corrections to the exchange integral Ktu include the kinetic exchange, the hole polarisation effect, the particle polarisation effect, the internal → active double excitations, the active → virtual double excitations, the dynamic spin polarisation effect, and the dynamic charge polarisation effect.21
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) u〉 and |ϕu
u〉 and |ϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) t〉 are coupled via determinants with ionic configurations within the active space. Consequently, the space of excited determinants is defined by {|ϕt
t〉 are coupled via determinants with ionic configurations within the active space. Consequently, the space of excited determinants is defined by {|ϕt![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) t〉, |ϕu
t〉, |ϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) u〉}, which are illustrated in Fig. 2.
u〉}, which are illustrated in Fig. 2.
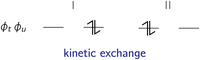 | ||
| Fig. 2 The kinetic exchange effect stems from the interaction of the ionic forms (I and II) within the active space with the reference determinants (i.e. the neutral forms within the active space). | ||
The correction of the exchange integral through the kinetic exchange is given by the contributions of two excited state configurations:
 | (25) |
Here, we will approximate the off-diagonal terms in the nominator through the CASSCF Fock matrix elements Ftu, where only the active part of the Fock matrix might cause a deviation from the corresponding off-diagonal element of Ĥ. Thus, only a minor deviation should be expected. This leads to a final contribution of:
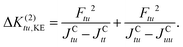 | (26) |
 . The reason for this is to circumvent the divergence of the perturbational approach. Note that JCtu corresponds to the two-electron integral (tt|uu) and JCtt corresponds to (tt|tt), whereby the chemist's notation54 is used.
. The reason for this is to circumvent the divergence of the perturbational approach. Note that JCtu corresponds to the two-electron integral (tt|uu) and JCtt corresponds to (tt|tt), whereby the chemist's notation54 is used.
As can be seen from the denominator, the kinetic exchange always favours anti-ferromagnetic coupling.
![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) = {|
= {|![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) iϕt
iϕt![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) tϕu〉, |
tϕu〉, |![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) iϕtϕu
iϕtϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) u〉, |ϕiϕt
u〉, |ϕiϕt![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) t
t![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) u〉, |ϕi
u〉, |ϕi![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) tϕu
tϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) u〉}, which are illustrated in Fig. 3.
u〉}, which are illustrated in Fig. 3.
This class of excited state determinants leads to the following contributions:
 | (27) |
which, in summary, give a total correction of:
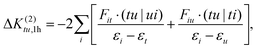 | (28) |
![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) = {|ϕt
= {|ϕt![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) a〉, |ϕu
a〉, |ϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) a〉, |
a〉, |![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) uϕa〉, |
uϕa〉, |![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) tϕa〉}, which are illustrated in Fig. 4.
tϕa〉}, which are illustrated in Fig. 4.
The 1p determinants yield the following contributions to the exchange integral:
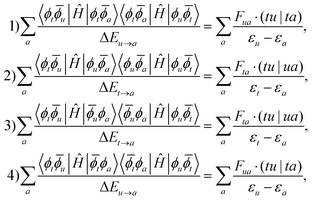 | (29) |
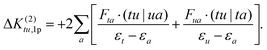 | (30) |
As in the case of the 1h excitation class, the single excitation terms in the nominator are approximated by the corresponding CASSCF Fock matrix elements.
All further excitation classes involve only double excitations relative to the reference determinants.
![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) = {|ϕi
= {|ϕi![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) jϕt
jϕt![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) tϕu
tϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) u〉}, illustrated in Fig. 5. This results in the following contribution to the exchange integral:
u〉}, illustrated in Fig. 5. This results in the following contribution to the exchange integral: | (31) |
![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) = {|ϕa
= {|ϕa![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) b〉} illustrated in Fig. 6.
b〉} illustrated in Fig. 6.
The correction to the exchange integral is then given by:
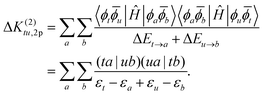 | (32) |
The dynamic spin-polarised determinants are generated by coupled triplet excitations, where two different types of excited state determinants ![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) = {|ϕi
= {|ϕi![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) t
t![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) uϕa〉, |
uϕa〉, |![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) iϕtϕu
iϕtϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) a〉}, which are illustrated in Fig. 7, can interact with the reference determinants.
a〉}, which are illustrated in Fig. 7, can interact with the reference determinants.
The corresponding contributions to the exchange integral are given by:
 | (33) |
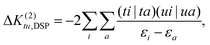 | (34) |
The dynamic charge-polarised determinants are generated by a singlet excitation from the internal space to the virtual space coupled with a singlet excitation within the active space, producing a charge polarisation within the active space. Here, four different types of excited state determinants ![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) = {|
= {|![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) iϕu
iϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) uϕa〉, |
uϕa〉, |![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) iϕt
iϕt![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) tϕa〉, |ϕiϕu
tϕa〉, |ϕiϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) u
u![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) a〉, |ϕiϕt
a〉, |ϕiϕt![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) t
t![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) a〉}, which are illustrated in Fig. 8, can interact with the reference determinants.
a〉}, which are illustrated in Fig. 8, can interact with the reference determinants.
The corresponding contributions are given by:
 | (35) |
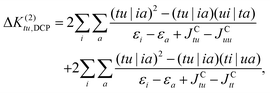 | (36) |
The kinetic exchange is corrected by including interactions with the excited states shown in Fig. 9: ![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) r = {|ϕtϕv
r = {|ϕtϕv![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) v〉, |ϕuϕv
v〉, |ϕuϕv![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) v〉, |ϕt
v〉, |ϕt![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) tϕu〉, |ϕtϕu
tϕu〉, |ϕtϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) u〉}.
u〉}.
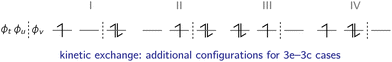 | ||
| Fig. 9 In the case of a 3c–3e system, four additional ionic configurations within the active space contribute to the kinetic exchange. | ||
The corrections to the exchange integral are given by:
 | (37) |
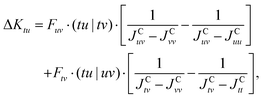 | (38) |
The excited state determinant space of the additional 1h contribution is given by: ![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) r = {|ϕiϕu
r = {|ϕiϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) uϕv
uϕv![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) v〉, |ϕiϕt
v〉, |ϕiϕt![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) tϕv
tϕv![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) v〉, |ϕiϕt
v〉, |ϕiϕt![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) tϕu
tϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) u〉}. As can be seen in Fig. 10, these excited states are generated by a single excitation from the internal space to the active space coupled with a single excitation within the active space where the additional active orbital ϕv is involved.
u〉}. As can be seen in Fig. 10, these excited states are generated by a single excitation from the internal space to the active space coupled with a single excitation within the active space where the additional active orbital ϕv is involved.
 | ||
| Fig. 10 In the case of a 3c–3e system, three additional 1h configurations contribute to the exchange interaction. | ||
Thus, the corrections are given by:
 | (39) |
In summary, these contributions yield a correction of:
 | (40) |
As can be seen in Fig. 11, the excited state determinant space of the additional 1p configurations is generated in the same way as for the additional 1h configurations: ![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) r = {|ϕu
r = {|ϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) uϕa〉, |ϕt
uϕa〉, |ϕt![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) tϕa〉, |ϕtϕu
tϕa〉, |ϕtϕu![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) a〉}. Here, the corrections are given by:
a〉}. Here, the corrections are given by:
 | (41) |
 | (42) |
3.3 Summary of contributions
The contributions listed above are all effects that contribute to the effective exchange integral Ktu in a three-electron–three-centre case. Note that all off-diagonal elements of H, which correspond to single excitations, are approximated by the corresponding CASSCF Fock matrix elements. This approximation allows for a much easier implementation while the deviation from the actual off-diagonal elements of H may be expected to be small. Furthermore, we made another assumption by defining all energy differences of excitations within the active space by one-site repulsion energies instead of the orbital energies. Formally, this might be regarded as the usage of two different definitions for Ĥ(0) depending on the orbital space, which may seem arbitrary as we deviate from the definition of Ĥ(0) for charge polarised configurations. However, by using such an alternative definition of the energy differences within the active space the method gains a great deal of numerical stability since it avoids the most common causes of intruder states.4 Implementation of the perturbational approach
The method for calculating the effective exchange integrals, described above, has been implemented into the ORCA program package.56 The algorithm consists of the following steps:(1) Generation of a set of molecular orbitals
The first step may seem trivial, but is crucial, as the molecular orbitals have a significant impact on the convergence of the perturbative approach. The method requires a CASSCF(n,n) calculation for the orbital generation.51,57 It is also essential that the generated molecular orbitals are canonical, since the subsequent steps are invalid otherwise.
(2) Localise the orbitals inside the active space
The localisation of the active orbitals is necessary to obtain the so-called ‘magnetic’ orbitals, as the Heisenberg approach relies on local spins, thus requiring localised orbitals. To fulfill this requirement, the New-Boys algorithm is employed.58
(3) Calculation of the Fock matrix over molecular orbitals
This step underlines the necessity of starting with canonical orbitals, as they are indispensable for generating the Fock matrix over atomic orbitals with the following procedure. The canonical orbital energies correspond to the diagonal elements of the diagonalised Fock matrix Fdiag. Here, the Fock matrix over atomic orbitals FAO is constructed using the coefficient matrix of the canonical orbitals Cold along with the overlap matrix in the basis of atomic orbitals S.
| FAO = XY†, | (43) |
| X = SCold, | (44) |
| Y = SColdFdiag. | (45) |
| FMO = C†FAOC. | (46) |
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) CASSCF including the “internal-active” and “active-virtual” subspaces, which may not be necessarily true. Consequently, no contributions can be expected for the 1h and 1p excitations in case of two-spin systems. However, it simplifies the implementation.
CASSCF including the “internal-active” and “active-virtual” subspaces, which may not be necessarily true. Consequently, no contributions can be expected for the 1h and 1p excitations in case of two-spin systems. However, it simplifies the implementation.
(4) Transformation of the two-electron integrals
The conversion of two-electron integrals into the molecular orbital basis represents the most computationally demanding stage. However, the computational effort can be reduced notably as not all transformed integrals are essential for calculating Kefftu. By defining internal and virtual orbital windows, distinct integral classes can be derived. Incorporating active orbitals within both orbital windows enhances flexibility in selecting specific integrals from various classes. Within this implementation, only the (ik|jl) and (ia|jb) integral classes are computed.59
Furthermore, the transformation is expedited by employing the “resolution of identity” (RI) approximation, which is mandatory in our implementation.59 This necessitates the use of an auxiliary basis set that will be detailed below in the Results and discussion section. As a final and highly effective acceleration method, the “frozen core” approximation is employed. This technique excludes core orbitals from the transformation due to their minimal impact on the dynamic correlation energy, resulting in a substantial reduction in the integral transformation dimensionality and, with this, in significant computational time savings.
(5) Calculation of the effective exchange integrals
In the final step, the effective exchange integrals Kefftu are computed using the expressions from Section 3. Essentially, this involves calculating the matrix elements Ktu and their corrections. The output includes the first-order exchange matrix (including the Ktu), the individual second-order exchange matrices (including the ΔK(2)tu), and the final exchange matrix (including the Kefftu), where the indices t and u iterate over the active orbitals. These matrices are always symmetric, and their dimension is determined by the number of electrons (or orbitals) in the CASSCF(n,n) calculation.
5 Results and discussion
5.1 Choice of molecules
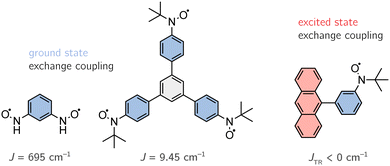
Since our discussion focuses on (organic) multi-spin systems, we chose an organic diradical (1,3-(phenylene)bis(nitroxide)), an organic triradical (1,3,5-triphenylbenzenetriyltris(N-tert-butyl nitroxide)) and an anthracene–radical system (9-[3-(4,4,5,5-tetramethyl-1-yloxyimidazolin-2-yl)phenyl]anthracene) to test the newly implemented method. The first two systems, shown on the left-hand side in Fig. 12, exhibit open-shell configurations in their ground state with known exchange coupling constants of J = 695 cm−1 and J = 9.45 cm−1.60,61 Note that the experimental value of the diradical was determined for the N-tert-butyl nitroxide. Here, we decided to truncate the tert-butyl groups in order to perform more accurate calculations. A benchmark on both of these systems, may also allow us to draw conclusions on the impact of the extent of the conjugated π-system. The latter system, depicted on the right-hand side in Fig. 12, forms an antiferromagnetically coupled open-shell system in its excited state.62 However, the magnitude of J for the anthracene system could not be determined experimentally, i.e. J < 0 cm−1.5.2 Computational details
The geometries of the structures shown in Fig. 12 were optimised at the B3LYP/def2-TZVP level of theory.63–67 Since the DDPT2 method requires a common set of orbitals, we calculated the exchange interaction using only one structure (vertical excitation energy). Here, the calculations were accelerated by the RIJCOSX approximation using the def2/J auxiliary basis set.68,69The magnetic couplings are either obtained by our own implemented method or, in order to compare the results, by the FIC-NEVPT2 method using the def2-SVP basis set or variational methods such as DDCI3, DDCI2 or CASCI+S, where the singles “S” include the 1h, 1p and 1h–1p excitations, also using the def2-SVP basis set.26–28 The Fock matrix formations were accelerated by the RIJCOSX method using the def2/J auxiliary basis set and the integral transformations were accelerated by the RI method using the def2-SVP/C auxiliary basis set.
In general, the calculations are based on CASSCF(3,3) or CASSCF(2,2) zeroth-order wavefunctions (depending on the multiplicity). It is important to note that the convergence criteria were set to ETol = 10−10 (energy gradient) and gTol = 10−7 (orbital gradient), which is tight compared to the default settings in ORCA.
For the variational calculations, the selection parameter Tsel was set to zero in order to include all possible configuration state functions in the CI. The variational methods were always used in combination with a common set of molecular orbitals (Q1-optimised orbitals or T1-optimised orbitals).
The NEVPT2 calculations were performed state-specific, i.e. the quartet state and the trip-doublet state were optimised separately.
Our implementation relies on a common set of molecular orbitals, where we used differently optimised orbitals in a series of calculations. Since, in our implementation, only the effective exchange integrals Kefftu are computed, the exchange interaction J for the three-spin systems (or specifically referred to as JTR in case of chromophore–radical systems) was calculated by Kefftu + Keffuv, where Kefftu and Keffuv are smaller in magnitude than Kefftv. In case of the two-spin system, J was calculated by 2Kefftu.
5.3 Benchmark results for ground state radicals
Since experimental values for the exchange interaction are known for the nitroxide diradical and triradical (J = 695 cm−1 and J = 9.45 cm−1),60,61 these systems are well suited to compare the accuracy of the DDPT2 method to other multireference methods such as the variational DDCI3, DDCI2, and CASCI+S methods as well as the perturbational NEVPT2 method.The NEVPT2 method is also chosen as a reference, since it is also a multi-reference second-order perturbation theory approach and is widely used for the calculation of exchange coupling constants. The differences between the NEVPT2 method and the DDPT2 method are: (1) the choice of the zeroth-order Hamiltonian (Dyall's Hamiltonian in the NEVPT2 method),70 (2) the inclusion of all possible excitation classes in the NEVPT2 method, which can be generated by single and double excitations, and (3) the fact that the NEVPT2 method relies on a contracted description of the first-order wavefunction, which is not the case for the DDPT2 method. Here, we will only use the fully-internally contracted NEVPT2 method (FIC-NEVPT2).
Since the DDPT2 method requires a common orbital basis, it makes sense to tailor the orbital optimisation to the ground state radicals and then to apply a corresponding protocol to the anthracene system.
| CASSCF(2,2) | DDCI3 | DDCI2 | CASCI+S | FIC-NEVPT2 | DDPT2 | Exp. | |
|---|---|---|---|---|---|---|---|
| a An additional series of calculations were performed with orbitals from a ROHF calculation on the open-shell singlet state. All values are given in cm−1. | |||||||
| w = 0 | 126 | 657 | 647 | 680 | 172 | 169 | 695 |
| w = 0.133 | 634 | 438 | 722 | ||||
| State-specific | 122 | 482 | |||||
| ROHFa | 104 | 649 | 629 | 658 | 154 | 140 | |
When the 2h and 2p excited determinants are introduced additionally (DDCI2), a slight decrease of J by −33 cm−1 can be observed, which means that the 2h and 2p excited states have a rather small anti-ferromagnetic effect on J. The additional inclusion of the 1h–2p and 2h–1p excited states (DDCI3) increases the J value by 10 cm−1 compared to the DDCI2 value. The contributions of the 2h–1p and 1h–2p excited states cancel each other out.49
The FIC-NEVPT2 method, using the triplet-optimised orbitals, yields a J value of 172 cm−1, which compares well to the DDPT2 value of J(w = 0) = 169 cm−1, where w is the weight of the ionic determinants in the CASSCF procedure. Both methods underestimate the exchange interaction severely indicating that the coupling of the FOIS functions among themselves (that come in at fourth and higher orders in perturbation theory) plays an important role, as discussed in depth by Calzado and Malrieu.21,44
However, the choice of orbitals also plays an important role, in particular in low order perturbation theory. In fact, NEVPT2 with state-specifically optimised orbitals yields a coupling of JNEVPT2(SS) = 482 cm−1. However, the coupling is still underestimated as higher-order effects are missing.
The use of orbitals from a ROHF calculation for the open-shell singlet state and the use of triplet-optimised orbitals yields almost identical results, since the same electronic configuration is modeled in both approaches.
It is known that the exchange interaction is strongly underestimated in multi-reference perturbation theory methods with minimal active space zeroth-order wavefunctions when the orbital optimisation primarily considers neutral determinants. The resulting orbitals are too compact; the exchange interaction can only be described well through higher-order interactions. As discussed by Angeli and co-workers,53 the charge polarising effect of the higher order terms can be crudely simulated by optimising a singlet CASSCF(2,2) wavefunction and artificially giving a higher weight to the ionic states (the second and third singlet roots) in the orbital optimisation. The increased weight of the ionic states then leads the optimisation to converge to more diffuse orbitals, which, subsequently, provides improved values for the exchange interaction at low orders of perturbation.53
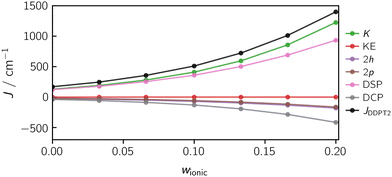
Fig. 13 illustrates the dependence of the calculated exchange interaction and its individual contributions on the weight w of the ionic states in the orbital optimisation. The calculations were performed for the diradical using the DDPT2 method. In the case of this system, the exchange coupling is barely influenced by the kinetic exchange (KE) contribution.
The 1h and 1p contributions are strictly zero for two-spin systems as we approximated the single-excitation Hamiltonian matrix elements by the SA-CASSCF Fock matrix elements, which we assumed to be diagonal.
Fig. 13 shows a strong (non-linear) dependence of J on w. To obtain accurate and meaningful J-values, the challenge will be to identify a suitable weight w which is a priori not known and will differ for systems of different size and nature. However, if the exchange interaction is known experimentally for a particular system, the distinct trend observed as a function of w will make it possible to identify an appropriate weighting factor that should allow us to calculate accurate J-values for a whole series of similar systems. For the diradical, a weight of 0.133 provides good orbitals for the calculation of J, where a value of J(w = 0.133) = 722 cm−1 is obtained, in good agreement with the experimental value of 695 cm−1.
A FIC-NEVPT2 calculation using the same weight of w = 0.133 yields an exchange coupling constant of JNEVPT2(w = 0.133) = 438 cm−1, which is smaller in magnitude than the DDPT2 value with the same ionic weight and even smaller than the corresponding CASSCF(2,2) value of 634 cm−1. The main reason for this deviation is the contribution of the 1h and 1p determinants in the NEVPT2 method, which are not taken into account in the DDPT2 method. The 1h and 1p determinants lead to an orbital relaxation and tend to act in favour of the singlet state. Interestingly, the effect of this orbital relaxation can become so large, that even a wrong sign can be predicted as illustrated in Fig. 14, showing the trend of the computed J values against w for DDPT2 and NEVPT2. For example, when using NEVPT2 with an ionic weight of w = 0.4, a coupling of JNEVPT2(w = 0.4) = −2.4 cm−1 is obtained. Consequently, one needs to be careful with state-averaging when using, for example, the NEVPT2 method. The current implementation of the DDPT2 method circumvents this problem intrinsically by assuming the SA-CASSCF Fock matrix to be diagonal.
Using the DDPT2 method, the J-values increase monotonically with w and converge to an upper bound. Using the NEVPT2 method, the values go through a local maximum and then converge to a negative value of J, due to the orbital relaxation. Interestingly, the most accurate J value for the NEVPT2 method is obtained at the maximum of the curve with JNEVPT2(w = 0.246) = 625 cm−1. However, the exact value is not reached. In future work, it may be worth investigating if this is a general behaviour of the NEVPT2 method for ferromagnetically coupled compounds.
| CASSCF(3,3) | FIC-NEVPT2 | DDPT2 | Exp. | |
|---|---|---|---|---|
| w = 0 | 0.191 | 0.497 | 0.283 | 9.45 |
| w = 0.375 | 5.87 | 6.00 | 11.4 | |
| State-specific | 0.190 | 0.741 |
To achieve a result with the DDPT2 method, that is relatively close to the experimental value of 9.45 cm−1, one might choose an ionic weight of w = 0.375, which yields a J value of JDDPT2(w = 0.375) = 11.4 cm−1. A FIC-NEVPT2 calculation with the same weight yields JNEVPT2(w = 0.375) = 6.00 cm−1, where the J-value is again damped by the anti-ferromagnetic orbital relaxation through the 1h and 1p determinants. This observation suggests that, for ferromagnetically-coupled systems, the optimal weight in state-averaged NEVPT2 calculations will be higher compared to the DDPT2 method. In case of antiferromagnetically-coupled systems, the optimal weight may be smaller compared to the DDPT2 method.
Comparing the optimal weights w for the triradical and the diradical, one finds that the optimal ionic weight may correlate with the system size, i.e. with the size of the π system. In order to calculate an accurate J value for a larger π system, a larger ionic weight w is likely to be necessary. The reason for this might be, that, in large π-systems, the ionic forms are better stabilised through the enhanced delocalisation. Now, if one increases w, only a slight expansion of the magnetic orbitals will be observed. This means, that, in case of a smaller π system, the relaxation of the ionic forms has to be connected with a larger expansion of the magnetic orbitals, which will lead to much more expanded orbitals at a smaller w.
5.4 Scaling of the DDPT2 method
The most elaborate step of the DDPT2 method is the transformation of the two-electron integrals. Only the (ik|jl) and (ia|jb) integrals are required for the computation of the effective exchange integrals. Therefore, in an optimal implementation, the computation time t should scale as follows:| t = m·N·(Nint4 + Nint2Nvirt2), | (47) |
| t = m·NNint2·(N2 − 2NNint + 2Nint2). | (48) |
Introducing the ratio c = Nint/N, we obtain:
| t = m·(c2 − 2c3 + 2c4)N5. | (49) |
To validate the above equation, 20 calculations were carried out, where, in each successive calculation, a xenon atom was added. This ensures that the ratio c remains constant. The calculations were performed using the def2-TZVP basis set and the def2-SVP/C auxiliary basis set. The computational time t as a function of the basis functions N is depicted in Fig. 15. With 8 cores (Apple M2 Max) and 8 GB of RAM per core, a computation time of 549.5 s was obtained for 920 basis functions (1000 basis functions including frozen core orbitals). Thus, medium to large systems (depending on the basis set size) can be calculated within a short time frame. The computation times were fitted with a function of the form: t = m·Nx, yielding a pre-factor of m = 4.69 × 10−12 s and an exponent of x ≈ 4.75. The exponent determined here approximately confirms the theoretically expected exponent of x = 5. The scaling of the DDPT2 method was also compared to the FIC-NEVPT2 method. In order to calculate the exchange interaction using the NEVPT2 method, two states need to be computed to obtain a meaningful comparison between the DDPT2 and NEVPT2 methods. Note that the RI approximation was also invoked in the FIC-NEVPT2 calculations. Using the same fit function as for the DDPT2 method, a scaling factor of x ≈ 4.32 was obtained. The scaling factor obtained for the FIC-NEVPT2 method is better than that of the DDPT2 method. However, the pre-factor is much larger with m = 1.21 × 10−10 s. As a consequence, it is expected that the DDPT2 method is faster for small and medium sized systems, whereas the FIC-NEVPT2 method should be faster for larger systems, due to its contracted nature.
The variational treatment of the exact same determinant space as in the DDPT2 method leads to the DDCI2 method. However, as can be seen in Fig. 15, the variational treatment becomes quickly unfeasible with an increasing number of basis functions making perturbational methods much more attractive for larger systems. Even with a smaller FOIS, such as that of the CASCI+S method, the scaling is still very steep compared to the perturbational methods.
The reason for the very large pre-factors of the DDCI2 and CASCI+S methods is largely of a technical nature since in the ORCA MRCI program matrix elements are being calculated one at a time which is far less efficient than constructing the sigma-vector through a series of matrix multiplications that only require a subset of the molecular integrals in each contraction. The reason for the ORCA implementation not following such an approach is that the program gains efficiency through individual selection, which interferes with a matrix driven construction. Secondly, a matrix driven, uncontracted MRCI approach is of high technical complexity and has, so far, not been attempted in the ORCA program. However, an internally contracted DDCI implementation has been available in ORCA since 2016 and will be numerically evaluated in a subsequent study.
5.5 A case study on the anthracene–radical system
In the orbital optimisation of the anthracene radical system, we used a weighting of the ionic states of w = 0.375, just as for the nitroxide triradical. This w should yield good values for J if the insights gained from the orbital optimisation of the nitroxide triradical, i.e. w depends on the size of the π-system, are applicable to the anthracene radical system.Calculations were performed using the def2-SVP and def2-TZVP basis sets to ascertain the dependence of the result on the basis set size. The obtained values are JDDPT2(w = 0.375,def2-SVP) = −4.76 cm−1 and JDDPT2(w = 0.375,def2-TZVP) = −5.01 cm−1. The results do not differ significantly and have the correct sign, suggesting that the calculated value of J is less dependent on the basis set size but more on the method used.
A FIC-NEVPT2 calculation with the same weight yields a value of JNEVPT2(w = 0.375) = −6.27 cm−1. This confirms the assumption that, for antiferromagnetic system, the NEVPT2 method should yield larger couplings than the DDPT2 method when considering the same w. Furthermore, the 2h–1p and 1h–2p contributions in the NEVPT2 method give a total contribution of −0.313 cm−1 justifying a perturbational treatment using only the DDCI2 space, as carried out within the DDPT2 method.
A DDCI2 calculation on this system with Q1-optimised orbitals using the def2-SVP basis set gave an exchange coupling constant of JDDCI2 = −6.14 cm−1, which is in good agreement. Since DDCI2 can yield excellent values for the exchange interaction in organic systems, as shown by Calzado et al. and Barone et al.49,71 we might expect the calculated values to be close to the exact value of JTR.
For the further discussion, only JDDPT2(w = 0.375,def2-SVP) will be used. Table 3 summarises all individual second-order contributions to the exchange interaction JTR. Here, the direct exchange sums up to 2.02 cm−1. The kinetic exchange contribution, which is often used to explain the negative sign of the exchange interaction, does only (almost) cancel out the direct exchange with a contribution of −1.93 cm−1.33 CASSCF(3,3) yields a J value of 0.313 cm−1, which approximately matches the result from the DDPT2 method, where only the direct and kinetic exchange contributions are included (J = 0.094 cm−1). This indicates that eqn (25) for calculating the kinetic exchange remains valid for this system, even though the equation is strictly only valid in the case of two degenerate orbitals.
| K ab + Kbc | KE | 1ö | 1p | 2h | 2p | DSP | DCP | J TR |
|---|---|---|---|---|---|---|---|---|
| 2.02 cm−1 | −1.93 cm−1 | ≈0 cm−1 | ≈0 cm−1 | −0.314 cm−1 | −0.166 cm−1 | −4.09 cm−1 | −0.265 cm−1 | −4.67 cm−1 |
The most important contribution stems from the dynamic spin polarisation effect with an anti-ferromagnetic contribution of −4.09 cm−1. Since this contribution is much larger than the direct exchange, its sign determines the sign of the final exchange interaction JTR. Assuming the dynamic spin polarisation to be equally important for other chromophore–radical systems, the sign of the exchange interaction JTR could be qualitatively predicted by predicting the sign of the dynamic spin polarisation contribution. All other second order contributions are small compared to the kinetic exchange and the dynamic spin polarisation and act in favour of the doublet state (i.e. anti-ferromagnetic coupling).
6 Conclusion
The DDPT2 implementation reported in this work is based on the perturbational approach by de Loth, et al. and allows for the direct calculation of the effective exchange integrals.22 The method seems to be promising for the calculation of exchange interactions of medium- and large-sized organic molecules (O(N5) scaling) in combination with molecular orbitals generated from state-averaged CASSCF calculations. We could show a non-linear dependence of the calculated J-value on the weight w of the ionic determinants in the orbital optimisation procedure of the CASSCF calculation. If the optimal weight for a specific system is known, it should, in principle, be possible to calculate accurate values for the exchange interaction for a series of similar molecules. The dependence of the J value on the ionic weight w might be seen as a drawback of the DDPT2 method. However, it is not a unique problem to the DDPT2 method but a common problem for low-order MRPT methods in general.The benchmark on the ground state radicals showed, that the optimal ionic weight w depends on the size of the conjugated π-system, where w increases with the size of the π system. In the case of the smaller diradical, the J-value was calculated to be JDDPT2(w = 0.133) = 722 cm−1, which is close to the experimental value of 695 cm−1. In the case of the triradical, the J-value was calculated to be JDDPT2(w = 0.375) = 11.4 cm−1, which is also in good agreement with the experimental value of 9.45 cm−1. The same weight as for the triradical was used in the calculation of the exchange interaction for the anthracene–radical system, where a value of J(w = 0.375) = −4.67 cm−1 was calculated, which is in good agreement with the DDCI2 value of −6.14 cm−1. Thus, we might expect the calculated result to be close to the exact value for the exchange interaction.48,49
In principle, it is also possible to obtain similar results for JTR with the NEVPT2 method when using molecular orbitals generated from state-averaged CASSCF calculations. However, DDPT2 allows the separation of the dynamic spin polarisation contribution from the dynamic charge polarisation contribution, which is very useful for the investigation of important exchange mechanisms. Using the DDPT2 method, we could show that the dynamic spin polarisation effect is significantly more important than the dynamic charge polarisation contribution (and all other contributions) in case of the photogenerated triplet–doublet system investigated in this work. This observation is likely applicable to other photoexcited chromophore–radical systems. Consequently, to predict the sign of the exchange interaction JTR qualitatively, one needs to be able to predict the sign of the dynamic spin polarisation effect in a qualitative manner,55 which will be the focus of our future work.
Regarding the DDPT2 method, future work will focus on (1) a less approximate treatment of the single excitations, which allows us to take the orbital relaxation through the 1h and 1p determinants into account. This way, a more accurate trend of the exchange interaction against w can be obtained, especially for ferromagnetically-coupled systems. (2) It should be investigated which higher-order effects have a significant effect on the exchange interaction in organic compounds. Here, the dynamic spin polarisation is likely to play an important role. (3) The reference space in the DDPT2 method may be expanded to a complete active space. However, only a minor improvement to the calculated exchange interaction might be expected for many organic compounds. (4) The usage of Dyall's Hamiltonian as Ĥ(0) will allow us to drop the approximations made in the derivation of the working equations, i.e. introducing two-electron interactions in case of charge-polarised active spaces. This way, a less approximate calculation strategy can be obtained.
Author contributions
Implementation of the code, quantum chemical calculations, investigation, methodology, formal analysis, data validation and visualisation, original draft writing M. F.; implementation, supervision, review and editing of the manuscript F. N.; conceptualisation, project administration, funding acquisition, supervision, review and editing of the manuscript S. R.Data availability
The data supporting the findings of this study are available within the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project numbers 417643975 and 536668010 (S. R.). The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 40/575-1 FUGG (JUSTUS 2 cluster). F. N. would like to thank the Max Planck Society for financial support. Open Access funding provided by the Max Planck Society.Notes and references
- T. Quintes, M. Mayländer and S. Richert, Nat. Rev. Chem., 2023, 7, 75–90 CrossRef PubMed.
- R. J. Hudson, T. S. C. MacDonald, J. H. Cole, T. W. Schmidt, T. A. Smith and D. R. McCamey, Nat. Rev. Chem., 2024, 8, 136–151 CrossRef PubMed.
- S. Bayliss, D. Laorenza, P. Mintun, B. Kovos, D. Freedman and D. Awschalom, Science, 2020, 370, 1309–1312 CrossRef CAS PubMed.
- S. Sanvito, Chem. Soc. Rev., 2011, 40, 3336–3355 RSC.
- M. Mayländer, S. Chen, E. R. Lorenzo, M. R. Wasielewski and S. Richert, J. Am. Chem. Soc., 2021, 143, 7050–7058 CrossRef PubMed.
- J. N. Nelson, J. Zhang, J. Zhou, B. K. Rugg, M. D. Krzyaniak and M. R. Wasielewski, J. Chem. Phys., 2020, 152, 014503 CrossRef CAS PubMed.
- J. H. Olshansky, J. Zhang, M. D. Krzyaniak, E. R. Lorenzo and M. R. Wasielewski, J. Am. Chem. Soc., 2020, 142, 3346–3350 CrossRef CAS PubMed.
- Y. Qiu, A. Equbal, C. Lin, Y. Huang, P. J. Brown, R. M. Young, M. D. Krzyaniak and M. R. Wasielewski, Angew. Chem., Int. Ed., 2023, 62, e202214668 CrossRef CAS PubMed.
- S. Gorgon, K. Lv, J. Grüne, B. H. Drummond, W. K. Myers, G. Londi, G. Ricci, D. Valverde, C. Tonnelé, P. Murto, A. S. Romanov, D. Casanova, V. Dyakonov, A. Sperlich, D. Beljonne, Y. Olivier, F. Li, R. H. Friend and E. W. Evans, Nature, 2023, 620, 538–544 CrossRef CAS PubMed.
- M. Mayländer, K. Kopp, O. Nolden, M. Franz, P. Thielert, A. Vargas Jentzsch, P. Gilch, O. Schiemann and S. Richert, Chem. Sci., 2023, 14, 10727–10735 RSC.
- M. Mayländer, P. Thielert, T. Quintes, A. Vargas Jentzsch and S. Richert, J. Am. Chem. Soc., 2023, 145, 14064–14069 CrossRef PubMed.
- A. Yamauchi, K. Tanaka, M. Fuki, S. Fujiwara, N. Kimizuka, T. Ryu, M. Saigo, K. Onda, R. Kusumoto, N. Ueno, H. Sato, Y. Kobori, K. Miyata and N. Yanai, Sci. Adv., 2024, 10, eadi3147 CrossRef CAS PubMed.
- R. M. Jacobberger, Y. Qiu, M. L. Williams, M. D. Krzyaniak and M. R. Wasielewski, J. Am. Chem. Soc., 2022, 144, 2276–2283 CrossRef CAS PubMed.
- Y. Qiu, H. J. Eckvahl, A. Equbal, M. D. Krzyaniak and M. R. Wasielewski, J. Am. Chem. Soc., 2023, 145, 25903–25909 CrossRef CAS PubMed.
- S. L. Bayliss, P. Deb, D. W. Laorenza, M. Onizhuk, G. Galli, D. E. Freedman and D. D. Awschalom, Phys. Rev. X, 2022, 12, 031028 CAS.
- E. M. Giacobbe, Q. Mi, M. T. Colvin, B. Cohen, C. Ramanan, A. M. Scott, S. Yeganeh, T. J. Marks, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2009, 131, 3700–3712 CrossRef CAS PubMed.
- M. T. Colvin, E. M. Giacobbe, B. Cohen, T. Miura, A. M. Scott and M. R. Wasielewski, J. Phys. Chem. A, 2010, 114, 1741–1748 CrossRef CAS PubMed.
- M. T. Colvin, A. L. Smeigh, E. M. Giacobbe, S. M. M. Conron, A. B. Ricks and M. R. Wasielewski, J. Phys. Chem. A, 2011, 115, 7538–7549 CrossRef CAS PubMed.
- S. Weber, eMagRes, 2017, 6, 255–270 CAS.
- M. Franz, F. Neese and S. Richert, Chem. Sci., 2022, 13, 12358–12366 RSC.
- J. P. Malrieu, R. Caballol, C. J. Calzado, C. De Graaf and N. Guihery, Chem. Rev., 2014, 114, 429–492 CrossRef CAS PubMed.
- P. De Loth, P. Cassoux, J. Daudey and J. Malrieu, J. Am. Chem. Soc., 1981, 103, 4007–4016 CrossRef CAS.
- J. P. Malrieu, P. Claverie and S. Diner, Theor. Chim. Acta, 1967, 8, 404–423 CrossRef CAS.
- J. Miralles, J.-P. Daudey and R. Caballol, Chem. Phys. Lett., 1992, 198, 555–562 CrossRef CAS.
- J. Miralles, O. Castell, R. Caballol and J.-P. Malrieu, Chem. Phys., 1993, 172, 33–43 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- P. A. M. Dirac, Proc. R. Soc. London, Ser. A, 1926, 112, 661–677 CAS.
- W. Heisenberg, Original Scientific Papers/Wissenschaftliche Originalarbeiten, Springer, 1985, pp. 580–597 Search PubMed.
- J. H. Van Vleck, Theory of Electric and Magnetic Susceptibilities, Clarendon Press, Oxford, 1932 Search PubMed.
- C. De Graaf and R. Broer, Magnetic Interactions in Molecules and Solids, Springer, Cham, 2016 Search PubMed.
- R. L. Ake and M. Gouterman, Theor. Chim. Acta, 1969, 15, 20–42 CrossRef CAS.
- M. G. Cory and M. C. Zerner, Chem. Rev., 1991, 91, 813–822 CrossRef CAS.
- F. Nepveu, W. Haase and H. Astheimer, J. Chem. Soc., Faraday Trans. 2, 1986, 82, 551–565 RSC.
- P. De Loth, P. Karafiloglou, J. P. Daudey and O. Kahn, J. Am. Chem. Soc., 1988, 110, 5676–5680 CrossRef CAS.
- P. de Loth, J.-P. Daudey, H. Astheimer, L. Walz and W. Haase, J. Chem. Phys., 1985, 82, 5048–5052 CrossRef CAS.
- H. Astheimer and W. Haase, J. Chem. Phys., 1986, 85, 1427–1432 CrossRef CAS.
- K. Handrick, J. P. Malrieu and O. Castell, J. Chem. Phys., 1994, 101, 2205–2212 CrossRef.
- O. Castell, R. Caballol, V. Garcia and K. Handrick, Inorg. Chem., 1996, 35, 1609–1615 CrossRef CAS PubMed.
- J. Cabrero, N. Ben Amor, C. De Graaf, F. Illas and R. Caballol, J. Phys. Chem. A, 2000, 104, 9983–9989 CrossRef CAS.
- C. J. Calzado, J. F. Sanz and J. P. Malrieu, J. Chem. Phys., 2000, 112, 5158–5167 CrossRef CAS.
- C. J. Calzado, C. Angeli, D. Taratiel, R. Caballol and J.-P. Malrieu, J. Chem. Phys., 2009, 131, 044327 CrossRef PubMed.
- O. Castell and R. Caballol, Inorg. Chem., 1999, 38, 668–673 CrossRef CAS.
- J. Cabrero, N. Ben-Amor and R. Caballol, J. Phys. Chem. A, 1999, 103, 6220–6224 CrossRef CAS.
- I. Negodaev, C. de Graaf and R. Caballol, Chem. Phys. Lett., 2008, 458, 290–294 CrossRef CAS.
- V. Barone, I. Cacelli, P. Cimino, A. Ferretti, S. Monti and G. Prampolini, J. Phys. Chem. A, 2009, 113, 15150–15155 CrossRef CAS PubMed.
- C. J. Calzado, C. Angeli, C. de Graaf and R. Caballol, Theor. Chem. Acc., 2011, 128, 505–519 Search PubMed.
- F. Illas, I. P. Moreira, C. De Graaf and V. Barone, Theor. Chem. Acc., 2000, 104, 265–272 Search PubMed.
- B. O. Roos, P. R. Taylor and P. E. Sigbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- B. O. Roos, Int. J. Quantum Chem., 1980, 18, 175–189 CrossRef.
- C. Angeli and C. J. Calzado, J. Chem. Phys., 2012, 137, 034104 CrossRef PubMed.
- A. Szabo and N. S. Ostlund, Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory, Courier Corporation, 2012 Search PubMed.
- P. Karafiloglou, J. Chem. Educ., 1989, 66, 816 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- C. Kollmar, K. Sivalingam, B. Helmich-Paris, C. Angeli and F. Neese, J. Comput. Chem., 2019, 40, 1463–1470 CrossRef CAS PubMed.
- S. F. Boys, Rev. Mod. Phys., 1960, 32, 296 CrossRef CAS.
- F. Neese, J. Comput. Chem., 2023, 44, 381–396 CrossRef CAS PubMed.
- T. Ishida and H. Iwamura, J. Am. Chem. Soc., 1991, 113, 4238–4241 CrossRef CAS.
- H. Iwamura, K. Inoue and N. Koga, New J. Chem., 1998, 22, 201–210 RSC.
- Y. Teki, S. Miyamoto, M. Nakatsuji and Y. Miura, J. Am. Chem. Soc., 2001, 123, 294–305 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- K. G. Dyall, J. Chem. Phys., 1995, 102, 4909–4918 CrossRef CAS.
- V. Barone, I. Cacelli and A. Ferretti, Phys. Chem. Chem. Phys., 2018, 20, 18547–18555 RSC.
| This journal is © the Owner Societies 2024 |