Probing the structure and dynamics of the heterocyclic PAH xanthene and its water complexes with infrared and microwave spectroscopy

Abstract

To assess the presence of oxygen-containing polycyclic aromatic hydrocarbons (OPAHs) in the interstellar medium and understand how water aggregates on an OPAH surface, we present a comprehensive gas-phase spectroscopy investigation of the OPAH xanthene (C₁₃H₁₀O) and its complexes with water using IR-UV ion dip spectroscopy and chirped-pulse Fourier transform microwave spectroscopy. The infrared spectrum of xanthene shows weak features at 3.42, 3.43, and 3.47 μm, which have been suggested to partly originate from vibrational modes of PAHs containing sp³ hybridized carbon atoms, in agreement with the molecular structure of xanthene. The high resolution of rotational spectroscopy reveals a tunneling splitting of the rotational transitions, which can be explained with an out-of-plane bending motion of the two lateral benzene rings of xanthene. The nature of the tunnelling motion is elucidated by observing a similar splitting pattern in the rotational transitions of the singly-substituted ¹³C isotopologues. The rotational spectroscopy investigation is extended to hydrates of xanthene with up to four water molecules. Different xanthene–water binding motifs are observed based on the degree of hydration, with O–H⋯π interactions becoming preferred over O–H⋯O_xanthene interactions as the degree of hydration increases. A structural comparison with water complexes of related molecular systems highlights the impact of the substrate's shape and chemical composition on the arrangement of the surrounding water molecules.

---

1 Introduction

Polycyclic aromatic hydrocarbons (PAHs) are a class of organic molecules with vast astrochemical implications.¹ They are detected across various regions of the interstellar medium (ISM) via the so-called aromatic infrared bands (AIBs), mid-infrared emissions linked to distinctive vibrational modes of aromatic species. The pervasive presence of the AIBs suggests that PAHs are ubiquitous in space² and points towards their pivotal role in shaping the physics and chemistry of the ISM.

Gaining insight into the structure of interstellar PAHs is paramount, as it is the basis for understanding their formation and evolution in space, and in turn, it can enable a deeper understanding of the unique physical properties of the interstellar environments in which PAHs are detected. However, because of the structural resemblances among PAHs, the variations in their vibrational frequencies are subtle and fall within the interstellar band profile, thus rendering the assignment of the AIBs to individual PAHs via infrared spectroscopy impossible. Identifying the exact nature of the AIBs carriers is nowadays one of the most important open challenges in carbon-based astrochemistry.³

Using radio astronomy for the detection of polar PAHs can overcome the challenges associated with infrared spectroscopy. While this approach is quite powerful, it still faces difficulties, primarily due to the inherently low electric dipole moments and large rotational partition functions of most PAHs. Still, the introduction of match filtering in the field of radio astronomy has facilitated the unambiguous detection of PAHs characterized by sizeable dipole moments and relatively low rotational partition functions. As of now, radio astronomy has successfully detected a few polar PAHs, namely, the non-substituted polycyclic aromatic hydrocarbon indene alongside with its cyano derivative 2-cyanoindene as well as the two isomers of cyanonaphthalene, 1- and 2-cyanonaphthalene, which were recently detected in the Taurus Molecular Cloud (TMC-1).^4–7 This highlights that functionalization with a group like –CN induces a large dipole moment thus yielding a spectroscopically bright molecule.

Beside cyano-substituted PAHs, oxygen-containing PAHs (OPAHs) have emerged as promising targets for astronomical detections, with suggestions that a C=O stretching vibration is responsible for the 6 μm feature in infrared emissions.⁸ OPAHs contain oxygen atoms either replacing a carbon atom in the PAH backbone, or substituting one of the aromatic hydrogen atoms with oxygen-containing functional groups, such as =O, –OH, and O–CH₃. In interstellar environments, OPAHs are expected to form within ice grains, where a fraction of PAHs is thought to be locked up. OPAHs could also form in regions characterized by elevated temperatures, where water does not condense onto grain surfaces as icy layers but may be present in the form of a few water molecules. Both scenarios can be considered plausible, as the formation of oxygenated PAHs has been observed in laboratory experiments, which involved UV irradiation of PAHs embedded in water ices as well as UV irradiation of complexes of PAHs with water molecules using matrix isolation.^9–13

Given the permanent electric dipole moments induced in PAHs by oxygenation, OPAHs could become observable by radio astronomy, providing crucial information to be complemented by infrared absorption or emission spectra recorded with the high resolution and sensitivity provided by the James Webb Space Telescope (JWST).¹⁴ Importantly, the detection of interstellar molecules typically stems from an interplay between laboratory experiments and astronomical observations. Therefore, conducting laboratory experiments on oxygenated PAHs is central to facilitate their detection in astronomical observations. Microwave and infrared spectroscopy are highly complementary in this respect. In this context, we present a comprehensive spectroscopy study focusing on the OPAH xanthene (C₁₃H₁₀O), involving IR-UV ion dip spectroscopy and broadband rotational spectroscopy. The structure of xanthene is non-planar and consists of three fused six-membered rings in a linear arrangement – two peripheral benzene rings and a central ring featuring an oxygen atom and a –CH₂ group, which bridge the two peripheral benzene rings (see Fig. 1). Interestingly, PAHs featuring carbon atoms with sp³ hybridization have also been suggested to contribute to the AIBs, potentially explaining the weaker features appearing near the 3.4 μm feature, seen at 3.4, 3.47, 3.51, and 3.56 μm.¹⁵

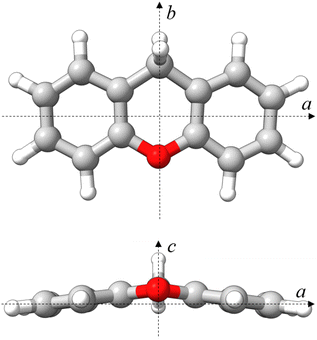Fig. 1 Molecular structure of xanthene calculated at the B3LYP-D3BJ/def2-TZVP level of theory in a top (ab) and front (ac) view. Rendered using UCSF ChimeraX software.¹⁶

In addition, the microwave spectroscopy study of xanthene presented here was extended to its hydrated complexes. The precise structure of water ices in interstellar environments remains elusive, as it depends on several factors such as the conditions under which they form and evolve and on their composition. Interstellar water ices are unlikely to exist in their chemically pure form, as molecules, i.e., OPAHs, may form simultaneously or accrete onto the ice. The presence of other molecules beside water may impact the structure of the water ice itself. This, in turn, may have an influence on the chemical processes taking place in these environments. Therefore, to understand the structure of interstellar ices and the chemical reactivity within such settings, it is important to understand how water molecules aggregate around a substrate, such as an OPAH, at the molecular level.

In previous experiments, we have investigated the aggregation process of water molecules around various PAH surfaces using broadband rotational spectroscopy.^17–20 Different binding motifs of the water molecules onto the PAH surfaces have been observed, dictated both by non-covalent interactions established between the water molecules themselves and between the water molecules and the PAH substrate. In this study, we investigated the aggregation of water molecules on the OPAH xanthene, using broadband rotational spectroscopy. We observed hydrated complexes of xanthene with up to four water molecules. Comparing these complexes with hydrated complexes of PAHs with a related structure to xanthene highlights the influence of the shape and composition of the PAH on the morphology of water complex formation.

2 Experimental methods

2.1 CP-FTMW spectroscopy

The broadband rotational spectra of xanthene and its hydrated clusters were recorded in the 2–8 GHz frequency range using the chirped-pulse Fourier transform microwave (CP-FTMW) spectrometer COMPACT in Hamburg.^21,22 Xanthene, with a purity of 99%, was purchased from Sigma Aldrich and used without any purification steps. The sample, which appears as a yellow powder at room temperature, was loaded into a heatable reservoir located inside the vacuum chamber and positioned directly before the orifice of a pulsed valve. A temperature between 115 °C and 135 °C was sufficient to generate enough concentration of the sample into the gas phase for probing using microwave spectroscopy. To generate a supersonic jet, neon at a backing pressure of 2.5 bar was flown through the reservoir containing the sample and supersonically expanded into the vacuum chamber through a 1-mm pinhole. For recording the spectra of xanthene's hydrated clusters, neon at a backing pressure of 3 bar was initially passed through a reservoir located outside the vacuum chamber, which contained deionized water, before passing through the internal reservoir containing xanthene. Weakly bound gas-phase clusters are expected to form at the onset of the supersonic expansion, where collisions are still occurring. These clusters can then be probed in isolation within the so-called “zone of silence” of the supersonic jet.

The supersonically cooled molecules were excited using microwave chirped pulses of 4 μs length, which were generated by an arbitrary waveform generator and amplified using a travelling-wave tube amplifier. Each excitation pulse was then subsequently broadcast into the vacuum chamber where it interacted with the molecules in the supersonic jet. After each excitation, the molecular emission signal was received by a horn antenna, amplified using a low-noise amplifier and digitized in the time domain in the form of a free induction decay (FID) for 40 μs on a fast oscilloscope. The repetition rate of the experiment was set to 8 Hz. To reduce measurement time and sample consumption, a train of eight chirp pulses was used to interact with each molecular pulse, thus resulting in an effective repetition rate of the experiment of 64 Hz. Final data sets were obtained from averaging 2.5 × 10⁶ and 5.1 × 10⁶ FIDs for the xanthene monomer and its hydrated clusters, respectively.

2.2 Infrared spectroscopy measurements

The infrared spectrum of neutral xanthene was recorded across a wide spectral range, covering from 120 to 1800 cm⁻¹ and from 2800 to 3200 cm⁻¹. For this, a similar methodology as discussed above was employed to create a gas pulse of neutral xanthene molecules. However, in this technique the gas pulse is skimmed before interacting with the infrared radiation, allowing only the coldest part of the beam to be probed. Additionally, the beam is injected into a perpendicularly extracted time-of-flight mass spectrometer (m/Δm = 2000 at 182 amu), as detailed in ref. 23. To record a mass spectrum, ionization of the molecular species in the beam is necessary, which is carried out differently depending on the covered infrared spectral range.

For the range from 2800 to 3200 cm⁻¹, ionization is performed via a (1 + 1) Resonance Enhanced Two-Photon Ionisation (R2PI) scheme, for which the UV light provided by a Nd:YAG laser pumped dye laser operating on Coumarin 153 in ethanol is aligned within the extraction plates of the mass spectrometer. Fixing the ionization wavelength to 279.79 nm, an infrared spectrum is recorded via IR-UV ion dip spectroscopy,²⁴ where the UV light is preceded by the laser light of a high-resolution tunable OPO/OPA laser (LaserVision), covering the 2800–3200 cm⁻¹ range in steps of 0.12 cm⁻¹. Upon resonant absorption of infrared light via vibrational transitions, the ionization efficiency is reduced, resulting in a depletion of signal in the mass spectra. To record the infrared spectra, mass spectra are consecutively measured with and without the excitation of the OPO/OPA laser, by running both UV and infrared lasers at 10 Hz (same as the pulsed valve), but by blocking every other infrared pulse with a shutter running at 5 Hz.

For the range from 120 to 1800 cm⁻¹, ionization is performed using the light of a Xe/Ar cell (10.5 eV), pumped by the third harmonic of a Nd:YAG laser (355 nm). In this case, ionization occurs after one-photon absorption, given the low ionization energy of xanthene (7.65 eV). To measure an infrared spectrum, prior to ionization, the molecular beam is merged with the counterpropagating laser light of the free electron laser FELIX, as described in ref. 25. Here, the scheme of Infrared Multiple Photon Dissociation (IRMPD) spectroscopy is employed, in which, given the high power of FELIX and its pulse structure of roughly 10 μs long macropulses, many photons can be absorbed on the same resonance, with the energy being rapidly redistributed via infrared vibrational redistribution (IVR), until the dissociation threshold is surpassed. This leads to a depletion in the signal of xanthene, which coincides with the signal in-growth of its dissociation channels.²⁶ As shown in the ESI,† dissociation occurs by losing one hydrogen atom. By running FELIX at 5 Hz while the molecular beam and its ionization laser at 10 Hz, consecutive mass spectra are recorded with and without vibrational excitation. FELIX is scanned in the 120 to 1800 cm⁻¹ range in steps of 1 cm⁻¹.

3 Theoretical methods

Density functional theory (DFT) calculations were conducted using the ORCA 5.0.4 software package.²⁷ The B3LYP exchange–correlation functional²⁸ was employed, together with the def2-TZVP basis set²⁹ and D3BJ dispersion corrections.³⁰ The geometry of xanthene, shown in Fig. 1, was optimized at the “verytight” convergence criteria for the self consistent field (SCF) and the geometry optimization cycles, as implemented in ORCA. Moreover, a very fine grid size was selected (defgrid3 option). For comparing and analysing the measured infrared spectra, harmonic vibrational frequencies were computed for the optimized structure, corroborating that all frequencies are positive. In addition, overtones and combination bands were calculated using the NEARIR formalism, where the frequencies of 2-quanta modes are computed without a direct perturbation of the fundamental frequencies, but with intensities determined using the vibrational second-order perturbation theory (VPT2) approach. All frequencies are scaled by a 0.9664 factor.³¹ The potential energy curve describing xanthene's butterfly-like motion was calculated using the nudged elastic band (NEB) method implemented in the ORCA software at the B3LYP-D3BJ/def2-TZVP level of theory.³²

The conformational landscapes of xanthene–(H₂O)_n, with n = 1–4, were investigated using the conformer–rotamer ensemble tool CREST at the GFN2-xTB level of theory.^33,34 The structures of the low-energy isomers were re-optimized at the B3LYP-D4/def2-QZVP level of theory³⁵ using the ORCA 5.0.4 quantum-chemistry program package. Harmonic frequency calculations were performed to provide zero-point energies (ZPE) as well as to verify that the calculated geometries are real minima of the potential energy surface (PES). This computational study revealed four isomers for each cluster size within an energy window of 5 kJ mol⁻¹. The hydrates have been labelled based on the number of their water molecules (1w, 2w, 3w, and 4w) as well as on their energy ordering (I, II, III, etc.). Their computed structures along with their calculated spectroscopic parameters and relative energies are provided in the ESI.†

4 Results and discussion

4.1 Infrared spectroscopy of xanthene

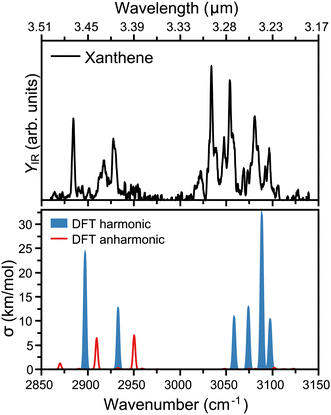
The measured infrared spectrum of xanthene in the 2800 to 3200 cm⁻¹ range (3.5 to 3.2 μm) is presented in the top panel of Fig. 2. The high resolution of the OPO/OPA laser allows us to distinguish many infrared features, notably at 2884, 2917, 2928, 3034, 3054, 3081, and 3097 cm⁻¹. In addition, the rich spectrum also shows minor but clearly visible bands at 3022, 3048, 3069, and 3106 cm⁻¹. The main modes above 3000 cm⁻¹ fall within the broader 3.3 μm band in the AIBs emissions,¹⁴ which are associated to the C–H stretch in PAHs, specifically at 3.23, 3.26, 3.27, and 3.30 μm. Similar features, however molecule specific, are seen in other PAHs.³⁶ Interestingly, xanthene also presents modes below 3000 cm⁻¹, which in wavelength are centered at 3.42, 3.43, and 3.47 μm. Thus, these features lie within the weakest AIBs band around 3.4 μm, which has been suggested to partly correspond to PAHs containing sp³ hybridized carbon atoms.³⁷

Fig. 2 Top: Infrared spectrum of neutral xanthene recorded in the 2850 to 3150 cm⁻¹ range, using an infrared OPO/OPA laser. The top axis presents the corresponding range in wavelength. Bottom: DFT calculated vibrational spectrum of xanthene, with harmonic computations in blue and combination bands and overtones in red. For visualization purposes, Gaussian functions are built around each vibration, with a FWHM of 2 cm⁻¹.

To rationalize the experimental infrared modes in terms of molecular vibrations, the vibrational spectrum of xanthene was computed by DFT calculations, as presented in the bottom panel of Fig. 2. In order to construct the spectrum and help its comparison with the experimental curve, each vibration was convoluted by Gaussian functions with a FWHM of 2 cm⁻¹. In blue, the computed spectrum presents the harmonic vibrations, which fairly reproduce the strongest experimental features. There is, however, a slight overall blue shift of the computed frequencies, in addition to an apparent compression of the bands into a narrower wavelength range. The modes at 3.23 and 3.26 μm are composed of two almost degenerate vibrations, which cannot be distinguished within the experimental bandwidth. As expected, the modes seen at 3.23, 3.26, 3.27, and 3.30 μm are all due to C–H stretches, which split into distinct vibrations given the lower symmetry of xanthene with respect to a fully aromatic PAH. In addition, the modes at 3.42 and 3.47 μm correspond to the symmetric and asymmetric C–H stretches involving the two out-of-plane H atoms in xanthene (see Fig. 1). We note that although the harmonic calculations provide a good match with the experiment, the latter has many unexplained features, which is not surprising given the known role anharmonicities can play in the C–H stretch region in PAHs.^38,39 This is addressed by also computing overtones or combination bands, shown in red in Fig. 2. While anharmonic features are seen around the 3.3 μm region, these vibrations are predicted with very low intensity, in contrast to the range around 3.4 μm, where two combination bands are clearly significant and help explaining the experimental 3.43 μm band.

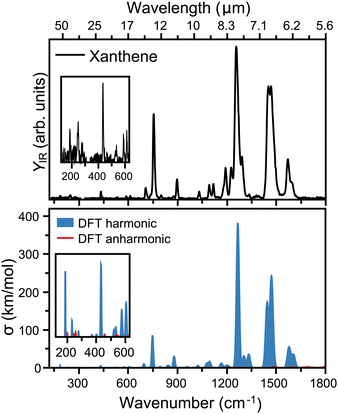
The top panel of Fig. 3 presents the infrared spectrum of xanthene in the far-infrared range, from 120 to 1800 cm⁻¹. Here, the most pronounced bands are seen at 6.38, 6.87, 7.97, 11.17 and 13.3 μm, falling into the ranges where the broad features in the AIBs are observed.¹⁴ Besides these bands, many other features are seen in the experiment, although of weaker intensity. Deep into the far-infrared, the experiment is sensitive enough to distinguish modes at long wavelengths, namely 16.37, 17.04, 23.09, 40.49, and 54.05 μm, which can be instrumental to differentiate xanthene from other PAHs. A comparison with harmonic DFT calculations, shown in the bottom panel of Fig. 3, provides a very good match with the experiment. In this case, the vibrational frequencies are convoluted with Gaussian functions having a wavelength-dependent FWHM (2% of the central wavelength), mimicking the linewidth of FELIX. As seen from the figure, most features are reproduced. We also note that anharmonic bands are presented in the figure, but while many are predicted in this spectral range, they all have very low infrared intensity. Of the most pronounced features, the bands at 6.38 and 6.87 μm (each composed by two close modes) correspond to in-plane C–C stretching modes, whereas the strongest band at 7.97 μm involves an in-plane bending of the O atom. Moreover, the band at 11.17 μm is a combination of C–C scissoring modes, and the 13.3 μm a C–H out-of-plane bending. Finally, the far-infrared modes involve variations of out-of-plane displacements of the entire structure of xanthene.

Fig. 3 Top: Infrared spectrum of neutral xanthene recorded in the 120 to 1800 cm⁻¹ range, using the infrared free electron laser FELIX. The top axis presents the corresponding range in wavelength. Bottom: DFT calculated vibrational spectrum of xanthene, with harmonic computations in blue and combination bands and overtones in red. For visualization purposes, Gaussian functions are built around each vibration with a FWHM corresponding to a 2% of the central wavenumber, mimicking the wavelength-dependent linewidth of FELIX.

4.2 Broadband rotational spectroscopy of xanthene

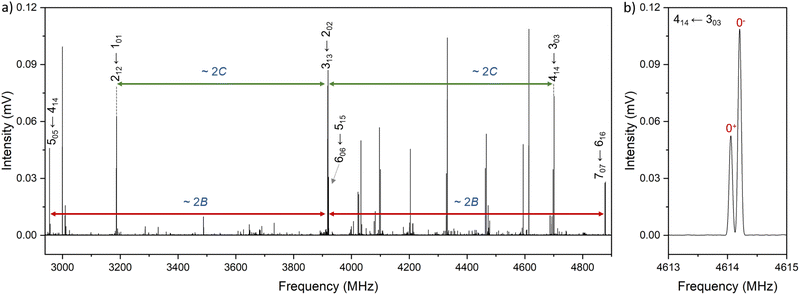
Xanthene exhibits characteristics of a near-prolate asymmetric top, with a value of the Ray's parameter κ calculated to be approximately −0.9. Owing to its symmetry with respect to the bc plane and its almost planar geometry, xanthene only possesses a measurable component of the dipole moment along the b principal axis. Therefore, the assignment of the rotational spectrum began by searching for R-branch b-type transitions within the series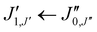 and 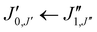which, due to the high symmetry of xanthene, are expected to be separated by ∼2B and ∼2C and to be among the most intense lines in the spectrum. A small section of the rotational spectrum recorded in the 2–8 GHz frequency range is depicted in Fig. 4.

Fig. 4 (a) Section of the rotational spectrum of xanthene recorded in the 2–8 GHz frequency range, displaying the typical spectral pattern observed for b-type transitions of a near-prolate asymmetric top. Transitions have been marked using the J_Ka,Kc notation, where J is the quantum number representing the total angular momentum, and K_a and K_c represent the projections of the angular momentum onto the a and c axes in the limiting case of prolate and oblate symmetric tops, respectively. (b) Highlight of the transition 4_1,4 ← 3_0,3 revealing the tunneling splitting caused by the butterfly-like motion. The two components of the tunneling splitting have been marked using the notation 0⁺ and 0⁻.

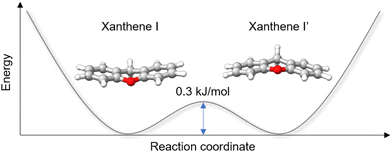
While analysing the rotational spectrum, we observed a splitting of the rotational transitions assigned to xanthene into two components. This splitting is assumed to be generated by a tunneling motion, which involves an out-of-plane bending motion of the two peripheral rings and connects two equivalent configurations of xanthene, as shown in Fig. 5. Despite the heavy mass of the motion, which would typically slow down the tunneling dynamics and thus cause small to negligible splittings, the small tunneling distance and the low barrier to the motion (0.3 kJ mol⁻¹ at the B3LYP-D3BJ/def2-TZVP level of theory) produce measurable splittings of the rotational transitions. The two tunneling components show a statistical weight of ∼3 : 1, which is known to be the typical intensity ratio generated by the inversion of equivalent hydrogen atoms. The butterfly-like motion observed in xanthene indeed leads to an inversion of the two equivalent hydrogen atoms of the –CH₂ group. The rotational spectrum was fitted using the S-reduction of the Watson's Hamiltonian in the I^r representation and using SPFIT/SPCAT implemented in Pickett's program.^40,41 The two sets of rotational constants obtained for the two tunneling states (0⁺ and 0⁻) are reported in Table 1.

Fig. 5 Schematic double-well potential energy curve describing the butterfly-like tunneling motion of xanthene. The pathway was simulated using the NEB method, and the energy barrier was calculated at the B3LYP-D3BJ/def2-TZVP level of theory.

Table 1 Experimental and theoretical spectroscopic constants (B3LYP-D3BJ/def2-TZVP) of xanthene

Parameters	Units	Theo.	Exp. (0^+)	Exp. (0^−)
a Total number (N) of lines in the fit. b Root-mean-square deviation of the fit, .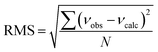
A	MHz	2065.0	2031.0404(12)	2032.1108(11)
B	MHz	464.9	466.05932(60)	465.95043(44)
C	MHz	384.0	385.25282(60)	385.12537(40)
D J	kHz		0.1180(49)	0.0192(29)
D JK	kHz		−0.258(23)	−0.298(18)
D K	kHz		1.17(15)	1.38(14)
|μa|, |μb|, |μc|	D	0, 1.0, 0.1	n, y, n
N			68
RMS^b	kHz		7.3

---

The signal-to-noise ratio of the rotational spectrum enabled the detection of all the singly substituted ¹³C isotopologues in natural abundance (1.1%). Due to the C_s symmetry of xanthene, all the C atoms, except the one associated with the –CH₂ group, are symmetrically equivalent in pairs. Therefore, the assignment of most of the isotopologues was facilitated by the doubling in intensity of their rotational spectra. A splitting of the rotational transitions into two components due to tunneling was also observed in the rotational spectra of the ¹³C isotopologues. This showed that the symmetry of the tunneling motion is not altered upon isotopic substitution and further confirmed the nature of the motion. The rotational spectra of the ¹³C isotopologues were fitted using the same Hamiltonian as for the parent species. The derived rotational spectroscopic parameters and the measured rotational transition frequencies are reported in the ESI.†

The availability of the experimental rotational constants of the parents and all the singly-substituted ¹³C isotopologues allowed for the determination of the experimental structure of xanthene. We used the Kraitchman's method,⁴² which exploits the changes in the moment of inertia upon isotopic substitution, to calculate the absolute values of the experimental coordinates for each substituted carbon atom (r_s structure) using the program KRA.⁴¹ Since this method only yields the coordinates in their absolute values, signs were taken from the equilibrium structure (r_e) calculated at the B3LYP-D3BJ/def2-TZVP level of theory. An overlay between the r_s and the r_e structures of xanthene is depicted in Fig. 6 and shows a very good agreement between the two structures. A table with the r_s and the r_e geometrical parameters is provided in the ESI.† Using dummy atoms derived from the experimental structure, the angle between the two planes formed by the lateral rings of xanthene was calculated to be ∼161°, thus reflecting the non-planarity of the molecule (Fig. 6).

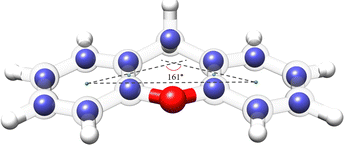Fig. 6 Overlay between the r_s and the r_e structures for the xanthene monomer calculated at the B3LYP-D3BJ/def2-TZVP level of theory. The blue spheres represent the carbon positions determined using the Kraitchman's equations (r_s), whereas the semi-transparent structure represents the theoretical structure (r_e) of xanthene. Rendered using UCSF ChimeraX software.¹⁶

4.3 Broadband rotational spectroscopy of xanthene–(H₂O)_n=1–4

The rotational spectrum of xanthene–(H₂O)_n=1–4 complexes was recorded across the 2–8 GHz frequency range. After isolating the rotational fingerprint of the monomer of xanthene from the spectrum, we distinguished over 1200 lines with a signal-to-noise ratio exceeding 2 : 1, predominantly arising from complexes of xanthene with a varying number of water molecules.

A distinct set of intense transitions exhibiting a typical b-type spectral pattern was immediately identified. Fitting these rotational transitions yielded a set of rotational constants which, with the aid of quantum chemical calculations, was assigned to the lowest-energy isomer of monohydrated xanthene (1w-I). The assignment was further confirmed by the observation of c-type transitions which could be fitted to the same set of rotational constants. Interestingly, a splitting of the c-type transitions into two components was observed. This splitting could be addressed in the fit as interstate transitions, indicating that the tunnelling motion causes an inversion of the electric dipole moment component along the c inertial axis. Interstate transitions occur between tunneling states of different symmetry, thus allowing for the determination of the difference in energy (ΔE) between the two tunneling states (0⁺ and 0⁻). For the 1w-I complex, this energy difference was determined to be 30.7(33) kHz. This tunneling splitting was attributed to a concerted motion, as a simple flip of the water's dangling hydrogen atom above and below the backbone of xanthene would not result in an equivalent configuration of the complex unless it is accompanied by a structural rearrangement of xanthene. The possible tunneling pathways are described later in the text.

Complexation of xanthene with one water molecule preserves the equivalence between the carbon atoms. This facilitated the observation of singly substituted ¹³C isotopologues in natural abundance, enabling the determination of the experimental structure of the carbon backbone of xanthene in the monohydrated complex. The derived spectroscopic parameters, Kraitchman's coordinates, and measured rotational transition frequencies are reported in the ESI.†

Once the rotational transitions arising from the 1w-I complex and its ¹³C isotopologues were removed from the spectrum, a series of weaker a- and b-type transitions was identified and fitted to a new set of rotational constants, which was assigned to one isomer of xanthene–(H₂O)₂ (2w-III). A closer inspection of the rotational spectrum further enabled the identification of two additional distinct sets of weak c- and b-type transitions, which were identified as the lowest energy conformer of xanthene–(H₂O)₃ (3w-I) and xanthene–(H₂O)₄ (4w-II), respectively. Portions of the experimental spectrum depicting the assignment of the four hydrates of xanthene are provided in the ESI.† The rotational spectra of all identified species were fitted using the A-reduction Watson's Hamiltonian in the I^r representation. The resulting spectroscopic parameters are listed in Table 2, whereas the structures of the identified hydrates are shown in Fig. 7.

Table 2 Experimental and theoretical spectroscopic constants of xanthene–(H₂O)_n=1–4 complexes

Parameters	1w-I			2w-III		3w-I		4w-II
	Theo.^d	Exp. (0^+)	Exp. (0^−)	Theo.	Exp.	Theo.	Exp.	Theo.	Exp.
a Difference in vibrational energy between the two tunneling states 0^+ and 0^−. b Total number (N) of lines in the fit. c Root-mean-square deviation of the fit, 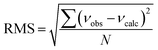. d Theoretical rotational constants and dipole moments calculated at the B3LYP-D4/def2-QZVP level of theory.
A (MHz)	934.2	913.47933(40)	913.47799(39)	625.7	610.66041(75)	690.8	668.50669(85)	569.3	558.1509(10)
B (MHz)	465.8	464.72502(26)	464.72511(26)	406.1	404.52319(18)	356.4	359.35148(40)	317.3	314.64302(37)
C (MHz)	318.4	317.02978(23)	317.02945(25)	255.6	255.01107(21)	319.4	313.21931(45)	289.7	286.93462(51)
Δ J (kHz)		0.0101(43)	0.0152(43)		0.0150(10)		0.0530(25)
Δ JK (kHz)		0.622(26)	0.588(26)		0.0832(76)		0.176(13)
Δ K (kHz)		−0.391(32)	−0.409(32)		0.126(27)				0.136(24)
δ K (kHz)		0.283(43)	0.359(43)						1.682(98)
ΔE^a (MHz)		0.0307(33)
|μa| (D)	0	n		2.3	y	0.3	n	0.1	n
|μb| (D)	2.6	y		1.2	y	0.8	n	2.7	y
|μc| (D)	1.3	y		0.7	y	1.7	y	2.4	y
N		436			107		49		44
RMS^c (kHz)		7.3			9.0		10.6		10.6

---

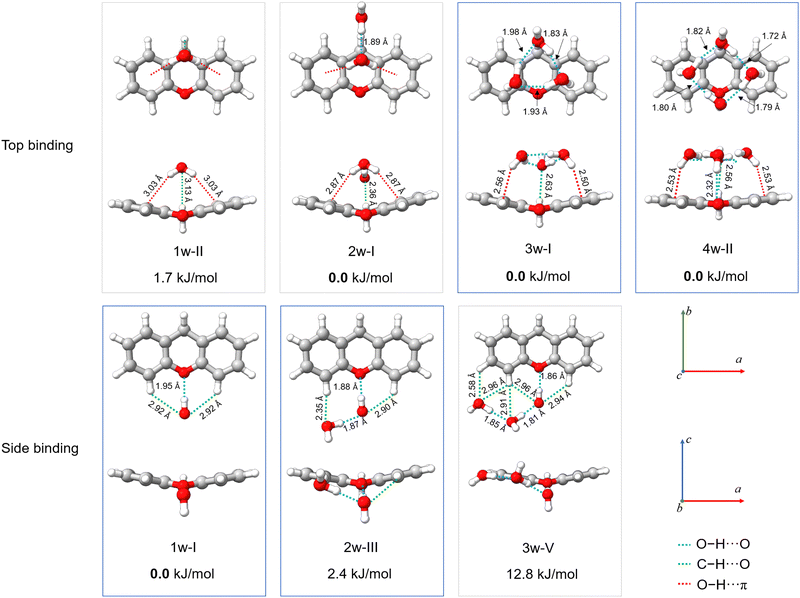Fig. 7 Theoretical structures of xanthene–(H₂O)_n=1–4 complexes, calculated at the B3LYP-D4/def2-QZVP level of theory, showcasing the lowest-energy top-binding and side-binding configurations predicted for each cluster size. Projections onto the ab and ac planes and relative energies are provided. The relevant O–H⋯O, C–H⋯O, and O–H⋯π interactions are highlighted with blue, green, and red dashed lines, respectively. The structures of the observed xanthene–(H₂O)_{n= 1−4} complexes are indicated with blue boxes. Rendered using UCSF ChimeraX software.¹⁶

The structures of all xanthene–water complexes are stabilized through the interplay of various intermolecular hydrogen bond interactions. In the monohydrated complex, the water molecule interacts with xanthene by forming a moderate O–H⋯O (1.94 Å) interaction with xanthene's oxygen atom in a side binding motif. The stability of the complex is then reinforced by van der Waals interactions of C–H⋯O type established between the free lone pairs of the water's oxygen atom and the nearest aromatic hydrogen atoms of xanthene. As mentioned earlier, the c-type transitions observed in the rotational spectrum of the 1w-I complex exhibit tunneling splitting. The nature of the tunneling motion was investigated using the climbing image nudge elastic band (CI-NEB) method.⁴³ This method is useful to find minimum energy pathways connecting two equivalent geometries. We have identified two nearly isoenergetic tunneling pathways, both describing a concerted motion. The first pathway involves a simple flip of the water's dangling hydrogen atom above and below xanthene's backbone, while xanthene undergoes a butterfly-like motion to tunnel between its two equivalent geometries. The second pathway also involves the butterfly-like motion of xanthene, but here, the water molecule exhibits a swinging motion with respect to the xanthene plane, resulting in a swap of the water's hydrogen atom involved in the O–H⋯O interaction. The energy barrier connecting the two equivalent minima in each motion is calculated to be 3.7 kJ mol⁻¹ and 3.3 kJ mol⁻¹ at the DLPNO-CCSD(T)/cc-pVTZ//B3LYP-D3(BJ)/def2-TZVP level of theory,⁴⁴ respectively. An illustration of the two tunneling pathways is provided in the ESI† (Fig. S6). Considering the energetics, both pathways are possible.

Tunnelling is not observed anymore for increased hydration. The addition of a second water molecule indeed reduces the mobility of the water's hydrogen atoms in addition to breaking the symmetry of the complex. In the 2w-III complex, xanthene's oxygen atom is still the binding site of choice, since the O–H⋯O interaction between one of the two water molecules and xanthene is preserved. The second water molecule forms a hydrogen bond with the first water molecule and anchors to xanthene through a C–H⋯O interaction with the proximate hydrogen atom of xanthene. The O–H⋯O_xanthene distance decreases from 1.94 Å in 1w-I to 1.88 Å in 2w-III, which can be ascribed to the cooperativity effects.⁴⁵

The 2w-III complex is predicted to be the third lowest energy conformer on the potential energy surface of xanthene–(H₂O)₂, lying 2.4 kJ mol⁻¹ higher in energy compared to the global minimum (2w-I). Observation of the first (2w-I) and second (2w-II) lowest-energy conformers was likely hindered by their weak dipole moment components along all three principal axes (Table S6, ESI†). Interestingly, 2w-I features a top binding motif of the water dimer, which interacts with the substrate via O–H⋯π interactions (Fig. 7), while intermolecular interactions with xanthene's oxygen atom are no longer established, as also highlighted by the non-covalent interactions (NCI) plots showcased in Fig. S13 of the ESI.† The higher stability of 2w-I and 2w-II compared to the experimentally observed 2w-III is also in agreement with their binding energies, calculated to be −34 kJ mol⁻¹, −33.7 kJ mol⁻¹, and −31.7 kJ mol⁻¹ at the B3LYP-D4/def2-QZVP level of theory for 2w-I, 2w-II, and 2w-III complexes, respectively.

While we did not probe the 2w-I and 2w-II complexes in the supersonic jet, the structure of the observed xanthene–(H₂O)₃ complex (3w-I) points towards their potential formation. The structure of the 3w-I complex features the water trimer in a top-binding configuration, anchoring to xanthene by forming a network of O–H⋯π and C–H⋯O interactions (Fig. 7). Unlike in the observed mono- and dihydrate complexes, the oxygen atom of xanthene is no longer a preferred binding site for the water molecules. A similar topology of the hydrogen bond network is also revealed in the structure of the observed xanthene–(H₂O)₄ complex (4w-II), where a top-binding motif is preserved. The addition of a fourth water molecule introduces an O–H⋯O interaction with xanthene's oxygen atom. However, the O–H⋯O distance is measured to be 2.32 Å, which corresponds to a weak O–H⋯O hydrogen bond.⁴⁶ This suggests that, as the degree of hydration increases, the oxygen atom in the carbon skeleton of xanthene may not act as the water's binding site of choice anymore.

The assignment of the xanthene–(H₂O)₄ complex based on a comparison between theoretical and experimental rotational constants was not straightforward. The computational study of the potential energy landscape yielded two nearly isoenergetic isomers of the xanthene–(H₂O)₄ complex. These isomers primarily differ in the orientation of the hydrogen bond network established within the water tetramer – clockwise or counterclockwise – and in the orientation of the dangling hydrogen atoms of the two water molecules lying on the b inertial axis, up–up and up–down, respectively (Fig. S10, ESI†). Due to the similarities in their structures, the two isomers exhibit closely matched rotational constants (Table S10, ESI†). Nevertheless, the different orientation of the dangling hydrogen atoms results in a significant difference in the magnitude of the dipole moment components along the b and c inertial axes, calculated to be 0.4 D and 0.9 D in the up–up configuration and 2.7 D and 2.4 D in the up–down configuration, respectively. We observe that the respective line intensities are better reproduced if values of 2.7 D and 2.4 D are considered for the μ_b and μ_c dipole moment components, respectively. This enabled a definitive assignment of the observed tetrahydrate to the 4w-II isomer.

An analysis of the evolution in the hydration shell of xanthene suggests that self-aggregation of the water molecules likely dominates the formation of the observed clusters. Indeed, the hydrogen bond network established within the water molecules closely resembles those typically found in pure water clusters, particularly in the 3w-I and 4w-II complexes. Furthermore, a look at the projection of the observed hydrates onto the ac plane in Fig. 7 indicates a change in the planarity of xanthene based on the degree of hydration: from 159° in the monomer and monohydrate (1w-I), to 152° in the dihydrate (2w-III), and further to 162° and 170° in the trihydrate (3w-I) and tetrahydrate (4w-II), respectively, revealing a structural flexibility of xanthene to maximize the interactions with the water clusters.

Exploration of the potential energy landscape reveals two main water binding motifs: a side-binding motif, in which xanthene's oxygen atom serves as a hydrogen-atom acceptor as the preferred binding site for water, and a top-binding motif, in which the water cluster primarily interacts with xanthene through O–H⋯π interactions with the aromatic π cloud of the two peripheral benzene rings of xanthene (Fig. 7). Previously, we explored phenanthridine,¹⁹ a planar PAH with a nitrogen atom functioning as a hydrogen acceptor. That study revealed that the side-binding motif is more favorable for phenanthridine when aggregated with up to three water molecules. In the case of xanthene, the two binding motifs are comparable in energy for its xanthene–(H₂O)_1,2 complexes, where the energy differences between them are predicted to be less than 2.5 kJ mol⁻¹. In the supersonic jet, both arrangements are likely to coexist. However, a net preference for the top-binding motif is predicted with increasing number of water molecules. With respect to the xanthene–(H₂O)₃ complex, the top-binding becomes 12.8 kJ mol⁻¹ more stable than its side-binding counterpart, while for the xanthene–(H₂O)₄ complex, no side-binding isomer was predicted within 25 kJ mol⁻¹. This clearly shows that the structural morphology of the PAH, mainly in terms of planarity, has a substantial influence on the aggregation mode of water molecules.

As the number of water molecules increases, xanthene exhibits a behaviour more akin to a pure hydrocarbon. A similar interaction network between water and a PAH molecule has been observed in water complexes of other PAHs such as phenanthrene and acenaphthene.^18,19 Specifically, when comparing the structures of their trihydrates a striking similarity emerges. They all feature the water trimer predominantly anchoring to the PAH via interactions with its aromatic cloud and oriented in a way that allows the water moiety to best take advantage of anchoring points on the PAH. These qualitative observations suggest that water effectively exploits the structure of the PAH to facilitate these interactions.

5 Conclusions

We have performed an exhaustive gas-phase spectroscopic investigation of the OPAH xanthene using IR-UV ion dip spectroscopy and chirped-pulse Fourier transform microwave spectroscopy. The combination of both techniques can aid its identification in the interstellar medium via infrared spectroscopy or radio astronomy. The infrared spectrum of xanthene exhibits many features between 6 and 16 μm, as well as weak ones at 3.42, 3.43, and 3.47 μm, which have previously been suggested to partly originate from PAHs containing sp³ hybridized carbon atoms. In xanthene, these bands are attributed to vibrational modes involving the hydrogen atoms of the –CH₂ group, therefore, corroborating this hypothesis further. The microwave spectrum of xanthene exhibits tunneling splitting originating from an out-of-plane bending motion of the two lateral benzene rings of xanthene. The nature of the tunneling motion was experimentally confirmed by the observation of the tunneling splitting in the spectrum of its singly-substituted ¹³C isotopologues.

The microwave investigation of xanthene was successfully expanded to its complexes with up to four water molecules. Water molecules can arrange on xanthene in a side-binding motif by primarily establishing O–H⋯O interactions or in a top-binding configuration by anchoring the substrate via O–H⋯π interactions. The two geometries are found to compete in the complexes with up to two water molecules, while a clear preference for the top-binding motif is observed as the number of interacting water molecules increases. This result suggests that, despite the presence of a polar group within the carbon skeleton of xanthene, its overall shape ultimately defines the binding sites of choice. Furthermore, in all observed xanthene–water complexes, and in particular in the trihydrate and tetrahydrate, the structure of the pure water clusters is mostly retained, whereas the degree of planarity of xanthene changes based on the number of water molecules to accommodate, thus suggesting that it is the OPAH xanthene to rearrange to increase the stability of the clusters and not the opposite. Overall, in addition to the possibility of identifying xanthene in interstellar environments, these results lay the foundation for a better understanding of water aggregation processes around an OPAH.

Data availability

The data supporting this article have been included as part of the ESI.† Further details can be requested to the corresponding authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

DL acknowledges the support of an Alexander von Humboldt postdoctoral fellowship. Theoretical calculations were performed by using the European XFEL and DESY funded Maxwell computational resources operated at Deutsches Elektronen-Synchrotron DESY, Hamburg, Germany. Scientific exchange within the Centre for Molecular Water Science (CMWS) is acknowledged. The research leading to the IR spectroscopy results has received funding from LASERLAB-EUROPE (grant agreement no. 871124, European Union's Horizon 2020 research and innovation programme). We gratefully acknowledge the support of Radboud University and of the Nederlandse Organisatie voor Wetenschappelijk Onder-zoek (NWO) for supporting the operation of the FELIX Laboratory, as well as the skillful assistance of the FELIX staff.

Notes and references

1. A. G. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337.
2. F. Galliano, S. C. Madden, A. G. Tielens, E. Peeters and A. P. Jones, Asian Pac. J., 2008, 679, 310.
3. C. S. Hansen, E. Peeters, J. Cami and T. W. Schmidt, Commun. Chem., 2022, 5, 94.
4. B. A. McGuire, R. A. Loomis, A. M. Burkhardt, K. L. K. Lee, C. N. Shingledecker, S. B. Charnley, I. R. Cooke, M. A. Cordiner, E. Herbst, S. Kalenskii and J. Tielens, et al. , Science, 2021, 371, 1265–1269.
5. J. Cernicharo, M. Agúndez, C. Cabezas, B. Tercero, N. Marcelino, J. R. Pardo and P. De Vicente, Astron. Astrophys., 2021, 649, L15.
6. M. L. Sita, P. B. Changala, C. Xue, A. M. Burkhardt, C. N. Shingledecker, K. L. K. Lee, R. A. Loomis, E. Momjian, M. A. Siebert and D. Gupta, et al. , Astrophys. J., Lett., 2022, 938, L12.
7. A. M. Burkhardt, K. L. K. Lee, P. B. Changala, C. N. Shingledecker, I. R. Cooke, R. A. Loomis, H. Wei, S. B. Charnley, E. Herbst and M. C. McCarthy, et al. , Astrophys. J., Lett., 2021, 913, L18.
8. E. Peeters, S. Hony, C. Van Kerckhoven, A. G. G. M. Tielens, L. J. Allamandola, D. M. Hudgins and C. W. Bauschlicher, Astron. Astrophys., 2002, 390, 1089–1113.
9. M. P. Bernstein, S. A. Sandford, L. J. Allamandola, J. S. Gillette, S. J. Clemett and R. N. Zare, Science, 1999, 283, 1135–1138.
10. A. De Barros, A. Mattioda, A. Ricca, G. Cruz-Diaz and L. Allamandola, Asian Pac. J., 2017, 848, 112.
11. J. Bouwman, H. Cuppen, M. Steglich, L. Allamandola and H. Linnartz, Astron. Astrophys., 2011, 529, 2035.
12. J. A. Noble, C. Jouvet, C. Aupetit, A. Moudens and J. Mascetti, Astron. Astrophys., 2017, 599, A124.
13. J. Noble, E. Michoulier, C. Aupetit and J. Mascetti, Astron. Astrophys., 2020, 644, A22.
14. R. Chown, A. Sidhu, E. Peeters, A. G. Tielens, J. Cami, O. Berné, E. Habart, F. Alarcón, A. Canin and I. Schroetter, et al. , Astron. Astrophys., 2024, 685, A75.
15. S. Cazaux, Y. Arribard, D. Egorov, J. Palotás, R. Hoekstra, G. Berden, J. Oomens and T. Schlathölter, Asian Pac. J., 2019, 875, 27.
16. E. C. Meng, T. D. Goddard, E. F. Pettersen, G. S. Couch, Z. J. Pearson, J. H. Morris and T. E. Ferrin, Prot. Sci., 2023, 32, e4792.
17. C. Pérez, A. L. Steber, A. M. Rijs, B. Temelso, G. C. Shields, J. C. Lopez, Z. Kisiel and M. Schnell, Phys. Chem. Chem. Phys., 2017, 19, 14214–14223.
18. A. L. Steber, C. Pérez, B. Temelso, G. C. Shields, A. M. Rijs, B. H. Pate, Z. Kisiel and M. Schnell, J. Phys. Chem. Lett., 2017, 8, 5744–5750.
19. D. Loru, A. L. Steber, P. Pinacho, S. Gruet, B. Temelso, A. M. Rijs, C. Pérez and M. Schnell, Phys. Chem. Chem. Phys., 2021, 23, 9721–9732.
20. D. Loru, A. L. Steber, C. Pérez, D. A. Obenchain, B. Temelso, J. C. López and M. Schnell, J. Appl. Chem. Sci., 2023, 145, 17201–17210.
21. D. Schmitz, V. A. Shubert, T. Betz and M. Schnell, J. Mol. Spectrosc., 2012, 280, 77–84.
22. C. Perez, A. Krin, A. L. Steber, J. C. Lopez, Z. Kisiel and M. Schnell, J. Phys. Chem. Lett., 2016, 7, 154–160.
23. V. J. Esposito, P. Ferrari, W. J. Buma, C. Boersma, C. J. Mackie, A. Candian, R. C. Fortenberry and A. G. Tielens, Mol. Phys., 2023, 122, e2261570.
24. A. M. Rijs and J. Oomens, Gas-phase IR spectroscopy and structure of biological molecules, Springer, 2015, vol. 364.
25. P. Ferrari, S. Lemmens and B. Redlich, Phys. Chem. Chem. Phys., 2024, 26, 12324–12330.
26. V. Yatsyna, D. J. Bakker, P. Salén, R. Feifel, A. M. Rijs and V. Zhaunerchyk, Phys. Rev. Lett., 2016, 117, 118101.
27. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
28. A. D. Becke, J. Chem. Phys., 1992, 96, 2155–2160.
29. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
30. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
31. D. S. Tikhonov, I. Gordiy, D. A. Iakovlev, A. A. Gorislav, M. A. Kalinin, S. A. Nikolenko, K. M. Malaskeevich, K. Yureva, N. A. Matsokin and M. Schnell, ChemPhysChem, 2024, e202400547.
32. V. Ásgeirsson, B. O. Birgisson, R. Bjornsson, U. Becker, F. Neese, C. Riplinger and H. Jónsson, J. Chem. Theory Comput., 2021, 17, 4929–4945.
33. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
34. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
35. E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122.
36. A. Lemmens, A. Rijs and W. Buma, Asian Pac. J., 2021, 923, 238.
37. P. Pla, Y. Wang, F. Martn and M. Alcami, Asian Pac. J., 2020, 899, 18.
38. V. J. Esposito, L. J. Allamandola, C. Boersma, J. D. Bregman, R. C. Fortenberry, A. Maragkoudakis and P. Temi, Mol. Phys., 2024, 122, e2252936.
39. C. J. Mackie, A. Candian, X. Huang, E. Maltseva, A. Petrignani, J. Oomens, W. J. Buma, T. J. Lee and A. G. Tielens, J. Chem. Phys., 2015, 143, 224314.
40. H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371–377.
41. Z. Kisiel, PROSPE-Programs for ROtational SPEctroscopy, https://info.ifpan.edu.pl/kisiel/prospe.htm (accessed: 09.07.2024).
42. J. Kraitchman, Am. J. Phys., 1953, 21, 17–24.
43. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
44. C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106.
45. C. Pérez, D. P. Zaleski, N. A. Seifert, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Angew. Chem., Int. Ed., 2014, 53, 14368–14372.
46. G. A. Jeffrey and G. A. Jeffrey, An introduction to hydrogen bonding, Oxford university press, New York, 1997, vol. 12.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03030c

---