Metal substrate engineering to modulate CO₂ hydrogenation to methanol on inverse Zr₃O₆/CuPd catalysts

Abstract

It is well known that the performance of some key catalytic reactions has a strong dependence on metal catalyst surfaces. In the current work, this concept is further extended to the CuPd alloy-supported zirconium oxide inverse catalyst for CO₂ hydrogenation to methanol. A combined DFT and microkinetic simulation study reveal that both the metal substrate surface and the precise exposed Cu or Pd metal atoms on the substrate have a pivotal influence on the catalytic mechanism and performance of the inverse catalyst for CO₂ hydrogenation to methanol. Herein, CuPd(100), (111), and (110) surfaces with either Cu and Pd terminations have been examined, which provided five metal substrates as support for the inverse catalyst. Three different mechanisms, including the formate pathway, RWGS + CO-hydro pathway, and CO₂ direct activation pathway, are explored under the same conditions; they take place at the interfacial sites between the metal alloy and oxide. The calculations indicated that the inverse catalyst with the CuPd(100) substrate demonstrates better performance than those with CuPd(110) and (111) for both formate and RWGS + CO-hydro mechanisms. Conversely, the reaction pathway is more sensitive to exposed atoms on the metal substrate. The best inverse catalyst, Zr₃O₆/CuPd(100) with either Cu or Pd terminations, demonstrated a methanol formation TOF above 0.30 site⁻¹ s⁻¹ and the selectivity was above 90% at 573 K, as evaluated from microkinetic simulation. The coverage analysis indicates the most populated species is HCOO*, which is consistent with experimental reports. Both kinetic and thermodynamics control steps are identified from DRC analysis for the best performing catalysts. Overall, the current study confirms the catalytic performance of the inverse Zr₃O₆/CuPd catalyst and demonstrates the tunable effects of the metal alloy substrate, which can facilitate effective optimization.

---

1. Inroduction

The combustion of fossil fuels over the past decades has led to the excessive emission of carbon dioxide. Consequently, the ever-increasing CO₂ concentration in the atmosphere has resulted in severe adverse effects, including the greenhouse effect, rising sea levels and ocean acidification.^1,2 A global consensus was attained to strictly control CO₂ emissions before the occurrence of any irreversible environmental damage. The carbon capture and utilization (CCU) technology, converting CO₂ to value-added chemicals through thermocatalytic, electrocatalytic^3,4 and photocatalytic^5,6 processes, is a very promising economical-viable strategy to reduce CO₂ and maintain sustainable developments.^7,8 However, it is well known that the CO₂ molecule is extremely stable thermodynamically. Furthermore, CO₂ activation is not a trivial task. Among various CO₂ catalytic conversion routes, the hydrogenation of CO₂ with the assistance of H₂ can generate many valuable chemicals, including methane,^9,10 formic acid,^11–13 alkene,¹⁴ and methanol^1,2,15–19 under mild conditions. Moreover, H₂ can be produced from a green and renewable energy source. Among various products of CO₂ hydrogenation, methanol stands out due to its distinctive benefits, including ease of transportation and storage, and high volumetric energy density.²⁰ It has also been suggested that the so-called “methanol economy” could potentially change the energy supply landscape.^20,21 Therefore, it is not surprising that extensive efforts have been devoted to developing an edge catalyst and technology for the catalytic carbon dioxide hydrogenation to methanol.

Cu/ZnO/Al₂O₃ catalysts are industrially employed in methanol synthesis for syngas feeding due to their good activity and affordability, although their activity is greatly decreased with high CO₂ concentrations.²² To address this issue, several strategies to improve the Cu-based catalysts for CO₂ hydrogenation to methanol were investigated. The alloying of a second metal with Cu is one effective method to adjust the CO₂ hydrogenation activity, and has been widely applied in methanol synthesis (e.g., CuPd,^23,24 CuNi,²⁵ CuZn,²⁶ PdZn^27,28). It should be noted that an appropriate chosen support for these metal alloy catalysts is vital for the catalytic performance. Among various oxide supports, ZrO₂ is considered to be one of the best options, particularly for the Cu catalyst, because of its basicity, weak hydrophilicity, and increased methanol formation rates. In addition to playing a role as an inert support and spectator in the reaction, ZrO₂ also actively participates in hydrogenation. It is generally accepted that the interface between ZrO₂ and the metal is the active site for CO₂ hydrogenation to methanol.^29,30 As a further extension from the conventional metal/oxide architecture, Wu et al.³¹ developed a superior active inverse catalyst, in which Cu and ZrO₂ switched their roles as the active material and support, respectively, and applied this inverse catalyst in the CO₂ hydrogenation to methanol. Therefore, an inverse catalyst is an architecture that uses metal oxide as the active material and metal as the support. They found that the inverse catalyst delivered a methanol formation rate that was 3.3 times greater than that of the conventional counterpart at 220 °C. The spectacular activity increase is attributed to the fast hydrogenation of the key elementary steps of formate to methoxy, and methoxy to methanol, as observed from operando DRIFTS measurements. Moreover, the unique adsorption configuration of CO₂, COO*–Cu, induced an adsorption-driven mechanism that is absent in the conventional metal/oxide catalyst. Senanayake et al.³² explored the relationship between the methanol formation rate and coverage of oxide on a metal support for the inverse CeO_x/Cu(111) catalyst. It was found that there is a volcano curve of activity, together with increasing oxide coverage, while the fully covered or empty metal surfaces possessed the lowest activity. This suggested that the interface between the oxide and metal is responsible for the observed catalytic performance. Consistent with this rationale, the exposed facets of the metal support, as a part of the oxide–metal interface, considerably affect the catalytic performance. For example, the methanol production rate of ZnO/Cu(100) is almost twice that of ZnO/Cu(111).³³ The barrier of the rate-limiting step of the bridge formate hydrogenation on inverse ZrO₂/Cu(111) is two times greater than the counterparts on Cu(100) and Cu(110).³⁴ The inverse catalyst showed distinct features from the traditionally accepted mechanism. From a combined density functional theory (DFT) and kinetic Monte Carlo (kMC) simulation, Kattel et al.¹⁹ suggested that CO₂ hydrogenation to methanol on Zr₃O₆H₆/Cu(111) preferred a RWGS + CO-hydro pathway over the conventional formate pathway due to the strong CO adsorption at the interfacial sites.

Overall, the exceptional performance of an inverse catalyst in CO₂ hydrogenation to methanol has been clearly demonstrated,^15,31,33 and the properties of the interfacial sites between oxide and metal are crucial to the catalytic activity. However, the origin of the significant improvements from the inverse catalyst over the conventional counterpart still remains elusive, particularly in consideration of the pronounced consequence induced by simply exchanging the metal and oxide. To solve this enigma, a DFT-based microkinetic simulation was performed to reveal and understand the reaction pathway and mechanism of CO₂ hydrogenation to methanol catalyzed by an inverse catalyst, Zr₃O₆/CuPd. The chosen bimetal alloy provides more options to modulate the properties of the interfacial sites, which serve to establish a structure–performance relationship, and potentially break the linear scaling relation associated with the single metal case. The supported CuPd bimetallic catalyst has been reported to have excellent activity in CO₂ hydrogenation to methanol.²³ However, the corresponding inverse counterpart or other oxide/bimetallic catalysts have not been explored to the best of our knowledge. Three facets of the CuPd alloy, including (100), (110), and (111), are chosen to construct the interfacial configurations with the Zr₃O₆ cluster. The adsorption and activation of CO₂ at the interfacial sites are carefully examined to reveal the origin of the activity. Three different pathways are examined and evaluated under the same conditions, including formate, RWGS + CO-hydro, and CO₂ direct activation. A microkinetic simulation is performed to reveal the different activities of the investigated inverse catalysts and identify the dominant reaction mechanism. The calculations verified the excellent performance of the inverse Zr₃O₆/CuPd catalyst, which is comparable with contemporary catalysts. It is also demonstrated that the fine-tuning of the atomic arrangement of the interfacial sites is key to adjusting both performance and mechanism. The current work paves the way for further advancing inverse catalyst applications in CO₂ hydrogenation and provides a solid optimization strategy.

2. Computational details

2.1. DFT calculations methods

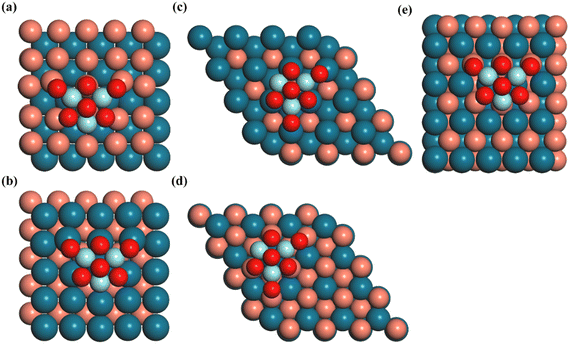
The Vienna ab initio simulation package (VASP) code^35,36 with the projector-augmented wave (PAW) method^37,38 was used to perform all calculations. The PBE exchange–correlation functional,³⁹ which incorporates the generalized gradient approximation (GGA), was utilized to characterize the exchange and correlation interactions. Additionally, the Grimme correction was applied to account for van der Waals interactions in all calculations. The integration over the Brillouin zone was conducted using a Monkhorst–Pack⁴⁰k-points grid with dimensions of 2 × 2 × 1. The atomic configurations were iteratively optimized until the forces acting on all unconstrained atoms reached a magnitude lower than 0.02 eV Å⁻¹ with the plane wave basis set with a cutoff energy of 400 eV, and the total energy was converged to an accuracy of 1 × 10⁻⁵ eV. To describe the London-dispersion interactions, the DFT-D3 correction was applied.⁴¹

The Zr₃O₆ cluster (denoted as Z) was modeled as the oxide moiety due to its successful imitation of the Cu–ZrO₂ interface⁴² and its validity in depicting the coordination of O and Zr atoms.⁴³ The (100), (110), and (111) surfaces of the CuPd alloy are used as support for the Zr₃O₆ cluster. The detailed information of each catalyst model is listed in Table S1 (ESI†). The (100) and (111) surfaces of the CuPd alloy both have two different terminations with either Cu or Pd, while the (110) surface of CuPd showed alternating Pd and Cu atom arrangements. The combinations between the Zr₃O₆ cluster and the CuPd alloy support resulted in five inverse catalysts, as shown in Fig. 1. The term ‘Z/CuPd(100)–Cu’ denotes the Zr₃O₆ cluster inverse catalyst supported on a metal substrate (100) surface with Cu termination.

Fig. 1 Top views of the DFT-optimized structures of the inverse catalysts for (a) Zr₃O₆/CuPd(100)–Cu, (b) Zr₃O₆/CuPd(100)–Pd, (c) Zr₃O₆/CuPd(111)–Pd, (d) Zr₃O₆/CuPd(111)–Cu, (e) Zr₃O₆/CuPd(110). Cu: orange, Pd: dark blue, Zr: light blue and O: red.

The adsorption energy of the intermediates (E_ads) is defined as

E_ads = E_total − E_slab − E_gas

where E_total represents the total energy of the slab containing the adsorbed intermediates, while E_gas corresponds to the energy of the gas phase molecules, and E_slab denotes the energy of the bare slab. The transition state (TS) is identified by dimer method,⁴⁴ and is confirmed with the presence of only one imagery frequency. The forward energy barrier, denoted as E_a, is defined as the energy difference between the transition state and initial state. Crystal orbital bond index (COBI) analysis⁴⁵ was performed by the local orbital basis suite towards electronic structure reconstruction (LOBSTER) package.⁴⁶ Bader charge analysis was performed to identify the charge distribution and transfer.⁴⁷

2.2. Microkinetic model

Microkinetic analysis was performed using the catalysis microkinetic analysis package (CatMAP).⁴⁸ The elementary reactions considered in this microkinetic model are listed in Table 1. During the simulation, two distinct sites were taken into account: h_site, designated for hydrogen atoms, and s_site, designated for other species involved in the reaction network. In this approach, hydrogen was adsorbed at a special “hydrogen reservoir” site, ensuring its adsorption occurred independently without any competition from other species.^49,50 The reaction was conducted under specific conditions, where the feed gas composition consisted of CO₂(g) : H₂(g) : inert gas in a ratio of 0.10 : 0.40 : 0.50 under 473–573 K and total pressure of 10 Bar.

Table 1 Activation energies of the forward reaction (E_a), and reaction energies (ΔE) (in eV) of the elementary reactions of methanol synthesis over Z/CuPd catalysts

Elementary reactions		Z/CuPd(100)–Cu		Z/CuPd(100)–Pd		Z/CuPd(110)		Z/CuPd(111)–Cu		Z/CuPd(111)–Pd
		E a/eV	ΔE/eV	E a/eV	ΔE/eV	E a/eV	ΔE/eV	E a/eV	ΔE/eV	E a/eV	ΔE/eV
R1	H2(g) + 2* ⇔ 2H*	0.39	−0.78	0.11	−0.83	0.21	−0.31	0.36	0.27	0.47	0.09
R2	CO2* ⇔ CO2(g) + *	1.51	1.51	1.65	1.65	1.67	1.67	1.42	1.42	1.73	1.73
R3	CO2* + H* ⇔ HCOO* + *	0.67	−0.24	0.33	0.11	0.66	0.05	0.19	−0.86	0.46	−0.28
R4	CO2* + H* ⇔COOH* + *	0.73	0.25	0.60	0.28	0.81	0.48	0.50	−0.30	0.90	−0.07
R5	CO2* + * ⇔ CO* + O*	0.71	0.31	1.34	0.35	1.13	0.75	0.74	−0.11	1.30	0.55
R6	HCOO* + H* ⇔ HCOOH* + *	1.11	0.79	0.74	0.63	0.74	0.59	1.19	1.10	1.08	0.89
R7	HCOO* + H* ⇔ CH2OO* + *	1.33	0.65	1.87	1.01	1.23	1.05	1.48	−0.07	1.64	1.39
R8	COOH* + * ⇔ CO* + OH*	1.52	1.04	0.82	1.01	1.05	0.14	2.05	1.18	1.94	0.81
R9	CO* + H* ⇔ HCO* + *	0.62	−0.52	0.79	0.63	0.97	0.40	0.98	−0.36	1.26	0.18
R10	HCOOH* + H* ⇔CH2OOH* + *	0.55	−0.46	0.72	0.16	0.61	0.11	0.22	−0.75	0.64	−0.15
R11	CH2OO* + H* ⇔ CH2OOH* + *	0.56	−2.23	0.48	−0.25	0.44	−0.11	0.60	0.06	0.64	−0.69
R12	HCO* + H* ⇔ CH2O* + *	0.74	−0.21	0.56	0.13	0.65	−0.11	0.49	−0.40	0.65	−0.08
R13	CH2OOH* + * ⇔ CH2O* + OH*	0.51	0.32	0.52	0.21	0.54	0.02	1.30	1.10	1.20	0.34
R14	CH2O* + H* ⇔ H3CO* + *	0.62	−0.66	0.60	0.00	0.43	−0.27	0.22	−0.63	0.56	0.02
R15	CH2O* + H* ⇔ CH2OH* + *	1.44	0.44	1.19	0.73	1.70	0.83	0.92	0.33	1.48	0.67
R16	CH3O* + H* ⇔ CH3OH* + *	1.34	0.87	0.74	0.44	0.89	0.67	0.73	0.29	0.81	0.61
R17	CH2OH* + H* ⇔ CH3OH* + *	1.15	−0.22	0.71	−0.26	0.54	−0.59	0.77	−0.29	0.64	−0.07
R18	OH* + H* ⇔ H2O* + *	1.41	0.95	0.70	0.45	0.94	0.69	1.08	0.82	0.83	0.61
R19	H2O* ⇔H2O(g) + *	1.29	1.29	1.30	1.30	1.63	1.63	1.33	1.33	1.46	1.46
R20	CO* ⇔ CO(g) + *	1.23	1.23	2.36	2.36	2.61	2.61	1.59	1.59	2.23	2.23
R21	CH3OH* ⇔ CH3OH(g) + *	1.56	1.56	1.55	1.55	1.87	1.87	1.59	1.59	1.56	1.56

---

The free energies of the adsorbates and transition states were estimated employing the harmonic approximation, and the entropy was evaluated using the following equation:

where k_B is the Boltzmann constant and T is the temperature. The number of harmonic energies (ε_i) used in the summation is denoted as the degree of freedom, which is generally 3N, where N is the number of atoms in the adsorbates or transition states.

Moreover, the free energies of the gas phase molecules are corrected through the following equation:

where C_p is the gas phase heat capacity as a function of temperature derived from the Shomate equations.

3. Results and discussion

3.1. CO₂ adsorption and activation

As shown in Fig. 1, two different exposed atoms, either Cu or Pd, form contacts with the Zr₃O₆ cluster to construct the interfacial structure for the investigated surfaces, including CuPd(100) and CuPd(111), respectively. It is noted that the interfacial atomic arrangement is different even for the same metal support surface, which will provide in-depth understandings of the catalytic mechanism beyond the pure surface-dependent regime. The interactions between the oxide and metal substrate induced a charge distribution polarization, as shown in Fig. 2. For facet (100), the Cu and Pd atoms in the top layer are mostly positively and negatively charged, respectively. More importantly, the interfacial atoms between the oxide cluster and metal support show different features from the other surface atoms. For Z/CuPd(100)–Cu, the interfacial copper atoms possessed around +0.37 |e⁻| charges, while the others are around +0.17 |e⁻|. For Z/CuPd(100)–Pd, the interfacial palladium atoms are less negatively charged (−0.02 |e⁻|) or even become positively charged (0.11 |e⁻|), while the others are negatively charged at around 0.13 |e⁻|. From charge analysis, the interfacial atoms showed a distinct charge pattern from the rest of the surface atoms, which is induced by the interaction between the oxide cluster and metal substrate. Moreover, the polarized charge distribution rendered the interfacial atoms with good activity to bind various intermediates, as discussed in the following sections.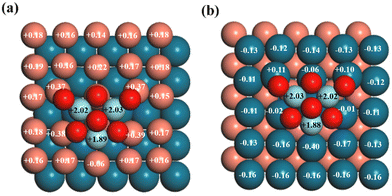

Fig. 2 Bader charge analysis (in |e|) of (a) Z/CuPd(100)–Cu and (b) Z/CuPd(100)–Pd. The numbers on the atoms are the calculated charge transfer from the Bader charge analysis.

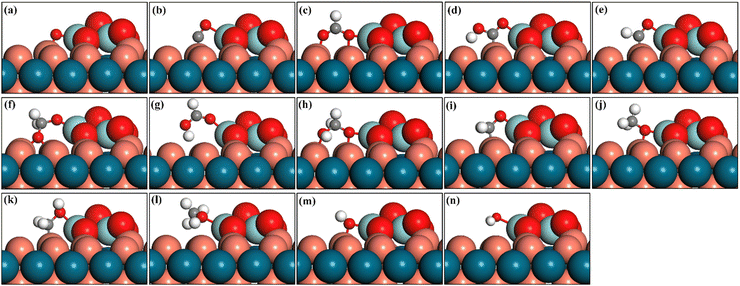
The polarized charge distribution directed the strong adsorption for the CO₂ molecule, as shown in Fig. 3a, which is a key step to initiate the reaction and lower the first hydrogenation barrier. For the Z/CuPd(100)–Cu catalyst, the CO₂ adsorption preferentially occurs at the interfacial sites and the adsorbed configuration is in the bent mode with an angle of 122.1°. This is significantly different from the linear configuration in the gas phase. Moreover, the C–O bond in CO₂ is elongated to 1.26 Å and 1.31 Å after adsorption. These geometry features clearly indicate that CO₂ is effectively activated upon adsorption. The adsorbed CO₂ molecule configurations on other inverse catalysts are shown in Fig. S1 (ESI†). The calculated adsorption energy is −1.51, −1.65, −1.67, −1.42, and −1.73 eV on Z/CuPd(100)–Cu, Z/CuPd(100)–Pd, Z/CuPd(110), Z/CuPd(111)–Cu, and Z/CuPd(111)–Pd, respectively. The calculated adsorption energies are much greater than previous reports including metal or other inverse catalysts, which are in the range from −0.20 eV to −1.10 eV.^19,42 The strong adsorption of CO₂ is mainly due to the covalent bond formation with the interfacial atoms, as shown in Fig. 3b and c. The strong adsorption is also witnessed as a significant charge is transferred from the catalyst surface to the adsorbed CO₂, as shown in Table S2 (ESI†). In addition to the CO₂ molecule, other key intermediates are explored, as shown in Fig. 4 and Fig. S3–S6 (ESI†). For all investigated Z/PdCu catalysts, the interfaces between Zr₃O₆ and PdCu served as the sites for the intermediate adsorption. The bonding scenarios can be categorized into three types: (1) no bonding with the PdCu substrate, such as HCOOH*, CH₃OH*, and H₂O*; (2) bonding through the carbon atom in the intermediate with the PdCu substrate, such as CO*, COOH*, and HCO*; and (3) bonding through the oxygen atoms in the intermediate with the PdCu substrate, including O*, OH*, HCOO*, CH₂OOH*, and CH₃O*. The adsorption energy for these key intermediates is illustrated in Fig. S1 (ESI†). Notably, for catalysts with the same PdCu support facet, the intermediates that bond through the oxygen atoms exhibit stronger adsorption on the Cu-terminated surface, i.e., Type III. Meanwhile, the intermediates that bond through the carbon atoms exhibit stronger adsorption on the Pd-terminated surface, i.e., Type II. For catalysts with the same support facet, the adsorption energy of the intermediates that do not bond with the support is very similar, i.e., Type I. The ability of the catalysts to interact with key intermediate species largely determines the mechanistic differences in the CO₂ hydrogenation-to-methanol process across various catalysts.

Fig. 3 (a) Geometry configuration and (b) and (c) calculated isosurfaces of the bonding orbital for CO₂ adsorbed on Z/CuPd(100)–Cu, where blue represents the negative lobe, while yellow represents the positive lobe. Cu: orange, Pd: dark blue, Zr: light blue, O: red and C: grey.

Fig. 4 Adsorbed structures of the intermediates involved in the synthesis of methanol through CO₂ hydrogenation over Z/CuPd(100)–Cu. (a) O*, (b) CO*, (c) HCOO*, (d) COOH*, (e) HCO*, (f) CH₂OO*, (g) HCOOH*, (h) CH₂OOH*, (i) CH₂O*, (j) CH₃O*, (k) CH₂OH*, (l) OH*, (m) OH*, (n) H₂O*. Cu: orange, Pd: dark blue, Zr: light blue, O: red and C: grey.

3.2. Reaction pathway

There are three major catalytic pathways for CO₂ hydrogenation to methanol, as shown in Fig. 5. The main difference lies in the first hydrogenation step on the pathway. There are three different products at the first step, HCOO*, COOH*, and CO* + O*, respectively, for the three pathways. Hydrogen bonding with carbon or oxygen in the CO₂ molecule formed HCOO* and COOH*, which distinguished the formate (PATH I) and RWGS + CO-hydro (PATH II) pathways (RWGS stands for reversed water–gas shift reaction). Conversely, CO₂ can undergo a direct breaking of the C–O bond to form CO* and O*, which corresponds to the CO₂ direction activation mechanism and is named as PATH III. However, PATH III became identical with PATH II after the first hydrogenation step. Therefore, only PATH I and II are mainly investigated. PATH I and II are basically paralleled until the formation of CH₂O*, where the two pathways meet. The targeted product, methanol, is obtained after two successive hydrogenation steps via either CH₃O* or CH₂OH* after CH₂O* formation. One of the main side products during the reaction is considered to be CO, which is mainly generated on PATH II and III.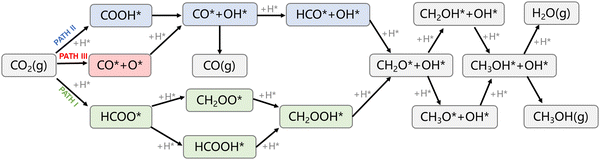

Fig. 5 Reaction network for CO₂ hydrogenation to methanol and carbon monoxide over Zr₃O₆/CuPd inverse catalysts. PATH I: formate, PATH II: RWGS + CO-hydro, PATH III: CO₂ direct activation.

3.2.1. Formate pathway (PATH I). For simplicity, Z/CuPd(100) with Pd and Cu terminations are selected to describe the reaction pathway, as shown in Fig. 6. For the first hydrogenation step to form HCOO*, it is clear that the Pd termination is more active than the Cu termination with a barrier of 0.33 eV, which is nearly half of the latter case (0.67 eV). At the transition state (TS1), CO₂ significantly deviated from a linear molecule in the gas phase. The angle of the CO₂ molecule at TS is 126.87° (Z/CuPd(100)–Cu) and 125.90° (Z/CuPd(100)–Pd), respectively. To quantitatively evaluate the bonding nature and strength, COBI analysis was performed, as shown in Fig. 7. The COBI method extended the rationale of the Mayer bond order to crystalline bonding,⁴⁵ providing an accurate and quantitative description of the bond strength, as well as the bonding nature (such as covalent or ionic). The value of the integrated COBI (ICOBI) is conversely related with ionicity, which means that a large ICOBI has a greater covalent bonding contribution. Summation of the ICOBI of the adsorbed CO₂ molecule is 0.56 and 0.59 for Z/CuPd(100)–Cu and Z/CuPd(100)–Pd, respectively, and the bonding nature is a mixed covalent and ionic. CO₂* also gained more stabilization on Z/CuPd(100)–Pd than Z/CuPd(100)–Cu, particularly from the carbon bonding with the metal atom. The stabilized transition state helped to reduce the barrier on Z/CuPd(100)–Pd.

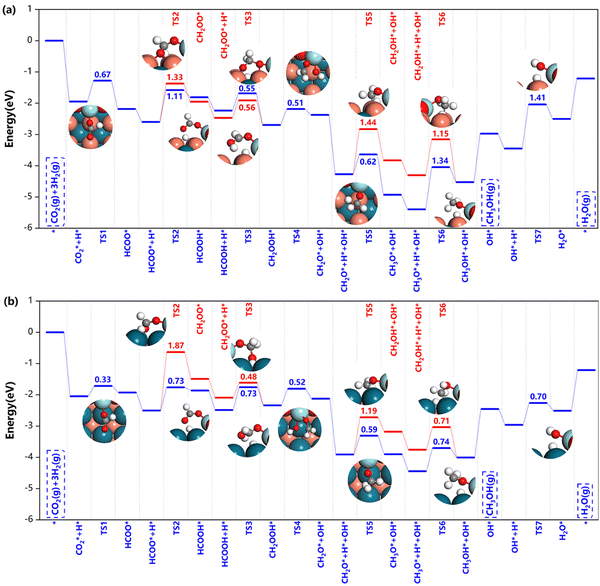Fig. 6 Potential energy diagrams and corresponding transition state structures of methanol formation over (a) Z/CuPd(100)–Cu and (b) Z/CuPd(100)–Pd on the formate pathway.

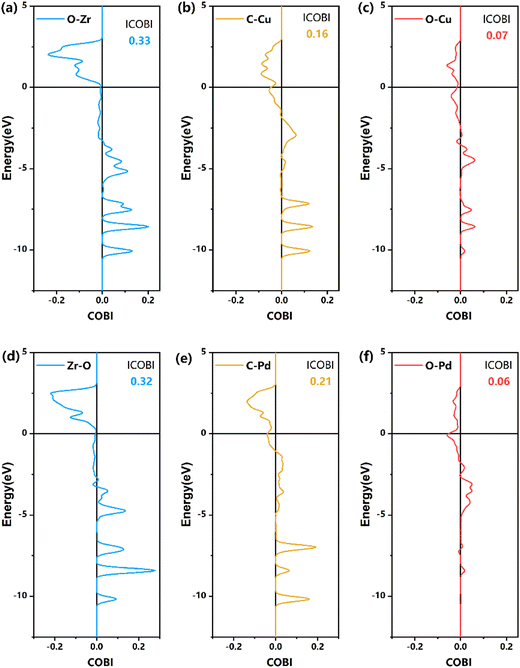Fig. 7 COBI analysis of the bonding nature and strength of TS1 on the formate pathway, as shown in Fig. 6. (a)–(c) Z/CuPd(100)–Cu, (d)–(f) Z/CuPd(100)–Pd.

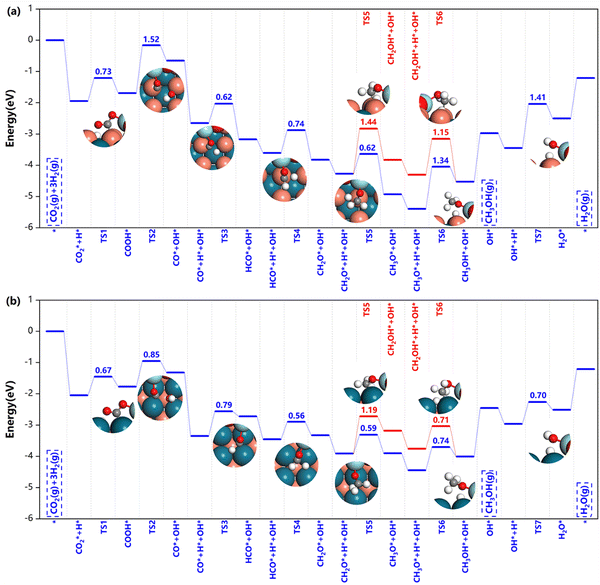
After HCOO* formation, there are two different catalytic routes to yield methanol, HCOOH → CH₂OOH → CH₂O → CH₃O → CH₃OH or CH₂OO → CH₂OOH → CH₂O → CH₂OH → CH₃OH, as indicated by the blue and red routes in Fig. 6. For Z/CuPd(100)–Cu, the red and blue pathways are quite similar regardless of the reaction barrier until the formation of CH₃O* (TS5), in which the blue pathway has a lower barrier than the red pathway. Therefore, Z/CuPd(100)–Cu probably followed the blue pathway. The largest barrier on the blue pathway is identified to be the hydrogenation of CH₃O* to methanol, which is 1.34 eV. For Z/CuPd(100)–Pd, the barrier of HCOO* hydrogenation to HCOOH* on the blue pathway and to CH₂OO* on the red pathway is 0.73 and 1.87 eV, respectively. This significant difference largely determined the blue pathway as being more favorable, which is consistent with Z/CuPd(100)–Cu. Conversely, the barriers on the blue pathway of Z/CuPd(100)–Pd are all less than 0.8 eV, which is more favorable than CuPd(100)–Cu, as shown in Fig. 6b. In particular, the critical step of CH₃O* hydrogenation to methanol has a barrier of 0.74 eV on Z/CuPd(100)–Pd, and it is calculated to be 1.34 eV on Z/CuPd(100)–Cu. Hence, Z/CuPd(100)–Pd is suggested to have better activity than Z/CuPd(100)–Cu from the formate pathway analysis. The performance demonstrated by different metal terminations of CuPd(100) is attributed to the bonding strength and properties of the intermediates and transition with interfacial atomic sites, particularly the Pd and Cu sites at the interfaces.

Moreover, the CuPd bimetallic support possessed better catalytic performance in comparison with other inverse catalysts. DFT calculations indicated that the reaction barrier is 1.32 eV and 1.39 eV on the Zr₃O₆H₆/Cu(111)¹⁹ and Zr₃O₆/Cu(110)⁴² inverse catalysts for *CH₂OOH dissociation, respectively, while it is calculated to be 0.5 eV in the current work. Furthermore, the calculated barriers on Z/CuPd(100)–Pd are much smaller than those of the counterparts on either Zr₃O₆H₆/Cu(111) or Zr₃O₆/Cu(110) in most cases for the formate pathway. The formate pathway on other surfaces, (110) and (111), are shown in Fig. S2 (ESI†). From comparison, Z/CuPd(100) generally has smaller barriers along the formate pathway than the Z/CuPd(110) and (111) surfaces, as shown in Fig. S3 (ESI†). In particular, for the key steps of the first hydrogenation and methanol formation, Z/CuPd(100)–Pd possessed the lowest barriers among the investigated catalysts.

3.2.2. RWGS + CO-hydro pathway. As shown in Fig. 8, the first step on the RWGS + CO-hydro pathway is CO₂ hydrogenation to form COOH*. For this hydrogenation step, the oxygen atom in the CO₂ molecule attracts hydrogen, rather than carbon on the formate pathway. The calculated barrier (TS1) of COOH* formation is 0.73 eV and 0.67 eV on Z/CuPd(100)–Pd or Cu, respectively. Unlike the continuous hydrogenation on the formate pathway, COOH* firstly underwent C–O bond breaking to generate CO* and OH*. It then evolved into CO* hydrogenation for the rest of the pathway, which explains why it is called the RWGS + CO-hydro pathway. With two successive hydrogen additions to carbon, CO* was hydrogenated to form CH₂O*. At the next hydrogenation step, there are two different options represented by blue and red pathways via either CH₃O* or CH₂OH*, respectively, to obtain the targeted methanol product. From a comparison of the barriers of TS5, the blue pathway via CH₃O* is more favorable than the red pathway via CH₂OH*. The former barrier is less than 0.7 eV, while the latter case is above 1.0 eV. Therefore, it can be concluded that the blue pathway is preferred on both Z/CuPd(100)–Pd and –Cu surfaces. On the blue pathway, there are two critical steps associated with significant barriers, which are COOH* dissociation (TS2) and methanol formation (TS6), respectively. Z/CuPd(100)–Pd exhibited smaller barriers compared with Z/CuPd(100)–Cu (0.67 eV and 0.74 eV), while they were calculated to be 0.73 and 1.34 eV on Z/CuPd(100)–Cu, respectively. Hence, Z/CuPd(100)–Pd more likely possessed better reactivity than CuPd(100)–Cu on the RWGS + CO-hydro pathway. Based on the above discussion, it is suggested that Z/CuPd(100)–Pd has better reactivity on both formate and RWGS + CO-hydro pathways. Similar to the formate pathway, Z/CuPd(100) also showed better activity than the (110) and (111) surfaces on the RWGS + CO-hydro pathway, as shown in Fig. S4 (ESI†).

Fig. 8 Potential energy diagrams and corresponding transition state structures of methanol formation over (a) Z/CuPd(100)–Cu and (b) Z/CuPd(100)–Pd on the RWGS + CO-hydro pathway.

3.2.3. Comparison of the three pathways. The major difference between the formate and RWGS + CO-hydro pathways lies in the first hydrogenation step. Whether the hydrogen is attached to carbon or oxygen in the activated CO₂ molecule determines if the reaction will take the formate or RWGS+ CO-hydro pathway. Therefore, this is a critical step to control the reaction mechanism. For Z/CuPd(100)–Pd, which has the best possible activity, the barrier of the first hydrogenation is 0.33 eV and 0.67 eV, respectively, for the formate and RWGS + CO-hydro pathways. Thus, CO₂ hydrogenation is more likely to take the formate pathway than the RWGS + CO-hydro pathway. After the first step, the continuous hydrogenation steps take place to reach the key intermediate, CH₃O*. Meanwhile, three hydrogens are added to the carbon or oxygen atoms accordingly on the formate and RWGS pathways, respectively. However, the first hydrogenation intermediate on the RWGS + CO-hydro pathway, COOH*, should firstly dissociate to yield CO* before further hydrogenations, which involved a noticeable barrier. This step served as an important signature of the RWGS + CO-hydro pathway.

Direct C–O bond breaking in the CO₂ molecule is an elementary step to generate CO* besides COOH* dissociation, as shown in Fig. 5. However, CO₂ direct activation has been rarely explored previously due to the assumption of a larger barrier associated with the strong C–O bond. The calculated barriers of CO₂ direct activation is 0.71, 1.34, 1.13, 1.14, 0.74 and 1.30 eV for Z/CuPd(100)–Cu and Pd, Z/CuPd(110)–Cu and Z/CuPd(111)–Cu and Pd, respectively. The previous DFT studies demonstrated that the barriers of CO₂ activation are around 1.00 eV on PdIn^51,52 alloy catalysts. Therefore, inverse Zr₃O₆/CuPd catalysts indeed demonstrated a remarkable ability to directly activate the C–O bond in the CO₂ molecule. This suggested that the inverse Zr₃O₆/CuPd catalysts will have great potential not only in CO₂ hydrogenation to methanol, but also in other catalytic reactions for CO₂ conversions with remarkable capability for C–O bond activation. Conversely, the calculated barriers of CO₂ activation are comparable with the counterparts of the first hydrogenation steps (HCOO* and COOH*) on the other pathways, which open a new channel for the reaction to proceed.

3.3. Microkinetic simulation

The reaction pathway analysis gave a preliminary evaluation of the catalytic performance for inverse catalysts. Based on the energetics of the elementary steps, as shown in Table 1 (obtained from DFT calculations), a microkinetic simulation was performed to further discern the catalytic capabilities. Firstly, the preference for the formate or RWGS + CO-hydro mechanism is explored for five different catalysts, as shown in Fig. 9. For both mechanisms, the TOF (turnover frequency) has a positive correlation with temperature, and it continuously increased with increasing temperature. For the formate pathway, the calculated TOF decreases with the following sequence: Z/CuPd(100)–Cu > Z/CuPd(100)–Pd > Z/CuPd(110) > Z/CuPd(111)–Pd > Z/CuPd(111)–Cu. The Z/CuPd(100) surfaces with either Cu or Pd terminations exhibit much better performances than the others throughout the whole investigated temperature range. For the Z/CuPd(100) surface, the Cu termination delivered a greater TOF than Pd termination. This indicated that the reactivity is not only dependent on a specific surface, but also significantly influenced by the exposed metal atoms. Conversely, this observation from the TOF calculations is different from the discussion of the reaction barrier comparison, which seems to suggest that Pd termination has better activity. For the RWGS + CO-hydro pathway, the reactivity with decreasing order is Z/CuPd(100)–Pd > Z/CuPd(110) > Z/CuPd(100)–Cu > Z/CuPd(111)–Pd > Z/CuPd(111)–Cu. The most significant change compared with the formate pathway is that the reactivity switched between Z/CuPd(100)–Cu and Z/CuPd(110). On the RWGS + CO-hydro pathway, Z/CuPd(110) exhibited improved activity compared to Z/CuPd(100)–Cu. This again demonstrated that not only reactivity, but also the reaction mechanism, is surface-dependent. The better reactivity of Z/CuPd(110) likely originated from the reduced barrier of the key step (TS2) over Z/CuPd(100)–Cu, as shown in Fig. S2b (ESI†). The common feature shared by both formate and RWGS-CO-hydro pathways is that Z/CuPd(100)–Pd has superior performance compared to others. A comparison of the performance regarding CO₂ direct activation (PATH III) is shown in Fig. S6 (ESI†) for the investigated catalysts. For each inversed catalyst, it also has a preferred reaction pathway. In particular, the most favorable pathway is determined to be formate on the Z/CuPd(100) surface, while it is CO₂ direct activation on the Z/CuPd(110) and Z/CuPd(111) surfaces. Furthermore, the reactivity sequence predicted from TOF calculations in Fig. 9 is inversely correlated with the trend of the largest barrier on the reaction pathway shown in Fig. 6 and 8 and Fig. S8 and S9 (ESI†), except CuPd(100)–Cu on the formate pathway, which further corroborated the validity of the calculations.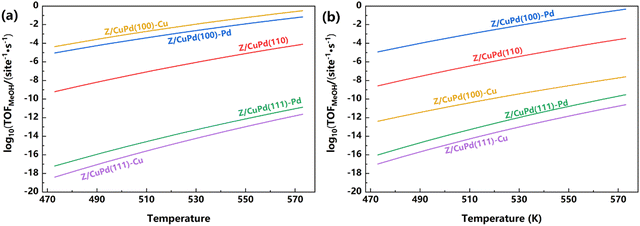

Fig. 9 The calculated TOF of Zr₃O₆/CuPd catalysts along the (a) formate pathway and (b) RWGS + CO-hydro pathway.

Besides the evaluation of the individual pathway, a total TOF is obtained by taking into account the elementary steps of all three pathways, as shown in Table 1, in the microkinetic simulation, which could eliminate any bias to a specific pathway and provide a thorough estimation of the performance. From Fig. 10a, it is clearly indicated that the Z/CuPd(100) surface outperformed both Z/CuPd(110) and Z/CuPd(111) surfaces. Hence, the performance of the Zr₃O₆/CuPd inverse catalyst has a strong dependence on the metal alloy support surface. From the above discussions, it can be concluded that the catalytic performance and mechanism of inverse Zr₃O₆/CuPd is largely determined by the metal surface and exposed atoms, respectively.

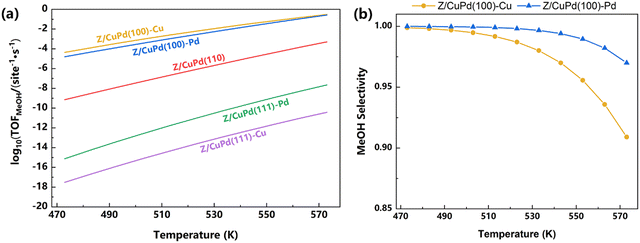Fig. 10 (a) The calculated TOF of Zr₃O₆/CuPd catalysts, including all elementary steps shown in Table 1. (b) Methanol selectivity of Z/CuPd(100)–Cu and Z/CuPd(100)–Pd.

For the two best catalysts Z/CuPd(100)–Cu and –Pd, the selectivity to methanol is also obtained, as shown in Fig. 10b. The selectivity of both catalysts showed a slow decline with increasing temperature, while Z/CuPd(100)–Cu exhibits a faster decrease in comparison with Z/CuPd(100)–Pd. Both catalysts demonstrate good selectivity above 90% in the investigated temperature range.

The degree of rate control (DRC) analysis, developed by Campbell, provides a quantitative method for analyzing the kinetics of multi-step reaction mechanisms.⁵³ Although the sum of DRC should be unity, there are cases in which unity is not reached. This is probably due to the incomplete elementary step list.^51,54 More information regarding the reaction key steps and mechanism are acquired from the coverage and DRC analysis, as shown in Fig. 11. For Z/CuPd(100)–Cu, the major species on the surface are determined to be HCOO*, CH₃O*, and OH*, as shown in Fig. 11a. Among them, HCOO* is the most populated species, which is consistent with previous experimental reports.^19,31,55 With increasing temperature, the coverage of HCOO* is slowly decreased from 0.6 ML to around 0.4 ML. However, it still occupied most surface sites. Conversely, the coverage of OH* steadily increased from 0.1 ML to 0.3 ML with increasing temperature, while the coverage of CH₃O* remains nearly unchanged. To further identify the key steps during the reaction, the general degree of control analysis was performed, as shown in Fig. 11c, which predicted both rate-limited and thermodynamics-limited steps accordingly. For the rate control step, TS4 (CH₂O–OH) on the formate pathway and CH₂OOH dissociation wielded the most significant influence on the reaction rate. The DRC of this step is calculated to be 0.5 at around 480 K, and it gradually decreased with increasing temperature. Conversely, water formation is also a kinetically relevant step, particularly at high temperature, although the DRC of water formation is below 0.15. The thermodynamics rate control analysis is conversely related with coverage, which is derived from its definition. The strong adsorptions of HCOO* or OH* inhibited the reaction and have adverse effects on rates. This adverse effect becomes less pronounced with increasing temperature for HCOO*, while the opposite trend is observed for OH*.

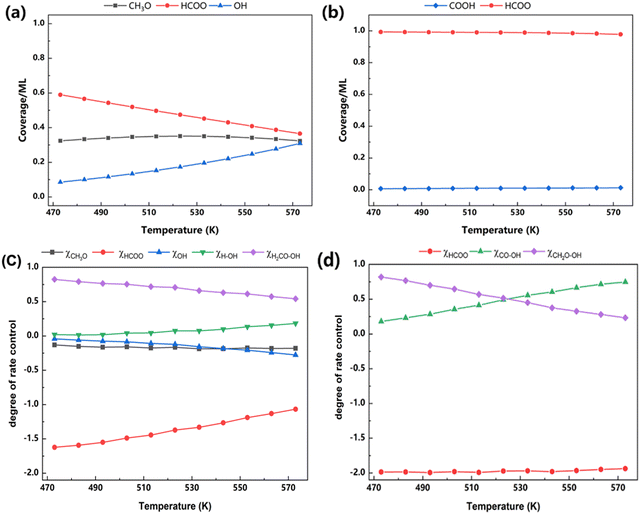Fig. 11 Coverage analysis of (a) Z/CuPd(100)–Cu and (b) Z/CuPd(100)–Pd, and DRC analysis of (c) Z/CuPd(100)–Cu and (d) Z/CuPd(100)–Pd.

For Z/CuPd(100)–Pd, HCOO* dominated the surface coverage with a negligible contribution from COOH*. Furthermore, the coverage distribution did not show an obvious dependence on temperature, as shown in Fig. 11b, which is quite different from Z/CuPd(100)–Cu. A more profound difference regarding the mechanism is revealed from DRC analysis, as shown in Fig. 11d. The kinetic control step is determined to be CH₂O–OH (TS4 on the formate pathway) and CO–OH (TS2 on the RWGS + CO-hydro pathway). Below 523 K, CH₂O–OH is dominant, and it switched to CO–OH at higher temperature. This seems to suggest that the formate and RWGS pathways have similar contributions to TOF, which is consistent with the observation shown in Fig. S5b (ESI†).

4. Conclusions

The rational optimization is crucial to further extend the application scope of promising inverse catalysts for CO₂ hydrogenation. In this work, it is found that the fine-tuning of the facets and exposed metal atoms on the substrate of inverse Zr₃O₆/CuPd catalysts is an effective strategy to enhance the performance and adjust the mechanism. The chosen CuPd alloy as support to construct inverse catalysts is proved to be crucial toward delivering excellent performance. The interface between the oxide and metal substrate provided active sites for CO₂ adsorption and activation, which initiated the reaction. COBI analysis gave a quantitative description of the bonding strength and nature of the transition state of key first hydrogenation step, which is used to determine the following pathway. Three mechanisms, including formate, RWGS + CO-hydro, and CO₂ direct activation, are explored and the former two are the dominant reactions. The preferred mechanism is largely determined by the exposed metal atom on the substrate. Moreover, this effect is manifested from the coverage and DRC analysis obtained from the microkinetic simulation. The calculated TOF indicated that the metal alloy substrate surfaces dominate the performance. Thus, Zr₃O₆/CuPd(100) has been predicted to possess the best performance among the investigated catalysts, which also outperformed the conventional CO₂ hydrogenation catalysts and other inverse catalysts on mono metal substrate. Overall, the current work applied a metal alloy-supported inverse catalyst in CO₂ hydrogenation to methanol, and validated its exceptional catalytic performance. More importantly, an effective strategy with the rational chosen metal substrate and exposed atoms has been verified, which opens a new direction for further optimization.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 22372105, 22172100), Basic Research Project of Education Office of Liaoning Province (JYTZD2023183), the Fundamental Research Funds for the Liaoning Universities (LJ212410166043), ShenYang Normal University (BS202208) and The Program for Excellent Talents in Shenyang Normal University.

References

1. X. Jiang, X. Nie, X. Guo, C. Song and J. G. Chen, Chem. Rev., 2020, 120, 7984–8034.
2. J. Zhong, X. Yang, Z. Wu, B. Liang, Y. Huang and T. Zhang, Chem. Soc. Rev., 2020, 49, 1385–1413.
3. T. Liu, S. Ali, Z. Lian, C. Si, D. S. Su and B. Li, J. Mater. Chem. A, 2018, 6, 19998–20004.
4. S. Chen, T. Liu, S. O. Olanrele, Z. Lian, C. Si, Z. Chen and B. Li, J. Energy Chem., 2021, 54, 143–150.
5. W. Xie, K. Li, X.-H. Liu, X. Zhang and H. Huang, Adv. Mater., 2023, 35, 2208132.
6. S. Yoshino, T. Takayama, Y. Yamaguchi, A. Iwase and A. Kudo, Acc. Chem. Res., 2022, 55, 966–977.
7. J. Artz, T. E. Muller, K. Thenert, J. Kleinekorte, R. Meys, A. Sternberg, A. Bardow and W. Leitner, Chem. Rev., 2018, 118, 434–504.
8. C. Hepburn, E. Adlen, J. Beddington, E. A. Carter, S. Fuss, N. Mac Dowell, J. C. Minx, P. Smith and C. K. Williams, Nature, 2019, 575, 87–97.
9. T. Dong, X. Liu, Z. Tang, H. Yuan, D. Jiang, Y. Wang, Z. Liu, X. Zhang, S. Huang, H. Liu, L. Zhao and W. Zhou, Appl. Catal., B, 2023, 326, 122176.
10. J. A. Onrubia-Calvo, A. Bermejo-López, B. Pereda-Ayo, J. A. González-Marcos and J. R. González-Velasco, Appl. Catal., B, 2023, 321, 122045.
11. K. Mori, H. Hata and H. Yamashita, Appl. Catal., B, 2023, 320, 122022.
12. E. H. Kim, M. H. Lee, J. Kim, E. C. Ra, J. H. Lee and J. S. Lee, Chin. J. Catal., 2023, 47, 214–221.
13. D. Wei, R. Sang, P. Sponholz, H. Junge and M. Beller, Nat. Energy, 2022, 7, 438–447.
14. S. Yang, L. Zhang and Z. Wang, Fuel, 2022, 324, 124503.
15. S. Kattel, B. Yan, Y. Yang, J. G. Chen and P. Liu, J. Am. Chem. Soc., 2016, 138, 12440–12450.
16. K. Larmier, W. C. Liao, S. Tada, E. Lam, R. Verel, A. Bansode, A. Urakawa, A. Comas-Vives and C. Coperet, Angew. Chem., Int. Ed., 2017, 56, 2318–2323.
17. T. Lunkenbein, J. Schumann, M. Behrens, R. Schlogl and M. G. Willinger, Angew. Chem., Int. Ed., 2015, 54, 4544–4548.
18. J. A. Rodriguez, P. Liu, D. J. Stacchiola, S. D. Senanayake, M. G. White and J. G. Chen, ACS Catal., 2015, 5, 6696–6706.
19. S. Kattel, B. Yan, Y. Yang, J. G. Chen and P. Liu, J. Am. Chem. Soc., 2016, 138, 12440–12450.
20. G. A. Olah, A. Goeppert and G. K. S. Prakash, Beyond Oil and Gas: The Methanol Economy, Wiley, 1st edn, 2009.
21. G. A. Olah, Angew. Chem., Int. Ed., 2005, 44, 2636–2639.
22. M. Behrens, F. Studt, I. Kasatkin, S. Kühl, M. Hävecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B.-L. Kniep, M. Tovar, R. W. Fischer, J. K. Nørskov and R. Schlögl, Science, 2012, 336, 893–897.
23. R. Qiu, Z. Ding, Y. Xu, Q. Yang, K. Sun and R. Hou, Appl. Surf. Sci., 2021, 544, 148974.
24. A. Mravak, S. Vajda and V. Bonačić-Koutecký, J. Phys. Chem. C, 2022, 126, 18306–18312.
25. C. Wang, Y. Fang, G. Liang, X. Lv, H. Duan, Y. Li, D. Chen and M. Long, J. CO2 Util., 2021, 49, 101542.
26. B. Hu, Y. Yin, G. Liu, S. Chen, X. Hong and S. C. E. Tsang, J. Catal., 2018, 359, 17–26.
27. F. Brix, V. Desbuis, L. Piccolo and É. Gaudry, J. Phys. Chem. Lett., 2020, 11, 7672–7678.
28. C. Quilis, N. Mota, B. Pawelec, E. Millán and R. M. Navarro Yerga, Appl. Catal., B, 2023, 321, 122064.
29. K. Li and J. G. Chen, ACS Catal., 2019, 9, 7840–7861.
30. S. Kattel, W. Yu, X. Yang, B. Yan, Y. Huang, W. Wan, P. Liu and J. G. Chen, Angew. Chem., Int. Ed., 2016, 55, 7968–7973.
31. C. Wu, L. Lin, J. Liu, J. Zhang, F. Zhang, T. Zhou, N. Rui, S. Yao, Y. Deng, F. Yang, W. Xu, J. Luo, Y. Zhao, B. Yan, X. D. Wen, J. A. Rodriguez and D. Ma, Nat. Commun., 2020, 11, 5767.
32. S. D. Senanayake, P. J. Ramírez, I. Waluyo, S. Kundu, K. Mudiyanselage, Z. Liu, Z. Liu, S. Axnanda, D. J. Stacchiola, J. Evans and J. A. Rodriguez, J. Phys. Chem. C, 2016, 120, 1778–1784.
33. R. M. Palomino, P. J. Ramírez, Z. Liu, R. Hamlyn, I. Waluyo, M. Mahapatra, I. Orozco, A. Hunt, J. P. Simonovis, S. D. Senanayake and J. A. Rodriguez, J. Phys. Chem. B, 2018, 122, 794–800.
34. W. Xiong, J. Ding, D. Wang and W. Huang, J. Phys. Chem. Lett., 2023, 14, 7229–7234.
35. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
36. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
37. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
38. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
39. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
40. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
41. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
42. L. Liu, X. Su, H. Zhang, N. Gao, F. Xue, Y. Ma, Z. Jiang and T. Fang, Appl. Surf. Sci., 2020, 528, 146900.
43. G. Zhao, B. Xiang, X. Shen, J. Sun, Y. Bai and Y. Wang, Acta Phys.-Chim. Sin., 2011, 27, 1095–1102.
44. G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022.
45. P. C. Müller, C. Ertural, J. Hempelmann and R. Dronskowski, J. Phys. Chem. C, 2021, 125, 7959–7970.
46. R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940.
47. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
48. A. J. Medford, C. Shi, M. J. Hoffmann, A. C. Lausche, S. R. Fitzgibbon, T. Bligaard and J. K. Nørskov, Catal. Lett., 2015, 145, 794–807.
49. A. Cao, J. Schumann, T. Wang, L. Zhang, J. Xiao, P. Bothra, Y. Liu, F. Abild-Pedersen and J. K. Nørskov, ACS Catal., 2018, 8, 10148–10155.
50. D. Garcia-Pintos, J. Voss, A. D. Jensen and F. Studt, J. Phys. Chem. C, 2016, 120, 18529–18537.
51. P. Wu and B. Yang, Catal. Sci. Technol., 2019, 9, 6102–6113.
52. P. Wu, J. Zaffran and B. Yang, J. Phys. Chem. C, 2019, 123, 13615–13623.
53. C. T. Campbell, ACS Catal., 2017, 7, 2770–2779.
54. X. Wang, J. Pan, H. Wei, W. Li, J. Zhao and Z. Hu, J. Phys. Chem. C, 2022, 126, 1761–1769.
55. F. C. Meunier, I. Dansette, A. Paredes-Nunez and Y. Schuurman, Angew. Chem., Int. Ed., 2023, 62, e202303939.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00927d

‡ These authors contributed equally to this work.

---