The effect of hydrogen bonding on the π depletion and the π–π stacking interaction

Abstract

Non-covalent interactions such as hydrogen bonding and π–π stacking are essential types of interactions governing molecular self-assembly. The π–π stacking ability of aromatic rings depends on the electron density of the π orbitals, which is affected by the electron-withdrawing or electron-donating properties of the substituents. We have here studied the effect of hydrogen bonding on the strength of the π–π stacking interactions by calculating the binding energies at the explicitly correlated Møller–Plesset (MP2-F12) perturbation theory level using polarized triple-ζ quality basis sets. The stacking interactions in the presence of hydrogen bonding are found to be stronger than in the absence of the hydrogen bonding suggesting that hydrogen bonds lead to π depletion, which affects the aromatic character of the aromatic rings and increases the strength of the π–π stacking interaction. We have also studied how hydrogen bonding affects the stacking interaction by calculating local orbital locator integrated pi over plane (LOLIPOP) indices. Comparing LOLIPOP indices with the stacking-interaction energies calculated at the MP2-F12 level shows that there is no clear correlation between the stacking-interaction energies and LOLIPOP indices.

---

1. Introduction

The π–π stacking interactions are one of the most commonly investigated types of non-covalent interactions and they are widely considered to be the most important type of weak interactions. Stacking interactions between aromatic rings containing π orbitals have been extensively studied during the past decades because they play a crucial role in a large number of applications. The π–π stacking interactions occur in molecular materials as well as in chemical and biological systems¹ where they stabilize molecular complexes and nanostructures.^2,3 The π–π interactions are responsible for the overall structural stability,^4–7 thermal stability⁸ and folding⁹ of proteins.

The π–π stacking interactions have also been studied for use in optoelectronic applications of organic crystals, where they were found to be responsible for electrical^10–17 and thermal conductivity¹⁸ in different devices. Materials with π–π interactions have also been used for sensing explosives^19,20 and in sensing dyes.²¹ The π–π interactions guide the favourite aggregation modes²² and are involved in the self-assembly of crystal structures.^23,24 They play a crucial role in the swelling of lignite, which is a type of low-rank coal.²⁵ The stacking-interaction energies improve the healability, self-healing properties, and the toughness of materials.^26–29 They also promote the delivery of chemical and biological drugs.^30–52

Hydrogen bonding is another type of non-covalent interaction that plays an important role in biological systems as well as in supramolecular chemistry.⁵³ Hydrogen bonding has been explored in the construction of crystalline and polymeric materials exhibiting novel and useful properties.^54–57

Hydrogen bonds affect the strength of π–π interactions because the cyclic π-electron delocalization of aromatic rings may limit an efficient stacking, whereas a stronger interaction can be obtained by depleting the π-electron density and thereby reducing the degree of aromaticity.⁵⁸

In this work, we investigate how hydrogen bonding interactions affect the π-stacking ability of aromatic rings. We have studied 17 aromatic molecules whose dimers are linked with quadruple hydrogen bonding. Seven dimers have the DDAA–AADD motif, where D denotes the donor and A is the acceptor of the hydrogen bond. Ten of the dimers have the DADA–ADAD motif. The studied dimers with the DDAA–AADD (DDAAn) and DADA–ADAD (DADAn) motifs are shown in Fig. 1 and 2, respectively. n is the running numbering of the molecules. More pictures of the molecular structures are reported in the ESI.†

Fig. 1 The quadruple hydrogen-bonded dimers with the more favourable DDAA–AADD hydrogen-bonding pattern. The figures are made with Jmol.⁵⁹

Fig. 2 The quadruple hydrogen-bonded dimers with the less favourable DADA–ADAD hydrogen-bonding pattern. The figures are made with Jmol.⁵⁹

The previously accepted notion was that the secondary A⋯D interactions are attractive, whereas the secondary A⋯A and D⋯D interactions are repulsive. The DDAA–AADD hydrogen-bonding structures are therefore expected to bind stronger than the DADA–ADAD ones.⁶⁰ However, in our recent study,⁶¹ we showed that the DDAA–AADD hydrogen bonding motifs have five attractive (D⋯A and A⋯A) and one repulsive (D⋯D) secondary interaction, while the DADA–ADAD motif have three attractive (A⋯A) and three repulsive (D⋯D) secondary interactions. The DDAA–AADD hydrogen bonding motif still binds stronger than the DADA–ADAD motif.⁶¹

We have here calculated the strength of π-stacking interactions and hydrogen-bonding strengths at the second-order Møller–Plesset (MP2) perturbation theory level. The hydrogen-bonding strengths are compared to benchmark values that we recently obtained in large-scale coupled-cluster calculations.⁶¹ We have also employed the LOLIPOP (local orbital locator integrated pi over plane) approach to estimate the extent of the π depletion and the π-stacking ability of the studied molecules.⁶²

We describe the employed computational methods in Section 2. The results are discussed in Section 3, which is followed by brief conclusions in Section 4.

2. Computational methods

The molecular structures of the studied molecules, their dimers and the benzene probe were optimized with Turbomole⁶³ at the density functional theory (DFT) level using the TPSSh functional,^64,65 the Davidson's contraction of the aug-cc-pVTZ basis sets^66,67 and the D3(BJ) dispersion correction.^68,69 The convergence threshold of the self-consistent field (SCF) optimization of the orbitals is 10⁻⁷ hartree and for the structure optimization the gradient norm is 3 × 10⁻⁴ hartree per bohr. The m5 integration grid was used in the DFT calculations.⁷⁰ The strengths of the π-stacking interactions and the hydrogen-bonding strengths were calculated at the MP2 level using the explicitly correlated (F12) approach^71,72 and basis-sets of polarized triple-ζ (def2-TZVP) quality.⁷³ We used the recommended F12 ansatz 2, model B and the corresponding auxiliary basis sets,⁷¹ which is the default F12 ansatz in Turbomole.⁶³ This ansatz in combination with the def2-TZVP basis sets yields almost the same interaction energies as obtained when using basis sets optimized for F12 calculations.⁷¹ We did not consider any vibrational energy corrections because the hydrogen-bonding energies are compared to reference data without them. We estimated the size of the vibrational effects by calculating the vibrational contribution to the hydrogen-bonding energy at the DFT level for one of the dimers using the aoforce program of Turbomole.⁷⁴ The molecular structures of the studied molecules and complexes are shown in Fig. 1 and 2 and in the ESI.† The Cartesian coordinates of the optimized molecular structures of the studied molecules, their dimers, and the molecules with the benzene probe are also given in the ESI.† The hydrogen-bonding interaction energies are compared to reference values that were calculated at the coupled-cluster singles and doubles level with a perturbational treatment of the triples (CCSD(T)) and extrapolated to the complete basis-set and Schrödinger limit.⁶¹ We also report the hydrogen-bonding energy for the nonaromatic DDAA05 dimer. The hydrogen bonding leads to π depletion that enhances the π-stacking ability of the aromatic rings.⁶² Population analysis was used for quantifying the π depletion of the aromatic rings of the dimers. The optimized structures were employed in the population analysis using the TPSSh functional.

The stacking-interaction energies were estimated by single-point calculations of the interaction energy between the studied systems and a benzene probe placed at a typical van der Waals distance of 3.8 Å above aromatic rings as shown in Fig. 3. The effect on the stacking-interaction energies due to hydrogen bonding were estimated by comparing stacking energies calculated for the monomers and dimers, respectively.

Fig. 3 The benzene probe above an aromatic ring is shown for (a) DDAA04-R, which is a monomer with the DDAA motif and for (b) DADA01, which is a monomer with the DADA motif. The figure is made with Jmol.⁵⁹

The effect of the hydrogen bonding on the stacking energy was also estimated by calculating the π depletion using the local orbital locator (LOL) approach.⁷⁵ LOL is a function of the kinetic energy density that can be used for depicting π bonds and for describing the nature and location of electron pairs.⁷⁵ LOLIPOP indices, which quantify the π depletion, were obtained by integrating the LOL function over a spatial domain consisting of a cylinder with a radius of 1.94 Å. The cylinder is placed in the middle of the benzene ring covering the main part of the π-electron density.⁶² The LOLIPOP analyses were performed using the Multiwfn software package⁷⁶ with the molecular orbital file in Molden⁷⁷ format as input. The Multiwfn input file was created with ORCA^78,79 at the TPSSh level of theory using the def2-SVP basis sets.^64,65,80

3. Results and discussion

3.1. Hydrogen bonding energies of the dimers

The binding energies of the quadruple hydrogen bonded dimers in Table 1 were calculated at the MP2-F12 level and compared to reference values calculated at the CCSD(T) level and extrapolated to the complete basis-set and Schrödinger limit.⁶¹ The naming scheme follows the notation of the hydrogen bonding motifs.

Table 1 Comparison of the hydrogen-bonding energies (in kJ mol⁻¹) of the studied molecules calculated at the MP2-F12/def2-TZVP level with reference CCSD(T) values extrapolated to the complete basis-set and Schrödinger limit⁶¹

Dimer	MP2-F12	CCSD(T)
DDAA01	−208.9	−210.8
DDAA02	−237.3	−222.7
DDAA03	−150.9	−141.0
DDAA04	−138.2	−129.0
DDAA05	−159.6	−153.0
DDAA06	−303.7	−293.3
DDAA07	−236.6	−229.0
DDAA08	−216.1	−211.0
DADA01	−141.2	−132.8
DADA02	−131.3	−121.3
DADA03	−127.7	−122.8
DADA04	−121.8	−115.5
DADA05	−123.7	−118.0
DADA06	−142.4	−129.6
DADA07	−141.1	−131.4
DADA08	−137.4	−132.3
DADA09	−196.3	−176.7
DADA10	−130.2	−124.2

---

The hydrogen bonding energies calculated at the MP2-F12 level agree well with the CCSD(T) reference energies. A linear regression fit yields an angular coefficient of 1.008 ± 0.022 and an offset of −7.11 ± 3.75 kJ mol⁻¹ with an root-mean-square (RMS) value of 4.7 kJ mol⁻¹ showing that the MP2-F12 and CCSD(T) energies correlate well as also seen in Fig. 4. However, the hydrogen bonding energies calculated at the MP2-F12 level are slightly larger than the CCSD(T) reference values, which is not surprising since MP2 is known to slightly overbind. The basis-set superposition error (BSSE) of the hydrogen bonding energies was estimated by repeating the MP2-F12 calculation on DADA01 using a basis set of quadruple-ζ polarization quality (def2-QZVP).⁷³ The estimated BSSE is 2.1 kJ mol⁻¹ or 1.5% of the hydrogen bonding energy. The reference energies of the DDAA01 and DADA09 species in Table 1 were calculated with smaller basis sets because the reference CCSD(T) energies could not be computed with the largest basis set. Since the hydrogen bonding energies calculated at the MP2-F12 level agree well with the CCSD(T) data, the stacking energies calculated at the MP2-F12 level are also expected to be accurate. Vibrational corrections to hydrogen-bonding energies are generally small. A vibrational correction of 5.5 kJ mol⁻¹ was obtained for the DADA01 dimer at the DFT level. Since the studied dimers have four hydrogen bonds, one can expect that the hydrogen-bonding energies of all the dimers have about the same vibrational contribution.

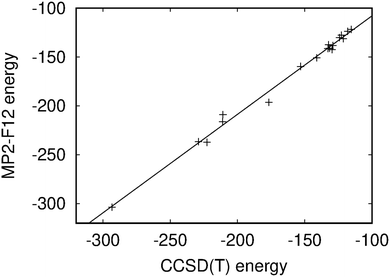Fig. 4 Correlation of the hydrogen bonding energies (in kJ mol⁻¹) calculated at the CCSD(T) and MP2-F12/def2-TZVP levels. The figure is made with GnuPlot.⁸¹

3.2. Stacking interaction energy

The π depletion of aromatic rings is related to the π-stacking ability of the molecules.^58,62 Hydrogen bonding leads to charge transfer from the donor (D) to the acceptor (A) of the hydrogen bond. It also leads to a localization of the electronic charge to the vicinity of the hydrogen bond implying that hydrogen bonding involving aromatic rings leads to charge transfer from the ring towards the hydrogen bond and thereby strengthening the stacking interaction. We study here the effect of hydrogen bonding on the π depletion and consequently on the molecular π-stacking energies. The stacking energies for the DDAA–AADD and DADA–ADAD hydrogen bonding motifs calculated at the MP2 level are summarized in Tables 2 and 3 respectively. A BSSE of 0.57 kJ mol⁻¹ was obtained for the stacking energy of DADA01 by repeating the MP2-F12 calculations using the def2-QZVP basis sets.⁷³ Changes in the stacking energies due to the hydrogen bonding were obtained by calculating the π-stacking energies for the monomers and the dimers. The stacking energies were obtained in single-point calculations with a benzene probe placed at a distance of 3.8 Å above the aromatic rings of the molecules. The obtained stacking energies of the DDAAn molecules and their dimers are given in Table 2. Some of the molecules have more than one aromatic ring as seen in Fig. 1 and 2. We introduce the label L (left) and R (right) to denote the studied aromatic ring of the DDAA and DADA molecules with two aromatic rings. The molecules are oriented with the first D to the left.

Table 2 Comparison of the stacking interaction energies (in kJ mol⁻¹) and LOLIPOP values of the DDAA–AADD molecules with and without the presence of hydrogen bonding. Labels L and R denote the left and the right ring, respectively. Molecule DDAA05 is omitted because it has no aromatic rings

Molecule	Dimer		Monomer
	Energy	LOLIPOP	Energy	LOLIPOP
DDAA01-R	−37.79	0.85	−34.84	1.96
DDAA01-L	−27.15	1.80	−26.13	2.14
DDAA02	−27.53	3.63	−23.32	4.03
DDAA03-R	−28.95	2.32	−24.41	2.69
DDAA03-L	−33.06	1.83	−27.17	3.41
DDAA04-L	−34.36	4.62	−28.43	4.69
DDAA04-R	−31.73	3.03	−27.12	3.14
DDAA06-L	−26.91	4.75	−25.18	4.98
DDAA06-R	−29.42	4.75	−25.84	4.94
DDAA07	−30.35	3.68	−25.44	4.09
DDAA08-R	−27.96	6.15	−26.10	6.25
DDAA08-L	−35.06	3.17	−29.64	3.59

---

Table 3 Comparison of the stacking interaction energies (in kJ mol⁻¹) and LOLIPOP values of the DADA–ADAD molecules with and without the presence of hydrogen bonding. Labels L and R denote the left and right ring, respectively

Molecule	Dimer		Monomer
	Energy	LOLIPOP	Energy	LOLIPOP
DADA01	−35.06	4.24	−28.19	4.33
DADA02	−22.60	2.80	−21.46	2.78
DADA03	−26.93	4.09	−24.33	4.19
DADA04	−30.56	4.47	−26.74	4.56
DADA05-L	−27.19	3.06	−26.41	3.10
DADA05-R	−32.59	3.30	−29.34	3.31
DADA06-R	−24.57	3.67	−22.26	4.71
DADA06-L	−22.80	4.55	−22.18	5.67
DADA07-R	−38.01	3.01	−36.55	3.92
DADA07-L	−35.10	3.84	−33.46	5.06
DADA08	−30.86	4.35	−27.86	4.41
DADA09-L	−30.57	1.22	−26.97	2.73
DADA09-R	−24.02	1.45	−20.24	2.05
DADA10-L	−30.33	4.82	−26.19	5.02
DADA10-R	−30.11	4.60	−26.03	4.70

---

The π-stacking ability of the aromatic rings of the dimers is stronger because the dimers are complexed through hydrogen bonding to their identical copy. This pattern can be clearly seen in Table 2 where the π-stacking interaction energies are larger for the hydrogen bonded dimers than for the monomers.

The left and right aromatic rings of DDAA01 exhibit different π-stacking strengths because the rings have different chemical environment. The stacking energy of the right ring of the DDAA01 dimer is −37.78 kJ mol⁻¹, whereas the stacking energy of the same ring of the DDAA01 monomer is −34.84 kJ mol⁻¹. The difference of 2.94 kJ mol⁻¹ in stacking energy is due to the π depletion caused by hydrogen bonds.

The stacking interaction energies of the monomers and dimers of the molecules with the DADA–ADAD hydrogen bonding motif are compared in Table 3 The same trend is obtained for the molecules with the DADA–ADAD hydrogen bonding motif as for the DDAA–AADD ones. The difference in the π-stacking energies is somewhat larger for the DDAA–AADD molecules than for the DADA–ADAD ones because the DDAA–AADD dimers have stronger hydrogen bonds than the DADA–ADAD ones. Stronger hydrogen bonds leads to a larger π depletion and a stronger stacking interaction.

3.3. Population analysis

A population analysis of the studied molecules was performed to corroborate the π depletion due to the hydrogen bonds of the dimers. The hydrogen bonds attract electrons from the nearest atoms of the aromatic rings. The electron attraction is stronger for the acceptor (A) part of the hydrogen bond than for the donor (D). The aromatic ring is for most of the studied molecules the acceptor of the hydrogen bond. The atoms of the aromatic rings donate electrons to the hydrogen bond making them less negatively charged in the dimer as compared to the monomer.

The electronic charges of the rings of the studied molecules are reported in Tables 4 and 5 The electronic charges are calculated for all atoms of the aromatic rings except for the one that is part of the hydrogen bond. Some of the studied molecules have fused aromatic rings. The electronic charge is then calculated separately for each ring implying that there is a double counting of the charges of the two common carbon atoms of the rings.

Table 4 Comparison of the charges (in e) of the aromatic rings with and without the presence of hydrogen bonding for the DDAA–AADD motif. The acceptor atom is excluded in the population analysis

Molecule	Dimer	Monomer	Difference
DDAA01-R	−0.17	−0.19	0.02
DDAA01-L	−0.64	−0.64	0.00
DDAA02	0.35	0.26	0.09
DDAA03-R	−0.12	−0.15	0.03
DDAA03-L	0.25	0.18	0.07
DDAA04-R	−0.04	−0.06	0.02
DDAA04-L	0.38	0.31	0.07
DDAA06-R	0.35	0.32	0.03
DDAA06-L	0.23	0.16	0.07
DDAA07	0.53	0.44	0.09
DDAA08-R	−0.56	−0.59	0.03
DDAA08-L	0.84	0.77	0.07

---

Table 5 Comparison of the charges (in e) of the aromatic rings with and without the presence of hydrogen bonding for the DADA–ADAD motif. The acceptor atom is excluded in the population analysis

Molecule	Dimer	Monomer	Difference
DADA01	0.21	0.18	0.03
DADA02	0.32	0.25	0.07
DADA03	0.12	0.11	0.01
DADA04	0.22	0.19	0.03
DADA05-R	0.67	0.66	0.01
DADA05-L	−0.50	−0.50	0.00
DADA06-R	−1.08	−1.08	0.00
DADA06-L	−1.10	−1.08	−0.02
DADA07-R	0.21	0.22	−0.01
DADA07-L	−0.21	−0.22	0.01
DADA08	0.18	0.16	0.02
DADA09-L	−0.39	−0.41	0.02
DADA09-R	−0.39	−0.41	0.02
DADA10-L	0.19	0.15	0.04
DADA10-R	0.37	0.35	0.02

---

Table 4 summarizes the charge of the rings for the DDAA–AADD molecules. For example, the DDAA01-R ring has a charge of −0.17 e and −0.19 e in the dimer and the monomer, respectively, whereas the DDAA01-L ring exhibits no change in the charge when forming the dimer. The DDAA01-R and the DDAA01-L rings do not participate in the hydrogen bonding, whereas on both sides of the rings there are acceptor and donor atoms leading to charge cancellation. The acceptor draws more electronic charge from the neighbouring atoms than the donor and therefore DDAA01-L exhibits no change in the charge when the monomers form the dimer. The hydrogen bonding of the dimers results in π depletion making the atoms of the ring near the donor of the hydrogen bond less negatively charged. The same pattern can be seen for all rings of the studied molecules except for DDAA01-L as discussed above.

Table 5 summarizes the charge of the aromatic rings of the DADA–ADAD molecules. The same trend is obtained for them as for DDAA–AADD. Aromatic rings are less negatively charged in the dimer than in the monomer. The DADA05-L, DADA06-R, DADA06-L and DADA07-L rings do not participate in the hydrogen bonding. When they form the dimer, the charges of the ring change by only 0.00, 0.00, −0.02 and −0.01 e, respectively. DADA05-L is on the opposite side of the molecule with respect to the hydrogen bonds implying that its charge does not change upon dimerization. The aromatic rings of DADA06 are distant from the hydrogen bonds. The left aromatic ring of DADA06 is further away from the hydrogen bond and is next to the donor. The right aromatic ring of DADA07 participates in the hydrogen bonding by donating a hydrogen, however, the ring is next to the carbonyl and hydroxyl functional groups. The presence of these functional groups leads to a resonance structure that directs more charge to the ring in the presence of hydrogen bonding.

3.4. LOLIPOP

The extent of the π depletion is also estimated using the local orbital locator (LOL) approach. LOL is a function of the kinetic energy density. LOLπ describes π depletion and provides information about the nature and location of electron pairs.⁸² The LOLIPOP index is a measure of the extent of π depletion reflecting the number and size of the LOLπ isosurfaces of the aromatic rings and can thus be used for quantifying the π-stacking ability. Large LOLIPOP values mean less π depletion which ultimately means a lower π-stacking ability, whereas smaller LOLIPOP values indicate that there is more π depletion and the π-stacking ability is expected to be stronger.

The LOLIPOP indices were calculated for the same aromatic rings of the monomer and the dimer. The first aim of the calculations was to investigate how the LOLIPOP values change when the molecules form dimers via hydrogen bonding. LOLIPOP indices for the molecules with the DDAA–AADD and DADA–ADAD hydrogen bonding motifs are summarized in Tables 2 and 3 respectively. It is evident from the Table 2 that the LOLIPOP indices decrease in the presence of the hydrogen bonds suggesting a depletion of π electrons and stronger π-stacking interaction of the dimers. All rings of the molecules follow the same trend. The LOLIPOP index for the right ring of the DDAA01 monomer is 1.96 and it decreases to 0.85 when it forms the dimer. The difference of 1.11 indicates π depletion. Similarly, the right ring of the DDAA04 monomer has a LOLIPOP index of 3.14 and it is 3.03 for the dimer. The LOLIPOP indices and the π-stacking energies predict π depletion.

The reliability of the LOLIPOP index for estimating π-stacking energies was studied by calculating the stacking energy as a function of the LOLIPOP index, which is shown in Fig. 5. A linear fit to the points in the graph yields an angular coefficient of 1.19 ± 0.52 kJ per mol per LI and an intercept of −33.22 ± 2.00 kJ mol⁻¹, where LI denotes the LOLIPOP value. The LOLIPOP calculations yield largely the correct general trend i.e., a larger LOLIPOP value means a weaker π–π interaction. However, there is not a very clear correlation between the binding energy and the LOLIPOP index as seen in Fig. 5 and in Tables 2 and 3. Thus, the LOLIPOP index is not a very accurate method for determining relative stacking energies.

Fig. 5 The stacking energy (in kJ mol⁻¹) of the aromatic rings of the monomers (M) and dimers (D) with the DDAA and DADA motif as a function of the LOLIPOP index. The line fitted to the points in the graph is also shown. The figure is made with GnuPlot.⁸¹

4. Conclusions

The effect of the hydrogen bonding on the π-stacking interaction of aromatic rings has been studied for quadruple hydrogen-bonded dimers. The hydrogen bonds lead to a transfer of π electrons from the aromatic rings towards the hydrogen bonds, which strengthens π-stacking interactions. We employed the MP2-F12 level of theory to calculate the energies of the hydrogen bonds and the π-stacking energies. The obtained strengths of the hydrogen bonds are compared to the benchmark energies computed at the CCSD(T) level.⁶¹ The strengths of the hydrogen bonds calculated at the MP2-F12 level correlate well with the ones obtained in the CCSD(T) calculations. The CCSD(T) binding energies are −27.3 ± 11.6 kJ mol⁻¹ stronger than the MP2-F12 ones. We show here that MP2-F12 calculations are a cost-effective method for calculating hydrogen-bonding energies since the obtained MP2-F12 energies agree within about 10% with CCSD(T) binding energies that are extrapolated to the Schrödinger limit. The agreement between the CCSD(T) and MP2-F12 energies suggest that also π-stacking energies calculated at the MP2-F12 level are accurate. The aromatic rings of the dimers exhibit stronger π-stacking interactions compared to the monomers as shown in Tables 2 and 3. Molecules with the DDAA–AADD and DADA–ADAD hydrogen-bonding motifs follow the same pattern. However, molecules with the DDAA–AADD hydrogen-bonding motif have stronger binding energies than the ones with the DADA–ADAD motif.

We also used the local orbital locator integrated pi over plane (LOLIPOP) approach and population analysis to estimate the depletion of π electrons from aromatic rings. The results obtained with the LOLIPOP approach also confirm that π electrons of the aromatic rings are transferred toward the hydrogen bonds. The population analysis shows that the atoms of the aromatic rings exhibit less electron charge in the dimers than in the monomers.

The MP2-F12 level of theory has proven to be an appropriate method for calculating the π-stacking energies for the monomers and the dimers. On the other hand, the absolute LOLIPOP indices do not correlate well with the stacking energies. The LOLIPOP approach can, however, be used for quantifying relative π-electron depletion of the aromatic rings upon changes to the immediate environment. Natural population analysis yields a general notion about the extent of the charge transfer from the aromatic rings towards the hydrogen bonds, which leads to a stronger π-stacking ability of the rings.

Author contributions

UA has performed the calculations under supervision of MPJ and DS. The results have been analyzed by UA and DS. All authors have contributed to writing the article.

Data availability

The data supporting this article have been included as part of the ESI.† The employed codes Turbomole version 7.8, Orca version 5.0, Molden version 7.2, Jmol version 14, and Gnuplot version 5.4 can be found at https://www.turbomole.org/, https://www.faccts.de/orca/, https://www.theochem.ru.nl/molden/, https://jmol.sourceforge.net/, and gnuplot.sourceforge.net, respectively. All programs except Turbomole are freely available.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work has been supported by the Academy of Finland through project numbers 314821 and 340583, by the Magnus Ehrnrooth Foundation, Oskar Öflund Foundation and by the Swedish Cultural Foundation in Finland. We acknowledge computational resources from CSC – IT Center for Science, Finland.

References

1. E. A. Meyer, R. K. Castellano and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 1210–1250.
2. C. G. Claessens and J. F. Stoddart, J. Phys. Org. Chem., 1997, 10, 254–272.
3. M. C. T. Fyfe and J. F. Stoddart, Acc. Chem. Res., 1997, 30, 393–401.
4. U. Samanta, D. Pal and P. Chakrabarti, Proteins: Struct., Funct., Bioinf., 2000, 38, 288–300.
5. S. Burley and G. Petsko, Science, 1985, 229, 23–28.
6. C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534.
7. P. Chakrabarti and U. Samanta, J. Mol. Biol., 1995, 251, 9–14.
8. N. Kannan and S. Vishveshwara, Protein Eng., Des. Sel., 2000, 13, 753–761.
9. R. Bhattacharyya, U. Samanta and P. Chakrabarti, Protein Eng., Des. Sel., 2002, 15, 91–100.
10. W. Yu, X.-Y. Wang, J. Li, Z.-T. Li, Y.-K. Yan, W. Wang and J. Pei, Chem. Commun., 2013, 49, 54–56.
11. L. S. Xie, E. V. Alexandrov, G. Skorupskii, D. M. Proserpio and M. Dinca, Chem. Sci., 2019, 10, 8558–8565.
12. J. Huang and M. Kertesz, J. Am. Chem. Soc., 2006, 128, 1418–1419.
13. J. Huang and M. Kertesz, J. Am. Chem. Soc., 2007, 129, 1634–1643.
14. J. Huang, S. Kingsbury and M. Kertesz, Phys. Chem. Chem. Phys., 2008, 10, 2625–2635.
15. Y.-H. Tian, J. Huang and M. Kertesz, Phys. Chem. Chem. Phys., 2010, 12, 5084–5093.
16. Y.-H. Tian and M. Kertesz, J. Phys. Chem. A, 2011, 115, 13942–13949.
17. X. Chen, F. Gao and W. Yang, Sci. Rep., 2016, 6, 29314.
18. Z. Su, H. Wang, K. Tian, W. Huang, C. Xiao, Y. Guo, J. He and X. Tian, Compos. Sci. Technol., 2018, 155, 1–10.
19. S. Shanmugaraju and P. S. Mukherjee, Chem. Commun., 2015, 51, 16014–16032.
20. L. Liu, J. Hao, Y. Shi, J. Qiu and C. Hao, RSC Adv., 2015, 5, 3045–3053.
21. N. Luisier, A. Ruggi, S. N. Steinmann, L. Favre, N. Gaeng, C. Corminboeuf and K. Severin, Org. Biomol. Chem., 2012, 10, 7487–7490.
22. H. Tang, S. Zhang, T. Huang, F. Cui and B. Xing, Environ. Sci.: Nano, 2020, 7, 984–995.
23. P. Venkatesan, M. Cerón, P. Ceballos, E. Pérez-Gutiérrez, S. Thamotharan and M. J. Percino, J. Mol. Struct., 2019, 1196, 306–322.
24. R. Shukla, T. Mohan, B. Vishalakshi and D. Chopra, J. Mol. Struct., 2017, 1134, 426–434.
25. R. Hou, W. Yuchi, Z. Bai, Z. Feng, Z. Guo, L. Kong, J. Bai and W. Li, Fuel, 2021, 299, 120920.
26. S. Burattini, B. W. Greenland, W. Hayes, M. E. Mackay, S. J. Rowan and H. M. Colquhoun, Chem. Mater., 2011, 23, 6–8.
27. G. Zhang, L. Lv, Y. Deng and C. Wang, Macromol. Rapid Commun., 2017, 38, 1700018.
28. J. Nie, J. Huang, J. Fan, L. Cao, C. Xu and Y. Chen, ACS Sustainable Chem. Eng., 2020, 8, 13724–13733.
29. J. Chen, Q. Peng, T. Thundat and H. Zeng, Chem. Mater., 2019, 31, 4553–4563.
30. W.-R. Zhuang, Y. Wang, P.-F. Cui, L. Xing, J. Lee, D. Kim, H.-L. Jiang and Y.-K. Oh, J. Controlled Release, 2019, 294, 311–326.
31. X. Yang, X. Zhang, Z. Liu, Y. Ma, Y. Huang and Y. Chen, J. Phys. Chem. C, 2008, 112, 17554–17558.
32. Y. Liang, X. Deng, L. Zhang, X. Peng, W. Gao, J. Cao, Z. Gu and B. He, Biomaterials, 2015, 71, 1–10.
33. F. Li, Y. Li, Z. Zhou, S. Lv, Q. Deng, X. Xu and L. Yin, ACS Appl. Mater. Interfaces, 2017, 9, 23586–23601.
34. J.-Y. Zeng, M.-Z. Zou, M. Zhang, X.-S. Wang, X. Zeng, H. Cong and X.-Z. Zhang, ACS Nano, 2018, 12, 4630–4640.
35. S.-Y. Fung, H. Yang, P. Sadatmousavi, Y. Sheng, T. Mamo, R. Nazarian and P. Chen, Adv. Funct. Mater., 2011, 21, 2456–2464.
36. X. Song, H. Guo, J. Tao, S. Zhao, X. Han and H. Liu, Chem. Eng. Sci., 2018, 187, 406–414.
37. R. Bao, B. Tan, S. Liang, N. Zhang, W. Wang and W. Liu, Biomaterials, 2017, 122, 63–71.
38. W. Miao, G. Shim, G. Kim, S. Lee, H.-J. Lee, Y. B. Kim, Y. Byun and Y.-K. Oh, J. Controlled Release, 2015, 211, 28–36.
39. N. Liu, J. Han, X. Zhang, Y. Yang, Y. Liu, Y. Wang and G. Wu, Colloids Surf., B, 2016, 145, 401–409.
40. C. Sun, Y. Liang, N. Hao, L. Xu, F. Cheng, T. Su, J. Cao, W. Gao, Y. Pu and B. He, Org. Biomol. Chem., 2017, 15, 9176–9185.
41. P.-F. Cui, W.-R. Zhuang, X. Hu, L. Xing, R.-Y. Yu, J.-B. Qiao, Y.-J. He, F. Li, D. Ling and H.-L. Jiang, Chem. Commun., 2018, 54, 8218–8221.
42. X. Deng, Y. Liang, X. Peng, T. Su, S. Luo, J. Cao, Z. Gu and B. He, Chem. Commun., 2015, 51, 4271–4274.
43. L. Yang, C. Zhang, C. Ren, J. Liu, Y. Zhang, J. Wang, F. Huang, L. Zhang and J. Liu, ACS Appl. Mater. Interfaces, 2019, 11, 331–339.
44. C. M. Spillmann, J. Naciri, W. R. Algar, I. L. Medintz and J. B. Delehanty, ACS Nano, 2014, 8, 6986–6997.
45. Y. Shi, R. van der Meel, B. Theek, E. Oude Blenke, E. H. E. Pieters, M. H. A. M. Fens, J. Ehling, R. M. Schiffelers, G. Storm, C. F. van Nostrum, T. Lammers and W. E. Hennink, ACS Nano, 2015, 9, 3740–3752.
46. X. Hu, J. Hu, J. Tian, Z. Ge, G. Zhang, K. Luo and S. Liu, J. Am. Chem. Soc., 2013, 135, 17617–17629.
47. H. Wang, J. Chen, C. Xu, L. Shi, M. Tayier, J. Zhou, J. Zhang, J. Wu, Z. Ye, T. Fang and W. Han, Theranostics, 2017, 7, 3638–3652.
48. Z. Liu, A. Fan, K. Rakhra, S. Sherlock, A. Goodwin, X. Chen, Q. Yang, D. Felsher and H. Dai, Angew. Chem., Int. Ed., 2009, 48, 7668–7672.
49. F. Li, Y. Zhu, B. You, D. Zhao, Q. Ruan, Y. Zeng and C. Ding, Adv. Funct. Mater., 2010, 20, 669–676.
50. C. Ge, J. Du, L. Zhao, L. Wang, Y. Liu, D. Li, Y. Yang, R. Zhou, Y. Zhao, Z. Chai and C. Chen, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16968–16973.
51. Y. Lai, Y. Long, Y. Lei, X. Deng, B. He, M. Sheng, M. Li and Z. Gu, J. Drug Targeting, 2012, 20, 246–254.
52. M.-G. Kim, Y. Shon, J. Kim and Y.-K. Oh, J. Natl. Cancer Inst., 2016, 109(1–10), djw186.
53. G. Cooke and V. M. Rotello, Chem. Soc. Rev., 2002, 31, 275–286.
54. O. Altintas, M. Artar, G. ter Huurne, I. K. Voets, A. R. A. Palmans, C. Barner-Kowollik and E. W. Meijer, Macromolecules, 2015, 48, 8921–8932.
55. X. Ji, K. Jie, S. C. Zimmerman and F. Huang, Polym. Chem., 2015, 6, 1912–1917.
56. K. M. Hutchins, R. H. Groeneman, E. W. Reinheimer, D. C. Swenson and L. R. MacGillivray, Chem. Sci., 2015, 6, 4717–4722.
57. M. Handke, T. Adachi, C. Hu and M. D. Ward, Angew. Chem., Int. Ed., 2017, 56, 14003–14006.
58. J. W. G. Bloom and S. E. Wheeler, Angew. Chem., Int. Ed., 2011, 50, 7847–7849.
59. Jmol: an open-source Java viewer for chemical structures in 3D., https://www.jmol.org/(accessed 21.7.2024).
60. P. K. Baruah and S. Khan, RSC Adv., 2013, 3, 21202–21217.
61. U. Ahmed, C. Daub, D. Sundholm and M. P. Johansson, Phys. Chem. Chem. Phys., 2024, 26, 24470–24476.
62. J. F. Gonthier, S. N. Steinmann, L. Roch, A. Ruggi, N. Luisier, K. Severin and C. Corminboeuf, Chem. Commun., 2012, 48, 9239–9241.
63. F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100.
64. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137.
65. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2004, 121, 11507.
66. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023.
67. E. R. Davidson, Chem. Phys. Lett., 1996, 260, 514–518.
68. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
69. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
70. O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346–354.
71. W. Klopper and C. C. M. Samson, J. Chem. Phys., 2002, 116, 6397–6410.
72. R. A. Bachorz, F. A. Bischoff, A. Glöβ, C. Hättig, S. Höfener, W. Klopper and D. P. Tew, J. Comp. Chem., 2011, 32, 2492–2513.
73. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
74. P. Deglmann and F. Furche, Chem. Phys. Lett., 2002, 362, 511–518.
75. H. Schmider and A. Becke, THEOCHEM, 2000, 527, 51–61.
76. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
77. G. Schaftenaar, Molden, https://www.theochem.ru.nl/molden/, (accessed 21.7.2024).
78. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
79. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
80. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
81. T. Williams, C. Kelley and Co-workers, Gnuplot 5.4: an interactive plotting program, https://gnuplot.sourceforge.net/(accessed 21.7.2024).
82. S. N. Steinmann, Y. Mo and C. Corminboeuf, Phys. Chem. Chem. Phys., 2011, 13, 20584–20592.

---

Footnote

† Electronic supplementary information (ESI) available: The Cartesian coordinates of the studied molecules and pictures of the molecular structures of the studied molecules. See DOI: https://doi.org/10.1039/d4cp02889a

---