An ab initio spectroscopic model of the molecular oxygen atmospheric and infrared bands†
Received
1st July 2024
, Accepted 20th September 2024
First published on 15th October 2024
Abstract
We present a unified variational treatment of the magnetic dipole matrix elements, Einstein coefficients and line strength for general open-shell diatomic molecules in the general purpose diatomic code Duo. Building on previous work in which similar expressions for the electric quadrupole transitions were developed, we also present a complete ab initio spectroscopic model for the infrared, electric dipole-forbidden, spectrum of the 16O2 molecule. The model covers seven states, namely the X 3Σ−g, a 1Δg, b 1Σ+g, I 1Πg, II 1Πg, I 3Πg and II 3Πg states, for which 7 potential energy, 6 electronic angular momentum, 7 spin–orbit, and 14 quadrupole moment curves are calculated using ic-MRCI theory and an aug-cc-pV5Z basis set. These curves are diabatised to remove avoided crossings between the excited Π states, and the resultant properties are used to produce a line list for higher-order transitions of astrophysical interest.
1. Introduction
Oxygen is the most abundant element on Earth, and the third most abundant element in the universe. In its diatomic molecular form, 16O2, it is also the second most abundant molecule in Earth's atmosphere and consequently plays a critical role in the metabolism of living organisms. Aside from its biological importance, oxygen also plays an important part in many chemical reactions, both industrial and geophysical. Due to it's ubiquity, 16O2 has been the focus of many studies and reviews spanning more than seven decades.1–8 The 16O2 molecule is also of special interest in an exoplanetary context, owing to both it's geophysical role9–14 and its potential as a biosignature on Earth-like exoplanets.15–18
Detecting the presence of 16O2 in exoplanetary atmospheres requires spectral characterisation across a broad range of frequencies, particularly in the infra-red region of the electromagnetic spectrum, where telescopes such as JWST and the ELT are primed to perform measurements of astronomical spectra.18–22 The existing body of work has produced extremely accurate spectrosopic data for a number of transitions, focused primarily on the narrow region of the spectrum that corresponds to Earth's atmospheric bands. However, Due to the limitations of experimental techniques, a broader characterisation of the 16O2 spectrum has yet to be completed.
Owing to it's molecular symmetry, the homonuclear diatomic 16O2 molecule has zero permanent electric dipole moment (E1) and, as a result, pure vibrational and rotational transitions are forbidden in the electric dipole approximation. The three lowest lying electronic states (X 3Σ−g, a 1Δg and b 1Σ+g), which comprise the infrared spectrum, all have gerade symmetries. Thus transitions between them are also forbidden by electric dipole selection rules. The strongest absorption bands for the oxygen molecule are electric dipole bands in the ultraviolet region. These include transitions to lowest energy ungerade states are c 1Σ−u, A′3Δu and A 3Σ+u, (known as the Herzberg bands) and the B 3Σ−u–b 1Σ+g bands, which borrow intensity from the electric dipole Schumman-Runge B 3Σ−u–X 3Σ−g transitions.23–27 However, the long wavelength of these absorption bands make them unlikely candidates for detection in an exoplanetary context. Telescopes for atmospheric remote sensing, such as CHEOPS, JWST, ARIEL and PLATO target the infrared and visible region, which is dominated in 16O2 by higher order magnetic dipole (M1) and electric quadrupole (E2) transitions.
The atmospheric A, B and γ-bands, due to the fundamental and first two overtone b 1Σ+g ← X 3Σ−g transitions,28–32 and infrared transitions in the ground electronic state have been the focus of numerous studies dating back to the 1920s.33–37 The structure of these bands was explained primarily by M1 interactions,38–40 and although it was known that these should be accompanied by significantly weaker E2 lines,39 they were not observed in terrestrial spectra until 1980.41 Infrared E2 transitions within the ground electronic state were also observed in 198142,43 and more recently measured in the laboratory.44 Additional quadrupole bands, due to the a 1Δg–X 3Σ−g transition,34,45 have also been observed in solar spectra,46 and the magnetic dipole counterparts in atmospheric afterglow.47
The Noxon band,48 which consists of transitions between the first two excited states, b 1Σ+g–a 1Δg, is also of interest. It is forbidden for both the E1 and M1 moments due to, respectively, the gerade symmetry of both states and the ΔΛ = 2 property. The absence of spin–orbit coupling between the two states means the Noxon band is purely electric quadrupolar in nature. Additionally, the same spin–orbit coupling between the two Σg states that generates the b 1Σ+g–B 3Σ−u transitions results in the Noxon band contributing significantly to the quadrupolar intensity of the b 1Σ+g–X 3Σ−g and a 1Δg–X 3Σ−g bands, a phenomenon first described by Sveshnikova and Minaev49 and subsequently observed in various experiments.50–52
The ExoMol project aims to provide accurate line lists for a wide range of molecules relevant to exoplanetary applications. In the case of diatomic molecules, the Duo program allows one to construct spectroscopic models for diatomic molecules with an arbitrary number of potential energy curves and couplings. These can be represented as either a grid of ab initio values or as an analytic representation using the various functional forms that are supported. For a full account of the Duo code we refer the reader to Yurchenko et al.53 Recent extensions to this program now allow for the calculation of magnetic dipole and electric quadrupole line strengths, which are crucial to the spectra of many homonuclear molecules such as 16O2. Once the absorption intensities have been computed, the ExoCross program allows one to create absorption cross-sections for a range of line profiles that account for effects such as collisional broadening and temperature dependence.54 In the case of molecular oxygen, for example, the terrestrial absorption lines are strongly determined by collisions with N2 and other O2 molecules.55 However, for other exoplanets, these effects are likely to vary considerably, and such considerations must be made on a case-by-case basis depending on the context (atmospheric pressure, abundance, etc.) in which the molecule at hand is studied.
A considerable amount of effort has been devoted to establishing highly accurate potential energy curves for a range of electronic states of 16O2. In 2010 Bytautas et al.56 employed Dunning's correlation-consistent triple and quadruple-zeta basis sets to determine the full configuration interaction energy for the three lowest-lying electronic states; X 3Σ−g, a 1Δg, and b 1Σ+g, including core-valence correlations and relativistic contributions. Using a method developed in earlier work, which they term correlation energy extrapolation by intrinsic scaling, they extrapolate these energies to the complete basis set limit.56,57 In 2014 Liu et al.58 produced accurate PECs for 22 electronic states as well 54 spin–orbit coupling curves via the complete active space self-consistent field (CASSCF) method, and a subsequent internally contracted multireference configuration interaction calculation including the Davidson correction (icMRCIQ).
2. Magnetic dipole linestrengths
In a previous work we reported expressions for the electric quadrupole linestrengths. These expressions were implemented in the variational spectroscopic program Duo,59 and verified using accurate spectral data for a variety of molecules, including H2 and the Noxon band of 16O2. Here we report similar expressions for general magnetic dipole transitions in diatomic molecules. Duo uses the Hund's case (a) basis set in the following form:| | | |φi〉 = |ξΛ〉|SΣ〉|ξv〉|JΩM〉 | (1) |
where J is the total angular momentum, M is a projection of J on the laboratory Z-axis in units of ħ, S is the total electronic spin angular momentum, Σ is the projection of the spin of electrons on molecular z-axis, ξ are indexes of the ξ-th electronic state, Λ is the projection of the electronic angular momentum on molecular z-axis, Ω = Λ + Σ (projection of the total angular momentum on molecule z-axis) and v is the vibrational quantum number.
The linestrengths in the representation of these basis set functions are then given by
| |  | (2) |
where
m′ indexes the spherical components of the magnetic dipole moment in the molecule-fixed frame. The Wigner 3
j symbol implies the following selection rules
The magnetic dipole moment ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) arises due to the motion of charged particles. In the case of diatomic molecules, the primary magnetic dipole moment is due to negatively charged electrons with non-zero angular momenta. This magnetic moment is the sum of the orbital electronic angular momentum, and the spin electronic angular momentum as
arises due to the motion of charged particles. In the case of diatomic molecules, the primary magnetic dipole moment is due to negatively charged electrons with non-zero angular momenta. This magnetic moment is the sum of the orbital electronic angular momentum, and the spin electronic angular momentum as
where
gs is the spin Lande
g-factor. The matrix elements can then be written in terms of the raising and lowering operators
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) ±
± and
Ŝ±| |  | (6) |
| |  | (7) |
| |  | (8) |
3. Intensity structure of the infrared bands b 1Σ+g–X 3Σ−g, a 1Δg–X 3Σ−g and X 3Σ−g–X 3Σ−g
The composition of the quadrupole and magnetic intensities of the forbidden atmospheric bands of 16O2 has been expounded in detail throughout the literature.50–52,60,61 In particular, we highlight the work of Minaev et al.,61 who provide a comprehensive account of individual contributions to the line strength of the b 1Σ+g–X 3Σ−g a 1Δg–X 3Σ−g, and Noxon b 1Σ+g–a 1Δg bands. The electric quadrupole transitions are, in general, weaker than magnetic dipole transitions, but nonetheless have been observed in both the laboratory30,48,62 and in atmospheric solar spectra.41,46 They are present in both the b 1Σ+g–X 3Σ−g, and a 1Δg–X 3Σ−g bands. Crucial to an account of the atmospheric bands are a set of highly excited Π states, namely the 1 1Πg, 2 1Πg, 1 3Πg, and 2 3Πg states.51,63 The two pairs of states with the same spin multiplicity each exhibit avoided crossings, with the 2 3Πg and 2 1Πg states being pre-dissociative in nature. In order to treat this collection of Π states we transform to the diabatic representation64 to produce the II 1Πg, I 1Πg, II 3Πg, and I 3Πg states. The II 1Πg and II 3Πg exhibit shallow potential wells with minima approximately 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 above the zero-point energy, which give rise to a small number of bound vibrational levels. In the following, we analyse the main contributions to the electric quadrupole and magnetic dipole line strengths for three systems b 1Σ+g–X 3Σ−g a 1Δg–X 3Σ−g and X 3Σ−g–X 3Σ−g.
000 cm−1 above the zero-point energy, which give rise to a small number of bound vibrational levels. In the following, we analyse the main contributions to the electric quadrupole and magnetic dipole line strengths for three systems b 1Σ+g–X 3Σ−g a 1Δg–X 3Σ−g and X 3Σ−g–X 3Σ−g.
3.1. Electric quadrupole transitions
The b 1Σ+g–X 3Σ−g electric quadrupole intensities are comprised of two quadrupole moments corresponding to components of the irreducible quadrupole moment operator, (see Somogyi et al.65 for discussion of the irreducible representation). The first is the Q(2)0 moment, which arises as a result of spin–orbit mixing between the X 3Σ−g and b 1Σ+g states, and generates two diagonal contributions to the total intensity for ΔΩ = 0 transitions. The second is the Q(2)±1 component, which generates ΔΩ = ±1 transitions via spin–orbit coupling of the X 3Σ−g state and the excited 1Πg states. Here Ω = Λ + Σ is the projection of the total electronic angular momentum on the molecular axis, with Λ and Σ the orbital and spin angular momenta respectively. Denoting the first-order SOC-perturbed expressions with a subscript p, for the b 1Σ+g–X 3Σ−g line strength we write| |  | (9) |
| |  | (10) |
| | 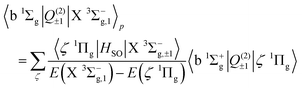 | (11) |
| | 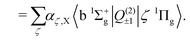 | (12) |
The 1Πg states lies far in energy above the X 3Σ−g, and the thus primary contribution to the b 1Σ+g–X 3Σ−g band comes from the difference in permanent electric quadrupole moments of the two Σ states.
We now turn to the quadrupole line strength of the a 1Δg–X 3Σ−g band, which consists of two components, as given by
| |  | (13) |
| |  | (14) |
| | 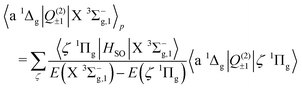 | (15) |
| |  | (16) |
The first component arises primarily from Q(2)±2, and borrows strength from the Noxon band (b 1Σ+g–a 1Δg) via spin–orbit mixing of the X 3Σ−g with the b 1Σ+g state. There is an additional contribution to this band from the 3Πg–X 3Σ−g quadrupole moments due to spin–orbit mixing of the a 1Δg state and the 3Πg states. The same 3Πg–X 3Σ−g quadrupole moment also contributes to the second (weaker) component of the a 1Δg–X 3Σ−g line strength, via Q(2)±1, together with the a 1Δg–1Πg quadrupole moment due to spin–orbit mixing between the X 3Σ−g and 1Πg states. The dominant contribution comes from the Noxon band, due to the fact that the b 1Σ+g state and a 1Δg state are closely separated in energy, and the transition quadrupole moment between them is reasonably strong. This hypothesis is supported by the work of Mishra et al.51, in which the ratio Q(2)±1/Q(2)±2 is calculated for various lines with a value in the range 0.012–0.055.
Finally, the electric quadrupole moment contribution to the X 3Σ−g–X 3Σ−g intensities arise predominantly from the diagonal quadrupole moment of the ground electronic state, but with additional contributions from the spin–orbit coupling with the 1Πg
| |  | (17) |
| | 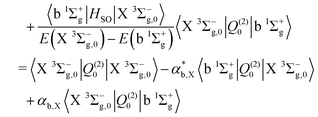 | (18) |
| |  | (19) |
| |  | (20) |
3.2. Magnetic dipole transitions
The strongest of the 16O2 atmospheric transitions are the magnetic dipole transitions in the b 1Σ+g–X 3Σ−g band with the main contributions to the line strengths given by| | 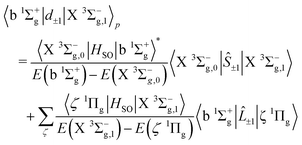 | (21) |
| |  | (22) |
which is composed of both spin and orbital angular momenta. However the relative strengths of the spin–orbit couplings imply that the primary contribution arises as a result of intensity borrowing from the spin–flip transitions between the Σ = 0 and Σ = ±1 sub-levels of the X 3Σ−g state through spin–orbit coupling between the b 1Σ+g and X 3Σ−g states. Electronic orbital magnetic moments contribute only weakly to this branch through spin–orbit mixing of the X 3Σ−g and 1Πg states, and of the b 1Σ+g and 3Πg states.
Magnetic dipole transitions in the a 1Δg–X 3Σ−g band are considerably weaker, and enabled only through spin–orbit coupling of the a 1Δg and X 3Σ−g states with the 3Πg and 1Πg states, respectively, as given by
| |  | (23) |
| | 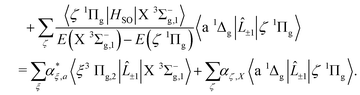 | (24) |
Finally, the X 3Σ−g–X 3Σ−g magnetic dipole line strength, composed of rotation–vibration and pure rotational transitions arises as a result of two magnetic dipole moments. The first couples spin sublevels in the X 3Σ−g state, and the second is composed of the diagonal spin magnetic moment, as given by
| | | 〈X 3Σ−g,1|d±1|X 3Σ−g,0〉p = 〈X 3Σ−g,1|S±1|X 3Σ−g,0〉 | (25) |
| | | 〈X 3Σ−g,Ω|d0|X 3Σ−g,Ω〉p = 〈X 3Σ−g,Ω|Ŝz|X 3Σ−g,Ω〉. | (26) |
4. Spectroscopic model
4.1. Electronic structure calculations
There are few ab initio calculations of the electric quadrupole moment functions in the literature. The earliest calculations of the E2 moment for 16O2 were made by Kotani et al.66 in 1957, followed by Varanasi67 in 1974. In recent years accurate multipole moment calculations at room temperature were made by Bartolomei et al.68 and Couling and Ntombela.69 In each case however, the quadrupole moment is given for only a single geometry. In 1997 Lawson and Harrison70 calculated the permanent E2 moment for a range of geometries. They use the aug-cc-pVQZ basis and MRCI method to obtain the permanent E2 moment of the X 3Σ−g state in the range 2 to 12a0. Minaev71 details MCSCF calculations for the permanent E2 moment for a narrow range of geometries between 1 to 1.8 Å, obtaining a variety of values for 〈X 3Σ−g|Qzz|X 3Σ−g〉 across different active space. The results broadly agree with experimental values and lie in the range −0.180 to −0.230ea02. The need for further calculations of electric quadrupole moments in order to obtain a spectroscopic model of the 16O2 atmospheric bands is evident, particularly transition moments and the permanent moments for excited states.
The necessary set of electric quadrupole moment curves (EQMC s), spin–orbit coupling curves (SOCs), orbital electronic angular momentum curves (EAMCs), and potential energy curves (PECs), are obtained with electronic structure calculations using the Molpro program.72 Initially MCSCF calculations are performed with CAS(12,12) and an diffusion augmented, correlation-consistent, polarized quintuple-zeta basis set (aug-cc-pV5Z). The optimized orbitals from this MCSCF calculation are then used as the orbitals for a subsequent MRCI calculation in the same active space.
The MRCI calculations include a variety of symmetry groups and spin multiplicities in order to obtain a complete set of wavefunctions and potential energy curves for the required electronic states, and are detailed in Table 1. Calculations are made for a number of geometries in the range 0.090–0.300 nm for the X 3Σ−g, a 1Δg and b 1Σ+g states, and in the range 0.094–0.300 nm for the 1 1Πg, 2 1Πg 1 3Πg, and 2 3Πg states. For some geometries the MOLPRO calculations fail to converge and these are omitted from the final dataset.
Table 1 This table details the number of states calculated for a given combination of irreducible symmetry group and spin multiplicity. It also shows the label of the corresponding states obtained from each calculation
| Symmetry |
(2S + 1) |
No. states |
State(s) |
| Ag |
1 |
2 |
b 1Σ+g, a 1Δg(xx) |
| B1g |
3 |
1 |
X
3Σ−g |
| B1g |
1 |
1 |
a 1Δg(xy) |
| B2g |
1 |
2 |
I 1Πg(x), II 1Πg(x) |
| B3g |
1 |
2 |
I 1Πg(y), II 1Πg(y) |
| B2g |
3 |
2 |
I 3Πg(x), II 3Πg(x) |
| B3g |
3 |
2 |
I 3Πg(y), II 3Πg(y) |
The wavefunctions obtained are used in subsequent MRCI calculations of the seven spin–orbit couplings, nine quadrupole moments, and the six orbital angular momentum curves required to reproduce the matrix elements in eqn (9)–(22). In addition to the quadrupole moments present in eqn (9)–(16), the permanent quadrupole moments of the a 1Δg, and the four Π states are also obtained. Finally, curves involving the Π states are transformed to the diabatic representation using the numerical procedure described by Brady et al.64 These diabatic curves are presented in Fig. 2–6.
 |
| | Fig. 1 The electric quadrupole and magnetic dipole line list at 296 K for 16O2 in the wavenumber range 0 to 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. 000 cm−1. | |
 |
| | Fig. 2 The PECs obtained from ab initio electronic structure calculations (dots) along with the continuous curves (solid lines) obtained by fitting the analytic potential energy functions to these ab initio data. | |
 |
| | Fig. 3 The SOCs obtained from ab initio electronic structure calculations (dots) along with the continuous curves (solid lines) obtained by fitting the analytic coupling functions to these ab initio data. | |
 |
| | Fig. 4 The permanent EQMCs obtained from ab initio electronic structure calculations (dots) along with the continuous curves (solid lines) obtained by fitting the analytic coupling functions to these ab initio data. | |
 |
| | Fig. 5 The transition EQMCs obtained from ab initio electronic structure calculations (dots) along with the continuous curves (solid lines) obtained by fitting the analytic coupling functions to these ab initio data. | |
 |
| | Fig. 6 The EAMCs obtained from ab initio electronic structure calculations (dots) along with the continuous curves (solid lines) obtained by fitting the analytic coupling functions to these ab initio data. | |
A challenge arises in evaluating the accuracy of ab initio quadrupole moment curves due to a dearth of experimental data. Typically such measurements consist of only a single value, usually vibrationally averaged over the v = 0 ground state. In 1968 Buckingham et al.73 obtained a value Q(2)0 = − 0.30 ± 0.08ea02via pressure induced birefringence. Cohen and Birnbaum74,75 obtain |Q(2)0| = 0.25ea02via far-infrared spectra, which is in agreement with the measurement of |Q(2)0| = 0.22ea02 made by Evans.76 More recently Couling and Ntombela69 accurately measured the room-temperature quadrupole moment via electric-field-gradient-induced birefringence (EFGIB) to be Q(2)0 = −0.2302 ± 0.0061ea02. The ground state vibrationally averaged quadrupole moment obtained via Duo from the ab initio data presented above has a value of Q(2)0 = −0.223ea02. The uncertainty quoted by Couling and Ntombela is the standard deviation, and so the ab initio value obtained in the present work lies well within two standard deviations from their mean experimental value.
4.2. Analytic curves
In order to fill in gaps in the ab initio data where the MOLPRO calculations fail to converge, and also to eliminate discontinuities that are characteristic of ab initio calculations across multiple geometries, we fit analytic functions for each of the curves described in Section 4.1. This also allows one to obtain spectroscopic parameters for the potential energy curves, and other characteristic quantities. The parameters obtained from fitting to the ab initio data can subsequently be used as a starting point for the empirical refinement of the calculated energy levels to experimental energies.
4.2.1. Potential energy curves.
To begin we fit the Morse/long-range (MLR) potential energy function to the five bound states under consideration. The Morse/long-range function was introduced by Le Roy et al.77 and later refined by Le Roy et al.,78 and improves on the well-known Morse potential by accounting for the long-range behaviour of molecular potential energy surfaces. We fit a form of the MLR potential described by the following expression,| |  | (27) |
with Te the potential minimum and Ae the dissociation energy, relative to the zero-point energy. The polynomial function β(r) and the long-range function u(r) ensure the function has the correct long-range behaviour,| | 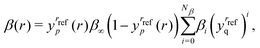 | (28) |
| | 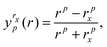 | (29) |
where p is an integer greater than 1, the value of which is a hyper-parameter of the fitting procedure. The long-range function is  , where one or more of the coefficients Cn may be equal to zero. In the limit r → ∞, the function approaches the
, where one or more of the coefficients Cn may be equal to zero. In the limit r → ∞, the function approaches the  where re is the equilibrium bond length, and rref is some reference geometry. In all fits we select rref := re for simplicity.
where re is the equilibrium bond length, and rref is some reference geometry. In all fits we select rref := re for simplicity.
For the two dissociative potentials (I 1Πg and I 3Πg) we fit a repulsive potential in the form of a Laurent power series in the radial distance,
| |  | (30) |
where
ai are the fitted coefficients. The fits for all potential energy curves are performed with the Python library scipy, using the Levenberg–Marquadt (LM) algorithm in the case of the dissociative potentials and the trust region reflective (TRF) algorithm with a soft L1 loss function in the case of the bound potentials. For each of the bound potentials we set a single dissociation parameter, namely
C6, to be non-zero and fix the value as
C6 = 2.95 × 10
5. The equilibrium bond length is bounded to remain within the range 0.9–3.0 Å, and the dissociation and excitation energies are bounded in the range of positive real numbers.
In Table 2 we compare several key spectroscopic parameters obtained from the bound potentials obtained in this work to experimental and other ab initio values.
Table 2 Key spectroscopic parameters obtained for the bound potentials presented in this work, compared to those obtained by Liu et al.58 and experimental parameters from Ruscic et al.79 and Herzberg.3 Values in square brackets indicate uncertain data, and those in rounded brackets indicate vibrationally averaged values obtained for the ground v = 0 state
|
|
D
e (eV) |
T
e (cm−1) |
R
e (nm) |
ω
e (cm−1) |
B
e (cm−1) |
102αe (cm−1) |
| X 3Σ−g |
5.2146 |
0.0 |
0.12078 |
1590.16 |
1.4478 |
1.6207 |
| Exp.79 |
5.2142 |
0.0 |
— |
— |
— |
— |
| Exp.3 |
5.2132 |
0.0 |
0.12075 |
1580.19 |
1.4456 |
1.59 |
| Cal.58 |
5.2203 |
0.0 |
0.12068 |
1581.61 |
1.4376 |
1.2539 |
| a 1Δg |
4.2313 |
7930.39 |
0.12229 |
1495.69 |
1.4083 |
1.4283 |
| Exp.2 |
4.2258 |
7918.11 |
0.12157 |
(1509.3) |
1.4263 |
1.71 |
| Exp.3 |
— |
7918.1 |
— |
[1483.5] |
1.4264 |
1.71 |
| Cal.58 |
4.2258 |
7776.43 |
0.12147 |
1491.07 |
1.3814 |
0.4238 |
| b 1Σ+g |
3.5786 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 195.4 195.4 |
0.12366 |
1423.20 |
1.3798 |
1.6138 |
| Exp.2 |
3.5772 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 195.31 195.31 |
0.12268 |
(1432.67) |
1.4005 |
1.8169 |
| Cal.58 |
3.6058 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 099.92 099.92 |
0.12258 |
1438.65 |
1.4030 |
1.8018 |
| II 3Πg |
0.6135 |
52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800.3 800.3 |
0.14880 |
625.40 |
0.9520 |
4.1312 |
| II 1Πg |
1.2633 |
63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500.6 500.6 |
0.14540 |
880.86 |
0.9964 |
2.0501 |
4.2.2. Spin–orbit coupling curves.
The use of a polynomial decay expansion as an analytic representation of the spin–orbit coupling interaction was introduced by Prajapat et al.80 and has been used in a number of diatomic spectroscopic models (see e.g. Semenov et al.81 or Yurchenko et al.82). The polynomial decay function has the form| |  | (31) |
where yp is the Šurkus variable defined by eqn (29), and z is taken as the damped coordinate| |  | (32) |
We use the same representation to parameterize all seven SOCs in the present work. Initially we attempt to fit a 3rd order polynomial for all SOCs, using TRF and a linear loss function. For each SOC the order of the polynomial is then increased until the fit converges with an R2 value greater than 0.95. This ensures a good fit whilst minimizing the degree of overfitting.
4.2.3. Transition moment curves.
Analytic representations of the EQMC s have not been widely used in the existing literature. We find that the LM algorithm is successful in parameterizing the fourteen quadrupole moment curves with the same polynomial decay function as for the spin–orbit curves. Though we find that higher order polynomials are often required in order to reach convergence. To obtain good fits of the EAMCs we find a variety of analytic forms are needed. The polynomial decay function defined by eqn (29) and (32) is used to represent the 〈a 1Δg|Ly|II 1Πg〉 curve, with a 6-th order polynomial. The 〈X 3Σ−g|Lx|I 3Πg〉 EAMC is represented by a simple polynomial expansion of the 10-th order with the form| | | F(r) = Te + a1(r − rref) + a2(r − rref)2+⋯ | (33) |
For all other EAMCs we find a good fit is possible using the so-called irregular Chebyshev polynomial, which was originally introduced by Medvedev and Ushakov83 to represent electronic dipole moment curves and has the form
| |  | (34) |
where
Tk(
z) are the Chebyshev polynomials of the first kind,
bk are the expansion coefficients and
maps the
r ∈ [0,∞] half-infinite interval to the
z ∈ [−1, +1] finite interval. The parameters
bi and
ci are the fitting parameters. As with the SOCs, we find a variety of polynomial orders are required to fit individual EAMCs. The parameters for all fitted curves are given in the ESI.
†
4.2.4. Spin–spin splitting curve.
In addition to the ab initio curves given above, we must also account for the spin splitting of the triplet ground state, which is crucial for the production of the b 1Σ+g–X 3Σ−g magnetic dipole transitions eqn (22). Tinkham and Strandberg84 estimated the magnitude of the separation as 1.17 cm−1. The spin splitting of the X 3Σ−g electronic state can be accounted for by including the phenomenological spin–spin operator term in the rovibronic Hamiltonian.59 Vahtras et al.85 present calculations of the spin–orbit and spin–spin contributions to the zero-field splitting (ZFS) of the X 3Σ−g ground state and estimate that the spin–spin contribution at the equlibrium geometry is approximately 40% of the total energy difference between the Ω = 0 and Ω = 1 states, DSS = 1.57 cm−1. We provide the values presented in their work at different internuclear geometries to the Duo program, which then performs a cubic spline interpolation on the grid of internuclear geometries described in Section 5.
5. Results
Using the analytic representation of the ab initio curves obtained in Section 4.2, we build a spectroscopic model for the electric quadrupole and magnetic dipole transitions of 16O2 in the infrared and visible region of the electromagnetic spectrum. We include transitions between all states lower in energy than 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. In solving the nuclear Schrödinger equation, a vibrational sinc-DVR basis set for each electronic state is defined on a grid of 1001 points in the range 0.90–3.00 Å. The vibronic basis sets are then truncated to the lowest 30 vibrational levels in the case of the X 3Σ−g, a 1Δg, and b 1Σ+g states, and to the lowest 300 vibrational levels for the II 1Πg, II 3Πg, I 1Πg, and I 3Πg states. We then solve for rotational levels up to J = 50. A large number of vibrational basis states are retained for the weakly bound and dissociative Π state in order to represent continuum states above the dissociation energy.86,87
000 cm−1. In solving the nuclear Schrödinger equation, a vibrational sinc-DVR basis set for each electronic state is defined on a grid of 1001 points in the range 0.90–3.00 Å. The vibronic basis sets are then truncated to the lowest 30 vibrational levels in the case of the X 3Σ−g, a 1Δg, and b 1Σ+g states, and to the lowest 300 vibrational levels for the II 1Πg, II 3Πg, I 1Πg, and I 3Πg states. We then solve for rotational levels up to J = 50. A large number of vibrational basis states are retained for the weakly bound and dissociative Π state in order to represent continuum states above the dissociation energy.86,87
In this work we present a line list using a purely ab initio model, without empirical refinement of the potential energy or coupling curves. In Fig. 1 we show the absorption intensities for the electric quadrupole and magnetic dipole moments, respectively, above a threshold of 10−30 cm molcule−1. In Fig. 7 we present stick spectra to compare the calculated intensities and line positions to accurate known data from the HITRAN database88, namely the X 3Σ−g(v = 1) → X 3Σ−g (v = 0) (E2), X 3Σ−g (v = 0) → X 3Σ−g (v = 0) (M1), a 1Δ−g (v = 0) → X 3Σ−g (v = 0), and b 1Σ+g (v = 0) → X 3Σ−g (v = 0) transitions. In addition to the six bands vibrational bands present in the HITRAN database, we also obtain intensities for 14 additional vibrational bands above the threshold intensity of 10−30 cm molcule.
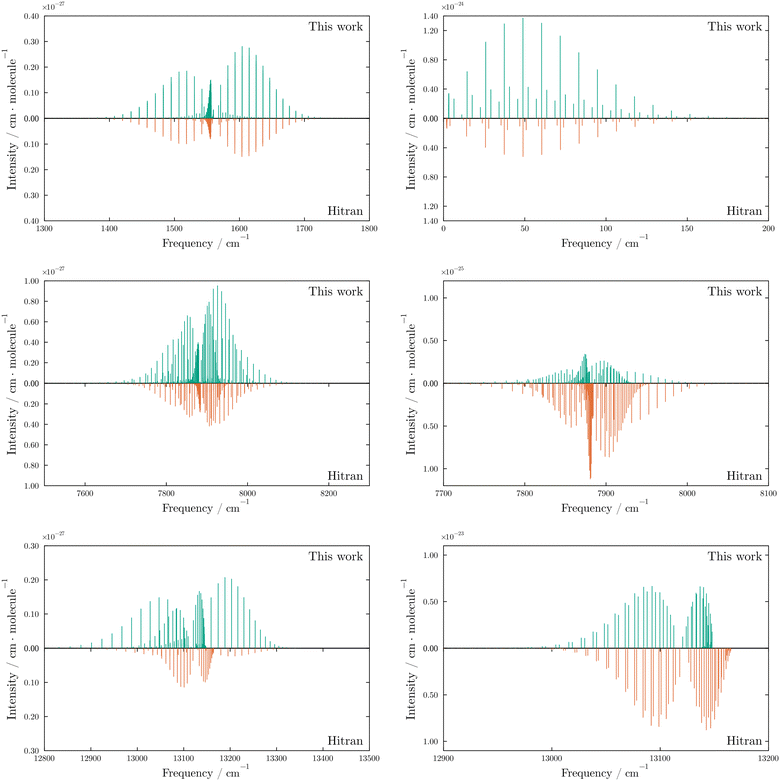 |
| | Fig. 7 Comparison of the most intense electric quadrupole (left) and magnetic dipole (right) transitions in the X 3Σ−g–X 3Σ−g (top), a 1Δg–X 3Σ−g (middle) and b 1Σ+g–X 3Σ−g (bottom) bands. The pink dots indicate the transition intensities recorded in the HITRAN database. In each case we show the v = 1 ← 0 transitions except for the X 3Σ−g–X 3Σ−g magnetic dipole band (top right), which is formed from the pure rotational v = 0 ← 0 transitions. The X 3Σ−g–X 3Σ−g bands contain closely separated lines as a result of the spin splitting of the triplet state produces Ω sub-levels with only small energy differences. The closely separated group of transitions below 10 cm−1 in the magnetic dipole moment X 3Σ−g–X 3Σ−gv = 0 ← 0 plot are the fine structure transitions between spin sub-levels in the same total rotational (J) state. | |
The ab initio model reproduces the expected intensities to the correct order of magnitude, with the largest discrepancies observed for the NO and TS branches of the b 1Σ+g–X 3Σ−g electric quadrupole transitions. These branches correspond to ΔN = −3, ΔJ = −2 and ΔN = +3, ΔJ = +2 transitions, respectively. Crucially, the combination of PECs and couplings present in the model successfully reproduces all of the observed rotational bands and the fine structure magnetic dipole transitions between spin sub-levels in the X 3Σ−g. To illustrate the role of the excited states we also reduce the model to a simple three state model that contains only the X 3Σ−g, a 1Δg, and b 1Σ+g with their respective couplings. Without the inclusion of the four Π states, we find that no intensities for the a 1Δg–X 3Σ−g magnetic dipole transitions are produced, and the PO and RS branches (ΔN = −1, ΔJ = −2 and ΔN = +1, ΔJ = +2) of the b 1Σ+g–X 3Σ−g electric quadrupole transitions are also not reproduced. In Fig. 8 we compare the intensities obtained with and without the inclusion of the Π states.
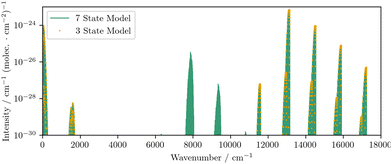 |
| | Fig. 8 A comparison of the magnetic dipole line list obtained using the only the three low-lying electronic states to that obtained when the excited Π states are included, which demonstrates the importance of the Π states in producing intensities for the a 1Δg–X 3Σ−g transitions. | |
6. Conclusions
The key result of this work is a novel set of ab initio electronic structure calculations for various properties of 7 electronic states of 16O2, namely the PECs of 7 electronic states, X 3Σ−g, a 1Δg, b 1Σ+g, I 1Πg, I 3Πg, II 1Πg and II 3Πg, along with a complete set of corresponding SOCs, EAMCs and EQMC s. These ab initio calculations have been used to produce a self-consistent ab initio spectroscopic model describing the magnetic dipole and electric quadrupole spectra of the three main atmospheric bands of O2, b 1Σ+g–X 3Σ−g a 1Δg–X 3Σ−g and X 3Σ−g–X 3Σ−g, which reproduces all the experimentally measured rotational branches within the dipole-forbidden electronic bands. We have shown that the highly excited Π states, although weakly coupled, are crucial for properly describing the observed bands in the infra-red region. The ab initio line list produced provides approximate intensities and line positions for the overtone transitions and rotational levels up to J = 50.
Due to the challenging nature of the electronic structure calculations, and the complex combination of couplings that contributes to each band, the line position and intensities of the purely ab initio model do no accurately reproduce experimentally measured lines. However, it is expected that the line positions and intensities can be improved significantly with respect to experimental data by empirical refinement of the potential energy and coupling curves. In future work this can be achieved by optimising the parameters of the analytic functions outlined in Section 4.2 in order to obtain an optimal fit to state energies, rather than to the ab initio values of the potential energy and coupling moments. We propose that the MARVEL analysis of Furtenbacher et al.89 is an ideal source of data with which to perform this refinement.
In this work we have restricted the model to consider only the first-order spin–orbit coupling perturbations and additional perturbations from other states such as the 1 5Πg state, which has previously been considered in the context of oxygen airglow by Minaev and Panchenko,90 have not been considered. Although these states are more highly excited and so coupled weakly around the equilibrium bond length, and longer bond lengths the strength of the coupling increases and these perturbations may provide small corrections to the rotational structure that further improve an empirically refined model.
Data availability
The code for Duo can be found at https://github.com/Trovemaster/Duo with DOI 10.1016/j.cpc.2015.12.021. The line list computed with Duo can be used directly with ExoCross to simulate the spectral properties. The code for ExoCross can be found at https://github.com/Trovemaster/exocross. The parameters for the analytic functions fitted to the ab initial data are included in the supplementary information, along with the calculated ab initio data itself.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the STFC Projects No. ST/Y001508/1 and ST/S506497/1. The authors acknowledge the use of the UCL Legion High Performance Computing Facility (Myriad@UCL) and associated support services in the completion of this work along with the Cambridge Service for Data Driven Discovery (CSD3), part of which is operated by the University of Cambridge Research Computing on behalf of the STFC DiRAC HPC Facility (https://www.dirac.ac.uk). The DiRAC component of CSD3 was funded by BEIS capital funding via STFC capital grants ST/P002307/1 and ST/R002452/1 and STFC operations grant ST/R00689X/1. DiRAC is part of the National e-Infrastructure. This work was also supported by the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation programme through Advance Grant number 883830. This work is partly supported by the European Metrology Partnership project “22IEM03 PriSpecTemp” (Funder ID 10.13039/100019599), which received funding from EPM Programme co-financed by the Participating States and from the European Unions Horizon 2020 research and motivation program and participating states.
Notes and references
- L. Wallace, Astrophys. J., Suppl. Ser., 1962, 7, 165 CrossRef CAS.
- P. H. Krupenie, J. Phys. Chem. Ref. Data, 1972, 1, 423–534 CrossRef CAS.
-
K. Huber and G. Herzberg, Molecular Spectra and Molecular Structure. IV. Constants of Diatomic Molecule, Springer, Boston, MA, 1979, vol. 4, pp. 1–716 Search PubMed.
- T. G. Slanger and P. C. Cosby, J. Phys. Chem., 1988, 92, 267–282 CrossRef CAS.
- B. J. Drouin, H. Gupta, S. Yu, C. E. Miller and H. S. P. Müller, J. Chem. Phys., 2012, 137, 024305 Search PubMed.
- S. Yu, C. E. Miller, B. J. Drouin and H. S. P. Müller, J. Chem. Phys., 2012, 137, 024304 Search PubMed.
- B. J. Drouin, S. Yu, B. M. Elliott, T. J. Crawford and C. E. Miller, J. Chem. Phys., 2013, 139, 144301 CrossRef PubMed.
- S. Yu, B. J. Drouin and C. E. Miller, J. Chem. Phys., 2014, 141, 174302 Search PubMed.
- A. E. Doyle, E. D. Young, B. Klein, B. Zuckerman and H. E. Schlichting, Science, 2019, 366, 356–359 CAS.
- T. Lichtenberg, D. J. Bower, M. Hammond, R. Boukrouche, P. Sanan, S.-M. Tsai and R. T. Pierrehumbert, J. Geophys. Res.-Planets, 2021, 126, e2020JE006711 CrossRef CAS PubMed.
- Y. Lin, W. van Westrenen and H.-K. Mao, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2110427118 CrossRef CAS PubMed.
- L. Schaefer, R. D. Wordsworth, Z. Berta-Thompson and D. Sasselov, Astrophys. J., 2016, 829, 63 CrossRef.
- L. Schaefer and B. Fegley, Astrophys. J., 2017, 843, 120 CrossRef.
- S. Konatham, J. Martin-Torres and M.-P. Zorzano, Proc. R. Soc. London, Ser. A, 2020, 476, 20200148 Search PubMed.
- V. S. Meadows, C. T. Reinhard, G. N. Arney, M. N. Parenteau, E. W. Schwieterman, S. D. Domagal-Goldman, A. P. Lincowski, K. R. Stapelfeldt, H. Rauer, S. DasSarma, S. Hegde, N. Narita, R. Deitrick, J. Lustig-Yaeger, T. W. Lyons, N. Siegler and J. L. Grenfell, Astrobiology, 2018, 18, 630–662 CrossRef PubMed.
- J. Krissansen-Totton, J. J. Fortney, F. Nimmo and N. Wogan, AGU Adv., 2021, 2, e2020AV000294 CrossRef.
- C. M. Lisse, S. J. Desch, C. T. Unterborn, S. R. Kane, P. R. Young, H. E. Hartnett, N. R. Hinkel, S.-H. Shim, E. E. Mamajek and N. R. Izenberg, Astrophys. J., 2020, 898, L17 CrossRef CAS.
- J. Krissansen-Totton, M. Thompson, M. L. Galloway and J. J. Fortney, Nat. Astronomy, 2022, 6, 189–198 CrossRef.
- T. P. Greene, M. R. Line, C. Montero, J. J. Fortney, J. Lustig-Yaeger and K. Luther, Astrophys. J., 2016, 817, 17 CrossRef.
- C. Danielski, J.-L. Baudino, P.-O. Lagage, A. Boccaletti, R. Gastaud, A. Coulais and B. Bezard, Astron. J., 2018, 156, 276 CrossRef CAS.
- M. López-Morales, S. Ben-Ami, G. Gonzalez-Abad, J. García-Mejía, J. Dietrich and A. Szentgyorgyi, Astron. J., 2019, 158, 24 CrossRef.
- K. K. Hardegree-Ullman, D. Apai, G. J. Bergsten, I. Pascucci and M. López-Morales, Astron. J., 2023, 165, 267 CrossRef.
- H. P. Broida and A. G. Gaydon, Proc. R. Soc. London, Ser. A, 1954, 222, 181–195 CAS.
- K. Yoshino, D. E. Freeman and W. H. Parkinson, J. Phys. Chem. Ref. Data, 1984, 13, 207–227 CrossRef CAS.
- A. Jenouvrier, M.-F. Mérienne, B. Coquart, M. Carleer, S. Fally, A. C. Vandaele, C. Hermans and R. Colin, J. Mol. Spectrosc., 1999, 198, 136–162 CrossRef CAS PubMed.
- B. R. Lewis, S. T. Gibson, T. G. Slanger and D. L. Huestis, J. Chem. Phys., 1999, 110, 11129–11132 CrossRef CAS.
- B. F. Minaev, Chem. Phys., 2000, 252, 25–46 CrossRef CAS.
- K. J. Ritter and T. D. Wilkerson, J. Mol. Spectrosc., 1987, 121, 1–19 CrossRef CAS.
- R. Schermaul and R. C. M. Learner, J. Quant. Spectrosc. Radiat. Transf., 1999, 61, 781–794 CrossRef CAS.
- D. A. Long, D. K. Havey, M. Okumura, H. M. Pickett, C. E. Miller and J. T. Hodges, Phys. Rev. A, 2009, 80, 042513 CrossRef.
- I. E. Gordon, L. S. Rothman and G. C. Toon, J. Quant. Spectrosc. Radiat. Transf., 2011, 112, 2310–2322 CrossRef CAS.
- B. J. Drouin, D. C. Benner, L. R. Brown, M. J. Cich, T. J. Crawford, V. M. Devi, A. Guillaume, J. T. Hodges, E. J. Mlawer, D. J. Robichaud, F. Oyafuso, V. H. Payne, K. Sung, E. H. Wishnow and S. Yu, J. Quant. Spectrosc. Radiat. Transf., 2017, 186, 118–138 CrossRef CAS PubMed.
- G. H. Dieke and H. D. Babcock, Proc. Natl. Acad. Sci. U. S. A., 1927, 13, 670–678 CrossRef CAS PubMed.
- L. Herzberg and G. Herzberg, Astrophys. J., 1947, 105, 353 CrossRef CAS.
- G. Herzberg, Can. J. Phys., 1952, 30, 185–210 CrossRef CAS.
- G. Herzberg, Can. J. Phys., 1953, 31, 657–669 CrossRef CAS.
- L. R. Zink and M. Mizushima, J. Mol. Spectrosc., 1987, 125, 154–158 CrossRef CAS.
- J. H. Burkhalter, R. S. Anderson, W. V. Smith and W. Gordy, Phys. Rev., 1950, 79, 651–655 CrossRef CAS.
- H. D. Babcock and L. Herzberg, Astrophys. J., 1948, 108, 167 CrossRef CAS.
- B. J. Drouin, S. Yu, C. E. Miller, H. S. P. Müller, F. Lewen, S. Brünken and H. Habara, J. Quant. Spectrosc. Radiat. Transf., 2010, 111, 1167–1173 CrossRef CAS.
- J. W. Brault, J. Mol. Spectrosc., 1980, 80, 384–387 CrossRef CAS.
- A. Goldman, J. Reid and L. S. Rothman, Geophys. Res. Lett., 1981, 8, 77–78 CrossRef CAS.
- L. S. Rothman and A. Goldman, Appl. Opt., 1981, 20, 2182–2184 CrossRef CAS PubMed.
- M. Toureille, S. Béguier, T. A. Odintsova, M. Yu. Tretyakov, O. Pirali and A. Campargue, J. Quant. Spectrosc. Radiat. Transf., 2020, 242, 106709 CrossRef CAS.
- O. Leshchishina, S. Kassi, I. E. Gordon, L. S. Rothman, L. Wang and A. Campargue, J. Quant. Spectrosc. Radiat. Transf., 2010, 111, 2236–2245 CrossRef CAS.
- I. E. Gordon, S. Kassi, A. Campargue and G. C. Toon, J. Quant. Spectrosc. Radiat. Transf., 2010, 111, 1174–1183 CrossRef CAS.
- C. Amiot and J. Verges, Can. J. Phys., 1981, 59, 1391–1398 CrossRef CAS.
- J. F. Noxon, Can. J. Phys., 1961, 39, 1110–1119 CrossRef CAS.
- E. B. Sveshnikova and B. F. Minaev, Opt. Spectrosc., 1983, 54, 320–322 Search PubMed.
- B. F. Minaev, Int. J. Quantum Chem., 1980, 17, 367–374 CrossRef CAS.
- A. P. Mishra, T. K. Balasubramanian and B. J. Shetty, J. Quant. Spectrosc. Radiat. Transf., 2011, 112, 2303–2309 CrossRef CAS.
- T. K. Balasubramanian and O. Narayanan, Acta Phys. Hung., 1994, 74, 341–353 CrossRef CAS.
- S. N. Yurchenko, L. Lodi, J. Tennyson and A. V. Stolyarov, Comput. Phys. Commun., 2016, 202, 262–275 CrossRef CAS.
- S. N. Yurchenko, A. F. Al-Refaie and J. Tennyson, Astron. Astrophys., 2018, 614, A131 CrossRef.
- T. Karman, A. van der Avoird and G. C. Groenenboom, J. Chem. Phys., 2017, 147, 084307 CrossRef PubMed.
- L. Bytautas, N. Matsunaga and K. Ruedenberg, J. Chem. Phys., 2010, 132, 074307 CrossRef PubMed.
- L. Bytautas and K. Ruedenberg, J. Chem. Phys., 2010, 132, 074109 CrossRef PubMed.
- H. Liu, D. Shi, J. Sun, Z. Zhu and Z. Shulin, Spectroc. Acta Pt. A-Molec. Biomolec. Spectr., 2014, 124, 216–229 CrossRef CAS PubMed.
- S. N. Yurchenko, L. Lodi, J. Tennyson and A. V. Stolyarov, Comput. Phys. Commun., 2016, 202, 262–275 CrossRef CAS.
- B. F. Minaev, Russ. Phys. J., 1978, 21, 1205–1209 Search PubMed.
- B. F. Minaev, N. A. Murugan and H. Ågren, Int. J. Quantum Chem., 2013, 113, 1847–1867 CrossRef CAS.
- E. H. Fink, H. Kruse, D. A. Ramsay and M. Vervloet, Can. J. Phys., 1986, 64, 242–245 CrossRef CAS.
- R. Klotz and S. D. Peyerimhoff, Mol. Phys., 1986, 573–594 CrossRef CAS.
- R. P. Brady, S. N. Yurchenko, G.-S. Kim, W. Somogyi and J. Tennyson, Phys. Chem. Chem. Phys., 2022, 24, 24076–24088 RSC.
- W. Somogyi, S. N. Yurchenko and A. Yachmenev, J. Chem. Phys., 2021, 155, 214303 CrossRef CAS PubMed.
- M. Kotani, Y. Mizuno, K. Kayama and E. Ishiguro, J. Phys. Soc. Jpn., 1957, 12, 707–736 CrossRef CAS.
- S. Sarangi and P. Varanasi, J. Quant. Spectrosc. Radiat. Transf., 1974, 14, 989–993 CrossRef CAS.
- M. Bartolomei, E. Carmona-Novillo, M. I. Hernández, J. Campos-Martínez and R. Hernández-Lamoneda, J. Comput. Chem., 2011, 32, 279–290 CrossRef CAS PubMed.
- V. W. Couling and S. S. Ntombela, Chem. Phys. Lett., 2014, 614, 41–44 CrossRef CAS.
- D. B. Lawson and J. F. Harrison, J. Phys. Chem., 1997, 101, 4781–4792 CrossRef CAS.
- B. F. Minaev, Spectrochim. Acta, Part A, 2004, 60, 1027–1041 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Sci., 2012, 2, 242–253 CrossRef CAS.
- A. D. Buckingham, R. L. Disch and D. A. Dunmur, J. Am. Chem. Soc., 1968, 90, 3104–3107 CrossRef CAS.
- E. R. Cohen and G. Birnbaum, J. Chem. Phys., 1977, 66, 2443–2447 CrossRef CAS.
- G. Birnbaum and E. R. Cohen, Mol. Phys., 1976, 32, 161–167 CrossRef CAS.
- M. Evans, Mol. Phys., 1975, 29, 1345–1351 CrossRef CAS.
- R. J. Le Roy, Y. Huang and C. Jary, J. Chem. Phys., 2006, 125, 164310 CrossRef PubMed.
- R. J. Le Roy, N. S. Dattani, J. A. Coxon, A. J. Ross, P. Crozet and C. Linton, J. Chem. Phys., 2009, 131, 204309 CrossRef PubMed.
- B. Ruscic, R. Pinzon, M. Morton, G. Von Laszevski, S. Bittner, S. Nijsure, K. Amin, M. Minkoff and A. Wagner, J. Phys. Chem. A, 2004, 108, 9979–9997 CrossRef CAS.
- L. Prajapat, P. Jagoda, L. Lodi, M. N. Gorman, S. N. Yurchenko and J. Tennyson, Mon. Not. Roy. Astron. Soc., 2017, 472, 3648–3658 CrossRef CAS.
- M. Semenov, N. Clark, S. N. Yurchenko, G.-S. Kim and J. Tennyson, Mon. Not. Roy. Astron. Soc., 2022, 516, 1158–1169 CrossRef CAS.
- S. N. Yurchenko, E. Nogué, A. A. A. Azzam and J. Tennyson, Mon. Not. Roy. Astron. Soc., 2022, 520, 5183–5191 CrossRef.
- E. S. Medvedev and V. G. Ushakov, J. Quant. Spectrosc. Radiat. Transf., 2022, 288, 108255 CrossRef CAS.
- M. Tinkham and M. W. P. Strandberg, Phys. Rev., 1955, 97, 937–951 CrossRef CAS.
- O. Vahtras, O. Loboda, B. Minaev, H. Ågren and K. Ruud, Chem. Phys., 2002, 279, 133–142 CrossRef CAS.
- M. Pezzella, J. Tennyson and S. N. Yurchenko, Mon. Not. Roy. Astron. Soc., 2022, 514, 4413–4425 CrossRef CAS.
- S. N. Yurchenko, W. Szajna, R. Hakalla, M. Semenov, A. Sokolov, J. Tennyson, R. R. Gamache, Y. Pavlenko and M. R. Schmidt, Mon. Not. Roy. Astron. Soc., 2023, stad3802 Search PubMed.
- I. Gordon, L. Rothman, R. Hargreaves, R. Hashemi, E. Karlovets, F. Skinner, E. Conway, C. Hill, R. Kochanov, Y. Tan, P. Wcisło, A. Finenko, K. Nelson, P. Bernath, M. Birk, V. Boudon, A. Campargue, K. Chance, A. Coustenis, B. Drouin, J.-M. Flaud, R. Gamache, J. Hodges, D. Jacquemart, E. Mlawer, A. Nikitin, V. Perevalov, M. Rotger, J. Tennyson, G. Toon, H. Tran, V. Tyuterev, E. Adkins, A. Baker, A. Barbe, E. Cané, A. Császár, A. Dudaryonok, O. Egorov, A. Fleisher, H. Fleurbaey, A. Foltynowicz, T. Furtenbacher, J. Harrison, J.-M. Hartmann, V.-M. Horneman, X. Huang, T. Karman, J. Karns, S. Kassi, I. Kleiner, V. Kofman, F. Kwabia-Tchana, N. Lavrentieva, T. Lee, D. Long, A. Lukashevskaya, O. Lyulin, V. Makhnev, W. Matt, S. Massie, M. Melosso, S. Mikhailenko, D. Mondelain, H. Müller, O. Naumenko, A. Perrin, O. Polyansky, E. Raddaoui, P. Raston, Z. Reed, M. Rey, C. Richard, R. Tóbiás, I. Sadiek, D. Schwenke, E. Starikova, K. Sung, F. Tamassia, S. Tashkun, J. V. Auwera, I. Vasilenko, A. Vigasin, G. Villanueva, B. Vispoel, G. Wagner, A. Yachmenev and S. Yurchenko, J. Quant. Spectrosc. Radiat. Transf., 2021, 277, 107949 CrossRef.
- T. Furtenbacher, M. Horváth, D. Koller, P. Sólyom, A. Balogh, I. Balogh and A. G. Császár, J. Phys. Chem. Ref. Data, 2019, 48, 023101 CrossRef.
- B. F. Minaev and A. A. Panchenko, J. Phys. Chem. A, 2020, 124, 9638–9655 CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Sergey N.
Yurchenko
*a,
Sergey N.
Yurchenko
 a and
Gap-Sue
Kim
b
a and
Gap-Sue
Kim
b

![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) arises due to the motion of charged particles. In the case of diatomic molecules, the primary magnetic dipole moment is due to negatively charged electrons with non-zero angular momenta. This magnetic moment is the sum of the orbital electronic angular momentum, and the spin electronic angular momentum as
arises due to the motion of charged particles. In the case of diatomic molecules, the primary magnetic dipole moment is due to negatively charged electrons with non-zero angular momenta. This magnetic moment is the sum of the orbital electronic angular momentum, and the spin electronic angular momentum as![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) =
= ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) + gs
+ gs![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) ,
,![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) ± and Ŝ±
± and Ŝ±


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 above the zero-point energy, which give rise to a small number of bound vibrational levels. In the following, we analyse the main contributions to the electric quadrupole and magnetic dipole line strengths for three systems b 1Σ+g–X 3Σ−g a 1Δg–X 3Σ−g and X 3Σ−g–X 3Σ−g.
000 cm−1 above the zero-point energy, which give rise to a small number of bound vibrational levels. In the following, we analyse the main contributions to the electric quadrupole and magnetic dipole line strengths for three systems b 1Σ+g–X 3Σ−g a 1Δg–X 3Σ−g and X 3Σ−g–X 3Σ−g.


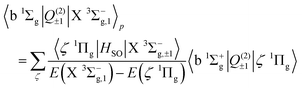
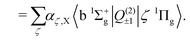


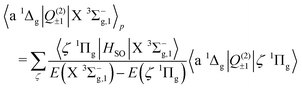


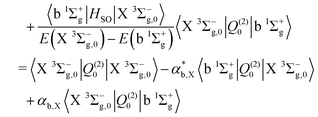


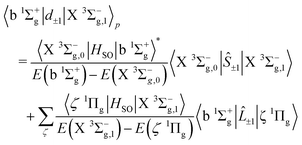


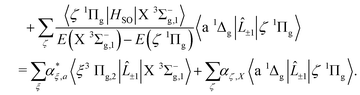

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1.
000 cm−1.
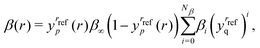
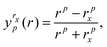
 , where one or more of the coefficients Cn may be equal to zero. In the limit r → ∞, the function approaches the
, where one or more of the coefficients Cn may be equal to zero. In the limit r → ∞, the function approaches the  where re is the equilibrium bond length, and rref is some reference geometry. In all fits we select rref := re for simplicity.
where re is the equilibrium bond length, and rref is some reference geometry. In all fits we select rref := re for simplicity.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 195.4
195.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 195.31
195.31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 099.92
099.92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800.3
800.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500.6
500.6


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. In solving the nuclear Schrödinger equation, a vibrational sinc-DVR basis set for each electronic state is defined on a grid of 1001 points in the range 0.90–3.00 Å. The vibronic basis sets are then truncated to the lowest 30 vibrational levels in the case of the X 3Σ−g, a 1Δg, and b 1Σ+g states, and to the lowest 300 vibrational levels for the II 1Πg, II 3Πg, I 1Πg, and I 3Πg states. We then solve for rotational levels up to J = 50. A large number of vibrational basis states are retained for the weakly bound and dissociative Π state in order to represent continuum states above the dissociation energy.86,87
000 cm−1. In solving the nuclear Schrödinger equation, a vibrational sinc-DVR basis set for each electronic state is defined on a grid of 1001 points in the range 0.90–3.00 Å. The vibronic basis sets are then truncated to the lowest 30 vibrational levels in the case of the X 3Σ−g, a 1Δg, and b 1Σ+g states, and to the lowest 300 vibrational levels for the II 1Πg, II 3Πg, I 1Πg, and I 3Πg states. We then solve for rotational levels up to J = 50. A large number of vibrational basis states are retained for the weakly bound and dissociative Π state in order to represent continuum states above the dissociation energy.86,87







