Product branching in the photodissociation of oxazole detected by broadband rotational spectroscopy

Abstract

The photodissociation of oxazole (c-C₃H₃NO) following excitation at 193 nm is studied using mm-Wave rotational spectroscopy in a uniform supersonic flow. Molecules entrained in the flow are excited to a ππ* state after which it is believed most relax back to the ground state via ring opening at the O–C[N] bond with subsequent fragmentation. From the line intensities of the probed products, we obtained the branching fractions for seven different products which are the result of five different dissociation pathways. The detected photoproducts and respective branching fractions (%) are the following: HCN (70.4), HCO (22.8), CH₂CN (4.2), CH₂CO (1.0), CH₃CN (1.0), HNC (0.9), HNCO (0.08). We suspect much of the HCO may be formed in conjunction with the isocyanomethyl radical, CH₂NC, which we did not probe. We discuss our results in relation to previous work, in particular our own study on the related isomer isoxazole, as well as direct dynamics theoretical simulations from the literature. We also studied the relaxation of a number of vibrationally excited levels of HCN produced at 20 K.

---

Introduction

Oxazole(c-C₃H₃NO) is a five membered heterocyclic molecule, containing C, H, O and N. The oxazole moiety is an important building block for many pharmaceutical molecules^1,2 and synthetic intermediates,^3,4 while its photochemical dynamics are of interest from the perspective of fundamental chemical physics. The UV dissociation of related isoelectronic heterocyclic molecules such as furan (c-C₄H₄O),^5–9 pyrrole (c-C₄H₅N)^10–14 and isoxazole (c-C₃H₃NO)^15,16 has been studied in some detail, while oxazole has received much less attention. The equilibrium geometry of oxazole and its isomer isoxazole are shown in Fig. 2.

The photodynamics of these isoelectronic molecules are governed by excitation to a ππ* state with ultrafast ring-opening leading to fragmentation. In Fig. 1 we show the possible asymptotic fragments and the associated energies. In this study we monitor asymptotic product branching in the photodissociation of oxazole and compare to our previous work on isoxazole¹⁵ and to theoretical direct dynamics studies of the early time behavior of isoxazole and oxazole from Cao^17,18 and Geng et al.¹⁶ and to theory and pyrolysis results of isoxazole from Nunes et al.¹⁹

Fig. 1 Products of the photodissociation of oxazole that are below the energy of the dissociating laser. Bold fonts indicate detected fragements. Black font is for closed-shell products, and red is for radical products. Orange indicates three body dissociation and green is for the non-dissociated molecules. The dashed line is the energy of the excitation. Energies are relative to oxazole and are taken from ref. 15 and ref. 20.

Here we employ chirped-pulse Fourier-transform mm-wave spectroscopy²¹ (CP-FTmmW) coupled with a pulsed uniform supersonic flow (a combination we term CPUF)^22,23 to study the photodissociation pathways of oxazole. Isoxazole has a fully conjugated set of π electrons, however, the ring may open at low energy owing to the weak N–O bond. Oxazole is more stable as the nitrogen and oxygen atoms are now separated by a carbon atom. It is possible to interconvert between the two molecules via a ring contraction-ring expansion mechanism involving the azirine intermediate (Fig. 2) which connects the potential energy surface of the two molecules, although it should be noted that isoxazole lies 1 eV higher in energy than oxazole.

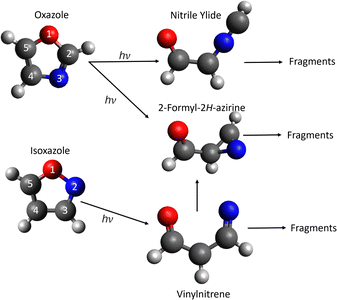Fig. 2 The structure of oxazole and isoxazole and the key stationary intermediate products in the photodissociation process. All structures are the geometry in the molecule on the ground state. The arrows indicate the most common pathways following excitation at ∼ 200 nm. The molecular geometry has been taken from Cao and co-workers.^17,18

Cao et al.^17,18 and Geng et al.¹⁶ have performed electronic structure and dynamical calculations following excitation to the (ππ*) state for both oxazole and isoxazole. For oxazole, Cao employed CASPT2 calculations of the energies with a 6-31G* basis set but CASSCF (10,8) with the same basis set for the dynamics. They identified the optically accessed ππ* state as S₂ and reported a conical intersection leading to S₁ which was identified as an nπ* state. Geng, however, suggested the nπ* state is actually S₂ based on calculations using an augmented basis set. It was argued that the N nonbonding orbital was raised in energy through the use of the non-augmented basis set, leading to the erroneous ordering in the Franck–Condon region. Using nonadiabatic surface-hopping direct dynamics simulations Cao et al. followed the dynamics from the S₂ state for 2 ps or until they reached a minimum. They found a very rapid transfer from the S₂ to S₁ state (on the order of ∼ 20 fs.) On the S₁ state the majority of trajectories undergo ring opening by O1–C2 bond scission. Then after about 300–350 fs the trajectories hop to the S₀ surface forming two different intermediates: nitrile ylide (66%) and 2-formyl-2H-azirine (15%), structures are shown in Fig. 2. Another important pathway to relaxation is the formation of a C2–C5 bond which can lead to either a bicyclic intermediate (8%) or reform the oxazole (8%). For the bicyclic intermediate, the hop to the S₀ state occurs around 250 fs and at about 400 fs for oxazole. The final 3% underwent ring opening via an O1–C5 bond break. They also considered the role of triplets up to T₃ but found only T₁ made a minor contribution as a conduit for flux from S₂ to S₀. Chief minima reached were the nitrile ylide, the bicyclic intermediate, and the 2-formyl-2H-azirine which is also observed during the ring opening of isoxazole.

Time resolved photoelectron spectroscopy (TRPES) measurements coupled with trajectories were reported by Geng et al.¹⁶ providing information about the early-time dynamics for isoxazole and oxazole. They identified the bright ππ* state as S₁, the nπ* state as S₂, and reported the key repulsive πσ* state is hidden in a dense set of highly excited Rydberg states and difficult to identify in the Franck–Condon region. The S₂ state was found not to play a role and was neglected in the dynamics. Their potential energy surfaces for oxazole showed a small barrier between the excited ππ* state and the dissociative πσ* state, unlike for isoxazole which is a barrierless decay. For isoxazole, their calculated surface order in the Franck–Condon region aligns with Cao's findings. Due to the small barrier in oxazole, the transition from the ππ* to the πσ* state occurs at a lower rate, with only 40% of oxazole molecules undergoing ring opening within the initial 100 fs, compared to 80% in the case of isoxazole in the trajectory calculations. In their TRPES measurements, isoxazole moves out of the observation window in 25 fs whereas oxazole takes 85 fs. Furthermore, in oxazole, a second longer-lived process is observed, lasting 6.5 ps, which is attributed to relaxation through ring puckering possibly via a bicyclic intermediate.

Our group reported product branching for the 193 nm photodissociation of isoxazole using CPUF.¹⁵ Seven products were detected ascribed to five dissociation channels. By comparison to pyrolysis results and high-level theoretical calculations from Nunes et al., and to Cao's dynamical calculations discussed above, it was concluded that most products likely arose from direct ultrafast dissociation while some involved a more extended exploration of S₀ prior to fragmentation.

In this work we observe the following five decomposition pathways following the excitation of oxazole at 193 nm, with detected products in bold:

C₃H₃NO + hν → HCN + CH₂CO (1)

→HCO + CH₂CN (2)

→HNC + CH₂CO (3)

→HNCO + C₂H₂ (4)

→CO + CH₃CN (5)

From the line intensities of the rotational spectra measured in a 20 K uniform supersonic flow using an extended Laval nozzle, we have determined the branching fractions among these pathways. We note that aside from HCN we examine only the ground vibrational levels. If there is a great variation in the vibrational distributions and vibrational cooling among the products, as may be the case, then this branching may be distorted. To gain some insight into this we also examine relaxation of vibrationally excited HCN in the flow. We obtain relaxation constants for six different vibrationally excited levels of HCN at 20 K. We interpret the branching and dynamics with the help of the calculations discussed above. We also compare our results for oxazole with our previous results from isoxazole.¹⁵

Experimental

The updated CPUF experimental apparatus has already been described in detail elsewhere^22,24 so only a brief description is provided here. The set-up consisted of two key components, an extended 20 K high-density helium Laval nozzle which is described in detail in ref. 24 and a pulsed mm-wave Fourier-transform spectrometer. A diagram of the experimental apparatus is shown in Fig. 3.

Fig. 3 A schematic of the CPUF chamber and components. The vacuum chamber consists of two turbomolecular pumps and a polycarbonate tube. The sample gas is introduced into the chamber by a piezoelectric stack valve with a Laval nozzle on the left side of the chamber. The 72–91 GHz spectrometer is placed 13 cm downstream from the Laval nozzle exit. The components at the bottom of the figure generate the mm-wave pulses and the components at the top of the figure record the signal. The 193 nm laser enters on the right side of the chamber. (LNA: low noise amplifier, AMC: active multiplier chain, PLDRO: phase locked dielectric resonator oscillator, BPFL: bandpass filter, and AWG: arbitrary waveform generator).

The conditions inside the nozzle have been characterized using resonant ionization of NO seeded in the flow along with computational fluid dynamics simulations. Within the nozzle the temperature is 19.7 ± 2.5 K and the total density 2.3 × 10¹⁷ cm⁻³. The total length of the uniform region within the nozzle is roughly 18 cm, giving a uniform hydrodynamic time of 225 μs. The chamber pressure is maintained at 0.02 torr which enables a shock free secondary expansion, creating a low temperature, low collision frequency environment ideal for CP-FTmmW detection.

The helium flow was seeded with less than 0.4% oxazole. The dissociation of oxazole is initiated with a 193 nm excimer laser pulse (Coherent COMPexPro 205F, ArF excimer laser employing unstable resonator optics) operated at 65 mJ per pulse, which is aligned along the axis of the flow and counter-propagating to it. The gas is pulsed using a home built piezoelectric stack valve to fill a stagnation volume of approximately 20 mL. The valve is opened for 3 ms and operated at a repetition rate of 2 Hz.

The spectrometer was oriented perpendicular to the flow 13 cm downstream from the nozzle exit. To generate the mm-Wave pulse we used signals from an arbitrary waveform generator (AWG 7082C, Tektronix) mixed with a constant 8.125 GHz from a phased locked dielectric resonator oscillator (PLDRO), which was then amplified before being multiplied by 8 with an active frequency multiplier chain (AMC, QuinnStar Technology, QMM-751020080). This produced frequencies in the range of 72–91 GHz, which was broadcast into the expanded flow by a standard gain horn. The pulse was then focused using a 150 mm focal length lens before entering the polycarbonate chamber perpendicular to the Laval flow. The transmitted pulse and free induction decay (FID) of the excited molecules were re-collimated with a 150 mm lens before being received by the horn and down-converted by mixing (Millitech, MXP-12-RFSL) with 10.7 GHz for 80–91 GHz and 9.0 GHz for the 72–80 GHz range from a low-noise microwave synthesizer (BNC-model 845-M) which is sent through an 8× AMC (Millitech, AMC-12-RFHOA). The down-converted signal is then amplified using a low-noise amplifier (LNA, Miteq AMF-4D-00100800-18-13P) and sent to the oscilloscope (Tektronic DPO 70804C). During each gas and photolysis laser pulse, the mm-Wave excitation and detection is pulsed 50 times, with each pulse spaced 5 μs apart. 50 pulses are used to ensure that the total excitation overlaps with the hydrodynamic time of the extended flow, followed by the secondary expansion. The photolysis laser is fired 37.5 μs after the first mm-Wave excitation pulse.

The data from the oscilloscope is read by a home-built Labview program. We use the FastFrame capabilities of the oscilloscope to record the last 20 ns of each excitation pulse and 0.7 μs of the free induction decay (FID). By limiting the total record length we reduced the amount of data to be transferred to the computer, and for these measurements high spectral resolution is not needed. All 50 frames are read by the computer together and the code then splits it back into the individual frames where each frame corresponds to each mm-wave pulse. The code then averages each frame in the time domain and fast Fourier transforms (FFT) the FID. This allows us to save both time domain and frequency domain signals, as well as having a real-time analysis of our experiment. A Kaiser–Bessel Window (β = 4) is used for the FFT.

To study product branching of the ground state fragments, we detect a single product at a time, sending in a single frequency pulse with a π/2 pulse length. The π/2 pulse length was experimentally determined for vinyl cyanide and then calculated for other molecules. This approach has been described in detail in previous publications.²⁵ The laser power was measured before and after the experiment to check for stability and the pressure and temperature of the oxazole bubbler were kept constant throughout the experiment. We probed several species based on our chemical intuition and prior experimental and theoretical results for oxazole and related molecules.^{15,17–19,26}

To study the relaxation of HCN we used broadband chirps, each chirp was 1 μs long and spanned 0.5 GHz from 87.85 to 89.45 GHz. The vibrationally excited HCN was created solely via the photolysis of oxazole. The flow and laser conditions used to detect the vibrationally excited HCN were identical to those for the ground state products. We studied the power dependence of the ground state HCN signal to verify we were within the single photon regime.

Results

Oxazole was photolyzed with a 193 nm excimer laser and seven distinct species from five different channels were observed, as shown in eqn (1) through (5) above. The products observed were HCN, CH₂CN, HCO, CH₂CO, HNC, HNCO, and CH₃CN. Table 1 shows the rotational transitions and corresponding frequencies that were employed in this experiment. The rotational lines used for all the species are for the vibrational ground state except for HCN as discussed below. The rotational lines are taken from the cologne database for molecular spectroscopy (CDMS)²⁷ and NIST.²⁸ As mentioned above, for every gas pulse the mm-wave pulse is broadcast 50 times in 5 μs intervals hence collecting the appearance time and evolution of the products over 250 μs.

Table 1 Rotational transitions associated with the vibrational ground state products detected from the photodissociation of oxazole

Photoproduct	Rotational transition	Frequency (GHz)
HCN	1–0	88.6316
CH2CN	4045–3034	80.4799
HCO	1–0	86.7084
CH2CO	422–321	81.5862
HNC	1–0	90.6636
HNCO	404–303	87.9252
CH3CN	400–300	73.5902

---

Fig. 4 shows the background subtracted spectra spanning the 73–91 GHz region.

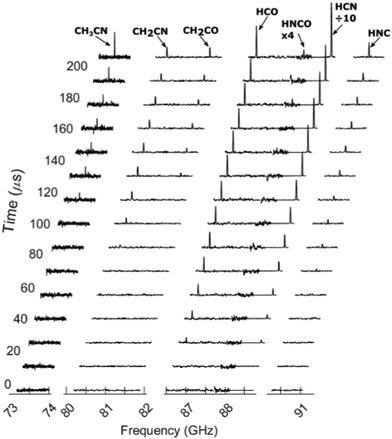Fig. 4 Rotational spectra of the photoproducts following excitation of oxazole with 193 nm. Every third frame is plotted.

Fig. 5 shows the integrated intensity of each fragment's peak as a function of time obtained from the data in Fig. 4. The first 5 broadcasts are before the laser fires and are used as a background to remove any peaks that are not laser-dependent. The last 5 broadcasts record the fragments formed in the throat of the nozzle and not in the uniform flow and therefore are not used for analysis. This is evident in the sharp increase in the peak intensities due to the increase in density. Fig. 5 also shows different appearance times for different photoproducts. In general, there is a delay between the formation of photoproducts and their detection by the CPUF spectrometer. This phenomenon has been studied previously²⁵ and the delayed appearance times have been attributed to vibrational and rotational cooling the molecules undergo once formed before they are detectable in the ground state. The appearance times of each fragment after the laser is fired are shown in.

Fig. 5 The time profile of the ground state fragments detected. The black lines show the region used to calculate the branching ratio. The intensity of HCN has been divided by 10 relative to the other fragments.

Table 2. HCN and HCO are the first fragments to appear about 15 μs after the laser is fired. HNC and CH₂CN appear next, 50 μs later, and finally CH₂CO appears 110 μs after HCN. (HNCO is too weak to see the appearance time clearly). From these observations, we can conclude that HCN and HCO fragments are formed with the least amount of vibrational and rotational excitation and CH₂CO is formed with the greatest excitation. We also studied the relaxation profile of vibrationally excited HCN. Fig. 5 also shows after the initial rise due to the vibrational relaxation the peak intensity for the majority of the fragments plateaus before the sharp increase due to the density in the nozzle throat. The exception is the HCN intensity which shows a continual increase which is discussed in more detail later.

Table 2 Branching fractions (%) and observation time for observed fragments from photodissociation of oxazole and isoxazole. (error one standard deviation)

Photoproduct	Observed time (oxazole)/μs	Oxazole branching	Isoxazole branching
HCN	12	70.4 ± 3.6	53.8 ± 1.7
HCO	17	22.8 ± 0.4	9.5 ± 2.3
CH2CN	77	4.2 ± 2.4	7.8 ± 2.9
CH2CO	122	1.0 ± 0.7	3.8 ± 0.9
HNC	67	0.9 ± 0.2	0.9 ± 0.2
HNCO	Unclear	0.08 ± 0.05	0
CH3CN	85	1.0 ± 0.6	23.4 ± 6.8
HCCCN	N/A	0	0.9 ± 0.2

---

Product formation

To calculate the product branching we use 6 frames corresponding to 160–190 μs. This is the region shown in Fig. 5 by the black lines and corresponds to the plateau just before the nozzle. We expect hundreds of collisions to have occurred by 160 μs.¹⁵ This means we believe the complete rotational cooling will have occurred. A small amount of vibrational excitation is still expected to be present.

The product branching can be calculated directly from the line strength as we are using π/2 mm-wave pulses to excite the fragments. The equation to calculate the relative number density is given below:

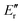where N_i is the total number density of the molecule, I is the signal intensity, T is the temperature of the flow, Q_i is the rotational partition function of the molecule, Sμ² is the transition strength, ν is the transition frequency is the lower state rotational energy. The derivation of this equation is discussed by Borengasser et al.²⁹ The temperature of the secondary expansion at the location of mm-Wave detection has been measured to be 5 ± 2 K.²⁴ The other values required to calculate N_i are obtained from the CDMS database.²⁷ The result of the product branching calculations are shown in Table 2 along with the product branching from the previous CPUF experiment with isoxazole.¹⁵ Neglecting possible vibrational dilution of the signal discussed below, the main source of uncertainty in the branching is the uncertainty in the temperature in the detection region, so we use that to calculate the error in the product branching. The reported error in the product branching is solely due to the uncertainty in temperature and does not include the uncertainty in the vibrational excitation.

Vibrational relaxtion of HCN

HCN has three vibrational modes, ν₁ is the C–H stretch, ν₂ is the bending mode and ν₃ is the C–N stretch. Fig. 6 shows the intensity time profile of the ground state HCN and 6 vibrationally excited HCN levels, (001), (100),(020), (021), (040), (041). To compare the intensities of the ground state HCN which was measured with a π/2 pulse with the vibrational excited HCN measured with a broadband chirp we scale the ground state intensity by 0.2.³⁰ The black lines in Fig. 6 are fits to the data. We fit the profiles to a logistic function multiplied with an exponential decay, given by the equation,Here a is a constant, t is the time, t₀ is the center time of the logistic function, and k₁ and k₂ are decay constants and define the rise and decay respectively. The logistic function is a common sigmoidal function and is used to model the rise in intensity associated with the transit of the molecules across the detection region and the increase in concentration as we start detecting molecules that were excited from within the nozzle. The exponential decay models the relaxation of the excited molecules. 1/k₂ gives the lifetime of the vibrationally excited level in the flow. We also used an error function to model the rise and obtained the same vibrational lifetimes, within error. For each excitation the fitted lifetime is given in Table 3. The lifetimes are determined by floating a, k₁, k₂ and t₀ and fitting the intensity profiles to eqn (7) using the nonlinear least squared method. The (100), (040), and (041) have a lifetime around ∼ 45 μs, giving an effective relaxation rate coefficient of ∼ 10 × 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹. The (001) and (020) had a longer relaxation time of around 85 μs, leading to an effective rate coefficient around ∼ 5.2 × 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹. Finally the (021) level had a lifetime of 21 μs and an effective rate coefficient of 20.5× 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹. Due to the low signal-to-noise ratio, there is a large uncertainty for the lifetime of (021). These are effective rates for the given experimental conditions assuming relaxation by the helium in the flow and neglecting incoming population from relaxation of higher excited levels. Collisions with molecules rather than helium in the flow may also contribute and may be far more effective at promoting vibrational relaxation despite the lower density.

Fig. 6 The integrated rotational line intensity of HCN for the ground state and vibrationally excited fragments. The black lines show the fit to the data. The data is fitted up to 190 μs.

Table 3 Detection frequency for each vibrationally excited HCN transition and the associated relaxation time (error one standard deviation)

Vibration	Frequency/GHz	Lifetime/μs	Rate coefficient × 10^−14 cm^3 molecules^−1 s^−1
(0,0,1)	88.0269	80 ± 5	5.4 ± 0.3
(1,0,0)	88.0063	43 ± 12	10.2 ± 1.4
(0,2,0)	89.0882	88 ± 6	5.0 ± 0.3
(0,2,1)	88.4679	21 ± 20	20.5 ± 9.9
(0,4,0)	89.5703	50 ± 8	8.6 ± 1.2
(0,4,1)	88.9333	46 ± 15	9.5 ± 2.3

---

Discussion

The object of this work was to study the asymptotic fragments of the dissociation of oxazole. Here, the products are produced in a dense cold flow and rotationally- and, to some extent, vibrationally-relaxed in the flow. In Fig. 5, the region marked by the black lines is used to calculate the product branching. By that time, the intensity of most fragments has plateaued, although HCN is an exception. We studied selected low vibrationally excited levels of HCN and showed they were largely relaxed with only about 6% remaining populated at 160 μs. This is not enough to explain the monotonic increase in the vibrational ground state population. The available energy for HCN + CH₂CO production is over 6 eV, so It may be that there is ongoing relaxation from long-lived very high vibrational states. However, we do not see ongoing relaxation into the excited levels we have probed, bringing that explanation into question. The other possibility is that there is a secondary pathway to HCN formation, although it is not clear what that might be.

The dominant photofragment observed from oxazole was HCN (70.4 ± 3.6%), which has the co-product CH₂CO (1.0 ± 0.7%). The abundance of CH₂CO is nonstoichiometric with HCN (nor HNC, as discussed later) which we attribute to the decomposition of CH₂CO produced at this high internal energy. While Cao's trajectories do not continue to final fragmentation, they do find 66% of their trajectories end at the nitrile ylide stationary point (structure shown in Fig. 2). Furthermore, 81% of the trajectories involving O1–C2 cleavage result in nitrile ylide. From this structure, an N3–C4 bond break followed by a 1,2 hydrogen shift would result in the HCN + CH₂CO product channel. We find a larger yield of HCN in oxazole than isoxazole (70.4% and 53.8% respectively) while less of the HCN co-product CH₂CO is detected in oxazole (1.0% and 3.8% respectively). This suggests CH₂CO is more likely to fragment for oxazole possibly due to greater internal energy when it is formed. This is interesting as oxazole is 1 ev more stable than isoxazole so overall less excess energy is available.

The next most abundant product is HCO (22.8 ± 0.4%), which is formed with the co-product CH₂CN(4.2 ± 2.4%). If the nitrile ylide breaks the C2–C3 bond instead of the N3–C4 then the two fragments are HCO + CHNCH. CHNCH can then rearrange to CH₂CN through a cationotropic 1,2-shift and 1,2-hydrogen shift. CH₂CN is a resonantly stabilized radical, isoelectronic to propargyl. Alternatively, a 1,3 H shift gives the isocyanomethyl radical, CH₂NC which is about 1 eV higher in energy than CH₂CN. We did not search for this product as the mm-wave frequencies are not available, but its formation likely accounts for the discrepancy between HCO and CH₂CN yields. Interestingly this channel is much weaker in the dissociation of isoxazole. Only 9.5% and 7.8% for HCO and CH₂CN respectively. In isoxazole, this pathway was due to a similar mechanism, ring opening followed by a C–C bond cleavage. Comparing oxazole to isoxazole, we find the percentage of HCO increased while its possible co-product CH₂CN decreased. Again this suggests that the main HCO co-fragment in oxazole is the isocyanomethyl radical. This is readily understood in that CH₂NC, with the nitrogen between two carbon atoms, is not part of the backbone structure of isoxazole while it is for oxazole. Fig. 1 also shows likely three-body fragmentation pathways below the energy of 193 nm, one of which involves the fragmentation of CH₂CO to CH₂ + CO while others involve secondary decomposition of HCO to H + CO.

These two channels correspond to 98% of the products formed, three other channels are responsible for the remaining 2% The third product channel observed was CH₃CN (1.0 ± 0.6%) + CO. We cannot observe CO as there are no rotational lines in the region of our spectrometer. This was the second most dominant channel for isoxazole (23.4%). In isoxazole it was suggested this pathway was from an indirect statistical dissociation, the result of spending an extended period on the ground state before dissociating and involving the azirine intermediate. From Cao's^17,18 calculation, about 15% of trajectories result in the azirine intermediate for oxazole and 53% result in the azirine intermediate or CH₃CN in isoxazole. Nunes et al.¹⁹ showed that azirine is an intermediate for several decomposition pathways. The lowest energy product was CH₃CN + CO. Another product channel from the azirine intermediate is H₂CCNH + CO which was observed exclusively in low-temperature flash-vacuum pyrolysis experiments of isoxazole;³¹ no equivalent experiments exist for oxazole. This was ascribed to the lower barrier to formation of H₂CCNH so that at lower energies the molecule does not have the energy to access the CH₃CN channel despite the fact that it is lower in energy. We did not detect any H₂CCNH either.

The fourth channel is HNC (0.9 ± 0.1%) + CH₂CO. HNC is ∼0.5 eV higher in energy than HCN with a 2 eV isomerization barrier, so HNC formed above that energy may relax on the HCN side of the barrier. This product channel has a similar branching ratio in isoxazole (HNC, 0.5%).

The final minor product is HNCO (0.08 ± 0.05%). The co-product is HCCH which does not have a dipole moment and hence cannot be detected by CPUF. All other products are the results of O1–C2 bond cleavage, however, this channel we believe arises from the O1–C5 scission followed by an N3–C4 scission and a 1,2 hydrogen shift. The trajectory calculations from Cao et al. had 3% of trajectories breaking the O1–C5 bond. This product channel is not observed in isoxazole as the N–O bond is always broken.

The HCCCN + H₂O channel which is observed in isoxazole (HCCCN – 1.0%) is not observed in oxazole. In isoxazole, the products are the result of two different processes. First, there is the direct non-statistical ultrafast dissociation which was suggested as the predominant mechanism for the HCN + CH₂CO and HCO + CH₂CN pathways. The second process is an indirect statistical dissociation which involves dynamics on the ground state prior to fragmentation. We attributed the formation of CH₃CN, HCCCN, and HNC to this process. The open-shell vinylnitrene intermediate controls both pathways. The intermediate is near the S₁/S₀ conical intersection and lies 3.9 kcal mol⁻¹ (0.17 eV) below the conical intersection. No equivalent structure exists on the oxazole surface. The nitirile ylide intermediate lies 39 kcal (1.7 eV) below the S₁/S₀ conical intersection. This means the molecule spends less time near the conical intersection therefore we believe the photodissociation of oxazole can be explained almost completely through an ultrafast direct mechanism.

While the majority of fragments have plateaued by the time we calculate the product branching, HCN is still increasing. The product branching percentage of HCN only increases by approximately 1% within the region used for the branching calculation. To investigate the cause of the increase we monitored selected vibrationally excited levels of HCN. There is likely more excited HCN that we did not probe. We did probe the (120) and (140) vibrational levels but did not detect them. From the intensity profiles of the vibrationally excited HCN, we can obtain the HCN relaxation coefficients. Sims et al. observed vibrationally excited HCN and HCCCN in a 10 K helium flow but did not characterize the relaxation.³² The only vibrational level that we observe for which the collisional relaxation rate has previously been reported, is (001) at 297 K with a value of 6.5 × 10⁻¹⁵ cm³ molecules⁻¹ s⁻¹.³³ Our value of 5.4 × 10⁻¹⁴ cm³ molecules⁻¹ s⁻¹ at 20 K would suggest an inverse temperature dependence, although given possible contributions from molecule-molecule collisions this trend should not be given much credence. In the region used to calculate the product branching, the percentage of observed excited HCN reduced from 6% to 4%. All the detected vibrationally excited HCN by this time is in the two longer lived vibrations, (001) and (020). The reduction in the population of the vibrationally excited HCN is significantly less than the increase in ground state HCN, therefore we believe there may be another pathway to HCN formation.

Conclusion

This experiment studies the final photoproducts of the dissociation of oxazole following the absorption of a single 193 nm photon. The major pathway observed is an O1–C2 bond scission giving a ring opened structure which then further fragments. The two major product channels HCN + CH₂CO and HCO + CH₂CN/CH₂NC. We also observe the minor products channels CH₃CN, HNC and HNCO. The HNCO product is evidence of a small amount of O1–C5 bond breakage. This is the first time the asymptotic fragments of oxazole have been studied. Our interpretation of the results is guided by Cao et al.¹⁷ and we compared our findings with our previous results on isoxazole.¹⁵ The major channel (HCN + CH₂CO) was the same for both molecules, although more HCN was formed in oxazole, and CH₂CO was more likely to fragment. The secondary pathways differed in the molecules. Over twice as much HCO was observed for oxazole than isoxazole however less of its co-product CH₂CN, suggesting the coproduct in the oxazole case is the isocyanomethyl radical which we did not probe. In isoxazole, the second most important channel was CH₃CN (23.4%) whereas in oxazole only 1.0% is observed. The CH₃CN fragment is expected to be a result of fragmentation of the azirine intermediate. We suggest the difference in this product yield is an effect of the low-lying vinylnitrene minimum near the S₁/S₀ conical intersection allowing isoxazole to spend an extended time near the conical intersection. Oxazole has no equivalent structure so rapidly moves away from the conical intersection. We also studied the relaxation of vibrationally excited HCN in our 20 K helium flow. We obtained effective collisional relaxation coefficients for (001), (100), (020), (021), (040) and (041). For (001) and (020) we obtained a rate coefficient of about ∼ 5.2 × 10⁻¹⁴ cm³ molecules⁻¹ s⁻¹ and for the (100), (040) and (041) vibrational modes, we found faster relaxation with a coefficient around 10 × 10⁻¹⁴ cm³ molecules⁻¹ s⁻¹. For (021) we obtained the fastest rate of 20 × 10⁻¹⁴ cm³ molecules⁻¹ s⁻¹, however there was very large uncertainty for the (021) value. These values do not account for more highly excited products causing a reduction of the decay rate, nor molecule-molecule collisions that may be important.

Data availability

Data for this article are available at MOspace at https://doi.org/10.32469/10355/104181.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Director, Office of Science, Office of Basic Energy Sciences, Division of Chemical Science, Geoscience and Bioscience, of the U.S. Department of Energy (DOE) under award number DE-SC0017130.

Notes and references

1. P. Lokwani, B. Nagori, N. Batra, A. Goyal, S. Gupta and N. Singh, J. Chem. Pharm. Res., 2011, 3, 302–311.
2. H.-Z. Zhang, Z.-L. Zhao and C.-H. Zhou, Eur. J. Med. Chem., 2018, 144, 444–492.
3. K. Neha, F. Ali, K. Haider, S. Khasimbi and S. Wakode, Synth. Commun., 2021, 51, 3501–3519.
4. V. S. Yeh, Tetrahedron, 2004, 60, 11995–12042.
5. O. Sorkhabi, F. Qi, A. H. Rizvi and A. G. Suits, J. Chem. Phys., 1999, 111, 100–107.
6. E. Gromov, C. Lévêque, F. Gatti, I. Burghardt and H. Köppel, J. Chem. Phys., 2011, 135, 164305.
7. E. Wang, S. Bhattacharyya, K. Chen, K. Borne, F. Ziaee, S. Pathak, H. V. S. Lam, A. S. Venkatachalam, X. Chen and R. Boll, et al., arXiv preprint, arXiv:2311.05099, 2023.
8. S. Oesterling, O. Schalk, T. Geng, R. D. Thomas, T. Hansson and R. de Vivie-Riedle, Phys. Chem. Chem. Phys., 2017, 19, 2025–2035.
9. R. Spesyvtsev, T. Horio, Y.-I. Suzuki and T. Suzuki, J. Chem. Phys., 2015, 143, 014302.
10. D. A. Blank, S. W. North and Y. T. Lee, Chem. Phys., 1994, 187, 35–47.
11. A. J. van den Brom, M. Kapelios, T. N. Kitsopoulos, N. H. Nahler, B. Cronin and M. N. Ashfold, Phys. Chem. Chem. Phys., 2005, 7, 892–899.
12. B. O. Roos, P.-A. Malmqvist, V. Molina, L. Serrano-Andrés and M. Merchán, J. Chem. Phys., 2002, 116, 7526–7536.
13. G. Wu, S. P. Neville, O. Schalk, T. Sekikawa, M. N. R. Ashfold, G. A. Worth and A. Stolow, J. Chem. Phys., 2015, 142, 074302.
14. M. Vazdar, M. Eckert-Maksić, M. Barbatti and H. Lischka, Mol. Phys., 2009, 107, 845–854.
15. N. Dias, B. Joalland, N. M. Ariyasingha, A. G. Suits and B. M. Broderick, J. Phys. Chem. A, 2018, 122, 7523–7531.
16. T. Geng, J. Ehrmaier, O. Schalk, G. W. Richings, T. Hansson, G. Worth and R. D. Thomas, J. Phys. Chem. A, 2020, 124, 3984–3992.
17. J. Cao, Z.-Z. Xie and X. Yu, Chem. Phys., 2016, 474, 25–35.
18. J. Cao, J. Chem. Phys., 2015, 142, 244302.
19. C. M. Nunes, I. Reva, T. M. V. D. Pinhoe Melo, R. Fausto, T. Šolomek and T. Bally, J. Am. Chem. Soc., 2011, 133, 18911–18923.
20. B. Ruscic and D. H. Bross, Active Thermochemical Tables values based on ver. 1.130 of the Thermochemical Network, https://atct.anl.gov.
21. G. G. Brown, B. C. Dian, K. O. Douglass, S. M. Geyer, S. T. Shipman and B. H. Pate, Rev. Sci. Instrum., 2008, 79, 053103.
22. J. M. Oldham, C. Abeysekera, B. Joalland, L. N. Zack, K. Prozument, I. R. Sims, G. B. Park, R. W. Field and A. G. Suits, J. Chem. Phys., 2014, 141, 154202.
23. C. Abeysekera, L. N. Zack, G. B. Park, B. Joalland, J. M. Oldham, K. Prozument, N. M. Ariyasingha, I. R. Sims, R. W. Field and A. G. Suits, J. Chem. Phys., 2014, 141, 214203.
24. S. Thawoos, N. Suas-David, R. M. Gurusinghe, M. Edlin, A. Behzadfar, J. Lang and A. G. Suits, J. Chem. Phys., 2023, 159, 214201.
25. B. M. Broderick, N. Suas-David, N. Dias and A. G. Suits, Phys. Chem. Chem. Phys., 2018, 20, 5517–5529.
26. N. Dias, R. M. Gurusinghe and A. G. Suits, J. Phys. Chem. A, 2022, 126, 5354–5362.
27. C. P. Endres, S. Schlemmer, P. Schilke, J. Stutzki and H. S. Müller, J. Mol. Spectrosc., 2016, 327, 95–104.
28. F. J. Lovas and R. Dragoset, Observed Interstellar Molecular Microwave Transitions, 2009, https://www.nist.gov/pml/observed-interstellar-molecular-microwave-transitions (accessed October 2023).
29. Q. Borengasser, T. Hager, A. Kanaherarachchi, D. Troya and B. M. Broderick, J. Phys. Chem. Lett., 2023, 14, 6550–6555.
30. J. McGurk, T. Schmalz and W. Flygare, J. Chem. Phys., 1974, 60, 4181–4188.
31. M. H. Palmer, G. Ganzenmüller and I. C. Walker, Chem. Phys., 2007, 334, 154–166.
32. T. Guillaume, B. M. Hays, D. Gupta, I. R. Cooke, O. Abdelkader Khedaoui, T. S. Hearne, M. Drissi and I. R. Sims, J. Chem. Phys., 2024, 160, 053103.
33. I. W. Smith and J. F. Warr, J. Chem. Soc., Faraday Trans., 1991, 87, 807–813.

---