Density-based quantification of steric effects: validation by Taft steric parameters from acid-catalyzed hydrolysis of esters†
Jingwen
Zhang
a,
Xin
He
b,
Bin
Wang
c,
Chunying
Rong
 *a,
Dongbo
Zhao
*a,
Dongbo
Zhao
 *d and
Shubin
Liu
*d and
Shubin
Liu
 *ef
*ef
aCollege of Chemistry and Chemical Engineering, Hunan Normal University, Changsha, Hunan 410081, China. E-mail: shubin@email.unc.edu
bInstitute of Frontier Chemistry, School of Chemistry and Chemical Engineering, Shandong University, Qingdao, Shandong 266237, China
cResearch Group of General Chemistry (ALGC), Vrije Universiteit Brussel (VUB), Pleinlaan 2, 1050 Brussels, Belgium
dInstitute of Biomedical Research, Yunnan University, Kunming 650500, Yunnan, China
eResearch Computing Center, University of North Carolina, Chapel Hill NC 27599-3420, USA
fDepartment of Chemistry, University of North Carolina, Chapel Hill NC 27599-3290, USA
First published on 16th August 2024
Abstract
The steric effect is one of the most widely used concepts for chemical understanding in publications and textbooks, yet a well-accepted formulation of this effect is still elusive. Experimentally, this concept was quantified by the acid-catalyzed hydrolysis of esters, yielding the so-called Taft steric parameter. Theoretically, we recently proposed a density-based scheme to quantify the effect from density functional theory. In this work, we directly compare these two schemes, one from theory and the other from experiment. To this end, we first establish the ester hydrolysis mechanism with multiple water molecules explicitly considered and then apply the energetic span model to represent the hydrolysis barrier height between the two schemes. Our results show that the barrier height of the reaction series is strongly correlated with both Taft steric parameters from experiment and steric quantification from theory. We also obtained strong correlations with steric potential, steric force, and steric charge from our theoretical scheme. Strong correlations with a few information-theoretic quantities are additionally unveiled. To the best of our knowledge, this is the first time in the literature that such a direct comparison between theoretical and experimental results is made. These results also suggest that our proposed two-water three-step mechanism for ester hydrolysis is effective, and our theoretical quantification of the steric effect is valid, robust, and experimentally comparable. In our view, this work should have satisfactorily addressed the issue of how the steric effect can be formulated and quantified, and thus it lays the groundwork for future applications.
Introduction
Density functional theory (DFT)1,2 has been widely accepted as the workhorse of electronic structure calculations for molecules and solids alike in the past few decades. Nevertheless, the endeavor to use density-based quantities from the DFT framework to enhance chemical understanding and predict chemical reactivity is still ongoing.3,4 The pioneering work on this topic is conceptual DFT1,5–9 by Parr and coworkers, who formulated concepts such as hardness and softness,10–12 Fukui function,13–15 and electrophilicity.16,17 Other examples along the line are the ELF (electron localization function) index,18–20 NCI (noncovalent interaction) index,21,22 SCI (strong covalent interaction) index,23,24 BNI (bonding and nonbonding interaction) index,25 electrophilicity/nucleophilicity,26–29 cooperativity/frustration,30–36etc. Bader's quantum theory of atom in molecules37 can also be regarded to belong to this category because it employs density-based quantities such as a density gradient and Laplacian for various applications.3,4Steric effects refer to the influence of the physical size and spatial arrangement of atoms or groups within a molecule on its reactivity. These effects can affect the rates of chemical reactions and the stability of intermediates. Earlier, we proposed a density-based formulation to quantify steric effects,38 which has been one of the most widely used chemical concepts in chemistry, but for which there is no unique way to define because no physical observable is associated with this effect. We have applied this DFT formulation of steric effects to account for its impact on numerous systems and phenomena,39–47 including conformational stability,41,47 anomeric effects,39,48,49 SN2 reactions,40,50,51 and stereoselectivity.51,52 On the other hand, experimentally, there exists an empirical scale using Taft steric parameters53–59 to quantitatively gauge the effect. This experimental scale employing the acid catalyzed hydrolysis of esters was obtained by the apparent rate constant of ester hydrolysis through a linear free energy relationship with the rate of the methyl group system as the reference.56,57 Given these two approaches to quantify the same effect, one from experiment and the other from theory, one natural question to ask is whether or not there is any correlation between the theoretical quantification and the Taft steric parameter. This question is what we will address in this work.
Methodology
Assuming that the total energy E of an electronic system comes from the contribution of three independent physicochemical effects, steric Es, electrostatic Ee, and quantum Eq, E![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Es + Ee + Eq, we have proved that the steric energy Es is simply the Weizsäcker kinetic energy TW,38
Es + Ee + Eq, we have proved that the steric energy Es is simply the Weizsäcker kinetic energy TW,38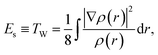 | (1) |
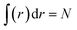 , with N as the total number of electrons and ∇ρ is the density gradient. Conventionally, in DFT,1 we have E = TS + Vne + J + Exc + Vnn, where Ts, Vne, J, Vnn, and Exc stand for the total non-interacting kinetic energy, nuclear–electron attraction, classical electron–electron Coulombic repulsion, nuclear–nuclear repulsion, and exchange-correlation energy, respectively. Since Vne, Vnn and J are all electrostatic, they can be put together yielding the total electrostatic energy Ee = Vne + J + Vnn and thus we have E = Ts + Ee + Exc. With this, we also have Eq = Ts − Es + EXC. For molecular systems in solvents, there is an extra term in the total energy partition coming from the contribution of the implicit solvent effect, ESolv, so the above two total energy decomposition schemes in DFT will each have this term added. It should also be noted that steric energy in eqn (1) is only different from Fisher information45,60–62 by a factor of 1/8 in the information-theoretic approach (ITA)63–65 in DFT, which has been found to be closely related to Shannon entropy and other ITA quantities.66–68 It should also be noted that eqn (1) has distinct physical meaning representing a hypothetical state and it satisfies homogeneous scaling properties.38
, with N as the total number of electrons and ∇ρ is the density gradient. Conventionally, in DFT,1 we have E = TS + Vne + J + Exc + Vnn, where Ts, Vne, J, Vnn, and Exc stand for the total non-interacting kinetic energy, nuclear–electron attraction, classical electron–electron Coulombic repulsion, nuclear–nuclear repulsion, and exchange-correlation energy, respectively. Since Vne, Vnn and J are all electrostatic, they can be put together yielding the total electrostatic energy Ee = Vne + J + Vnn and thus we have E = Ts + Ee + Exc. With this, we also have Eq = Ts − Es + EXC. For molecular systems in solvents, there is an extra term in the total energy partition coming from the contribution of the implicit solvent effect, ESolv, so the above two total energy decomposition schemes in DFT will each have this term added. It should also be noted that steric energy in eqn (1) is only different from Fisher information45,60–62 by a factor of 1/8 in the information-theoretic approach (ITA)63–65 in DFT, which has been found to be closely related to Shannon entropy and other ITA quantities.66–68 It should also be noted that eqn (1) has distinct physical meaning representing a hypothetical state and it satisfies homogeneous scaling properties.38| E = Ts + Ee + Exc + ESolv = Es + Ee + Eq + ESolv, | (2) |
The density-based quantification of steric effects in eqn (1) is an explicit electron density functional. With its expression analytically known, steric energy can be augmented by following three physical concepts, (i) steric potential υs(r), which is defined as the functional derivative of the steric energy with respect to the electron density,38
 | (3) |
| Fs(r) = −∇·υs(r) | (4) |
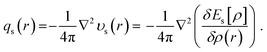 | (5) |
These quantities can be represented at molecular, group, and atomic levels using partition schemes such as Hirshfeld, Becke, and AIM (atoms-in-molecules).26,71–73 The above set of formulae in eqn (1), (3), (4), and (5), steric energy, steric potential, steric force, and steric charge, forms our density-based approach to quantify the steric effect in DFT from the theoretical perspective.
From the experimental perspective, on the other hand, the steric effect has been previously quantified in the literature by the following acid-catalyzed hydrolysis of esters,53,56,57,59,74
 | (6) |
 | (7) |
Before getting started, however, we have the following a few points in order. First, while these reaction rates in eqn (7), kS and kCH3, are experimentally accessible, computationally we approach the kinetic propensity of a reaction through its barrier height, which can be converted to the reaction rate through the Arrhenius equation if necessary. In this work, we directly use the barrier height for our purpose. Secondly, when hydrolysis is carried out in an acidic solvent, which can be simulated by the implicit solvent model in computation, multiple water molecules will explicitly participate in the reaction. It is impossible to computationally exhaust all combinations of different numbers of water molecules involved. Instead, we explore the mechanism using up to four water molecules and then ascertain the mechanism with the minimal number of water molecules required for the hydrolysis reaction to be effectively simulated.
Lastly, hydrolysis should proceed through a multiple-step mechanism, so the rates in eqn (7) are apparent reaction rates, not the ones from the rate-limiting step of the multi-step mechanism. We employ the energetic span model of Kozuch and Shaik75,76 as the effective barrier height to account for the apparent reaction rate in eqn (7). The energetic span model is a conceptual framework used in catalysis theory to understand and predict the performance of catalytic cycles. It focuses on identifying and analyzing the key energetic parameters that govern the overall catalytic efficiency. An energetic span is defined as the difference in energy between the highest energy transition state and the lowest energy intermediate (including the reactant) along the reaction pathway. This span represents the overall energy barrier that must be overcome for the catalytic cycle to proceed.
Computational details
All calculations were performed with the Gaussian 16 package, version C01,77 with ultrafine integration grids and tight self-consistent-field convergence. All molecular geometries were fully optimized first, and a single-point frequency calculation was followed to ensure that the final structure obtained has no imaginary frequency. We employed DFT functionals B3LYP and M06-2X and a few basis sets, such as Pople's standard triple-zeta split-valence basis set, 6-311+G(d), etc., with and without dispersion correction for the calculation and benchmark purposes in this work. The solvent effect was considered by using the implicit solvent model of the CPCM (conductor polarizable continuum model) and SMD (solvation model based on density). The “Multiwfn” program version 3.878 was employed to calculate energetic components, steric effect quantities (steric energy, steric potential, steric force, and steric charge), and information-theoretic quantities, such as Shannon entropy, Fisher information, alternative Fisher information, Ghosh–Berkowitz–Parr entropy, information gain, relative Fisher information, alternative relative Fisher information, etc. They were performed by using the checkpoint file from the Gaussian calculations as the input file. Details of these information-theoretic quantities in definition and implementation are available elsewhere.29,61,62,64,67,73,78–80 To consider the atomic contributions of these quantities, we employ the Hirshfeld scheme to partition atoms in molecules.81 The total number of mesh points for the Hirshfeld numerical quadrature in the radial part and spherical surface is 300 and 3890, respectively.Results and discussion
We first investigated the ester hydrolysis mechanism that can be employed for our study by changing the number of water molecules explicitly included in the reaction. For a mechanism to be feasible for our purpose, there is only one mandatory condition. That is, by increasing the size of the substituting group from H to methyl to t-butyl; for the rate-limiting step, the barrier height should be monotonically increased. This condition results from the very fact that this reaction has been employed to quantify the steric effect in the first place, so this condition must be true. The 3-step mechanism with multiple, m + n in total, water molecules explicitly considered is shown in Scheme 1. The first step is the formation of the C–O bond between the carboxyl group and an incoming water molecule, the second step involves proton transfer, and the third step is the break of the ester C–O bond to complete hydrolysis. It has three transition state (TS) structures and two intermediates. Fig. 1 elucidates the hydrolysis mechanism with up to 4 water molecules explicitly included for esters, which are attached by three different substituting groups R with R = H, methyl, and t-butyl. Their optimized molecule coordinates are included in the ESI.† From the figure, it can be seen that (i) the rate-limiting step is TS2 for all three species and (ii) only 2- and 3-water mechanisms correctly reproduce the order of the steric effect for the three groups. This result suggests that we need at least two water molecules to reasonably simulate the hydrolysis process for esters. Also, we notice that the “reactant” in Fig. 1 was the starting molecule complex, as shown in Scheme 1, of the acid-catalyzed ester with multiple water molecules, which indeed is an intermediate from the perspective of the energetic span model. In this study, the energetic span is the difference of the total energy between TS2 and the reactant in Scheme 1. | ||
| Fig. 1 Acid-catalyzed ester hydrolysis mechanisms of different groups (R = H, CH3, and tBu) with (a) one (m = 0 and n = 1), (b) two (m = 0 and n = 2), (c) three (m = 0 and n = 3), and (d) four (m = 1 and n = 3) water molecules explicitly included in Scheme 1. | ||
Can the result obtained in Fig. 1 be extended to groups other than alkyl groups, such as aromatic groups or strongly electronegative ones? Fig. 2 illustrates the comparison of the hydrolysis mechanism with F and Ph3C groups together with that of the t-butyl group. For F and Ph3C groups, the rate-limiting step is changed to TS3, but for the alkyl group, we know from Fig. 1, it is TS2. This difference in the mechanism suggests that different functional groups can result in different rate-limiting steps, so they do not belong to the same category from the mechanism viewpoint. For this reason, we only consider alkyl groups in this study.
 | ||
| Fig. 2 The 2-water acid-catalyzed ester hydrolysis mechanism with three R groups (R = tBu, F, and Ph3C) of vastly different (alkly, aromatic, and strongly electronegative) groups in Scheme 1. | ||
Table 1 summarizes the effective barrier height results for the 2-water reaction mechanism obtained from five different methodologies for 20 alkyl groups in solvent water. Their corresponding Taft steric parameters ES from the literature53 are also tabulated in the table. The last row is the correlation coefficient R2 value between Taft steric parameters and calculated barrier heights for the 20 alkyl groups. As an illustrative example, Fig. 3a exhibits the strong correlation of Taft steric parameters with the barrier height results from the M06-2X/6-311++G(d,p) level of theory in water solvent using the SMD implicit solvent model. As can be seen from the table and Fig. 3a, (i) the correlations between Taft steric parameters and barrier heights are markedly strong across all five different methods that we examined in this work, all with R2 better than 0.93, suggesting that the 2-water reaction mechanism in Fig. 1 is a valid and reliable representation of the acid-catalyzed hydrolysis of esters with alkyl groups; and (ii) the choice of methodologies does significantly impact the barrier height values, especially when different exchange–correlation functionals are employed. We considered other methodologies as well, including MP2 (not shown). No matter what methodologies are employed, the correlation between Taft steric parameters and barrier heights is always strong, confirming the validity and robustness of the correlation and independence of our results on functionals and basis sets.
| Alkyl group–R | Taft ES | Method 1 | Method 2 | Method 3 | Method 4 | Method 5 |
|---|---|---|---|---|---|---|
| Taft steric parameters are from ref. 53. All methods employed the SMD implicit solvent model. Method 1 is at the M06-2X/6-311++G(d,p) level of theory; method 2 is at M062X/6-311++G(d,p) with the GD3 dispersion correction; method 3 is at M062X/6-311+G(d) with the GD3 dispersion correction; method 4 is same as method 2 except that M062X was replaced by B3LYP; method 5 is same as method 2 except that a larger basis set, aug-cc-pVDZ, was utilized. | ||||||
| C2H5 | 0.08 | 7.51 | 7.49 | 5.44 | 14.70 | 7.45 |
| C3H7 | 0.36 | 7.51 | 7.48 | 5.43 | 14.78 | 7.32 |
| C4H9 | 0.39 | 7.57 | 7.54 | 5.48 | 14.87 | 7.38 |
| CH3 | 0.00 | 7.00 | 7.00 | 4.85 | 14.15 | 6.86 |
| Cyclohexane | 0.69 | 8.21 | 8.16 | 6.03 | 15.91 | 7.53 |
| Et2CH | 2.00 | 12.82 | 12.82 | 10.74 | 18.87 | 12.73 |
| EtMe2C | 2.28 | 11.83 | 11.81 | 9.74 | 19.85 | 11.59 |
| H | −1.12 | 0.41 | 0.39 | −1.58 | 6.82 | 0.28 |
| iBut | 0.93 | 9.08 | 9.01 | 6.21 | 17.35 | 7.54 |
| iPrEtCH | 3.23 | 15.44 | 15.42 | 13.35 | 23.90 | 16.60 |
| iPr | 0.47 | 7.56 | 7.56 | 5.68 | 15.29 | 6.96 |
| Pr2CH | 2.03 | 12.84 | 12.85 | 10.80 | 18.98 | 12.78 |
| PrEtCH | 2.00 | 12.27 | 12.22 | 9.81 | 18.77 | 11.02 |
| PrMeCH | 1.02 | 9.37 | 9.34 | 7.15 | 17.14 | 8.90 |
| sBut | 1.00 | 9.40 | 9.39 | 7.35 | 16.60 | 9.25 |
| tBuCH2Me2C | 2.48 | 12.29 | 12.25 | 10.04 | 20.89 | 12.64 |
| tBuCH2MeCH | 1.81 | 12.05 | 11.86 | 9.79 | 17.88 | 11.11 |
| tBuCH2 | 1.63 | 11.05 | 10.96 | 8.79 | 18.71 | 10.46 |
| tBuMeCH | 3.21 | 15.86 | 15.86 | 13.63 | 23.49 | 15.68 |
| tBu | 1.43 | 10.35 | 9.87 | 7.78 | 17.77 | 9.70 |
| R 2 | 0.947 | 0.946 | 0.944 | 0.935 | 0.942 | |
 | ||
| Fig. 3 Strong linear correlations of the 2-water hydrolysis barrier height from method 1 with (a) experimental Taft parameters and (b) the difference of the steric energy between TS2 and the reactant in the 2-water hydrolysis mechanism in Fig. 2 on the central carbon atom for 20 alkyl groups. | ||
With the hydrolysis mechanism computationally established, we are ready to answer the question that we posed earlier. That is, is there any correlation between the theoretical quantification of steric effect and the Taft steric parameter obtained from experiment? The correlation between the barrier height of 20 systems studied in this work and the difference of steric energy, eqn (1), on the central carbon atom with the correlation coefficient R2 = 0.929 is shown in Fig. 3b. The difference of steric energy is between TS2 and the reactant, same as the barrier height defined by the energetic span model.75,76 When the Taft steric parameter and the steric energy difference on the central carbon are directly correlated, we obtain the correlation coefficient R2 = 0.904. These results indicate that the answer to the above question is positive and decisively favorable. We obtained a strong correlation between theoretical and experimental quantifications of steric effects.
Moreover, we correlate the barrier height results with the three other physical variables from the scheme of our quantification, steric potential, steric force, and steric charge, defined in eqn (3)–(5), respectively. Fig. 4 shows the result of these additional correlations for the central carbon atom. From the figure, we can see that steric potential and steric charge are positively correlated with the barrier height, whereas the magnitude of the steric force is negatively correlated. Even though the correlation with the steric force is the least strong (with R2 = 0.83), the one with steric potential and steric charge is significantly stronger, with R2 = 0.92 and 0.95, respectively. When Taft steric parameters are directly correlated with the steric charge, we obtained R2 = 0.94. These results confirm what we have obtained in Fig. 3b, suggesting that experimental and theoretical quantifications of steric effects are strongly correlated. Put together, these results from steric energy, steric potential, steric force, and steric charge validate the effectiveness of our theoretical approach to formulate and quantify the steric effect using density-based quantities.
 | ||
| Fig. 4 Strong linear correlations of the barrier height with the difference of the (a) steric potential, (b) magnitude of the steric force, and (c) steric charge between TS2 and the reactant in the 2-water hydrolysis mechanism in Fig. 2 on the central carbon atom for 20 alkyl groups. | ||
We employed the steric propensities on the central carbon atom in Scheme 1 to correlate with Taft steric parameters in Fig. 3b and 4. There is a reason for this. No matter what substituent groups R are replaced in eqn (6), their impact on the reactivity of hydrolysis should eventually be passed to the central carbon atom, which is the reaction center, and thus reflected by the change of its properties. In this regard, it makes sense that we utilize different steric-related propensities of the central carbon atom for the correlation purpose. However, can we still use the results from the molecular level to do that? Using the difference at the molecular level between TS2 and the reactant, even though the correlation with steric energy and steric force is less strong, the correlation with steric potential (R2 = 0.87) and steric charge (R2 = 0.91) is still considerably significant. In this regard, our answer to the above question is still favorable.
Let us now examine the results from the two total energy partition schemes in DFT, eqn (2), for these systems. Table 2 shows the decomposition results for the hydrolysis barrier height of the 2-water reaction mechanism for 20 alkyl groups at the M062X/6-311++G(d,p) level of theory in solvent water using the SMD implicit solvent model. From the table, we can see that (i) with the conventional DFT partition scheme, ΔE = ΔESolv + ΔTs + ΔEe + ΔExc, the only positive and thus dominant contributor to ΔE is from the electrostatic component ΔEe, and all other three terms contribute negatively. This is the same as what we previously observed for other systems,39–41,45–47,50,82 However, different from the previous systems, the correlation between ΔEe and ΔE is not significant (with R2 = 0.467 only). (ii) With the second partition scheme, ΔE = ΔESolv + ΔEs + ΔEe + ΔEq, both ΔEe and ΔEs contribute positively but the magnitude of ΔEs is much larger than that of ΔEe, suggesting that the barrier height is dominated by the steric effect. Nevertheless, no strong correlation at the molecular level is obtained for ΔE with any of these two components. Using multivariant fittings, however, same as what we did previously,39,47,50,82 better correlations can be obtained from both partition schemes. For example, with ΔESolv, ΔEe, and ΔEs, we have R2 = 0.822, and with ΔESolv, ΔEe, and ΔExc, we obtain R2 = 0.811 (not shown). These results are the same as the other systems that we previously investigated.39–41,45–47,50,82
| Alkyl group–R | ΔE | ΔESolv | ΔTs | ΔExc | ΔEe | ΔEs | ΔEq |
|---|---|---|---|---|---|---|---|
| C2H5 | 7.51 | −5.27 | −37.47 | −16.69 | 66.94 | 300.04 | −354.20 |
| C3H7 | 7.51 | −6.80 | −34.69 | −17.26 | 66.26 | 307.45 | −359.41 |
| C4H9 | 7.57 | −6.75 | −35.60 | −17.13 | 67.04 | 306.52 | −359.25 |
| CH3 | 7.00 | −4.45 | −37.31 | −16.77 | 65.52 | 306.17 | −360.24 |
| Cyclohexane | 8.21 | −4.16 | −41.30 | −18.69 | 72.35 | 350.41 | −410.40 |
| Et2CH | 12.82 | −0.16 | −37.71 | −19.25 | 69.94 | 347.83 | −404.79 |
| EtMe2C | 11.83 | −3.26 | −40.07 | −19.61 | 74.77 | 353.16 | −412.84 |
| H | 0.41 | −3.74 | −32.06 | −16.57 | 52.78 | 296.53 | −345.16 |
| iBut | 9.08 | −3.39 | −41.19 | −18.99 | 72.65 | 354.73 | −414.92 |
| iPrEtCH | 15.44 | −1.63 | −43.47 | −18.17 | 78.71 | 329.32 | −390.96 |
| iPr | 7.56 | −6.91 | −45.58 | −17.62 | 77.68 | 333.90 | −397.10 |
| Pr2CH | 12.84 | −0.44 | −36.68 | −19.43 | 69.39 | 350.64 | −406.75 |
| PrEtCH | 12.27 | −0.93 | −34.08 | −21.68 | 68.97 | 377.29 | −433.06 |
| PrMeCH | 9.37 | −4.04 | −45.49 | −19.03 | 77.92 | 357.23 | −421.76 |
| sBut | 9.40 | −3.30 | −37.95 | −18.58 | 69.23 | 342.47 | −399.01 |
| tBuCH2Me2C | 12.29 | −8.14 | −45.83 | −18.99 | 85.26 | 341.92 | −406.75 |
| tBuCH2MeCH | 12.05 | −10.58 | −47.16 | −18.80 | 88.59 | 350.86 | −416.82 |
| tBuCH2 | 11.05 | −5.97 | −37.97 | −18.86 | 73.84 | 340.76 | −397.58 |
| tBuMeCH | 15.86 | −1.88 | −43.20 | −18.21 | 79.15 | 328.40 | −389.80 |
| tBu | 10.35 | −5.68 | −45.30 | −18.40 | 79.73 | 346.35 | −410.05 |
Since steric energy differs from Fisher information only by a factor of 1/8, and the latter was proven to be intrinsically related67,83 to other quantities from the information-theoretic approach (ITA),63–65 we next examine correlations of the barrier height with ITA quantities. Strong correlations of the barrier height with the difference of six ITA quantities, including Shannon entropy ΔSS, alternative Fisher information ΔI′F, information gain ΔIG, relative alternative Fisher information ΔrI′F, second-order relative Rényi entropy ΔrR2, and third-order relative Rényi entropy ΔrR3, are shown in Fig. 5. The difference of these ITA quantities was taken between TS2 and the reactant of the 2-water hydrolysis mechanism in Fig. 2 on the central carbon atom for 20 alkyl groups. As can be seen from the figure, all these six ITA quantities are strongly correlated with the barrier height of ester hydrolysis for 20 alkyl groups. These results not only verify the intrinsic relationship among ITA quantities, but also suggest that we could have more quantitative descriptors for Taft steric parameters.
 | ||
| Fig. 5 Strong linear correlations of the 2-water hydrolysis barrier height with the difference of (a) Shannon entropy, (b) alternative Fisher information, (c) information gain, (d) relative alternative Fisher information, (e) second-order relative Rényi entropy, and (f) third-order relative Rényi entropy from the information-theoretic approach in DFT between TS2 and the reactant of the 2-water hydrolysis mechanism in Fig. 2 on the central carbon atom for 20 alkyl groups. | ||
Finally, as a further piece of evidence, as shown in Fig. 6, we directly correlated Taft steric parameters with the descriptors from both steric quantifications (steric potential and steric charge) and ITA quantities (Shannon entropy and alternative Fisher information) on the carbon center. From the figure, we can see all four descriptors generated significantly strong correlations with Taft constants, all with the correlation coefficient larger than 0.90. These results confirm, again, the effectiveness and validity of employing the DFT scheme and ITA quantities to quantitatively describe the steric effect.
 | ||
| Fig. 6 Strong linear relationships between the Taft steric parameter of 20 systems studied in this work and the atomic difference of (a) Shannon entropy, (b) alternative Fisher information, (c) steric potential, and (d) steric charge on the reaction center. The difference was taken between TS2 and the reactant of the 2-water hydrolysis mechanism in Fig. 2 on the central carbon atom for 20 alkyl groups using the Hirshfeld partition. | ||
Conclusions
To summarize, in this work, we applied the theoretical quantification scheme from density functional theory for the acid catalyzed hydrolysis of esters with 20 different substituent groups, whose experimental scale of Taft steric parameters was previously established in the literature. The main results from this work are as follows. Firstly, a computational model to effectively simulate the hydrolysis mechanism in acidic solvents is established. At least two water molecules must be explicitly considered. Secondly, to represent the effective barrier height of the multi-step mechanism for ester hydrolysis and to correlate it with the apparent reaction rate from experimental measurements, the energetic span model from the literature must be employed. Thirdly, we observed strong correlations of the barrier height with Taft steric parameters and with the four steric effect related variables, including steric energy, steric potential, steric force, and steric charge. Lastly, we obtained strong correlations of the barrier height with six different information-theoretic quantities. These results provide pieces of strong evidence in support that the density-based quantification of steric effects using Weizsäcker kinetic energy and its derivatives is a valid and robust one, and that steric effects can be quantitatively described and well accounted for by numerous density-based quantities in the framework of density functional theory. It is our humble view that this work should have satisfactorily addressed the issue of how the steric effect can be formulated in such a way that a direct comparison with experiments is made possible. It is our hope that this work might have laid the groundwork for future applications, where both steric, electrostatic, and quantum can be quantitatively accounted for.Data availability
Cartesian coordinates of optimized reactants and transition state structures are included in ESI.† The data that support the findings of this study are available from the corresponding author, SL, upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. Y. R. acknowledges support from the National Natural Science Foundation of China (Grant No. 22373034) and the Hunan Province College Students Research Learning and Innovative Experiment project (S202310542078). D. B. Z. is supported by the start-up funding of Yunnan University, the Yunnan Fundamental Research Projects (Grant No. 202101AU070012). A part of the computations were performed using the high-performance computers of the Advanced Computing Center of Yunnan University.References
- R. G. Parr and W. T. Yang, Density-functional theory of atoms and molecules, Oxford University Press, New York, 1989 Search PubMed.
- A. M. Teale, T. Helgaker, A. Savin, C. Adamo, B. Aradi, A. V. Arbuznikov, P. W. Ayers, E. J. Baerends, V. Barone and P. Calaminici, et al. , Phys. Chem. Chem. Phys., 2022, 24, 28700–28781 RSC.
- C. Y. Rong, D. B. Zhao, X. He and S. B. Liu, J. Phys. Chem. Lett., 2022, 13, 11191–11200 CrossRef CAS PubMed.
- X. He, M. Li, C. Y. Rong, D. B. Zhao, W. J. Liu, P. W. Ayers and S. B. Liu, J. Phys. Chem. A, 2024, 128, 1183–1196 CrossRef CAS PubMed.
- R. G. Parr and W. T. Yang, Annu. Rev. Phys. Chem., 1995, 46, 701–728 CrossRef CAS PubMed.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1873 CrossRef CAS PubMed.
- P. Geerlings, E. Chamorro, P. K. Chattaraj, F. De Proft, J. L. Gázquez, S. B. Liu, C. Morell, A. Toro-Labbé, A. Vela and P. W. Ayers, Theor. Chem. Acc., 2020, 139, 36 Search PubMed.
- S. B. Liu, Acta Phys. Chim. Sin., 2009, 25, 590–600 CAS.
- S. B. Liu, Conceptual Density Functional Theory: Towards a New Chemical Reactivity Theory, Wiley-VCH, Germany, 2022 Search PubMed.
- P. K. Chattaraj and P. W. Ayers, J. Chem. Phys., 2005, 123, 086101 CrossRef PubMed.
- R. G. Pearson, Acc. Chem. Res., 1993, 26, 250–255 CrossRef CAS.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- W. T. Yang and R. G. Parr, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 6723–6726 CrossRef CAS PubMed.
- T. L. Li, S. B. Liu, S. X. Feng and C. E. Aubrey, J. Am. Chem. Soc., 2005, 127, 1364–1365 CrossRef CAS PubMed.
- W. T. Yang, R. G. Parr and R. Pucci, J. Chem. Phys., 1984, 81, 2862–2863 CrossRef CAS.
- P. K. Chattaraj, U. Sarkar and D. R. Roy, Chem. Rev., 2006, 106, 2065–2091 CrossRef CAS PubMed.
- R. G. Parr, L. v Szentpály and S. B. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- A. D. Becke and K. E. Edgecombe, J. Am. Chem. Soc., 1990, 92, 5397–5403 CAS.
- B. Silvi and A. Savin, Nature, 1994, 371, 683–686 CrossRef CAS.
- A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832 CrossRef CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. T. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. T. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- S. Liu, C. Rong, T. Lu and H. Hu, J. Phys. Chem. A, 2018, 122, 3087–3095 CrossRef CAS PubMed.
- Y. Huang, L. Liu, C. Rong, T. Lu, P. W. Ayers and S. Liu, J. Mol. Model., 2018, 24, 213 CrossRef PubMed.
- S. J. Zhong, X. He, S. Y. Liu, B. Wang, T. Lu, C. Y. Rong and S. B. Liu, J. Phys. Chem. A, 2022, 126, 2437–2444 CrossRef CAS PubMed.
- S. B. Liu, C. Y. Rong and T. Lu, J. Phys. Chem. A, 2014, 118, 3698–3704 CrossRef CAS PubMed.
- B. Wang, C. Y. Rong, P. K. Chattaraj and S. B. Liu, Theor. Chem. Acc., 2019, 138, 124 Search PubMed.
- S. B. Liu, J. Phys. Chem. A, 2015, 119, 3107–3111 CrossRef CAS PubMed.
- S. B. Liu, J. Chem. Phys., 2014, 141, 194109 CrossRef PubMed.
- C. Y. Rong, D. B. Zhao, T. J. Zhou, S. Y. Liu, D. H. Yu and S. B. Liu, J. Phys. Chem. Lett., 2019, 10, 1716–1721 CrossRef CAS PubMed.
- C. Y. Rong, D. B. Zhao, D. H. Yu and S. B. Liu, Phys. Chem. Chem. Phys., 2018, 20, 17990–17998 RSC.
- J. Nochebuena, J.-P. Piquemal, S. Liu and G. A. Cisneros, J. Chem. Theory Comput., 2023, 19, 7715–7730 CrossRef CAS PubMed.
- S. B. Liu and C. Y. Rong, J. Phys. Chem. A, 2021, 125, 4910–4917 CrossRef CAS PubMed.
- M. Li, X. He, J. Chen, B. Wang, S. B. Liu and C. Y. Rong, J. Phys. Chem. A, 2021, 125, 1269–1278 CrossRef CAS PubMed.
- S. B. Liu, J. Phys. Chem. Lett., 2020, 11, 8690–8696 CrossRef CAS PubMed.
- S. B. Liu, J. Phys. Chem. Lett., 2021, 12, 8720–8725 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules, Oxford University Press, 1989 Search PubMed.
- S. B. Liu, J. Chem. Phys., 2007, 126, 244103 CrossRef PubMed.
- Y. Huang, A. G. Zhong, Q. Yang and S. B. Liu, J. Chem. Phys., 2011, 134, 084103 CrossRef PubMed.
- S. B. Liu, H. Hu and L. G. Pedersen, J. Phys. Chem. A, 2010, 114, 5913–5918 CrossRef CAS PubMed.
- D. H. Ess, S. B. Liu and F. De Proft, J. Phys. Chem. A, 2010, 114, 12952–12957 CrossRef CAS PubMed.
- M. Torrent-Sucarrat, S. B. Liu and F. De Proft, J. Phys. Chem. A, 2009, 113, 3698–3702 CrossRef CAS PubMed.
- V. G. Tsirelson, A. I. Stash and S. B. Liu, J. Chem. Phys., 2010, 133, 114110 CrossRef PubMed.
- D. Fang, J.-P. Piquemal, S. B. Liu and G. A. Cisneros, Theor. Chem. Acc., 2014, 133, 1484 Search PubMed.
- R. O. Esquivel, S. B. Liu, J. C. Angulo, J. S. Dehesa, J. Antolín and M. Molina-Espíritu, J. Phys. Chem. A, 2011, 115, 4406–4415 CrossRef CAS PubMed.
- S. B. Liu and N. Govind, J. Phys. Chem. A, 2008, 112, 6690–6699 CrossRef CAS PubMed.
- S. B. Liu, J. Phys. Chem. A, 2013, 117, 962–965 CrossRef CAS PubMed.
- X. F. Cao, S. Y. Liu, C. Y. Rong, T. Lu and S. B. Liu, Chem. Phys. Lett., 2017, 687, 131–137 CrossRef CAS.
- X. Zhou, D. H. Yu, C. Y. Rong, T. Lu and S. B. Liu, Chem. Phys. Lett., 2017, 684, 97–102 CrossRef CAS.
- Z. Wu, C. Y. Rong, T. Lu, P. W. Ayers and S. B. Liu, Phys. Chem. Chem. Phys., 2015, 17, 27052–27061 RSC.
- S. B. Liu, L. H. Liu, D. H. Yu, C. Y. Rong and T. Lu, Phys. Chem. Chem. Phys., 2018, 20, 1408–1420 RSC.
- S. B. Liu, C. Y. Rong and T. Lu, Phys. Chem. Chem. Phys., 2017, 19, 1496–1503 RSC.
- J. A. MacPhee, A. Panaye and J.-E. Dubois, Tetrahedron, 1978, 34, 3553–3562 CrossRef CAS.
- B. Bumbăcilă and M. V. Putz, New Frontiers in Nanochemistry: Concepts, Theories, and Trends, Apple Academic Press, 2020 Search PubMed.
- B. Pinter, T. Fievez, F. M. Bickelhaupt, P. Geerlings and F. De Proft, Phys. Chem. Chem. Phys., 2012, 14, 9846–9854 RSC.
- R. W. Taft, J. Am. Chem. Soc., 1952, 74, 3120–3128 CrossRef CAS.
- R. W. Taft, J. Am. Chem. Soc., 1953, 75, 4538–4539 CrossRef CAS.
- M. Charton, J. Org. Chem., 1978, 43, 3995–4001 CrossRef CAS.
- M. Charton, J. Am. Chem. Soc., 1975, 97, 1552–1556 CrossRef CAS.
- Á. Nagy, Int. J. Quantum Chem., 2022, 122, e26679 CrossRef.
- B. Wang, D. B. Zhao, T. Lu, S. B. Liu and C. Y. Rong, J. Phys. Chem. A, 2021, 125, 3802–3811 CrossRef CAS PubMed.
- R. A. Fisher, Math. Proc. Camb. Phil. Soc., 1925, 22, 700–725 CrossRef.
- C. Y. Rong, B. Wang, D. B. Zhao and S. B. Liu, WIREs Comput. Mol. Sci., 2020, 10, e1461 CrossRef CAS.
- S. B. Liu, Acta Phys. Chim. Sin., 2016, 32, 98–118 Search PubMed.
- X. Y. Zhou, C. Y. Rong, T. Lu, P. P. Zhou and S. B. Liu, J. Phys. Chem. A, 2016, 120, 3634–3642 CrossRef CAS PubMed.
- S. B. Liu, J. Chem. Phys., 2022, 157, 101103 CrossRef CAS PubMed.
- S. B. Liu, J. Chem. Phys., 2007, 126, 191107 CrossRef PubMed.
- X. He, T. Lu, C. Y. Rong, S. B. Liu, P. W. Ayers and W. J. Liu, J. Chem. Phys., 2023, 159, 054112 CrossRef CAS PubMed.
- S. B. Liu, P. W. Ayers and R. G. Parr, J. Chem. Phys., 1999, 111, 6197–6203 CrossRef CAS.
- G. Menconi, D. J. Tozer and S. B. Liu, Phys. Chem. Chem. Phys., 2000, 2, 3739–3742 RSC.
- F. Heidar-Zadeh, P. W. Ayers, T. Verstraelen, I. Vinogradov, E. Vöhringer-Martinez and P. Bultinck, J. Phys. Chem. A, 2018, 122, 4219–4245 CrossRef CAS PubMed.
- R. F. Nalewajski and R. G. Parr, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 8879–8882 CrossRef CAS PubMed.
- C. Y. Rong, T. Lu, P. K. Chattaraj and S. B. Liu, Indian. J. Chem. Sect. A, 2014, 53, 970–977 Search PubMed.
- R. W. Taft, J. Am. Chem. Soc., 1952, 74, 2729–2732 CrossRef CAS.
- S. Kozuch, WIREs Comput. Mol. Sci., 2012, 2, 795–815 CrossRef CAS.
- S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakat-suji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. L. F. Ding, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas and J. B. Foresman, Gaussian16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- C. E. Shannon, Bell Syst. Tech. J., 1948, 27, 3–55 CrossRef.
- S. B. Liu, C. Y. Rong, Z. M. Wu and T. Lu, Acta Phys. Chim. Sin., 2015, 31, 2057–2063 CAS.
- F. L. Hirshfeld, Theor. Chem. Acc., 1977, 44, 129–138 Search PubMed.
- S. B. Liu and C. K. Schauer, J. Chem. Phys., 2015, 142, 054107 CrossRef PubMed.
- S. B. Liu, J. Chem. Phys., 2019, 151, 141103 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02702g |
| This journal is © the Owner Societies 2024 |

