Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Carbon–sulfur bond elongation as the promoting reaction coordinate in the efficient sub-nanosecond intersystem crossing in thianaphthene derivatives†
Cameron
Griffith
,
Erqian
Mao
,
Sean J.
Hoehn
 ,
Sarah E.
Krul
and
Carlos E.
Crespo-Hernández
,
Sarah E.
Krul
and
Carlos E.
Crespo-Hernández
 *
*
Department of Chemistry, Case Western Reserve University, Cleveland, Ohio 44106, USA. E-mail: carlos.crespo@case.edu
First published on 23rd August 2024
Abstract
Thiophene derivatives have become integral to OLEDs, photovoltaics, and photodynamic therapy research. A deeper understanding of their excited state dynamics and electronic relaxation mechanisms is expected to provide important physical insights of direct relevance for these applications. In this study, thianaphthene (TN), 2-methylbenzothiophene (2MBT), and 3-methylbenzothiophene (3MBT) are investigated using femtosecond broadband transient absorption and steady-state spectroscopy techniques along with time-dependent density functional calculations in cyclohexane and acetonitrile. The photophysical properties and electronic relaxation mechanisms of these derivatives are elucidated. Small fluorescence quantum yields ranging from 0.4 to 1.1% are measured. It is demonstrated that excitation of TN at 290 nm leads primarily to intersystem crossing to the triplet manifold with a lifetime of 400 ± 15 ps in either solvent, whereas four- to twofold shorter intersystem crossing lifetimes are measured for 2MBT and 3MBT depending on whether cyclohexane or acetonitrile is used. Linear interpolation of internal coordinates evidence that elongation of the S–C bonds enables ultrafast intersystem crossing in these thiophene derivatives involving singlet and triplet states with ππ* and πσ* characters. Excitation at 266 nm results in an additional 5 ± 1 ps lifetime, which is assigned to intramolecular vibrational relaxation dynamics occurring in the excited singlet state.
Introduction
Thiophene derivatives are widely employed as building blocks in the design of various π-conjugated organic semiconductors,1–7 such as organic light-emitting diodes (OLED) and organic solar cells, in which they served as chromophores or light harvesting agents. Thiophene derivatives are also gaining attention in the field of photodynamic therapy due to their cytotoxic and phototoxic properties.8,9 Therefore, understanding the photophysical properties and excited state dynamics of thiophene derivatives, particularly, the intersystem crossing relaxation pathway and its time scale, should offer critical physical insights for their prospective use in these applications.10 Equally important, thiophene derivatives have been identified as a significant source of sulfur oxides released into the atmosphere during the consumption of petroleum products.11–16 Hence, understanding their photophysics and electronic relaxation mechanisms would aid in evaluating their sunlight-induced fate in the environment and in designing photocatalysts17 for their removal.The electronic relaxation mechanism of the thiophene monomer has been previously investigated by Salzmann et al.18 and Weinkauf et al.,19 using ab initio computations and ultrafast spectroscopy, respectively. Upon photoexcitation to the S1 state, thiophene undergoes an ultrafast, three-step internal conversion to the ground state on the femtosecond timescale. Accordingly, the S1 population initially decay to a ππ* region of the S1 adiabatic potential energy surface (PES), which subsequently transitions into an S–C stretched ring-opening πσ* region, and finally decays back to the ground state.19,20 In a nonadiabatic dynamic simulation study reported by Schnappinger et al.,21 the authors proposed that in addition to internal conversion, intersystem crossing is likely to occur because of a small energy gap between singlet and triplet states at the flat potential of the ring-opened πσ* region. Interestingly, however, the relaxation mechanism is different when the π-conjugated system is extended from the thiophene monomer to oligothiophenes.21 According to the computational study by Kölle et al.,22 conducted to explain the experimental work done by Paa et al.,23 such π-conjugation stabilizes both πσ* and ππ* states, thereby hindering access from the ππ* state to the πσ* state. Consequently, fluorescence and intersystem crossing are observed more prominently in the oligothiophenes than in the thiophene monomer, and it was proposed that intersystem crossing primarily occurs from non-planar, ring puckered 1ππ* structures in the oligothiophenes, which enhanced the spin–orbit coupling between the S1 and T3 states.
Recently, the photophysical properties and excited state dynamics of dibenzothiophene, 4-methyldibenzothiophene, and 4,6-dimethyldibenzothiophene were investigated using femtosecond broadband transient absorption, steady-state absorption and emission spectroscopy, and time-dependent density functional (TD-DFT) calculations.24 It was found that excitation of these dibenzothiophene derivatives at 320 nm populates the S1(ππ*) state directly. Surprisingly, most of the S1 population was shown to undergo efficient intersystem crossing to the triplet manifold with lifetimes ranging from 820 ± 50 to 900 ± 30 ps, despite all accessible triplet states below the S1(ππ*) state also exhibiting ππ* character in the Franck Condon region. TD-DFT calculations, however, provided evidence that C–S bond elongation and the mixing of σ and π orbitals along the excited state reaction coordinate play a key role in facilitating the near unity intersystem crossing to the triplet manifold in these dibenzothiophene derivatives.24 While it has been shown that ring puckering and ring opening minima structures in the S1 potential energy surface (PES) of the oligothiophenes are populated almost simultaneously on an ultrafast timescale, and play an important role in their relaxation mechanisms,22 a ring puckering minimum was not located in the case of the dibenzothiophene derivatives.24
In this study, we investigate the photophysics and excited state dynamics of thianaphthene and two of its methylated derivatives at the C2 and C3 positions (Scheme 1), to better understand the photophysical properties of monomeric thiophene derivatives of relevance to n-conjugated thiophene systems. Steady state absorption and emission spectroscopy, femtosecond broadband pump–probe transient absorption, and density functional theory calculations are used. The measurements show small fluorescence quantum yields ranging from 0.4 to 1.1%. When TN is excited at 290 nm, it primarily undergoes intersystem crossing to the triplet manifold with a lifetime of 400 ± 15 ps in either solvent. Four- to twofold shorter intersystem crossing lifetimes are measured for 2MBT and 3MBT depending on whether cyclohexane or acetonitrile is used. The TDDFT calculations indicate that the elongation of the S–C bonds enables ultrafast intersystem crossing in these thiophene derivatives, involving singlet and triplet states of ππ* and πσ* characters. Contrary to what was found in the dibenzothiophene derivatives,24 we show that methylation significantly affects the intersystem crossing lifetime of these thianaphthene derivatives. In addition, excitation of TN, 2MBT, and 3MBT at 266 nm results in an additional lifetime of 5 ± 1 ps, which is assigned to intramolecular vibrational relaxation dynamics occurring in the S1 state.
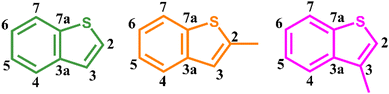 | ||
| Scheme 1 Structures with carbon atom numbering of thianaphthene (green), 2-methylbenzothiophene (orange), and 3-methylthianaphthene (pink). | ||
Experimental
Chemicals
Thianaphthene (TN) was obtained from Sigma-Aldrich (98% purity). 2-Methylbenzothiophene (2MBT) and 3-methylbenzothiophene (3MBT) were obtained from Alfa Aesa with 98% purity. Cyclohexane (CHX, 99% purity, Millipore Corporation) and acetonitrile (ACN, 99.8% purity, Fisher Scientific) were all used as received.Steady-state measurements
Steady-state absorption and emission spectra were taken using Varian Cary 100 and Varian Cary Eclipse, respectively. Emission spectra were collected using a PMT voltage of 540 V with 5 nm slit widths and excitation at 280 nm. Molar absorption coefficients were determined from five solutions of various concentrations prepared from a known stock concentration. Fluorescence quantum yields were measured using L-tryptophan as a standard.25 Bathochromic shifts in fluorescence emission (Fig. S1, ESI†) at concentrations above 7 × 10−5 M in either solvent were observed, as have been observed previously in other polycyclic aromatic hydrocarbons.26,27 This observation evidence the formation of aggregates at higher concentrations that 7 × 10−5 M. Therefore, all the spectroscopic experiments were done at lower concentrations to avoid aggregate formation.Femtosecond broadband transient absorption spectroscopy
The femtosecond broadband pump–probe transient absorption used in this study is described in detail elsewhere.28–31 Briefly, a 800 nm fundamental pulse (4.0 W, 100 fs pulse, Libra-HE from Coherent, Inc.) is split into a pump and probe pulse. The 290 nm excitation pulse was generated from a fraction the fundamental beam after being sent through an optical parametric amplifier where it was tuned. The remaining small fraction of the fundamental pulse was sent to a delay stage and focused on a translating CaF2 crystal to generate a probe white light continuum in a spectral range of ∼320 to 700 nm. An optical rail kit (FKE series, EKSMA optics) was used to generate the excitation pulse at 266![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm.32–34 A 2 mm fused silica cuvette with a stir bar was used to ensure homogeneity of the solutions. Steady-state absorbance measurements were taken before and after transient experiments to check for photodegradation. No photodegradation of the samples were observed under the experimental conditions used in this study.
nm.32–34 A 2 mm fused silica cuvette with a stir bar was used to ensure homogeneity of the solutions. Steady-state absorbance measurements were taken before and after transient experiments to check for photodegradation. No photodegradation of the samples were observed under the experimental conditions used in this study.
The femtosecond transient absorption data were collected using the SurfaceXplorer program and analyzed using global and target analysis35 in the Glotaran 1.5.1 graphical user interfaced to the R-package TIMP software.36 A two-component sequential model was required to model the transient data for 2MBT and 3MBT upon excitation at 290 nm, while a three-sequential model was needed for the transient data of TN upon excitation at 290 nm. A three-component sequential model was required to model of the transient absorption data of the three TN derivatives upon excitation at 266 nm. The evolution associated decay spectra EADS were extracted from the global fitting of the transient data sets. For the three TN derivatives in acetonitrile, the transient data from 320 to 340 nm were excluded from the global analysis due to the observation of stimulated Raman emission of the solvent. The lifetimes of the longer-lived species persisting for time delays longer than the 3 ns timescale used in this study are reported as >3 ns because their decay lifetimes cannot be accurately determined. All transient absorption measurements were performed in duplicate on different days to ensure reproducibility. Time-zero was defined as the time of maximum overlap of the pump and probe pulses, as judged from the stimulated Raman emission signal of acetonitrile. Errors of the lifetimes are reported as twice the standard deviation from repeating the experiments in duplicate.
The effect of changing the concentration of the TN derivatives on the transient absorption signals were also studied. The global, target kinetic analysis of the data at different concentrations showed no variation in the extracted lifetimes and only minor spectral changes in the extracted evolution associated difference spectra (EADS) (Fig. S2–S13, ESI†), while red shifts in the fluorescence bands were observed in the steady state emission spectra as a function of concentration (Fig. S1, ESI†). Regardless, the transient absorption data, lifetimes, and EADS reported in the main text where collected for concentrations bellow 7 × 10−5 M for the TN derivatives in either solvent.
Computational method
All the density functional theory calculations were carried out in the Orca 5.0.3 quantum chemistry program package.37 Electronic ground state geometries were optimized at B3LYPG-D3BJ/def2-TZVPD level of theory in vacuum.38–43 Excited state geometries were optimized at TDA-PBE0-D3BJ/def2-TZVPD level,44,45 while the triplet excited state geometries were optimized using unrestricted DFT at UPBE0-D3BJ/def2-TZVPD level. The RIJCOSX46 density fitting and the def2/J47 auxiliary Coulomb fitting basis set were used throughout to accelerate the computations. No symmetry constraints were employed throughout. Harmonic vibrational frequencies48 were evaluated to confirm no imaginary modes in all the optimized geometries. Vertical excitation energies (VEE) and oscillator strengths were obtained at TDA-PBE0/def2-TZVPD level of theory in vacuum, acetonitrile, and cyclohexane. Dielectric effects of acetonitrile and cyclohexane were described using the C-PCM implicit solvation model,49 as implemented in Orca 5.0.3. Linear interpolation of internal coordinates (LIIC) was performed from the ground state minimum to the S1(πσ*) minimum of the three thianaphthene derivatives. The spin–orbit mean-field method50 was employed to obtain spin–orbit coupling constants (SOCCs), and its magnitude is reported by the square root of the sum of squares using the x, y, and z components of the spin–orbit coupling matrix elements.Results
Steady-state spectroscopy
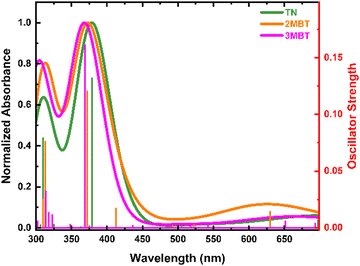
Fig. 1 depicts the absorption and emission spectra of TN, 2MBT, and 3MBT in acetonitrile and cyclohexane. Vibronic fine structures in the S1 state can be observed in the spectral region between 285 to 300 nm. The TN derivatives exhibit larger absorption cross-sections (ca. 103 M−1 cm−1) in cyclohexane than in acetonitrile with negligible spectral shifts. A reduction in vibronic fine structure is observed in going from cyclohexane to acetonitrile indicative of stronger solvent–solute interactions in acetonitrile, as observed previously for dibenzothiophene derivatives.24 The fluorescence quantum yields slightly increase in going from acetonitrile to cyclohexane, and decrease with methylation of TN at the 2 and 3 positions, as is shown in Table 1.| Compound | Solvent | λ abs/nm | ε(λmax)/M−1 cm−1 at 298 nm | λ em/nm | E 00/cm−1 ± 100 | Φ fl (×10−2) |
|---|---|---|---|---|---|---|
| a λ max/M−1 cm−1 is at 299 nm. | ||||||
| TN | Acetonitrile | 258, (264), 281, 288, 290, 298 | 2120 ± 30a | 299, 311, (323) | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
0.9 ± 0.1 |
| Cyclohexane | 258, 264, 281, 288, 291, 298 | 3810 ± 30 | 300, 311, (323) | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
1.1 ± 0.2 | |
| 2MBT | Acetonitrile | 258, 264, 281, 288, 291, 298 | 1322 ± 30 | 300, 311, (324) | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
0.4 ± 0.1 |
| Cyclohexane | 260, 265, 281, 288, 291, 298 | 2180 ± 30 | 300, 311, (324) | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
0.6 ± 0.1 | |
| 3MBT | Acetonitrile | 264, (283), 291, 299 | 2060 ± 30a | 303, 313, (327) | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
0.5 ± 0.1 |
| Cyclohexane | 262, (270), (282), 290, 299 | 4210 ± 30a | 303, 313, (327) | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
0.8 ± 0.1 | |
For completeness, we also investigate how the concentration of the TN derivatives affects their steady state photochemical properties. No significant spectral changes were observed in the steady-state absorption spectra (not shown). However, the higher energy emission band of TN in the fluorescence spectra in acetonitrile shows a small bathochromic shift of ca. 2 nm, a decrease in intensity of the emission band at ca. 300 nm, an increase in intensity of a shoulder band ca. 312 nm, and extension of the emission tail to up to 400 nm with an increase in concentration (Fig. S1, ESI†).
Ground state geometries and simulated ground state absorption spectra
In this study, the nomenclature: S1, S2, …, T1, T2, …, represents the adiabatic order of electronic states at a given geometry, followed by the character of the electronic structure in parentheses. All the optimized ground state geometries for the TN derivatives exhibit a planar ring system. VEEs, oscillator strengths, and electronic structure of the low-lying singlet and triplet excited states are presented in Table 2 for TN in vacuum, and in Tables S1–S8 (ESI†) for TN, 2MBT, and 3MBT in vacuum, acetonitrile, and cyclohexane. The electron density of the Kohn–Sham orbitals associated to the electronic states can be found in Fig. 2 and Fig. S14, S15 (ESI†). The simulated ground state absorption spectra for the TN derivatives are depicted in Fig. 3 based on the Franck–Condon principle. The simulated absorption spectra of 2MBT and 3MBT are available in Fig. 2. Tables S1, S2, S4, S5, S7, and S8 (ESI†) present the VEEs and oscillator strengths, obtained with the C-PCM implicit solvation solvent model.| State | Electronic structure | VEE/eV | f (r) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1(ππ*) | H | → | L | 0.47; | H−1 | → | L | 0.23; | H | → | L+1 | 0.14; | 4.77 | 0.0474 |
| S2(ππ*) | H | → | L+1 | 0.47; | H | → | L | 0.32; | H−1 | → | L+1 | 0.14; | 4.99 | 0.0251 |
| S3(πσ*) | H−1 | → | L+2 | 0.92; | 5.25 | 0.0000 | ||||||||
| S4(ππ*) | H−1 | → | L | 0.42; | H | → | L+1 | 0.22; | H−1 | → | L+5 | 0.13; | 5.77 | 0.2455 |
| T1(ππ*) | H | → | L | 0.82; | 3.40 | |||||||||
| T2(ππ*) | H | → | L+1 | 0.68; | H−1 | → | L | 0.10; | 4.11 | |||||
| T3(ππ*) | H−1 | → | L | 0.74; | H | → | L | 0.11; | 4.16 | |||||
| T4(ππ*) | H−1 | → | L+1 | 0.76; | H | → | L+1 | 0.13; | 4.55 | |||||
| T5(ππ*) | H | → | L+5 | 0.47; | H−2 | → | L | 0.28; | 4.94 | |||||
| T6(πσ*) | H−1 | → | L+2 | 0.82; | 4.97 | |||||||||
 | ||
| Fig. 2 Electron density of TN frontier Kohn–Sham orbitals at the S0 minimum in vacuum, contour value of the isosurfaces was set to 0.02, visualized by the Multiwfn51 and VMD52 program. | ||
 | ||
| Fig. 3 Normalized absorption spectra of TN, 2MBT, and 3MBT calculated in vacuum at TDA-PBE0/def2-TZVPD level of theory. The full width at maximum (FWHM) of the Gaussian broadening function were set to 0.3 eV, plotted with Multiwfn.51 | ||
Excited state geometries
Harmonic frequency analyses were performed on all the optimized geometries in vacuum, acetonitrile, and cyclohexane. No imaginary frequencies were found, showing that the geometries are local minima on the PES. A complete list containing excited state energies and spin–orbit couplings at the S1(ππ*) minima for the three TN derivatives in vacuum, acetonitrile, and cyclohexane can be found in Tables S9–S16 (ESI†).For the three TN derivatives, the geometry at the S1(ππ*) minima conserves the Cs symmetry. The calculated E0,0 align well with the experimental results, as can be seen in Table 1. The T1(ππ*) minima are ca. 1.3 eV lower in energy than the optimized S1(ππ*) minima counterparts. Additionally, the C2–H bond shows a puckering of the H–C2–C3–C3a dihedral; from 180° in the singlet minima to a 157° in the triplet minima.
S1(πσ*) minima with planar geometries were found for the TN derivatives. In comparison to the S1(ππ*) minima, S1(πσ*) minima exhibited elongated S–C bonds due to occupation in the S–C σ* orbital. Stretching either the S–C2 or S–C7a bond leads to different electronic configurations and corresponding minima, as depicted in Fig. 4, while the minima resulting from the S–C7a bond stretch are lower in energy than those from the S–C2 bond stretch. The SOCCs for TN were evaluated at the S1 and T1 optimized minima in vacuum, as listed in Table 3. The large energy gap and small SOCCs between the S1(ππ*) and T1(ππ*) states suggest that a direct intersystem crossing from the S1(ππ*) to the T1(ππ*) state is unlikely. Nevertheless, it is reasonable to expect that the ππ* states could intersect with πσ* states upon S–C elongation, creating conditions for both a small energy gap difference and considerable SOCCs, which could facilitate favorable intersystem crossing between them.21,24
 | ||
| Fig. 4 Geometries and electronic structure of (a) TN S–C2 stretched and (b) S–C7a stretched S1(πσ*) minima, optimized at TDA-PBE0/def2-TZVPD level of theory. Visualized by the Multiwfn51 and VMD52 programs. | ||
| S1(ππ*) minimum | S–C2 stretched S1(πσ*) minimum | S–C7a stretched S1(πσ*) minimum | ||||||
|---|---|---|---|---|---|---|---|---|
| State | E/eV | SOCC(S1–Tn)/cm−1 | State | E/eV | SOCC(S1–Tn)/cm−1 | State | E/eV | SOCC(S1–Tn)/cm−1 |
| S1(ππ*) | 4.70 | — | S1(πσ*) | 4.48 | — | S1(πσ*) | 4.16 | — |
| T1(ππ*) | 3.12 | 0.0 | T1(πσ*) | 4.06 | 0.7 | T1(πσ*) | 3.80 | 0.2 |
| T2(ππ*) | 4.11 | 0.0 | T2(σσ*) | 4.99 | 92.7 | T2(σσ*) | 4.92 | 75.1 |
| T3(ππ*) | 4.31 | 0.0 | T3(πσ*) | 5.20 | 0.3 | T3(ππ*) | 5.46 | 52.4 |
| T4(ππ*) | 4.88 | 0.0 | T4(ππ*) | 5.94 | 44.4 | T4(πσ*) | 5.64 | 0.6 |
| T5(ππ*) | 4.93 | 0.0 | ||||||
| T6(πσ*) | 5.22 | 22.5 | ||||||
Linear interpolation of internal coordinates
All the ππ* and πσ* geometries in the S1 and T1 states feature a planar ring system. The energy shift between ππ* and πσ* geometries is primarily contributed by the S–C stretch, as minimal changes in all other bonds, angles, and dihedrals are observed. Thus, it is reasonable to employ linear interpolation of internal coordinates to connect the ππ* region at the Franck–Condon point and the πσ* minima, to produce a two-dimensional slice that depicts the potential energy hypersurface. Twenty-four geometries were interpolated with an averaged step size between the ground state minima and the S1(πσ*) minima associated with each respective S–C ring-opening, the calculated energy barriers are collected in Table 4. In addition, extrapolated geometries were generated beyond S–C stretched S1 minima to search for an S1(πσ*)/S0(ππ*) avoided crossing (see, Fig. 5).| Bond | S–C/Å | ΔES1–FC/eV | |
|---|---|---|---|
| TN | S–C2 | 1.96 | 0.32 |
| S–C7a | 1.91 | 0.21 | |
| 2MBT | S–C2 | 1.96 | 0.26 |
| S–C7a | 1.90 | 0.17 | |
| 3MBT | S–C2 | 1.98 | 0.36 |
| S–C7a | 1.90 | 0.19 |
Among the linear interpolated geometries, several energy crossings between the S1 and the triplet states were found. The SOCCs of the singlet–triplet crossing geometries are reported in Table 5. For the three TN derivatives, the energies and singlet–triplet crossings in the linear interpolations follow a similar pattern in vacuum and in both solvents. The LIIC of the TN S–C7a stretch is presented in Fig. 5, while the analogous LIICs and SOCMEs for the remaining systems are presented in Fig. S16–S20 and Tables S9–S16 (ESI†), respectively.
| S–C/Å | T | S | ΔES1–FC/eV | SOCC/cm−1 |
|---|---|---|---|---|
| 1.80 | T5(πσ*) | S1(ππ*) | 0.07 | 33.4 |
| 1.94 | T5(ππ*) | S1(πσ*) | 0.15 | 2.4 |
| 1.97 | T4(ππ*) | S1(πσ*) | 0.09 | 9.6 |
| 2.04 | T3(ππ*) | S1(πσ*) | −0.05 | 18.6 |
| 2.23 | T2(ππ*) | S1(πσ*) | −0.40 | 39.0 |
Triplet excited state geometries and simulated transient absorption spectra
The optimized structures of T1(ππ*), S–C2 stretched T1(πσ*), and S–C7a stretched T1(πσ*) for TN, 2MBT, and 3MBT were obtained from unrestricted DFT calculations. Compared to their singlet minima counterparts, the H–C2–C3–C3a dihedral angle in T1(ππ*) minima departs by 23°, 34°, and 25° from the plane in TN, 2MBT (CH3–C2–C3–C3a angle in the case of 2MBT), and 3MBT, respectively, whereas the T1(πσ*) minima remain planar. The VEEs and the SOCMEs between the low-lying singlet and triplet states in vacuum are collected in Table 6. The simulated absorption spectra of the TN derivatives in vacuum are presented in Fig. 6. The lower energy band is due to ππ* transitions from T1 to T5, T6, and T7 states. The 375 nm band is consistent with the triplet → triplet absorption from the T1(ππ*) state to doubly excited triplet states.| T1(ππ*) minimum | S–C2 stretched T1(πσ*) minimum | S–C7a stretched T1(πσ*) minimum | ||||||
|---|---|---|---|---|---|---|---|---|
| State | E/eV | SOCC(Sn–T1)/cm−1 | State | E/eV | SOCC(Sn–T1)/cm−1 | State | E/eV | SOCC(Sn–T1)/cm−1 |
| T1(ππ*) | 3.04 | — | T1(πσ*) | 4.11 | — | T1(πσ*) | 3.84 | — |
| S0 | 0.61 | 2.2 | S0 | 3.34 | 142.8 | S0 | 3.33 | 124.3 |
| S1(ππ*) | 4.94 | 4.3 | S1(πσ*) | 4.52 | 0.5 | S1(πσ*) | 4.19 | 0.1 |
| S2(ππ*) | 5.21 | 1.9 | S2(πσ*) | 5.67 | 0.3 | S2(πσ*) | 6.17 | 0.5 |
| S3(πσ*) | 5.52 | 27.5 | S3(ππ*) | 6.82 | 82.7 | S3(πσ*) | 6.44 | 0.4 |
 | ||
| Fig. 6 Normalized absorption spectra of T1(ππ*) of TN, 2MBT, and 3MBT in vacuum at UTDA-PBE0/def2-TZVPD level of theory. The unrestricted density matrices of T1(ππ*) were used to calculate higher triplet excited states at T1(ππ*) optimized geometry. The full width at maximum (FWHM) of the Gaussian broadening function was set to 0.5 eV, plotted with Multiwfn.51 | ||
Femtosecond broadband transient absorption
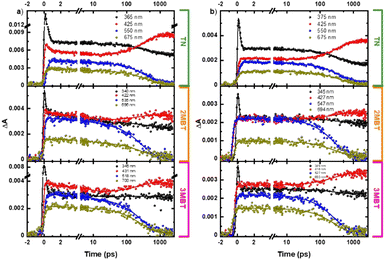
Femtosecond transient absorption measurements were obtained for the TN derivatives in acetonitrile and cyclohexane to unravel their electronic relaxation mechanisms (Fig. S21–S23, ESI†). Representative contour plots (heat maps) of the transient absorption data are shown in Fig. 7. No significant spectral changes were observed in the transient absorption data as a function of concentration for the three TN derivatives in both solvents (Fig. S2–S13, ESI†). Fig. 8 displays the evolution associated difference spectra (EADS) of TN, 2MBT, and 3MBT after excitation at 266 and 290 nm in both acetonitrile and cyclohexane. Fig. S2–S7 (ESI†) further display the EADS of the TN derivatives at different concentrations, where these molecules are either present as monomers or as aggregates according to the steady-state emission spectra (Fig. S1, ESI†). Table S17 (ESI†) highlights the band maxima and shoulders seen in the EADS of the TN derivatives upon excitation at 266 nm and 290 nm. Representative kinetic traces and best fits based on global analyses using two or three component sequential models for excitation at wavelengths of 290 or 266 nm, respectively, are shown in Fig. 9 and Fig. S7–S13 (ESI†) for each TN derivative in both solvents. The lifetimes extracted from these global and target analyses are presented in Table 7. | ||
| Fig. 8 Evolution associated difference spectra of TN, 2MBT, and 3MBT in cyclohexane upon excitation at (a) 266 nm and (b) 290 nm. | ||
| Compound | Solvent | Ecx. λ (nm) | τ 1 (ps) | τ 2 (ps) | τ 3 (ns) |
|---|---|---|---|---|---|
| TN | Acetonitrile | 266 | 5 ± 1 | 400 ± 10 | >3 |
| 290 | 5 ± 1 | 387 ± 10 | >3 | ||
| Cyclohexane | 266 | 5 ± 1 | 397 ± 15 | >3 | |
| 290 | 5 ± 1 | 397 ± 15 | >3 | ||
| 2MBT | Acetonitrile | 266 | 6 ± 1 | 205 ± 20 | >3 |
| 290 | — | 170 ± 15 | >3 | ||
| Cyclohexane | 266 | 6 ± 1 | 275 ± 15 | >3 | |
| 290 | — | 277 ± 15 | >3 | ||
| 3MBT | Acetonitrile | 266 | 5 ± 1 | 186 ± 15 | >3 |
| 290 | — | 168 ± 10 | >3 | ||
| Cyclohexane | 266 | 5 ± 1 | 265 ± 15 | >3 | |
| 290 | — | 260 ± 15 | >3 |
Within experimental uncertainties, the first lifetime of ca. 5 ps is independent of the solvent and TN derivative under investigation upon excitation at 266 nm. Interestingly, the first lifetime is also independent of the solvent and TN derivative but it is not observed in either solvent for 2MBT and 3MBT upon excitation at 290 nm (Table 7). The second lifetime depends on the solvent and excitation wavelength for 2MBT and 3MBT, but not for TN within the experimental errors. Table 7 shows that the third lifetime is longer than the time window used in this study of 3 ns independent of the TN derivative, solvent, or excitation wavelength. As shown in Table S17 (ESI†) and Fig. 8, minor spectral shifts are observed in the EADSs for each TN derivatives depending on the compound, solvent, and excitation wavelength.
Discussion
Steady-state and computational studies
As shown in Fig. 1 and Table 1, the absorption and emission spectra of the TN derivatives are only minimally perturbed by methylation of TN at the C2 and C3 positions. The E0,0 energies are the same within the experimental uncertainties, independent of solvent, while the molar absorption coefficients are ca. 1.6 to 2-fold larger in cyclohexane than in acetonitrile. Similarly, the fluorescence quantum yields are slightly larger in cyclohexane than in acetonitrile, varying from 0.4 to 1.1% depending on the solvent and the TN derivative studied. On average, methylation of TN reduces it fluorescence quantum yield by ca. 2-fold in acetonitrile and 1.6-fold in cyclohexane.The relatively small fluorescence quantum yields for the three TN derivatives evidence that nonradiative relaxation pathways play a primary role in the electronic relaxation mechanisms of these molecules.
VEEs of the TN derivatives (Fig. 3, Table 2 and Fig. S1–S8, ESI†) are in fair agreement with the experimental absorption spectra reported in Fig. 1a. The simulated absorption spectra in vacuum (Fig. 3) are blue-shifted by approximately 30 nm in comparison with the experimental spectra (Fig. 1a), which is expected given the reported ±0.2 to 0.3 eV error of these calculations.53–56 A slight red shift of the VEEs and an increase in oscillator strengths for the TN derivatives upon inclusion of solvent effects using the CPCM model (Tables S1–S8, ESI†) are in good agreement with the steady-state absorption spectra shown in Fig. 1a. Based on the VEEs, the lower energy absorption band between 285 to 305 nm for the TN derivatives is due to a combination of the electronic transition from the S0 to the S1(ππ*) and S2(ππ*) states. The higher energy absorption band at 260 nm is assigned to be a combination of transitions to the S4(ππ*), and S6(ππ*) states, due to their high oscillator strengths (Tables S1–S8, ESI†). The S3 and S5 states have πσ* character and negligible oscillator strength. Similarly, the experimental and computational E0,0 energies, Tables 1, 2 and Tables S1–S8 (ESI†), are in good agreement and provide support that fluorescence emission occurs from the S1(min)(ππ*) state. The agreement between the steady state results and the computations lend support to the use of TD-DFT to describe the photophysics of these TN derivatives in this study. Hence, based on the TD-DFT calculations, excitation of the TN derivatives at 290 nm directly populates the S1(ππ*) state, while excitation at 266 nm can directly populate both the S4(ππ*) and S6(ππ*) states simultaneously.
Assignment of the transient absorption spectra and lifetimes for the TN derivatives
According to the TD-DFT calculations, excitation of the TN derivatives at 290 nm populates the vibrationally excited S1(ππ*) state, while excitation at 266 nm primarily populates the vibrationally excited S4(ππ*) and S6(ππ*) states. Hence, the EADS1 reported in Fig. 8a is due to the absorption spectrum of the vibrationally excited S1(ππ*) state upon excitation at 290 nm. Similarly, the EADS1 is assigned to a minor contribution from the absorption spectra of the S4(ππ*) and S6(ππ*) states together with a significant contribution from the absorption spectrum of the vibrationally excited S1(ππ*) state upon excitation at 266 nm. In other words, we expect that most of the initial population reaching the S4(ππ*) and S6(ππ*) states would internally converge to the vibrationally excited S1(ππ*) state within the time resolution of the experimental setup of ca. 250 fs. This is supported by the similarity of the spectral shape of the EADS1 at both excitation wavelengths (Fig. 8).The EADS2 is assigned to the absorption spectra of the S1(ππ*) minimum at both excitation wavelengths in the three TN derivatives in both solvents (Fig. 8). Hence, the first lifetime of ca. 5 ps reported in Table 7 represents a minor contribution ultrafast internal conversion from the S4(ππ*) and S6(ππ*) states to the vibrationally excited S1(ππ*) state and intramolecular vibrational relaxation to the S1(ππ*) minimum upon excitation at 266 nm, while it represents intramolecular vibrational relaxation to the S1(ππ*) minimum upon excitation at 290 nm. For 2MBT and 3MBT, it seems that vibrational relaxation occurs faster than our time resolution upon excitation at 290 nm independent of the solvent (Table 7). The inability to observe the intramolecular vibrational relaxation lifetime to the S1(min)(ππ*) in 2MBT and 3MBT upon excitation at 290 nm highlights the significance of the additional vibrational degrees of freedom due to methylation, which allows for faster vibrational relaxation.
The EADS3 is assigned to the absorption spectrum of the T1(ππ*) minimum for each TN derivative. This is supported by the agreement between the computed transient absorption spectra for the T1(ππ*) minimum in Fig. 6 and the EADS3 reported in Fig. 8 independent of the excitation wavelength. Seixas et al.57 has previously observed the population of the triplet state in TN with a triplet quantum yield of >98% in ethanol, whose absorption spectrum is similar to those reported for the EADS3 in Fig. 8. Therefore, the second lifetime is unequivocally assigned to intersystem crossing to the T1(ππ*) state in the three TN derivatives, independent of solvent or excitation wavelength. The T1(ππ*) state is populated with a faster lifetime in 2MBT and 3MBT than in TN and significantly faster in acetonitrile than in cyclohexane for 2MBT and 3MBT (Table 7), in excellent agreement with the steady state observation that the fluorescence quantum yield of TN decreases by 2-fold in acetonitrile and 1.6-fold in cyclohexane upon methylation. The observation that intersystem crossing occurs in a few hundred of picoseconds also supports the idea of efficient and near unity triplet yield in these TN derivatives.57 The triplet state of these TN derivatives is long-lived (τ3 in Table 7) and for TN, it decays with a lifetime of 3 μs in ethanol.57
Electronic relaxation mechanism leading to the efficient population of the triplet state
Analysis of the transient absorption data and comparison with the excited state calculations evidence that the population of the triplet state in these TN derivatives is highly efficient independent of the excitation wavelength (i.e., 266 versus 290 nm) or solvent used (i.e., acetonitrile versus cyclohexane). The observation that the fluorescence quantum yield of the TN derivatives is less than or equal to 1.1% and that the intersystem crossing lifetimes occur in less than or equal to 400 ps, lend further support to the idea that intersystem crossing is the primary relaxation pathway in these molecules. This is further supported by the work of Seixas et al.,57 which reported a triplet quantum yield of >98% for TN in ethanol. The proposal that intersystem crossing is both efficient and the primary relaxation pathway is surprising given that the TD-DFT calculations reported in Table 2 and Tables S1–S8 (ESI†) predict that the S1 and the triplet states below it all have ππ* character in the Franck–Condon region of the PESs.Recently, the excited state dynamics of dibenzothiophene (DBT) derivatives were investigated using femtosecond transient absorption and TD-DFT calculations.24 The authors demonstrated that intersystem crossing in these DBT derivatives occurs in a sub-1 ns timescale and with near unity triplet yield despite a similar observation that the singlet and triplet states all have ππ* character in the Franck–Condon region. However, LIIC at the TD-DFT level of theory revealed the chemical basis for relaxing the spin-forbidden intersystem crossing in these DBT derivatives.24 It was shown that C–S bond elongation and the mixing of σ and π orbitals along the reaction coordinate relaxes the El-Sayed rules and enable the near unity triplet yield.24 Therefore, in this study, we have performed similar LIIC at the TD-DFT level of theory to provide physical insights about the electronic relaxation mechanism giving rise to ultrafast intersystem crossing and near unity triplet yield in the TN derivatives.
Based on the stationary points and LIIC reported in Fig. 5, two favorable intersystem crossing pathways are identified with a reasonably low energy barrier of ca. 0.19 and a reasonably large SOCME of 33 cm−1. The first intersystem crossing pathway involves an energy crossing between the S1(ππ*) and the T5(πσ*) states at the early stage of the S–C stretching, while the second involves an energy crossing between the S1(πσ*) and the T2(ππ*) states, near the S1(πσ*) minimum (Fig. 5). After intersystem crossing occurs, the TN derivatives are expected to populate one or both T1(ππ*) and T1(πσ*) minima in the T1 PES. In the absence of nonadiabatic dynamics simulations, and under the assumption that the nonradiative transition is primarily dominated by the S–C elongation, we could use the Landau–Zener formula58 as a first approximation to provide a rationale for the intersystem crossing event. Accordingly, for an efficient nonradiative transition to ensue, it requires not only the crossing seam to be energetically accessible but also a considerable nuclear velocity along the branching-plane. From this perspective, the S1(πσ*)/T2(ππ*) crossing region should be more favorable than the S1(ππ*)/T5(πσ*) region because it is lower in energy than the former, thus, having a larger kinetic energy to aid in the intersystem crossing event.
Once the triplet state is populated, intersystem crossing to the ground state should occur in a microsecond time scale, as reported by Seixas et al. for TN in ethanol.57 From the LIIC, the predicted S1(πσ*)/S0(ππ*) avoided crossing is at a similar energy than the S1(πσ*)/T2(ππ*) crossing, and internal conversion is usually considered to be much faster than intersystem crossing. However, the dynamic study for thiophene by Schnappinger et al.21 found that thiophene, which has a similar topological landscape of PES at the S–C stretched region than TN, does not effectively decay to the ground state minimum because it requires the inversion of the velocity vector, which means contraction of the C–S bond instead of stretching. In addition, in the study of Schnappinger et al.,21 the S1(πσ*)/T2(ππ*) is partially active at the S–C stretched region, which further supports the participation of a similar pathway in TN derivatives. 2MBT and 3MBT have smaller energy barriers of 0.04 and 0.02 eV to access the S–C stretched S1(πσ*) region, respectfully, than the energy barrier of TN (0.21), which correlates with their second lifetime being shorter than the intersystem crossing lifetime of TN.
In the work on oligo-thiophene by Kölle et al.,22 the intersystem crossing yield increases with the barrier to the S–C stretched region as more thiophene units are introduced to the system. Their dynamic study found that the El-Sayed forbidden intersystem crossing between singlet ππ* and triplet ππ* occurs at non-planar geometries, which results from either non-planar character of the ground state geometries or thermal torsional fluctuations. For the TN derivatives investigated in our study, the SOCMEs between singlet ππ* and triplet ππ* at S1(ππ*) minima are minimal (<0.1 cm−1). However, at the slightly puckered T1(ππ*) minima, the SOCME increases to a range of 1–10 cm−1. This could be due to a small mixing of πσ* character into the ππ* state at the non-planar geometry, which correlates with the observation from oligo-thiophene. Although a direct S1(ππ*)/T1(ππ*) is unlikely due to the large energy gap, we cannot exclude the possibility of S1(ππ*)/T3(ππ*) or S1(ππ*)/T4(ππ*) occurring from a puckered structure, and then decaying to the T1 adiabatic PES. A systematic study of the vibronic effect on the nonradiative transition in TN derivatives would require non-adiabatic dynamics simulations, which are beyond the scope of this study. Regardless, of whether a puckered S1(ππ*)structure could also give rise to intersystem crossing, the population of T1(ππ*) in TN derivatives is supported by both transient absorption spectra and simulated transient absorption signal in this study. The large energy gap and small SOCCs indicating the nonradiative T1(ππ*)/S0 transitions are inefficient, resulting in the T1(ππ*) state having a long lifetime in the microseconds.
Conclusions
The efficient intersystem crossing to the T1 state in three TN derivatives was demonstrated using time-resolved absorption spectroscopy and steady-state absorption/emission. The electronic relaxation mechanism leading to the efficient population of the T1(ππ*) state was further revealed using ground and excited state TD-DFT calculations. Population of the S1(ππ*) state leads to roughly 1% of the population decaying by fluorescence emission. The remaining 98–99% of the population is proposed to follow the S1 adiabatic PES that leads to internal conversion between the S1(ππ*) and S1(πσ*) states due to S–C bond elongation. The primary intersystem crossing is proposed to occur between S1(πσ*) and T2(ππ*) states given the significant SOCME, minimal energy barrier, and larger kinetic energy than the pathways between S1(ππ*) and T5(πσ*) states. The smaller energy barriers of 0.04 and 0.02 eV to access the S–C stretched S1(πσ*) region seen in 2MBT and 3MBT supports than the energy barrier of 0.21 in TN lend support to their shorter intersystem crossing lifetimes compared to that of TN. The decrease in the triplet state population lifetime upon methylation in these TN derivatives contrasts with what was observed recently for dibenzothiophene derivatives.24 In that study, the addition of methyl groups to the dibenzothiophene derivatives does not affect the intersystem crossing lifetime to populate the T1(ππ*) state. This observation suggests that the addition of a benzene group at the C2–C3 bond of the TN derivatives hinders the vibrational degrees of freedom necessary to increase the intersystem crossing rate to the T1(ππ*) state in the TN derivatives. To further explore this hypothesis, experiments are currently underway to investigate the excited state dynamics and intersystem crossing rate on 2,3-dimethylbenzothiophene (a.k.a., benzo[b]thiophene, 2,3-dimethyl). Collectively, this study lends further support to the proposal that the S–C ring opening of thiophene21 and bond elongation of dibenzothiophene24 is the primary relaxation pathway for intersystem crossing, which relaxes the El-Sayed propensity rules for intersystem crossing to the T1(ππ*) state.Author contributions
Cameron Griffith: investigation, formal analysis, and writing – original draft. Erqian Mao: investigation, formal analysis, writing – original draft, and editing. Sean J. Hoehn: investigation, manuscript review, writing – original draft, and editing. Sarah E. Krul: investigation, manuscript review, writing – original draft, and editing. Carlos E. Crespo-Hernández: conceptualization, funding acquisition, project administration, resources, supervision, manuscript review, and editing.Data availability
Experimental and computational procedures and all relevant data are available in the main text, ESI,† and from the authors upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by the donors of the American Chemical Society Petroleum Research Fund. It made use of the High Performance Computing Resource in the Core Facility for Advanced Research Computing at Case Western Reserve University. We thank Mr Chris Acquah for assistance with making Fig. 7.References
- I. F. Perepichka, D. F. Perepichka, H. Meng and F. Wudl, Adv. Mater., 2005, 17, 2281–2305 CrossRef CAS.
- G. Hadziioannou and P. F. Van Hutten, Semiconducting Polymers: Chemistry, Physics and Engineering, Wiley-VCH, Weinheim, Germany, 2000 Search PubMed.
- M. Pomerantz, J. Wang, S. Seong, K. P. Starkey, L. Nugyen and D. S. Marynick, Phosphorus, Sulfur Silicon Relat. Elem., 1994, 95, 507–508 CrossRef.
- Y. Kunugi, K. Takimiya, Y. Toyoshima, K. Yamashita, Y. Aso and T. Otsubo, J. Mater. Chem., 2004, 14, 1367–1369 RSC.
- D. Fichou, Handbook of Oligo- and Polythiophene, Wiley-VCH, Weinheim, Germany, 1999 Search PubMed.
- W. Jiang, Y. Li and Z. Wang, Chem. Soc. Rev., 2013, 42, 6113–6127 RSC.
- X. Guo, M. Baumgarten and K. Müllen, Prog. Polym. Sci., 2013, 38, 1832–1908 CrossRef CAS.
- T. P. Kubrak, P. Kołodziej, J. Sawicki, A. Mazur, K. Koziorowska and D. Aebisher, Molecules, 2022, 27, 1–19 Search PubMed.
- S. Pathania, R. K. Narang and R. K. Rawal, Eur. J. Med. Chem., 2019, 180, 486–508 CrossRef CAS PubMed.
- C. Griffith, S. E. Krul, S. J. Hoehn, T. Phan and C. E. Crespo-Hernández, Chem. – Eur. J., 2024 DOI:10.1002/chem.202402721.
- T. A. Saleh, Trends Environ. Anal. Chem., 2020, 25, e00080 CrossRef CAS.
- T. Harner, C. Rauert, D. Muir, J. K. Schuster, Y.-M. Hsu, L. Zhang, G. Marson, J. G. Watson, J. Ahad, S. Cho, N. Jariyasopit, J. Kirk, J. Korosi, M. S. Landis, J. W. Martin, Y. Zhang, K. Fernie, G. R. Wentworth, A. Wnorowski, E. Dabek, J.-P. Charland, B. Pauli, F. Wania, E. Galarneau, I. Cheng, P. Makar, C. Whaley, J. C. Chow and X. Wang, Environ. Rev., 2018, 26, 430–468 CrossRef CAS.
- M. G. Ehrhardt and K. A. Burns, Mar. Pollut. Bull., 1993, 27, 187–197 CrossRef CAS.
- C. A. Manzano, C. Marvin, D. Muir, T. Harner, J. Martin and Y. Zhang, Environ. Sci. Technol., 2017, 51, 5445–5453 CrossRef CAS PubMed.
- S. Bobinger and J. T. Andersson, Environ. Sci. Technol., 2009, 43, 8119–8125 CrossRef CAS PubMed.
- E. M. Fathalla and J. T. Andersson, Environ. Toxicol. Chem., 2011, 30, 2004–2012 CrossRef CAS PubMed.
- I. A. Mkhalid and A. Shawky, Ceram. Int., 2020, 46, 20769–20776 CrossRef CAS.
- S. Salzmann, M. Kleinschmidt, J. Tatchen, R. Weinkauf and C. M. Marian, Phys. Chem. Chem. Phys., 2008, 10, 380–392 RSC.
- R. Weinkauf, L. Lehr, E. W. Schlag, S. Salzmann and C. M. Marian, Phys. Chem. Chem. Phys., 2008, 10, 393–404 RSC.
- S. Salzmann, M. Kleinschmidt, J. Tatchen, R. Weinkauf and C. M. Marian, Phys. Chem. Chem. Phys., 2008, 10, 380–392 RSC.
- T. Schnappinger, P. Kölle, M. Marazzi, A. Monari, L. González and R. De Vivie-Riedle, Phys. Chem. Chem. Phys., 2017, 19, 25662–25670 RSC.
- P. Kölle, T. Schnappinger and R. De Vivie-Riedle, Phys. Chem. Chem. Phys., 2016, 18, 7903–7915 RSC.
- W. Paa, J. P. Yang and S. Rentsch, Appl. Phys. B: Lasers Opt., 2000, 71, 443–449 CrossRef CAS.
- C. Griffith, S. E. Krul, S. J. Hoehn, E. Mao, G. Sleyko and C. E. Crespo-Hernández, J. Phys. Chem. B, 2023, 127, 5924–5932 CrossRef CAS PubMed.
- R. F. Chen, Anal. Lett., 1967, 1, 35–42 CrossRef CAS.
- M. Kastler, W. Pisula, D. Wasserfallen, T. Pakula and K. Müllen, J. Am. Chem. Soc., 2005, 127, 4286–4296 CrossRef CAS PubMed.
- H. Narita, H. Choi, M. Ito, N. Ando, S. Ogi and S. Yamaguchi, Chem. Sci., 2022, 13, 1484–1491 RSC.
- C. Reichardt, R. A. Vogt and C. E. Crespo-Hernández, J. Chem. Phys., 2009, 131, 224518 CrossRef PubMed.
- M. M. Brister, L. E. Pinero-Santiago, M. Morel, R. Arce and C. E. Crespo-Hernandez, J. Phys. Chem. Lett., 2016, 7, 5086–5092 CrossRef CAS PubMed.
- M. Pollum, S. Jockusch and C. E. Crespo-Hernandez, J. Am. Chem. Soc., 2014, 136, 17930–17933 CrossRef CAS PubMed.
- L. A. Ortiz-Rodríguez, S. J. Hoehn, A. Loredo, L. Wang, H. Xiao and C. E. Crespo-Hernández, J. Am. Chem. Soc., 2021, 143, 2676–2681 CrossRef PubMed.
- S. E. Krul, S. J. Hoehn, K. J. Feierabend and C. E. Crespo-Hernández, J. Chem. Phys., 2021, 154, 075103 CrossRef CAS PubMed.
- S. E. Krul, G. J. Costa, S. J. Hoehn, D. Valverde, L. M. F. Oliveira, A. C. Borin and C. E. Crespo-Hernández, Photochem. Photobiol., 2023, 99, 693–705 CrossRef CAS PubMed.
- S. J. Hoehn, S. E. Krul, B. J. Skory and C. E. Crespo-Hernández, Chem. – Eur. J., 2022, 28, e202103667 CrossRef CAS PubMed.
- I. H. M. van Stokkum, D. S. Larsen and R. van Grondelle, Biochim. Biophys. Acta, 2004, 1657, 82–104 CrossRef CAS PubMed.
- J. Snellenburg, S. Laptenok, R. Seger, K. M. Mullen and I. H. M. van Stokkom, J. Stat. Software, 2012, 49, 1–22 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephen, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- B. A. Heß, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371 CrossRef.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- R. Improta, V. Barone and F. Santoro, J. Phys. Chem. B, 2007, 111, 14080–14082 CrossRef CAS PubMed.
- D. Jacquemin, V. Wathelet, E. A. Perpète and C. Adamo, J. Chem. Theory Comput., 2009, 5, 2420–2435 CrossRef CAS PubMed.
- Y. Shao, Y. Mei, D. Sundholm and V. R. I. Kaila, J. Chem. Theory Comput., 2020, 16, 587–600 CrossRef PubMed.
- A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039 CrossRef CAS.
- J. Seixas de Melo, J. Pina, L. M. Rodrigues and R. S. Becker, J. Photochem. Photobiol., A, 2008, 194, 67–75 CrossRef CAS.
- M. Desouter-Lecomte, D. Dehareng, B. Leyh-Nihant, M. T. Praet, A. J. Lorquet and J. C. Lorquet, J. Phys. Chem., 1985, 89, 214–222 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02849j |
| This journal is © the Owner Societies 2024 |