Fulminic acid: a quasibent spectacle

Abstract

Fulminic acid (HCNO) played a critical role in the early development of organic chemistry, and chemists have sought to discern the structure and characteristics of this molecule and its isomers for over 200 years. The mercurial nature of the extremely flat H–C–N bending potential of fulminic acid, with a nearly vanishing harmonic vibrational frequency at linearity, remains enigmatic and refractory to electronic structure theory, as dramatic variation with both orbital basis set and electron correlation method is witnessed. To solve this problem using rigorous electronic wavefunction methods, we have employed focal point analyses (FPA) to ascertain the ab initio limit of optimized linear and bent geometries, corresponding vibrational frequencies, and the HCN + O(³P) → HCNO reaction energy. Electron correlation treatments as extensive as CCSDT(Q), CCSDTQ(P), and even CCSDTQP(H) were employed, and complete basis set (CBS) extrapolations were performed using the cc-pCVXZ (X = 4–6) basis sets. Core electron correlation, scalar relativistic effects (MVD1), and diagonal Born–Oppenheimer corrections (DBOC) were all included and found to contribute significantly in determining whether vibrationless HCNO is linear or bent. At the all-electron (AE) CCSD(T)/CBS level, HCNO is a linear molecule with ω₅(H–C–N bend) = 120 cm⁻¹. However, composite AE-CCSDT(Q)/CBS computations give an imaginary frequency (51i cm⁻¹) at the linear optimized geometry, leading to an equilibrium structure with an H–C–N angle of 173.9°. Finally, at the AE-CCSDTQ(P)/CBS level, HCNO is once again linear with ω₅ = 45 cm⁻¹, and inclusion of both MVD1 and DBOC effects yields ω₅ = 32 cm⁻¹. A host of other topics has also been investigated for fulminic acid, including the dependence of r_e and ω_i predictions on a variety of CBS extrapolation formulas, the question of multireference character, the N–O bond energy and enthalpy of formation, and issues that give rise to the quasibent appellation.

---

1. Introduction

Fulminic acid (HCNO) and its isomers isocyanic acid (HNCO), cyanic acid (HOCN), and isofulminic acid (HONC) have played pivotal roles in the history of chemistry,¹ and these compounds are still the target of much current research.^2–5 Although fulminic acid is compositionally simple, this molecule has challenged generations of chemists and physicists seeking to uncover its structure and properties. Fulminic acid has been a test case for the development of spectroscopic methods of analysis owing to its intriguing rovibrational dynamics,^6,7 and the species even has considerable astrochemical interest as a precursor to prebiotic molecules.^8–12

In 1800 the English chemist Edward Howard first prepared salts of fulminic acid by reacting mercury oxide, nitric acid, and ethanol.^1,13–15 The explosive properties of these salts led Howard to call them “fulminating,” appropriately drawing from the Latin fulminare meaning “to strike like lightning.”^1,13,16 However, the primitive methods of quantitative analysis at the time were unable to elucidate the true identity of the compounds. Liebig was particularly fascinated by silver fulminate and in 1824 discovered that its percentage composition was identical to that of the silver cyanate prepared by Wöhler.^1,15,17 As such, fulminic and cyanic acids gained widespread acclaim as examples of the newly discovered phenomenon of isomerism.¹⁷ Fulminate salts emerged as the predominant detonator for firing projectiles in the 19th century, and Alfred Nobel even introduced fulminate cartridges for the safe use of dynamite.^1,14

The quest to definitively establish the bonding in fulminic acid persisted for over a century.^1,18–31 Fulminic acid was initially regarded as a two-carbon compound originating from ethanol, leading to many erroneous attempts at structural characterization.^1,28–31 However, in 1894 Nef asserted that experimental evidence pointed to a one-carbon CNOH structure for fulminic acid, making it identical to carbyloxime.^19–21 A formyl nitrile oxide structure (HCNO) was proposed²² as early as 1899 and favored by a theoretical analysis of free energies by Pauling in 1926,²³ but retention of the oxime formula persisted well into the 1950s.¹ Proof of the formyl nitrile oxide structure was finally obtained by Beck and coworkers in 1965–66 after the IR spectrum of pure gaseous fulminic acid revealed H–C–N–O connectivity.^24,25

Even after the connectivity was ascertained accurately, characterizing fulminic acid still proved elusive, as suspicions grew that the species was quasilinear. This classification is generally given to molecules with a nonlinear electronic minimum but a low barrier to linearity, allowing large-amplitude bending motion that engenders rovibrational spectra reminiscent of a linear framework.^7,32 Fitting the microwave spectrum recorded by M. Winnewisser and Bodenseh³³ to a linear structure gave rise to a disturbingly short r_s(C–H) distance; moreover, the lowest-frequency bending vibration ν₅ could not be located by Beck and Feldl²⁵ in the IR spectrum. The first experimental information for ν₅ was later obtained from analysis of the rotational transitions of seven HCNO excited vibrational states in 1969.³⁴

Although a wealth of low-resolution microwave, millimeter-wave, and infrared data had accumulated by 1974,^35–37 the highly anharmonic, large-amplitude nature of the H–C–N bending vibration of fulminic acid was not clearly established until measurement and analysis in that year of the high-resolution far-infrared spectrum between 180 and 420 cm⁻¹ with 0.1 cm⁻¹ resolution.³⁸ One year later, Stone³⁹ performed a rigid-bender treatment of the ν₅ fundamental and overtone bands of HCNO and DCNO and extracted an associated one-dimensional model potential function with an equilibrium H–C–N angle of 161° and a barrier to linearity of 70 cm⁻¹. Shortly thereafter, the anomalous vibrational dependence of the observed rotational constants and l-doubling interactions were analyzed with a simple rovibrational Hamiltonian, placing the H–C–N angle near 170° and the barrier to linearity at only 2 cm⁻¹.⁴⁰ Substantial improvements in the previous analyses were made in 1979 by Bunker and coworkers,⁴¹ who used a semirigid bender Hamiltonian to fit the entire body of known HCNO and DCNO rovibrational energy separations.^{33–38,42–51} They concluded that vibrationless HCNO is linear within the uncertainty of the analysis but zero-point motion or vibrational excitation of the complementary stretching modes produces a nonlinear minimum on the effective potential curve for large-amplitude H–C–N bending.⁴¹ In 1983 Jensen⁵² extended the semirigid bender Hamiltonian to also account for the ν₄ C–N–O bending mode and confirmed the conclusions reached by Bunker et al.⁴¹ Technical details of this landmark research^41,52 that deemed the molecule “quasibent” are discussed below when our new theoretical results are presented.

High-resolution rovibrational spectroscopy of the ground electronic state of HCNO and DCNO continued in earnest through the early 2000s. Additional infrared bands of HCNO in the 500–657 cm⁻¹ region were characterized;⁵³ moreover, 46 l-sublevel vibrational satellites were assigned in the millimeter wave spectrum involving rotational transitions within excited vibrational manifolds having up to 4 quanta of bending.⁶ The vibrational band origins of HCNO were ascertained for nearly every state in the 700–7000 cm⁻¹ region, revealing networks of anharmonic resonances.^54–57 Far-infrared data for HCNO and DCNO were further refined to a precision of 0.0012 cm⁻¹ (FWHM) in 2000.⁵⁴ Infrared, far-infrared, microwave, and millimeter wave spectra were obtained and analyzed for five isotopologues of HCNO.^58–65 Finally, in recent years the paradigmatic energy levels of fulminic acid involving the H–C–N bending mode have been analyzed via several novel approaches, including Lie algebraic methods,⁶⁶ as well as quantum monodromy⁶⁷ and quantum phase transitions^68,69 within a champagne-bottle potential.

Even almost two centuries after its initial discovery, fulminic acid and its isomers captivated quantum chemists.^32,70–84 Electronic structure computations gave muddled results for the equilibrium geometry of HCNO, as strong dependence on the orbital basis set and electron correlation method were observed. The struggles of early ab initio work with low levels of theory and small basis sets revealed the difficulty of the problem.^70,71 In 1982, Farnell, Nobes, and Radom⁷² obtained a linear equilibrium structure for HCNO at the MP3/6-31G** level and computed harmonic vibrational frequencies as a function of the H–C–N angle; the zero-point vibrational energy of the complementary modes was shown to favor a bent structure, but this correction was not sufficient to overcome the Born–Oppenheimer potential function that favored linearity. In contrast, in 1989 a bent equilibrium structure was obtained at MP2/6-31G** with a nonnegligible barrier to linearity of 0.64 kcal mol⁻¹.⁷³ Similarly, in 1991 both the 6-31G** and 6-311G** basis sets produced bent structures at the MP2 and MP4 levels but linear structures at MP3 and CISD; MCSCF/DZP also gave a bent molecule, while MRCISD computations built on these MCSCF wave functions yielded either linear or bent structures depending on the choice of reference space.⁷⁴ The robust and newly popularized CCSD(T) theory was applied to HCNO for the first time in 1992 by Rendell, Lee, and Lindh,⁷⁵ predicting a linear structure upon use of a TZ2P basis set; however, four years later another study found that improving the method to CCSD(T)/cc-pVQZ produced a bent equilibrium geometry with a minuscule 7 cm⁻¹ barrier to linearity.⁷⁶ This led Albert and Quack⁸⁵ to comment in a 2007 report that prevailing quantum chemical research had failed to provide a full understanding of the observed rovibrational spectra of HCNO.

More recently in 2008, Mladenović and Lewerenz⁷⁷ computed both frozen-core and all-electron CCSD(T) results with the cc-pVXZ (X = 2–6) and cc-pCVXZ (X = 2–5) basis sets. The optimized H–C–N bending angle of fulminic acid varied nearly 30° with basis set, but the best results trended toward a true linear equilibrium structure. The CCSD(T) computations were extended in 2009 to the aug-cc-pCVXZ (X = 2–5) family of basis sets, which predicted a linear HCNO structure at the complete basis set (CBS) limit.³² Thus far, only one ab initio study from Cambridge in 1993 has performed full 6-dimensional variational computations for HCNO rovibrational states.⁷⁸ Practical limitations dictated a rather low level of theory (MP2/DZP) for generating 561 energy points, which were fit to various model potentials constructed from expansions in simple internal coordinates comprising up to 55 terms.⁷⁸ Considerable difficulty was encountered in obtaining good analytical fits, and the ν₅ results proved to be unstable with respect to the choice of model potential.⁷⁸ While a full 6-dimensional treatment of the HCNO problem was a cutting-edge accomplishment in 1993, the underlying MP2/DZP surface exhibits a bent HCNO minimum with ∠H–C–N = 148.1° and a barrier to linearity of 332 cm⁻¹, features now known to be unrealistic.

To date, the quasibent/quasilinear nature of fulminic acid has not been probed by any high-order coupled cluster method beyond CCSD(T), and the impact of relativistic effects (MVD1) and diagonal Born–Oppenheimer corrections (DBOC) has not been assessed. Moreover, structures at the CBS limit are sparse, and corresponding harmonic vibrational frequencies are nonexistent in the current literature. We have discovered that previous work failed to converge to the ab initio limit and that even more rigorous quantum chemical methods are essential in finally solving the HCNO problem. Therefore, in the present study, high-level electron-correlation methods as extensive as CCSDT(Q), CCSDTQ(P), and even CCSDTQP(H) are employed in conjunction with complete basis set (CBS) extrapolations using the cc-pCVXZ (X = 4–6) basis sets to accurately pinpoint the equilibrium structure, harmonic vibrational frequencies, and relative energies of HCNO via focal point analyses (FPA). Scalar relativistic effects (MVD1) and diagonal Born–Oppenheimer corrections (DBOC) are also studied. The well-established linear HCN molecule was used as a benchmark to demonstrate the extreme accuracy of our computational techniques used on HCNO.

2. Theoretical methods

A systematic progression of electronic wavefunction methods was employed to target the ab initio limit of molecular geometries and harmonic vibrational frequencies for HCN and HCNO, as well as the HCN + O(³P) → HCNO reaction energy. The progression of methods incorporated Hartree–Fock theory;^86,87 second-order Møller–Plesset (MP2)⁸⁸ perturbation theory; and coupled cluster (CC)^89,90 theory, including full single and double excitations (CCSD),⁹¹ perturbative treatment of connected triple excitations [CCSD(T)],⁹² full triple excitations (CCSDT),⁹³ perturbative treatment of quadruple excitations [CCSDT(Q)],⁹⁴ full quadruple excitations (CCSDTQ),⁹⁵ perturbative treatment of pentuple excitations [CCSDTQ(P)],^96,97 full pentuple excitations (CCSDTQP), and perturbative treatment of hextuple excitations [CCSDTQP(H)].^96–98

The wavefunction computations were executed using the family of correlation-consistent polarized-valence orbital basis sets cc-pVXZ (X = D, T, Q, 5, 6) and the related core-valence basis sets cc-pCVXZ (X = D, T, Q, 5, 6) developed by Dunning and coworkers.^99–101 To make the CCSDTQ(P) and CCSDTQP(H) jobs tractable, the 6-31G* Pople basis set¹⁰² was used instead of cc-pVDZ; the legitimacy of this replacement was carefully established. The electronic energies for CCSD(T) and lower levels were computed with the CFOUR 2.0^103,104 package, while those of CCSDT and higher levels through CCSDTQP(H) were obtained with the MRCC^105,106 program, either as a standalone package or interfaced with CFOUR.

The primary CBS extrapolations of the cc-pCV(Q,5,6)Z Hartree–Fock total energies (E_HF) and the cc-pCV(5,6)Z all-electron MP2, CCSD, and CCSD(T) correlation energies (E_corr) were performed according to the following equations:^107,108

E_HF(X) = E_HF,CBS + be^−cX (1)

E_corr(X) = E_corr,CBS + bX⁻³ (2)

where X is the cardinal number of the correlation-consistent basis set series. Additional extrapolation formulas from the literature were also tested:^109–111

E_HF(X) = E_HF,CBS + be^−(X−1) + ce^−(X−1)2 (3)

Moreover, the Schwenke¹¹² and SchwenkeAug¹¹² extrapolation schemes were investigated for both Hartree–Fock and correlation energies. Two final correlation energy extrapolations are introduced in this work that entail three-parameter fits to X = 4, 5, 6 data:

E_corr(X) = E_corr,CBS + bX^−c (6)

E_corr(X) = E_corr,CBS + b(X − c)⁻³ (7)

A composite focal point analysis (FPA) scheme^113,114 was utilized to obtain CCSDT, CCSDT(Q), CCSDTQ, CCSDTQ(P), CCSDTQP, and CCSDTQP(H) energies targeting the CBS limit. The following correlation increments (δ) were employed:

δ[CCSDT] = E_corr(CCSDT/cc-pVTZ) − E_corr(CCSD(T)/cc-pVTZ) (8)

δ[CCSDT(Q)] = E_corr(CCSDT(Q)/cc-pVTZ) − E_corr(CCSDT/cc-pVTZ) (9)

δ[CCSDTQ] = E_corr(CCSDTQ/6-31G*) − E_corr(CCSDT(Q)/6-31G*) (10)

δ[CCSDTQ(P)] = E_corr(CCSDTQ(P)/6-31G*) − E_corr(CCSDTQ/6-31G*) (11)

δ[CCSDTQP(H)] = E_corr(CCSDTQP(H)/6-31G*) − E_corr(CCSDTQ(P)/6-31G*) (12)

One-electron mass-velocity and Darwin terms (MVD1)^115–117 were evaluated perturbatively to obtain scalar relativistic corrections at the AE-CCSD(T)/cc-pCV5Z level of theory. Diagonal Born–Oppenheimer (DBOC) corrections¹¹⁸ were computed at the AE-CCSD/cc-pCVQZ level and compared to corresponding HF/cc-pCVQZ values. These auxiliary corrections (Δ) were added to yield final FPA energies as follows:

E_FPA = E_HF,CBS + E_corr,CBS[CCSD(T)] + δ[CCSDT] + δ[CCSDT(Q)] + δ[CCSDTQ] + δ[CCSDTQ(P)] + Δ(MVD1) + Δ(DBOC) (13)

The small but extremely costly δ[CCSDTQP(H)] increment was added only when the HCN + O(³P) → HCNO reaction energy was computed.

A custom Mathematica¹¹⁹ program was written for this research to evaluate composite FPA energies, optimize geometries, and calculate harmonic vibrational frequencies in internal coordinates, all by specifying lists of energy points to be computed with the electronic structure codes and then processing the data upon completion of the sundry jobs. Energy gradients and diagonal quadratic force constants were obtained numerically from customary 3-point single-displacement formulas, whereas off-diagonal quadratic force constants were determined from two additional double displacements [(+, +) and (−,−)]; the displacement sizes were 0.005 Å for bond distances and 0.02 rad for angles. A key to getting results at such high levels of theory was the implementation of highly efficient optimization algorithms. Steps in the optimization of linear structures were found by defining an analytic potential function within Mathematica for the force field expansion complete through fourth order and then minimizing this function via built-in modules; for this purpose, the gradients and quadratic force constants evaluated at the given level of theory were augmented with AE-CCSD(T)/CBS cubic and quartic force constants¹²⁰ listed in the ESI.† Steps in the optimization of bent geometries were taken via the full Newton-Raphson method elaborated with controlled damping or dilation of the step vector. Finally, the Mathematica program was used for error analyses in which random fuzz of a chosen order of magnitude was added to the input energies followed by recalculation of the final results for geometric parameters and harmonic frequencies. Such simulations were executed 1000 times to ascertain standard deviations in the final results as a function of the imparted uncertainty in the energies. In our computations, the largest final step in the CC iterations was (2.9 × 10⁻¹⁰, 9.8 × 10⁻¹¹) E_h for energies around (linear, bent) stationary points, while the underlying HF energies were more tightly converged. The key conclusion from our simulations is that such energy convergence yields accuracy better than (10⁻⁵ Å, 0.01°, 0.1 cm⁻¹) in the predicted (distance, angles, frequencies). The lone exception is the pair of C–N–O bending frequencies of bent HCNO at the AE-CCSDT(Q)/CBS level, whose accuracy is better than 1 cm⁻¹, despite the numerical difficulties associated with a very nearly linear heavy-atom framework.

3. Results and discussion

3.1. Electronic structure of HCNO

To assess the possibility of multireference character in HCNO, the CCSD(T)/cc-pVTZ values shown in Table 1 for the traditional T₁, T_2,max, D₁, and D₂ diagnostics^121–123 were computed using Psi4¹²⁴ for linear HCNO and HCN at their respective AE-CCSDTQ(P)/CBS + MVD1 geometries and for bent HCNO at its AE-CCSDT(Q)/CBS structure. A T₁ diagnostic greater than 0.02 was proposed decades ago by Lee and Taylor¹²¹ as a criterion for closed-shell species exhibiting substantial multireference character. The linear and bent HCNO T₁ diagnostics are near 0.018, somewhat larger than the HCN value (0.012) but still comfortably below the stated multireference threshold. Moreover, the absolute maximum T₂ amplitudes (T_2,max) of both HCNO species are not large (0.075) and are actually less than their HCN counterpart (0.087). Original testing of the D₁ and D₂ diagnostics^122,123 indicated that molecules with D₁(CCSD) ≤ 0.02 and D₂(CCSD) ≤ 0.15 display excellent agreement between CCSD and CCSD(T) bond distances and harmonic vibrational frequencies, whereas inadequacies of the CCSD method occur for molecules with D₁(CCSD) > 0.050 and D₂(CCSD) > 0.18. By these D₁ standards, HCN is intermediate in character, while both linear and bent HCNO are problematic for CCSD. In contrast, the D₂ diagnostic indicates that all three species are borderline for the performance of CCSD. Nevertheless, the D₁ and D₂ criteria for CCSD are not precisely relevant to our current research on HCNO, for which the real question is whether high-order single-reference coupled-cluster treatments at or beyond CCSD(T) can yield accurate results, especially within the context of the FPA approach.

Table 1 Comparative T₁, T_2,max, D₁, and D₂ diagnostics [CCSD(T)/cc-pVTZ] and largest CASSCF CI coefficients (C₀–C₃) for linear and bent HCNO and the HCN benchmark

	T 1	T 2,max	D 1	D 2	C 0	C 1	C 2	C 3
a At the AE-CCSDTQ(P)/CBS + MVD1 optimized geometries. b At the AE-CCSDT(Q)/CBS optimum geometry.
HCN^a	0.012	0.0867	0.029	0.178	0.958	−0.121	−0.121	0.078
Linear HCNO^a	0.018	0.0745	0.053	0.179	0.943	−0.113	−0.113	0.080
Bent HCNO^b	0.018	0.0746	0.053	0.179	0.942	−0.114	−0.113	0.080

---

The development of new diagnostics for multireference electronic character and criticism of traditional metrics is an ongoing topic of research.^125–129 Fortunately, in the current study we can obtain definitive electronic structure information using MOLPRO^130–133 to perform full-valence CASSCF/cc-pVXZ (X = D, T) computations for HCNO and HCN with (16, 13) and (10, 9) active spaces, respectively. The resulting CI coefficients based on CASSCF natural orbitals were virtually independent of whether the cc-pVDZ or cc-pVTZ basis set was utilized or whether the geometries were optimized at the CASSCF level or set to our highest-quality structures. A representative sample of results is given in Table 1. For all three species, the HF reference has C₀ > 0.94, and the next most important contributions arise from a pair of π² → (π*)² excited determinants with CI coefficients near −0.12. No other configuration has a coefficient greater than 0.08 in magnitude. Such CI coefficients are typical of molecules widely considered to be single-reference species. In brief, HCNO is indeed strongly dominated by a single configuration, and the nature of its electronic structure is very similar to that of HCN. Finally, the similarity of the coupled-cluster diagnostics and CASSCF CI coefficients indicates that a change to multireference behavior is not a factor in the large-amplitude H–C–N bending motion of fulminic acid.

3.2. HCN Benchmark

To verify the extreme accuracy of the wavefunction methods applied here to HCNO, the computations summarized in Table 2 were first performed on HCN, which has been exhaustively studied by high-resolution spectroscopy. Systematic and strong convergence with respect to basis set is achieved to the level of 0.0001 Å and 0.1 cm⁻¹ for bond distances and harmonic frequencies. Similar convergence with respect to electron correlation treatment is also accomplished for these quantities to within 0.00006 Å and 1.0 cm⁻¹, as shown by the difference between AE-CCSDT(Q)/CBS and AE-CCSDTQ(P)/CBS results. Scalar relativistic effects shorten the bond distances slightly (≤0.0002 Å) and alter the frequencies by less than 0.5 cm⁻¹. Our best theoretical HCN results are near-identical matches to the best existing spectroscopic parameters. The empirical equilibrium bond distances (r_e) were extracted from ground-state rotational constants for eight different isotopologues, namely every combination of H, D, ¹²C, ¹³C, ¹⁴N, and ¹⁵N; the requisite B₀−B_e corrections were obtained from rigorous variational computations of the vibration-rotation energy levels and wavefunctions.¹³⁴ The empirical harmonic frequencies were derived from a least-squares fit of 50 vibrational band origins of HCN up to 10 631 cm⁻¹ in energy; the best fit employing ω₁, ω₂, ω₃, g₂₂, and 20 anharmonicity constants (x_ij, y_ijk, y_ill, and z₃₃₃₃) was selected for comparison to our present ab initio HCN results.¹³⁵ The highest-level computations [AE-CCSDTQ(P)/CBS + MVD1] match the empirical r_e and ω_i values to 0.00017 Å and 1.6 cm⁻¹, respectively. Such astounding agreement is very gratifying and bodes well for a definitive solution of the HCNO problem.

Table 2 HCN bond distances (r_e, Å) and harmonic vibrational frequencies (ω_i, cm⁻¹)

Level of theory	r e(H–C)	r e(C–N)	ω 1(σ)	ω 2(π)	ω 3(σ)
HF/cc-pCVQZ	1.05698	1.12326	3607.8	877.1	2408.4
HF/cc-pCV5Z	1.05690	1.12319	3608.5	876.7	2407.9
HF/cc-pCV6Z	1.05689	1.12319	3608.6	876.5	2407.8
HF/CBS	1.05688	1.12319	3608.6	876.5	2407.8
AE-MP2/cc-pCV5Z	1.06264	1.15969	3475.2	727.5	2051.0
AE-MP2/cc-pCV6Z	1.06260	1.15942	3475.3	729.8	2051.9
AE-MP2/CBS	1.06255	1.15907	3475.4	733.3	2053.1
AE-CCSD/cc-pCV5Z	1.06311	1.14549	3474.9	756.6	2201.2
AE-CCSD/cc-pCV6Z	1.06303	1.14519	3475.5	758.4	2202.5
AE-CCSD/CBS	1.06292	1.14478	3476.2	761.1	2204.2
AE-CCSD(T)/cc-pCV5Z	1.06524	1.15300	3444.6	728.5	2134.8
AE-CCSD(T)/cc-pCV6Z	1.06516	1.15271	3445.0	730.3	2135.9
AE-CCSD(T)/CBS	1.06508	1.15232	3445.6	733.1	2137.4
AE-CCSDT/CBS	1.06495	1.15175	3447.0	734.8	2144.3
AE-CCSDT(Q)/CBS	1.06509	1.15333	3443.5	728.7	2126.7
AE-CCSDTQ/CBS	1.06504	1.15303	3444.5	729.3	2130.8
AE-CCSDTQ(P)/CBS	1.06505	1.15327	3444.0	728.6	2127.7
AE-CCSDTQ(P)/CBS + MVD1	1.06491	1.15307	3444.1	728.5	2127.3
Empirical^134,135	1.06501(8)	1.15324(2)	3442.5(1)	726.9(2)	2127.2(4)

---

3.3. HCNO structures and vibrational frequencies

Linear HCNO bond distances, harmonic vibrational frequencies, and bending quadratic force constants are reported in Table 3 for all levels of theory employed in this study. The HF bond distances are essentially converged to the CBS limit once the cc-pCV5Z basis set is employed. The HF/CBS distances are too short compared to those of AE-CCSDTQ(P)/CBS, the disparities being 0.007, 0.037, and 0.012 Å for r_e(H–C), r_e(C–N), and r_e(N–O), respectively. The r_e(C–N) error is larger than usual but mirrors that seen in Table 2 for HCN. For the MP2, CCSD, and CCSD(T) methods, the cc-pCV6Z distances differ from the corresponding CBS limits by only 0.0004 Å or less. In the [AE-MP2, AE-CCSD, AE-CCSD(T)] correlation series, r_e(H–C) and r_e(N–O) increase monotonically in modest steps, while r_e(C–N) exhibits highly oscillatory increments of (+0.048, −0.023, +0.011) Å at the CBS limit. At the AE-CCSD(T)/CBS level, [r_e(H–C), r_e(N–O)] are within (0.0001, 0.0003) Å of the corresponding AE-CCSDTQ(P)/CBS limits. In contrast, r_e(C–N) continues to oscillate with variations of (–0.0010, +0.0024, −0.0004, +0.0001) Å as the [CCSDT, CCSDT(Q), CCSDTQ, CCSDTQ(P)] levels of theory are reached, similar to the HCN benchmark except with larger step sizes. Overall, the convergence of the linear HCNO bond distances with respect to both orbital basis set and electron correlation treatment is almost as good as that witnessed for the HCN benchmark, so that similar high accuracy is expected in the predictions. Nonetheless, it is apparent from Table 3 that post-CCSD(T) methods are essential to achieving this accuracy.

Table 3 Linear HCNO bond distances (r_e, Å), harmonic vibrational frequencies (ω_i, cm⁻¹), and bending quadratic force constants (F₄₄, F₄₅, F₅₅, aJ rad⁻²)

Level of theory	r e(H–C)	r e(C–N)	r e(N–O)	ω 1(σ)	ω 2(σ)	ω 3(σ)	ω 4(π)	ω 5(π)	F 44	F 45	F 55
HF/cc-pCVQZ	1.0526	1.1226	1.1894	3640	2499	1313	647	603	0.204	0.153	0.875
HF/cc-pCV5Z	1.0526	1.1223	1.1898	3639	2497	1310	646	604	0.205	0.152	0.871
HF/cc-pCV6Z	1.0526	1.1223	1.1899	3639	2497	1310	646	604	0.206	0.152	0.870
HF/CBS	1.0526	1.1223	1.1899	3639	2497	1310	646	604	0.206	0.152	0.869
AE-MP2/cc-pCV5Z	1.0564	1.1706	1.1910	3529	2264	1325	560	283i	−0.0003	0.164	0.690
AE-MP2/cc-pCV6Z	1.0564	1.1703	1.1911	3528	2263	1324	559	273i	0.002	0.163	0.687
AE-MP2/CBS	1.0564	1.1700	1.1911	3527	2263	1324	558	260i	0.005	0.162	0.685
AE-CCSD/cc-pCV5Z	1.0575	1.1481	1.1978	3525	2346	1291	576	318	0.081	0.153	0.729
AE-CCSD/cc-pCV6Z	1.0574	1.1478	1.1977	3525	2346	1291	576	325	0.083	0.152	0.728
AE-CCSD/CBS	1.0574	1.1474	1.1976	3525	2347	1291	576	334	0.086	0.152	0.727
FC-CCSD(T)/cc-pCV5Z	1.0605	1.1609	1.2041	3492	2278	1266	551	82i	0.033	0.157	0.673
AE-CCSD(T)/cc-pCV5Z	1.0593	1.1587	1.2019	3498	2287	1272	554	54	0.037	0.154	0.680
FC-CCSD(T)/cc-pCV6Z	1.0605	1.1607	1.2042	3492	2278	1266	551	54i	0.035	0.157	0.673
AE-CCSD(T)/cc-pCV6Z	1.0593	1.1584	1.2019	3497	2286	1272	554	89	0.039	0.154	0.677
FC-CCSD(T)/CBS	1.0606	1.1604	1.2042	3491	2278	1266	550	65	0.038	0.156	0.670
AE-CCSD(T)/CBS	1.0592	1.1580	1.2019	3497	2287	1272	553	120	0.042	0.153	0.676
AE-CCSDT/CBS	1.0591	1.1570	1.2021	3499	2292	1270	553	146	0.045	0.152	0.676
AE-CCSDT(Q)/CBS	1.0592	1.1594	1.2034	3496	2275	1261	546	49i	0.034	0.152	0.660
AE-CCSDTQ/CBS	1.0592	1.1590	1.2029	3497	2279	1265	548	52	0.036	0.152	0.664
AE-CCSDTQ(P)/CBS	1.0591	1.1591	1.2022	3497	2276	1268	548	45	0.036	0.153	0.665
AE-CCSDTQ(P)/CBS + MVD1	1.0590	1.1588	1.2024	3497	2275	1266	548	19	0.035	0.153	0.664
AE-CCSDTQ(P)/CBS + MVD1 + DBOC/HF	1.0591	1.1588	1.2024	3497	2275	1267	548	41	0.036	0.153	0.664
AE-CCSDTQ(P)/CBS + MVD1 + DBOC/CCSD	1.0591	1.1588	1.2024	3497	2275	1267	548	32	0.036	0.153	0.664

---

All of the vibrational modes of linear HCNO exhibit (cc-pCV5Z, cc-pCV6Z, CBS) sets of HF harmonic frequencies in internal agreement to better than 1 cm⁻¹. In accord with expectation, the HF/CBS stretching frequencies (ω₁, ω₂, ω₃) are too large compared to those of AE-CCSDTQ(P)/CBS by (4.1, 9.7, 3.3)%; however, the HF/CBS overestimation of ω₄ (17.9%) is substantially greater than normal for this level of theory. For the AE-MP2, AE-CCSD, and AE-CCSD(T) methods, the cc-pCV6Z ω₁–ω₄ values are within 1 cm⁻¹ of the corresponding CBS limits, revealing tight basis set convergence. For AE-MP2/CBS the (ω₁, ω₂, ω₃, ω₄) errors vis-à-vis AE-CCSDTQ(P)/CBS are (0.9, −0.6, 4.4, 1.8)%; because ω₃(AE-MP2/CBS) is peculiarly greater than ω₃(HF/CBS) by 14 cm⁻¹, its accuracy is diminished. For AE-CCSD/CBS the (ω₁, ω₂, ω₃, ω₄) errors relative to the benchmark are (0.8, 3.1, 1.8, 5.1)%, so that ω₂ and ω₄ are actually less accurate than their AE-MP2/CBS counterparts. The rather erratic behavior of (ω₁, ω₂, ω₃, ω₄) in the electron correlation series settles down at the AE-CCSD(T)/CBS level, which yields values that are slightly too large by (0.0, 0.5, 0.3, 0.9)%. Beyond this level, subtle variations accumulate to net downward shifts. The (P) effect on (ω₁, ω₂, ω₃, ω₄) is only (0, −3, +3, 0) cm⁻¹, which indicates strong convergence with respect to electron correlation.

The critical feature of Table 3 is the remarkable variation of the doubly-degenerate H–C–N bending frequency, ω₅(π), as depicted for the primary AE coupled cluster series at the CBS limit in Fig. 1. The CBS extrapolations prove to be important in evaluating ω₅ with correlated methods, as seen most dramatically by comparing the AE-CCSD(T)/cc-pCV6Z value (89 cm⁻¹) with its CBS counterpart (120 cm⁻¹). At the HF/CBS level, HCNO is a linear molecule with a sizable ω₅ = 604 cm⁻¹. However, all AE-MP2 computations give an imaginary frequency at the linear optimized structure; in particular, ω₅ = 260i cm⁻¹ at the CBS limit. A rebound effect is provided by AE-CCSD, which gives ω₅ = (318, 325, 334) cm⁻¹ in the cc-pCV(5,6,∞)Z computations. Intriguingly, CCSD(T) with basis sets smaller than cc-pCV5Z can yield imaginary ω₅ values,^76,77 but as the AE-CCSD(T)/CBS limit is approached, ω₅ steadily increases to 120 cm⁻¹. The post-CCSD(T) predictions for ω₅ continue to waver in a virtually unprecedented manner. Most notably, ω₅ = 49i cm⁻¹ results from CCSDT(Q) theory, so that HCNO constitutes a remarkable case in which the perturbative (Q) correlation correction actually changes the qualitative nature of the equilibrium structure. The bending quadratic force constants in Table 3 reveal a surprising aspect about the CCSDT(Q)/CBS imaginary ω₅ frequency, viz., the diagonal constants F₄₄ and F₅₅ are both positive, showing that F₄₅ coupling is essential to lowering the vibrational potential energy along the ω₅ mode. In other words, simultaneous trans-bending is required to achieve an imaginary frequency.

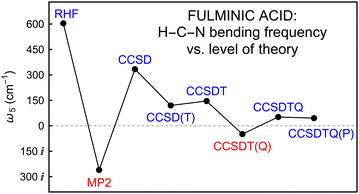Fig. 1 Variation of ω₅ (HCNO) in the all-electron coupled-cluster series at the CBS limit. The quantity actually plotted is |ω₅|·sgn(ω₅²), but the ticks are labeled with the corresponding ω₅ values.

The amazing saga of ω₅ for fulminic acid is not complete even at the CCSDT(Q) level! A full accounting of connected quadruple excitations leads back to a linear minimum structure with ω₅ = 52 cm⁻¹ for CCSDTQ theory. Thereafter, the (P) effect on ω₅ is only −7 cm⁻¹, suggesting that the AE-CCSDTQ(P)/CBS frequency of 45 cm⁻¹ is very near complete convergence, pending inclusion of auxiliary MVD1 and DBOC terms. As observed for HCN, the MVD1 relativistic effects shorten the HCNO bond distances by 0.0001–0.0003 Å; the corresponding changes for (ω₁, ω₂, ω₃, ω₄) are merely (0, −1, −2, 0) cm⁻¹. However, MVD1 provides a driving force toward nonlinearity that reduces ω₅ to a minuscule 19 cm⁻¹ at the AE-CCSDTQ(P)/CBS + MVD1 level. Therefore, our ultimate conclusion for the Born–Oppenheimer potential energy surface is that HCNO exists as a linear minimum structure with an H–C–N bending frequency barely above zero. Because ω₅ is so small, room is thus left for first-order, mass-dependent, non-Born–Oppenheimer terms to influence the equilibrium structure. As shown in Table 3, such terms have a negligible effect on the bond distances and ω₁–ω₄, yet ω₅ is increased to stanch the MVD1 reductions. To ensure reliability, DBOC computations were run with the cc-pCVQZ basis set and both the HF and AE-CCSD methods, the latter providing ω₅ = 32 cm⁻¹. One can genuinely say that both the MVD1 and DBOC effects, which are normally just auxiliary corrections, play a decisive role in determining the final equilibrium structure of HCNO, and if the DBOC were to augment rather than compensate for the MVD1 shift on ω₅, then vibrationless fulminic acid would be bent rather than linear.

While core electron correlation was fully incorporated and embedded in our FPA analyses of linear HCNO, insight is gained by singling out this effect, which is commonly treated as an auxiliary correction. For this purpose, frozen-core (FC) CCSD(T)/cc-pCV(5,6,∞)Z computations were performed for the r_e and ω_i parameters of linear HCNO (Table 3). The differences between FC and AE results are quite insensitive to basis set and reveal that 1s correlation changes [r_e(H–C), r_e(C–N), r_e(N–O)] by about (–0.001, −0.002, −0.002) Å, in accord with earlier findings on diatomic molecules.¹³⁶ The concomitant overall shifts in the (ω₁, ω₂, ω₃) stretching frequencies are (+6, +9, +6) cm⁻¹, as expected from Badger's Rule.¹³⁷ For diatomic molecules such overall shifts can be deceptive, because the direct effect of core correlation is actually curvature reduction of V(r), which is compensated by the indirect effect of r_e contraction. We find that linear HCNO exhibits the same phenomenon. In particular, evaluating the FC-CCSD(T)/cc-pCV6Z force constants at the AE-CCSD(T)/cc-pCV6Z equilibrium geometry yields (ω₁, ω₂, ω₃) = (3504, 2296, 1277) cm⁻¹, exposing the direct 1s correlation effect as (–7, −9, −5) cm⁻¹. In turn, the indirect effect of bond-length contraction on the stretching frequencies is (+13, +18, +11) cm⁻¹. The sum of these competing effects produces the aforementioned overall phenomenological shifts arising from 1s correlation. In the (cc-pCV5Z, cc-pCV6Z, CBS) cases, the FC → AE CCSD(T) shifts are very striking for ω₅: (82i → 54, 54i → 89, 65 → 120) cm⁻¹. Clearly, core correlation is a pivotal factor favoring the linear structure.

Trans-bent HCNO minima are obtained at the AE-MP2/cc-pCV(5,6,∞)Z and AE-CCSDT(Q)/CBS levels of theory by following the imaginary-frequency ω₅ mode of the respective linear structures (Table 3). The optimized geometries, barriers to linearity (E_B), and harmonic frequencies of these bent HCNO minima are provided in Table 4. The AE-MP2 results for r_e, θ_CNO, ω₁–ω₄, and ω₆ of bent HCNO display basis-set convergence that is only slightly less rapid than found for linear HCNO. Such is not the case for the (θ_HCN, E_B, ω₅) values of AE-MP2, for which the CBS limit is removed from cc-pCV6Z by (+0.6°, −11.3 cm⁻¹, −15 cm⁻¹). Upon bending, AE-MP2/CBS yields [r_e(H–C), r_e(C–N)] elongations of (0.0026, 0.0071) Å and associated (ω₁, ω₂) reductions of (36, 11) cm⁻¹; simultaneously, r_e(N–O) contracts by approximately 0.002 Å while ω₃ is unchanged. The AE-MP2/CBS θ_HCN and θ_CNO angles deviate from linearity by 23.5° and 5.5°, respectively, but these distortions only engender E_B = 73 cm⁻¹. A similar comparison between bent and linear AE-CCSDT(Q)/CBS structures shows strikingly smaller differences. The r_e(H–C) and r_e(C–N) bond distances elongate by merely 0.0002 Å and 0.0006 Å, respectively, whereas r_e(N–O) contracts by 0.0002 Å; frequency differences upon bending are no more than 2 cm⁻¹. The CCSDT(Q) (θ_HCN, θ_CNO) angles are bent from linearity by merely (6.1°, 1.4°), and the resulting E_B = 0.1 cm⁻¹ is shockingly small.

Table 4 Trans-bent HCNO optimized bond distances (r_e, Å) and bond angles (θ), barriers to linearity (E_B, cm⁻¹), and harmonic frequencies (ω_i, cm⁻¹)

Level of theory	r e(H–C)	r e(C–N)	r e(N–O)	θ HCN	θ CNO	E B	ω 1(a′)	ω 2(a′)	ω 3(a′)	ω 4(a′)	ω 5(a′)	ω 6(a′′)
AE-MP2/cc-pCV5Z	1.0591	1.1783	1.1885	155.4°	174.2°	92.4	3491	2253	1325	555	404	569
AE-MP2/cc-pCV6Z	1.0591	1.1778	1.1887	155.9°	174.3°	83.9	3491	2253	1324	554	393	568
AE-MP2/CBS	1.0590	1.1771	1.1888	156.5°	174.5°	72.6	3491	2252	1324	554	378	567
AE-CCSDT(Q)/CBS	1.0594	1.1600	1.2032	173.9°	178.6°	0.1	3494	2273	1261	546	70	545

---

The energy profile for the H–C–N bending is so flat that zero-point vibrational energy (ZPVE) of the complementary modes comes into play. In the AE-MP2/CBS case, this ZPVE shift increases the effective barrier to linearity from 73 to 94 cm⁻¹, assuming the geometries are fixed at the r_e structure. Because the AE-CCSDT(Q)/CBS bending distortions are much smaller, the corresponding ZPVE shift is only +2.5 cm⁻¹. However, this phenomenon overwhelms the tiny 0.1 cm⁻¹ vibrationless barrier and enhances the barrier to linearity. A central question to be answered in future studies on fulminic acid is whether an accounting of complementary-mode ZPVE at a very high level of theory sufficiently amends the positive curvature of the AE-CCSDTQ(P)/CBS + MVD1 H–C–N bending curve to produce a nonlinear minimum for the effective vibrational potential.

Our best level of theory [AE-CCSDTQ(P)/CBS + MVD1] within the Born–Oppenheimer regime predicts that fulminic acid has a linear equilibrium structure with [r_e(H–C), r_e(C–N), r_e(N– O)] = (1.0590, 1.1588, 1.2024) Å and (ω₁, ω₂, ω₃, ω₄) = (3497, 2275, 1266, 548) cm⁻¹. Previously, the best theoretical r_e structures for HCNO came from the AE-CCSD(T) work of Mladenović and coworkers.^32,77 Their cc-pCV5Z results exactly match ours, while their CBS extrapolation produced [r_e(H–C), r_e(C–N), r_e(N–O)] distances differing from our corresponding values by (+0.0001, +0.0004, +0.0002) Å. Variations in the CBS extrapolation methods are responsible for these differences. In ref. 32, AE-CCSD(T)/aug-cc-pCV(3,4,5)Z total energies were fit to the three-parameter exponential form of eqn (1). In contrast, our methodology applied eqn (1) only to HF/cc-pCV(4,5,6)Z energies and appended the correlation energy derived from extrapolation of AE-CCSD(T)/cc-pCV(5,6)Z points viaeqn (2).

Our AE-CCSDTQ(P)/CBS + MVD1 prediction of ω₅ = 19 cm⁻¹ for linear HCNO warrants assessment with respect to the experimental literature. Using high-resolution rovibrational spectroscopy, Winnewisser and coworkers^{33–38,42–46} assigned thousands of absorptions for the ground vibrational states of HCNO and DCNO, as well as the ν₁ and ν₂ fundamental levels of HCNO. The ν₅(HCNO) band origin indisputably lies at 224.1 cm⁻¹,^38,47 but this frequency is pushed up considerably by the quartic anharmonicity of large-amplitude H–C–N bending. The analysis of experimental data by Bunker et al.⁴¹ adopted a sudden/adiabatic model in which the low-frequency H–C–N bending was separated from the complementary vibrational modes. For each vibrational state of the complementary modes, a semirigid bender Hamiltonian was used to fit the observed rotational levels for J ≤ 5 to a two-parameter effective potential function for H–C–N bending comprised of a quadratic and quartic term. For the ground vibrational states of HCNO and DCNO, the resulting curves displayed minima with deviations from linearity of 15.83° and 12.90° and corresponding barriers to linearity of 11.5 and 5.4 cm⁻¹, respectively. Vibrational excitation of the ν₁ and ν₂ stretching modes increased the effective barriers to linearity to 40.6 and 35.3 cm⁻¹, respectively. The analysis found that for the H–C–N bending potential of the complementary-mode ground vibrational state, the zero-point energy lies at 146.9 cm⁻¹, well above the 11.5 cm⁻¹ barrier to linearity. Thus, the large-amplitude H–C–N motion occurs over the top of a small bump on the potential curve at linearity.

Bunker and coworkers⁴¹ finally employed an extrapolation scheme to work backwards from the vibrationally adiabatic H–C–N bending curves for the various states of the complementary vibrational modes; thus, a vibrationless (Born–Oppenheimer) potential function for the pure H–C–N bending mode was inferred. This function displayed a remarkably small barrier to linearity of 0.2 cm⁻¹. A key conclusion was then made: “To within the uncertainties inherent in the fitting procedure, and the uncertainty introduced by the choice of model for the shape of the potential, … the molecule is linear at equilibrium.” Of course, the same uncertainties prevent one from excluding the possibility that the molecule might instead have a very small barrier to linearity on the Born–Oppenheimer surface. Nevertheless, the ultimate conclusion of ref. 41 is in full accord with our best theoretical predictions.

Our AE-CCSDTQ(P)/CBS + MVD1 results show that the H–C bond of fulminic acid has one of the shortest lengths (1.0590 Å) and highest harmonic frequencies (3497 cm⁻¹) known for organic compounds.^5,138 For comparison, experimental values for the [r_e(H–C), ω₁] pair are (1.0606 Å, 3495 cm⁻¹) for acetylene,¹³⁹ (1.0591 Å, 3501 cm⁻¹) for monofluoroacetylene,^140,141 and (1.0650 Å, 3443 cm⁻¹) for HCN.^134,135 We find the C–N bond in fulminic acid to be 0.0058 Å longer than in HCN, but the associated stretching frequency is 148 cm⁻¹ higher due to coupling with the N–O stretch. The N–O bond distance obtained here for HCNO is 0.017 Å longer than that of the isoelectronic N₂O species, and this substantial change is accompanied by a harmonic frequency decrease of 32 cm⁻¹ for the N–O stretching mode.^142,143

The characteristics of HCNO can be placed into context by comparison with the properties of other small nitrile oxide compounds XCNO (X = F, Cl, Br, CN, CH₃, CF₃) that have been investigated by gas-phase, high-resolution rovibrational spectroscopy^144–155 and by varying levels of electronic structure theory.^152–164 Generally, the XCNO equilibrium structures are strongly dependent on both the orbital basis set and the electron correlation method, as observed in the HCNO case. The propensity for X–C–N bending in these compounds can be understood in terms of a competition between two Lewis structures:

Electron-withdrawing substituents tilt the balance toward the secondary structure and favor bending, whereas electron-donating or π-accepting substituents elevate the importance of the primary structure and maintain linearity. Thus, for the halogen fulminates, the X–C–N angle decreases and the barrier to linearity (E_B) increases with increasing electronegativity (X = Br, Cl, F). At CCSD(T)/CBS, fluorofulminate has ∠(F–C–N) = 135.1° and a relatively high E_B = 1870 cm⁻¹, so that FCNO is not quasilinear, but rather the first example of a truly bent nitrile oxide.^156,157 Employing CCSD(T) with a mixed cc-pV5Z/cc-pVQZ basis set for X/(C,N,O) demonstrated that ClCNO¹⁵⁸ and BrCNO¹⁶⁰ are more weakly bent with [∠(X–C–N), E_B] = (152.2°, 156 cm⁻¹) and (153.1°, 119 cm⁻¹), respectively. This conclusion is supported by the effective barriers to linearity (167, 131) cm⁻¹ derived from spectroscopy¹⁴⁴ for (ClCNO, BrCNO). In contrast, acetonitrile N-oxide (X = CH₃, electron donating) and cyanofulminate (X = NC, π-accepting) have linear structures at the CCSD(T)/cc-pVQZ and CCSD(T)-F12/aug-cc-pVTZ-F12 levels of theory, respectively.^161,164 Interestingly, a gas-phase mid-infrared and ab initio study of CF₃CNO was conducted by Havasi and coworkers¹⁵⁴ to ascertain the effect of the strongly withdrawing CF₃ group on the molecular framework. Their FC-CCSD(T)/cc-pVTZ computations gave a substantially bent structure with [∠(C–C–N), E_B] = (148.9°, 174 cm⁻¹), while their experiments suggested but did not prove that the molecule has a near-linear backbone. In summary, the series for bending disposition in XCNO compounds is F ≫ CF₃ > Cl > Br > H > CH₃ > CN, and the parent fulminic acid lies almost precisely on the cusp for breaking linearity of the equilibrium structure.

3.4. Assessing CBS extrapolation schemes

The sensitivity of the H–C–N bending potential of the fulminic acid to orbital basis set calls for an assessment of CBS extrapolation methods. In Table 5, AE-CCSDTQ(P)/CBS optimized bond distances and harmonic frequencies of linear HCNO are presented for nine different combinations of the E_HF and E_corr extrapolation schemes specified above in Section 2. While substantial research exists on energetic results from various CBS approaches in quantum chemistry, very little information is known on the sensitivity of r_e and ω_i predictions to the choice of CBS methodology. Our focus here is not on estimating CBS values using modest basis sets, rather we investigate possibilities for making the final step from rigorous cc-pCV(4,5,6)Z computations to the CBS limit. It is gratifying that the [r_e(H–C), r_e(C–N), r_e(N–O)] values in Table 5 lie within narrow intervals of width (0.00014, 0.00023, 0.00005) Å while the (ω₁, ω₂, ω₃, ω₄) frequencies vary by no more than (0.1, 0.6, 1.6, 0.3) cm⁻¹. Not surprisingly, the ω₅ frequencies exhibit larger variations as the extrapolation method is changed. The Schwartz-4 result (22.5 cm⁻¹) of eqn (5) is clearly an outlier, and the Schwenke schemes may suffer by a few cm⁻¹ because they are not calibrated on the cc-pCVXZ basis set series. The remaining 6 results for ω₅ all reside within the range [44.0, 45.6] cm⁻¹. The essential observation from Table 5 is that the primary approach employed here [eqn (1) (4,5,6), eqn (2) (5,6)] is buttressed by numerous reasonable alternatives. This conclusion is further supported by analyzing the c parameters resulting from the fits of X = (4,5,6) data to eqn (6) and (7). Remarkably, the MP2 correlation energies in the vicinity of the AE-CCSDTQ(P)/CBS equilibrium geometry are characterized by an X exponent of 2.9953(5) in eqn (6) or an X shift of 0.0056(6) in eqn (7). On the other hand, the corresponding (exponent, shift) pair is [3.4760(4), −0.5162(4)] for CCSD and [3.5014(4), −0.5406(4)] for CCSD(T). Therefore, the coupled-cluster correlation energies for linear HCNO may be slightly better described by either an X^−3.5 or (X + ½)⁻³ decay, but the assumption of X⁻³ dependence viaeqn (2) yields virtually indistinguishable results for r_e and ω_i.

Table 5 Linear HCNO FPA bond distances (r_e, Å) and harmonic vibrational frequencies (ω_i, cm⁻¹) at the AE-CCSDTQ(P)/CBS level as a function of the CBS extrapolation method^a

E HF	E corr [CCSD(T)]	r e(H–C)	r e(C–N)	r e(N–O)	ω 1(σ)	ω 2(σ)	ω 3(σ)	ω 4(π)	ω 5(π)
a The applied CBS extrapolation equations from the text are listed in the first two columns along with the X values of the fitted points for the Hartree–Fock (EHF) and CCSD(T) correlation energy (Ecorr). The Schwenke extrapolation schemes^112 (Schw, augSchw) do not have explicit extrapolation formulas.
eqn (1) (4,5,6)	eqn (2) (5,6)	1.05913	1.15910	1.20229	3496.9	2275.9	1268.1	548.3	45.3
eqn (4) (5,6)	eqn (2) (5,6)	1.05913	1.15910	1.20229	3496.9	2275.9	1268.1	548.3	45.6
eqn (1) (4,5,6)	eqn (2) (4,5,6)	1.05907	1.15901	1.20231	3496.9	2275.6	1267.4	548.4	44.4
eqn (3) (4,5,6)	eqn (2) (5,6)	1.05913	1.15909	1.20231	3496.9	2275.9	1268.0	548.1	45.9
eqn (1) (4,5,6)	eqn (6) (4,5,6)	1.05921	1.15924	1.20226	3496.9	2276.5	1269.0	548.1	44.0
eqn (1) (4,5,6)	eqn (7) (4,5,6)	1.05919	1.15920	1.20227	3496.9	2276.3	1268.7	548.2	44.7
eqn (1) (4,5,6)	eqn (5) (5,6)	1.05913	1.15919	1.20230	3496.9	2275.9	1268.1	548.4	22.5
Schw (5,6)	Schw (5,6)	1.05913	1.15913	1.20229	3496.9	2276.0	1268.1	548.4	37.3
augSchw (5,6)	augSchw (5,6)	1.05913	1.15913	1.20229	3496.9	2275.9	1268.1	548.4	39.4

---

3.5. Reaction energy for HCNO formation

The electronic wavefunction methods employed here for the quasilinear/quasibent problem of fulminic acid were put to a stern test by application to the HCN + O(³P) → HCNO reaction energy. The two-dimensional FPA grid for extrapolation to both the orbital basis set (CBS) and electron correlation (FCI) limits comprises Table 6. The HF/CBS reaction energy is +15.2 kcal mol⁻¹, while the MP2/CBS correction to this starting point is a prodigious −78.4 kcal mol⁻¹. Thus, the reaction is substantially endoergic with HF and strongly exoergic with MP2, demonstrating the demands placed on the coupled-cluster series to reach a converged answer. Toward this end the [CCSD, CCSD(T)] increments are (+20.1, −8.3) kcal mol^{− 1} at the CBS limit, after which ΔE_e[CCSD(T)/CBS] = −51.4 kcal mol⁻¹ is obtained. In brief, a phenomenal oscillatory series is witnessed that is unfettered until the triple excitations are accounted for by coupled-cluster theory. The convergence of the energetic predictions with respect to orbital basis set displays the characteristic properties of the FPA method.^165–173 In particular, HF reaches the CBS limit very rapidly, δ[MP2] displays a protracted decay that varies 0.7 kcal mol⁻¹ even after cc-pCV6Z, and the higher-order correlation increments are increasingly insensitive to basis set as the electronic excitation level builds up.

Table 6 Vibrationless reaction energy (ΔE_e, kcal mol⁻¹) of HCN + O(³P) → HCNO^a

	ΔEe(HF)	δ[MP2]	δ[Ȼ]	δ[Ȼ(T)]	δ[ȻT]	δ[ȻT(Q)]	δ[ȻTQ]	δ[ȻTQ(P)]	δ[ȻTQP]	δ[ȻTQP(H)]	NET
D e(HCN–O) = −[ΔEe(FPA) + Δ(MVD1) + Δ(DBOC) + Δ(SOC)] ⇒ De(HCN–O) = −(–51.62 + 0.35 − 0.03 + 0.22) = 51.08 kcal mol^−1. D0(HCN–O) = De(HCN–O) + Δ(ZPVE) = 51.08 − 2.00 = 49.08 kcal mol^−1.a AE-CCSDTQ(P)/CBS + MVD1 reference geometries. Ȼ is shorthand for CCSD. The symbol δ denotes increments in ΔEe with respect to the preceding level of theory in the electron correlation series HF → MP2 → CCSD → CCSD(T) → CCSDT → CCSDT(Q) → CCSDTQ → CCSDTQ(P) → CCSDTQP→ CCSDTQP(H). Brackets signify results from primary CBS extrapolations (eqn (1) and (2)) or additivity assumptions. The sum across each row yields the NET column entry, which approximates the CCSDTQP(H) (or FCI) result with the corresponding basis set. UHF orbitals were employed for O(^3P), given that the spin contamination of the UHF reference wavefunction is negligible. (FC, AE) specifies whether a given row pertains to (frozen-core, all-electron) computations.
6-31G* (FC)	18.29	−66.05	16.69	−5.62	0.20	−0.95	0.21	0.12	−0.15	0.01	−37.23
cc-pVDZ (FC)	19.77	−65.98	16.12	−5.92	0.22	−0.96	0.24	0.14	[–0.15]	[0.01]	[–36.50]
cc-pVTZ (FC)	15.96	−72.43	18.82	−7.54	0.50	−0.95	[0.24]	[0.14]	[–0.15]	[0.01]	[–45.40]
cc-pCVQZ (FC)	15.34	−75.39	19.48	−7.91	[0.50]	[–0.95]	[0.24]	[0.14]	[–0.15]	[0.01]	[–48.70]
cc-pCVQZ (AE)	15.34	−75.96	19.53	−8.07	[0.50]	[–0.95]	[0.24]	[0.14]	[–0.15]	[0.01]	[–49.38]
cc-pCV5Z (AE)	15.18	−77.16	19.82	−8.18	[0.50]	[–0.95]	[0.24]	[0.14]	[–0.15]	[0.01]	[–50.55]
cc-pCV6Z (AE)	15.16	−77.69	19.95	−8.22	[0.50]	[–0.95]	[0.24]	[0.14]	[–0.15]	[0.01]	[–51.01]
CBS	[15.16]	[–78.40]	[20.13]	[–8.29]	[0.50]	[–0.95]	[0.24]	[0.14]	[–0.15]	[0.01]	[–51.62]

---

Our FPA of the reaction energy embeds the 1s effects in the AE-[MP2, CCSD, CCSD(T)] computations with the cc-pCV(Q,5,6)Z basis sets, superseding any auxiliary correction for core correlation. To proceed toward a definitive reaction energy, AE results have been carefully seamed together in Table 6 with frozen-core treatments up to CCSDTQP(H). The inclusion of rows for both FC- and AE-CCSD(T)/cc-pCVQZ effectuates a smooth fusion and yields a new type of construction for FPA layouts. For example, the difference of the NET entries for these two rows gives −0.68 kcal mol⁻¹ as the 1s correlation effect on ΔE_e, similar in size to the corresponding bond-energy shift for the NO diatomic.¹³⁶ The oscillatory pattern for the correlation increments persists with (δ[CCSDT], δ[CCSDT(Q)], δ[CCSDTQ]) = (+0.50, −0.95, +0.24) kcal mol⁻¹, after which the net effect is essentially zero. The 6-31G* and cc-pVDZ increments past the CCSD(T) level are virtually identical, justifying use of the smaller basis set in the extension toward the FCI limit. The final FC-CCSDTQP(H)/6-31G* job on HCNO required 10 weeks of continuous CPU time on a high-performance cluster, yielding an FPA table of unprecedented reach. The coup de grâce is the final increment revealing that hextuple excitations change the reaction energy by only 0.01 kcal mol⁻¹.

The dual extrapolation in Table 6 yields ΔE_e(FPA) = −51.6 kcal mol⁻¹, which is appended with Δ(MVD1) = 0.35 kcal mol⁻¹ [AE-CCSD(T)/cc-pCV5Z], Δ(DBOC) = −0.03 kcal mol⁻¹ [AE-CCSD/cc-pCVQZ], and Δ(SOC) = 0.22 kcal mol⁻¹. The last auxiliary term is a spin–orbit correction for the O atom, derived as usual by taking a weighted average of the relative energies (0, 158.265, 226.977) cm⁻¹ pinpointed spectroscopically for the (³P₂, ³P₁, ³P₀) multiplets.¹⁷⁴ The final result for ΔE_e translates into the vibrationless dissociation energy D_e(HCN–O) = 51.1 kcal mol⁻¹.

Constructing the ZPVE correction for the HCN–O dissociation energy is complicated by the anharmonicity of the large-amplitude H–C–N bending mode (ν₅) of fulminic acid. Fortunately, an optimum effective one-dimensional potential for the ν₅ mode is available from semirigid bender fits of high-resolution spectroscopic data, and the vibrational states supported by this potential have been determined by matrix diagonalization of the corresponding effective Hamiltonian.⁴¹ As discussed above in Section 3.3, a ZPVE of 146.9 cm⁻¹ is found for ν₅ on the adiabatic curve given by the ground state of the complementary vibrational modes.⁴¹ Combining this ν₅ value with the ZPVEs given by our AE-CCSDTQ(P)/CBS + MVD1 harmonic frequencies (Tables 2 and 3) for the other vibrational modes of HCNO and HCN, we arrive at Δ(ZPVE) = −2.00 kcal mol⁻¹. Hence, we ascertain D₀(HCN–O) = 49.08 kcal mol⁻¹, with a rough uncertainty estimate of ±0.15 kcal mol^{− 1}. This bond energy for fulminic acid is over 10 kcal mol⁻¹ larger than the value D₀(N₂–O) = 38.44 kcal mol⁻¹ given by current thermochemical tabulations¹⁷⁵ for the isoelectronic nitrous oxide molecule.

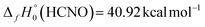The D₀(HCN–O) result obtained in this research by high-level computations provides an important alternative route for the determination of for fulminic acid. Utilizing the precisely known¹⁷⁵ values and , our D₀(HCN–O) yields . The current ATcT value for this enthalpy of formation (40.81 ± 0.11 kcal mol⁻¹) appears to come essentially from and the isocyanic acid → fulminic acid isomerization energy of 68.5 ± 0.2 kcal mol⁻¹ surmised in a 2004 computational study.⁸⁰ This ATcT quantity is in accord with our alternative derivation of , and the level of agreement is certainly within the collective error bars of the two numbers. Nevertheless, our result provides valuable new information for the ATcT refinement algorithm.

4. Summary

This comprehensive quantum chemical investigation of fulminic acid has performed numerous analyses and reached an abundance of conclusions, as summarized in the following bullet points:

(1) Previous theoretical work on fulminic acid through the CCSD(T) level is not sufficiently converged to the ab initio limit to definitively solve longstanding, vexing problems posed by this paradigmatic molecule of historical prominence.

(2) For HCN, our best ab initio [AE-CCSDTQ(P)/CBS + MVD1] equilibrium bond distances and harmonic vibrational frequencies match the empirically derived values to within 0.00017 Å and 1.6 cm⁻¹, respectively, constituting a genuine triumph of modern theoretical and experimental chemical physics.

(3) In our final analysis, fulminic acid (HCNO) manifests a linear minimum on the Born–Oppenheimer potential energy surface with [r_e(H–C), r_e(C–N), r_e(N–O)] = (1.0590, 1.1588, 1.2024) Å and (ω₁, ω₂, ω₃, ω₄) = (3497, 2275, 1266, 548) cm⁻¹, as provided by the same level of theory [AE-CCSDTQ(P)/CBS + MVD1] that yields essentially exact results for the HCN benchmark.

(4) The extensive series of AE correlation methods applied here with CBS extrapolation to the H–C–N bending frequency of linear HCNO generates phenomenal fluctuations: ω₅(π) = (604, 260i, 334, 120, 146, 49i, 52, 45) cm⁻¹ for [HF, MP2, CCSD, CCSD(T), CCSDT, CCSDT(Q), CCSDTQ, CCSDTQ(P)]. With incorporation of MVD1 relativistic effects, ω₅ = 19 cm⁻¹ is obtained as the final Born–Oppenheimer frequency. Accordingly, without ZPVE modulation from complementary vibrations, the ω₅ mode of linear HCNO is an almost perfect quartic oscillator with a nearly vanishing quadratic component.

(5) Core electron correlation, the diagonal Born–Oppenheimer correction (DBOC), and scalar relativistic effects (MVD1) all play a pivotal role in determining whether vibrationless HCNO is linear or bent; the cooperation of the first two driving forces against MVD1 preserves the linear structure. The influence of 1s correlation on the H–C–N bending frequency is particularly dramatic, as FC-CCSD(T)/CBS yields ω₅ = 65 cm⁻¹, but AE-CCSD(T)/CBS gives ω₅ = 120 cm⁻¹.

(6) The AE-MP2/CBS method incorrectly favors a bent optimum structure of HCNO that lies 73 cm⁻¹ below the linear form; the associated (θ_HCN, θ_CNO) angles deviate from linearity by (23.5°, 5.5°).

(7) Remarkably, the (Q) electron correlation contribution wrongly changes the structure of HCNO from linear to bent; nevertheless, the AE-CCSDT(Q)/CBS barrier to linearity is a microscopic 0.1 cm⁻¹, and the (θ_HCN, θ_CNO) angles are bent by only (6.1°, 1.4°) from linearity.

(8) Although both AE-MP2/CBS and AE-CCSDT(Q)/CBS give an imaginary ω₅ frequency for linear HCNO, the diagonal force constants F₄₄(H–C–N bend) and F₅₅(C–N–O bend) are both positive; accordingly, favorable F₄₅ coupling via simultaneous trans-bending is necessary to drive the molecule downhill in energy.

(9) With correlated methods the CBS limit for ω₅ is reached slowly, making basis-set extrapolations paramount to accurate conclusions. Notably, the AE-CCSD(T)/cc-pCV6Z frequency of linear HCNO is raised by 31 cm⁻¹ upon extrapolation, and at the FC-CCSD(T) level the cc-pCV6Z imaginary ω₅ (54i cm⁻¹) actually becomes real (65 cm⁻¹) at the CBS limit.

(10) The energy profile for H–C–N bending in fulminic acid is so flat that complementary-mode ZPVE becomes an important factor; the H–C and C–N bonds elongate upon bending, reducing the ZPVE in these modes, but contraction of the N–O bond may partially compensate for this effect.

(11) Novel work has been completed for linear HCNO investigating the dependence of AE-CCSDTQ(P)/CBS r_e and ω_i values on a litany of CBS extrapolation schemes and substantiating our final predictions. Nonlinear fits to new extrapolation formulas reveal that the all-electron correlation energy within the cc-pCVXZ basis set series exhibits almost perfect X⁻³ decay for MP2 but either an X^−3.5 or (X + ½)^–3 dependence for CCSD and CCSD(T).

(12) The D₁ and D₂ wavefunction diagnostics indicate that HCNO has borderline multireference electronic character, but full-valence CASSCF wavefunctions contradict this notion and show that this issue is not the cause of sensitivity to level of theory.

(13) Core electron correlation contracts the bond distances in HCNO by 0.001–0.002 Å, an order of magnitude more than MVD1. Incorporating 1s correlation causes an overall increase in harmonic stretching frequencies by 6–9 cm⁻¹; however, these frequency shifts are deceptive because the direct effect without geometry relaxation is to decrease ω₁–ω₃ by 5–9 cm⁻¹.

(14) Fulminic acid has one of the shortest r_e(H–C) distances and highest C–H stretching frequencies known for organic compounds, perhaps rivaled only by monofluoroacetylene.

(15) The facility of bending in XCNO compounds follows the order CN < CH₃ < H < Br < Cl < CF₃ ≪ F, with the parent fulminic acid appearing just before the critical point for breaking the symmetry of the linear equilibrium structure.

(16) The dissociation energy D_e(HCN–O) has been investigated by the first FPA computations to reach the CCSDTQP(H) level (at least for a tetra-atomic or larger system); new ground is thus broken in showing that the final correlation increment in the coupled cluster series for a challenging bond cleavage can be reduced to 0.01 kcal mol⁻¹.

(17) The final N–O bond energy of fulminic acid from cutting-edge FPA computations is D₀(HCN–O) = 49.1 kcal mol⁻¹, which is 28% larger than that of nitrous oxide; the 1s correlation effect on D₀(HCN–O) is a sizable 0.7 kcal mol⁻¹.

(18) Our final theoretical analysis supports the spectroscopic characterization that fulminic acid is by strict criteria a quasibent rather than a quasilinear molecule, because its true Born–Oppenheimer equilibrium structure is linear but the effective one-dimensional potential for large-amplitude H–C–N bending has a small protuberance at linearity.

The rovibrational quantum structure of fulminic acid remains a worthwhile and inviting target for future theoretical investigations. The current study reveals the severe demands for generating an accurate potential energy surface of full dimensionality for variational computations. A less formidable intermediate goal is to use high levels of theory to map out the most favorable course for H–C–N bending from linearity and rigorously determine the energy profile and complementary-mode ZPVE along this route. Such an endeavor would aim to cement the quasibent status of fulminic acid by showing that the empirical one-dimensional effective H–C–N bending potentials surmised from voluminous spectroscopic data are consonant with purely ab initio quantum chemical computations at the highest possible levels.

Data availability

The data supporting this article have been included as a part of the ESI.†

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This research was supported by the U.S. Department of Energy, Basic Energy Sciences, Division of Chemistry, Computational and Theoretical Chemistry (CTC) Program under Contract DE-SC0018412.

References

1. F. Kurzer, Fulminic Acid in the History of Organic Chemistry, J. Chem. Educ., 2000, 77, 851.
2. F. Arab, F. Nazari and F. Illas, Artificial Neural Network-Derived Unified Six-Dimensional Potential Energy Surface for Tetra Atomic Isomers of the Biogenic [H, C, N, O] System, J. Chem. Theory Comput., 2023, 19, 1186–1196.
3. A. Rey Planells and A. Espinosa Ferao, CHNO isomers and derivatives – a computational overview, New J. Chem., 2022, 46, 5771–5778.
4. D. Bégué, W. Lafargue-Dit-Hauret, A. Dargelos and C. Wentrup, CHNO – Formylnitrene, Cyanic, Isocyanic, Fulminic, and Isofulminic Acids and their Interrelationships at DFT and CASPT2 Levels of Theory, J. Phys. Chem. A, 2023, 127, 9088–9097.
5. D. P. Chong, MP2 or B3LYP: computed bond distances compared with CCSD(T)/cc-pVQZ, Can. J. Chem., 2018, 96, 336–339.
6. B. P. Winnewisser, M. Winnewisser, C. W. Mathews and K. M. T. Yamada, The rotational spectrum of HCNO in excited bending combination states, J. Mol. Spectrosc., 1987, 126, 460–479.
7. B. P. Winnewisser, The Spectra, Structure, and Dynamics of Quasilinear Molecules with Four or More Atoms, Molecular Spectroscopy: Modern Research, ed. K. N. Rao, Academic Press, 1985, pp. 321–419.
8. M. Gerlach, T. Preitschopf, E. Karaev, H. M. Quitián-Lara, D. Mayer, J. Bozek, I. Fischer and R. F. Fink, Auger electron spectroscopy of fulminic acid, HCNO: an experimental and theoretical study, Phys. Chem. Chem. Phys., 2022, 24, 15217–15229.
9. N. Marcelino, J. Cernicharo, B. Tercero and E. Roueff, Discovery of Fulminic Acid, HCNO, in Dark Clouds, Astrophys. J., 2009, 690, L27–L30.
10. E. Mendoza, B. Lefloch, A. López-Sepulcre, C. Ceccarelli, C. Codella, H. M. Boechat-Roberty and R. Bachiller, Molecules with a peptide link in protostellar shocks: a comprehensive study of L1157, Mon. Not. R. Astron. Soc., 2014, 445, 151–161.
11. B. Lefloch, R. Bachiller, C. Ceccarelli, J. Cernicharo, C. Codella, A. Fuente, C. Kahane, A. López-Sepulcre, M. Tafalla and C. Vastel, et al., Astrochemical evolution along star formation: overview of the IRAM Large Program ASAI, Mon. Not. R. Astron. Soc., 2018, 477, 4792–4809.
12. N. Marcelino, M. Agúndez, J. Cernicharo, E. Roueff and M. Tafalla, Discovery of the elusive radical NCO and confirmation of H₂NCO⁺ in space, Astron. Astrophys., 2018, 612, L10.
13. E. Howard, On a New Fulminating Mercury, Philos. Trans. R. Soc. London, 1800, 90, 204–238.
14. F. Kurzer, The Life and Work of Edward Charles Howard FRS, Ann. Sci., 1999, 56, 113–141.
15. W. Beck, The First Chemical Achievements and Publications by Justus von Liebig (1803–1873) on Metal Fulminates and Some Further Developments in Metal Fulminates and Related Areas of Chemistry, Eur. J. Inorg. Chem., 2003, 4275–4288.
16. Fulminate, Merriam-Webster Dictionary, https://www.merriam-webster.com/dictionary/fulminate, (accessed 2024 June 21).
17. S. Esteban, Liebig–Wöhler Controversy and the Concept of Isomerism, J. Chem. Educ., 2008, 85, 1201–1203.
18. H. Wieland, Eine neue Knallsäuresynthese. Über den Verlauf der Knallsäurebildung aus Alkohol und Salpetersäure, Ber. Dtsch. Chem. Ges., 1907, 40, 418–422.
19. J. U. Nef, On the Constitution of the Nitroparaffine Salts, Proc. Am. Acad. Arts Sci., 1894, 30, 124–150.
20. J. U. Nef, On Bivalent Carbon. Second Paper, Proc. Am. Acad. Arts Sci., 1894, 30, 151–193.
21. J. U. Nef, Ueber das zweiwerthige Kohlenstoffatom, Justus Liebigs Ann. Chem., 1894, 280, 291–342.
22. H. Ley and H. Kissel, Beiträge zur Chemie des Quecksilbers, Ber. Dtsch. Chem. Ges., 1899, 32, 1357–1368.
23. L. Pauling and S. B. Hendricks, The Prediction of the Relative Stabilities of Isoteric Isomeric Ions and Molecules, J. Am. Chem. Soc., 1926, 48, 641–651.
24. W. Beck, E. Schuierer and K. Feldl, Fulminato-Metall-Komplexe, Angew. Chem., 1965, 77, 722.
25. W. Beck and K. Feldl, The Structure of Fulminic Acid, HCNO, Angew. Chem., Int. Ed. Engl., 1966, 5, 722–723.
26. W. Beck, P. Swoboda, K. Feldl and R. S. Tobias, Eigenschaften und IR-Spektrum der Knallsäure HCNO, Chem. Ber., 1971, 104, 533–543.
27. W. Beck, G. Fischer and P. Swoboda, Some Comments on Fulminic Acid (Knallsäure) and a Praise to Heinrich Wieland and his Work on Organic Derivatives of Nitrogen, Z. Anorg. Allg. Chem., 2017, 643, 353–356.
28. A. Kekulé, Ueber die Constitution des Knallquecksilbers, Justus Liebigs Ann. Chem., 1857, 105, 279–286.
29. E. Divers and M. Kawakita, On the constitution of the fulminates, J. Chem. Soc., Trans., 1884, 45, 13–24.
30. E. Divers and M. Kawakita, On Liebig's production of fulminating silver without the use of nitric acid, J. Chem. Soc., Trans., 1884, 45, 27–30.
31. H. E. Armstrong, Note on the formation and on the constitution of the fulminates, J. Chem. Soc., Trans., 1884, 45, 25–27.
32. M. Mladenović, M. Elhiyani and M. Lewerenz, Quasilinearity in tetratomic molecules: An ab initio study of the CHNO family, J. Chem. Phys., 2009, 130, 154109.
33. M. Winnewisser and H. K. Bodenseh, Mikrowellenspektrum, Struktur und l-Typ-Dublett-Aufspaltung der HCNO (Knallsäure), Z. Naturforsch., A, 1967, 22, 1724–1737.
34. H. K. Bodenseh and M. Winnewisser, Rotation-Vibration Interaction in the Microwave Spectrum of Fulminic Acid, HCNO, Z. Naturforsch., A, 1969, 24, 1966–1972.
35. M. Winnewisser and B. P. Winnewisser, Centrifugal Distortion Parameters of Fulminic Acid, HCNO, from the Millimeter-Wave Rotational Spectra, Z. Naturforsch., A, 1971, 26, 128–131.
36. M. Winnewisser and B. P. Winnewisser, Millimeter wave rotational spectrum of HCNO in vibrationally excited states, J. Mol. Spectrosc., 1972, 41, 143–176.
37. M. Winnewisser and B. P. Winnewisser, The Millimeter Wave Spectrum of DCNO: An Example of Current Measurements in the Frequency Range from 60 to 350 GHz, Z. Naturforsch., A, 1974, 29, 633–641.
38. B. P. Winnewisser, M. Winnewisser and F. Winther, The bending-rotation spectrum of fulminic acid and deuterofulminic acid, J. Mol. Spectrosc., 1974, 51, 65–96.
39. J. M. R. Stone, The large amplitude motion-rotation Hamiltonian for tetratomic molecules, application to HCNO and HNCO, J. Mol. Spectrosc., 1975, 54, 1–9.
40. J. A. Duckett, A. G. Robiette and I. M. Mills, The two-dimensional anharmonic oscillator: Vibration-rotation constants of fulminic acid, HCNO, J. Mol. Spectrosc., 1976, 62, 19–33.
41. P. R. Bunker, B. M. Landsberg and B. P. Winnewisser, HCNO as a semirigid bender, J. Mol. Spectrosc., 1979, 74, 9–25.
42. B. P. Winnewisser, High resolution infrared spectrum of HCNO: Analysis of the bands at 3300 cm⁻¹, J. Mol. Spectrosc., 1971, 40, 164–176.
43. B. P. Winnewisser and M. Winnewisser, Millimeter wave rotational spectrum of deuterofulminic acid, DCNO, in excited vibrational states, J. Mol. Spectrosc., 1975, 56, 471–483.
44. K. Yamada, B. P. Winnewisser and M. Winnewisser, Vibration-rotation interaction in HCNO caused by accidental resonances and enhanced by the quasilinearity of the molecule, J. Mol. Spectrosc., 1975, 56, 449–470.
45. H. K. Bodenseh and M. Winnewisser, Microwave Spectrum, Structure and Rotation-Vibration Interaction of Deutero-Fulminic Acid, DCNO, Z. Naturforsch., A, 1969, 24, 1973–1979.
46. B. P. Winnewisser and M. Winnewisser, On the high resolution infrared spectrum of HCNO, J. Mol. Spectrosc., 1969, 29, 505–507.
47. E. L. Ferretti and K. Narahari Rao, Infrared bands of the HCNO molecule, J. Mol. Spectrosc., 1974, 51, 97–106.
48. F. Winther, Weak bands in the far-infrared spectrum of HCNO, J. Mol. Spectrosc., 1976, 62, 232–246.
49. E. L. Ferretti and K. Narahari Rao, Infrared spectrum of DCNO: ν₂ band at 4.8 μm, J. Mol. Spectrosc., 1975, 56, 494–496.
50. E. L. Ferretti, Infrared-bands of Fulminic Acid and Deuterated Fulminic Acid, PhD thesis, The Ohio State University, 1974.
51. W. D. Sheasley, C. W. Mathews, E. L. Ferretti and K. Narahari Rao, Infrared spectra of DCNO: Rotational analysis of the ν₁ band, J. Mol. Spectrosc., 1971, 37, 377–379.
52. P. Jensen, HCNO as a semirigid bender: The degenerate ν₄ state, J. Mol. Spectrosc., 1983, 101, 422–439.
53. B. P. Winnewisser and P. Jensen, The infrared spectrum of fulminic acid, HCNO, in the ν₄ fundamental region, J. Mol. Spectrosc., 1983, 101, 408–421.
54. G. Schulze, O. Koja, B. P. Winnewisser and M. Winnewisser, High resolution FIR spectra of DCNO and HCNO, J. Mol. Struct., 2000, 517–518, 307–325.
55. S. Albert, M. Winnewisser and B. P. Winnewisser, Networks of anharmonic resonance systems in the rovibrational overtone spectra of the quasilinear molecule HCNO, Ber. Bunsen-Ges. Phys. Chem., 1996, 100, 1876–1898.
56. S. Albert, M. Winnewisser and B. P. Winnewisser, The v₁, v₂, 2v₃, v₂ + v₃ band systems and the overtone region of HCNO above 4000 cm⁻¹: A Network of Resonance Systems, Ber. Bunsen-Ges. Phys. Chem., 1997, 101, 1165–1186.
57. R. Takashi, K. Tanaka and T. Tanaka, CO₂ laser-microwave double resonance spectroscopy of HCNO: Precise measurement of the dipole moment and its vibrational dependence, J. Mol. Spectrosc., 1989, 138, 450–466.
58. B. P. Winnewisser, M. Winnewisser, G. Wagner and J. Preusser, The effects of a strong Coriolis resonance in the far infrared spectrum and rotational transitions of H¹³CNO, J. Mol. Spectrosc., 1990, 142, 29–56.
59. W. Quapp, S. Albert, B. P. Winnewisser and M. Winnewisser, The FT-IR Spectrum of HC¹⁵NO: The ν₁, ν₂, 2ν₃, and ν₂ + ν₃ Band Systems, J. Mol. Spectrosc., 1993, 160, 540–553.
60. G. Wagner, B. P. Winnewisser, M. Winnewisser and K. Sarka, The Infrared-Spectrum of HC¹⁵NO in the Range 170-1300 cm⁻¹, J. Mol. Spectrosc., 1993, 162, 82–119.
61. K. Islami, W. Jabs, J. Preusser, M. Winnewisser and B. P. Winnewisser, The Rotational and Rotation-Bending Spectrum of HC¹⁵NO: An Extended Analysis of the Spectral Regions 18–40 GHz, 90–440 GHz and 170–1300 cm⁻¹, Ber. Bunsen-Ges. Phys. Chem., 1995, 99, 565–582.
62. K. Islami, J. Preusser, R. Schermaul, B. P. Winnewisser and M. Winnewisser, Analysis of the Coriolis Resonance System (00002)/(00010) in Four Isotopomers of Fulminic Acid, J. Mol. Spectrosc., 1996, 176, 416–424.
63. J. Preusser, R. Schermaul, B. P. Winnewisser and M. Winnewisser, Rotational and Rovibrational Spectra of H¹³C¹⁵NO in the Spectral Regions 18–40 GHz, 110–440 GHz, and 170–1850 cm⁻¹, J. Mol. Spectrosc., 1996, 176, 99–123.
64. S. Albert, K. K. Albert, M. Winnewisser and B. P. Winnewisser, The FT-IR Spectrum of H¹³C¹⁵NO in the ranges 1800–3600 and 6300–7000 cm⁻¹, J. Mol. Struct., 2001, 599, 347–369.
65. G. Wagner, B. P. Winnewisser and M. Winnewisser, The effects of a strong Coriolis resonance on rovibrational line intensities of H¹³CNO, J. Mol. Spectrosc., 1991, 146, 104–119.
66. F. Iachello, F. Pérez-Bernal and P. H. Vaccaro, A novel algebraic scheme for describing nonrigid molecules, Chem. Phys. Lett., 2003, 375, 309–320.
67. M. Winnewisser, B. P. Winnewisser, I. R. Medvedev, F. C. De Lucia, S. C. Ross and L. M. Bates, The hidden kernel of molecular quasi-linearity: Quantum monodromy, J. Mol. Struct., 2006, 798, 1–26.
68. D. Larese and F. Iachello, A study of quantum phase transitions and quantum monodromy in the bending motion of non-rigid molecules, J. Mol. Struct., 2011, 1006, 611–628.
69. D. Larese, Quantum monodromy and quantum phase transitions in floppy molecules, AIP Conf. Proc., 2012, 1488, 358–365.
70. D. Poppinger, L. Radom and J. A. Pople, A theoretical study of the CHNO isomers, J. Am. Chem. Soc., 1977, 99, 7806–7816.
71. A. D. McLean, G. H. Loew and D. S. Berkowitz, Structures and spectra of the isomers HNCO, HOCN, HONC, and HCNO from ab Initio quantum mechanical calculations, J. Mol. Spectrosc., 1977, 64, 184–198.
72. L. Farnell, R. H. Nobes and L. Radom, A theoretical consideration of the quasi-bent nature of the HCNO molecule, J. Mol. Spectrosc., 1982, 93, 271–280.
73. J. H. Teles, G. Maier, B. Andes Hess Jr., L. J. Schaad, M. Winnewisser and B. P. Winnewisser, The CHNO Isomers, Chem. Ber., 1989, 122, 753–766.
74. M. T. Nguyen, K. Pierloot and L. G. Vanquickenborne, Fulminic acid (HCNO): bent versus linear equilibrium structure?, Chem. Phys. Lett., 1991, 181, 83–87.
75. A. P. Rendell, T. J. Lee and R. Lindh, Quantum chemistry on parallel computer architectures: coupled-cluster theory applied to the bending potential of fulminic acid, Chem. Phys. Lett., 1992, 194, 84–94.
76. J. Koput, B. P. Winnewisser and M. Winnewisser, An ab initio study on the equilibrium structure and HCN bending potential energy function of fulminic acid, Chem. Phys. Lett., 1996, 255, 357–362.
77. M. Mladenović and M. Lewerenz, Equilibrium structure and energetics of CHNO isomers: Steps towards ab initio rovibrational spectra of quasi-linear molecules, Chem. Phys., 2008, 343, 129–140.
78. N. Pinnavaia, M. J. Bramley, M.-D. Su, W. H. Green and N. C. Handy, A study of the ground electronic state of the isomers of CHNO, Mol. Phys., 1993, 78, 319–343.
79. A. M. Mebel, A. Luna, M. C. Lin and K. Morokuma, A density functional study of the global potential energy surfaces of the [H,C,N,O] system in singlet and triplet states, J. Chem. Phys., 1996, 105, 6439–6454.
80. M. S. Schuurman, S. R. Muir, W. D. Allen and H. F. Schaefer III, Toward subchemical accuracy in computational thermochemistry: Focal point analysis of the heat of formation of NCO and [H,N,C,O] isomers, J. Chem. Phys., 2004, 120, 11586–11599.
81. M. Mladenović, M. Elhiyani and M. Lewerenz, Electric and magnetic properties of the four most stable CHNO isomers from ab initio CCSD(T) studies, J. Chem. Phys., 2009, 131, 034302.
82. A. Luna, A. M. Mebel and K. Morokuma, Density functional study of the global potential energy surfaces of the [H,C,N,O]⁺ system in doublet and quartet states, J. Chem. Phys., 1996, 105, 3187–3205.
83. M. Mladenović, M. Lewerenz, M. C. McCarthy and P. Thaddeus, Isofulminic acid, HONC: Ab initio theory and microwave spectroscopy, J. Chem. Phys., 2009, 131, 174308.
84. M. Mladenović, Six-dimensional potential energy surface and rotation-vibration energy levels of HNCO in the ground electronic state, J. Serb. Chem. Soc., 2019, 84, 845–859.
85. S. Albert and M. Quack, High Resolution Rovibrational Spectroscopy of Chiral and Aromatic Compounds, Chem. Phys. Chem., 2007, 8, 1271–1281.
86. C. C. J. Roothaan, New Developments in Molecular Orbital Theory, Rev. Mod. Phys., 1951, 23, 69–89.
87. J. A. Pople and R. K. Nesbet, Self-Consistent Orbitals for Radicals, J. Chem. Phys., 1954, 22, 571–572.
88. C. Møller and M. S. Plesset, Note on an Approximation Treatment for Many-Electron Systems, Phys. Rev., 1934, 46, 618–622.
89. J. Čížek, On the Correlation Problem in Atomic and Molecular Systems. Calculation of Wavefunction Components in Ursell-Type Expansion Using Quantum-Field Theoretical Methods, J. Chem. Phys., 1966, 45, 4256–4266.
90. T. D. Crawford and H. F. Schaefer III, An Introduction to Coupled Cluster Theory for Computational Chemists, Rev. Comput. Chem., 2000, 33–136.
91. G. D. Purvis III and R. J. Bartlett, A full coupled-cluster singles and doubles model: The inclusion of disconnected triples, J. Chem. Phys., 1982, 76, 1910–1918.
92. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, A fifth-order perturbation comparison of electron correlation theories, Chem. Phys. Lett., 1989, 157, 479–483.
93. J. Noga and R. J. Bartlett, The full CCSDT model for molecular electronic structure, J. Chem. Phys., 1987, 86, 7041–7050.
94. Y. J. Bomble, J. F. Stanton, M. Kállay and J. Gauss, Coupled-cluster methods including noniterative corrections for quadruple excitations, J. Chem. Phys., 2005, 123, 054101.
95. S. A. Kucharski and R. J. Bartlett, The coupled-cluster single, double, triple, and quadruple excitation method, J. Chem. Phys., 1992, 97, 4282–4288.
96. M. Kállay and J. Gauss, Approximate treatment of higher excitations in coupled-cluster theory, J. Chem. Phys., 2005, 123, 214105.
97. M. Kállay and J. Gauss, Approximate treatment of higher excitations in coupled-cluster theory. II. Extension to general single-determinant reference functions and improved approaches for the canonical Hartree–Fock case, J. Chem. Phys., 2008, 129, 144101.
98. M. Kállay and P. R. Surján, Higher excitations in coupled-cluster theory, J. Chem. Phys., 2001, 115, 2945–2954.
99. T. H. Dunning Jr., Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023.
100. A. K. Wilson, T. van Mourik and T. H. Dunning Jr., Gaussian basis sets for use in correlated molecular calculations. VI. Sextuple zeta correlation consistent basis sets for boron through neon, J. Mol. Struct. THEOCHEM, 1996, 388, 339–349.
101. D. E. Woon and T. H. Dunning Jr., Gaussian basis sets for use in correlated molecular calculations. V. Core-valence basis sets for boron through neon, J. Chem. Phys., 1995, 103, 4572–4585.
102. P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chem. Acc., 1973, 28, 213–222.
103. CFOUR, a quantum chemical program package written by J. F. Stanton, J. Gauss, L. Cheng, M. E. Harding, D. A. Matthews, P. G. Szalay with contributions from A. Asthana, A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, S. Blaschke, Y. J. Bomble, S. Burger, O. Christiansen, D. Datta, F. Engel, R. Faber, J. Greiner, M. Heckert, O. Heun, M. Hilgenberg, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, T. Kirsch, M.-P. Kitsaras, K. Klein, G. M. Kopper, W. J. Lauderdale, F. Lipparini, J. Liu, T. Metzroth, L. A. Mück, T. Nottoli, D. P. O'Neill, J. Ostwald, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, T. Uhlířová, J. Vázquez, F. Wang, J. D. Watts, P. Yergün, C. Zhang, X. Zheng and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, and J. Olsen), and ECP routines by, A. V. Mitin and C. van Wüllen, For the current version, see https://www.cfour.de.
104. D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, Coupled-cluster techniques for computational chemistry: The CFOUR program package, J. Chem. Phys., 2020, 152, 214108.
105. MRCC, a quantum chemical program suite written by M. Kállay, P. R. Nagy, D. Mester, L. Gyevi-Nagy, J. Csóka, P. B. Szabó, Z. Rolik, G. Samu, J. Csontos, B. Hégely, Á. Ganyecz, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and R. A. Horváth. See https://www.mrcc.hu.
106. M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy and B. Hégely, et al., The MRCC program system: Accurate quantum chemistry from water to proteins, J. Chem. Phys., 2020, 152, 07410.
107. D. Feller, Application of systematic sequences of wave functions to the water dimer, J. Chem. Phys., 1992, 96, 6104–6114.
108. T. Helgaker, W. Klopper, H. Koch and J. Noga, Basis-set convergence of correlated calculations on water, J. Chem. Phys., 1997, 106, 9639–9646.
109. K. A. Peterson, D. E. Woon and T. H. Dunning Jr., Benchmark calculations with correlated molecular wave functions. IV. The classical barrier height of the H + H₂ → H₂ + H reaction, J. Chem. Phys., 1994, 100, 7410–7415.
110. A. Karton and J. M. L. Martin, Comment on: “Estimating the Hartree–Fock limit from finite basis set calculations” [Jensen F (2005) Theor Chem Acc 113:267], Theor. Chem. Acc., 2006,(115), 330–333.
111. J. M. L. Martin, Ab initio total atomization energies of small molecules—towards the basis set limit, Chem. Phys. Lett., 1996, 259, 669–678.
112. D. W. Schwenke, The extrapolation of one-electron basis sets in electronic structure calculations: How it should work and how it can be made to work, J. Chem. Phys., 2004, 122, 014107.
113. A. L. L. East and W. D. Allen, The heat of formation of NCO, J. Chem. Phys., 1993, 99, 4638–4650.
114. A. G. Császár, W. D. Allen and H. F. Schaefer III, In pursuit of the ab initio limit for conformational energy prototypes, J. Chem. Phys., 1998, 108, 9751–9764.
115. K. Balasubramanian, Relativistic Effects in Chemistry, Wiley Interscience, 1997.
116. R. D. Cowan and D. C. Griffin, Approximate relativistic corrections to atomic radial wave functions, J. Opt. Soc. Am., 1976, 66, 1010–1014.
117. C. Michauk and J. Gauss, Perturbative treatment of scalar-relativistic effects in coupled-cluster calculations of equilibrium geometries and harmonic vibrational frequencies using analytic second-derivative techniques, J. Chem. Phys., 2007, 127, 044106.
118. N. C. Handy, Y. Yamaguchi and H. F. Schaefer III, The diagonal correction to the Born–Oppenheimer approximation: Its effect on the singlet–triplet splitting of CH₂ and other molecular effects, J. Chem. Phys., 1986, 84, 4481–4484.
119. Wolfram Research, Inc., Mathematica, Version 14.0, Champaign, IL, 2024.
120. S. R. Barua, High-level ab initio quantum chemical studies of the competition between cumulenes, carbenes, and carbones, PhD thesis, University of Georgia, 2014.
121. T. J. Lee and P. R. Taylor, A diagnostic for determining the quality of single-reference electron correlation methods, Int. J. Quantum Chem., 1989, 36, 199–207.
122. C. L. Janssen and I. M. B. Nielsen, New diagnostics for coupled-cluster and Møller–Plesset perturbation theory, Chem. Phys. Lett., 1998, 290, 423–430.
123. I. M. B. Nielsen and C. L. Janssen, Double-substitution-based diagnostics for coupled-cluster and Møller–Plesset perturbation theory, Chem. Phys. Lett., 1999, 310, 568–576.
124. D. G. A. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. Di Remigio and A. Alenaizan, et al., Psi4 1.4: Open-source software for high-throughput quantum chemistry, J. Chem. Phys., 2020, 152, 184108.
125. J. P. Coe and M. J. Paterson, Investigating Multireference Character and Correlation in Quantum Chemistry, J. Chem. Theory Comput., 2015, 11, 4189–4196.
126. R. J. Bartlett, Y. C. Park, N. P. Bauman, A. Melnichuk, D. Ranasinghe, M. Ravi and A. Perera, Index of multi-determinantal and multi-reference character in coupled-cluster theory, J. Chem. Phys., 2020, 153, 234103.
127. F. M. Faulstich, H. E. Kristiansen, M. A. Csirik, S. Kvaal, T. B. Pedersen and A. Laestadius, S-Diagnostic—An a Posteriori Error Assessment for Single-Reference Coupled-Cluster Methods, J. Phys. Chem. A, 2023, 127, 9106–9120.
128. X. Xu, L. Soriano-Agueda, X. López, E. Ramos-Cordoba and E. Matito, All-Purpose Measure of Electron Correlation for Multireference Diagnostics, J. Chem. Theory Comput., 2024, 20, 721–727.
129. W. Jiang, N. J. DeYonker and A. K. Wilson, Multireference Character for 3d Transition-Metal-Containing Molecules, J. Chem. Theory Comput., 2012, 8, 460–468.
130. H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona and D. A. Kreplin, et al., The Molpro quantum chemistry package, J. Chem. Phys., 2020, 152, 144107.
131. H.-J. Werner, P. J. Knowles, P. Celani, W. Györffy, A. Hesselmann, D. Kats, G. Knizia, A. Köhn, T. Korona, D. Kreplin, R. Lindh, Q. Ma, F. R. Manby, A. Mitrushenkov, G. Rauhut, M. Schütz, K. R. Shamasundar, T. B. Adler, R. D. Amos, J. Baker, S. J. Bennie, A. Bernhardsson, A. Berning, J. A. Black, P. J. Bygrave, R. Cimiraglia, D. L. Cooper, D. Coughtrie, M. J. O. Deegan, A. J. Dobbyn, K. Doll and M. Dornbach, F. Eckert, S. Erfort, E. Goll, C. Hampel, G. Hetzer, J. G. Hill, M. Hodges and T. Hrenar, G. Jansen, C. Köppl, C. Kollmar, S. J. R. Lee, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, B. Mussard, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. A. Peterson, K. Pflüger, R. Pitzer, I. Polyak, P. Pulay, M. Reiher, J. O. Richardson, J. B. Robinson, B. Schröder, M. Schwilk and T. Shiozaki, M. Sibaev, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, J. Toulouse, M. Wang, M. Welborn and B. Ziegler, MOLPRO, version 2010.1, a package of ab initio programs, see https://www.molpro.net.
132. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Molpro: a general-purpose quantum chemistry program package, WIREs Comput. Mol. Sci., 2012, 2, 242–253.
133. D. A. Kreplin, P. J. Knowles and H.-J. Werner, Second-order MCSCF optimization revisited. I. Improved algorithms for fast and robust second-order CASSCF convergence, J. Chem. Phys., 2019, 150, 194106.
134. S. Carter, I. M. Mills and N. C. Handy, The equilibrium structure of HCN, J. Chem. Phys., 1992, 97, 1606–1607.
135. A. M. Smith, S. L. Coy, W. Klemperer and K. K. Lehmann, Fourier transform spectra of overtone bands of HCN from 5400 to 15100 cm⁻¹, J. Mol. Spectrosc., 1989, 134, 134–153.
136. A. G. Császár and W. D. Allen, The effect of 1s correlation on D_e, r_e, and ω_e of first-row diatomics, J. Chem. Phys., 1996, 104, 2746–2748.
137. R. M. Badger, A Relation Between Internuclear Distances and Bond Force Constants, J. Chem. Phys., 1934, 2, 128–131.
138. J. R. Durig, K. W. Ng, C. Zheng and S. Shen, Comparison of Ab Initio MP2/6-311+G(d,p) Predicted Carbon–Hydrogen Bond Distances with Experimentally Determined r₀ (C–H) Distances, Struct. Chem., 2004, 15, 149–157.
139. G. Strey and I. M. Mills, Anharmonic force field of acetylene, J. Mol. Spectrosc., 1976, 59, 103–115.
140. P. Botschwina, M. Ostwald, J. Flügge, Ä. Heyl and R. Ostwald, Ab initio spectroscopic constants and the equilibrium geometry of HCCF, Chem. Phys. Lett., 1993, 209, 117–125.
141. J. K. Holland, D. A. Newnham, I. M. Mills and M. Herman, Vibration-rotation spectra of monofluoroacetylene: 1700 to 7500 cm⁻¹, J. Mol. Spectrosc., 1992, 151, 346–368.
142. J.-L. Teffo and A. Chédin, Internuclear potential and equilibrium structure of the nitrous oxide molecule from rovibrational data, J. Mol. Spectrosc., 1989, 135, 389–409.
143. M. Kobayashi and I. Suzuki, Sextic force field of nitrous oxide, J. Mol. Spectrosc., 1987, 125, 24–42.
144. H. Lichau, C. W. Gillies, J. Z. Gillies, S. C. Ross, B. P. Winnewisser and M. Winnewisser, On the Anharmonic XCN Bending Modes of the Quasilinear Molecules BrCNO and ClCNO, J. Phys. Chem. A, 2001, 105, 10065–10079.
145. C. W. Gillies, J. Z. Gillies, H. Lichau, B. P. Winnewisser and M. Winnewisser, Gas phase detection of the unstable halofulminate BrCNO by millimeter wave spectroscopy, Chem. Phys. Lett., 1998, 285, 391–397.
146. H. Lichau, S. C. Ross, M. Lock, S. Albert, B. P. Winnewisser, M. Winnewisser and F. C. De Lucia, On the Low-Lying CCN Bending Mode of the Nearly Linear Molecule NCCNO, J. Phys. Chem. A, 2001, 105, 10080–10088.
147. B. Guo, T. Pasinszki, N. P. C. Westwood, K. Zhang and P. F. Bernath, High resolution infrared spectroscopy of cyanogen N-oxide, NCCNO, J. Chem. Phys., 1996, 105, 4457–4460.
148. T. Brupbacher, R. K. Bohn, W. Jäger, M. C. L. Gerry, T. Pasinszki and N. P. C. Westwood, Microwave Spectrum and Geometry of Cyanogen N-Oxide, NCCNO, J. Mol. Spectrosc., 1997, 181, 316–322.
149. T. Pasinszki and N. P. C. Westwood, Gas-phase generation and spectroscopy of the unstable NCCNO molecule, J. Chem. Soc., Chem. Commun., 1995, 1901–1902.
150. M. Winnewisser, E. F. Pearson, J. Galica and B. P. Winnewisser, Millimeter wave spectrum of acetonitrile oxide, CH₃CNO, in the ν₁₀ vibrational manifold: The ground state and the state v₁₀ = 1, J. Mol. Spectrosc., 1982, 91, 255–268.
151. W. G. Isner and G. L. Humphrey, Acetonitrile N-oxide. Infrared spectrum and symmetry force constants, J. Am. Chem. Soc., 1967, 89, 6442–6444.
152. T. Pasinszki and N. P. C. Westwood, Ground, Excited, and Ionic States of the NCCNO Molecule:  A HeI Photoelectron, Infrared, Ultraviolet, and ab Initio Investigation, J. Phys. Chem., 1996, 100, 16856–16863.
153. T. Pasinszki and N. P. C. Westwood, Gas-Phase Spectroscopy of the Unstable Acetonitrile N-Oxide Molecule, CH₃CNO, J. Phys. Chem. A, 2001, 105, 1244–1253.
154. B. Havasi, T. Pasinszki and N. P. C. Westwood, Gas-Phase Infrared and ab Initio Study of the Unstable CF₃CNO Molecule and Its Stable Furoxan Ring Dimer, J. Phys. Chem. A, 2005, 109, 3864–3874.
155. T. Pasinszki and N. P. C. Westwood, Unstable Chloronitrile Oxide, ClCNO, and Its Stable Ring Dimer: Generation, Spectroscopy, and Structure, J. Phys. Chem. A, 1998, 102, 4939–4947.
156. T. Pasinszki and N. P. C. Westwood, Structure and stability of fluoronitrile oxide, FCNO: A quantum-chemical study, Phys. Chem. Chem. Phys., 2002, 4, 4298–4304.
157. J. Koput, Ab Initio Prediction of the Equilibrium Structure and Vibrational−Rotational Energy Levels of Fluorofulminate, J. Phys. Chem. A, 2002, 106, 12064–12066.
158. J. Koput, An ab Initio Study on the Equilibrium Structure and XCN Bending Energy Levels of Halofulminates:  ClCNO, J. Phys. Chem. A, 1999, 103, 2170–2174.
159. T. Pasinszki and N. P. C. Westwood, Gas-Phase Generation of the Unstable BrCNO Molecule and Its Stable Dibromofuroxan Dimer. HeI Photoelectron, Photoionization Mass Spectroscopy, Mid-Infrared, and ab Initio Studies, J. Phys. Chem., 1995, 99, 6401–6409.
160. J. Koput, Ab Initio Study on the Equilibrium Structure and XCN Bending Energy Levels of Halofulminates: BrCNO, J. Phys. Chem. A, 1999, 103, 6017–6022.
161. J. Koput, Ab Initio Study on the Equilibrium Structure and CCN Bending Energy Levels of Cyanofulminate (NCCNO), J. Phys. Chem. A, 2001, 105, 11347–11350.
162. D. Poppinger and L. Radom, A theoretical study of substituted CHNO isomers, J. Am. Chem. Soc., 1978, 100, 3674–3685.
163. V. M. Rodriguez-Betancourtt, V. M. Quezada-Navarro, M. Neff and G. Rauhut, Anharmonic frequencies of [F,C,N,X] isomers (X = O,S) obtained from explicitly correlated coupled-cluster calculations, Chem. Phys., 2011, 387, 1–4.
164. S. Dalbouha, M. L. Senent, N. Komiha and R. Domínguez-Gómez, Structural and spectroscopic characterization of methyl isocyanate, methyl cyanate, methyl fulminate, and acetonitrile N-oxide using highly correlated ab initio methods, J. Chem. Phys., 2016, 145, 124309.
165. X. Zhang, A. T. Maccarone, M. R. Nimlos, S. Kato, V. M. Bierbaum, G. B. Ellison, B. Ruscic, A. C. Simmonett, W. D. Allen and H. F. Schaefer III, Unimolecular thermal fragmentation of ortho-benzyne, J. Chem. Phys., 2007, 126, 044312.
166. H. Feng and W. D. Allen, The problematic C₂H₄ + F₂ reaction barrier, J. Chem. Phys., 2010, 132, 094304.
167. A. G. Császár and W. D. Allen, The Composite Focal-Point Analysis (FPA) Approach, in Molecular Quantum Mechanics: From Methylene to DNA and Beyond, Selected Papers by H. F. Schaefer III, ed. R. J. Bartlett, T. D. Crawford, M. Head-Gordon and C. D. Sherrill, Brandon's Printing, 2010, pp. 261–265.
168. N. J. DeYonker and W. D. Allen, Taming the low-lying electronic states of FeH, J. Chem. Phys, 2012, 137, 234303.
169. S. R. Barua, W. D. Allen, E. Kraka, P. Jerabek, R. Sure and G. Frenking, Nearly Degenerate Isomers of C(BH)₂: Cumulene, Carbene, or Carbone?, Chem. – Eur. J., 2013, 19, 15941–15954.
170. M. A. Bartlett, T. Liang, L. Pu, H. F. Schaefer III and W. D. Allen, The multichannel n-propyl + O₂ reaction surface: Definitive theory on a model hydrocarbon oxidation mechanism, J. Chem. Phys., 2018, 148, 094303.
171. M. A. Bartlett, A. H. Kazez, H. F. Schaefer III and W. D. Allen, Riddles of the structure and vibrational dynamics of HO₃ resolved near the ab initio limit, J. Chem. Phys., 2019, 151, 094304.
172. P. Vermeeren, M. Dalla Tiezza, M. E. Wolf, M. E. Lahm, W. D. Allen, H. F. Schaefer III, T. A. Hamlin and F. M. Bickelhaupt, Pericyclic reaction benchmarks: hierarchical computations targeting CCSDT(Q)/CBS and analysis of DFT performance, Phys. Chem. Chem. Phys., 2022, 24, 18028–18042.
173. M. E. Lahm, M. A. Bartlett, T. Liang, L. Pu, W. D. Allen and H. F. Schaefer III, The multichannel i-propyl + O₂ reaction system: A model of secondary alkyl radical oxidation, J. Chem. Phys., 2023, 159, 024305.
174. C. E. Moore, Tables of spectra of hydrogen, carbon, nitrogen, and oxygen atoms and ions, CRC Press, 1993.
175. Active Thermochemical Tables, Version 1.122. Argonne National Laboratory, https://atct.anl.gov/Thermochemical%20Data/version%201.122/species/?species_number=392 (accessed 2024 June 21).

---

Footnotes

† Electronic supplementary information (ESI) available: Supplementary Information contains the quartic force field of linear HCNO [AE-CCSD(T)/CBS)] and the total energies for the FPA computation of D_e(HCN–O). See DOI: https://doi.org/10.1039/d4cp02700k

‡ Integrated Space Science and Technology Institute, Department of Physics, American University, 4400 Massachusetts Avenue, NW, Washington, DC, USA 20016 and Planetary Systems Laboratory, Code 693, NASA Goddard Space Flight Center, Greenbelt, MD, USA 20771.

---