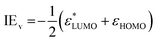Photoelectron spectra of functionalized adamantanes

Abstract

Diamondoids are a class of aliphatic molecules with cage-like structures and serve as a bridge between small hydrocarbons and large nanodiamond macromolecules. Because their optical properties are highly dependent on the size, shape, and functionalization of the carbon network, they have many applications in the fields of nanotechnology and spectroscopy. Still, much remains to understand the geometric and electronic effects induced by functionalization of diamondoids. To this end, we perform gas phase photoelectron spectroscopy (PES) of functionalized adamantanes using a helium discharge lamp as a photon source and a hemispherical electron analyzer. We present the photoelectron spectra of 1-cyanoadamantane, 1-amantadine, and 2-adamantanol and compare these to the known PES spectra of adamantane, 1-adamantanol, and urotropine, remeasured herein with improved resolution and a more thorough assignment of vibronic features, with the aid of time-dependent density functional theory calculations.

---

1. Introduction

Diamondoids are a well-known class of hydrocarbon molecules that resemble diamonds on the molecular scale, with diverse applications across photonics, materials science, and medicine due to their unique properties.^1–3 Particularly, the tunability of their optical properties based on size and functionalization makes them ideal candidates for emerging research in developing molecular building blocks for nanoscale devices.^2,4–9 Moreover, their spectroscopic characteristics exhibit intriguing correlations with unidentified infrared emission bands observed in circumstellar environments, suggesting potential astrophysical implications.^10,11 For these reasons and more, there has been a continuing focus devoted to unraveling the structural, vibrational, and optical properties of diamondoids over recent decades. With ongoing advancements in extraction and synthesis methodologies, the opportunities to study more complex diamondoids, particularly their functionalized derivatives, are more accessible than ever.^2,12

A recent application of adamantane (C₁₀H₁₆), the simplest diamondoid, as a solid propellant for Hall-effect thrusters especially highlights the value of measuring ionization energies (IE) of diamondoid derivatives.¹³ Whereas large ion thrusters typically use atomic ion propellants, such as xenon or krypton, due to their high mass-to-IE ratio, these fuels are costly and require impractical storage solutions for miniaturized spacecraft.¹⁴ Alternatively, adamantane has a similar mass as xenon with a substantially lower IE, potentially offering greater thrust efficiency. Its low molar volume is also beneficial while still having a significant vapor pressure at room temperature.¹³ The tunability of the IE of diamondoids by functionalization combined with a thorough understanding of their fragmentation patterns may provide new insights into their use as molecular propellants in the future.¹⁵

Photoelectron spectroscopy (PES) is a powerful method to study the electronic properties of molecules in all states of matter. The earliest PES studies of isolated diamondoids mostly focused on comparing ionization potentials of simple diamondoids (adamantane, diamantane, triamantane) with their mono-substituted derivatives.^16–19 Schmidt presented the first He(I) PES spectrum of both adamantane and urotropine (an isoelectronic nitrogen-substituted equivalent of adamantane) in the range of 7.5–19 eV and made rough orbital assignments of the observed bands by simple SCF calculations.²⁰ This work was extended by several other experimental PES studies of adamantane,^18,21–23 as well as some functionalized adamantanes including 1-adamantanol.^9,24 The orbital structure of the amino-substituted adamantane, amantadine, was investigated by low-resolution electron momentum spectroscopy.²⁵ Furthermore, Lenzke et al. employed synchrotron total-ion-yield spectroscopy to determine the first IE of the five simplest bare diamondoids.⁵ Supporting these experimental investigations, several theoretical studies provide insight into the observed band structures.^7,26–30 One important outcome of these studies is that the lowest unoccupied molecular orbitals (LUMO) and the LUMO+n orbitals of diamondoids exhibit Rydberg-like character.¹⁹ For adamantane, the energy gap between the highest occupied molecular orbital (HOMO) and the LUMO is larger than 6 eV.^4,31 The gap becomes smaller as the size of the cage network increases, generally following the principle of a delocalized particle in a three-dimensional box model where the boundary conditions are determined by the cage surfaces.^4,5 Thus, diamondoids are excellent analytes for exploring the tunability of optical properties in nanomaterials. The interesting consequence of the large optical gaps in diamondoids is that the absorption spectra for their open-shell cations closely correspond to the PES spectra of the neutral species (after accounting for the first ionization energy) because typically the first several excited states are transitions of the form HOMO ← HOMO−n.^26,32,33 Recently, our group recorded the first optical spectra of the adamantane,³⁴ diamantane,³⁵ and 1-cyanoadamantane³⁶ cations in the gas phase by electronic photodissociation spectroscopy (EPD) using a cryogenic ion trap. In each case, the spectra exhibit broad absorption bands with widths between 1 and 2 eV. After ruling out other factors, the broadness of the bands is attributed to ultrafast relaxation (<100 fs) of the excited states and Franck–Condon (FC) congestion of close-lying vibronic excitations. This was further supported by measurements of Ada⁺ doped into helium-droplets using electronic spectroscopy, which ensures a low-temperature environment of 0.37 K and can observe electronic states below the dissociation limit.³² It is peculiar that the EPD spectrum of the adamantane cation closely resembles previous PES spectra of adamantane despite large differences in the resolution achieved by the two methods (4–8 vs. 320–400 cm⁻¹, respectively) and differences in selection rules.^9,34 Fundamentally, the two methods differ in that PES probes the excited ionic states by measuring the kinetic energy of electrons ejected from neutral molecules, whereas EPD first ionizes the neutral and then excites the cation ground state by absorption of a photon. It is known at least for amantadine (C₁₀H₁₅NH₂) and cyanoadamantane (C₁₀H₁₅CN), which are functionalized derivatives of adamantane, certain ionizing conditions can cause the adamantyl cage to open, as revealed by infrared photodissociation (IRPD) spectroscopy, which results in more than one isomer and contaminates the spectrum.^37–39 PES has the advantage that no measurement is directly made of the nascent ion, meaning that if the cage opens after ionization, it has no effect on the PES spectrum. Nevertheless, considering that absorption spectra of diamondoid cations are remarkably broad at low temperatures, it remains an open question whether high-resolution PES techniques are able to further resolve vibronic features. To our knowledge, only adamantane has been measured by threshold PES, which can discriminate the kinetic energy of photoelectrons with a resolution below 1 meV.²⁹ However, the relatively large step size (13 meV) limited this study from interpreting the broad nature of the band representing the cation ground state. Therefore, further high-resolution investigations are necessary to elucidate the effect of lifetime broadening in the PES spectra of diamondoids.

Within this work, we present the He(I) ultraviolet PES spectra of four functionalized derivatives of adamantane (Ada), namely, 1-amantadine (AdNH₂), 1-cyanoadamantane (AdCN), 1-adamantanol (1-AdOH), and 2-adamantanol (2-AdOH). Among these, the PES spectra of AdNH₂, AdCN, and 2-AdOH are presented for the first time. Additionally, the influence of the functional groups on the adamantyl cage is explored by comparing the Ada derivatives with remeasured spectra of Ada and urotropine (Uro), which is isoelectronic to Ada but has all four CH groups of the cage substituted by N atoms. The experimental spectra are presented together with a detailed analysis of the cation ground state (D₀) using Franck–Condon (FC) simulations based on density functional theory (DFT) calculations. The DFT calculations are also used within the framework of Koopman's Theorem (KT) to assign the higher-energy bands arising from excited electronic states of the cation (D_n, where n is the number of the state). In parallel, time-dependent (TD)-DFT calculations determine vertical excitation energies (E_v) to the higher ionic states from the cation ground state in both the optimized neutral (D_n ← D₀*) and cation (D_n ← D₀) geometries. Finally, we analyze the resultant Kohn–Sham molecular orbitals (MOs) and natural transition orbitals (NTOs) to correlate the first 12 ionic states of Ada to the ionic states of each molecule, providing further insight into the effects induced by the functional groups on the electronic and optical properties of the adamantyl cage.

2. Experimental and computational techniques

2.1. Experimental

The PES spectra are measured with a Scienta SES-2002 photoelectron spectrometer equipped with a hemispherical electron analyzer.^9,23 A helium lamp (SPECS UVS 10/35) provides a collimated beam of quasi-monoenergetic photons with an energy of 21.22 eV (He(I), ≥95% contribution). The instrument is configured with a pass energy of 20 eV and a curved entrance slit width of 0.8 mm to achieve a resolution of 38–40 meV, as measured for the spin–orbit coupling components of gaseous Xe (Air Liquide, 99.995% purity) at 12.130 (²P_3/2) and 13.433 (²P_1/2) eV.⁴⁰ These peaks also serve to calibrate the energy scale and optimize the signal intensity prior to measuring the diamondoid samples. Average error of the calibration peaks is typically 4–5 meV, close to the stepsize of the electron energy analyzer of 3.74 meV. Measurements are taken at a speed of five frames per second between 7.5 and 15 eV (18 eV for Uro). Each sample is then measured 30 times and the scans are accumulated to increase the signal-to-noise ratio. For each measurement, a small amount of powdered sample (Sigma Aldrich) is loaded into a sample holder contained within the vacuum chamber prior to evacuating to 5 × 10⁻⁷ mbar. The sample holder is mounted onto a translatable stage that can be heated up to 200 °C by a resistively heated oven to increase the vapor pressure of the sample. The temperature is increased until a static pressure of (2–5) × 10⁻⁵ mbar is reached (Ada: 25 °C; AdCN: 65 °C, AdNH₂: 35 °C, 1-AdOH: 60 °C, 2-AdOH: 60 °C, Uro: 70 °C). The resulting gas then exits through a small nozzle that is positioned to align horizontally with the photon beam and vertically with the entrance lenses of the electron analyzer.

2.2. Computational

Features in the PES spectra are assigned with the aid of DFT calculations.⁴¹ We compare the results computed with several dispersion-corrected DFT functionals, namely B3LYP,⁴² CAM-B3LYP,⁴³ B3PW91,⁴⁴ and M06-2X,⁴⁵ using the cc-pVTZ basis set.^46,47 For the M06-2X functional, Grimme's dispersion correction (D3)⁴⁸ is included while the other functionals also incorporate Becke–Johnson damping factors (D3BJ).⁴⁹ The spin-restricted (R) formalism is used for neutral species, whereas the cation structures are optimized using the unrestricted (U) formalism. First, the geometry of the neutral species in its electronic ground state (S₀) is optimized and its minimum on the potential energy surface is verified by harmonic frequency analysis. This calculation provides the minimum electronic energy of the neutral structure (E_n) and the harmonic zero-point energy (ZPE_n) correction. Then, an electron is removed, and both the vertical ionization energy (IE_v) and the ZPE-corrected adiabatic ionization energy (IE_a) is determined. We follow similar methods and formalisms used in previous theoretical diamondoid studies for these values (Fig. S1, ESI†).^26,30 Briefly, IE_v is defined as

IE_v = E₊* − E_n,

where E₊* is the energy of the cation in the optimized neutral geometry (S₀). This structure is subsequently optimized to find the minimum energy (E₊) and ZPE correction (ZPE₊) of the D₀ cation ground state, again verified by harmonic frequency analysis. IE_a is then given as

IE_a = E₀ + ΔZPE,

where E₀ is the minimum adiabatic separation energy between E₊ and E_n and ΔZPE is the difference between ZPE₊ and ZPE_n. From these values, the relaxation energy (E_rel) of the cation ground state is obtained by

E_rel = IE_v − E₀.

By these equations, the relationship between IE_a and IE_v is thus

IE_v = IE_a + E_rel − ΔZPE.

In some cases, IE_a values can be determined experimentally by PES when the FC factor between the ground vibrational states of both the neutral and cation is large (i.e., their geometries are similar). For large organic molecules like diamondoids, however, the bands observed are often broad and convoluted from close-lying vibrational and/or electronic states, making only determinations of IE_v values possible. Herein, we make assignments of the ionic states observed in the PES spectra using three methods: (i) an application of KT to Kohn–Sham DFT orbitals, (ii) TD-DFT calculations of vertical excitations (E_v) of the cation in the optimized neutral geometry (D₀*), and (iii) TD-DFT of the cation in its relaxed geometry (D₀). In the first method, we analyze the canonical molecular orbitals (MOs) of the neutral structure and approximate the vertical ionization energies as the negative eigenenergies (−ε) of the MOs. Previous applications of this method, however, have been shown to not accurately estimate the IE_v values observed in the experimental PES spectra of many diamondoids.²³ It is generally understood that employing Kohn–Sham orbitals to predict IE values can be prone to many errors and typically underestimates them,⁹ although certain functionals perform better than others depending on how the electron exchange correlation is handled, among other factors. The second approach uses TD-DFT at the same computational level to determine transition energies into higher electronic states from D₀*, following the Born–Oppenheimer approximation. The E_v values are then shifted by the vertical S₀ → D₀* ionization energy. The last method using TD-DFT calculations from D₀ is more applicable to EPD spectra of the cations. Nonetheless, these results are provided in ESI† for comparison.

Correlating the ionic states assigned by TD-DFT to the MOs of the neutral is feasible by also calculating natural transition orbitals (NTOs). These calculations show that in nearly every case, the ionic states relevant to the energy range of the PES spectra consist of transitions involving only two orbitals with significant contribution and are always of the type SOMO ← SOMO−n, where SOMO refers to the semi-occupied molecular orbital. We also shift the eigenenergies of the MOs such that −ε_HOMO matches the vertical S₀ → D₀* ionization energy (IE_v + ε_HOMO).

To provide a more complete assessment of the lowest-energy PES bands and assign vibronic features, we also carry out FC simulations for the D₀ ← S₀ transition at the same temperature as the experiment.⁴¹ The obtained stick spectra are then convoluted with a Gaussian line profile having a FWHM of 40 meV to match the resolution of the PES spectrometer. Efforts to optimize the geometries of the excited cation states have been mostly unsuccessful, as has been reported in other studies, likely due to conical intersections and vibronic coupling with nearby states.^{26,30,33,34,50} Thus, a full FC analysis for transitions into higher ionic states is not considered and beyond the scope of the present work.

3. Results and discussion

The PES spectra, along with the structures of all six molecules, are compared in Fig. 1 and are arranged from top to bottom in order of decreasing first IE_v. With the exception of Uro, the spectra for all functionalized molecules show similar band structures as Ada in the measured energy range and the largest differences are observed in the first bands representing the ground states of the respective cations. Due to FC congestion, lifetime broadening, and Jahn–Teller (JT) effects, many of the electronic bands overlap and create broad and unresolved profiles that are difficult to interpret in detail at the current resolution. Comparing the spectra in Fig. 1, the first observation is the substantial variation in the position of the lowest IE band. Clear IE_a peaks are observed only for Ada, AdCN, and Uro. For the others, the IE_a value is estimated by aligning the simulated FC spectrum with the experimental spectrum and then marking the position of the calculated 0–0 peak. Uro has the lowest IE_a at (8.03 ± 0.01) eV, followed by AdNH₂ at the estimated value of 8.27 eV. Both are significantly lower than that of Ada at (9.30 ± 0.01) eV and display bands with symmetrical FC envelopes and weak vibrational fine structure. The alcohol derivatives of Ada, 1-AdOH and 2-AdOH, lack any vibrational fine structure over the whole measured range but have an onset of the first band between 9.0 and 9.2 eV, indicating that IE_a falls in this range with a weak FC overlap for the 0–0 transition. Finally, AdCN has a prominent IE_a peak at the relatively high energy of (9.78 ± 0.01) eV, and the remaining spectrum has several corresponding features with the Ada spectrum that appear blue shifted by approximately 0.5 eV. Thus, the IE_a values spread over an energy range of (1.75 ± 0.02) eV through either functionalization or modification of the adamantane cage. A thorough description of each spectrum is provided in Sections 3.1–3.6.

Fig. 1 PES spectra and structures of AdCN, Ada, 2-AdOH, 1-AdOH, AdNH₂, and Uro. The spectra are arranged by decreasing first IE_v energy, and discernable IE_a peaks with their position values are marked by an arrow. IE_a values in parentheses are derived from FC simulations. Due to many overlapping bands, orbital assignments are approximately positioned near the energies predicted by DFT calculations (see Sections 3.1–3.6), and those which are calculated to be nearly degenerate are grouped in parentheses. Orbitals in red are primarily attributed to the respective functional groups or isoelectronic substitution (Uro). An extended PES spectrum of Uro recorded up to 18 eV is available in Section 3.6.

The calculated IE_a values, using various DFT functionals, are compared in Table 1 to the experimental IE_a values. While the B3LYP functional is commonly used in diamondoid studies,^{7,9,22,28,51,52} the M06-2X functional consistently predicts the IE_a value closest to its experimental value.²³ In every case besides 2-AdOH, the difference between calculation and experiment (ΔIE_a) is 0.2 eV or less. When assuming the local maximum of the first PES bands in each spectrum represents the experimental vertical S₀ → D₀* ionization energy, the IE_v values calculated with the M06-2X functional are in excellent agreement (Table 2). Only the calculated IE_v values for Ada and AdCN differ more than 0.12 eV from the experimental IE_v. These molecules also have considerably larger ΔZPE corrections by a factor of 2 to 3 compared to the other molecules. This may be related to JT activity as these molecules exhibit broadening in their spectra due to JT distortion and thus IE_v is more difficult to extract precisely from experiment.^34,36 Nonetheless, their calculated IE_v values are also within 0.1–0.2 eV when considering the center of the bands as a better representation of the experimental IE_v. Overall, the relaxation energy is rather large for all diamondoids considered, E_rel = 0.43–0.77 eV, indicative of their large geometry changes upon ionization.

Table 1 Comparison of experimental IE_a values with calculated IE_a values at various DFT levels^a

Molecule	Exp.	B3LYP	CAM-B3LYP	B3PW91	M06-2X
a All values are given in eV. Values in parentheses are estimated.
Ada	9.30	8.82	9.06	8.78	9.10
AdCN	9.78	9.31	9.65	9.28	9.67
AdNH2	(8.27)	7.89	8.05	7.87	8.17
1-AdOH	(9.03)	8.59	8.78	8.56	8.87
2-AdOH	(9.17)	8.51	8.71	8.51	8.81
Uro	8.03	7.77	7.95	7.76	8.08

---

Table 2 Determination of various energies at the M06-2X(D3)/cc-pVTZ level^a

Energies	Ada	AdCN	AdNH2	1-AdOH	2-AdOH	Uro
a All values are given in eV. Values in parentheses are estimated. b ΔIEv = IEv − Exp. IEv. c ΔIEa = IEa − Exp. IEa.
E 0	9.39	9.91	8.23	8.96	8.90	8.12
ΔZPE	−0.29	−0.24	−0.06	−0.09	−0.09	−0.04
−εHOMO	8.98	9.52	8.09	8.75	8.85	7.77
	10.70	11.18	9.86	10.36	10.52	9.49
	9.84	10.35	8.97	9.56	9.68	8.63
IEv	9.83	10.34	8.88	9.54	9.67	8.60
Exp. IEv	9.46 ± 0.01	10.10 ± 0.02	8.89 ± 0.06	9.52 ± 0.05	9.58 ± 0.05	8.48 ± 0.05
ΔIEv^b	0.37	0.24	−0.01	0.02	0.09	0.12
IEv + εHOMO	0.86	0.82	0.79	0.79	0.83	0.84
E rel	0.45	0.43	0.65	0.58	0.77	0.48
IEa	9.10	9.67	8.17	8.87	8.81	8.08
Exp. IEa	9.30 ± 0.01	9.78 ± 0.01	(8.27)	(9.03)	(9.17)	8.03 ± 0.01
ΔIEa^c	−0.20	−0.11	−0.10	−0.16	−0.36	0.05

---

Table 2 also compares IE_v to −ε of the HOMO, which should agree according to KT. Here again, the M06-2X functional yields values closest to the experimental IE_v and there is a close agreement between the vertical S₀ → D₀* ionization energy (IE_v in Table 2) and −ε. For example, the vertical S₀ → D₀* ionization energy of Ada is 9.83 eV and −ε of the 7t₂ orbital is 8.98 eV (Table 2). These values are notably more similar than for B3LYP or B3PW91. B3LYP yields a vertical S₀ → D₀* ionization energy of 9.43 eV, while −ε_HOMO is only 7.60 eV. CAM-B3LYP yields values with closer agreement than M06-2X (−ε_HOMO = 9.15, IE_v = 9.77 eV), but still gives less accurate IE_a values than M06-2X when compared to experiment (Table 1). After shifting the MO eigenenergies by 0.85 eV (IE_v + ε, Table 2), the KT model using M06-2X is in excellent agreement with the measured spectrum (Section 3.1), and this holds true for all functionalized adamantanes studied herein as well. It has been reported that for large molecular systems, IE_v + ε approximates the classical Coulomb electrostatic energy needed to remove an electron from the system, which is not accurately handled in the calculation of DFT Kohn–Sham MO eigenenergies.⁵³ Additionally, if the MO is generally delocalized over a large molecule, IE_v can also be approximated by

where is the eigenenergy of the unoccupied β orbital belonging to the SOMO of the D₀* cation in an unrestricted DFT single-point energy calculation. These values are also reported in Table 2 for comparison with IE_v and −ε_HOMO values, along with other relevant energies.

3.1. Adamantane (Ada)

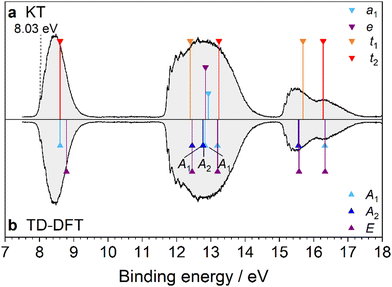
Although the PES spectrum of Ada has been measured extensively in previous works,^{18,20–22,29} we include our remeasured spectrum for comparison with the functionalized adamantanes and an improved computational assignment. The spectrum in Fig. 2 is mirrored to compare the assignments of the bands using (i) KT (Fig. 2a) and (ii) TD-DFT (Fig. 2b), and all other PES spectra are presented in the same manner. At the M06-2X level, the electronic configuration of Ada is

…(5a₁)²(5t₂)⁶(1t₁)⁶(6t₂)⁶(3e)⁴(2t₁)⁶(7t₂)⁶

and corresponding assignments in the PES spectrum are included in Fig. 1. The distortion of bond lengths and bond angles in Ada upon ionization has been investigated in several previous studies using various DFT functionals and basis sets.^26,54–56 As our results do not provide further structural insights, we do not discuss them in detail here. It is essential, however, to highlight that the degenerate orbitals of neutral Ada are subject to JT splitting upon ionization, and the symmetry of the cation is lowered from T_d to C_3v.⁵⁴ By nature of the symmetry correlation rules for these point groups, the degenerate orbitals in T_d split in C_3v according to: t₁ → a₂ + e, t₂ → a₁ + e, e → a₁ + a₂.

Fig. 2 PES spectrum of Ada combined with DFT analysis. In panel (a), the spectrum is assigned by the KT method, wherein the IE_v values are approximated by the negative eigenenergies of the MOs of neutral Ada at the M06-2X/cc-pVTZ level (−ε). In panel (b), the same level of theory is used to calculate the vertical transition energies from D₀* into the excited ionic states using TD-DFT. The transition energies are then shifted by the calculated IE_v (9.83 eV). The MO eigenvalues in (a) are shifted by 0.85 eV to have the same origin as the TD-DFT method. The peak at 12.6 eV (marked by an asterisk) is attributed to water contamination in the vacuum chamber.

The PES spectrum reveals four broad bands between 9 and 15 eV, with an evident 0–0 peak appearing at (9.30 ± 0.01) eV. This value matches IE_a reported previously^19,57 and is consistent with the generally accepted value of (9.25 ± 0.04) eV.⁵⁸ The first band, appearing between 9.2 and 10.6 eV, is assigned to ionization from the triply degenerate 7t₂ HOMO, which has mainly CC bonding character (Fig. S2, ESI†), and results in the ²A₁ ground state (D₀) and a ²E first excited state (D₁, Table S1, ESI†). The second band in the PES spectrum lies between 10.6 and 12.4 eV and is attributed to close-lying ionic states (D₂–D₅) caused by ionization from the 2t₁ and 3e orbitals, which are also CC bonding orbitals. The third band has contributions from the two triply degenerate orbitals, 6t₂ (D₆/D₇) and 1t₁ (D₈/D₉), with σ_CH and π_CH2 bonding character, respectively. Vibronic peaks also appear between 12.8 and 13.1 eV but are not well resolved. Finally, the fourth band, appearing near 14.8 eV, is small and featureless and is assigned to ionization from the close-lying 5t₂ (D₁₀/D₁₁) and 5a₁ (D₁₂) orbitals, having π_CH2 and σ_CH bonding character, respectively. Also observed is a small peak at 12.6 eV (marked by an asterisk in Fig. 2a), arising from minor water contamination in the vacuum chamber.⁵⁹

Small differences exist between the KT and TD-DFT models, especially when considering degenerate ionic states. For example, the first transition of the cation, described as D₁(²E) ← D₀*(²A), has E_v = 0.06 eV (Table S1 and Fig. S3, ESI†). Both Candian et al.²⁹ and Roy et al.³⁰ also calculated D_n ← D₀* vertical transitions of Ada using TD-DFT and report similar values. This discrepancy between the ground state and first excited states does not accurately adhere to what should be a symmetry-imposed degeneracy in the D₀* (T_d) geometry. However, it is a known artifact of linear response DFT, which gives different and somewhat unbalanced treatments to calculating ground state and excited state energies, and this issue has been meticulously discussed elsewhere.⁶⁰ A far more pronounced splitting of these states is calculated for the D₁(²E) ← D₀(²A₁) transition of the cation (E_v = 1.16 eV) and is the result of its reduced symmetry resulting from JT distortion.³⁴ This value has been verified experimentally by Kappe et al. (E_v = 1.12 eV) for cold Ada⁺ ions doped into superfluid helium nanodroplets.³² Regarding the second band, the KT model predicts the 2t₁ orbital to be slightly higher in energy than the 3e orbital, although previous assignments suggest the order is dependent on the level of theory.^18,21,22 The TD-DFT approach indicates that the 2t₁ and 3e orbitals undergo splitting and the resulting four ionic states (two ²A₂, one ²A₁, and one doubly degenerate ²E) of the cation overlap. Again, the ionic states are more separated at the relaxed cation geometry.³⁴ Ultimately, an accurate ordering is nontrivial using computational methods alone, and the resolution of the PES spectrum is insufficient to distinguish a separation of these ionic states. Although neither KT nor TD-DFT can explain the broad nature of the bands, Gali et al. employed a many-body perturbation theory (MBPT) approach to demonstrate convincingly that Ada and other diamondoids exhibit strong electron-vibration coupling in addition to JT distortion, and these effects give rise to various satellite peaks that further broaden the bands,²⁷ in addition to FC congestion (unresolved (ro)vibrational structure) and possibly lifetime broadening.³⁴

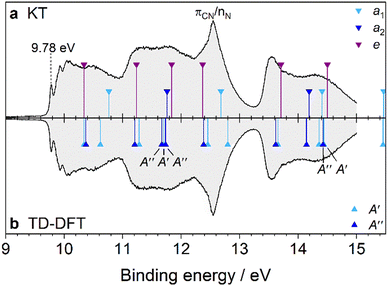
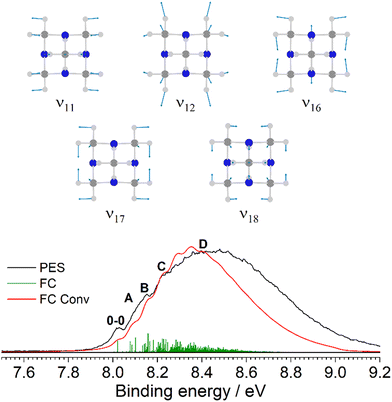
Fig. 3 provides an expanded view of the PES spectrum of Ada in the energy range between 9 and 10 eV. The 0–0 peak at 9.30 eV (IE_a) has a FWHM of 49 meV, which is slightly broader than the Xe calibration peaks and likely due to sequence hot bands and unresolved rotational structure. Subsequently, four vibronic peaks, labeled A–D, are observed toward higher energy at 9.40, 9.46, 9.55, and 9.63 eV (810, 1290, 2020, 2660 cm⁻¹ above 0–0), respectively. In previous analyses, similar progressions are also reported, but a wide range of values are given by Schmidt²⁰ (734 and 1175 cm⁻¹), Kovac and Klasinc²¹ (800 and 1260 cm⁻¹), and Candian et al.²⁹ (900 and 1284 cm⁻¹). The FC analysis of the band, represented by the green stick spectrum, is convoluted with a Gaussian line profile (FWHM = 40 meV) to simulate the PES spectrum (red). The results are shifted to align the origin at 9.30 eV. Although the simulated peaks do not closely resemble the measured spectrum in their relative intensities (particularly for the underestimated 0–0 peak), their positions on the binding energy scale are in good agreement and adequately allow for a vibrational assignment. We also note that no contribution from hot bands is observable at 300 K, which is reflected by the simulation. Peaks A and B arise from two fundamental modes, 12¹₀ (ν₁₂ = 886 cm⁻¹) and 9¹₀ (ν₉ = 1270 cm⁻¹), both of which are symmetric C–C stretching modes combined with C–H bending motions. These modes correspond to JT active vibrations that are excited upon ionization and reduce the high symmetry by distorting the cage. Peak C arises mostly from the 9¹₀12¹₀ combination band while peak D is attributed to the 9²₀ overtone. More combination bands and overtones of these modes contribute to the band intensity toward higher energy but become congested and therefore unresolved in the measured spectrum (Table S2, ESI†). Additionally, a broader satellite feature appears near 10 eV (peak E). This feature corresponds to the satellite peak described by Gali et al. and is attributed to electron coupling with 43 different vibrational modes, with the largest contribution belonging to a t₂ twisting mode with an energy of 78.2 meV (630 cm⁻¹).²⁷ Nevertheless, a Born–Oppenheimer approach as used here still performs considerably well to interpret the major vibronic features below this satellite peak.

Fig. 3 The D₀(²A₁) ← S₀(¹A₁) transition band from the PES spectrum of Ada (black) compared to the simulated FC stick spectrum (green) at 300 K, which is convoluted with a FWHM of 40 meV (red). The observed vibronic features are assigned to the calculated vibrational modes ν₉ = 1270 and ν₁₂ = 886 cm⁻¹.

3.2. Cyanoadamantane (AdCN)

The PES spectrum of AdCN shown in Fig. 4 is the first to be reported for this molecule. As stated, the EPD spectrum of AdCN⁺ was recently reported,³⁶ and despite large differences in the experimental conditions including selection rules for the excited state transitions, both spectra share a similar line profile (Fig. S16, ESI†). There are still notable differences, with the largest being that EPD provides no information of the cation ground state, which is readily observed in the PES spectrum. The electronic configuration of AdCN is

…(11a₁)²(7e)⁴(12a₁)²(8e)⁴(13a₁)²(1a₂)²(9e)⁴(14a₁)²(10e)⁴(11e)⁴(2a₂)²(12e)⁴(15a₁)²(13e)⁴

and corresponding bands in the PES spectrum are labeled in Fig. 1. Thus, it possesses an additional four valence MOs compared to Ada, three of which are predicted to be observable in the measured energy range (both π_CN and n_N). The H → CN substitution at the 1-position of the adamantyl cage reduces the tetrahedral symmetry of Ada from T_d to C_3v in AdCN, and the 13e HOMO and 15a₁ HOMO−1 in AdCN correspond to the triply degenerate 7t₂ HOMO of Ada (Fig. 4a). Ionization of AdCN also leads to JT distortion, and the point group is further lowered from C_3v to C_s.^36,39 Thus, the TD-DFT model predicts that all degenerate ionic states are split in the cation and the 13e HOMO further splits into a′ and a′′ orbitals (Fig. 4b). A detailed description of the changes in bond angles and bond lengths of AdCN⁺ upon ionization has been previously discussed at the (u)B3LYP-D3BJ/cc-pVTZ level,^36,39 and there are only negligible differences using the M06-2X functional. At the relaxed cation geometry, the CN group bends slightly toward one of the adjacent CH₂ groups, and the C–H bond within the mirror plane is elongated to produce a characteristic low-frequency stretching mode that was recently measured spectroscopically.³⁹

Fig. 4 PES spectrum of AdCN assigned by DFT. In panel (a), the spectrum is assigned by the KT method. In panel (b), TD-DFT is used to calculate the vertical transition energies of AdCN⁺ in the D₀* geometry. The transition energies are shifted by the calculated first IE_v (10.34 eV). The MO eigenvalues in (a) are then shifted by 0.82 eV to have the same origin as the TD-DFT method.

Like Ada, the PES spectrum of AdCN exhibits a well-pronounced IE_a band, which lies at (9.78 ± 0.01) eV. To our knowledge, it possesses the highest IE_a of any measured pristine or monosubstituted diamondoid to date, due to the small size of the cage relative to higher order diamondoids and the strong inductive effect of the nitrile group.^4,9 In the measured energy range, five overlapping bands appear with only the first exhibiting clear vibronic features. This band spans between 9.7 and 10.8 eV and is analogous to the first band of Ada. It is the result of ionization from the 13e and 15a₁ orbitals, which are CC bonding orbitals from the adamantyl cage (Table S3 and Fig. S4, ESI†). An expanded view is given in Fig. 5 and the interpretation is again aided by a FC simulation. The convolution of the stick spectrum with 40 meV FWHM yields a band contour (red) that is in excellent agreement with the measured spectrum, although the strength of the origin peak is underestimated, as is the case for Ada (Table S4, ESI†). Again, we see no clear evidence of hot bands at 340 K, except that the 0–0 band is slightly broader than the Xe calibration peak when fitted with a Gaussian profile (47 vs. 40 meV). Four vibronic peaks, labeled A–D, can be distinguished toward higher energy. Peak A appears as a shoulder of peak B near 9.88 eV (+810 cm⁻¹) and is assigned to two close-lying fundamental vibrations, 52¹₀ (ν₅₂ = 848 cm⁻¹) and 50¹₀ (ν₅₀ = 890 cm⁻¹). Peak B, with its maximum at 9.93 eV (+1210 cm⁻¹), is attributed to mode 33¹₀ (ν₃₃ = 1221 cm⁻¹). Peak C at 10.03 eV (+2020 cm⁻¹) is therefore assigned to the combination bands 33¹₀52¹₀, 33¹₀50¹₀ and peak D near 10.08 eV (+2420 cm⁻¹) is the 33²₀ overtone. These strongly FC active modes are along the cage-opening coordinates.³⁹ Another feature with a local maximum near 10.5 eV is primarily assigned to ionization from 15a₁, which has a calculated IE_v of 10.76 eV according to KT or 10.62 eV by TD-DFT. Vibronic coupling that dynamically induces JT distortion could also contribute to this feature, as it resembles the satellite peak previously investigated by MBPT in the Ada spectrum at 10.0 eV.²⁷ It likewise appears approximately 0.7 eV above the first IE_a. However, a thorough investigation of these effects is beyond the scope of our study.

Fig. 5 The D₀(²A) ← S₀(¹A₁) transition band from the PES spectrum of AdCN (black) compared to the simulated FC stick spectrum (green) at 340 K, which is convoluted with a FWHM of 40 meV (red). The observed vibronic features are assigned to the calculated vibrational modes ν₃₃ = 1221, ν₅₀ = 890, and ν₅₂ = 848 cm⁻¹.

The second PES band, spanning between 10.8 and 13.2 eV, is comparable to the second band in the PES spectrum of Ada, as the 2t₁ and 3e orbitals in Ada correlate with the 12e + 2a₂ and 11e orbitals in AdCN, respectively. However, the nearly degenerate nature of the 2t₁ and 3e orbitals in Ada is lost in the corresponding orbitals of AdCN. Substituting one of the primary H atoms in Ada with a CN group results in two of the eigenstates of the 2t₁ orbital to mix with the π orbitals of the nitrile group to form the degenerate 12e orbital of AdCN (Fig. S5, ESI†). The 2a₂ orbital of AdCN correlates with the remaining 2t₁ eigenstate of Ada. Since its Kohn–Sham MO exhibits no CN character, it stands to reason that the 2a₂ orbital possesses a similar energy gap from the 13e HOMO as the 7t₂/2t₁ gap in Ada (1.40 vs. 1.35 eV). Additionally, mixing of the π orbitals of the nitrile group with those of the cage effectively lowers the binding energy of the 12e electrons by 0.52 eV according to the KT model. These arguments then satisfyingly explain the broader nature of the second band in the AdCN spectrum compared to that of Ada.

In the range of 12–13 eV occurs an overlapping and more prominent peak, which is unique to the AdCN spectrum. To interpret this feature, we compare the spectrum to that of acetonitrile (CH₃CN), which is a simple alkyl nitrile wherein the adamantyl cage of AdCN (C₁₀H₁₅) is replaced by CH₃. The PES spectrum of CH₃CN exhibits two bands that lie close together between 12 and 13.5 eV.⁶¹ The first contains a distinct progression of peaks and is assigned to removal of a bonding π_CN electron. The second is a sharp, “needle-like” band and is typical for an electron being ejected from the nonbonding nitrogen lone pair (n_N). In fact, it is generally observed that alkyl nitriles exhibit broader FC-active π_CN bands lying slightly below a narrow n_N band, and AdCN appears to behave similarly.⁶² As the size of the alkyl group increases, the bands attributed to the CC and CH orbitals decrease in binding energy and eventually obscure the n_N band, as in tertbutylnitrile, (CH₃)₃CCN.⁶³ Both the KT and TD-DFT models predict 10e to lie 0.3–0.4 eV above 14a₁. We therefore rationalize that in the AdCN spectrum, the broadness of the peak, especially on the low-energy side, is likely due to ionization from the 10e orbitals with π_CN character (Fig. S4, ESI†). However, this assignment is stated with some reservation as no corresponding resolved features are clearly discernable in the measured spectrum. This would leave the sharp peak at 12.55 eV to be assigned to ionization from the 14a₁ orbital, occupied by the n_N lone pair electrons.

Lastly, several overlapping transitions are observed between 13.3 and 15.0 eV, yielding a contour that resembles the bands belonging to the 6t₂ and 1t₁ orbitals of Ada but without displaying any vibronic features. These are attributed to ionic states resulting from ionization of the 9e, 1a₂, 13a₁, and 8e orbitals. The 9e and 13a₁ orbitals correlate with 6t₂ of Ada and are separated by 0.70 eV, whereas 1a₂ and 8e correlate with 1t₁ of Ada. From the TD-DFT perspective, transitions into the D₁₁(²A′′) and D₁₂(²A′) ionic states (corresponding to the JT-split 9e orbitals) are nearly isoenergetic to the D₆(²E) ← D₀*(²A₁) transition in Ada⁺ (Fig. S5, ESI†). This again is because the 9e orbitals have essentially no influence from the CN group. The 13a₁ orbital, however, exhibits strong mixing between the σ_CN orbital of the nitrile group with one of the 6t₂ orbitals in Ada, which increases the binding energy of the occupying electrons.

3.3. Amantadine (AdNH₂)

The pyramidal amino group in AdNH₂ reduces the symmetry of Ada from T_d to C_s, yielding only nondegenerate orbitals (Table S5, ESI†). AdNH₂ has the electronic configuration

…(16a′)²(17a′)²(18a′)²(19a′)²(8a′′)²(20a′)²(9a′′)²(21a′)²(10a′′)²(22a′)²

(11a′′)²(23a′)²(12a′′)²(24a′)²(13a′′)²(14a′′)²(25a′)²(26a′)²(15a′′)²(27a′)²

and corresponding bands in the PES spectrum are labeled in Fig. 1. Three of these valence orbitals are unique to AdNH₂ compared to Ada with orbital character analogous to the n_N and π_NH2 orbitals of NH₃. Litvinyuk et al. provided the only previous investigation of the AdNH₂⁺ ionic states using low resolution electron momentum spectroscopy.²⁵ They conclude that the 27a′ HOMO of AdNH₂ mainly manifests as the nonbonding lone pair from N, with a binding energy roughly measured at 8.6 eV. George and Dopfer explored the geometry of the cation and its solvated clusters by IRPD spectroscopy and found ionization into the D₀(²A′) ground state distorts the pyramidal NH₂ group toward a planar configuration.^37,38,64 Additionally, the apical C–C bond within the σ_h mirror plane is severely elongated due to conjugation with the n_N orbital. A cage-opening mechanism along this bond was measured and it was determined that the π-electron-donating nature of the NH₂ group drastically lowers the barrier of the reaction compared to the equivalent reaction in Ada⁺.

Fig. 6 shows the first PES spectrum reported for this molecule and four bands between 8 and 15 eV are observed. The first band is weakest in intensity and is a symmetrical FC band exhibiting weak, yet still visible vibronic structure on the low-energy side. It is similar to the lowest-lying band observed in the PES spectra of many alkyl amines that assign the HOMO to the localized lone pair electrons of the NH₂ group (n_N character). Unlike Ada, IE_a is not easily determined due to the broad, gradual rise of the band profile, which begins to increase near 8.30 eV. Five vibronic peaks can be identified (labeled A–E), which progressively become more difficult to discern, at 8.37, 8.45, 8.54, 8.62, and 8.70 eV, respectively. The spacings between the peaks are nearly uniform, with an average energy difference of 80 meV (650 cm⁻¹). The FC simulation (Fig. 7) of the cation ground state predicts the 0–0 origin to have nearly no intensity and that two vibrational progressions make significant contributions to the band intensity (Table S6, ESI†). Assuming the small peak at 8.37 eV (peak A) to be the first vibronic peak, the IE_a is calculated to lie at 8.27 eV. Peaks A–D are attributed to a progression of 36ⁿ₀ (ν₃₆ = 615 cm⁻¹), which is known as the NH₂ umbrella inversion mode. A long progression in this mode is expected because the NH₂ group becomes nearly planar in the cation upon ionization of the n_N electron. Peak E is the start of the unresolved band continuum, caused by FC congestion of many transitions. However, it is also near the calculated energy of the symmetric N–H stretching mode, 1¹₀ (ν₁ = 3505 cm⁻¹), which forms combination bands with a progression in ν₃₆ toward higher energies, further contributing to the broadness of the band. The predicted frequency of this mode is in close agreement with the fundamental determined experimentally by George and Dopfer³⁷ (3322 cm⁻¹) after applying a scaling factor of 0.95 to account for anharmonicity.

Fig. 6 PES spectrum of AdNH₂ assigned by DFT. In panel (a), the spectrum is assigned by the KT method. In panel (b), TD-DFT is used to calculate the vertical transition energies of AdNH₂⁺ in the D₀* geometry. The transition energies are shifted by the calculated IE_v (8.88 eV). The MO eigenvalues in (a) are then shifted by 0.79 eV to have the same origin as the TD-DFT method. The peak at 12.6 eV (marked by an asterisk) is attributed to water contamination in the vacuum chamber.

Fig. 7 The D₀(²A′) ← S₀(¹A′) transition band from the PES spectrum of AdNH₂ (black) compared to the simulated FC stick spectrum (green) at 310 K, which is convoluted with a FWHM of 40 meV (red). The observed vibronic features are in close agreement with the calculated vibrational frequencies ν₁ = 3505 and ν₃₆ = 615 cm⁻¹.

The next three bands in the spectrum have a similar appearance as the first three bands in the PES spectrum of Ada, signaling that the MOs giving rise to these features are mainly localized on the adamantyl cage. Inspection of the Kohn–Sham MOs (Fig. S6, ESI†) and NTOs (Fig. S7, ESI†) illustrates the correlation between the 7t₂ HOMO of Ada with the orbitals 15a′′, 26a′, and 25a′ in AdNH₂. Furthermore, the other orbitals of Ada correlate with those in AdNH₂ as (i) 2t₁ → 14a′′ + 13a′′ + 23a′, (ii) 3e → 24a′ + 12a′′, (iii) 6t₂ → 11a′′ + 22a′ + 21a′, (iv) 1t₁ → 10a′′ + 9a′′ + 20a′, and (v) 5t₂ → 8a′′ + 19a′ + 18a′. Such correlations were also discussed by Litvinyuk et al., but with the assumption that the order of the correlating MOs between Ada and AdNH₂ is the same.²⁵ They argue that because several of the split orbitals in AdNH₂ are still quasi degenerate, the ionic states are separated by large gaps even at their low resolution of 1.5 eV and thus the orbitals of Ada remain almost unchanged by H → NH₂ substitution. While this is essentially the case for orbitals correlating with the 7t₂ orbitals of Ada, our assignments for the higher energy bands yield new interpretations. For instance, the comparison of the MOs and NTOs reveals the relationship between the D₄ and D₈ ionic states of AdNH₂⁺ and the D₃ degenerate state of Ada⁺. The 14a′′ and 23a′ orbitals of AdNH₂ both exhibit delocalized spatial wavefunctions that correlate with the degenerate 2t₁ orbitals of Ada. However, their eigenenergies are separated by 0.42 eV because of the bonding (23a′) vs. nonbonding (14a′′) character of the π_NH2 electrons with the cage orbitals. A similar relationship applies to the 10a′′ and 20a′ orbitals, which experience a larger splitting of 0.73 eV. In these cases, the conjugation of the n_N lone pair with the alkyl group in the symmetric a′ orbitals increases the transition energies to the respective ²A′ ionic states, whereas the ²A′′ states have lower transition energies with respect to the correlating states of Ada⁺. In summary, the largest splittings occur for orbitals related to the 7t₂, 2t₁, and 1t₁ orbitals in Ada, as these have the largest overlap with the orbitals contributed by the NH₂ group.

Fig. 8 PES spectrum of 1-AdOH assigned by DFT. In panel (a), the spectrum is assigned by the KT method. In panel (b), TD-DFT is used to calculate the vertical transition energies of 1-AdOH⁺ in the D₀* geometry. The transition energies are shifted by the calculated IE_v (9.54 eV). The MO eigenvalues in (a) are then shifted by 0.79 eV to have the same origin as the TD-DFT method.

3.4. 1-Adamantanol (1-AdOH)

Several rotamers of 1-AdOH are optimized to find the global minimum geometry, which is determined to have C_s symmetry with the O–H bond in the anti-position relative to one of the adjacent apical C–C bonds, as shown in Fig. 1. The electronic configuration of the ground state is computed as

…(17a′)²(18a′)²(7a′′)²(19a′)²(20a′)²(8a′′)²(21a′)²(9a′′)²(22a′)²(10a′′)²

(23a′)²(11a′′)²(12a′′)²(24a′)²(13a′′)²(25a′)²(26a′)²(14a′′)²(27a′)²(15a′′)²

and the corresponding bands are labeled in Fig. 1. By this configuration, ionization from the 15a′′ orbital results in a D₀*(A′′) state, meaning that symmetries are reversed when comparing KT orbital assignments with TD-DFT ionic states due to the cross product with a′′. At the relaxed cation geometry, the C_s symmetry is reduced to C₁ as several bonds are distorted disproportionately. The apical C–C bond within the mirror plane undergoes the largest change, being elongated by 0.29 Å (or 18%). This may again indicate instability of the adamantyl cage structure that leads to a cage-opening reaction, as was observed for the isoelectronic AdNH₂⁺ cation by IRPD spectroscopy.³⁷

The first PES measurement of 1-AdOH was reported by Bodor et al.,¹⁶ however only IE_v values were provided without discussion. Tian et al. presented the only available spectrum,²⁴ wherein 1-AdOH was also measured by He*(2³S) Penning ionization electron spectroscopy (PIES). Our measurement shows differences in the band intensities and yields slightly more pronounced features due to the improved resolution (40 vs. 80 meV). The first notable difference is a peak at (9.52 ± 0.07) eV, followed by another weak feature near 9.88 eV (Fig. 8). These were previously observed as shoulders to a peak at 10.6 eV by Tian et al.,²⁴ who estimated the IE_v values to be at 9.6 and 10.0 eV by the slope of the band contour and compared them to values calculated by Outer Valence Green's Function (OVGF) at 9.25 and 9.61 eV, respectively. Both peaks are well resolved in our spectrum and accurately predicted by our models. We calculate the S₀(¹A′) → D₀*(²A′′) IE_v at 9.54 eV, and both KT and TD-DFT give 9.89 eV for the D₁(²A′′) state (Table S7, ESI†). The output of the FC simulation for the IE band is shown in Fig. 9. It reproduces the smooth contour seen in the experimental spectrum with no apparent vibronic features. The simulation yields a 0–0 peak with extremely low intensity at 71559 cm⁻¹ (8.872 eV), which is then shifted by 0.16 eV to align the center of the band with the experimental curve (Table S8, ESI†). This gives a best estimate of the experimental IE_a near 9.03 eV. The broad band is composed of densely congested vibrational excitations, although no fundamentals are predicted to have pronounced intensity. Instead, various combination bands involving several modes contribute to the convoluted line profile in red. Many of these modes involve activation of the C–C bond that is elongated upon ionization, and the large geometry changes between 1-AdOH and 1-AdOH⁺ result in small FC overlap.

Fig. 9 The D₀(²A′) ← S₀(¹A′) transition band from the PES spectrum of 1-AdOH (black) compared to the simulated FC stick spectrum (green) at 335 K, which is convoluted with a FWHM of 40 meV (red).

At the current resolution, the low symmetry increases the degree of overlapping bands and complicates the ability to interpret the spectrum, especially with regards to identifying the OH orbitals. For comparison, the PES spectrum of 1-diamantanol has also been measured and similarly shows a smooth band contour with no apparent n_O band.⁹ Two possibilities for assigning the nonbonding lone pair orbital are the ground state band at 9.52 eV or the sharper and more prominent peak at 10.46 eV. The MOs suggest that the 15a′′ HOMO is analogous to one of the eigenstates of the AdCN HOMO and the HOMO−1 of AdNH₂ (Fig. S8, ESI†), but also possesses nonbonding n_O character. However, the 14a′′ HOMO−2 has similar character and it is unclear to access which one correlates more strongly with the 7t₂ HOMO of Ada by a visual comparison. Tian et al. assigned both to the two n_O lone pairs, stating 15a′′ to be perpendicular and 14a′′ to be parallel to the cage, but with respect to orthogonal reference planes.²⁴ We contend the nonbonding lone pair should be out of plane from the C_s axis, whereas the other will have bonding character between the acidic proton and the cage, analogous to the MOs of H₂O. Using another model to describe the nature of the cation ground state, NBO charges at the same level of theory are computed for the neutral and cation ground state of 1-AdOH. The difference of the charges indicates that the cage experiences a net change of +0.787e for S₀ → D₀. This is similar to the AdCN HOMO, which has net change of +0.891e localized on the cage and contrasts with AdNH₂, which experiences a net change of +0.554e on the NH₂ group. Although NBO charges represent local charge density at equilibrium, this consideration would seem to indicate that the 15a′′ HOMO more closely correlates with the 7t₂ HOMO of Ada. The peak at 10.46 eV is attributed to two quasi-degenerate ionic states, D₂ and D₃ at 10.51 and 10.52 eV, respectively (Fig. S9, ESI†). The near degeneracy and relative isolation of these states explain the observed peak prominence. The 26a′ orbital, however, correlates closely with the 7t₂ HOMO of Ada together with the 27a′ orbital. We therefore correlate the MOs of Ada as: (i) 7t₂ → 15a′′ + 27a′ + 26a′, (ii) 2t₁ → 25a′ + 13a′′ + 11a′′, (iii) 3e → 24a′ + 12a′′, (iv) 6t₂ → 10a′′ + 22a′ + 21a′, (v) 1t₁ → 9a′′ + 8a′′ + 20a′, and (vi) 5t₂ → 19a′ + 7a′′ + 18a′. The bonding valence OH orbital is 23a′, which is assigned to the small shoulder not observed in the other spectra at 12.73 eV. We find that strong mixing between the adamantyl and OH orbitals induces significant splitting of the Ada 7t₂ HOMO, 2t₁ HOMO−1, and 1t₁ HOMO−4 over an energy range of about 1 eV in each case.

3.5. 2-Adamantanol (2-AdOH)

The PES spectrum of 2-AdOH in Fig. 10 is the first to be reported for this molecule. Here, the OH group substitutes an H atom in the 2-position of Ada. The global minimum geometry is characterized by C₁ symmetry, with the O–H bond at a dihedral angle of 64.7° relative to the adjacent C–H bond (Fig. 1). Upon ionization, the global minimum geometry undergoes a decrease in this H–C–O–H dihedral angle to 15.5°, and like 1-AdOH, the C–C bond attached to the OH group is significantly elongated by 0.32 Å (21%). This observation again points toward an instability of the adamantyl cage in the cation caused by an inductive effect of the OH group through the C–C bonds.

Fig. 10 PES spectrum of 2-AdOH assigned by DFT. In panel (a), the spectrum is assigned by the KT method. In panel (b), TD-DFT is used to calculate the vertical transition energies of 2-AdOH⁺ in the D₀* geometry. The transition energies are shifted by the calculated IE_v (9.67 eV). The MO eigenvalues in (a) are then shifted by 0.83 eV to have the same origin as the TD-DFT method.

The PES spectrum exhibits several differences from that of 1-AdOH, demonstrating the significant effect of the substitution position on the ionic states (Table S9, ESI†). There are three bands appearing between 9 and 15 eV, the profiles of which are generally broader and smoother in appearance with no distinguishable vibrational fine structure. The onset of the first band is enlarged in Fig. 11 and is compared with a FC simulation of the transition into the cation ground state. The 0–0 peak is calculated at 70 958 cm⁻¹ (8.798 eV) with low intensity (Table S10, ESI†). The simulated spectrum is then shifted by 0.37 eV to align it with the experimental band contour to give a best estimate of the experimental IE_a near 9.17 eV. After the stick spectrum is convoluted to match the resolution of the spectrometer, the simulated spectrum closely mirrors the measured curve. Four vibrations give the largest contribution to the band intensity: ν₃₈ = 1195, ν₅₀ = 949, ν₆₅ = 506, and ν₇₅ = 68 cm⁻¹. These mainly contribute in the form of combination bands that are highly congested, which explains the smoothness of the band profile. However, the broadness of the band is not fully reproduced by the FC simulation, indicating that there are overlapping ionic states nearby toward higher energy. Both the KT and TD-DFT models match closely to the measured spectrum after adjusting by the vertical S₀ → D₀* ionization energy. Analyzing the Kohn–Sham MOs identifies 39a, predicted at 10.34 eV, to be a novel OH orbital not correlating with the MOs of Ada and having n_O character (Fig. S10, ESI†). The other valence OH orbital is 33a (bonding n_O), with a calculated IE_v at 12.69 eV. Thus, the valence OH orbitals have slightly lower binding energy when Ada is functionalized at the 2-position compared to the tertiary 1-position.

Fig. 11 The D₀(²A) ← S₀(¹A) transition band from the PES spectrum of 2-AdOH (black) compared to the simulated FC stick spectrum (green) at 335 K, which is convoluted with a FWHM of 40 meV (red). The calculated vibronic modes with highest intensity have frequencies ν₃₈ = 1195, ν₅₀ = 949, ν₆₅ = 506, and ν₇₅ = 68 cm⁻¹.

3.6. Urotropine (Uro)

The last molecule of this study is Uro, which has a PES spectrum significantly distinct from that of Ada despite the two molecules being isoelectronic and possessing the same symmetry (Fig. 12). Optimizing the structure of Uro by DFT yields the electronic configuration

…(5t₂)⁶(1t₁)⁶(6t₂)⁶(5a₁)²(3e)⁴(2t₁)⁶(7t₂)⁶

(Table S11, ESI†) and corresponding assignments in the PES spectrum are included in Fig. 1. The only previous PES measurement of Uro was reported by Schmidt et al.²⁰ Our measurement shows the same three broad and well separated bands between 7 and 18 eV, with nearly 4 eV separating the first two. Substitution of the four tertiary CH groups in Ada with N atoms drastically affects the orbital character of the 7t₂ HOMO, which is dominated by the n_N lone pairs in Uro (Fig. S12, ESI†). Because the orbitals are more localized, the S₀ → D₀* IE_v is greatly reduced compared to Ada. An important difference in our measurement is the observation of vibronic activity in the first three bands that was not resolved in the earlier study,²⁰ perhaps due to the slightly better resolution (40 vs. 50 meV) and improved signal-to-noise ratio. The first band possesses a mostly symmetric FC envelope, with the 0–0 band observed at (8.03 ± 0.03) eV. However, it is not as pronounced as the first IE_a band in Ada, and the subsequent vibronic peaks are barely distinguishable from the band profile. Fig. 13 shows the cation ground state band in more detail, together with the corresponding FC simulation. Peaks A–C are the discernable vibronic features, observed at 8.12, 8.15, and 8.22 eV (890, 1060, and 1660 cm⁻¹ above 0–0), respectively. Peak D marks the band maximum at 8.48 eV. The FC simulation yields five fundamental modes that give considerable contribution to the band intensity: ν₁₁ = 1065, ν₁₂ = 1019, ν₁₆ = 647, ν₁₇ = 518, and ν₁₈ = 451 cm⁻¹ (Table S12, ESI†). These modes induce JT distortion of the cation, reducing the symmetry from T_d to C_2v. Peak A is a broad shoulder and assigned to the low frequency fundamentals ν₁₈, ν₁₇, and ν₁₆, which are symmetric cage stretching vibrations. Peak B is mostly attributed to the 16¹₀17⁰₀ combination band and 16²₀ overtone. Toward higher energies, the FC states become congested with various combination bands, eventually forming a smooth line profile.

Fig. 12 PES spectrum of Uro assigned by DFT. In panel (a), the spectrum is assigned by the KT method. In panel (b), TD-DFT is used to calculate the vertical transition energies of Uro⁺ in the D₀* geometry. The transition energies are shifted by the calculated IE_v (8.60 eV). The MO eigenvalues in (a) are then shifted by 0.84 eV to have the same origin as the TD-DFT method.

Fig. 13 The D₀(¹B₁) ← S₀(²A₁) transition band from the PES spectrum of Uro (black) compared to the simulated FC stick spectrum (green) at 345 K, which is convoluted with a FWHM of 40 meV (red). The observed vibronic features are in close agreement with the calculated vibrational frequencies ν₁₁ = 1065, ν₁₂ = 1019, ν₁₆ = 647, ν₁₇ = 518, and ν₁₈ = 451 cm⁻¹.

As we are unable to optimize the excited state geometries, we cannot give similar treatment to interpret vibronic features observed in the JT split D₂(²A₂)/D₃(²E) and D₉(²A₂)/D₁₀(²E) ionic states near 12.45 and 15.56 eV, respectively (Fig. S13, ESI†). For the first progression, we observe a 0–0 band at (11.73 ± 0.02) eV, followed by peaks at 11.81, 11.90 (shoulder), 11.96, and 12.12 eV (650, 1370, 1860, and 3150 cm⁻¹ above the origin, respectively). Two more peaks are observed at 12.62 and 13.28 eV but are not likely to belong to the same state. The peak at 12.62 eV could be contamination of water in the vacuum chamber. The progression seen in the third band near 15.5 eV has an apparent 0–0 band at (15.15 ± 0.02) eV. Subsequent peaks are observed at 15.24, 15.31 (shoulder), 15.34, and 15.41 eV (730, 1290, 1530, and 2100 cm⁻¹ above 0–0).

Lastly, correlation of the MOs of Uro with those of Ada highlights the inductive effect of the nitrogen lone pairs on the ionic states of Uro⁺. Much of this discussion has been given by Schmidt.²⁰ Isolation of the MOs on the lone pairs significantly lowers the binding energy of the 7t₂ and 5a₁ orbitals by 1.23 and 2.25 eV, respectively. Meanwhile, conjugation of the lone pair electrons into the CN bonds increases the binding energies of the 2t₁, 3e, 1t₁, and 5t₂ orbitals by 1.21, 1.59, 2.08, and 1.34 eV, respectively. The 6t₂ orbitals of Ada and Uro, however, are nearly degenerate as these orbitals are mainly σ_CH2 bonding orbitals.

3.7. Correlation of states

Correlation diagrams comparing the first 19 valence MOs of Ada (12 states) to those of the functionalized adamantanes as well as Uro are shown in Fig. 14. Orbitals are plotted by their −ε values, calculated at the M06-2X(D3)/cc-pVTZ level. The dashed lines identify which orbitals correlate with each other and orbitals highlighted in red signify those which are mainly attributed to n or π electrons belonging to the respective functional groups. For convenience, a copy of Fig. 1 with the correlations overlaid is given in Fig. S14 and correlating MOs are illustrated in Fig. S15 (ESI†).

Fig. 14 Correlation diagrams of the MO eigenvalues (−ε) of Ada compared to those of the functionalized adamantanes and Uro. Orbitals in red are attributed to the respective functional groups.

All derivatives of Ada measured in this work, apart from 2-AdOH, affect one of the tertiary CH groups, and Uro replaces all four with N atoms. Thus, close inspection of the Kohn–Sham MOs with respect to the CH groups provides qualitative insight into the trends observed in the PES spectra. The 7t₂ and 6t₂ orbitals of Ada show σ_CH bonding character in all four tertiary CH groups whereas two of the six CH₂ groups are bonding and the remaining four are nonbonding with the neighboring H. The 2t₁ and 1t₁ orbitals have no contributions from the tertiary CH groups and two of the CH₂ groups, with the remaining CH₂ groups again having nonbonding character. The 3e orbital also has no contribution from the CH groups but shows π_CH2 bonding character in all six CH₂ groups. Finally, 5a₁ has bonding character in all CH and CH₂ groups. These descriptions qualitatively agree with the equivalence orbital model used by Schmidt.²⁰ Therefore, we classify the character of the orbitals as: 7t₂ (CC, σ_CH), 2t₁ (CC), 3e (CC, σ_CH), 6t₂ (σ_CH), 1t₁ (π_CH2), 5t₂ (π_CH2), and 5a₁ (σ_CH, σ_CH2).²⁰

Fig. 14a compares −ε values of orbitals that correlate with the 7t₂ orbital of Ada. The largest effect is demonstrated in the comparison between Ada and Uro, which differ in their energies by 1.23 eV and is caused by localization of the corresponding MOs in Uro to the n_N lone pairs. The largest splitting of the orbital degeneracy, however, is manifested in 1-AdOH, which has a difference of 1.00 eV between 15a′′ and 26a′. As discussed, assignment of the nonbonding lone pair orbitals in 1-AdOH and 2-AdOH is not as straightforward as in the cases of AdNH₂ and AdCN because both the HOMO and HOMO-2 orbitals are described by similar spatial wavefunctions. Fig. 14b and c depict the same energy range but separate the 2t₁ and 3e orbital correlations for clarity. The 2t₁ orbital of Ada again undergoes large splittings with the addition of the OH group. All orbitals corresponding to the 3e orbitals of Ada maintain quasi-degeneracy except for 2-AdOH, which undergoes a large splitting of 1 eV. This observation validates the assignment of the 3e orbital as CH₂ bonding in Ada, because only functionalization at the secondary carbon has a noticeable effect. Comparing correlations with the 6t₂ orbital of Ada (Fig. 14d) reveals that the nitrile group induces the largest change, with 13a₁ and 9e both exhibiting increased binding energy and a large splitting of 0.71 eV between them. 1-AdOH is affected similarly whereas AdNH₂ and 2-AdOH exhibit relatively small splittings in their correlated orbitals. 6t₂ of Uro is nearly degenerate with 6t₂ of Ada. However, considering most orbitals of Uro experience a shift towards higher binding energy by the inductive effect of the N atoms in the cage, similar to the effect of the nitrile group in AdCN, this implies that the 6t₂ binding energy of Uro is actually redshifted relative to the nearby orbitals. Fig. 14f again shows that the 5t₂ orbital Ada is CH₂ bonding as there is quasi-degeneracy for correlating orbitals in the functionalized adamantanes except for 2-AdOH. Lastly, the 5a₁ orbital of Uro has a lower binding energy by several eV due to small overlap of lone pair electrons with the remaining hydrocarbon cage orbitals (just like 7t₂).

4. Conclusions

We present the PES spectra of four functionalized derivatives of Ada, namely, AdCN, AdNH₂, 1-AdOH, and 2-AdOH. Only 1-AdOH has been measured previously. Comparison with the parent molecule, Ada, provides valuable insight into the electronic differences induced by effects of electron-withdrawing and electron-donating functional groups. Furthermore, differences between the spectra of 1-AdOH and 2-AdOH help to emphasize the influence of symmetry on the excited states of their respective cations. Additionally, our remeasured spectrum of Uro is the first to reveal vibronic fine structure in the bands representing the cation ground state and first ionic excited states. We expand on this work, as well as previous PES studies of Ada,^{18,20–22,29} 1-AdOH,²⁴ and Uro,²⁰ with a FC analysis of the ground state cation bands for each molecule. The combined laboratory and theoretical (TD-)DFT analysis reveals the vibrational modes contributing to Jahn–Teller distortion of the cation ground states. In the case of the functionalized adamantanes that were not previously measured, we again see evidence that vibronic coupling effects are important to consider for diamondoids. However, the DFT methods employed here, combined with qualitative reasoning using Kohn–Sham molecular orbitals, effectively provide an accurate interpretation of the observed differences in the PES spectra.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no competing interests to declare.

Acknowledgements

This work was supported by Deutsche Forschungsgemeinschaft (DFG, DO 729/8-2). P. C. was also partly supported by the International Max Planck Research School for Elementary Processes in Physical Chemistry. The authors thank Thomas Möller for use of the spectrometer. We thank Uwe Hergenhahn for offering his expertise to improve the experimental setup, Peter Saalfrank and Evengii Titov for the valuable conversations related to the theoretical methods, and Alexander Breier for fruitful discussions.

References

1. J. E. Dahl, S. G. Liu and R. M. K. Carlson, Isolation and Structure of Higher Diamondoids, Nanometer-Sized Diamond Molecules, Science, 2003, 299, 96–99.
2. H. Schwertfeger, A. A. Fokin and P. R. Schreiner, Diamonds are a chemist's best friend: Diamondoid chemistry beyond adamantane, Angew. Chem., Int. Ed., 2008, 47, 1022–1036.
3. L. Wanka, K. Iqbal and P. R. Schreiner, The lipophilic bullet hits the targets: Medicinal chemistry of adamantane derivatives, Chem. Rev., 2013, 113, 3516–3604.
4. L. Landt, K. Klünder, J. E. Dahl, R. M. K. Carlson, T. Möller and C. Bostedt, Optical response of diamond nanocrystals as a function of particle size, shape, and symmetry, Phys. Rev. Lett., 2009, 103, 047402.
5. K. Lenzke, L. Landt, M. Hoener, H. Thomas, J. E. Dahl, S. G. Liu, R. M. K. Carlson, T. Möller and C. Bostedt, Experimental determination of the ionization potentials of the first five members of the nanodiamond series, J. Chem. Phys., 2007, 127, 084320.
6. C. S. Sarap, B. Adhikari, S. Meng, F. Uhlig and M. Fyta, Optical properties of single- and double-functionalized small diamondoids, J. Phys. Chem. A, 2018, 122, 3583–3593.
7. A. A. Fokin, B. A. Tkachenko, P. A. Gunchenko, D. V. Gusev and P. R. Schreiner, Functionalized Nanodiamonds Part I. An Experimental Assessment of Diamantane and Computational Predictions for Higher Diamondoids, Chem. – Eur. J., 2005, 11, 7091–7101.
8. P. Khan, T. Mahmood, K. Ayub, S. Tabassum and M. Amjad Gilani, Turning diamondoids into nonlinear optical materials by alkali metal Substitution: A DFT investigation, Opt. Laser Technol., 2021, 142, 107231.
9. T. Rander, M. Staiger, R. Richter, T. Zimmermann, L. Landt, D. Wolter, J. E. Dahl, R. M. K. Carlson, B. A. Tkachenko, N. A. Fokina, P. R. Schreiner, T. Möller and C. Bostedt, Electronic structure tuning of diamondoids through functionalization, J. Chem. Phys., 2013, 138, 024310.
10. J. Oomens, N. Polfer, O. Pirali, Y. Ueno, R. Maboudian, P. W. May, J. Filik, J. E. Dahl, S. Liu and R. M. K. Carlson, Infrared spectroscopic investigation of higher diamondoids, J. Mol. Spectrosc., 2006, 238, 158–167.
11. O. Pirali, M. Vervloet, J. E. Dahl, R. M. K. Carlson, A. G. G. M. Tielens and J. Oomens, Infrared Spectroscopy of Diamondoid Molecules: New Insights into the Presence of Nanodiamonds in the Interstellar Medium, Astrophys. J., 2007, 661, 919–925.
12. J. E. P. Dahl, J. M. Moldowan, Z. Wei, P. A. Lipton, P. Denisevich, R. Gat, S. Liu, P. R. Schreiner and R. M. K. Carlson, Synthesis of Higher Diamondoids and Implications for Their Formation in Petroleum, Angew. Chem., Int. Ed., 2010, 49, 9881–9885.
13. V.-G. Tirila, A. Demairé and C. N. Ryan, Review of alternative propellants in Hall thrusters, Acta Astronaut., 2023, 212, 284–306.
14. P. Dietz, W. Gärtner, Q. Koch, P. E. Köhler, Y. Teng, P. R. Schreiner, K. Holste and P. J. Klar, Molecular propellants for ion thrusters, Plasma Sources Sci. Technol., 2019, 28, 084001.
15. M. A. Bretti, IEPC-2022-349, Electric Rocket Propulsion Society, 2022, pp. 1–25.
16. N. Bodor, M. J. S. Dewar and S. D. Worley, Photoelectron spectra of molecules. III. Ionization potentials of some cyclic hydrocarbons and their derivatives, and heats of formation and ionization potentials calculated by the MINDO SCF MO method, J. Am. Chem. Soc., 1970, 92, 19–24.
17. M. J. S. Dewar and S. D. Worley, Photoelectron Spectra of Molecules. I. Ionization Potentials of Some Organic Molecules and Their Interpretation, J. Chem. Phys., 1969, 50, 654–667.
18. S. D. Worley, G. D. Mateescu, C. W. McFarland, R. C. Fort and C. F. Sheleyld, Photoelectron Spectra and MINDO-SCF-MO Calculations for Adamantane and Some of Its Derivatives, J. Am. Chem. Soc., 1973, 95, 7580–7586.
19. J. W. Raymonda, Rydberg States in Cyclic Alkanes, J. Chem. Phys., 1972, 56, 3912–3920.
20. W. Schmidt, Photoelectron spectra of diamondoid molecules: Adamantane, silamantane and urotropine, Tetrahedron, 1973, 29, 2129–2134.
21. B. Kovač and L. Klasinc, Photoelectron Spectroscopy of Adamantane and Some Adamantanones, Croat. Chem. Acta, 1978, 51, 55–74.
22. S. X. Tian, N. Kishimoto and K. Ohno, Two-Dimensional Penning Ionization Electron Spectroscopy of Adamantanes and Cyclohexanes: Electronic Structure of Adamantane, 1 -Chloroadamantane, Cyclohexane, and Chlorocyclohexane and Interaction Potential with He*(2³S), J. Phys. Chem. A, 2002, 106, 6541–6553.
23. T. Zimmermann, R. Richter, A. Knecht, A. A. Fokin, T. V. Koso, L. V. Chernish, P. A. Gunchenko, P. R. Schreiner, T. Möller and T. Rander, Exploring covalently bonded diamondoid particles with valence photoelectron spectroscopy, J. Chem. Phys., 2013, 139, 084310.
24. S. X. Tian, N. Kishimoto and K. Ohno, Electronic structures of 1-adamantanol, cyclohexanol and cyclohexanone and anisotropic interactions with He*(2³S) atoms: collision-energy-resolved Penning ionization electron spectroscopy combined with quantum chemistry calculations, J. Electron Spectrosc. Relat. Phenom., 2002, 127, 167–181.
25. I. V. Litvinyuk, Y. Zheng and C. E. Brion, Electron momentum spectroscopy study of amantadine: binding energy spectra and valence orbital electron density distributions, Chem. Phys., 2000, 261, 289–300.
26. T. Xiong, R. Włodarczyk, L. Gallandi, T. Körzdörfer and P. Saalfrank, Vibrationally resolved photoelectron spectra of lower diamondoids: A time-dependent approach, J. Chem. Phys., 2018, 148, 44310.
27. A. Gali, T. Demján, M. Vörös, G. Thiering, E. Cannuccia and A. Marini, Electron–vibration coupling induced renormalization in the photoemission spectrum of diamondoids, Nat. Commun., 2016, 7, 11327.
28. M. Steglich, F. Huisken, J. E. Dahl, R. M. K. Carlson and T. Henning, Electronic spectroscopy of FUV-irradiated diamondoids: a combined experimental and theoretical study, Astrophys. J., 2011, 729, 91.
29. A. Candian, J. Bouwman, P. Hemberger, A. Bodi and A. G. G. M. Tielens, Dissociative ionisation of adamantane: a combined theoretical and experimental study, Phys. Chem. Chem. Phys., 2018, 20, 5399–5406.
30. B. Roy, E. Titov and P. Saalfrank, Computational study of the adamantane cation: simulations of spectroscopy, fragmentation dynamics, and internal conversion, Theor. Chem. Acc., 2023, 142, 71.
31. L. Landt, W. Kielich, D. Wolter, M. Staiger, A. Ehresmann, T. Möller and C. Bostedt, Intrinsic photoluminescence of adamantane in the ultraviolet spectral region, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205323.
32. M. Kappe, A. Schiller, S. A. Krasnokutski, M. Ončák, P. Scheier and E. M. Cunningham, Electronic spectroscopy of cationic adamantane clusters and dehydrogenated adamantane in helium droplets, Phys. Chem. Chem. Phys., 2022, 24, 23142–23151.
33. S. Banerjee, T. Stüker and P. Saalfrank, Vibrationally resolved optical spectra of modified diamondoids obtained from time-dependent correlation function methods, Phys. Chem. Chem. Phys., 2015, 17, 19656–19669.
34. P. B. Crandall, D. Müller, J. Leroux, M. Förstel and O. Dopfer, Optical Spectrum of the Adamantane Radical Cation, Astrophys. J. Lett., 2020, 900, L20.
35. P. B. Crandall, R. Radloff, M. Förstel and O. Dopfer, Optical Spectrum of the Diamantane Radical Cation, Astrophys. J., 2022, 940, 104.
36. P. B. Crandall, V. D. Lovasz, R. Radloff, S. Stahl, M. Förstel and O. Dopfer, Optical spectrum of the cyanoadamantane radical cation, Mol. Phys., 2023, 122, e2231566.
37. M. A. R. George and O. Dopfer, Infrared Spectrum of the Amantadine Cation: Opening of the Diamondoid Cage upon Ionization, J. Phys. Chem. Lett., 2022, 13, 449–454.
38. M. A. R. George and O. Dopfer, Opening of the Diamondoid Cage upon Ionization Probed by Infrared Spectra of the Amantadine Cation Solvated by by Ar, N₂, and H₂O, Chem. – Eur. J., 2022, 28, e202200577.
39. P. T. Rubli and O. Dopfer, Infrared spectrum of the 1-cyanoadamantane cation: evidence of hydrogen transfer and cage-opening upon ionization, Phys. Chem. Chem. Phys., 2023, 25, 22734–22743.
40. Handbook of Chemistry and Physics, ed. D. R. Lide, 1992, pp. 10–211.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision C.02, 2019.
42. A. D. Becke, A new mixing of Hartree-Fock and local density-functional theories, J. Chem. Phys., 1993, 98, 1372–1377.
43. T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57.
44. J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 1, 1–23.
45. Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241.
46. T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023.
47. F. Jensen, Atomic orbital basis sets, WIREs Comput. Mol. Sci., 2013, 3, 273–295.
48. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
49. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465.
50. T. Xiong and P. Saalfrank, Vibrationally Broadened Optical Spectra of Selected Radicals and Cations Derived from Adamantane: A Time-Dependent Correlation Function Approach, J. Phys. Chem. A, 2019, 123, 8871–8880.
51. P. A. Gunchenko, A. A. Novikovskii, M. V. Byk and A. A. Fokin, Structure and transformations of diamantane radical cation: Theory and experiment, Russ. J. Org. Chem., 2014, 50, 1749–1754.
52. K. Lenzke, L. Landt, M. Hoener, H. Thomas, J. E. Dahl, S. G. Liu, R. M. K. Carlson, T. Möller and C. Bostedt, Experimental determination of the ionization potentials of the first five members of the nanodiamond series, J. Chem. Phys., 2007, 127, 084320.
53. J. Luo, Z. Q. Xue, W. M. Liu, J. L. Wu and Z. Q. Yang, Koopmans’ theorem for large molecular systems within density functional theory, J. Phys. Chem. A, 2006, 110, 12005–12009.
54. A. Patzer, M. Schütz, T. Möller and O. Dopfer, Infrared Spectrum and Structure of the Adamantane Cation: Direct Evidence for Jahn-Teller Distortion, Angew. Chem., Int. Ed., 2012, 51, 4925–4929.
55. M. A. R. George, M. Förstel and O. Dopfer, Infrared Spectrum of the Adamantane⁺–Water Cation: Hydration-Induced C−H Bond Activation and Free Internal Water Rotation, Angew. Chem., Int. Ed., 2020, 59, 12098–12104.
56. M. A. R. George and O. Dopfer, Microhydration of the adamantane cation: intracluster proton transfer to solvent in [Ad(H₂O)_{n= 1–5}]⁺ for n ≥ 3, Phys. Chem. Chem. Phys., 2023, 25, 13593–13610.
57. L. L. Miller, V. R. Koch, T. Koenig and M. Tuttle, Photoelectron spectroscopy and the anodic fragmentation of adamantane derivatives, J. Am. Chem. Soc., 1973, 95, 5075–5077.
58. P. J. Linstrom and W. G. Mallard, NIST Chemistry WebBook, Gaithersburg, MD: NIST, https://webbook.nist.gov/chemistry/, (accessed 26 January 2022).
59. D. W. Turner, C. Baker, A. D. Baker, C. R. Brundle and D. A. Shirley, Molecular Photoelectron Spectroscopy, Wiley Interscience, London, 1970, vol. 268.
60. X. Zhang and J. M. Herbert, Analytic derivative couplings for spin-flip configuration interaction singles and spin-flip time-dependent density functional theory, J. Chem. Phys., 2014, 141, 064104.
61. J. Delwiche and J. E. Collin, High-resolution spectrum of acetonitrile, Chem. Phys. Lett., 1992, 193, 41–48.
62. H. Stafast and H. Bock, Triple-Bonded Functional Groups, John Wiley & Sons, Ltd., Chichester, UK, 2010, vol. 1, pp. 137–185.
63. R. H. Staley, J. E. Kleckner and J. L. Beauchamp, Relationship between orbital ionization energies and molecular properties. Proton affinities and photoelectron spectra of nitriles, J. Am. Chem. Soc., 1976, 98, 2081–2085.
64. M. A. R. George, F. Buttenberg, M. Förstel and O. Dopfer, Microhydration of substituted diamondoid radical cations of biological relevance infrared spectra of amantadine⁺-(H₂O)_n=1–3 clusters, Phys. Chem. Chem. Phys., 2020, 22, 28123–28139.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02425g

---