Fully quantal description of combined internal conversion and intersystem crossing processes in the smallest Criegee intermediate CH2OO
Received
22nd May 2024
, Accepted 22nd August 2024
First published on 27th August 2024
Abstract
A quantal description of nuclear motion using coupled fifteen-state potential energy and spin–orbit coupling surfaces for studying the photodissociation of CH2OO to H2CO(X1A1) + O1D and H2CO(X1A1) + O3P channels is presented. For the evaluation of surfaces, multireference electronic wave functions are employed. For the fully quantal description of the nuclear motion, we diabatize the PESs of the two and four lowest excited singlet and triplet states, respectively, within the three sets of vibronically coupled states, i.e. (B1A′, C1A′), (a3A′, b3A′) and (a3A′′, b3A′′), employing the diabatization by ansatz method. This yields three different adiabatic-to-diabatic mixing angles, which are used for the diabatization of the spin–orbit coupling surfaces and allow to investigate simultaneously the internal conversion and intersystem crossing processes in CH2OO using a nuclear quantum dynamical approach for the first time. Our calculation predicts the presence of a weak spectral band with irregular and discrete structures, which originates from the role of spin–orbit couplings. This band of the spectrum is mainly located between the minimum energy of the a3A′ state and the onset of the B1A′ ← X1A′ spectral band. Furthermore, sizable SOC between the B1A′ and a3A′′ states mixes them via intersystem crossing. Due to the vibronic interaction between the a3A′′ and a3A′ states, the molecule finally relaxes to the a3A′ state and is dissociated to H2CO(X1A1) and O3P products.
1 Introduction
Internal conversion (IC) and intersystem crossing (ISC) are two important processes that are to be treated properly when studying theoretically the photochemistry of molecular systems.1–7 The IC which is typically generated by an electronic degeneracy (e.g. conical intersection), drives a nonadiabatic process (e.g. IC) between two states with the same spin multiplicity.8–11 In contrast, the ISC refers to a nonadiabatic process occurring between two electronic states with different spin multiplicities.12,13
If spin–orbit coupling (SOC) is present, when potential energy surfaces of the excited singlet and triplet states approach at the avoided crossing, there may be mixing of the singlet and triplet states at this point.14 The spin–orbit interaction for polyatomic molecules is effective in promoting ISC close to the avoided crossing geometries only if (i) the orbital transition involved has the character of px → py orbital jump to induce orbital angular momentum and (ii) the orbital transition is localized on a single atom.15
For molecular systems including carbonyl groups (e.g. formaldehyde oxide), the possible ISC can take place between an initial state with 1ππ* character and a final state with 3nπ* character. For 1ππ* → 3nπ* transitions, some of the atomic orbitals have a one-center py → px spin–orbit coupling with the 3nπ* state. As a result of that, a 1ππ* → 3nπ* transition is allowed.16,17 This is known as the El-Sayed rule providing a selection rule for transitions from the singlet to the triplet states involving a change of orbital type.16,17
The dynamic simulation including IC and ISC requires PESs of the singlet and triplet states, vibronic coupling as well as SOC, which are generally computed by employing ab initio electronic structure methods. Incorporating the aforementioned electronic structure data for a fully quantal approach describing both IC and ISC for a specific molecule is not a trivial task. In order to achieve this task, we firstly diabatize separately each group of excited singlet and triplet states. In particular, diabatization is a crucial step for molecular systems when their PESs represent an avoided crossing in the adiabatic picture and are not smooth and slowly varying functions of the nuclear coordinates.8,9,18,19 Thus, the diabatization provides a path way for understanding of nonadiabatic processes (e.g. IC) within the group of two states with smooth diagonal and off-diagonal elements of a potential Hamiltonian in the diabatic picture. Secondly, the SOC matrices as function of the nuclear coordinates are diabatized by using the adiabatic to diabatic (ATD) transformation evaluated in the previous step. The advantage of using PESs and SOC matrices in the diabatic picture is to remove not only the singular derivative couplings and discontinuities in PESs (owing to the presence of avoided crossings in the adiabatic picture) but also the discontinuities in SOCs as a function of the nuclear coordinates. As a result of the diabatization procedure, one obtains an analytical expression for the potential, in which the contributions of the vibronic coupling and SOC matrices are incorporated and, thus this provides a good starting point for the fully quantal description of the IC–ISC in a molecule.
The photodissociation dynamics of formaldehyde oxide can be considered as an example for studying the competition between the IC and ISC processes. Formaldehyde oxide possessing a carbonyl group for which the explicitly correlated multi-reference methods20,21 (MRCI-F12b and RS2-F12) can be used for the evaluation of the PESs of the excited singlet and triplet states and SOCs.22–26 Several investigations on the electronic structure of this molecule for the ground and excited states have been reported in the literature.25,26 Excited state dynamics investigations focusing on the B1A′ ← X1A′ absorption spectrum were reported, where only the vibronic coupling between the excited states was taken into account.25,26 Due to limitations imposed by the potential consisting of only the excited singlet states and their vibronic coupling, one could explain the photodissociation of formaldehyde oxide via CH2OO(X1A′) → H2CO(X1A1) + O1D.25–29 However, CH2OO can be dissociated via CH2OO(X1A′) → H2CO(X1A1) + O3P as well, which is energetically lower than the previous dissociation channel.30,31 For a full quantum dynamic study of this channel, it is required to construct a model as indicated above, in which the PESs of the excited singlet and triplet states together with the vibronic coupling as well as SOC are incorporated. Due to lack of an accurate analytical representation of PESs data and SOCs in the diabatic representation, such a investigation relying on a fully quantal description of IC and ISC processes has not been reported comprehensively yet in the literature.31 Investigation of these nonadiabatic processes and their roles for studying thoroughly the absorption spectroscopy in CH2OO with considering the contributions of the relevant excited triplet states and SOCs constitutes the main research topic in the current manuscript. So far, the contributions of the excited singlet states have been treated for studying the absorption spectroscopy of this molecular system (see for instance ref. 25 and 26).
In this work, our aim is to build the diabatic representation for the PESs of the excited singlet and triplet states B1A′, C1A′, a3A′, b3A′, a3A′′ and b3A′′ and eventually diabatize the SOC between the excited singlet states and the triplet states. Within this unified diabatic representation, we carry out a nuclear quantum dynamics investigation which provides a theoretical basis for understanding the dissociation of CH2OO in more detail.
2 Vibronic Hamiltonian
We use the vibronic Hamiltonian constructed in our previous work,26 which has been already employed for studying the nonadiabatic dynamics of CH2OO following the B1A′ ← X1A′ electronic transition. The model was constructed using the adiabatic ground state X and the diabatic B and C excited states. In this work, we extent the model and include the relevant diabatic triplet states. In other words, the vibronic Hamiltonian H is constructed in the adiabatic state of X1A′ as well as diabatic states a3+A′, a30A′, a3−A′, b3+A′, b30A′, b3−A′, a3+A′′, a30A′′, a3−A′′, b3+A′′, b30A′′, b3−A′′, B1A′ and C1A′ (see e.g. ref. 8 and 9). The Hamiltoniancontains the kinetic part TN (1 stands for the 15 × 15 unit matrix), which is already computed in our previous work26 by employing the the familiar G-matrix method of Wilson et al.32,33 The potential part is W(S). In our previous work,26 we consider the O–O and C–O stretching and the C–O–O bending modes, which are totally symmetric, with a′ symmetry for planar conformations (Cs point group). In the diabatic representation for the excited states, W(S) reads| |  | (2) |
In eqn (2), the vector S refers to the relevant internal coordinates, O–O and C–O stretch and C–O–O bend for our present purposes. Furthermore, the diagonal elements refer to the PESs of the adiabatic state X1A′ as well as diabatic states a3+A′, a30A′, a3−A′, b3+A′, b30A′, b3−A′, a3+A′′, a30A′′, a3−A′′, b3+A′′, b30A′′, b3−A′′, B1A′ and C1A′. The off-diagonal elements SOCa(S), SOCc(S), SOCe(S), SOCg(S) and SOCi(S) are the spin–orbit coupling (SOC) between the B1A′ and the a3−A′, a3+A′′, a30A′′, b3−A′, b3+A′′ and b30A′′ states, respectively. The off-diagonal elements SOCb(S), SOCd(S), SOCf(S), SOCh(S), SOCj(S) and SOCl(S) are the SOC matrix elements between the C1A′ and the a3−A′, a3+A′′, a30A′′, b3−A′, b3+A′′ and b30A′′ states, respectively. The notation SOC in eqn (2) stands for the spin–orbit coupling matrix elements.
In eqn (2), WBC(S), Wa′b′(S) and Wa′′b′′(S) are the vibronic coupling terms between the pairs of coupled states (B1A′,C1A′), (a3A′,b3A′) and (a3A′′,b3A′′), respectively. The numerical values for the coupling constants WBC, Wa′b′ and Wa′′b′′ are 0.049 eV, 0.1 eV and 0.1 eV, respectively (see below for the detailed information regarding the method of calculation). The vibronic coupling constants are computed as the minimum energy difference of the lower and upper potential energy curves along ROO at the avoided crossing geometries (shown in Fig. 3). As can be seen, they are in the excitation energy range of the singlet and triplet transitions relevant to the absorption spectrum. As a result, these avoided crossing shown in in Fig. 3 are relevant in our quantum dynamical calculations. We compute these vibronic coupling by taking the matrix elements to be simple analytical functions of the coordinates, for example, taking the off-diagonal element of the coupling matrix W as constant and the diagonal elements as linear functions of the coordinates25,26 (see eqn (2)). However, in a higher-dimensional treatment, vibronic coupling constants are not taken globally as constant, but rather the minimum energy difference is determined separately for different angles θCOO (90 < θCOO < 180) and rCO (1.12 < rCO < 1.32). Detailed information regarding the evaluations of the vibronic coupling constants was given in our previous work25,26 and we thus skip it here. We should mention that the vibronic coupling of the C state with higher excited singlet states is not treated in the current work, because the energy at their avoided crossing is relatively high and thus its influence on the dynamics may not be important.
As will be explained below, the ISC process happens more likely in the vicinity of the avoided crossing geometries. Thus, we consider the SOC matrices at the minimum energy gaps between the singlet B and C states with the relevant triplet states and average this over the O–O, C–O–O and C–O coordinates in our nuclear quantum dynamical calculation. More details regarding the average values of SOC matrices at the minimum energy gaps will be provided in Section 4, (see also Fig. 12 and 13).
3 Diabatization by ansatz
3.1 Diabatization of excited state PESs
For the purpose of carrying out the nuclear quantum dynamical calculation, we need to diabatize the PESs computed in the adiabatic picture in the first place. For this task, we use a so-called diabatization-by-ansatz method, which is well described in the literature.8,9 As indicated, the singlet and triplet electronic states a3A′, b3A′, a3A′′, b3A′′, B1A′ and C1A′ are involved in the dynamics. Thus, we need to diabatize the PESs corresponding to these states. For this task, we diabatize these states considering three different blocks in the Hamiltonian model (by employing the diabatization-by-ansatz method). The first block involves the a3A′, b3A′ states, while the second block includes the a3A′′ and b3A′′ states. The two singlet B and C states constitute the third block.
Diagonalizing blocks of the potential matrix in eqn (2) results in the energies of the a3A′, b3A′, a3A′′, b3A′′ B1A′ and C1A′ states in the adiabatic picture. The diagonalization of each block can be represented as follows:
| |  | (3) |
where
i ∈ {a
3A′, a
3A′′, B
1A′} and
j ∈ {b
3A′, b
3A′′, C
1A′}. The off-diagonal term
Wij(
S) refers to the vibronic coupling between the coupled states (a
3A′,b
3A′), (a
3A′′,b
3A′′) and (B
1A′,C
1A′) which are shown as
Wa′b′(
S),
Wa′′b′′(
S) and
WBC(
S), respectively, in the Hamiltonian model. In this equation,
Uij(
S) is a unitary transformation and reads
| |  | (4) |
where
α(
S) is the adiabatic to diabatic (ATD) transformation angle and given by
| |  | (5) |
We define the matrix elements of the unitary transformation using the sin and cosine functions depending on the ATD angle (see
eqn (4) and (5)). However, we can also get explicit expressions for the matrix elements of the unitary transformation in
eqn (4) in terms of PESs of the excited state directly rather than using trigonometric functions.
34 In other words, the matrix elements of the unitary transformation
U can be evaluated in terms of
Wi(
S),
Wj(
S),
Wij(
S),
Vi(
S) and
Vj(
S), (where indexes
i and
j are defined above) as follows,
| |  | (6) |
where,
xi(
S) and
xj(
S) read
| | 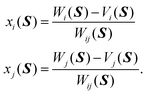 | (7) |
Taking the eigenvalue problem in
eqn (3) to be solved, we compute the diabatic PESs in terms of adiabatic energies
Vi(
S) and
Vj(
S) obtained from the electronic structure methods discussed in the previous section. Thus, the diabatized surfaces can be computed using the following relations,
| |  | (8) |
Here
Wij is computed as the minimum energy difference between the
j and
i states along
ROO, as referred in Section 2 and detailed in ref.
25 and
26.
3.2 Diabatization of SOC matrix elements
As mentioned in the previous section, the three sets of (B1A′,C1A′), (a3A′,b3A′) and (a3A′′,b3A′′) are diabatized by using eqn (3) and (8). This diabatization results in the three separate ATD transformation angles as given in eqn (5). We used these ATD transformation angles and diabatize the SOC matrix elements as described in the following. For the sake of simplicity, we use the three angles α1, α2 and α3 for the representation of the ATD transformation angles in the three sets of (B1A′,C1A′), (a3A′,b3A′) and (a3A′′,b3A′′), respectively, instead of using the two index notations (ij) as used in eqn (5).
For the three sets of (B1A′,C1A′), (a3A′,b3A′) and (a3A′′,b3A′′), the ATD transformations from the adiabatic to the diabatic picture for each ATD transformation angle can be written as rotation matrices
| | 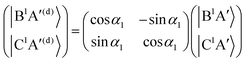 | (9) |
| |  | (10) |
| |  | (11) |
Inserting the diabatic states obtained from
eqn (9)–(11) into the SOC matrix elements results in the diabatized SOC matrix elements between the singlet states B
1A′, C
1A′ and the triplet states a
3A′, b
3A′, a
3A′′, b
3A′′,
| |  | (12) |
| | 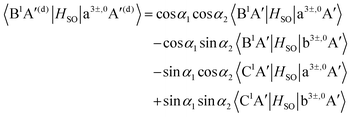 | (13) |
| | 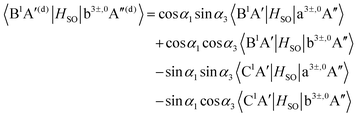 | (14) |
| |  | (15) |
| |  | (16) |
| |  | (17) |
| |  | (18) |
| | 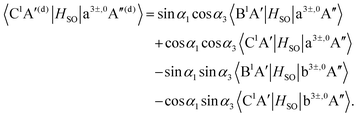 | (19) |
As mentioned in Section 3.1, the matrix elements of the unitary transformation of eqn (4) can be defined in terms of the diabatic and adiabatic PESs (see eqn (6) and (7)). Thus, for the purpose of the evaluations of the SOC in the diabatic picture using eqn (12)–(19), we will use eqn (6) and (7) to compute the sin and cosine functions mentioned in eqn (12)–(19) and eventually calculate the SOC matrix elements in the diabatic picture. In Fig. 5, 6 and 7, the matrix elements of the unitary transformation of eqn (4) (or eigenvectors) for the three sets of states (B1A′,C1A′), (a3A′,b3A′) and (a3A′′,b3A′′) are shown.
Inserting the unitary transformations of eqn (6) and (7) into eqn (12)–(19) results in the SOC matrix elements in the diabatic representation as function of ROO stretching coordinate shown in Fig. 8–11 (shown by dashed lines). Comparing the diabatized SOC curves with their corresponding version in the adiabatic representation reveals that the diabatization procedure removes the zig-zag features of SOC curves in the adiabatic representation and instead creates smooth SOC curves in the diabatic representation (as shown by dashed lines in Fig. 8–11). As a result, the diabatization procedure is able to generate SOC curves, which are slowly varying functions of the nuclear coordinates as also observed in the case of PESs of the relevant excited states (see Fig. 4).
4 Quantum chemistry results
For our electronic structure calculations, we use the ground state electronic structure of CH2OO taken from our previous work,25 where the UCCSD(T)-F12b/cc-pVTZ-F12 level of theory35,36 imposing planarity (Cs point group) was employed (see Fig. 1). For the evaluation of the excited state potential energy surfaces (PESs), we use the CASPT2-F12 (hereafter RS2-F12)21 methods employing the cc-pVTZ-F12 basis set for all atoms.36 We employ the full-valence complete active space (CAS), with 18 electrons distributed in 14 orbitals (18e,14o) as already used in our previous works.25,26 In the current work, the PESs along the O–O and C–O stretching as well as C–O–O bending modes for the four triplet states a3A′, b3A′, a3A′′ and b3A′′ are computed. The 3D PESs of the singlet states X1A′, B1A′, C1A′ along rOO, rCO and θCOO were computed in our previous work.26 The PESs are computed in the range 1.09 < rOO < 4, 1.12 < rCO < 1.32 and 92° < θCOO < 120°. The intervals between adjacent points along rOO, rCO and θCOO are 0.05, 0.05 and 2°, respectively. For the evaluation of PESs along the relevant coordinates, we keep the other coordinates fixed at the equilibrium values at the ground state obtained in our previous work25 and shown in Fig. 1. In total, we compute 4720 points for the construction of the PESs for each triplet state using the RS2-F12 method. Spin–orbit couplings (SOCs) among the aforementioned singlet and triplet states along the O–O and C–O stretching as well as C–O–O bending modes are computed by employing the MRCI wavefunction. In this calculation, we consider absolute values of SOCs. However, we should mention that this is an approximation and more accurate way regarding adjusting the signs of wavefunctions can be found in ref. 37. For this calculation, the same active space is employed as used for the evaluation of the PESs. However, the extension F12 from the aforementioned basis set for all atoms is dropped as we use the MRCI wavefunction in this case. For MRCI wavefunctions, the full Breit–Pauli operator is employed for evaluating the spin–orbit matrix elements between internal configurations (no electrons in external orbitals), while for contributions of external configurations a mean-field one-electron fock operator is employed (see ref. 38 for more information). The electronic structure calculations are carried out by using the MOLPRO 2019.2 suite of programs.39
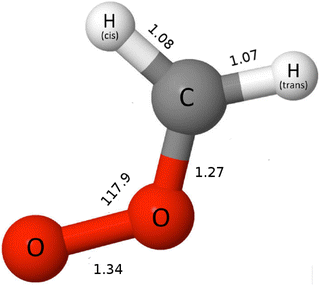 |
| | Fig. 1 The ground state equilibrium structure of CH2OO.25 The bond length and bond angle are given in angstrom and degrees, respectively. | |
In Fig. 2, the vertical excitation energies of the excited singlet and triplet states are depicted and shown in ascending order. In the upper panel of Fig. 3, the adiabatic PE curves along the O–O stretching mode for X1A′, a3A′, b3A′, a3A′′, b3A′′, B1A′ and C1A′ are presented (based on the ordering of the diabatic basis introduced in eqn (3)). For this PE cut, the stretching mode O–O is varied within the range shown in Fig. 3 and the other bond lengths and angles are kept at the equilibrium structure values as shown partly in Fig. 1. In this figure, the PE curves of excited singlet states are shown by solid lines while the PE curves for the excited triplet states are shown by dashed lines. From this figure, one can see several avoided crossings between the PE curves of the excited singlet and triplet states with the same symmetry. As inferred from the lower panel of Fig. 3, the avoided crossings occur between the two singlet states B1A′ and C1A′ at 3.06 eV with ROO = 1.741, between the excited triplet states a3A′ and b3A′ at 2.35 eV with ROO = 1.591 and finally between the excited triplet states a3A′′ and b3A′′ at 2.57 eV with ROO = 1.591. SOCs along the O–O stretching mode in the adiabatic representation are presented in Fig. 8–11. All SOC matrix elements in the adiabatic representation are shown by gray and green solid lines in these figures. We compute the SOCs among the singlet B and C states with the a3A′, b3A′, a3A′′ and b3A′′ states for different spin components 0, ±1.
 |
| | Fig. 2 Pictorial representation of the vertical excitation energies of the singlet and triplet states of CH2OO computed using the RS2-F12 method. The different dissociation channels are shown. UV absorption excites CH2OO from its ground to the excited B states resulting in photodissociation the products H2CO(X) and O1D. The other dissociation channel (energetically lower than the first one) occurs through the ISC between B1A′ and a3A′′ as well as the vibronic coupling between the a3A′′ and a3A′ leading to the products H2CO(X) and O3P. | |
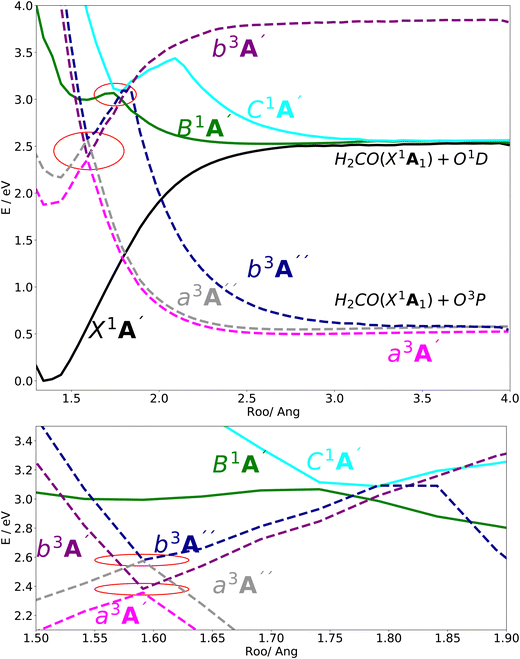 |
| | Fig. 3 (upper) The adiabatic PE curves along the OO stretching mode for the X1A′, B1A′, C1A′, a3A′, b3A′, a3A′′ and b3A′′ states. (lower) The adiabatic PE curves along O–O stretching mode, zooming in geometries in the range 1.55 < ROO < 1.80 (indicated by red circles in the upper panel). The bonding angle θCOO and the stretching mode RCO are fixed at the equilibrium structure values 117.905° and 1.27, respectively. | |
 |
| | Fig. 4 (upper) The diabatic PE curves along the OO stretching mode for the X1A′, B1A′, C1A′, a3A′, b3A′, a3A′′ and b3A′′ states. The CAP is included as the dashed-dotted green curve. (lower) The diabatic PE curves along O–O stretching mode, zooming in geometries in the range 1.55 < ROO < 1.80 (indicated by red circles in the upper panel). | |
 |
| | Fig. 5 The eigenvectors or the unitary transformation matrix elements obtained from the diabatization of the B1A′ and C1A′ states. | |
 |
| | Fig. 6 The eigenvectors or the unitary transformation matrix elements obtained from the diabatization of the a3A′ and b3A′ states. | |
 |
| | Fig. 7 The eigenvectors or the unitary transformation matrix elements obtained from the diabatization of the a3A′′ and b3A′′ states. | |
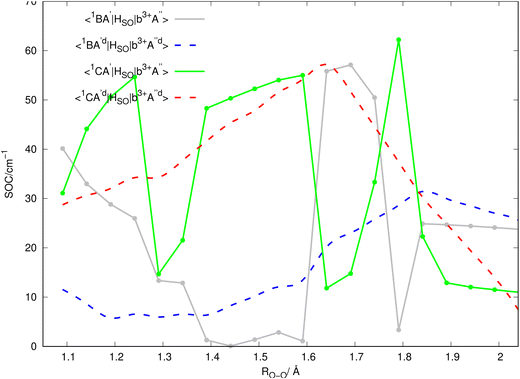 |
| | Fig. 8 SOC matrix elements (shown in the caption of the figure) in the adiabatic (solid lines) and diabatic (dashed lines) representations. | |
 |
| | Fig. 9 SOC matrix elements (shown in the caption of the figure) in the adiabatic (solid lines) and diabatic (dashed lines) representations. | |
 |
| | Fig. 10 SOC matrix elements (shown in the caption of the figure) in the adiabatic (solid lines) and diabatic (dashed lines) representations. | |
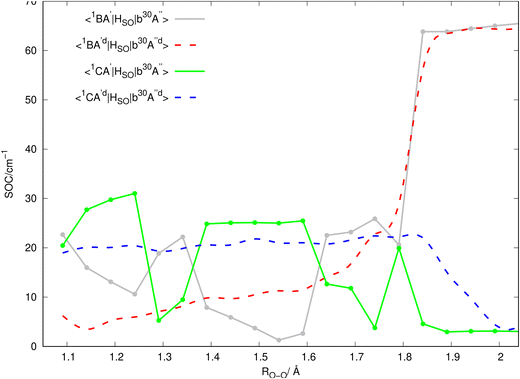 |
| | Fig. 11 SOC matrix elements (shown in the caption of the figure) in the adiabatic (solid lines) and diabatic (dashed lines) representations. | |
The dissociation channel along the O–O stretching coordinate after excitation to the B state leads to the H2CO(X1A1) and O1D products. The electronic states X1A′, B1A′ and C1A′ correlate with this same asymptotic limit generating the H2CO(X1A1) and O1D products (see upper panel of Fig. 3). The dissociation energy corresponds for this channel is estimated ≈57 kcal mol−1 or 2.47 eV, which is in close agreement with the experimental value ≈54 kcal mol−1 or 2.34 eV.40 As can be seen in the upper panel of Fig. 3, the three triplet states a3A′, a3A′′ and b3A′′ correlate adiabatically with the same state in the asymptotic O–O stretching range and this represents a dissociation channel, which is energetically lower than the aforementioned dissociation channel. In this new channel, CH2OO(X1A′) is dissociated into H2CO(X1A1) and O3P products. Based on our calculation, the dissociation energy corresponding to this channel is estimated ≈13 kcal mol−1 or 0.56 eV.
Since the 3D PESs and SOCs matrix elements are inherently computed in the adiabatic picture within the electronic structure formalism, we need to diabatize them for the nuclear quantum dynamics purposes. Hence, we diabatize the 3D excited PESs and SOCs matrix elements using the method explained in Sections 3.1 and 3.2. The diabatic PE curves along the relevant singlet and triplet states are shown in the upper panel of Fig. 4 and the new features of the crossing (in contrast to the adiabatic picture) among the excited states PESs are shown in the lower panel of Fig. 4. The diabatized SOC matrix elements are computed using the method explained in Section 3.2 and are shown by red and blue dashed lines in Fig. 8–11. Due to the diabatization process, the PESs and SOC matrix elements become often smooth and slowly varying functions of the nuclear coordinates which does not hold for the adiabatic and SOC matrix elements. As shown below, the SOC matrix elements along O–O stretching coordinate have large values below ∼2, where the energy gaps between PESs of the singlet and triplet states are minimum, i.e. the ISC process can more likely happen there (see Fig. 12 and 13). Thus, we plot the SOC matrix elements along O–O stretching coordinate until 2. In Table 1, the minimum energies and barrier heights for the diabatic B1A′ and a3−A′′ states are shown.
 |
| | Fig. 12 (a) The energy difference (in eV) between the PESs of the B1A′ and a3A′′ states along the ROO and θCOO coordinates. (b) The energy difference between the PESs of the C1A′ and a3A′′ states along the ROO and θCOO coordinates. (c) The size of SOC at the geometries close to the B1A′ and a3+A′′ avoided crossing. The corresponding average value is 0.005 eV (42 cm−1). (d) The size of SOC at the geometries close to the C1A′ and a3+A′′ avoided crossing. The corresponding average value is 0.001 eV (8 cm−1). | |
 |
| | Fig. 13 (a) The energy difference between the PESs (in eV) of the B1A′ and b3A′′ states along the ROO and θCOO coordinates. (b) The energy difference between the PESs of the C1A′ and b3A′′ states along the ROO and θCOO coordinates. (c) The size of SOC at the geometries close to the B1A′ and b3+A′′ avoided crossing. The corresponding average value is 0.001 eV (8 cm−1). (d) The size of SOC at the geometries close to the C1A′ and b3+A′′ avoided crossing. The corresponding average value is 0.005 eV (42 cm−1). | |
Table 1 The minimum and barrier energies of PE curves of the diabatic states B1A′ and a3−A′′ as shown in Fig. 4
| Diabatic states |
E
min.
|
E
barr.
|
Barr. height |
| B1A′ |
3.00 |
3.44 |
0.44 |
| a3A′′ |
2.35 |
3.09 |
0.74 |
In the panels of Fig. 12a and b, the contour plots of the energy differences between the 2D PESs for the (B1A′, a3A′′) and (C1A′, a3A′′) are depicted. In the panels of Fig. 12c and d, the sizes of SOC matrix elements at the geometries, where the energy gap between the (B1A′, a3A′′) and (C1A′, a3A′′) are minimum, are depicted. In Fig. 12a, the small energy gap in the range of 1.40 < ROO < 1.85 is in the range of 0–0.6 eV. Fig. 12c reveals that the size of SOCs in the range of 1.56 < ROO < 1.64 and 100 ≤ θCOO ≤ 120 has the average value of 5 × 10−3 eV (or 42 cm−1). This small energy gap between the PESs of the B1A′, a3A′′ states and the relatively strong SOC between them (within the range of 1.50 < ROO < 1.60 and 100 ≤ θCOO ≤ 120) leads an efficient intersystem crossing (ISC).
In Fig. 12b, within the range 1.60 < ROO < 1.70, there is an energy gap of 0.5–1.5 eV between the PESs of the C1A′ and a3A′′ states. As inferred from Fig. 12d, the size of the SOC in the range 1.60 < ROO < 1.70 is considerable (average value of 0.001 eV or 8 cm−1). We should mention that at some specific geometries, (namely ROO ∼ 1.64 and 100 ≤ θCOO ≤ 102.5), the energy gap between the C1A′ and a3A′′ states is between 0.5–0.6 eV (see Fig. 12b), where the size of SOC is considerable. Thus, in this case one would expect to have a moderately efficient ISC process, but it is not as efficient as for the case of the B1A′ and a3A′′ states. In Fig. 13, the contour plots of the energy differences between the 2D PESs for the (B1A′, b3A′′) and (C1A′, b3A′′) are shown. In Fig. 13c and d, the size of SOC matrix elements at the geometries close to the (B1A′, b3A′′) and (C1A′, b3A′′) avoided crossing are shown, respectively. In general, Fig. 13 indicates that the size of SOC matrix elements are not large enough at the avoided crossing geometries, where the energy gap is small. Thus, we do not expect an efficient ISC crossing to occur between the (B1A′, b3A′′) and (C1A′, b3A′′) states.
As a result of the aforementioned reasoning, one may conclude that the ISC mechanism is more likely to happen between the two states B1A′ and a3A′′. This finding is also consistent with the El-Sayed rule indicating that the rate of intersystem crossing is relatively large if the radiationless transition involves a change of orbital type.16,17 Based on this rule, the mixing between the B1A′(1ππ*) and a3A′′(3nπ*) states is allowed to occur via SOC, because these states have different orbital characters.
5 Dynamics
5.1 Excitation spectrum
For the evaluation of the spectrum, we perform a propagation calculation using the Hamiltonian model of eqn (2) with a time step 0.05 fs for 1000 fs. This follows after lifting the initial wavepacket from the ground X to the excited B state. The initial wavepacket is computed via propagation in imaginary time by employing the ground state PES of CH2OO.41,42 The method is known as relaxation technique not only in the MCTDH formalism, but quite generally.42–45 In the MCTDH wavepacket propagation,42–45 one needs to choose an appropriate DVR, which yields an efficient and accurate form of the wavefunction Ψ. In this work, we choose the harmonic oscillator (HO) DVR and fast Fourier transform (FFT) in the propagation.42,45 In Table 2, we list the size of the primitive basis and number of single particle functions (SPFs) employed in the current work.
Table 2 Number of basis functions for the primitive harmonic and SPF basis used for the MCTDH calculation. The ordering of the SPF basis for the states involved in the dynamics is the X1A′, a3A′, b3A′, a3A′′, b3A′′, B1A′ and C1A′ states
| Modes |
DVR |
Primitive basis |
SPF basis |
|
R
OO
|
FFT |
128 |
9, 10, 9, 9, 9, 9, 9 |
|
R
CO
|
HO |
88 |
9, 10, 9, 9, 9, 9, 9 |
|
θ
COO
|
HO |
80 |
9, 10, 9, 9, 9, 9, 9 |
Since we study the photodissociation process via the O–O bond cleavage, the wavepacket can be reflected, or it penetrates the other side of the grid when periodic boundary conditions (e.g. FFT) are employed. This leads to the depreciation of the wavefunction. As stated by Leforestier and Wyatt,46 and later Kosloff,47 one uses a complex absorbing potential (CAP) along the O–O stretching mode to avoid the convergence issue in the WP propagation. The CAP is a negative imaginary potential used to absorb the wavepacket as it approaches the end of the grid and thus helps the propagation to converge better along the O–O stretching coordinate. The CAP is usually defined as follows42
| | | iW(Q) = −iη(Q − Qc)bθ(Q − Qc) | (19) |
In this equation,
Qc,
b and
η are the starting point, order, and strength of the CAP, respectively. The parameters
Qc,
b and
η used in the current work are 2.1 Å, 3.1 × 10
−4 a.u., 3, respectively. The symbol
θ(
x) denotes Heaviside's step function. The distance between the starting point of the CAP and the end of the grid determines the length of the CAP, which is usually determined by visualizing the topology of potential energy cuts. The optimal CAP order is 2 or 3 as suggested in ref.
48. In our study, the length of CAP is ∼1 Å resulting in a smaller CAP strength
η to produce unwanted CAP reflections in the quantum dynamical calculation (see ref.
48 for more information for determining the CAP parameters). We thus modify the potential part of the Hamiltonian in eqn (2) by adding
iW(
Q) according to
eqn (20).
In Fig. 14, we present the computed spectrum for the different energy ranges. In the upper panel of Fig. 14, the spectral band with an energy larger than 2.8 eV (black color) corresponding to the B1A′ ← X1A′ transition is shown. This part of the spectrum is in excellent agreement with the experiment28,29 as also shown in our previous work.26 In the lower panel, the spectrum in the energy range below 2.8 eV, shown by the red color, represents the spectral band, in which the contributions of the two lowest triplet states with a3A′ and a3A′′ symmetry including their SOCs with the B1A′ and C1A′ states (see eqn (2)) play a role. This spectral band showing an irregular and discrete structure is ∼0.9 eV above the minimum energy of the 3D PESs of a3A′ (Emin = 1.45 eV). This spectral band is below the energy barrier of the a3A′′ state (3.09 eV) as shown in Table 1 and Fig. 4. As can be seen from Fig. 4, the barrier height of a3A′′ state (0.74 eV) is larger than the one in B1A′ (0.44 eV) indicated explicitly in Fig. 4. Due to this deeper well of the diabatic state a3A′′ at ROO = 1.791 Å, (which is below the starting point of the CAP at Qc = 2.1 shown by the green dashed-dotted line in Fig. 4), the wavepackets corresponding to the a3+A′′ and a30A′′ states as shown in Fig. 17 are partly reflected by the barrier to the right of the shallow well at ROO = 1.791 Å (shown in Fig. 4) resulting in the discrete structure. The intensity of the triplet band in the lower panel in Fig. 14 is considerably smaller than that of the singlet band in the upper panel. The intensity ratio between the highest peaks of the triplet and singlet bands is ∼0.006. This small intensity of the triplet band is expected, which is due to the average value of SOC between the B1A′ and a3A′′ (0.005 eV, see Fig. 12c).
 |
| | Fig. 14 The excitation spectrum of CH2OO computed by the model Hamiltonian in eqn (1) with the coupled singlet and triplet states. For the evaluation of the spectrum, the average values of SOC matrix elements at the geometries close to the avoided crossing (see Fig. 12 and 13) are used. The upper panel (black color) is the spectral band corresponding to the B1A′ ← X1A′ transition, while the lower panel spectrum (red color) is the spectral band caused by the triplet states and SOCs. The oneset of the B1A′ ← X1A′ spectral band is above the minimum energy of 3D PESs of B1A′ (Emin = 2.41 eV). The onset of the spectrum in the lower panel is above the minimum energy of 3D PESs of a3A′ (Emin = 1.45 eV) and below the barrier energy of a3A′′ (3.09 eV) as shown in Fig. 4 and Table 1. | |
5.2 Time-dependent population analysis
This section is devoted to the study of the time-dependent populations Pα(t) of the electronic states α involved in the photodissociation dynamics of CH2OO. Pα(t) is computed via 〈Ψα(t)|Ψα(t)〉, where Ψα(t) is the propagated wavefunction (for the method of computing |Ψα(t)〉 see ref. 42 and 43). In Fig. 15 and 16, the diabatic electronic populations of the singlet and triplet sates considering their spin components are shown. In the lower panel of Fig. 15, the diabatic populations of the B1A′ and C1A′ states are depicted. At t = 0, the system is in the B state due to the fact that the initial wavefunction is lifted from the X1A′ to the B1A′ state. Within the propagation time, while the B state population decreases relatively fast within the lifetime τ = 74 fs (obtained via fitting ae−t/τ to the population of the B state), the C state population has a moderate increase at t = 50 fs. For the later propagation times t ≫ 50 fs, the populations decrease less than ∼0.001. In the upper panel of Fig. 15, the populations of the states a3+A′′ and a30A′′ are shown. The population of a3+A′′ (the green line) has a relatively sharp increase until t ∼ 50 fs and thereafter, it oscillates and decreases very slowly until the end of the propagation time at 1000 fs. In this figure, the population of a30A′′ (the gray line) is shown representing a similar behavior compared to the population of a3+A′′ state but with less enhancement in its population at t = 50 fs. In Fig. 16, the populations of other triplet states are also shown. It can be seen that amount population transfer from the diabatic populations of states depicted in Fig. 15 to the states in Fig. 16 is small.
 |
| | Fig. 15 The diabatic electronic populations of the singlet and triplet states involved in the dynamics of CH2OO following excitation to the B state. For more details see the text. | |
 |
| | Fig. 16 The diabatic electronic populations of the triplet states involved in the dynamics of CH2OO following excitation to the B state. For more details see the text. | |
For a better understanding, Fig. 17 shows WP snapshots (reduced densities) for the B1A′, a3+A′′ and a30A′′ states for the selected propagation times given in the legend of the figure. For both states, the WP moves to the right (larger O–O distances) and broadens, (especially in the case of the a3+A′′ and a30A′′ states). The a3+A′′ population oscillates and decreases as depicted by Fig. 15 and this is due to the fact that the WP is moving towards and within the range of the CAP, see green dashed line in Fig. 4. Strictly speaking, the WP gets partly reflected within the deep shallow well corresponding to the a3+A′′ near 1.791 Å, which causes the discrete structure in the spectrum in the lower panel of Fig. 14. The parts moving out are suppressed by the CAP and the population decreases which represents photodissociation of CH2OO into the H2CO(X1A1) and O3P products.
 |
| | Fig. 17 One-dimensional reduced densities for the B1A′, a3+A′′ and a30A′′ states along the OO stretching mode. | |
It can be seen that there is a population transfer from the B to the relevant triplet states, which cannot be ignored, especially there is a considerable transfer to the a3+A′′ and a30A′′ states (see the upper panel of Fig. 15). This considerable amount of population transfer to the a3+A′′ and a30A′′ states seems to be realistic. This can be understood by using the results provided in Fig. 12a and c, showing a sizable SOC at the geometries close to the avoided crossings between the B1A′ to the a3A′′ state. Due to this considerable SOC at those specific geometries, we observe a population transfer from the B1A′ to a3+A′′ states. This considerable population transfer between these two states represents the role of SOC in the dynamics, which eventually allows for an efficient ISC between the B1A′ and a3A′′ states and provides a path for a spin-forbidden dissociation channel as shown in Fig. 3.
While the population transfer between B1A′ and C1A′ is due to the presence of vibronic coupling WBC (see eqn (2)), the SOCs play a dominant role for transferring the population between the B1A′ to the a3A′′ state as mentioned above. Due to the weakly avoided crossing of the PE curves of the singlet and triplet states, the fast population transfer occurs within the time scale of 50–100 fs. However, we can observe a small population transfer in the triplet manifold due to the small value for the SOC (0.01 eV), which is related to the small intensity ratio of the triplet and singlet spectra (0.006) mentioned in Section 5.1. We can conclude that both vibronic coupling and SOC are essential for understanding of dynamics. In fact, the later one can be used for understanding another dissociation channel for CH2OO occurring via the ISC mechanism in CH2OO (see below).
Based on the theoretical considerations provided above, we suggest a photodissociation channel for CH2OO relying on the triplet states a3A′′ and a3A′ as well as the ISC between B1A′ and a3A′′ as shown schematically in Fig. 2; the UV absorption process excites CH2OO from its ground state to the excited state B1A′. The SOC can mix the B1A′(1ππ*) and a3A′′(3nπ*) based on the El-Sayed's rule. In fact, this mixing originates from the sizable SOC between the B1A′ and a3A′′ states (as shown in Fig. 12a and c) at the geometries close to the avoided crossing. Due to vibronic interaction between the two triplet states a3A′′ and a3A′ (as a result of the avoided crossings between the triplet states shown in Fig. 3 and the vibronic terms of Wa′b′ and Wa′′b′′ in eqn (2)), the molecule relaxes to the a3A′ state and is dissociated into H2CO(X1A1) and O3P products.
Our findings demonstrate the role of ISC in the (spin-forbidden) dissociation channel of CH2OO, which has not been addressed fully quantally so far in the literature.31 This enabled us to treat the excitation spectrum and the electronic populations on an equal footing, a novel step for the Criegee intermediates. Similar findings for other molecular systems with nearly the same size as formaldehyde oxide, such as formaldehyde and acetaldehyde have already been reported in the literature,49 wherein photodissociation is driven by eventual formation of a triplet state manifold mediated by efficient intersystem crossing from an initially excited bright singlet state. Van veen et al. measured the absorption spectra of formaldehyde and acetaldehyde including spectral bands with important contributions from the lowest triplet states and possible SOCs between the singlet and triplet states in these aldehydes.49
6 Summary and conclusion
In this article we have presented a unified Hamiltonian model, in which the contributions of the SOC and vibronic couplings for describing the photodissociation dynamics of CH2OO via the two dissociation channels H2CO(X1A1) + O1D and H2CO(X1A1) + O3P are taken into account and treated on an equal footing. Contributions PESs of triplet states with different spin components Ms = 0, ±1 and their spin–orbit couplings with the other singlet states B and C are explicitly taken into account in our calculation. This is a novel step in the theoretical treatment of the photodynamics of the Criegee intermediates. The PESs and SOCs are computed using the RS2-F12 method and MRCI wavefunction, respectively. The ATD angles obtained from the diabatization of the three sets of the coupled states (B1A′,C1A′), (a3A′,b3A′) and (a3A′′,b3A′′) lead to the diabatizations of the relevant SOC matrix elements and remove the discontinuities in the PESs and SOCs as function of the O–O stretching coordinate. Combining a perturbative explicit-correlation treatment for the electronic motion with a fully quantal approach for the fifteen coupled PESs (via vibronic and SOC couplings) enabled us to compute the spectral band generated due to the presence of SOCs, which is located below the onset of the B1A′ ← X1A′ absorption spectrum. This in turn shows that both vibronic and SOC couplings need to be considered to properly describe the photodissociation dynamics of CH2OO. The population transfer between B1A′ and a3A′′ occurring during the propagation time is indicative of the efficient ISC process between these two states and hence, the dissociation CH2OO into the H2CO(X1A1) and O3P products.
Data availability
The data that support the findings of this study are available based on a reasonable request from authors.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We are indebted to the Deutsche Forschungsgemeinschaft (DFG) for financial support (KO 945/22-1). The authors acknowledge support by the state of Baden-Württemberg through bwHPC (JUSTUS 2 cluster).
Notes and references
- R. S. Minns, D. S. N. Parker, T. J. Penfold, G. A. Worth and H. H. Fielding, Phys. Chem. Chem. Phys., 2010, 12, 15607–15615 RSC
 .
.
- M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Phys. Chem. Lett., 2012, 3, 3090–3095 CrossRef CAS PubMed
 .
.
- M. Richter, S. Mai, P. Marquetand and L. González, Phys. Chem. Chem. Phys., 2014, 16, 24423–24436 RSC
 .
.
- A. Sidat, F. J. Hernández, L. Stojanović, A. J. Misquitta and R. Crespo-Otero, Phys. Chem. Chem. Phys., 2022, 24, 29437–29450 RSC
 .
.
- B. F. E. Curchod, C. Rauer, P. Marquetand, L. González and T. J. Martínez, J. Chem. Phys., 2016, 144, 101102 CrossRef PubMed
 .
.
- B. Nikoobakht and H. Köppel, Chem. Phys. Lett., 2016, 651, 221–232 CrossRef CAS
 .
.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025 CrossRef CAS PubMed
 .
.
-
W. Domcke, D. R. Yarkony and H. Köppel, Conical Intersections: Electronic Structure, Dynamics and Spectroscopy, World Scientific, New Jersey, 2004 Search PubMed
 .
.
- H. Köppel, W. Domcke and L. S. Cederbaum, Adv. Chem. Phys., 1984, 57, 59–246 CrossRef
 .
.
- S. Fernandez-Alberti, A. E. Roitberg, T. Nelson and S. Tretiak, J. Chem. Phys., 2012, 137, 014512 CrossRef PubMed
 .
.
- J. P. Heritage and A. Penzkofer, Chem. Phys. Lett., 1976, 44, 76–81 CrossRef CAS
 .
.
- M. A. El-Sayed, J. Chem. Phys., 1962, 36, 573–574 CrossRef CAS
 .
.
- M. A. El-Sayed, J. Chem. Phys., 1964, 41, 2462–2467 CrossRef CAS
 .
.
- C.-H. Ting, Photochem. Photobiol., 1969, 9, 17–31 CrossRef CAS PubMed
 .
.
-
N. J. Turro, V. Ramamurthy and J. C. Scaiano, Principles of Molecular Photochemistry: An Introduction, University Science Books, Sausalito, California, 1945 Search PubMed
 .
.
- M. A. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS
 .
.
- S. K. Lower and M. A. El-Sayed, Chem. Rev., 1966, 66, 199 CrossRef CAS
 .
.
- A. Thiel and H. Köppel, J. Chem. Phys., 1999, 110, 9371–9383 CrossRef CAS
 .
.
- H. Köppel, J. Gronki and S. Mahapatra, J. Chem. Phys., 2001, 115, 2377–2388 CrossRef
 .
.
- T. Shiozaki and H.-J. Werner, J. Chem. Phys., 2011, 134, 184104 CrossRef PubMed
 .
.
- T. Shiozaki and H.-J. Werner, J. Chem. Phys., 2010, 133, 141103 CrossRef PubMed
 .
.
- P. Aplincourt, E. Henon, F. Bohr and M. Ruiz-López, Chem. Phys., 2002, 285, 221–231 CrossRef CAS
 .
.
- M. T. Nguyen, T. L. Nguyen, V. T. Ngan and H. M. T. Nguyen, Chem. Phys. Lett., 2007, 448, 183–188 CrossRef CAS
 .
.
- M. C. McCarthy, L. Cheng, K. N. Crabtree, O. Martinez, T. L. Nguyen, C. C. Womack and J. F. Stanton, J. Phys. Chem. Lett., 2013, 4, 4133–4139 CrossRef CAS
 .
.
- B. Nikoobakht and H. Köppel, Mol. Phys., 2021, e1958019 CrossRef
 .
.
- B. Nikoobakht and H. Köppel, Phys. Chem. Chem. Phys., 2022, 24, 12433–12441 RSC
 .
.
- L. Sheps, J. Phys. Chem. Lett., 2013, 4, 4201–4205 CrossRef CAS PubMed
 .
.
- W.-L. Ting, Y.-H. Chen, W. Chao, M. C. Smith and J. J.-M. Lin, Phys. Chem. Chem. Phys., 2014, 16, 10438–10443 RSC
 .
.
- E. S. Foreman, K. M. Kapnas, Y. Jou, J. Kalinowski, D. Feng, R. B. Gerber and C. Murray, Phys. Chem. Chem. Phys., 2015, 17, 32539–32546 RSC
 .
.
- J. H. Lehman, H. Li, J. M. Beames and M. I. Lester, J. Chem. Phys., 2013, 139, 141103 CrossRef PubMed
 .
.
- V. J. Esposito, O. Werba, S. A. Bush, B. Marchetti and T. N. V. Karsili, Photochem. Photobiol., 2022, 98, 763–772 CrossRef CAS PubMed
 .
.
-
E. B. Wilson, J. C. Decius and P. Cross, Molecular vibrations: the theory of infrared and Raman vibrational spectra, McGraw-Hill, New York City, 1955 Search PubMed
 .
.
- E. B. Wilson, J. Chem. Phys., 1939, 7, 1047–1052 CrossRef CAS
 .
.
- Horst Köppel, Unpublished results (2024).
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed
 .
.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS
 .
.
- Y. Guan, H. Guo and D. R. Yarkony, J. Chem. Theory Comput., 2020, 16, 302–313 CrossRef PubMed
 .
.
- A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823–1833 CrossRef CAS
 .
.
-
H.-J. Werner and P. Knowles, MOLPRO, version 2019.2, a package of ab initio programs, 2019, For the current version, see https://www.molpro.net/ Search PubMed
 .
.
- H. Li, Y. Fang, J. M. Beames and M. I. Lester, J. Chem. Phys., 2015, 142, 214312 CrossRef PubMed
 .
.
- R. Kosloff and H. Tal-Ezer, Chem. Phys. Lett., 1986, 127, 223–230 CrossRef CAS
 .
.
- M. Beck, A. Jäckle, G. Worth and H.-D. Meyer, Phys. Rep., 2000, 324, 1–105 CrossRef CAS
 .
.
- H.-D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73–78 CrossRef CAS
 .
.
-
M. Beck, A. Jäckle, G. Worth and H.-D. Meyer, MCTDH, The Heidelberg MCTDH Package Version 8.4.20, For the current version, see https://www.pci.uni-heidelberg.de/tc/usr/mctdh/doc/index.html Search PubMed
 .
.
-
H.-D. Meyer, F. Gatti and G. Worth, Multidimensional Quantum Dynamics: MCTDH Theory and Applications, Wiley-VCH Verlag GmbH and Co. KGaA, Weinheim, 2009 Search PubMed
 .
.
- C. Leforestier and R. E. Wyatt, J. Chem. Phys., 1983, 78, 2334–2344 CrossRef CAS
 .
.
- R. Kosloff and D. D. Kosloff, J. Comput. Phys., 1986, 63, 363–376 CrossRef
 .
.
- U. V. Riss and H.-D. Meyer, J. Chem. Phys., 1996, 105, 1409–1419 CrossRef CAS
 .
.
- E. H. van Veen, W. L. van Dijk and H. H. Brongersma, Chem. Phys., 1976, 16, 337–345 CrossRef CAS
 .
.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article * and
Horst
Köppel
* and
Horst
Köppel






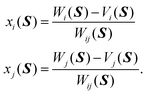

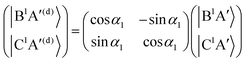



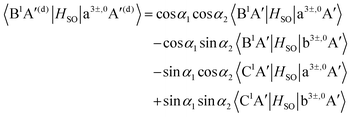
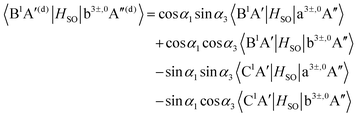




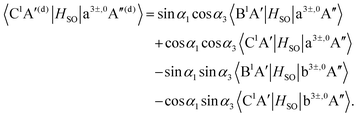












.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.





