Reaction pathways leading to HPALD intermediates in the OH-initiated oxidation of isoprene

Abstract

In this study, we revisited the mechanism of isoprene oxidation by OH radicals, focusing on the formation of hydroperoxyaldehydes (HPALDs) in the reactions following O₂-addition at the α-position to Z,Z′-OH-allyl radical products of the 1,6-H shift of the 1st-generation Z-δ-OH-isoprenylperoxy radicals. Utilizing high-level ab initio quantum chemical calculations and a master equation approach, we provide theoretical confirmation that the formation of δ-HPALDs dominates by far and show that production of β-HPALDs by the mechanism proposed by Wennberg et al. (Chem. Rev., 2018, 118, 3337–3390) is negligible. Besides the dominance of the δ-HPALD formation channel, our investigation also reveals a novel though minor reaction channel resulting in the formation of an allylic δ-hydroperoxy acid and OH radical. Of primary importance for the assessment of the respective channels is the identification of a chemically activated mechanism driving the δ-HPALD formation process under atmospheric conditions. Different from traditional thermally activated pathways, we found that the rovibrationally hot peroxy radicals resulting from O₂ addition to Z,Z′-OH-allyl radicals undergo prompt rearrangement and decomposition at a rate faster than their collisional relaxation, predominantly yielding δ-HPALDs in a chemically activated manner with high efficiency under atmospheric conditions.

---

1 Introduction

Isoprene is a naturally occurring compound synthesized by plant leaves during photosynthesis and released into the atmosphere. Its global emissions are on par with methane and substantially exceed the total emissions of man-made volatile organic compounds (VOCs). Global estimates of isoprene emissions vary widely, ranging from approximately 210 to 990 Tg C per year.^1,2 In addition to its terrestrial emissions, marine isoprene emissions correlated with phytoplankton productivity have also been observed, although the annual yield is likely small³ but very uncertain.⁴

The atmospheric oxidation of isoprene, primarily by the hydroxyl (OH) radical, is a rapid process, with a lifetime of the order of 1 hour at an OH concentration of 1–5 × 10⁶ molecules cm⁻³. This fast reaction results in a cascade of oxidation products, influencing factors such as the hydroxyl radical balance,⁵ tropospheric ozone production,⁶ nitrogen oxide production,^7,8 and the formation of secondary organic aerosols (SOAs).⁹ Isoprene oxidation is highly dependent on local atmospheric conditions, particularly the concentration of nitrogen oxides (NO_x). In pristine environments, where NO_x levels are low, the oxidation mechanism follows a different pathway compared to polluted areas with high NO_x concentrations. Understanding these mechanisms is essential for accurate atmospheric modeling and for predicting the environmental impacts of isoprene, especially in regions where anthropogenic influences are minimal.

Extensive theoretical and laboratory studies^10–27 have developed intricate mechanisms for OH-induced isoprene oxidation, aiming to identify the main oxidation pathways, quantify the product yields, and explore the potential for OH radical regeneration. These studies have identified or confirmed the critical steps in the isoprene oxidation mechanism, which is initiated by the addition of OH radicals to the isoprene molecule, occurring through two distinct pathways: attachment to either the 1-carbon (HO–CH₂–C(CH₃)–CH=CH₂) or the 4-carbon atom (H₂C=C(CH₃)–CH–CH₂–OH).^20,24 These pathways are denoted as case I and case II, respectively. The subsequent addition of an O₂ molecule to isoprene-OH radicals leads to the formation of the first-generation isoprene hydroxy-peroxy (ISOPOO) radicals, which according to the LIM1 mechanism of Peeters et al.^11,12 quickly interconvert, even tending to equilibration (Fig. 1). In LIM1, subsequent unimolecular isomerization reactions of specific peroxy radical isomers by 1,6-H- and 1,5-H-shifts – competing with the bimolecular peroxy reactions – are considered essential for OH and HO_x radical generation pathways in isoprene oxidation. The role of these isomerization reactions, particularly the 1,6-H-shift of the Z-δ-OH-peroxy radical leading to the Z,Z′-OH-allyl radical 1, is crucial under typical atmospheric conditions due to their significant rate constant, in particular for case II, which makes it the most favorable reaction pathway for the degradation of isoprene in a pristine environment.^12,17,18,28

Fig. 1 A simplified reaction schematic of the reaction pathways in the LIM1 model after the addition of O₂ to the isoprene-OH radical for case I.

The further reactions of the resulting Z,Z′-OH-allyl radical may result in the formation of either hydroperoxy aldehydes (HPALDs) following O₂ addition at the position α to the HOC°H-group or dihydroperoxy carbonylperoxy radicals (di-HPCARPs) following O₂ addition at the γ-position, both of which have been proposed to be the main sources of OH radical recycling in the isoprene oxidation mechanism.^12,16,22,29 However, the various experimental measurements of the relative yields of HPALDs and di-HPCARPs differ considerably.^{17,19,21,28,30} In addition to the 1,6-H shift channel, the 1,5-H shift of β-OH-peroxy radicals yields either methyl vinyl ketone (MVK) or methacrolein (MACR), in addition to a hydroperoxy radical (HO₂),^11,14 potentially contributing to the OH radical regeneration, although in very low amounts due to its rate being two orders of magnitude lower than that of the 1,6-H shift.¹²

Despite several thorough investigations in the past 15 years resulting in a consensus on the main pathways, significant differences still exist between currently available chemical mechanisms, i.e. LIM1,¹² the master chemical mechanism of Jenkin et al.³¹ (MCM v3.3.1), and the Caltech mechanism of Wennberg et al.¹⁸ Specifically, the assumed relative yields of HPALD vary between 0.4 and 0.76, and the rate coefficients for the 1,6-H shift differ by as much as a factor of 5. Furthermore, the assumed relative contributions of case I and II as well as of the formed β- and δ-HPALD isomers are also different in these models.

In an early experimental study conducted by Berndt et al.,³⁰ the HPALD yield resulting from the 1,6-H shift of the Z-δ-OH peroxy was estimated to be of the order of 0.04 within a factor of 2. However, in later experiments,^17,19,21,28 it became evident that the HPALD yield is higher and better aligned with the theoretical predictions of Peeters et al.,^11,12 who suggested the di-HPCARP as the other main product of the follow-up chemistry of the Z,Z′-OH-allyl radical. The experimental study conducted by Teng et al.¹⁷ used GC-MS to separate the different isomeric products and intermediates formed in the isoprene oxidation process. They observed six peaks in the GC trace with an m/z ratio of 116 g mol⁻¹ and assigned the two larger peaks to δ-HPALD isomers (cases I and II), while two other lower-abundance peaks were assigned to β-HPALD isomers. By assuming the same HPALD yield for cases I and II, the obtained yield for the δ-HPALD was 0.25 (within a factor of 2), while two further peaks with an m/z ratio of 116 g mol⁻¹ remained unidentified with a yield of 0.15 (again within a factor of 2). Later, Wennberg et al.¹⁸ reexamined these measurements and assigned these two peaks to the β-HPALD, which gives a total HPALD yield of 0.4 (δ: 0.25 and β: 0.15); they also proposed a mechanism for β-HPALD formation, which will be duly examined in this work. Subsequently, Berndt et al.¹⁹ reported a significantly higher HPALD yield (0.76) without distinction between the β- and δ-isomers. Novelli et al.²⁸ also conducted chamber experiments under near-atmospheric conditions and provided direct evidence for the efficient OH recycling. They could not determine the HPALD yield, although a high HPALD yield of 0.75 was found to be consistent with their measurements of other compounds. The most recent experiment of Medeiros et al.²¹ based on direct time-resolved OH measurements serves as a validation of the theory-based LIM1 mechanism. However, from their experiment, they indirectly determined a 0.19 HPALD yield with an uncertainty factor of 2.5, where cases I and II as well as the β- and δ-HPALD could not be distinguished.

In the case of such a complex chemical network, where numerous pathways compete, detailed theoretical analysis can provide valuable complementary insights that make it possible to interpret the experimental results and refine the mechanism. The proposed pathways for HPALD formation might achieve numerical consistency with kinetic simulations from experiments, but the reasoning does not stem from in-depth quantitative theoretical analysis of each elementary reaction step. As a result, it may lack the ability to distinguish between different mechanisms or outcomes in such intricate and subtle chemical processes. In this study, our goal is to explore the formation mechanism of HPALD species in the oxidation of the Z,Z′-OH-allyl radical using quantum chemical methodology together with statistical rate theories, thereby aiming also to assess the validity of the β-HPALD formation mechanism proposed by Wennberg et al.¹⁸

2 Computational details

2.1 Electronic structure calculations

Density functional theory (DFT), along with ab initio methodologies, has been employed to characterize the potential energy surface of the system. DFT, using the M06-2X+D3 functional that includes Grimmes D3 dispersion correction – crucial for the hydrogen-bonded structures under investigation – and the aug-cc-pVTZ basis set were utilized for geometry optimization and frequency analysis of molecular structures. We used the 0.974 scaling factor for the frequencies obtained using the M06-2X+D3 functional. This approach enabled the determination of reliable partition functions, zero-point energy (ZPE) corrected potential energies (at 0 K), and Gibbs free energies within the harmonic oscillator–rigid rotor approximation. For key rate-limiting reaction steps, the geometries of the lowest-energy conformers of reactants and reaction barriers were identified, and their single-point energies were calculated using the high-performance UCCSD(T)-F12 method (an explicitly correlated coupled-cluster method) with the specific cc-pVDZ-F12 basis set. The spin densities are obtained from the Mulliken population analysis and the DFT calculations. All DFT calculations were conducted using the Orca 5.04 program suite,³² and the coupled-cluster calculations were performed using the Molpro 2023 program³³ ensuring a robust and comprehensive computational approach. Chemaxon Marvin was used for drawing chemical structures and reactions.³⁴

2.2 Kinetics calculations

To understand how the Z,Z′-OH-allyl radical 1 behaves after O₂-addition under different conditions, we run energy-resolved master equation (ME) simulations for the elementary reaction steps depicted in Fig. 2 and 3. ME analysis rather than a thermal reaction kinetics approach is in order here, since the nascent peroxy radical 2 formed from Z,Z′-OH-allyl + O₂ has ca. 23 kcal internal energy, while the lowest energy barrier of reactions of 2 is only ca. 11 kcal mol⁻¹. For the ME computations, we utilized the MESS software³⁵ to compute phenomenological rate coefficients by diagonalization of the global energy-resolved relaxation matrix. This matrix characterizes collisional energy relaxation, unimolecular isomerization, and dissociation processes, as well as the formation of bimolecular products, as sinks and the capture of reactants as source terms.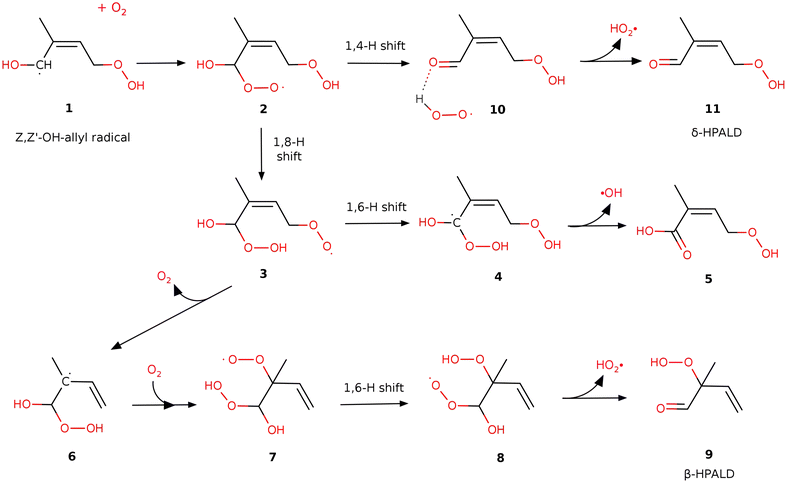

Fig. 2 Reaction pathways leading to products (9 (β-HPALD), 11 (δ-HPALD) and acid 5) after the addition of O₂ to the Z,Z′-OH-allyl radical at the α-position for case I. The structures of case II are displayed in Fig. 3.

Fig. 3 Potential energy profiles for the Z,Z′-allyl radical + O₂ reactions. Zero-point corrected energies are given in kcal mol⁻¹ for case I and in brackets for case II. The structures of the intermediates and products are displayed only for case II.

To model the energy relaxation, we used the exponential down collisional energy transfer model with an exponent of 0.85 and Lennard-Jones (LJ) collision frequencies. In the collision model, the same set of empirical LJ parameters were used as in the work of Li et al.²⁷ on first-generation isorepene-OH-peroxides that are originally derived for δ-pinene chemistry by Kurten et al.³⁶ The empirical LJ parameters σ = 6.5 Å and ε = 417 cm⁻¹ were used for the Z,Z′-OH-allyl radical and σ = 3.9 Å and ε = 33.4 cm⁻¹ for the bath N₂ gas. The average energy transferred during the downward energy transfer was set to 〈ΔE〉 = 200 cm⁻¹. The two barrierless reactions, (i) the capture process of O₂ to Z,Z′-OH-allyl radicals and (ii) the dissociation of peroxy 10 to δ-HPALD + HO₂, are treated within the phase space theory model, where the transition state of the barrierless process was modeled using an attractive V(R) = −C₆/R⁶ long-range potential and then the number of states at the corresponding transition state on the model potential is estimated using the phase space theory. Furthermore, the asymmetric Eckart barrier model^37,38 was used to take into account tunneling in RRKM calculations with an energy grain size of 10 cm⁻¹.

The microcanonical rate constant (RRKM) calculations needed for the master equation are complicated by the presence of numerous (at least 7) internal rotors in each peroxy species. While the high-pressure kinetics of reactions involved in our mechanism can be effectively estimated using the accurate multi-conformer method, simulating the pressure-dependent kinetics with the master equation taking into account all the hindered rotors becomes cumbersome. Because of this, only the lowest energy conformers are considered in our master equation simulations within the rigid rotor–harmonic oscillator approximation. Nevertheless, the lowest frequencies, particularly those below 50 cm⁻¹, may introduce uncertainty in the calculated number of states and rate constants. To mitigate this error, we adopted Truhlar's approach.³⁹ Frequencies in the range of 50–100 cm⁻¹ are uniformly adjusted to 100 cm⁻¹, while those below 50 cm⁻¹ are adjusted to 50 cm⁻¹.

3 Results and discussion

The product radicals 1 (Fig. 2) resulting from 1,6-H shifts of the Z-δ-OH-peroxy radical HO–CH–C(CH₃)–CH=CH₂–OOH in case I and HOO–CH₂=C(CH₃)–CH–CH₂–OH in case II are anticipated to primarily form in the Z,Z′ conformations, which facilitate the formation of the most stable cyclic H-bonded structures.¹² As was shown earlier, the energy barriers for the various unimolecular isomerization and decomposition processes of the Z,Z′-OH-allyl radicals are generally too high for these steps to play a significant role.¹² Therefore, the collisional stabilization of the radical dominates at atmospheric pressures. Then, an oxygen molecule may attach without a barrier to either the allylic 1-carbon in the alpha position or the 3-carbon in the γ position to the HOC°H-group. Adding O₂ at the allylic α-position, which has a spin density of 0.81, is likely slightly more favorable than adding to the γ carbon, where the spin density is 0.55. Moreover, the addition to the α-carbon can subsequently lead to the formation of HPALDs via HO₂ elimination from 8 and 10, whereas addition to the γ position is expected to lead to di-HCARPs. Therefore, in this work, we only consider the addition of O₂ to the allylic α-carbon of the Z,Z′-OH-allyl radical in both cases I and II. The formed adduct with an additional peroxy group on the allylic α-carbon is denoted as radical 2 (see Fig. 2 and 3).

3.1 δ-HPALD formation channel

Based on the theoretical work of the Leuven group (e.g. Peeters et al.^11,12) confirmed experimentally by the Caltech group (see Crounse et al.¹⁰), it is generally accepted (see e.g. Wennberg et al.¹⁸) that the further isomerization reactions of peroxy 2 result in the formation of hydroperoxy aldehydes (δ-HPALDs), assumed to be some of the main sources of secondary OH radicals produced in the isoprene oxidation process. The reaction path for δ-HPALD production from peroxy 2 proposed by Peeters et al.^11,12 is the well-known general mechanism of α-OH-alkylperoxy type radicals (see e.g. Hermans et al.⁴⁰), i.e. a concerted 1,4-H shift of the hydroxyl-H to the peroxy function and C–OO rupture, followed by HO₂ elimination from the resulting complex. In the present work, we could confirm and kinetically quantify this mechanism, with the concerted reaction proceeding through a transition state (TS-2-10) over barriers of 11.4 and 10.7 kcal mol⁻¹ in cases I and II, respectively. This 1,4 H-shift yields a strongly H-bonded complex 10 by the reaction between HO₂ and a newly formed carbonyl function on the α-carbon. Then, peroxy 10 can rapidly decompose without significant exit barrier into δ-HPALD and a free HO₂, requiring 11.8 and 7.4 kcal mol⁻¹ energy in cases I and II, respectively.

3.2 β-HPALD formation channel

After the work of Teng et al.¹⁷ (see above), Wennberg et al.¹⁸ proposed a mechanism for the formation of the β-HPALD isomer to which one of the GC-MS elution peaks observed by Teng¹⁷ was tentatively assigned. In this mechanism, as implemented in this work (see Fig. 2 or the green reaction path in Fig. 3), after the addition of a second O₂ moiety to the α-carbon of the Z,Z′-OH-allyl radical, peroxy 2 can transform into peroxy 3 by an intramolecular 1,8-H shift from the preexisting –OOH to the –O₂ group. The barrier of the tight transition state connecting peroxy 2 and species 3 is relatively high with energies of 18.5 and 16.2 kcal mol⁻¹ in cases I and II, respectively. Then, the newly formed –O₂ group may dissociate as an O₂ molecule from peroxy 3 leaving behind an α-hydroperoxy allyl radical (3 → 6). For case I, this reaction shows a small but real exit barrier above an endothermic energy of 3.4 kcal mol⁻¹, due to multiple H-bonding interactions in peroxy 3 (see Fig. S1, ESI†). Re-addition of an O₂ molecule may happen to the allylic β-carbon to form species 7, which opens the way to a 1,6-H shift between the –O₂ and –OOH groups resulting in peroxy 8. From this, β-HPALD can form through the expulsion of an HO₂ radical that occurs without any potential barrier. According to our present calculations, the rate-limiting step in case I is the dissociation of O₂ in the reaction 3 → 6 over a 21.3 kcal mol⁻¹ barrier, and in case II is 1,6-H transfer from peroxy 7 → 8 through a tight transition state over a barrier of 20.9 kcal mol⁻¹. Furthermore, the O₂ re-addition to the allylic beta carbon in the reaction 6 → 7 also has small barriers of 2.6 kcal mol⁻¹ and 0.5 kcal mol⁻¹ in cases I and II, respectively. It is worth noting that in the dissociation of the O₂ from peroxy 3 to form radical 6 and the re-addition of a different O₂ molecule to form 7, intermediate radical 6 is assumed here to be collisionally stabilized. However, even without collisional stabilization of radical 6, one can still justify this transformation of peroxy 3 → 7 through radical 6 by assuming the “somersault” of O₂ involving its dissociation from 7 and its prompt re-addition, which implies a roaming mechanism. Although this reaction pathway can explain the tentatively proposed β-HPALD formation, the associated barriers (TS-3-6 and TS-7-8) are too high to permit a significant reaction rate.

3.3 δ-Hydroperoxy acid formation channel

In addition to the two HPALD formation channels, another reaction mechanism has been explored here (blue lines in Fig. 3), which leads to a non-HPALD product. This starts with the formation of radical 3 from 2, as in the β-HPALD + HO₂ reaction. Besides TS-3-6, discussed above, we found another lower energy barrier (TS-3-4) that involves a 1,6-H shift from the initial α-carbon (in radical 2) to the –O₂ group. The product of this exothermic reaction is a bis-hydroperoxy allylic radical (species 4 in Fig. 2 and 3) with one HOO- and one HO-group on the α-carbon. The unstable α-hydroperoxy radical 4 will spontaneously undergo a barrierless and highly exothermic concerted O–O bond homolysis to yield a beta-unsaturated acid (5) and an OH radical, which lie lower in energy than 4 by 37 kcal mol⁻¹. The discovery of a new reaction pathway that leads to the formation of acid 5 and OH might have implications for the interpretation of experimental results. Besides HPALDs, a C₅H₈O₄ product with a yield of 3.5% has been observed by Teng et al.,¹⁷ though it remained unidentified. Berndt et al.¹⁹ measured the same C₅H₈O₄ product but with a significantly higher yield of 15% and assigned it as the hydroperoxy-carbonly-epoxide (HPCE), which may form through another reaction channel following O₂ addition to Z,Z′-OH-allyl in the γ-position (Wennberg 2018). However, unsaturated acid 5 can also be identified as a C₅H₈O₄ product. The main bottleneck for the formation of acid 5 is the high-lying TS-3-4, although with a large imaginary frequency (i1800 cm⁻¹), which makes it prone to rate enhancement through quantum-mechanical tunneling. Indeed, in our calculations, the tunneling contributes to making this pathway nearly 3 orders of magnitude faster than the competing β-HPALD formation through TS-3-6. Nonetheless, this reaction channel is still predicted to be negligible under atmospheric conditions, with the main pathway being predicted to be that leading through TS-2-10 to the δ-HPALD products by far. Based on our calculations, acid 5 formation may have no significant contribution to the observed C₅H₈O₄ product with a molecular weight of 132 g mol⁻¹.^17,19

3.4 Chemical vs. thermal activation kinetics

Based on the energetics (see Fig. 3) as well as the high-pressure rate coefficients (see Fig. S2, ESI†), the formation of δ-HPALD is predicted to be far more favorable than all competing processes of peroxy 2. The calculated high-pressure thermal rate coefficient for 2 → 10 δ-HPALD formation is 7 orders of magnitude larger in case I than that of the 3 → 6 reactions leading to β-HPALD and 4 orders of magnitude larger than that of the sequence leading to the non-HPALD compound (acid 5).

Nonetheless, in the case of the nascent hot peroxy intermediate 2 formed from Z,Z′-OH-allyl + O₂ in the atmospheric oxidation of isoprene, one expects a competition between its prompt rearrangement (2 → 10), followed by decomposition of 10, and collisional stabilization so that thermal high-pressure rate coefficients provide only part of the story. In the atmospheric process, in which prompt reactivity of the chemically activated species 2 competes with its stabilization, the relative rates of 2 → 10 and its competing reactions are expected to differ appreciably from those of the thermal reactions, though reaction 2 → 10 should still be predominant. To derive the relative rates and the product yields of the initially chemically activated 2 under atmospheric conditions, we have performed master-equation modelling of the reaction network.

Beyond the treatment of well-to-well and well-to-product channels, it is crucial to account for the incoming flux of 2 stemming from the bimolecular association of O₂ with the Z,Z′-OH-allyl radical (1). This consideration is especially important because most of the barriers (TS-2-10 and TS-2-3) are submerged or have slightly positive energy (TS-3-6, TS-6-7, and TS-7-8) relative to the energy level of the reactants, O₂ + Z,Z′-OH-allyl radical 1, making the entire chemical network susceptible to chemical activation. In such a case, the thermally equilibrated reactants (O₂ + 1) form a ro-vibrationally hot adduct (peroxy radical 2). The energy distribution of the reactive complex immediately after the O₂ capture can be given by P(E) = (2πQ_R)⁻¹N^#(E)exp(−E/k_BT), where Q_R is the product of the partition functions of the reactants, and N^#(E) is the number of states for the transition state of the capture step.³⁵ This adduct with the energy distribution P(E) may react at a rate similar to or faster than the timescale for its collisional energy relaxation. Consequently, the chemically activated (non-thermalized) fraction of the incoming reactant flux may significantly contribute to or even dominate product formation, in addition to the usual thermal reaction channels.

A similar scenario has been explored by Pfeifele & Olzmann²³ in the study of first-generation isoprene-OH-peroxys. In their work, alongside the conventional thermal activation channels, they investigated the effects of both single and double chemical activation under steady-state conditions. This was achieved by coupling two master equations for the bimolecular chemical activation steps: one for isoprene + OH and another for isoprene-OH + O₂ → ISOPOO, after which the Z,Z′-OH-allyl radical is generated via the 1,6 H-shift of the Z-δ-peroxy radical. Their findings indicated that neither the double nor the single activation mechanisms substantially affect the rate coefficients or branching ratios, owing to the rapid thermalization of both the isoprene-OH and the ISOPOO radicals under atmospheric conditions.

Based on the above considerations, we ran master equation simulations of the reaction system considering the chemical activation stemming from the association reaction of O₂ + Z,Z′-OH-allyl radical. The Z,Z′-OH-allyl radicals (1) having achieved thermal equilibrium within ca. 1 ns following sufficient random collisions react fast with O₂ molecules to yield 2 upon O₂-addition in the alpha position. Besides the reactants, we have taken into account in our ME simulation the following potential wells: 2, 3, 10, and barriers TS-2-3, TS-2-10, and TS-3-6 (see Fig. 3) and also three distinct product channels: acid 5 and both HPALDs (9 and 11).

When complex 2 forms through the bimolecular association of thermalized reactants (O₂ + Z,Z′-OH-peroxy radical) under atmospheric conditions, the resulting adduct (2) possesses an average internal (ro-vibrational) energy of 23 kcal mol⁻¹, 5 kcal mol⁻¹ of which is inherited from the thermal reactants O₂ + 1. The energy dependence of the phenomenological rate constants, derived from solving the chemical master equation (ME), can provide insights into the probability of the different fates of the hot 2 as a function of its energy, which are displayed in Fig. 4 for case I. At an energy of 23 kcal mol⁻¹, the probability of prompt δ-HPALD formation from radical 2 through the hot complex 10 is notably high (0.7). This contrasts with the probabilities for thermal stabilization and decomposition of radical 2 back to reactants, which are 0.14 and 0.15, respectively, and the probability of isomerization of 2 to 10 and stabilization of the latter, which is less than 0.01. These probabilities underscore the prominence of chemically activated (the prompt decomposition of the energized radical 2 to δ-HPALD + HO₂) over conventional thermally activated reaction pathways. Additionally, it is worth noting that at energies well below the thermal average for radical 2 (below ca. 19 kcal mol⁻¹), collisional stabilization of 2 is the dominant process. However, at higher energies, the reverse reaction (re-decomposition into reactants 1 and O₂) becomes the most favorable. reaction

Fig. 4 Energy-dependent probabilities of various reaction pathways for the ro-vibrationally excited adduct peroxy 2 as a function of its internal energy in case I at T = 298 K and p = 760 Torr: collisional stabilization of radical 2 (black curve), isomerization of radical 2 to stabilized complex 10 (green line), prompt decomposition to δ-HPALD (red curve), and redissociation back to the reactants 1 + O₂ (blue line). The vertical dotted line indicates the average thermal energy of the reactants (O₂ + Z,Z′-OH-peroxy radical) from which radical 2 is formed under atmospheric conditions.

The energy-dependent probabilities offer valuable insights into the underlying physicochemical processes. However, quantifying the relative contributions of thermally and chemically activated processes requires examining the temperature and pressure dependencies of our chemical system. Fig. 5 displays the temperature dependence of chemically activated δ-HPALD formation yields at 760 Torr, as well as at two other pressures. At 760 Torr, 76–90% of the incoming reactant flux instantaneously yields quasi-solely δ-HPALD + HO₂ products via chemical activation, across the whole considered temperature range of 250–330 K. The remaining 10–24% of the reactant flux initially stabilizes through collisions as radical 2, with its subsequent fate determined by the thermal rate constants, such that it almost entirely undergoes thermal transformation to complex 10, eventually leading to 11, δ-HPALD + HO₂. At lower pressures, the thermal relaxation of 2 is less effective; therefore, at p = 500 Torr, the yield from chemically activated 2 increases to 85–95%. Although the thermal reaction occurs in the fall-off regime at atmospheric pressures, the thermally activated formation of δ-HPALD from peroxy 2 remains significantly predominant with 99.7% yield of the thermalized flux at 300 K and 760 Torr (see Fig. S5, ESI†) compared to the other two products (5 and 9).

Fig. 5 Thermally and chemically activated yields of δ-HPALD in the Z,Z′-OH-allyl radical + O₂ reactions at different pressures for case I.

We conducted additional simulations to investigate the effects of the energy transfer parameter (ΔE) and non-tropospheric pressures and temperatures on chemically activated product yields, especially on the possible formation of δ-acid + OH. On the other hand, the production calculations above were based on ΔE = 200 cm⁻¹; to assess the impact of collisional energy transfer, we extended the simulations by using ΔE = 100 cm⁻¹. Additionally, we broadened the temperature range (250–580 K) and pressure range (100–1400 Torr) in our simulations (see Fig. S4 in the ESI†) to align more closely with the conditions of the most recent experimental work of Medeiros et al.²¹ The chemically activated yields reported in Table S4 (ESI†) are those of the minor products δ-acid-5 + OH and β-HPALD + HO₂, as produced from the chemically activated peroxy 2 while skipping the wells of all intermediates 3 and 4 and for β-HPALD also 7 and 8, i.e. without counting the contributions after collisional thermalization of these intermediates. Even at 100 Torr and 580 K, when using ΔE = 100 cm⁻¹, the so-calculated chemically activated formation of δ-acid remains low, with a yield of 3.1 × 10⁻⁴, indicating that the chemically activated formation of δ-acid (as well as the β-HPALD) remains negligible across a wide temperature (250–580 K) and pressure range (100–1400 Torr), regardless of the energy transfer parameter.

Until now, the results of our simulations were based on the assumption of thermalized reactants Z,Z′-OH-allyl + O₂. In order to explore the impact of a possibly not fully thermalized Z,Z′-OH-allyl radical upon reaction with O₂, we performed additional master equation simulations over an extended temperature (250–580 K) and pressure range (100–1400 Torr). In these simulations, we artificially increased the energy level of the reactants by +5 kcal mol⁻¹ to mimic a residual excess energy content of the Z,Z′-OH-allyl radicals from their formation. Our simulations (see Table S4 in the ESI†) indicate that, even with non-thermalized hot reactants, the chemically activated formation of δ-acid + OH remains negligible, with a yield of 5 × 10⁻⁴ at low pressures (100 Torr) and high temperatures (580 K).

Note that at tropospheric temperatures and pressures, the total yield of δ-acid + OH (5) is substantially higher than the chemically activated yields (for example, 1.4 × 10⁻⁶ in case 2 at 300 K and 760 Torr), as shown in Table S4 (ESI†). This is due to the more significant production of 5 from thermalized peroxy 2, owing to the high tunneling factors at 300 K of ca. 220 for 2 → 3 and ca. 100 for 3 → 4, versus only ca. 2 for 2 → 10, on account of the very high imaginary frequencies (see Table S2, ESI†) of ca. i2200 cm⁻¹ for TS-2-3 and ca. i1800 cm⁻¹ for TS-3-4, while that of TS-2-10 is only ca. i830 cm⁻¹. Nevertheless, the thermal yield of δ-acid + OH remains below 2.5×10⁻⁴ overall under atmospheric conditions (see Fig. S5 and S6, ESI† for the fraction δ-acid in the total thermal flux). At 500 K, the thermal contribution to δ-acid + OH is much smaller, because of the lower fraction of thermalized peroxy 2 among others.

These results imply that under atmospheric conditions, as well as in the extended pressure and temperature range explored in the experiments by Medeiros et al.,²¹ the addition of O₂ to 1 in the α-position predominantly leads to the formation of δ-HPALD and HO₂. The formation of other products, such as δ-acid + OH and β-HPALD + HO₂, is negligible in both thermally and chemically activated pathways.

4 Conclusion

In this study, we re-examined the HPALD formation pathways in the reaction of Z,Z′-OH-allyl radical + O₂, using high-level ab initio quantum chemical calculations combined with energy-dependent master equation modeling of the reactive chemical network. Our calculations strongly suggest that the earlier proposed pathway leading to δ-HPALD + HO₂ is by far the most dominant fate peroxy 2 resulting from O₂ addition to Z,Z′-OH-allyl in the α-position. We confirmed that the peroxy radical 2 can isomerize into a doubly H-bonded product (10), which eventually dissociates in a barrier-free process to δ-HPALD + HO₂. We have shown that the previously suggested multi-step mechanism for β-HPALD formation (Wennberg et al.¹⁸) is negligibly slow, both in the high-pressure limit and under atmospheric conditions. In addition to the two HPALD formation channels, we also discovered another reaction route leading to an allylic δ-hydroperoxy acid (5) and OH radical. This reaction is more favorable than the β-HPALD formation; however, it is still negligible compared to the δ-HPALD formation.

Another important result of our work is that we demonstrated that the δ-HPALD formation occurs for the most part (ca. 85%) promptly by reaction of the initially formed, chemically activated adduct peroxy radicals (2) as the rate of HPALD formation through the instantaneous rearrangement and decomposition of 2 is faster than the nanosecond timescale for its collisional relaxation. Reaction of the thermalized adduct 2 contributes additionally by ca. 15% to δ-HPALD + HO₂ production, with an overall δ-HPALD yield very close to 100%.

The reaction channels confirmed and energetically as well as kinetically quantified in this work may significantly impact the isoprene oxidation mechanism by predicting quasi 100% δ-HPALD production from the Z,Z′-OH-allyl radical upon O₂ addition at the α-position, given also the proposed OH radical recycling through the subsequent photolysis of δ-HPALD.^16,18,29 Another significant finding is that in our proposed mechanism, while the production of β-HPALD by the mechanism proposed by Wennberg et al.¹⁸ is found to be negligible, the only HPALD product is the δ-isomer, formed mainly through a chemically activated mechanism. In experiments, it is difficult to distinguish between the β and δ-isomers of HPALD, though this aspect could be revisited in light of the current predictions.

Author contributions

P. Szabó: investigation and analysis (quantum chemical calculations and all kinetics calculations), writing and editing; Z. Liu: investigation and analysis (quantum chemical calculations); J.-F. Müller: formal analysis, funding acquisition, resources, validation, reviewing and editing; J. N. Harvey: formal analysis, funding acquisition, resources, validation, reviewing and editing; and J. Peeters: conceptualization, formal analysis, validation, reviewing and editing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors have no conflicts to disclose.

Acknowledgements

P. S. expresses gratitude to Yuri Georgievski for his invaluable assistance in clarifying the intricate details of the MESS code. This research was funded by the Belgian Science Policy Office (BELSPO), FED-tWIN REVOCS.

Notes and references

1. A. Arneth, G. Schurgers, J. Lathiere, T. Duhl, D. J. Beerling, C. N. Hewitt, M. Martin and A. Guenther, Atmos. Chem. Phys., 2011, 11, 8037–8052.
2. A. B. Guenther, X. Jiang, C. L. Heald, T. Sakulyanontvittaya, T. Duhl, L. K. Emmons and X. Wang, Geosci. Model Dev., 2012, 5, 1471–1492.
3. P. Rodríguez-Ros, M. Galí, P. Cortés, C. M. Robinson, D. Antoine, C. Wohl, M. Yang and R. Simó, Geophys. Res. Lett., 2020, 47, e2020GL087888.
4. V. Ferracci, J. Weber, C. G. Bolas, A. D. Robinson, F. Tummon, P. Rodríguez-Ros, P. Cortés-Greus, A. Baccarini, R. L. Jones, M. Galí, R. Simó, J. Schmale and N. R. P. Harris, Nat. Commun., 2024, 15, 2571.
5. J. Lelieveld, T. Butler, J. Crowley, T. J. Dillon, H. Fischer, L. Ganzeveld, H. Harder, M. G. Lawrence, M. Martinez, D. Taraborrelli and J. Williams, Nature, 2008, 452, 737–740.
6. O. J. Squire, A. T. Archibald, P. T. Griffiths, M. E. Jenkin, D. Smith and J. A. Pyle, Atmos. Chem. Phys., 2015, 15, 5123–5143.
7. Y. Xie, F. Paulot, W. P. L. Carter, C. G. Nolte, D. J. Luecken, W. T. Hutzell, P. O. Wennberg, R. C. Cohen and R. W. Pinder, Atmos. Chem. Phys., 2013, 13, 8439–8455.
8. J. Mao, F. Paulot, D. J. Jacob, R. C. Cohen, J. D. Crounse, P. O. Wennberg, C. A. Keller, R. C. Hudman, M. P. Barkley and L. W. Horowitz, J. Geophys. Res.: Atmos., 2013, 118, 256.
9. A. G. Carlton, C. Wiedinmyer and J. H. Kroll, Atmos. Chem. Phys., 2009, 9, 4987–5005.
10. J. D. Crounse, F. Paulot, H. G. Kjaergaardc and P. O. Wennberg, Phys. Chem. Chem. Phys., 2011, 13, 13607–13613.
11. J. Peeters, T. Nguyen and L. Vereecken, Phys. Chem. Chem. Phys., 2009, 11, 5935–5939.
12. J. Peeters, J.-F. Müller, T. Stavrakou and V. S. Nguyen, J. Phys. Chem. A, 2014, 118, 5935–5939.
13. T. Nguyen, L. Vereecken and J. Peeters, ChemPhysChem, 2010, 11, 3996–4001.
14. G. da Silva, C. Graham and Z.-F. Wang, Environ. Sci. Technol., 2010, 44, 250–256.
15. G. M. Wolfe, J. D. Crounse, J. D. Parrish, J. M. S. Clair, M. R. Beaver, F. Paulot, T. P. Yoon, P. O. Wennberg and F. N. Keutscha, Phys. Chem. Chem. Phys., 2012, 14, 7276–7286.
16. Z. Liu, V. S. Nguyen, J. Harvey, J.-F. Müller and J. Peeters, Phys. Chem. Chem. Phys., 2017, 19, 9096–9106.
17. A. P. Teng, J. D. Crounse and P. O. Wennberg, J. Am. Chem. Soc., 2017, 139, 5367–5377.
18. P. O. Wennberg, K. H. Bates, J. D. Crounse, L. G. Dodson, R. C. McVay, L. A. Mertens, T. B. Nguyen, E. Praske, R. H. Schwantes, M. D. Smarte, J. M. St Clair, A. P. Teng, X. Zhang and J. H. Seinfeld, Chem. Rev., 2018, 118, 3337–3390.
19. T. Berndt, N. Hyttinen, H. Herrmann and A. Hansel, Commun. Chem., 2019, 2, 21.
20. D. J. Medeiros, M. A. Blitz, P. W. Seakins and L. K. Whalley, J. Phys. Chem. A, 2018, 122, 7239.
21. D. J. Medeiros, M. A. Blitz, P. W. Seakins and L. K. Whalley, JACS Au, 2022, 2, 809–818.
22. J.-F. Müller, T. Stavrakou and J. Peeters, Geosci. Model Dev., 2019, 12, 2307–2356.
23. M. Pfeifle and M. Olzmann, Chem. Kinet., 2014, 46, 231–244.
24. E. E. Greenwald, S. W. North, Y. Georgievskii and S. J. Klippenstein, J. Phys. Chem. A, 2007, 111, 5582–5592.
25. I. R. Piletic, R. Howell, L. J. Bartolotti, T. E. Kleindienst, S. M. Kaushik and E. O. Edney, J. Phys. Chem. A, 2019, 123, 906–919.
26. K. H. Møller, K. H. Bates and H. G. Kjaergaard, J. Phys. Chem. A, 2019, 123, 920.
27. Y. Li, R. Zhang and X. Xu, Ecotoxicol. Environ. Saf., 2023, 266, 115553.
28. A. Novelli, L. Vereecken, B. Bohn, H.-P. Dorn, G. I. Gkatzelis, A. Hofzumahaus, F. Holland, D. Reimer, F. Rohrer, S. Rosanka, D. Taraborrelli, R. Tillmann, R. Wegener, Z. Yu, A. Kiendler-Scharr, A. Wahner and H. Fuchs, Atmos. Chem. Phys., 2020, 20, 3333–3355.
29. J. Peeters and J.-F. Müller, Phys. Chem. Chem. Phys., 2010, 12, 14227–14235.
30. T. Berndt, J. Atmos. Chem., 2012, 69, 253–272.
31. M. E. Jenkin, J. C. Young and A. R. Rickard, Atmos. Chem. Phys., 2015, 15, 11433–11459.
32. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
33. H.-J. Werner, et al., MOLPRO, version 2023, A package of ab initio programs, 2023.
34. Chemaxon-Marvin 17.21.0, https://www.chemaxon.com, 2024.
35. Y. Georgievskii, J. A. Miller, M. P. Burke and S. J. Klippenstein, J. Phys. Chem. A, 2013, 117, 12146–12154.
36. T. Kurtén, M. P. Rissanen, K. Mackeprang, J. A. Thornton, N. Hyttinen, S. Jorgensen, M. Ehn and H. G. Kjaergaard, J. Phys. Chem. A, 2015, 119, 11366–11375.
37. C. Eckart, Phys. Rev., 1930, 35, 1303.
38. H. S. Johnston and J. Heicklen, J. Phys. Chem., 1962, 66, 532–533.
39. R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562.
40. I. Hermans, T. L. Nguyen, P. A. Jacobs and J. Peeters, ChemPhysChem, 2005, 6, 637–645.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02106a

---