pH-Controlled enzymatic computing for digital circuits and neural networks

Abstract

Unconventional computing paradigms explore new methods for processing information beyond the capabilities of traditional electronic architectures. In this work, we present our approach to digital computation through enzymatic reactions in chemically buffered environments. A key aspect of this approach is its reliance on pH-sensitive enzymatic reactions, with the direction of the reaction controlled by maintaining pH levels within a specific range. When the pH crosses a defined threshold, the reaction moves forward and vice versa, akin to the switching action of electronic switches in digital circuits. The binary signals (0 and 1) are encoded as different concentrations of strong acids or bases, offering a bio-inspired method for computation. The final readout is done using UV-vis spectroscopy after applying detection reactions to indicate whether the output is 1 (indicated by the presence of the enzymatic reaction's product) or 0 (indicated by the absence of the enzymatic reaction's product). We build and evaluate a set of digital circuits in the lab using our proposed methodology to model the circuits using chemical reactions. In addition, we demonstrate the implementation of a neural network classifier using our framework.

---

Introduction

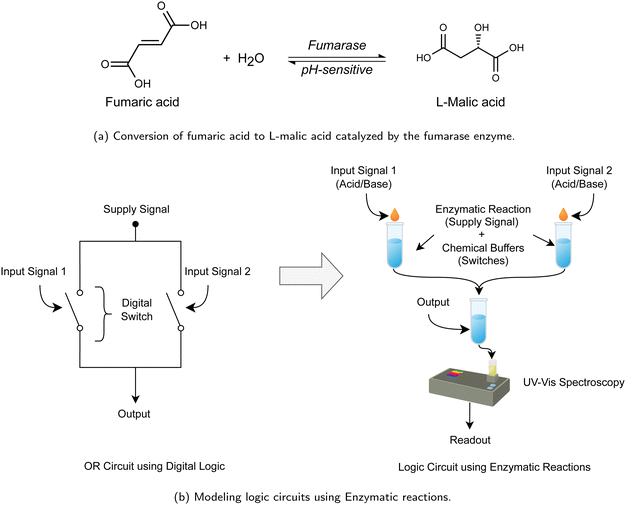
The evolution of computing technology has experienced several paradigm shifts, transitioning from the initial mechanical systems to the current advancements in electronic computing. These developments have paved the way for exploring unconventional methods of information processing. Unconventional computing explores novel computing mechanisms, often inspired by biological, chemical, or physical phenomena.^1–5 While some advancements, such as DNA computing and quantum computing, utilize the intrinsic capabilities of DNA molecules for data storage and the principles of quantum mechanics for enhanced computational power,^6–10 there remains a vast potential in other biological systems. Among these, we observe that enzymes offer a unique opportunity for developing computational systems due to their inherent biological properties and behaviors.

In this work, we introduce a computational model based on enzymatic reactions. Enzymes are catalysts that accelerate biochemical reactions and offer a high degree of specificity.¹¹ They are not only environmentally benign but also demonstrate energy-efficient characteristics.¹² Additionally, their kinetic properties can be influenced and controlled by external factors such as pH levels, which motivates our approach to using pH-controlled enzymatic reactions for information processing. Building on this premise, we use the enzyme fumarase to build our system.

Fumarase is an enzyme involved in the citric acid cycle, catalyzing the hydration of fumarate to L-malate, as shown in Fig. 1. This reaction is a critical step in the metabolic processes that contribute to energy production within cells. Fumarase's activity is influenced by the pH of its environment,¹³ a feature that allows for the regulation of the reaction's direction based on pH levels. The enzyme's response to pH changes enables a degree of control over its catalytic function, making it a subject of interest for applications extending beyond its biological role. In this study, we utilize the pH-sensitive nature of fumarase to develop a computational model. In our system, we promote the forward reaction by elevating the buffer's pH above 7.2, while lowering the pH results in inhibition or reversal of the reaction. We use acids and bases for signal encoding to modulate the pH of the reaction medium, ensuring controlled activation or inhibition of fumarase activities to model computational logic.

Fig. 1 (a) Enzymatic reaction for converting fumaric acid to L-malic acid. (b) Overview of modeling logic circuits using enzymatic reaction showing a traditional circuit for an OR gate comprised of two switches compared to the same circuits modeled using enzymatic reactions. The enzymatic reaction and the buffer provide the switching mechanism; the substrate represents the supply signal, the acids and bases are used to model the input signal, and the reaction product models the output signal. The final readout is done using UV-Vis spectroscopy to detect the presence or absence of the product of the enzymatic reactions (indicating an output of 1 or 0, respectively).

Building on this foundation, we propose a new class of digital logic circuits and analog computing. A major advantage of our proposed method compared to many existing approaches^14,15 is decoupling the propagated supply signal (modeled as enzymatic reaction's substrate) and the input signals (encoded as acids and bases), providing extensibility in modeling logic functionalities and cascading computations. Moreover, in computational systems, it is often preferred to have a non-linear relation between the inputs and the outputs for its ability to enable functions beyond what is achievable with simple linear operations, such as the mere addition of two inputs or reagents. In digital circuit design, the ability to incorporate non-linear relationships between inputs and outputs facilitates the creation of more complex and adaptable computing architectures.^16,17 Our model introduces non-linearity through two components. The first involves chemical buffers that host the enzymatic reactions. These buffers are characterized by attributes such as buffering capacity and range, which impart a non-linear relationship with the input that affects the solution's pH. Additionally, the enzymatic reactions themselves contribute to the non-linearity of the system. The activity of enzymes, including fumarase, demonstrates a non-linear relation to the pH of the medium.¹³ We provide more details about the non-linearity of our system in the ESI.† Our contributions can be summarized as follows:

• We introduce a novel computational paradigm that uses pH-sensitive enzymatic reactions in a chemical buffer to model digital logic gates. Fig. 1(b) shows that traditional logic circuits are comprised of a supply signal (e.g., power signal) that gets propagated through electronic switches controlled by the input signals. Similarly, in our model, the enzymatic reaction models a switching mechanism; the substrate acts as the supply signal, while the acid/base encoding models the input signal that controls the pH of the chemical buffers, which regulates the direction of the enzymatic reaction (supply signal). For the final readout, we apply an established detection method to generate NADH if the forward enzymatic reaction is successful. We use UV-vis spectroscopy to detect the presence or absence of NADH (which indicates an output of 1 corresponding to the success of the enzymatic reaction or 0 otherwise).

• We formulate the problem of finding the proper encoding for the input signals (the acids and bases that are used to represent the signal), and we propose a corresponding optimization approach. Our method identifies the concentrations of acids and bases to control pH levels in the buffer solution (promoting or inhibiting enzymatic reactions) to align with the behavior of the digital design.

• We experimentally model different logic circuits as enzymatic computation using our framework. We also demonstrate examples of cascading logic gates. We implemented and evaluated the different circuits in the laboratory conducted using chemical reactions.

• We extend our enzymatic computation framework to design and model a machine-learning classifier that we carry out through chemical reactions conducted in the laboratory. The implemented model performs binary classification of data points into positive or negative groups based on their respective coordinates. Our framework translates the traditional weights and inputs of a neural network perceptron into concentrations of chemical buffers while the acids and bases are used to encode the input coordinates.

Related work & preliminaries

Molecular computation

Molecular computation extends beyond DNA computing to encompass a broad spectrum of molecular interactions used for computational tasks. This field exploits the specific and affinity-driven interactions of various molecular substrates, including peptides, proteins, and small molecules like neurotransmitters, to perform complex computations.^18–20 While these molecules offer unique computational capabilities due to their inherent properties, they often lack the robustness or flexibility required for complex computational architectures.

For instance, peptides and proteins are particularly notable for their structural versatility, which allows them to fold into specific three-dimensional shapes that can act as molecular computing devices. Researchers have utilized these properties to develop protein-based logic gates and self-assembling peptide structures, which respond to external stimuli to execute computational operations.^18,21 However, these systems typically face challenges in stability and complexity, which are crucial for computing applications.

Intrinsically disordered proteins (IDPs) showcase another avenue for unconventional computing, offering unique features due to their conformational heterogeneity. Unlike structured proteins, IDPs lack a rigid 3D structure and exist as dynamic ensembles capable of sampling a range of conformations. This flexibility allows IDPs to exhibit context-dependent behavior and physicochemical multiplicity, features that are particularly suitable for implementing fuzzy sets and processing fuzzy logic.^22,23 The ability of IDPs to adapt their conformation in response to environmental factors provides flexibility and adaptability in computing systems, suggesting a promising direction for further exploration in molecular computing.

Another example is small molecules, including neurotransmitters, which have been used to mimic neural network behaviors in bio-inspired computing systems.²⁴ These molecules can participate in signal transduction pathways, serving as messengers that relay information within and between cells. By harnessing these signaling molecules, researchers have developed computational models that mimic neural networks, leveraging the natural communication pathways of the brain for information processing. This approach highlights the computational capacity of small molecules and their potential for creating bio-inspired computing systems that emulate the efficiency and complexity of biological processes. Nevertheless, the complexity and control of these molecular interactions remain limited, restricting their application to simple signal-processing tasks.

Moreover, the field of molecular computing has been enriched by the integration of synthetic biology techniques, which enable the design and construction of novel biological circuits with predefined functionalities. This has led to the development of biosensors, memory storage devices, and even computational systems capable of decision-making processes based on molecular inputs.^25–30

Enzymes, such as fumarase, provide a promising alternative to other biomolecules due to their specificity and efficiency. Enzymes are highly specific to their substrates, which reduces the likelihood of side reactions and allows for precise control over the biochemical reactions necessary for computation.¹¹ Additionally, enzymes operate effectively under controlled conditions where parameters such as temperature, pH, and ionic strength can be regulated to enhance their activity and stability.³¹ This specificity and controllability make enzymes suitable for constructing logic gates and performing complex computational tasks. However, the use of enzymes as practical components in computing devices also presents challenges. Enzymes can be sensitive to environmental changes, leading to issues with stability and consistency over long periods. However, there are also techniques to chemically modify enzymes to enhance their stability, which remains a potential avenue for future research to further improve enzyme stability for practical applications.³²

While there are some criticisms of molecular computing based on chemical inputs, such as the progressive dilution of solutions and the difficulty in cascading logic gates, our approach tries to mitigate these issues. The use of buffered solutions maintains consistent pH levels, minimizing the impact of dilution. Additionally, the non-linearity in our model makes the threshold values more reliable. By decoupling the supply signal from the input signal using enzymatic reaction substrates and acids/bases, our method mitigates signal neutralization, facilitating the construction of more complex binary circuits. For example, existing work^14,15 demonstrates modeling a single gate or a decoder circuit (which does not involve cascading computation) since, beyond the first gate, the acid/base input/supply signals can get neutralized (destroying the propagated signal), and only the biasing input signal is left to represent the output. However, in our method, we model the supply signal using the enzymatic reaction's substrate while the input signals are encoded as variations in acid/base concentrations that modulate the enzymatic activity by altering the buffer's pH, which reduces the effect of dilution or neutralization, providing further flexibility and extensibility for the system as we demonstrate cascading more than one gate.

Enzymatic reactions

Enzymes serve as biological catalysts, enabling chemical reactions to proceed at rates that would otherwise be unattainable under mild conditions. Governed by the principles of enzymatic kinetics, these biomolecules have been widely studied in biochemistry and molecular biology. Their ability to facilitate reactions is controlled by a range of factors, including but not limited to temperature, ionic strength, and pH levels. However, their potential use in computational systems has been less explored. While enzymes offer the advantage of highly specific and energy-efficient catalytic actions, their sensitivity to various environmental conditions presents challenges that need to be carefully managed.

Digital circuits

Digital circuits serve as the fundamental infrastructure powering all electronic systems. These circuits operate on the principles of Boolean algebra, employing binary logic where signals are designated as either “0” or “1”. The elemental components in these circuits are logic gates, such as AND, OR, and NOT gates, which execute basic Boolean functions. These gates accept binary signals as inputs and produce a binary output based on predetermined logical operations.

Complex digital systems are constructed by assembling these basic gates into hierarchical arrangements that can perform sophisticated computational tasks. Over the years, technological advancements have facilitated the miniaturization and increased efficiency of these circuits, contributing to the development of electronic devices that are both potent and compact.

Although traditional digital circuits predominantly employ silicon-based components, the limitations inherent to these materials have spurred interest in alternative computational paradigms.^3,14,33,34 Among these alternatives, systems modeled on biological or chemical phenomena are subjects of active research, as they offer novel methods of signal processing and computation.

Results & discussion

Modeling logic gates using enzymatic reactions

As mentioned earlier, our approach utilizes the enzymatic conversion of fumarate to L-malate, catalyzed by the fumarase enzyme as shown in eqn (1), as a biochemical proxy for switches in digital logic gates. This enzymatic reaction offers a convenient feature: its directionality is modulated by the pH level of the chemical buffer in which it occurs.¹³

The initial step is to map each switch in a conventional digital logic gate to a chemical buffer. Each buffer, containing the enzyme and its substrates, acts as a medium for the enzymatic reaction (the supply signal). Initially, these buffers are prepared with a pH value situated approximately at pH = 6.8, the midpoint of the ranges that favor forward and reverse reactions. This intermediate pH serves as the starting point, from which we can shift the reaction's course by adding either strong acids or bases (the input signals).

For the realization of these enzymatic gates, the concentration levels of strong acids and bases, corresponding to the binary signals “0” and “1”, are determined through an optimization process that we explain in the following subsection. The concentrations thus derived serve as the inputs for each chemical buffer. The introduction of these strong acids or bases drives the enzymatic reaction either forward or backward, in accordance with the pH-modulated reaction kinetics.

Subsequent to this input phase, the reactions are propagated from one buffer to the next, following the switches’ connections in the original digital design. The enzymatic reactions mimic the signal flow in digital design, moving from one buffer to the next in a manner analogous to signal transmission across switches in the conventional circuit.

The presence or absence of the malic acid at the terminal buffer serves as the chemical analog of the binary output signal (“0” or “1”) from the digital circuit.

Computing the concentrations for the input signals

An important aspect of our system is the computation of concentrations necessary for representing the signals “0” and “1”. The goal is to adjust the input signal, in terms of concentration, to make the buffer fall within a pH range that either promotes or inhibits the forward enzymatic reaction, corresponding to the desired outputs of “1” or “0”, respectively. To model the buffer's pH, we employ the Henderson–Hasselbalch equation, shown in eqn (2), which serves to calculate the expected pH of the buffers where pKa represents the acid dissociation constant of the material forming the buffer, [HA] is the concentration of the acid, [A⁻] denotes the concentration of the conjugate base, and pH is the final buffer's concentration.

Determining the requisite concentrations is approached as a linear programming problem, where the objective is to identify values that satisfy a series of inequalities that describe the target pH range for each input pattern. For instance, consider a basic design incorporating a single buffer (switch) for an inverter circuit, which necessitates that an input of “0” produces an output of “1”, and an input of “1” results in an output of “0”. Let pH_forward be the minimum pH required for the enzymatic reaction to proceed (so we need the buffer's pH to be greater than pH_forward to execute the forward reaction), and pH_reverse be the pH at which the reaction reverses. Δ[OH⁻] represents the change in concentration of [OH⁻] ions when applying the concentration of input signal 0, while Δ[H⁺] represents the change in concentration of [H⁺] ions when applying the concentration of input signal 1. The objective is for a “0” signal to set the buffer's pH within the pH_forward range and conversely for a “1” signal. To find these concentrations, we solve the inequalities (3) and (4). Realizing the envisioned enzymatic circuit relies on the feasibility of solving these inequalities.

As the design complexity increases with additional buffers, the inequalities are expanded to model the buffer states in response to varying input patterns. While we can try to find the concentrations experimentally, we prefer to formulate the problem based on the characterization of the enzyme, making it easier to design different gates. Using this formulation, the concentrations are determined by solving the given inequalities. One method to solve these inequalities is through iterative optimization techniques through neural networks and gradient descent, which are further detailed in the ESI.†

Signal readout

The output in our system is defined as the presence or absence of the reaction's product, which also acts as a thresholding mechanism. Hence, we measure the system's state by detecting the presence or absence of the final output (as a binary state) defined by the absorbance level at 340 nm. We use the common method of detecting L-malic acid by applying assay reactions to generate NADH (which can then be detected through UV-Vis spectroscopy). The reaction details are highlighted in the ESI.† After the reaction, an increase in absorbance at 340 nm serves as a reliable proxy for the presence of L-malic acid and, by extension, the binary output of the original logic gate. This readout mechanism provides a quantifiable method for translating the chemical activity into discernable digital signals. Moreover, alongside qualitative assessments derived from the absorbance curve, we established a quantitative method to analyze the presence of NADH. Considering the baseline absorbance at 340 nm typically sits at around 0.2, and NADH's peak absorbance occurs near 0.4 at 340 nm, our goal is to refine these observations to binary-like values, closely mapping the presence or absence of NADH to 1 or 0, respectively. To facilitate this, we employ the following equation for quantifying the output based on the absorbance at 340 nm:

Absorbance score = |A_340 nm − 0.2| × 5.0 (5)

In this formula, A_340 nm represents the measured absorbance at the 340 nm wavelength. Applying a threshold value of 0.5 allows for a binary interpretation of the data: readings below 0.5 are classified as indicating an absence of NADH (quantified as 0), and those above 0.5 as indicating its presence (quantified as 1). Thus, an absorbance measurement at 340 nm close to 0.2 translates to an absorbance score near 0, reflecting minimal or no NADH presence. Meanwhile, an absorbance measurement at 340 nm around 0.4 results in an absorbance score close to 1, indicating a significant presence of NADH. This approach enhances the precision of our model's output interpretation by quantitatively reflecting the enzymatic reaction outcomes.

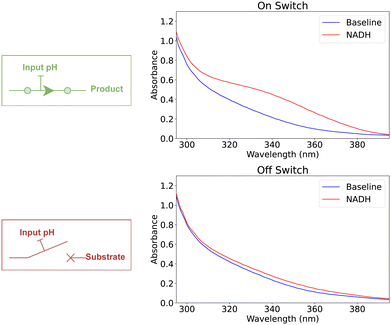
Modeling switch mechanism

The concept of a digital switch is modeled by using a single enzymatic reaction. In this model, the binary state of the switch is determined by the presence or absence of L-malic acid, with its presence indicating an “on” state (“1”) and its absence denoting an “off” state (“0”). We use one buffer solution to modulate the enzymatic reaction, where the application of a strong base or acid determines the switch's state. Specifically, the introduction of a strong base into the buffer induces a pH increase, catalyzing the enzymatic reaction to produce L-malic acid and effectively turning the switch “on.” Conversely, adding a strong acid decreases the pH, inhibiting the enzymatic reaction and switching the device “off.” Fig. 2 demonstrated the experimental validation of the model showcasing controlling the switch state, while Table 1 shows the corresponding Absorbance scores.

Fig. 2 UV-vis spectroscopy for the outputs of a switch mechanism modeled using enzymatic reactions.

Table 1 Absorbance score for modeling a switch mechanism using enzymatic reactions. The “state” column indicates the state of the switch (on or off). The “pH encoding” column indicates the pH used to set the switch into the corresponding state. The “abs.” column lists the measured absorbance at 340 nm corresponding to NADH presence. The “abs. score” is calculated from the absorbance using the provided equation, and the “normalized” column presents the final binary output after applying the thresholding value

State	pH encoding	Abs.	Abs. score	Normalized
On	14.00	0.427	1.137	1
Off	0.60	0.215	0.077	0

---

Modeling NAND gate

The NAND gate, a fundamental two-input logic gate, is designed to output a “1” for all input combinations except when both inputs are “1”. To model this behavior using our enzymatic reaction framework, the input signals are configured to inhibit the enzymatic reaction when both are “1”, allowing the reaction to proceed in all other cases. The encoding of binary signals into chemical concentrations uses a pH of 14.27 for encoding a signal of value “0” and a pH of 0.62 for encoding a signal of value “1”. This approach ensures that the enzymatic reaction is selectively inhibited based on the input combination, mirroring the logical function of a NAND gate. The reactions were carried out in 2.5 mL of phosphate buffer with an initial concentration of 1.01 gm mL⁻¹ containing 100 μL of the fumarase enzyme and 128 μL of the Fumaric acid. The encoded signal was applied using 10 μL of the given concentration; we expect the pH of the buffer to be above 7.2 (promoting the forward reaction) for all cases except for the input signals of all “1s”. Hence, Fig. 3 illustrates the absorbance curves for the outputs generated by our enzymatic NAND gate for various input patterns, demonstrating the gate's ability to replicate the expected logical outcomes through biochemical means. Additionally, Table 2 shows the absorbance score for the modeled computation and its alignment with the expected output from the equivalent digital computation. The table shows three entries only for the two-input function (which should have four input patterns) because the missing fourth entry is symmetric to the second entry.

Fig. 3 UV-vis spectroscopy for the outputs of the NAND circuit modeled using enzymatic reactions.

Table 2 Quantitative analysis of NAND gate operation using enzymatic reactions. The “digital output” column indicates the expected binary output based on the input combinations “In 1” and “In 2,” while “input pH encoding” represents the pH values used to encode the input signals. The “abs.” column lists the measured absorbance at 340 nm, which corresponds to NADH presence. The “abs. score” is calculated from the absorbance using the provided equation, and the “normalized” column presents the final binary output after applying the thresholding value

In 1	In 2	Input pH encoding	Digital output	Abs.	Abs. score	Normalized
0	0	(14.27, 14.27)	1	0.435	1.177	1
1	0	(14.27, 0.62)	1	0.406	1.030	1
1	1	(0.62, 0.62)	0	0.230	0.148	0

---

Modeling NOR gate

The NOR gate, another essential two-input logic gate, outputs a “1” only when both inputs are “0”. In our enzymatic model, this principle is applied by configuring the input signals to prevent the enzymatic reaction from proceeding unless both inputs are “0”. For the chemical encoding of binary signals, we use a pH of 12.87 for encoding a signal of value “0” and a pH of 0.3 for encoding a signal of value 1. This setup is designed to ensure that the enzymatic reaction is inhibited in the presence of any “1” input, effectively simulating the NOR gate's logical operation. Table 3 presents the absorbance scores for outputs observed from our enzymatic NOR gate when subjected to different input patterns. The corresponding UV-vis absorbance curves are shown in the ESI.†

Table 3 Quantitative analysis of NOR gate operation using enzymatic reactions. The “digital output” column indicates the expected binary output based on the input combinations “In 1” and “In 2,” while “input pH encoding” represents the pH values used to encode the input signals. The “abs.” column lists the measured absorbance at 340 nm corresponding to NADH presence. The “Abs. score” is calculated from the absorbance using the provided equation, and the “normalized” column presents the final binary output after applying the thresholding value

In 1	In 2	Input pH encoding	Digital output	Abs.	Abs. score	Normalized
0	0	(12.87, 12.87)	1	0.411	1.057	1
1	0	(12.87, 0.30)	0	0.223	0.116	0
1	1	(0.30, 0.30)	0	0.233	0.163	0

---

Modeling OR gate

The OR gate, fundamentally the inverse of the NOR gate, outputs a “1” if at least one of its inputs is “1”. To model this gate effectively within our enzymatic system, we incorporate a third buffer to model the additional computational stage. This addition necessitates a re-evaluation of the concentration levels for the signals “0” and “1”, ensuring that the overall system accurately reflects the OR gate's logic. Hence, we use a pH of 0.6 for encoding a signal of value “0” and a pH of 14.39 for encoding a signal of value “1”, respectively. By adjusting these concentrations, we align the enzymatic reactions to mirror the expected behavior of an OR gate. Table 4 presents the absorbance scores for outputs observed from our enzymatic OR gate when subjected to different input patterns. The corresponding UV-vis absorbance curves are shown in the ESI.†

Table 4 Quantitative analysis of OR gate operation using enzymatic reactions. The “digital output” column indicates the expected binary output based on the input combinations “In 1” and “In 2,” while “input pH encoding” represents the pH values used to encode the input signals. The “abs.” column lists the measured absorbance at 340 nm corresponding to NADH presence. The “abs. score” is calculated from the absorbance using the provided equation, and the “normalized” column presents the final binary output after applying the thresholding value

In 1	In 2	Input pH encoding	Digital output	Abs.	Abs. score	Normalized
0	0	(0.60, 0.60)	0	0.235	0.175	0
1	0	(14.39, 0.60)	1	0.404	1.018	1
1	1	(14.39, 14.39)	1	0.419	1.094	1

---

Cascading AND-OR gates

For the purpose of demonstrating the cascading capability of 2-input gates within our enzymatic system, we model a 3-input circuit configuration as depicted in Fig. 4. This arrangement consists of an AND gate followed by an OR gate. The AND gate is realized through two buffers, whose output is subsequently integrated with another input via a third buffer to emulate the OR gate functionality. We used a pH of 0.3 for encoding a signal of value “0” and a pH of 14.6 for encoding a signal of value “1”. Fig. 5 illustrates the resulting outputs from our enzymatic cascaded gate system for two sample inputs, additional absorbance curves are provided in the ESI,† while Table 5 shows Absorbance scores for different input points.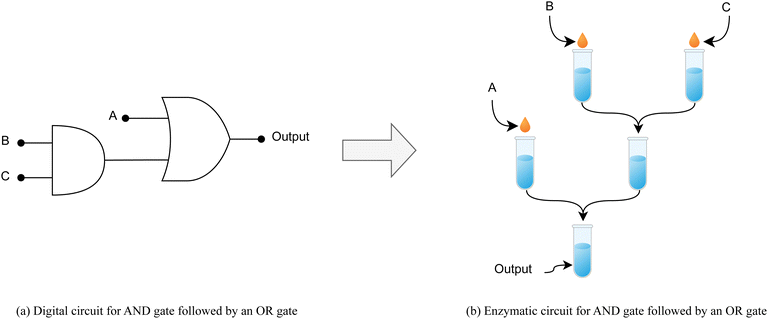

Fig. 4 (a) Conventional digital circuit comprised of cascading AND gate with OR gate. (b) Representing the same circuit using the enzymatic reactions model.

Fig. 5 UV-vis spectroscopy for the outputs of the AND-OR circuit modeled using enzymatic reactions.

Table 5 Quantitative analysis of the AND-OR circuit gate modeled using enzymatic reactions. The “digital output” column indicates the expected binary output based on the input combinations “A,” “B,” and “C,” where we use a pH of 14.6 to encode a signal of value “1” and a pH of 0.3 to encode a signal of value “0”. The “abs.” column lists the measured absorbance at 340 nm corresponding to NADH presence. The “abs. score” is calculated from the absorbance using the provided equation, and the “normalized” column presents the final binary output after applying the thresholding value

A	B	C	Digital output	Abs.	Abs. score	Normalized
0	0	0	0	0.224	0.118	0
0	1	0	0	0.239	0.195	0
1	0	0	1	0.391	0.956	1
0	1	1	1	0.396	0.982	1
1	0	1	1	0.411	1.055	1
1	1	1	1	0.420	1.101	1

---

Enzymatic machine learning model

Building upon the foundational principles outlined in preceding sections, we extend the application of enzymatic reactions to the realm of machine learning, specifically for the task of binary classification using a perceptron model. A perceptron is a classification model that can decide whether or not an input vector is a member of a specific class, as shown in Fig. 6(a). Hence, we propose a model analogous to a neural network perceptron, as illustrated in Fig. 6(b). In this model, what would traditionally be weights of a perceptron are instead represented by the concentration levels of chemical buffers. Input signals are modeled through variations in the concentrations of acids and bases within these buffers. The primary objective of this model is to classify a set of data points (x, y) into either positive or negative categories. For example, if a coordinate point (1, 1) is represented by the acid/base concentrations (x, y), then the point (2, 3) would be encoded with concentrations (2x, 3y) to reflect the proportional relationship between the points. Additionally, if we use concentrations of bases to represent positive coordinates, we choose acids with the same concentrations to represent their negative counterparts. Fig. 6(c) shows the mapping of different values into their corresponding pH encoding. This transformation allows for a straightforward mapping of input data into the biochemical domain, enabling the enzymatic network to process the information. Similar to how we compute the concentration for encoding the input signal, we adopt the same logic to calculate the correct buffer concentrations that mimic the neural network's weights, where we want to promote the forward reaction for positive samples and inhibit it for negative samples. Once these concentrations are computed, the model can classify data points based on the presence or absence of L-malic acid, respectively, wherein the presence of L-malic acid signifies a positive classification outcome, whereas its absence denotes a negative classification. To model our perceptron, two buffers were designated to handle the x and y coordinates, with their pH levels adjusted to 6.6 and 7.0 to model the network's weights. We validated 100 sample points with in silico simulation of the reaction. In addition, we evaluated four distinct points chemically, encompassing two positive samples and two negative samples. The positive samples were represented by coordinates (1, 1) and encoded with pH values of (13.0, 13.0) for the first point and (2, 3) encoded as (13.3, 13.48) for the second point, respectively. Conversely, the negative samples were represented by coordinates (−1, −1) and encoded with pH values of (1.0, 1.0) for the first point and (1, −3) encoded with pH values of (13.0, 0.52) for the second point. Fig. 6(d) provides a visual representation of the classification outcome of a sample point, while Table 6 shows the absorbance scores for the four points, showcasing the capability of our enzymatic model to distinguish between positive and negative classes.

Fig. 6 Enzymatic machine learning perceptron. (a) A conventional machine learning perceptron classifies points into positive and negative classes. (b) An equivalent enzymatic machine learning perceptron for point classification. The chemical buffers encode the weights, while the acids/bases encode the inputs. (c) Mapping of the input coordinates into pH values to be applied to the perceptron. (d) Sample absorbance curves for classifying the point (1, 1) using the enzymatic machine learning perceptron.

Table 6 Absorbance score for classification results of 4 different coordinate points using enzymatic machine learning classifier. The “input” column presents the input point coordinates, and the “abs.” column lists the measured absorbance at 340 nm, which corresponds to NADH presence. The “abs. score” is calculated from the absorbance using the provided equation, and the “normalized” column presents the final label after applying the thresholding value

Input	Input pH encoding	Digital label	Abs.	Abs. score	Normalized label
(1, 1)	(13.00, 13.00)	1	0.402	1.012	1
(−1, −1)	(1.00, 1.00)	0	0.242	0.210	0
(2, 3)	(13.30, 13.48)	1	0.425	1.124	1
(1, −3)	(13.00, 0.52)	0	0.254	0.269	0

---

Conclusion

In this paper, we introduced our approach to digital computation that utilizes enzymatic reactions to emulate the functionalities of digital logic gates and machine learning neurons. Our method leverages the pH sensitivity of the enzymatic reaction to encode binary signals through the concentrations of strong acids or bases. We explained the problem formulation to tune the concentrations of acids and bases to encode the input signals properly. Our empirical evaluations demonstrated the capability of our framework through the construction of digital gates and machine learning perceptron in the laboratory setting, illustrating the practical application of enzymatic reactions in computational tasks. The potential of enzymatic reactions in computing opens avenues for future research, including refining and exploring the integration of biological and electronic components to enhance computational performance or improve biomedical devices.

Methods

All solutions for the experiment were prepared using deionized water as a solvent (Millipore Milli-Q). For the signal encoding, we used 20 μL (per input) of hydrochloric acid (HCl, 36.5% to 38.0%, Fisher Chemical) and sodium hydroxide (NaOH, ≥97%, Fisher Chemical). The enzyme utilized was fumarase, obtained from a porcine heart (Sigma Aldrich, Natick, MA) dissolved in 0.1% bovine serum albumin solution (Sigma Aldrich, Natick, MA). The chemical buffers were based on a phosphate buffer solution (pH 7.00, Fluka). pH Meter Kit (PH700, Apera) was used to verify the pH across different reactions. Fumaric acid (>99.0%, Sigma Aldrich, Natick, MA) was used to prepare the reagent solutions. To detect the enzymatic reaction outcomes, we employed NAD+ and a glutamate-oxaloacetate suspension (Megazyme, Lansing, MI). The final measurements were conducted using UV spectroscopy (Varian Cary 50 Bio UV-Vis Spectrophotometer) to assess the success of the enzymatic processes.

Author contributions

A. A. designed the experiments. A. A. and S. M. performed the experiments. A. A., S. M., J. K. R., E. K., and S. R. analyzed the results. E. K., J. K. R., and S. R. provided direction and oversight. All authors provided notes and edits to the manuscript.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was partially supported by the National Science Foundation (NSF 2027108). The content is solely the responsibility of the authors and does not necessarily represent the official views of NSF.

References

1. A. Adamatzky, L. Bull and B. D. L. Costello, Unconventional computing 2007, Luniver Press, 2007.
2. A. Adamatzky, Advances in unconventional computing: Volume 1: Theory, Springer, 2016, vol. 22.
3. Y. Benenson, Nat. Rev. Genet., 2012, 13, 455–468.
4. A. Adamatzky, B. D. L. Costello and T. Asai, Reaction-diffusion computers, Elsevier, 2005.
5. J. Gorecki, K. Gizynski, J. Guzowski, J. Gorecka, P. Garstecki, G. Gruenert and P. Dittrich, Philos. Trans. R. Soc., A, 2015, 373, 20140219.
6. Z. Ezziane, Nanotechnology, 2005, 17, R27.
7. R. Binti abu Bakar and J. Watada, ICIC Exp. Lett. ICIC Int., 2008, 2, 101–108.
8. E. Rieffel and W. Polak, ACM Comput. Surv., 2000, 32, 300–335.
9. M. Savchuk and A. Fesenko, Cybern. Syst. Anal., 2019, 55, 10–21.
10. S. B. Ramezani, A. Sommers, H. K. Manchukonda, S. Rahimi and A. Amirlatifi, 2020 International joint conference on neural networks (IJCNN), 2020, pp. 1-8.
11. P. A. Frey and A. D. Hegeman, Enzymatic reaction mechanisms, Oxford University Press, 2007.
12. P. K. Agarwal, Microb. Cell Fact., 2006, 5, 1–12.
13. C. Frieden and R. A. Alberty, J. Biol. Chem., 1955, 212, 859–868.
14. A. A. Agiza, K. Oakley, J. K. Rosenstein, B. M. Rubenstein, E. Kim, M. Riedel and S. Reda, Nat. Commun., 2023, 14, 496.
15. E. Katz and V. Privman, Chem. Soc. Rev., 2010, 39, 1835–1857.
16. D. Harris and S. Harris, Digital design and computer architecture, Morgan Kaufmann, 2010.
17. N. H. Weste and D. Harris, CMOS VLSI design: a circuits and systems perspective, Pearson Education, India, 2015.
18. M. Sakthi Balan and H. Jürgensen, Nat. Comput., 2008, 7, 71–94.
19. H. Hug and R. Schuler, Bioinformatics, 2001, 17, 364–368.
20. R. Unger and J. Moult, Proteins: Struct., Funct., Bioinf., 2006, 63, 53–64.
21. T. Miyamoto, S. Razavi, R. DeRose and T. Inoue, ACS Synth. Biol., 2013, 2, 72–82.
22. P. Kulkarni, V. B. Leite, S. Roy, S. Bhattacharyya, A. Mohanty, S. Achuthan, D. Singh, R. Appadurai, G. Rangarajan and K. Weninger, et al. , Biophys. Rev., 2022, 3, 011306.
23. P. L. Gentili, Biomimetics, 2024, 9, 121.
24. A. Hjelmfelt, E. D. Weinberger and J. Ross, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 10983–10987.
25. A. S. Khalil and J. J. Collins, Nat. Rev. Genet., 2010, 11, 367–379.
26. W. Weber and M. Fussenegger, Nat. Rev. Genet., 2012, 13, 21–35.
27. O. Purcell and T. K. Lu, Curr. Opin. Biotechnol, 2014, 29, 146–155.
28. J. K. Rosenstein, C. Rose, S. Reda, P. M. Weber, E. Kim, J. Sello, J. Geiser, E. Kennedy, C. Arcadia and A. Dombroski, et al. , IEEE Trans. NanoBiosci., 2020, 19, 378–384.
29. C. E. Arcadia, E. Kennedy, J. Geiser, A. Dombroski, K. Oakley, S.-L. Chen, L. Sprague, M. Ozmen, J. Sello and P. M. Weber, et al. , Nat. Commun., 2020, 11, 691.
30. C. E. Arcadia, A. Dombroski, K. Oakley, S. L. Chen, H. Tann, C. Rose, E. Kim, S. Reda, B. M. Rubenstein and J. K. Rosenstein, Chem. Sci., 2021, 12, 5464–5472.
31. A. I. Bentez-Mateos, M. L. Contente, D. R. Padrosa and F. Paradisi, React. Chem. Eng., 2021, 6, 599–611.
32. F. H. Arnold, Acc. Chem. Res., 1998, 31, 125–131.
33. S. Yang, B. W. Bögels, F. Wang, C. Xu, H. Dou, S. Mann, C. Fan and T. F. de Greef, Nat. Rev. Chem., 2024, 1–16.
34. L. Grozinger, M. Amos, T. E. Gorochowski, P. Carbonell, D. A. Oyarzún, R. Stoof, H. Fellermann, P. Zuliani, H. Tas and A. Goñi-Moreno, Nat. Commun., 2019, 10, 5250.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02039a

---