Open Access Article
Open Access ArticleFull optimization of dynamic nuclear polarization on a 1 tesla benchtop polarizer with hyperpolarizing solids†‡
Ewoud
Vaneeckhaute
 *a,
Charlotte
Bocquelet
*a,
Charlotte
Bocquelet
 a,
Léa
Bellier
a,
Huu-Nghia
Le
b,
Nathan
Rougier
a,
Shebha Anandhi
Jegadeesan
a,
Léa
Bellier
a,
Huu-Nghia
Le
b,
Nathan
Rougier
a,
Shebha Anandhi
Jegadeesan
 c,
Sanjay
Vinod-Kumar
c,
Sanjay
Vinod-Kumar
 c,
Guinevere
Mathies
c,
Guinevere
Mathies
 c,
Laurent
Veyre
b,
Chloe
Thieuleux
c,
Laurent
Veyre
b,
Chloe
Thieuleux
 b,
Roberto
Melzi
d,
Daniel
Banks
b,
Roberto
Melzi
d,
Daniel
Banks
 e,
James
Kempf
e,
Quentin
Stern
e,
James
Kempf
e,
Quentin
Stern
 a and
Sami
Jannin
a and
Sami
Jannin
 a
a
aUniversité Claude Bernard Lyon 1, CNRS, ENS Lyon, UCBL, CRMN UMR 5082, 69100 Villeurbanne, France. E-mail: ewoud.vaneeckhaute@univ-lyon1.fr
bUniversité Claude Bernard Lyon 1, Institut de Chimie de Lyon, CP2M UMR 5128 CNRS-UCBL-CPE Lyon, 69616 Villeurbanne, France
cDepartment of Chemistry, University of Konstanz, Universitätsstr. 10, 78464, Konstanz, Germany
dBruker Italia S.r.l., Viale V. Lancetti 43, 20158 Milano, Italy
eBruker Biospin, Billerica, Massachusetts 01821, USA
First published on 11th July 2024
Abstract
Hyperpolarization by dissolution dynamic nuclear polarization (dDNP) provides the opportunity to dramatically increase the weak nuclear magnetic resonance (NMR) signal of liquid molecular targets using the high polarization of electron radicals. Unfortunately, the solution-state hyperpolarization can only be accessed once since freezing and melting of the hyperpolarized sample happen in an irreversible fashion. A way to expand the application horizon of dDNP can therefore be to find a recyclable DNP alternative. To pursue this ambitious goal, we recently introduced the concept of recyclable hyperpolarized flow (HypFlow) DNP where hyperpolarization happens in porous hyperpolarizing solids placed in a compact benchtop DNP polarizer at a magnetic field of 1 T and a temperature of 77 K. Here we aim to optimize the radical concentrations immobilized in hyperpolarizing solids with the objective of generating as much polarization as possible in a timeframe (<1 s) compatible with future recyclable DNP applications. To do so, the solid-state DNP enhancement factors, build-up rates and DNP spectra of different hyperpolarizing solids containing various nitroxide radical loadings (20–74 μmol cm−3) are compared against the DNP performance of varying nitroxide concentrations (10–100 mM) solvated in a glassy frozen solution. We demonstrate that in <1 s, polarization enhancement goes up to 56 and 102 with surface-bound and solvated radicals, respectively, under the optimized conditions. For the range of nitroxide concentrations used cross effect DNP seems to be the dominant mechanism under benchtop conditions. This was deduced from the electron paramagnetic resonance (EPR) lineshape of TEMPOL investigated using Q-band EPR measurements.
1. Introduction
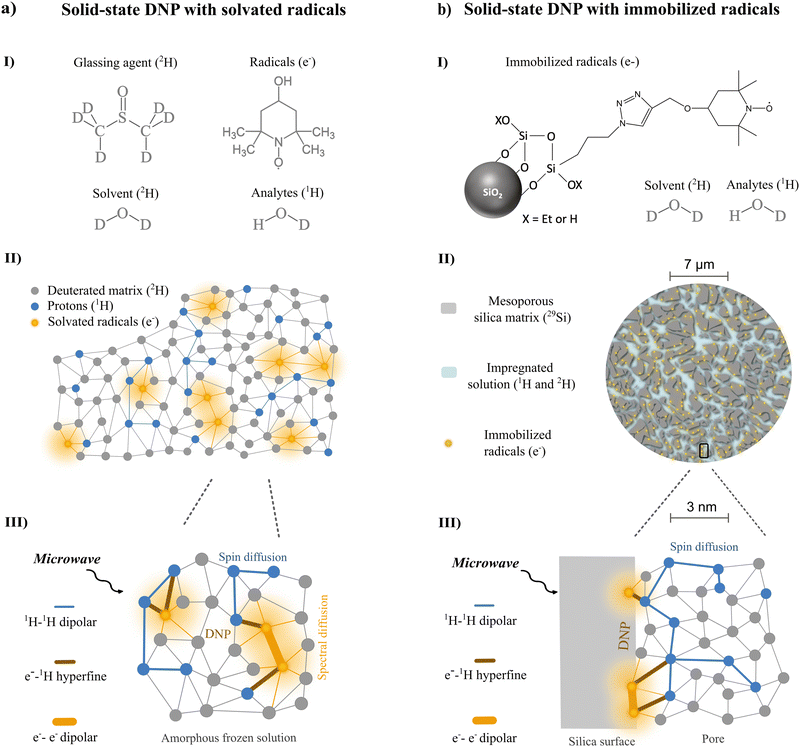
Nuclear magnetic resonance (NMR) is an indispensable spectroscopic tool for the analysis of complex analyte mixtures.1–3 Liquid-state NMR excels in providing structurally rich spectroscopic output that is robust, reliable, and reproducible due to the non-destructive properties of the technology. Moreover, the sensitivity constraints that are traditionally limiting NMR applications can be circumvented by recent advancements in hyperpolarization strategies temporarily bringing molecular targets into a transient hyperpolarized – or signal-enhanced – state.4–6Dissolution dynamic nuclear polarization (dDNP) is uniquely fitted for providing the higher sensitivity required for advancing mixture analysis applications via liquid-state NMR.7–9 Using dDNP, any analyte brought in close contact (1–5 nm) with a neighbouring paramagnetic radical with highly spin-polarized electrons in a frozen (1–4 K), glassy state can become transiently fuelled with nuclear spin hyperpolarization through microwave (μw) assisted polarization transfer inside a magnetic field.10 Then, spin diffusion, that thrives on energy-conservative dipolar flip-flops, allows for spontaneous redistribution of nuclear polarization to any analyte target (Fig. 1a).11 Afterwards, rapid dissolution with hot pressurized water melts and transfers the sample for hyperpolarized liquid-state NMR detection where fine structural features (Hz) of the analytes are revealed, previously obscured by strong dipolar interactions (kHz) in the frozen state.12 The general applicability of bringing analytes in close contact with a polarizing agent explains why sensitivity enhancement by dDNP is exceptionally promising towards hyperpolarization of multi-component chemical mixtures.13,14
However, the presence of the paramagnetic polarizing agents for fuelling hyperpolarization in the frozen state, also induces detrimental hyperpolarization losses both during and after the phase transition when in intricate contact with the analytes.15 As hyperpolarized analytes are forced into an out-of-equilibrium magnetic state, paramagnetic relaxation caused by the close presence of unpaired electrons drastically reduces the longitudinal relaxation time of the nuclear spins. This is caused by stochastic fluctuations of the electron spin state that are similar in frequency to the nuclear Larmor frequency. In solids, the main source of these fluctuations are spontaneous electron-pair flip-flops or electron longitudinal relaxation processes, while in liquids, the main source is considered molecular translational diffusion.16–18 Yet in all cases, the presence of electrons acts as a strong hyperpolarization sink. Consequentially, within milliseconds in solids and seconds in liquids, hyperpolarization after the phase transition is mostly lost. Therefore, after transferring the paramagnetic hyperpolarized mixture into a dedicated liquid-state NMR detection unit, only a limited one-shot window exists in which structural analysis of complex mixtures can be performed. This is considered an important bottleneck in applying dDNP for hyperpolarized NMR.19,20
Hyperpolarizing solids offer an elegant way to circumvent this roadblock. They are composed of porous materials (e.g. silica- or polymer-based) containing covalently immobilized radicals in which the analytes of interest can be impregnated (Fig. 1b).21–23 There is additional control over the physical distance between the unpaired electrons, distributed along the silica pore channels or even embedded in the solid framework, and the impregnated analytes residing in the pores.24 Since the rate of direct paramagnetic induced relaxation is dependent on the inverse sixth power of the distance between the electron and nuclear spins,10,11,25 optimization of pore geometry and radical immobilization can reduce the relaxation sink.26,27 On top, the ability to physically extrude the hyperpolarized analytes after melting has even more opportunities: the production of pure analyte solutions not contaminated and affected by any paramagnetic species becomes suddenly feasible.28,29
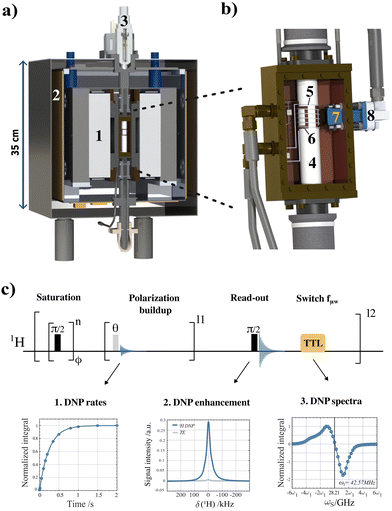
We aim to reach a new horizon of DNP applications by establishing methods, equipment and chemical systems that enable a repeated sequence of DNP hyperpolarization and solution-state NMR observation. This approach takes advantage of hyperpolarizing solids which will be key to developing a recyclable DNP alternative without dilution nor radical contamination. To pursue this ambitious goal, we recently introduced the concept of recyclable hyperpolarized flow (HypFlow) DNP in Bocquelet et al.30 The HypFlow DNP approach aims at operating with a closed loop cycle where hyperpolarization is generated in a heterogenous stationary phase of silica-based polarizing matrices (HYPSO) positioned in a compact and helium-free benchtop DNP polarizer which is schematically summarized in Fig. 2a and b. By utilizing a benchtop DNP polarizer at a magnetic field of 1 T and a temperature of 77 K, we gain a more modest sensitivity boost compared to traditional dDNP, but the higher temperature and accessible conditions also create the opportunity when hyperpolarizing matrices are used, to enable rapid melt and pure sample extraction in the future.31,32 A single sample could therefore be hyperpolarized several times if a dilution-free melting step is envisioned.33,34 When the sample is then pumped through a closed loop coupled to a benchtop NMR spectrometer for liquid-state detection, this could allow for compatibility with hyperpolarized two-dimensional NMR structural characterization advancing in-depth chemical mixture analysis.35
In this context, we present a general systematic DNP study for a series of different nitroxide radical concentrations solvated in a glassy frozen solution (Fig. 1a) and immobilized in hyperpolarizing solids (Fig. 1b) using the benchtop DNP polarizer (Fig. 2a and b). Our goal is to optimize the nitroxide radical concentration immobilized in hyperpolarizing solids with the objective of generating as much polarization as possible in a timeframe (<1 s) compatible with future recyclable DNP applications. Moreover, we want to probe the underlying DNP mechanism at play when working at these optimal radical concentrations in HypFlow DNP conditions. This way, future design of the hyperpolarizing solids might be distinctively optimized to allow for larger enhancement factors, suitable polarization build-up rates, and finally longer relaxation times for more efficient dilution-free melting to be performed.
More specifically, signal enhancements and corresponding build-up rates together with their characteristic relaxation times were measured for silica-immobilized nitroxide radical concentrations ranging from 20–74 μmol cm−3 and compared to solvated TEMPOL from 10–100 mM in a glassy state. At each set of radical concentrations, DNP spectra were also obtained by stepping the microwave frequency (fμw) between 27.7 and 28.3 GHz and plotting it against the proton enhancement factor. A fully automated experimental and processing approach was used on the benchtop DNP polarizer (Fig. 2a and b) to reach this goal. In Fig. 2c, the methodology to do so is summarized and is based on a single pseudo-3d pulse sequence that was able to extract (i) the DNP build-up rates, (ii) the thermal and DNP hyperpolarized NMR spectra and (iii) the DNP spectra via MATLAB (MathWorks, Massachusetts, USA) using a processing pipeline that is available via the Zenodo repository.†
Finally, initial investigation into the main hyperpolarization transfer mechanisms responsible for DNP at 1 T and 77 K using nitroxide radicals was assisted by performing Q-band (1.2 T) continuous-wave (CW) EPR experiments. The EPR lineshape of 50 mM TEMPOL radical in frozen solution at 1.2 T was used to rationalize the shape of the DNP spectra. From this, conclusive remarks on the optimization and rationalization of performing DNP at 1 T and 77 K using nitroxide radicals in amorphous frozen solutions and immobilized states are contextualized with the prospect of advancing DNP into a recyclable hyperpolarization technique.
2. Results and discussion
To compare the DNP performances of nitroxide radicals at 1 T and under cryogenic measurement conditions of 77 K in amorphous and immobilized conditions, a series of TEMPOL concentrations ranging from 10–100 mM were dissolved using a partially protonated 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 H2O
6 H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O
D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO-d6 (v
DMSO-d6 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v
v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) solution (1) to allow for good glassing capabilities when flash-frozen. TEMPOL was chosen as the reference DNP radical due to its chemical stability, proven DNP performance, and high compatibility towards immobilization onto porous materials as immobilization is essential for the envisioned recyclable DNP application.22,24,27
v) solution (1) to allow for good glassing capabilities when flash-frozen. TEMPOL was chosen as the reference DNP radical due to its chemical stability, proven DNP performance, and high compatibility towards immobilization onto porous materials as immobilization is essential for the envisioned recyclable DNP application.22,24,27
For immobilizing the nitroxide radicals, commercially available silica beads with an average pore diameter of 5 nm (Fig. S1, ESI‡) were used to generate a set of silica-based hyperpolarizing solids with varying nitroxide radical concentrations ranging from 20–74 μmol cm−3 referred to as HYPSO-5. The material properties of the used hyperpolarizing solids are summarized in Table 1.21 The exact pore volume of the HYPSO-5 samples was finally impregnated with a partially protonated 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 H2O
8 H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O (v
D2O (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) solution (2).
v) solution (2).
| [Nitroxide] (μmol cm−3) | Porous volume (cm3 g−1) | Pore diameter (nm) | Enhancement | Build-up rate (s−1) |
|---|---|---|---|---|
| 20 | 0.65 | 4 | 8 | — |
| 25 | 0.69 | 5 | 28 | 1.14 ± 0.19 |
| 43 | 0.63 | 4 | 42 | 0.94 ± 0.03 |
| 58 | 0.57 | 5 | 24 | 2.08 ± 0.18 |
| 74 | 0.55 | 4 | 19 | 2.08 ± 0.37 |
The main output of the systematic hyperpolarization study using the pseudo-3d pulse sequence shown in Fig. 2c is reported in Fig. 3a for the different nitroxide radical concentrations under amorphous frozen conditions and in Fig. 3b for the different immobilized nitroxide radicals concentrations. Based on the pulse sequence highlighted in Fig. 2c, DNP build-up rates (τdnp−1) were measured at each fμw which was then stepped automatically to obtain the overall DNP spectra. Afterwards, the MATLAB-based processing pipeline provided the enhancement factors (Fig. 3-I and II) together with the corresponding build-up rates at both the positive and negative extrema (Fig. 3-III and IV) of the DNP spectra (Fig. 3-V). The automated and systematic approach minimized any external factors that potentially could hinder comparison of the DNP performances between radical concentrations. More detailed information on the sample preparation, NMR acquisition, DNP enhancement factor calculation, DNP build-up rate extraction and processing workflow can be found in the Materials and methods section and in the ESI.‡
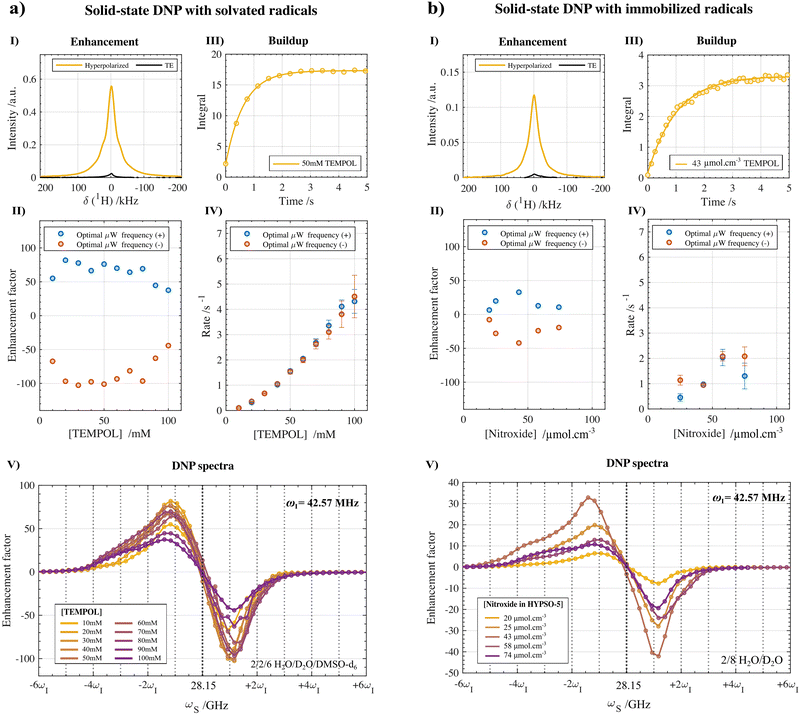 | ||
Fig. 3 Solid-state 1H-DNP performances at 1 T and 77 K with varying concentrations of TEMPOL radicals (a) randomly distributed in an amorphous frozen solution (10–100 mM in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 H2O 6 H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO-d6 (v DMSO-d6 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) solution) and (b) under chemically immobilized conditions in the HYPSO-5 silica mesoporous matrix (20–74 μmol cm−3 impregnated with a partially protonated 2 v) solution) and (b) under chemically immobilized conditions in the HYPSO-5 silica mesoporous matrix (20–74 μmol cm−3 impregnated with a partially protonated 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 H2O 8 H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O (v D2O (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) solution). A single pulse sequence (Fig. 2c) with the corresponding MATLAB processing pipeline (available in Zenodo†) enabled us to capture the thermal and DNP hyperpolarized NMR spectra (at the optimal fμw) (I), the enhancement factors (II), the hyperpolarization build-up profiles (III), the corresponding rates τdnp−1 (IV) and the DNP spectra (V) in a single NMR experiment. The enhancement factors were calculated according to eqn (2) in the experimental section, while τdnp−1 were fitted using the monoexponential function shown in eqn (3) with typically 15 build-up points. The error boundaries correspond to a 95% confidence interval. More information about the processing and experimental parameters can be found in the Materials and methods section. v) solution). A single pulse sequence (Fig. 2c) with the corresponding MATLAB processing pipeline (available in Zenodo†) enabled us to capture the thermal and DNP hyperpolarized NMR spectra (at the optimal fμw) (I), the enhancement factors (II), the hyperpolarization build-up profiles (III), the corresponding rates τdnp−1 (IV) and the DNP spectra (V) in a single NMR experiment. The enhancement factors were calculated according to eqn (2) in the experimental section, while τdnp−1 were fitted using the monoexponential function shown in eqn (3) with typically 15 build-up points. The error boundaries correspond to a 95% confidence interval. More information about the processing and experimental parameters can be found in the Materials and methods section. | ||
2.1. DNP enhancement factors
As shown in Fig. 3a-I and II, a maximal proton enhancement factor of 102 was obtained with solvated TEMPOL at a concentration of 50 mM using solution (1) after fμw optimization of 28.2 GHz and correction for the probe background (Fig. S2, ESI‡). With respect to the radical concentration, the enhancement shows a steep increase in amplitude from 10 mM up until 30 mM followed by a plateau until 50 mM with a fall-off in efficiency from 60 mM TEMPOL onward (the calculated enhancement at 70 mM is recognized as an outlier). For each concentration of TEMPOL, the maximal enhancement occurred systematically at the negative lobe of the DNP spectra (circles, red) and shows 25% higher polarization compared to optimal fμw inducing positive hyperpolarization (squares, blue). Overall, the dependency on concentration is analogues to what is observed under traditional dDNP conditions at 6.7 T and 1–4 K, yet in our case already at lower radical concentrations (>20 mM) enhancement starts reaching optimal values. The optimal DNP enhancement when using HYPSO-5 powders reaches a factor of 42 at a concentration of 43 μmol cm−3 using solution (2) as shown in Fig. 3b-I and II and reported in Table 1. The hyperpolarization dependency on the radical loading shows a narrower window of optimal concentrations when the nitroxide radicals are immobilized onto the silica matrix than when dissolved in solution before freezing. At a higher nitroxide concentration of 74 μmol cm−3, the enhancement factor therefore drops below 20.2.2. DNP build-up rates
The overall DNP build-up rates (τdnp−1) in the benchtop DNP polarizer for different solvated and immobilized nitroxide radical concentrations are plotted against each other in Fig. 3-IV. Specifically, the DNP rates that were measured at the optimal fμw for obtaining positive (circles, blue) and negative (circles, red) DNP optima are shown. The individual build-up curve of the optimal radical concentrations and microwave conditions are represented in Fig. 3-III. In general, the position of the fμw for optimal (−) DNP and (+) DNP did not seem to impact the bulk polarization transfer rate much. Both for the positive and negative maxima of the DNP spectra show in Fig. 3-IV, τdnp−1 was found to be equal within the error boundaries of the exponential fit for most radical concentrations (besides 25 μmol cm−3). This statement can be generalized to any microwave frequency and to any nitroxide concentration either in a frozen solution or in HYPSO-5. In Fig. 4a this is illustrated by plotting τdnp−1 at each corresponding fμw for the 50 mM TEMPOL. Note that outside the fμw range where DNP is inefficient, τdnp−1 could not be fitted properly anymore as observed in Fig. 4b. The remaining concentrations for the solvated and immobilized nitroxide radicals are provided in Fig. S6 and S7 that are found in the ESI.‡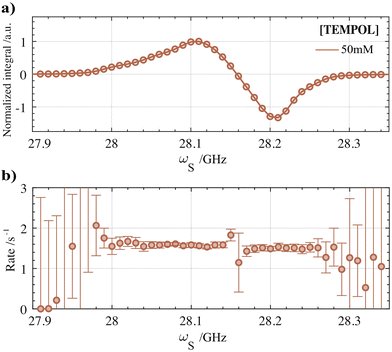 | ||
| Fig. 4 (a) 1H-DNP spectrum measured for the optimal TEMPOL concentration of 50 mM at 1 T and 77 K. (b) 1H-DNP build-up rates (τdnp−1) at each corresponding fμw of the DNP spectrum. τdnp−1 values were extracted using the MATLAB processing pipeline after correction for the background build-up (see Fig. S4 and S5 (ESI‡)). The same methodology was used for each nitroxide concentration in frozen solution or in the hyperpolarizing solids. The results are presented in Fig. S6 and S7 of the ESI.‡ | ||
For solvated TEMPOL, a non-linear correlation of τdnp−1 with an increasing nitroxide concentration is also noticeable in Fig. 3a-IV. In the benchtop DNP polarizer, τdnp−1 ranges from 0.2 s−1 for 10 mM TEMPOL towards 4.5 s−1 for 100 mM TEMPOL. By increasing the number of electrons (e) in the amorphous frozen solution, the dipolar interaction strength between electrons is influenced in particular. Assuming a random statistical distribution of electrons, the e–e dipolar interaction will increase proportionally with concentration as well.36,37 This gives us the ability to gain insight into the dependency of τdnp−1 on the e–e dipolar interaction strength. In Fig. S3 (ESI‡), the relationship between the build-up time and the radical concentration was fitted with a simple non-linear model according to:
| τdnp−1 = αCλe with Dee ∝ Ce, | (1) |
In the pores of HYPSO-5, the impact of varying the immobilized nitroxide concentration on τdnp−1 of the impregnated partially protonated solution (2) is less predictable than in the case of nitroxides in a glassy state. This can be noticed when comparing Fig. 3a-IV with Fig. 3b-IV. Instead of the monotonically increasing τdnp−1 for solvated nitroxides, the build-up rates for immobilized nitroxides feature a plateau when reaching higher concentrations. This is not entirely unexpected since during immobilization of the nitroxide precursor in the pores of HYPSO-5, effects such as clustering of the radicals are thought to be significant especially at higher radical loading. The consequences that the clustering has on DNP in hyperpolarizing solids are however not yet fully understood.39
At the optimal concentration of 43 μmol cm−3, the polarization rate during fμw equals 0.94 ± 0.03 s−1. When comparing this with typical 1H build-up rates for HYPSO-5 under dissolution DNP conditions,21 the gain in speed approximates two orders of magnitude, which is beneficial for limiting the total recycle time and therefore using it in the context of the future HypFlow DNP approach.
2.3. DNP spectra
The DNP spectra plotted for each of the nitroxide concentrations are overlayed in Fig. 3a-V. For the lowest concentration of 10 mM, a quasi-symmetrical positive and negative lobe of the DNP spectra is apparent separated by slightly more than 2 times the Larmor frequency (ωI of 42.57 MHz) of the hyperpolarized proton nuclei under observation. A separate representation of the DNP spectra for each concentration is provided in Fig. S8 (ESI‡). Increasing to higher nitroxide concentrations gradually results in more asymmetry. In particular, for the positive lobe, a broader polarization enhancement profile becomes apparent at high nitroxide concentrations. One of the possible explanations could be that the high concentration of electrons is affecting the overall line shape of the EPR profile. This will in principle also be reflected in the DNP spectra. A general methodology for rationalizing the shape of the DNP spectra in these low-field conditions is given later (Fig. 6 and 7). However, deeper investigation to explain the change in 1H-DNP spectra with radical concentration is planned for the future. This could include radical clustering effects or the influence of the increased e–e dipolar interactions at higher radical concentrations.For HYPSO-5, an overlay of the measured DNP spectra after immobilizing different amounts of nitroxide radical on the mesoporous silica is shown in Fig. 3b-V and Fig. S9 (ESI‡) for a separate representation. The DNP spectra have a similar appearance as observed for solvated TEMPOL in frozen solution, again showing maximal and minimal hyperpolarization at respectively around +ωI and −ωI. However, an overall lower proton enhancement factor is observed when comparing it with Fig. 3a-V where the performance of TEMPOL in an amorphous glassy state is shown. A completely random distribution of radicals which is believed to benefit DNP efficiency, cannot be guaranteed when immobilizing the TEMPOL derivative in the pores of HYPSO-5. However, as previously reported,21 the pore geometry of HYPSO-5 has been tailored to imitate the random distribution of radicals compared to previous generations of structured silica-based hyperpolarizing solids with highly ordered porosity.24,27
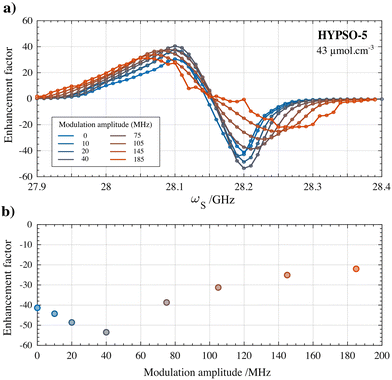
Finally, the influence of fμw modulation on the DNP performance in the HYPSO-5 powders was also investigated. The beneficial effect of using fμw modulation was much more pronounced in HYPSO-5 powders (>25% increase) than for the glassy solution where it did not improve DNP substantially. Inhomogeneities in radical distribution in HYPSO-5 can lead to inefficient spectral diffusion compared to radicals in a glassy frozen solution. Frequency modulation thus could potentially compensate for a lack of spectral diffusion in some regions of the HYPSO-5 powder. Fig. 5a shows the effect of varying the frequency modulation bandwidth Δfμw on the DNP spectrum of the best performing HYPSO-5 powder with 43 μmol cm−3 of nitroxide radical loading. In Fig. 5b, the polarization enhancement at optimal DNP is plotted. A maximum enhancement of 56 is reached at Δfμw of 40 MHz using a modulation frequency (fmod) of 60 kHz with a triangular shape. With further increasing Δfμw, the enhancement factor drops. The DNP spectra become broader and less resolved as seen in Fig. 5a. The reason is the simultaneous generation of both positive and negative nuclear spin hyperpolarization due to the large fμw irradiation bandwidth. Note that the overall comparison made in Fig. 3a-V was done without the use of any fμw modulation to ensure reliable comparison of the DNP characteristics of nitroxide radicals under solvated and immobilized conditions.
2.4. DNP mechanism for polarization transfer
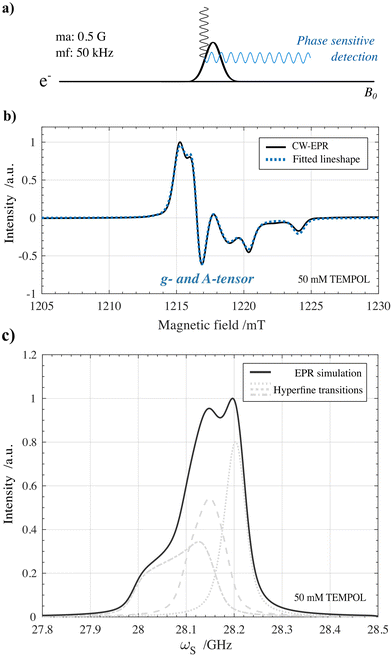
Insights into the polarization transfer mechanism which is dominant when performing DNP can be crucial for tailoring the radicals used for hyperpolarization. In high-field MAS-DNP, large research efforts have been made in this regard where the cross effect mechanism has been determined to be the dominant DNP mechanism for broad nitroxide-based radicals at optimal concentrations.40–42 We found a first set of indications that when performing static solid-state DNP using optimized TEMPOL concentrations at 1 T and 77 K, the cross effect polarization transfer mechanism should also be taken into account.The indications are based on rationalizing the shape of the 1H DNP spectra in Fig. 3(V) for either solid effect or cross effect. The line shape is based on the expected EPR profile of 50 mM solvated TEMPOL in frozen solution at 1 T and 77 K. For this, first a continuous-wave (CW) EPR measurement shown in Fig. 6a was performed on an identical 50 mM TEMPOL frozen solution under similar conditions of 1.2 T (Q-band, 34 GHz) and 77 K. The resulting EPR spectrum is shown in Fig. 6b. After fitting the CW-EPR spectrum using the Easyspin MATLAB package,43 the anisotropic g-tensor and hyperfine A-tensor values were extracted together with the homogeneous broadening parameters for 50 mM TEMPOL (Table 2).
| Inhomogeneous broadening (Δ) | Homogeneous broadening (δ) | ||||
|---|---|---|---|---|---|
| g-tensor (unitless) | A-tensor (MHz) | Lorentzian (MHz) | Gaussian (MHz) | ||
| g xx | 2.008 | A xx | 24.23 | 17.65 | 15.63 |
| g yy | 2.005 | A yy | 16.96 | ||
| g zz | 2.001 | A zz | 103.33 | ||
Afterwards, the extracted parameters were used to predict the fμw-swept EPR profile for 50 mM TEMPOL under HypFlow DNP conditions shown in Fig. 6c. The exact conditions in which the benchtop DNP polarizer was operating were derived from the chemical shift of the solid-state proton peak (ωI = 42.669 MHz which corresponds to a field of 1.0022 T). A detailed description on the EPR experiment and fitting procedure can be found in the Materials and methods section. The large anisotropy of the g-tensor and hyperfine tensor due to the spin-1 14N nucleus results in the large inhomogeneous broadening spanning over 350 MHz as can be seen in Fig. 6c. Especially at low temperatures (1–4 K) and moderate magnetic fields (up to 7 T) these EPR properties have been recognized to enable effective hyperpolarization of high-gamma nuclei such as protons by means of thermal mixing induced polarization transfer.44–47 However, in a magnetic field of 1 T and at an operating temperature of 77 K, field- and temperature-dependent electronic and nuclear interactions including their relaxation rates change, reducing the thermal mixing efficiency, making room for the solid effect or cross effect polarization transfer to become dominant.48–50
While for narrow line radicals the resulting DNP spectra and optimal fμw positions can be discriminated for either the solid effect or cross effect case, for broad line radicals this becomes less straightforward.51 We therefore attempted to rationalize the corresponding DNP spectra inspired by the electron bin model in the case of TEMPOL described in Kundu et al.52 For now, we chose to disregard any effect of hole burning or spectral diffusion to remain in scope of the paper.38,52 By discretizing the EPR profile in 1024 points, an estimation of the shape of the DNP spectrum assuming the solid effect and cross effect could be calculated using respectively eqn (4) and (5) available in the Materials and methods section. After implementing the correct matching condition, the experimental DNP spectrum acquired for 50 mM TEMPOL in a glassy frozen solution was compared to the resulting DNP spectra simulations. The results of this analysis are shown in Fig. 7.
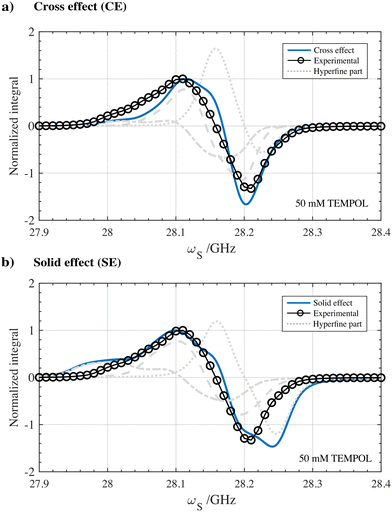 | ||
| Fig. 7 Simulated 1H DNP spectra assuming (a) cross effect and (b) solid effect type of polarization transfer using 50 mM TEMPOL in a partially protonated frozen glassy solution at 77 K and 1 T. The calculated line shapes assuming the cross effect and solid effect are overlayed with the experimental 1H DNP spectrum as a comparison. Solid-state EPR simulations of TEMPOL at 1.0022 T were performed using the Easyspin MATLAB package and based on experimental CW-EPR measured at 1.2 T as can be seen in Fig. 6. The 1H-DNP spectrum simulations are based on a straightforward analytical electron bin model assuming monochromatic microwave hole burning without spectral diffusion. Detailed information on the acquisition and simulation of the DNP spectra can be found in the Materials and methods section. | ||
Despite the simplicity of the model, the calculated DNP spectrum assuming the cross effect shown in Fig. 7a seems to reflect the characteristics of the experimental 1H DNP spectrum. In particular, the position and shape of the negative lobe of the calculated DNP spectrum are in better agreement. In contrast, assuming the solid effect, the calculated DNP spectrum illustrated in Fig. 7b shows a broader DNP profile with polarization being generated up to 28.25 GHz. The DNP simulations presented in Fig. 7 together with the non-linear dependency of the DNP build-up rate on the radical concentration shown in Fig. 3a-IV are therefore a first set of indications that the cross effect seems an important contributor to enhancing nuclear spins at 1 T and 77 K using solvated nitroxide radicals. Surprisingly, the cross effect seems dominant over the entire range of nitroxide concentration from 10–100 mM, while one would expect solid effect contributions to become more significant at lower concentrations.48 However, in Fig. 2a-V, the position of the DNP optima and the overall shape of the DNP profiles are only slightly influenced by the radical concentration. Which minimum nitroxide concentration is required for the cross effect to be dominant over the solid effect could therefore be an interesting question to solve in the future. Finally, the experimental solid-state DNP spectra measured for solvated 50 mM TEMPOL and for 43 μmol cm−3 HYPSO-5 are overlayed and showcased in Fig. S10 (ESI‡). The overlapping line shape could be an indication that, also when using hyperpolarizing solids at benchtop conditions, cross effect polarization transfer from the dipolar coupled electrons on the surface of the pores needs to be considered. Yet, more definite insights can only be realized when considering all other processes impacting DNP such as spectral diffusion, spin diffusion and paramagnetic induced relaxation. This is aimed for future investigation.
3. Conclusions
Optimization of the radical concentration used in a benchtop DNP polarizer operating at 1 T and 77 K has indicated that for HYPSO-5 an optimal loading of 43 μmol cm−3 nitroxide radical gives proton polarization enhancement inside the pores up to 56 in under a second. Solvated nitroxide radicals in the form of TEMPOL embedded in frozen solution, even allows for proton enhancement factors up to 100 for the optimal concentration of 50 mM. This is particularly promising in view of future HypFlow DNP applications. Two-dimensional experiments can benefit from a fast recycle time giving an approximate acquisition time of 10 minutes for 2D liquid-state hyperpolarized experiments with 512 transients. Moreover, we found the first indications that DNP using broad line nitroxide radicals at a low-magnetic field and high temperatures is dominated by cross effect polarization transfer. This indication includes analytical cross effect DNP spectrum simulations derived from the Q-band EPR profile of TEMPOL that agree well with the experimentally obtained 1H DNP spectrum. Future optimization of hyperpolarizing solids towards cross effect DNP will therefore benefit our goal to achieve recyclable hyperpolarization that is produced under accessible conditions.4. Materials and methods
4.1. 1H-DNP experiments at 1 T and 77 K
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 H2O
6 H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O
D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO-d6 (v
DMSO-d6 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v
v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) (1) was doped with varying quantities of a stock polarizing agent solution containing TEMPOL radicals to finally generate 10 samples with a varying nitroxide concentration of 10 mM to 100 mM in steps of 10 mM. All chemicals were purchased from Sigma-Aldrich and the deuteration purity for D2O and DMSO-d6 were respectively 99.5% and 99.96%. This sample formulation with the corresponding preparation procedure ensured good amorphous glass-forming capabilities to end up with a random distribution of radicals. The final amount of proton spins eligible for DNP hyperpolarization amounts to a concentration of 22 M. Finally, by filling a 4 mm (o.d.) Wilmad quartz EPR sample holder with 200 μL of the 1H DNP test solution, the solid-state DNP performances at 1 T and 77 K could be benchmarked according to the experimental design described later.
v) (1) was doped with varying quantities of a stock polarizing agent solution containing TEMPOL radicals to finally generate 10 samples with a varying nitroxide concentration of 10 mM to 100 mM in steps of 10 mM. All chemicals were purchased from Sigma-Aldrich and the deuteration purity for D2O and DMSO-d6 were respectively 99.5% and 99.96%. This sample formulation with the corresponding preparation procedure ensured good amorphous glass-forming capabilities to end up with a random distribution of radicals. The final amount of proton spins eligible for DNP hyperpolarization amounts to a concentration of 22 M. Finally, by filling a 4 mm (o.d.) Wilmad quartz EPR sample holder with 200 μL of the 1H DNP test solution, the solid-state DNP performances at 1 T and 77 K could be benchmarked according to the experimental design described later.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 H2O
8 H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O (v
D2O (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) solution (2) amounting to the total pore volume (determined via N2 physisorption) of each of the HYPSO-5 samples (Table 1) was impregnated in approximately 40 mg of the corresponding powder using an incipient wetness impregnation technique with continuous stirring, until the sample appeared dry again. No DMSO-d6 was required since the amorphous distribution of radicals which is beneficial for DNP is already achieved by immobilization via silica coating. The 2
v) solution (2) amounting to the total pore volume (determined via N2 physisorption) of each of the HYPSO-5 samples (Table 1) was impregnated in approximately 40 mg of the corresponding powder using an incipient wetness impregnation technique with continuous stirring, until the sample appeared dry again. No DMSO-d6 was required since the amorphous distribution of radicals which is beneficial for DNP is already achieved by immobilization via silica coating. The 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 ratio between H2O and D2O gave rise to 0.88 mmol of proton spins available for DNP hyperpolarization under immobilized conditions of radicals.
8 ratio between H2O and D2O gave rise to 0.88 mmol of proton spins available for DNP hyperpolarization under immobilized conditions of radicals.
Specifically, the benchmarking protocol started with a saturation block using hard π/2 rf-pulses with alternating phases that are separated by a short delay and repeated 50 times. After destroying the residual magnetization on the proton rf-channel, the hyperpolarization build-up was monitored via a small π/36 flip angle rf-pulse that allowed us to trace the 1H-NMR signal. A total of 15 small angle rf-pulses were typically used to monitor the build-up with a delay that was depending on the DNP rate. Note that during the entire duration of the pulse sequence the microwave was switched on at maximum power (5 W) since no TTL gating was available. After the build-up sequences, a hard π/2 rf-pulse was used to maximize the detected hyperpolarized signal for finally constructing the DNP spectra and calculating the enhancement factor (vide infra). Finally, a TTL pulse generated by the NMR console positioned after the final acquisition was read by an Arduino board to trigger the microwave source to change frequency by 10 MHz during a given delay of 5 s, after which the pulse sequence reinitialized its saturation and detection cycle. The fμw was swept from 27.8 to 28.44 GHz and generated 65 separate DNP build-ups (15 FID's) and a single 1H-NMR spectrum (1 FID) in series, thus resulting in 1040 transients in the pseudo F1 dimension. Since the DNP build-up rates are considerably fast at optimal nitroxide concentrations (around 2 s−1 for 50 mM), the total acquisition time for fully benchmarking the DNP samples was on average 12 minutes. For the lower radical concentration samples, the total acquisition time was prolonged up to 72 minutes.
A MATLAB-based processing pipeline, available in the ESI,‡ automatically rearranged the F1 dimension into the small and large flip-angle 1D NMR spectra which after integration generates the DNP build-up plots and the DNP spectra shown in Fig. 3. The signal enhancement factors were calculated according to the following formula:
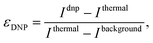 | (2) |
Next, the extraction of the build-up rates was performed by fitting the integrated small flip-angle signals (Idnpt) according to the exponential build-up:
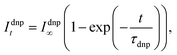 | (3) |
Finally, the DNP spectra were constructed based on the enhancement factor calculation of eqn (2). Additionally, to counteract a drift of the magnetic field due to potential temperature instabilities in the magnet, the microwave frequency values used for constructing the DNP spectra were corrected according to the Larmor frequency of the 1H signal. Also, to make sure the absolute integration values (Idnp) were consistent over the different concentrations, all processing was performed using 8k datapoints in the F2 dimension and the same exponential line broadening of 1 kHz. Since the MATLAB processing pipeline only imported frequency domain NMR data, the fast Fourier transform, and line broadening were performed using Topspin.
4.2. Q-band EPR experiments at 1.2 T and 77 K
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 H2O
6 H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O
D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO-d6 (v
DMSO-d6 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v
v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v). After dilution to the desired radical concentration (50 mM), 1 μL of the DNP solution was taken in a 1.6 mm (o.d.) quartz tube to perform the EPR experiments.
v). After dilution to the desired radical concentration (50 mM), 1 μL of the DNP solution was taken in a 1.6 mm (o.d.) quartz tube to perform the EPR experiments.
4.2.3.1. CW EPR. Field-swept CW EPR experiments were conducted with a field modulation amplitude of 0.5 G at a modulation frequency of 50 kHz for phase-sensitive detection of the reflected microwave signal. The microwave power was set to 60 μW (25 dB attenuation), and the microwave frequency was 34.1842 GHz.
4.3. DNP simulations
First, the anisotropic g- and A-tensor and homogeneous broadening parameters for the 50 mM TEMPOL sample were derived by fitting the experimental CW Q-band EPR measurement (1.2 T, 34 GHz) on an identical sample. Afterwards, an Easyspin43 simulated frequency-swept EPR profile was simulated at the exact magnetic field of 1.0022 T (deduced from ωI) in which the DNP spectrum was acquired. The resulting electron density profile was discretized into N = 1024 points, for which the following equations52,53 were used to calculate the shape of the DNP spectrum assuming solid effect and cross effect respectively: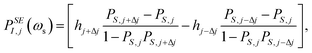 | (4) |
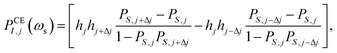 | (5) |
Author contributions
SJ conceived the project. EV and QS supervised the work performed. EV, CB, LB, and NR performed the experimental work. HNL synthesized the hyperpolarizing solids used in this work under the supervision of CT and LV. SVK, SAJ and GM provided the Q-band CW-EPR measurements on TEMPOL. JK, DB and RM provided the prototype benchtop DNP polarizer and further technological and scientific support. EV wrote the manuscript and all authors contributed to refining the manuscript.Data availability
The main data reported in the manuscript consists of NMR and EPR data for which the raw data is available in the Zenodo repository: https://zenodo.org/records/11120019. The DOI is also included in the main manuscript. The data folder contains the raw NMR and EPR data used in the manuscript to benchmark the DNP performance of different hyperpolarizing solids containing various nitroxide radical loadings compared against the DNP performance of varying nitroxide concentrations (10–100 mM) solvated in a glassy frozen solution. The NMR data is formatted in a pseudo-3d data Bruker format. The EPR data is formated in a text file. The code folder contains the script to process the pseudo-3d data to extract the DNP parameters. The code folder also contains the script to estimate the lineshape of the DNP spectra in the solid effect and cross effect case using the EPR data as input.Conflicts of interest
There are no conflicts to declare. The authors declare no competing financial interest. JK, DB and RM are employees of Bruker who co-developed the benchtop 1 T DNP prototype polarizer system.Acknowledgements
We acknowledge Bruker Biospin for providing the prototype benchtop DNP polarizer. We additionally acknowledge C. Jose and C. Pages for use of the ISA Prototype Service, and S. Martinez of the UCBL mechanical workshop for machining parts of the experimental apparatus. This research was supported by ENS-Lyon, the French CNRS, Lyon 1 University, the Deutsche Forschungsgemeinschaft (Grant No: SFB 1527, Project No. 454252029), the European Research Council under the European Union's Horizon 2020 research and innovation program (ERC Grant Agreements No. 101044726/HypFlow) and the French National Research Agency (project ‘HyMag’ ANR-18-CE09-0013).References
- C. K. Larive, G. A. Barding and M. M. Dinges, Anal. Chem., 2015, 87, 133–146 CrossRef CAS PubMed.
- T. W.-M. Fan, Prog. Nucl. Magn. Reson. Spectrosc., 1996, 28, 161–219 CrossRef CAS.
- J. Marchand, E. Martineau, Y. Guitton, G. Dervilly-Pinel and P. Giraudeau, Curr. Opin. Biotechnol., 2017, 43, 49–55 CrossRef CAS PubMed.
- V. Ribay, C. Praud, M. P. M. Letertre, J.-N. Dumez and P. Giraudeau, Curr. Opin. Chem. Biol., 2023, 74, 102307 CrossRef CAS PubMed.
- J.-N. Dumez, J. Milani, B. Vuichoud, A. Bornet, J. Lalande-Martin, I. Tea, M. Yon, M. Maucourt, C. Deborde, A. Moing, L. Frydman, G. Bodenhausen, S. Jannin and P. Giraudeau, Analyst, 2015, 140, 5860–5863 RSC.
- L. Sellies, I. Reile, R. L. E. G. Aspers, M. C. Feiters, F. P. J. T. Rutjes and M. Tessari, Chem. Commun., 2019, 55, 7235–7238 RSC.
- S. Jannin, J.-N. Dumez, P. Giraudeau and D. Kurzbach, J. Magn. Reson., 2019, 305, 41–50 CrossRef CAS PubMed.
- C. Hilty and S. Bowen, Org. Biomol. Chem., 2010, 8, 3361–3365 RSC.
- B. Plainchont, P. Berruyer, J.-N. Dumez, S. Jannin and P. Giraudeau, Anal. Chem., 2018, 90, 3639–3650 CrossRef CAS PubMed.
- A. Abragam and M. Goldman, Rep. Prog. Phys., 1978, 41, 395–467 CrossRef CAS.
- G. R. Khutsishvili, Phys.-Usp., 1966, 8, 743 CrossRef.
- J. H. Ardenkjær-Larsen, B. Fridlund, A. Gram, G. Hansson, L. Hansson, M. H. Lerche, R. Servin, M. Thaning and K. Golman, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10158–10163 CrossRef PubMed.
- K. Singh, C. Jacquemmoz, P. Giraudeau, L. Frydman and J.-N. Dumez, Chem. Commun., 2021, 57, 8035–8038 RSC.
- J. Eills, D. Budker, S. Cavagnero, E. Y. Chekmenev, S. J. Elliott, S. Jannin, A. Lesage, J. Matysik, T. Meersmann, T. Prisner, J. A. Reimer, H. Yang and I. V. Koptyug, Chem. Rev., 2023, 123, 1417–1551 CrossRef CAS PubMed.
- W. E. Blumberg, Phys. Rev., 1960, 119, 79–84 CrossRef CAS.
- A. Abragam, V. Bouffard and Y. Roinel, J. Magn. Reson., 1969, 1976(22), 53–63 Search PubMed.
- I. J. Lowe and D. Tse, Phys. Rev., 1968, 166, 279–291 CrossRef CAS.
- C. D. Jeffries, Proc. Phys. Soc., 1966, 88, 257–258 CrossRef CAS.
- P. R. Vasos, A. Comment, R. Sarkar, P. Ahuja, S. Jannin, J.-P. Ansermet, J. A. Konter, P. Hautle, B. van den Brandt and G. Bodenhausen, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18469–18473 CrossRef CAS PubMed.
- X. Ji, A. Bornet, B. Vuichoud, J. Milani, D. Gajan, A. J. Rossini, L. Emsley, G. Bodenhausen and S. Jannin, Nat. Commun., 2017, 8, 1–7 CrossRef PubMed.
- M. Cavaillès, A. Bornet, X. Jaurand, B. Vuichoud, D. Baudouin, M. Baudin, L. Veyre, G. Bodenhausen, J.-N. Dumez, S. Jannin, C. Copéret and C. Thieuleux, Angew. Chem., Int. Ed., 2018, 57, 7453–7457 CrossRef PubMed.
- D. Gajan, A. Bornet, B. Vuichoud, J. Milani, R. Melzi, H. A. van Kalkeren, L. Veyre, C. Thieuleux, M. P. Conley, W. R. Grüning, M. Schwarzwälder, A. Lesage, C. Copéret, G. Bodenhausen, L. Emsley and S. Jannin, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 14693–14697 CrossRef CAS PubMed.
- K. Nishimura, H. Kouno, Y. Kawashima, K. Orihashi, S. Fujiwara, K. Tateishi, T. Uesaka, N. Kimizuka and N. Yanai, Chem. Commun., 2020, 56, 7217–7232 RSC.
- D. L. Silverio, H. A. van Kalkeren, T.-C. Ong, M. Baudin, M. Yulikov, L. Veyre, P. Berruyer, S. Chaudhari, D. Gajan, D. Baudouin, M. Cavaillès, B. Vuichoud, A. Bornet, G. Jeschke, G. Bodenhausen, A. Lesage, L. Emsley, S. Jannin, C. Thieuleux and C. Copéret, Helv. Chim. Acta, 2017, 100, e1700101 CrossRef.
- S. F. J. Cox, S. F. J. Read and W. T. Wenchebach, J. Phys. C-Solid State Phys., 1977, 10, 2917 CrossRef CAS.
- T. El Daraï, S. F. Cousin, Q. Stern, M. Ceillier, J. Kempf, D. Eshchenko, R. Melzi, M. Schnell, L. Gremillard, A. Bornet, J. Milani, B. Vuichoud, O. Cala, D. Montarnal and S. Jannin, Nat. Commun., 2021, 12, 1–9 CrossRef PubMed.
- D. Baudouin, H. A. van Kalkeren, A. Bornet, B. Vuichoud, L. Veyre, M. Cavaillès, M. Schwarzwälder, W.-C. Liao, D. Gajan, G. Bodenhausen, L. Emsley, A. Lesage, S. Jannin, C. Copéret and C. Thieuleux, Chem. Sci., 2016, 7, 6846–6850 RSC.
- T. Cheng, M. Mishkovsky, M. J. N. Junk, K. Münnemann and A. Comment, Macromol. Rapid Commun., 2016, 37, 1074–1078 CrossRef CAS PubMed.
- R. Kircher, H. Hasse and K. Münnemann, Anal. Chem., 2021, 93, 8897–8905 CrossRef CAS PubMed.
- C. Bocquelet, N. Rougier, H.-N. Le, L. Veyre, C. Thieuleux, R. Melzi, A. Purea, D. Banks, Q. Stern, E. Vaneeckhaute and S. Jannin, ChemRxiv, preprint, 2024 DOI:10.26434/chemrxiv-2024-3nlndn.
- R. Kircher, S. Mross, H. Hasse and K. Münnemann, Molecules, 2022, 27, 6402 CrossRef CAS PubMed.
- M. Sharma, G. Janssen, J. Leggett, A. P. M. Kentgens and P. J. M. van Bentum, J. Magn. Reson., 2015, 258, 40–48 CrossRef CAS PubMed.
- C.-G. Joo, K.-N. Hu, J. A. Bryant and R. G. Griffin, J. Am. Chem. Soc., 2006, 128, 9428–9432 CrossRef CAS PubMed.
- P. J. M. van Bentum, M. Sharma, S. G. J. van Meerten and A. P. M. Kentgens, J. Magn. Reson., 2016, 263, 126–135 CrossRef CAS PubMed.
- L. Frydman and D. Blazina, Nat. Phys., 2007, 3, 415–419 Search PubMed.
- N. Bloembergen, Physica, 1949, 15, 386–426 CrossRef CAS.
- O. S. Leifson and C. D. Jeffries, Phys. Rev., 1961, 122, 1781–1795 CrossRef CAS.
- K. Kundu, A. Feintuch and S. Vega, J. Phys. Chem. Lett., 2018, 9, 1793–1802 CrossRef CAS PubMed.
- A. Equbal, S. K. Jain, Y. Li, K. Tagami, X. Wang and S. Han, Prog. Nucl. Magn. Reson. Spectrosc., 2021, 126–127, 1–16 CrossRef CAS PubMed.
- G. Menzildjian, J. Schlagnitweit, G. Casano, O. Ouari, D. Gajan and A. Lesage, Chem. Sci., 2023, 14, 6120–6148 RSC.
- A. Venkatesh, G. Casano, Y. Rao, F. De Biasi, F. A. Perras, D. J. Kubicki, D. Siri, S. Abel, H. Karoui, M. Yulikov, O. Ouari and L. Emsley, Angew. Chem., Int. Ed., 2023, e202304844 Search PubMed.
- D. Wisser, G. Karthikeyan, A. Lund, G. Casano, H. Karoui, M. Yulikov, G. Menzildjian, A. C. Pinon, A. Purea, F. Engelke, S. R. Chaudhari, D. Kubicki, A. J. Rossini, I. B. Moroz, D. Gajan, C. Copéret, G. Jeschke, M. Lelli, L. Emsley, A. Lesage and O. Ouari, J. Am. Chem. Soc., 2018, 140, 13340–13349 CrossRef CAS PubMed.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- S. Jannin, A. Comment and J. J. Van Der Klink, Appl. Magn. Reson., 2012, 43, 59–68 CrossRef CAS.
- A. Bornet and S. Jannin, J. Magn. Reson., 2016, 264, 13–21 CrossRef CAS PubMed.
- D. Guarin, S. Marhabaie, A. Rosso, D. Abergel, G. Bodenhausen, K. L. Ivanov and D. Kurzbach, J. Phys. Chem. Lett., 2017, 8, 5531–5536 CrossRef CAS PubMed.
- F. Jähnig, A. Himmler, G. Kwiatkowski, A. Däpp, A. Hunkeler, S. Kozerke and M. Ernst, J. Magn. Reson., 2019, 303, 91–104 CrossRef PubMed.
- D. Shimon, Y. Hovav, A. Feintuch, D. Goldfarb and S. Vega, Phys. Chem. Chem. Phys., 2012, 14, 5729–5743 RSC.
- Y. Zhao, H. El Mkami, R. I. Hunter, G. Casano, O. Ouari and G. M. Smith, Commun. Chem., 2023, 6, 1–12 CrossRef PubMed.
- T. El Daraï and S. Jannin, Chem. Phys. Rev., 2021, 2, 041308 CrossRef.
- W. T. Wenckebach, Essentials of Dynamic Nuclear Polarization, Spindrift Publications, 2016 Search PubMed.
- K. Kundu, M. R. Cohen, A. Feintuch, D. Goldfarb and S. Vega, Phys. Chem. Chem. Phys., 2018, 21, 478–489 RSC.
- Y. Hovav, I. Kaminker, D. Shimon, A. Feintuch, D. Goldfarb and S. Vega, Phys. Chem. Chem. Phys., 2015, 17, 226–244 RSC.
Footnotes |
| † Raw data and MATLAB codes are available in the Zenodo repository https://doi.org/10.5281/zenodo.11120018. |
| ‡ Electronic supplementary information (ESI) available: Additional NMR and DNP results and HYPSO-5 material properties. See DOI: https://doi.org/10.1039/d4cp02022g |
| This journal is © the Owner Societies 2024 |