Water and ions in electrified silica nano-pores: a molecular dynamics study

Abstract

Solid–liquid interfaces (SLIs) are ubiquitous in science and technology from the development of energy storage devices to the chemical reactions occurring in the biological milieu. In systems involving aqueous saline solutions as the liquid, both the water and the ions are routinely exposed to an electric field, whether the field is externally applied, or originating from the natural surface charges of the solid. In the current study a molecular dynamics (MD) framework is developed to study the effect of an applied voltage on the behaviour of ionic solutions located in a ∼7 nm pore between two uncharged hydrophilic silica slabs. We systematically investigate the dielectric properties of the solution and the organisation of the water and ions as a function of salt concentration. In pure water, the interplay between interfacial hydrogen bonds and the applied field can induce a significant reorganisation of the water orientation and densification at the interface. In saline solutions, at low concentrations and voltages the interface dominates the whole system due to the extended Debye length resulting in a dielectric constant lower than that for the bulk solution. An increase in salt concentration or voltage brings about more localized interfacial effects resulting in dielectric properties closer to that of the bulk solution. This suggests the possibility of tailoring the system to achieve the desired dielectric properties. For example, at a specific salt concentration, interfacial effects can locally increase the dielectric constant, something that could be exploited for energy storage.

---

1. Introduction

Solid–liquid interfaces (SLI) are central to many scientific and technologically active areas such as materials science, chemistry, physics, biology and medicine.^1–15 Examples span from the design of materials for more efficient batteries^1,16 to the fate of therapeutic nanoparticles in nanomedicine^17,18 and the efficiency of heterogeneous catalysis.¹⁹

SLIs involving aqueous solutions as the liquid phase are among the most common in nature and technology. Water always contains naturally occurring hydronium and hydroxide ions, but additional metal ions are often present in much larger concentrations, influencing the solution electric conductivity,²⁰ facilitating chemical reactions,²¹ buffering the pH¹¹ and underpinning the survival of living organisms.²² Even ionic concentrations below 10⁻³ molar can have a significant effect on the well-known water properties such as dielectric constant,²³ electric and thermal conductivity,²⁴ boiling and freezing temperatures, density and surface tension,^25,26 but also at SLIs.^27–31 Higher salt concentrations lead to a decrease in the water dielectric constant²³ and can trigger self-assembly at SLIs as well as controlling colloidal stability.³² In all cases, the behaviour and properties of liquid molecules at the SLI or confined in nano-pores tend to differ from that of bulk water.^33–35 For example, various computational and experimental studies with different SLIs have reported a sharp reduction in the water dielectric constant near the interface^35–37 or in confinement.³⁸ This has been explained by an anisotropy of the dipolar electric field and lower dielectric constant of the surrounding walls (solid phase), rather than an ice-like behaviour of the water molecules.³⁹ Generally, the behaviour of aqueous SLIs depends on the properties of interface/confined water, from the electrostatically dominated adsorption of ions^28,29 to water-mediated correlation effects^27,31,40 and the enhanced charge storage ability of water–gold and water–platinum SLIs compared to mean-field calculations.⁴¹

Continuum theoretical models such as the Gouy–Chapman–Stern model^42–44 usually assume a mean field representation of ions in a continuum of water molecules.⁴⁵ The ions arrange so as to negate the effect of any electrical potential at the surface of the solid, creating an electrical double layer (EDL) of counter-ions at the SLI. The standard continuum description can be improved, for example, using a Landau–Ginzburg-type continuum model to capture a transition from overscreening to crowding through increasing voltage,⁴⁶ as confirmed by computer simulation.^47–50 However, the description of ions as average densities in continuum models limits the molecular understanding which is required for applications where local structure is relevant, for example at atomic or step defects in the solid. Another issue is the assumption of a fixed dielectric constant for water since the water screening ability has been shown to change with distance from the SLI.^{38,48,51–53} Experimental approaches, devoid of continuum assumptions tend to provide a more accurate picture of SLIs, with methods such as scattering techniques, sum frequency generation and scanning probe microscopies.^{27,30,32,54–58} However, experimental methods often struggle to provide both high spatial and temporal resolution simultaneously. This can be overcome by computational approaches such as MD simulations and density functional theory (DFT). For example, MD simulation of ionic liquids under an electric field demonstrated the existence of an electric potential range for a disorder to order ionic transition in the interface⁵⁹ which is hard to pursue through experimental approaches.

In the present study, a MD framework is developed to investigate the effect of an externally applied voltage on the behaviour of water and monovalent metal ions (NaCl) confined between two silica surfaces placed ∼7 nm apart. We focus on the effect of the voltage and ionic concentration on the molecular organisation, orientation and dielectric properties at the SLI. Silica is used here as a generic model system for a hydrophilic interface as often found in science and technology.^60–62 Biological membranes, for example, expose hydrophilic blocking electrodes (the lipid headgroups) that naturally operate under a significant trans-membrane potential.^63,64 Similarly, the development of electrolyte-based energy storage solutions^1,8,65–67 as well as biosensing technology^68,69 often relies on thin insulating layers at the interface with an electrolytic solution under an applied trans-interface potential. In terms of electrolyte, NaCl is the most abundant salt naturally present in aqueous solutions. Accordingly, here we investigate the interface of aqueous NaCl solutions with silica surfaces under DC potentials. The results point out the delicate balance between ions and water in screening the electric field.

2. Method

2.1 System setup

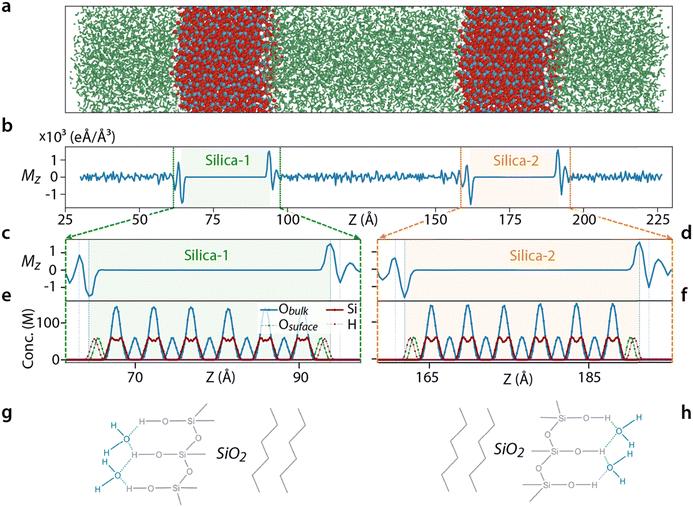
A system composed of two silica slabs (Fig. 1a) with an aqueous solution in-between was considered. The silica coordinates were taken from the Interface forcefield database for the Q3 surfaces as defined by Emami et al.,⁷⁰ each having a thickness of 2.3 nm and 4.7 silanol groups per nm², with no SiO⁻Na⁺ groups. The simulation box dimensions (3.83 × 3.92 × 19.5 nm³) were carefully chosen to ensure that the separation between two silica slabs (∼7.3 nm) is equivalent to the separation between each slab and its nearest periodic image. This choice effectively obviates the requirement for corrections in the calculation of the water dielectric constant, as it guarantees uniformity in the water conditions across the system. We used SPC/Fw for its accurate prediction of the water dielectric constant⁷¹ and the ionic parameter was taken from the CHARMM forcefield.⁷² The simulation box was solvated with ∼8000 SPC/Fw water molecules. More information on the number of ions and water molecules is provided in Table S1 (ESI†).

Fig. 1 Water molecular organisation near uncharged silica surfaces. The whole simulation box (a) is used to calculate the distribution of the z-component of (M_z) of water molecular dipoles along the z direction (b). Magnified view of M_z at the interface with each silica slab (c) and (d) highlighting the water molecular orientation dominated by interfacial hydrogen bonds. This is confirmed by atomistic densities (e)–(f), and illustrated schematically (g)–(h). Errors are shown as shades around plotted values in (b)–(f).

The simulations were pursued in several different steps. First, the system was energy minimized. In all cases, there was a short equilibration simulation of 100 ps prior to the main simulation of 10 ns, except for simulations with 8 V potential which lasted for 20 ns. The initial 2 ns (12 ns) simulation time was discarded as equilibration and the last 8 ns was used for the analysis. The Nosé–Hoover thermostat and barostat were deployed to keep the system at a temperature and pressure of 300 K and 1 bar. An external voltage was applied between the silica slabs through a constant electric field as described by Gumbart et al.⁷³ In this method, the value of the external field E needed to create a potential difference of ΔV must be equal to ΔV/d where d is the simulation box size. However, our simulations showed that d must be taken as the closest distance between the silica surfaces to impose a voltage difference of ΔV across the solution inside the pore region. Thanks to the periodic boundary conditions the same voltage is applied to the solution outside the pore region. The upper and lower SLIs are called positive and negative interfaces, respectively. The simulations were run on LAMMPS,⁷⁴ the visualisations were done through OVITO⁷⁵ and matplotlib library of python⁷⁶ and several C++ and python codes were written for data analysis. In the current study, 60 different simulation sets were done, each repeated six times with a cumulative simulation time of 4.29 μs.

2.2 Analysis

Several physical quantities were obtained from the simulations. The bulk dielectric constant of water was calculated according to eqn (1) in which M, ε₀, V_w, k, T, 〈 〉 and ε stand for the total water dipole, the vacuum permittivity, the water volume, Boltzmann's constant, temperature, ensemble average and the dielectric constant, respectively. The ensemble average was calculated through time averaging according to the ergodic hypothesis.⁷⁷ A C++ code was written for this purpose. The convergence of the dielectric constant was judged through the dielectric constant-time plot (Fig. S1, ESI†).The ion and water density profiles over the whole simulation were obtained using a moving average coded in python. The profiles are composed of 1000 points evenly distributed across the simulation box. The value at each point was obtained by averaging over all the relevant molecules or ions within a 1 Å-wide window centred around the point, unless stated otherwise. The voltage distribution was calculated through integrating the Poisson equation (eqn (2)) in which V, ρ, z, and ε₀, represent the electrostatic potential, charge density, position perpendicular to the silica surface and the vacuum permittivity. Meshes along the z direction placed 0.1 Å apart were used to calculate the charge density distribution. Test analyses showed 0.1 Å to be the minimum mesh size over which the z-voltage distribution does not change with mesh size. To obtain the voltage through the Poisson equation, the boundary conditions were taken as 0 and the imposed voltage difference ΔV at the minimum and maximum z position of the simulation box. We note that this is different from the voltage imposed across the system; it is a measure of the local potential once the system has reached equilibrium.

To identify the role of water in screening the external electric field and ultimately the molecular origin of the dielectric properties of the SLI, the total water dipole in the direction of the field (M_z) was utilized as a proxy for its dielectric constant perpendicular to the interface.^39,78,79 Positive M_z values imply the alignment of the water dipoles in the direction of the field with larger values indicating a more effective screening and a lower perpendicular dielectric constant. Values of M_z close to zero and relatively higher standard deviation indicate less organization of the water dipoles in the direction of the field and higher perpendicular dielectric constant (eqn (1)).

3. Results

3.1 Spatial organisation of pure water

Before exploring the impact of ions on the SLI molecular behaviour, we examine the arrangement of pure water molecules between two uncharged silica slabs in the absence of any electric field. This serves as a reference to help disentangle the field effect from that of the hydrophilic interfaces. The three components M_x, M_y and M_z are used to quantify the average orientation of the water molecules. M_z and M_x experience sharp changes near the interface (Fig. 1b–d, see also and Fig. S2, ESI†), in contrast to M_y where changes appear negligible (Fig. S3, ESI†). The net value of M_z is zero except for the three interfacial water layers closest to the silica surface where an alternating water orientation indicates a layering that decays into the bulk (Fig. 1b). The water layer closest to the silica surface has the highest net dipole, with the molecular dipoles oriented outward from the surface (dashed lines in Fig. 1c and d). The water oxygens in the surface layer align predominantly towards the silica, with a position coinciding with the surface hydrogen atoms (dashed lines in Fig. 1d and e). This suggests the formation of hydrogen bonds between the water molecules and the silica surface (Fig. 1g–h) being at the origin of the interfacial water organization. The second and third layers (dotted lines Fig. 1c and d) adopt an arrangement aiming to cancel the dipole of the first and the second layers, respectively, leading to the alternating M_z sign between adjacent layers.

The crystalline structure of the silica also influences the in-plane component of water's organisation: M_x is non-zero at the interface owing to the specific arrangement of the Si–O–H groups of the silica slab considered here. The highly polar Si–O bonds are aligned at a specific angle with respect to the x coordinate, and while the total dipole of these bonds is zero inside bulk silica, at the surface a non-zero in-plane dipole moment exists. However, the Si–O bonds in the y–z plane are perpendicular to the y-direction resulting in a net zero value of M_y at the interface (Fig. S3, ESI†).

When a voltage is applied, the M_z distribution of water shows a net increase throughout the pore (Fig. 2a–c), but the M_x and M_y remain unchanged. This reflects an alignment of the water molecules in the z-direction to oppose the applied electric field, something they successfully achieve in most cases except near the electrodes (Fig. 2d). The field affects the relatively positive and negative interfaces differently (respectively green and orange highlights in Fig. 2a–c). Near the positive interface the applied potential reinforces the three-layered M_z organisation (Fig. 2b), while the opposite is observed at the negative interface where the three-layer structure disappears at higher voltages (Fig. 2c). The field screening is also better at the positive interface (inset Fig. 2d) compared to the negative interface where a competition between opposing the field and hydrogen bonding with the silica takes place: below 200 mV, the molecular arrangement at the negative interface is fully dominated by the interface hydrogen bonds which prevent water molecules to screen the field. Between 200 mV and 4 V, both driving forces are at play, progressively reversing the shape of the M_z distribution with the apparition of a single maximum (orange arrows in Fig. 2a). Beyond 4 V, the molecular ordering induced by the hydrogen bonds becomes negligible and no oscillations in M_z are visible (Fig. 2c).

Fig. 2 Organisation of the water molecules under an externally applied electrical potential across the system. The distributions of M_z (a) depend on the magnitude of the voltage at the interface with silica (b)–(c). The relatively positive (b) and negative (c) interfaces with respect to the applied potential exhibit different behaviour, with the field either reinforcing (b) or opposing (c) the water molecule orientation induced by the water–silica hydrogen bonds. The voltage distribution perpendicular to the interfaces (d) shows an average linear drop across the non-conducting solid with minimal change across the liquid (inset). The dashed lines indicate the silica–water boundary. Errors appear as shades around the plotted curves.

3.2 Impact of adding ions: changes in the molecular organisation

Having examined the molecular organisation of water molecules at the interface when exposed to an applied voltage, we now explore the impact of adding NaCl. To better evidence the effect of the applied voltage, we focus on results obtained at the maximum test voltage (8 V) but a similar behaviour can be seen at lower voltages, although less pronounced (Fig. S4–S9, ESI†). In all cases, the analysis focuses on the z-component of the water dipole (M_z) and the ion's atomistic densities in the solution.

In the absence of salt, M_z behaves as shown in Fig. 2 (black line in Fig. 2a). If we define the bulk solution as the region where 〈M_z〉 = 0, none of the pure water molecules can be seen as ‘bulk’ with the interface effectively extending beyond the pore.

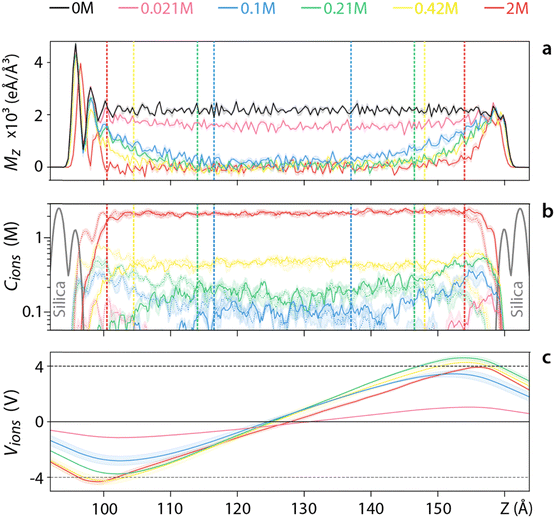
Adding salt to the system reduces the size of the interface and M_z becomes distance-dependent in the pore region (Fig. 3a). At the lowest salt concentrations (<0.1 M), M_z decays when moving away from the slabs but never reaches 〈M_z〉 = 0, similarly to pure water. This implies that water molecules are involved in the screening of the applied voltage throughout the whole system. This can be directly visualised from the difference between the co- and counter-ions distribution across the pore (Fig. 3b), and the associated electrical potential created by this ionic distribution (Fig. 3c) which is insufficient to compensate for the externally imposed voltage (dashed lines in Fig. 3c).

Fig. 3 Molecular orientation and ionic densities across the pore under an external voltage of 8 V. Adding salt (a) progressively screens the electric potential, allowing water to behave as bulk (〈M_z〉 = 0) in the middle of the pore for salt concentrations >0.1 M (between dashed vertical lines). Comparison of the potential decay with the ionic density distributions for each concentration (b) shows a similar range of decay to bulk values (dashed vertical lines) with the cation (solid line) and anion (dotted lines) behaving symmetrically. The average voltage or electrical potential distribution created by the ions across the pore (c) cannot fully screen the applied voltage (black dashed lines) for concentrations <0.21 M. Errors are depicted as shades around the plots.

For ionic concentrations above >0.1 M, ions completely screen the applied potential in the middle of the system with 〈M_z〉 dropping to zero. At the interface with the silica, the water orientation is almost identical to the system without ions (Fig. 3a), with an exclusion region for co-ions enabling the screening (Fig. 3b). Outside this electrical double layer (EDL) region, defined as the adsorbed counter-ions alongside the diffusive layer of ions in the solution, the ions have fully screened the potential. The boundary (dashed lines in Fig. 4b) coincides with the place where the M_z reaches the bulk value. As expected, the EDL region decreases with increasing the ionic concentration, consistent with the thermodynamic picture underpinning continuum models of the EDL Poisson–Boltzmann model.⁸⁰ A similar dependence of the screening behaviour on the ionic concentration is observed for lower voltages (see Fig. S4–S9, ESI†), but with full ionic screening achieved at lower ionic concentrations.

Fig. 4 Molecular orientation and ionic densities across the pore under different external voltages for an ionic concentration of 0.042 M (42 mM). As the voltage increases, the low ionic concentration can no longer screen the potential with 〈M_z〉 decaying over longer distances (a). Unlike with varying ionic concentration, there is no obvious correlation between the size of the EDL (b) and the decay length of 〈M_z〉 with the cation (solid lines) and anion (dotted lines) distributed symmetrically across the pore. The average voltage or electrical potential distribution created by the ions across the pore (c) is insufficient to fully screen the applied voltage (horizontal dashed lines) at most voltages. Errors are depicted as shades around the plots.

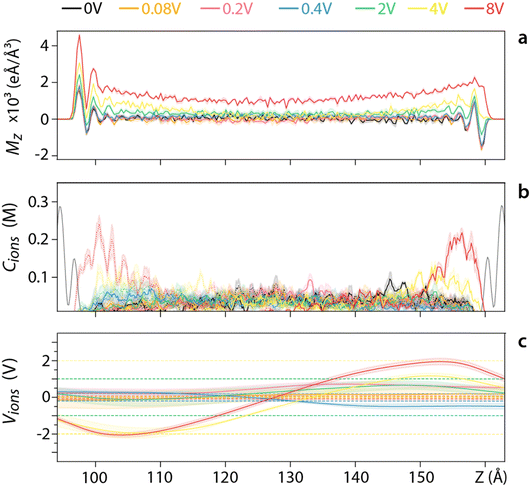
Having explored the effect of varying the salt concentration at a given applied voltage (Fig. 3), we now investigate varying the applied voltage for a given ionic concentration. A relatively low salt concentration (0.042 M) is used to better evidence the response of the system even at lower voltages (Fig. 4). For voltages <0.4 V, ions appear to be able to screen the resulting field with 〈M_z〉 remaining zero in the middle of the pore (Fig. 4a). This is confirmed by examining the voltage created by the ions (Fig. 4c) although the error is too large to draw any comparative conclusion. For voltages >0.4 V water is also involved in screening the field, with 〈M_z〉 gradually decreasing to a non-zero value at the centre of the pore (Fig. 4a). The ionic distribution still responds to the applied field (Fig. 4b), but the effect is insufficient to screen the external voltage (dashed lines in Fig. 4c). A similar behaviour is observed for higher ionic concentrations (Fig. S11–S15, ESI†), but an increased ability to screen the applied voltage before the involvement of the water in the pore. This inverse is true for lower ionic concentrations (Fig. S10, ESI†). Overall, higher voltages intensify interfacial effects, increasing the size of the region where water contributes to the electrostatic screening.

3.3 Consequences for the dielectric constant of water

Having explored the spatial details of the molecular-level response of the water and the ions to the applied voltage, we now investigate the consequences for the average dielectric constant of water across the whole pore. In the absence of the silica slabs and with no external voltage, the dielectric constant decreases linearly with increasing salt concentration (Fig. 5a). This well-established result^23,81–86 acts here as a control, confirming that the simulations quantitatively capture the dielectric behaviour of the solution. When the two silica slabs are present, although salt still induces a change in the average dielectric constant between slabs, the decrease is no longer linear with the salt concentration. The interfaces have a significant and salt-dependent impact on the dielectric constant of the whole system due to its finite size. At lower salt concentrations, the interface extends further into the bulk, hence lowering the global dielectric constant of the liquid. This is consistent with the interfacial liquid being more structurally ordered than the bulk.^27,87 As the salt concentration increases, the relative contribution of the interface diminishes, and the dielectric constant converges towards that value of the silica-free system. As a result, the dielectric constant exhibits a non-monotonic behaviour with the increasing salt concentration, first increasing up to a maximum at ∼0.21 M and then decreasing linearly (Fig. 5a).

Fig. 5 Average dielectric constant of the water in the pore as a function of salt concentration (a) and the applied external voltage (b). The dielectric constant reaches a maximum around 0.21 M when plotted against the solution's salt concentration (a), regardless of the applied voltage. For the pore size used here, interfacial effects dominate <0.21 M with the expected bulk solution behaviour appearing at higher concentrations. When the dielectric constant is plotted against the applied voltage (b), three different regimes can be observed: (i) constant at low voltages, (ii) increasing at medium voltages, and (iii) a salt concentration-dependent decrease beyond 2 V.

This non-monotonic behaviour remains at all the voltages investigated (Fig. 5a), but the effect of the voltage follows a consistent pattern (Fig. 5b): typically, three regimes can be observed for all the salt concentrations considered here. At lower voltages (<0.4 V) the dielectric constant remains broadly unchanged with voltage, followed by a slight dielectric recovery over intermediate voltages (0.4–2 V), and finally a salt concentration-dependent decrease of the dielectric constant with increasing voltage (>2 V). For higher ionic concentrations, the change between stages occurs at larger voltage values and the changes in dielectric constant in the second and third stages are lower, consistent with better ionic screening at the interface.

Generally, the non-monotonic effects in voltage and ionic concentration observed here are interface-driven. They are therefore dependent on the system size and become negligible for macroscopic systems. Nonetheless, the present results shown that these effects are still significant for pores as large as 7 nm.

4. Discussion

In many natural and technological systems, aqueous solutions occupy nano-pores between solid surfaces. The surface of the solid is often charged, either naturally such as with oxides and minerals^88,89 or due to an applied potential in technological application.^1,65 The present computational work explores the behaviour of water and ions in nanopores formed by hydrophilic silica surfaces. We focus on the interplay between water–surface interactions at equilibrium and externally applied electric fields across the whole system, using the average water dipole at any given distance from the surfaces as a proxy for water's molecular orientation.

Our results show high dipole moment density along z and x directions near the silica surface due to hydrogen bonding with the surface's Si–O–H groups. M_y does not change with distance from the surface due to a lack of Si–O–H orientation along the y surface direction. Previous studies have reported an anisotropic screening behaviour for water near the SLI,^{35,37,39,78,90} usually associated with a low dielectric constant near the SLI. Here, the simulations indicate a strong alignment of the water molecules with the silica crystal, with M_z and M_x decaying to zero over a similar distance to that needed for the dielectric constant to reach its bulk value.^39,78 The shape of the M_z distribution, its number of maxima in this range, are also similar to the reported perpendicular dielectric constant of water near a SLI.^39,78

Interfacial water orientation is expected with silica due to direct hydrogen bonds with the surface. We note that similar orientational effects can occur in graphene or metals through surface polarization due to fluctuating surface charges,⁹⁰ something often missing in computational studies with non-polarizable forcefields. Moreover, in the computational studies on the dielectric constant variation near the surface the parallel components of the dielectric constant are considered the same^48,53,78,79 (a semi-isotropic behaviour), while this study highlights the importance of considering an anisotropic behaviour for realistic surfaces such as silica in which the hydrogen bond donor/acceptor groups have preferential orientations.

Applying an external electric field across the system can have a significant impact on the molecular orientation of the water, even when ions are present. Significantly, the present results show that the dielectric response of the solution is not linear with the applied potential. For the sake of the discussion, we refer to the silica interfaces as ‘positive’ and ‘negative’ electrodes despite the silica being non-conducting. In this mindset, the silica surfaces can be thought of as blocking electrodes, with the positive (respectively negative) electrode being the interface with the highest (respectively lowest) electrical potential. A strong screening is observed near the positive electrode due to an enhancement in the three-layer structure observed in M_z while this molecular ordering is opposed at the negative electrode resulting in a weaker screening. This is due to interfacial hydrogen bonds and orientation of the water dipoles with the applied field opposing each other. Interestingly this is in line with results from simulations of water between two polarizable graphene sheets,⁹⁰ also consistent with the observation of slower water reorientation near the positive electrode for graphene based SLIs.^90,91 Both enhanced molecular orientation at the positive electrode and slower water reorientation dynamics likely play a role in the present study, but further work would be needed to disentangle the two effects.

The impact of the electric field on the water dielectric constant is non-trivial due to a significant effect of the interfaces, themselves depending on the ionic concentration of the solution. Besides, the expected linear dielectric response of bulk water with the ionic concentration no longer applies here. For lower salt concentrations (≲0.21 M), the dielectric constant increases with the salt concentration, in opposition to the well-known bulk behaviour.^23,81–86 This can be explained by interfacial effects dominating the dielectric response of the solution in the pore. Water molecules are oriented throughout most or even the whole pore (non-zero 〈M_z〉). Ions also extend further from the silica surfaces, with the length of the ionic density decaying from the interface depending only on the NaCl concentration. This is captured classically by the Poisson–Boltzmann formalism⁸⁰ whereby lower ionic concentrations lead to larger Debye lengths. The dielectric constant reaches maximum around 0.21 M, a value expected to depend on the size of the system with larger systems behaving more bulk-like. Preliminary simulation results suggest a lower salt concentration threshold for larger pore size.

At higher salt concentration the trend reverses and falls back in line with the expected bulk behaviour. This is due to thinner interfacial regions hence leaving most of the pore with a bulk-like solution. This reduced length of the ionic density decay from the solid is expected (smaller Debye length) from Poisson–Boltzmann.⁸⁰

Overall, the fact that interfacial effects dominate in nano-pores is not surprising, with multiple examples available in experimental and computational studies. The remarkable findings here come from the range of the effect with water exhibiting its maximum dielectric constant near 0.21 M in a ∼7 nm pore which is an order of magnitude larger than the Debye length of ∼0.66 nm predicted by the Poisson–Boltzmann for this salt concentration. In contrary to the widely accepted idea of water having bulk-like behaviour in separation distances larger than the Debye length, this observation suggests that interfacial effects are important beyond the short-range molecular interactions. The salt concentration of 0.15 M in biological entities and the fact the most biomolecular processes occur over ≾10 nm, the typical size range of biological molecules, makes this observation relevant in the biological milieu. Besides, the present findings could have implications in various areas such as energy storage devices and batteries. For instance, in the case of nano-porous capacitors, the present simulations suggest that salt addition can lead to up to 50% increase in the dielectric constant and energy storage capacity.

In terms of voltage dependence, three different regimes are observed regardless of the salinity regime. At lower voltages (<0.4 V), the ions fully screen the electric field which has limited impact on the behaviour of the water molecules. The dielectric constant does not evolve with changes in voltage in this regime. At intermediate voltages (0.4–2 V), increased ionic concentration near the silica creates a depleted region with less ions in the middle of the pore, leading to a higher dielectric constant. Finally, at higher voltages both water and ions are involved in the screening, leading to a decrease in the dielectric constant with increasing voltage. Consistently, the voltage threshold for each regime increases with salt concentration.

Overall, the results of this study paint a complex but consistent picture of the behaviour of water and ions in nano-pores. Part of the present simulations was conducted with significant applied voltages (2–8 V), several order of magnitude larger than the amount required for the water dielectric breakdown in a conducting system. We believe that the use of such voltages is appropriate here for several reasons. First, higher voltages help ameliorate the limited time and length scales of the MD simulations. The time scale accessible through MD is limited (<microseconds) and high voltages help speed up the ionic diffusion and the water dipole arrangement. Second lower voltages can be challenging when in conjunction with lower ionic concentrations due to limitations in the system size needed to achieve effective sampling. Finally, neither charge transfer, water polarization nor water dissociation have been observed in our simulations, suggesting that we always operate in the linear regime. We therefore expect the physics of the system to behave similarly at higher and lower voltages.

Another point worth mentioning is the fact that silica exposed to an aqueous solution at neutral pH carries a negative net surface charge. However, when immersed into an ionic solution, the surface charge density tends to be reduced by the adsorption of counterions from the solution.⁹² The interaction between these ions and the surface charges can be strong, even at relatively low salt concentration,^27,30,93 with the ions often remaining stable over the timescale of the simulations.^27,28,31,93 Here, this was further confirmed by preliminary simulations conducted with charged silica surfaces (results not shown). We therefore considered these ions as effectively part of the surface in the present study, validating the use of a neutral silica electrode to investigate the general behaviour of SLIs under electric fields. While still a simplification, this avoids unnecessary complications without limiting the scope of the findings. A question remains as to the atomic structure of a representative silica surface. Although most silica surfaces are not crystalline, creating a non-crystalline silica surface risks biasing the results towards a particular silica structure due to the relatively small size of the MD system. The use of crystalline silica creates an in-plane dipole and hence affects the arrangement of water dipoles parallel to the surface (see Fig. S16, ESI†). However, the applied voltage has a significantly larger impact on the out of plane dipole arrangement, the focus of the current study.

5. Conclusions

In this study an all-atom molecular dynamics (MD) framework was developed to study the response of water dipoles and dissolved salt ions to an applied electric field, when in a silica nanopore. The results highlight the interplay between hydrogen bonds with the silica surface and dipole orientation with the applied field for the interfacial water molecules. The field can compete with, or enhance the hydrogen bond-dominated water organisation, leading to lower dielectric constants. For a ∼7 nm pore, the effect of the interfaces dominated the behaviour of the solution for NaCl concentrations lower than ∼0.2 M, with the average dielectric constant of the solution increasing with the salt concentration regardless of the applied voltage. The trend is reversed at higher salt concentrations, following well-established results for bulk solutions. As expected, both the applied voltage and ions decrease the size of the interface region beyond which the water dielectric properties reach its bulk value. The finding highlights the intricate balance between water dipoles and ions in electrostatic screening in nano-pores, showing that significant interfacial effect can dominate in common ionic solutions even for systems and an order of magnitude larger than the Debye length. This could have implications for our understanding of biological systems when nanoscale pores are common and in the development of water-based energy-related applications.

Data availability

Derived data supporting the findings of this study are available from the corresponding authors MT and KV on request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge funding from the UK Engineering and Physical Sciences Research Council (EPSRC grant EP/S028234/1). The authors also wish to acknowledge the Advanced research computing group of Durham University for the provision of the computational facilities and support for the Hamilton HPC.

References

1. Y. Chen, W. Wu, S. Gonzalez-Munoz, L. Forcieri, C. Wells, S. P. Jarvis, F. Wu, R. Young, A. Dey, M. Isaacs, M. Nagarathinam, R. G. Palgrave, N. Tapia-Ruiz and O. V. Kolosov, Nat. Commun., 2023, 14, 1321.
2. C. M. Magin, S. P. Cooper and A. B. Brennan, Mater. Today, 2010, 13, 36–44.
3. M. Tavakol, A. Montazeri, R. Naghdabadi, M. J. Hajipour, S. Zanganeh, G. Caracciolo and M. Mahmoudi, Nanoscale, 2018, 10, 7108–7115.
4. T. Minato, K. Umeda, K. Kobayashi, Y. Araki, H. Konishi, Z. Ogumi, T. Abe, H. Onishi and H. Yamada, Jpn. J. Appl. Phys., 2021, 60, 0806.
5. G. Buckton, Int. J. Pharm., 1988, 44, 1–8.
6. C. Cafolla and K. Voïtchovsky, Nanoscale, 2018, 10, 11831–11840.
7. C. Cafolla, J. Philpott-Robson, A. Elbourne and K. Voïtchovsky, ACS Appl. Mater. Interfaces, 2024, 16, 44–53.
8. S. Zhao, Y. Fu, H. Cao and Y. Chai, J. Mater. Chem. A, 2023, 11, 21009–21028.
9. G. Macfie, B. A. Brookes and R. G. Compton, J. Phys. Chem. B, 2001, 105, 12534–12546.
10. T. Fukuma and R. Garcia, ACS Nano, 2018, 12, 11785–11797.
11. W. Trewby, D. Livesey and K. Voitchovsky, Soft Matter, 2016, 12, 2642–2651.
12. N. Giovambattista, P. J. Rossky and P. G. Debenedetti, Annu. Rev. Phys. Chem., 2012, 63, 179–200.
13. A. Haji-Akbari and P. G. Debenedetti, J. Chem. Phys., 2015, 143, 214501.
14. J. R. Vella, M. Chen, S. Fürstenberg, F. H. Stillinger, E. A. Carter, P. G. Debenedetti and A. Z. Panagiotopoulos, Nucl. Fusion, 2017, 57, 116036.
15. G. Stirnemann, S. R.-V. Castrillón, J. T. Hynes, P. J. Rossky, P. G. Debenedetti and D. Laage, Phys. Chem. Chem. Phys., 2011, 13, 19911–19917.
16. J. Zheng, Y. Hou, Y. Duan, X. Song, Y. Wei, T. Liu, J. Hu, H. Guo, Z. Zhuo, L. Liu, Z. Chang, X. Wang, D. Zherebetskyy, Y. Fang, Y. Lin, K. Xu, L.-W. Wang, Y. Wu and F. Pan, Nano Lett., 2015, 15, 6102–6109.
17. J. K. Patra, G. Das, L. F. Fraceto, E. V. R. Campos, M. del, P. Rodriguez-Torres, L. S. Acosta-Torres, L. A. Diaz-Torres, R. Grillo, M. K. Swamy, S. Sharma, S. Habtemariam and H.-S. Shin, J. Nanobiotechnol., 2018, 16, 1–33.
18. H. Mohammad-Beigi, A. Hosseini, M. Adeli, M. R. Ejtehadi, G. Christiansen, C. Sahin, Z. Tu, M. Tavakol, A. Dilmaghani-Marand, I. Nabipour, F. Farzadfar, D. E. Otzen, M. Mahmoudi and M. J. Hajipour, ACS Nano, 2019, 13, 3243–3256.
19. J.-M. Andanson and A. Baiker, Chem. Soc. Rev., 2010, 39, 4571–4584.
20. A. Marandi, M. Polikarpus and A. Jõeleht, Appl. Geochem., 2013, 38, 103–109.
21. N. V. Bhagavan, ed., in Medical Biochemistry, Academic Press, San Diego, 4th edn, 2002, p. iii.
22. W. Sim, R. T. Barnard, M. a T. Blaskovich and Z. M. Ziora, Antibiotics, 2018, 7, 93.
23. N. Gavish and K. Promislow, Phys. Rev. E, 2016, 94, 012611.
24. N. Kumar, J. Hirschey, T. J. LaClair, K. R. Gluesenkamp and S. Graham, J. Energy Storage, 2019, 24, 100794.
25. M. Bostrom, D. R. M. Williams and B. W. Ninham, Langmuir, 2001, 17, 4475–4478.
26. A.-H. A. Shah, K. Ali and S. Bilal, Colloids Surf., A, 2013, 417, 183–190.
27. M. Ricci, P. Spijker and K. Voitchovsky, Nat. Commun., 2014, 5, 4400.
28. M. Ricci, P. Spijker, F. Stellacci, J.-F. Molinari and K. Voitchovsky, Langmuir, 2013, 29, 2207–2216.
29. I. Siretanu, D. Ebeling, M. P. Andersson, S. L. S. Stipp, A. Philipse, M. C. Stuart, D. van den Ende and F. Mugele, Sci. Rep., 2015, 4, 4956.
30. M. Ricci, W. Trewby, C. Cafolla and K. Voïtchovsky, Sci. Rep., 2017, 7, 43234.
31. W. Trewby, J. Faraudo and K. Voïtchovsky, Nanoscale, 2019, 11, 4376–4384.
32. R. Steitz, V. Leiner, R. Siebrecht and R. v. Klitzing, Colloids Surf., A, 2000, 163, 63–70.
33. S. Chakraborty, H. Kumar, C. Dasgupta and P. K. Maiti, Acc. Chem. Res., 2017, 50, 2139–2146.
34. J. F. van der Veen and H. Reichert, MRS Bull., 2011, 29, 958–962.
35. L. Fumagalli, A. Esfandiar, R. Fabregas, S. Hu, P. Ares, A. Janardanan, Q. Yang, B. Radha, T. Taniguchi, K. Watanabe, G. Gomila, K. S. Novoselov and A. K. Geim, Science, 2018, 360, 1339–1342.
36. K.-Y. Chiang, T. Seki, C.-C. Yu, T. Ohto, J. Hunger, M. Bonn and Y. Nagata, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2204156119.
37. O. Teschke, G. Ceotto and E. F. de Souza, Phys. Rev. E, 2001, 64, 011605.
38. M. H. Motevaselian and N. R. Aluru, ACS Nano, 2020, 14, 12761–12770.
39. J.-F. Olivieri, J. T. Hynes and D. Laage, J. Phys. Chem. Lett., 2021, 12, 4319–4326.
40. J. Wang, H. Li, M. Tavakol, A. Serva, B. Nener, G. Parish, M. Salanne, G. G. Warr, K. Voïtchovsky and R. Atkin, ACS Nano, 2024, 18, 1181–1194.
41. M. Azimzadeh Sani, N. G. Pavlopoulos, S. Pezzotti, A. Serva, P. Cignoni, J. Linnemann, M. Salanne, M.-P. Gaigeot and K. Tschulik, Angew. Chem., 2022, 134, e202112679.
42. M. Gouy, J. Phys. Theor. Appl., 1910, 9, 457–468.
43. D. L. Chapman, Philos. Mag. J. Sci., 1913, 25, 475–481.
44. R. Kant and M. B. Singh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 052303.
45. C. Tournassat, Y. Chapron, P. Leroy, M. Bizi and F. Boulahya, J. Colloids Interface Sci., 2009, 339, 533–541.
46. M. Z. Bazant, B. D. Storey and A. A. Kornyshev, Phys. Rev. Lett., 2011, 106, 046102.
47. Y. Wang and G. Tian, Langmuir, 2021, 37, 14059–14071.
48. D. J. Bonthuis, S. Gekle and R. R. Netz, Langmuir, 2012, 28, 7679–7694.
49. M. Sha, Q. Dou, F. Luo, G. Zhu and G. Wu, ACS Appl. Mater. Interfaces, 2014, 6, 12556–12565.
50. J. G. Hedley, H. Berthoumieux and A. A. Kornyshev, J. Phys. Chem. C, 2023, 127, 8429–8447.
51. M. H. Motevaselian, S. Y. Mashayak and N. R. Aluru, Phys. Rev. E, 2018, 98, 052135.
52. F. Deißenbeck, C. Freysoldt, M. Todorova, J. Neugebauer and S. Wippermann, Phys. Rev. Lett., 2021, 126, 136803.
53. S. Ruiz-Barragan, D. Muñoz-Santiburcio, S. Körning and D. Marx, Phys. Chem. Chem. Phys., 2020, 22, 10833–10837.
54. J. H. Lakey, Curr. Opin. Colloid. Interface. Sci., 2019, 42, 33–40.
55. O. B. Tarun, H. I. Okur, P. Rangamani and S. Roke, Commun. Chem., 2020, 3, 1–8.
56. O. B. Tarun, C. Hannesschläger, P. Pohl and S. Roke, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 4081–4086.
57. R. Garcia, Amplitude Modulation Atomic Force Microscopy, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2010.
58. E. J. Miller, W. Trewby, A. F. Payam, L. Piantanida, C. Cafolla and K. Voïtchovsky, J. Visualized Exp., 2016, e54924.
59. C. Merlet, D. T. Limmer, M. Salanne, R. van Roij, P. A. Madden, D. Chandler and B. Rotenberg, J. Phys. Chem. C, 2014, 118, 18291–18298.
60. W. Tan, K. Wang, X. He, X. J. Zhao, T. Drake, L. Wang and R. P. Bagwe, Med. Res. Rev., 2004, 24, 621–638.
61. S. Minakata and M. Komatsu, Chem. Rev., 2009, 109, 711–724.
62. C. Strong, Y. Carrier and F. Handan Tezel, Appl. Energy, 2022, 312, 118533.
63. B. Alberts, A. Johnson, J. Lewis, D. Morgan, M. C. Raff, K. Roberts, P. Walter, J. H. Wilson and T. Hunt, Molecular biology of the cell, Garland Science, Taylor and Francis Group, New York, NY, 6th edn, 2015.
64. X. Lin, V. Nair, Y. Zhou and A. A. Gorfe, Phys. Chem. Chem. Phys., 2018, 20, 15841–15851.
65. M. Yang, Y. Zhong, J. Ren, X. Zhou, J. Wei and Z. Zhou, Adv. Energy Mater., 2015, 5, 1500550.
66. C.-Z. Zhao, B.-C. Zhao, C. Yan, X.-Q. Zhang, J.-Q. Huang, Y. Mo, X. Xu, H. Li and Q. Zhang, Energy Storage Mater., 2020, 24, 75–84.
67. S. Sun, B. Liu, H. Zhang, Q. Guo, Q. Xia, T. Zhai and H. Xia, Adv. Energy Mater., 2021, 11, 2003599.
68. J. Riu and B. Giussani, TrAC, Trends Anal. Chem., 2020, 126, 115863.
69. A. Poghossian and M. J. Schöning, Sensors, 2020, 20, 5639.
70. F. S. Emami, V. Puddu, R. J. Berry, V. Varshney, S. V. Patwardhan, C. C. Perry and H. Heinz, Chem. Mater., 2014, 26, 2647–2658.
71. Y. Wu, H. L. Tepper and G. A. Voth, J. Chem. Phys., 2006, 124, 024503.
72. J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmüller and A. D. MacKerell, Nat. Methods, 2017, 14, 71–73.
73. J. Gumbart, F. Khalili-Araghi, M. Sotomayor and B. Roux, Biochim. Biophys. Acta, Biomembr., 2012, 1818, 294–302.
74. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. In’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
75. A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012.
76. J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95.
77. M. P. Allen and D. J. Tildesley, Comput. Simul. Liquids, Oxford University Press, 2017.
78. P. Loche, C. Ayaz, A. Wolde-Kidan, A. Schlaich and R. R. Netz, J. Phys. Chem. B, 2020, 124, 4365–4371.
79. A. Schlaich, E. W. Knapp and R. R. Netz, Phys. Rev. Lett., 2016, 117, 048001.
80. J. N. Israelachvili, Intermolecular and surface forces, Academic Press, 3rd edn, 2011.
81. A. Stogryn, IEEE Trans. Microwave Theory Tech., 1971, 19, 733–736.
82. A. Levy, D. Andelman and H. Orland, Phys. Rev. Lett., 2012, 108, 227801.
83. J. B. Hasted, D. M. Ritson and C. H. Collie, J. Chem. Phys., 1948, 16, 1–21.
84. P. Wang and A. Anderko, Fluid Phase Equilib., 2001, 186, 103–122.
85. B. Hess, C. Holm and N. van der Vegt, Phys. Rev. Lett., 2006, 96, 147801.
86. H. Weingärtner, Z. Phys. Chem., 2006, 220, 1395–1405.
87. S. Pintea, W. de Poel, A. E. F. de Jong, V. Vonk, P. van der Asdonk, J. Drnec, O. Balmes, H. Isern, T. Dufrane, R. Felici and E. Vlieg, Langmuir, 2016, 32, 12955–12965.
88. X. Yin, V. Gupta, H. Du, X. Wang and J. D. Miller, Adv. Colloid Interface Sci., 2012, 179–182, 43–50.
89. H. Li, W. Xu, F. Jia, J. Li, S. Song and Y. Nahmad, Int. J. Miner., Metall. Mater., 2020, 27, 857–871.
90. Y. Zhang, G. Stirnemann, J. T. Hynes and D. Laage, Phys. Chem. Chem. Phys., 2020, 22, 10581–10591.
91. Y. Zhang, H. B. de Aguiar, J. T. Hynes and D. Laage, J. Phys. Chem. Lett., 2020, 11, 624–631.
92. I. Siretanu, S. R. van Lin and F. Mugele, Faraday Discuss., 2023, 246, 274–295.
93. S. S. Lee, P. Fenter, K. L. Nagy and N. C. Sturchio, Nat. Commun., 2017, 8, 15826.

---

Footnote

† Electronic supplementary information (ESI) available: This article contains supplementary information describing details of the simulation procedure and additional detailed results summarised in the article. See DOI: https://doi.org/10.1039/d4cp00750f

---