Water splitting at imine-linked covalent organic frameworks

Abstract

Covalent organic frameworks (COFs) are a promising class of metal-free catalysts, offering a high structural and functional variety. Here, we systematically study imine-linked COFs with donor (D) and acceptor (A) groups using density functional theory (DFT). Using water splitting as a model reaction, we analyze the effects of protonation of the catalyst, the orientation of the imine linkage leading to different constitutional isomers, and solvation. In agreement with experimental results, we show that protonation decreases the band gap. In addition, COFs in which the donor is closer to the nitrogen atom of the imine group (DNCA) have lower band gaps than those in which the donor is closer to the carbon atom (DCNA). Three different D/A COFs are compared in this work, for which energies for the hydrogen evolution reaction (HER) and oxygen evolution reaction (OER) and corresponding electrochemical overpotentials are computed. We show that reaction energies are very similar for DCNA and DNCA COFs. The differences in hydrogen evolution rates between the constitutional isomers observed experimentally in (photocatalytic) HER (Yang et al., Nat. Commun., 2022, 13, 6317), are proposed to be at least in part a consequence of differences in charge distribution.

---

1 Introduction

Obtaining hydrogen from water using photo(electro)catalysts is a promising route towards sustainable energy production.^1–3 In this context, two-dimensional carbon-based materials^4–9 have recently been the focus of intense research. Compared to traditional metal-based catalysts, they are cheap and easy to produce while providing large structural flexibility. In particular, covalent-organic frameworks (COFs)^10–14 may be synthesized using a wide range of monomeric building blocks. This flexibility enables the introduction of additional functionality and offers the potential to tune their optoelectronic properties. For instance, incorporating electron-donating alongside electron-accepting groups may result in better separation of charge carriers and increased catalytic performance.^15–19

However, optimizing the COFs for specific catalytic applications requires a detailed understanding of the relationship between structure and properties. The large number of possible donor, acceptor, and linkage groups necessitates systematic studies. Even for a given combination of building units, structural variation may also be possible regarding the orientation of donor and acceptor groups with respect to the linkage. For example, when employing imine linkages, there are two constitutional isomers, depending on whether the carbon atom of the imine group is closer to the donor (DCNA) or to the acceptor (DNCA) groups, respectively. This has recently been shown to significantly affect hydrogen evolution rates²⁰ in photocatalytic water splitting. In that work, we achieved good agreement between observed and calculated band gaps for both isomers of one particularly active donor–acceptor combination, called DCNA-1 and DNCA-1. In ref. 20 it was observed that the HER production rate in particular for protonated DCNA-1, called DCNA-1_AC there (with protonation done by ascorbic acid) was excellent, while DNCA-1_AC performed less good. In ref. 20, also two other classes of D/A imine-linked COFs with different D and A combinations were investigated (see below), DCNA-2/DNCA-2 and DCNA-3/DNCA-3, which both showed good HER performance in their protonated forms and with DCNA-X_AC (X = 2,3) peforming better than DNCA-X_AC.

Here, we extend our previous computational studies to compare the mentioned three different donor–acceptor combinations in detail. In addition to band gaps and band positions for unprotonated and protonated species, we also calculate reaction energies of the hydrogen evolution and oxygen evolution reactions, and corresponding overpotentials relevant in particular for electrochemistry. Furthermore, we study the effect of solvation on these COFs. As one determinant for the HER efficiency of various D/A COFs, differences in charge distributions will be identified. The possible performance of the studied COFs in OER, not realized experimentally so far, will also be addressed.

2 Computational details

All calculations were performed using VASP, version 5.4.4.^21,22 The PBE functional²³ was employed together with the D3 dispersion correction²⁴ with Becke–Johnson damping.²⁵ Additional calculations using the hybrid functional HSE^26,27 were performed at the PBE-optimized structures to obtain accurate band gaps. Lattice parameters of the hexagonal unit cells were optimized using bulk models, which were then transformed into single-layer models by increasing the c vector to 20 Å. The optimized values for a (=b) are 23.22, 23.26, 23.43, 23.48, 25.47, and 25.50 Å for DCNA-1, DNCA-1, DCNA-2, DNCA-2, DCNA-3, and DNCA-3, respectively. The angle γ is 119.6° for DCNA-3 and DNCA-3 and 120.0° for the other COFs. The plane wave energy cutoff was set to 600 eV, and a 2 × 2 × 1 k-point grid was used. Harmonic vibrational frequencies were calculated numerically with a displacement of 1.5 pm. Only the adsorbed atoms were considered, while atoms of the catalyst surface and - in the case of protonated COFs - the ascorbate were fixed. These frequencies were used to obtain vibrational contributions to the Gibbs free energy. Calculations including implicit solvation effects were performed using a polarizable continuum model (PCM) as implemented in the VASPsol package.^28,29 Bader charges³⁰ were calculated using a grid-based approach.³¹

The oxygen evolution reaction (OER) can be described by four one-electron steps (* represents the catalyst):

A: * + H₂O → *OH + H⁺ + e⁻

B: *OH → *O + H⁺ + e⁻

C: *O + H₂O → *OOH + H⁺ + e⁻

D: *OOH → * + O₂ + H⁺ + e⁻

The reaction path of the OER under alkaline conditions is, from a thermodynamic viewpoint, related to the acidic path shown above via the dissociation of water to protons and hydroxide ions, which is represented by the pH correction term discussed below.

The hydrogen evolution reaction (HER) proceeds via two one-electron steps:

E: * + H⁺ + e⁻ → *H

F: *H + H⁺ + e⁻ →* + H₂

To compute Gibbs free reaction energies for individual steps in presence of finite pH and voltage, U, we employ Nørskov's computational hydrogen electrode model.³² That is (ref. 32 and 33)

ΔG_e = ΔG + Δ_pH − eU (1)

with the corrected (ΔG_e) and uncorrected (ΔG) Gibbs free energies of a given reaction step. The latter is calculated as ΔG = ΔH − TΔS with ΔH = ΔE_DFT + ΔZPE +ΔΔH(T) including DFT and zero point energy changes and thermal corrections ΔΔH(T) (due to vibrations, and possible rotations and translations). Spin-polarized calculations were performed for structures containing unpaired electrons. No constraints were imposed, so that the spin state could change freely to the optimal one during the calculation. The spin state was then assigned based on the total magnetization value. ΔE_DFT was determined by considering the respective species in their most stable spin states, i.e., *O, H₂O and H₂ as singlets, OH, OOH, *OH, *OOH and *H as doublets, and O₂ as triplet. We performed test calculations for *O to ensure that the singlet state that was obtained from the unconstrained calculation was indeed more stable than a triplet state. ΔS is the reaction entropy. Further, in eqn (1) Δ_pH = ±kT ln(10)pH is the pH correction term, with the sign depending on whether protons are reactants (HER, then +) or product (OER, then −). The temperature was chosen as T = 293.15 K if not stated otherwise. Finally, eU is the electrostatic correction term for a single-electron process at voltage U. The voltage is given using the standard hydrogen electrode as a reference. No additional charges or electric fields are applied to the unit cells. Thus, the formal surface charge only changes in integer steps in each reaction step (and is compensated by the adsorbate to keep the whole structure charge-neutral).

The overpotential η is calculated as η = U_L − U_eq, with U_eq as the voltage required to reach equilibrium, i.e., ΔG_e of the overall reaction (OER or HER) is 0 (this is independent of the catalyst used), and U_L as the voltage at which all individual steps are exergonic. Barriers between the reaction steps are neglected. Note that, while U_L and U_eq are affected by the pH value, the pH correction term cancels out when calculating the overpotential (assuming a constant pH value throughout the reaction). Overpotentials are determined both for OER, η^OER and HER, η^HER, respectively. Note that within the computational hydrogen electrode approach, reaction energies of E and F at U = 0 and pH = 0 have the same absolute values, just with an opposite sign. Thus, the overpotential for the HER corresponds to the absolute value of the Gibbs free energy of step E (or, equivalently, F).

While our analysis emphasizes electrochemical reactions with OER being the anodic half reaction and HER the cathodic one, the energetics are relevant for photocatalytic water splitting as well. In this case electrons are photoexcited from the valence to the conduction band and drive the HER while the OER is driven by holes in the valence band.

Graphical representations of structures and spin densities were prepared using Jmol³⁴ and VESTA,³⁵ respectively.

3 Results and discussion

3.1 Structure and band gaps

The structures of the different COFs are shown in Fig. 1 (see (Fig. 2) for schematic representations). All of them have hexagonal unit cells and show the same sequence of units: donor-imine-acceptor-imine. The direction of the imine linkage (–N=CH–) can be varied, so that its carbon atom is either closer to the donors (DCNA) or closer to the acceptors (DNCA). We further use the numbering established earlier²⁰ and described above for the specific combination of donor and acceptor. The donors are nitrogen, N, (DA-1 and DA-2) or phenyl, C₆H₃ (DA-3), while the acceptors are triazine, C₃N₃ (DA-1 and DA-3) or phenyl (DA-2). Each of these is connected to three phenyl groups, which are then bonded to imine groups. Note that all these structures are non-planar due to rotations of the phenyl groups bonded to the imine-N atoms and to the donor groups. As stated above, the COFs most active for HER are protonated forms. As in ref. 20, we protonate in computational models one of the (three) imine groups per cell, giving [–NH=CH–]⁺ and species DCNA-X_AC and DNCA-X_AC, respectively (for X = 1,2,3). These have one ascorbate anion (C₆H₇O₆⁻) hydrogen-bonded near the protonated group – see ref. 20, Fig. 5 for optimized structures of protonated DCNA-1 and DNCA-1 as an example.

Fig. 1 Structures of (a) DCNA-1, (b) DNCA-1, (c) DCNA-2, (d) DNCA-2, (e) DCNA-3, (f) DNCA-3, optimized at the PBE+D3 level of theory. H: white; C: grey; N: blue. Solid lines indicate hexagonal elementary cells used in simulations. The optimized values for a (=b) are 23.22, 23.26, 23.43, 23.48, 25.47, and 25.50 Å for DCNA-1, DNCA-1, DCNA-2, DNCA-2, DCNA-3, and DNCA-3, respectively. The angle γ is 119.6° for DCNA-3 and DNCA-3 and 120.0° for the other COFs.

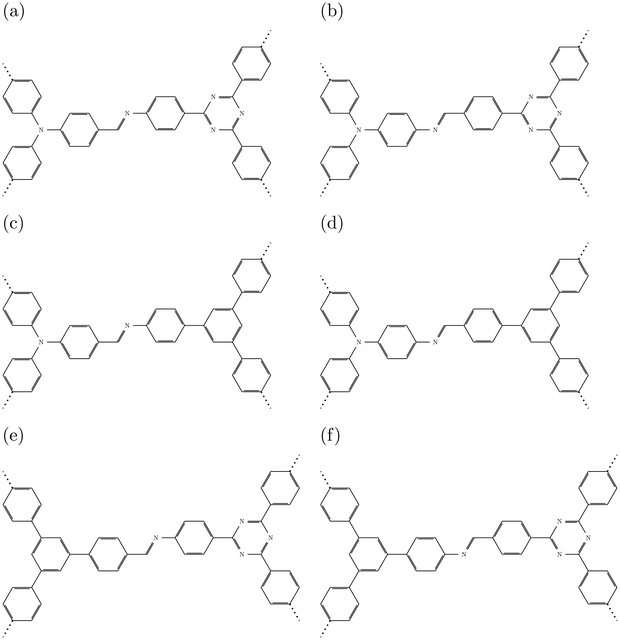Fig. 2 Schematic representations of the central motif (donor, imine linkage, and acceptor) of (a) DCNA-1, (b) DNCA-1, (c) DCNA-2, (d) DNCA-2, (e) DCNA-3, (f) DNCA-3.

To be suitable for water splitting, band gaps of photo(electro)catalysts should be larger than 1.23 eV, the energy required for the overall reaction. All investigated COFs fulfill this minimal requirement. Band gaps of unprotonated DNCA-COFs are lower compared to the corresponding DCNA-COFs by 0.2 to 0.7 eV (see Fig. 3(a)). PBE and HSE results both show this trend, but PBE underestimates the values compared to HSE, as expected. The HSE results are in very good agreement with experimental results.²⁰ Also the experimental trends for gaps with DCNA-1 ∼ DCNA-2 < DCNA-3 and DNCA-1 < DNCA-2 < DNCA-3 are nicely followed.

Fig. 3 Band gaps of (a) DA-COFs and (b) protonated DA-COFs obtained from experiment²⁰ (black circles) and calculated using PBE (red triangles) and HSE (blue squares).

In further agreement with experimental results,²⁰ protonation results in lower band gaps (see Fig. 3(b)). Similar to the non-protonated COFs, HSE results are in very good agreement with experimental values, while PBE underestimates them. Note that apart from the diminished band gaps, the overall trends observed for the protonated species are similar to those found for the non-protonated COFs.

3.2 Oxygen evolution reaction

For the COFs studied in this work, photo- or electrochemical OER has not been reported experimentally so far. Still, a theoretical investigation of the four (electrochemical) steps A–D given above is worthwhile. The relevant intermediates O, OH, and OOH were adsorbed at the imine group and all potential donor and acceptor groups. O is covalently bound in all cases, either to a nitrogen atom (amine, triazine, and imine) or to two carbon atoms (phenyl). OH can be either covalently bound to carbon (triazine, phenyl, and imine) or van der Waals-bound (amine). The OOH intermediate, in most cases, actually consists of both of the two aforementioned species, O and OH. We also considered the formation of a peroxide (OOH) group, but this is much less stable except for adsorption at amine groups, because it is only weakly bound via hydrogen bonds to nitrogen or van der Waals interactions with phenyl groups. Corresponding structures, all optimized on the PBE+D3 level of theory, are shown in Fig. 4.

Fig. 4 OER intermediates at (a)–(c) imine, (d)–(f) amine, (g)–(i) triazine, and (j)–(l) phenyl groups, optimized at the PBE+D3 level of theory. H: white; C: grey; N: blue; O: red.

The different binding sites also lead to differences in the Gibbs free energy profiles of the OER (see Fig. 5). The figures show these profiles at pH = 0 and U = 0, for DCNA-X and DNCA-X, with the three different adsorption sites (donor, acceptor, imine) in each case. Step A, which involves adsorption of an OH group, is endergonic in all cases, but significantly more so when the reaction takes place at amine or triazine groups. The following step B, leading to an adsorbed O atom, is exergonic at triazine groups, but endergonic at imine, amine and phenyl groups. Step C, involving adsorption of another OH, is strongly endergonic at all groups, in particular at triazine groups. Finally, step D, in which O₂ is formed and the catalyst is regenerated, is exergonic at amine groups, close to thermoneutral at triazine groups, and endergonic at phenyl and imine groups. Step A is the one with the highest increase in energy (corresponding to the rate-determining step) at all groups. Because this step is most favorable at imine groups, they are the most probable reaction sites (based on purely thermodynamical considerations).

Fig. 5 OER reaction profiles of (a) DCNA-1, (b) DNCA-1, (c) DCNA-2, (d) DNCA-2, (e) DCNA-3, (f) DNCA-3.

Independent of adsorption site and catalyst, the reaction energy for the entire half reaction, H₂O → O₂+ 4 H⁺+ 4e⁻ is 4.32 eV. Note that this value is much lower than the expected 4.92 eV due to the overbinding of the oxygen molecule (see, for instance,³⁶). However, this applies to all COFs equally and does not affect comparability between them. When applying the equilibrium voltage of U_eq = 4.32/4 = 1.08 V, each individual step will be stabilized by 1.08 eV. Since step A is rate-limiting and most favourable when adsorption takes place at imine sites, the corresponding (minimal) overpotentials (see Table 1) are rather similar for the different donor–acceptor combinations. However, they are lower for DNCA-COFs compared to the DCNA-COFs, demonstrating the importance of the constitutional isomerism. Note that OH and O preferentially bind to the C and N atom of the imine group, respectively. Consequently, the transformation of OH to O in step B would also involve a change in binding site and a corresponding energy barrier. However, step B requires around 1 eV less than step A, so even with the inclusion of this barrier, step A likely remains rate-determining.

Table 1 Overpotentials η in eV for the HER and OER reaction. In case of the HER, overpotentials for the protonated COFs (AC) are given as well. Values in parentheses were obtained by correcting the energy of the oxygen molecule based on the experimental Gibbs free energy of the water splitting reaction

COF	η ^HER	η ^HER AC	η ^OER
DCNA-1	0.26	0.01	0.64 (0.59)
DNCA-1	0.24	0.05	0.41 (0.63)
DCNA-2	0.22	0.31	0.56 (0.51)
DNCA-2	0.23	0.23	0.37 (0.50)
DCNA-3	0.17	0.11	0.64 (0.60)
DNCA-3	0.14	0.03	0.54 (0.60)

---

If we correct the energy of the oxygen molecule such that the experimental value of the overall water splitting reaction is obtained (4.92 eV), step D becomes the rate-limiting step at imine groups. The overpotentials change by up to 0.22 eV (see the values in parentheses in Table 1), reducing the differences between the various COFs. In this case, the overpotentials for DCNA-2, DNCA-2, and DNCA-3 are slightly lower at phenyl groups compared to imine groups.

3.3 Hydrogen evolution reaction

Photocatalytic HER has been achieved for all six protonated COFs DCNA-XAC studied in this work in ref. 20, with the trends outlined above, namely H₂ evolution rates DCNA-X_AC > DNCA-X_AC and DCNA-1_AC > DCNA-2_AC ∼ DCNA-1_AC. We studied HER for all six protonated and un-protonated COFs.

We investigated hydrogen adsorption at the imine groups and the donor and acceptor groups. Imine groups are the most stable adsorption sites, showing slightly exothermic binding energies of −0.06 to −0.17 eV. All other sites show endothermic adsorption energies, increasing from triazine (0.15 to 0.22 eV) to phenyl (0.51 to 0.68 eV) to amine (1.67 to 1.91 eV). These trends also apply to the protonated COFs, but the adsorption energies are generally lower (stronger binding). The exception are imine and phenyl groups in DCNA-2 and the imine group in DNCA-2, which show slightly higher adsorption energies (weaker binding) compared to the corresponding non-protonated COFs.

Using Gibbs free energies instead of electronic energies increases the energy of the adsorbed state with respect to free H₂. The enthalpic and entropic corrections are similar for the pure and protonated COFs. Thus, while step E is endergonic in most cases, this is generally much more pronounced for the pure COFs (0.14 eV up to 0.26 eV). The Gibbs free energy profiles for the HER of DCNA-1 and DNCA-1 are shown in Fig. 7 (black lines without any solvation effects).

At the protonated COFs 1 and 3, step E is only slightly endergonic or slightly exergonic (DNCA-3_AC). Thus, the overpotentials (see Table 1) are particularly low for COFs 1 and 3. Differences between DCNA and DNCA structures are small. This is apparently in contrast to the experimentally observed large HER activity differences between the constitutional isomers,²⁰ and the better performance of DCNA-1_AC compared to DCNA-2_AC and DCNA-3_AC. This may be either because of other factors affecting the catalytic activity (e.g., the separation of charge carriers or the precise positioning of the conduction band), or because our computational models are too simple. We will explore some of these aspects in the following sections.

3.4 Band positions

In order for HER to be energetically feasible, not only the overall band gap is important but also the conduction band minimum, ε_CBM, corrected by η^HER should be above the H⁺/H₂ reduction potential. Similarly, for OER the valence band maximum, ε_VBM, corrected by η^OER, must be below the O₂/H₂O electrochemical potential.

In Fig. 6(a), we show the conduction and valence band edges of DCNA-X and DNCA-X (X = 1,2,3) with and without overpotential corrections. Uncorrected band edges are obtained with HSE, the overpotentials are taken from Table 1. Fig. 6(b) gives the same information for the protonated species, DCNA-X_AC and DNCA-X_AC. (For overpotentials of the OER reaction, the values of the unprotonated species of Table 1, η^OER, were taken for simplicity.) Also shown are the electrochemical potentials for H⁺/H₂ and O₂/H₂O at pH = 7 (blue and red horizontal lines) and a range of pH values between 0 and 14 (shaded areas), at T = 298.15 K. Note that all values are given w.r.t. the vacuum energy. On this absolute scale, the electrochemical potential for H⁺/H₂ at pH = 0 is −4.44 V³⁷ (rather than 0 V as for the normal hydrogen electrode potential), while that of O₂/H₂O at pH = 7 is −4.44 V −1.23 V = −5.67 V. At finite pH, these values are up-shifted by kT ln(10)pH.

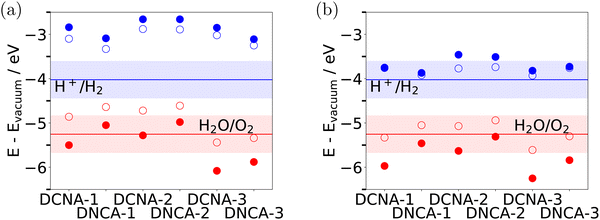Fig. 6 Band edges relative to vacuum energy for (a) unprotonated DCNA-X without (filled symbols) and with overpotential correction (open symbols). (b) The same for protonated DCNA-X_AC. Band edges were calculated with HSE, overpotentials are taken from Table 1. (For η^OERAC in (b), the η^OER were taken for simplicity.) Also shown are the electrochemical potentials for H⁺/H₂ and O₂/H₂O at pH = 7 (blue and red horizontal lines) and a range of pH values between 0 and 14 (lower and upper boundaries of the shaded areas), all at T = 298.15 K.

From the conduction band edges we note that all COFs fulfill the energy criterion for HER, ε_CBM − η^HER > U (H⁺/H₂), at least for not too basic pH values, in agreement with experimental findings. Note that the corrected band edges are closer to the HER potential for the protonated species. In the sense of a Golden Rule type argument, which predicts electron transfer rates to be large when initial and final states are close in energy, this may help to explain the better performance of the protonated species. The experimentally observed differences between DCNA-1_AC, DCNA-2_AC, and DCNA-3_AC, however, cannot be rationalized on the basis of this criterion either.

Inspecting overpotential-corrected valence band edges we note that OER will be difficult for most COFs studied in this work, at least when based on a simple energy criterion ε_VBM + η^OER < U (H₂O/O₂). At pH = 7, only DCNA-1_AC as well as DCNA-3 and DNCA-3 in protonated and unprotonated form are predicted to be possible candidates. Note that this result is not qualitatively affected when using the overpotentials corrected as described above (using the experimental value of the Gibbs free energy of the water splitting reaction).

3.5 Hydration effects

Returning to the experimentally known HER at the studied COFs, we also investigated the effect of hydration. For DCNA-1 and DNCA-1, we compared calculations including implicit solvation (via a polarizable continuum model, PCM) and explicit solvation (including one water molecule hydrogen-bonded to the catalyst). The water molecule was placed close to the imine group, forming hydrogen bonds: H_water⋯N_imine (pure COF) or N_imine–H⋯O_water (product of step E). A single water molecule is a very simplistic model for explicit solvation, but a more thorough investigation involving molecular dynamics simulations of extended water networks is beyond the scope of the present work.

Solvation leads to stronger binding of hydrogen to the COF, reducing the energy required for step E of the HER (see Fig. 7). The effect is approximately twice as large when using the PCM compared to explicit solvation, or, in other words, the differences in energy between no solvent and explicit solvent and between explicit solvent and implicit solvent are very similar. The energy difference is much higher for DCNA-1 (ca. 0.1 eV) compared to DNCA-1 (ca. 0.05 eV). Thus, while both show very similar reaction energies in the absence of solvation, the reaction energy (and, consequently, the overpotential) in water is much smaller for DCNA-1 compared to DNCA-1. However, the overpotentials of both isomers are small compared to the separation between conduction band and hydrogen evolution potential, especially at the low pH values used in experiment (cf.Fig. 6). The observed differences in hydrogen evolution rates is, therefore, unlikely to be based on the differences in overpotentials. Nevertheless, the impact of solvation on the HER overpotentials highlights the important role of electrostatic effects.

Fig. 7 Free energies of the hydrogen evolution reaction at (a) DCNA-1 and (b) DNCA-1, calculated without solvent (black), with a single water molecule (cyan), and with implicit solvation (pink).

3.6 Electron density redistribution during the hydrogen evolution reaction

We analyzed the changes in electron density during the HER to better understand the differences in reactivity between the constitutional isomers. The electron density differences and spin densities show that reaction step E, i.e., addition of a hydrogen atom, leads to rather localized increases in electron density. The largest changes in electron density upon hydrogen adsorption occur at the imine group, in particular at the carbon atom. Bader charge analysis shows that this C atom is more negatively charged by ≈0.2 e compared to the pure COF (see Table 2). There is also some spin density on the phenyl group that is bound to the carbon atom of the imine (see Fig. 8). (Charge and spin density analysis was done for unprotonated DCNA-1 and DNCA-1, an additional proton at another imine group does not change these values significantly.)

Table 2 Change in Bader charge upon hydrogen adsorption at an imine group for different functional groups of the protonated COFs

COF	Imine	Donor	Acceptor
DCNA-1	−0.21	−0.11	−0.06
DNCA-1	−0.20	+0.01	−0.25
DCNA-2	−0.22	−0.15	−0.01
DNCA-2	−0.21	+0.01	−0.21
DCNA-3	−0.25	−0.09	−0.09
DNCA-3	−0.19	+0.04	−0.27

---

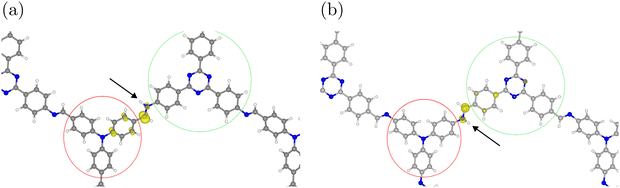Fig. 8 Spin densities (yellow) after hydrogen adsorption at (a) DCNA-1 and (b) DNCA-1. An isosurface level of 0.01 eV Å⁻³ was used. The arrow indicates the adsorbed hydrogen. Donor and acceptor groups as defined for the charge analysis in Table 2 are indicated in red and green, respectively.

Our analysis thus demonstrates that the changes in electron density occur near the donor and acceptor groups for DCNA-1 and DNCA-1, respectively. This suggests that the isomers behave differently in terms of charge separation and/or charge transport during the HER, which affects their catalytic performance.

3.7 Comparison to other water splitting catalysts

Water splitting at COFs has been studied in the literature using DFT calculations similar to ours. For instance, Wan et al.³⁸ compared various combinations of building units and linkages. Their COFs contained only one type of building unit, so there was no donor–acceptor motif. Nevertheless, they also used imine linkages connected to amine, phenyl, and triazine units via phenyl groups, leading to similar structures as the ones used in this work. Consequently, their results are also similar to ours. For instance, the high energy of the valence band maximum of the amine-containing COFs 1 and 2 is in good agreement with the results shown in ref. 38. Using the same active sites (phenyl groups) and the same pH value (7, not shown here), the OER reaction profiles are also very similar. However, as discussed in the previous sections, the reactivity can be influenced by the donor–acceptor combination, protonation, and the orientation of the imine linkage, and these factors have not been investigated in ref. 38.

Metal–organic frameworks (MOFs) are also frequently studied as electrocatalysts for water splitting. For example, Das et al.³⁹ investigated metallophthalocyanine-based MOFs using PBE+D3. The lowest HER overpotential that they reported is 0.08 V, which is comparable to our HER overpotentials for COFs 1 and 3 (see Table 1, η^HER AC). The lowest overpotential for the OER in their work is 0.58 V, which is also very similar to our values (Table 1, η^OER). DNCA-1 and DNCA-2 have even lower OER overpotentials than the values reported in ref. 39, but the valence band position of these two COFs limits their suitability for the OER.

Thus, in terms of band alignment and overpotentials, the performance of the COFs presented here is on par with other recently studied water-splitting catalysts. However, charge separation and carrier mobility are also important characteristics affecting the catalytic performance, which may be improved using two-dimensional hetero-structures (see, for example, ref. 40).

4 Conclusions

In this work, we investigated the suitability of different imine-linked COFs for water splitting using DFT calculations. Band gaps calculated using the HSE functional are in very good agreement with experiment and are larger than the 1.23 eV required to enable water splitting. As expected, PBE underestimates band gaps.

The COFs investigated here fulfill the additional energy criterion for the HER half reaction based on conduction band edges, as suggested by experiment. For the OER half reaction, however, only few of the COFs fulfill an analogous criterion based on valence band edges.

Imine groups are the most active sites for both reactions. This suggests a competition between the OER and HER reactions, but the presence of multiple imine groups and the fact that the OER overpotentials are only moderately higher at phenyl groups may still enable both reactions to take place at the same COF. Overpotentials for the OER and HER are rather similar at the different COFs. This suggests that the experimentally observed large differences in hydrogen production rates during HER between DCNA and DNCA COFs are not based on differences in the stabilization of adsorbed hydrogen, but rather on other photochemical descriptors. Based on the charge density differences and spin densities, we propose that the separation and/or transport of excited charge carriers are more decisive factors. In particular for photocatalysis, also differences in oscillator strengths for relevant optical excitations may be of importance.^20,41 Based purely on the combination of band positions and overpotentials, protonated DCNA-3 is expected to show the best overall water splitting performance, followed by DCNA-1 (which shows the highest HER rates in experiment).

Our calculations also showed the importance of taking into account solvation effects. The reaction energies of the HER (and, consequently, overpotentials) are affected even by the presence of a single explicit water molecule. Using an implicit solvation model leads to even stronger changes in reaction energies. Further work is needed to address this in more detail by using more explicit water molecules and combining explicit and implicit solvation.

Data availability

Data for this article, in particular files of all optimized structures, are available at Zenodo (https://doi.org/10.5281/zenodo.12683320).

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We thank Arne Thomas (TU Berlin) and his coworkers for fruitful discussions. Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy - EXC 2008/1-390540038 - UniSysCat (C. P. and P. S.). The authors gratefully acknowledge the computing time made available to them on the high-performance computer “Lise” at the NHR Center NHR@ZIB. This center is jointly supported by the Federal Ministry of Education and Research and the state governments participating in the NHR (https://www.nhr-verein.de/unsere-partner).

References

1. X. Zou and Y. Zhang, Noble metal-free hydrogen evolution catalysts for water splitting, Chem. Soc. Rev., 2015, 44, 5148–5180.
2. M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Solar Water Splitting Cells, Chem. Rev., 2010, 110, 6446–6473.
3. I. Roger, M. A. Shipman and M. D. Symes, Earth-abundant catalysts for electrochemical and photoelectrochemical water splitting, Nat. Rev. Chem., 2017, 1, 0003.
4. A. Savateev and M. Antonietti, Ionic Carbon Nitrides in Solar Hydrogen Production and Organic Synthesis: Exciting Chemistry and Economic Advantages, ChemCatChem, 2019, 11, 6166–6176.
5. M. Zhao, J. Feng, W. Yang, S. Song and H. Zhang, Recent Advances in Graphitic Carbon Nitride Supported Single-Atom Catalysts for Energy Conversion, ChemCatChem, 2021, 13, 1250–1270.
6. L. Tan, C. Nie, Z. Ao, H. Sun, T. An and S. Wang, Novel TwoDimensional Crystalline Carbon Nitrides beyond g-C₃N₄: Structure and Applications, J. Mater. Chem. A, 2021, 9, 17–33.
7. V. W.-h Lau and B. V. Lotsch, A Tour-Guide through Carbon NitrideLand: Structure- and Dimensionality-Dependent Properties for Photo-(Electro)Chemical Energy Conversion and Storage, Adv. Energy Mater., 2022, 12, 2101078.
8. H. Jin, C. Guo, X. Liu, J. Liu, A. Vasileff, Y. Jiao, Y. Zheng and S.-Z. Qiao, Emerging Two-Dimensional Nanomaterials for Electrocatalysis, Chem. Rev., 2018, 118, 6337–6408.
9. J. Zhang, Y. Chen and X. Wang, Two-dimensional covalent carbon nitride nanosheets: synthesis, functionalization, and applications, Energy Environ. Sci., 2015, 8, 3092–3108.
10. A. P. Côté, A. I. Benin, N. W. Ockwig, M. O’Keeffe, A. J. Matzger and O. M. Yaghi, Porous, Crystalline, Covalent Organic Frameworks, Science, 2005, 310, 1166–1170.
11. R. Liu, K. T. Tan, Y. Gong, Y. Chen, Z. Li, S. Xie, T. He, Z. Lu, H. Yang and D. Jiang, Covalent organic frameworks: an ideal platform for designing ordered materials and advanced applications, Chem. Soc. Rev., 2021, 50, 120–242.
12. S. J. Lyle, P. J. Waller and O. M. Yaghi, Covalent Organic Frameworks: Organic Chemistry Extended into Two and Three Dimensions, Trends Chem., 2019, 1, 172–184.
13. S. Kandambeth, K. Dey and R. Banerjee, Covalent Organic Frameworks: Chemistry beyond the Structure, J. Am. Chem. Soc., 2019, 141, 1807–1822.
14. H. M. El-Kaderi, J. R. Hunt, J. L. Mendoza-Cortés, A. P. Côté, R. E. Taylor, M. O’Keeffe and O. M. Yaghi, Designed Synthesis of 3D Covalent Organic Frameworks, Science, 2007, 316, 268–272.
15. M. Calik, F. Auras, L. M. Salonen, K. Bader, I. Grill, M. Handloser, D. D. Medina, M. Dogru, F. Löbermann, D. Trauner, A. Hartschuh and T. Bein, Extraction of Photogenerated Electrons and Holes from a Covalent Organic Framework Integrated Heterojunction, J. Am. Chem. Soc., 2014, 136, 17802–17807.
16. P. Pachfule, A. Acharjya, J. Roeser, R. P. Sivasankaran, M.-Y. Ye, A. Brückner, J. Schmidt and A. Thomas, Donor–acceptor covalent organic frameworks for visible light induced free radical polymerization, Chem. Sci., 2019, 10, 8316–8322.
17. S. Jin, K. Furukawa, M. Addicoat, L. Chen, S. Takahashi, S. Irle, T. Nakamura and D. Jiang, Large pore donor–acceptor covalent organic frameworks, Chem. Sci., 2013, 4, 4505.
18. A. Chatterjee, J. Sun, K. S. Rawat, V. Van Speybroeck and P. Van Der Voort, Exploring the Charge Storage Dynamics in Donor–Acceptor Covalent Organic Frameworks Based Supercapacitors by Employing Ionic Liquid Electrolyte, Small, 2023, 19, 2303189.
19. P. Das, B. Ball and P. Sarkar, Theoretical investigation of a tetrazine based covalent organic framework as a promising anode material for sodium/calcium ion batteries, Phys. Chem. Chem. Phys., 2022, 24, 21729–21739.
20. J. Yang, et al., Constitutional Isomerism of the Linkages in Donor–Acceptor Covalent Organic Frameworks and Its Impact on Photocatalysis, Nat. Commun., 2022, 13, 6317.
21. G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15–50.
22. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
23. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
24. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
25. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465.
26. J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid Functionals Based on a Screened Coulomb Potential, J. Chem. Phys., 2003, 118, 8207–8215.
27. J. Heyd, G. E. Scuseria and M. Ernzerhof, Erratum: “Hybrid Functionals Based on a Screened Coulomb Potential” [J. Chem. Phys.118, 8207 (2003)], J. Chem. Phys., 2006, 124, 219906.
28. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways, J. Chem. Phys., 2014, 140, 084106.
29. K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, Implicit self-consistent electrolyte model in plane-wave densityfunctional theory, J. Chem. Phys., 2019, 151, 234101.
30. R. F. W. Bader, Atoms in Molecules: A Quantum Theory; The International Series of Monographs on Chemistry 22, Clarendon Press, Oxford University Press, Oxford [England]: New York, 1994.
31. W. Tang, E. Sanville and G. A. Henkelman, Grid-Based Bader Analysis Algorithm without Lattice Bias, J. Phys.: Condens. Matter, 2009, 21, 084204.
32. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108, 17886–17892.
33. J. Wirth, R. Neumann, M. Antonietti and P. Saalfrank, Adsorption and Photocatalytic Splitting of Water on Graphitic Carbon Nitride: A Combined First Principles and Semiempirical Study, Phys. Chem. Chem. Phys., 2014, 16, 15917–15926.
34. Jmol: an open-source Java viewer for chemical structures in 3D. https://www.jmol.org/.
35. K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276.
36. S. Kurth, J. P. Perdew and P. Blaha, Molecular and solid-state tests of density functional approximations: LSD, GGAs, and meta-GGAs, Int. J. Quant. Chem., 1999, 75, 889–909.
37. S. Trasatti, The Absolute Electrode Potential: An Explanatory Note, J. Electroanal. Chem., 1986, 209, 417–428.
38. Y. Wan, L. Wang, H. Xu, X. Wu and J. Yang, A Simple Molecular Design Strategy for Two-Dimensional Covalent Organic Framework Capable of Visible-Light-Driven Water Splitting, J. Am. Chem. Soc., 2020, 142, 4508–4516.
39. P. Das, B. Ball and P. Sarkar, Bifunctional Electrocatalytic Activity of Two-Dimensional Metallophthalocyanine-Based Metal–Organic-Frameworks for Overall Water Splitting: A DFT Study, ACS Catal., 2023, 13, 16307–16317.
40. S. Sannigrahi, A. Ghosh, B. Ball and P. Sarkar, Exploring the Ti 2 CO 2 –WSe 2 Heterostructure as a Direct Z -Scheme Photocatalyst for Water Splitting: A Non-Adiabatic Study, J. Phys. Chem. C, 2022, 126, 20852–20863.
41. C. Penschke, R. E. Von Zander, A. Beqiraj, A. Zehle, N. Jahn, R. Neumann and P. Saalfrank, Water on Porous, Nitrogen-Containing Layered Carbon Materials: The Performance of Computational Model Chemistries, Phys. Chem. Chem. Phys., 2022, 24, 14709–14726.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02019g

---