Open Access Article
Open Access ArticleWater vapor effect on the physico-geometrical reaction pathway and kinetics of the multistep thermal dehydration of calcium chloride dihydrate†
Kazuki
Kato
,
Mito
Hotta
and
Nobuyoshi
Koga
 *
*
Department of Science Education, Division of Educational Sciences, Graduate School of Humanities and Social Sciences, Hiroshima University, 1-1-1 Kagamiyama, Higashi-Hiroshima 739-8524, Japan. E-mail: nkoga@hiroshima-u.ac.jp; Fax: +81-82-424-7092; Tel: +81-82-424-7092
First published on 18th June 2024
Abstract
This study investigated how water vapor influences the reaction pathway and kinetics of the multistep thermal dehydration of inorganic hydrates, focusing on CaCl2·2H2O (CC-DH) transforming into its anhydride (CC-AH) via an intermediate of its monohydrate (CC-MH). In the presence of atmospheric water vapor, the thermal dehydration of CC-DH stoichiometrically proceeded through two distinct steps, resulting in the formation of CC-AH via CC-MH under isothermal conditions and linear nonisothermal conditions at a lower heating rate (β). Irrespective of atmospheric water vapor pressure (p(H2O)), these reaction steps were kinetically characterized by a physico-geometrical consecutive process involving the surface reaction and phase boundary-controlled reaction, which was accompanied by three-dimensional shrinkage of the reaction interface. In addition, a significant induction period was observed for the second reaction step, that is, the thermal dehydration of CC-MH intermediate to form CC-AH. With increasing p(H2O), a systematic increase in the apparent Arrhenius parameters was observed for the first reaction step, that is, the thermal dehydration of CC-DH to form CC-MH, whereas the second reaction step exhibited unsystematic variations of the Arrhenius parameters. At a larger β in the presence of atmospheric water vapor, the first and second reaction steps partially overlapped; moreover, an alternative reaction step of the thermal dehydration of CC-MH to form CaCl2·0.3H2O was observed between these reaction steps. The physico-geometrical phenomena influencing the reaction pathway and kinetics of the multistep thermal dehydration were elucidated by considering the effects of atmospheric and self-generated water vapor in a geometrically constrained reaction scheme.
1. Introduction
The kinetics and mechanism underlying the thermal dehydration of inorganic hydrates have been extensively studied over the past century, with the aim of establishing the theoretical basis for solid-state reactions accompanied by the evolution of gaseous products.1–5 This class of reactions, categorized as the thermal decomposition of solids with a reversible nature, has consistently garnered attention as a potential candidate for thermochemical energy storage via the reaction cycle comprising endothermic thermal dehydration and exothermic hydration.6–9 In order to develop practical thermochemical energy storage systems that utilize thermal dehydration and hydration of inorganic hydrates, it is necessary to gain further insight into the kinetics of forward and reverse reactions, as well as to have a comprehensive understanding of the phase relationships in the reaction system based on reliable thermodynamics. With regard to the reaction kinetics, the existing kinetic theory, which characterizes the reaction rate as a function of temperature (T) and degree of reaction (α), requires expansion in order to incorporate the interactions between solid reactants and products with gaseous products. Therefore, the incorporation of a term representing the partial pressure of the gaseous product species in the reaction atmosphere and at the reaction interface into the kinetic equation is essential. This challenge, also spanning over a century,10 has recently been addressed by achieving a universal kinetic description of the reaction rate as a function of T, α, and the partial pressure of the gas. This was achieved by introducing an accommodation function (AF) based on the partial pressure of the gaseous product species and the equilibrium pressure of the reaction (Peq(T)), demonstrated in simple single-step reactions such as the thermal decomposition of metal carbonates11–14 and hydroxides,15–17 as well as thermal dehydration of inorganic hydrates.18–21 Nevertheless, to enhance our comprehension of the thermal dehydration of inorganic hydrates and facilitate the design of thermochemical energy storage systems, more advanced kinetic modeling is necessary because many potential thermal dehydration reactions entail multistep processes and proceed through several intermediate hydrates. In multistep thermal dehydration reactions, each component reaction step can be regulated by different physico-geometrical constraints. Overlaps of the different reaction steps generate complex physico-geometrical constraints for the reaction. In addition, the kinetics of each reaction step can be influenced by atmospheric and self-generated water vapor, which modify the chemical and physico-geometrical reaction pathways. Consequently, the physico-geometrical kinetic behaviors must be comprehended by considering geometrical constraints in multistep reactions and the effect of atmospheric and self-generated water vapor on the reaction pathway and kinetics of the component reaction steps.The thermal dehydration of calcium chloride hydrates exemplifies a multistep process, where various intermediate hydrates are involved in the formation of anhydride. The thermal dehydration–hydration cycle of calcium chloride hydrates is potentially suitable for thermochemical energy storage systems.22–30 Calcium chloride dihydrate (CC-DH) is a relatively stable crystalline hydrate that is commonly utilized as a dehumidifying and snow-melting agent in daily life. Thermal dehydration of CC-DH results in the formation of its anhydride (CC-AH) via an intermediate of monohydrate (CC-MH).
 | (1) |
 | (2) |
In our previous study,31 we examined the thermal dehydration of CC-DH in a stream of dry N2 to understand the impact of self-generated water vapor on the reaction pathway and kinetics of the component reaction steps. The process was comprised of three distinct steps: (1) direct dehydration of CC-DH to CC-AH on the particle surface, resulting in a core–shell structure with CC-DH core and CC-AH shell; (2) contraction of the CC-DH core with the three-dimensional (3D) interface shrinkage to form CC-MH; and (3) contraction of the CC-MH core with the 3D interface shrinkage to form CC-AH. The transition from the first to second reaction steps was associated with an elevation in the partial pressure of water vapor (p(H2O)) at the reaction interface of the first reaction step. Furthermore, the kinetic analysis indicated an acceleration in the linear advancement rates of the reaction interfaces during the second and third reaction steps as they advanced. These acceleration behaviors were explained by the gradual decrease in p(H2O) at the corresponding reaction interfaces, influenced by the changes in the overlapping features with the other reaction steps.
The presence of atmospheric water vapor can induce changes in the reaction pathway and kinetic features of the component reaction steps. Molenda et al. have reported a distinct two-step mass loss process during the thermal dehydration of CC-DH to yield CC-AH via stable CC-MH at elevated atmospheric p(H2O) levels (≈5 kPa).22 The change in the mass loss process owing to differing atmospheric p(H2O) levels indicates the varying effects of p(H2O) on each reaction step. In addition, they observed the formation of an alternative intermediate hydrate, CaCl2·0.3H2O (CC-0.3H), during thermal dehydration at high p(H2O) values (≥10 kPa) and during the hydration of CC-AH. This indicates a variation in the reaction pathway influenced by atmospheric p(H2O).22 Herein, we systematically monitored the thermal dehydration of CC-DH at various atmospheric p(H2O) values using humidity-controlled thermogravimetry (TG). We examined variations in the overlapping features of the component reaction steps with atmospheric p(H2O) through kinetic analysis of multistep reactions. Furthermore, we elucidated the physico-geometrical kinetic features of individual reaction steps using kinetic analysis based on a physico-geometrical consecutive reaction model comprising the induction period (IP), surface reaction (SR), and phase boundary-controlled reaction (PBR).32–36 We also observed variations in the kinetic features of individual physico-geometrical reaction processes, i.e., IP, SR, and PBR, at each reaction step with atmospheric p(H2O) by tracking changes in the apparent Arrhenius parameters. The reaction behaviors with specific physico-chemical and physico-geometrical phenomena in the presence of atmospheric water vapor were interpreted considering the effects of atmospheric and self-generated water vapor, in comparison with those observed in a stream of dry N2, as reported previously. 31 The integrated findings of the mutually correlated variations in the reaction behaviors and atmospheric and self-generated p(H2O) during the multistep thermal dehydration of CC-DH in our study, along with previous studies, serve as the basis for the further advanced universal kinetic modeling aimed at using thermal dehydration and hydration of inorganic hydrates as a thermochemical energy storage system.
2. Experimental
2.1 Sample description
The same CC-DH sample used in our previous study to monitor the thermal decomposition process in a stream of dry N231 was used in this study, focusing on examining the effect of water vapor on the thermal dehydration pathway and kinetics. The CC-DH sample (special grade, >99.9%, FUJIFILM Wako Chem.) underwent characterization via powder X-ray diffraction and Fourier transform infrared spectroscopy, confirming its crystallographic structure (orthorhombic, SG = Pbcn(60), a = 5.8930, b = 7.4690, c = 12.0700, α = β = γ = 90.000, ICCD-PDF 01-070-0385)37 and revealing infrared absorption peaks indicative of O–H stretching, H–O–H bending, and calcium chloride lattice vibrations.29,38 The sample, comprised cuboidal particles with a sieved particle size fraction of 300–500 μm, was used for the thermoanalytical (TA) measurements. Notably, the sample demonstrated substantial deliquesce during sampling for TA measurements at room temperature in ambient atmospheres. To recover CC-DH in the deliquesced surface portion, the weighed samples were adequately dried at room temperature (approximately 303 K) in a stream of dry N2 before conducting the TA measurements. Sample characterization was detailed in our previous article.312.2 Kinetic measurements in a stream of wet N2
The thermal dehydration process of CC-DH in the presence of atmospheric water vapor at various controlled p(H2O) values was measured using a TG–differential thermal analysis (DTA) instrument (TG-8122, Thermoplus Evo2 system, Rigaku) fitted with a humidity controller (me-40DP-2PHW, Micro equipment Co.). The initial sample mass (m0) for the humidity-controlled TG measurements was fixed to be 3.0 mg and weighed into a Pt pan (5 mm in diameter and 2.5 mm in depth). Initially, the sample placed in the TG–DTA instrument was left at room temperature in a stream of dry N2 at a qv of 200 cm3 min−1 for 90 min before the measurement. Those sampling procedures including m0 value, sample pan, and pretreatment in the TG–DTA instrument are the same with those used for the TG–DTA measurements in a stream of dry N2 in our previous study.31 The sample temperature was increased at a β of 2 K min−1 in steps with 10 min-isothermal holding sections inserted every 10 K to a temperature below the reaction initiation temperature. In addition, the p(H2O) value in the flowing gas was increased with a step-by-step manner at each isothermal holding section to attain the preset p(H2O) value for the TG–DTA measurements, after switching the flowing gas to wet N2 (qv = 200 cm3 min−1) generated by the humidity controller. Following stabilization of the measurement system at a constant temperature and a preset p(H2O) value for 30 min, the sample was heated at a β of 5 K min−1 to 473 K in a stream of wet N2 with various p(H2O) values (0.1 ≤ p(H2O)/kPa ≤ 9.8), facilitating the recording of the TG–derivative TG (DTG)–DTA curves for the thermal dehydration of CC-DH. Notably, temperature and relative humidity of the flowing gas were continuously recorded in the anterior chamber of the reaction tube of the TG–DTA instrument using a hygrometer (HF5 sensor with an HF535 converter, rotronic) to calculate the actual p(H2O) value during the TG–DTG–DTA measurements.TG–DTG curves for the kinetic analysis were obtained in linear nonisothermal and isothermal modes in a stream of wet N2 with four different p(H2O) values: 0.8 ± 0.1, 1.8 ± 0.1, 4.2 ± 0.2, and 7.5 ± 0.2 kPa. In the linear nonisothermal mode, the sample was heated at different β values (0.5 ≤ β/K min−1 ≤ 10) following stabilization of the measurement system at constant temperatures below the reaction initiation temperature and the preset p(H2O) value. Isothermal mass loss curves were recorded for the two component mass loss steps during the thermal dehydration of CC-DH. The sample temperature was increased at a β of 5 K min−1 to reach the first preset temperature after stabilizing the measurement system at the preset p(H2O), held until completion of the first mass loss step, then further raised to reach the second preset temperature and held for recording the mass loss curve for the second mass loss step.
3. Results and discussion
3.1 Effect of water vapor on the reaction pathway
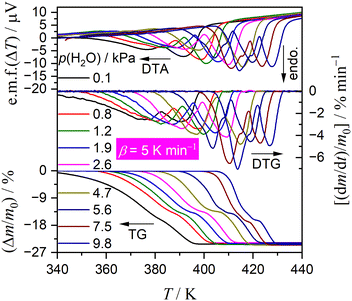
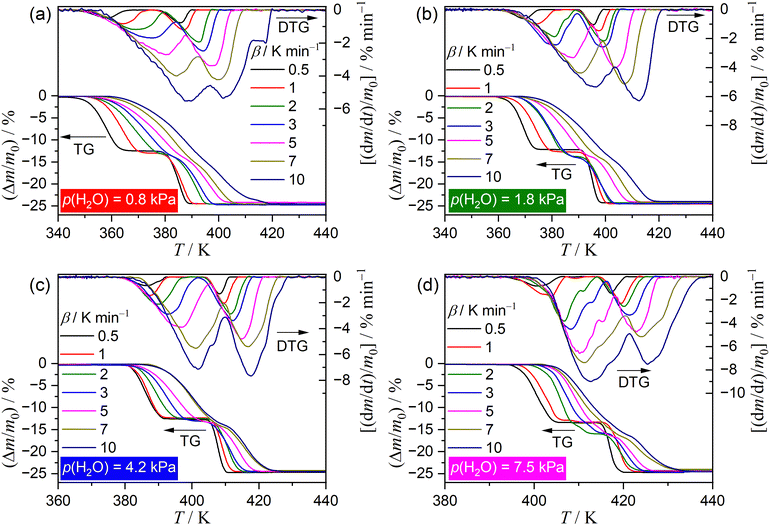
Fig. 1 shows TG–DTG–DTA curves of the thermal dehydration of CC-DH to form CC-AH at a β of 5 K min−1 in a stream of wet N2 with different p(H2O) values (0.1 ≤ p(H2O)/kPa ≤ 9.8). As p(H2O) increased, TA curves shifted systematically to higher temperatures, emphasizing a more pronounced shift in onset temperature of the mass loss compared with the endpoint temperature. Therefore, the higher p(H2O) values led to thermal dehydration occurring at elevated temperatures with increased reaction rates. The mass loss process involved two steps, akin to that in a stream of dry N2.31 The mass loss values of the first and second mass loss steps vary with increasing p(H2O) value. The magnitude relation of the mass loss values of the first and second mass loss steps, Δm1 and Δm2, respectively, was Δm1 > Δm2 at low p(H2O), aligning with that in a stream of dry N2.31 However, with increasing p(H2O), Δm1 gradually decreased until it equaled Δm2 in a p(H2O) range of 2.6–4.7 kPa. Further increase in p(H2O) led to an additional mass loss step emerging toward the end of the first mass loss step, causing a decrease in the Δm2 value. Regarding the TA curve shift along the temperature coordinate with p(H2O) corresponding to the respective mass loss steps, the shift width of the first mass loss step was greater than that of the second mass loss step, indicating the overlap of two mass loss steps became more significant with increasing p(H2O) value.Fig. 2 shows a series of TG–DTG curves obtained at different β values in a stream of wet N2, with four selected p(H2O) values of 0.8, 1.8, 4.2, and 7.5 kPa. Across all p(H2O) values, the well-separated two-step mass loss process via CC-MH was observed at lower β values. At larger β values, an alternative mass loss step emerged after the first mass loss step, resulting in a characteristic of a three-step mass loss process. Consequently, through mathematical deconvolution analysis (MDA)39–43 using a statistical function F(t) (Weibull function eqn (S1), (ESI†) in this study) depicted in Fig. S1–S4 (ESI†), DTG peaks representing the overall process was segregated into two or three peaks.
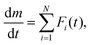 | (3) |
Fig. 3 illustrates the typical results of MDA, showcasing two and three mass loss steps as exemplified by the reactions at β = 1 and 10 K min−1 at p(H2O) = 4.2 kPa. At β = 1 K min−1 (Fig. 3(a)), two mass loss steps were well separated along the temperature coordinate. Furthermore, the comparable areas of these separated peaks suggest a two-step thermal dehydration of CC-DH to form CC-AH via stable CC-MH (eqn (1) and (2)). Conversely, at β = 10 K min−1 (Fig. 3(b)), the first and second mass loss steps observed at lower β values overlap, superimposed by the shift of the first mass loss step to higher temperatures, resulting in an additional mass loss step in the superimposed region, hence forming a three-step overall process. The MDA results for the reactions at various β values at individual p(H2O) values were shown in Fig. S1–S4 in ESI.†Fig. 4 depicts variations in the contributions (ci) of component step i with β for the reactions at individual p(H2O) values. Across all p(H2O) values, the contribution of the first mass loss step (c1) remained steady at approximately 0.5, regardless of β, indicating consistent thermal dehydration from CC-DH to CC-MH (eqn (1)). At higher β values, an alternative mass loss step emerged at the onset of second mass loss step at lower β values. The contribution of the newly developed step at larger β values increased with β, whereas the contribution of the original second mass loss step decreased with increasing β values, aligning with the three-step mass loss behavior. In addition, at a fixed high β value (e.g., 10 K min−1), the contribution of the developed second mass loss step exhibited an increasing trend with increasing p(H2O). Notably, the well-separated two-step mass loss behavior was evident at β ≤ 1 K min−1 for p(H2O) values of 0.8, 1.8, and 7.5 kPa, whereas, at p(H2O) = 4.2 kPa, the ideal two-step process persisted until β reached 3 K min−1. Therefore, the variation in the multistep thermal dehydration behavior is influenced by the combined effects of T and p(H2O), which are regulated by the thermodynamic phase relationship between the reactant, intermediate, and final product, as well as the physico-geometrical kinetic behavior of the component reaction steps.
 | ||
| Fig. 3 Typical MDA results highlighting the two and three mass loss steps of the thermal dehydration process of CC-DH at p(H2O) = 4.2 kPa at different β values: (a) 1 K min−1 and (b) 10 K min−1. | ||
Notably, the onset temperature of the developed second mass loss step observed at higher β values was lower than that of the original second reaction step at lower β values, while maintaining stoichiometric thermal dehydration from CC-MH to CC-AH, as typically observed in the TG–DTG curves at different β values at p(H2O) = 7.5 kPa (Fig. 2(d) and 4(d)). Consequently, an alternative intermediate hydrate may form during the developed second reaction step at higher β values. Molenda et al. reported the formation of a stable intermediate hydrate, CC-0.3H, during the hydration of CC-AH under linear cooling at p(H2O) ≥ 5 kPa and the dehydration of CC-DH under linear heating at p(H2O) ≥ 10 kPa.22 This observation was reconfirmed in our study for the hydration of CC-AH at a cooling rate of 1 K min−1 across various p(H2O) values ranging from 0.8 to 8.4 kPa, as shown in Fig. S5 (ESI†). A plateau in the TG curve corresponding to mass change associated with the formation of CC-0.3H was evident during the hydration of CC-AH at p(H2O) values exceeding 3.3 kPa. Therefore, the formation of CC-0.3H during the initial stage of the thermal dehydration of CC-MH could be a contributing factor to the emergence of the second reaction step at higher atmospheric p(H2O) values and elevated β values with increased self-generated p(H2O) at the reaction site. In the context of the contracting geometry of thermal dehydration, the particle surfaces of CC-MH, generated during the first reaction step by the thermal dehydration of CC-DH, serve as potential sites for the formation of CC-0.3H temporarily creating a core–shell structure with a CC-MH core surrounded by a surface layer of CC-0.3H. Upon further heating, thermal dehydration of CC-0.3H on the particle surface and CC-MH in the core successively proceed by the movement of the reaction interface to form CC-AH in the third reaction step.
3.2 Kinetics of the component reaction steps at different p(H2O) values
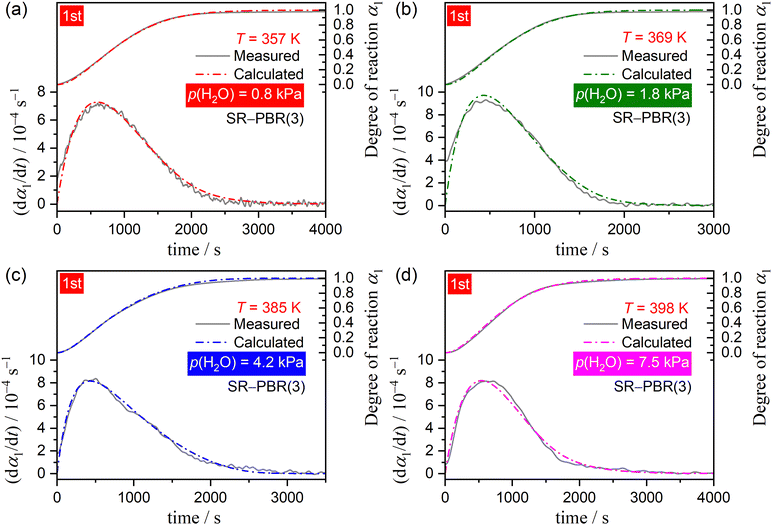
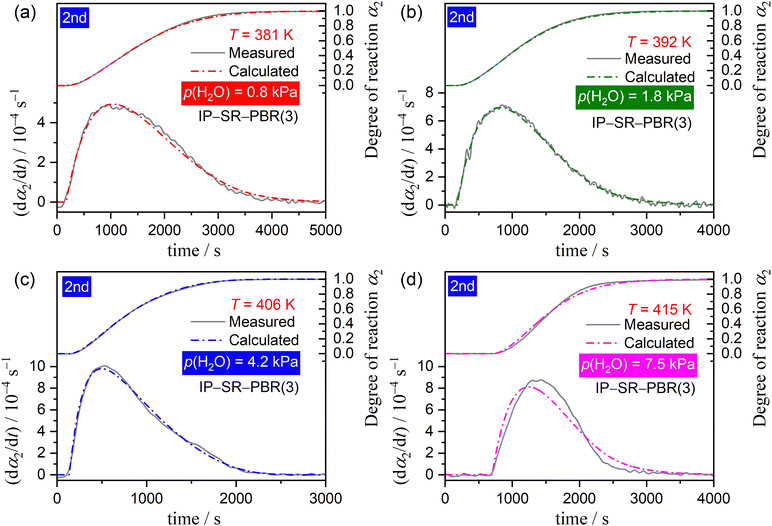
The well-defined two-step thermal dehydration of CC-DH to form CC-AH via CC-MH (eqn (1) and (2)) observed under linear nonisothermal conditions at lower β values, regardless of p(H2O) value, suggests the feasibility of experimentally tracking the individual reaction steps separately. This was enabled by employing the two-step isothermal heating protocol as shown in Fig. S6 (ESI†). A series of TG–DTG curves representing the first and second reaction steps of the two-step thermal dehydration of CC-DH to form CC-AH via CC-MH at different T and p(H2O) values are shown in Fig. 5 and 6, respectively. For both the reaction steps, the mass loss curves at constant T values displayed a sigmoidal shape, independent of the p(H2O) values. Furthermore, the mass loss curves for the second reaction step exhibited a detectable IP. These TG–DTG curves were transformed into the kinetic curves by calculating α values for the individual reaction steps with reference to the total mass loss value at each reaction step (i.e., α1 and α2 for the first and second reaction steps, respectively).A series of kinetic curves for each reaction step at various constant T values, obtained at individual p(H2O) values, were integrated with those obtained under linear nonisothermal conditions at lower β values using MDA, as shown in Fig. S7 and S8 (ESI†) for the first and second reaction steps, respectively. Subsequently, the kinetic curves for each reaction step at individual p(H2O) values, depicted in Fig. S9 and S10 (ESI†) in the 3D kinetic coordinate of T−1, αi, and ln(dαi/dt), underwent formal kinetic analysis according to the basic kinetic equation for a single-step reaction, disregarding the influence of p(H2O).44–46
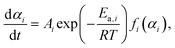 | (4) |
 | (5) |
The 3D kinetic coordinate represented in Fig. S9 and S10 (ESI†) is based on eqn (5), describing the variation in ln(dαi/dt) as a function of T−1 and αi.
Fig. 7 and 8 illustrate the results of the formal kinetic analysis at individual p(H2O) values for the first and second reaction steps in the thermal dehydration process of CC-DH to form CC-AH via CC-MH, respectively. In the 3D kinetic coordinate (Fig. S9 and S10, ESI†), the isoconversional kinetic relationship, which describes the dependence of ln(dαi/dt) on T−1, represented by specific two-dimensional (2D) planes perpendicular to the αi axis. According to eqn (5), plotting ln(dαi/dt) against T−1 at a fixed αi (i.e., Friedman plot47) results in a straight line with the slope of −Ea,i/R. In both reaction steps, the Friedman plots generally exhibited a linear correlation, regardless of the p(H2O) value; however, a convex feature of the plot was also observed, particularly evident in plots at αi = 0.5, as depicted in Fig. 7(a) and 8(a). This convex characteristic was similarly observed at different αi values, as shown in Fig. S11 and S12 (ESI†). In the first reaction step, the slope of the Friedman plot at α1 = 0.5 systematically increased with raising p(H2O) value (Fig. 7(a)). Conversely, in the second reaction step, Friedman plots at α2 = 0.5 at higher p(H2O) values of 1.8, 4.2, and 7.5 kPa exhibited a parallel shift with a slope larger than that at p(H2O) = 0.8 kPa (Fig. 8(a)). Throughout both reaction steps, the slope of the Friedman plot at p(H2O) values of 0.8, 1.8, and 4.2 kPa displayed a slight decreasing trend as the reaction progressed (Fig. S11 and S12, ESI†), whereas an increasing trend was observed at p(H2O) = 7.5 kPa. The variations in the slope of the Friedman plot with αi and p(H2O) were mirrored by the calculated Ea,i values at different αi values, as shown in Fig. 7(b) and 8(b) for the first and second reaction steps, respectively. Regarding the first reaction step, the Ea,1 values exhibited a gradual decrease as the reaction progressed at p(H2O) values of 0.8, 1.8, and 4.2 kPa. Conversely, at p(H2O) = 7.5 kPa, there was an initial increase in the Ea,1 value during the first half of the reaction. The second reaction step exhibited the similar Ea,2 variation with α2 as in the first reaction step at the corresponding p(H2O) values. However, in both the reaction steps, the Ea,i values were approximately constant in the established stage of the reaction at each p(H2O).
Table 1 presents the average Ea,i values determined through the Friedman plots for the established stage of the respective reaction steps at different p(H2O) values. In the established stage of the first reaction step, the Ea,1 values systematically increased with increasing p(H2O), ranging from 116 kJ mol−1 at p(H2O) = 0.8 kPa to 285 kJ mol−1 at p(H2O) = 7.5 kPa. Notably, these Ea,1 values are significantly larger than that reported previously for the thermal dehydration of CC-DH to form CC-MH in a stream of dry N2, which stood at 72 kJ mol−1.31 Such an increase in the Ea value, derived from the basic kinetic equation, with rising partial pressure of the gaseous product in the reaction atmosphere, is a common phenomenon in reversible thermal decomposition of solids,11–21 often seen as a superficial variation caused by the simplified kinetic approach that neglects the effect of p(H2O). In the second reaction step, the average Ea,2 value at p(H2O) = 0.8 kPa, that is, 333 kJ mol−1, was more than four times larger than that reported previously for the thermal dehydration of CC-MH to form CC-AH in a stream of dry N2, that is, 82 kJ mol−1.31 The Ea,2 value further rose at higher p(H2O) values, reaching 628 kJ mol−1 at p(H2O) = 1.8 kPa, remaining consistently above 500 kJ mol−1. The apparent variation in Ea,2 value with p(H2O) value suggests a more significant influence of p(H2O) on CC-MH dehydration kinetics to form CC-AH compared to the first reaction step. Additionally, the unsystematic variation in the Ea,2 value with p(H2O) highlights the significant influence of self-generated p(H2O) at the reaction interface, alongside atmospheric p(H2O).
| Reaction step i | p(H2O)/kPa | E a,i/kJ mol−1 | |||||
|---|---|---|---|---|---|---|---|
| A i /s−1 | m i | n i | p i |
R
2,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
|
|||
| a Averaged over 0.2 ≤ αi ≤ 0.9. b Averaged over 0.3 ≤ αi ≤ 0.9. c Averaged over 0.4 ≤ αi ≤ 0.8. d Determination coefficient of the nonlinear least-squares analysis. | |||||||
| 1 | 0.8 | 116.4 ± 8.3,a | (1.00 ± 0.02) × 1014 | −0.96 ± 0.06 | 1.20 ± 0.02 | 1.21 ± 0.06 | 0.9997 |
| 1.8 | 164.3 ± 12.2,a | (2.06 ± 0.02) × 1018 | −1.11 ± 0.09 | 1.27 ± 0.04 | 1.40 ± 0.09 | 0.9994 | |
| 4.2 | 223.8 ± 15.9,a | (5.22 ± 0.02) × 1025 | −0.17 ± 0.03 | 1.01 ± 0.01 | 0.54 ± 0.03 | 0.9999 | |
| 7.5 | 285.1 ± 4.0,b | (4.26 ± 0.06) × 1034 | −1.31 ± 0.10 | 1.30 ± 0.04 | 1.58 ± 0.09 | 0.9994 | |
| 2 | 0.8 | 332.6 ± 8.3,a | (3.02 ± 0.07) × 1042 | 0.08 ± 0.16 | 0.72 ± 0.06 | 0.18 ± 0.16 | 0.9967 |
| 1.8 | 627.7 ± 27.9,a | (3.77 ± 0.06) × 1080 | 1.52 ± 0.11 | 0.45 ± 0.04 | −1.19 ± 0.11 | 0.9992 | |
| 4.2 | 522.2 ± 45.8,b | (2.66 ± 0.05) × 1064 | 0.73 ± 0.17 | 0.60 ± 0.06 | −0.49 ± 0.17 | 0.9983 | |
| 7.5 | 623.5 ± 5.3,c | (4.87 ± 0.07) × 1075 | 0.25 ± 0.12 | 0.90 ± 0.05 | 0.29 ± 0.11 | 0.9988 | |
The isothermal kinetic relationship appeared on the specific 2D plane perpendicular to T−1 axis in the 3D kinetic coordinate (Fig. S9 and S10, ESI†) was analyzed at an infinite temperature using the Ozawa's generalized time (θ) concept.48–50 This involved calculating the hypothetical reaction rate (dαi/dθi) at infinite temperature at different αi values, which assumed a constant Ea,i value during each reaction step i,51–55 that is, the average Ea,i values in the selected αi ranges in each reaction step at various p(H2O) values listed in Table 1.
 | (6) |
Regardless of p(H2O), the experimental master plots of (dα1/dθ1) versus α1 for the first reaction step (Fig. 7(c)) displayed the maximum reaction rate in the first half of the reaction, with the α1 value at the maximum reaction rate increasing systematically with higher p(H2O) levels, from α1 = 0.30 at p(H2O) = 0.8 kPa to α1 = 0.36 at p(H2O) = 7.5 kPa. Notably, although different Ea,1 variation trends were observed for the reaction at p(H2O) = 7.5 kPa compared to those at lower p(H2O) values, they did not so significantly alter the shape of the experimental master plot. Regarding the second reaction step, the shape of the experimental master plot of (dα2/dθ2) versus α2 exhibited the maximum reaction rate occurring midway through the reaction at all p(H2O) values (Fig. 8(c)). However, at p(H2O) = 7.5 kPa, the shape differed from those at lower p(H2O) values due to the distinct Ea,2 variation trend as the reaction progressed, unlike reactions at lower p(H2O) values. The α2 value at the maximum reaction rate slightly shifted toward smaller values with increasing p(H2O), that is, from α2 = 0.24 at 0.8 kPa to α2 = 0.21 at 4.2 kPa, while at p(H2O) = 7.5 kPa, the maximum reaction rate was observed at α2 = 0.44. To formally evaluate Ai values for each reaction step at individual p(H2O) values according to eqn (6), the experimental master plot was fitted using an empirical kinetic model function, that is, Šesták–Berggren model with three kinetic exponents: SB(m, n, p).56–58
| f(α) = αm(1 − α)n[−ln(1 − α)]p | (7) |
By optimizing the kinetic exponents in SB(mi, ni, pi) and Ai value for each reaction step i at various p(H2O) values, the experimental master plots were nearly perfectly fitted, owing to the high flexibility of SB(m, n, p) to accommodate various types of rate behaviors. The optimized kinetic exponents SB(mi, ni, pi) and Ai values for individual reaction steps i are detailed in Table 1. The optimized kinetic exponents for individual reaction steps exhibited unsystematic variations with p(H2O) and should be viewed as empirical values aimed at achieving the best fit to the experimental master plot. Additionally, the optimized Ai values exhibited certain systematic variation trends with p(H2O), particularly noticeable in the first reaction step, where the optimized A1 value systematically increased with rising p(H2O) values, accompanied by a systematic increase in the Ea,1 value. The compensative variations in A1 and Ea,1 with p(H2O), including those values previously determined for the reactions in a stream of dry N2,31 revealed a general trend known as the kinetic compensation effect (KCE) (Fig. S13, ESI†): the apparent linear correlation between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A and Ea values determined across a series of chemical reactions, that is, ln
A and Ea values determined across a series of chemical reactions, that is, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A = a + bEa, where a and b are constants.59–68 Moreover, the A2 values for the second reaction step at different p(H2O) values exhibited unsystematic variation with p(H2O); however, the variations in A2 were accompanied by the compensative variations in Ea,2, following an apparent trend of KCE (Fig. S13, ESI†).
A = a + bEa, where a and b are constants.59–68 Moreover, the A2 values for the second reaction step at different p(H2O) values exhibited unsystematic variation with p(H2O); however, the variations in A2 were accompanied by the compensative variations in Ea,2, following an apparent trend of KCE (Fig. S13, ESI†).
Formal kinetic analyses employing isoconversional and master plot methods, based on the basic kinetic equation to elucidate the kinetic behavior as a function of T and α, have highlighted several important points toward advancing the understanding of the two-step thermal dehydration process from CC-DH to form CC-AH via CC-MH. One such insight concerns the apparent Arrhenius parameters and their variations with p(H2O) in the individual reaction steps. Both reaction steps of the thermal dehydration process demonstrated variations in the kinetic behavior with atmospheric p(H2O); however, the basic kinetic equation does not consider the effect of p(H2O). Therefore, the Arrhenius parameters derived from the formal kinetic approach represent essentially empirical values, primarily useful for replicating kinetic behavior at a given p(H2O) value. Nevertheless, the observed variations in the apparent Arrhenius parameters with p(H2O) signify distinct characteristics of the effect of p(H2O) on the kinetics. The systematic and interrelated variations in A1 and Ea,1 values with p(H2O) noted in the first reaction step are general trends for the reversible thermal decomposition of solids. This behavior suggests that the effect of p(H2O) is not limited to A1 but also extends to Ea,1, indicating a dependency of the p(H2O) effect also depends on T. The temperature dependent influence of p(H2O) is related to the equilibrium water vapor pressure of each reaction step, Peq,i(T). Hence, a possible solution involves integrating an AF comprising both p(H2O) and Peq,i(T), denotes as hi(p(H2O), Peq,i(T)), into the basic kinetic equation.11–21,55
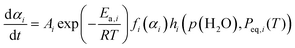 | (8) |
Notably, eqn (8) is expected to universally depict the kinetics of each reaction step across different p(H2O) values as a function of T, αi, p(H2O), and Peq,i(T). To achieve this ideal solution, an appropriate AF is required. Recently, we formulated an analytical form for AF with variable exponents (ai, bi) drawing from theoretical considerations of the surface and interfacial processes as the respective consecutive/concurrent processes of various elementary steps.11–21,55
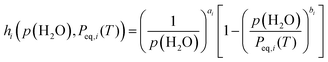 | (9) |
The combination of eqn (8) and (9) has enabled us to universally characterize the kinetics of reversible thermal dehydrations in inorganic hydrates and hydroxides.15–21 Similarly, employing the advanced kinetic approach based on eqn (8) and (9) proved effective for analyzing the reversible thermal decompositions of inorganic carbonates.11–14 However, for the second reaction step, the unsystematic variations in A2 and Ea,2 values with p(H2O) cannot be adequately explained by eqn (8) and (9). One possible explanation is the significant influence of self-generated p(H2O) at the reaction interface due to the physico-geometrical constraints for the diffusional removal of the water vapor generated by the reaction. In such scenarios, optimizing the effective p(H2O) by considering both atmospheric and self-generated p(H2O) has been suggested as a possible solution to achieve a universal kinetic description across different T and p(H2O) values.13,14,21 Indeed, such a universal kinetic description, considering the effect of p(H2O), represents next crucial step toward advancing the understanding of the multistep thermal dehydration process from CC-DH to form CC-AH via CC-MH. This endeavor necessitates reliable thermodynamic parameters for CC-DH and CC-MH, in addition to the well-established parameters for CC-AH,69 to calculate Peq,i(T) for each reaction step i.
Another consideration pertains to the physico-geometrical reaction mechanism as described by fi(αi). Fundamentally, the thermal dehydration reaction initiates on the particle surface, after which the reaction interface progresses inward, toward the center of each particle. In cases where the SR occurs promptly, the rate behavior of overall thermal dehydration, characterized by a contracting geometry model, demonstrates a deceleration as the reaction progresses. This is evidenced by the convex and concaved shapes of decelerating experimental master plots, representing interfacial reactions controlled by chemical reaction and diffusion, respectively. Unlike the ideal behavior expected from a contracting geometry-type reaction, both experimental master plots for the first and second reaction steps of the two-step thermal dehydration from CC-DH to form CC-AH via CC-MH displayed the maximum reaction rate midway through each reaction step at a constant temperature (Fig. 7(c) and 8(c)). Previously, we reported similar experimental master plots for the partially overlapping two-step thermal dehydration process from CC-DH to form CC-AH via CC-MH in a stream of dry N2.31 In that scenario in a stream of dry N2, the two reaction steps of the thermal dehydration process of CC-DH to CC-MH and CC-MH to CC-AH occurred through the successive movements of two reaction interfaces in the same 3D interface shrinkage schemes in each particle, subsequent to the particle surfaces being covered with the surface product layer of CC-AH. The rate behavior displaying the maximum reaction rate midway through each reaction step was explained by the acceleration of the linear advancement rate of the reaction interface as the reaction progressed, attributed to the decrease in p(H2O) at the reaction interface due to the termination of the other reaction step that partially overlapped with the subjected reaction. This explanation was corroborated by the nearly perfect fit of the Galway–Hood model70,71 characterized by 3D interface shrinkage and an acceleration of the linear advancement rate of the reaction interface to the experimental master plots. In contrast to reactions conducted in a stream of dry N2, the two reaction steps involved in the thermal dehydration of CC-DH in a stream of wet N2 occurred separately in terms of time and temperature coordinates, under isothermal and linear nonisothermal conditions, respectively. Consequently, the acceleration of the linear advancement rate of the reaction interface, attributed to the decrease in p(H2O) at the reaction interface, could not be anticipated as the factor behind the maximum reaction rate midway through the reaction at a constant temperature. An alternative physico-geometrical reaction model that demonstrates the maximum reaction rate midway through the reaction at a constant temperature of the contracting geometry reaction could be the physico-geometrical consecutive SR–PBR model.32–36 The sigmoidal mass loss curves observed in both reaction steps at a constant temperature (Fig. 5 and 6) lend support to the possible applicability of the SR–PBR model in elucidating the rate behavior. Additionally, the appearance of IP preceding the second reaction step of the thermal dehydration process is generally observed for reactions described by the SR–PBR model, suggesting potential relevance of the consecutive IP–SR–PBR model.
3.3 Kinetic modeling based on the IP–SR–PBR(n) models
The physico-geometrical consecutive SR–PBR model, derived from Mampel's model,32,33 describes acceleration and deceleration periods attributed to SR and PBR, respectively. Furthermore, Ogasawara and Koga developed differential kinetic equations for the consecutive IP–SR–PBR(n) models at a constant temperature, considering assumptions such as zero-order process for IP, the first-order process for SR, and n-dimensional interface shrinkage for PBR.34 Recently, Favergeon et al. reformulated these kinetic models as surface nucleation and anisotropic growth models. 35 Table S1 (ESI†) provides the differential kinetic equations for the IP–SR–PBR(n) models. Utilizing these kinetic equations, the differential kinetic curves for the first and second reaction steps of the thermal dehydration process from CC-DH to form CC-AH via CC-MH at constant temperatures and various p(H2O) values were fitted using SR–PBR(n) and IP–SR–PBR(n) models, respectively. This involved optimizing the rate constants for IP, SR, and PBR(n), that is, kIP, kSR, and kPBR(n), through nonlinear least-squares analysis. Initially, fittings of the SR–PBR(3) or IP–SR–PBR(3) model were investigated, given the identification of 3D interface shrinkage for both reaction steps in a stream of dry N2 in our previous research.31Fig. 9 and 10 present typical fitting results for the first and second reaction steps at various p(H2O) values using SR–PBR(3) and IP–SR–PBR(3) models, respectively. Regardless of the p(H2O) value, statistically significant fits of these physico-geometrical consecutive models to the experimental kinetic curves were observed in both reaction steps. Significantly, the SR–PBR(2) and IP–SR–PBR(2) models, assuming a 2D interface shrinkage, yielded comparable fitting results in terms of the determination coefficient (R2) obtained from the nonlinear least-squares analysis, as shown in Fig. S14 and S15 (ESI†) for the first and second reaction steps, respectively. These fitting results suggest a satisfactory description of the rate behaviors utilizing the physico-geometrical consecutive processes of SR–PBR and IP–SR–PBR models for the first and second reaction steps, respectively. Moreover, the similarity in fitting results between assumptions of PBR(3) and PBR(2) suggests interface shrinkage with a nonintegral or fractal dimension between 2 and 3 in both reaction steps.72–74Tables S2 and S3 (ESI†) detail the optimized kIP, kSR, and kPBR(n) values at specific temperatures and p(H2O) values, as determined by the SR–PBR(n) and IP–SR–PBR(n) models for the first and second reaction steps, respectively. The temperature dependence of the rate constants for the individual physico-geometrical processes at different p(H2O) values in each reaction step was formally analyzed using conventional Arrhenius plots, without considering the influence of p(H2O).
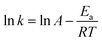 | (10) |
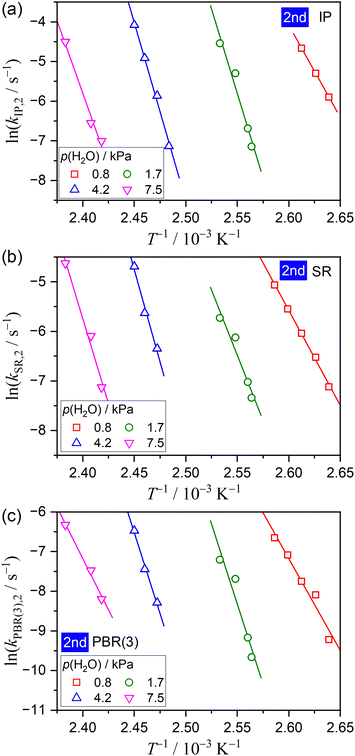
Fig. 11 and 12 illustrate the Arrhenius plots of the component physico-geometrical processes in the SR–PBR(3) and IP–SR–PBR(3) models for the first and second reaction steps, respectively. Corresponding plots based on SR–PBR(2) and IP–SR–PBR(2) models are presented in Fig. S16 and S17 (ESI†). Each Arrhenius plot exhibited a statistically significant linear correlation, enabling the determination of the apparent Arrhenius parameters. In the first reaction step of the thermal dehydration of CC-DH to CC-MH, the slope of the Arrhenius plots systematically increased with the increasing p(H2O), regardless of the component physico-geometrical process (Fig. 11 and Fig. S16, ESI†), consistent with the Ea,1 variation trend observed in the formal analysis utilizing the Friedman plot (Fig. 7(b)). In the second reaction step of the thermal dehydration of CC-MH to CC-AH, a systematic increase in the slope of the Arrhenius plot with p(H2O) was generally observed until p(H2O) = 4.2 kPa, but this trend discontinued at p(H2O) = 7.5 kPa. This behavior of the second reaction step aligned with the expectation from the formal analysis using the Friedman plot (Fig. 8(a)).
Table 2 summarizes the apparent Arrhenius parameters for each physico-geometrical reaction process at different p(H2O) values for the first and second reaction steps based on SR–PBR(3) and IP–SR–PBR(3) models. Additionally, counterparts based on SR–PBR(2) and IP–SR–PBR(2) are presented in Table S4 (ESI†) for comparison purpose. In the first reaction step, a systematic increase in the Ea,1 value with increasing p(H2O) was observed in both SR and PBR(n) processes, accompanied by a compensative increase in the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A1 value. While the variations in the apparent Arrhenius parameters with p(H2O) were more significant for the second reaction step compared with those in the first one, the similar compensatory increases in the Ea,2 and ln
A1 value. While the variations in the apparent Arrhenius parameters with p(H2O) were more significant for the second reaction step compared with those in the first one, the similar compensatory increases in the Ea,2 and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 values with increasing p(H2O) were observed across all physico-geometrical reaction steps in the second reaction step until p(H2O) = 4.2 kPa; however, these values dropped at p(H2O) = 7.5 kPa. Notably, the apparent Arrhenius parameters of individual physico-geometrical reaction processes at varying p(H2O) values, along with their variations with p(H2O), showed similar trends between those determined using SR–PBR(3) and SR–PBR(2) models for the first reaction step and IP–SR–PBR(3) and IP–SR–PBR(2) models for the second reaction step. The variations in these parameters with p(H2O) in each physico-geometrical reaction process demonstrated a strong mutual correlation between Ea and ln
A2 values with increasing p(H2O) were observed across all physico-geometrical reaction steps in the second reaction step until p(H2O) = 4.2 kPa; however, these values dropped at p(H2O) = 7.5 kPa. Notably, the apparent Arrhenius parameters of individual physico-geometrical reaction processes at varying p(H2O) values, along with their variations with p(H2O), showed similar trends between those determined using SR–PBR(3) and SR–PBR(2) models for the first reaction step and IP–SR–PBR(3) and IP–SR–PBR(2) models for the second reaction step. The variations in these parameters with p(H2O) in each physico-geometrical reaction process demonstrated a strong mutual correlation between Ea and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A values following the KCE, as illustrated in Fig. S18 (ESI†) for the series of apparent Arrhenius parameters determined using the SR–PBR(3) model for the first reaction step and IP–SR–PBR(3) model for the second reaction step. Of particular note is the nearly identical slope of the KCE line between different physico-geometrical processes, with ∼0.26 and ∼0.29 for the first and second reaction steps, respectively (Fig. S18, ESI†). These values closely align with those obtained from the apparent Arrhenius parameters determined through the formal kinetic analysis (Fig. S13, ESI†). The empirical observations of the KCE have always been used in investigations on relevant physico-chemical origins, as well as various artificial origins.59–68 For example, we recently identified a linear correlation among a series of apparent ln
A values following the KCE, as illustrated in Fig. S18 (ESI†) for the series of apparent Arrhenius parameters determined using the SR–PBR(3) model for the first reaction step and IP–SR–PBR(3) model for the second reaction step. Of particular note is the nearly identical slope of the KCE line between different physico-geometrical processes, with ∼0.26 and ∼0.29 for the first and second reaction steps, respectively (Fig. S18, ESI†). These values closely align with those obtained from the apparent Arrhenius parameters determined through the formal kinetic analysis (Fig. S13, ESI†). The empirical observations of the KCE have always been used in investigations on relevant physico-chemical origins, as well as various artificial origins.59–68 For example, we recently identified a linear correlation among a series of apparent ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A and Ea values for the thermal decomposition of CaCO3 at different CO2 partial pressures, as determined through the extended kinetic approach based on eqn (8) and (9).14,21,68
A and Ea values for the thermal decomposition of CaCO3 at different CO2 partial pressures, as determined through the extended kinetic approach based on eqn (8) and (9).14,21,68
 | (11) |
| Reaction step i | Physico-geometrical process | p(H2O)/kPa | E a,i/kJ mol−1 | ln(Ai/s−1) | −γa |
|---|---|---|---|---|---|
| a Correlation coefficient of the linear regression analysis for the Arrhenius plot. | |||||
| 1 | SR | 0.8 | 151.2 ± 8.4 | 45.4 ± 2.9 | 0.9939 |
| 1.7 | 264.7 ± 19.4 | 80.6 ± 6.4 | 0.9921 | ||
| 4.1 | 271.5 ± 33.9 | 79.1 ± 10.6 | 0.9923 | ||
| 7.4 | 295.4 ± 46.3 | 83.4 ± 14.0 | 0.9651 | ||
| PBR(3) | 0.8 | 212.1 ± 12.1 | 63.7 ± 4.1 | 0.9935 | |
| 1.7 | 239.3 ± 15.8 | 70.7 ± 5.2 | 0.9935 | ||
| 4.1 | 266.9 ± 31.6 | 76.3 ± 9.9 | 0.9931 | ||
| 7.4 | 340.2 ± 18.0 | 95.4 ± 5.4 | 0.9958 | ||
| 2 | IP | 0.8 | 386.2 ± 1.6 | 116.7 ± 0.5 | 0.9999 |
| 1.7 | 707.6 ± 103.1 | 211.2 ± 31.6 | 0.9794 | ||
| 4.2 | 746.5 ± 44.1 | 216.0 ± 13.1 | 0.9965 | ||
| 7.5 | 607.9 ± 73.2 | 169.7 ± 21.2 | 0.9928 | ||
| SR | 0.8 | 318.8 ± 8.8 | 94.1 ± 2.8 | 0.9989 | |
| 1.7 | 437.4 ± 78.5 | 127.7 ± 24.1 | 0.9692 | ||
| 4.2 | 618.4 ± 80.6 | 177.5 ± 23.9 | 0.9916 | ||
| 7.5 | 571.3 ± 78.1 | 159.2 ± 22.6 | 0.9908 | ||
| PBR(3) | 0.8 | 385.2 ± 45.8 | 113.3 ± 14.4 | 0.9794 | |
| 1.7 | 671.2 ± 142.9 | 197.5 ± 43.9 | 0.9575 | ||
| 4.2 | 678.0 ± 64.6 | 193.3 ± 19.1 | 0.9955 | ||
| 7.5 | 430.3 ± 45.4 | 117.0 ± 13.1 | 0.9945 | ||
3.4 Physico-geometrical reaction pathway
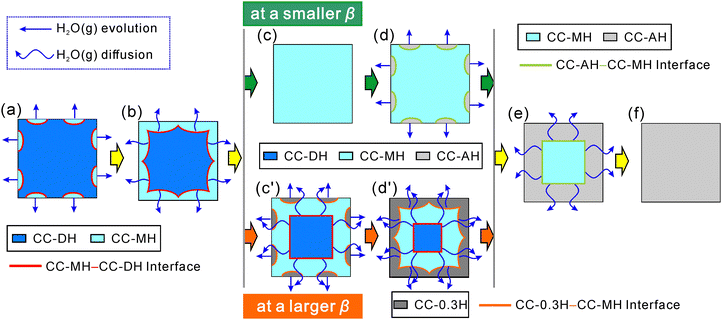
The variations observed in the TA curves with p(H2O) and the kinetic results of the each reaction step and its component physico-geometrical processes have revealed distinctive characteristics of the multistep thermal dehydration of CC-DH to form CC-AH via CC-MH in the presence of atmospheric water vapor. Fig. 13 schematically illustrates the physico-geometrical reaction pathway of this multistep thermal dehydration as revealed in our study. In the presence of atmospheric water vapor, direct dehydration of CC-DH surface to CC-AH did not occur, leading to the characterization of the first reaction step by the stoichiometric dehydration of CC-DH to form CC-MH. The first dehydration step proceeded followed a contracting geometry-type reaction model, displaying sigmoidal mass loss curves and reaching the maximum reaction rate midway through the reaction at a constant temperature. The observed rate behavior, independent of the p(H2O) value, was effectively captured by the physico-geometrical consecutive SR–PBR(3) model, underscoring the significant role of SR in the overall kinetics (Fig. 13(a)) and 3D interface shrinkage with a constant linear advancement rate of the reaction interface at a constant temperature (Fig. 13(b), (c), (c′), and (d′)). The consistent linear advancement rate of the CC-MH–CC-DH interface at a constant temperature, different from the accelerated linear advancement rate observed in a stream of dry N2,31 indicates a constant p(H2O) at the reaction interface during the reaction. In both SR and PBR(3) processes, the temperature range for the first reaction step systematically shifted to higher temperatures, accompanied by a systematic increase in the apparent Arrhenius parameters with increasing p(H2O), demonstrating a general trend of KCE. This behavior formally signifies a more pronounced increase in the reaction rate with the temperature escalation.The subsequent process of the thermal dehydration of intermediate CC-MH was found to vary primarily with β rather than p(H2O). At a lower β, this process occurred at well-separated temperatures from the first reaction step (Fig. S1–S4, ESI†), proceeding stoichiometrically to form CC-AH (Fig. 13(d)–(f)). Regardless of p(H2O) value, the second reaction step under isothermal conditions displayed a noticeable IP. Under linear nonisothermal conditions, the IP led the reaction onset to higher temperatures, by which the second reaction step proceeded at relatively high reaction rates due to the temperature effect. The mass loss exhibited sigmoidal curves under isothermal conditions, with maximum reaction rates occurring midway through the reaction as in the first reaction step. Consequently, the IP–SR–PBR(3) model satisfactorily described the process, emphasizing the significant contributions of IP and SR to 3D shrinkage of the CC-AH–CC-MH interface proceeding at a constant rate. Compared to the first reaction step, a greater increase in the apparent Arrhenius parameters was observed across all physico-geometrical reaction processes at higher p(H2O) values, albeit with unsystematic variations differing from the first reaction step. The kinetic results indicated the more significant influence of atmospheric p(H2O) and the contribution of self-generated p(H2O) to the second reaction step of the thermal dehydration of CC-MH to form CC-AH under both isothermal and nonlinear nonisothermal conditions at a lower β values.
When the CC-DH sample was subjected to linear nonisothermal heating at higher β values in the presence of atmospheric water vapor, a different reaction pathway emerged. Under this condition, the two observed mass loss steps at lower β values became partially overlapped along the temperature coordinate (Fig. S1–S4, ESI†). An additional mass loss step appeared between original reaction steps of CC-DH to CC-MH and CC-MH to CC-AH, initiating at lower temperatures compared to CC-MH dehydration. This suggested the formation of an intermediate hydrate phase, CC-0.3H. The thermal dehydration of CC-MH to form CC-0.3H should initiate at the surfaces of the reacting particle (Fig. 13(c′)). Notably, during this process, the CC-MH–CC-DH reaction interface of the first reaction step continued to progress inward toward the center of the reacting particles, while the CC-0.3H–CC-MH reaction interface served as the water vapor diffusion path that evolved at the internal CC-MH–CC-DH reaction interface and in the state at a high p(H2O) (Fig. 13(d′)). The formation of stable CC-0.3H was observed during CC-AH hydration at a high p(H2O) value (Fig. S5, ESI†). Therefore, self-generated p(H2O) from the overlapping reaction steps likely facilitated the formation of CC-0.3H intermediate phase during thermal dehydration. The self-generated p(H2O) decreases in the reacting particles as the first reaction step proceeds to termination, creating favorable conditions for CC-MH dehydration to form CC-AH. Consequently, CC-0.3H in the particle shell and CC-MH in the particle core underwent successive dehydration to form CC-AH in a contracting geometry scheme (Fig. 13(e) and (f)).
4. Conclusions
The thermal dehydration of CC-DH to CC-AH primarily involved the CC-MH intermediate. However, the actual reaction pathway of multistep thermal dehydration is further complicated by the physico-geometrical constraints of solid-state reactions coupled with the evolution of water vapor. Furthermore, because of the reversible dehydration and hydration nature, the reaction pathways and kinetics of the thermal dehydration are significantly influenced by atmospheric and self-generated water vapor.In a stream of dry N2, thermal dehydration exhibited a partially overlapping three-step process, as reported in our previous study.31 The first reaction step is initiated on the reactant surface to directly form CC-AH. However, in the presence of atmospheric water vapor, direct dehydration of CC-DH to CC-AH was prevented, prompting the first-step reaction to proceed stoichiometrically to form stable CC-MH instead. This deviation stems from the influence of atmospheric water vapor. In another example, in a stream of dry N2, the second and third reaction steps of the thermal dehydration of CC-DH to CC-MH and CC-MH to CC-AH, respectively, occurred as successive 3D contractions of the respective reaction interfaces by partially overlapping. However, in the presence of atmospheric water vapor, these reactions occurred as a well-separated reaction processes along the temperature coordinate under isothermal and linear nonisothermal conditions at lower β. Enhanced stability of CC-MH on the particle surface, along with significant IP for the thermal dehydration of CC-MH due to atmospheric water vapor, accounted for the well-separated two-step thermal dehydration process from CC-DH to form CC-AH via CC-MH. Self-generated water vapor significantly influences the physico-geometrical reaction pathway, leading to a shift in the reaction mode from direct thermal dehydration of CC-DH to CC-AH formation to the formation of CC-MH intermediate in a stream of dry N2.31 This phenomenon occurs when the reactant surface becomes coated with CC-AH product, increasing p(H2O) at the CC-AH–CC-DH reaction interface due to self-generated water vapor. Additionally, a combined effect of atmospheric and self-generated water vapor contributes to the formation of CC-0.3H intermediate during CC-DH thermal dehydration of under linear nonisothermal conditions at a high β in the presence of atmospheric water vapor. CC-0.3H forms on the CC-MH surface when the process begins midway through the preceding reaction step of CC-DH thermal dehydration to CC-MH, facilitated by 3D interface shrinkage. In this scenario, the CC-MH particle surface is exposed to high p(H2O) due to the self-generated water vapor at the internal reaction interface and atmospheric water vapor, creating suitable T and p(H2O) conditions for CC-0.3H formation.
The kinetic behavior of individual reaction steps involved in the thermal dehydration of CC-DH to CC-MH, described by the physico-geometrical consecutive SR–PBR(3) model, exhibits a systematic change with the atmospheric p(H2O). The apparent Arrhenius parameters increase with atmospheric p(H2O) in both SR and PBR(3) processes, empirically indicating the influence of atmospheric water vapor on the kinetic behavior. Additionally, self-generated p(H2O) affects kinetics, observed in the second reaction step of CC-DH thermal dehydration to form CC-MH and the third reaction step of CC-MH to CC-AH in a stream of dry N2.31 These partially overlapping steps, characterized by 3D interface shrinkage, show accelerated linear advancement rates attributed to gradual reduction of p(H2O) at the reaction interfaces as the preceding steps progresses to terminate. A combined effect of atmospheric and self-generated p(H2O) on the kinetics is expected in the thermal dehydration of CC-MH to CC-AH in the presence of atmospheric water vapor, evidenced by unsystematic variations in apparent Arrhenius parameters with p(H2O).
This study, examining the thermal dehydration of CC-DH in the presence of atmospheric water vapor, combined with the results of a previous study in a stream of dry N2,31 highlights the significant impact of atmospheric and self-generated water vapor on both the physico-geometrical reaction pathway and kinetics. Notably, these effects manifest specifically in individual reaction steps and their component physico-geometrical reaction processes, such as IP, SR, and PBR. Therefore, consideration of atmospheric and self-generated p(H2O) is essential in kinetic modeling of multistep thermal dehydration of inorganic hydrates that exhibit reversible dehydration–hydration properties. Reliable thermodynamic parameters for each compound and reaction step are necessary for rigorous modeling of the reaction pathway and kinetics. At the same time, empirical observation of KCE in the apparent Arrhenius parameters determined at different p(H2O) values in each reaction steps and physico-geometrical process warrants further investigation for its relevance to intrinsic kinetic behavior and practical applicability in formal kinetic descriptions across different T and p(H2O) values.
Data availability
Data will be made available on request.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The present work was supported by JSPS KAKENHI Grant Numbers 22H01011, 22K02946, 23K22282, and 24K05970.References
- D. A. Young, Decomposition of Solids, Pergamon, Oxford, 1966 Search PubMed.
- A. K. Galwey and M. E. Brown, Thermal Decomposition of Ionic Solids, Elsevier, Amsterdam, 1999 Search PubMed.
- H. Tanaka, N. Koga and A. K. Galwey, J. Chem. Educ., 1995, 72, 251–256 CrossRef CAS.
- A. K. Galwey, Thermochim. Acta, 2000, 355, 181–238 CrossRef CAS.
- N. Koga and H. Tanaka, Thermochim. Acta, 2002, 388, 41–61 CrossRef CAS.
- H. U. Rammelberg, T. Schmidt and W. Ruck, Energy Procedia, 2012, 30, 362–369 CrossRef CAS.
- K. E. N’Tsoukpoe, T. Schmidt, H. U. Rammelberg, B. A. Watts and W. K. L. Ruck, Appl. Energy, 2014, 124, 1–16 CrossRef.
- F. Trausel, A.-J. de Jong and R. Cuypers, Energy Procedia, 2014, 48, 447–452 CrossRef CAS.
- P. A. J. Donkers, L. C. Sögütoglu, H. P. Huinink, H. R. Fischer and O. C. G. Adan, Appl. Energy, 2017, 199, 45–68 CrossRef CAS.
- S. Vyazovkin, Int. Rev. Phys. Chem., 2020, 39, 35–66 Search PubMed.
- N. Koga, Y. Sakai, M. Fukuda, D. Hara, Y. Tanaka and L. Favergeon, J. Phys. Chem. C, 2021, 125, 1384–1402 CrossRef CAS.
- M. Hotta, T. Tone, L. Favergeon and N. Koga, J. Phys. Chem. C, 2022, 126, 7880–7895 CrossRef CAS.
- M. Hotta, L. Favergeon and N. Koga, J. Phys. Chem. C, 2023, 127, 13065–13080 CrossRef CAS.
- M. Hotta and N. Koga, Thermochim. Acta, 2024, 733, 179699 CrossRef CAS.
- M. Fukuda, L. Favergeon and N. Koga, J. Phys. Chem. C, 2019, 123, 20903–20915 CrossRef CAS.
- N. Koga, L. Favergeon and S. Kodani, Phys. Chem. Chem. Phys., 2019, 21, 11615–11632 RSC.
- S. Kodani, S. Iwasaki, L. Favergeon and N. Koga, Phys. Chem. Chem. Phys., 2020, 22, 13637–13649 RSC.
- Y. Yamamoto, L. Favergeon and N. Koga, J. Phys. Chem. C, 2020, 124, 11960–11976 CrossRef CAS.
- J. G. D. Preturlan, L. Vieille, S. Quiligotti and L. Favergeon, J. Phys. Chem. C, 2020, 124, 26352–26367 CrossRef CAS.
- Y. Zushi, S. Iwasaki and N. Koga, Phys. Chem. Chem. Phys., 2022, 24, 29827–29840 RSC.
- M. Hotta, Y. Zushi, S. Iwasaki, S. Fukunaga and N. Koga, Phys. Chem. Chem. Phys., 2023, 25, 27114–27130 RSC.
- M. Molenda, J. Stengler, M. Linder and A. Wörner, Thermochim. Acta, 2013, 560, 76–81 CrossRef CAS.
- K. E. N'Tsoukpoe, H. U. Rammelberg, A. F. Lele, K. Korhammer, B. A. Watts, T. Schmidt and W. K. L. Ruck, Appl. Therm. Eng., 2015, 75, 513–531 CrossRef.
- C. Barreneche, A. I. Fernández, L. F. Cabeza and R. Cuypers, Appl. Energy, 2015, 137, 726–730 CrossRef CAS.
- H. U. Rammelberg, T. Osterland, B. Priehs, O. Opel and W. K. L. Ruck, Sol. Energy, 2016, 136, 571–589 CrossRef CAS.
- A. D. Pathak, S. Nedea, H. Zondag, C. Rindt and D. Smeulders, Phys. Chem. Chem. Phys., 2016, 18, 10059–10069 RSC.
- K. S. P. Karunadasa, C. H. Manoratne, H. M. T. G. A. Pitawala and R. M. G. Rajapakse, J. Phys. Chem. Solids, 2018, 120, 167–172 CrossRef CAS.
- M. Gaeini, A. L. Rouws, J. W. O. Salari, H. A. Zondag and C. C. M. Rindt, Appl. Energy, 2018, 212, 1165–1177 CrossRef CAS.
- S. Wei, R. Han, Y. Su, W. Zhou, J. Li, C. Su, J. Gao, G. Zhao and Y. Qin, Energy Convers. Manage., 2020, 212, 112694 CrossRef CAS.
- K. Heijmans, S. Nab, B. Klein Holkenborg, A. D. Pathak, S. Gaastra-Nedea and D. Smeulders, Comput. Mater. Sci., 2021, 197, 110595 CrossRef CAS.
- K. Kato and N. Koga, Phys. Chem. Chem. Phys., 2024, 26, 12358–12371 RSC.
- K. L. Mampel, Z. Phys. Chem. Abt. A, 1940, 187, 43–57 Search PubMed.
- K. L. Mampel, Z. Phys. Chem. Abt. A, 1940, 187, 234–249 Search PubMed.
- H. Ogasawara and N. Koga, J. Phys. Chem. A, 2014, 118, 2401–2412 CrossRef CAS PubMed.
- L. Favergeon, M. Pijolat and M. Soustelle, Thermochim. Acta, 2017, 654, 18–27 CrossRef CAS.
- M. Hotta, T. Tone and N. Koga, J. Phys. Chem. C, 2021, 125, 22023–22035 CrossRef CAS.
- A. Leclaire and M. M. Borel, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 1608–1610 CrossRef.
- D. Agarwal and V. K. Kasana, Int. Res. J. Pure Appl. Chem., 2019, 18, 1–10 CrossRef.
- N. Koga, Y. Goshi, S. Yamada and L. A. Pérez-Maqueda, J. Therm. Anal. Calorim., 2013, 111, 1463–1474 CrossRef CAS.
- N. Koga, in Handbook of Thermal Analysis and Calorimetry, ed. S. Vyazovkin, N. Koga and C. Schick, Elsevier, Amsterdam, 2nd edn, 2018, vol. 6, ch. 6, pp. 213–251 Search PubMed.
- S. Vyazovkin, A. K. Burnham, L. Favergeon, N. Koga, E. Moukhina, L. A. Perez-Maqueda and N. Sbirrazzuoli, Thermochim. Acta, 2020, 689, 178597 CrossRef CAS.
- A. Perejón, P. E. Sánchez-Jiménez, J. M. Criado and L. A. Pérez-Maqueda, J. Phys. Chem. B, 2011, 115, 1780–1791 CrossRef PubMed.
- R. Svoboda and J. Málek, J. Therm. Anal. Calorim., 2013, 111, 1045–1056 CrossRef CAS.
- S. Vyazovkin, A. K. Burnham, J. M. Criado, L. A. Pérez-Maqueda, C. Popescu and N. Sbirrazzuoli, Thermochim. Acta, 2011, 520, 1–19 CrossRef CAS.
- N. Koga, J. Therm. Anal. Calorim., 2013, 113, 1527–1541 CrossRef CAS.
- N. Koga, J. Šesták and P. Simon, in Thermal Analysis of Micro, Nano- and Non-Crystalline Materials, ed. J. Šesták and P. Simon, Springer, Dordrecht, 2013, ch. 1, pp. 1–28 Search PubMed.
- H. L. Friedman, J. Polym. Sci., Part C: Polym. Symp., 1964, 6, 183–195 CrossRef.
- T. Ozawa, J. Therm. Anal., 1970, 2, 301–324 CrossRef CAS.
- T. Ozawa, Bull. Chem. Soc. Jpn., 1965, 38, 1881–1886 CrossRef CAS.
- T. Ozawa, Thermochim. Acta, 1986, 100, 109–118 CrossRef CAS.
- J. Málek, Thermochim. Acta, 1992, 200, 257–269 CrossRef.
- N. Koga, Thermochim. Acta, 1995, 258, 145–159 CrossRef CAS.
- F. J. Gotor, J. M. Criado, J. Málek and N. Koga, J. Phys. Chem. A, 2000, 104, 10777–10782 CrossRef CAS.
- J. M. Criado, L. A. Pérez-Maqueda, F. J. Gotor, J. Málek and N. Koga, J. Therm. Anal. Calorim., 2003, 72, 901–906 CrossRef CAS.
- N. Koga, S. Vyazovkin, A. K. Burnham, L. Favergeon, N. V. Muravyev, L. A. Pérez-Maqueda, C. Saggese and P. E. Sánchez-Jiménez, Thermochim. Acta, 2023, 719, 179384 CrossRef CAS.
- J. Šesták and G. Berggren, Thermochim. Acta, 1971, 3, 1–12 CrossRef.
- J. Šesták, J. Therm. Anal., 1990, 36, 1997–2007 CrossRef.
- J. Šesták, J. Therm. Anal. Calorim., 2011, 110, 5–16 CrossRef.
- N. Koga and H. Tanaka, J. Therm. Anal., 1991, 37, 347–363 CrossRef CAS.
- N. Koga and J. Šesták, Thermochim. Acta, 1991, 182, 201–208 CrossRef CAS.
- N. Koga and J. Šesták, J. Therm. Anal., 1991, 37, 1103–1108 CrossRef.
- N. Koga, Thermochim. Acta, 1994, 244, 1–20 CrossRef CAS.
- A. K. Galwey and M. Mortimer, Int. J. Chem. Kinet., 2006, 38, 464–473 CrossRef CAS.
- P. J. Barrie, Phys. Chem. Chem. Phys., 2012, 14, 318–326 RSC.
- P. J. Barrie, Phys. Chem. Chem. Phys., 2012, 14, 327–336 RSC.
- D. Xu, M. Chai, Z. Dong, M. M. Rahman, X. Yu and J. Cai, Bioresour. Technol., 2018, 265, 139–145 CrossRef CAS PubMed.
- A. Mianowski, T. Radko and T. Siudyga, React. Kinet., Mech. Catal., 2020, 132, 37–58 CrossRef.
- R. E. Lyon, J. Phys. Chem. A, 2023, 127, 2399–2406 CrossRef CAS PubMed.
- D. D. Wagman, W. H. Evans, V. B. Parker, R. H. Schumm, I. Halow, S. M. Bailey, K. L. Churney and R. L. Nuttall, The NBS Tables of Chemical Thermodynamic Properties. Selected Values for Inorganic and C1 and C2 Organic Substances in SI Units, American Chemical Society, Washington, DC, 1982 Search PubMed.
- A. K. Galwey and W. J. Hood, J. Phys. Chem., 1979, 83, 1810–1815 CrossRef CAS.
- T. Wada and N. Koga, J. Phys. Chem. A, 2013, 117, 1880–1889 CrossRef CAS PubMed.
- R. Ozao and M. Ochiai, J. Ceram. Soc. Jpn., 1993, 101, 263–267 CrossRef CAS.
- N. Koga and H. Tanaka, J. Therm. Anal., 1994, 41, 455–469 CrossRef CAS.
- N. Koga and J. Málek, Thermochim. Acta, 1996, 283, 69–80 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Water vapor effect on the reaction pathway (Fig. S1–S5); S2. Kinetics of the component reaction steps at different p(H2O) values (Fig. S6–S13); S3. Kinetic modeling based on the IP–SR–PBR(n) models (Fig. S14–S18 and Tables S1–S4). See DOI: https://doi.org/10.1039/d4cp01870b |
| This journal is © the Owner Societies 2024 |