Why alloying with noble metals does not decrease the oxidation of platinum: a DFT-based ab initio thermo-dynamics study†
Received
4th May 2024
, Accepted 26th August 2024
First published on 3rd September 2024
Abstract
Despite its well-known nobility, even platinum is subject to corrosion under the harsh conditions that many technical applications require. Based on the assumption that the platinum loss is mainly caused by the formation of volatile PtO2, alloying is a promising strategy to reduce it. This investigation explores the bulk stability of Pt–Au, Pt–Ir, Pt–Re, Pt–W, Pt–Ag, Pt–Rh, Pt–Cu, Pt–Ni and Pt–Co, as well as their oxides, utilizing density functional theory, as well as ab initio and literature thermodynamic data. The alloy model combines special-quasi random structures with thermodynamic properties interpolated from the constituting metals, which are complemented by the configuration entropy. The results suggest that reducing platinum oxidation by alloying decreases the overall nobility of the alloy, since platinum- and oxygen affinity of the alloying metal are related to each other. Despite this limitation, copper was identified as a promising candidate for stabilizing the platinum catalyst in the Ostwald process.
1. Introduction
Synthetic fertilizers are without doubt one of the most important accomplishments of chemistry. Synthesis of nitrate on a large industrial scale was accomplished more than a century ago by oxidation of ammonia using the Ostwald process.1–3 Still, central parts of the mechanism are not completely understood due to the fast4,5 and highly exothermic reaction4,6 and the complexity of the reaction network.4,6 While direct observation is impossible at least for now, computational chemistry may be able to answer some of the remaining questions. One issue in the practical implementation concerns catalyst corrosion: although the platinum catalyst employed in the process is highly active, half of it is lost over the catalyst lifetime due to corrosion.7 Techniques to minimize this loss include flow related modifications of the catalyst like knitting and catchment gauzes, as well as alloying the platinum with around 10% rhodium.7 While the former two techniques have improved considerably over time, no addition to or replacement of rhodium has been found to further enhance the catalyst stability via alloying, since the mechanism of the corrosion is still not completely known.
By examining worn out catalyst gauzes, it was found, that the surface of the wires is reconstructed extensively in the form of “cauliflower” in the reaction zone (see Fig. 1).5,7–9 The most advanced mechanism5,8,10 of their formation postulates Pt-transport through the gas phase, which is powered by the high temperature of localized reaction hot-spots on the surface. The transport process is most likely mediated by PtO2, since platinum sublimation alone is not severe enough to account for the amount of platinum lost in an oxygen atmosphere. The PtO2 then either re-deposits nearby or is carried out. Hence, the unusual shape of the structures results from the crystallite extending into the reaction feed, but at the same time also shielding the surface from it.
 |
| | Fig. 1 Platinum catalyst surface reconstruction during ammonia oxidation. Image taken from Hannevold et al.8 | |
The Pt–Rh catalyst itself adds another layer of complexity by featuring conflicting properties like the oxidation of rhodium11 on one hand and the ability of platinum to reversibly4,12 absorb oxygen on the other, as well as oxygen-dependant surface segregation.13–16 At present, modelling all of these effects at once is not feasible due to vastly different time- and length-scales of catalytic reaction and catalyst degradation. The sheer scale of the reconstruction discussed above however demonstrates that the corrosion of platinum is mostly driven by bulk thermodynamics. Conversely, the influence of the surface is probably too small, to completely prevent the oxidation of a thermodynamically unstable phase, especially at a temperature above 1000 K. Its effect is therefore only kinetic in nature. Consequently, the investigation at hand focusses on screening platinum-rich alloys of Au, Ir, Re, W, Ag, Rh, Cu, Ni and Co for their thermodynamic resistance to oxidation combining periodic bulk-DFT calculations and ab initio thermodynamics with literature data. The stability of the alloys was estimated based on their ideal Gibbs free energy of mixing, which was then used to model their thermic oxidation in dry oxygen or their electro-chemical oxidation under OER conditions. This approach allows for a streamlined treatment of rather different alloys by not considering surface properties, the most important of which are catalytic activity and selectivity, as well as kinetic effects. According to the results, the stability of an alloy against platinum oxidation is closely related to the reactivity of the second metal, which however not only determines its affinity for platinum, but also that for oxygen. An independent adjustment of these two properties is therefore not possible and the resulting concentration-dependence of the overall nobility severely limits the number of viable alloying elements and -compositions. Still, copper was found to optimize both aspects much better than rhodium.
2. Computational details
2.1 Density functional theory calculations
All structures and energies were obtained by means of density functional theory (DFT). The calculations were done spin-polarized using VASP 5.3.5,17–21 employing the PBE-functional,22 the standard ultrasoft PAW-pseudopotentials provided by VASP,23 a Monkhorst–Pack–Mesh24,25 (∼32k-pts Å−1) and Gaussian smearing (sigma = 0.005 eV). Electronic and geometric convergence thresholds were set to 1 × 10−6 eV and 5 × 10−6 eV, respectively, and a cutoff of 500 eV was chosen. Gas phase molecules were calculated at the Γ-point only.
2.1.1 Dispersion correction.
The investigation at hand compares phases with vastly different mass densities. The common assumption of similar van der Waals interactions is therefore not valid. VASP provides several methods to account for this and a selection of them was tested on platinum and the solid and gaseous modifications of PtO2. Of these, only the combination of PBE and D3/BJ26,27 (D4 is not available in VASP 5) provides reliable energies of formation for condensed and gaseous states of matter, whereas the other tested dispersion functionals were found to predict unreasonably low energies for the endothermic formation of gaseous PtO2 (see Table S3, ESI†). Additionally, many of the methods overestimate lattice constants and bond lengths similar to or even worse, than bare PBE, which is known to underbind.28,29 This agrees with literature results,30 where nonlocal methods were found to reproduce errors of the underlying GGA functionals. For the computation of thermodynamic properties, which requires vibrational frequencies, a comparison between PBE and PBE-D3/BJ for the above test set yielded negligible entropy differences of about 2 J mol−1 K−1 at 298.15 K. PBE was therefore chosen for this task.
2.1.2 Magnetic structures.
Magnetism is not relevant for most of the solid-state calculations because most of the investigated transition elements are not able to collectivize their uncompensated spins. Nevertheless, there are exceptions like the oxides of cobalt and nickel, whose unit cells require adjustments to be compatible with the correct magnetic structure (thereby lowering the respective symmetry from Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and Fm
m and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m to I41/amd and P2/m for Co3O4 and CoO/NiO). While all calculations were conducted employing the spin-unrestricted scheme, in some cases the structures had to be pre-relaxed with a set total spin. Especially some of the cobalt alloys were found to not converge without this treatment. Still, the ground state was not found in all cases, which results in a comparatively large scattering of the Pt–Co energies. In contrast, the geometries and energies of molecular phases were determined for fixed integer values of the total spin. Several values were tested for each species and the following magnetic moments were determined: PtO2 (0μB), IrO2 (1μB), IrO3 (1μB), Re2O7 (0μB), WO2 (0μB), WO3 (0μB), RhO2 (1μB).
m to I41/amd and P2/m for Co3O4 and CoO/NiO). While all calculations were conducted employing the spin-unrestricted scheme, in some cases the structures had to be pre-relaxed with a set total spin. Especially some of the cobalt alloys were found to not converge without this treatment. Still, the ground state was not found in all cases, which results in a comparatively large scattering of the Pt–Co energies. In contrast, the geometries and energies of molecular phases were determined for fixed integer values of the total spin. Several values were tested for each species and the following magnetic moments were determined: PtO2 (0μB), IrO2 (1μB), IrO3 (1μB), Re2O7 (0μB), WO2 (0μB), WO3 (0μB), RhO2 (1μB).
2.2 Mean empirical enthalpy correction
Local and semi-local density functional functionals are known to penalize localized electronic states due to the self-interaction error.31 This affects radicals (especially oxygen) and -anions, as well as band gaps (Mott–Hubbard- and charge-transfer-insulators32), especially in transition metal compounds. Unfortunately, there is no method to account for this easily in case of periodic boundary calculations. Wave-function based methods (and hybrid functionals), for example, are prohibitively expensive due to nonlocal terms, whereas alternative methods, like the semi-empirical GGA+U approach, are not transferable between different chemical systems. Slightly different from the oxygen correction scheme by Wang et al.,33 the oxide Gibbs free energies are therefore adjusted empirically by −38.27 kJ mol−1 per metal atom based on the mean deviation from experimental enthalpies of formation. Averaging is unavoidable here due to missing reference values for some oxides. Still, this procedure nearly halves the standard deviation of the enthalpy to +32.53 kJ mol−1 per metal atom (the error is mostly concentrated on NiO, CoO and Co3O4) and allows for a comparison of the oxidation properties to that of other metals, as well as experimental data. The remaining errors should not affect the conclusions of this work, since the energies do not influence the trends versus T. This is due to the smaller, less error-prone normal modes dominating the heat capacity. No correction has been applied to the electrochemical reactions, since molecular oxygen is not involved in this case, while there is no way to determine the oxide component of the error.
The following solid phases were considered for the enthalpy comparison and the calculation of the mean (the literature cited for the metals refers to entropy data): Ir,34 IrO2,35,36 Re,37 ReO2,38–41 ReO3,41,42 Re2O7,41 W,43 WO2,44,45 W18O49,44,45 WO3,44–46 Ag,47 Ag2O,48 Rh,34 Rh2O3,49,50 RhO2,51 Cu,52,53 Cu2O,53,54 CuO,54 Ni,53,55 NiO,53 Co,53,56 CoO53,57,58 and Co3O4.57 Due to unreliable data, the oxide of gold, as well as the ones of platinum were excluded from the averaging (this also prevented an individual adjustment). They were however corrected nonetheless for the sake of consistency.
The enthalpy errors of the gaseous oxides seemingly differ from the solid ones. Including them in the average thus worsens the overall result. A separate or individual correction of the gaseous phases is not an option either, since literature data is scarce and its reliability uncertain (PtO2,59–61 IrO3,62 Re2O7,42 WO2,45 WO3,45 RhO259–61). The reference data for O2, H2 and water vapour was taken from the NIST-JANAF tables.45
2.3 Crystalline phases
The DFT energies were complemented by an evaluation of the thermodynamic properties to obtain the Gibbs free energy:In case of the regular solid phases only phononic contributions to the enthalpy and the entropy were accounted for, which was done using the phonopy package63,64 (version 2.15.1, accessed 13.06.2022) applying the finite difference method with atomic displacements of 0.01 Å. To obtain a continuous representation of the discrete values provided by phonopy, the heat capacities were fitted to the Shomate equation65,66| |  | (2) |
within the interval 300 ≤ T ≤ 1300 K. Integration of the heat capacity in eqn (2) yields the vibrational entropy| |  | (3) |
and -enthalpy| |  | (4) |
The parameters a, f and g were constrained to allow for a perfect reproduction of the respective phonopy values at 300 K. All parameters obtained this way are provided in Table S2 and the corresponding data file in the ESI.† By adding the single-point energy E and the mean empirical enthalpy correction 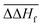 of −38.27 kJ mol−1 per metal atom (0 kJ mol−1 for electrochemical reactions) to Hvib(T), one obtains the total enthalpy
of −38.27 kJ mol−1 per metal atom (0 kJ mol−1 for electrochemical reactions) to Hvib(T), one obtains the total enthalpy| | 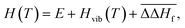 | (5) |
where the thermal expansion of the solid phases is assumed to be negligible.
2.4 Gas phase model
In contrast to the solid state, the translational and rotational degrees of freedom dominate the enthalpy H(T) and entropy S(T) of the gas phase:| | | H(T) = E + Htrans(T) + Hrot(T) + Hvib(T) | (6) |
| | | S(T) = Strans(T) + Srot(T) + Svib(T) + Sel(T). | (7) |
The energy E was determined by means of DFT calculations at the Γ-point using VASP. The contributions to H and S are expressible in terms of their partition functions, which were adopted from Irikura.67 Doing so for the translational degrees of freedom yields| |  | (8) |
for the associated change in enthalpy and| |  | (9) |
for the translational entropy, where R, kB and h are the universal gas constant, the Boltzmann constant and the Planck constant, respectively. M denotes the total mass of the molecule and the pressure is fixed to p = 1 bar. Eqn (8) already includes the thermodynamic work pΔV = RT. Due to missing one rotational degree of freedom, the enthalpy- and entropy expressions for the rotation of non-linear molecules| |  | (10) |
| |  | (11) |
differ from that of linear ones| |  | (13) |
An additional symmetry number σ is necessary to describe the number of equivalent orientations. The total moment of inertia I was obtained using the determinant of the inertia tensor. Despite being small, the vibrational contributions to the enthalpy| |  | (14) |
and the entropy| |  | (15) |
have been included to ensure correct behaviour at elevated temperatures. Depending on the molecular geometry, there are either 3N − 6 (non-linear) or 3N − 5 (linear) normal modes (N being the number of atoms). The normal mode frequencies νi were obtained using the finite-difference algorithm implemented in VASP with two displacements of 0.01 Å per direction and atom (NFREE = 2), skipping symmetry equivalent calculations (IBRION = 6). In case of Re2O7(g) two of the normal modes correspond to internal rotations. These have been modelled as free, symmetric rotors instead| |  | (17) |
| |  | (18) |
| |  | (19) |
where Irotor and σrotor represent the moment of inertia of the rotating fragment and its symmetry. The angles α, β and γ specify the inclination of the rotation axis with respect to the global moments of inertia IA, IB and IC. Finally, a simplified representation of the electronic degrees of freedom was added to the entropy, which considers the 2S + 1 degenerate spin states (S being the total spin in this particular case):| | Sel = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2S + 1) ln(2S + 1) | (20) |
This does not only concern the gaseous oxides of rhodium and iridium, which share a total spin of S = 1/2, but is especially important in case of the triplet ground state of oxygen.
2.5 Random alloys
The alloys with at least fifty percent platinum content were modelled as randomized bulk supercells containing 108 atoms. Alloy randomization was achieved by applying the SQS-scheme by Zunger et al.,68 which is implemented in the sqsgenerator package69 (version 0.2, accessed 13.06.2022) and provides structures that mimic the properties of fully random alloys. The alloy energies of at least four random structures per composition with a standard deviation of at most 0.53 kJ mol−1 per atom or 6.5% of the mixing energy were fitted to a cubic polynomial describing the total energy E as a function of the composition x, which hereafter refers to the concentration of the non-platinum metal (x2). The energy of pure platinum was obtained from a separate calculation and fixed in the fitting process. To obtain the Gibbs free energy G(x, T) of the alloy, its energy per metal atom E(x)/nM was combined with enthalpy- and entropy contributions, which were interpolated between the Gibbs free energies Gi(T) of the two constituting metals i:| |  | (21) |
To avoid expansive cluster expansion calculations70 for each alloy, the configurational entropy ΔSmix(x) was calculated assuming an ideal solution:| |  | (22) |
To estimate the boundaries of the random phase, the alloy data obtained this way is compared to stable intermetallic structures of like composition, which exist for the platinum alloys of copper,71,72 nickel,73 cobalt74 and tungsten.75
3. Results
3.1 Alloying
While oxidation of the alloys is the main focus of this investigation, it is tied to their general thermodynamic stability, which will therefore be addressed here first. On a qualitative level, there are four types of alloys:
– Elements forming type sA alloys interact strongly attractive, which favours intermetallic phases over the random structure in most areas of the phase diagram.
– Interactions in type wA alloys are less attractive, hence the disordered phase is stable over a wide range of compositions and temperatures.
– Element combinations of type wR interact weakly repulsive, thereby opening up a miscibility gap at low temperatures.
– The phase diagrams of type sR combinations are completely dominated by the miscibility gap. As a result of this, alloys of this type are only stable for very specific compositions and/or temperatures.
The classification described above can be illustrated by considering the Gibbs free energy of mixing, which compares the alloy to an idealized mixture of its components i:
| | 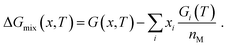 | (23) |
Fig. 2 depicts Δ
Gmix(
x,
T) of three representative platinum alloys for a temperature interval that covers many technical applications. It is important to note, that these plots should not be mistaken for complete phase diagrams, since besides neglecting liquid phases they do not contain information about phase mixtures. To maintain catalytic activity, a high content of platinum was assumed to be required, so only compositions with 0 ≤
x ≤ 0.5 were investigated. Accordingly, only the face-centred (fcc) structure of the platinum matrix is considered for the disordered alloys, which is favoured at high platinum content and shared by most metals investigated here. The only two exceptions – alloys rich in tungsten (
Fig. 2c) and rhenium (Fig. S7b, ESI
†), which crystallize in body-centred and hexagonal structures, respectively – are expected to occur only in case of a significant excess of the alloying metal.
 |
| | Fig. 2 Gibbs free energy of mixing (ΔGmix) of Pt–Au (a), Pt–Cu (b) and Pt–W (c) per metal atom mapped onto alloy composition x and temperature T. Vertical black lines represent stable intermetallic phases of like composition. | |
As can be seen from Pt–Au in Fig. 2a, at high temperatures the configurational entropy completely compensates the repulsive interaction even in sR-type alloys. Likewise, the transition between weakly and strongly attractive categories (see Fig. 2b and c for examples, black bars indicate the stable temperature range of the respective ordered phase) is smooth. The weak/strong-subdivision established at the beginning of this section is therefore somewhat arbitrary. Moreover, it relies on experimental data to some extent. This is in contrast to the general attractive/repulsive character of the interaction, which is unambiguously defined by the sign of the mixing energy. Fortunately though, according to the summary in Table 1, the deviation of the most stable/unstable composition xmin/max from 0.5 might be a viable indicator for the interaction strength, since there are four alloys (Pt–W, Pt–Re, Pt–Au and Pt–Ag) with deviations of more than 0.1. Considering the sparse experimental data and the rather unexpected absence of intermetallic phases in such a well mixing system, Pt–Re is hence relabelled as a type sA alloy (in fact, the existence of regular phases is assumed based on theoretical predictions76). A welcome side effect of basing the classification on xmin/max is the connection to the gradient of ΔGmix along x, which will be important for the oxidation in Sections 3.2 and 3.3. In the discussion below the results will be presented starting with the late 5d alloys, which are most similar to platinum, and ending with the more complex 3d alloys.
Table 1 Classification of the investigated platinum alloys and the properties it is based on (extremal energy ΔEmin/maxmix per metal atom and the corresponding composition xmin/max, oxide energy of formation ΔEf)
| Alloy |
ΔEmin/maxmix [kJ mol−1] |
x
min/max
|
Alloyability-typea |
ΔEf/metal atom [kJ mol−1] |
Nobility-typeb |
|
sA = strongly attractive, wA = weakly attractive, wR = weakly repulsive, sR = strongly repulsive.
N = noble, B = base in comparison to ΔEf (PtO2,s) = −147.67 kJ mol−1.
Relabelled based on xmin/max.
|
| Pt–Au |
5.3 |
0.38 |
sR |
−19.80 (Au2O3) |
N |
| Pt–Ir |
∼6.0 |
∼0.55 |
wR |
−230.45 (IrO2) |
B |
| Pt–Re |
−8.3 |
0.34 |
sA (wA)c |
−637.68 (Re2O7) |
B |
| Pt–W |
−18.6 |
0.25 |
sA |
−822.09 (WO3) |
B |
| Pt–Ag |
2.6 |
0.33 |
sR |
−5.91 (Ag2O) |
N |
| Pt–Rh |
∼−1.1 |
∼0.55 |
wA |
−243.29 (RhO2) |
B |
| Pt–Cu |
< −8.5 |
> 0.50 |
wA |
−108.38 (CuO) |
N |
| Pt–Ni |
−3.4 |
0.48 |
wA |
−125.43 (NiO) |
N |
| Pt–Co |
−3.8 |
0.48 |
wA |
−233.78 (Co3O4) |
B |
3.2 Pt-Alloys of Au and Ir
While most considered elements mix attractively with platinum, gold and iridium do not. In Fig. 2a (see Fig. S5b for the iridium results, ESI†) this is indicated by the positive sign of ΔGmix(x, T) at low temperatures. Even at 1300 K the Gibbs free energy of mixing does not exceed −3 kJ mol−1 for both elements. Still, the miscibility gaps reported in the literature extend up to 1473 K for Pt–Au77 and 1300 K in case of Pt–Ir,78 indicating an overstabilization of the random phase in our model. An improved description of ΔGmix can be achieved by combining a cluster expansion model with Monte Carlo sampling70 (see for example ref. 79). This is, however, out of the scope for the present screening investigation and even the lower demixing temperatures fall within range of the working conditions of the Ostwald process.
3.2.1 Pt-Alloys of Re and W.
The rhenium alloy mixes strongly attractively (type sA), with minimum ΔGmix(x, T) values ranging between around −10 kJ mol−1 at 300 K and nearly −16 kJ mol−1 at 1300 K for a rhenium content of 25% (Fig. S7b, ESI†). The compositional range is reduced in this case due to rhenium crystallizing in a hcp structure and the related miscibility gap around x ≈ 0.5, which is hinted at by a minimum of ΔGmix(x, T) along x. The presence of the latter somewhat contradicts the attractive interaction with platinum and indeed calculations by Levy et al.76 suggest the existence of Pt3Re. The behaviour of tungsten (Fig. 2c) is very similar, the only differences being the even stronger interaction with platinum (−20 kJ mol−1 up to −25 kJ mol−1 at x = 0.25) and the intermetallic phase at x = 0.33.75,80 Still, both elements appear to be useful for alloying, since the limited compositional range is made up for by the steep gradient of ΔGmix along x, which permits the use of less alloying metal.
3.2.2 Pt-Alloys of Ag.
The platinum alloy with silver (Fig. S1a, ESI†) is similar to that of gold (Fig. 2a) but about 3 kJ mol−1 more stable. Based on the large deviation of the miscibility gap's maximum temperature from the experimental phase diagram,81 the stability is probably overestimated, though. Please note that neither the liquid phase, which is required for the peritectic reaction, nor intermetallic PtAg at low temperatures81 were considered.
3.2.3 Pt-Alloys of Rh.
The Gibbs free energy of mixing of rhodium in platinum (Fig. 7a) is mostly driven by entropic contributions, while the enthalpy of mixing is negligible. Thus, despite being an attractive alloy (type wA) and the default choice for alloying, it needs around 1300 K to reach the Gibbs free energy of mixing of Pt–Re at 300 K.
3.2.4 Pt-Alloys of Cu.
Modelling the late 3d platinum alloys is slightly more complicated, since there are order–disorder transitions within the investigated temperature range. For the sake of this discussion, the alloys are assigned to the weakly attractive category. This agrees with the classification based on xmin/max, which was proposed above (see Table 1). The copper alloy (Fig. 2b) outperforms all other wA-alloys in terms of stability (ΔGmix decreasing from −10.6 kJ mol−1 to −16.4 kJ mol−1 in the chosen temperature interval). This is accompanied by the emergence of the unique L13- (Cmmm)82–84 and L11-structures (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m)72,83,84 for Pt3Cu and PtCu (please see Table S1 in the ESI† for a complete listing of all considered phases and their thermodynamic properties). Still, the order–disorder transition at 50% copper occurs almost 200 K lower than expected71 (no data was found for Pt3Cu), supporting the notion expressed earlier for Pt–Au and Pt–Ir that the stability of the random alloys is overestimated.
m)72,83,84 for Pt3Cu and PtCu (please see Table S1 in the ESI† for a complete listing of all considered phases and their thermodynamic properties). Still, the order–disorder transition at 50% copper occurs almost 200 K lower than expected71 (no data was found for Pt3Cu), supporting the notion expressed earlier for Pt–Au and Pt–Ir that the stability of the random alloys is overestimated.
3.2.5 Pt-Alloys of Co and Ni.
Except for the negligible fcc–hcp transition of cobalt both alloys resemble each other very closely, with ΔGmix of Pt–Co decreasing from −5.5 kJ mol−1 at 300 K to almost −11.5 kJ mol−1 at 1300 K and Pt–Ni only adding +0.5 kJ mol−1 to this (Fig. S3b and S6b, ESI†). Both elements carry a magnetic moment, which in some cases prevents the identification of the ground state. Especially for compositions with 20% and 30% cobalt the energies are notably less negative than expected (see Fig. S3a, ESI†). Consequently, the transition to the L12 structure (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) sets in 450 K too low, whereas the transition at 50% to the L10 structure (P4/mmm) deviates by 400 K from the experimental phase diagram.74 The analogous nickel deviations of +110 K for PtNi and −40 K for Pt3Ni on the other hand compare much better to the literature.73,85,86
m) sets in 450 K too low, whereas the transition at 50% to the L10 structure (P4/mmm) deviates by 400 K from the experimental phase diagram.74 The analogous nickel deviations of +110 K for PtNi and −40 K for Pt3Ni on the other hand compare much better to the literature.73,85,86
3.3 Oxidation of platinum
Despite being known as noble, platinum forms at least one gaseous oxide – which is the main focus of this investigation – as well as several solid oxide phases. While the latter do not contribute to the volatility directly, they may form at the surface, thereby potentially passivating it or acting as a precursor for the formation of PtO2 vapour. Thermodynamically, the volatilization can be described in three steps (which are not identical to the reaction mechanism). In the first step a platinum atom is released from the alloy:| | | Pt(1−x)sMx·s → Pt(1−x)s−1Mx·s + Pt. | (I) |
This is equivalent to increasing x to the final concentration x:
| | 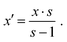 | (24) |
Herein,
s denotes the system size in terms of the total number of atoms. Conversely, 1/
s can be thought of as the fraction of the system, which is affected by oxidation. In the following calculations
s was set to 100 atoms, though reducing it to ten atoms or less does not change the results for the platinum oxidation significantly (it does however affect that of the second metal). Please note, that the intermediate state of the released metal atom, which results from the separation of step I and II, has not been considered explicitly. Hence, in the second step the released platinum atom directly reacts to form the thermodynamically stable oxide:
| |  | (II) |
In case of the latter being solid, a third step – subsequent oxidation, decomposition or direct sublimation – is necessary to complete formation of a volatile species:
| |  | (III) |
All Gibbs free energies presented hereafter will follow this scheme (negative values signifying oxidation taking place spontaneously). The gaseous product being transported out of the reaction zone by the gas feed renders the third reaction a non-equilibrium process in a technical reactor. As a consequence, this process may take place, regardless of sign.
As can be seen from equations I to III, alloy composition and properties only affect the very first step, whereas the oxidation of the released platinum is identical for all alloys and depends only on the reaction conditions. The four alloy types introduced in the alloying section – strongly attractive (sA), attractive (wA), repulsive (wR) and strongly repulsive (sR) – thus apply here as well. Despite most platinum oxides being solid, the three reaction steps are combined here to assess the resistance against platinum volatilization via PtO2(g). The total Gibbs free energy of reaction thus reduces to
| | | ΔGr,Pt(x, T) = ΔG−Pt(x, T) + GPtO2(T) − GO2(T). | (25) |
GO2 and
GPtO2 are calculated as described in the computational details. The Gibbs free energy necessary to release one platinum atom from the alloy, Δ
G−Pt, is expressed by
| | | ΔG−Pt(x, T) = (s − 1)G(x′, T) − sG(x, T). | (26) |
Eqn (26) implies that Δ
Gr,Pt(
x,
T) is related to the derivative of Δ
Gmix(
x,
T) with respect to
x, since the change of the Gibbs free energy is calculated for a constant change in concentration. As a result of this, the trends along
x of associated plots oppose each other in
Fig. 2 and 3. The dependence on the temperature, on the other hand, is mostly determined by the large entropy difference of the gaseous and solid phases, which results from the latter lacking translational and rotational degrees of freedom. This translates to a declining stability at elevated temperatures for the solid oxides, whose entropy is too small to compensate for the loss of gaseous oxygen, whereas the formation of gaseous metal oxides results in an entropy gain if a maximum of one oxygen molecule is bound in the process. Both states of matter are observed in the oxidation of platinum, which below will be discussed for pure platinum (
x = 0) first. As for the Gibbs free energy of mixing, only a representative selection of the results is shown in
Fig. 3. The remaining plots can be found in the ESI.
†
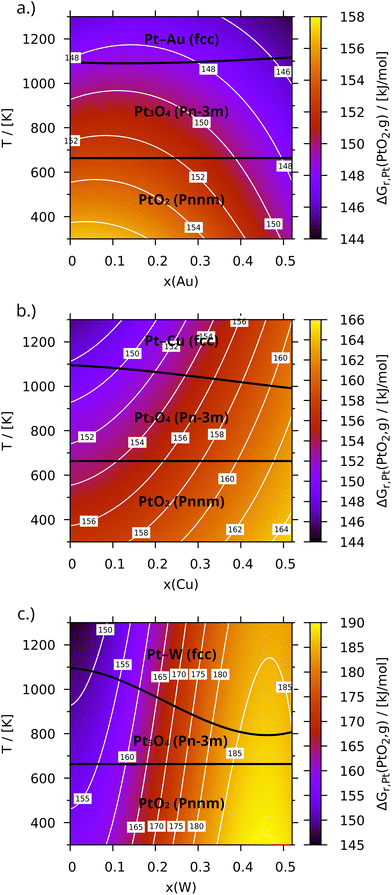 |
| | Fig. 3 Gibbs free energy for the formation of gaseous PtO2 (ΔGr,Pt) from Pt–Ir (a), Pt–Cu (b) and Pt–W (c) per metal atom mapped onto alloy composition x and Temperature T. Phases and their boundaries are signified in black. | |
3.3.1 Oxidation of pure platinum.
Besides gaseous PtO2, four solid phases – α-PtO2 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), β-PtO2 (Pnnm), Pt3O4 (Pm
m), β-PtO2 (Pnnm), Pt3O4 (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n) and PtO (P42/mmc) – were considered as possible oxidation products. Reproducing their very different structures and properties correctly requires the inclusion of dispersion forces, which especially lowers the relative stability of the gaseous- and the layered a-modifications of PtO2 in accordance with their lower mass density. In the present case, the D3/BJ approach by Grimme et al.26,27 was chosen to complement the PBE density functional. Consequently, only two oxides are observed in Fig. 3: β-PtO2 is predicted to be stable at low temperatures. At 663 K the rapidly growing gas-phase entropy of oxygen causes some of it to be released from the solid. The resulting Pt3O4 is then stable again up to 1094 K in case of pure platinum (x = 0), where it finally decomposes. Unfortunately, experimental data on the phase transitions between platinum oxides is sparse, especially at moderate or low temperatures and pressures, where equilibration is difficult. Electrical resistance measurements by Berry87 suggest a decomposition of β-PtO2 between 870 K and 920 K. This is consistent with more recent thermogravimetric results by Punnose et al.,88 who additionally found Pt3O4 between 908 K and 1073 K. Both measurements were conducted in air, where the transition temperatures are lower than in pure oxygen due to the lower partial pressure. A comparison to other theoretical results, like that of Chen and Yang89 or Seriani et al.,90 is difficult due to differences in the employed models, since either the phonon contribution or the corrections of the DFT oxygen and oxide energies are missing. The seemingly better Pt3O4-boundary temperatures of 870 K and 970 K by Seriani et al.90 might thus be coincidental and caused by error cancellation. The corrected values for (β-)PtO2 and Pt3O4 calculated here differ by about −10.1 kJ mol−1 and +12.0 kJ mol−1 per platinum atom, respectively, compared to the empirical relation proposed by Wang et al.91 for example (please see the Table S1 for a complete list of all thermodynamic properties, ESI†). The combined deviation can easily cause a boundary shift of the observed magnitude. It needs to be kept in mind, though, that the metal–oxide transition is much more important for the present investigation.
n) and PtO (P42/mmc) – were considered as possible oxidation products. Reproducing their very different structures and properties correctly requires the inclusion of dispersion forces, which especially lowers the relative stability of the gaseous- and the layered a-modifications of PtO2 in accordance with their lower mass density. In the present case, the D3/BJ approach by Grimme et al.26,27 was chosen to complement the PBE density functional. Consequently, only two oxides are observed in Fig. 3: β-PtO2 is predicted to be stable at low temperatures. At 663 K the rapidly growing gas-phase entropy of oxygen causes some of it to be released from the solid. The resulting Pt3O4 is then stable again up to 1094 K in case of pure platinum (x = 0), where it finally decomposes. Unfortunately, experimental data on the phase transitions between platinum oxides is sparse, especially at moderate or low temperatures and pressures, where equilibration is difficult. Electrical resistance measurements by Berry87 suggest a decomposition of β-PtO2 between 870 K and 920 K. This is consistent with more recent thermogravimetric results by Punnose et al.,88 who additionally found Pt3O4 between 908 K and 1073 K. Both measurements were conducted in air, where the transition temperatures are lower than in pure oxygen due to the lower partial pressure. A comparison to other theoretical results, like that of Chen and Yang89 or Seriani et al.,90 is difficult due to differences in the employed models, since either the phonon contribution or the corrections of the DFT oxygen and oxide energies are missing. The seemingly better Pt3O4-boundary temperatures of 870 K and 970 K by Seriani et al.90 might thus be coincidental and caused by error cancellation. The corrected values for (β-)PtO2 and Pt3O4 calculated here differ by about −10.1 kJ mol−1 and +12.0 kJ mol−1 per platinum atom, respectively, compared to the empirical relation proposed by Wang et al.91 for example (please see the Table S1 for a complete list of all thermodynamic properties, ESI†). The combined deviation can easily cause a boundary shift of the observed magnitude. It needs to be kept in mind, though, that the metal–oxide transition is much more important for the present investigation.
Gaseous PtO2, despite being unstable, most likely plays a key role in the corrosion of platinum due to its formation being irreversible in a fixed bed reactor with a directional gas flow. In contrast to the solid phases, its entropy is larger than that of platinum and oxygen combined, which results in a decrease of the Gibbs free energy of reaction from +156.9 kJ mol−1 at 300 K to +146.0 kJ mol−1 at 1300 K, promoting its formation at elevated temperatures. The corresponding enthalpy of formation amounts to +160.6 kJ mol−1 at 298.15 K, whereas the literature data spans values from about 164 kJ mol−1 (ref. 59–61) to 218 kJ mol−1.92 Fortunately, changes induced by alloying are not affected by this uncertainty. The following discussion will therefore focus on how alloying alters the relative stability of the alloys compared to pure platinum.
3.3.2 Oxidation of Pt in Au- and Ir-alloys.
Pt–Au and Pt–Ir are repulsive alloys of type sR and wR, respectively. These types are characterized by a positive Gibbs free energy of mixing, which lowers the energy required for releasing platinum from alloys with high gold or iridium content, thereby also promoting their oxidation. This is illustrated by Fig. 3a, which presents the Gibbs free energy for forming PtO2(g) from the gold alloy (see Fig. S5c for the iridium results, ESI†). As can be seen, at 300 K alloying with gold decreases ΔGr,Pt(x, T) from +156.7 kJ mol−1 to +149.8 kJ mol−1 (to +153.2 kJ mol−1 in case of iridium), which increases the vapour pressure at that temperature by almost 17 times. At 1300 K, on the other hand, the configurational entropy almost compensates the repulsive enthalpy and the gradient of ΔGr,Pt(x, T) along x nearly vanishes. Another inversion is observed at low x, where decreasing the platinum content slightly increases ΔGr,Pt(x, T), which results in a small maximum along x (in case of iridium, the maximum less narrow and shifted to larger x). The reason for this is the infinite mixing entropy at x = 0, which translates to a rapidly decreasing chemical potential of gold at low concentrations. Thus, alloying platinum with small amounts of any other metal generally reduces its oxidation tendency. This is also reflected by the boundary between Pt3O4 and the metallic state, which is – in contrast to oxide–oxide transitions–composition dependant.
3.3.3 Oxidation of Pt in Re- and W-alloys.
Pt–Re and Pt–W are of the strongly attractive type, where the minimum Gibbs free energy of mixing is reached well below x = 0.5. In Fig. 3c, which presents the formation of PtO2(g) from Pt–W, this translates to a steep increase of ΔGr,Pt(x, T) to +176.0 kJ mol−1 already at 300 K and x = 0.25 (results for larger x are not discussed due to adjacent intermetallic phases). Alloying with rhenium yields almost +163.4 kJ mol−1 for the same conditions (see Fig. S7c, ESI†). Both values decrease by only about 8.5 kJ mol−1 at 1300 K (the vapour pressures at this temperature are thus reduced to 14% and 44%, respectively). A comparably strong dependence on x was found for the metal–oxide phase transition, which drops by around 175 K in case of alloying with tungsten (around 70 K for rhenium). Unlike the repulsive alloys, all trends are monotonous, since the stabilizing effect of the mixing entropy adds to an already negative mixing energy.
3.3.4 Oxidation of Pt in Ag-alloys.
The mixing behaviour of silver in platinum is similar to that of gold. Nevertheless, its mixing energy is smaller, which reduces the gradient of ΔGr,Pt(x, T) along x and results in a plot that blends properties of Pt–Au and Pt–Ir (Fig. S1c, ESI†). Consequently, the Gibbs free energy of reaction at x = 0.5 is always above that of the gold alloy (+152.4 kJ mol−1 at 300 K, +147.3 kJ mol−1 at 1300 K).
3.3.5 Oxidation of Pt in Rh-alloys.
The rhodium alloy belongs into the wA-category, which is represented by Pt–Cu in Fig. 3b (see Fig. 7b for the rhodium plot). Alloys of this type mix attractively over the whole range of x, allowing for synergy with the configurational term at high temperatures. The gradient along x therefore opposes that of the repulsive alloys. In case of Pt–Rh the mixing behaviour turned out to be almost ideal. This leaves the configurational entropy as the only contribution that influences the oxidation, which is not sufficient to compensate the surplus entropy of PtO2(g). At x = 0.5 ΔGr,Pt is therefore higher at 300 K (+159.5 kJ mol−1), than at 1300 K (+154.4 kJ mol−1). Still, the vapour pressure at 1300 K decreases to 46% compared to pure platinum.
3.3.6 Oxidation of Pt in Cu-, Ni- and Co-alloys.
The late 3d elements are miscible with platinum regardless of composition already at 0 K (type wA). The Gibbs free energy needed for the formation of gaseous PtO2 therefore steadily increases with x. The largest value of ΔGr,Pt(x, T) is found for 50% copper at 300 K and amounts to +164.4 kJ mol−1. This is a lower bound to the actual value, since ordered PtCu is preferred at this temperature. At 1300 K, this composition still yields +159.3 kJ mol−1. Alloying nickel or cobalt lowers ΔGr,Pt to +162.4 kJ mol−1 and +157.3 kJ mol−1 in case of the former and to +163.2 kJ mol−1 and +158.1 kJ mol−1 for the latter. Despite seemingly compensating the influence of temperature on pure platinum, alloying however cannot completely suppress its volatilization, since the weight of the Gibbs energy difference decreases at high temperatures according to exp(−ΔΔGr,Pt/RT). Still, the difference of ΔΔGr,Pt = 13.4 kJ mol−1, which was calculated for the copper alloy at 1300 K, is equivalent to a reduction of the PtO2 vapour pressure by 71%.
3.4 Oxidation of the alloying metal
With some minor adjustments the reaction scheme established for platinum is also valid for the second alloy component. The adaption of eqn (25) for other oxide stoichiometries then yields the following more general expression of the Gibbs free energy of reaction for the oxidation of the alloying metal M:| |  | (27) |
In contrast to platinum, though, releasing M from the alloy decreases x. The final concentration x′ therefore needs to be redefined to| |  | (28) |
This is equivalent to| | | Pt(1−x)sMx·s → Pt(1−x)sMx·s−1 + M. | (IV) |
Despite the similar reaction sequence, the additional complexity of M denoting more than one element, each of them with its own, distinct oxidation behaviour, still exists. This property, which will be referred to as “nobility”, also needs to be accounted for in the alloy classification scheme introduced in Section 3.1 by subdividing the alloy types. Oxygen affinity and alloyability are, however, not independent of each other, since both are connected to the reactivity. This results in opposing behaviour in terms of stability. Accordingly, elements of subtype N (“noble”), which are comparatively stable with regards to oxidation, usually mix repulsively (the opposite is the case for subtype B, “base”). Since all metals oxidize to some extent, the normalized oxidation energy of the pure metals (without any correction) was chosen as a criterion for assigning them to one of the two subgroups by comparing it to the formation of β-PtO2 from platinum. The resulting assignments are listed in Table 1.
The following section compares metals with very different properties and not all of them form volatile oxides. Consequently, the Gibbs free energy of reaction ΔGr,M(x, T) of the most stable oxide phases – regardless of their state of matter – is shown in Fig. 4. Besides the replacement of the gold alloy with that of iridium (gold is not expected to oxidize notably), the plots are similar to that for the oxidation of platinum in Fig. 3. There are however several important differences. Most obviously, the trends along x are inverted due to the complementary element concentration, while the inversion along T is related to the mostly solid oxides, whose entropy is much lower than that of (gaseous) oxygen. Additionally, the oxidized metal being different for each alloy adds an element- and temperature-dependant offset to the Gibbs free energy of reaction. A final detail is the gap at low x, where the amount of the non-platinum metal decreases below x = 1/100 = 1/s, which is equivalent to x = 0. This was implemented, since the configurational entropy (which is based on ln(x)) is not defined for x < 0. At the same time, alloying effects are most prominent at low concentrations due to the logarithm tending to negative infinity.
 |
| | Fig. 4 Gibbs free energy for the oxidation of the alloying metal (ΔGr,M) within Pt–Ir (a), Pt–Cu (b) and Pt–W (c) per metal atom mapped onto alloy composition x and temperature T. Phases and their boundaries are signified in black. | |
3.4.1 Oxidation of Ir in Pt-alloys.
Iridium is the only element tested, that is oxygen-affine in comparison to platinum and repulsive at the same time (type wR/B). Fig. 4a therefore exhibits an increase of ΔGr,Ir for most compositions at 300 K from −218.4 kJ mol−1 at x = 0.1 to −210.0 kJ mol−1 at x = 0.5 due to the positive mixing energy. Above 1000 K the latter is compensated by the configurational entropy, which results in an increase from −13.3 kJ mol−1 to −18.6 kJ mol−1 at 1300 K. Below x ≈ 0.1 the logarithmic mixing term inverts the trend even at 300 K. While iridium oxide is known to be volatile, this is not reflected in Fig. 4a, even though both, the enthalpy of formation and the entropy of IrO3 at 298.15 K are overestimated62 by −32.1 kJ mol−1 and +27.0 J mol−1 K−1, respectively (see Table S1, ESI†). Instead, solid IrO2 (P42/mnm) is observed up to 1300 K, whose properties differ much less from the literature. This implies, that the nobility of iridium – like that of rhenium and tungsten – is at least partly caused by passivation.
3.4.2 Oxidation of Re in Pt-alloys.
Similar to Pt–W in Fig. 4c, Pt–Re (type sA/B, see Fig. S7d, ESI†) features a steep drop in ΔGr,M from −504.5 kJ mol−1 to −561.1 kJ mol−1 at 300 K (−238.6 kJ mol−1 to −330.1 kJ mol−1 at 1300 K) while increasing the rhenium content to 25%. Just a single oxidation state – Re2O7 – is found to dominate this temperature interval, though there is a change of its state of matter. A direct comparison of the transition temperature with literature data is not possible due to the neglected liquid state but according to the enthalpies of formation solid Re2O7 (P212121) is −35.8 kJ mol−1 per metal atom too stable,40,41 whereas the gaseous equivalent differs by −1.7 kJ mol−1.42 (which is offset by the 15.7 kJ mol−1 larger42,93 entropy per metal atom). Adjusting the enthalpy of the solid oxide thus lowers the boundary from 780 K to 635 K. The roles of ReO2 and ReO3 might be comparable to that of WO2 (see below).
3.4.3 The oxidation of W on Pt-alloys.
Tungsten (type sA/B, Fig. 4c) behaves very similar to rhenium but eclipses the latter not only in terms of platinum – but also oxygen affinity. ΔGr,M thus spans a huge range of values, from −596.6 kJ mol−1 and −750.5 kJ mol−1 at 300 K and x = 0.25 to −301.5 kJ mol−1 and −490.3 kJ mol−1 at 1300 K. The large variety of phases described in the literature94 is, however, not reflected by Fig. 4c: besides solid WO3 no other oxide is present. And while WO2 and W18O49 are limited to very specific conditions95 and their occurrence on oxidized tungsten surfaces is likely related to their low oxygen permeability,96,97 only two of the four expected98,99 WO3 modifications (P21/c at low – and Pnma at high temperatures) are observed. The latter is not a major concern, though, since the properties of the WO3 phases are very similar and compare well with the values of Charlu and Kleppa44 (please see Table S1, ESI†). The absence of gaseous phases, on the other hand, is not a sign of instability but results from the overwhelming stability of solid WO3. In fact, the formation of WO3(g) is predicted to be about half as endergonic, as that of the solid phase. Moreover, the resulting volatility is probably underestimated due to not accounting for the formation of tungstic acid (H2WO4)100,101 or dimerization.102
3.4.4 Oxidation of Ag in Pt-alloys.
Ag2O is one of very few oxides, whose enthalpy of formation is severely worsened by the empirical correction (−43.4 kJ mol−1 instead of −15.3 kJ mol−1 ref. 48 per silver atom). But besides raising the corresponding phase boundary by more than 600 K48 (see Fig. S1d, ESI†), the impact of this error is limited, since it is only additive and does not influence the observed trends. As a repulsive alloy, Pt–Ag shares several characteristics with Pt–Ir in Fig. 4a, like the small minimum of ΔGr,M with regards to alloy composition at x ≈ 0.1. Unlike iridium, however, silver is of the noble subtype sR/N, as can be seen from the still small enthalpy of formation. Accordingly, the Gibbs free energy of reaction between x = 0.1 and x = 0.5 only increases from −38.9 kJ mol−1 to −29.4 kJ mol−1 at 300 K (+11.2 kJ mol−1 to +7.0 kJ mol−1 at 1300 K).
3.4.5 Oxidation of Rh in Pt-alloys.
The wA/B-classification of the rhodium alloy (Fig. 7c) is only shared by that of cobalt, which is however much easier oxidizable (see below). The corresponding change of the Gibbs free energy of oxidation is negligible at 300 K but grows to nearly −55 kJ mol−1 at 1300 K (+28.3 kJ mol−1 to −26.4 kJ mol−1). Compositions with up to 5% rhodium are thus stable at this temperature, which conforms with the pure oxide dissociating at 1400 K103 and the phase diagram by Muller and Roy.104 Unfortunately, neither of the expected103,104 Rh2O3 polymorphs is observed due to an overcorrection of RhO2 by −31.5 kJ mol−1.51,105 Indeed, Rh2O3 appears above 956 K, if the oxides are corrected individually based on their enthalpies of formation, which also widens the stable range to x ≈ 0.24 (see Fig. S10c and d, ESI†). According to Jacob et al.11 this is still too narrow, though. Finally, rhodium also forms a gaseous oxide similar to PtO2, whose formation is slightly more endothermic (ΔH0f = +173.2 kJ mol−1, ΔH0f,lit ≥ +188.9 kJ mol−1 ref. 59–61).
3.4.6 Oxidation of Cu in Pt-alloys.
Contrary to expectation the close relation of the copper oxides to superconductivity does not influence their thermodynamic properties noticeably. The remaining enthalpy errors of +9.9 kJ mol−1 (CuO) and +1.7 kJ mol−1 (Cu2O) per copper atom are however still large enough to lower the CuO–Cu2O-transition in Fig. 4b by roughly 230 K compared to the hypothetical literature value (at 1 bar CuO melts54 well before this happens). Consequently, the Gibbs free energies calculated for the oxidation of copper are likely too positive at high temperatures (+56.6 kJ mol−1 to −19.6 kJ mol−1 at 1300 K), while the low-temperature region remains mostly unaffected (−68.8 kJ mol−1 to −104.3 kJ mol−1 at 300 K). Indeed, the range of stable alloy compositions reduces to about 17% copper at 1300 K, if the oxide enthalpies are corrected individually (see Fig. S10a and b, ESI†). This is slightly smaller than the fully corrected rhodium alloy, which is however not as stable against platinum oxidation. Copper is thus the only element, that can potentially strengthen platinum without oxidizing itself (type wA/N).
3.4.7 Oxidation of Ni and Co in Pt-alloys.
Despite all similarities found for the cobalt- and nickel alloys (type wA/B and wA/N, see Fig. S3d and d, ESI†), the elements themselves behave rather differently, since nickel in contrast to cobalt avoids high oxidation states.106,107 Consequently, with Co3O4 a cobalt oxide with two different oxidation states is found to dominate over the whole temperature range, even though its calculated enthalpy of formation deviates by +36.3 kJ mol−1 per metal atom from to the literature value of −305.1 kJ mol−1.57 Given that the deviation53 of the prototypical charge-transfer insulators108–110 CoO and NiO is about twice as large, this is probably related to the self-interaction error.31 The Gibbs free energies of reaction calculated for Pt–Co (−210.5 kJ mol−1 to −225.3 kJ mol−1 at 300 K, −39.1 kJ mol−1 to −94.7 kJ mol−1 at 1300 K) and Pt–Ni (−111.7 kJ mol−1 to −132.7 kJ mol−1 at 300 K, +14.8 kJ mol−1 to −47.1 kJ mol−1 at 1300 K) are thus too low as well.
3.5 Electrochemical oxidation
Platinum and its alloys are highly relevant electrode materials, and electrooxidation of platinum-based catalyst materials is a frequently observed degradation mechanism, for example in fuel cells.111–114 To provide more insight into the thermodynamic behaviour of platinum-based alloys in this context, the model presented in the last sections was adapted to the electrochemical oxidation. This mainly requires the replacement of oxygen by liquid water, with electron holes acting as the electrochemical oxidizer. The Gibbs free energy of liquid water is approximated based on the vapour–liquid phase equilibrium| | 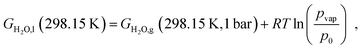 | (29) |
where pvap = 0.032 bar indicates the vapour pressure of water at room temperature and GH2O,g represents the calculated Gibbs free energy of a water molecule in the gas phase (see Section 2.4 for details). Only total oxidation is considered here, which is preferred for most metals investigated here at typical oxygen evolution (OER) overpotentials.115–118 In case of Nickel119 and Cobalt120 the hydroxides are not stable at strongly acidic conditions. Neither the formation of complex ions, nor the direct dissolution to metal ions, which are usually preferred instead, have been included in the calculations presented below.
The oxidation reaction of the released metal atom M, which can be either platinum or the alloying metal, thus reads
| |  | (V) |
Adapting the model of the computational hydrogen electrode,
121,122 the chemical potential of the protons is defined by the H
2/H
+-equilibrium. At standard conditions (
pH2 = 1 bar, pH = 0,
T = 298.15 and
U = 0 V relative to the standard hydrogen electrode), the Gibbs free energy of the protons is therefore identical to that of gaseous hydrogen, while increasing the voltage (
U) facilitates the electrochemical reduction of water. The total Gibbs free energy of reaction thus reads
| |  | (30) |
The dependence of the oxidation on voltage (
U) and pH is described by the Gibbs free energy of the electron transfer (
Ge), which is defined as:
| |  | (31) |
Eqn (31) is specified in kJ mol
−1 and therefore includes a conversion factor, where
F denotes Faraday's constant. The Gibbs free energy
G−M(
x,
T) needed to release a metal atom is calculated according to the
eqn (26) and (24) or (28), respectively, while the Gibbs free energies of the oxides are adopted from the previous sections. The pH is fixed to pH = 0.
Since the release of platinum from the alloy is modelled similarly to the thermal oxidation, the trend with regards to alloying is reproduced in case of the electrochemical oxidation. Fig. 5 illustrates this by plotting the Gibbs free energy of reaction for the oxidation of platinum in the tungsten alloy. As is evident from the more or less horizontal isolines, the dependence of ΔGU,Pt on x is weak compared to that on U. Due to the effect of alloying being even smaller for the other alloys, none of them are shown here (see the ESI,† for the respective diagrams). While the dependence on the pH is not plotted here in favour of the compositional dependence, a comparison to the Pourbaix diagram of platinum118 is still possible at x = 0 and U = 0, which reveals several differences. Most importantly, there is no dissolution of platinum around 1.0 V. Even though this is expected, as Pt2+ was neglected here, it is still not a sufficient explanation for the markedly lower metal–oxide phase transition at 0.81 V (solid black line at ΔGU,Pt = 0). Besides the enthalpies of formation of the platinum oxides themselves (see the discussion above about platinum oxidation or Table S1 in the ESI†), the lowering of the phase transition is probably caused by components of the calculation, which were not present in the dry reaction with oxygen, for example the energy of water vapour. Judging the quality of the latter requires a suitable comparison, for example the enthalpy of formation, which however also relies on the inaccurate energy of oxygen. Hence, no empirical correction was employed for the electrochemical reactions, even though some of the oxides have special electronic properties on their own. But since the oxide phases very likely differ in their DFT errors, the mean empirical correction cannot account for these deviations anyway. This is especially notable for PtO, which – in contrast to the thermal oxidation – is expected to separate solid PtO2 and the metallic state in absence of Pt2+. This intermediate phase is not observed here, since the PtO–PtO2 boundary (dashed line in Fig. 5) is shifted below the metal–oxide boundary. Lastly, some of the underlying assumptions of the electrode model probably contribute to the deviations as well.
 |
| | Fig. 5 Gibbs free energy for the electro-chemical oxidation of platinum (ΔGU,Pt) from within Pt–W per metal atom at 298.15 K and pH = 0 mapped onto alloy composition x and applied voltage U. Phases and their boundaries are signified in black. | |
The compositional dependence is generally slightly more pronounced for the oxidation of the second metal, where halving the platinum content shifts the isolines by roughly 0.1 V for the majority of the investigated alloys (the direction of the shift is determined by the mixing characteristics). Notable exceptions are the alloys of copper and tungsten (shown in Fig. 6b and c, respectively), the former of which features a transition to Cu2O, that increases the already larger gradient below 0.66 V, but is unstable with respect to the metallic phase. Pt–W in turn continues a trend already discussed above for the electrochemical oxidation of platinum, namely the emergence of additional intermediate oxide phases – in this case W18O49 (P2/m) between Pt–W and WO3 – below 0.04 V. In the case of rhenium (figure Fig. S7f, ESI†), two additional phases – ReO3 (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and ReO2 (Pbcn) – are observed below 0.89 V and 0.31 V, respectively (the alloy is stable below 0.29 V, depending on composition). The transition from Rh2O3 (Pbca) to RhO2 at U = 0.55 V, on the other hand, happens well below the metal–oxide transition below 0.60 V. The phases in the iridium (IrO2 above 0.56 V to 0.59 V), cobalt (Co3O4 above U = 0.41 V to 0.31 V) and nickel plots (NiO above 0.55 to 0.44 V) are the same as for the thermal oxidation (see Fig. S5f, S3f and S6f in the ESI†). The same is the case for the oxidation of gold (Au2O3-formation above 1.03 V, Fig. S2f, ESI†) and silver (Ag2O starting to form between 0.72 V and 0.83 V, Fig. S1f, ESI†). The comparability of these results to literature data is limited, since only x ≤ 0.5 was considered here. Moreover, Co,120 Ni,119 Cu,115 Ag118 and even Au118 are expected to dissolve at pH = 0, provided the applied potential is sufficiently large. This is neglected here, as is the formation of perrhenate ions117 in case of rhenium. The solid oxides are thus only relevant for the electrochemical oxidation of rhodium, iridium and tungsten.116,118
m) and ReO2 (Pbcn) – are observed below 0.89 V and 0.31 V, respectively (the alloy is stable below 0.29 V, depending on composition). The transition from Rh2O3 (Pbca) to RhO2 at U = 0.55 V, on the other hand, happens well below the metal–oxide transition below 0.60 V. The phases in the iridium (IrO2 above 0.56 V to 0.59 V), cobalt (Co3O4 above U = 0.41 V to 0.31 V) and nickel plots (NiO above 0.55 to 0.44 V) are the same as for the thermal oxidation (see Fig. S5f, S3f and S6f in the ESI†). The same is the case for the oxidation of gold (Au2O3-formation above 1.03 V, Fig. S2f, ESI†) and silver (Ag2O starting to form between 0.72 V and 0.83 V, Fig. S1f, ESI†). The comparability of these results to literature data is limited, since only x ≤ 0.5 was considered here. Moreover, Co,120 Ni,119 Cu,115 Ag118 and even Au118 are expected to dissolve at pH = 0, provided the applied potential is sufficiently large. This is neglected here, as is the formation of perrhenate ions117 in case of rhenium. The solid oxides are thus only relevant for the electrochemical oxidation of rhodium, iridium and tungsten.116,118
 |
| | Fig. 6 Gibbs free energy for the electro-chemical oxidation of the alloying metal (ΔGU,M) in Pt–Ir (a), Pt–Cu (b) and Pt–W (c) per metal atom at 298.15 K and pH = 0 mapped onto alloy composition x and applied voltage U. Phases and their boundaries are signified in black. | |
The low compositional dependence of the metal–oxide transition is also reflected by the intermetallic phases of the late 3d metals (see Table 2). Assuming total stoichiometric decomposition, the corresponding voltages are confined to a rather narrow interval of 0.17 V below the phase transition of pure platinum at 0.81 V (see x = 0 in Fig. 5 for comparison). Accordingly, the nobility-related drop between the Cu- and Co-compounds with like platinum concentration amounts to only 0.13 V even for the PtM with less platinum content. In contrast to this, Pt2W is only stable up to 0.33 V and PtW already decomposes at 0.09 V.
Table 2 Decomposition voltage Ud of the investigated intermetallic phases at 298.15 K assuming complete oxidation to the stable oxides at these conditions
| Compound |
Oxide 1 |
Oxide 2 |
U
d/[V] |
|
Structure distorted due to magnetic structure.
|
| Pt3Cu (Cmmm) |
PtO2 (Pnnm) |
CuO (C2/c) |
0.80 |
PtCu (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
PtO2 (Pnnm) |
CuO (C2/c) |
0.76 |
Pt3Ni (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
PtO2 (Pnnm) |
NiO (P2/m) |
0.77 |
| PtNi (P4/mmm) |
PtO (P42/mmc) |
NiO (P2/m) |
0.69 |
Pt3Co (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
PtO2 (Pnnm) |
Co3O4 (I41/amd)a |
0.76 |
| PtCo (P4/mmm) |
PtO (P42/mmc) |
Co3O4 (I41/amd)a |
0.63 |
| Pt2W (Immm) |
PtO (P42/mmc) |
WO3 (P21/c) |
0.33 |
PtW (P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2) m2) |
PtO (P42/mmc) |
WO3 (P21/c) |
0.09 |
4. Discussion
The oxidation of several platinum alloys was investigated based on their Gibbs free energy of mixing ΔGmix(x, T), which was modelled by combining the ideal mixing energy, interpolation from the pure metals and the ideal configurational entropy. It was observed, that the “alloyability” follows expected reactivity trends of the alloying metals. Thus, ΔGmix(x, T) of the gold alloy is positive and decreases towards copper and tungsten. This is also reflected by the tendency to form intermetallic phases. Hence, whereas the miscibility gabs observed for platinum alloys of the late 4d and 5d-elements (Au, Ir and Ag) highlights the repulsive interaction with platinum, the attractively mixing 3d-metals tend to form intermetallic phases. In case of the late 3d-metals this results in an order–disorder transition within the investigated temperature range.
The formation of gaseous PtO2 mirrors the mixing trends for most elements, since atom removal is modelled based on the nominal change in concentration. Thus, one might expect that releasing platinum – thereby increasing x – should be advantageous in case of attractively mixing alloys with high platinum content, since the initial mixing energy is less negative, than the final one. Instead, the opposite is true and platinum oxidation is related to the derivative of ΔGmix with respect to x. This apparent contradiction is resolved by considering ΔGmix as part of the binding energy of the released platinum atom. A notable conclusion to be drawn from this is that contrary to intuition very unreactive elements like gold are not suited to stabilize platinum against oxidation, since the stability of the latter in the alloy is not directly related to the that of the elements involved, but to their mixture.
Alloying platinum with one of the very early transition metals instead will not increase the catalyst durability either: while these elements are indeed capable of compensating the volatilization of PtO2, they have a strong affinity for oxygen themselves. In fact, the formation of – in some cases even volatile – oxides is favourable thermodynamically for most tested elements, thereby opening up another possible route for corrosion. Consequently, the compositional dependence opposes that of platinum oxidation in that higher x promotes oxidation of the second metal, thereby undermining the positive effects of alloying. Hence, alloyability and nobility of the alloying element need to be balanced.
Even though the above general trends still apply, the Ostwald process modifies some of the underlying conditions the results were obtained for. Besides the total pressure, whose influence is small despite covering a range of several bar in actual production plants7 (the entropy of oxygen decreases by only ∼20 J mol−1 K−1 at 10 bar and 1300 K), this is especially true considering the composition of the gas feed, which contains ammonia, nitric oxides, and water vapour. This has several possible effects: as for tungstic acid (H2WO4),100,101 the formation of volatile hydrides or hydrates might accelerate the volatilization. Indeed, our calculations suggest the formation of gaseous Pt(OH)2 from PtO2 and hydrogen to be exergonic even at 1300 K (−42.1 kJ mol−1). Replacing hydrogen by ammonia is expected to lower this Gibbs free energy of formation to about −116.0 kJ mol−1 due to its endergonic formation at this temperature. Hydrates like Pt(OH)4, on the other hand, are found to be unstable already at comparatively low temperatures. However, such species could be formed at the surfaces of platinum as intermediates during the formation of the volatile PtO2 or Pt(OH)2. Likewise, the amount of surface sites available for oxygen decreases due to the presence of other adsorbates. Since oxygen competes with other reactants for sites, the prediction of corrosion rates requires a more complete picture of the catalytic reaction mechanism than considered here. While the role of the surface in corrosion cannot be overstated, the overall thermodynamic stability of the material is governed by its bulk properties, as is reflected by the total Gibbs free energy. This study identifies two alloys that significantly enhance the stability of platinum in the bulk: Pt–Cu and Pt–W. The following detailed literature discussion about their properties also includes surface information that might impact the above findings.
4.1 Pt–Cu
Considering only the oxidation of the platinum atoms, all late 3d alloys are calculated to outperform the rhodium alloy (Fig. 7b) in terms of suppressing the formation of PtO2. In this group, copper optimizes the stability of platinum, despite being the noblest of the three metals. Still, the available concentration range is limited by its oxidation, whose dependence on x opposes that of the platinum and can not be extended by taking advantage of the order–disorder transition, since lowering the operational temperature also decreases the selectivity of the ammonia oxidation reaction. Moreover, intermetallic phases tend to be brittle due to decreased dislocation mobility and/or reduced grain boundary cohesion,123 even though the L13 and L11 phases of Pt3Cu82–84 and PtCu72,83,84 are both superstructures of the fcc random alloy. Given the knitted design of modern ammonia oxidation catalysts,7 this might pose a problem for manufacturing.
 |
| | Fig. 7 Gibbs free energy of mixing (ΔGmix, a), Gibbs free energy of PtO2 formation (ΔGr,PtO2, b) and Gibbs free energy of rhodium oxidation (ΔGr,Rh, c) of Pt–Rh metal atom. Phases and their boundaries are signified in black. | |
As is the case for rhodium, platinum-copper alloys are subject to surface segregation. But unlike Pt–Rh13–16,124–126 (and most127,128 other platinum alloys) copper is usually found atop,128–134 even though contradicting measurements135,136 and some calculations127 indicate the segregation tendency to be weak. Cluster expansion calculations of nanoparticles by Li et al.137 suggest, that the presence of oxygen suppresses the preference for platinum segregation at high platinum content due to the stronger oxygen affinity of copper. Not only does this possibly reduce the catalyst activity, it also has implications for stability, since surface atoms are likely more prone to oxidation.
Being situated in the bulk does however not protect the copper atoms either, since noble metal alloys are known to oxidize from within (“internal oxidation”),138–141 which has also been discussed for Pt–Cu.142 Even without alloying, platinum has the ability to reversibly integrate oxygen into its structure.4,12 The latter probably involves a place-exchange of adsorbed oxygen and surface platinum discussed143–147 in the context of Pt-electrode degradation or interstitial absorption of oxygen atoms148,149 at high surface-occupation, both of which might be important for PtO2 formation as well.
Fortunately, DFT calculations150–153 suggest, that alloying platinum with more electropositive elements electronically saturates it, thereby also reducing its interaction with oxygen. Moreover, segregation of platinum to the surface might limit copper oxidation due to the subsurface platinum acting as a diffusion barrier154 (copper atoms can however leave the surface on their own to oxidize on top, as was found by Luo et al.155,156 for copper containing up to 10% platinum).
4.2 Pt–W
The strongly attractive interaction of tungsten with platinum stabilizes the latter even more against volatilization than copper. Accordingly, the intermetallic phase at x = 1/3, which likely crystallizes in a fcc-like superstructure75,157 as well, was found to be stable over the whole temperature interval. Unlike for copper, however, the calculated Gibbs free energy of mixing of the tungsten alloy decreases rapidly, when approaching the intermetallic composition, which might affect the catalyst stability negatively, if the intermetallic phase cannot be realized for whatever reason. At the same time, the strong compositional dependence at low x can be utilized to leverage the effect of alloying, while still retaining high platinum content. This might be useful to maintain the catalytical properties.
While tungsten is famous for its high thermal and chemical resistance, the latter is based on surface passivation rather than extraordinary thermodynamic stability, as is evident from the highly exergonic oxidation. And although calculations by Ruban et al.128 predict platinum segregation for Pt–W, it is known from Pt–Rh, that the presence of oxygen can not only influence, but reverse segregation tendencies.13,14 Considering the presence of oxygen, it is therefore likely that tungsten will segregate to the surface and passivate it, which will also alter the catalytic properties. Indeed, WO3 is used as promoter for the NH3-based selective catalytic reduction of NO to N2,158 which suggests it to be inactive, if not detrimental to the Ostwald process. Finally, tungsten is also known to be volatile, which is caused by a multitude of molecular oxide species102 and accelerated in presence of water vapour due to the formation of tungstic acid (H2WO4), which was neglected here.100,101,159
The benefit of alloying platinum with tungsten in the context of the Ostwald process is therefore dependant on the presence of WO3 on the surface, and its properties. If passivation of the catalyst indeed occurs, a strategy to circumvent this problem could be utilizing the very strong effect of tungsten on platinum by only alloying the surface or subsurface with small amounts of it to minimize the amount of tungsten at the surface and its thermodynamic oxidation tendency, as well as its volatility. If, on the other hand, the catalyst remains active despite passivation, the high affinity of tungsten for oxygen would be turned into an advantage, since this would allow for alloy optimization based on other criteria. According to a directed literature search, neither the alloy of tungsten, nor that of copper have been tested for the Ostwald process so far.
5. Summary and conclusion
Platinum alloys of several transition metals have been investigated using density functional theory and ab initio thermodynamics to identify elements that thermodynamically stabilize platinum against the formation of volatile PtO2, which is assumed to mediate the extensive reconstruction of the platinum catalyst in the Ostwald process. It was found that for platinum-rich alloys a high resistance to platinum oxidation is associated with a negative Gibbs energy of mixing, which is however also correlated with a high reactivity of the alloying element. Conversely, the repulsive interaction of very noble elements like gold pushes platinum out of the alloy, thereby facilitating its oxidation. The oxidation tendencies of platinum and the alloying element thus oppose each other and cannot be separated, but only optimized, which limits the overall stability of the alloy and introduces a concentration dependence. Still, alloying is a viable strategy to inhibit platinum oxidation and volatilization under harsh oxidizing conditions, if the affinities of the alloying element for platinum and oxygen are well-balanced. Based on the thermodynamic stability, the platinum alloy of copper is expected to be the most promising candidate in this regard.
Conversely, the elements that can compensate most of the PtO2 vapour pressure at temperatures as high as 1300 K – tungsten and rhenium – are prone to oxidation themselves. The formation of gaseous Re2O7(g) even at moderate temperatures, for instance, rules out the use of Pt–Re alloys for the intended application as a catalyst in the Ostwald process. The lower volatility of tungsten oxides, on the other hand, makes Pt–W an interesting candidate, if the expected passivation of the surface does not affect ammonia oxidation negatively. Rhodium is thus neither the only, nor the optimal alloying element to suppress platinum corrosion.
Data availability
The raw D3/BJ-corrected energies and structures are publicly available at the NOMAD data repository (DOI: 10.17172/NOMAD/2024.08.22-1, Dataset ID: vU6ILzWbROCinlWCLXRZcQ). A second dataset created for raw PBE-data without dispersion correction (DOI: 10.17172/NOMAD/2024.08.21-1, Dataset ID: hwdvWSk6TeaCM5d70F8q_Q) additionally contains either phonopy output files for the regular solid phases (raw thermodynamic results and the force sets to recreate them) or – in case of gaseous phases – vibrational data obtained directly with VASP. The thermodynamic data of the pure phases was processed using two custom scripts based on bash 4.4.20(1), gawk 4.2.1 and gnuplot 5.2, which are available at github (https://github.com/axkf/HEATh, last accessed at 02.09.2024, and https://github.com/axkf/HEATher, last accessed at 02.09.2024). The script used for combining the latter results with the alloy data is not easily portable and therefore not published at the moment. The procedure is however described in detail within the article.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
A. Kafka acknowledges funding for this project by the Fund of the German Chemical Industry (“Fonds der Chemischen Industrie”) with a Liebig Fellowship.
References
- L. B. Hunt, Platinum Met. Rev., 1958, 2, 129–134 CrossRef.
- F. Kuhlmann, Ann. Pharm., 1839, 29, 272–291 CrossRef.
- W. Ostwald, Berg- und Hüttenm. Rsch., 1906, 20, 16 Search PubMed.
-
R. Krähnert, PhD thesis, Technische Universität, Berlin, 2005.
- O. Nilsen, A. Kjekshus and H. Fjellvåg, Appl. Catal., A, 2001, 207, 43–54 CrossRef CAS.
- R. Imbihl, A. Scheibe, Y. F. Zeng, S. Günther, R. Krähnert, V. A. Kondratenko, M. Baerns, W. K. Offermans, A. P. J. Jansen and R. A. van Santen, Phys. Chem. Chem. Phys., 2007, 9, 3522–3540 RSC.
- J. Ashcroft, Johnson Matthey Technol. Rev., 2021, 65, 44–53 CrossRef.
- L. Hannevold, O. Nilsen, A. Kjekshus and H. Fjellvåg, Appl. Catal., A, 2005, 284, 163–176 CrossRef.
- J. Pura, P. Wiecinski, P. Kwasniak, M. Zwolinska, H. Garbacz, J. Zdunek, Z. Laskowski and M. Gierej, Appl. Surf. Sci., 2016, 388, 670–677 CrossRef.
- L. Hannevold, O. Nilsen, A. Kjekshus and H. Fjellvåg, J. Cryst. Growth, 2005, 279, 206–212 CrossRef.
- K. T. Jacob, S. Priya and Y. Waseda, Bull. Mater. Sci., 1998, 21, 99–103 CrossRef.
- L. R. Velho and R. W. Bartlett, Metall. Trans., 1972, 3, 65–72 CrossRef.
- F. C. M. J. M. van Delft, B. E. Nieuwenhuys, J. Siera and R. M. Wolf, ISIJ Int., 1989, 29, 550–559 CrossRef.
- B. Moest, S. Helfensteyn, P. Deurinck, M. Nelis, A. W. Denier van der Gon, H. H. Brongersma, C. Creemers and B. E. Nieuwenhuys, Surf. Sci., 2003, 536, 177–190 CrossRef.
- S. Müller, M. Stöhr and O. Wieckhorst, Appl. Phys. A: Mater. Sci. Process., 2006, 82, 415–419 CrossRef.
- K. Yuge, A. Seko, A. Kuwabara, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 174202 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef.
- G. Kresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245–8257 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- J. D. Pack and H. J. Monkhorst, Phys. Rev. B: Condens. Matter Mater. Phys., 1977, 16, 1748–1749 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- Z. Wu and R. E. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235116 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- J. Zaanen, G. A. Sawatzky and J. W. Allen, Phys. Rev. Lett., 1985, 55, 418–421 CrossRef CAS.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- J. W. Arblaster, Platinum Met. Rev., 1996, 40, 62–63 CrossRef.
- E. H. P. Cordfunke, Thermochim. Acta, 1981, 50, 177–185 CrossRef.
- H. S. C. O’Neill and J. Nell, Geochim. Cosmochim. Acta, 1997, 61, 5279–5293 CrossRef.
- J. W. Arblaster, CALPHAD, 1996, 20, 343–352 CrossRef.
- K. T. Jacob, S. Mishra and Y. Waseda, Thermochim. Acta, 2000, 348, 61–68 CrossRef.
- M. I. Pownceby and H. S. C. O’Neill, Contrib. Mineral. Petrol., 1994, 118, 130–137 CrossRef.
-
E. G. King, R. V. Mrazek and D. W. Richardson, Heats of Formation of three Oxides of Rhenium, Dept. of the Interior, Bureau of Mines, Washington, DC, 1969 Search PubMed.
-
J. M. Stuve and M. J. Ferrante, Thermodynamic properties of rhenium oxides, 8 to 1,400 K, Dept. of the Interior, Bureau of Mines, Washington, DC, 1976 Search PubMed.
- H. Oppermann, Z. Anorg. Allg. Chem., 1985, 523, 135–144 CrossRef.
- J. W. Arblaster, J. Phase Equilib. Diffus., 2018, 39, 891–907 CrossRef.
- T. V. Charlu and O. J. Kleppa, J. Chem. Thermodyn., 1973, 5, 325–330 CrossRef.
-
M. W. J. Chase, NIST-JANAF Thermochemical Tables, American Institute of Physics, Washington, DC, 4th edn, 1998 Search PubMed.
- B.-y Han, A. V. Khoroshilov, A. V. Tyurin, A. E. Baranchikov, M. I. Razumov, O. S. Ivanova, K. S. Gavrichev and V. K. Ivanov, J. Therm. Anal. Calorim., 2020, 142, 1533–1543 CrossRef.
- J. W. Arblaster, J. Phase Equilib. Diffus., 2015, 36, 573–591 CrossRef.
- J. Assal, B. Hallstedt and L. J. Gauckler, J. Am. Ceram. Soc., 1997, 80, 3054–3060 CrossRef.
- K. T. Jacob, T. Uda, T. H. Okabe and Y. Waseda, High. Temp. Mater. Pr.-ISR, 2000, 19, 11–16 Search PubMed.
- J. Nell and H. S. C. O’Neill, Geochim. Cosmochim. Acta, 1997, 61, 4159–4171 CrossRef.
- K. T. Jacob and D. Prusty, J. Alloys Compd., 2010, 507, L17–L20 CrossRef.
- J. W. Arblaster, J. Phase Equilib. Diffus., 2015, 36, 422–444 CrossRef.
- R. D. Holmes, H. S. C. O’Neill and R. J. Arculus, Geochim. Cosmochim. Acta, 1986, 50, 2439–2452 CrossRef.
- B. Hallstedt, D. Risold and L. J. Gauckler, J. Phase Equilib., 1994, 15, 483–499 CrossRef.
- P. D. Desai, Int. J. Thermophys., 1987, 8, 763–780 CrossRef.
- A. Fernández Guillermet, Int. J. Thermophys., 1987, 8, 481–510 CrossRef.
- M. Chen, B. Hallstedt and L. J. Gauckler, J. Phase Equilib., 2003, 24, 212–227 CrossRef.
- H. S. C. O’Neill, Am. Mineral., 1987, 72, 280–291 Search PubMed.
- C. B. Alcock and G. W. Hooper, Proc. R. Soc. London, Ser. A, 1960, 254, 551–561 Search PubMed.
- C. B. Alcock, Platinum Met. Rev., 1961, 5, 134–139 CrossRef.
- A. Olivei, J. Less-Common Met., 1972, 29, 11–23 CrossRef.
- J. H. Carpenter, J. Less-Common Met., 1989, 152, 35–45 CrossRef CAS.
- A. Togo, J. Phys. Soc. Jpn., 2023, 92, 012001 CrossRef.
- A. Togo, L. Chaput, T. Tadano and I. Tanaka, J. Phys.: Condens. Matter, 2023, 35, 353001 CrossRef CAS PubMed.
- C. H. Shomate, J. Am. Chem. Soc., 1944, 66, 928–929 CrossRef CAS.
- C. H. Shomate, J. Phys. Chem., 1954, 58, 368–372 CrossRef CAS.
-
K. K. Irikura, in Computational Thermochemistry, ed. K. K. Irikura and D. J. Frurip, American Chemical Society, Washington, DC, 1998, of ACS Symposium Series, ch. 22, vol. 677, pp. 402–418 Search PubMed.
- A. Zunger, S.-H. Wei, L. G. Ferreira and J. E. Bernard, Phys. Rev. Lett., 1990, 65, 353–356 CrossRef CAS PubMed.
- D. Gehringer, M. Friák and D. Holec, Comput. Phys. Commun., 2023, 286, 108664 CrossRef CAS.
- A. van de Walle, JOM, 2013, 65, 1523–1532 CrossRef CAS.
- T. Abe, B. Sundman and H. Onodera, J. Phase Equilib. Diffus., 2006, 27, 5–13 CrossRef CAS.
- C. Mshumi, C. I. Lang, L. R. Richey, K. C. Erb, C. W. Rosenbrock, L. J. Nelson, R. R. Vanfleet, H. T. Stokes, B. J. Campbell and G. L. W. Hart, Acta Mater., 2014, 73, 326–336 CrossRef CAS.
- A. A. Popov, A. D. Varygin, P. E. Plyusnin, M. R. Sharafutdinov, S. V. Korenev, A. N. Serkova and Y. V. Shubin, J. Alloys Compd., 2022, 891, 161974 CrossRef.
- H. Okamoto, J. Phase Equilib. Diffus., 2019, 40, 743–756 CrossRef.
- P. Kiruthika and A. Paul, J. Phase Equilib. Diffus., 2014, 35, 36–42 CrossRef.
- O. Levy, M. Jahnátek, R. V. Chepulskii, G. L. W. Hart and S. Curtarolo, J. Am. Chem. Soc., 2010, 133, 158–163 CrossRef PubMed.
- X.-N. Xu, Y.-P. Ren, C.-F. Li, S. Li and G.-W. Qin, Trans. Nonferrous Met. Soc. China, 2012, 22, 1432–1436 CrossRef.
- H. Okamoto, J. Phase Equilib. Diffus., 2014, 35, 208–219 CrossRef CAS.
- L. Cao, C. Li and T. Mueller, J. Chem. Inf. Model., 2018, 58, 2401–2413 CrossRef CAS PubMed.
- A. G. Knapton, Platinum Met. Rev., 1980, 24, 64–69 CrossRef CAS.
- G. L. W. Hart, L. J. Nelson, R. R. Vanfleet, B. J. Campbell, M. H. F. Sluiter, J. H. Neethling, E. J. Olivier, S. Allies, C. I. Lang, B. Meredig and C. Wolverton, Acta Mater., 2017, 124, 325–332 CrossRef CAS.
- R. S. Irani and R. W. Cahn, J. Mater. Sci., 1973, 8, 1453–1472 CrossRef CAS.
- V. V. Kulagina, A. A. Chaplygina, L. A. Popova, M. D. Starostenkov, A. I. Potekaev and A. A. Klopotov, Russ. Phys. J., 2012, 55, 814–824 CrossRef CAS.
- L. J. Nelson, G. L. W. Hart and S. Curtarolo, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 054203 CrossRef.
- C. E. Dahmani, M. C. Cadeville, J. M. Sanchez and J. L. Morán-López, Phys. Rev. Lett., 1985, 55, 1208–1211 CrossRef.
- H. Okamoto, J. Phase Equilib. Diffus., 2010, 31, 322 CrossRef.
- R. J. Berry, Surf. Sci., 1978, 76, 415–442 CrossRef.
- A. Punnoose, M. S. Seehra and I. Wender, Fuel Process. Technol., 2001, 74, 33–47 CrossRef.
- Q. Chen and Y. Yang, Comput. Mater. Sci., 2020, 180, 109708 CrossRef.
- N. Seriani, W. Pompe and L. C. Ciacchi, J. Phys. Chem. B, 2006, 110, 14860–14869 CrossRef CAS PubMed.
- C.-B. Wang, H.-K. Lin, S.-N. Hsu, T.-H. Huang and H.-C. Chiu, J. Mol. Catal. A: Chem., 2002, 188, 201–208 CrossRef CAS.
- M. Citir, R. B. Metz, L. Belau and M. Ahmed, J. Phys. Chem. A, 2008, 112, 9584–9590 CrossRef CAS PubMed.
- R. H. Busey, J. Am. Chem. Soc., 1956, 78, 3263–3266 CrossRef CAS.
- H. A. Wriedt, Bull. Alloy Phase Diagrams, 1989, 10, 368–384 CrossRef CAS.
-
G. K. Schwenke, Proceedings of the 15th International Plansee Seminar, Reutte, 2001, pp. 647–661 Search PubMed.
- S. C. Cifuentes, M. A. Monge and P. Pérez, Corros. Sci., 2012, 57, 114–121 CrossRef CAS.
- J. Habainy, S. Iyengar, K. B. Surreddi, Y. Lee and Y. Dai, J. Nucl. Mater., 2018, 506, 26–34 CrossRef CAS.
- K. R. Locherer, I. P. Swainson and E. K. H. Salje, J. Phys.: Condens. Matter, 1999, 11, 6737–6756 CrossRef CAS.
- C. C. Mardare and A. W. Hassel, Phys. Status Solidi A, 2019, 216, 1900047 CrossRef.
- G. R. Belton and R. L. McCarron, J. Phys. Chem., 1964, 68, 1852–1856 CrossRef CAS.
- T. Millner and J. Neugebauer, Nature, 1949, 163, 601–602 CrossRef CAS.
- P. O. Schissel and O. C. Trulson, J. Chem. Phys., 1965, 43, 737–743 CrossRef CAS.
- G. Bayer and H. G. Wiedemann, Thermochim. Acta, 1976, 15, 213–226 CrossRef.
- O. Muller and R. Roy, J. Less-Common Met., 1968, 16, 129–146 CrossRef.
- S. Gossé, S. Bordier, C. Guéneau, E. Brackx, R. Domenger and J. Rogez, J. Nucl. Mater., 2018, 500, 252–264 CrossRef.
- J. P. Neumann, T. Zhong and Y. A. Chang, Bull. Alloy Phase Diagrams, 1984, 5, 141–144 CrossRef.
- J. R. Taylor and A. T. Dinsdale, Int. J. Mater. Res., 1990, 81, 354–366 CrossRef.
- A. Fujimori and F. Minami, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 957–971 CrossRef.
- G. A. Sawatzky and J. W. Allen, Phys. Rev. Lett., 1984, 53, 2339–2342 CrossRef.
- Z.-X. Shen, J. W. Allen, P. A. P. Lindberg, D. S. Dessau, B. O. Wells, A. Borg, W. Ellis, J. S. Kang, S.-J. Oh, I. Lindau and W. E. Spicer, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 1817–1828 CrossRef.
- N. Arulmozhi, D. Esau, R. P. Lamsal, D. Beauchemin and G. Jerkiewicz, ACS Catal., 2018, 8, 6426–6439 CrossRef.
- S. Cherevko, N. Kulyk and K. J. J. Mayrhofer, Nano Energy, 2016, 29, 275–298 CrossRef.
- M. J. Eckl, Y. Mattausch, C. K. Jung, S. Kirsch, L. Schmidt, G. Huebner, J. E. Mueller, L. A. Kibler and T. Jacob, Electrochem. Sci. Adv., 2021, 2, e2100049 CrossRef.
- J. Zhang, Y. Yuan, L. Gao, G. Zeng, M. Li and H. Huang, Adv. Mater., 2021, 33, 2006494 CrossRef.
- B. Beverskog and I. Puigdomenech, J. Electrochem. Soc., 1997, 144, 3476–3483 CrossRef.
- M. I. Nave and K. G. Kornev, Metall. Mater. Trans. A, 2017, 48, 1414–1424 CrossRef.
- P. A. Nikolaychuk, Chem. Thermodyn. Thermal Anal., 2022, 7, 100068 CrossRef.
- M. Schalenbach, O. Kasian, M. Ledendecker, F. D. Speck, A. M. Mingers, K. J. J. Mayrhofer and S. Cherevko, Electrocatalysis, 2018, 9, 153–161 CrossRef.
- B. Beverskog and I. Puigdomenech, Corros. Sci., 1997, 39, 969–980 CrossRef.
- J. Chivot, L. Mendoza, C. Mansour, T. Pauporté and M. Cassir, Corros. Sci., 2008, 50, 62–69 CrossRef.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- J. Rossmeisl, A. Logadottir and J. K. Nørskov, Chem. Phys., 2005, 319, 178–184 CrossRef.
- C. T. Liu and J. O. Stiegler, Science, 1984, 226, 636–642 CrossRef PubMed.
- D. Brown, P. D. Quinn, D. P. Woodruff, T. C. Q. Noakes and P. Bailey, Surf. Sci., 2002, 497, 1–12 CrossRef.
- J. Florencio, D. M. Ren and T. T. Tsong, Surf. Sci., 1996, 345, L29–L33 CrossRef.
- T. T. Tsong, D. M. Ren and M. Ahmad, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 7428–7435 CrossRef CAS.
- Y. Ma and P. B. Balbuena, Surf. Sci., 2008, 602, 107–113 CrossRef.
- A. V. Ruban, H. L. Skriver and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 15990–16000 CrossRef.
- M. J. Kelley, D. G. Swartzfager and V. S. Sundaram, J. Vac. Sci. Technol., 1979, 16, 664–667 CrossRef.
- Y. G. Shen, D. J. O’onnor and K. Wandelt, Surf. Sci., 1998, 406, 23–31 CrossRef.
- Y. G. Shen, D. J. O’Connor and K. Wandelt, Surf. Sci., 1998, 410, 1–14 CrossRef.
- Y. G. Shen, D. J. O’Connor, K. Wandelt and R. J. MacDonald, Surf. Sci., 1995, 328, 21–31 CrossRef.
- A. D. van Langeveld and V. Ponec, Appl. Surf. Sci., 1983, 16, 405–423 CrossRef.
- A. D. van Langeveld and V. Ponec, Surf. Sci., 1983, 126, 702–707 CrossRef.
- Y. Gauthier, A. Senhaji, B. Legrand, G. Tréglia, C. Becker and K. Wandelt, Surf. Sci., 2003, 527, 71–79 CrossRef.
- R. Yang, P. Strasser and M. F. Toney, J. Phys. Chem. C, 2011, 115, 9074–9080 CrossRef.
- C. Li, D. Raciti, T. Pu, L. Cao, C. He, C. Wang and T. Mueller, J. Phys. Chem. C, 2018, 122, 18040–18047 CrossRef.
- D. L. Douglass, Oxid. Met., 1995, 44, 81–111 CrossRef CAS.
-
R. A. Rapp, in Encyclopedia of Materials: Science and Technology, ed. K. H. J. Buschow, R. W. Cahn, M. C. Flemings, B. Ilschner, E. J. Kramer, S. Mahajan and P. Veyssière, Elsevier, Oxford, 2001, pp. 4265–4268 Search PubMed.
- F. H. Stott and G. C. Wood, Mater. Sci. Technol., 1988, 4, 1072–1078 CrossRef CAS.
- C. Wagner, Z. Elektrochem., 1959, 63, 772–782 CrossRef CAS.
- C. Wagner, Corros. Sci., 1968, 8, 889–893 CrossRef CAS.
- Z. Nagy and H. You, Electrochim. Acta, 2002, 47, 3037–3055 CrossRef.
- G. Jerkiewicz, G. Vatankhah, J. Lessard, M. P. Soriaga and Y.-S. Park, Electrochim. Acta, 2004, 49, 1451–1459 Search PubMed.
- A. A. Topalov, S. Cherevko, A. R. Zeradjanin, J. C. Meier, I. Katsounaros and K. J. J. Mayrhofer, Chem. Sci., 2014, 5, 631–638 RSC.
- D. Fantauzzi, J. E. Mueller, L. Sabo, A. C. T. van Duin and T. Jacob, ChemPhysChem, 2015, 16, 2797–2802 CrossRef.
- M. J. Eslamibidgoli and M. H. Eikerling, Electrocatalysis, 2016, 7, 345–354 CrossRef.
- Z. Gu and P. B. Balbuena, J. Phys. Chem. C, 2007, 111, 9877–9883 CrossRef CAS.
- Z. Gu and P. B. Balbuena, J. Phys. Chem. C, 2007, 111, 17388–17396 CrossRef CAS.
- Z. Gu and P. B. Balbuena, J. Phys. Chem. C, 2008, 112, 5057–5065 CrossRef CAS.
- Y. Ma and P. B. Balbuena, J. Phys. Chem. C, 2008, 112, 14520–14528 CrossRef CAS.
- Y. Ma and P. B. Balbuena, Surf. Sci., 2009, 603, 349–353 CrossRef CAS.
- Y. Ma and P. B. Balbuena, J. Electrochem. Soc., 2010, 157, B959 CrossRef.
- C. Li, Y. Zhu, D. Wu, J. A. Boscoboinik and G. Zhou, Phys. Rev. Mater., 2022, 6, 025801 CrossRef.
- L. Luo, Y. Kang, J. C. Yang, D. Su, E. A. Stach and G. Zhou, Appl. Phys. Lett., 2014, 104, 121601 CrossRef.
- L. Luo, Y. Kang, J. C. Yang and G. Zhou, J. Appl. Phys., 2015, 117, 065305 CrossRef.
- A. Fernández Guillermet, V. Ozolinš, G. Grimvall and M. Körling, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 10364–10374 CrossRef PubMed.
- F. Can, X. Courtois and D. Duprez, Catalysts, 2021, 11, 703 CrossRef CAS.
- P. J. Meschter, E. J. Opila and N. S. Jacobson, Annu. Rev. Mater. Res., 2013, 43, 559–588 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: A complete set of figures for each element and a summary of the thermodynamic properties at 298.15 K, as well as the corresponding fit parameters of the regular solid phases between 300 K and 1300 K. The calculated energies, thermodynamic properties and fit parameters are also available as data files. See DOI: https://doi.org/10.1039/d4cp01807a |
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Franziska
Hess
and
Franziska
Hess
 *
*

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and Fm
m and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m to I41/amd and P2/m for Co3O4 and CoO/NiO). While all calculations were conducted employing the spin-unrestricted scheme, in some cases the structures had to be pre-relaxed with a set total spin. Especially some of the cobalt alloys were found to not converge without this treatment. Still, the ground state was not found in all cases, which results in a comparatively large scattering of the Pt–Co energies. In contrast, the geometries and energies of molecular phases were determined for fixed integer values of the total spin. Several values were tested for each species and the following magnetic moments were determined: PtO2 (0μB), IrO2 (1μB), IrO3 (1μB), Re2O7 (0μB), WO2 (0μB), WO3 (0μB), RhO2 (1μB).
m to I41/amd and P2/m for Co3O4 and CoO/NiO). While all calculations were conducted employing the spin-unrestricted scheme, in some cases the structures had to be pre-relaxed with a set total spin. Especially some of the cobalt alloys were found to not converge without this treatment. Still, the ground state was not found in all cases, which results in a comparatively large scattering of the Pt–Co energies. In contrast, the geometries and energies of molecular phases were determined for fixed integer values of the total spin. Several values were tested for each species and the following magnetic moments were determined: PtO2 (0μB), IrO2 (1μB), IrO3 (1μB), Re2O7 (0μB), WO2 (0μB), WO3 (0μB), RhO2 (1μB).



 of −38.27 kJ mol−1 per metal atom (0 kJ mol−1 for electrochemical reactions) to Hvib(T), one obtains the total enthalpy
of −38.27 kJ mol−1 per metal atom (0 kJ mol−1 for electrochemical reactions) to Hvib(T), one obtains the total enthalpy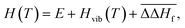










![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2S + 1)
ln(2S + 1)

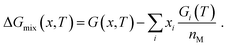
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m)72,83,84 for Pt3Cu and PtCu (please see Table S1 in the ESI† for a complete listing of all considered phases and their thermodynamic properties). Still, the order–disorder transition at 50% copper occurs almost 200 K lower than expected71 (no data was found for Pt3Cu), supporting the notion expressed earlier for Pt–Au and Pt–Ir that the stability of the random alloys is overestimated.
m)72,83,84 for Pt3Cu and PtCu (please see Table S1 in the ESI† for a complete listing of all considered phases and their thermodynamic properties). Still, the order–disorder transition at 50% copper occurs almost 200 K lower than expected71 (no data was found for Pt3Cu), supporting the notion expressed earlier for Pt–Au and Pt–Ir that the stability of the random alloys is overestimated.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) sets in 450 K too low, whereas the transition at 50% to the L10 structure (P4/mmm) deviates by 400 K from the experimental phase diagram.74 The analogous nickel deviations of +110 K for PtNi and −40 K for Pt3Ni on the other hand compare much better to the literature.73,85,86
m) sets in 450 K too low, whereas the transition at 50% to the L10 structure (P4/mmm) deviates by 400 K from the experimental phase diagram.74 The analogous nickel deviations of +110 K for PtNi and −40 K for Pt3Ni on the other hand compare much better to the literature.73,85,86
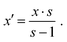


![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), β-PtO2 (Pnnm), Pt3O4 (Pm
m), β-PtO2 (Pnnm), Pt3O4 (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n) and PtO (P42/mmc) – were considered as possible oxidation products. Reproducing their very different structures and properties correctly requires the inclusion of dispersion forces, which especially lowers the relative stability of the gaseous- and the layered a-modifications of PtO2 in accordance with their lower mass density. In the present case, the D3/BJ approach by Grimme et al.26,27 was chosen to complement the PBE density functional. Consequently, only two oxides are observed in Fig. 3: β-PtO2 is predicted to be stable at low temperatures. At 663 K the rapidly growing gas-phase entropy of oxygen causes some of it to be released from the solid. The resulting Pt3O4 is then stable again up to 1094 K in case of pure platinum (x = 0), where it finally decomposes. Unfortunately, experimental data on the phase transitions between platinum oxides is sparse, especially at moderate or low temperatures and pressures, where equilibration is difficult. Electrical resistance measurements by Berry87 suggest a decomposition of β-PtO2 between 870 K and 920 K. This is consistent with more recent thermogravimetric results by Punnose et al.,88 who additionally found Pt3O4 between 908 K and 1073 K. Both measurements were conducted in air, where the transition temperatures are lower than in pure oxygen due to the lower partial pressure. A comparison to other theoretical results, like that of Chen and Yang89 or Seriani et al.,90 is difficult due to differences in the employed models, since either the phonon contribution or the corrections of the DFT oxygen and oxide energies are missing. The seemingly better Pt3O4-boundary temperatures of 870 K and 970 K by Seriani et al.90 might thus be coincidental and caused by error cancellation. The corrected values for (β-)PtO2 and Pt3O4 calculated here differ by about −10.1 kJ mol−1 and +12.0 kJ mol−1 per platinum atom, respectively, compared to the empirical relation proposed by Wang et al.91 for example (please see the Table S1 for a complete list of all thermodynamic properties, ESI†). The combined deviation can easily cause a boundary shift of the observed magnitude. It needs to be kept in mind, though, that the metal–oxide transition is much more important for the present investigation.
n) and PtO (P42/mmc) – were considered as possible oxidation products. Reproducing their very different structures and properties correctly requires the inclusion of dispersion forces, which especially lowers the relative stability of the gaseous- and the layered a-modifications of PtO2 in accordance with their lower mass density. In the present case, the D3/BJ approach by Grimme et al.26,27 was chosen to complement the PBE density functional. Consequently, only two oxides are observed in Fig. 3: β-PtO2 is predicted to be stable at low temperatures. At 663 K the rapidly growing gas-phase entropy of oxygen causes some of it to be released from the solid. The resulting Pt3O4 is then stable again up to 1094 K in case of pure platinum (x = 0), where it finally decomposes. Unfortunately, experimental data on the phase transitions between platinum oxides is sparse, especially at moderate or low temperatures and pressures, where equilibration is difficult. Electrical resistance measurements by Berry87 suggest a decomposition of β-PtO2 between 870 K and 920 K. This is consistent with more recent thermogravimetric results by Punnose et al.,88 who additionally found Pt3O4 between 908 K and 1073 K. Both measurements were conducted in air, where the transition temperatures are lower than in pure oxygen due to the lower partial pressure. A comparison to other theoretical results, like that of Chen and Yang89 or Seriani et al.,90 is difficult due to differences in the employed models, since either the phonon contribution or the corrections of the DFT oxygen and oxide energies are missing. The seemingly better Pt3O4-boundary temperatures of 870 K and 970 K by Seriani et al.90 might thus be coincidental and caused by error cancellation. The corrected values for (β-)PtO2 and Pt3O4 calculated here differ by about −10.1 kJ mol−1 and +12.0 kJ mol−1 per platinum atom, respectively, compared to the empirical relation proposed by Wang et al.91 for example (please see the Table S1 for a complete list of all thermodynamic properties, ESI†). The combined deviation can easily cause a boundary shift of the observed magnitude. It needs to be kept in mind, though, that the metal–oxide transition is much more important for the present investigation.


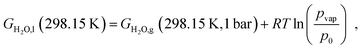



![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and ReO2 (Pbcn) – are observed below 0.89 V and 0.31 V, respectively (the alloy is stable below 0.29 V, depending on composition). The transition from Rh2O3 (Pbca) to RhO2 at U = 0.55 V, on the other hand, happens well below the metal–oxide transition below 0.60 V. The phases in the iridium (IrO2 above 0.56 V to 0.59 V), cobalt (Co3O4 above U = 0.41 V to 0.31 V) and nickel plots (NiO above 0.55 to 0.44 V) are the same as for the thermal oxidation (see Fig. S5f, S3f and S6f in the ESI†). The same is the case for the oxidation of gold (Au2O3-formation above 1.03 V, Fig. S2f, ESI†) and silver (Ag2O starting to form between 0.72 V and 0.83 V, Fig. S1f, ESI†). The comparability of these results to literature data is limited, since only x ≤ 0.5 was considered here. Moreover, Co,120 Ni,119 Cu,115 Ag118 and even Au118 are expected to dissolve at pH = 0, provided the applied potential is sufficiently large. This is neglected here, as is the formation of perrhenate ions117 in case of rhenium. The solid oxides are thus only relevant for the electrochemical oxidation of rhodium, iridium and tungsten.116,118
m) and ReO2 (Pbcn) – are observed below 0.89 V and 0.31 V, respectively (the alloy is stable below 0.29 V, depending on composition). The transition from Rh2O3 (Pbca) to RhO2 at U = 0.55 V, on the other hand, happens well below the metal–oxide transition below 0.60 V. The phases in the iridium (IrO2 above 0.56 V to 0.59 V), cobalt (Co3O4 above U = 0.41 V to 0.31 V) and nickel plots (NiO above 0.55 to 0.44 V) are the same as for the thermal oxidation (see Fig. S5f, S3f and S6f in the ESI†). The same is the case for the oxidation of gold (Au2O3-formation above 1.03 V, Fig. S2f, ESI†) and silver (Ag2O starting to form between 0.72 V and 0.83 V, Fig. S1f, ESI†). The comparability of these results to literature data is limited, since only x ≤ 0.5 was considered here. Moreover, Co,120 Ni,119 Cu,115 Ag118 and even Au118 are expected to dissolve at pH = 0, provided the applied potential is sufficiently large. This is neglected here, as is the formation of perrhenate ions117 in case of rhenium. The solid oxides are thus only relevant for the electrochemical oxidation of rhodium, iridium and tungsten.116,118![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m)
m)![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m)
m)![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m)
m)![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2)
m2)





