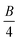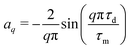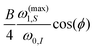Pulsed dynamic nuclear polarization: a comprehensive Floquet description†
Received
30th April 2024
, Accepted 5th June 2024
First published on 5th June 2024
Abstract
Dynamic nuclear polarization (DNP) experiments using microwave (mw) pulse sequences are one approach to transfer the larger polarization on the electron spin to nuclear spins of interest. How the result of such experiments depends on the external magnetic field and the excitation power is part of an ongoing debate and of paramount importance for applications that require high chemical-shift resolution. To date numerical simulations using operator-based Floquet theory have been used to predict and explain experimental data. However, such numerical simulations provide only limited insight into parameters relevant for efficient polarization transfer, such as transition amplitudes or resonance offsets. Here we present an alternative method to describe pulsed DNP experiments by using matrix-based Floquet theory. This approach leads to analytical expressions for the transition amplitudes and resonance offsets. We validate the method by comparing computations by these analytical expressions to their numerical counterparts and to experimental results for the XiX, TOP and TPPM DNP sequences. Our results explain the experimental data and are in very good agreement with the numerical simulations. The analytical expressions allow for the discussion of the scaling behaviour of pulsed DNP experiments with respect to the external magnetic field. We find that the transition amplitudes scale inversely with the external magnetic field.
1 Introduction
Dynamic nuclear polarization (DNP) has become a routine method to increase the nuclear polarization of solid samples by transferring the higher electron polarization to the nuclei of interest typically at cryogenic temperatures.1,2 Two different implementations of DNP are currently in wide-spread use: (i) magic-angle spinning (MAS) DNP operated typically at around 100 K to investigate materials, surfaces, and biomolecules.2–5 (ii) Dissolution DNP operated typically at around 1 K to generate highly polarized small molecules for metabolic imaging or spectroscopic applications.6–11 Both modes of DNP use continuous-wave (CW) irradiation of microwaves (mw) on the sample to generate a high polarization on the nuclei. In MAS DNP, polarization transfer to protons is the most common mode followed by a subsequent polarization-transfer step to other nuclei. In dissolution DNP, direct enhancement of 13C is quite common but transfer to protons with subsequent polarization transfer to other nuclei has also been implemented. A number of different mechanisms (Overhauser effect (OE),12 solid effect (SE),13–16 cross effect (CE),17–19 and thermal mixing (TM)20,21) have been identified that explain the polarization transfer. They all have in common that increasing static magnetic fields lead to a decrease of the polarization transfer efficiency. Typically, they are described in an incoherent way using arguments that rely on the saturation of certain transitions and relaxation properties.
Some time ago, the nuclear orientation via electron spin locking (NOVEL) sequence was introduced where the microwave nutation frequency is matched to the nuclear Zeeman frequency.22–25 Both fields modulate the pseudo-secular part of the hyperfine coupling leading to a time-independent effective Hamiltonian if the two frequencies are matched. A number of additional pulsed polarization-transfer techniques for DNP have been introduced recently that can also be described by a coherent effective time-averaged Hamiltonian in a suitable frame of reference.26–30 They all rely on modulation by a pulse sequence that in some way matches the nuclear Larmor frequency, thus generating a time-independent part of the Hamiltonian from the pseudo-secular part of the hyperfine interaction that promotes polarization transfer. Different irradiation schemes have been proposed but this principal mode of operation is the same for all of them.
In this publication, we analyze pulsed DNP sequences in more detail, using two different approaches. In a first approach, we use operator-based Floquet theory to calculate effective Hamiltonians at the resonance conditions that drive the double-quantum or zero-quantum polarization transfer.31,32 This provides theoretical understanding under which conditions we can expect DNP to happen and allows to estimate the efficiency. In a second, complementary approach, we use matrix-based Floquet theory33–36 to connect the Fourier coefficients of the pulse sequence to the various resonance conditions and to get a better understanding of the scaling behavior of pulsed DNP as a function of the static magnetic field.
2 Theoretical concepts
We will first discuss pulsed DNP sequences in the framework of operator-based Floquet theory (Section 2.1) which gives effective Hamiltonians that promote polarization transfer at resonance conditions. These effective Hamiltonians can be calculated only numerically due to the complexity of the interaction-frame transformation that hides the direct connection between the Fourier coefficients of the microwave irradiation and the transition probabilities. In a complementary treatment in the framework of classical matrix-based Floquet theory (Section 2.3), analytical diagonalization in connection with perturbation theory can be used to establish this connection. This treatment allows a better understanding of transition amplitudes and their dependence on the experimental parameters like microwave amplitude and static magnetic field.
2.1 Operator-based Floquet theory
In this section, we present an operator-based Floquet theory formalism31 to describe pulsed DNP. The formalism introduced in this section is similar to the one presented in ref. 29 and we repeat some of the results but in a slightly different notation. The two-spin Hamiltonian for a spin system consisting of one electron spin (S) in the Zeeman rotating frame and one nuclear spin (I) in the laboratory frame is given as| | 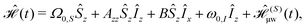 | (1) |
where Ω0,S = ω0,S − ωμw is the offset of the microwave irradiation, Azz the secular and 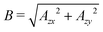 the pseudo-secular part of the hyperfine coupling. The electron resonance frequency is given by
the pseudo-secular part of the hyperfine coupling. The electron resonance frequency is given by  and for the nucleus by ω0,I = −γIB0 while ωμw is the microwave frequency and B0 is the external static magnetic field applied along the laboratory z-axis. The orientation-dependent gzz value determines the frequency offset from the mw irradiation. For low static magnetic fields, the isotropic value giso can be used instead. The Hamiltonian
and for the nucleus by ω0,I = −γIB0 while ωμw is the microwave frequency and B0 is the external static magnetic field applied along the laboratory z-axis. The orientation-dependent gzz value determines the frequency offset from the mw irradiation. For low static magnetic fields, the isotropic value giso can be used instead. The Hamiltonian  refers to the Hamiltonian of the μw irradiation and can be written as
refers to the Hamiltonian of the μw irradiation and can be written as| |  | (2) |
where ω1,S(t) is the time-dependent pulse amplitude and ϕ(t) the time-dependent phase. To describe the effect of the microwave irradiation, it is best to transform the Hamiltonian of eqn (1) into an interaction frame with respect to  . Such a transformation can be analytically written as
. Such a transformation can be analytically written as| |  | (3) |
with  where
where ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is the Dyson time-ordering operator37 and a(S)ξχ(t) are the time-dependent elements of a 3 × 3 rotation matrix. Note that in the following we drop the “dash” on the S spin operators when referring to the interaction frame. We consider time-periodic irradiation schemes with a modulation period τm with
is the Dyson time-ordering operator37 and a(S)ξχ(t) are the time-dependent elements of a 3 × 3 rotation matrix. Note that in the following we drop the “dash” on the S spin operators when referring to the interaction frame. We consider time-periodic irradiation schemes with a modulation period τm with  . This results in a modulation frequency
. This results in a modulation frequency| |  | (4) |
Operator-based Floquet theory can then be used to describe the effect of the irradiation. The interaction-frame transformation, as given in eqn (3), corresponds to rotation around an effective field axis in the spin space of the electron spin. The effective frequency is| |  | (5) |
where βeff,S describes the rotation angle around the effective field axis within one period τm. Note the functional dependence of ωeff,S on the offset frequency Ω0,S. The Fourier coefficients of the Hamiltonian can be calculated from the rotation-matrix elements a(S)ξχ(t) as| |  | (6) |
Now we transform the Hamiltonian into a frame rotating with the nuclear Larmor frequency ω0,I and insert the Fourier coefficient of eqn (6) for the electron spin. This leads to| |  | (7) |
where a(k,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )± = a(k,
)± = a(k,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )zx ∓ ia(k,
)zx ∓ ia(k,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )zy and Ŝ± = Ŝx ± iŜy. Please note that we assumed a negative Larmor frequency for the nuclear spin corresponding to a positive gyromagnetic ratio. The Hamiltonian in eqn (7) contains three fundamental frequencies |ω0,I|, ωeff,S and ωm and we can write it as a Fourier series (see last line in eqn (7)). The first-order effective Hamiltonian based on triple-mode Floquet theory is, thus, given by
)zy and Ŝ± = Ŝx ± iŜy. Please note that we assumed a negative Larmor frequency for the nuclear spin corresponding to a positive gyromagnetic ratio. The Hamiltonian in eqn (7) contains three fundamental frequencies |ω0,I|, ωeff,S and ωm and we can write it as a Fourier series (see last line in eqn (7)). The first-order effective Hamiltonian based on triple-mode Floquet theory is, thus, given by| |  | (8) |
In eqn (8)n0, k0 and ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 0 sum over only the values where the resonance condition
0 sum over only the values where the resonance condition| | n0|ω0,I| + k0ωm + ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 0ωeff,S = 0 0ωeff,S = 0 | (9) |
is fulfilled. Polarization transfer between the electron spin (S) and the nuclear spin (I) can only be mediated by the double-quantum (DQ) terms (Ŝ±Î±) or the zero-quantum (ZQ) terms (Ŝ±Î∓). Therefore, if we now define a tuple (−1, k0, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 0) and its negative (1, −k0, −
0) and its negative (1, −k0, −![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 0), we obtain a first-order effective Hamiltonian for the ZQ and DQ-transfer given by
0), we obtain a first-order effective Hamiltonian for the ZQ and DQ-transfer given by| | 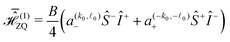 | (10) |
| |  | (11) |
Note that for a negative gyromagnetic ratio (positive Larmor frequency) for the nuclear spin the sign for the indices k0 and ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 0 changes, e.g.,
0 changes, e.g.,  in case of a negative Larmor frequency is
in case of a negative Larmor frequency is  in case of a positive Larmor frequency. The polarization transfer ρ0 → Îz can be calculated following ref. 29 by
in case of a positive Larmor frequency. The polarization transfer ρ0 → Îz can be calculated following ref. 29 by| |  | (12) |
where  and the upper binary operator in this equation refers to the ZQ case and the lower one to the DQ case, respectively. Again, eqn (12) is valid for the case of a positive gyromagnetic ratio of the nuclear spin (negative Larmor frequency). For the case of a negative gyromagnetic ratio of the nuclear (positive Larmor frequency) the sign for the indices k0 and
and the upper binary operator in this equation refers to the ZQ case and the lower one to the DQ case, respectively. Again, eqn (12) is valid for the case of a positive gyromagnetic ratio of the nuclear spin (negative Larmor frequency). For the case of a negative gyromagnetic ratio of the nuclear (positive Larmor frequency) the sign for the indices k0 and ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 0 changes, e.g. for the ZQ case
0 changes, e.g. for the ZQ case  would change to
would change to 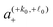 . Also note that in case of a positive gyromagnetic ratio of the nuclear spin the ZQ enhancement gets negative and the DQ enhancement positive due to the ratio
. Also note that in case of a positive gyromagnetic ratio of the nuclear spin the ZQ enhancement gets negative and the DQ enhancement positive due to the ratio 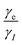 . However, for a negative gyromagnetic ratio of the nuclear spin the ZQ enhancement is positive and the DQ enhancement is negative. The factor 〈ρ0|Ŝz〉 takes into account that only the part of the electron polarization that is along the effective field can be transferred to the nuclei. For small times t and using
. However, for a negative gyromagnetic ratio of the nuclear spin the ZQ enhancement is positive and the DQ enhancement is negative. The factor 〈ρ0|Ŝz〉 takes into account that only the part of the electron polarization that is along the effective field can be transferred to the nuclei. For small times t and using  the performance of a certain pulse scheme can be roughly estimated by29
the performance of a certain pulse scheme can be roughly estimated by29| | | εZQ/DQ = ∓〈ρ0|Ŝz〉aeff | (13) |
where| |  | (14) |
For CW irradiation (time-independent pulse amplitude ω1,S and phase offset ϕ in eqn (2)), we can calculate the Fourier coefficients of the Hamiltonian of eqn (7) analytically which leads to an effective Hamiltonian relevant for DNP of the form
| |  | (15) |
where

describes the direction of the effective field in the electron spin coordinate system (see Fig. S1 in ESI,
† Section A). In case of the solid effect
16 we can invoke the small-angle approximation (
Ω0,S ≫
ω1,S), where

leads to a prefactor of

. For NOVEL
23,25
and the prefactor is

. Section A of the ESI
† contains the derivation to calculate the Fourier coefficients of the Hamiltonian analytically starting from
eqn (6). The effective Hamiltonian of
eqn (15) as well as the scaling factor for NOVEL and SE were already reported in ref.
38.
2.2 Microwave irradiation scheme
So far we did not specify the microwave irradiation scheme characterized by 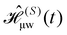 in eqn (1) in detail. In order to apply Floquet theory the only requirement is that the mw irradiation is time periodic with a modulation period τm. When we limit the discussion to amplitude-modulated monochromatic pulses (ϕ(t) = ϕ), the pulse amplitude ω1,S(t) becomes the only parameter that has to fulfill the time-periodic restriction. In the following we set ϕ = 0 for simplicity of the notation. Any time-periodic amplitude modulation can then be represented as a half-range Fourier expansion of the form
in eqn (1) in detail. In order to apply Floquet theory the only requirement is that the mw irradiation is time periodic with a modulation period τm. When we limit the discussion to amplitude-modulated monochromatic pulses (ϕ(t) = ϕ), the pulse amplitude ω1,S(t) becomes the only parameter that has to fulfill the time-periodic restriction. In the following we set ϕ = 0 for simplicity of the notation. Any time-periodic amplitude modulation can then be represented as a half-range Fourier expansion of the form| |  | (16) |
where a0, aq and bq are the Fourier coefficients of the microwave irradiation scheme and q ∈ ![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) . ω(max)1,S is the maximum value of the time-dependent pulse amplitude ω1,S(t). Note the difference between the Fourier coefficients of the microwave irradiation scheme (aq and bq) as given in eqn (16) and the Fourier coefficients of the interaction-frame trajectory (a(k,
. ω(max)1,S is the maximum value of the time-dependent pulse amplitude ω1,S(t). Note the difference between the Fourier coefficients of the microwave irradiation scheme (aq and bq) as given in eqn (16) and the Fourier coefficients of the interaction-frame trajectory (a(k,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )zχ) as calculated in eqn (6). For CW irradiation all Fourier coefficients in eqn (16) are zero except for a0, which is equal to 2 and ω1,S(t) = ω(max)1,S. For an even pulse amplitude function ω1,S(t) all odd Fourier coefficients (bq) are 0. In contrast for an odd function ω1,S(t) all even coefficients are 0, e.g. a0 and aq. In the following three sections we will discuss pulsed DNP schemes, first the Time-optimized Pulsed (TOP) DNP27 sequence, second the XiX (X-inverse-X) DNP sequence28,29 and last the Two-Pulse Phase Modulation (TPPM) DNP sequence.30 We represent them by the half-range Fourier expansion as given in eqn (16).
)zχ) as calculated in eqn (6). For CW irradiation all Fourier coefficients in eqn (16) are zero except for a0, which is equal to 2 and ω1,S(t) = ω(max)1,S. For an even pulse amplitude function ω1,S(t) all odd Fourier coefficients (bq) are 0. In contrast for an odd function ω1,S(t) all even coefficients are 0, e.g. a0 and aq. In the following three sections we will discuss pulsed DNP schemes, first the Time-optimized Pulsed (TOP) DNP27 sequence, second the XiX (X-inverse-X) DNP sequence28,29 and last the Two-Pulse Phase Modulation (TPPM) DNP sequence.30 We represent them by the half-range Fourier expansion as given in eqn (16).
2.2.1 TOP pulse scheme.
The TOP DNP sequence is presented in Fig. 1(a) and consists of a delay τd and a pulse with length τp.27 In this representation, the TOP DNP sequence is an even irradiation scheme in the sense of the half-range Fourier expansion which means that all odd Fourier coefficients bq are 0. The value of a0 is given for arbitrary values of τd and τp as| |  | (17) |
The Fourier coefficients aq for the TOP sequence are obtained as| |  | (18) |
One can clearly see from eqn (17) and (18) that the Fourier coefficients of the microwave irradiation scheme depend on the duty cycle τp/τm of the TOP sequence. The coefficient a0 describes the average field and can have values between zero (no pulse) and two (cw irradiation). The Fourier coefficients aq for q ∈ ![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) exhibit a much more complex behaviour. For certain combinations of the parameters τd, τp and q certain coefficients aq can be 0. This is summarized in Table 1 and has important consequences for the discussion in Section 3.3.
exhibit a much more complex behaviour. For certain combinations of the parameters τd, τp and q certain coefficients aq can be 0. This is summarized in Table 1 and has important consequences for the discussion in Section 3.3.
 |
| | Fig. 1 Half-range Fourier expansion of (a) the TOP DNP pulse scheme and (b) the XiX DNP pulse scheme according to eqn (16). The DNP pulse sequence is represented with a blue solid line. The TOP DNP sequence consists of a pulse with length τp and a delay τd, whereas the XiX DNP sequence consists of two pulses with opposite phase. The different Fourier modes are shown with dashed lines. In the TOP sequence the unmodulated Fourier mode described by the Fourier coefficient a0 is represented in dashed red. The first Fourier mode a1 and the second mode a2 are represented by magenta and violet dashed lines respectively. A fraction 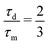 is used for this particular TOP sequence (see Table 1). In the XiX case, the first Fourier mode b1, the third mode b3 and the fifth mode b5 are represented by red, magenta and violet dashed lines respectively. is used for this particular TOP sequence (see Table 1). In the XiX case, the first Fourier mode b1, the third mode b3 and the fifth mode b5 are represented by red, magenta and violet dashed lines respectively. | |
Table 1 Fourier coefficients for different duty cycles for the TOP DNP sequence. For certain combinations of τd, τp and q some coefficients aq are 0. The first entry represents the case where τd = 0 e.g. CW irradiation. The Fourier coefficient a0 is scaled by the maximal possible value obtained by CW which is two
|
τ
d/τp |
τ
p/τm |
τ
d/τm |
a
0/2 |
a
q
|
| 0 |
1 |
0 |
1 |
0 for all q |
| 1 |
1/2 |
1/2 |
1/2 |
0 for all q = 2, 4, 6, 8,… |
| 2 |
1/3 |
2/3 |
1/3 |
0 for all q = 3, 6, 9, 12,… |
| 3 |
1/4 |
3/4 |
1/4 |
0 for all q = 4, 8, 12, 16,… |
2.2.2 XiX pulse scheme.
The XiX DNP sequence is shown schematically in Fig. 1(b).28,29 Although XiX is a phase-modulated pulse scheme, it can be considered as well as an amplitude modulation scheme with equal pulse length τp and inverted amplitude. Such an amplitude modulation can be described by an odd half-range Fourier expansion. The odd coefficients bq are given by| |  | (19) |
and are independent of the pulse length and modulation period. Another difference to the TOP sequence is that the Fourier coefficients bq are non-zero only for odd q.
2.2.3 TPPM pulse scheme.
The TPPM pulse scheme consists of two consecutive pulses with phases ±ϕ (see Fig. 2(a) and (b)). This scheme can be considered as an amplitude-modulated XiX sequence with an additional orthogonal CW part as indicated in Fig. 2(c). This can be easily understood by starting from the Hamiltonian 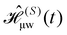 as given in eqn (2). By inserting a function ϕ(t) switching from +ϕ to −ϕ at a modulation frequency ωm we obtain
as given in eqn (2). By inserting a function ϕ(t) switching from +ϕ to −ϕ at a modulation frequency ωm we obtain| | 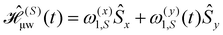 | (20) |
with| | | ω(x)1,S = cos(ϕ)ω(max)1,S | (21) |
and| |  | (22) |
The coefficients bq in eqn (22) are the same as for the XiX case as given in eqn (19). Please note that in the TPPM case we multiply coefficients bq by a factor sin(ϕ) to account for the phase modulation. This results in a new definition ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) q = sin(ϕ)bq as performed in the last step of eqn (22). The amplitude of the CW contribution is given by eqn (21). Hence, due to the effective CW part in TPPM, the a0 Fourier coefficient of the microwave irradiation is
q = sin(ϕ)bq as performed in the last step of eqn (22). The amplitude of the CW contribution is given by eqn (21). Hence, due to the effective CW part in TPPM, the a0 Fourier coefficient of the microwave irradiation is| |  | (23) |
This coefficient is not zero unless  , which corresponds to the XiX limit of TPPM with phase y. Therefore, the TPPM sequence can be viewed as a combination of the CW irradiation and an orthogonal XiX DNP sequence. The time-dependent modulation can be treated in a similar way as in the XiX sequence with the exception that there is an additional time-independent CW part.
, which corresponds to the XiX limit of TPPM with phase y. Therefore, the TPPM sequence can be viewed as a combination of the CW irradiation and an orthogonal XiX DNP sequence. The time-dependent modulation can be treated in a similar way as in the XiX sequence with the exception that there is an additional time-independent CW part.
 |
| | Fig. 2 (a) Schematic representation of the TPPM pulse sequence consisting of two pulses of length τp with opposite phases ϕ and −ϕ, respectively. (b) Cartesian representation of the opposite phases in a TPPM experiment. The x-part of the phase of the two pulses is identical. The y-part of the phase of the two pulses changes sign and results in an XiX type irradiation. (c) The TPPM sequence can be viewed as a combination of an amplitude-modulated XiX pulse sequence with amplitude ω(y)1,S and phase y (blue dashed lines) and an additional orthogonal CW irradiation with amplitude ω(x)1,S and phase x (red dotted lines). | |
2.3 Matrix-based Floquet theory
While operator-based Floquet theory can be used to calculate effective Hamiltonians that describe the polarization transfer in DNP, the direct connection to the various harmonics of the mw irradiation is often lost in the complexities of the interaction-frame transformation. In principle, the connection can be recovered through an analytical Bessel function formulation of the interaction-frame transformation39 but insights are limited due to the complexity of the expressions. In this section we consider matrix-based Floquet theory as an alternative description that provides a direct connection between transition probabilities and the microwave irradiation scheme. The Hamiltonian as defined in eqn (1) can be rewritten with the amplitude modulation of the mw irradiation schemes as discussed in Section 2.2 to| |  | (24) |
For the TOP- and XiX DNP sequence χ = x. The analytical expressions for the Fourier coefficients of the TOP sequence can be found in eqn (17) and (18) and for the XiX sequence in eqn (19), respectively. As shown in Fig. 2 the TPPM sequence can also be regarded as an amplitude-modulated pulse sequence with phase +y with an orthogonal CW part with phase +x. Therefore, χ = y in eqn (24) for the TPPM case. In TPPM 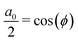 and aq = 0 ∀ q ≠ 0. The Fourier coefficients are
and aq = 0 ∀ q ≠ 0. The Fourier coefficients are 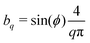 for odd values of q. The Hamiltonian in eqn (24) can be expressed as a Fourier expansion
for odd values of q. The Hamiltonian in eqn (24) can be expressed as a Fourier expansion
| | 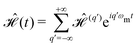 | (25) |
with the Fourier components
| |  | (26) |
and
| |  | (27) |
Be aware that in contrast to the expansion in
eqn (16) and (24) the Fourier index
q′ of the Hilbert space Hamiltonian in
eqn (25) can also be negative while
q = |
q′| is always limited to positive values. Now we can use the Fourier components in
eqn (26) and (27) to express the Floquet matrix

. We thus obtain the elements of the infinite-dimensional Floquet matrix
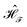
as
36| |  | (28) |
In
eqn (28)δij represents the Kronecker delta.

is a specific element of the Floquet matrix, which can be obtained from
eqn (26) and (27). In the upcoming sections, we use Greek letters to represent the eigenvalues of the spin operator in Hilbert-space and Latin letters to denote the Fourier harmonics of amplitude modulation of the μw irradiation scheme. Be aware that in
eqn (28) the difference
c1 −
c2 between two Fourier indices in Floquet space has to match the Fourier index
q′ in
eqn (25)–(27). According to
eqn (28) the central blocks of the infinite-dimensional Floquet matrix (blocks where
q′ =
c1 −
c2 = 0) contain the Fourier component

(
eqn (26)) with frequency offsets

(last term of
eqn (28)). The off-diagonal blocks (blocks where
q′ =
c1 −
c2 ≠ 0) contain the Fourier components

as given in
eqn (27). In the upcoming sections we will use the Fourier index
q′ of the Fourier expansion in Hilbert space to denote connected Fourier states in Floquet space. For a two-spin 1/2 system, the Fourier components

are 4 × 4 matrices within the basis set |
κ,
η〉 where
κ ∈ {
αS,
βS} and
η ∈ {
αI,
βI}. Part of the infinite-dimensional Floquet matrix

is presented in
Fig. 3.
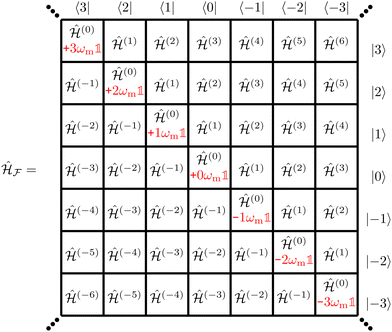 |
| | Fig. 3 Schematic representation of the infinite-dimensional Floquet matrix. Each block is represented by the corresponding Fourier component  , which is in case of a two-spin system consisting of spin 1/2 particles a 4 × 4 matrices. The expression , which is in case of a two-spin system consisting of spin 1/2 particles a 4 × 4 matrices. The expression  in red on the central block in red on the central block 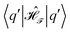 results from last term of eqn (28). results from last term of eqn (28). | |
As outlined in Section 2.2.1 in the TOP DNP sequence the even Fourier coefficients a0 and aq are non-zero (see eqn (17) and (18)). Therefore, eqn (27) simplifies to
| |  | (29) |
All diagonal blocks in the infinite-dimensional Floquet matrix for the TOP DNP sequence contain the Fourier component

as given in
eqn (26). In case of the XiX DNP sequence (see Section 2.2.2) the odd Fourier coefficients
bq are the non-zero ones (see
eqn (19)) resulting in
| |  | (30) |
for
eqn (26) and in
| |  | (31) |
for
eqn (27). According to Section 2.2.3, the TPPM sequence can be regarded as a combination of the CW irradiation scheme and the XiX DNP sequence. The diagonal and off-diagonal blocks in Floquet space are given by the Fourier components in
eqn (26) and (27) with phase +
y, respectively. Inserting the Fourier coefficients for the TPPM case leads to
| |  | (32) |
for the diagonal block and
| |  | (33) |
for the off-diagonal block, respectively. Compared to the XiX sequence, in the TPPM the phase of the off-diagonal block changes from
x to
y and the block contains an additional factor sin(
ϕ) as mentioned in Section 2.2.3. The diagonal block

in the infinite-dimensional Floquet matrix is given in
eqn (26) in its most general analytical form.

is similar for the TOP and the TPPM sequence (except for the definition of Fourier coefficient
a0) and the XiX case differs by a missing term with the
Ŝx operator due to
a0 = 0. However, we still can define a general diagonalization of
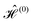
that is valid for all three pulse schemes. This will be further discussed in Section 2.4.
2.4 Diagonalization of the central Floquet block
In order to apply perturbation theory for the side-diagonal parts of the Floquet Hamiltonian that originate from the time-dependent mw irradiation, we first diagonalize the spin-degrees of freedom of the central blocks of the Floquet Hamiltonian  which have the form
which have the form| |  | (34) |
The offset terms 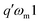 do not influence diagonalization, since the unit operator is invariant under rotation. Direct diagonalization of eqn (34) leads to results that are very complex and not easy to interpret. Therefore,
do not influence diagonalization, since the unit operator is invariant under rotation. Direct diagonalization of eqn (34) leads to results that are very complex and not easy to interpret. Therefore,  is approximately diagonalized in a two-step approach like outlined in ref. 40. In the first step, the reduced Hamiltonian
is approximately diagonalized in a two-step approach like outlined in ref. 40. In the first step, the reduced Hamiltonian| |  | (35) |
is diagonalized exactly and the additional term  (contained in eqn (34)) is subjected to this first transformation leading to a term of the form Ŝx
(contained in eqn (34)) is subjected to this first transformation leading to a term of the form Ŝx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(η) + 2ŜyÎy
cos(η) + 2ŜyÎy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(η). From this resulting term Ŝx
sin(η). From this resulting term Ŝx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(η) is treated as a perturbation in a second unitary transformation (see Fig. S2 in ESI,† Section B). All the details of this two consecutively applied unitary transformations are given in ESI,† Section B in much more detail and were adapted from ref. 40. Here we present only the relevant results needed for further discussion. The same set of transformations is then applied to the off-diagonal parts of the Floquet Hamiltonian
cos(η) is treated as a perturbation in a second unitary transformation (see Fig. S2 in ESI,† Section B). All the details of this two consecutively applied unitary transformations are given in ESI,† Section B in much more detail and were adapted from ref. 40. Here we present only the relevant results needed for further discussion. The same set of transformations is then applied to the off-diagonal parts of the Floquet Hamiltonian  with q′ ≠ 0 (see eqn (27)). In a final step, we can then apply second-order perturbation theory to calculate the transition frequencies and probabilities enabled by the Fourier components of the various mw irradiation schemes.
with q′ ≠ 0 (see eqn (27)). In a final step, we can then apply second-order perturbation theory to calculate the transition frequencies and probabilities enabled by the Fourier components of the various mw irradiation schemes.
The first unitary transformation that diagonalizes the Hamiltonian in eqn (35) is given by
| | | Û1 = exp(−i(−ηαŜαÎy + ηβŜβÎy)). | (36) |
Since the first diagonalization takes place in the
I-spin sub space, we have to distinguish between a positive Larmor frequency
ω0,I and a negative one to diagonalize
eqn (35). In the following we restrict our discussion to negative Larmor frequencies (see Fig. S2 in ESI,
† Section B). The angles
ηα and
ηβ describing the first unitary transformation can be obtained from Fig. S2 in ESI,
† Section B and are given as
| | 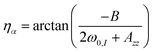 | (37) |
| | 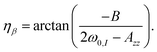 | (38) |
The angles are chosen such that 0° ≤
ηα,
ηβ ≤ 90°. The Hamiltonian

of
eqn (35) after the first unitary transformation is given by
| |  | (39) |
with
| |  | (40) |
| |  | (41) |
and the nuclear frequencies
| |  | (42) |
| |  | (43) |
The full diagonal block of the Floquet Hamiltonian (see
eqn (34)) contains in addition the spin operator
Ŝx which transforms into
| | Û1−1ŜxÛ1 = Ŝx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(η) + 2ŜyÎy cos(η) + 2ŜyÎy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(η), sin(η), | (44) |
with

. The angle 2
η is shown in Fig. S2 (ESI
†) and can take values from 0° to 180°. The case 2
η < 90° is obtained for spin systems in the weak coupling regime, where |
Azz|,|
B| < |
ω0,I|. 2
η > 90° is attained in the strong-coupling regime, meaning that |
Azz| > |
ω0,I|. Near the weak-coupling limit, we have 2
η ≈ 0° and near the strong-coupling limit, we have 2
η ≈ 180°. In both these cases, sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η
η ≈ 0, meaning the excitation of formally forbidden electron-nuclear transitions is weak. The total Hamiltonian in
eqn (34) after the first unitary transformation is thus given by
| |  | (45) |
Using
eqn (27) and (44) the off-diagonal blocks containing the Fourier components

with
q′ ≠ 0 after the first diagonalization step can be written as
| | 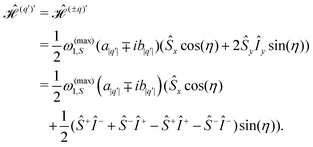 | (46) |
As outlined later in more detail, for spin systems near the weak-coupling limit, the angle
η is very small. Therefore, we perform the second diagonalization step only with respect to the
Ŝx term, leaving the term 2
ŜyÎy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin(
η) in
eqn (45) as a remaining off-diagonal perturbation. We thus diagonalize the Hamiltonian
| |  | (47) |
with

. Diagonalization of
eqn (47) takes place in the subspace of the
S-spin. Thus, we need to take into account the sign of
Ω0,S (see Fig. S2 in ESI,
† Section B). The upper binary operator in the following equations corresponds to the +
Ω0,S case and the lower one to the −
Ω0,S case, respectively. The unitary transformation to diagonalize
eqn (47) is given by
| | | Û2 = exp(−i(±θαŜyÎα ± θβŜyÎβ)). | (48) |
The angles
θα and
θβ as shown in Fig. S2 (ESI
†) can be calculated as
| |  | (49) |
| |  | (50) |
and can take any values from 0° to 90°. In the doubly tilted frame the truncated Hamiltonian can be expressed as
| | 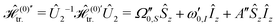 | (51) |
with
| | 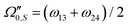 | (52) |
and the electronic frequencies
| | 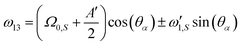 | (54) |
| |  | (55) |
The angle 2
θ = (
θα −
θβ) is depicted in Fig. S2 (ESI
†). The spin operator
Ŝx from the off-diagonal parts of the Floquet Hamiltonian

in the doubly tilted frame can be expressed as
| |  | (56) |
In this doubly tilted frame, the total Hamiltonian including also the term 2ŜyÎy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(η) as given in eqn (45) can be expressed as
sin(η) as given in eqn (45) can be expressed as
| |  | (57) |
Eqn (57) can be used to derive the Fourier coefficients of the Hamiltonian for DNP experiments like solid effect DNP
16 and NOVEL
23,25 (see
eqn (15) and ESI,
† Section B).
In case of TPPM, the diagonal blocks of the Floquet Hamiltonian in the doubly tilted frame have the same form as given in eqn (57). The modulated part contained in the off-diagonal parts of the Floquet Hamiltonian is phase shifted by 90° and contains the spin operator Ŝy (see eqn (33)). In the doubly tilted frame we obtain
| |  | (58) |
with
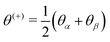
. Please note, that we have to set

for the term

in the TPPM case,
e.g., in
eqn (49) and (50) for the angles
θα and
θβ and all other equations containing

. The ZQ- and DQ terms are contained in the operator

. In the ESI,
† Section B we present a detailed step-by-step derivation of this entire section.
3 Results and discussion
3.1 Fourier synthesized DNP
In the following sections we use the Fourier expansion of eqn (16) and the matrix representation of the Floquet Hamiltonian in the electron rotating frame to explain the occurrence of certain resonance peaks in the DNP profile. We artificially set some Fourier coefficients of the microwave irradiation scheme to 0 and see which resonance peaks are left/unchanged compared to the original sequence. For this Fourier-synthesized (FS) DNP sequences we use the name FS-XiX in case where the original sequence is the XiX sequence or FS-TOP for the TOP sequence, respectively. In the following Section the original sequence will be always represented by blue color and the FS case by red color. All experiments were conducted with the parameters/procedures as given in Section 5. As a chemical system we used the trityl radical Ox063 dissolved in DNP juice at 80 K which gives high enhancement factors as first described in ref. 24. We discuss the details for the XiX sequence and only give a more summary description for the TOP and TPPM sequence since many of the properties are very similar.
3.2 XiX sequence
3.2.1 DNP profile.
The experimental comparison of the DNP profile of the standard XiX DNP sequence with the FS-XiX case for bq = 0 ∀ q \{1} at X-band (0.35 T) using τp = 15 ns and 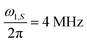 is shown in Fig. 4. Examples for pulse lengths of τp = 5, 9 and 45 ns can be found in ESI,† Section J. We only discuss the case where we set all Fourier coefficients of the microwave irradiation to 0 except the one for q = 1. All others can be converted to this case by scaling the modulation frequency of the XiX DNP sequence to the considered harmonic.
is shown in Fig. 4. Examples for pulse lengths of τp = 5, 9 and 45 ns can be found in ESI,† Section J. We only discuss the case where we set all Fourier coefficients of the microwave irradiation to 0 except the one for q = 1. All others can be converted to this case by scaling the modulation frequency of the XiX DNP sequence to the considered harmonic.
 |
| | Fig. 4 DNP profile for XiX (blue line) and FS-XiX (red line) recorded at X-band (0.35 T) with a Rabi frequency of 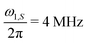 and a pulse length τp = 15 ns (further experimental parameters are given in Section 5). The dots and asterisks represent the estimated enhancement εZQ/DQ as given in eqn (13). and a pulse length τp = 15 ns (further experimental parameters are given in Section 5). The dots and asterisks represent the estimated enhancement εZQ/DQ as given in eqn (13). | |
In Fig. 4 we see that only some select resonances remain visible for the FS-XiX sequence. This is confirmed by calculating the transfer efficiency using operator-based Floquet theory. The theoretical values were calculated numerically (see Section 2.1 or ESI,† Section L) and are indicated by circles or asterisks in Fig. 4. We can group the resonance conditions (Ω0,S for which eqn (9) is fulfilled) obtained from numerical calculations using operator-based Floquet theory in three groups, i.e., resonance conditions that are present (non-zero) in the XiX case and the FS-XiX case like  or ±48 MHz, resonance conditions that are non-zero in the XiX case, but 0 in the FS-XiX case like
or ±48 MHz, resonance conditions that are non-zero in the XiX case, but 0 in the FS-XiX case like  and resonance conditions that are zero in both cases, e.g.,
and resonance conditions that are zero in both cases, e.g.,  . This behavior can be better explained by using the matrix representation of the infinite-dimensional Floquet Hamiltonian as described in Section 2.3. In case of XiX we only need the first diagonalization step from Section 2.4 because a0 = 0. The four eigenvalues can be calculated according to eqn (39) and are given as
. This behavior can be better explained by using the matrix representation of the infinite-dimensional Floquet Hamiltonian as described in Section 2.3. In case of XiX we only need the first diagonalization step from Section 2.4 because a0 = 0. The four eigenvalues can be calculated according to eqn (39) and are given as
| |  | (59) |
| |  | (60) |
| | 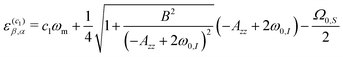 | (61) |
| |  | (62) |
In
eqn (59)–(62) the superscript in
e.g.
denotes the Fourier index, the first subscript index refers to the electron spin state and the second to the nuclear spin state, respectively. For weak irradiation, meaning that
ω1,S ≪
ωm, the off-diagonal blocks that are relevant are the ones that connect almost degenerate Floquet states in the diagonal blocks (see
Fig. 5). These off-diagonal blocks contain the transition amplitudes of the corresponding transition. For DQ transitions in Floquet space,
e.g. (|
αS,
αI,
c1〉 ↔ |
βS,
βI,
c2〉), this means that
| |  | (63) |
has to hold resulting in the following expression for the microwave offset at resonance
| |  | (64) |
For ZQ transitions, we need to consider (|
αS,
βI,
c1〉 ↔ |
βS,
αI,
c2〉) and we obtain
| |  | (65) |
For spin systems in the weak coupling regime, where |
Azz|,|
B| ≪ |
ω0,I|, the resonance offset in
eqn (64) and (65) can be approximated by
| | | Ω(res,DQ)0,S ≈ (c2 − c1)ωm − |ω0,I| | (66) |
and
| | | Ω(res,ZQ)0,S ≈ (c2 − c1)ωm + |ω0,I|, | (67) |
respectively. The results in
eqn (66) and (67) have two important consequences. First of all, we can assign the different resonance peaks in the experimental DNP profile in
Fig. 4 to a specific Fourier index
q′ of the pulse sequence. So each resonance peak can be viewed as a modulation side band resulting from the fundamental modulation period of the applied pulse sequence. Second, according to
eqn (66) and (67) we observe that the resonance offset
Ω0,S for
c2 −
c1 =
q′ = ±1 (the resonance offset with largest transition amplitude in the DNP profile see discussion later) shifts towards larger offsets when going towards larger magnetic fields.
E.g. for a XiX sequence with
τp = 1 ns corresponding to

at a magnetic field of 28 T

, this would lead to resonance offset

for
c2 −
c1 =
q′ = ±1 of ∓700 MHz and ±1700 MHz. This can have important consequences for the hardware design of a pulsed DNP spectrometer. The relation between operator-based Floquet theory and matrix-based Floquet theory in the weak irradiation limit and weak coupling regime is discussed in ESI,
† Section K.
 |
| | Fig. 5 Part of the infinite-dimensional Floquet matrix of Fig. 3 for the Fourier states 〈1|, 〈0| and 〈−1|. We consider systems consisting of four sub-blocks in Fourier space. The system comprising the Fourier states 0 and −1 is indicated by an orange frame. There arise four different transitions marked in yellow, greenish-blue, brown and purple. These transitions can be further grouped in two ZQ- and two DQ-transitions (see Section 3.2.1). In the system comprising the Fourier states 〈1| and 〈−1| (light-green frames), the four sub-blocks in Fourier space are not connected. | |
At this point we need to consider the matrix elements that connect the ZQ/DQ transitions for the Fourier states c1 and c2, because these elements represent the transition amplitudes. A transition |c1〉 ↔ |c2〉 in Fourier space is connected by the off-diagonal blocks  with
with  as indicated in Fig. 5 by the orange frame for the case |0〉 ↔ |−1〉 and green frames for |1〉 ↔ |−1〉, respectively. In such a constellation one can observe a total of four different transitions (two ZQ- and two DQ-transitions) as marked with yellow and purple for the DQ case and greenish-blue and brown for the ZQ case, respectively. The transition amplitudes can be obtained from the prefactor of the DQ- and ZQ-operators terms in the off-diagonal elements
as indicated in Fig. 5 by the orange frame for the case |0〉 ↔ |−1〉 and green frames for |1〉 ↔ |−1〉, respectively. In such a constellation one can observe a total of four different transitions (two ZQ- and two DQ-transitions) as marked with yellow and purple for the DQ case and greenish-blue and brown for the ZQ case, respectively. The transition amplitudes can be obtained from the prefactor of the DQ- and ZQ-operators terms in the off-diagonal elements  in eqn (46) and are given by
in eqn (46) and are given by
| |  | (68) |
In the XiX case, whenever q′ = c2 − c1 is odd, the off-diagonal block in the Floquet matrix is non-zero and, therefore, the transition amplitudes are non-zero as can be seen by eqn (68) and Fig. 5. This results in a resonance in the DNP profile that we observe experimentally by a polarization transfer. These resonance conditions are also confirmed by a non-zero Fourier coefficient for the Hamiltonian  arising in numerical simulations using operator-based Floquet theory, e.g. for
arising in numerical simulations using operator-based Floquet theory, e.g. for  , ±48 or ±115 MHz in Fig. 4. Whenever q′ = c2 − c1 is even, we do not observe a resonance peak in the experimental DNP profile. In numerical simulation using operator-based Floquet theory we obtain a match in the resonance condition, but with the Fourier coefficient of the Hamiltonian
, ±48 or ±115 MHz in Fig. 4. Whenever q′ = c2 − c1 is even, we do not observe a resonance peak in the experimental DNP profile. In numerical simulation using operator-based Floquet theory we obtain a match in the resonance condition, but with the Fourier coefficient of the Hamiltonian  equal to 0. This represent cases like
equal to 0. This represent cases like 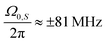 in Fig. 4.
in Fig. 4.
In the FS-XiX case, all Fourier coefficients of the microwave irradiation scheme are 0 except for |q′| = 1 and all off-diagonal blocks in the matrix-based Floquet representation are 0 except for the  block. Therefore, in the FS-XiX case only those resonance peaks remain in the DNP profile for which c2 − c1 = q′ = ±1 holds, i.e.,
block. Therefore, in the FS-XiX case only those resonance peaks remain in the DNP profile for which c2 − c1 = q′ = ±1 holds, i.e.,  and ±48 MHz in Fig. 4. By using eqn (66) and (67), these four resonance peaks can be grouped into two DQ transitions (
and ±48 MHz in Fig. 4. By using eqn (66) and (67), these four resonance peaks can be grouped into two DQ transitions ( and +18 MHz) and two ZQ transitions (
and +18 MHz) and two ZQ transitions (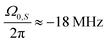 and +48 MHz). They are indicated in Fig. 5 by yellow colour for the DQ transition at
and +48 MHz). They are indicated in Fig. 5 by yellow colour for the DQ transition at  , by purple colour for the DQ transition at
, by purple colour for the DQ transition at 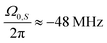 , by greenish-blue colour for the ZQ transition at
, by greenish-blue colour for the ZQ transition at 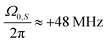 and by brown colour for the ZQ transition at
and by brown colour for the ZQ transition at  . All other resonances resulting from |c2 − c1| = |q′| ≠ 1 are absent in the experimental DNP profile. Numerical simulations using operator-based Floquet theory results in zero transition amplitude for these resonances.
. All other resonances resulting from |c2 − c1| = |q′| ≠ 1 are absent in the experimental DNP profile. Numerical simulations using operator-based Floquet theory results in zero transition amplitude for these resonances.
As outlined above, we can group the resonance peaks in Fig. 4 according to the Fourier index q′ (see Fig. 6 and Fig. S14 in ESI,† Section M). In Fig. 6 and Fig. S14 (ESI†) we compare the approach using the infinite-dimensional Floquet Hamiltonian, which results in analytical expressions for the resonance offset Ω0,S and transition amplitudes, with the numerical approach using operator-based Floquet theory for the DQ and ZQ resonance conditions. Both these approaches agree well with each other in the weak coupling regime (|Azz|,|B| ≪ |ω0,I|). The resonance offsets obtained by numerical simulation using operator-based Floquet theory are shown in dashed lines in those two figures. They overlap with the intersection points obtained by eqn (59) and (62) for DQ resonances and eqn (60) and (61) for ZQ resonances, respectively. The dashed lines are color-coded according to transitions between Floquet states that have a non-zero transition amplitude (black) and a zero transition amplitude (gray) according to eqn (68).
 |
| | Fig. 6 Comparison between the eigenvalues of a specific diagonal block in the infinite-dimensional Floquet Hamiltonian as given in eqn (59) (red color code) and eqn (62) (blue color code) with the numerical simulation using operator-based Floquet theory (dashed lines) for the XiX DNP sequence at 0.35 T and a pulse length τp of 15 ns. Shown here are resonance conditions for DQ transitions. A resonance condition occurs at a mw offset Ω0,S, where the eigenvalues are equal i.e. with c2 − c1 = q′. The Fourier components with c2 − c1 = q′. The Fourier components 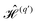 with Fourier index q′ are indicated above the dashed lines. In the weak irradiation regime (ω1,S ≪ ωm), each resonance condition can be assigned to a Fourier index of the infinite Floquet Hamiltonian and therefore to a mode in the Fourier expansion of the mw irradiation. The color code for the dashed lines indicates the strength of the resonance condition (see eqn (68)). For the analytical calculations of the eigenvalues according to eqn (59) and (62) the following parameters were used: with Fourier index q′ are indicated above the dashed lines. In the weak irradiation regime (ω1,S ≪ ωm), each resonance condition can be assigned to a Fourier index of the infinite Floquet Hamiltonian and therefore to a mode in the Fourier expansion of the mw irradiation. The color code for the dashed lines indicates the strength of the resonance condition (see eqn (68)). For the analytical calculations of the eigenvalues according to eqn (59) and (62) the following parameters were used:  , , 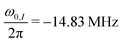 , Azz = B = 1 MHz. Hyperfine constants are given here in linear frequency, whereas they are expressed in angular frequency in eqn (59)–(62). , Azz = B = 1 MHz. Hyperfine constants are given here in linear frequency, whereas they are expressed in angular frequency in eqn (59)–(62). | |
A closer look at Fig. 4 reveals that there are some small peaks visible at the foot of the large assigned enhancements. As already explained in ref. 41 and 29 these small peaks correspond to three-spin electron-1H–1H transitions. One can use the same formalism described above for the two-spin case to obtain analytical expressions for the resonance offset Ω0,S and the transition amplitudes for the three-spin case (see ESI,† Section N).
3.2.2 Transition amplitudes.
The transition amplitudes according to eqn (68) can be compared to the numerically calculated Fourier coefficients of the Hamiltonian, as given in eqn (13), and to the experimental enhancements. This is graphically represented in Fig. 7. Note that, unlike the transition amplitudes, the numerical estimate for the enhancement as given in eqn (13) also contains the projection of ρ0 onto the effective field (factor 〈ρ0|Ŝz〉 in eqn (13)). However, for the pulsed DNP experiments presented in this work and for pulsed DNP experiments using low to moderate Rabi frequencies ω1,S, such that ω1,S ≪ ωm, this factor is close to 1 since the resonance offsets are large and the irradiation is weak. The experimental values were obtained by taking the maximal or minimal intensity of the DNP profile of Fig. 4. They were scaled linearly so that they agreed best with the theoretical black curve that represents the function 1/q. As seen from Fig. 7, both, the transition amplitudes obtained by matrix-based Floquet theory (analytical) and the Fourier coefficients of the Hamiltonian obtained from operator-based Floquet theory (numerical), scale with the inverse of the Fourier coefficient q′ (see black line in Fig. 7). For the analytical transition amplitudes this follows from inserting eqn (19) into eqn (68). There are a number of reasons for the observed differences between theory and experiments. In the theory so far we completely neglect relaxation effects, electron/proton concentrations or nuclear spin diffusion processes. These effects can contribute to the efficiency of the polarization transfer and therefore to the enhancement observed in experiments. Imperfections of the spectrometer, such as limited width of the microwave resonator mode or differences in non-linearity of the traveling wave tube amplifier at different frequencies can also influence the polarization enhancement. We tried to minimize effects of spectrometer imperfections during the acquisition by the techniques described in Section 5, and the ESI,† Sections E and F.
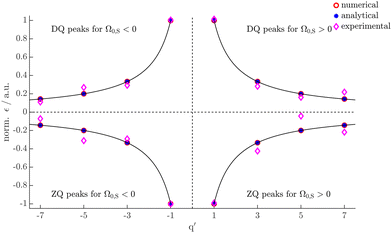 |
| | Fig. 7 Comparison between the transition amplitudes obtained by the analytical expression of eqn (68) obtained by matrix-based Floquet theory (red dots), the numerically calculated Fourier coefficients of the Hamiltonian in operator-based Floquet theory as given in eqn (14) (blue asterisks) and the experimental enhancements (magenta diamonds). The experimental values were obtained from a non-linear fit of the DNP profile presented already in Fig. 4. The black line is plotted to indicate the inverse scaling with respect to the Fourier index q of the analytical and numerical values. | |
3.2.3 Field dependence of DNP sequences.
In order to discuss the field dependence of a particular DNP sequence we need to emphasize some important points. We use the Fourier coefficients of the effective Hamiltonian obtained from operator-based Floquet theory (especially eqn (12) and (13)) for the analysis of the performance of a certain sequence.27–30 In the previous Section we presented analytical expressions for transition amplitudes obtained from the off-diagonal blocks in the infinite-dimensional Floquet matrix and showed that they are identical with the numerically calculated counterparts obtained from operator-based Floquet theory. Such an analysis does not cover any experimental parameters such as relaxation times, electron and proton concentration, nuclear spin diffusion, repeated application of the DNP sequence, or electronic imperfections. However, these parameters can play an important role in the polarization transfer and in the magnitude of the enhanced signal that is measured.
We restrict our discussion to the weak-irradiation regime, i.e., ω1,S ≪ ωm. In this regime the transition amplitude and, therefore, the transition probability between two almost degenerate Floquet states can be described by the matrix elements in the off-diagonal block of the Floquet matrix connecting the almost degenerate states. For a typical XiX sequence with short pulses τp, the modulation frequency ωm becomes large, which results for the sequence to be in the weak irradiation regime even for large Rabi frequencies ω1,S. The transition amplitudes as given by eqn (68) for non-zero resonance conditions (for odd values of c2 − c1 = q′) are
| |  | (69) |
First we notice that the transition amplitude is independent of the pulse length
τp (remember that

for odd
q). The rightmost approximate expression results from the definitions of the angles

,

and

. The argument inside the arctan function scales with the inverse of the Larmor frequency of the nuclei and, therefore, with the inverse of the external magnetic field. In the weak coupling regime, where |
Azz|,|
B| ≪ |
ω0,I|, we can invoke the small angle approximation and simplify

in
eqn (69). This approximation was already used to derive the prefactors for the solid-effect DNP mechanism in operator-based Floquet theory. We again obtain an unfavorable inverse scaling of the transition probability with larger magnetic fields. As
eqn (69) contains also
ω(max)1,S as a pre-factor, the transition amplitude can be kept field-independent by increasing the Rabi frequency linearly with the external
B0-field. This is the same scaling as required in CW DNP schemes.
To demonstrate our conclusion, we plotted in Fig. 8 the Fourier coefficient aeff, the offset Ω0,S and k0 obtained from operator-based Floquet theory at the resonance condition for two different cases. In the first case we look at a XiX DNP sequence with a pulse length τp = 15 ns and a fixed Rabi frequency 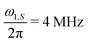 but for different magnetic fields. This case is shown in Fig. 8 in red circles. In blue diamonds in Fig. 8 we look at a XiX DNP sequence with a pulse length τp = 5 ns
but for different magnetic fields. This case is shown in Fig. 8 in red circles. In blue diamonds in Fig. 8 we look at a XiX DNP sequence with a pulse length τp = 5 ns  for the following nutation frequency and external magnetic field combinations i.e.
for the following nutation frequency and external magnetic field combinations i.e. ∈ {(0.1 MHz, 0.1 T), (0.35 MHz, 0.35 T), (1.3 MHz, 1.3 T), (3.5 MHz, 3.5 T), (7 MHz, 7 T), (14 MHz, 14 T), (28 MHz, 28 T)}. The pulse length of the second case was chosen to ensure that the weak irradiation regime (ω1,S ≪ ωm) is fulfilled for all combinations. For both cases we discuss and compare the DQ resonances for the difference in Fourier indices c2 − c1 = 1. The ZQ case with c2 − c1 = 1 is treated in Fig. S16 in ESI,† Section O. Note that the cases ZQ c2 − c1 = +1 and DQ c2 − c1 = −1 are equivalent (except for the sign of aeff and Ω0,S) due to the point symmetry of the ideal DNP profile.
∈ {(0.1 MHz, 0.1 T), (0.35 MHz, 0.35 T), (1.3 MHz, 1.3 T), (3.5 MHz, 3.5 T), (7 MHz, 7 T), (14 MHz, 14 T), (28 MHz, 28 T)}. The pulse length of the second case was chosen to ensure that the weak irradiation regime (ω1,S ≪ ωm) is fulfilled for all combinations. For both cases we discuss and compare the DQ resonances for the difference in Fourier indices c2 − c1 = 1. The ZQ case with c2 − c1 = 1 is treated in Fig. S16 in ESI,† Section O. Note that the cases ZQ c2 − c1 = +1 and DQ c2 − c1 = −1 are equivalent (except for the sign of aeff and Ω0,S) due to the point symmetry of the ideal DNP profile.
 |
| | Fig. 8 Calculated values for aeff, Ω0,S and k0 at resonance for different magnetic fields (0.1, 0.35, 1.3, 3.5, 7, 14, 28) T for DQ peaks with c2 − c1 = 1. The red circles represent a XiX DNP sequence with a fixed Rabi frequency  and pulse length τp = 15 ns. XiX DNP sequences with τp = 5 ns and Rabi frequencies that increase linearly with the external B0-field e.g. (0.1 MHz, 0.1 T), (0.35 MHz, 0.35 T), (1.3 MHz, 1.3 T), (3.5 MHz, 3.5 T), (7 MHz, 7 T), (14 MHz, 14 T) and (28 MHz, 28 T) for the Rabi frequency and the external magnetic field, respectively, are shown in blue diamonds. The linear behaviour of Ω0,S with respect to the external magnetic field can be explained by the approximation in eqn (66). Due to eqn (9) also k0 shows a similar linear behaviour. For the red circles, a fraction of aeff for two different magnetic fields scale with the inverse fraction of the corresponding magnetic fields, respectively. In contrast, aeff is constant over the different magnetic fields for a Rabi frequency that scales linearly with the magnetic field (blue diamonds). This is indicated by the dashed blue line. Please note the logarithmic scale in the y axis in the plot for aeff. and pulse length τp = 15 ns. XiX DNP sequences with τp = 5 ns and Rabi frequencies that increase linearly with the external B0-field e.g. (0.1 MHz, 0.1 T), (0.35 MHz, 0.35 T), (1.3 MHz, 1.3 T), (3.5 MHz, 3.5 T), (7 MHz, 7 T), (14 MHz, 14 T) and (28 MHz, 28 T) for the Rabi frequency and the external magnetic field, respectively, are shown in blue diamonds. The linear behaviour of Ω0,S with respect to the external magnetic field can be explained by the approximation in eqn (66). Due to eqn (9) also k0 shows a similar linear behaviour. For the red circles, a fraction of aeff for two different magnetic fields scale with the inverse fraction of the corresponding magnetic fields, respectively. In contrast, aeff is constant over the different magnetic fields for a Rabi frequency that scales linearly with the magnetic field (blue diamonds). This is indicated by the dashed blue line. Please note the logarithmic scale in the y axis in the plot for aeff. | |
From the first case with fixed Rabi frequency ω1,S, but varying magnetic field (red circles in Fig. 8) we can confirm the unfavorable scaling of the transition probability with larger magnetic fields. The numerically calculated Fourier coefficients of the Hamiltonian aeff as given in eqn (14) scale with the inverse of the magnetic field e.g. the fraction  . This relation is true for all comparisons within the used magnetic fields and is predicted by eqn (69). In Fig. 8 one can nicely observe the linear increase of the resonance offset Ω0,S for resonant DNP as already outlined in eqn (66) and (67). We find that k0 also depends linearly on the magnetic field within the quantization error of a discrete parameter. This can be explained by the increase of ω0,I in the resonance condition of eqn (9). k0 selects the Fourier coefficients
. This relation is true for all comparisons within the used magnetic fields and is predicted by eqn (69). In Fig. 8 one can nicely observe the linear increase of the resonance offset Ω0,S for resonant DNP as already outlined in eqn (66) and (67). We find that k0 also depends linearly on the magnetic field within the quantization error of a discrete parameter. This can be explained by the increase of ω0,I in the resonance condition of eqn (9). k0 selects the Fourier coefficients  of the effective Hamiltonian relevant for DNP (see eqn (10) and (11)). The Fourier coefficients
of the effective Hamiltonian relevant for DNP (see eqn (10) and (11)). The Fourier coefficients  tend to decrease for larger values of k0, which can be seen from eqn (6) and which is the actual reason for the decreased transition probability towards larger magnetic fields.
tend to decrease for larger values of k0, which can be seen from eqn (6) and which is the actual reason for the decreased transition probability towards larger magnetic fields.
Increasing the Rabi frequency linearly with the external B0-field keeps the transition amplitude field independent as one can see from the blue diamonds in Fig. 8. aeff is constant over the seven different combinations used in our simulations. Again, this behaviour can be explained with the right-hand side of eqn (69). Assuming that the strength of the pseudo-secular term B does not change (we assume that we polarize the same proton), the only terms that change within the seven combinations are ω(max)1,S and ω0,I. The ratio 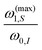 is kept constant here. Accordingly, the numerically calculated Fourier coefficients of the effective Hamiltonian in operator-based Floquet theory are the same.
is kept constant here. Accordingly, the numerically calculated Fourier coefficients of the effective Hamiltonian in operator-based Floquet theory are the same.
We discussed here the three parameters aeff, Ω0,S and k0 to reveal the behaviour of the XiX DNP pulse sequence when increasing the external magnetic field. As outlined in Section 2.1 the parameters ωeff,S and 〈ρ0|Ŝz〉 at resonance condition also influence the performance of the XiX DNP sequence. However, the behaviour of ωeff,S and 〈ρ0|Ŝz〉 with respect to different magnetic fields is difficult to predict/explain due to the merging of different effects (see Fig. S17 and S18 in ESI,† Section O). Cases for c2 − c1 = ±3 or even higher values are equivalent and are not discussed explicitly here.
3.2.4 Linewidth in the DNP profile.
So far our theory as outlined in Sections 2.1 and 2.3 does not include a line width provided by either relaxation of the electrons or the orientation dependence of the g value. In this situation, our theory predicts a DNP profile with infinitely narrow lines, since the resonance condition in eqn (9) and the analytical expression for the microwave offset at resonance (see eqn (64) and (65)) are fulfilled for only a single Ω0,S. However, the experimental DNP profile (see Fig. 4) clearly shows broadened lines. The fit of a field-swept EPR spectrum at X band (9.8 GHz) to a Gaussian line shape gave a FWHM of 6.23 MHz for the allowed transition (see Fig. S4 in ESI,† Section D). The resonances in the DNP profile in Fig. 4 were also fitted to a Gaussian line shape (see Fig. S19 in ESI,† Section P) and the FWHM of each individual peak was extracted (Table S2 in ESI,† Section P) with an average width of about 5.59 MHz.
A full numerical simulation using GAMMA42 showed that the line width in the DNP profile is influenced by the g-anisotropy of the electron and dominated by this effect in W band. The resulting simulated field profiles for XiX with τp = 5 ns and  at 80 K for B0 fields of 0.35 and 3.5 T are plotted in Fig. 9. We simulated the field profile using a two-spin electron–proton system with an electron–proton distance ren = 4.5 Å with either an axial g-tensor with a slight g-anisotropy of gxx = gyy = 2.00319 and gzz = 2.00258 or an isotropic g-tensor with giso = 2.00299.43 A more detailed description of the GAMMA simulations can be found in ESI,† Section Q. At 0.35 T one can barely see a difference between the field profile with g-anisotropy and with isotropic g-tensor because of the small g-anisotropy. However, at 3.5 T the field profile of the simulation using a g-anisotropy show resonance peaks that resemble the powder lineshape for a g-tensor with axial symmetry.
at 80 K for B0 fields of 0.35 and 3.5 T are plotted in Fig. 9. We simulated the field profile using a two-spin electron–proton system with an electron–proton distance ren = 4.5 Å with either an axial g-tensor with a slight g-anisotropy of gxx = gyy = 2.00319 and gzz = 2.00258 or an isotropic g-tensor with giso = 2.00299.43 A more detailed description of the GAMMA simulations can be found in ESI,† Section Q. At 0.35 T one can barely see a difference between the field profile with g-anisotropy and with isotropic g-tensor because of the small g-anisotropy. However, at 3.5 T the field profile of the simulation using a g-anisotropy show resonance peaks that resemble the powder lineshape for a g-tensor with axial symmetry.
 |
| | Fig. 9 Full numerical simulation of the field profile for XiX DNP with τp = 5 ns and  at 80 K for B0 fields of 0.35 T (X-band) top and 3.5 T (W-band) bottom for an isotropic g-tensor (red) and with an axial g-tensor with a slight g-anisotropy (blue). At X-band the difference between the simulations with and without g-anisotropy are very minor due to the small magnitude of the g-anisotropy. However, at W-band the resonance peaks in the DNP profile using a slight g-anisotropy are much broader than for the isotropic counterpart and resemble the g-tensor of the electron spin. All details of the numerical simulation can be found in ESI,† Section Q. at 80 K for B0 fields of 0.35 T (X-band) top and 3.5 T (W-band) bottom for an isotropic g-tensor (red) and with an axial g-tensor with a slight g-anisotropy (blue). At X-band the difference between the simulations with and without g-anisotropy are very minor due to the small magnitude of the g-anisotropy. However, at W-band the resonance peaks in the DNP profile using a slight g-anisotropy are much broader than for the isotropic counterpart and resemble the g-tensor of the electron spin. All details of the numerical simulation can be found in ESI,† Section Q. | |
3.3 TOP sequence
The discussion of the TOP DNP sequence in terms of its Fourier coefficients is not as straightforward as in the XiX case because the Fourier coefficients of the mw irradiation scheme now depend on pulse length τp and delay τd (see eqn (17) and (18)). In addition, the unmodulated Fourier coefficient a0 is non-zero. Therefore, we need two consecutively applied unitary transformations to approximately diagonalize  (see Section 2.4 or ESI,† Section B for more details). As a consequence of this second unitary transformation the transition amplitudes now depend on the mw offset. However, the resonance conditions in the TOP DNP sequence can still be assigned to a certain Fourier index q′ as will become clear later in this section.
(see Section 2.4 or ESI,† Section B for more details). As a consequence of this second unitary transformation the transition amplitudes now depend on the mw offset. However, the resonance conditions in the TOP DNP sequence can still be assigned to a certain Fourier index q′ as will become clear later in this section.
First let us take a closer look on how the four eigenvalues for the TOP DNP case look like. The four eigenvalues can be obtained from eqn (51) and are given as
| |  | (70) |
| |  | (71) |
| |  | (72) |
| |  | (73) |
The exact analytical expressions for

and
A′ can be found in
eqn (40) and (41), respectively. We can now invoke the same steps as for the XiX case and solve
| |  | (74) |
and
| |  | (75) |
for
Ω(res,DQ)0,S and
Ω(res,ZQ)0,S, respectively. This leads to simplified expressions for these conditions in the weak coupling regime (|
Azz|,|
B| ≪ |
ω0,I|). However, compared to the XiX case, we need to make an additional approximation. If the condition
| |  | (76) |
is fulfilled, we find the same approximate resonance conditions as in the XiX case (
e.g.eqn (66) and (67)), namely
| | | Ω(res,DQ)0,S ≈ (c2 − c1)ωm − |ω0,I| | (77) |
and
| | | Ω(res,ZQ)0,S ≈ (c2 − c1)ωm + |ω0,I|. | (78) |
Note that one needs to check for each case if the condition
eqn (76) is fulfilled for all resonances. If so, the transition amplitudes for the TOP case are given according to
eqn (56)| | 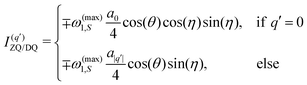 | (79) |
where

(see
eqn (49) and (50) for analytical expression for
θα and
θβ). As expected also the transition amplitudes for the TOP DNP sequence contain the term sin(
η). As explained in Section 3.2.3 this term scales unfavorably with the inverse of
B0 when invoking the weak coupling regime. For low to moderate
ω(max)1,Se.g. the weak irradiation regime,
θ is small and therefore cos(
θ) ≈ 1 holds.
We can now test the theory derived for TOP DNP against experimental observations reported in ref. 27. Tan et al. performed a TOP DNP experiment at 0.35 T (corresponding to ν0,I ≈ −14.83 MHz) using trityl radical Ox063 with the following parameters: 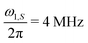 , τp = 28 ns, τd = 56 ns. This results in
, τp = 28 ns, τd = 56 ns. This results in  and a linear modulation frequency of
and a linear modulation frequency of 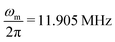 . They measured the DNP profile for this particular TOP DNP experiment from
. They measured the DNP profile for this particular TOP DNP experiment from  to +30 MHz and found the following values for the resonance offsets:
to +30 MHz and found the following values for the resonance offsets:  and ±27 MHz.27 They also found a DNP enhancement at
and ±27 MHz.27 They also found a DNP enhancement at  in numerical calculations using operator-based Floquet theory but with zero DNP enhancement in experiments. They explained the absence of DNP enhancement at this particular offset by assuming that the “ZQ- and DQ terms” (Fourier coefficients
in numerical calculations using operator-based Floquet theory but with zero DNP enhancement in experiments. They explained the absence of DNP enhancement at this particular offset by assuming that the “ZQ- and DQ terms” (Fourier coefficients  in eqn (10) and (11) in our notation) “have almost equal sizes” (and different sign). We can now use eqn (77)–(79) to explain the occurrence and absence of resonance peaks in the TOP DNP profile reported in ref. 27. In Table 2 we list the Fourier indices for the TOP DNP experiment for the fraction
in eqn (10) and (11) in our notation) “have almost equal sizes” (and different sign). We can now use eqn (77)–(79) to explain the occurrence and absence of resonance peaks in the TOP DNP profile reported in ref. 27. In Table 2 we list the Fourier indices for the TOP DNP experiment for the fraction  (see eqn (17) and (18)) along with the estimated values according to eqn (77) and (78) for different values of c2 − c1 = q′. We see that the approximations in eqn (77) and (78) give very accurate predictions for the microwave offsets Ω0,S, where DNP enhancements are expected. Eqn (79) together with eqn (17) and (18) fairly well predicts the amount of polarization transfer in the DNP profile presented in Fig. 2 in ref. 27. The resonances at
(see eqn (17) and (18)) along with the estimated values according to eqn (77) and (78) for different values of c2 − c1 = q′. We see that the approximations in eqn (77) and (78) give very accurate predictions for the microwave offsets Ω0,S, where DNP enhancements are expected. Eqn (79) together with eqn (17) and (18) fairly well predicts the amount of polarization transfer in the DNP profile presented in Fig. 2 in ref. 27. The resonances at  and 27 MHz show the largest enhancement, whereas the peak at
and 27 MHz show the largest enhancement, whereas the peak at 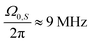 shows only a small enhancement, as predicted from theory. However, the resonance offset
shows only a small enhancement, as predicted from theory. However, the resonance offset  should in theory result in a similar enhancement as
should in theory result in a similar enhancement as  . The data shown in Fig. 2 in ref. 27 indicate a slightly smaller enhancement for
. The data shown in Fig. 2 in ref. 27 indicate a slightly smaller enhancement for  than for
than for 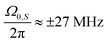 . We tentatively attribute this difference between simulation and experiment to the fact that the ZQ- and DQ enhancements occur at a frequency difference that is within the FWHM (∼6 MHz) of the EPR line of the trityl radical Ox063. This case is similar to the enhancements close to
. We tentatively attribute this difference between simulation and experiment to the fact that the ZQ- and DQ enhancements occur at a frequency difference that is within the FWHM (∼6 MHz) of the EPR line of the trityl radical Ox063. This case is similar to the enhancements close to  in the XiX field profile for τp = 45 ns shown in Fig. S13 (ESI†). As discussed in Section 3.2.4, the width of the experimental DNP profile at 0.35 T resembles the width of the EPR line. This may result in a partial cancellation of the ZQ- and DQ-enhancement due to the overlap of both peaks in the DNP profile and the different sign of their amplitudes. Using the theory outlined here, we can also explain the absence of DNP enhancement for
in the XiX field profile for τp = 45 ns shown in Fig. S13 (ESI†). As discussed in Section 3.2.4, the width of the experimental DNP profile at 0.35 T resembles the width of the EPR line. This may result in a partial cancellation of the ZQ- and DQ-enhancement due to the overlap of both peaks in the DNP profile and the different sign of their amplitudes. Using the theory outlined here, we can also explain the absence of DNP enhancement for  MHz. According to eqn (17) and (18) and Table 1 all Fourier coefficients of the pulse sequence are non-zero except for Fourier indices of q = 3, 6, 9, 12,…. Therefore, for c2 − c1 = q′ = ±3 we can calculate (by using eqn (77) and (78)) one pair of the offset to be
MHz. According to eqn (17) and (18) and Table 1 all Fourier coefficients of the pulse sequence are non-zero except for Fourier indices of q = 3, 6, 9, 12,…. Therefore, for c2 − c1 = q′ = ±3 we can calculate (by using eqn (77) and (78)) one pair of the offset to be 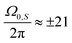 MHz. This means that the enhancement at this resonance offset is zero because the Fourier coefficient a3 is zero.
MHz. This means that the enhancement at this resonance offset is zero because the Fourier coefficient a3 is zero.
Table 2 Fourier coefficients of the TOP DNP sequence according to eqn (17) and (18) for 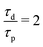 and the expected resonance offsets according to eqn (77) and (78) calculated for different c2 − c1 = q′. The values for the resonance offsets are compared to a DNP profile measured from
and the expected resonance offsets according to eqn (77) and (78) calculated for different c2 − c1 = q′. The values for the resonance offsets are compared to a DNP profile measured from  to
to  at 0.35 T with
at 0.35 T with  , τp = 28 ns, τd = 56 ns as reported in ref. 27. The italic entries are those resonances which were also observed experimentally in ref. 27. The bold entries were reported as being observed by numerical simulations using operator-based Floquet theory, but gave zero enhancement in the experimental DNP profile (see Table 1 for
, τp = 28 ns, τd = 56 ns as reported in ref. 27. The italic entries are those resonances which were also observed experimentally in ref. 27. The bold entries were reported as being observed by numerical simulations using operator-based Floquet theory, but gave zero enhancement in the experimental DNP profile (see Table 1 for  )
)
|
c
2 − c1 = q′ |
a
|q′|
|
(c2 − c1)νm + |ν0,I| [MHz] |
(c2 − c1)νm − |ν0,I| [MHz] |
| −4 |
0.138 |
−32.789 |
−62.449 |
| −3 |
0
|
−20.884
|
−50.544 |
| −2 |
−0.276 |
−8.980
|
−38.640 |
| −1 |
0.551 |
2.925
|
−26.735
|
| 0 |
0.667 |
14.830
|
−14.830
|
| 1 |
−0.551 |
26.735
|
−2.925
|
| 2 |
0.276 |
38.640 |
8.980
|
| 3 |
0
|
50.544 |
20.884
|
| 4 |
−0.138 |
62.449 |
32.789 |
3.4 TPPM sequence
The analytical expressions for the diagonal blocks of the Floquet matrix after the two diagonalization steps ( in eqn (57)) are similar for the TPPM and TOP sequences. Hence, we can adapt the results obtained for the TOP DNP sequence in Section 3.3 to the TPPM case. The only difference is the definition of the Fourier coefficient
in eqn (57)) are similar for the TPPM and TOP sequences. Hence, we can adapt the results obtained for the TOP DNP sequence in Section 3.3 to the TPPM case. The only difference is the definition of the Fourier coefficient  (compare eqn (17) and (23)). In both cases
(compare eqn (17) and (23)). In both cases 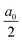 cannot exceed one. Therefore, the condition in eqn (76) is also valid in the TPPM case, resulting in the same approximations for Ω0,S as in the TOP DNP and XiX DNP case, e.g.eqn (77) and (78). Therefore, in the weak irradiation regime the resonance offsets Ω0,S of the three DNP sequences (TOP, XiX and TPPM) occur at the same spectral position when using the same modulation period ωm. Using eqn (57) and (58) the transition amplitudes between the Fourier states c1 and c2 for the TPPM case are then given as
cannot exceed one. Therefore, the condition in eqn (76) is also valid in the TPPM case, resulting in the same approximations for Ω0,S as in the TOP DNP and XiX DNP case, e.g.eqn (77) and (78). Therefore, in the weak irradiation regime the resonance offsets Ω0,S of the three DNP sequences (TOP, XiX and TPPM) occur at the same spectral position when using the same modulation period ωm. Using eqn (57) and (58) the transition amplitudes between the Fourier states c1 and c2 for the TPPM case are then given as| |  | (80) |
where q′ = c2 − c1 and  . For the angles θα and θβ one needs to insert
. For the angles θα and θβ one needs to insert  into in eqn (49) and (50). For the weak irradiation regime, i.e., for low to moderate ω(max)1,S and sufficient large ωm, cos(θ(+)) ≈ 1 holds. Thus for ϕ → 0 we obtain the same transition amplitude as for the SE and for
into in eqn (49) and (50). For the weak irradiation regime, i.e., for low to moderate ω(max)1,S and sufficient large ωm, cos(θ(+)) ≈ 1 holds. Thus for ϕ → 0 we obtain the same transition amplitude as for the SE and for  the transition amplitude as for the XiX sequence, respectively.
the transition amplitude as for the XiX sequence, respectively.
In Table 3 we compare the transition amplitudes for different DNP sequences applying the weak irradiation regime and the weak coupling regime. Please note that we do not distinguish between ZQ- and DQ-polarization transfer in that table and that q = |q′| = |c2 − c1|. Pulsed DNP sequences like XiX, TPPM or TOP in general show an inverse scaling of transfer efficiency with respect to the external magnetic field B0: the same as the CW experiments like SE.
Table 3 Comparison of transition amplitudes of different DNP sequences
| Experiment |
Transition amplitude |
Comment |
| NOVEL |
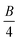
|
ω
(max)1,S = ω0,I |
| SE |

|
|
| XiX |

|
For odd q′,  |
| TOP |

|

|
|
|

|
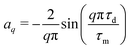
|
| TPPM |
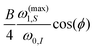
|
|
|
|

|
For odd q′,  |
4 Conclusions
Combining operator- and matrix-based Floquet theory for the description of a general amplitude-modulated pulsed DNP sequence, we can explain the origin of the resonance offsets where enhancement occurs and the corresponding enhancement factors for pulsed DNP experiments TOP,27 XiX28,29 or TPPM30 sequences. We show experimentally that the resonances in the XiX DNP case can be excited by a simple sine wave and originate from a single frequency mode of the Fourier expansion. The TPPM sequence can be viewed as an XiX sequence with an additional orthogonal CW component and will, therefore, have a similar excitation profile. Using matrix-based Floquet theory, we obtain analytical expressions for the mw offsets that correspond to resonance conditions as well as expressions for the corresponding transition amplitudes. The latter quantities allow a better understanding of the scaling behavior of pulsed DNP experiments with respect to the external magnetic B0-field.
The frequency offset at the resonance conditions and the magnitude of the transition amplitudes agree very well with the numerical results obtained using operator-based Floquet theory. Both complementary approaches are able to predict experimental observations, e.g., the mw offsets corresponding to resonance conditions and the magnitude of polarization transfer in an experimental DNP profile. However, important effects that influence experimental enhancements, such as relaxation, spin diffusion processes, experimental parameters like concentration of the radical and imperfections in mw irradiation are not covered by the presented theory. Regardless, the numerical results using effective Hamiltonians in operator-based Floquet theory as well as the analytical expressions resulting from matrix-based Floquet theory reveal an unfavorable scaling of the transition amplitudes with magnetic field. This result is not unexpected, since the effectiveness of the pseudo-secular BŜzÎx term in the Hamiltonian of eqn (1) for mixing tends to zero when the external magnetic field approaches the high-field limit for the nuclear spin.
The performance of a particular pulsed DNP sequence can be maintained if and only if the Rabi frequency on the electron spin is increased linearly with the external B0-field. Therefore, pulsed DNP at high B0-fields requires the use of high-power mw devices. Such devices are not yet readily available at higher mw frequencies.
An alternative approach is simultaneous irradiation of electrons and protons by mw and rf, respectively. Such techniques, reminiscent of Hartmann–Hahn cross polarization, do not rely on the pseudo-secular part of the hyperfine coupling. In these schemes, mixing is achieved by the modulation of the secular part of the hyperfine coupling AzzŜzÎz. A possible disadvantage of this approach would be that the transfer rate of polarization needs to compete with relaxation of the electrons and nuclei in the modulated spin-lock frame rather than with longitudinal relaxation of electrons and nuclei.
As confirmed by numerical simulations, part of the line width observed in experimental DNP profiles can be attributed to the anisotropy of the g-tensor. As expected, the g tensor contribution becomes dominant at larger magnetic fields. At higher fields, this effect could lead to an overlap of ZQ- and DQ-transfer resulting in a diminished polarization transfer if the bandwidth of the sequence is large. However, sequences currently in use have a quite narrow DNP matching profile and will result in orientation selection for the g tensor.
The observations in this publication have implications for the future design of new pulsed DNP sequences to circumvent the unfavorable scaling of the effective Hamiltonian with respect to the external B0-field. Moreover, we were able to show that an enhanced NMR signal can be achieved by a simple cosine or sine wave. This opens new possibilities since those trigonometric functions are already implemented on most AWG and are less prone to electronic imperfections (pulse transients, finite rise times) than rectangular pulses. On the other hand, limited rise time of rectangular pulses corresponds to an attenuation of higher harmonics of the modulation frequency and is, thus, not expected to substantially reduce performance of pulsed DNP schemes.
5 Materials and methods
5.1 Sample preparation
In all experiments a 5 mM sample of OX063 trityl radical dissolved in DNP juice (glycerol-d8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O
D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O, 6
H2O, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume) was used. The sample was prepared by the following procedure: 1.69 mg of the trityl (MW = 1359 g mol−1) were dissolved in 24.15 mg water (MW = 18.02 g mol−1, ρ0 = 0.997 g mL−1) and 80.93 mg D2O (MW = 20.03 g mol−1, ρ0 = 1.11 g mL−1). This gives a ∼1.2 μmol solution of trityl dissolved in a D2O
1 by volume) was used. The sample was prepared by the following procedure: 1.69 mg of the trityl (MW = 1359 g mol−1) were dissolved in 24.15 mg water (MW = 18.02 g mol−1, ρ0 = 0.997 g mL−1) and 80.93 mg D2O (MW = 20.03 g mol−1, ρ0 = 1.11 g mL−1). This gives a ∼1.2 μmol solution of trityl dissolved in a D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O matrix of 3
H2O matrix of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume. From that resulting solution 48.6 μL were added to 99.92 mg glycerol-d8 (MW = 100.14 g mol−1, ρ0 = 1.371 g mL−1) to give the desired 5 mM solution of trityl in DNP juice. 40 μL of that final solution were added to a 3 mm OD quartz capillary. All masses were weighted in with a AT261 Delta Range scale with a precision of 0.01 mg. A pipetman from GILSON (P100) with volumes adjustable to 0.1 μL precision was used to transfer and measure the volumes.
1 by volume. From that resulting solution 48.6 μL were added to 99.92 mg glycerol-d8 (MW = 100.14 g mol−1, ρ0 = 1.371 g mL−1) to give the desired 5 mM solution of trityl in DNP juice. 40 μL of that final solution were added to a 3 mm OD quartz capillary. All masses were weighted in with a AT261 Delta Range scale with a precision of 0.01 mg. A pipetman from GILSON (P100) with volumes adjustable to 0.1 μL precision was used to transfer and measure the volumes.
All experiments were conducted at 80 K and an external magnetic field of 0.35 T (X-band). The sample was flash frozen in liquid nitrogen before measuring in the resonator.
5.2 EPR/NMR spectroscopy
All experiments were acquired on a home-built X-band spectrometer similar to the spectrometer as described in ref. 44. A constant temperature of 80 K was achieved with closed cycle cryogen-free cryostat from Cryogen Limited. An arbitrary waveform generator (Keysight model M8190A) was used to generate mw pulses and the pulses were amplified using a 1 kW traveling wave tube (TWT) amplifier. The Hahn echoes were recorded using a digitizer running at 1.8 GSa s−1 (SP devices ADQ412). A Bruker EN4118A-MD4 resonator was used with a home-built external rf tuning and matching box. NMR experiments were performed with an OpenCore spectrometer.45,46 A schematic representation of a general DNP experiment used in this work can be seen in Fig. 10. Each DNP sequence was started with a 1H saturation pulse train consisting of eleven 100° pulses spaced by 1 ms to destroy any polarization on the protons. Afterwards, each basic DNP block was repeated k times to give a total contact time tcon = k·τm (gray loop in Fig. 10). The total DNP experiment was then repeated h times to give a total build-up time tDNP = h·trep (outer black loop in Fig. 10). The enhanced proton signal was finally read out by a solid echo consisting of two 90° pulses of 2.5 μs length separated by tSE = 20 μs. For the solid echo a eight step phase cycle was used with {x, x, y, y, −x, −x, −y, −y} for the first pulse and detection and {y, −y, x, −x, y, −y, x, −x} for the second pulse. For most of the experiments the following values were used: tcon = 5 μs, trep = 2 ms and h = 1000. To record a DNP profile, the mw frequency on the EPR spectrometer was adjusted accordingly and a total of 8 scans were recorded for every mw frequency. The build-up curves were recorded by incrementing either h or k at a given resonance offset and keeping all other parameters constant. The reference experiment was recorded the same way with the exception that the mw irradiation was turned off and a delay of 180 s ≈ 5·T1,n was used between two consecutive scans. A total of 512 scans were recorded and accumulated for the reference experiment. To process the data, a cosine-squared apodization function was used and time-domain data was zero-filled to twice the number of recorded data points. After Fourier transformation of the resulting time-domain data, the peak was fitted by a Lorentzian function and integrated using a standard library function in MATLAB over a symmetric integration window. The range of the integration window was constant for all individual recordings as well as for the reference experiment. The experimental enhancement was calculated by dividing the integral of the enhanced signal by the integral of the reference signal normalized by the number of scans e.g. normalized by 8 for a DNP experiment and by 512 for the reference experiment.
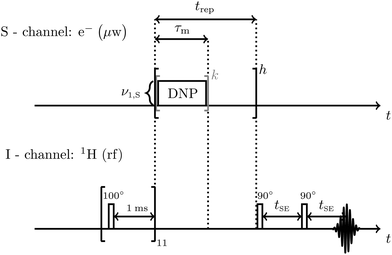 |
| | Fig. 10 General DNP pulse sequence used in the realm of this work. The saturation train on the 1H channel is followed by a repeated DNP cycle (h-loop). The actual DNP sequence, either XiX or FS-XiX is repeated k-times. The enhanced 1H signal is afterwards recorded with a solid echo with two 90° pulses of 2.5 μs length separated by tSE = 20 μs. A eight-step phase cycle was used for the solid echo with {x, x, y, y, −x, −x, −y, −y} for the first pulse and detection and {y, −y, x, −x, y, −y, x, −x} for the second pulse. | |
An echo-detected nutation experiment was used to compensate for the limited width of the microwave resonator mode and differences in non-linearity of the traveling wave tube amplifier at different frequencies.47 The result of those experiments can be found in the ESI,† Sections E and F. All experimental spectra and plots for the DNP, EPR and NMR experiments together with the complete experimental parameters can be found in ESI,† Sections C–I.
Data availability
The data that support the findings of this study are available at https://doi.org/10.3929/ethz-b-000675865.
Author contributions
M. E. and G. J. designed the research. Simulation and data evaluation script were written by G. M. C., N. W. and M. E., G. M. C. performed all experimental measurements. G. M. C. and M. E. wrote the first draft and all authors were involved in editing the final manuscript.
Conflicts of interest
The authors declare that they have no conflicts of interest.
Acknowledgements
Daniel Klose and Rene Tschaggelar are acknowledged for building the EPR spectrometer and Kazuyuki Takeda for help and discussion about the Opencore NMR spectrometer. We thank Mohammed M. Albannay for help in installing the Opencore NMR spectrometer. Oliver Oberhänsli is acknowledged for mechanical support. This research has been supported by the ETH Zürich and the Schweizerischer Nationalfonds zur Förderung der Wissenschaftlichen Forschung (grant no. 200020_188988 and 200020_219375).
Notes and references
- A. Abragam and M. Goldman, Rep. Prog. Phys., 1978, 41, 395–467 CrossRef CAS.
- A. S. Lilly Thankamony, J. J. Wittmann, M. Kaushik and B. Corzilius, Prog. Nucl. Magn. Reson. Spectrosc., 2017, 102–103, 120–195 CrossRef CAS PubMed.
- L. R. Becerra, G. J. Gerfen, R. J. Temkin, D. J. Singel and R. G. Griffin, Phys. Rev. Lett., 1993, 71, 3561–3564 CrossRef CAS PubMed.
- B. Corzilius, A. A. Smith and R. G. Griffin, J. Chem. Phys., 2012, 137, 21–27 CrossRef PubMed.
- T. Biedenbänder, V. Aladin, S. Saeidpour and B. Corzilius, Chem. Rev., 2022, 122, 9738–9794 CrossRef PubMed.
- J. H. Ardenkjær-Larsen, B. Fridlund, A. Gram, G. Hansson, L. Hansson, M. H. Lerche, R. Servin, M. Thaning and K. Golman, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10158–10163 CrossRef PubMed.
- F. Jähnig, G. Kwiatkowski and M. Ernst, J. Magn. Reson., 2016, 264, 22–29 CrossRef PubMed.
- F. Jähnig, G. Kwiatkowski, A. Däpp, A. Hunkeler, B. H. Meier, S. Kozerke and M. Ernst, Phys. Chem. Chem. Phys., 2017, 19, 19196–19204 RSC.
- D. Kurzbach and S. Jannin, eMagRes, 2018, 7, 117–132 CAS.
- S. Jannin, J. N. Dumez, P. Giraudeau and D. Kurzbach, J. Magn. Reson., 2019, 305, 41–50 CrossRef CAS PubMed.
- S. J. Elliott, Q. Stern, M. Ceillier, T. El Daraï, S. F. Cousin, O. Cala and S. Jannin, Prog. Nucl. Magn. Reson. Spectrosc., 2021, 126–127, 59–100 CrossRef CAS PubMed.
- A. W. Overhauser, Phys. Rev., 1953, 92, 411–415 CrossRef CAS.
- C. D. Jeffries, Phys. Rev., 1957, 106, 164–165 CrossRef CAS.
-
A. Abragam and W. G. Proctor, Une nouvelle methode de polarization dynamique des noyaux atomiques dans les solides, Comptes Rendus Hebdomadaires des Seances de l Academie des Sciences, 246th edn, 1958, pp. 2253–2256 Search PubMed.
- C. D. Jeffries, Phys. Rev., 1960, 117, 1056–1069 CrossRef CAS.
- W. T. Wenckebach, Appl. Magn. Reson., 2008, 34, 227–235 CrossRef.
- C. F. Hwang and D. A. Hill, Phys. Rev. Lett., 1967, 18, 110–112 CrossRef CAS.
- C. F. Hwang and D. A. Hill, Phys. Rev. Lett., 1967, 19, 1011–1014 CrossRef CAS.
- A. Equbal, A. Leavesley, S. K. Jain and S. Han, J. Phys. Chem. Lett., 2019, 10, 548–558 CrossRef CAS PubMed.
- B. N. Provotorov, Sov. Phys. – JETP, 1962, 14, 1126–1131 Search PubMed.
- M. Borghini, Phys. Rev. Lett., 1968, 20, 419–421 CrossRef CAS.
- A. Henstra, P. Dirksen, J. Schmidt and W. T. Wenckebach, J. Magn. Reson., 1988, 77, 389–393 Search PubMed.
- T. V. Can, J. J. Walish, T. M. Swager and R. G. Griffin, J. Chem. Phys., 2015, 143, 1–8 CrossRef PubMed.
- G. Mathies, S. Jain, M. Reese and R. G. Griffin, J. Phys. Chem. Lett., 2016, 7, 111–116 CrossRef CAS PubMed.
- T. V. Can, R. T. Weber, J. J. Walish, T. M. Swager and R. G. Griffin, J. Chem. Phys., 2017, 146, 1–7 CrossRef PubMed.
- K. O. Tan, S. Jawla, R. J. Temkin and R. G. Griffin, eMagRes, 2019, 8, 339–352 CAS.
- K. O. Tan, C. Yang, R. T. Weber, G. Mathies and R. G. Griffin, Sci. Adv., 2019, 5, 1–7 Search PubMed.
- V. S. R. Redrouthu and G. Mathies, J. Am. Chem. Soc., 2022, 144, 1513–1516 CrossRef CAS PubMed.
- N. Wili, A. B. Nielsen, L. A. Völker, L. Schreder, N. C. Nielsen, G. Jeschke and K. O. Tan, Sci. Adv., 2022, 8, 1–13 Search PubMed.
- V. S. R. Redrouthu, S. Vinod-Kumar and G. Mathies, J. Chem. Phys., 2023, 159, 1–12 CrossRef PubMed.
- I. Scholz, J. D. Van Beek and M. Ernst, Solid State Nucl. Magn. Reson., 2010, 37, 39–59 CrossRef CAS PubMed.
- M. Leskes, P. K. Madhu and S. Vega, Prog. Nucl. Magn. Reson. Spectrosc., 2010, 57, 345–380 CrossRef CAS PubMed.
- J. H. Shirley, Phys. Rev., 1965, 138, B979–B987 CrossRef.
- A. D. Bain and R. S. Dumont, Concepts Magn. Reson., 2001, 13, 159–170 CrossRef.
- S. Vega, eMagRes, 2007, 2007, 1–16 Search PubMed.
- K. L. Ivanov, K. R. Mote, M. Ernst, A. Equbal and P. K. Madhu, Prog. Nucl. Magn. Reson. Spectrosc., 2021, 126–127, 17–58 CrossRef CAS PubMed.
- F. J. Dyson, Phys. Rev., 1949, 75, 486–502 CrossRef.
- S. K. Jain, G. Mathies and R. G. Griffin, J. Chem. Phys., 2017, 147, 1–13 CrossRef PubMed.
- M. Ernst, H. Geen and B. H. Meier, Solid State Nucl. Magn. Reson., 2006, 29, 2–21 CrossRef CAS PubMed.
- G. Jeschke and A. Schweiger, J. Chem. Phys., 1996, 105, 2199–2211 CrossRef CAS.
- K. O. Tan, M. Mardini, C. Yang, J. H. Ardenkjær-Larsen and R. G. Griffin, Sci. Adv., 2019, 5, 1–7 Search PubMed.
- S. A. Smith, T. O. Levante, B. H. Meier and R. R. Ernst, J. Magn. Reson., Ser. A, 1994, 106, 75–105 CrossRef CAS.
- L. Lumata, Z. Kovacs, A. D. Sherry, C. Malloy, S. Hill, J. Van Tol, L. Yu, L. Song and M. E. Merritt, Phys. Chem. Chem. Phys., 2013, 15, 9800–9807 RSC.
- A. Doll and G. Jeschke, J. Magn. Reson., 2017, 280, 46–62 CrossRef CAS PubMed.
- K. Takeda, Rev. Sci. Instrum., 2007, 78, 1–6 CrossRef PubMed.
- K. Takeda, J. Magn. Reson., 2008, 192, 218–229 CrossRef CAS PubMed.
- A. Doll, S. Pribitzer, R. Tschaggelar and G. Jeschke, J. Magn. Reson., 2013, 230, 27–39 CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Nino
Wili
a,
Nino
Wili
 b,
Gunnar
Jeschke
b,
Gunnar
Jeschke
 *a and
Matthias
Ernst
*a and
Matthias
Ernst
 *a
*a
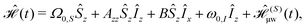
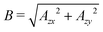 the pseudo-secular part of the hyperfine coupling. The electron resonance frequency is given by
the pseudo-secular part of the hyperfine coupling. The electron resonance frequency is given by  and for the nucleus by ω0,I = −γIB0 while ωμw is the microwave frequency and B0 is the external static magnetic field applied along the laboratory z-axis. The orientation-dependent gzz value determines the frequency offset from the mw irradiation. For low static magnetic fields, the isotropic value giso can be used instead. The Hamiltonian
and for the nucleus by ω0,I = −γIB0 while ωμw is the microwave frequency and B0 is the external static magnetic field applied along the laboratory z-axis. The orientation-dependent gzz value determines the frequency offset from the mw irradiation. For low static magnetic fields, the isotropic value giso can be used instead. The Hamiltonian  refers to the Hamiltonian of the μw irradiation and can be written as
refers to the Hamiltonian of the μw irradiation and can be written as
 . Such a transformation can be analytically written as
. Such a transformation can be analytically written as
 where
where ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is the Dyson time-ordering operator37 and a(S)ξχ(t) are the time-dependent elements of a 3 × 3 rotation matrix. Note that in the following we drop the “dash” on the S spin operators when referring to the interaction frame. We consider time-periodic irradiation schemes with a modulation period τm with
is the Dyson time-ordering operator37 and a(S)ξχ(t) are the time-dependent elements of a 3 × 3 rotation matrix. Note that in the following we drop the “dash” on the S spin operators when referring to the interaction frame. We consider time-periodic irradiation schemes with a modulation period τm with  . This results in a modulation frequency
. This results in a modulation frequency



![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )± = a(k,
)± = a(k,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )zx ∓ ia(k,
)zx ∓ ia(k,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )zy and Ŝ± = Ŝx ± iŜy. Please note that we assumed a negative Larmor frequency for the nuclear spin corresponding to a positive gyromagnetic ratio. The Hamiltonian in eqn (7) contains three fundamental frequencies |ω0,I|, ωeff,S and ωm and we can write it as a Fourier series (see last line in eqn (7)). The first-order effective Hamiltonian based on triple-mode Floquet theory is, thus, given by
)zy and Ŝ± = Ŝx ± iŜy. Please note that we assumed a negative Larmor frequency for the nuclear spin corresponding to a positive gyromagnetic ratio. The Hamiltonian in eqn (7) contains three fundamental frequencies |ω0,I|, ωeff,S and ωm and we can write it as a Fourier series (see last line in eqn (7)). The first-order effective Hamiltonian based on triple-mode Floquet theory is, thus, given by
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 0 sum over only the values where the resonance condition
0 sum over only the values where the resonance condition![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 0ωeff,S = 0
0ωeff,S = 0![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 0) and its negative (1, −k0, −
0) and its negative (1, −k0, −![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 0), we obtain a first-order effective Hamiltonian for the ZQ and DQ-transfer given by
0), we obtain a first-order effective Hamiltonian for the ZQ and DQ-transfer given by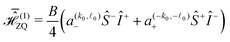

![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 0 changes, e.g.,
0 changes, e.g.,  in case of a negative Larmor frequency is
in case of a negative Larmor frequency is  in case of a positive Larmor frequency. The polarization transfer ρ0 → Îz can be calculated following ref. 29 by
in case of a positive Larmor frequency. The polarization transfer ρ0 → Îz can be calculated following ref. 29 by
 and the upper binary operator in this equation refers to the ZQ case and the lower one to the DQ case, respectively. Again, eqn (12) is valid for the case of a positive gyromagnetic ratio of the nuclear spin (negative Larmor frequency). For the case of a negative gyromagnetic ratio of the nuclear (positive Larmor frequency) the sign for the indices k0 and
and the upper binary operator in this equation refers to the ZQ case and the lower one to the DQ case, respectively. Again, eqn (12) is valid for the case of a positive gyromagnetic ratio of the nuclear spin (negative Larmor frequency). For the case of a negative gyromagnetic ratio of the nuclear (positive Larmor frequency) the sign for the indices k0 and ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 0 changes, e.g. for the ZQ case
0 changes, e.g. for the ZQ case  would change to
would change to 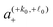 . Also note that in case of a positive gyromagnetic ratio of the nuclear spin the ZQ enhancement gets negative and the DQ enhancement positive due to the ratio
. Also note that in case of a positive gyromagnetic ratio of the nuclear spin the ZQ enhancement gets negative and the DQ enhancement positive due to the ratio 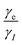 . However, for a negative gyromagnetic ratio of the nuclear spin the ZQ enhancement is positive and the DQ enhancement is negative. The factor 〈ρ0|Ŝz〉 takes into account that only the part of the electron polarization that is along the effective field can be transferred to the nuclei. For small times t and using
. However, for a negative gyromagnetic ratio of the nuclear spin the ZQ enhancement is positive and the DQ enhancement is negative. The factor 〈ρ0|Ŝz〉 takes into account that only the part of the electron polarization that is along the effective field can be transferred to the nuclei. For small times t and using  the performance of a certain pulse scheme can be roughly estimated by29
the performance of a certain pulse scheme can be roughly estimated by29

 describes the direction of the effective field in the electron spin coordinate system (see Fig. S1 in ESI,† Section A). In case of the solid effect16 we can invoke the small-angle approximation (Ω0,S ≫ ω1,S), where
describes the direction of the effective field in the electron spin coordinate system (see Fig. S1 in ESI,† Section A). In case of the solid effect16 we can invoke the small-angle approximation (Ω0,S ≫ ω1,S), where  leads to a prefactor of
leads to a prefactor of  . For NOVEL23,25
. For NOVEL23,25 and the prefactor is
and the prefactor is  . Section A of the ESI† contains the derivation to calculate the Fourier coefficients of the Hamiltonian analytically starting from eqn (6). The effective Hamiltonian of eqn (15) as well as the scaling factor for NOVEL and SE were already reported in ref. 38.
. Section A of the ESI† contains the derivation to calculate the Fourier coefficients of the Hamiltonian analytically starting from eqn (6). The effective Hamiltonian of eqn (15) as well as the scaling factor for NOVEL and SE were already reported in ref. 38.
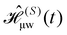 in eqn (1) in detail. In order to apply Floquet theory the only requirement is that the mw irradiation is time periodic with a modulation period τm. When we limit the discussion to amplitude-modulated monochromatic pulses (ϕ(t) = ϕ), the pulse amplitude ω1,S(t) becomes the only parameter that has to fulfill the time-periodic restriction. In the following we set ϕ = 0 for simplicity of the notation. Any time-periodic amplitude modulation can then be represented as a half-range Fourier expansion of the form
in eqn (1) in detail. In order to apply Floquet theory the only requirement is that the mw irradiation is time periodic with a modulation period τm. When we limit the discussion to amplitude-modulated monochromatic pulses (ϕ(t) = ϕ), the pulse amplitude ω1,S(t) becomes the only parameter that has to fulfill the time-periodic restriction. In the following we set ϕ = 0 for simplicity of the notation. Any time-periodic amplitude modulation can then be represented as a half-range Fourier expansion of the form
![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) . ω(max)1,S is the maximum value of the time-dependent pulse amplitude ω1,S(t). Note the difference between the Fourier coefficients of the microwave irradiation scheme (aq and bq) as given in eqn (16) and the Fourier coefficients of the interaction-frame trajectory (a(k,
. ω(max)1,S is the maximum value of the time-dependent pulse amplitude ω1,S(t). Note the difference between the Fourier coefficients of the microwave irradiation scheme (aq and bq) as given in eqn (16) and the Fourier coefficients of the interaction-frame trajectory (a(k,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) )zχ) as calculated in eqn (6). For CW irradiation all Fourier coefficients in eqn (16) are zero except for a0, which is equal to 2 and ω1,S(t) = ω(max)1,S. For an even pulse amplitude function ω1,S(t) all odd Fourier coefficients (bq) are 0. In contrast for an odd function ω1,S(t) all even coefficients are 0, e.g. a0 and aq. In the following three sections we will discuss pulsed DNP schemes, first the Time-optimized Pulsed (TOP) DNP27 sequence, second the XiX (X-inverse-X) DNP sequence28,29 and last the Two-Pulse Phase Modulation (TPPM) DNP sequence.30 We represent them by the half-range Fourier expansion as given in eqn (16).
)zχ) as calculated in eqn (6). For CW irradiation all Fourier coefficients in eqn (16) are zero except for a0, which is equal to 2 and ω1,S(t) = ω(max)1,S. For an even pulse amplitude function ω1,S(t) all odd Fourier coefficients (bq) are 0. In contrast for an odd function ω1,S(t) all even coefficients are 0, e.g. a0 and aq. In the following three sections we will discuss pulsed DNP schemes, first the Time-optimized Pulsed (TOP) DNP27 sequence, second the XiX (X-inverse-X) DNP sequence28,29 and last the Two-Pulse Phase Modulation (TPPM) DNP sequence.30 We represent them by the half-range Fourier expansion as given in eqn (16).


![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) exhibit a much more complex behaviour. For certain combinations of the parameters τd, τp and q certain coefficients aq can be 0. This is summarized in Table 1 and has important consequences for the discussion in Section 3.3.
exhibit a much more complex behaviour. For certain combinations of the parameters τd, τp and q certain coefficients aq can be 0. This is summarized in Table 1 and has important consequences for the discussion in Section 3.3.

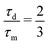 is used for this particular TOP sequence (see Table 1). In the XiX case, the first Fourier mode b1, the third mode b3 and the fifth mode b5 are represented by red, magenta and violet dashed lines respectively.
is used for this particular TOP sequence (see Table 1). In the XiX case, the first Fourier mode b1, the third mode b3 and the fifth mode b5 are represented by red, magenta and violet dashed lines respectively.
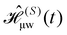 as given in eqn (2). By inserting a function ϕ(t) switching from +ϕ to −ϕ at a modulation frequency ωm we obtain
as given in eqn (2). By inserting a function ϕ(t) switching from +ϕ to −ϕ at a modulation frequency ωm we obtain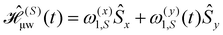

![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) q = sin(ϕ)bq as performed in the last step of eqn (22). The amplitude of the CW contribution is given by eqn (21). Hence, due to the effective CW part in TPPM, the a0 Fourier coefficient of the microwave irradiation is
q = sin(ϕ)bq as performed in the last step of eqn (22). The amplitude of the CW contribution is given by eqn (21). Hence, due to the effective CW part in TPPM, the a0 Fourier coefficient of the microwave irradiation is
 , which corresponds to the XiX limit of TPPM with phase y. Therefore, the TPPM sequence can be viewed as a combination of the CW irradiation and an orthogonal XiX DNP sequence. The time-dependent modulation can be treated in a similar way as in the XiX sequence with the exception that there is an additional time-independent CW part.
, which corresponds to the XiX limit of TPPM with phase y. Therefore, the TPPM sequence can be viewed as a combination of the CW irradiation and an orthogonal XiX DNP sequence. The time-dependent modulation can be treated in a similar way as in the XiX sequence with the exception that there is an additional time-independent CW part.

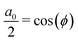 and aq = 0 ∀ q ≠ 0. The Fourier coefficients are
and aq = 0 ∀ q ≠ 0. The Fourier coefficients are 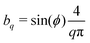 for odd values of q. The Hamiltonian in eqn (24) can be expressed as a Fourier expansion
for odd values of q. The Hamiltonian in eqn (24) can be expressed as a Fourier expansion


 . We thus obtain the elements of the infinite-dimensional Floquet matrix
. We thus obtain the elements of the infinite-dimensional Floquet matrix  as36
as36
 is a specific element of the Floquet matrix, which can be obtained from eqn (26) and (27). In the upcoming sections, we use Greek letters to represent the eigenvalues of the spin operator in Hilbert-space and Latin letters to denote the Fourier harmonics of amplitude modulation of the μw irradiation scheme. Be aware that in eqn (28) the difference c1 − c2 between two Fourier indices in Floquet space has to match the Fourier index q′ in eqn (25)–(27). According to eqn (28) the central blocks of the infinite-dimensional Floquet matrix (blocks where q′ = c1 − c2 = 0) contain the Fourier component
is a specific element of the Floquet matrix, which can be obtained from eqn (26) and (27). In the upcoming sections, we use Greek letters to represent the eigenvalues of the spin operator in Hilbert-space and Latin letters to denote the Fourier harmonics of amplitude modulation of the μw irradiation scheme. Be aware that in eqn (28) the difference c1 − c2 between two Fourier indices in Floquet space has to match the Fourier index q′ in eqn (25)–(27). According to eqn (28) the central blocks of the infinite-dimensional Floquet matrix (blocks where q′ = c1 − c2 = 0) contain the Fourier component  (eqn (26)) with frequency offsets
(eqn (26)) with frequency offsets  (last term of eqn (28)). The off-diagonal blocks (blocks where q′ = c1 − c2 ≠ 0) contain the Fourier components
(last term of eqn (28)). The off-diagonal blocks (blocks where q′ = c1 − c2 ≠ 0) contain the Fourier components  as given in eqn (27). In the upcoming sections we will use the Fourier index q′ of the Fourier expansion in Hilbert space to denote connected Fourier states in Floquet space. For a two-spin 1/2 system, the Fourier components
as given in eqn (27). In the upcoming sections we will use the Fourier index q′ of the Fourier expansion in Hilbert space to denote connected Fourier states in Floquet space. For a two-spin 1/2 system, the Fourier components  are 4 × 4 matrices within the basis set |κ, η〉 where κ ∈ {αS,βS} and η ∈ {αI,βI}. Part of the infinite-dimensional Floquet matrix
are 4 × 4 matrices within the basis set |κ, η〉 where κ ∈ {αS,βS} and η ∈ {αI,βI}. Part of the infinite-dimensional Floquet matrix  is presented in Fig. 3.
is presented in Fig. 3.

 , which is in case of a two-spin system consisting of spin 1/2 particles a 4 × 4 matrices. The expression
, which is in case of a two-spin system consisting of spin 1/2 particles a 4 × 4 matrices. The expression  in red on the central block
in red on the central block 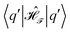 results from last term of eqn (28).
results from last term of eqn (28).
 as given in eqn (26). In case of the XiX DNP sequence (see Section 2.2.2) the odd Fourier coefficients bq are the non-zero ones (see eqn (19)) resulting in
as given in eqn (26). In case of the XiX DNP sequence (see Section 2.2.2) the odd Fourier coefficients bq are the non-zero ones (see eqn (19)) resulting in



 in the infinite-dimensional Floquet matrix is given in eqn (26) in its most general analytical form.
in the infinite-dimensional Floquet matrix is given in eqn (26) in its most general analytical form.  is similar for the TOP and the TPPM sequence (except for the definition of Fourier coefficient a0) and the XiX case differs by a missing term with the Ŝx operator due to a0 = 0. However, we still can define a general diagonalization of
is similar for the TOP and the TPPM sequence (except for the definition of Fourier coefficient a0) and the XiX case differs by a missing term with the Ŝx operator due to a0 = 0. However, we still can define a general diagonalization of 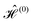 that is valid for all three pulse schemes. This will be further discussed in Section 2.4.
that is valid for all three pulse schemes. This will be further discussed in Section 2.4.
 which have the form
which have the form
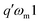 do not influence diagonalization, since the unit operator is invariant under rotation. Direct diagonalization of eqn (34) leads to results that are very complex and not easy to interpret. Therefore,
do not influence diagonalization, since the unit operator is invariant under rotation. Direct diagonalization of eqn (34) leads to results that are very complex and not easy to interpret. Therefore,  is approximately diagonalized in a two-step approach like outlined in ref. 40. In the first step, the reduced Hamiltonian
is approximately diagonalized in a two-step approach like outlined in ref. 40. In the first step, the reduced Hamiltonian
 (contained in eqn (34)) is subjected to this first transformation leading to a term of the form Ŝx
(contained in eqn (34)) is subjected to this first transformation leading to a term of the form Ŝx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(η) + 2ŜyÎy
cos(η) + 2ŜyÎy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(η). From this resulting term Ŝx
sin(η). From this resulting term Ŝx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(η) is treated as a perturbation in a second unitary transformation (see Fig. S2 in ESI,† Section B). All the details of this two consecutively applied unitary transformations are given in ESI,† Section B in much more detail and were adapted from ref. 40. Here we present only the relevant results needed for further discussion. The same set of transformations is then applied to the off-diagonal parts of the Floquet Hamiltonian
cos(η) is treated as a perturbation in a second unitary transformation (see Fig. S2 in ESI,† Section B). All the details of this two consecutively applied unitary transformations are given in ESI,† Section B in much more detail and were adapted from ref. 40. Here we present only the relevant results needed for further discussion. The same set of transformations is then applied to the off-diagonal parts of the Floquet Hamiltonian  with q′ ≠ 0 (see eqn (27)). In a final step, we can then apply second-order perturbation theory to calculate the transition frequencies and probabilities enabled by the Fourier components of the various mw irradiation schemes.
with q′ ≠ 0 (see eqn (27)). In a final step, we can then apply second-order perturbation theory to calculate the transition frequencies and probabilities enabled by the Fourier components of the various mw irradiation schemes.
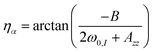
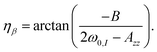
 of eqn (35) after the first unitary transformation is given by
of eqn (35) after the first unitary transformation is given by




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(η) + 2ŜyÎy
cos(η) + 2ŜyÎy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(η),
sin(η), . The angle 2η is shown in Fig. S2 (ESI†) and can take values from 0° to 180°. The case 2η < 90° is obtained for spin systems in the weak coupling regime, where |Azz|,|B| < |ω0,I|. 2η > 90° is attained in the strong-coupling regime, meaning that |Azz| > |ω0,I|. Near the weak-coupling limit, we have 2η ≈ 0° and near the strong-coupling limit, we have 2η ≈ 180°. In both these cases, sin
. The angle 2η is shown in Fig. S2 (ESI†) and can take values from 0° to 180°. The case 2η < 90° is obtained for spin systems in the weak coupling regime, where |Azz|,|B| < |ω0,I|. 2η > 90° is attained in the strong-coupling regime, meaning that |Azz| > |ω0,I|. Near the weak-coupling limit, we have 2η ≈ 0° and near the strong-coupling limit, we have 2η ≈ 180°. In both these cases, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η ≈ 0, meaning the excitation of formally forbidden electron-nuclear transitions is weak. The total Hamiltonian in eqn (34) after the first unitary transformation is thus given by
η ≈ 0, meaning the excitation of formally forbidden electron-nuclear transitions is weak. The total Hamiltonian in eqn (34) after the first unitary transformation is thus given by
 with q′ ≠ 0 after the first diagonalization step can be written as
with q′ ≠ 0 after the first diagonalization step can be written as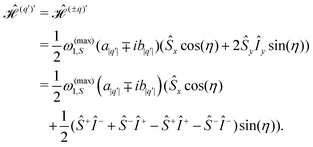
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(η) in eqn (45) as a remaining off-diagonal perturbation. We thus diagonalize the Hamiltonian
sin(η) in eqn (45) as a remaining off-diagonal perturbation. We thus diagonalize the Hamiltonian
 . Diagonalization of eqn (47) takes place in the subspace of the S-spin. Thus, we need to take into account the sign of Ω0,S (see Fig. S2 in ESI,† Section B). The upper binary operator in the following equations corresponds to the +Ω0,S case and the lower one to the −Ω0,S case, respectively. The unitary transformation to diagonalize eqn (47) is given by
. Diagonalization of eqn (47) takes place in the subspace of the S-spin. Thus, we need to take into account the sign of Ω0,S (see Fig. S2 in ESI,† Section B). The upper binary operator in the following equations corresponds to the +Ω0,S case and the lower one to the −Ω0,S case, respectively. The unitary transformation to diagonalize eqn (47) is given by

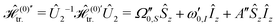
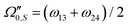
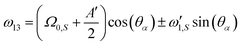

 in the doubly tilted frame can be expressed as
in the doubly tilted frame can be expressed as
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(η) as given in eqn (45) can be expressed as
sin(η) as given in eqn (45) can be expressed as

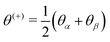 . Please note, that we have to set
. Please note, that we have to set  for the term
for the term  in the TPPM case, e.g., in eqn (49) and (50) for the angles θα and θβ and all other equations containing
in the TPPM case, e.g., in eqn (49) and (50) for the angles θα and θβ and all other equations containing  . The ZQ- and DQ terms are contained in the operator
. The ZQ- and DQ terms are contained in the operator  . In the ESI,† Section B we present a detailed step-by-step derivation of this entire section.
. In the ESI,† Section B we present a detailed step-by-step derivation of this entire section.
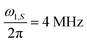 is shown in Fig. 4. Examples for pulse lengths of τp = 5, 9 and 45 ns can be found in ESI,† Section J. We only discuss the case where we set all Fourier coefficients of the microwave irradiation to 0 except the one for q = 1. All others can be converted to this case by scaling the modulation frequency of the XiX DNP sequence to the considered harmonic.
is shown in Fig. 4. Examples for pulse lengths of τp = 5, 9 and 45 ns can be found in ESI,† Section J. We only discuss the case where we set all Fourier coefficients of the microwave irradiation to 0 except the one for q = 1. All others can be converted to this case by scaling the modulation frequency of the XiX DNP sequence to the considered harmonic.

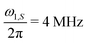 and a pulse length τp = 15 ns (further experimental parameters are given in Section 5). The dots and asterisks represent the estimated enhancement εZQ/DQ as given in eqn (13).
and a pulse length τp = 15 ns (further experimental parameters are given in Section 5). The dots and asterisks represent the estimated enhancement εZQ/DQ as given in eqn (13). or ±48 MHz, resonance conditions that are non-zero in the XiX case, but 0 in the FS-XiX case like
or ±48 MHz, resonance conditions that are non-zero in the XiX case, but 0 in the FS-XiX case like  and resonance conditions that are zero in both cases, e.g.,
and resonance conditions that are zero in both cases, e.g.,  . This behavior can be better explained by using the matrix representation of the infinite-dimensional Floquet Hamiltonian as described in Section 2.3. In case of XiX we only need the first diagonalization step from Section 2.4 because a0 = 0. The four eigenvalues can be calculated according to eqn (39) and are given as
. This behavior can be better explained by using the matrix representation of the infinite-dimensional Floquet Hamiltonian as described in Section 2.3. In case of XiX we only need the first diagonalization step from Section 2.4 because a0 = 0. The four eigenvalues can be calculated according to eqn (39) and are given as

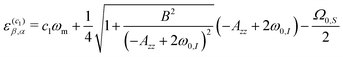

 denotes the Fourier index, the first subscript index refers to the electron spin state and the second to the nuclear spin state, respectively. For weak irradiation, meaning that ω1,S ≪ ωm, the off-diagonal blocks that are relevant are the ones that connect almost degenerate Floquet states in the diagonal blocks (see Fig. 5). These off-diagonal blocks contain the transition amplitudes of the corresponding transition. For DQ transitions in Floquet space, e.g. (|αS,αI,c1〉 ↔ |βS,βI,c2〉), this means that
denotes the Fourier index, the first subscript index refers to the electron spin state and the second to the nuclear spin state, respectively. For weak irradiation, meaning that ω1,S ≪ ωm, the off-diagonal blocks that are relevant are the ones that connect almost degenerate Floquet states in the diagonal blocks (see Fig. 5). These off-diagonal blocks contain the transition amplitudes of the corresponding transition. For DQ transitions in Floquet space, e.g. (|αS,αI,c1〉 ↔ |βS,βI,c2〉), this means that


 at a magnetic field of 28 T
at a magnetic field of 28 T  , this would lead to resonance offset
, this would lead to resonance offset  for c2 − c1 = q′ = ±1 of ∓700 MHz and ±1700 MHz. This can have important consequences for the hardware design of a pulsed DNP spectrometer. The relation between operator-based Floquet theory and matrix-based Floquet theory in the weak irradiation limit and weak coupling regime is discussed in ESI,† Section K.
for c2 − c1 = q′ = ±1 of ∓700 MHz and ±1700 MHz. This can have important consequences for the hardware design of a pulsed DNP spectrometer. The relation between operator-based Floquet theory and matrix-based Floquet theory in the weak irradiation limit and weak coupling regime is discussed in ESI,† Section K.

 with
with  as indicated in Fig. 5 by the orange frame for the case |0〉 ↔ |−1〉 and green frames for |1〉 ↔ |−1〉, respectively. In such a constellation one can observe a total of four different transitions (two ZQ- and two DQ-transitions) as marked with yellow and purple for the DQ case and greenish-blue and brown for the ZQ case, respectively. The transition amplitudes can be obtained from the prefactor of the DQ- and ZQ-operators terms in the off-diagonal elements
as indicated in Fig. 5 by the orange frame for the case |0〉 ↔ |−1〉 and green frames for |1〉 ↔ |−1〉, respectively. In such a constellation one can observe a total of four different transitions (two ZQ- and two DQ-transitions) as marked with yellow and purple for the DQ case and greenish-blue and brown for the ZQ case, respectively. The transition amplitudes can be obtained from the prefactor of the DQ- and ZQ-operators terms in the off-diagonal elements  in eqn (46) and are given by
in eqn (46) and are given by
 arising in numerical simulations using operator-based Floquet theory, e.g. for
arising in numerical simulations using operator-based Floquet theory, e.g. for  , ±48 or ±115 MHz in Fig. 4. Whenever q′ = c2 − c1 is even, we do not observe a resonance peak in the experimental DNP profile. In numerical simulation using operator-based Floquet theory we obtain a match in the resonance condition, but with the Fourier coefficient of the Hamiltonian
, ±48 or ±115 MHz in Fig. 4. Whenever q′ = c2 − c1 is even, we do not observe a resonance peak in the experimental DNP profile. In numerical simulation using operator-based Floquet theory we obtain a match in the resonance condition, but with the Fourier coefficient of the Hamiltonian  equal to 0. This represent cases like
equal to 0. This represent cases like 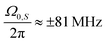 in Fig. 4.
in Fig. 4. block. Therefore, in the FS-XiX case only those resonance peaks remain in the DNP profile for which c2 − c1 = q′ = ±1 holds, i.e.,
block. Therefore, in the FS-XiX case only those resonance peaks remain in the DNP profile for which c2 − c1 = q′ = ±1 holds, i.e.,  and ±48 MHz in Fig. 4. By using eqn (66) and (67), these four resonance peaks can be grouped into two DQ transitions (
and ±48 MHz in Fig. 4. By using eqn (66) and (67), these four resonance peaks can be grouped into two DQ transitions ( and +18 MHz) and two ZQ transitions (
and +18 MHz) and two ZQ transitions (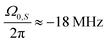 and +48 MHz). They are indicated in Fig. 5 by yellow colour for the DQ transition at
and +48 MHz). They are indicated in Fig. 5 by yellow colour for the DQ transition at  , by purple colour for the DQ transition at
, by purple colour for the DQ transition at 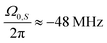 , by greenish-blue colour for the ZQ transition at
, by greenish-blue colour for the ZQ transition at 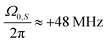 and by brown colour for the ZQ transition at
and by brown colour for the ZQ transition at  . All other resonances resulting from |c2 − c1| = |q′| ≠ 1 are absent in the experimental DNP profile. Numerical simulations using operator-based Floquet theory results in zero transition amplitude for these resonances.
. All other resonances resulting from |c2 − c1| = |q′| ≠ 1 are absent in the experimental DNP profile. Numerical simulations using operator-based Floquet theory results in zero transition amplitude for these resonances.
 with c2 − c1 = q′. The Fourier components
with c2 − c1 = q′. The Fourier components  with Fourier index q′ are indicated above the dashed lines. In the weak irradiation regime (ω1,S ≪ ωm), each resonance condition can be assigned to a Fourier index of the infinite Floquet Hamiltonian and therefore to a mode in the Fourier expansion of the mw irradiation. The color code for the dashed lines indicates the strength of the resonance condition (see eqn (68)). For the analytical calculations of the eigenvalues according to eqn (59) and (62) the following parameters were used:
with Fourier index q′ are indicated above the dashed lines. In the weak irradiation regime (ω1,S ≪ ωm), each resonance condition can be assigned to a Fourier index of the infinite Floquet Hamiltonian and therefore to a mode in the Fourier expansion of the mw irradiation. The color code for the dashed lines indicates the strength of the resonance condition (see eqn (68)). For the analytical calculations of the eigenvalues according to eqn (59) and (62) the following parameters were used:  ,
, 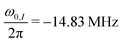 , Azz = B = 1 MHz. Hyperfine constants are given here in linear frequency, whereas they are expressed in angular frequency in eqn (59)–(62).
, Azz = B = 1 MHz. Hyperfine constants are given here in linear frequency, whereas they are expressed in angular frequency in eqn (59)–(62).

 for odd q). The rightmost approximate expression results from the definitions of the angles
for odd q). The rightmost approximate expression results from the definitions of the angles  ,
,  and
and  . The argument inside the arctan function scales with the inverse of the Larmor frequency of the nuclei and, therefore, with the inverse of the external magnetic field. In the weak coupling regime, where |Azz|,|B| ≪ |ω0,I|, we can invoke the small angle approximation and simplify
. The argument inside the arctan function scales with the inverse of the Larmor frequency of the nuclei and, therefore, with the inverse of the external magnetic field. In the weak coupling regime, where |Azz|,|B| ≪ |ω0,I|, we can invoke the small angle approximation and simplify  in eqn (69). This approximation was already used to derive the prefactors for the solid-effect DNP mechanism in operator-based Floquet theory. We again obtain an unfavorable inverse scaling of the transition probability with larger magnetic fields. As eqn (69) contains also ω(max)1,S as a pre-factor, the transition amplitude can be kept field-independent by increasing the Rabi frequency linearly with the external B0-field. This is the same scaling as required in CW DNP schemes.
in eqn (69). This approximation was already used to derive the prefactors for the solid-effect DNP mechanism in operator-based Floquet theory. We again obtain an unfavorable inverse scaling of the transition probability with larger magnetic fields. As eqn (69) contains also ω(max)1,S as a pre-factor, the transition amplitude can be kept field-independent by increasing the Rabi frequency linearly with the external B0-field. This is the same scaling as required in CW DNP schemes.
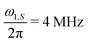 but for different magnetic fields. This case is shown in Fig. 8 in red circles. In blue diamonds in Fig. 8 we look at a XiX DNP sequence with a pulse length τp = 5 ns
but for different magnetic fields. This case is shown in Fig. 8 in red circles. In blue diamonds in Fig. 8 we look at a XiX DNP sequence with a pulse length τp = 5 ns  for the following nutation frequency and external magnetic field combinations i.e.
for the following nutation frequency and external magnetic field combinations i.e. ∈ {(0.1 MHz, 0.1 T), (0.35 MHz, 0.35 T), (1.3 MHz, 1.3 T), (3.5 MHz, 3.5 T), (7 MHz, 7 T), (14 MHz, 14 T), (28 MHz, 28 T)}. The pulse length of the second case was chosen to ensure that the weak irradiation regime (ω1,S ≪ ωm) is fulfilled for all combinations. For both cases we discuss and compare the DQ resonances for the difference in Fourier indices c2 − c1 = 1. The ZQ case with c2 − c1 = 1 is treated in Fig. S16 in ESI,† Section O. Note that the cases ZQ c2 − c1 = +1 and DQ c2 − c1 = −1 are equivalent (except for the sign of aeff and Ω0,S) due to the point symmetry of the ideal DNP profile.
∈ {(0.1 MHz, 0.1 T), (0.35 MHz, 0.35 T), (1.3 MHz, 1.3 T), (3.5 MHz, 3.5 T), (7 MHz, 7 T), (14 MHz, 14 T), (28 MHz, 28 T)}. The pulse length of the second case was chosen to ensure that the weak irradiation regime (ω1,S ≪ ωm) is fulfilled for all combinations. For both cases we discuss and compare the DQ resonances for the difference in Fourier indices c2 − c1 = 1. The ZQ case with c2 − c1 = 1 is treated in Fig. S16 in ESI,† Section O. Note that the cases ZQ c2 − c1 = +1 and DQ c2 − c1 = −1 are equivalent (except for the sign of aeff and Ω0,S) due to the point symmetry of the ideal DNP profile.
 and pulse length τp = 15 ns. XiX DNP sequences with τp = 5 ns and Rabi frequencies that increase linearly with the external B0-field e.g. (0.1 MHz, 0.1 T), (0.35 MHz, 0.35 T), (1.3 MHz, 1.3 T), (3.5 MHz, 3.5 T), (7 MHz, 7 T), (14 MHz, 14 T) and (28 MHz, 28 T) for the Rabi frequency and the external magnetic field, respectively, are shown in blue diamonds. The linear behaviour of Ω0,S with respect to the external magnetic field can be explained by the approximation in eqn (66). Due to eqn (9) also k0 shows a similar linear behaviour. For the red circles, a fraction of aeff for two different magnetic fields scale with the inverse fraction of the corresponding magnetic fields, respectively. In contrast, aeff is constant over the different magnetic fields for a Rabi frequency that scales linearly with the magnetic field (blue diamonds). This is indicated by the dashed blue line. Please note the logarithmic scale in the y axis in the plot for aeff.
and pulse length τp = 15 ns. XiX DNP sequences with τp = 5 ns and Rabi frequencies that increase linearly with the external B0-field e.g. (0.1 MHz, 0.1 T), (0.35 MHz, 0.35 T), (1.3 MHz, 1.3 T), (3.5 MHz, 3.5 T), (7 MHz, 7 T), (14 MHz, 14 T) and (28 MHz, 28 T) for the Rabi frequency and the external magnetic field, respectively, are shown in blue diamonds. The linear behaviour of Ω0,S with respect to the external magnetic field can be explained by the approximation in eqn (66). Due to eqn (9) also k0 shows a similar linear behaviour. For the red circles, a fraction of aeff for two different magnetic fields scale with the inverse fraction of the corresponding magnetic fields, respectively. In contrast, aeff is constant over the different magnetic fields for a Rabi frequency that scales linearly with the magnetic field (blue diamonds). This is indicated by the dashed blue line. Please note the logarithmic scale in the y axis in the plot for aeff. . This relation is true for all comparisons within the used magnetic fields and is predicted by eqn (69). In Fig. 8 one can nicely observe the linear increase of the resonance offset Ω0,S for resonant DNP as already outlined in eqn (66) and (67). We find that k0 also depends linearly on the magnetic field within the quantization error of a discrete parameter. This can be explained by the increase of ω0,I in the resonance condition of eqn (9). k0 selects the Fourier coefficients
. This relation is true for all comparisons within the used magnetic fields and is predicted by eqn (69). In Fig. 8 one can nicely observe the linear increase of the resonance offset Ω0,S for resonant DNP as already outlined in eqn (66) and (67). We find that k0 also depends linearly on the magnetic field within the quantization error of a discrete parameter. This can be explained by the increase of ω0,I in the resonance condition of eqn (9). k0 selects the Fourier coefficients  of the effective Hamiltonian relevant for DNP (see eqn (10) and (11)). The Fourier coefficients
of the effective Hamiltonian relevant for DNP (see eqn (10) and (11)). The Fourier coefficients  tend to decrease for larger values of k0, which can be seen from eqn (6) and which is the actual reason for the decreased transition probability towards larger magnetic fields.
tend to decrease for larger values of k0, which can be seen from eqn (6) and which is the actual reason for the decreased transition probability towards larger magnetic fields.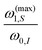 is kept constant here. Accordingly, the numerically calculated Fourier coefficients of the effective Hamiltonian in operator-based Floquet theory are the same.
is kept constant here. Accordingly, the numerically calculated Fourier coefficients of the effective Hamiltonian in operator-based Floquet theory are the same. at 80 K for B0 fields of 0.35 and 3.5 T are plotted in Fig. 9. We simulated the field profile using a two-spin electron–proton system with an electron–proton distance ren = 4.5 Å with either an axial g-tensor with a slight g-anisotropy of gxx = gyy = 2.00319 and gzz = 2.00258 or an isotropic g-tensor with giso = 2.00299.43 A more detailed description of the GAMMA simulations can be found in ESI,† Section Q. At 0.35 T one can barely see a difference between the field profile with g-anisotropy and with isotropic g-tensor because of the small g-anisotropy. However, at 3.5 T the field profile of the simulation using a g-anisotropy show resonance peaks that resemble the powder lineshape for a g-tensor with axial symmetry.
at 80 K for B0 fields of 0.35 and 3.5 T are plotted in Fig. 9. We simulated the field profile using a two-spin electron–proton system with an electron–proton distance ren = 4.5 Å with either an axial g-tensor with a slight g-anisotropy of gxx = gyy = 2.00319 and gzz = 2.00258 or an isotropic g-tensor with giso = 2.00299.43 A more detailed description of the GAMMA simulations can be found in ESI,† Section Q. At 0.35 T one can barely see a difference between the field profile with g-anisotropy and with isotropic g-tensor because of the small g-anisotropy. However, at 3.5 T the field profile of the simulation using a g-anisotropy show resonance peaks that resemble the powder lineshape for a g-tensor with axial symmetry.
 at 80 K for B0 fields of 0.35 T (X-band) top and 3.5 T (W-band) bottom for an isotropic g-tensor (red) and with an axial g-tensor with a slight g-anisotropy (blue). At X-band the difference between the simulations with and without g-anisotropy are very minor due to the small magnitude of the g-anisotropy. However, at W-band the resonance peaks in the DNP profile using a slight g-anisotropy are much broader than for the isotropic counterpart and resemble the g-tensor of the electron spin. All details of the numerical simulation can be found in ESI,† Section Q.
at 80 K for B0 fields of 0.35 T (X-band) top and 3.5 T (W-band) bottom for an isotropic g-tensor (red) and with an axial g-tensor with a slight g-anisotropy (blue). At X-band the difference between the simulations with and without g-anisotropy are very minor due to the small magnitude of the g-anisotropy. However, at W-band the resonance peaks in the DNP profile using a slight g-anisotropy are much broader than for the isotropic counterpart and resemble the g-tensor of the electron spin. All details of the numerical simulation can be found in ESI,† Section Q. (see Section 2.4 or ESI,† Section B for more details). As a consequence of this second unitary transformation the transition amplitudes now depend on the mw offset. However, the resonance conditions in the TOP DNP sequence can still be assigned to a certain Fourier index q′ as will become clear later in this section.
(see Section 2.4 or ESI,† Section B for more details). As a consequence of this second unitary transformation the transition amplitudes now depend on the mw offset. However, the resonance conditions in the TOP DNP sequence can still be assigned to a certain Fourier index q′ as will become clear later in this section.




 and A′ can be found in eqn (40) and (41), respectively. We can now invoke the same steps as for the XiX case and solve
and A′ can be found in eqn (40) and (41), respectively. We can now invoke the same steps as for the XiX case and solve


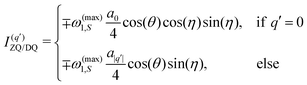
 (see eqn (49) and (50) for analytical expression for θα and θβ). As expected also the transition amplitudes for the TOP DNP sequence contain the term sin(η). As explained in Section 3.2.3 this term scales unfavorably with the inverse of B0 when invoking the weak coupling regime. For low to moderate ω(max)1,Se.g. the weak irradiation regime, θ is small and therefore cos(θ) ≈ 1 holds.
(see eqn (49) and (50) for analytical expression for θα and θβ). As expected also the transition amplitudes for the TOP DNP sequence contain the term sin(η). As explained in Section 3.2.3 this term scales unfavorably with the inverse of B0 when invoking the weak coupling regime. For low to moderate ω(max)1,Se.g. the weak irradiation regime, θ is small and therefore cos(θ) ≈ 1 holds.
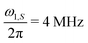 , τp = 28 ns, τd = 56 ns. This results in
, τp = 28 ns, τd = 56 ns. This results in  and a linear modulation frequency of
and a linear modulation frequency of 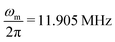 . They measured the DNP profile for this particular TOP DNP experiment from
. They measured the DNP profile for this particular TOP DNP experiment from  to +30 MHz and found the following values for the resonance offsets:
to +30 MHz and found the following values for the resonance offsets:  and ±27 MHz.27 They also found a DNP enhancement at
and ±27 MHz.27 They also found a DNP enhancement at  in numerical calculations using operator-based Floquet theory but with zero DNP enhancement in experiments. They explained the absence of DNP enhancement at this particular offset by assuming that the “ZQ- and DQ terms” (Fourier coefficients
in numerical calculations using operator-based Floquet theory but with zero DNP enhancement in experiments. They explained the absence of DNP enhancement at this particular offset by assuming that the “ZQ- and DQ terms” (Fourier coefficients  in eqn (10) and (11) in our notation) “have almost equal sizes” (and different sign). We can now use eqn (77)–(79) to explain the occurrence and absence of resonance peaks in the TOP DNP profile reported in ref. 27. In Table 2 we list the Fourier indices for the TOP DNP experiment for the fraction
in eqn (10) and (11) in our notation) “have almost equal sizes” (and different sign). We can now use eqn (77)–(79) to explain the occurrence and absence of resonance peaks in the TOP DNP profile reported in ref. 27. In Table 2 we list the Fourier indices for the TOP DNP experiment for the fraction  (see eqn (17) and (18)) along with the estimated values according to eqn (77) and (78) for different values of c2 − c1 = q′. We see that the approximations in eqn (77) and (78) give very accurate predictions for the microwave offsets Ω0,S, where DNP enhancements are expected. Eqn (79) together with eqn (17) and (18) fairly well predicts the amount of polarization transfer in the DNP profile presented in Fig. 2 in ref. 27. The resonances at
(see eqn (17) and (18)) along with the estimated values according to eqn (77) and (78) for different values of c2 − c1 = q′. We see that the approximations in eqn (77) and (78) give very accurate predictions for the microwave offsets Ω0,S, where DNP enhancements are expected. Eqn (79) together with eqn (17) and (18) fairly well predicts the amount of polarization transfer in the DNP profile presented in Fig. 2 in ref. 27. The resonances at  and 27 MHz show the largest enhancement, whereas the peak at
and 27 MHz show the largest enhancement, whereas the peak at 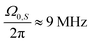 shows only a small enhancement, as predicted from theory. However, the resonance offset
shows only a small enhancement, as predicted from theory. However, the resonance offset  should in theory result in a similar enhancement as
should in theory result in a similar enhancement as  . The data shown in Fig. 2 in ref. 27 indicate a slightly smaller enhancement for
. The data shown in Fig. 2 in ref. 27 indicate a slightly smaller enhancement for  than for
than for 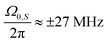 . We tentatively attribute this difference between simulation and experiment to the fact that the ZQ- and DQ enhancements occur at a frequency difference that is within the FWHM (∼6 MHz) of the EPR line of the trityl radical Ox063. This case is similar to the enhancements close to
. We tentatively attribute this difference between simulation and experiment to the fact that the ZQ- and DQ enhancements occur at a frequency difference that is within the FWHM (∼6 MHz) of the EPR line of the trityl radical Ox063. This case is similar to the enhancements close to  in the XiX field profile for τp = 45 ns shown in Fig. S13 (ESI†). As discussed in Section 3.2.4, the width of the experimental DNP profile at 0.35 T resembles the width of the EPR line. This may result in a partial cancellation of the ZQ- and DQ-enhancement due to the overlap of both peaks in the DNP profile and the different sign of their amplitudes. Using the theory outlined here, we can also explain the absence of DNP enhancement for
in the XiX field profile for τp = 45 ns shown in Fig. S13 (ESI†). As discussed in Section 3.2.4, the width of the experimental DNP profile at 0.35 T resembles the width of the EPR line. This may result in a partial cancellation of the ZQ- and DQ-enhancement due to the overlap of both peaks in the DNP profile and the different sign of their amplitudes. Using the theory outlined here, we can also explain the absence of DNP enhancement for  MHz. According to eqn (17) and (18) and Table 1 all Fourier coefficients of the pulse sequence are non-zero except for Fourier indices of q = 3, 6, 9, 12,…. Therefore, for c2 − c1 = q′ = ±3 we can calculate (by using eqn (77) and (78)) one pair of the offset to be
MHz. According to eqn (17) and (18) and Table 1 all Fourier coefficients of the pulse sequence are non-zero except for Fourier indices of q = 3, 6, 9, 12,…. Therefore, for c2 − c1 = q′ = ±3 we can calculate (by using eqn (77) and (78)) one pair of the offset to be 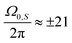 MHz. This means that the enhancement at this resonance offset is zero because the Fourier coefficient a3 is zero.
MHz. This means that the enhancement at this resonance offset is zero because the Fourier coefficient a3 is zero.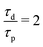 and the expected resonance offsets according to eqn (77) and (78) calculated for different c2 − c1 = q′. The values for the resonance offsets are compared to a DNP profile measured from
and the expected resonance offsets according to eqn (77) and (78) calculated for different c2 − c1 = q′. The values for the resonance offsets are compared to a DNP profile measured from  to
to  at 0.35 T with
at 0.35 T with  , τp = 28 ns, τd = 56 ns as reported in ref. 27. The italic entries are those resonances which were also observed experimentally in ref. 27. The bold entries were reported as being observed by numerical simulations using operator-based Floquet theory, but gave zero enhancement in the experimental DNP profile (see Table 1 for
, τp = 28 ns, τd = 56 ns as reported in ref. 27. The italic entries are those resonances which were also observed experimentally in ref. 27. The bold entries were reported as being observed by numerical simulations using operator-based Floquet theory, but gave zero enhancement in the experimental DNP profile (see Table 1 for  )
)
 in eqn (57)) are similar for the TPPM and TOP sequences. Hence, we can adapt the results obtained for the TOP DNP sequence in Section 3.3 to the TPPM case. The only difference is the definition of the Fourier coefficient
in eqn (57)) are similar for the TPPM and TOP sequences. Hence, we can adapt the results obtained for the TOP DNP sequence in Section 3.3 to the TPPM case. The only difference is the definition of the Fourier coefficient  (compare eqn (17) and (23)). In both cases
(compare eqn (17) and (23)). In both cases 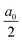 cannot exceed one. Therefore, the condition in eqn (76) is also valid in the TPPM case, resulting in the same approximations for Ω0,S as in the TOP DNP and XiX DNP case, e.g.eqn (77) and (78). Therefore, in the weak irradiation regime the resonance offsets Ω0,S of the three DNP sequences (TOP, XiX and TPPM) occur at the same spectral position when using the same modulation period ωm. Using eqn (57) and (58) the transition amplitudes between the Fourier states c1 and c2 for the TPPM case are then given as
cannot exceed one. Therefore, the condition in eqn (76) is also valid in the TPPM case, resulting in the same approximations for Ω0,S as in the TOP DNP and XiX DNP case, e.g.eqn (77) and (78). Therefore, in the weak irradiation regime the resonance offsets Ω0,S of the three DNP sequences (TOP, XiX and TPPM) occur at the same spectral position when using the same modulation period ωm. Using eqn (57) and (58) the transition amplitudes between the Fourier states c1 and c2 for the TPPM case are then given as
 . For the angles θα and θβ one needs to insert
. For the angles θα and θβ one needs to insert  into in eqn (49) and (50). For the weak irradiation regime, i.e., for low to moderate ω(max)1,S and sufficient large ωm, cos(θ(+)) ≈ 1 holds. Thus for ϕ → 0 we obtain the same transition amplitude as for the SE and for
into in eqn (49) and (50). For the weak irradiation regime, i.e., for low to moderate ω(max)1,S and sufficient large ωm, cos(θ(+)) ≈ 1 holds. Thus for ϕ → 0 we obtain the same transition amplitude as for the SE and for  the transition amplitude as for the XiX sequence, respectively.
the transition amplitude as for the XiX sequence, respectively.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O
D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O, 6
H2O, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume) was used. The sample was prepared by the following procedure: 1.69 mg of the trityl (MW = 1359 g mol−1) were dissolved in 24.15 mg water (MW = 18.02 g mol−1, ρ0 = 0.997 g mL−1) and 80.93 mg D2O (MW = 20.03 g mol−1, ρ0 = 1.11 g mL−1). This gives a ∼1.2 μmol solution of trityl dissolved in a D2O
1 by volume) was used. The sample was prepared by the following procedure: 1.69 mg of the trityl (MW = 1359 g mol−1) were dissolved in 24.15 mg water (MW = 18.02 g mol−1, ρ0 = 0.997 g mL−1) and 80.93 mg D2O (MW = 20.03 g mol−1, ρ0 = 1.11 g mL−1). This gives a ∼1.2 μmol solution of trityl dissolved in a D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O matrix of 3
H2O matrix of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume. From that resulting solution 48.6 μL were added to 99.92 mg glycerol-d8 (MW = 100.14 g mol−1, ρ0 = 1.371 g mL−1) to give the desired 5 mM solution of trityl in DNP juice. 40 μL of that final solution were added to a 3 mm OD quartz capillary. All masses were weighted in with a AT261 Delta Range scale with a precision of 0.01 mg. A pipetman from GILSON (P100) with volumes adjustable to 0.1 μL precision was used to transfer and measure the volumes.
1 by volume. From that resulting solution 48.6 μL were added to 99.92 mg glycerol-d8 (MW = 100.14 g mol−1, ρ0 = 1.371 g mL−1) to give the desired 5 mM solution of trityl in DNP juice. 40 μL of that final solution were added to a 3 mm OD quartz capillary. All masses were weighted in with a AT261 Delta Range scale with a precision of 0.01 mg. A pipetman from GILSON (P100) with volumes adjustable to 0.1 μL precision was used to transfer and measure the volumes.