A highly accurate potential energy surface for carbonyl sulphide (OCS): how important are the ab initio calculations?

Abstract

Ab initio quantum chemical methods can produce accurate molecular potential energy surfaces (PESs) capable of predicting the fundamental vibrational wavenumbers to within 1 cm⁻¹. However, for high-resolution applications this is simply not good enough and empirical refinement is necessary, i.e. adjusting the PES to better match laboratory spectroscopic data. Here, the impact of the underlying ab initio calculations is rigorously investigated within the context of empirical refinement. For carbonyl sulphide (OCS), state-of-the-art electronic structure calculations are employed to construct higher- and lower-level ab initio PESs, which are then empirically refined in near-identical procedures. The initial ab initio calculations are shown to considerably affect the accuracy of the final refined PES, with an order-of-magnitude improvement in computed rotation-vibration energy levels achieved for OCS. In demonstrating this, the most accurate PES of the electronic ground state of OCS is produced, reproducing the fundamentals with a root-mean-square error (RMSE) of 0.004 cm⁻¹, and 884 rovibrational energy levels below 14 000 cm⁻¹ with an RMSE of 0.060 cm⁻¹.

---

1 Introduction

Knowledge of the potential energy surface (PES) is crucial in studies of molecular structure, spectroscopy, and dynamics. The use of wavefunction-based quantum chemical methods, such as coupled cluster or multireference configuration interaction, in conjunction with large basis sets usually of quadruple-zeta quality and above, will produce an accurate ab initio PES, i.e. predicting the fundamental vibrational wavenumbers to within 2–5 cm⁻¹. To improve the accuracy further, one must treat the basis set incompleteness error and smaller additional effects to recover more of the electron correlation energy, known as higher-level corrections.^1,2 Numerous highly accurate ab initio PESs have been constructed in this manner, e.g. LiOH,³ H₂CS,⁴ CH₃Cl,⁵ CH₄,⁶ reproducing the fundamentals to within 1 cm⁻¹ on average. Although impressive, purely ab initio PESs are simply not good enough for high-resolution spectroscopic applications where sub-wavenumber accuracy is required.

To overcome the limits of ab initio theory, the PES must be empirically refined to high-resolution laboratory spectroscopic data, i.e. adjusting the expansion parameters of the analytic function used to represent the ab initio data to better match experiment. Doing so can lead to orders-of-magnitude improvements in the accuracy of the calculated rotation-vibration (rovibrational) energy levels, better wavefunctions, and more reliable molecular properties as a result. The refinement procedure can be viewed as “pulling” and “pushing” the potential hypersurface in nuclear configuration space to better match the “true” molecular PES, with the original ab initio surface acting as the starting point. This poses the question: how significant are the initial ab initio calculations if the PES is going to be empirically refined?

Anecdotally, there are arguments for and against more sophisticated ab initio calculations of the initial PES. On the one hand, a more accurate ab initio PES should be closer to the “true” surface, thus leading to a smoother refinement and better final product. However, it could be argued that any reasonably accurate ab initio PES can serve as a starting point. The refinement procedure will mask the contribution from higher-level corrections and largely negate the additional computational effort associated with generating a highly accurate ab initio PES.

In this work, the impact of the initial ab initio calculations on the accuracy of a PES that is subsequently empirically refined is rigorously investigated. The carbonyl sulphide molecule (main isotopologue ¹⁶O¹²C³²S) is investigated as there is strong interest in its infrared spectrum. Prominent studies of extrasolar planets, known as exoplanets, are actively searching for spectroscopic signatures of OCS.^7,8 However, there is currently no infrared OCS molecular line list suitable for the high-temperature environments found on exoplanets, hindering its potential detection. In general, sulphur chemistry is expected to play a key role in the formation of hazes and clouds in the atmospheres of exoplanets⁹ with OCS an essential atmospheric molecule. On Earth, carbonyl sulphide is one of the most widespread sulphur-containing molecules in the atmosphere with a long atmospheric lifetime (over 2 years).¹⁰ OCS may even play a vital role in the prebiotic formation of biomolecules, challenging conventional assumptions about prebiotic chemistry on Earth.¹¹

The purpose of this paper is twofold: (i) to critically evaluate the influence of the underlying ab initio calculations in the context of empirical refinement of the PES, and (ii) to produce the most accurate PES of the electronic ground state of OCS in the literature. There have been several theoretical studies of the PES and rovibrational spectrum of OCS^12–19 but none at the accuracy or completeness targeted in this study.

2 Potential energy surface

2.1 Electronic structure calculations

To generate the PES of OCS, a focal-point approach²⁰ has been utilised with the total electronic energy represented as,

E_tot = E_CBS + ΔE_CV + ΔE_HO + ΔE_SR + ΔE_DBOC. (1)

These terms are known as “higher-level” energy corrections to the PES arising from extrapolating the energy to the complete basis set (CBS) limit, core-valence (CV) electron correlation, higher-order (HO) correlation, scalar relativistic (SR) effects, and the diagonal Born–Oppenheimer correction (DBOC).^1,2 In principle, their inclusion should lead to a more accurate PES.

The largest contribution is from the energy at the complete basis set (CBS) limit E_CBS, computed using the explicitly correlated coupled cluster method CCSD(T)-F12b,²¹ in conjunction with the F12-optimized correlation consistent basis sets, cc-pVTZ-F12 and cc-pVQZ-F12.^22,23 Extrapolation to the CBS limit was done using the two-point formula,²⁴

E^C_CBS = F^C(E^C_QZ − E^C_TZ) + E^C_TZ, (2)

where the C = CCSD − F12b and (T) components of the total correlation energy were extrapolated separately with the parameter F^C assuming values of F^CCSD−F12b = 1.363388 and F^(T) = 1.769474, respectively. Here, E^C_TZ and E^C_QZ refers to the correlation energy component computed with the cc-pVTZ-F12 and cc-pVQZ-F12 basis sets, respectively. No extrapolation was applied to the Hartree–Fock (HF) energy, rather the HF + CABS (complementary auxiliary basis set) singles correction²¹ computed in the larger cc-pVQZ-F12 basis set was taken. Calculations used the frozen core approximation and the diagonal fixed amplitude ansatz 3C(FIX)²⁵ with a Slater geminal exponent value of β = 1.0 a₀⁻¹.²⁴ For the auxiliary basis sets (ABS) required in explicitly correlated calculations, the resolution of the identity OptRI²⁶ basis, and the cc-pV5Z/JKFIT²⁷ and aug-cc-pwCV5Z/MP2FIT²⁸ basis sets for density fitting were employed. The quantum chemistry package MOLPRO2015^29,30 was used for calculations unless stated otherwise.

The contribution of CV electron correlation ΔE_CV was computed at the CCSD(T)-F12b/cc-pCVTZ-F12^23,31 level of theory. The same ansatz and ABS were used as before but with a Slater geminal exponent value of β = 1.4 a₀⁻¹. The (1s) orbital of sulphur was frozen in all-electron calculations due to the difficulty basis sets have in describing this orbital.

The effect of truncating the coupled cluster expansion, termed HO correlation, was accounted for using the hierarchy of coupled cluster methods such that ΔE_HO = ΔE_T + ΔE_(Q). Here, the full triples contribution ΔE_T = E_CCSDT − E_CCSD(T), and the perturbative quadruples contribution ΔE_(Q) = E_CCSDT(Q) − E_CCSDT. Calculations using the CCSD(T), CCSDT, and CCSDT(Q) methods were performed in the frozen core approximation using the general coupled cluster approach^32,33 implemented in the MRCC code³⁴ interfaced to the CFOUR quantum chemistry program.³⁵ The correlation consistent basis sets cc-pVTZ(+d for S) and cc-pVDZ(+d for S)^36,37 were utilised for the full triples and perturbative quadruples calculations, respectively.

The correction from SR effects ΔE_SR was accounted for using the second-order Douglas–Kroll–Hess approach^38,39 at the CCSD(T)/cc-pVQZ-DK⁴⁰ level of theory employing the frozen core approximation. Lastly, the DBOC ΔE_DBOC was determined from all-electron calculations (with the (1s) orbital of S frozen) using the CCSD method⁴¹ as implemented in CFOUR with the aug-cc-pCVDZ(+d for S) basis set.^42–44 The DBOC arises from the nuclear kinetic energy operator acting on the ground electronic state wavefunction and is dependent on nuclear mass, hence its inclusion means the PES is isotopologue-specific for ¹⁶O¹²C³²S. It is worth stating that the natural abundance of the main isotopologue ¹⁶O¹²C³²S on Earth is approximately 94% compared to the other OCS isotopologues.

In Fig. 1, the higher-level contributions are illustrated for OCS where one-dimensional cuts of the different corrections have been plotted. They are generally much smaller in magnitude, noticeably around the equilibrium geometry, and vary in a smooth fashion. As the molecule distorts, the higher-level corrections grow in magnitude which has the effect of “pulling” and “pushing” the potential hypersurface closer to its “true” shape.

Fig. 1 One-dimensional cuts of the core-valence (CV), higher-order (HO), scalar relativistic (SR), and diagonal Born–Oppenheimer (DBOC) energy correction surfaces (ΔE in cm⁻¹) with all other coordinates held at their equilibrium values.

All terms in eqn (1) were calculated on a grid of 6082 nuclear geometries with energies E up to hc 30 000 cm⁻¹, where h is the Planck constant and c is the speed of light (from here on in we drop the h and c factors when discussing energies in wavenumbers). The grid was constructed in terms of three internal coordinates: the O–C bond length 0.95 ≤ r_OC ≤ 1.59 Å the C–S bond length 1.27 ≤ r_CS ≤ 2.46 Å and the interbond angle 107.5 ≤ ∠(OCS) ≤ 180.0°. Points were distributed randomly with a higher concentration around the equilibrium region as this is more spectroscopically important. It is possible that fewer points could have been utilised to obtain a satisfactory description of the OCS PES and studies have explored this, for example, in a highly accurate ab initio PES of CH₃Cl.⁴⁵

The basis sets used to compute the higher-level corrections were chosen pragmatically to ensure timely calculations with less emphasis on tightly converged energies. This was done because the corrections are (i) formed from differences between two absolute energies, and (ii) somewhat cancel each other out when summed up together, further negating the convergence error, for example, the CV and HO contributions along the stretch coordinates in Fig. 1 have similar magnitude but opposing sign. This strategy has been successfully utilised before in calculations of highly accurate ab initio PESs of SiH₄,⁴⁶ CH₄,⁶ and CH₃F.⁴⁷ It is also relevant that the PES of OCS will be empirically refined to laboratory spectroscopic data.

The higher-level corrections were computed at every grid point, which although computationally intensive, was time-effective. An alternative strategy is to design reduced grids for each correction, fit a suitable analytic representation to the ab initio data, and obtain values across the global grid of nuclear geometries by interpolation, for example, as was done in ref. 4,5. While this is less computationally intensive, achieving a satisfactory description of each higher-level correction requires careful consideration and may not be trivial; issues that are avoided in the present approach.

For the purposes of this study, two ab initio PESs were produced. The first (and main) PES of OCS, referred to as CBS-HL^ai, contained the CBS extrapolated energies plus all the higher-level corrections, i.e. all terms in eqn (1). The second PES, named VQZ-F12^ai, was determined from CCSD(T)-F12b/cc-pVQZ-F12 energies and can be regarded as a reference surface. This level of theory is still a very good approximation to the “true” surface and many theoretical studies would regard this as accurate and sufficient. Comparisons between the two surfaces will enable a valuable assessment of the impact of the CBS extrapolation and higher-level corrections on the accuracy of the PES, especially regarding the results of the empirical refinement.

2.2 Analytic representation

Each ab initio dataset was fitted using the analytic expression,with maximum expansion order i₁ + i₂ + i₃ = 6. Three vibrational coordinates were used,

ξ₁ = 1 − exp[−a(r₁ − r^eq₁)], (4)

ξ₂ = 1 − exp[−b(r₂ − r^eq₂)], (5)

ξ₃ = sin(π − α) − sin(π − α_eq), (6)

in terms of the internal stretching coordinates r₁ = r_OC and r₂ = r_CS (in Å), the interbond angle α = ∠(OCS) (in radians), the Morse parameters a and b (in Å⁻¹), and the equilibrium structural parameters r^eq₁, r^eq₂, and α_eq, the latter being fixed to 180° as OCS is linear at equilibrium.

The second and third terms in eqn (3) introduce a repulsive contribution to the PES^48,49 if the distance between the O and S atoms

becomes small, i.e. at very small bond angles. The values of the parameters b₁, b₂, g₁, g₂ were adopted from ref. 49 (see the ESI† for the complete list of expansion parameters of the OCS PESs). In actuality, these very small bond angles are never sampled in the variational calculations performed in this study to validate the PESs (dis cussed in Section 3.1) and the repulsive contribution is negligible. However, these terms are still recommended as a safeguarding measure.

The expansion parameters f_i1,i2,i3 were established through a least-squares fitting to the ab initio data, weighted using factors of the form⁵⁰

Here, Ẽ_i^(w) = max (Ẽ_i, 10 000) where Ẽ_i is the potential energy at the ith geometry above equilibrium and the normalization constant N = 0.0001 (all values in cm⁻¹). The weighting favoured energies below 15 000 cm⁻¹, producing a more spectroscopically relevant PES. The fit also employed Watson's robust fitting scheme,⁵¹ which reduced the weights of outliers and improved the overall description of the PESs.

The ab initio CBS-HL^ai PES was fitted using a total of 90 parameters (81 expansion parameters, 3 equilibrium parameters, 2 Morse parameters, 4 damping parameters) achieving a weighted root-mean-square error (wRMSE) of 0.011 cm⁻¹ for energies up to 30 000 cm⁻¹. The VQZ-F12^ai PES was fitted by 89 parameters (80 expansion parameters, 3 equilibrium parameters, 2 Morse parameters, 4 damping parameters) with a wRMSE of 0.015 cm⁻¹ for energies up to 30 000 cm⁻¹. The expansion parameters of the CBS-HL^ai and VQZ-F12^ai PESs are provided along with a program to construct them in the ESI.†

3 Variational calculations

3.1 Rotation-vibration energy level calculations

To assess the accuracy of the PESs, variational calculations of the rovibrational energy level structure of OCS were carried out using the nuclear motion code TROVE.⁵² TROVE is a well-established program used extensively by the ExoMol database^53–55 to generate comprehensive molecular line lists (catalogues of transitions and their probabilities) for exoplanetary science. The methodology of TROVE is well described in the literature^52,56–61 and it has been used to compute the spectra of several triatomic molecules including CO₂,⁶² SiO₂,⁶³ CaOH,⁶⁴ KOH and NaOH⁶⁵ (amongst numerous other larger polyatomics). Full details of the TROVE approach for treating linear and quasi-linear molecules can be found in ref. 60. The key calculation steps for OCS were as follows.

The rovibrational Schrödinger equation in the ground electronic state was solved using the exact kinetic energy operator for triatomic molecules⁶⁰ (based on the bisector embedding^66,67) with the potential energy operator represented as a sixth-order power-series expansion. A multi-step procedure⁵⁹ was employed to build the vibrational basis set from contracted and symmetry-adapted products of one-dimensional basis functions ϕ_n1, ϕ_n2 and 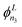associated with the three vibrational modes of OCS. In TROVE, the two stretching and one bending vibrational mode have the respective quantum numbers n₁, n₂ and n₃, with L being the vibrational angular momentum quantum number associated with the bending mode. These primitive one-dimensional functions were determined numerically through solution of one-dimensional Schrödinger equations for a given mode (stretch or bend) with all other modes set to their equilibrium values. For the stretches, the Numerov–Cooley method^68,69 was used on grids of 1000 points each, while the bending mode required the use of Laguerre polynomials as a basis and a grid of 3000 points. The total size of the vibrational basis set was controlled by the polyad number condition 2(n₁ + n₂) + n₃ ≤ 58. Convergence testing was done with respect to the number of basis functions defined through the polyad number condition, and with respect to the number of grid points used to define the primitive one-dimensional basis sets. Vibrational J = 0 states were converged to 10⁻⁶ cm⁻¹ (on average) up to 5000 cm⁻¹, and to 10⁻⁴ up to 8000 cm⁻¹.

The full rovibrational basis set was constructed from symmetrized products of the symmetry-adapted vibrational basis functions 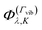and symmetry-adapted rigid rotor functions |J,k,m〉^(Γ_rot), classified according to the irreducible representations of the C_s(M) molecular group symmetry. That is,

Here, J is the total angular momentum quantum number, k and m are the rotational quantum numbers associated with the projection of the rotational angular momentum onto the molecular z and laboratory Z axes (in units of ħ), respectively, K = |k|, λ denotes a set of vibrational state quantum numbers, Γ_vib, Γ_rot, and Γ denote the symmetry of the vibrational, rotational, and total wavefunctions, respectively. An energy cut-off of E = 40 000 cm⁻¹ was used to contract the J = 0 eigenfunctions for states up to K ≤ 20.

Thus, for a rovibrational state i with total angular momentum J and total symmetry Γ, the total wavefunction Ψ^(Γ)_i,J is a linear combination of rovibrational basis set functions,

where the linear expansion coefficients c^(i,J,Γ)_λ,K were found by solving the eigenvalue problem for the full rovibrational Hamiltonian. Calculations employed atomic mass values of 15.99491463 Da (oxygen), 12.0 Da (carbon), and 31.9720707 Da (sulphur), taken from the Ame2012 atomic mass evaluation database.⁷⁰

3.2 Empirical refinement procedure

There is a substantial amount of high-resolution, laboratory spectroscopic data on OCS. Very recently, an exhaustive review was performed⁷¹ that resulted in the extraction and analysis of 14 071 independently measured and assigned rovibrational transitions. This was carried out using the MARVEL (measured active rotational-vibrational energy levels) procedure,^72–75 which takes a user-constructed dataset of assigned spectroscopic transitions with measurement uncertainties and inverts them to yield a consistent set of empirically-derived energy levels with quantum number labelling and uncertainties. Such a dataset is invaluable for refining the PES. For OCS, 13 056 of the extracted transitions were validated to produce a list of 5729 rovibrational energy levels up to J = 95 with energies up to 14 551 cm⁻¹, of which 884 rovibrational energy levels (covering 106 vibrational states) up to J = 10 were utilised in the refinement.

Empirical refinement of the CBS-HL^ai and VQZ-F12^ai PESs was carried out in two steps. Firstly, the equilibrium structural parameters r^eq₁ and r^eq₂ were adjusted in a nonlinear least-squares fitting procedure to the pure rotational energies up to J = 10 in the ground vibrational state. Two iterations were sufficient to obtain converged parameters. Secondly, the full refinement was performed using an efficient least-squares fitting procedure⁷⁶ in TROVE. Here, the effect of the refinement was treated as a perturbation ΔV to the original ab initio PES V_ai such that the refined surface V′ = V_ai + ΔV. Using the same vibrational coordinates, see eqn (4), the perturbation was expanded as

where the coefficients Δf_i1,i2,i3 are corrections to the original PES expansion parameters f_i1,i2,i3 with i₁ + i₂ + i₃ ≤ 6. Note that the Morse and damping parameters were not varied in the refinement. The new perturbed rovibrational Hamiltonian H′ = H + ΔV was diagonalized in a basis set of eigenfunctions from the initial unperturbed Hamiltonian H eigenvalue problem. Each iteration of the least-squares fitting refinement procedure utilised the previous iteration “unperturbed” basis set in this manner until a PES of desirable quality was achieved. To stop any unphysical distortions of the PES in the refinement, the expansion parameters were simultaneously fitted⁷⁷ to both the empirically-derived energies and the original ab initio datasets.

In rovibrational calculations, computed states are assigned TROVE quantum numbers (n₁, n₂, n₃, L) based on the largest contribution from the vibrational basis functions in the basis set expansion of eqn (10). These need to be correlated with the standard spectroscopic normal mode quantum numbers (v₁,v^L₂,v₃) for linear triatomic molecules to enable the computed values to be matched with the empirically-derived values. In OCS, the fundamentals are the C–S stretch ν₁ at ≈859 cm⁻¹, the bending mode ν₂ at ≈520 cm⁻¹, and the C–O stretch ν₃ at ≈2062 cm⁻¹. The additional vibrational angular momentum quantum number L is needed to describe excitation of the ν₂ bending mode since motion can occur in two orthogonal planes with different phases. The following correlation rules were used: v₁ = n₂, v^L₂ = 2n₃ + L, and v₃ = n₁.

The weighting scheme, i.e. the weights assigned to the empirically-derived values being refined to, is an important aspect of the procedure. Practically speaking, the relative weighting between energies is far more significant than the absolute values. A benefit of the MARVEL OCS dataset is that each energy level possesses a measurement uncertainty and information on the number of transitions that it was established from. Energy levels that are only involved in one transition may not be wholly reliable, whereas an energy level involved in multiple transitions can be deemed more trustworthy and assigned a larger weight in the refinement.

Different weighting schemes were tested that factored in the measurement uncertainty, as was used previously, for example, in ref. 78. However, the most successful scheme was based only on the number of transitions that the energy level was involved in. In Fig. 2, the final weighting scheme used in the refinement of the OCS PESs is illustrated. Pure rotational energies were weighted the largest to ensure rotational band structure was better reproduced. Energies below 5000 cm⁻¹ were weighted an order-of-magnitude larger than energies above 5000 cm⁻¹ to accurately capture the more important spectroscopic region of the PES. Overall, this weighting scheme produced a balanced and highly accurate refinement.

Fig. 2 Illustration of the weighting scheme used in the empirical refinement to produce the CBS-HL^ref and VQZ-F12^ref PESs of OCS. The relative weighting between energy levels is more important than the absolute values. Note the y-axis is log scale.

4 Results and Discussion

4.1 Equilibrium geometry and pure rotational energies

In the following, the empirically refined PESs of OCS are referred to as CBS-HL^ref and VQZ-F12^ref, corresponding to the refined versions of the ab initio CBS-HL^ai and VQZ-F12^ai PESs, respectively. In Table 1, the equilibrium bond lengths and rotational constant of OCS determined from the different PESs are listed along with experimental values^79–81 derived from measured OCS microwave spectra. The computed values are in close agreement with experiment, with only marginal differences between the ab initio and refined PES bond lengths, especially for the CBS-HL PESs. Comparing the CBS-HL and VQZ-F12 PESs, the difference in equilibrium geometry is approximately 0.001–0.002 Å for the O–C bond length and 0.002–0.003 Å for the C–S bond length. Interestingly, the B rotational constant does not change between the CBS-HL PESs and is close to the refined VQZ-F12^ref value.

Table 1 Equilibrium bond lengths and rotational constant of OCS determined from the ab initio and empirically refined PESs

	r(O–C)/Å	r(C–S)/Å	B/cm^−1
a From microwave spectroscopy. b From laser Stark measurements.
Experiment^79^a	1.1612 ± 0.0058	1.5604 ± 0.0049
Experiment^80,81^b	1.1543 ± 0.0010	1.5628 ± 0.0010	0.202857
CBS-HL^ref	1.1560	1.5619	0.203434
CBS-HL^ai	1.1561	1.5616	0.203434
VQZ-F12^ref	1.1576	1.5638	0.203447
VQZ-F12^ai	1.1577	1.5647	0.202717

---

Calculations of pure rotational energies up to J = 20 in the ground vibrational state, shown in Table 2, magnifies the seemingly small differences in equilibrium geometries. The CBS-HL^ref PES shows the closest agreement with the empirically-derived MARVEL energies⁷¹ indicating that the equilibrium geometry derived from this PES is the most accurate of the four. The residual errors (observed–calculated) of the computed rotational energies using the CBS-HL^ai PES are approximately a factor of two larger than the refined CBS-HL^ref PES values. They are still much more accurate than the VQZ-F12 PES results. Advanced ab initio calculations that treat higher-level corrections can be highly accurate when describing molecular structure⁸² and the results of Table 1 confirm this.

Table 2 Pure rotational energies (in cm⁻¹) of OCS computed using the ab initio and empirically refined PESs. Results are compared against the empirically-derived MARVEL energies⁷¹ with the residual errors (observed–calculated) given in the last four columns

J	Observed	CBS-HL^ai (A)	VQZ-F12^ai (B)	CBS-HL^ref (C)	VQZ-F12^ref (D)	o–c (A)	o–c (B)	o–c (C)	o–c (D)
0	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
1	0.4057	0.4057	0.4043	0.4057	0.4046	0.0001	0.0014	0.0000	0.0011
2	1.2171	1.2170	1.2128	1.2170	1.2139	0.0002	0.0043	0.0001	0.0032
3	2.4343	2.4339	2.4256	2.4341	2.4278	0.0004	0.0087	0.0002	0.0065
4	4.0571	4.0565	4.0426	4.0568	4.0463	0.0006	0.0145	0.0003	0.0108
5	6.0857	6.0848	6.0639	6.0852	6.0695	0.0009	0.0217	0.0005	0.0162
6	8.5199	8.5186	8.4895	8.5192	8.4973	0.0013	0.0304	0.0007	0.0226
7	11.3598	11.3581	11.3193	11.3589	11.3297	0.0017	0.0406	0.0009	0.0302
8	14.6055	14.6033	14.5533	14.6043	14.5667	0.0022	0.0521	0.0012	0.0388
9	18.2568	18.2540	18.1916	18.2553	18.2083	0.0027	0.0652	0.0014	0.0485
10	22.3137	22.3104	22.2341	22.3119	22.2545	0.0033	0.0797	0.0018	0.0592
11	26.7763	26.7723	26.6807	26.7742	26.7053	0.0040	0.0956	0.0021	0.0711
12	31.6446	31.6399	31.5316	31.6421	31.5606	0.0047	0.1130	0.0025	0.0840
13	36.9185	36.9130	36.7867	36.9156	36.8205	0.0055	0.1318	0.0029	0.0980
14	42.5980	42.5916	42.4459	42.5946	42.4849	0.0064	0.1521	0.0034	0.1131
15	48.6831	48.6758	48.5093	48.6793	48.5539	0.0073	0.1738	0.0039	0.1292
16	55.1738	55.1656	54.9769	55.1694	55.0274	0.0083	0.1970	0.0044	0.1464
17	62.0701	62.0608	61.8485	62.0652	61.9054	0.0093	0.2216	0.0049	0.1647
18	69.3719	69.3615	69.1243	69.3664	69.1878	0.0104	0.2476	0.0055	0.1841
19	77.0793	77.0678	76.8042	77.0732	76.8747	0.0115	0.2751	0.0061	0.2046
20	85.1922	85.1794	84.8881	85.1854	84.9661	0.0128	0.3041	0.0068	0.2261

---

4.2 Rotation-vibration energy levels

In Table 3, computed J = 0 and J = 1 energy levels using the different PESs are compared against the empirically-derived MARVEL energies.⁷¹ For illustrative purposes, only a small selection is given, enough to clearly demonstrate the relative accuracies of the different PESs. Rovibrational energy levels are labelled by the rigorous quantum numbers J and the rotationless parity e/f where states with L = 0 correspond to e parity only, while states with L > 0 can possess both e and f components. The vibrational quantum numbers are approximate and follow the normal mode notation (v₁,v^L₂,v₃) for linear triatomic molecules discussed in Section 3.1.

Table 3 Computed energy levels (in cm⁻¹) of OCS using the ab initio and empirically refined PESs. For illustrative purposes, only a small selection is shown and compared against the empirically-derived MARVEL energies⁷¹ with the residual errors (observed--calculated) given in the last four columns. For J = 1, L = 1 states only e parity levels are shown despite both e and f components being available. A full comparison of the CBS-HL^ref and VQZ-F12^ref PESs against the MARVEL energies is provided as ESI

J	e/f	(v1,v^L2,v3)	Observed	CBS-HL^ai (A)	VQZ-F12^ai (B)	CBS-HL^ref (C)	VQZ-F12^ref (D)	o–c (A)	o–c (B)	o–c (C)	o–c (D)
1	e	(0,1^1,0)	520.828	521.474	522.516	520.829	520.841	−0.646	−1.042	−0.001	−0.013
0	e	(1,0^0,0)	858.967	858.320	860.309	858.961	859.020	0.647	−1.989	0.006	−0.053
0	e	(0,2^0,0)	1047.042	1048.281	1050.516	1047.043	1047.125	−1.239	−2.236	−0.001	−0.083
1	e	(1,1^1,0)	1372.864	1372.927	1375.905	1372.869	1372.880	−0.063	−2.978	−0.004	−0.016
1	e	(0,3^1,0)	1573.774	1575.576	1578.908	1573.772	1573.772	−1.803	−3.332	0.001	0.001
0	e	(2,0^0,0)	1710.976	1709.598	1713.848	1710.979	1711.018	1.378	−4.250	−0.003	−0.042
0	e	(1,2^0,0)	1892.229	1892.878	1896.889	1892.245	1892.168	−0.649	−4.011	−0.017	0.060
0	e	(0,0^0,1)	2062.201	2060.822	2063.908	2062.200	2062.238	1.379	−3.086	0.002	−0.036
0	e	(0,4^0,0)	2104.828	2107.081	2111.729	2104.854	2104.718	−2.254	−4.647	−0.026	0.109
1	e	(2,1^1,0)	2218.433	2217.832	2223.005	2218.429	2218.470	0.601	−5.173	0.004	−0.038
1	e	(1,3^1,0)	2412.526	2413.729	2418.787	2412.532	2412.519	−1.203	−5.058	−0.006	0.007
0	e	(3,0^0,0)	2555.991	2553.796	2560.523	2556.004	2555.922	2.195	−6.728	−0.013	0.069
1	e	(0,1^1,1)	2575.712	2575.003	2579.275	2575.708	2575.753	0.708	−4.272	0.003	−0.041
1	e	(2,2^0,0)	2731.804	2731.792	2737.857	2731.812	2731.725	0.012	−6.065	−0.008	0.079
0	e	(1,0^0,1)	2918.105	2916.240	2921.264	2918.125	2918.156	1.865	−5.024	−0.020	−0.051
0	e	(0,2^0,1)	3095.554	3095.482	3101.154	3095.536	3095.667	0.072	−5.672	0.018	−0.112
1	f	(1,1^1,1)	3424.543	3423.398	3429.531	3424.548	3424.380	1.145	−6.133	−0.005	0.163
1	e	(0,3^1,1)	3615.750	3616.278	3623.216	3615.728	3616.024	−0.528	−6.938	0.022	−0.274
0	e	(2,0^0,1)	3768.496	3766.931	3774.825	3768.489	3768.584	1.565	−7.894	0.007	−0.088
0	e	(1,2^0,1)	3937.427	3936.898	3944.311	3937.421	3937.371	0.530	−7.413	0.006	0.056
1	e	(1,6^0,0)	3990.515	3992.934	4002.173	3990.522	3991.784	−2.420	−9.239	−0.007	−1.269
0	e	(0,0^0,2)	4101.410	4098.179	4105.020	4101.388	4101.400	3.232	−6.841	0.022	0.010

---

The ab initio CBS-HL^ai and VQZ-F12^ai PESs reproduce the three fundamental wavenumbers with root-mean-square errors (RMSEs) of 0.955 cm⁻¹ and 2.203 cm⁻¹, respectively. The residual errors increase for combination and overtone states, with the CBS-HL^ai PES noticeably more accurate than the VQZ-F12^ai PES. The refined CBS-HL^ref and VQZ-F12^ref PESs reproduce the fundamentals with RMSEs of 0.004 cm⁻¹ and 0.038 cm⁻¹, respectively. This is a substantial improvement over the respective ab initio surfaces but is somewhat expected.

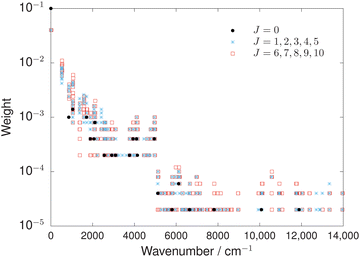
More surprising is the difference in accuracy between the two refined PESs. In Fig. 3 and Table 4, the main results of this study are summarised. The CBS-HL^ref PES exhibits superior accuracy, reproducing all known empirically-derived rovibrational energy levels of OCS up to J = 10 below 5000 cm⁻¹ with an RMSE of 0.016 cm⁻¹. This is an order-of-magnitude better than the VQZ-F12^ref PES, which possesses an RMSE of 0.167 cm⁻¹. The improvement in accuracy extends across all the energy levels used in the refinement up to 14 000 cm⁻¹, clearly seen in Fig. 3. Overall, the CBS-HL^ref PES reproduces the 884 empirically-derived energies with an RMSE of 0.060 cm⁻¹ compared to 0.383 cm⁻¹ of the VQZ-F12^ref PES, over a factor of six better.

Fig. 3 Direct comparison of the residual errors ΔE_obs−calc (in cm⁻¹) between the empirically-derived MARVEL energies⁷¹ and the corresponding computed values up to J = 10 using the CBS-HL^ref and VQZ-F12^ref PESs of OCS.

Table 4 Comparison of the empirically refined VQZ-F12^ref and CBS-HL^ref PESs of OCS. The table shows values for the root-mean-square error (RMSE) and mean absolute deviation (MAD) (both in cm⁻¹) of the computed rovibrational energy levels up to J = 10 when compared against the empirically-derived MARVEL values. The comparison is for a total of 884 energies with 434 of those below 5000 cm⁻¹ and 450 above 5000 cm⁻¹

	VQZ-F12^ref	CBS-HL^ref
RMSE (<5000 cm^−1)	0.167	0.016
MAD (<5000 cm^−1)	0.072	0.010
RMSE (>5000 cm^−1)	0.511	0.083
MAD (>5000 cm^−1)	0.280	0.053
RMSE (all)	0.383	0.060
MAD (all)	0.178	0.032

---

A closer inspection of the residual errors between the observed and computed energy levels for the refined PESs is shown in Fig. 4. The overall trend in residual errors is fairly similar between the CBS-HL^ref and VQZ-F12^ref PESs, with larger differences seen between 6000–7000 cm⁻¹ for levels within, e.g. the (v₁,v^L₂,v₃) = (4,2⁰,1) vibrational state. Several of these energy levels were only determined from one measured transition in the MARVEL procedure. Although weighted lower in the refinement, both PESs struggle more than expected to reproduce these levels, suggesting possible issues in the underlying spectroscopic experiments used to determine them. The VQZ-F12^ref PES performs particularly poorly for the (1,6⁰,0) vibrational state around ≈3991 cm⁻¹ with residual errors around −1.25 cm⁻¹ compared to errors of less than −0.01 cm⁻¹ for the CBS-HL^ref PES. It is not clear why the VQZ-F12^ref exhibits this behaviour.

Fig. 4 Closer inspection of the residual errors ΔE_obs−calc (in cm⁻¹) between the empirically-derived MARVEL energies⁷¹ and the corresponding computed values up to J = 10 using the CBS-HL^ref (left panel) and VQZ-F12^ref (right panel) PESs of OCS.

In the refinement procedure, the PES expansion parameters are simultaneously fitted to both the empirically-derived energies and the original ab initio dataset. This stops overfitting and unrealistic distortions arising in the PES. However, the fit will be somewhat constrained to the quality of the original ab initio dataset, potentially limiting the accuracy that can be achieved in the refinement.

To test the impact of constraining the refinement to the ab initio dataset, the CBS-HL^ref PES (defined by the expansion parameters) was refined to the empirical-quality MARVEL energy levels but constrained to the VQZ-F12 ab initio dataset. The 434 empirically-derived rovibrational energy levels of OCS below 5000 cm⁻¹ were reproduced with an RMSE of 0.027 cm⁻¹ (compared to 0.016 cm⁻¹ in the original CBS-HL^ref PES refinement), while the full dataset of 884 energies was reproduced with an RMSE of 0.071 cm⁻¹ (compared to 0.060 cm⁻¹ in the original CBS-HL^ref PES refinement). Thus, the results of the refinement do not change significantly upon constraining to a different, less-accurate ab initio dataset.

Both refined PESs used the same analytic representation, and were determined using the same least-squares fitting refinement procedure in the computer program TROVE. This process varied the PES expansion parameters until they converged on an optimum solution in which the computed rovibrational energy levels matched the empirically-derived values as closely as possible for the given PES. The ab initio PES expansion parameters were the starting point of each refinement and seem to dictate the path that the refinement procedure takes to converge on a final solution. It suggests that the accuracy of the starting ab initio PES strongly influences the accuracy that can be achieved for the final refined PES.

5 Conclusions

The purpose of the present work was twofold. Firstly, the influence of the underlying ab initio calculations on the accuracy of a PES refined to experimental data has been critically investigated. Using carbonyl sulphide as an example, two PESs were generated with different levels of ab initio theory and subsequently refined to laboratory spectroscopic data in near-identical procedures. Interestingly, the quality of the underlying ab initio calculations was shown to considerably affect the accuracy of the final refined PES. For OCS, an order-of-magnitude improvement in the accuracy of the computed rovibrational energies was shown. This was achieved using a refined PES based on higher-quality ab initio calculations; a substantial improvement in accuracy that should be factored into future high-resolution theoretical studies.

The second outcome of this work was constructing the most accurate PES in the literature for the electronic ground state of carbonyl sulphide. The empirically refined CBS-HL^ref PES, recommended for future applications, was based on state-of-the-art electronic structure calculations that pushed the limits of ab initio accuracy. The PES was rigorously refined to a comprehensive list of empirically-derived rovibrational energy levels up to J = 10; a list established from an exhaustive analysis of the literature on high-resolution spectra of OCS.⁷¹ The CBS-HL^ref PES reproduced 884 energy levels below 14 000 cm⁻¹ with an RMSE of 0.060 cm⁻¹ and 434 energies below 5000 cm⁻¹ with an RMSE of 0.016 cm⁻¹, demonstrating unprecedented accuracy.

There is strong motivation to study the infrared spectrum of OCS. Major studies of exoplanets are actively searching for spectroscopic signatures of carbonyl sulphide, e.g. in the spectra of the gas giant WASP-39b using the James Webb Space Telescope (JWST),^7,8 but a lack of suitable spectroscopic data is hindering its potential detection. Exoplanets can possess temperatures ranging into the thousands of Kelvin but only room-temperature OCS line list data with incomplete coverage is available from the HITRAN spectroscopic database.⁸³ A comprehensive molecular line list of OCS, based on the CBS-HL^ref PES, has recently been computed⁸⁴ for the ExoMol database,^53–55 which is providing extensive high-temperature spectroscopic data for exoplanets.

Data availability

The data that support the findings of this study are available within the article and its ESI.†

Conflicts of interest

The authors have no conflicts to disclose.

Acknowledgements

The author is grateful to Sergey Yurchenko for valuable discussions on the TROVE calculations and to Jonathan Tennyson for sharing the MARVEL dataset of empirically-derived energy levels of OCS before publication. The author acknowledges support from the Engineering and Physical Sciences Research Council [grant number EP/S021582/1]. The author also acknowledges the use of the UCL Legion High Performance Computing Facility (Legion@UCL) and associated support services in the completion of this work, along with the Cambridge Service for Data Driven Discovery (CSD3), part of which is operated by the University of Cambridge Research Computing on behalf of the STFC Dirac HPC Facility (https://www.dirac.ac.uk). The Dirac component of CSD3 was funded by BEIS capital funding via STFC capital grants ST/P002307/1 and ST/R002452/1 and STFC operations grant ST/R00689X/1.

References

1. T. Helgaker, W. Klopper and D. P. Tew, Mol. Phys., 2008, 106, 2107.
2. K. A. Peterson, D. Feller and D. A. Dixon, Theor. Chem. Acc., 2012, 131, 1079.
3. J. Koput, J. Chem. Phys., 2013, 138, 234301.
4. A. Yachmenev, S. N. Yurchenko, T. Ribeyre and W. Thiel, J. Chem. Phys., 2011, 135, 074302.
5. A. Owens, S. N. Yurchenko, A. Yachmenev, J. Tennyson and W. Thiel, J. Chem. Phys., 2015, 142, 244306.
6. A. Owens, S. N. Yurchenko, A. Yachmenev, J. Tennyson and W. Thiel, J. Chem. Phys., 2016, 145, 104305.
7. S.-M. Tsai, E. K. H. Lee, D. Powell, P. Gao, X. Zhang, J. Moses, E. Hébrard, O. Venot, V. Parmentier, S. Jordan, R. Hu, M. K. Alam, L. Alderson, N. M. Batalha, J. L. Bean, B. Benneke, C. J. Bierson, R. P. Brady, L. Carone, A. L. Carter, K. L. Chubb, J. Inglis, J. Leconte, M. Line, M. Lopez-Morales, Y. Miguel, K. Molaverdikhani, Z. Rustamkulov, D. K. Sing, K. B. Stevenson, H. R. Wakeford, J. Yang, K. Aggarwal, R. Baeyens, S. Barat, M. de Val-Borro, T. Daylan, J. J. Fortney, K. France, J. M. Goyal, D. Grant, J. Kirk, L. Kreidberg, A. Louca, S. E. Moran, S. Mukherjee, E. Nasedkin, K. Ohno, B. V. Rackham, S. Redfield, J. Taylor, P. Tremblin, C. Visscher, N. L. Wallack, L. Welbanks, A. Youngblood, E.-M. Ahrer, N. E. Batalha, P. Behr, Z. K. Berta-Thompson, J. Blecic, S. L. Casewell, I. J. M. Crossfield, N. Crouzet, P. E. Cubillos, L. Decin, J.-M. Desert, A. D. Feinstein, N. P. Gibson, J. Harrington, K. Heng, T. Henning, E. M.-R. Kempton, J. Krick, P.-O. Lagage, M. Lendl, J. D. Lothringer, M. Mansfield, N. J. Mayne, T. Mikal-Evans, E. Palle, E. Schlawin, O. Shorttle, P. J. Wheatley and S. N. Yurchenko, Nature, 2023, 617, 483.
8. L. Alderson, H. R. Wakeford, M. K. Alam, N. E. Batalha, J. D. Lothringer, J. Adams Redai, S. Barat, J. Brande, M. Damiano, T. Daylan, N. Espinoza, L. Flagg, J. M. Goyal, D. Grant, R. Hu, J. Inglis, E. K. H. Lee, T. Mikal-Evans, L. Ramos-Rosado, P.-A. Roy, N. L. Wallack, N. M. Batalha, J. L. Bean, B. Benneke, Z. K. Berta-Thompson, A. L. Carter, Q. Changeat, K. D. Colon, I. J. M. Crossfield, J.-M. Desert, D. Foreman-Mackey, N. P. Gibson, L. Kreidberg, M. R. Line, M. Lopez-Morales, K. Molaverdikhani, S. E. Moran, G. Morello, J. I. Moses, S. Mukherjee, E. Schlawin, D. K. Sing, K. B. Stevenson, J. Taylor, K. Aggarwal, E.-M. Ahrer, N. H. Allen, J. K. Barstow, T. J. Bell, J. Blecic, S. L. Casewell, K. L. Chubb, N. Crouzet, P. E. Cubillos, L. Decin, A. D. Feinstein, J. J. Fortney, J. Harrington, K. Heng, N. Iro, E. M.-R. Kempton, J. Kirk, H. A. Knutson, J. Krick, J. Leconte, M. Lendl, R. J. MacDonald, L. Mancini, M. Mansfield, E. M. May, N. J. Mayne, Y. Miguel, N. K. Nikolov, K. Ohno, E. Palle, V. Parmentier, D. J. M. Petit dit de la Roche, C. Piaulet, D. Powell, B. V. Rackham, S. Redfield, L. K. Rogers, Z. Rustamkulov, X. Tan, P. Tremblin, S.-M. Tsai, J. D. Turner, M. de Val-Borro, O. Venot, L. Welbanks, P. J. Wheatley and X. Zhang, Nature, 2023, 614, 664.
9. R. Hobbs, P. B. Rimmer, O. Shorttle and N. Madhusudhan, Mon. Not. R. Astron. Soc., 2021, 506, 3186.
10. M. A. K. Khalil and R. A. Rasmussen, Atmos. Environ., 1984, 18, 1805.
11. L. Leman, L. Orgel and M. R. Ghadiri, Science, 2004, 306, 283.
12. A. Foord, J. Smith and D. Whiffen, Mol. Phys., 1975, 29, 1685.
13. K. A. Peterson, R. C. Mayrhofer and R. C. Woods, J. Chem. Phys., 1991, 94, 431.
14. J. Martin, J. Francois and R. Gijbels, J. Mol. Spectrosc., 1995, 169, 445.
15. Y. Pak and R. C. Woods, J. Chem. Phys., 1997, 107, 5094.
16. J. Zuniga, A. Bastida, M. Alacid and A. Requena, J. Chem. Phys., 2000, 113, 5695.
17. D. Xie, Y. Lu, D. Xu and G. Yan, Chem. Phys., 2001, 270, 415.
18. D. Xie and Y. Lu, Chin. Sci. Bull., 2002, 47, 641.
19. L. Shirkov, T. Korona and R. Moszynski, Struct. Chem., 2012, 23, 1425.
20. A. G. Csaszar, W. D. Allen and H. F. Schaefer, J. Chem. Phys., 1998, 108, 9751.
21. T. B. Adler, G. Knizia and H. J. Werner, J. Chem. Phys., 2007, 127, 221106.
22. K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102.
23. J. G. Hill and K. A. Peterson, Phys. Chem. Chem. Phys., 2010, 12, 10460.
24. J. G. Hill, K. A. Peterson, G. Knizia and H.-J. Werner, J. Chem. Phys., 2009, 131, 194105.
25. S. Ten-No, Chem. Phys. Lett., 2004, 398, 56–61.
26. K. E. Yousaf and K. A. Peterson, J. Chem. Phys., 2008, 129, 184108.
27. F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291.
28. C. Hättig, Phys. Chem. Chem. Phys., 2005, 7, 59–66.
29. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Sci., 2012, 2, 242–253.
30. H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107.
31. J. G. Hill, S. Mazumder and K. A. Peterson, J. Chem. Phys., 2010, 132, 054108.
32. M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 214105.
33. M. Kállay and J. Gauss, J. Chem. Phys., 2008, 129, 144101.
34. M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy, B. Hégely, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and Á. Ganyecz, J. Chem. Phys., 2020, 152, 074107.
35. D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108.
36. T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023.
37. T. H. Dunning Jr., K. A. Peterson and A. K. Wilson, J. Chem. Phys., 2001, 114, 9244.
38. M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155.
39. B. A. Heß, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742–3748.
40. W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48–53.
41. J. Gauss, A. Tajti, M. Kallay, J. F. Stanton and P. G. Szalay, J. Chem. Phys., 2006, 125, 144111.
42. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
43. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1995, 103, 4572–4585.
44. K. A. Peterson and T. H. Dunning, J. Chem. Phys., 2002, 117, 10548.
45. P. O. Dral, A. Owens, S. N. Yurchenko and W. Thiel, J. Chem. Phys., 2017, 146, 244108.
46. A. Owens, S. N. Yurchenko, A. Yachmenev and W. Thiel, J. Chem. Phys., 2015, 143, 244317.
47. A. Owens, A. Yachmenev, J. Küpper, S. N. Yurchenko and W. Thiel, Phys. Chem. Chem. Phys., 2019, 21, 3496.
48. S. E. Choi and J. C. Light, J. Chem. Phys., 1992, 97, 7031.
49. V. G. Tyuterev, S. A. Tashkun and D. W. Schwenke, Chem. Phys. Lett., 2001, 348, 223–234.
50. H. Partridge and D. W. Schwenke, J. Chem. Phys., 1997, 106, 4618–4639.
51. J. K. G. Watson, J. Mol. Spectrosc., 2003, 219, 326–328.
52. S. N. Yurchenko, W. Thiel and P. Jensen, J. Mol. Spectrosc., 2007, 245, 126–140.
53. J. Tennyson and S. N. Yurchenko, Mon. Not. R. Astron. Soc., 2012, 425, 21–33.
54. J. Tennyson, S. N. Yurchenko, A. F. Al-Refaie, E. J. Barton, K. L. Chubb, P. A. Coles, S. Diamantopoulou, M. N. Gorman, C. Hill, A. Z. Lam, L. Lodi, L. K. McKemmish, Y. Na, A. Owens, O. L. Polyansky, T. Rivlin, C. Sousa-Silva, D. S. Underwood, A. Yachmenev and E. Zak, J. Mol. Spectrosc., 2016, 327, 73–94.
55. J. Tennyson, S. N. Yurchenko, A. F. Al-Refaie, V. H. J. Clark, K. L. Chubb, E. K. Conway, A. Dewan, M. N. Gorman, C. Hill, A. E. Lynas-Gray, T. Mellor, L. K. McKemmish, A. Owens, O. L. Polyansky, M. Semenov, W. Somogyi, G. Tinetti, A. Upadhyay, I. Waldmann, Y. Wang, S. Wright and O. P. Yurchenko, J. Quant. Spectrosc. Radiat. Transf., 2020, 255, 107228.
56. S. N. Yurchenko, R. J. Barber, A. Yachmenev, W. Thiel, P. Jensen and J. Tennyson, J. Phys. Chem. A, 2009, 113, 11845–11855.
57. A. Yachmenev and S. N. Yurchenko, J. Chem. Phys., 2015, 143, 014105.
58. J. Tennyson and S. N. Yurchenko, Int. J. Quantum Chem., 2017, 117, 92–103.
59. S. N. Yurchenko, A. Yachmenev and R. I. Ovsyannikov, J. Chem. Theory Comput., 2017, 13, 4368–4381.
60. S. N. Yurchenko and T. M. Mellor, J. Chem. Phys., 2020, 153, 154106.
61. T. M. Mellor, S. N. Yurchenko and P. Jensen, Symmetry, 2021, 13, 548.
62. S. N. Yurchenko, T. M. Mellor, R. S. Freedman and J. Tennyson, Mon. Not. R. Astron. Soc., 2020, 496, 5282–5291.
63. A. Owens, E. K. Conway, J. Tennyson and S. N. Yurchenko, Mon. Not. R. Astron. Soc., 2020, 495, 1927–1933.
64. A. Owens, V. H. J. Clark, A. Mitrushchenkov, S. N. Yurchenko and J. Tennyson, J. Chem. Phys., 2021, 154, 234302.
65. A. Owens, J. Tennyson and S. N. Yurchenko, Mon. Not. R. Astron. Soc., 2021, 502, 1128–1135.
66. S. Carter, N. Handy and B. Sutcliffe, Mol. Phys., 1983, 49, 745–748.
67. B. T. Sutcliffe and J. Tennyson, Int. J. Quantum Chem., 1991, 39, 183–196.
68. B. V. Noumerov, Mon. Not. R. Astron. Soc., 1924, 84, 592–602.
69. J. W. Cooley, Math. Comp., 1961, 15, 363–374.
70. M. Wang, G. Audi, A. Wapstra, F. Kondev, M. MacCormick, X. Xu and B. Pfeiffer, Chin. Phys. C, 2012, 36, 1603.
71. E. Xu and J. Tennyson, Mol. Phys., 2023, e2279694.
72. T. Furtenbacher, A. G. Császár and J. Tennyson, J. Mol. Spectrosc., 2007, 245, 115–125.
73. A. G. Császár, G. Czakó, T. Furtenbacher and E. Mátyus, Annu. Rep. Comput. Chem., 2007, 3, 155–176.
74. T. Furtenbacher and A. G. Csaszar, J. Mol. Struct., 2012, 1009, 123.
75. R. Tóbiás, T. Furtenbacher, J. Tennyson and A. G. Császár, Phys. Chem. Chem. Phys., 2019, 21, 3473–3495.
76. S. N. Yurchenko, R. J. Barber, J. Tennyson, W. Thiel and P. Jensen, J. Mol. Spectrosc., 2011, 268, 123–129.
77. S. Yurchenko, M. Carvajal, P. Jensen, F. Herregodts and T. Huet, Chem. Phys., 2003, 290, 59.
78. A. Owens, A. Mitrushchenkov, S. N. Yurchenko and J. Tennyson, Mon. Not. R. Astron. Soc., 2022, 516, 3995.
79. T. W. Dakin, W. E. Good and D. K. Coles, Phys. Rev., 1947, 71, 640.
80. A. G. Maki and D. R. Johnson, J. Mol. Spectrosc., 1973, 47, 226.
81. A. G. Maki, J. Phys. Chem. Ref. Data, 1974, 3, 221.
82. C. Puzzarini, Int. J. Quantum Chem., 2016, 116, 1513.
83. I. E. Gordon, L. S. Rothman, R. J. Hargreaves, R. Hashemi, E. V. Karlovets, F. M. Skinner, E. K. Conway, C. Hill, R. V. Kochanov, Y. Tan, P. Wcislo, A. A. Finenko, K. Nelson, P. F. Bernath, M. Birk, V. Boudon, A. Campargue, K. V. Chance, A. Coustenis, B. J. Drouin, J.-M. Flaud, R. R. Gamache, J. T. Hodges, D. Jacquemart, E. J. Mlawer, A. V. Nikitin, V. I. Perevalov, M. Rotger, J. Tennyson, G. C. Toon, H. Tran, V. G. Tyuterev, E. M. Adkins, A. Baker, A. Barbe, E. Canè, A. G. Császár, A. Dudaryonok, O. Egorov, A. J. Fleisher, H. Fleurbaey, A. Foltynowicz, T. Furtenbacher, J. J. Harrison, J.-M. Hartmann, V.-M. Horneman, X. Huang, T. Karman, J. Karns, S. Kassi, I. Kleiner, V. Kofman, F. Kwabia–Tchana, N. N. Lavrentieva, T. J. Lee, D. A. Long, A. A. Lukashevskaya, O. M. Lyulin, V. Y. Makhnev, W. Matt, S. T. Massie, M. Melosso, S. N. Mikhailenko, D. Mondelain, H. S. P. Müller, O. V. Naumenko, A. Perrin, O. L. Polyansky, E. Raddaoui, P. L. Raston, Z. D. Reed, M. Rey, C. Richard, R. Tóbiás, I. Sadiek, D. W. Schwenke, E. Starikova, K. Sung, F. Tamassia, S. A. Tashkun, J. Vander Auwera, I. A. Vasilenko, A. A. Vigasin, G. L. Villanueva, B. Vispoel, G. Wagner, A. Yachmenev and S. N. Yurchenko, J. Quant. Spectrosc. Radiat. Transf., 2022, 277, 107949.
84. A. Owens, S. N. Yurchenko and J. Tennyson, Mon. Not. R. Astron. Soc., 2024, 530, 4004.

---

Footnote

† Electronic supplementary information (ESI) available: See the supplementary material for input files containing the expansion parameters and a program to construct the PESs of OCS, along with a full comparison of computed rovibrational energy levels up to J = 10 using the CBS-HL^ref and VQZ-F12^ref PESs. See DOI: https://doi.org/10.1039/d4cp01205d

---