Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Partial density of states representation for accurate deep neural network predictions of X-ray spectra†
Clelia
Middleton
a,
Basile F. E.
Curchod
b and
Thomas J.
Penfold
 *a
*a
aChemistry, School of Natural and Environmental Sciences, Newcastle University, Great North Road, Newcastle upon Tyne, NE1 7RU, UK. E-mail: tom.penfold@newcastle.ac.uk
bCentre for Computational Chemistry, School of Chemistry, Cantock's Close, University of Bristol, Bristol, BS8 1TS, UK
First published on 30th August 2024
Abstract
The performance of a machine learning (ML) algorithm for chemistry is highly contingent upon the architect's choice of input representation. This work introduces the partial density of states (p-DOS) descriptor: a novel, quantum-inspired structural representation which encodes relevant electronic information for machine learning models seeking to simulate X-ray spectroscopy. p-DOS uses a minimal basis set in conjunction with a guess (non-optimised) electronic configuration to extract and then discretise the density of states (DOS) of the absorbing atom to form the input vector. We demonstrate that while the electronically-focused p-DOS performs well in isolation, optimal performance is achieved when supplemented with nuclear structural information imparted via a geometric representation. p-DOS provides a description of the key electronic properties of a system which is not only concise and computationally efficient, but also independent of molecular size or choice of basis set. It can be rapidly generated, facilitating its application with large training sets. Its performance is demonstrated using a wide variety of examples at the sulphur K-edge, including the prediction of ultrafast X-ray spectroscopic signal associated with photoexcited 2(5H)-thiophenone. These results highlight the potential for ML models developed using p-DOS to contribute to the interpretation and prediction of experimental results e.g. in operando measurements of batteries and/or catalysts and femtosecond time-resolved studies, especially those made possible by emergent cutting-edge technologies, especially X-ray free electron lasers.
1 Introduction
As in innumerable other areas of modern life, the impact of Machine learning (ML) algorithms is emerging as a transformative force within the fields of computational chemistry and physics.1–3 It is vital that when developing an effectual ML algorithm in chemistry that careful attention is paid to representational formatting, i.e. the approach used to encode information about molecular or material composition and structure.4–6 A high-quality representation should efficiently encapsulate both important differences between input cases and the physics relevant to the problem under consideration, enabling the model to develop descriptive power which can render target properties accurately for a wide breadth of inputs. A ML model that operates on molecular structures must map each system, i.e. the atomic identities and their Cartesian coordinates, onto a suitable (lower-dimensional) representation or feature vector. These representations aim to capture the key ingredients required to support a model's capacity to extract abstract and nuanced patterns and relationships in the training set data, facilitating the accurate prediction of properties and observables. The ideal feature vector should be (i) local, such that it encodes the immediate molecular structure at an arbitrary point up to a cutoff distance, (ii) invariant with respect to transformations that do not alter the target property (iii) unique, such that it should vary when the target property varies; associating different outputs with identical representations and (iv) efficient, such that it should not take a long time to construct.There exists a number of representations for which these criteria are fulfilled: examples include smooth overlap of atomic positions (SOAP),7 the atomic cluster expansion (ACE),8 many body tensor representation (MBTR)9 and atomic centred symmetry functions (ACSF).10 Importantly, these representations focus solely on the position and charge of the nuclei to build a representation. Consequently while computationally inexpensive to generate, they are limited by an incapacity to provide direct insights into the relationship between electronic structure of the input and target properties of a system. They are also unable to supply distinct representations for species with identical geometries which differ in their electronic configurations, i.e. anions and cations.
To overcome this challenge, quantum-inspired representations which do include electronic structural information have been developed. Such representations include molecular orbital basis machine learning (MOB-ML)11 and the F (Fock), J (Coulomb), and K (exchange) matrices (FJK) representation.12 However, both of these require some a priori calculations: hence they only operate within a ‘Δ-learning’ framework, where a ML model corrects a calculation performed at a lower level of theory to provide a result consistent with a higher level of theory. Alternatively, the spectrum of approximated Hamiltonian matrices (SPAHM)13 and matrix of orthogonalised atomic orbital coefficients (MAOC)14 algorithms generate representations based upon a guess electronic Hamiltonian. These representations are thus quicker to encode, and models applying them are also able to provide predictions using electronic information from the input.
In recent years, computational spectroscopy has become an indispensable tool for the modern spectroscopist, capable of providing predictions – and, consequently, interpretations – of experimental observables. The predominance of computational spectroscopy is perhaps best illustrated within X-ray spectroscopy,15–17 where the transformative effects of next-generation light sources18,19 are rapidly advancing the capabilities of the technique. The increased understanding of mechanisms responsible for X-ray spectral lineshapes alongside the availability of increasing quantities of data arising from the performance of more numerous and sophisticated calculations presents the opportunity to develop data-driven and ML techniques, which can complement the first-principles based techniques of computational spectroscopy.20,21 A number of works have developed such ML models for the simulation and analysis of X-ray spectroscopy.22–32 For example, Rankine et al.33 applied the weighted atomic centred symmetry functions (wACSF)34 descriptor within a deep neural network (DNN) – XANESNET – to predict X-ray absorption near-edge structure (XANES) K-edge spectra of transition metal complexes. This approach, which predicts spectra instantaneously, was able to provides K-edge XANES spectra with an average accuracy of ∼±2–4% in which the positions of prominent peaks are matched with a >90% hit rate to sub-eV (∼0.8 eV) error.
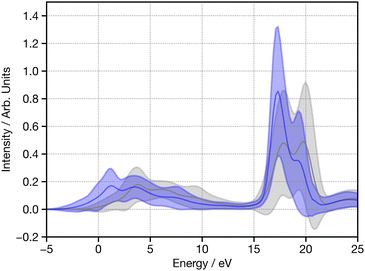
When observing transition metal spectra (an example of which is supplied in Fig. 1(a)), it is apparent that many prominent lineshape features arise above the ionisation potential. These resonant features result from scattering events of the excited electron with neighbouring atoms, and therefore are largely dependent upon the nuclear geometric structure of the system around the absorbing atom.35 The XANESNET network was later extended by Watson et al. to the Pt L2/3-edge,36 which – in contrast to the transition metal K-edges – exhibits a strong absorption edge, or white line transition in the low-energy region of the spectrum. The shape and position of this white line is determined by the character of the d-orbitals of the absorbing atom, and therefore is also influenced by electronic structure. In this work, Watson et al. demonstrated that although the network was able to describe the whole spectrum containing both electronic and nuclear structural information, the poorest performance was found to be in region of the spectrum near the white line – where the electronics of the system are deterministic. This shortfall in predictive capability is due to limitations of the wACSF descriptor, which only directly encodes nuclear geometrics. Models where purely geometric representations are used will naturally struggle to describe regions of the XANES where electronic factors dominate the formation of prominent features in the lineshape.
When approaching the problem of encoding electronic information, Carbone et al.37 developed a graph neural network, which went beyond purely nuclear geometrics by including information about donor acceptor status and hybridisation of the absorbing atom (or “absorber”). In this work, the authors demonstrated that the network could predict spectra at the O and N K-edges, which – like the Pt L2/3 edge spectra – are sensitive to the electronic structure, particularly close to the white line. The sulphur K-edge, a typical spectrum for which is shown in Fig. 1(b), presents a similar case, where the prominent first peaks arise from 1s → π* and 1s → σ* transitions. The sharpness of these peaks and their strong sensitivity to the electronic configuration of the system38,39 means that for a model to cogently map out the structure–spectrum relationship, a robust physics-based description of the initial and final states of these transitions must be available. A representation which can be generated with computational efficiency also remains a desirable goal, as this leverages the benefits of efficient machine learning architectures when contrasted with the run-times and computational costs of first-principles calculations.
To tackle these challenges, we herein introduce a new descriptor based upon a partial density of states (p-DOS), which encodes relevant electronic information for ML models seeking to simulate X-ray spectroscopy. We demonstrate that using a minimal basis set in conjunction with a guess (non-optimised) electronic configuration of the molecule, this representation can be generated quickly and delivers a compact descriptor, independent in size from the size of either the input species or the basis set. Using a diverse variety of examples at the sulphur K-edge, we demonstrate that while this representation performs well in isolation, optimal performance is achieved when the descriptor is supplemented with nuclear structural information imparted via a geometric representation (Fig. 2).
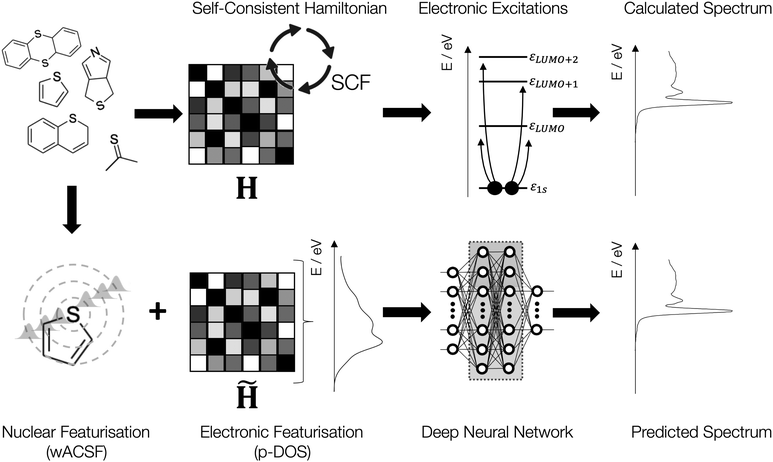 | ||
| Fig. 2 Schematic of the architecture used in this work: during first principles calculations, the Hamiltonian is set up and then converged using self-consistent field cycles. Subsequently, the spectra can be calculated using electronic excitations of the core-orbitals. Our DNN combines the nuclear structure descriptor based upon weighted atom-centred symmetry functions (wACSF)34 with the partial density of states (p-DOS) obtained from a guess (non-optimised) electronic wavefunction. This descriptor is subsequently fed to the DNN to develop a forward structure-to-spectrum mapping via the iterative optimisation of the internal weights. | ||
2 Methods and computational details
2.1 Partial density of states (p-DOS) descriptor
An X-ray absorption spectrum records the transition probability between an initial ground state and a final core–hole excited state of the system. This may be expressed using Fermi's golden rule as: | (1) |
 represents the interaction Hamiltonian, with light radiation of frequency ω.
represents the interaction Hamiltonian, with light radiation of frequency ω.
Assuming the one-electron state approximation (i.e. one electron transitions to generate each final state) and an interaction limited to the dipole approximation (which even in the short wavelength regime is usually 3 orders of magnitude larger than high-order terms such as the electric transition quadrupole) we can rewrite eqn (1) as:
 | (2) |
 to be non-zero, the selection rule ΔL = ±1 applies, and there must be spatial overlap between the initial and final states. Consequently, we can take advantage of the localised nature of the initial core-state and approximate a XANES spectrum using a partial density of states (p-DOS) corresponding to a dipole-allowed transition from the initial core orbital. For the sulphur K-edge, this corresponds to electronic transitions from s → p orbitals on the absorber and therefore the spectrum can be approximated as the sulphur p-orbital DOS.
to be non-zero, the selection rule ΔL = ±1 applies, and there must be spatial overlap between the initial and final states. Consequently, we can take advantage of the localised nature of the initial core-state and approximate a XANES spectrum using a partial density of states (p-DOS) corresponding to a dipole-allowed transition from the initial core orbital. For the sulphur K-edge, this corresponds to electronic transitions from s → p orbitals on the absorber and therefore the spectrum can be approximated as the sulphur p-orbital DOS.
Within this approximation, our p-DOS descriptor is obtained by extracting the absorber's atomic orbital contribution to each unoccupied molecular orbital, which is obtained using a guess (non-optimised) electronic configuration of the system. We express the guess molecular orbital configuration as in eqn (3):
 | (3) |
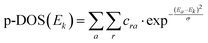 | (4) |
The p-DOS descriptor aims to encapsulate the electronic information which produces spectroscopic observables. To encode nuclear structural information which also acts as a contributor to the spectrum, one can supplement this descriptor with the wACSF descriptor previously described in ref. 33 For an arbitrary absorption site, i, wACSF is constructed via using a single global (G1), n radial (G2; two-body), and m angular (G4; three-body) terms. The descriptor is available in the latest version of XANESNET found here.40
2.2 Training data and quantum chemistry simulations
Contextualising the ML training data in terms of “samples” and “labels”, our reference datasets comprise X-ray absorption site geometries (“samples”) of small organic molecule complexes containing a single sulphur atom, extracted from the GBD13 dataset.41 All molecules have ≤10 heavy (non-hydrogen) atoms. Overall, the dataset comprises a total of 134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 877 samples.
877 samples.
Sulphur K-edge XAS spectra (“labels”) for all of the structures in our reference datasets were calculated using a restricted excitation window time-dependent density functional theory (REW-TDDFT)42 as implemented in the ORCA quantum chemistry package.43 For all calculations, the BP86 exchange and correlation functional44,45 and DKH-def2-TZVP basis set46 were used, and scalar relativistic effects were described using a Douglas–Kroll–Hess (DKH) Hamiltonian of 2nd order.47 The light–matter interaction was described using electric dipole, magnetic dipole, and electric quadrupole transition moments.48 After calculation, each spectrum was broadened using a Gaussian function with a fixed width of 1.0 eV. A final pre-processing step was carried out to scale the target spectra for each reference dataset into the 0 → 1 range independently by dividing through by the largest calculated cross-section in the reference dataset. The dataset is freely available at the following location.49
2.3 Network details and training
In this work, our network is based on the deep multilayer perceptron (MLP) model and comprises an input layer, two hidden layers, and an output layer. All layers are dense, i.e.: fully connected, and each hidden layer perform nonlinear transformations using the rectified linear unit (ReLU) activation function. The input layer, where an input feature vector has length N, comprises N neurons, the hidden layers each comprise 512 neurons, and the output layer comprises 400 neurons from which the discretised K-edge XANES spectrum is retrieved after regression. In other words, XANESNET is a multi-output MLP where each output neuron corresponds to the spectral intensity at a given energy gridpoint. The XANESNET DNN contains by [N × 512 × 512 × 400] points overall and therefore has, depending on the size of N, ∼400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 internal weights (W).
000 internal weights (W).
The internal weights, W, are optimised via iterative feed-forward and backpropagation cycles to minimise the empirical loss, J(W), defined here as the mean-squared error (MSE) between the predicted, μpredict, and calculated, μcalculated, K-edge XANES spectra over the reference dataset. In other words, the algorithm hunts for an optimal set of internal weights, W*, to satisfy  . Gradients of the empirical loss with respect to the internal weights, δJ(W)/δW, were estimated over minibatches of 64 samples and updated iteratively according to the adaptive moment estimation (ADAM)50 algorithm. An annealed learning rate was used throughout, with the learning rate initially set to 2 × 10−3, then reduced by a factor of 2 every 100 epochs. Internal weights were initially set according to ref. 51. Unless explicitly stated in this Article, optimisation was carried out over 500 iterative cycles through the network (commonly termed epochs). Regularisation was implemented to avert any over-fitting of the network to the training dataset.
. Gradients of the empirical loss with respect to the internal weights, δJ(W)/δW, were estimated over minibatches of 64 samples and updated iteratively according to the adaptive moment estimation (ADAM)50 algorithm. An annealed learning rate was used throughout, with the learning rate initially set to 2 × 10−3, then reduced by a factor of 2 every 100 epochs. Internal weights were initially set according to ref. 51. Unless explicitly stated in this Article, optimisation was carried out over 500 iterative cycles through the network (commonly termed epochs). Regularisation was implemented to avert any over-fitting of the network to the training dataset.
The DNN is programmed in Python 3 with Pytorch.52 The atomic simulation environment53 (ase) API is used to handle and manipulate molecular structures. For this work, the required electronic properties as described in Section 2.1 were extracted using the pySCF package,54 as incorporated within the XANESNET code.40 The code is publicly available under the GNU Public License (GPLv3) on GitLab.40
3 Results
We now detail and discuss the results of the studies, which are undertaken as follows: firstly, we optimise a suitable p-DOS descriptor and assess the influence of its parameters – including basis set, energy range, broadening and discretisation – on performance. We additionally assess the influence of concatenating p-DOS with a nuclear structure descriptor based upon wACSF.34 Secondly, the performance of the XANESNET DNN for predicting S K-edge XANES spectra using the new descriptor is investigated. Third and finally, we extend the investigation into the capability of p-DOS at the S K-edge with an interesting test case: the ultrafast time-resolved experimental signal associated with the ground state interconversion of highly vibrationally excited photoproducts of 2(5H)-thiophenone.3.1 p-DOS descriptor: featurisation and optimisation
In this section, we address the way p-DOS represents the electronic configuration of an input system, and investigate the influence of user-adjustable parameters on the performance of the ML algorithm.p-DOS uses coefficients from orthogonalised atomic orbitals and therefore the basis set used impacts both the performance of the network and the time required to generate the descriptor. Fig. 3 shows the relative performance as a function of the transformation rate (i.e. the speed at which an input geometry can be converted into the p-DOS descriptor) calculated using a training subset of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structure–spectrum pairs randomly selected from the full dataset. For reference, translation into the wACSF descriptor occurs at a rate of ∼300 transformations per s using an off-the-shelf commercial-grade CPU (AMD Ryzen Threadripper 3970X; 3.7–4.5 GHz). As expected, the rate of generation for p-DOS is significantly slower for larger basis sets – although in agreement with observations for the MAOC representation,14 we find that the use of larger basis sets does not improve performance, with the 3-21G and pc1 basis sets achieving the best results. 3-21G is found to be faster than pc1 by a factor of four: consequently it was applied for the remainder of this study. In the context of future studies at other absorption edges where larger basis (e.g. def2-TZVP) may be requisite, we emphasise that although transformation times may increase for large training sets, once the model has been developed and is run in ‘predict’ mode individual predictions by end users can be produced rapidly, with rates of ≥6 predictions per minute.
000 structure–spectrum pairs randomly selected from the full dataset. For reference, translation into the wACSF descriptor occurs at a rate of ∼300 transformations per s using an off-the-shelf commercial-grade CPU (AMD Ryzen Threadripper 3970X; 3.7–4.5 GHz). As expected, the rate of generation for p-DOS is significantly slower for larger basis sets – although in agreement with observations for the MAOC representation,14 we find that the use of larger basis sets does not improve performance, with the 3-21G and pc1 basis sets achieving the best results. 3-21G is found to be faster than pc1 by a factor of four: consequently it was applied for the remainder of this study. In the context of future studies at other absorption edges where larger basis (e.g. def2-TZVP) may be requisite, we emphasise that although transformation times may increase for large training sets, once the model has been developed and is run in ‘predict’ mode individual predictions by end users can be produced rapidly, with rates of ≥6 predictions per minute.
Although the computational efficiency of p-DOS is achieved by use of the guess wavefunction, we study the influence of varying degrees of SCF convergence of the wavefunction to assess the relative benefit of implementing some SCF cycles. Fig. S1 (ESI†) shows the relative performance as a function of the number of SCF cycles used while developing the p-DOS descriptor with a 3-21G basis set. Very little improvement in performance is gleaned as the number of SCF cycles is increased. This lack of effectual benefit can be explained when we plot the average p-DOS descriptor calculated with the training subset as shown in Fig. 4. The blue line shows the average and standard deviation without SCF optimisation, while the grey shows the same metrics when SCF has been used. Overall, only a small shift at low energy (−5 → 10 eV) and a slight change of lineshape between 15 → 20 eV is observed. These are comparatively small changes, and the behaviour is not significantly distinct from shifts in p-DOS lineshape observed when selecting sample structures from the training set (examples shown in Fig. S2, ESI†). Hence increasing the number of SCF cycles does not intelligently enhance the p-DOS descriptor, and so the performance of the network is not improved. Finally, the initial guess may also influence performance. In the present case, we found a different initial guess (e.g. Hückel or superposition of atomic densities) do not have a significant influence on performance however it may at other absorption edges and therefore should be considered when developing and optimising models.
When generating the p-DOS descriptor, the number of points (features), the energy range (Ek) and the broadening used (σ) (see eqn (4)) each influence performance. Fig. S3 (ESI†) shows the relative performance as a function of the energy range, where the energy grid starts at −10 eV, and the highest energy point climbs to increment the full grid across a range. We observe gradual improvement up to an energy range of 40 eV, a range which is sufficient to enclose all of the major features seen in Fig. 4. Using this energy range, Fig. 5 displays the relative performance as a function of the number of points (features) and broadening (σ). This shows that optimal performance is achieved with Gaussian broadening of 0.8 eV and grid points >50. Consequently, throughout the remainder of this study we adopt σ = 0.8, and discretise the p-DOS descriptor using 80 input features.
3.2 p-DOS descriptor: performance
In this section, we apply a p-DOS descriptor with optimal parameters as described in the previous section and turn our attention towards assessing the performance of the model when predicting sulphur K-edge XANES spectra. Unless otherwise stated, all results in this section have been obtained using a model-training set comprised of 129![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 877 structure–spectrum pairs, and tested against a held-out set of 5000 structure–spectrum pairs.49 Throughout this section, we apply the Wasserstein distance as an alternative error metric to measure the similarity of the expected and predicted spectral shapes. Low values of Wasserstein distance implicate shape-adherence somewhat more closely than pure mean-squared error. This metric is sometimes referred to as earth-mover's distance and can intuitively be understood as the work done to transform between one probability distribution and another.
877 structure–spectrum pairs, and tested against a held-out set of 5000 structure–spectrum pairs.49 Throughout this section, we apply the Wasserstein distance as an alternative error metric to measure the similarity of the expected and predicted spectral shapes. Low values of Wasserstein distance implicate shape-adherence somewhat more closely than pure mean-squared error. This metric is sometimes referred to as earth-mover's distance and can intuitively be understood as the work done to transform between one probability distribution and another.
The performance of the network as a function of the number of epochs (i.e. optimisation cycles of the network) for three permutations of the descriptor – p-DOS, wACSF, and p-DOS appended with wACSF (“combined”) – is shown in Fig. S3 (ESI†). In each case, the wACSF descriptor includes 22 G2 functions and 10 G4 functions, consistent with the optimisation described by Gastegger et al.34 We see that optimum performance is achieved for the combined descriptor at ≥500 epochs. The second best performer, with relative performance 10% worse than the combined descriptor, is the p-DOS only descriptor; in spite of diminished performance, convergence is much quicker with p-DOS only, occurring within 50 forward passes through the network. Finally, while the wACSF only descriptor shows a similar convergence trend to the combined descriptor, its relative performance is 25% worse. Overall this demonstrates that the combination of nuclear and electronic structural information provides superior performance. We hence carry forward the combined descriptor for the subsequent studies in this paper. Additionally, we note that the rapidity of the network's training, taking <30 min using an off-the-shelf commercial-grade CPU (AMD Ryzen Threadripper 3970X; 3.7–4.5 GHz) or GPU (nVidia RTX 3070, 5888 CUDA cores; 1.5–1.7 GHz) illustrates that once training data has been curated our DNN can be quickly reoptimised to estimate XANES spectra at other absorption edges, and for other absorbing elements.
As a function of the number of training samples, all three descriptors show similar behaviour when assessed using k-fold cross validation (see Fig. S4, ESI†). In all cases, performance improves most rapidly when using the first 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samples; subsequent improvements are slow as set size increases 120
000 samples; subsequent improvements are slow as set size increases 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samples. The modest and diminishing rate of improvement that while there remains scope to further improve on the results by growing the dataset, further sample-size boosts should be executed carefully to prevent the development of an over-fitted network.
000 samples. The modest and diminishing rate of improvement that while there remains scope to further improve on the results by growing the dataset, further sample-size boosts should be executed carefully to prevent the development of an over-fitted network.
Fig. 6 shows a histogram of Wasserstein distance for the held-out testing set of 5000 samples. The median Wasserstein distance from this distribution is 0.0050 and the interquartile range is 0.0026. These low values, alongside the high positive skewness coefficient of 1.02 across the held-out dataset, demonstrate that predictions are generally clustered towards the higher-performance region of the histogram, indicating the strong performance of the network. Fig. S5 (ESI†) contextualises these results by showing the comparison between 6 predicted and target sulphur K-edge XANES spectra from the held-out. It can be observed that even for those spectra in the 90th–100th percentiles, i.e. the worst performers, capture spectral lineshape well, and error is mostly derived from discrepancies in peak intensity.
Fig. 7 shows experimental (dashed), TDDFT calculated (grey) and DNN predicted (black) S K-edge spectra for the species (a) thianthrene, (b) thiohemianthraquinone, dibenzothiophene (c), and tetramethylenesulfone (d). Overall, good agreement is observed, even for the cases of species thiohemianthraquinone and tetramethylenesulfone, which respectively exhibit a strong pre-edge feature at 2466 eV arising from the formation of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S double bond and a strong blue shift due to the electron-withdrawing character of the S
S double bond and a strong blue shift due to the electron-withdrawing character of the S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety. Fig. S7 (ESI†) shows the same spectra predicted using a ML model trained using only the nuclear geometric wACSF descriptor. The comparison of the spectra shows clear distinctions and evidences significant improvement, especially for species a and b, upon the incorporation of electronic information via the p-DOS descriptor. To facilitate interpretation, Fig. S8 (ESI†) shows normalised feature importance resulting from SHAP value analysis.55 In all cases, as confirmed by the average SHAP analysis performed over the entire held-out set (Fig. S9, ESI†), this shows important contributions from both the electronic (p-DOS) and structural (wACSF) descriptors. Indeed, the relative importance of each p-DOS feature closely follows, as expected, the general shape of the spectrum. The agreement with lineshape is particularly marked with thiohemianthraquinone, which shows a strong peak at feature 18, lower than the other examples, which gives rise to the strong pre-edge just above 2466 eV. The geometric wACSF G2 functions (features 80–102) show peaks at 1.8 Å, 1.7 Å, 1.8 Å and 1.4 Å for thianthrene (a), thiohemianthraquinone (b), dibenzothiophene (c) and tetramethylenesulfone (d). These distances correspond to first coordination shell bond lengths to the sulphur absorber in each case.
O moiety. Fig. S7 (ESI†) shows the same spectra predicted using a ML model trained using only the nuclear geometric wACSF descriptor. The comparison of the spectra shows clear distinctions and evidences significant improvement, especially for species a and b, upon the incorporation of electronic information via the p-DOS descriptor. To facilitate interpretation, Fig. S8 (ESI†) shows normalised feature importance resulting from SHAP value analysis.55 In all cases, as confirmed by the average SHAP analysis performed over the entire held-out set (Fig. S9, ESI†), this shows important contributions from both the electronic (p-DOS) and structural (wACSF) descriptors. Indeed, the relative importance of each p-DOS feature closely follows, as expected, the general shape of the spectrum. The agreement with lineshape is particularly marked with thiohemianthraquinone, which shows a strong peak at feature 18, lower than the other examples, which gives rise to the strong pre-edge just above 2466 eV. The geometric wACSF G2 functions (features 80–102) show peaks at 1.8 Å, 1.7 Å, 1.8 Å and 1.4 Å for thianthrene (a), thiohemianthraquinone (b), dibenzothiophene (c) and tetramethylenesulfone (d). These distances correspond to first coordination shell bond lengths to the sulphur absorber in each case.
 | ||
| Fig. 7 Experimental (grey dashed-line), TDDFT(BP86) calculated (grey solid-line) and DNN predictions (black line) sulphur K-edge spectra of (a) thianthrene, (b) thiohemianthraquinone, (c) dibenzothiophene and (d) tetramethylenesulfone. Experimental spectra have been digitised from ref. 38. All calculated and DNN predicted spectra have been shifted horizontally by 66 eV to account for the routine error in absolute transition energies of TDDFT spectra. | ||
3.3 Case study: application to ground state interconversion of highly vibrationally excited photoproducts
Having demonstrated the strong performance of the model developed using the p-DOS and wACSF combined descriptor, we now apply it to the prediction of the sulphur K-edge XANES signal arising from the athermal ground state dynamics following photorelaxation of 266 nm excited 2(5H)-thiophenone. Previous experimental investigations into the photoproducts has been performed using photoelectron spectroscopy and electron diffraction:56,57 the simulations in this work will provide insights into the complementary information obtainable via ultrafast X-ray absorption spectroscopy.As illustrated schematically in Fig. 8, following photoexcitation 2(5H)-thiophenone exhibits a fast ring-opening wherein one C–S bond breaks to form a ring-opened (acyclic) form and an ultrafast decay towards the ground (S0) electronic state is triggered. The ring-opening and decay occurs within ∼300 fs. Upon reaching the ground state, intra-molecular rearrangements of the highly vibrationally excited species may lead to the reformation of a thiophenone and/or isomerisation to various ketenes. A recent ultrafast electron diffraction study57 has demonstrated that ∼25% of the photoproducts reform 2(5H)-thiophenone (1) and ∼50% form 2-(2-thiiranyl)ketene (2) – an exciting photoproduct containing a strained 3-membered ring – within ∼1 ps of photoexcitation. The remaining ∼25% form the ring-open forms 2-thioxoethylkene (3) and 2-(2-sulfanylethyl)kentene (4), which are theoretically differentiable due to the protonation of the sulphur in the latter structure. However, due to the weak scattering cross section of hydrogen, electron diffraction experiments have been unable to distinguish between these species. In contrast, S K-edge X-ray absorption is well documented to be very sensitive to electronic structure, which would be expected to vary upon protonation. It is therefore reasonable to posit that the sulphur K-edge XANES of each species would show distinct signals, and therefore that XANES spectroscopy could be applied to deliver a more detailed insight into photoproduct formation.
Fig. 9 shows the calculated (dashed) and DNN predicted (solid) sulphur K-edge spectra for photoproducts 1–4. Overall there is good agreement between the DNN predicted and calculated spectra, highlighting the accuracy of the DNN and the p-DOS descriptor. Compared to 1, the spectrum of 2 exhibits a red shift, associated with the increase in electron density of the sulphur. The spectrum of 4 is somewhat similar to 2, within the energy range considered with only a slight reduction in red shift and loss of intensity of the band at 2473 eV. However, the spectrum for 3 shows a significant change, with a strong pre-edge peak arising at 2468 eV. This arises from transitions into a low energy π* orbital along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S double bond (similarly to the observations made for thiohemianthraquinone in the previous section). For comparison, Fig. S10 (ESI†) shows the predictions of the same photoproducts using a DNN developed using only the nuclear structural wACSF descriptor. A substantial decrease in performance is clearly observed, especially for 2-thioxoethylkene (3) and 2-(2-sulfanylethyl)ketene (4). While these snapshots appear to indicate a strong sensitivity to differences between the two ring-open products, it is critical to account for the effect of the high internal energy of the photoproducts, which gives rise to a substantial diversity of molecular configurations for each photoproduct.
S double bond (similarly to the observations made for thiohemianthraquinone in the previous section). For comparison, Fig. S10 (ESI†) shows the predictions of the same photoproducts using a DNN developed using only the nuclear structural wACSF descriptor. A substantial decrease in performance is clearly observed, especially for 2-thioxoethylkene (3) and 2-(2-sulfanylethyl)ketene (4). While these snapshots appear to indicate a strong sensitivity to differences between the two ring-open products, it is critical to account for the effect of the high internal energy of the photoproducts, which gives rise to a substantial diversity of molecular configurations for each photoproduct.
Fig. 10(a) shows the time-resolved S K-edge X-ray absorption spectra to be simulated by the DNN, based upon the molecular dynamics trajectories from ref. 56 and 57. Our interest in the present study is in investigating the network's ability to capture the photoproduct spectra, therefore we have not included initial dynamics in the excited state (up to ∼250 fs), and only simulated the species when they populate the electronic ground state. The most prominent feature is the formation of the derivative profile associated with an edge shift between 2471–2472 eV, arising due to the formation of 2. There is a weak positive feature around 2468 eV which, as indicated in Fig. 9, likely arises from photoproduct 4. Fig. 10(b) overlaps the dynamics of this pre-edge peak with the populated kinetics of 3 (the relative populations of all of the species are shown in Fig. S11, ESI†) and excellent agreement is observed between the two, confirming proposed ability of sulphur K-edge XANES to distinguish between the ring open conformers 3 and 4.
To further review the accuracy of the DNN predictions, Fig. 11 show a comparison between the DNN predicted (Fig. 11(a)) and TDDFT(BP86) calculated (Fig. 11(b)) at 140 (solid) and 1000 (dashed) fs respectively. While there are some small deviations, especially with regards to the position and intensity of the pre-edge, the key transient features and the changes between the two time steps are very well reproduced, further confirming the capability and aptness of the combined-descriptor DNN model. The differences in the pre-edge, which arises from the formation C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S, is consistent with the differences arising from Fig. 7(b) and therefore represents an area for improvement in future work. Fig. S12 and S13 (ESI†) show the same simulations, using the DNN developed solely with a wACSF descriptor. As is consistent with previous observations, the wACSF DNN clearly exhibits a significant deviation in features between the DNN and TDDFT, again evidencing that due to the importance of electronic information wACSF in isolation is an insufficient representational format for the simulation of these spectra.
S, is consistent with the differences arising from Fig. 7(b) and therefore represents an area for improvement in future work. Fig. S12 and S13 (ESI†) show the same simulations, using the DNN developed solely with a wACSF descriptor. As is consistent with previous observations, the wACSF DNN clearly exhibits a significant deviation in features between the DNN and TDDFT, again evidencing that due to the importance of electronic information wACSF in isolation is an insufficient representational format for the simulation of these spectra.
 | ||
| Fig. 11 The DNN predicted (a) and TDDFT(BP86) calculated (b) S K-edge spectra at 140 (solid) and 1000 (dashed) fs. | ||
Overall, this section demonstrates the potential of incorporating electronic information in the form of our p-DOS descriptor compared to solely using nuclear information through the wACSF descriptor when applied to predicting ultrafast time-resolved X-ray signals.58 With the upgrade of the LCLS, time-resolved X-ray experiments have moved from 120 pulses per second to 1 million pulses per second, making such ultrafast X-ray experiments increasingly common. Consequently, computations that efficiently and accurately support analysis are also becoming increasingly desirable. We emphasise that this is not design to replace first-principles techniques, but rather to add an additional tool for researchers to enhance analysis. In addition, while this present analysis is focused on time-resolved experiments, it should be noted that similar benefits could be expected for other experimental types, e.g., in operando measurements of batteries and/or catalysts, with the principal benefits being the ability to speed up spectral predictions and therefore rapidly screen potential outcomes and scenarios.
4 Conclusions
The proliferation of high-brilliance light sources such as third-generation synchrotrons and X-ray free-electron lasers (XFELs) means that it is increasingly possible for X-ray spectroscopy to deliver highly-detailed information about the local geometric and electronic structure of matter in a broad range of different environments and under challenging operating conditions, such as femtosecond time-resolved studies. These advances increase the importance of computational spectroscopy to interpret and predict experimental signals to guarantee that the detailed information contained within these observables can be efficiently extracted.59 Accurate ML models have the potential to equip researchers with easy-to-use, computationally inexpensive, and accessible tools for the fast and automated analysis and prediction of X-ray spectroscopy.21To this end, this work has introduced a quantum-inspired representation for ML specifically tailored towards the simulation of X-ray spectra. The form of the p-DOS descriptor is directly inspired by the spectral shapes within the single-particle and dipole approximations and enables, for the first time, the inclusion of explicit electronic information of the absorbing atom into structural featurisation. The p-DOS is generated within the XANESNET code40 and constructed from the coefficients of the non-optimised (guess) wavefunction obtained from the pySCF code54 and while it depends on the basis set used, we have shown that even small basis sets are able to exhibit strong performance while simultaneously converting the atomic nuclear coordinates into the descriptor at rapid rates.
Optimal performance is achieved by combining this newly developed p-DOS descriptor with nuclear structural information obtained from the wACSF descriptor used in previous work.33 This is shown to facilitate the accurate description of sulphur K-edge X-ray absorption spectra from a held-out set and delivers predictions in good agreement with experimental observables. We demonstrate that the performance is substantially better than the wACSF-only descriptor, which can be explained by the SHAP feature importance analysis of the input descriptor showing that on average the p-DOS component represents >40% of the overall feature importance for the held-out training set. Further testing of the descriptor and the network developed is achieved by applying it to predict ultrafast sulphur K-edge XANES signals of the products of 2(5H)-thiophenone formed after 266 nm photoexcitation.56,57 This demonstrates, consistent with first principles simulations, that in contrast to previous photoelectron spectrum and electron diffraction experiments, X-ray absorption spectroscopy can distinguish between some of the ring-open isomers formed in the vibrationally excited ground state. Here the DNN is especially important, due to the high level of conformational disorder of the molecule which must be captured, meaning that many spectral simulations are required to simulate an experimental observable.
Overall, this paper introduces an accurate and affordable descriptor, generaliseable with respect to the identity of the absorber, which encapsulates the electronic properties that contribute to spectroscopic observables. Although, owing to the strong influence of the electronic structure on spectral shape,38,39 the present work focuses on the application of p-DOS descriptor to sulphur K-edge X-ray absorption spectra, the method is equally applicable to other absorption edges and spectroscopic methods (i.e. an XES ML-model could be developed if the method were applied to the occupied rather than unoccupied DOS), which will be the focus of future work. Previous work33 demonstrated that when developing machine learning algorithms to produce transition metal K-edge spectra, a purely geometric structural representation facilitated the production of an accurate and affordable machine learning model. This is as the transition metal spectra are principally derived from structural properties, with the strongest spectral features appearing at – or slightly above – the absorption edge. For this group, transitions from core orbitals into the low-lying unoccupied valence states correspond to dipole-forbidden (3d ← 1s) excitations, and consequently provide limited insight into the electronic configuration of the absorber, because such forbidden transitions typically give rise to both broad and weak spectral features. In the present work, SHAP analysis highlights the importance of the electronic (p-DOS) representation, and therefore it should be established whether p-DOS might also demonstrate an appreciable benefit for species where the XANES spectra are principally derived from geometric features. In addition, the role of quadrupole transitions raises the question of whether s and d orbitals should also be considered by an electronic representation, in spite of the weakness of these transitions. In the present work a non-optimised (guess) wavefunction has been used, as this limits the computational expense of generating the descriptor. We note that while the guess wavefunction performs sufficiently within the present work, it may represent a limitation for some systems with a more complex electronic structure. To overcome this, optimised wavefunctions from lower-level semi-empirical methods, such as GFN-xTB60 could be used to generate the p-DOS. These are therefore the recommended directions of focus for future investigations based upon the novel p-DOS descriptor.
Data availability
Data supporting this publication is openly available. The software can be obtained from ref. 40, while the data can be obtained from ref. 49.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research made use of the Rocket High Performance Computing service at Newcastle University and computational resources from ARCHER2 UK National Computing Service which was granted via HPC-CONEXS, the UK High-End Computing Consortium (EPSRC grant no. EP/X035514/1). We also acknowledge the COSMOS Programme grant (EPSRC grant no. EP/X026973/1). T. J. P. would like to thank the EPSRC for an Open Fellowship (EP/W008009/1) and Leverhulme Trust (Project RPG-2020-268).Notes and references
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Müller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872 CrossRef CAS PubMed.
- G. B. Goh, N. O. Hodas and A. Vishnu, J. Comput. Chem., 2017, 38, 1291–1307 CrossRef CAS PubMed.
- J. Westermayr, M. Gastegger, K. T. Schütt and R. J. Maurer, J. Chem. Phys., 2021, 154, 230903 CrossRef CAS PubMed.
- J. Damewood, J. Karaguesian, J. R. Lunger, A. R. Tan, M. Xie, J. Peng and R. Gómez-Bombarelli, Annu. Rev. Mater. Res., 2023, 53, 399–426 CrossRef CAS.
- P. van Gerwen, A. Fabrizio, M. D. Wodrich and C. Corminboeuf, Mach. Learn.: Sci. Technol., 2022, 3, 045005 Search PubMed.
- F. Musil, A. Grisafi, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Chem. Rev., 2021, 121, 9759–9815 CrossRef CAS PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- R. Drautz, Phys. Rev. B, 2019, 99, 014104 CrossRef CAS.
- H. Huo and M. Rupp, Mach. Learn.: Sci. Technol., 2022, 3, 045017 Search PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- M. Welborn, L. Cheng and T. F. Miller III, J. Chem. Theory Comput., 2018, 14, 4772–4779 CrossRef CAS PubMed.
- K. Karandashev and O. A. von Lilienfeld, J. Chem. Phys., 2022, 156, 114101 CrossRef CAS PubMed.
- A. Fabrizio, K. R. Briling and C. Corminboeuf, Digital Discovery, 2022, 1, 286–294 RSC.
- S. Llenga and G. Gryn’ova, J. Chem. Phys., 2023, 158, 214116 CrossRef CAS PubMed.
- J. J. Rehr, J. J. Kas, F. D. Vila, M. P. Prange and K. Jorissen, Phys. Chem. Chem. Phys., 2010, 12, 5503–5513 RSC.
- C. J. Milne, T. J. Penfold and M. Chergui, Coord. Chem. Rev., 2014, 277, 44–68 CrossRef.
- T. J. Penfold, C. J. Milne and M. Chergui, Adv. Chem. Phys., 2013, 153, 1–41 CrossRef CAS.
- Y. Hwu and G. Margaritondo, J. Synchrotron Radiat., 2021, 28, 1014–1029 CrossRef PubMed.
- J. Hastings, C. Pellegrini and A. Marinelli, Physics of and Science with X-ray Free-electron Lasers, IOS Press, 2020, vol. 199 Search PubMed.
- Z. Chen, N. Andrejevic, N. C. Drucker, T. Nguyen, R. P. Xian, T. Smidt, Y. Wang, R. Ernstorfer, D. A. Tennant and M. Chan, et al. , Chem. Phys. Rev., 2021, 2, 031301 CrossRef.
- T. Penfold, L. Watson, C. Middleton, T. David, S. Verma, T. Pope, J. Kaczmarek and C. D. Rankine, Mach. Learn.: Sci. Technol., 2024, 5, 021001 Search PubMed.
- M. R. Carbone, M. Topsakal, D. Lu and S. Yoo, Phys. Rev. Lett., 2020, 124, 156401 CrossRef CAS PubMed.
- M. R. Carbone, S. Yoo, M. Topsakal and D. Lu, Phys. Rev. Mater., 2019, 3, 033604 CrossRef CAS.
- C. D. Rankine, M. M. Madkhali and T. J. Penfold, J. Phys. Chem. A, 2020, 124, 4263–4270 CrossRef CAS PubMed.
- M. M. Madkhali, C. D. Rankine and T. J. Penfold, Molecules, 2020, 25, 2715 CrossRef CAS PubMed.
- J. Timoshenko and A. I. Frenkel, ACS Catal., 2019, 9, 10192–10211 CrossRef CAS.
- J. Timoshenko, C. J. Wrasman, M. Luneau, T. Shirman, M. Cargnello, S. R. Bare, J. Aizenberg, C. M. Friend and A. I. Frenkel, Nano Lett., 2019, 19, 520–529 CrossRef CAS PubMed.
- J. Timoshenko, D. Lu, Y. Lin and A. I. Frenkel, J. Phys. Chem. Lett., 2017, 8, 5091–5098 CrossRef CAS PubMed.
- S. B. Torrisi, M. R. Carbone, B. A. Rohr, J. H. Montoya, Y. Ha, J. Yano, S. K. Suram and L. Hung, npj Comput. Mater., 2020, 6, 109 CrossRef.
- S. Tetef, V. Kashyap, W. M. Holden, A. Velian, N. Govind and G. T. Seidler, J. Phys. Chem. A, 2022, 126, 4862–4872 CrossRef CAS PubMed.
- S. Tetef, N. Govind and G. T. Seidler, Phys. Chem. Chem. Phys., 2021, 23, 23586–23601 RSC.
- E. Falbo, C. Rankine and T. Penfold, Chem. Phys. Lett., 2021, 780, 138893 CrossRef CAS.
- C. D. Rankine and T. Penfold, J. Chem. Phys., 2022, 156, 164102 CrossRef CAS PubMed.
- M. Gastegger, L. Schwiedrzik, M. Bittermann, F. Berzsenyi and P. Marquetand, J. Chem. Phys., 2018, 148, 241709 CrossRef CAS PubMed.
- J. J. Rehr and R. C. Albers, Rev. Mod. Phys., 2000, 72, 621 CrossRef CAS.
- L. Watson, C. D. Rankine and T. J. Penfold, Phys. Chem. Chem. Phys., 2022, 24, 9156–9167 RSC.
- M. R. Carbone, M. Topsakal, D. Lu and S. Yoo, Phys. Rev. Lett., 2020, 124, 156401 CrossRef CAS PubMed.
- G. N. George and M. L. Gorbaty, J. Am. Chem. Soc., 1989, 111, 3182–3186 CrossRef CAS.
- G. N. George, I. J. Pickering, J. J. H. Cotelesage, L. I. Vogt, N. V. Dolgova, N. Regnier, D. Sokaras, T. Kroll, E. Y. Sneeden, M. J. Hackett, K. Goto and E. Block, Phosphorus, Sulfur Silicon Relat. Elem., 2019, 194, 618–623 CrossRef CAS.
- XANESNET, gitlab.com/team-xnet/xanesnet, 2023.
- L. C. Blum and J.-L. Reymond, J. Am. Chem. Soc., 2009, 131, 8732–8733 CrossRef CAS PubMed.
- S. DeBeer George and F. Neese, Inorg. Chem., 2010, 49, 1849–1853 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. Reiher, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 139–149 CAS.
- S. DeBeer George, T. Petrenko and F. Neese, J. Phys. Chem. A, 2008, 112, 12936–12943 CrossRef CAS PubMed.
- XANESNET Training Data, gitlab.com/team-xnet/training-sets, 2023.
- D. P. Kingma and J. L. Ba, arXiv, preprint, 2014, DOI:10.48550/arXiv.1412.6980.
- X. Glorot and Y. Bengio, Proceedings of the thirteenth international conference on artificial intelligence and statistics, 2010, pp. 249-256.
- N. Ketkar, J. Moolayil, N. Ketkar and J. Moolayil, Deep Learning with Python: Learn Best Practices of Deep Learning Models with PyTorch, 2021, pp. 27–91 Search PubMed.
- A. Hjorth Larsen, J. Jorgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer and C. Hargus, et al. , J. Phys.: Condens. Mater., 2017, 29, 273002 CrossRef PubMed.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova and S. Sharma, et al. , Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1340 Search PubMed.
- S. M. Lundberg and S.-I. Lee, Advances in neural information processing systems, 2017, vol. 30 Search PubMed.
- S. Pathak, L. M. Ibele, R. Boll, C. Callegari, A. Demidovich, B. Erk, R. Feifel, R. Forbes, M. Di Fraia and L. Giannessi, et al. , Nat. Chem., 2020, 12, 795–800 CrossRef CAS PubMed.
- J. P. Figueira Nunes, L. M. Ibele, S. Pathak, A. R. Attar, S. Bhattacharyya, R. Boll, K. Borne, M. Centurion, B. Erk and M.-F. Linet al., J. Am. Chem. Soc., 2024, 146(6), 4134–4143.
- M. Chergui and E. Collet, Chem. Rev., 2017, 117, 11025–11065 CrossRef CAS PubMed.
- J. D. Elliott, V. Rogalev, N. Wilson, M. Duta, C. J. Reynolds, J. Filik, T. J. Penfold and S. Diaz-Moreno, J. Synchrotron Radiat., 2024, 31, 1276–1284 CrossRef CAS PubMed.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01368a |
| This journal is © the Owner Societies 2024 |