Benchmark ab initio characterization of the multi-channel Cl + CH₃X [X = F, Cl, Br, I] reactive potential energy surfaces

Abstract

We determine benchmark geometries and relative energies for the stationary points of the Cl + CH₃X [X = F, Cl, Br, I] reactions. We consider four possible reaction pathways: hydrogen abstraction, hydrogen substitution, halogen abstraction, and halogen substitution, where the substitution processes can proceed via either Walden inversion or front-side attack. We perform geometry optimizations and obtain harmonic vibrational frequencies at the explicitly-correlated UCCSD(T)-F12b/aug-cc-pVTZ level of theory, followed by UCCSD(T)-F12b/aug-cc-pVQZ single-point computations to make finite-basis-set error negligible. To reach chemical (<1 kcal mol⁻¹), or even subchemical (<0.5 kcal mol⁻¹) accuracy, we include core-correlation, scalar relativistic, post-(T), spin–orbit-splitting and zero-point-energy contributions, as well, in the relative energies of all the stationary points. Our benchmark 0 K reaction enthalpies are compared to available experimental results and show good agreement. The stationary-point structures and energetics are interpreted in terms of Hammond's postulate and used to make predictions related to the dynamical behavior of these reactive systems.

---

Introduction

Reactions of chlorine atom with small molecules have long been ideal test systems in reaction dynamics studies. Besides the investigations of the Cl + H₂/H₂O/NH₃ reactions,^1–3 the scientific interest turned towards more complex processes: the Cl + CH₄ reaction served as the new benchmark of polyatomic reactions inspiring extensive experimental and theoretical studies.^4–10 Experiments were then extended to study the reactions of Cl with larger alkanes, and other small functionalized organic molecules. Several initial experimental kinetics studies, motivated by the atmospheric relevance of the title reactions, provided rate constants^11–24 and investigated the kinetic isotope effects^25–31 for the hydrogen-abstraction reactions of Cl atom with halogenated methane molecules. Furthermore, early scattering experiments investigated the dynamics of the Cl + CH₃I reaction and revealed integral cross sections, angular and velocity distributions for the I-abstraction reaction path.³² In addition, reaction rates for the halogen-substitution, i.e., methyl-chloride formation have been determined in the case of the Cl + CH₃Br and CH₃I-reactions.³³ Also, I-substitution in the reactions of Cl atom with alkyl-iodides has been observed in kinetics experiments.²¹ In 2004, Orr-Ewing and coworkers reported the first comprehensive resonance-enhanced multiphoton ionization experiments for the Cl + CH₃X [X = F, Cl, Br, I] reactions and provided detailed insights into the dynamics of the H-abstraction channel.³⁴ They set a special focus on the stereodynamics of the reactions by analyzing the HCl product rotational-state distributions.³⁴ In conjunction with their dynamics results for the reactions of Cl with other functionalized small organic molecules,^35–39 they found that the degree of rotational excitation of HCl is in correlation with the dipole moment of the radical co-product. Thus, the HCl rotational distribution turned out to be a characteristic property of the angular anisotropy of the potential energy surfaces (PESs) of these reactions.^34–39

A number of theoretical investigations on some of the stationary-point structures and energetics of mostly the H-abstraction path of the title reactions have been carried out, as well.^{15,17,18,28,40–44} For the Cl + CH₃F reaction, G2-level energies, consisting of MP2/triple-zeta and QCISD(T)/triple-zeta single-point values, were computed on MP2/double-zeta geometries along the minimum energy path (MEP) of the H-abstraction reaction.⁴⁰ After early ab initio computations on the transition state (TS) structures,¹⁵ more advanced CCSD(T)/aug-cc-pVTZ single-point energies on CCSD/aug-cc-pVDZ geometries were calculated for the TS, and the MEP of the Cl + CH₃Cl → HCl + CH₂Cl reaction was also studied at the MP2/aug-cc-pVTZ level of theory.²⁸ Also, a density-functional-theory (DFT) and QCISD(T)/triple-zeta study has been performed for the Cl + CH₃Cl and CH₃Br H-abstraction reactions.⁴³ Various MP2,¹⁷ G2,¹⁸ DFT^18,33 and G4⁴¹ (including also CCSD(T)-level correlation-energy terms) computations were performed for the Cl + CH₃Br → HCl + CH₂Br reaction, as well. In case of the Cl + CH₃I → HCl + CH₂I reaction, an early MP2/double-zeta investigation proposed the presence of a bent pre-reaction complex.⁴² In 2013, a comprehensive G2-level theoretical study of the TS, as well as pre- and post-reaction complex structures for the Cl + CH₃X [X = F, Cl, Br] reactions was carried out, suggesting 8–10 kJ mol⁻¹ high barriers of H-abstraction.⁴⁴ As to the dynamics of these reactions, due to the high number of the degrees of freedom, only lower-level direct dynamics methods have been available to study their mechanisms. In 2004, along with the experiments of the Orr-Ewing group, G2//MP2/6-311G(d,p)-level direct dynamics simulations, i.e., when the gradients of the potential energy necessary for the classical trajectories are computed on-the-fly, were carried out, together with the systematic characterization of the stationary points at the same level of theory.³⁴ In the above studies, apart from some exceptions, the H-abstraction channel is considered to be the main pathway of the title reactions, however, other interesting, even high-energy reaction routes are worth being investigated, for which experimental techniques are also accessible.⁴⁵

In the present work we aim to characterize the stationary points of all chemically interesting reaction channels of the title reactions. We investigate the hydrogen-abstraction (HA), hydrogen-substitution (HS), halogen-abstraction (XA), and halogen-substitution (XS) pathways. We determine benchmark geometries and relative energies using the best available electronic-structure methods. The benchmark energies provided include (1) core-correlation, (2) scalar relativistic, (3) post-(T), and (4) spin–orbit corrections, as well as (5) zero-point-energy contributions to the explicitly-correlated CCSD(T)-F12/aug-cc-pVQZ single-point energies computed at the CCSD(T)-F12/aug-cc-pVTZ stationary-point structures. These auxiliary energy terms are calculated to ensure the (sub)chemical (<0.5 kcal mol⁻¹) accuracy of the results. The benchmark adiabatic relative energies obtained are compared to experimental results, as well.

Computational details

We investigate the Cl + CH₃X [X = F, Cl, Br, I] reactions by characterizing their potential energy surfaces by using state-of-the-art electronic-structure methods. We determine the benchmark geometries and energies of the stationary points, and even compare the obtained 0 K reaction enthalpies to available experimental data. As an initial step we search for stationary-point structures using the restricted open-shell Hartree–Fock (ROHF)-based second-order Møller–Plesset perturbation method⁴⁶ with aug-cc-pVDZ basis set⁴⁷ (RMP2/aug-cc-pVDZ), by performing geometry-optimization and harmonic-frequency calculations. Next, we further optimize the RMP2/aug-cc-pVDZ geometries with the ROHF-based explicitly-correlated unrestricted coupled-cluster singles, doubles, and perturbative triples method⁴⁸ with the aug-cc-pVDZ and aug-cc-pVTZ basis sets⁴⁷ (UCCSD(T)-F12b/aug-cc-pVDZ and UCCSD(T)-F12b/aug-cc-pVTZ), followed by harmonic-frequency computations at each level of theory. At the most accurate benchmark UCCSD(T)-F12b/aug-cc-pVTZ geometries we perform additional single-point energy computations to obtain auxiliary energy corrections to achieve chemical (<1 kcal mol⁻¹) or even subchemical (<0.5 kcal mol⁻¹) accuracy of the final benchmark energies.

For this (a) we compute UCCSD(T)-F12b/aug-cc-pVQZ single-point energies to make the finite basis-set error negligible, (b) we determine core-correlation effects by also correlating the sub-valence-shell electrons applying the corresponding aug-cc-pwCVTZ basis set,⁴⁹ as

Δ_core = ΔE(AE-UCCSD(T)/aug-cc-pwCVTZ) − ΔE(FC-UCCSD(T)/aug-cc-pwCVTZ), (1)

where FC and AE refer to frozen-core (only the valence electrons are correlated) and all-electron (the valence and the sub-valence-shell electrons are correlated), respectively, (c) we obtain post-(T) energy corrections by computing UHF-based UCCSDT⁵⁰ and UCCSDT(Q)⁵¹ energies with the aug-cc-pVDZ basis set to consider higher-order correlation effects, as well:

δ[CCSDT] = ΔE(UCCSDT/aug-cc-pVDZ) − ΔE(UCCSD(T)/aug-cc-pVDZ) (2)

δ[CCSDT(Q)] = ΔE(UCCSDT(Q)/aug-cc-pVDZ) − ΔE(UCCSDT/aug-cc-pVDZ) (3)

(d) we also improve our relative energies by computing scalar relativistic contributions using the second-order Douglas–Kroll (DK) Hamiltonian⁵² and the corresponding triple-zeta basis sets:⁵³

Δ_rel = ΔE(DK-AE-UCCSD(T)/aug-cc-pwCVTZ-DK) − ΔE(AE-UCCSD(T)/aug-cc-pwCVTZ), (4)

(e) as the reactants and the halogen-substitution products of the title reactions involve free halogen atoms, the energy-lowering effect of the relativistic spin–orbit (SO) interaction must be taken into account. For this, we apply the multi-reference configuration interaction method augmented with Davidson-correction (MRCI+Q),^54,55 estimating higher-order contributions, and the Breit–Pauli operator in the interacting-states approach⁵⁶ with the aug-cc-pVDZ basis set. In order to be able to consider the spin–orbit splitting of both halogen atoms along the halogen-substitution reaction path, the MRCI active space involves 21 electrons on 11 spatial orbitals (MRCI+Q(21,11)/aug-cc-pVDZ), while the core orbitals are doubly occupied and are all closed, in all of the SO computations. SO corrections (Δ_SO) are calculated as follows: (1) in the case of all stationary points except the XS products, the SO correction is the difference between the 1/3 of the experimental⁵⁷ SO splitting of the free Cl atom (0.84 kcal mol⁻¹) and the calculated SO-correction at the given stationary point (including XS stationary points, as well), (2) for the XS products, the SO correction is obtained in the same way as in (1), but we use the experimental splittings for all the free halogen atoms.

Finally, we also include the energy contribution stemming from the zero-point vibrations (Δ_ZPE) at the stationary points in the harmonic-oscillator approach, calculated at the UCCSD(T)-F12b/aug-cc-pVTZ level of theory, to obtain vibrationally adiabatic relative energies.

The final classical, which refers to the classical, i.e., static nuclei, benchmark energies are determined as

ΔE_classical = ΔE(UCCSD(T)-F12b/aug-cc-pVQZ) + δ[CCSDT] + δ[CCSDT(Q)] + Δ_core + Δ_rel + Δ_SO, (5)

while the benchmark adiabatic energies are calculated as

ΔE_adiabatic = ΔE_classical + Δ_ZPE (6)

In all of the computations, except those of the DK-AE-UCCSD(T)/aug-cc-pwCVTZ-DK energy, effective core potentials (ECPs)⁵⁸ and the appropriate pseudo-potential (-PP) basis sets⁵⁸ are applied to replace the 10 inner-core electrons (1s² 2s² 2p⁶) of the Br atom and the 28 inner-core electrons (1s² 2s² 2p⁶ 3s² 3p⁶ 3d¹⁰) of the I atom. These ECPs partly cover the scalar relativistic effects present in the Br and I atoms. We use the frozen-core approach in all computations, unless otherwise noted.

All computations are carried out with the MOLPRO 2015.1 software package⁵⁹ (for some problematic cases we use MOLPRO 2023.2⁶⁰), except for the post-(T) energy corrections, where the MRCC program^61,62 is applied.

In some cases, we encounter electronic-structure convergence problems: (1) the XS Walden (W) TS geometries could only be optimized at the RMP2/aug-cc-pVDZ level of theory (UMP2 for X = I), and in the X = F case we had to increase the robustness of the HF convergence by using the SO-SCI keyword in MOLPRO 2023.2. (2) In the case of the X = Br and I XA W TSs the Douglas–Kroll computations do not converge, (3) the geometry of the Cl-substitution front-side (FS) post-reaction minimum (postmin) could only be optimized at the UCCSD(T)-F12b/aug-cc-pVTZ level by using MOLPRO 2023.2, (4) the SO-corrections for the X = I system could only be calculated using MOLPRO 2023.2.

For all the mid-reaction stationary points we perform ManyHF calculations,⁶³ to check if the original Hartree–Fock calculation is converged to the right electronic state. The ManyHF procedure has been recently developed in our group and involves multiple HF, DFT and multi-configurational self-consistent-field (MCSCF) calculations to generate different initial orbital guesses and selects the lowest-energy HF solution to the problem.⁶³ In the case of the XS channel we experienced significant deviations from the original HF energy, thus we applied ManyHF-based calculations for all these stationary points. For the other pathways we do not face HF misconvergence.

Results and discussion

We characterize the potential energy surfaces of the Cl + CH₃X [X = F, Cl, Br, I] systems by determining benchmark stationary-point geometries (UCCSD(T)-F12b/aug-cc-pVTZ) and classical energies by adding several auxiliary energy terms to the UCCSD(T)-F12b/aug-cc-pVQZ relative-energy values: (1) core-correlation, (2) post-(T)-corrections, (3) relativistic effects including scalar relativistic and spin–orbit-corrections (see Computational details for additional information). The vibrationally-adiabatic relative energies are then obtained by including ZPE-contributions. Both the classical and adiabatic energies of the stationary points of the title reactions relative to those of the reactants are plotted in Fig. 1 and listed in Table 1. Cartesian coordinates and absolute energies of each optimized stationary-point structure are given in the ESI.†

Fig. 1 Schematic potential energy diagrams of the Cl + CH₃X [X = F, Cl, Br, I] reactions showing the benchmark geometries and classical (adiabatic) relative energies of the stationary points, as well as the possible reaction paths. The stationary points marked with * correspond to MP2/aug-cc-pVDZ-optimized geometries.

Table 1 Energies (in kcal mol⁻¹) of the stationary points of the Cl + CH₃X [X = F, Cl, Br, I] reactions relative to those of the reactants obtained at different levels of theory (CC denotes CCSD(T)-F12b, and DZ, TZ, and QZ denote aug-cc-pVnZ with n = D, T, Q, respectively) along with auxiliary energy corrections (for details and notations of the corrections see Computational details)

		MP2/DZ	CC/DZ	CC/TZ	CC/QZ	δ[T]	δ[(Q)]	Δ core	Δ rel	Δ SO	Δ ZPE	Classical	Adiabatic
a Relative energies and corrections correspond to MP2/aug-cc-pVDZ geometries. b CCSD(T)-F12b/aug-cc-pV5Z relative energy. c Classical and adiabatic relative energies obtained by using the CCSD(T)-F12b/aug-cc-pV5Z relative energy.
Cl + CH3F
H abstraction	HCl + CH2F	3.99	0.89	1.59	1.50	−0.07	−0.06	−0.12	0.23	0.84	−4.92	2.32	−2.60
	TS	5.69	4.52	5.15	5.11	−0.15	−0.19	−0.11	0.08	0.83	−4.19	5.57	1.38
	Postmin	1.61	−1.41	−0.43	−0.44	−0.09	−0.08	−0.14	0.23	0.84	−3.75	0.31	−3.44
F abstraction	ClF + CH3	58.00	51.84	52.89	52.87	−0.06	−0.29	−0.02	−0.03	0.84	−4.96	53.31	48.35
H substitution	H + CH2ClF	18.48	18.49	20.18	20.16	0.13	−0.18	−0.11	0.18	0.84	−5.14	21.02	15.87
	Walden TS	49.55	45.93	46.50	46.47	−0.25	−0.33	0.06	0.05	0.83	−4.03	46.82	42.79
	W Postmin	18.28	18.32	19.94	19.94	0.12	−0.18	−0.11	0.18	0.84	−4.91	20.79	15.88
F substitution	F + CH3Cl	30.72	26.54	27.23	27.23	0.05	0.02	−0.13	0.05	0.45	−0.98	27.67	26.69
	Walden TS^a	64.30	—	—	45.10	−0.50	−0.53	−0.02	0.10	0.83	−0.51	44.99	44.48
Cl + CH3Cl
H abstraction	HCl + CH2Cl	2.92	−1.05	−0.10	−0.21	−0.11	−0.07	−0.15	0.26	0.84	−5.30	0.56	−4.74
	TS	4.87	3.54	4.63	4.59	−0.15	−0.22	−0.13	0.07	0.82	−4.17	4.98	0.81
	Postmin	0.01	−3.56	−2.22	−2.26	−0.12	−0.09	−0.18	0.24	0.84	−3.88	−1.58	−5.46
Cl abstraction	Cl2 + CH3	37.64	28.80	29.18	29.02	−0.07	−0.15	0.00	−0.06	0.84	−4.31	29.58	25.27
H substitution	H + CH2Cl2	21.91	22.47	24.39	24.33	0.15	−0.20	−0.13	0.15	0.72	−5.22	25.03	19.81
	Walden TS	51.14	47.90	49.10	49.04	−0.22	−0.37	0.03	0.02	0.83	−4.15	49.32	45.17
	W Postmin	21.65	22.28	24.09	24.04	0.15	−0.20	−0.13	0.15	0.84	−5.01	24.85	19.84
Cl substitution	Cl + CH3Cl	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	Walden TS^a	28.72	—	—	24.23	−0.45	−0.35	0.07	−0.16	0.79	−0.44	24.12	23.68
	W Postmin	−0.64	−0.55	—	−0.62	−0.01	−0.01	−0.03	0.00	0.09	0.18	−0.58	−0.40
	FS Postmin	−3.20	−4.87	−4.24	−4.33	−0.11	−0.08	−0.08	−0.05	0.78	0.34	−3.87	−3.53
Cl + CH3Br
H abstraction	HCl + CH2Br	3.79	0.32	1.19	1.10	−0.14	−0.07	−0.04	0.28	0.82	−5.30	1.95	−3.35
	TS	4.67	4.25	4.97	4.95	−0.17	−0.23	−0.12	0.08	0.82	−4.26	5.31	1.05
	Postmin	0.66	−2.26	−1.16	−1.18	−0.16	−0.10	−0.11	0.25	0.82	−3.85	−0.47	−4.32
Br abstraction	ClBr + CH3	28.27	20.98	21.00	20.69	−0.06	−0.14	0.30	0.23	0.84	−4.06	21.86	17.80
	TS	15.29	17.28	—	11.24	−0.47	−0.39	0.12	0.07	0.83	−1.28	11.39	10.11
H substitution	H + CH2ClBr	22.29	23.38	25.08	25.01	0.16	−0.21	−0.17	0.21	0.84	−5.23	25.84	20.61
	Walden TS	50.68	48.47	49.13	49.05	−0.21	−0.39	0.00	0.07	0.83	−4.20	49.36	45.16
	W Postmin	22.01	23.10	24.74	24.68	0.16	−0.21	−0.19	0.20	0.84	−4.93	25.47	20.55
Br substitution	Br + CH3Cl	−10.95	−12.13	−11.76	−11.89	0.04	−0.01	0.38	0.48	−2.67	0.41	−13.66	−13.26
	Walden TS^a	20.83	—	—	15.92	−0.44	−0.32	0.14	—	0.79	−0.35	16.09	15.74
	W Postmin	−11.65	—	—	−12.53	0.03	−0.02	0.29	0.39	−2.39	0.56	−14.23	−13.67
	FS TS	40.08	—	—	35.59	−1.27	−0.71	0.24	0.03	0.38	0.20	34.27	34.47
	FS Postmin	−14.17	−15.96	−15.45	−15.63	−0.03	−0.06	0.18	0.35	−0.44	0.75	−15.62	−14.87
Cl + CH3I
H abstraction	HCl + CH2I	4.59	0.51	1.26	1.19	−0.18	−0.07	0.03	0.21	0.75	−5.09	1.92	−3.17
	TS	4.28	3.78	4.48	4.49	−0.21	−0.26	−0.15	0.11	0.82	−4.25	4.80	0.55
	Postmin	1.31	−2.25	−1.26	−1.24	−0.21	−0.11	−0.09	0.23	0.71	−3.68	−0.71	−4.40
I abstraction	ClI + CH3	16.82	10.53	10.19	9.64(9.38^b)	−0.05	−0.10	0.78	0.11	0.84	−3.74	11.22(10.96^c)	7.48(7.22^c)
	TS	11.58	—	—	3.64	−0.45	−0.31	0.52	0.15	0.47	−1.77	4.01	2.23
	Postmin	11.31	—	—	4.52	−0.21	−0.22	0.59	0.16	0.53	−1.97	5.37	3.40
H substitution	H + CH2ClI	23.03	24.31	25.94	25.85	0.17	−0.22	−0.21	0.20	0.84	−5.19	26.64	21.45
	Walden TS	49.81	47.41	47.98	47.89	−0.22	−0.42	−0.02	0.10	0.83	−4.17	48.16	43.99
	W Postmin	22.74	23.99	25.53	25.45	0.16	−0.22	−0.24	0.20	0.82	−4.89	26.18	21.29
I substitution	I + CH3Cl	−21.72	−22.63	−22.46	−22.68	0.06	0.01	0.94	0.34	−6.41	0.81	−27.74	−26.93
	Walden TS^a	14.53	—	—	9.03	−0.46	−0.31	0.15	—	0.81	−0.17	9.21	9.05
	W Postmin	−22.43	—	—	−23.40	0.05	0.00	0.71	—	−5.65	0.86	−28.29	−27.43
	FS TS	32.36	28.54	27.96	27.74	−1.48	−0.77	0.50	0.09	−1.17	−0.24	24.90	24.66
	FS Postmin	−24.83	−25.87	−25.62	−25.91	0.03	−0.03	0.63	0.32	−3.80	1.06	−28.76	−27.70

---

In Fig. 1 we show the energy profiles for the title reactions. All four reactions feature four possible product channels: (1) hydrogen abstraction with the products HCl + CH₂X, (2) hydrogen substitution leading to H + CH₂ClX, (3) halogen abstraction forming ClX + CH₃, and (4) halogen substitution resulting in X + CH₃Cl. The substitution products can form either via Walden inversion or front-side-attack, for which we refer to as W and FS, respectively, in the nomenclature of the stationary points.

In the case of the X = F and Cl reactions the XA channel is the most endothermic, with 0 K reaction enthalpies 48.4 kcal mol⁻¹ and 25.3 kcal mol⁻¹, respectively, and H-abstraction is the lowest-energy and adiabatically even exothermic reaction path with product relative adiabatic energies −2.6 kcal mol⁻¹ and −4.7 kcal mol⁻¹, respectively. In contrast, HA has only the second lowest reaction energy for X = Br (−3.4 kcal mol⁻¹) and I (−3.2 kcal mol⁻¹) and it is also exothermic adiabatically in these cases. The most exothermic pathway is X-substitution for X = Br and I, while this route is the second and third most endothermic for X = F and Cl, respectively. The decreasing tendency of the XS product relative energies (from 26.7 to −26.9 kcal mol⁻¹) as the size of X increases is not surprising, because the breaking C–X bonds become weaker and weaker with increasing X size, and the forming C–Cl bond exceeds their stability in case of X = Br and I. The two highest-energy channels for the Br and I systems are HS and XA. With increasing halogen atom size, the dihalide product of XA becomes more and more stable due to increased polarizability of the X atom, explaining the considerable decrease in XA reaction enthalpy (from 48.4 kcal mol⁻¹ to 7.5 kcal mol⁻¹). On the other hand, regarding H-substitution the 0 K reaction enthalpies cover a much smaller energy range (15.9–21.5 kcal mol⁻¹) for all halogens, because there is no significant difference between the stability of the CH₂ClX products. Similarly, the HA exothermicity varies only between −2.6 (X = F) and −4.74 (X = Cl) kcal mol⁻¹ as the relative energies of the CH₂X radicals differ only slightly.

H-abstraction, which is considered as the main route of the title reactions in the literature, has a small positive barrier, with 0.6–1.4 kcal mol⁻¹ adiabatic, and 4.8–5.6 kcal mol⁻¹ classical heights, indicating a significant ZPE effect. In all cases, HA has the lowest-energy TSs amongst the possible reaction paths. The HA pathways also feature shallow exit-channel minima with small negative relative energies (except the X = F classical value of 0.3 kcal mol⁻¹), considerably smaller when ZPE is taken into account. Interestingly, we could not identify any stationary point other than the products for the X = F and Cl XA reactions. For X = Br and I, the XA TSs are not much above in energy with respect to those of HA. For the CH₃F reaction the highest barrier corresponds to the Walden-inversion XS pathway, at 44.5 kcal mol⁻¹ adiabatic relative energy, however, this route lacks an exit-channel minimum. The HS TS is just slightly lower, with a 42.8 kcal mol⁻¹ adiabatic height, than the XS TS for the X = F reaction. In the case of the other three halogens, H-substitution opens at similar energies. The HS reaction always seems to occur via Walden inversion, as we were not able to locate a front-side-attack TS geometry in either case. The thermoneutral Cl + CH₃Cl reaction can also take place only through Walden-inversion (with a 23.7 kcal mol⁻¹ adiabatic barrier), since a front-side TS arrangement could not be found. In the case of the X-substitution channels of the CH₃Br and CH₃I reactions, however, both Walden-inversion and front-side-attack TSs are found, with the FS TSs being around 20 and 15 kcal mol⁻¹ higher in energy, respectively. The geometries of the Walden TSs for all four XS reactions could only be optimized at the RMP2/aug-cc-pVDZ level of theory (except when X = I, where UMP2 method had to be applied), and all of the related energy-correction computations turned out to be very problematic. This is interesting, especially compared to the Walden-inversion TSs of the similar, but negatively charged, thus closed shell, systems, i.e., in the S_N2 pathways of ion–molecule reactions.^64,65 These S_N2 Walden TSs are usually submerged and straightforward to identify if the nucleophile is Cl⁻,⁶⁵ though they can be problematic or may not exist if it is F⁻ or OH⁻.^64,66 On the other hand, exit-channel minima both for the XS W and FS pathways are quite deep, found at adiabatic relative energies of −13.7 and −14.9 kcal mol⁻¹ for X = Br, and −27.4 and −27.7 kcal mol⁻¹ for X = I, respectively. In fact, most of the post-reaction minima identified are rather close in energy to the product asymptote, leaving the studied reaction paths without deep exit-channel wells.

In Table 1 we also show the relative energies of each stationary point of the title reactions obtained by optimizing the geometries at three different levels of theory: MP2/aug-cc-pVDZ, CCSD(T)-F12b/aug-cc-pVDZ, and CCSD(T)-F12b/aug-cc-pVTZ. We can see that the MP2/aug-cc-pVDZ values can differ by even 6–9 kcal mol⁻¹ from the CCSD(T)-F12b/aug-cc-pVDZ relative energies in the case of the XA products, indicating the importance of the accurate description of electron correlation. In contrast, the MP2 relative energies deviate only by a few 0.1 kcal mol⁻¹ from the CCSD(T)-F12b/aug-cc-pVDZ values for the HS postmin and product when X = F and Cl, and for the HA TS structures when X = Br and I. For the remaining stationary structures, the MP2 – CCSD(T)-F12b difference using the aug-cc-pVDZ basis set is around 1–4 kcal mol⁻¹, suggesting an overall necessity for coupled-cluster calculations.

In Fig. 2 and Table 1 we show the convergence behavior of the aug-cc-pVnZ (n = D, T, Q) basis sets applied with the CCSD(T)-F12b method. Large differences, up to 1.8 kcal mol⁻¹, can be seen between the DZ and TZ basis sets, with the double-zeta set usually underestimating the relative energies. These deviations are the largest for the HS products and post-reaction minima. In contrast, the QZ and TZ values agree much better, with deviations mostly around 0.1 kcal mol⁻¹, reflecting the excellent convergence properties of the explicitly-correlated CCSD(T)-F12b method. The QZ – TZ differences are always negative, with the largest absolute values for the XA products of the X = Br (0.3 kcal mol⁻¹) and I (0.55 kcal mol⁻¹) reactions. Note, that in the latter case we also perform a CCSD(T)-F12b/aug-cc-pV5Z computation, which results in a 0.26 kcal mol⁻¹ further lowering effect. The TZ – DZ difference has a negative sign only for the XS FS TS and the XA product channel of the X = I reaction.

Fig. 2 Deviations between the CCSD(T)-F12b/aug-cc-pVDZ and CCSD(T)-F12b/aug-cc-pVTZ (TZ – DZ), and those of between the CCSD(T)-F12b/aug-cc-pVTZ and CCSD(T)-F12b/aug-cc-pVQZ (QZ – TZ) relative energies for the stationary points of the Cl + CH₃X [X = F, Cl, Br, I] reactions.

Various auxiliary corrections to the relative energies are presented in Fig. 3 and in Table 1, as well. It is clear, that the scalar relativistic effects are of a few 0.1 kcal mol⁻¹, mostly within 0.5 kcal mol⁻¹, in the case of all four reactions, and are usually positive, except for the XA products when X = F and Cl, and for the XS W TS and XS FS postmin of the Cl + CH₃Cl reaction. The largest relativistic corrections are seen for the Br + CH₃Cl products. As to the correlation of the sub-valence-shell electrons, with increasing X atom size, the core-correction is more and more positive and larger and larger in magnitude (from 0.1–0.2 kcal mol⁻¹ for the F to around 1 kcal mol⁻¹ for the I reaction), probably (1) due to the larger number of electrons on the sub-valence shell, as well as (2) to the increased nuclear charge with increasing atomic number. The core-correlation effect is more significant in the case of reaction routes involving multiple halogen-bond breaking and forming, i.e., XA and XS pathways, especially for the CH₃I reaction. To take higher-order excitations into account we also determine CCSDT/aug-cc-pVDZ and CCSDT(Q)/aug-cc-pVDZ relative energies. The deviations between the CCSDT(Q) and CCSDT (δ[(Q)]) values, a few 0.1 kcal mol⁻¹ and mostly negative, are similar in absolute value as the CCSDT and CCSD(T) (δ[T]) differences. We can see some exceptions, e.g., the XS W TS structure (optimized only at the MP2/aug-cc-pVDZ level) for the X = F reaction, and for the XS FS TS geometries when X = Br and I, where these corrections exceed 1 kcal mol⁻¹.

Fig. 3 Scalar relativistic (ΔE(DK-AE-CCSD(T)/aug-cc-pwCVTZ-DK) − ΔE(AE-CCSD(T)/aug-cc-pwCVTZ)), core-correlation (ΔE(AE-CCSD(T)/aug-cc-pwCVTZ) − ΔE(FC-CCSD(T)/aug-cc-pwCVTZ)) and post-(T) (δ[T] = ΔE(CCSDT/aug-cc-pVDZ) − ΔE(CCSD(T)/aug-cc-pVDZ) and δ[(Q)] = ΔE(CCSDT(Q)/aug-cc-pVDZ) − ΔE(CCSDT/aug-cc-pVDZ)) energy corrections for the stationary points of the Cl + CH₃X [X = F, Cl, Br, I] reactions.

To obtain vibrationally adiabatic relative energies we determine the harmonic frequencies of each stationary point, and calculate their ZPE contributions to the classical relative energy values, which are shown in Fig. 4, and also in Table 1. In the case of the halogen substitution channel, we find small ZPE contributions (both positive and negative), around or below 1 kcal mol⁻¹ absolute value, which is not surprising as the breaking C–X bonds are replaced by the forming C–Cl bonds that are similar in strength (or the same in case of the X = Cl reaction). Since the imaginary frequencies are not included in the ZPEs of the transition-state geometries, the reactant/product-like nature cannot be unambiguously deducted from the ZPE corrections. As can be expected, since a C–Cl bond is forming in all four reactions, the relative strength of the breaking C–X bonds determines the sign and magnitude of the ZPE correction in the XS reaction. This is nicely reflected in Fig. 4 by the small negative value corresponding to the F + CH₃Cl products and the increasingly positive ZPE contributions for the X = Br and I reaction energies. As to the halogen-abstraction channel, the ZPE effect is dominated by the strength of the breaking C–X bond with respect to the forming Cl–X bond. For the F reaction, this difference is manifested in a large negative ZPE contribution, which suggests that the C–F bond has much higher frequency that the Cl–F bond. We see less and less negative, but still considerable, ZPE contributions to the relative energies of the XA stationary points as the size of X increases, indicating a smaller difference in the C–X and the Cl–X bond-strengths. For the HA and HS pathways, the ZPE effects are the largest, between −4 and −5 kcal mol⁻¹. In both reactions a C–H bond breaks, which is replaced by a C–Cl, and a H–Cl bond in HS and HA, respectively. Thus, we see very similar ZPE contributions, differing only within a few 0.1 kcal mol⁻¹, for the stationary points of both of these channels.

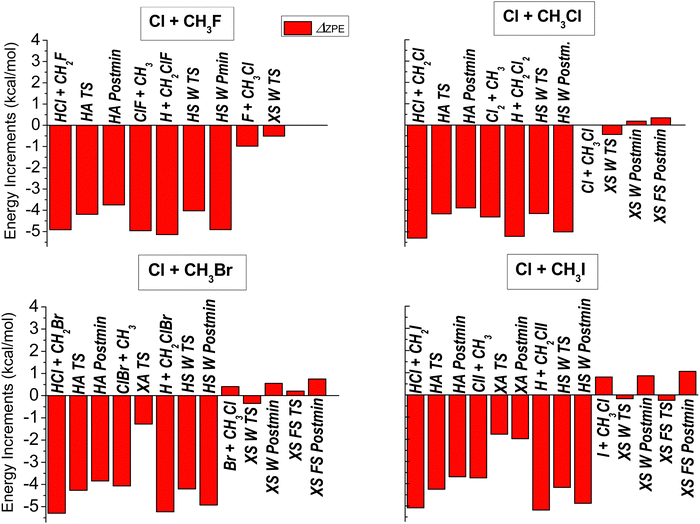Fig. 4 Zero-point-energy contributions obtained at the CCSD(T)-F12b/aug-cc-pVTZ level of theory for the stationary points of the Cl + CH₃X [X = F, Cl, Br, I] reactions.

In Fig. 5 we present the relevant structural parameters of the stationary-point geometries of the title reactions, which makes possible to judge if a transition-state geometry resembles more to the reactants (early-barrier reaction) or to the products (late-barrier reaction). Such a comparison allows for making some prediction regarding the dynamics behavior of these reactive systems. The H-abstraction path involves a TS structure that is very similar for all four reactions, which is not surprising at all, because a C–H bond breaks and a H–Cl bond forms in all of the HA processes. The TS can be referred to as a so-called central barrier, because the H–Cl bond is lengthened to about the same extent as the C–H bond is stretched in this arrangement. On the other hand, all the HA Postmin structures have clearly product-like geometries with only 0.01 Å longer H–Cl distances than in the HCl molecule. As to H-substitution, both the C–H and C–Cl bond-lengths are considerably longer in the HS W TS than in the reactant and the product molecules, respectively, however, this lengthening is much more significant for the C–H bond, making HS a late-barrier pathway. Similar to HA, the geometries of the HS W Postmins are very close to those of the CH₂ClX products, with extremely long C–H distances. In the case of the X-abstraction channel, we find a late-barrier Br and I reaction, while for F- and Cl-abstraction we could locate neither the TS nor the Postmin. Interestingly, for the Br-abstraction TS a slightly bent structure is found (with 158.5° Cl–Br–C bond angle). We can only identify a XA Postmin for the I reaction, where it has a linear C–I–Cl arrangement, with short Cl–I distance. For halogen substitution (XS), we find both Walden-inversion and front-side TSs, as well, the latter ones only for X = Br and I. The XS Walden TS geometry, which could only be optimized at the MP2/aug-cc-pVDZ level of theory in all four cases, is increasingly reactant-like as going from F to I, with very product-like XS W Postmin structures featuring extremely long C–X distances. The methyl group is nearly planar in the TS, while it is bent towards X in the Postmin arrangement (which is not found for X = F). The XS FS TSs of the Br and I reactions seem to be rather product-like or central, also with very long C–X separation. The X–C–Cl angles are a bit smaller for the XS FS Postmin than for XS FS TS.

Fig. 5 Relevant structural parameters of the stationary points of the Cl + CH₃X [X = F, Cl, Br, I] reactions obtained at the CCSD(T)-F12b/aug-cc-pVTZ level of theory. Bond lengths are in angström, and bond angles are in degrees. The values marked with * correspond to MP2/aug-cc-pVDZ-optimized geometries.

Knowing the reaction energy of the different channels of the title reactions allows for interpreting the structural parameters of the stationary points in the framework of Hammond's postulate,⁶⁷ as visualized by the schematic graphs of Fig. 6. The postulate presumes that an exothermic reaction has a reactant-like transition-state arrangement, whereas endothermic reactions have product-like TS geometries.⁶⁷ Hammond's idea is often explained by intersecting harmonic parabola potential energy functions corresponding to the breaking bond of the reactant and the forming bond of the product. For example, in the case of the H-abstraction pathway of the title reactions, which is not far from a thermoneutral reaction for all X atoms, the intersection of the parabolae corresponding to the breaking C–H bond and the forming H–Cl bonds results in a central-barrier to the reaction, in accordance with what we see in Fig. 5. In contrast, the 21–27 kcal mol⁻¹ endothermicity of the H-substitution reaction, i.e., the up-shifting harmonic potential curve of the forming C–Cl bond with respect to that of the tearing C–H bond, leads to product-like TS structures, as also reflected in Fig. 5. However, when the different X halogen atoms participate explicitly in the chemical reaction, we have different parabolae for the reactants (XS channel), or both for the reactant and product species (XA channel). In these cases, not only the position of the minimum of the functions, but their widths play an important role, as well, which depend on the strength of the given bond. The interplay of these two effects, shown schematically in Fig. 6, culminates in increasingly product-like TS structures in the XA case as the size of the halogen increases. However, in Fig. 5, we find an interesting tendency for the halogen-substitution reaction, which features more and more reactant-like XS W TS geometries, which are always the lowest-lying TSs in the XS reactions, as going from F to I. Here, the impact of the widening harmonic functions, which contributes to determining the position of the TS along the reaction coordinate, is counteracted by the decreasing reaction energy as the halogen size increases. This finding can be clearly seen in the last panel of Fig. 6.

Fig. 6 Schematic representations of the crossing harmonic potential energy curves corresponding to the reactant and product wells of the different reaction pathways of the Cl + CH₃X [X = F, Cl, Br, I] reactions to demonstrate the validity of Hammond's postulate.⁶⁷

Stepping further from the stationary-point picture of the Cl + CH₃X [X = F, Cl, Br, I] reactions, we can make some preliminary predictions based on the so-called Polanyi-rules.⁶⁸ These rules of thumb are based on the dynamical observations obtained for atom + diatom reactions, and say that early-barrier reactions can be more effectively promoted by translational excitation of the reactants, while vibrational excitation can increase the reactivity more efficiently of late-barrier reactions.⁶⁸ Thus, we expect vibrational enhancement in the case of the HS and XA channels, and more and more pronounced translational promotion in the XS reaction. However, for these complex reactions only detailed dynamics simulations can ultimately tell which form of energy is more efficient in increasing reactivity. Additionally, in the case of these polyatomic systems, several deviations from the Polanyi rules are expected due to the increase in the number of degrees of freedom with respect to atom + diatom reactions.

The spin–orbit corrections to the relative energies are also listed in Table 1 and shown for the XS channel in Fig. 7. As can be seen in Table 1, the spin–orbit coupling in the mid-reaction stationary points and products of the HA, HS and XA channels is not significant, we can only see small deviation (less than 0.15 kcal mol⁻¹) from the 0.84 kcal mol⁻¹ SO-splitting of the reactant Cl atom in two cases: (1) for the HS products in the Cl reaction and (2) for the HA stationary points for X = Br and I. As to the halogen-substitution products, the SO splitting of the forming halogen atom, of course, has a notable effect, larger and larger in magnitude as the halogen size, along with the splitting itself, increases. More interestingly, such effects are also seen in Fig. 7 in the case of the TS and Postmin geometries, where the SO splitting is usually considered as quenched. The quenching, i.e., the unaffected 0.84 kcal mol⁻¹ SO-correction value of the reactant Cl atom in Fig. 7, is only seen for the XS W TS structures, which can be explained by the increasing reactant-like character of these stationary points, as discussed above (see Fig. 5 and 6), which prevents the more and more strongly bound X, with increasing SO splitting, to impact the relative energy. In contrast, the product-like geometry of the XS W Postmin results in a large negative SO correction for X = Br and I, and visible decrease in the SO-splitting in the X = Cl case. Regarding the XS FS TS geometry the forming Br atom has only a slight influence on the SO-splitting of the TS, whereas the breaking C–I bond in the XS FS TS leads to a small negative SO correction. Similar, but larger effects are found for the X = Br and I XS FS Postmin structures, reflecting their more product-like character. For the I reaction, a small SO effect is also found for the XA TS (0.4 kcal mol⁻¹) and Postmin (0.3 kcal mol⁻¹).

Fig. 7 Spin–orbit corrections for the stationary points of the halogen-substitution pathway of the Cl + CH₃X [X = F, Cl, Br, I] reactions obtained at the MRCI+Q(21,11)/aug-cc-pVDZ level of theory.

Our 0 K reaction enthalpies can be directly compared to “experimental” values taken from the active thermochemical tables (ATcT),⁶⁹ which comparison is shown in Table 2. In most cases the differences are below 0.4 kcal mol⁻¹, and are always below 0.7 kcal mol⁻¹, except for the ClI + CH₃ I-abstraction channel, where the difference between the ATcT data and ours is 1.28 kcal mol⁻¹. This unexpectedly⁷⁰ large deviation indicates either problems with the present computations and/or with the ATcT data. From the theoretical side, additional basis-set effects and anharmonic ZPE contributions could be considered, while verification of the enthalpy of formation value of ClI in ATcT would also be needed.

Table 2 Comparison between the benchmark theoretical 0 K Cl + CH₃X reaction enthalpies of the present work with the values taken from the 1.130 version of active thermochemical tables (ATcT).⁶⁹ All data are given in kcal mol⁻¹

X	Reaction channel	ATcT	This work	Difference
F	ClF + CH3	48.27 ± 0.05	48.35	−0.08
	H + CH2ClF	16.09 ± 0.21	15.61	0.49
	F + CH3Cl	26.35 ± 0.06	26.69	−0.33
Cl	HCl + CH2Cl	−4.40 ± 0.21	−4.74	0.34
	Cl2 + CH3	25.08 ± 0.04	25.06	0.02
	H + CH2Cl2	20.12 ± 0.08	19.81	0.31
Br	ClBr + CH3	17.44 ± 0.04	17.61	−0.17
	H + CH2ClBr	21.26 ± 0.29	20.61	0.65
	Br + CH3Cl	−13.27 ± 0.03	−13.26	−0.02
I	Cll + CH3	5.94 ± 0.04	7.22	−1.28
	I + CH3Cl	−26.66 ± 0.05	−26.93	0.27

---

Summary

We determine benchmark geometries and energies of the stationary points of the Cl + CH₃X [X = F, Cl, Br, I] reactions by optimizing their structures at the explicitly-correlated UCCSD(T)-F12b/aug-cc-pVTZ level of theory, and augmenting the quality of their relative energies with auxiliary energy corrections, computed at the above geometries. We study four possible pathways of the title reactions: hydrogen abstraction, halogen abstraction, hydrogen substitution, and halogen substitution. We compute UCCSD(T)-F12b/aug-cc-pVQZ single-point energies at the benchmark geometries to make finite-basis-set error negligible. We consider the energy correction stemming from the correlation of the sub-valence-shell electrons at the AE/FC-UCCSD(T)/aug-cc-pwCVTZ level of theory, and also from scalar-relativistic effects using the second-order Douglas–Kroll (DK) Hamiltonian. We take higher-order electron-correlation effects into account by determining post-(T) corrections as energy increments between UCCSD(T), UCCSDT and UCCSDT(Q) relative energies applying the aug-cc-pVDZ basis set. Due to the presence of free halogen atoms in the title reactions, we also account for spin–orbit splittings at the multi-reference MRCI+Q(21,11)/aug-cc-pVDZ level of theory in case of all the stationary points. Zero-point-energy contributions, determined at the UCCSD(T)-F12b/aug-cc-pVTZ level, are also included in the benchmark adiabatic relative energies, which are compared to experimental values and show generally good agreement. It turns out that the above-detailed energy correction terms are necessary to reach chemical accuracy of the results. Based on the energetics and structural parameters of the studied stationary points we interpret our results in terms of Hammond's postulate and make predictions for the expected dynamics behavior of the title reactions based on the Polanyi rules, which may motivate future theoretical dynamics investigations of the present reactive systems.

Data availability

The data that support the findings of this study are available from the corresponding authors upon reasonable request.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We thank the National Research, Development and Innovation Office–NKFIH, K-146759; Project no. TKP2021-NVA-19, provided by the Ministry of Culture and Innovation of Hungary from the National Research, Development and Innovation Fund, financed under the TKP2021-NVA funding scheme; and the Momentum (Lendület) Program of the Hungarian Academy of Sciences for the financial support.

References

1. A. Persky, J. Chem. Phys., 1977, 66, 2932.
2. B. Jiang and H. Guo, J. Am. Chem. Soc., 2013, 135, 15251.
3. M. Monge-Palacios and J. Espinosa-Garcia, J. Phys. Chem. A, 2010, 114, 4418.
4. S. Yan, Y. T. Wu, B. Zhang, X.-F. Yue and K. Liu, Science, 2007, 316, 1723.
5. S. J. Greaves, R. A. Rose, F. Abou-Chahine, D. R. Glowacki, D. Troya and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2011, 13, 11438.
6. G. Czakó and J. M. Bowman, Science, 2011, 334, 343.
7. F. Meng, W. Yan and D. Wang, Phys. Chem. Chem. Phys., 2012, 14, 13656.
8. G. Czakó and J. M. Bowman, J. Phys. Chem. A, 2014, 118, 2839.
9. B. Fu, X. Shan, D. H. Zhang and D. C. Clary, Chem. Soc. Rev., 2017, 46, 7625.
10. H. Pan, F. Wang, G. Czakó and K. Liu, Nat. Chem., 2017, 9, 1175.
11. L. N. Krasnoperov and V. N. Panfflov, React. Kinet. Catal. Lett., 1979, 10, 191.
12. E. C. Tuazon, R. Atkinson and S. B. Corchnoy, Int. J. Chem. Kinet., 1992, 24, 639.
13. K. Hitsuda, K. Takahashi, Y. Matsumi and T. J. Wallington, J. Phys. Chem. A, 2001, 105, 5131.
14. K. M. Brahan, A. D. Hewitt, G. D. Boone and S. A. Hewitt, Int. J. Chem. Kinet., 1996, 28, 397.
15. M. G. Bryukov, I. R. Slagle and V. D. Knyazev, J. Phys. Chem. A, 2002, 106, 10532.
16. T. Gierczak, L. Goldfarb, D. Sueper and A. R. Ravishankara, Int. J. Chem. Kinet., 1994, 26, 719.
17. K. G. Kambanis, Y. G. Lazarou and P. Papagiannakopoulos, J. Phys. Chem. A, 1997, 101, 8496.
18. C. A. Piety, R. Soller, J. M. Nicovich, M. L. McKee and P. H. Wine, Chem. Phys., 1998, 231, 155.
19. I. K. Larin, A. I. Spasskii, E. M. Trofimova and N. G. Proncheva, Kinet. Catal., 2018, 59, 11.
20. K. G. Kambanis, Y. G. Lazarou and P. Papagiannakopoulos, Chem. Phys. Lett., 1997, 268, 498.
21. E. S. N. Cotter, N. J. Booth, C. E. Canosa-Mas, D. J. Gray, D. E. Shallcross and R. P. Wayne, Phys. Chem. Chem. Phys., 2001, 3, 402.
22. R. C. Sharma, M. Blitz, R. Wada and P. W. Seakins, Spectrochim. Acta, Part A, 2014, 128, 176.
23. S. Enami, S. Hashimoto, M. Kawasaki, Y. Nakano, T. Ishiwata, K. Tonokura and T. J. Wallington, J. Phys. Chem. A, 2005, 109, 1587.
24. V. Dookwah-Roberts, J. M. Nicovich and P. H. Wine, J. Phys. Chem. A, 2008, 112, 9535.
25. M. Marinkovic, M. Gruber-Stadler, J. M. Nicovich, R. Soller, M. Mülhäuser, P. H. Wine, L. Bache-Andreassen and C. J. Nielsen, J. Phys. Chem. A, 2008, 112, 12416.
26. D. Sarzyński, A. A. Gola, K. Brudnik and J. T. Jodkowski, Chem. Phys. Lett., 2012, 525–526, 32.
27. A. A. Gola, B. D’Anna, K. L. Feilberg, S. R. Sellevåg, L. Bache-Andreassen and C. J. Nielsen, Atmos. Chem. Phys., 2005, 5, 2395.
28. S. R. Sellevåg, G. Nyman and C. J. Nielsen, J. Phys. Chem. A, 2006, 110, 141.
29. D. Sarzyński, A. A. Gola, A. Dryś and J. T. Jodkowski, Chem. Phys. Lett., 2009, 476, 138.
30. A. A. Gola, D. Sarzyński, A. Dryś and J. T. Jodkowski, Chem. Phys. Lett., 2010, 486, 7.
31. M. Bilde and T. J. Wallington, J. Phys. Chem. A, 1998, 102, 1550.
32. S. M. A. Hoffmann, D. J. Smith, A. González Ureña, T. A. Steele and R. Grice, Mol. Phys., 1984, 53, 1067.
33. W. S. Goliff and F. S. Rowland, Geophys. Res. Lett., 1997, 24, 3029.
34. C. Murray, B. Retail and A. J. Orr-Ewing, Chem. Phys., 2004, 301, 239.
35. S. Rudić, D. Ascenzi and A. J. Orr-Ewing, Chem. Phys. Lett., 2000, 332, 487.
36. S. Rudić, C. Murray, D. Ascenzi, H. Anderson, J. N. Harvey and A. J. Orr-Ewing, J. Chem. Phys., 2002, 117, 5692.
37. S. Rudić, C. Murray, J. N. Harvey and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2003, 5, 1205.
38. C. Murray and A. J. Orr-Ewing, Int. Rev. Phys. Chem., 2004, 23, 435.
39. C. Murray, J. K. Pearce, S. Rudić, B. Retail and A. J. Orr-Ewing, J. Phys. Chem. A, 2005, 109, 11093.
40. E. Rosenman and M. L. McKee, J. Am. Chem. Soc., 1997, 119, 9033.
41. G. da Silva, Chem. Phys. Lett., 2018, 706, 371.
42. Y. G. Lazarou, K. G. Kambanis and P. Papagiannakopoulos, Chem. Phys. Lett., 1997, 271, 280.
43. J.-F. Xiao, Z.-S. Li, Y.-H. Ding, J.-Y. Liu, X.-R. Huang and C.-C. Sun, Phys. Chem. Chem. Phys., 2001, 3, 3955.
44. K. Brudnik, M. Twarda, D. Sarzyński and J. T. Jodkowski, J. Mol. Model., 2013, 19, 1489.
45. D. Troya, G. C. Schatz, D. J. Garton, A. L. Brunsvold and T. K. Minton, J. Chem. Phys., 2004, 120, 731.
46. R. D. Amos, J. S. Andrews, N. C. Handy and P. J. Knowles, Chem. Phys. Lett., 1991, 185, 256.
47. T. H. DunningJr, J. Chem. Phys., 1989, 90, 1007.
48. G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104.
49. K. A. Peterson and T. H. Dunning, Jr., J. Chem. Phys., 2002, 117, 10548.
50. J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041.
51. M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 214105.
52. M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89.
53. W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48.
54. K. R. Shamasundar, G. Knizia and H.-J. Werner, J. Chem. Phys., 2011, 135, 054101.
55. S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61.
56. A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823.
57. The National Institute of Standards and Technology (NIST), Handbook of basic atomic spectroscopic data, https://www.nist.gov/pml/data/handbook/.
58. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113.
59. MOLPRO, version 2015.1, a package of ab initio programs, H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz and others, see https://www.molpro.net.
60. MOLPRO, version 2023.2, a package of ab initio programs, H.-J. Werner, P. J. Knowles and others, see https://www.molpro.net.
61. M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, B. P. Szabó, L. Gyevi-Nagy, B. Hégely, et al. MRCC, a quantum chemical program suite, see https://www.mrcc.hu.
62. M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy and B. Hégely, et al. , J. Chem. Phys., 2020, 152, 074107.
63. T. Győri and G. Czakó, J. Chem. Phys., 2022, 156, 071101.
64. I. Szabó and G. Czakó, J. Phys. Chem. A, 2017, 121, 9005.
65. I. Szabó and G. Czakó, J. Phys. Chem. A, 2017, 121, 5748.
66. D. A. Tasi, T. Győri and G. Czakó, Phys. Chem. Chem. Phys., 2020, 22, 3775.
67. G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334.
68. J. C. Polanyi, Science, 1987, 236, 680.
69. B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) values based on ver. 1.130 of the Thermochemical Network, Argonne National Laboratory, 2019, available at https://ATcT.anl.gov.
70. G. Czakó, T. Győri, B. Olasz, D. Papp, I. Szabó, V. Tajti and D. A. Tasi, Phys. Chem. Chem. Phys., 2020, 22, 4298.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates (in Å) and absolute energies (in E_h) of each optimized stationary-point structure. See DOI: https://doi.org/10.1039/d4cp01578a

---