 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Importance sampling within configuration space integration for adsorbate thermophysical properties: a case study for CH3/Ni(111)†
Katrín
Blöndal‡
a,
Kirk
Badger‡
 a,
Khachik
Sargsyan
a,
Khachik
Sargsyan
 b,
David H.
Bross
b,
David H.
Bross
 c,
Branko
Ruscic
c,
Branko
Ruscic
 c and
C. Franklin
Goldsmith
c and
C. Franklin
Goldsmith
 *a
*a
aChemical Engineering Group, School of Engineering, Brown University, Providence, RI 02912, USA. E-mail: franklin_goldsmith@brown.edu
bSandia National Laboratories, Livermore, CA 94550, USA
cChemical Sciences and Engineering Division, Argonne National Laboratory, Lemont, IL 60439, USA
First published on 22nd May 2024
Abstract
A new strategy is presented for computing anharmonic partition functions for the motion of adsorbates relative to a catalytic surface. Importance sampling is compared with conventional Monte Carlo. The importance sampling is significantly more efficient. This new approach is applied to CH3* on Ni(111) as a test case. The motion of methyl relative to the nickel surface is found to be anharmonic, with significantly higher entropy compared to the standard harmonic oscillator model. The new method is freely available as part of the Minima-Preserving Neural Network within the ADTHERM package.
1 Introduction
First-principle based methods in heterogeneous catalysis are increasingly important tools in catalyst development and reactor design. Fortunately, the computational cost of an individual single-point calculation continues to decrease, even as the accuracy of these methods increases, and calculations that would have been challenging a few years ago are now increasingly commonplace. Accordingly, it is now feasible to move beyond the standard harmonic-oscillator model when computing the partition function for adsorbates on metals.1,2 By providing a more accurate depiction of the entropy of adsorbates, these anharmonic models provide a more accurate estimate of the free energy of the system.2–15A common requirement in all of these methods is sampling a broader number of nuclear configurations, particularly configurations that are further from the minima than what would be used to compute the gradients in forces that are required by the Hessian. In principle, this configurational sampling can be done directly by using a first-principle method – e.g. direct sampling with density functional theory (DFT). In practice, however, the large number of configurations required frequently necessitates the construction of a surrogate potential energy surface (PES). This surrogate PES is trained to DFT data, and the design of the surrogate model should prioritize accuracy where it matters the most – i.e. near the stationary points.
In ref. 16 the authors introduced the minima-preserving neural network (MPNN) as an accurate surrogate PES, which was used within Monte Carlo (MC) integration routines to solve a 3-dimensional integral for H* adsorbed on Cu(111); this method was released as an open-source package, ADTHERM. In ref. 17 this phase space integration approach was extended to 6-dimensions for polyatomic adsorbates, including CO/Pt(111) and CH3OH/Cu(111). In all three cases, conventional MC integration was used to compute the phase space integrals and hence the partition function. Although the MC integration was performed using the MPNN surrogate PES, and thus was several orders of magnitude faster than direct calls to a DFT calculator, the approach still required ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (7) single-point calculations. However, alternative integration strategies are possible. In particular, integration strategies based upon importance sampling could reduce the number of required single-point calculations. Indeed, with a sufficient reduction, it might be possible to combine importance sampling with direct DFT sampling and avoid the need for a surrogate model altogether.
(7) single-point calculations. However, alternative integration strategies are possible. In particular, integration strategies based upon importance sampling could reduce the number of required single-point calculations. Indeed, with a sufficient reduction, it might be possible to combine importance sampling with direct DFT sampling and avoid the need for a surrogate model altogether.
In the present work, we extend ADTHERM to include importance sampling in the evaluation of the 6D phase space integrals required to evaluate the entropy and other thermophysical properties of adsorbates. The method is here applied for the specific case of adsorbed methyl, CH3*, on Ni(111). A previous study by Henkelman et al.18 demonstrated a counterintuitive minimum-energy path for the rotation parallel to the surface. The optimal mechanism of rotation of CH3* in the fcc site is not through rotation about the carbon atom; instead, the binding C atom is displaced from the fcc site to an adjacent hcp site through rotation about one of the H atoms, due to the strong hydrogen-metal binding energy. To return to the fcc site and obtain the 120° rotated geometry, the methyl rotates again about a different hydrogen atom. This rather unexpected minimum-energy path makes CH3/Ni(111) an interesting candidate to study with the phase space integration approach, since it confirms that a chemisorbed species (otherwise presumed to be tightly bound and thus harmonic) can have a complicated, anharmonic motion relative to the surface. Such behavior suggests that conventional analytical models, such as the harmonic oscillator, are unlikely to capture the number of thermally accessible states and thus will underestimate the entropy of methyl on metal surfaces.
2 Methods
2.1 Electronic structure theory
Density functional theory (DFT) calculations were used for the geometry optimization, generation of the Hessian, and for the generation of the training data. The DFT calculations were performed with the plane-wave code Quantum ESPRESSO.19–21 The Perdew–Burke–Ernzerhof functional22 was used with Grimmes D3 corrections23 including three-body Axilrod–Teller–Muto corrections,24,25 PBE-D3(ABC). Projector augmented wave method (PAW) pseudopotentials generated using the “atomic” code by Dal Corso26,27 were used. A plane-wave cutoff of 60 Ry and a (7 × 7 × 1) k-point grid were used for the energy calculations, as well as the Marzari–Vanderbilt smearing method28 with a smearing width of 0.01 Ry. The limited-memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS) algorithm in the atomic simulation environment (ASE),29 with a maximum force convergence criterion of 0.01 eV Å−1 along all directions was used for geometry relaxations.The optimized lattice constant with the PBE-D3(ABC) functional was found to be 3.47 Å for Ni. The CH3/Ni(111) system was modeled using a 4-layer Ni(111) slab with a 3 × 3 unit cell, corresponding to a 1/9th monolayer coverage, and a 17 Å vacuum between the top of the adsorbed CH3* and the bottom of the repeated image. All Ni surface atoms were held fixed in their bulk geometry while the CH3* adsorbate was relaxed on the surface. The fcc binding site was found to be the optimal position of CH3* on the Ni(111) surface, where the adsorption energy is −2.16 eV, converged within 10 meV. A slightly less stable minimum was found with CH3* in the hcp site.
For the gas-phase CH4(g), coupled cluster calculations were performed. The geometry optimization and normal mode analysis were performed at the UCCSD(T)/cc-pVTZ level in Molpro.30
2.2 CH3/Ni(111) training data generation
The position of the adsorbed methyl relative to the surface can be described by six degrees of freedom: x,y,z,α,β,γ. The first three degrees of freedom (x,y,z) correspond to translation of CH3* in space (i.e. surface diffusion and desorption), and the latter three degrees of freedom (α,β,γ) correspond to rotation about principal axes (i.e. libration, or frustrated tumbling, and “helicopter” rotation). The potential energy as a function of these degrees of freedom, V(x,y,z,α,β,γ), was calculated at a total of 9930 (x,y,z,α,β,γ) configurations of CH3* on the rhombus-shaped surface of the unit cell volume. The z values ranged from 0.75 Å below the optimal z value of CH3* to 2.5 Å above the optimal z value, which was 1.62 Å in the fcc position. The boundaries on the α, β, and γ angles were [−π,π], [−π/2,π/2], and [−π,π], respectively.The generation of these training data consisted of multiple steps. First, the selection of training data was intentionally biased towards the fcc and hcc minima. This set included both minima, as well as 84 displacements required to calculate the rigid Hessian matrix at each minimum for a total of 168 displacements. Second, multivariate normal (MVN) distributions centered at each minimum were obtained using the corresponding inverse-Hessian matrices as covariance matrices. This scheme, which prioritizes the minima and distributions around them, was intended to ensure ample sampling in the low-energy region, which is the highest Boltzmann weight area. The distribution centered at the fcc minimum included 2891 geometries, and the hcp distribution included 2833 geometries. In order to properly capture a relatively dense sampling at the lowest energies, scaled MVN distributions were included as well. A total of 1000 geometries were generated from scaled covariance matrices and added to the training data: 500 each for fcc and hcp, both with MVN 1% scaling. To ensure that a sufficient number of repulsive configurations were included in the surrogate model, 3036 geometries were distributed over the whole constrained volume, 2024 of them being generated according to a 6-dimensional Sobol sequence, and the remaining 1012 generated randomly. Finally, we removed all geometries with z > 3.0 Å, leading to a total number of N = 8861 training points.
In theory, some of the training data could be degenerate, owing to the three-fold symmetry of methyl, and this degeneracy could be utilized in the generation of training data. In the present work, however, external symmetry was not considered. ADTHERM and the MPNN procedure are designed for arbitrary adsorbates, irrespective of symmetry. Future versions of the software may utilize symmetry.
2.3 Surrogate potential energy surface
We denote the input feature vector as x = (x,y,z,α,β,γ). Given a set of training input configurations and their corresponding energy evaluations {x(j),V(x(j))} for j = 1,…,N, we approximate V(x) as a neural network of a special form that preserves the minima information. Specifically, we employ the minima-preserving NN (MPNN) surrogate form described in ref. 16, 17 and implemented in a python-based library.31 The MPNN surrogate is a weighted linear combination of multiple surrogates of form | (1) |
We trained the NN function NN(·) within the PyTorch framework, after transforming the input-output training data according to eqn (1). The neural network surrogate was trained using a standard multilayer perceptron architecture, with 3 hidden layers, 111 neurons in each layer, and sigmoid activation functions. The training employed the Adam optimization method, with 5000 epochs, batch size of 2000 and a learning rate of 0.01. We also separated 10% of the training data as a validation set to check the overall minimization objective during training, and selected the NN with the smallest validation error as the final result.
2.4 Importance sampling
In order to compute the thermodynamic quantities, phase space integration needs to evaluate the following integrals: | (2) |
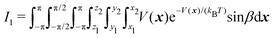 | (3) |
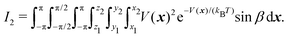 | (4) |
As detailed in ref. 16 the entropy is proportional to the logarithm of I0 and to the ratio I1/I0, the latter being related to the enthalpy increment, while the ratio I2/I0 is required for the heat capacity. Note that all the integrals are of the form
 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β, and V(x)2sin
β, and V(x)2sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β, respectively. In ref. 16 and 17 we computed these integrals via conventional Monte Carlo integration:
β, respectively. In ref. 16 and 17 we computed these integrals via conventional Monte Carlo integration: | (6) |
In this work we consider an alternative approach to conventional MC that is more efficient, i.e. achieves higher accuracy of integration with fewer integrand evaluations. Namely, we use an importance sampling integration scheme where the integral in eqn (5) is computed via weighted summation as
 | (7) |
Unlike conventional MC from eqn (6), here the integration sample set {xm}Mm=1 is sampled according to a pre-defined probability density function (PDF) p(x).32 The efficiency of the importance sampling estimator, eqn (7), depends on a choice of the PDF p(x), which ideally should be as close to e−V(xm)/(kBT) as possible, up to a constant factor. For example, in an idealized scenario where p(x) coincides with e−V(x)/(kBT), the integration scheme becomes a simple averaging of the function f(x).
However, sampling from p(x) ∼ e−V(x)/(kBT) is challenging, hence we rely on Gaussian mixtures as p(x) to enable sampling while sharing minima and curvature information with e−V(x)/(kBT). Indeed, the shape of the potential surface (or its MPNN surrogate) V(xm) is dominated by the quadratic approximation anchored at each of the minima locations, hence an efficient p(x) choice is a Gaussian (in case of one minimum) or a Gaussian mixture model (GMM, in case of multiple minima), truncated to the domain Ω = [−π,π] × [−π/2,π/2] × [−π,π] × [z1,z2] × [y1,y2] × [x1,x2]. We refer to such truncated Gaussian mixture model integration scheme as GMMT.
2.5 Direct state counting
Direct state counting of the six external degrees of freedom (x,y,z,α,β,γ) for the motion of CH3* relative to the nickel surface were used to obtain a reference set of thermodynamic functions using a discrete variable representation (DVR) method. Dense eigensolves were carried out using the open-source DVR package33 that implements the universal DVR approach originally proposed by Colbert and Miller.34 In order to attain sufficiently converged densities of states for all degrees of freedom, separate treatment of some degrees of freedom was required, as was done previously.16,17 The direct count of eigenstates from 2D scans of x, y translation along the surface, as well as 1D translation away from the surface in z, was solved via DVR basis functions that corresponded to Cartesian basis functions in these coordinates. The CH3* x, y surface was calculated on a rectangular grid of 238 × 185 grid points spanning 2.786 Å in x and 2.413 Å in y by using the surrogate. The z, α, β, and γ coordinates were relaxed on the x, y surface. The libration of the adsorbate was also treated using DVR, with each rotational degree of freedom examined separately while the other degrees of freedom were relaxed, as was done previously.17 The product of the resulting xy, α, β, γ, and z states was used via state counting to compute the relevant contributions to the desired quantum mechanical thermodynamic functions.353 Results and discussion
3.1 MPNN surrogate construction
Fig. 1 demonstrates the quality of the approximation of the exponential e−V(x)/kT resulting from the surrogate approximation V(x) ≈ Vs(x), for varying values of temperature T. We reported relative root-mean-squared error (rRMSE) for the full training set, defined as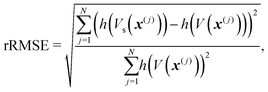 | (8) |
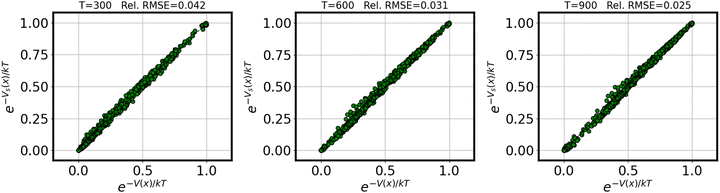 | ||
| Fig. 1 Parity plot demonstrating the surrogate quality across temperatures for the exponential functional e−V(x)/kT. | ||
These results suggest that 8000 training samples are sufficient to converge the partition function to within ±5% over a useful range of temperatures (indeed, in many cases fewer samples would likely be entirely adequate).
3.2 Integration via GMMT importance sampling
The GMMT importance sampling weight PDF is a truncated Gaussian mixture model and has the form: | (9) |
 | (10) |
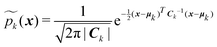 | (11) |
The GMM weights wk 's are selected according to
 | (12) |
This approach ensures  and that the weight function p(x) has consistent weighting of mixture elements with the underlying integrand e−V(x)/kBT. The extra volume factor
and that the weight function p(x) has consistent weighting of mixture elements with the underlying integrand e−V(x)/kBT. The extra volume factor 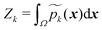 captures the truncation effect and is analytically available.36 We select the mean μk that matches the k-th minimum location and covariance which is a factor away from the corresponding inverse Hessian Ck = rkBTHk−1(x).
captures the truncation effect and is analytically available.36 We select the mean μk that matches the k-th minimum location and covariance which is a factor away from the corresponding inverse Hessian Ck = rkBTHk−1(x).
The latter expression ensures that the behavior of the weight function p(x) mimics that of the integrand e−V(x)/kBT. The selection of this factor r has an impact on the effectiveness of importance sampling. If r is selected to be very small, then the weight function will become a mixture of narrow Gaussians. These narrow Gaussians will force all samples to be taken from smaller neighborhoods near the minima, missing out on potentially significant points further away from minima. The result would be that the integration will converge more quickly, but to a biased value. Conversely, if r is chosen to be very large, then the weight function will be closer to a uniform distribution, so the integration would perform similarly to MC integration. To determine the best value of r for this system, the convergence of I0 was tested with different covariance factors and across a variety of temperatures. The results are plotted in Fig. 3 below:
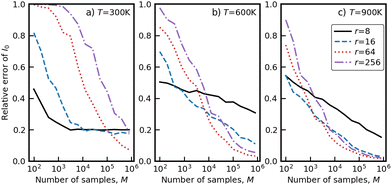 | ||
| Fig. 3 Integral I0 as a function of the number of integration samples, M, for different temperatures T and covariance factors r. | ||
As seen for all three temperatures in Fig. 3, for low values of r, the integral I0 converges quickly but to the wrong value, whereas for high values of r, the integral converges to the correct value, but the convergence is slow and unstable. The intermediate value of r = 64 strikes a balance between the rate of convergence and stability, and was used in all subsequent integration.
3.3 Comparison with Monte Carlo integration and convergence of GMMT
Whereas our prior work relied on conventional MC sampling, importance sampling should offer improved performance both in terms of sampling efficiency and in terms of convergence. Conventional MC integration runs the risk of underestimating the integrals in low-temperature regimes, particularly for a low number of integration samples, since the integrands have sharp peaks, and MC samples do not resolve these peaks sufficiently well.
Fig. 4 compares the two methods directly at three different temperatures (columns) for each of the three integrals (rows). In lieu of the exact value, we report the relative error with respect to the highest, M = 107 solution, i.e. . The GMMT results at M = 107 were used in both cases as the reference. As can be seen, the GMMT results converge more quickly. For example, a relative convergence to within 10% at 300 K requires approximately M = 5 × 105 samples using GMMT, but MC requires nearly two orders of magnitude more samples to obtain the same convergence. Higher temperatures require fewer samples in both cases. Overall, the GMMT estimator is more robust, and it possesses both reduced bias and variance compared to MC integration.
. The GMMT results at M = 107 were used in both cases as the reference. As can be seen, the GMMT results converge more quickly. For example, a relative convergence to within 10% at 300 K requires approximately M = 5 × 105 samples using GMMT, but MC requires nearly two orders of magnitude more samples to obtain the same convergence. Higher temperatures require fewer samples in both cases. Overall, the GMMT estimator is more robust, and it possesses both reduced bias and variance compared to MC integration.
Fig. 4 further demonstrates the convergence of GMMT integration as the number of training samples, M, increases, for the three integrals needed to compute the thermophysical properties. Given that the surrogate PES required nearly 9000 samples, we can conclude that performing the phase space integration with a direct DFT approach, particularly one that uses fewer single-point calculations, would have resulted in a relative error ≈25% at 300 K for all three integrals. Accordingly, we do not recommend direct DFT sampling for the evaluation of phase space integrals, even when a well-tuned importance sampling procedure is used.
3.4 CH3/Ni(111) thermophysical properties
The Monte Carlo amd GMMT configuration space integration (both using the MPNN surrogate PES) were performed at 21 evenly spaced temperature values between 290–1030 K. The results of the two PSI methods are shown in Fig. 5. The conventional MC sampling are the solid red line, and the GMMT approach are the blue triangles. The benchmark DVR results are the black stars. Also included in Fig. 5 are the common analytical models for the two limiting cases, harmonic oscillator (black dash-dot line) and free translator (cyan dashed line), as well as the hindered translator and hindered translator/rotor models of Sprowl et al.4 (yellow and magenta dotted lines, respectively). In order to allow direct comparison, the free-translator model is confined to the same unit cell area as the PSI model. Both the MC and GMMT PSI models are in excellent agreement with the DVR results.A useful measure of the anharmonicity is the ratio of the PSI (or DVR) partition function to the harmonic oscillator partition function, or the anharmonic correction factor, fPSI = qPSI/qHO. For CH3/Ni(111), the anharmonic correction factor increases from a nominal value of fPSI ≈ 1 at 300 K to fPSI≈6 at 1000 K. The DVR results are quantitatively similar, apart from a constant offset of fDVR ≈ fPSI + 0.5 (see ESI† for details). As detailed below, this offset does not translate to a meaningful difference in thermophysical properties.
The Helmholtz free energy, F = –kBTln(q), entropy S/R; enthalpy increment, [H(T)−H(0)]/RT; and isobaric heat capacity, Cp/R, were derived from the partition function. In our approach, the six transitional (“external”) degrees of freedom (x,y,z,α,β,γ) are assumed to be coupled and anharmonic, but they are still separated from the 6 “internal” degrees of freedom of CH3* (i.e. those resulting in C–H stretches, HCH bending modes, etc). Those degrees of freedom would be treated the same in all the models represented in Fig. 5 (e.g. as harmonic oscillators). Accordingly, only the contributions of the six transitional degrees of freedom are represented in Fig. 6. Notably, for all thermophysical properties, the PSI method is in excellent agreement with the DVR benchmark.
Although confirming or validating the interesting saddle point observed by Henkelman et al.18 was not the aim of this work, our results are consistent with their observation that the motion of methyl relative to the Ni(111) surface is indeed quite labile. This high degree of mobility contributes significantly to the entropy of the adsorbate, and the entropy of CH3* is considerably larger than that predicted by the harmonic oscillator model.
The heat capacity shows a maximum value between 400 and 600 K for the PSI and state counting from DVR state solutions, which is a consequence of anharmonic effects. Namely, the harmonic oscillator eigenstates are an infinite equidistant set, causing the heat capacity to rise monotonically with temperature and approach asymptotically a fixed value of 1R for each degree of freedom. However, for a finite set of bound states, such as those encountered in a typical anharmonic oscillator, the function will change depending on the density of states. In an anharmonic oscillator, where there is initially a higher density of states in a given region than predicted by the harmonic model, the result is an initial increase in heat capacity exceeding the value predicted by the harmonic oscillator model, but at higher temperatures the attained value begins to decline and eventually approaches zero when all bound eigenstates become equally saturated.35,37
The results in Fig. 6 only include the six degrees of freedom for the motion of the adsorbate relative to the surface, since the phase space integration approach does not consider the anharmonicity of internal modes. Our current assumption is that those six internal modes are still reasonably well described by the harmonic oscillator model, at least for the temperatures considered relevant for catalysis. The CH3* umbrella mode is arguably the most likely to exhibit some degree of anharmonicity, but explicit consideration of that mode is beyond the scope of this work.
It is useful to consider how analogous results would compare for methyl adsorbed on different metals. Broadly speaking, the weaker the binding energy (i.e. less negative), the greater the contribution of anharmonicity to the total partition function. If we compare the binding energy for CH3* on Ni(111) versus Pt(111),38–40 we see methyl binds more strongly to Ni(111) than to Pt(111) (by roughly −17 kJ mol−1 at 0 K). We would therefore expect that CH3/Pt(111) would be slightly more anharmonic than CH3/Ni(111) (e.g. CH3/Pt(111) would exhibit greater entropy at a given temperature). As we move from Ni(111) and Pt(111) to Cu(111) and Ag(111), the binding energy of CH3* progressively weakens.41,42 We would expect, therefore, that 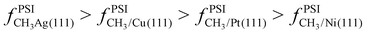 . We plan to test this hypothesis in a subsequent manuscript.
. We plan to test this hypothesis in a subsequent manuscript.
3.5 Dissociative adsorption of methane on nickel
Finally, to give a broader context to the implications of these results, we discuss the impact of anharmonicity on the equilibrium constant for the dissociative adsorption of methane, CH4(g) + 2* ⇌ CH3* + H*. Fig. 7 presents the equilibrium constant, as computed from the partition functions: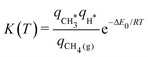 | (13) |
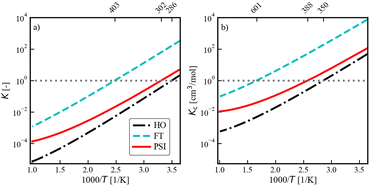 | ||
| Fig. 7 van't Hoff Plot for the dissociative adsorption of CH4 on Ni(111). (a) is the equilibrium constant, and (b) is the equilibrium constant in concentration units, obtained via(14). | ||
The partition function for methane, qCH4(g), was computed using the standard rigid-rotor harmonic-oscillator model; the geometry optimization and normal mode analysis were performed using CCSD(T)/cc-pVTZ, as detailed above. The partition function for adsorbed methyl,  , was taken from the results in the previous section. For the hydrogen adatom,
, was taken from the results in the previous section. For the hydrogen adatom,  , we performed the geometry optimization and normal mode analysis for H/Ni(111) using the same electronic structure method as for CH3/Ni(111). However, we did not perform new phase space integration results for H/Ni(111). Instead, as an approximation, we scaled our new harmonic oscillator results,
, we performed the geometry optimization and normal mode analysis for H/Ni(111) using the same electronic structure method as for CH3/Ni(111). However, we did not perform new phase space integration results for H/Ni(111). Instead, as an approximation, we scaled our new harmonic oscillator results, 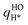 , by the same anharmonic correction factor we obtained for H/Cu(111), fPSIH/Cu(111), in ref. 16 In ref. 16 the anharmonic correction factor ranged from fPSIH/Cu(111) ≈ 2.5 at 300 K to fPSIH/Cu(111) ≈ 3.5 at 1000 K, and the PSI results suggested that even tightly bound H/Cu(111) has entropy that is closer to that of a free translator than that of a harmonic oscillator.
, by the same anharmonic correction factor we obtained for H/Cu(111), fPSIH/Cu(111), in ref. 16 In ref. 16 the anharmonic correction factor ranged from fPSIH/Cu(111) ≈ 2.5 at 300 K to fPSIH/Cu(111) ≈ 3.5 at 1000 K, and the PSI results suggested that even tightly bound H/Cu(111) has entropy that is closer to that of a free translator than that of a harmonic oscillator.
The ΔE0 in eqn (13) is the difference in zero-point corrected electronic energy between the adsorbates and the gas-phase methane. Although the purpose of the present work is not to provide the most accurate value for the equilibrium constant, we would prefer, nonetheless, to do better than using the raw DFT values from the binding energies. Instead, we used experimentally derived enthalpies of formation at  . The enthalpy of formation for methane,
. The enthalpy of formation for methane,  , was taken from the ATcT database.43,44 For the two adsorbed species, we started with published enthalpies of formation at 298.15 K:
, was taken from the ATcT database.43,44 For the two adsorbed species, we started with published enthalpies of formation at 298.15 K:  = −46.5 kJ mol−1 and
= −46.5 kJ mol−1 and  , both of which were obtained from calorimetery experiments by Campbell and coworkers from ref. 45 and 40 respectively. These values were then corrected from 298 K to 0 K using the DFT frequencies, as described in ref. 39 The corrected results were
, both of which were obtained from calorimetery experiments by Campbell and coworkers from ref. 45 and 40 respectively. These values were then corrected from 298 K to 0 K using the DFT frequencies, as described in ref. 39 The corrected results were  and
and  , for a final value of ΔE0 = −173.2 kJ mol−1.
, for a final value of ΔE0 = −173.2 kJ mol−1.
Fig. 7b presents the concentration equilibrium constant:
 | (14) |
The results in Fig. 7 demonstrate that adsorbate anharmonicity can have a quantifiable impact on reaction thermochemistry, even at lower temperatures. The phase space integration results (solid red line) are larger than the harmonic oscillator results (dash-dot black line) for all temperatures, which implies that the increase in adsorbate entropy results in higher coverages at equilibrium for a fixed temperature. If we consider the ratio of the phase space integration result to the more conventional harmonic oscillator model (i.e. normalize the solid red line by the dash-dot black line in Fig. 7), this ratio is equivalent to product of the anharmonic correction factors for the adsorbates: 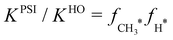 . Accordingly, the impact of anharmonicity on the equilibrium constant increases from approximately a factor of 3 at 300 K, to a factor of 8 at 600 K, and to a factor of 16 at 900 K. Although the spread between the phase space integration results and the harmonic model increases with increasing temperature, the PSI model still does not reach the free translator limit (at least not at any temperature that would be of relevance for heterogeneous catalysis). It is worth re-emphasizing that the two adsorbates in question, CH3* and H* are typically thought of as tightly bound and thus suitable candidates for the harmonic oscillator approximation, yet the present work suggests that this approximation could lead to an error of roughly an order of magnitude at industrially relevant temperatures. We expect similar results to be true for equilibrium constants for other adsorption reactions.
. Accordingly, the impact of anharmonicity on the equilibrium constant increases from approximately a factor of 3 at 300 K, to a factor of 8 at 600 K, and to a factor of 16 at 900 K. Although the spread between the phase space integration results and the harmonic model increases with increasing temperature, the PSI model still does not reach the free translator limit (at least not at any temperature that would be of relevance for heterogeneous catalysis). It is worth re-emphasizing that the two adsorbates in question, CH3* and H* are typically thought of as tightly bound and thus suitable candidates for the harmonic oscillator approximation, yet the present work suggests that this approximation could lead to an error of roughly an order of magnitude at industrially relevant temperatures. We expect similar results to be true for equilibrium constants for other adsorption reactions.
4 Conclusions
Importance sampling is explored as an alternative to “naïve” Monte Carlo sampling in computing the phase space integrals for adsorbates on metals. The new sampling procedure is significantly more efficient than the conventional Monte Carlo implementation. The thermophysical properties of CH3* on Ni(111) are investigated. It was found that the motion of methyl relative to the nickel terrace is anharmonic, despite the fact that it is typically considered to be strongly bound. This improved sampling procedure is now part of the open-source ADTHERM package.46 The calculations were performed in the low-coverage limit, but anharmonic, coverage-dependent partition functions are underway.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to thank Prof. Hannes Jónsson and Dr. Bjarne Kreitz for helpful suggestions. This work was done within the Exascale Catalytic Chemistry (ECC) Project, which is supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Chemical Sciences, Geosciences and Biosciences Division, as part of the Computational Chemistry Sciences Program (KBl, KS, DHB, KBa, CFG). BR was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Chemical Sciences, Geosciences and Biosciences Division, as part of the Gas-Phase Chemical Physics Program. KBl, KBa, and CFG acknowledge support from DOE BES award number No. 0000232253; DHB and BR acknowledge support from Contract No. DE-AC02-06CH11357 (ANL); KS acknowledges support from Contract No. DE-NA0003525 (SNL). Sandia National Laboratories is a multimission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC., a wholly owned subsidiary of Honeywell International, Inc., for the U.S. Department of Energys National Nuclear Security Administration. This research used resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357. The Active Thermochemical Tables (ATcT) are a U.S. Department of Energy Office of Science Public Reusable Research (DOE SC PuRe) Data Resource.47References
- G. Collinge, S. F. Yuk, M.-T. Nguyen, M.-S. Lee, V.-A. Glezakou and R. Rousseau, ACS Catal., 2020, 10, 9236–9260 CrossRef CAS.
- J. Amsler, P. N. Plessow, F. Studt and T. Bučko, J. Chem. Theory Comput., 2021, 17, 1155–1169 CrossRef CAS PubMed.
- G. Piccini and J. Sauer, J. Chem. Theory Comput., 2014, 10, 2479–2487 CrossRef CAS PubMed.
- L. H. Sprowl, C. T. Campbell and L. Árnadottir, J. Phys. Chem. C, 2016, 120, 9719–9731 CrossRef CAS.
- M. Jørgensen and H. Grönbeck, J. Phys. Chem. C, 2017, 121, 7199–7207 CrossRef.
- Z. Zhang, X. Liu, Z. Chen, H. Zheng, K. Yan and J. Liu, J. Chem. Phys., 2017, 147, 034109 CrossRef PubMed.
- M. Jørgensen, L. Chen and H. Grönbeck, J. Phys. Chem. C, 2018, 122, 20351–20357 CrossRef.
- A. H. Bajpai, P. Mehta, K. Frey, A. M. Lehmer and W. F. Schneider, ACS Catal., 2018, 8, 1945–1954 CrossRef CAS.
- Z. Zhang, X. Liu, K. Yan, M. E. Tuckerman and J. Liu, J. Phys. Chem. A, 2019, 123, 6056–6079 CrossRef CAS PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- C. Waitt, A. R. Miles and W. F. Schneider, J. Phys. Chem. C, 2021, 125, 20331–20342 CrossRef CAS.
- M. Rybicki and J. Sauer, J. Chem. Theory Comput., 2022, 18, 5618–5635 CrossRef CAS PubMed.
- K. De Wispelaere, P. N. Plessow and F. Studt, ACS Phys. Chem. Au, 2022, 2, 399–406 CrossRef CAS PubMed.
- B. X. Shi, A. Zen, V. Kapil, P. R. Nagy, A. Grüneis and A. Michaelides, J. Am. Chem. Soc., 2023, 145, 25372–25381 CrossRef CAS PubMed.
- K. Blöndal, K. Sargsyan, D. H. Bross, B. Ruscic and C. F. Goldsmith, J. Phys. Chem. C, 2021, 125, 20249–20260 CrossRef.
- K. Blöndal, K. Sargsyan, D. Bross, B. Ruscic and C. F. Goldsmith, ACS Catal., 2023, 13, 19–32 CrossRef.
- G. Henkelman, A. Arnaldsson and H. Jónsson, J. Chem. Phys., 2006, 124, 044706 CrossRef PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens.Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, P. Delugas, R. A. DiStasio Jr., A. Ferreti, A. Floris, G. Fratesi, G. Fugalio, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Tronhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- Quantum ESPRESSO, https://www.quantum-espresso.org/, Accessed: 2022-27-01.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- B. M. Axilrod and E. Teller, J. Chem. Phys., 1943, 11, 299 CrossRef CAS.
- Y. Muto, Proc. Phys.-Math. Soc. Jpn., 1943, 17, 629 CAS.
- A. D. Corso, Comput. Mater. Sci., 2014, 95, 337–350 CrossRef.
- pslibrary by A. Dal Corso, 2013, https://dalcorso.github.io/pslibrary/, We used the pseudopotentials Pt.pbe-n-kjpaw_psl.1.0.0.UPF, C.pbe-n-kjpaw_psl.1.0.0.UPF, O.pbe-nl-kjpaw_psl.1.0.0.UPF, H.pbe-kjpaw_psl.1.0.0.UPF and Cu.pbe-dn-kjpaw_psl.1.0.0.UPF, accessed: 2019-08-01.
- N. Marzari, D. Vanderbilt, A. De Vita and M. C. Payne, Phys. Rev. Lett., 1999, 82, 3296 CrossRef CAS.
- S. R. Bahn and W. K. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Gia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2022. 1 a package of ab initio programs 2022 Search PubMed.
- Minima-preserving neural network construction library by K. Sargsyan, https://github.com/sandialabs/MPNN, Accessed: 2022-08-24.
- M. F. Bugallo, V. Elvira, L. Martino, D. Luengo, J. Miguez and P. M. Djuric, IEEE Signal Process. Mag., 2017, 34, 60–79 Search PubMed.
- Multidimensional DVR program to generate and solve 1D and 2D potentials, a program by D. Bross, https://github.com/Dbross/CM_DVR, Accessed: 2022-07-08.
- W. H. Colbert and D. T. Miller, J. Chem. Phys., 1992, 96, 1982–1991 CrossRef.
- B. Ruscic and D. H. Bross, Comput.-Aided Chem. Eng., 2019, 45, 3–114 CAS.
- R. Kan and C. Robotti, J. Comput. Graph. Stat., 2017, 26, 930–934 CrossRef.
- B. Ruscic and D. H. Bross, Mol. Phys., 2021, 119, e1969046 CrossRef.
- E. M. Karp, T. L. Silbaugh and C. T. Campbell, J. Am. Chem. Soc., 2013, 135, 5208–5211 CrossRef CAS PubMed.
- B. Kreitz, K. Abeywardane and C. F. Goldsmith, J. Chem. Theory Comput., 2023, 19, 4149–4162 CrossRef CAS PubMed.
- S. J. Carey, W. Zhao, A. Frehner, C. T. Campbell and B. Jackson, ACS Catal., 2017, 7, 1286–1294 CrossRef CAS.
- G.-C. Wang, J. Li, X.-F. Xu, R.-F. Li and J. Nakamura, J. Comput. Chem., 2005, 26, 871–878 CrossRef CAS PubMed.
- F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 016105 CrossRef CAS PubMed.
- B. Ruscic, R. E. Pinzon, M. L. Morton, G. von Laszevski, S. J. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, J. Phys. Chem. A, 2004, 108, 9979–9997 CrossRef CAS.
- B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) Values Based on ver. 1.130 of the Thermochemical Network, https://atct.anl.gov, (accessed 2023-11-30).
- T. L. Silbaugh and C. T. Campbell, J. Chem. Phys., 2016, 120, 25161–25172 CAS.
- AdTherm, https://github.com/franklingoldsmith/adtherm, v. 0.2, accessed: 2022-09-22.
- PuRe Data Resources at a Glance, https://science.osti.gov/Initiatives/PuRe-Data/Resources-at-a-Glance, accessed: 2024-01-31.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01197j |
| ‡ These authors contributed equally. |
| This journal is © the Owner Societies 2024 |




