The SCAN+U method in the investigation of complex transition metal oxides: a case study on YSr₂Cu₂FeO_7+δ (δ = 0, 1)

Abstract

Assessment of DFT methods is essential to sustain reliability in the computational investigation of complex transition metal oxides. This work evaluates the performance of the strongly constrained and appropriately normed (SCAN) functional and its extended Hubbard-U methodology (SCAN+U) to model the YSr₂Cu₂FeO_7+δ (0 < δ < 1) perovskite-based system. The influence of the individual U_Cu and U_Fe Hubbard parameters (0 < U < 4 eV) on the calculated electronic, magnetic and crystal structures of the end members δ = 1 (metallic) and δ = 0 (insulating) is analyzed. The introduction of the U-correction terms enhances the reproduction of the crystal structures, with a U_Cu value of 1 eV improving the band gap accuracy for the YSr₂Cu₂FeO₇ phase, while maintaining the metallic characteristics of YSr₂Cu₂FeO₈. At a fixed U_Cu value, the results are almost insensitive to the U_Fe value used in the calculations. The findings emphasize that for oxides containing several TM ions, the optimal U_TM values may differ from those of the simple TM oxides.

---

Introduction

Transition metal (TM) oxides are one of the most interesting classes of solids, exhibiting excellent properties and applications in a wide variety of fields. Methods based on density functional theory (DFT) play a central role in designing advanced functional oxides. They enable the identification of promising materials through property prediction and facilitate the understanding of the underlying structure–composition–property relationships. A current challenge is selecting a DFT methodology capable of modelling complex TM oxides with strongly interacting d-electrons. The GGA + U method has been extensively used in the last few decades; to the GGA exchange–correlation functional, a TM-specific Hubbard U parameter is added describing the on-site Coulomb interaction between localized electrons. However, progress in the modelling of correlated TM oxides requires testing and evaluating advanced exchange–correlation functionals.

The recently developed strongly constrained and appropriately normed (SCAN) meta-GGA functional¹ has demonstrated a superior performance in reproducing the fundamental physical properties and phenomena associated with correlated oxides.^2–8 Furthermore, studies have shown that incorporating the SCAN functional into the DFT+U framework (SCAN+U) can enhance the accuracy in reproducing certain physical properties of transition metal oxides.^9–13 For example, Carter and coworkers demonstrated that the introduction of the Hubbard term improves the reproduction of the ground-state properties of binary 3d TM oxides, being critical for the prediction of the most stable polymorphs of Mn₂O₃ and Fe₃O₄.^9,10 The SCAN+U method has also been used to evaluate the formation energy of anion vacancies, which are highly involved in properties related to energy applications, of ABO₃ perovskites with various A and B (TM) elements and diverse electronic structures.¹¹ For BiFeO₃ polymorphs, the effect of Fe-site doping on the phase stability, as well as on the structural and ferroelectric properties, has been assessed.¹² For oxides containing two TM ions, double Nb-perovskites (Sr₂SmNbO₆, Sr₂CoNbO₆ and Ba₂CoNbO₆) have been investigated,¹⁴ although the authors dropped the treatment of correlation in Nb to simplify the analysis.

Assessing the performance of the SCAN+U method in modelling complex transition metal oxides represents a crucial step forward in the predictive design of functional oxides, especially defying for oxides containing different TM ions. This study focuses on the SCAN+U method in the investigation of complex oxides YSr₂Cu₂FeO_7+δ, for which the SCAN functional correctly captures the metal-to-insulating transition as a function of the oxygen content.⁸ The perovskite-related crystal structure of the YSr₂Cu₂FeO_7+δ system (Fig. 1) can be referred to the YBaCuO-type structure with the replacement of one layer of Cu atoms with Fe.^15,16 The YSr₂Cu₂FeO₈ (δ = 1) idealized compound, with [FeO₆] octahedral units in the FeO₂ layers (Fig. 1a), is a metallic oxide with a superconducting transition at a T_c of 70 K.¹⁷ Lowering the oxygen content creates vacancies in the O3 positions of the FeO_1+δ layer, which leads to a tetrahedral coordination for all Fe atoms in the idealized YSr₂Cu₂FeO₇ (δ = 0) compound (Fig. 1b). The synthetized compounds with δ ∼ 0 are insulators with mainly Fe³⁺ and Cu²⁺ ions.^8,16,18,19

Fig. 1 Crystal structures of the idealized models of YSr₂Cu₂FeO_7+δ stoichiometric oxides: (a) YSr₂Cu₂FeO₈ (S.G. P4/mmm) and (b) YSr₂Cu₂FeO₇ (S.G. Ima2). Color code: Fe in brown, Cu in blue, Sr in green, Y in grey and O in red.

The combination of Cu and Fe ions in different oxidations states, and the evolution of the electronic properties of the YSr₂Cu₂FeO_7+δ series, provides an excellent framework to examine the applicability of the SCAN+U approach in the DFT investigation of complex oxides. This study delves into the effects of U_Cu and U_Fe correction terms on the crystallographic, magnetic and electronic structures of the idealized end-members of YSr₂Cu₂FeO_7+δ (δ = 0 and 1). By conducting calculations with individual U terms ranging from 0 to 4 eV, we determine and discuss the appropriate set of U values for accurately describing the system. A relevant question arises regarding the transferability of U_TM parameters from simple oxides to their combinations in complex TM oxides. We will demonstrate that such transferability cannot be guaranteed.

Methodology

Calculations for the ideal stoichiometric end-members of the YSr₂Cu₂FeO_7+δ family, YSr₂Cu₂FeO₈ and YSr₂Cu₂FeO₇, have been performed using the ab initio total energy and molecular dynamics program VASP (Vienna Ab initio Simulation Package) developed at the Universität Wien.^20,21 The interaction of core electrons with the nuclei is described using the projector augmented wave (PAW) method²² with 2s²2p⁴ of O, 3s²3p⁶3d⁷4s¹ of Fe, 3p⁶3d¹⁰4p¹ of Cu, 4s²4p⁶5s² of Sr, and 4s²4p⁶4d¹5s² of Y being treated as valence electrons. The energy cut-off for the plane wave basis set was fixed at a constant value of 600 eV throughout the calculations. The integration in the Brillouin zone was done on appropriate k-point sets determined by the Monkhorst–Pack scheme. The k-point meshes were set at 2 × 8 × 8 for YSr₂Cu₂FeO₇ and 10 × 10 × 4 for YSr₂Cu₂FeO₈, using a Gaussian smearing parameter of 0.05 eV. For the density of states (DOS) calculations, the tetrahedron method with Bloch corrections²³ was used. Self-consistency was achieved with a tolerance in total energy of 1 × 10⁻⁴ eV for geometry optimization and 1 × 10⁻⁶ eV for DOS calculations.

A local Hubbard-U (SCAN+U) was added to Fe and Cu atoms, following the simplified rotationally invariant framework developed by Dudarev et al.²⁴ Typically, U is formulated as U_eff = U − J, where U is the onsite Coulomb term and J is the exchange term. In this work, this effective parameter is simply referred as U. The J value was fixed to 1 eV. Effective U values between 0 and 4 eV were used for the 3d orbitals of Cu and Fe. It should be noted that a value of 4 eV for Fe and Cu was found appropriate in GGA + U investigations.^25–27 The local magnetic moments were taken from the difference between the projected electron density of up and down spins onto a 1 Å ionic radius sphere. Bader charge analysis²⁸ was performed on the charge density files²⁹ using the pymatgen package.³⁰

The crystallographic models of YSr₂Cu₂FeO₈ and YSr₂Cu₂FeO₇ were, respectively, constructed taking the initial positions from YSr₂Cu₂FeO_7.86 (ICSD file 11514)¹⁷ and YSr₂Cu₂GaO₇ (ICSD file 71263).³¹ For the metallic YSr₂Cu₂FeO_7.86, López et al.¹⁷ found a magnetic structure consisting of in-plane FM coupling within the FeO_1+δ layers and a weak AFM coupling between layers along the c-axis (A-type AFM ordering). Due to the soft character of the inter-plane magnetic interactions (T_N ∼ 20 K³²), subsequent DFT calculations utilized a ferromagnetic (FM) structure to model the idealized YSr₂Cu₂FeO₈,⁸ which is also employed in the present study. Investigation of the idealized YSr₂Cu₂FeO₇ is carried out in the antiferromagnetic ground state (C-type AFM) and the metastable ferromagnetic structure (FM). Additional SCAN+U calculations have been conducted with the maximum U values tested (U_Cu = U_Fe = 4 eV) using the A-type AFM magnetic ordering for YSr₂Cu₂FeO_7+δ with δ = 0 and 1. More details of magnetic structures are given in ref. 8.

Results

The experimental lattice parameters and bond distances of YSr₂Cu₂FeO_7+δ (δ = 0,1) crystal structures are reproduced well using both SCAN and SCAN+U methods, with errors below 3%. For conciseness, Table 1 lists only the values for SCAN+U with the highest U values tested, 4 eV for Fe and Cu. Noteworthily, introducing the U correction term reduces the discrepancies between the theory and experimental structural data. For instance, within the SCAN+U approach, the calculated unit cell volumes (errors of 0.9% and 0.7% for YSr₂Cu₂FeO₈ and YSr₂Cu₂FeO₇, respectively) are closer to the experimental values than those within the SCAN approach (errors of 2% and 1.2% for YSr₂Cu₂FeO₈ and YSr₂Cu₂FeO₇, respectively). Since the Cu-3d states play a critical role in the metal-to-insulating transition in high-Tc cuprate superconductors,³³ the Cu–O distances are analyzed in detail. Fig. 2 shows the calculated Cu–O1 (apical oxygen) and Cu–O2 (equatorial oxygen) distances as a function of the U_Cu and U_Fe values. The results show that, for both YSr₂Cu₂FeO₈ and YSr₂Cu₂FeO₇, increasing U_Cu results in a better agreement with the experimental available values. It can be seen in Fig. 2a that, for the metallic phase YSr₂Cu₂FeO₈, at a fixed U_Cu, applying U_Fe produces a decrease in d Cu-O1 (a maximum variation of 4% for U_Cu = 0) and a subtle increase in d Cu–O2 (a maximum variation of 0.7% at U_Cu = 0). On the other hand, for the C-type AFM-YSr₂Cu₂FeO₇, the Cu–O distance depends mostly on U_Cu. Hence, at a fixed U_Cu, changing U_Fe has little to no effect on the Cu–O bonding distances.

Table 1 Calculated unit cell parameters (Å), unit cell volumes (ų), volume per atom (ų) and selected bond lengths (Å) for the YSr₂Cu₂FeO₇ and YSr₂Cu₂FeO₈ idealized oxides. The experimental data of YSr₂Cu₂FeO_7.86 (ICSD-11514¹⁷) and YSr₂Cu₂FeO_7.12 (ICSD-151654¹⁹) are included for comparison. Within the SCAN+U method U = 4 eV is used for Cu and Fe

YSr2FeCu2O8	Experimental	SCAN	SCAN+U	YSr2FeCu2O7	Experimental	SCAN AFM-C	SCAN+U AFM-C	SCAN FM	SCAN+U FM
a	3.8145(3)	3.7861	3.7989	a	22.9241(8)	22.8529	22.8568	22.9157	22.8640
c	11.327(7)	11.2755	11.3116	b	5.4584(2)	5.4411	5.4536	5.4365	5.4646
V	164.81(1)	161.62	163.26	c	5.4080(2)	5.3744	5.3893	5.3608	5.3956
V per atom	11.77	11.54	11.66	V	676.70	668.22	671.79	675.96	674.14
d Fe–O3	1.9072(2)	1.8930	1.8994	V per atom	12.89	12.85	12.91	13.00	12.96
d Fe–O1	1.8434(4)	1.8417	1.8591	Mean d Fe–O	1.8757	1.8732	1.8888	1.8880	1.8987
d Fe–O1/d Fe–O3	0.9663	0.9729	0.9788	Fe–O3–Fe	125.5°	124.5°	123.2°	120.1°	121.0°
d Cu–O2	1.9244(4)	1.9147	1.9232	Mean d Cu–O2	1.9335	1.9237	1.9368	1.9207	1.9366
d Cu–O1	2.117(4)	2.0812	2.0738	d Cu–O1	2.312(4)	2.3449	2.3210	2.3600	2.3071
d Cu–O1/d Cu–O2	1.1000	1.0870	1.0783	d Cu–O1/d Cu–O2	1.1958	1.2148	1.2019	1.2288	1.1913
d Cu–Cu	3.407(4)	3.4297	3.4459	d Cu–Cu	3.338(0)	3.3095	3.3379	3.3119	3.3676
d Cu–Fe	3.960(3)	3.9229	3.9329	d Cu–Fe	4.085(8)	4.0815	4.0681	4.0946	4.0543

---

Fig. 2 Calculated Cu–O bond lengths (Å) within the SCAN+U approach as a function of U_Cu and U_Fe values for (a) YSr₂Cu₂FeO₈ and (b) YSr₂Cu₂FeO₇ idealized oxides. The experimental bond lengths are depicted as dashed blue lines. The PBE (U_Fe and U_Cu = 0 eV) and PBE+U (U_Fe and U_Cu = 4 eV) results from a previous investigation⁸ are denoted by blue and yellow asterisks, respectively.

For the sake of completeness, Fig. 2 incorporates data from a preceding PBE and PBE+U (U_Cu = U_Fe = 4 eV) investigation.⁸ As previously discussed, the PBE functional tends to yield larger bonding lengths than the SCAN functional. Specifically, the Cu–O1 distance in the YSr₂Cu₂FeO₇ oxide exhibits the most significant deviation from experimental values (5.7%). Introducing the U parameter to the PBE method results in changes in the Cu–O bond distances, with d Cu–O1 for δ = 0 decreasing and the others increasing, following the same trends observed with SCAN+U.

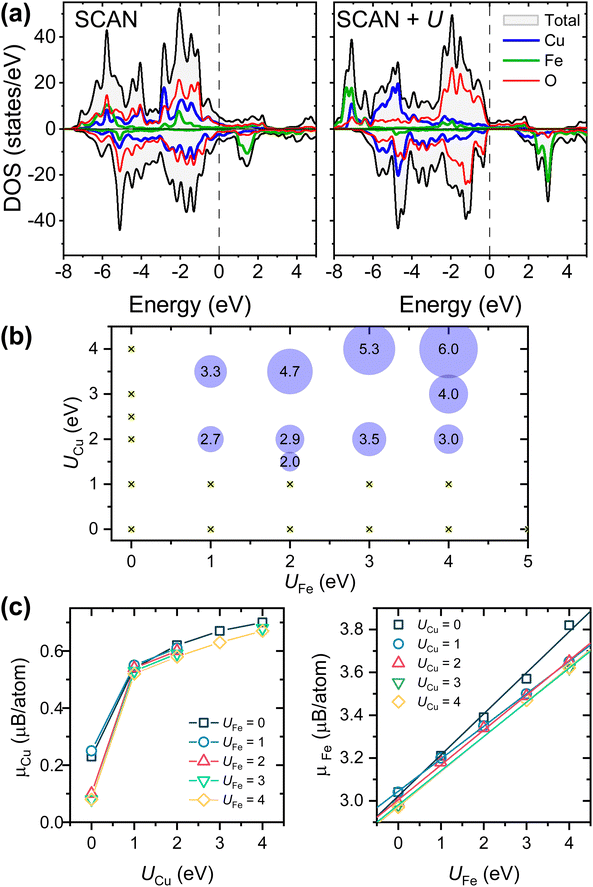
Regarding the electronic properties of YSr₂Cu₂FeO₈, the SCAN functional correctly reproduces the itinerant electron character and metallic behavior of the oxide (calculated DOS in Fig. 3a). Applying the Hubbard correction (SCAN+U) produces a downshift of the occupied Fe/Cu-3d states, keeping the 3d orbitals atomic-like and diminishing their hybridization with the 2p-oxygen (less covalent TM–O bonding). This is clearly observed in Fig. 3a for the case with U_Cu and U_Fe = 4 eV. Moreover, since U penalizes the fractional occupation on metal ions, the electrons tend to localize in the majority spin in Cu-3d and Fe-3d orbitals and a band gap opens in the minority spin channel, resulting in a half-metal compound. Fig. 3b shows the dependence of the down-spin band gap with the U_Cu and U_Fe values employed in the SCAN+U calculations. Half-metallicity is largely influenced by the U value used for the Cu-3d states. When U_Cu < 1.0 eV, independent of the U_Fe tested (maximum 5 eV), the DOS corresponds to a metallic compound. For U_Cu > 1.0 eV and U_Fe > 0, an energy gap opens in the down spin channel, whose energy increases with larger U_Fe (see the band gap values in the circles). In addition to half-metallicity, the introduction of the U parameter, and associated electron localization, produces increasing local magnetic moments (Fig. 3c) that deviate from the experimental observations, that is, μ₀(Fe) = 1.7–2 μB per ion and μ₀(Cu) = 0 μB.¹⁷ In this regard, the introduction of the U term does not benefit property prediction.

Fig. 3 (a) Calculated total and atom-projected density of states (DOS) for YSr₂Cu₂FeO₈ within the SCAN and SCAN+U approximation (U_eff = 4 eV for Cu and Fe). The Fermi level is set as the zero of energy. DOS units refer to the calculated cell. Up spin (or majority) and down spin (or minority) contributions are shown. Color code: total black, Cu blue, Fe green, and O red. (b) Effect of the on-site Coulomb repulsion parameters U_Feand U_Cu within the SCAN+U approximation on the electronic properties of the YSr₂Cu₂FeO₈ idealized model. A metal (green dots) to half-metal (purple circles) transition occurs at U_Cu ∼ 2 eV. For half-metallicity, the magnitude of the band gap in the down-spin channel is shown inside the purple circles. (c) Calculated local magnetic moments on Cu and Fe ions as a function of the U_Fe and U_Cu values employed in the SCAN+U method.

Interestingly, as depicted in Fig. 3b and c, maintaining metallic characteristics in YSr₂Cu₂FeO₈ is possible with combinations such as U_Cu = 0 eV and U_Fe = 5 eV, as well as U_Fe = 0 and U_Cu = 4 eV. This is to say, electron localization does not occur when either U_Cu or U_Fe is set to zero. Fig. 4 reveals the impact of increasing only U_Fe or U_Cu, while keeping the other U-value equal to zero. It can be inferred that since both Cu-3d and Fe-3d states contribute to the Fermi level, electron localization only occurs when both U-terms are greater than zero. Furthermore, the predominant contribution of Cu 3d-states at the Fermi level, characterized by a higher number of states compared to Fe 3d-states, results in U_Cu exerting a greater influence on the magnetic and electronic properties as well as on the Cu–O distances.

Fig. 4 Calculated atom-projected density of states for YSr₂Cu₂FeO₈ within the SCAN+U apporach. The evolution of the pDOS with U values for both TMs can be followed in columns. In the left column, U_Cu is set to zero and the metallic character is perserved independently of the U_Fe value. In the right column, U_Fe is set to zero, and increasing U_Cu drastically reduces the number of states at the Fermi level. The Fermi level is set as the zero of energy. Color code: Cu blue and Fe black.

Fig. 5a shows the calculated SCAN-DOS for the idealized model of C-type AFM-YSr₂Cu₂FeO₇. For this insulating oxide, the band gap extracted from diffuse reflectance spectroscopy (DRS) is in the range of 0.73–1.2 eV.⁸ As previously reported, the PBE+U (U_Cu and U_Fe = 4 eV) predicts a band gap of 0.85 eV, while the bare PBE fails to reproduce the insulating character of YSr₂Cu₂FeO₇. The SCAN functional yields a band gap of 0.63 eV, which widens when the U term is applied (SCAN+U). With U = 4 eV for Fe and Cu (Fig. 5a), the band gap is as wide as 2.3 eV. Fig. 5b unveils how the band gap can be tuned by the choice of the U values. Noteworthily, the band gap depends linearly on U_Cu, but it is almost insensitive to the choice of U_Fe, similarly with the afore-mentioned trend in the calculated Cu–O distances in this oxide. The experimental band gap is reproduced for 0 < U_Cu < 1 eV. For U_Cu = 0 eV, appropriate values of U_Fe range from 1 to the maximum value tested (4 eV), whereas for U_Cu = 1 eV, any U_Fe value (including U_Fe = 0) yields the same band gap. Fig. 6 depicts the specific effects of U_Cu and U_Fe in the calculated DOS. While both, Cu and Fe-3d states, are significant parts of the top of the valence band, the bottom of the conduction band is formed exclusively by Cu-3d states. As U_Cu increases, these empty states shift up in energy, thereby opening the band gap.

Fig. 5 (a) Calculated total and atom-projected density of states for YSr₂Cu₂FeO₇ in the C-type AFM configuration within the SCAN and SCAN+U approximation (U_eff = 4 eV for Cu and Fe). The Fermi level is set as the zero of energy. DOS units refer to the calculated cell. Up spin (or majority) and down spin (or minority) contributions are shown. Color code: total black, Cu blue, Fe green, and O red. (b) Dependence of the band gap for C-type AFM-YSr₂Cu₂FeO₇ with the U values on Fe and Cu utilized in the SCAN+U calculations. The experimental band gap range is denoted by a gray region. The PBE (U_Fe and U_Cu = 0 eV) and PBE+U values (U_Fe and U_Cu = 4 eV) from a previous investigation⁸ are denoted by blue and yellow asterisks, respectively.

Fig. 6 Calculated atom-projected density of states for C-type AFM-YSr₂Cu₂FeO₇ within the SCAN+U methodology, showing the major impact of U_Cu on the electronic properties. The evolution of the pDOS with U values for both TMs can be followed in columns. In the left column, U_Cu is set to zero and the band gap value is perserved independently of the U_Fe value. In the right column, U_Fe is set to zero, and band gap widens with the increasing U_Cu values. Color code: Cu blue and Fe black.

Investigation of the hypothetical FM-YSr₂Cu₂FeO₇ supports the minor impact of U_Fe in property prediction. The calculated DOSs for the FM configuration (shown in Fig. 7a), indicate that within the SCAN+U approach, the U term drives the oxide from a metallic state (as described by the SCAN) to an insulating state. Fig. 7b shows the band gap opening as a function of the U_Cu and U_Fe values used in the calculations. In the same way as in the C-type AFM-YSr₂Cu₂FeO₇, the U_Cu dominates the band gap opening, being the critical value U = 2 eV. In the insulating state, the magnitude of the band gap is nearly insensitive to U_Fe; for instance, a band gap of 0.8 eV is obtained when U_Cu = 4 eV and U_Fe ranging from 0 to 4 eV. It should be noted that due to the lack of experimental data for FM-YSr₂Cu₂FeO₇, it is not conceivable to extract an optimal U value to model its properties. FM-YSr₂Cu₂FeO₇ is metastable relative to C-type AFM under any DFT approximation, with energy differences per formula unit of 0.248 eV (PBE),⁸ 0.414 eV (SCAN),⁸ 0.424 eV (PBE+U, U_Fe = U_Cu = 4 eV),⁸ and 0.330 eV (SCAN+U, U_Fe = U_Cu = 4 eV). It is therefore unlikely that such a phase could ever be prepared.

Fig. 7 (a) Calculated total and atom-projected density of states for YSr₂Cu₂FeO₇ in the FM configuration. The Fermi level is set as the zero of energy. DOS units refer to the calculated cell. Up spin (or majority) and down spin (or minority) contributions are shown. Color code: total black, Cu blue, Fe green, and O red. (b) FM-YSr₂Cu₂FeO₇ evolves from metallic (blue) to insulating behavior with increasing U_Cu values. The metal-to-insulator transition occurs at a critical U_Cu value of approximately 2.5 eV.

The stabilization of the C-type AFM magnetic structure in insulating YSr₂Cu₂FeO₇ is attributed to local antiferromagnetic ordering within the Cu/Fe plane layer arising from superexchange interactions via oxygen bridges.^8,34 In contrast, in-plane AFM ordering is not observed in the metallic YSr₂Cu₂FeO₈, for which an A-type AFM magnetic structure is reported.¹⁷ Noteworthily, the inter-plane magnetic interactions are weak throughout the YSr₂Cu₂FeO_7+δ system.^8,17,32,34 This is consistent with the small energy differences found between the inter-plane ferromagnetic and antiferromagnetic couplings in YSr₂Cu₂FeO₇ within the PBE, PBE+U and SCAN approximations.⁸ For this oxide, the SCAN+U (U_Fe = U_Cu = 4 eV) yields a negligible energy (E_TotalFM – E_TotalFM) difference of 0.004 eV per formula unit. Similarly, for the metallic YSr₂Cu₂FeO₈, the A-type AFM configuration is only 0.018 eV per formula unit more stable than the FM configuration within the SCAN +U (U_Fe = U_Cu = 4 eV).

Discussion

The principal drawback of the DFT+U schemes lies in the selection of the adjustable parameter, U. While U values can be derived from self-consistent calculations,³⁵ a common approach involves choosing these in order to match the experimental data, such as equilibrium volumes, formation energies, band gap values, transition pressures, intercalation voltages, and so on.^{10,25,26,36–38} It is impossible to pinpoint an exact and universally applicable value for the U parameter to accurately reproduce all material properties.³⁷ In this study, suitable ranges of U values are determined through comparison with experimental data on crystalline, magnetic and electronic structures.

The appropriate Hubbard U parameter varies depending on the nature and oxidation state of the transition metal (TM) as well as the crystal structure.²⁵ YSr₂Cu₂FeO_7+δ (δ = 0,1) shares the same structural type, and for both compounds incorporating a U correction improves the reproduction of lattice parameters and Cu–O bond lengths. In the YSr₂Cu₂FeO_7+δ system, the oxygen content determines the oxidation states of Cu and Fe as well as the magnetic interactions. For the magnetic structures, the SCAN+U method performs equally well compared to the SCAN, PBE and PBE+U methods: they all capture the occurrence of in-plane AFM ordering for δ ∼ 0, and the soft character of the inter-plane interactions throughout the YSr₂Cu₂FeO_7+δ system. These DFT-trends, even when extracted from the idealized oxides with δ = 0 and 1, are in good agreement with the observed magnetic properties of YSr₂Cu₂FeO_7+δ.^17,32,34

The primary impact of U is observed in the electronic properties. In the metallic phase YSr₂Cu₂FeO₈, as expected, the U parameter penalizes electron delocalization, with U_Cu > 1 eV being detrimental for property prediction. On the other hand, for the insulating phase YSr₂Cu₂FeO₇, the electron correlation is better captured with 0 < U_Cu < 1 eV and U_Fe =1–4 eV. Considering these findings, the YSr₂Cu₂FeO_7+δ system is better described with U_Cu = 1 eV, which improves the accuracy of the band gap for the insulating C-type AFM-YSr₂Cu₂FeO₇, while maintaining the metallic behavior of YSr₂Cu₂FeO₈. Importantly, once U_Cu is set to 1 eV, varying U_Fe between 0 and 4 eV has a minor impact on the calculated metal/insulating behavior of YSr₂Cu₂FeO₈/YSr₂Cu₂FeO₇ (Fig. 3b and 5b). The predominant role of U_Cu is consistent with the specific contributions of Cu-3d and Fe-3d states on the valence and conduction bands of YSr₂Cu₂FeO_7+δ.

In the DFT+U framework, there exists dependence of the appropriate U values on the XC-functional used. Despite the limited number of studies addressing the estimation of suitable U values within the SCAN+U approach, a widespread observation is that the optimal U values for electronic property prediction are notably lower than those within the PBE+U method.^9,12,27 This remark is supported by comparing the current SCAN+U results for YSr₂Cu₂FeO₇ with a previous investigation using PBE+U (Fig. 5b).⁸ In the PBE+U approach, applying U_eff values of ∼4 eV for Cu and Fe ions, a calculated band gap of 0.85 eV is achieved, which falls in the experimental range. However, using the same U values in the SCAN+U method significantly overestimates the band gap, widening it to 2.3 eV. Fig. 2 and 5b suggest that the calculated bonding distances and band gaps exhibit a linear trend with the U value, displaying similar slopes for both SCAN+U and PBE+U methods. Since the bare PBE and SCAN produce different values (either for band gaps or bond-lengths), the optimal U values matching the experimental data definitely depend on the chosen XC functional.

Finally, within the SCAN+U method, the optimal U values for modelling the YSr₂Cu₂FeO_7+δ compounds can be compared to those previously reported for the simple Fe and Cu oxides. Previous studies have suggested that the optimal U_Fe value is around ∼3 eV for FeO/Fe₂O₃/Fe₃O₄⁹ and BiFeO₃.¹² Carter et al. demonstrated that, while SCAN is sufficient to reproduce the crystal structure and formation energies of CuO and Cu₂O, the proper simulation of the electronic structure requires the introduction of U_Cu at around ∼2 eV.¹⁰ However, applying the combination extracted from simple oxides (U_Cu = 2 eV and U_Fe = 3 eV), a poor description of the electronic properties of the YSr₂Cu₂FeO_7+δ system is given. This combination leads to a half-metallic behavior (and electron localization) for YSr₂Cu₂FeO₈, and band gaps that deviate from the experimental values for YSr₂Cu₂FeO₇. In short, the appropriate U parameters found for the simple Cu/Fe oxides are not suitable for reproducing the properties of the complex oxides YSr₂Cu₂FeO_7+δ. The differences between the optimal U-values for simple and complex TM oxides are linked to the specific contributions of the TM-d states in the electronic structure.

Conclusions

The SCAN functional effectively models the crystal structure and basic electronic and magnetic properties of complex oxides YSr₂Cu₂FeO_7+δ (0 < δ < 1). Although adding a U correction on top is not necessary, it is found that applying a U_Cu value of 1 eV leads to a more accurate description of properties. In this case study, the Cu-3d states dominate, respectively, the Fermi level of YSr₂Cu₂FeO₈ and the bottom of the conduction band of YSr₂Cu₂FeO₇. Consequently, U_Cu has a greater impact than U_Fe in the calculated electronic properties and magnetic moments. Indeed, for a fixed U_Cu, the results are almost insensitive to U_Fe.

This case study highlights the importance of analyzing the role of the individual U parameters for the reliable SCAN+U investigations of complex oxides containing several TM ions. The optimal U-values certainly depend on the material under investigation (chemical composition and crystal structure), and U-transferability among materials is particularly risky for such complex oxides. The appropriate combination of U_TM terms may differ from the optimal values in the respective simple oxides. Therefore, the convenience of using the SCAN+U approach in the study of oxides containing several TM ions should be assessed for each material, considering whether the benefits in property prediction (compared to the SCAN functional) outweigh the efforts made in determining the optimal combination of individual U_TM values.

Author contributions

Marianela Gómez-Toledo: investigation, methodology, software, data curation, validation, formal analysis, visualization, and writing – original draft. Elena M. Arroyo-de Dompablo: investigation, conceptualization, supervision, funding acquisition, project administration, and writing – original draft.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research is part of the project ECSAWE-PID2022-139501OB-C22 funded by the MCIN/AEI/10.13039/501100011033 and by the “ERDF A way of making Europe”. The authors thank funding from the MCIN/AEI/10.13039/501100011033-“NextGenerationEU”/PRTR (project TED2021-130452B-C21) and from the Universidad Complutense de Madrid (FEI-EU-22-01-4129585). Computational resources from the MALTA–cluster (Universidad de Oviedo) and I2Basque are acknowledged. The authors are grateful to S.A. López-Paz and S.García-Martín for their valuable discussions and helpful insights into the experimental aspects of the YSr₂Cu₂FeO_7+δ system.

References

1. J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402.
2. Y. Hinuma, H. Hayashi, Y. Kumagai, I. Tanaka and F. Oba, Phys. Rev. B, 2017, 96.
3. D. A. Kitchaev, H. Peng, Y. Liu, J. Sun, J. P. Perdew and G. Ceder, Phys. Rev. B, 2016, 93, 045132.
4. J. W. Furness, Y. Zhang, C. Lane, I. G. Buda, B. Barbiellini, R. S. Markiewicz, A. Bansil and J. Sun, Commun. Phys., 2018, 1.
5. J. Varignon, M. Bibes and A. Zunger, Phys. Rev. B, 2019, 100.
6. L. Iglesias, M. Bibes and J. Varignon, Phys. Rev. B, 2021, 104, 035123.
7. J. Kaczkowski, M. Pugaczowa-Michalska and I. Płowaś-Korus, J. Magn. Magn. Mater., 2022, 548, 168984.
8. M. Gómez-Toledo, S. A. López-Paz, S. García-Martín and M. E. Arroyo-de Dompablo, Inorg. Chem., 2023, 62, 3445–3456.
9. G. S. Gautam and E. A. Carter, Phys. Rev. Mater., 2018, 2, 095401.
10. O. Y. Long, G. S. Gautam and E. A. Carter, Phys. Rev. Mater., 2020, 4, 045401.
11. R. B. Wexler, G. S. Gautam, E. B. Stechel and E. A. Carter, J. Am. Chem. Soc., 2021, 143, 13212–13227.
12. J. Kaczkowski, M. Pugaczowa-Michalska and I. Plowas-Korus, Phys. Chem. Chem. Phys., 2021, 23, 8571–8584.
13. M. Verma and R. Pentcheva, Phys. Rev. Res., 2022, 4.
14. Y. Zeng, Q. Hu, M. Pan, K. Zhang, S. Grasso, C. Hu and Q. Feng, Adv. Powder Mater., 2022, 1, 100019.
15. J. Shimoyama, K. Otzschi, T. Hinouchi and K. Kishio, Physica C, 2000, 341, 563–564.
16. T. Mochiku, Y. Nakano, A. Hoshikawa, S. Sato, K. Oikawa, T. Ishigaki, T. Kamiyama, K. Kadowaki and K. Hirata, Phys. C, 2004, 412, 115–119.
17. S. A. Lopez-Paz, X. Martinez de Irujo-Labalde, J. Sanchez-Marcos, C. Ritter, E. Moran and M. A. Alario-Franco, Inorg. Chem., 2019, 58, 12809–12814.
18. J. E. H. Sansom, E. Kendrick, H. A. Rudge-Pickard, M. S. Islam, A. J. Wright and P. R. Slater, J. Mater. Chem., 2005, 15, 2321–2327.
19. T. Mochiku, Y. Nakano, K. Oikawa, T. Kamiyama, H. Fujii, Y. Hata, I. Suzuki, I. Kakeya, K. Kadowaki and K. Hirata, Phys. C, 2003, 400, 43–52.
20. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
21. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
22. P. E. Bloch, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
23. P. E. Blochl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233.
24. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, Z. Szotek, W. M. Temmerman and A. P. Sutton, Phys. Status Solidi A, 1998, 166, 429–443.
25. L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107.
26. M. E. Arroyo y de Dompablo, Y.-L. Lee and D. Morgan, Chem. Mater., 2010, 22, 906–913.
27. A. M. Ritzmann, J. M. Dieterich and E. A. Carter, Phys. Chem. Chem. Phys., 2016, 18, 12260–12269.
28. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, UK, 1990.
29. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
30. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319.
31. G. Roth, P. Adelmann, G. Heger, R. Knitter and T. Wolf, J. Phys. I, 1991, 1, 721–741.
32. Y. Hata, Y. Mihara, T. Mochiku, J.-I. Suzuki, I. Kakeya, K. Kadowaki, E. Kita and H. Yasuoka, Phys. C, 2004, 417, 17–24.
33. M. Imada, A. Fujimori and Y. Tokura, Rev. Mod. Phys., 1998, 70, 1039.
34. M. Pissas, G. Kallias, A. Simopoulos, D. Niarchos and R. Sonntag, Physica B, 1998, 253, 1–9.
35. F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 15, 235121.
36. K. W. Lee and W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 174428.
37. M. E. Arroyo-de Dompablo, A. Morales-Garcia and M. Taravillo, J. Chem. Phys., 2011, 135, 054503.
38. M. E. Arroyo-de Dompablo, P. Rozier, M. Morcrette and J. M. Tarascon, Chem. Mater., 2007, 19, 2411–2422.

---