Optical characterization of a single molecule complete spatial orientation using intra-molecular triplet–triplet absorption

Abstract

Progress in single molecule fluorescence experiments have enabled an in-depth characterization of fluorophores, ranging from their photophysical rates to the orientation of their emission dipole moments in three dimensions. However, one crucial spatial information remains elusive: the molecule orientation relative to its emission dipole moment. One can retrieve the latter only by the use of another non-colinear transition dipole moment. We experimentally demonstrate the optical retrieval of this information for single terrylene (Tr) molecules in a 30 nm thin para-terphenyl matrix. We show, through second-order correlation measurements at varying excitation power and polarization, that Tr molecules experience an optically induced deshelving of their triplet states, mediated by two orthogonal intra-molecular triplet–triplet absorption dipole moments. We take advantage of these two transition dipole moments to retrieve the full orientation of the Tr molecule, employing a 3-level scheme for the molecule photophysics and analytical calculations for the exciting electric field distribution. This modelling approach enables us to accurately describe both varying power and polarization measurements, giving access to the molecule's photophysical rates and to its complete orientation in three dimensions. This includes the orientation of the singlet emission dipole moment in the laboratory frame, and the orientation of the molecule plane with respect to the singlet emission dipole moment.

---

1 Introduction

The groundbreaking work of Moerner and Kador¹ demonstrated the feasability of reaching the single molecule limit with absorption optical measurements. Shortly thereafter, Orrit and Bernard² demonstrated that fluorescence provides a much better signal to noise ratio. The sensitivity achieved at the single-molecule level allowed for the observation of blinking, caused by quantum jump of the molecule from the bright singlet to the dark triplet manifold.³ Progress in the field over the past decades enabled a profound understanding of phenomena at play in the photophysics of single emitters.⁴ This has given rise to numerous applications, methods and experimental works in spectroscopy, super resolution microscopy and photonic quantum technologies.^5,6

An important property of a single-photon emitter is the orientation of its absorption and emission transition dipole moment. The interaction of both dipoles with their local environment strongly depends on their spatial orientation. This applies to the interaction of the absorption dipole with the excitation light, as well as the interaction of the emission dipole with its environment (such as interfaces or nearby objects) via the local density of optical states (LDOS). Knowledge of the intrinsic and extrinsic properties of single emitters provides valuable information for their use as probes, spanning from fundamental physics experiments to practical applications.

Many experimental efforts have been devoted to measuring the orientation of the singlet emission dipole moment of emitters. Various techniques have been employed, including polarization analysis of fluorescence,^7,8 back-focal plane imaging,^9,10 defocused images¹¹ or excitation point-spread-function engineering.¹² For more detailed information on these methods and additional references, we direct the reader to reviews from Moerner's¹³ and Brasselet's¹⁴ groups. However, to the best of our knowledge, there is currently no experimental optical technique capable of retrieving the orientation of the emitter around its emission dipole moment.To obtain this last information, another transition dipole moment is required. We will show that intra-molecular triplet–triplet transition dipole moments can serve this purpose and outline how we experimentally access this information, despite the fact that triplet states are usually dark.

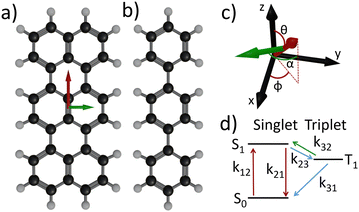
To achieve this, we use terrylene molecules (Tr, C₃₀H₁₆) embedded in a para-terphenyl matrix (pT, C₁₈H₁₄), a paradigmatic guest/host system in single molecule fluorescence experiments (see Fig. 1). We chose this particular system for the following reasons: (i) Tr is highly photostable in a pT matrix, (ii) the molecules are oriented preferentially perpendicular to the glass substrate, (iii) the pT matrix has domains of low thicknesses (≈30 nm) and (iv) it is a well-studied system. The earliest report on this dates back to 1994.¹⁵ Since then, numerous studies have been conducted, spanning from liquid helium temperature^3,16,17 to room temperature,^18–20 and involving thick (several microns) pT crystals. In a notable study, Fleury et al.¹⁹ characterized all the photophysical rates of Tr, using a 3-level scheme (Fig. 1d). They observed an excitation power-dependent deshelving of the triplet state (k₃₂ in Fig. 1d). This observation was later confirmed by the group of Kozankiewicz²¹ who measured this deshelving rate across a large range of temperatures (5 K to room temperature).

Fig. 1 Molecular system of the study. (a) Guest: terrylene, (b) Host: para-terphenyl, (c) Coordinate system with angle definition for the terrylene molecule orientation. The black arrows (x, y, z) correspond to the laboratory frame. The red arrow correspond to the absorption/emission transition dipole moment of the singlet manifold. The smaller green arrow correspond the dipole moment transition of the “orthogonal” triplet–triplet absorption (see text for details), (d) 3-level system for terrylene and associated rates.

The Tr/pT guest/host system has also been employed in a thin film configuration, where Tr molecules showed an aligned emission dipole almost perpendicular to the glass substrate, accompanied by a remarkably high photo-stability.²² This thin film configuration paved the way for pioneering nano-photonics experiments, enabling the quantitative measurement of the influence of nanoantennas on the very same single molecule, through scanning probe microscopy.^23,24 Furthermore, the thin film configuration allowed the integration of single Tr molecules as tools to inverstigate the impact of more complex structures on their emission properties and photophysics, such as plasmonic nanoparticles,^23–26 dielectric and metallic local probes,²⁷ planar dielectric antennas,²⁸ or hybrid nanostructures.²⁹ In our specific case, the thin film configuration is particularly appealing as it provides a good knowledge of the excitation electric field distribution.

In this paper, we report fluorescence measurements of single Tr molecules in a sub-30 nm thick pT film under ambient conditions. We measure the second order auto-correlation function of the fluorescence signal with respect to excitation power and polarization on the same single molecule. Our findings reveal that two transition dipole moments are necessary to describe the optically induced deshelving of the triplet state. This intricate process involves two intramolecular triplet–triplet transitions followed by reverse InterSystem Crossing (r-ISC) to the singlet manifold. Thanks to the simple excitation field distribution inside the thin film and within the framework of a 3-level system, we utilize these two triplet–triplet transitions to obtain the complete molecule orientation. This includes the three-dimensional orientation of the singlet transition dipole moment and the orientation of the molecule's plane around its singlet transition dipole moment. Furthermore, we extract all the rates involved in Tr fluorescence photophysics, identifying two populations of molecules, distinguished by the magnitude of the triplet state deshelving rate as a function of the excitation polarization.

2 Results and discussion

The electronic states involved in the fluorescence process of Tr molecules can be reduced to a 3-level system as illustrated in Fig. 1d.^18–20 S₀ denotes the ground singlet state, S₁ is the first excited singlet state and T₁ is the lowest triplet state. Experimental findings have demonstrated that the spin degeneracy of the triplet state is only lifted at temperatures below 17.5 K.³⁰ Since our work is conducted at room temperature, we consider only a single triplet level T₁. The population dynamics of the various levels are governed by a system of three linear differential equations:where for example n_S0 represents the population of the S₀ level, and ṅ_S0 denotes its time derivative.

Referring to Fig. 1d, k₁₂ represents the excitation rate from the singlet ground state S₀ to the bright excited state S₁, while 1/k₂₁ is the fluorescence lifetime, k₂₃ the intersystem crossing (ISC) rate from S₁ to a dark triplet state T₁, k₃₁ the T₁ to ground singlet non-radiative depopulation rate, and k₃₂ a power dependent triplet deshelving rate.¹⁹ The latter can be interpreted as a process in which the triplet level is pumped into higher triplet states (T₁–T_n transition, with n = 5 or 6³¹), followed by a r-ISC to the singlet manifold. It's worth noting that such process is not unique to Tr but is observed in many other molecules.³² A 4-level system model was tested in ref. 33 using data from ref. 28 and it showed no difference compared to the 3-level system beyond the experimental noise. In the end, in agreement with the literature,^18–20 the electronic structure of the Tr molecule at the excitation wavelength used in this work (532 nm) is described by a 3-level system.

Solving eqn (1) yields the time evolution of the level populations, from which one can derive an analytical formula for the second order correlation function g⁽²⁾(τ) for the steady state under a continuous-wave excitation:³⁴

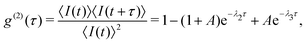where (−λ₂) 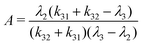and (−λ₃) denotes the eigenvalues of the system in eqn (1), and A is the bunching amplitude given by (see details in ESI†):

Assuming an emission quantum yield of 1 for Tr,¹⁰ the total rate of photon emission R_t is given by:

These four quantities (λ₂, λ₃, A and R_t) are solely function of the rates of the system. The detected count rates R is then given by:

R = ηR_t, (5)

where η is the detection efficiency of our experimental system (around 4.5%).

The excitation rate k₁₂ and the triplet state deshelving rate k₃₂ both exhibit a linear dependence on excitation power.^19,20,28,33 Therefore, by measuring g⁽²⁾(τ) at different powers, one can extract all the rates involved in the fluorescence process, including those related to the dark triplet state, which is responsible for the molecule blinking. However, previous reports did not consider the respective orientation of the excitation electric field and the molecule. For instance, the power experienced by an absorption transition dipole moment varies with the input polarization as |μ·E|², where μ is the transition dipole moment of the molecule and E is the excitation field. In our study, we employ two complimentary measurements: a variation of excitation power at fixed excitation polarization and a variation of the excitation polarization at fixed excitation power. Subsequently, we demonstrate that the latter type of measurement unveils a complex behavior: k₃₂ involves two transition dipole moments.

Experimentally, we utilize a home-made confocal inverted microscope that is equipped with a spectrometer, a Hanbury–Brown–Twiss detection scheme and a home-made tuning-fork based atomic force microscope (TF-AFM). Terrylene molecules were synthetized following the procedure outlined in ref. 35 and samples were prepared as in ref. 22. Using TF-AFM, we ensure that Tr molecules in pT films of thickness below 30 nm are studied (see ESI†). The excitation is provided by a 532 nm continuous-wave laser in total internal reflection via a high numerical aperture microscope objective. The laboratory reference frame is illustrated in Fig. 1c, where (x, z) is the plane of incidence. We specifically select molecules exhibiting a maximum fluorescence intensity at 578 ± 1 nm. Employing a combination of half-wave plate and polarizer allows us to vary the excitation power in a continuous way. Another half-wave plate is used to rotate the excitation polarization before entering the microscope. The excitation polarization can thus be changed from transverse magnetic (or p, electric field in the (x, z) plane) to transverse electric (or s, electric field in the (y, z) plane). Fluorescence photons are collected through the same objective, filtered and recorded while continuously varying one of the half-wave plate (either for power or polarization). For clarity, we refer hereafter to a “power scan” for the measurement at different excitation power, and a “polarization scan” for the measurement at different excitation polarization angle. More comprehensive details on sample preparation, the optical setup and measurement procedures are provided in the ESI.†

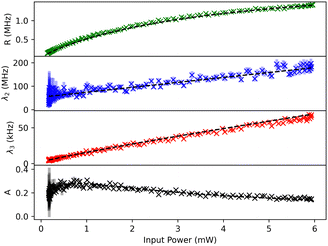
The result of a typical power scan are depicted in Fig. 2, where the measured count rates R, λ₂, λ₃ and A are plotted as a function of excitation power (see ESI† for all molecules).

Fig. 2 Typical evolution of the measured count rates R, λ₂, λ₃ and the bunching amplitude A as a function of excitation power (ramping up and down). The colored areas represent the 68% confidence intervals of the second order correlation function fit results. Dashed black lines are result of a global fit function (see text for details).

The measurement includes data points for both increasing and decreasing excitation powers, which are almost indistinguishable in Fig. 2. This shows the stability of the measurement apparatus, the pT matrix and the Tr molecule up to an excitation power density of 370 kW cm⁻².

The polarization scan measurements are illustrated in Fig. 3 and 4, presenting R, λ₂, λ₃ and A as function of the excitation polarization angle (see ESI† for all molecules). When the detected count rate becomes very low, we lack sufficient photons to construct a meaningful g⁽²⁾(τ) function, which accounts for the absence of experimental data points at excitation polarization angles with a low-emission rate.

Fig. 3 Evolution of R, λ₂, λ₃ and A and as a function of input polarization angle for an in-phase (ip) molecule. Colored markers are experimental data points. Dashed black lines are result of a global fit function (see text for details). The colored areas represent the 68% confidence intervals of the second order correlation function fit results. Left and right panels are respectively linear and polar representation of the same data.

Fig. 4 Evolution of R, λ₂, λ₃, and A as a function of input polarization angle for an out-of-phase (oop) molecule. Colored markers are experimental data points. Dashed black lines are result of a global fit function (see text for details). The colored areas represent the 68% confidence intervals of the second order correlation function fit results. Left and right panels are respectively linear and polar representation of the same data.

Two distinct types of behavior are evident. The first one (Fig. 3) where the count rates R, λ₂, λ₃ have their maxima at the same excitation polarization angle. The bunching amplitude A shows a behavior that aligns with the power scan: it starts with a low value at low count rates, reaches a maximum when R ≈ 500 kHz and then decreases at higher count rates. A slight asymmetry is observed for the value of A at 30° and 125° excitation polarization angles, which will be discussed later. We refer to such molecules as in-phase (ip) molecules.

The second population (Fig. 4) exhibits a similar behavior for R and λ₂, but a distinctly different dependence for λ₃ and A: λ₃ is out of phase with R and λ₂, with its lowest value being ≈ 10 kHz higher than the lowest values of ip molecules. The bunching amplitude shows a maximum, close to the count rates maximum, with a clear asymmetry around 100°. For these molecules, the evolution of λ₃ and A do not align with the power scans and cannot be easily explained. We refer to these molecules as out-of-phase (oop) molecules. It's worth noting that the values of λ₃ and A are very similar for both ip and oop molecules at the maximum count rate polarization angle, rendering them indistinguishable if one analyzes only power scans.

Theoretical calculations³⁶ show that the absorption dipole (S₀–S₁ transition) and the emission dipole (S₁–S₀ radiative transition) are oriented along the long axis of the molecule (red arrow in Fig. 1a). Experimentally it was confirmed that the absorption and emission dipoles are aligned.³⁷ Therefore, we assume colinear absorption and emission dipoles along the long-axis direction of the terrylene molecule (red arrow in Fig. 1a and c).

In our initial attempt to model the polarization scans, we considered a vertically oriented dipole above the interface, utilizing the rates deduced solely from power scans. We could reproduce qualitatively the main features of most of the ip molecules (except for the asymmetry in A, and an offset of the curves along the excitation polarization axis). However, it proved impossible to replicate the behavior of the oop molecules.

Subsequently, we incorporated the molecule's orientation with respect to the sample plane and to the excitation beam (i.e. the laboratory frame (x,y,z) in Fig. 1c). We defined θ for the polar angle, ϕ for the azimuth angle (see Fig. 1c for a schematic with angle definitions). For an accurate depiction of the molecule's interaction with the excitation field, we calculated the distribution of the excitation field both analytically³⁸ and numerically.³⁹ We emphasize here the critical role played by the 30 nm thickness of the para-terphenyl film. Although we do not precisely know the molecule's depth within the film, the excitation field components remain relatively constant within the 30 nm pT thickness (see ESI†). This is not the case for thicker films.

However, considering the long-axis orientation of the molecule was not sufficient to describe the asymmetry in the bunching amplitude for ip molecule, and we couldn't even qualitatively reproduce the behavior of oop molecules. To develop a model capable of describing both ip and oop molecules, we must introduce two absorption transition dipole moments to characterize the triplet state deshelving process. These can be regarded as two distinct T₁–T_n transitions that later cross back to the singlet manifold by r-ISC. This hypothesis is consistent with a density functional theory (DFT) study, predicting a T₁–T₅ transition and a T₁–T₆ transition respectively at 2.34 eV and 2.40 eV, with non-zero oscillator strength.³¹ These energies are close to our excitation energy (2.33 eV). Additionally, this is in line with transient absorption experimental measurements of 2,5,10,13-tetra-t-butylterrylene (a Tr derivative with similar spectral properties) in benzene⁴⁰ revealing two triplet–triplet absorption broad peaks centered at 2.25 eV and 2.42 eV, overlapping at our excitation laser energy (2.33 eV). Consequently, we can excite these two intramolecular triplet–triplet transitions with our excitation laser. However, the orientation of the associated transition dipole moment in the molecule's reference frame is not reported to our knowledge. Symmetry consideration, as Tr belongs to the D_2h symmetry point group, suggests a contribution aligned with the singlet absorption dipole moment, i.e. along the long molecule axis, red arrow in Fig. 1a, and a second one orthogonal to the singlet absorption dipole, i.e. along the molecule short axis, green arrow in Fig. 1a. We then express k₃₂ as the sum of these two orthogonal transitions:

k₃₂ = σ_32a|μ_32a·E|² + σ_32o|μ_32o·E|², (6)

where we introduce two distinct triplet deshelving absorption cross-sections: σ_32a and σ_32o, respectively for aligned and orthogonal to the singlet transition dipole moment, μ_32a and μ_32o are the T₁–T_n transition dipole moment vectors and E the electric field of the excitation laser. The molecule orientation around the singlet dipole should then be specified. We define the angle α for the molecule rotation around its singlet dipole transition moment (see Fig. 1c). It's important to note that σ_32a and σ_32o are not the direct T₁–T_n absorption cross sections, but the product of the T₁–T_n absorption cross sections and the r-ISC rate from the T_n levels back to the singlet manifold.

Considering all these elements, we define a global fit function to simultaneously adjust R, λ₂, λ₃ and A, for both power and polarization scans. To obtain meaningful results in this fitting procedure, we fix the depth of the molecule inside the pT film at 15 nm above the pT–glass interface. We also fix the singlet absorption cross-section of Tr at σ₁₂ = 1.2 × 10⁻¹⁶ cm², which will be justified later. The free parameters include the molecular rates k₂₁, k₂₃ and k₃₁, the molecule orientation angles θ, ϕ and α, and the two triplet deshelving absorption cross-sections σ_32a and σ_32o. This model allows for a perfect adjustment of all the measured molecules (both ip and oop), providing an excellent description of the small asymmetry in the bunching amplitude (A) of ip molecules polarization scans, and accurately describing the excitation polarization behavior of oop molecules. The power scans are also well reproduced, the global character of the fit function ensuring coherence between power scans and polarization scans. This is illustrated in Fig. 3 and 4 where the fit result is represented by a black dashed line over the experimental datapoints.

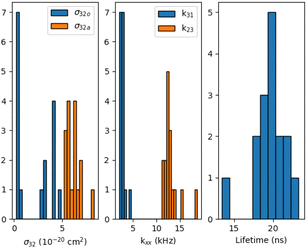
The results obtained for 16 measured Tr molecules are presented in Fig. 5 (see also ESI†). Except for one molecule, the Tr fluorescence lifetime (1/k₂₁) ranges within 17.5 to 23.2 ns, with a mean value of 19.78 ns, consistent with previous reports for Tr in pT thin films.^10,23 For k₂₃, we obtain a mean value around 13 kHz. The dark triplet depopulation rate k₃₁ has a mean value of 2.6 kHz. These results falls within the range of previously reported values.^18,19,21 It's noteworthy that our results show much lower dispersion in k₂₃ and k₃₁ values than the previous reports. We believe that this is due to our illumination conditions being more constant from molecule to molecule in the thin film configuration, and to our spectral selection. Also, only stable molecules withstand our full measurement procedure and are thus selected in those statistics.

Fig. 5 Results for 16 Tr molecules. Triplet deshelving cross-sections power: σ_32a for the component aligned with the singlet transition dipole moment and σ_32o for the component orthogonal to the singlet transition dipole moment, the power independent rates (k₂₃, k₃₁) and the fluorescence lifetime (1/k₂₁).

Regarding the triplet deshelving absorption cross-sections (see Fig. 5), σ_32a shows lower dispersion for all molecules, with a mean value of 6.2 × 10⁻²⁰ cm², while σ_32o clearly shows two distinct populations: one around 3.7 × 10⁻²¹ cm² and the other around 3.8 × 10⁻²⁰cm². The low values of σ_32o correspond to ip molecules, while the higher values of σ_32o correspond to oop molecules. Setting σ_32o to zero for oop molecules completely changes the evolution of λ₃ and the bunching amplitude A in the polarization scan, making it similar to that of ip molecules, which contradicts experimental observations reported in Fig. 4. Concerning ip molecules, setting σ_32o to zero restores a perfect symmetry of the bunching amplitude, giving equal maximum values of A for an excitation polarization angle of 30° and 125°, also contradicting experimental results presented in Fig. 3. So, although σ_32o is one order of magnitude lower than σ_32a for ip molecules, it does have a noticeable influence on the polarization scan.

A single value for the singlet absorption cross-section σ₁₂ is imposed for all molecules. The global fit procedure manages to find solutions for values of σ₁₂ ∈ [1 × 10⁻¹⁶–1 × 10⁻¹⁵] cm². Outside this range, the fit quality starts to degrade (higher residuals), and some molecules cannot be fitted properly (unable to match both polarization and power scan). To assess σ₁₂ with better accuracy, we compare θ and ϕ obtained from the global fit with results from detection polarization scans for 6 of the 16 molecules, using two analytical models^7,8 (see ESI†).

The global fit gives a very good match for ϕ, and very close values for θ with a singlet absorption cross-section fixed at σ₁₂ = 1.2 × 10⁻¹⁶ cm². This value is 2 to 10 times higher than previously reported ones for single molecule measurements in thick crystals.^19,20 Measurements in a CH₂Cl₂ solution gives 6.7 × 10⁻¹⁶ cm² possibly measured at 568.2 nm, where absorption is higher than at 532 nm.¹⁸ Another measurement of 2,5,10,13-tetra-t-butylterrylene (Tr derivative with similar spectral properties) in cyclohexane gives 7.8 × 10⁻¹⁶ cm² at 557 nm.⁴⁰ We do not have any experimental means to check the angle α. The obtained values do not show any particular trend. The main uncertainty source in the molecule angle determination is the depth of the molecule inside the film because the weights of the electric field contributions (E_x and E_z) change. We did calculations assuming the extreme cases of a 1 nm and 29 nm depth and obtained uncertainties of ± 9° for θ, ± 8° for ϕ and ± 4° for α. These uncertainties are much larger than the state-of-the-art single molecule orientation-localization microscopy methods,^14,41–43 but we provide an additional information: the molecule orientation around its emission dipole moment.

It is tempting to discuss the Tr orientation in terms of possible insertion sites in the pT matrix. However, as observed by Werley and Moerner,⁴⁴ thin pT crystal can show different orientation domains with cracks between them, which imposes special care in the analysis of ϕ and α as our 16 molecules are located in different areas in the pT film and thus likely to belong to different domains. Furthermore, we see no clear trends in angle values between ip and oop molecules.

We turn now to a discussion on the possible physical origin of populations of ip and oop molecules. As mentioned previously, our model is able to extract the optically induced deshelving rate of the triplet state T₁. This quantity is the product of the triplet–triplet (T₁–T_n) absorption cross-section and the subsequent r-ISC rate from the triplet to the singlet manifold. The difference between ip and oop molecules can thus come from either of these processes. We hypothesize that geometrical distortions of Tr molecules in the pT crystal could be at the origin of the existence of the two populations. At low temperature, pT has a complex crystalline structure with four non-equivalent pT sites resulting from the locking of the central phenyl ring of pT.⁴⁵ Tr fluorescence measurements at 1.4 K indeed showed four different 0–0 phonon lines, suggesting a simple Tr substitution with a pT molecule of the crystal in these four non-equivalent sites.¹⁵ However, at room temperature, the central phenyl rings or pT undergo large libration movements, making the molecule on average flat, leading to a mono-clinic P2_1a symmetry group with only 2 degenerate pT sites.⁴⁵ Consequently we expect a single type of Tr insertion configuration in our room temperature experiments. The observation of two molecule populations is therefore surprising and suggests that a simple pT substitution might not be the only possible Tr configuration in the pT crystal.

Two different insertion schemes should thus lead to two distinct conformations and/or environments for the Tr molecule. Geometrical distortions can impact the triplet energy levels, resulting in different T₁–T_n oscillator strengths or absorption energies (and thus cross-sections at a fixed excitation energy). Additionally, these distortions can alter the energy and number of vibrationnal levels, as change in molecular symmetry affects possible vibrationnal eigenmodes. This, in turn may influence the T_n → S_n r-ISC rate. Surprisingly, the S₁ → T₁ intersystem crossing rate (k₂₃) is similar for both ip and oop molecules. A more detailed discussion can be found in the ESI.† Based on the experimental absorption cross-sections of the T₁–T_n transitions,⁴⁰ we estimate the r-ISC probability (T_n → S_n) to be ≈ 5 × 10⁻³. Verification of these hypotheses requires challenging experiments and involving DFT calculations which are beyond the scope of the present paper.

3 Conclusions

In conclusion, our investigation, combining excitation power and polarization scans on single fluorescent Tr molecules in a thin pT host matrix, revealed that the optically pumped deshelving rate of the T₁ state involves two orthogonal transition dipole moments. We attribute these dipole moments to T₁–T₅ and T₁–T₆ transitions with subsequent r-ISC to the singlet manifold. We derive values for all the rates at play in the molecule photophysics within a 3-level system framework. The presence of two orthogonal triplet–triplet transition dipole moments enables us to determine the full three-dimensional orientation of the molecule in the laboratory frame: the singlet dipole orientation and the orientation of the molecule plane in respect to the singlet transition dipole moment. The observation of two distinct molecule populations, exhibiting different T₁ deshelving rate along the Tr short-axis raises questions on the insertion geometry of Tr in pT at room-temperature and on the possible distortion of the Tr geometry. Nevertheless, our comprehensive photophysical characterization of Tr provides valuable insights and paves the way for its enhanced utilization as a single photon source and a potent probe for various applications. The low dispersion of the obtained rates instills confidence for future experiments on the triplet state-associated rates at the single molecule level. In a more general perspective, we hope that our measurement method will enable progress where molecular orientation is crucial, such as the generation of pure spin state from single molecules where magnetic fields aligned with the molecule principal axis are needed,⁴⁶ or the design of organic light emitting devices, where orientation plays an important role for both optical and electrical properties.^47,48

Author contributions

Conceptualization, data curation, formal analysis: R. T. and S. V., funding acquisition and visualization: S. V., investigation and writing – original draft: R. T., methodology: R. T., S. V. and F. C., project administration, supervision and validation: S. V. and F. C., resources: L. S. V., L. D. and S. V., software: R. T., L. D. and S. V., writing review and editing: all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge Bruno Delomez, Philippe Forget and the SPEC mechanical workshop for their help with the experiment. This work was funded by the French National Research Agency (ANR) under the grant ANR-CE09-0009.

References

1. W. E. Moerner and L. Kador, Phys. Rev. Lett., 1989, 62, 2535–2538.
2. M. Orrit and J. Bernard, Phys. Rev. Lett., 1990, 65, 2716–2719.
3. T. Basché, S. Kummer and C. Bräuchle, Nature, 1995, 373, 132–134.
4. T. Basché, W. Moerner, M. Orrit and U. E. Wild, Single-molecule optical detection, imaging and spectroscopy, John Wiley & Sons, 2008.
5. S. Adhikari and M. Orrit, J. Chem. Phys., 2022, 156, 160903.
6. C. Toninelli, I. Gerhardt, A. S. Clark, A. Reserbat-Plantey, S. Götzinger, Z. Ristanovic, M. Colautti, P. Lombardi, K. D. Major, I. Deperasinska, W. H. Pernice, F. H. L. Koppens, B. Kozankiewicz, A. Gourdon, V. Sandoghdar and M. Orrit, Nat. Mater., 2021, 20, 1615–1628.
7. J. T. Fourkas, Opt. Lett., 2001, 26, 211–213.
8. C. Lethiec, J. Laverdant, H. Vallon, C. Javaux, B. Dubertret, J.-M. Frigerio, C. Schwob, L. Coolen and A. Matre, Phys. Rev. X, 2014, 4, 021037.
9. M. A. Lieb, J. M. Zavislan and L. Novotny, J. Opt. Soc. Am. B, 2004, 21, 1210–1215.
10. B. C. Buchler, T. Kalkbrenner, C. Hettich and V. Sandoghdar, Phys. Rev. Lett., 2005, 95, 063003.
11. M. Böhmer and J. Enderlein, J. Opt. Soc. Am. B, 2003, 20, 554–559.
12. M. P. Backlund, M. D. Lew, A. S. Backer, S. J. Sahl, G. Grover, A. Agrawal, R. Piestun and W. E. Moerner, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19087–19092.
13. M. P. Backlund, M. D. Lew, A. S. Backer, S. J. Sahl and W. E. Moerner, Chem. Phys. Chem., 2014, 15, 587–599.
14. S. Brasselet and M. A. Alonso, Optica, 2023, 10, 1486–1510.
15. S. Kummer, T. Basché and C. Bräuchle, Chem. Phys. Lett., 1994, 229, 309–316.
16. M. Vogel, A. Gruber, J. Wrachtrup and C. Von Borczyskowski, J. Phys. Chem., 1995, 99, 14915–14917.
17. A. C. Brouwer, E. J. Groenen and J. Schmidt, Phys. Rev. Lett., 1998, 80, 3944–3947.
18. F. Kulzer, F. Koberling, T. Christ, A. Mews and T. Basché, Chem. Phys., 1999, 247, 23–34.
19. L. Fleury, J. M. Segura, G. Zumofen, B. Hecht and U. P. Wild, Phys. Rev. Lett., 2000, 84, 1148–1151.
20. L. Fleury, J.-M. Segura, G. Zumofen, B. Hecht and U. Wild, J. Lumin., 2001, 94–95, 805–809.
21. M. Banasiewicz, O. Morawski, D. Wiacek and B. Kozankiewicz, Chem. Phys. Lett., 2005, 414, 374–377.
22. R. J. Pfab, J. Zimmermann, C. Hettich, I. Gerhardt, A. Renn and V. Sandoghdar, Chem. Phys. Lett., 2004, 387, 490–495.
23. S. Kühn, U. Håkanson, L. Rogobete and V. Sandoghdar, Phys. Rev. Lett., 2006, 97, 017402.
24. H. Eghlidi, K. G. Lee, X.-W. Chen, S. Götzinger and V. Sandoghdar, Nano Lett., 2009, 9, 4007–4011.
25. K.-G. Lee, H. Eghlidi, X.-W. Chen, A. Renn, S. Götzinger and V. Sandoghdar, Opt. Express, 2012, 20, 23331–23338.
26. X. W. Chen, K. G. Lee, H. Eghlidi, S. Götzinger and V. Sandoghdar, Opt. Express, 2015, 23, 32986–32992.
27. S. Kühn, G. Mori, M. Agio and V. Sandoghdar, Mol. Phys., 2008, 106, 893–908.
28. K. G. Lee, X.-W. Chen, H. Eghlidi, P. Kukura, R. Lettow, A. Renn, S. Götzinger and V. Sandoghdar, Nat. Photonics, 2011, 5, 166–169.
29. X.-L. Chu, S. Götzinger and V. Sandoghdar, Nat. Photonics, 2017, 11, 58–62.
30. M. Białkowska, A. Makarewicz, M. Banasiewicz and B. Kozankiewicz, Chem. Phys. Lett., 2013, 555, 131–134.
31. T. Minami, S. Ito and M. Nakano, J. Phys. Chem. Lett., 2012, 3, 2719–2723.
32. I. Carmichael and G. L. Hug, J. Phys. Chem. Ref. Data, 1986, 15, 1–250.
33. K.-G. Lee, J. Korean Phys. Soc., 2014, 64, 1792–1796.
34. R. Loudon, The quantum theory of light, OUP Oxford, 2000.
35. Y. Avlasevich, C. Kohl and K. Müllen, J. Mater. Chem., 2006, 16, 1053–1057.
36. T. M. Halasinski, J. L. Weisman, R. Ruiterkamp, T. J. Lee, F. Salama and M. Head-Gordon, J. Phys. Chem. A, 2003, 107, 3660–3669.
37. J. Sepioł, J. Jasny, J. Keller and U. P. Wild, Chem. Phys. Lett., 1997, 273, 444–448.
38. D. Axelrod, J. Microscopy, 2012, 247, 147–160.
39. J. Waxenegger, A. Trügler and U. Hohenester, Comput. Phys. Commun., 2015, 193, 138–150.
40. Y. Meyer, P. Plaza and K. Müllen, Chem. Phys. Lett., 1997, 264, 643–648.
41. O. Zhang, W. Zhou, J. Lu, T. Wu and M. D. Lew, Nano Lett., 2022, 22, 1024–1031.
42. O. Zhang, Z. Guo, Y. He, T. Wu, M. D. Vahey and M. D. Lew, Nat. Photonics, 2023, 17, 179–186.
43. P. Jouchet, A. R. Roy and W. Moerner, Opt. Commun., 2023, 542, 129589.
44. C. A. Werley and W. E. Moerner, J. Phys. Chem. B, 2006, 110, 18939–18944.
45. P. Bordat and R. Brown, Chem. Phys., 1999, 246, 323–334.
46. O. G. Reid, J. C. Johnson, J. D. Eaves, N. H. Damrauer and J. E. Anthony, Acc. Chem. Res., 2023, 57, 59–69.
47. T. D. Schmidt, T. Lampe, P. I. Djurovich, M. E. Thompson and W. Brütting, et al. , Phys. Rev. Appl., 2017, 8, 037001.
48. A. Hofmann, M. Schmid and W. Brütting, Adv. Opt. Mater., 2021, 9, 2101004.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00867g

---