Simultaneous switching of two different CO₂-switchable amines in the same solution

Abstract

Most CO₂-responsive systems operate by using a base in water that is expected to be mostly deprotonated when under an atmosphere of air and mostly protonated under an atmosphere of CO₂. This concept has led to the development of many different CO₂-responsive materials such as solvents, polymers, surfactants, and solutes. As CO₂-responsive materials research continues, more complex systems may be developed, including systems containing two different bases with different basicities. Understanding the influence each base has on the protonation equilibrium of the other base is important for designing systems in which effective deprotonation and protonation occur. This article presents a model that can predict the solution pH and the % protonation of two different bases at various concentrations under air and CO₂. Experimental data was collected to demonstrate the successful simultaneous switching of two amines and to evaluate the accuracy of the predictive model. The simultaneous switching of two different CO₂-switchable amines in the same solution was determined to be possible but only if the amine concentrations and basicities are within certain ranges, and only if the pK_aH values of the two bases differ by no more than 3 units.

---

1. Introduction

Stimuli-responsive or switchable materials have been a very active area of research in the past two decades as these materials offer the solution to processes that have time-separated conflicting requirements. For example, sunglasses should be dark when the wearer is outside, but light when they’re inside. An ideal extraction solvent would dissolve the desired solute very well during the extraction stage but not at all when the solute and solvent subsequently need to be separated. Stimuli-responsive materials can address such conflicting requirements by reversibly altering their properties when a specific stimulus is added or removed. Different stimuli have been used including voltage, light, oxidants/reductants, acids/bases, and CO₂.¹ Using CO₂ as a stimulus is particularly interesting as it provides some advantages over other stimuli such as easy removal with no residual salt accumulation, low toxicity, and no need for the material to be transparent or electrically conductive.² CO₂ is a cheap and effective trigger that can be used in many different industrial processes to allow for multiple properties to be changed on demand.

Many CO₂-responsive materials use the acid–base reaction between a neutral organic base and hydrated CO₂ to form a charged bicarbonate salt³ (eqn (1)). These are the simplest CO₂-responsive materials and the most widely explored because bicarbonate salt formation can often be easily reversed under mild conditions (T ≤ 60 °C and/or sparging with a non-acidic gas like air). Tertiary amines are the most common choice of base for these reactions but any basic group with a free lone pair and suitable basicity such as amidines or guanidines can achieve this reaction. It is also possible with anionic bases such as carboxylate anions but that scenario is not considered in this paper.

B + CO₂ + H₂O ⇌ [BH⁺][HCO₃⁻] (1)

The ability of an organic base to be CO₂-switchable in water depends upon the organic compound having appropriate basicity. If it is too basic, then it will have a high % protonation under air and under CO₂, so that its properties will be those of the bicarbonate salt regardless of whether CO₂ is present or absent. Such a system is not switchable. Similarly, if it is too weakly basic, then it will have a low % protonation under air and under CO₂, so that its properties will be those of the neutral amine and again largely unaffected by the introduction or removal of CO₂. Fortunately, if the basicity is in an appropriate range between these two extremes, the % protonation will be low under air and high under CO₂, leading to a significant change in properties. Thus the pK_aH (the pK_a of the protonated base) must be within a range that is appropriate for the concentration, temperature, and pressure being used. For an amine of appropriate basicity, the majority of the amine in aqueous solution will be neutral under an atmosphere of air. However, upon the addition of CO₂ (usually at 0.1 MPa) into the aqueous system, the amine will become mostly protonated.⁴ Removal of the CO₂ will cause the base to easily revert back to its neutral form. Thus the greatest switch in properties can only be achieved if an amine of the correct basicity is used.

Protonation of the chosen base depends on the solution's pH relative to the system midpoint, defined as the pH at which half of the base, regardless of its location in the system, is protonated. Here, and for the rest of the discussion, we will assume that all of the amine, regardless of the degree of protonation, remains in the aqueous phase. In that situation, the system midpoint is the same as the aqueous midpoint, defined as the pH at which the base located in the aqueous phase is 50% protonated. This occurs when the pH is equal to the pK_aH.

To achieve switching using CO₂ as the trigger there are two key requirements or criteria (Scheme 1). First, the pH of the solution under air must be greater than the system midpoint, preferably at least one unit above, so that the base is no more than 10% protonated. The second requirement is that when the solution is under an atmosphere of CO₂, the pH must be lower than the midpoint, preferably at least one unit below so that at least 90% of the base is in its protonated form. The choices of 10 and 90% are somewhat arbitrary. One could argue that 15 and 85% might be adequate, if not as good. However, for the mathematical exercise it was convenient to choose specific limits.

Scheme 1 The two criteria for CO₂-responsive materials to be effectively switched using CO₂.

As research into stimuli-responsive materials continues to expand, increasingly complex systems are being designed. Many authors have reported a material that responds to two or more stimuli (Scheme 2A) such as CO₂ and temperature.^5–8 On the other hand, there has been less attention paid to the reverse situation: using one stimulus to simultaneously switch two or more materials (Scheme 2B). In one example, Yan et al. showed that a local temperature rise triggered responses simultaneously in two thermoresponsive polymers in a bilayer structure.⁹ In our own research on CO₂-switchable systems, we have found it useful to simultaneously switch two different chemicals at the same time.

Scheme 2 Complex stimuli responsive systems. (A) A single object that can respond to two different stimuli. (B) Two objects that can respond to the same stimulus simultaneously.

Having two or more species in a system respond to CO₂ increases the complexity, with the risk that one switchable chemical may interfere with the switching of the other. An example of a more complex system is the polymerization of a CO₂-switchable monomer using a CO₂-responsive initiator while in the presence of carbonated water. The monomer and initiator may have different basicities and different concentrations, with the monomer being at much higher concentration. Understanding the monomer's influence on the initiator's ability to switch, and vice versa, is important for designing the system. The initiator may need to be protonated, in order for it to sufficiently rapidly generate radicals at the reaction temperature.

The monomer may also need to be protonated, or it will not adequately dissolve. Similar arguments apply once the CO₂ is removed; if both the initiator (or its residues at the chain ends) and the monomer repeat units in the polymer chain are to be CO₂-switchable, then they must switch to largely unprotonated when the CO₂ is removed. The basicity and concentration of each base in an aqueous solution will influence its own equilibrium as well as the other base's equilibrium in a predictable way. Understanding this, and being able to make predictions mathematically can lead to the design of complex CO₂-switchable systems that operate correctly when under air or CO₂.

Previous work in our group developed a model for single base CO₂-switchable systems and their behaviour in water under air and under an atmosphere of CO₂.¹ Two equations were derived allowing for the prediction of [H₃O⁺] and therefore the pH of different base solutions at various concentrations under air and under CO₂ (eqn (2) and (3) respectively). Once the pH of the solution is known, the % protonation of the base in solution can be predicted with eqn (4).

In these equations, [B]₀ is the nominal concentration of base, so that [B]₀ = [B] + [BH⁺]. Because these equations use molarities rather than activities, they are not accurate at higher concentrations. However, comparisons to experimental data showed them to predict pH values within 0.3 units of the observed pH at concentrations up to 1 M.¹

0 = [H₃O⁺]³ + (K_aH + [B]₀)[H₃O⁺]² − K_W[H₃O⁺] − K_WK_aH (2)

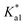The concentration of CO₂ in solution is governed by the Henry's law constant (K_H) and is highly temperature dependent.¹⁰ CO₂ is a weak acid and therefore only partially dissociates in water to bicarbonate ions in the pH range typical for CO₂-switching chemistry (pH 4 to 10). The observed equilibrium between dissolved CO₂ and bicarbonate in solution is governed by the equilibrium constant . These two factors limit the lowest accessible pH of aqueous solutions saturated with CO₂ to approximately 3.9 and 3.5 under 0.1 MPa and 1 MPa of CO₂ respectively at 22 °C.

From the models derived from eqn (2)–(4) it was observed that the pK_aH of a base and its concentration in solution are critical factors that determine whether it can be effectively switched with an atmosphere of CO₂ (Fig. 1).¹ To meet criterion #1 (<10% protonation under air), a minimum concentration of base in solution is required, as indicated by the turquoise dashed line in Fig. 1. This is due to partial protonation of the base by water forming the hydroxide salt [BH⁺][OH⁻]. As the pK_aH of a base increases a larger fraction is protonated by water, raising the minimum concentration required to meet criterion #1. On the other hand, as the concentration of base in solution increases it becomes harder for weaker bases (pK_aH ≤ 8) to be >90% protonated under 0.1 MPa of CO₂ (Criterion #2). This is due to the pH of the system approaching the pK_aH of both the base and bicarbonate ( at 25 °C)¹⁰ creating a buffer. The solution will become saturated with CO₂ before the buffer is consumed preventing complete protonation of the base in solution. This paper describes the factors that influence the behaviour of aqueous CO₂-responsive systems containing two different bases. We assume that the system is being designed in the hope that both bases will be CO₂-switchable and therefore that both pK_aH bases affect each other under air and under CO₂ with varying concentrations of each amine. Predictions from this model were then compared to experimental data to evaluate the accuracy and consistency of the model.

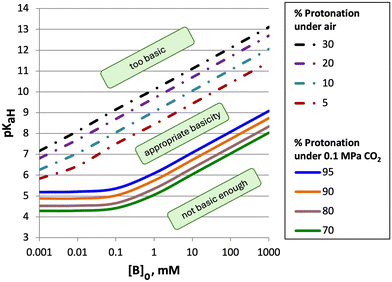Fig. 1 The pK_aH required of a base to have a specific percent protonation when mixed with water or carbonated water at 25 °C. Dashed lines represent the pK_aH required to achieve the specific percent protonation under air. Solid lines represent the pK_aH required to achieve the specific percent protonation of a base under an atmosphere of CO₂. A base having a pK_aH value between the dashed lines and the solid lines has appropriate basicity to be an effective CO₂-switchable compound, as it satisfies both criteria at the indicated concentration.¹

2. Results and discussion

2.1. Predictions of the mathematical model

To effectively predict the [H₃O⁺] and pH of aqueous solutions of two bases, eqn (2) and (3) must be modified to account for the second base present. There are now two bases: X and Y that have their own unique K_aH constants K_X and K_Y respectively. For the purposes of this paper, the pK_aH of base X is always equal to or less than the pK_aH of base Y. Adding in the new terms for the second base we get eqn (5) and (6) for the [H₃O⁺] (and therefore pH) of two base solutions under air and CO₂ respectively (derivations shown in the ESI†).As these are both quartic equations there will be four possible x-intercepts for these equations, but only one of those answers should be reasonable and therefore the real pH of solution. With the predicted [H₃O⁺] of these solutions, the % protonation of each base can be calculated using eqn (7) and (8).Using the above equations, we are able to accurately predict both the pH and % protonation of 2 bases in solution under air and under an atmosphere of CO₂. These predictions were verified by comparing experimental pH values to the predicted values. We are able to predict the effective range of concentrations in which two bases of different basicity both meet the required criteria and therefore can be effectively switched using CO₂ as the stimulus. Scenarios where the two bases in solution had the same concentration, and where they had differing concentrations were both explored.

2.2. Scenario 1: two bases with the same concentration: [X]₀ = [Y]₀

To illustrate the approach to the problem, we will first discuss the example of two bases X and Y, where X is the weaker base (pK_X = 8.0) and Y is the stronger (pK_Y = 10.0), and where they are both at the same nominal concentration ([Y]₀ = [X]₀). Several assumptions were made in this model: bases X and Y are infinitely soluble in both their neutral and bicarbonate salt forms; the pH never rises high enough that significant amounts of carbonate ions are formed or present in solution; the solutions containing CO₂ are completely saturated; T = 25 °C; and P_CO2 = 0.1 MPa. For a given nominal concentration of the two bases in water under air, eqn (5) was used to predict the [H₃O⁺]. This was repeated for nominal concentrations ranging from 1 μM to 10 M. Using the predicted [H₃O⁺] of these different solutions, the percent protonation of each base was calculated using eqn (7) and (8). The % protonation of bases X and Y under air was then plotted against their nominal concentration in solution (Fig. 2A). From this graph it is clear that above 10 mM, both bases are <10% protonated, which satisfies the first criterion for CO₂ switching.

Fig. 2 Results for the example case of two bases X and Y, where the nominal concentrations of the bases are identical and the pK_aH values are 8 and 10, respectively. (A) Predicted percent protonation of bases X and Y under air. In the shaded area both bases are <10% protonated under air. (B) Predicted percent protonation of bases X and Y under an atmosphere of CO₂. In the shaded area both bases are >90% protonated under an atmosphere of CO₂. (C) Wedge graph indicating the conditions in which both bases meet both criteria. The basicity of the stronger base is again fixed at pK_Y = 10, but the weaker base (pK_X) is allowed to vary in basicity.

Next, we wanted to determine the percent protonation of the same two bases X and Y at various nominal concentrations under an atmosphere of CO₂. To achieve this, the [H₃O⁺] of the different solutions was predicted using eqn (6). From these predictions, eqn (7) and (8) were used to determine the percent protonation of bases X and Y at concentrations from 1 μM to 1 M. In Fig. 2B, it is evident that the maximum concentration where both bases are >90% protonated under an atmosphere of CO₂ is 100 mM. Therefore, from the data shown in Fig. 2A and B, we can conclude that these two bases are both CO₂-switchable only if their nominal concentrations fall in the range of 10 to 100 mM. That is a fairly narrow range, which might restrict the applications of solutions containing these two CO₂-switchable amines.

What would happen if ΔpK_aH, meaning the difference between the pK_aH values of the two amines, was larger or smaller than 2? Would that affect the range of viable concentrations?

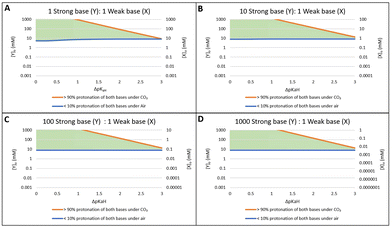
To evaluate this question, we retained the assumptions that Y has a pK_Y of 10 and that the bases have equal nominal concentrations. However, we allowed the pK_X of base X, and therefore also ΔpK_aH, to vary. With the data above, we plotted the minimum and maximum concentrations whereby both criteria are simultaneously met for both bases. In other words, both bases (X and Y) are <10% protonated under air and >90% protonated under an atmosphere of CO₂. These minimum and maximum concentrations are plotted against ΔpK_aH (Fig. 2C). This graph shows the effective concentration range where both bases can be effectively switched using CO₂ at atmospheric pressure.

Between the two lines (the green triangle) is considered the “Goldilocks zone” where both bases satisfy both criteria for effective switching. At concentrations above the effective range the bases are too concentrated and at least one of them will be <90% protonated under 0.1 MPa of CO₂ (i.e. criterion #2 is not satisfied). Conversely if the concentration of the bases is below the effective range at least one base will be >10% protonated under air (i.e. criterion #1 is not satisfied). Evidently, having a smaller ΔpK_aH expands the range of concentrations in which both amines are CO₂-switchable. However, having a ΔpK_aH greater than 3 makes it impossible for both amines to be switchable, at any concentration.

Similar wedge-shaped diagrams were obtained for the situations where the stronger base has a pK_Y of 8, 9, 10, or 11 (Fig. 3). Solutions with base concentrations that fall between the two lines will satisfy both requirements to be considered effectively switched from mostly protonated to mostly deprotonated. For every unit decrease in pK_Y, both the minimum and maximum effective concentrations decrease by 10-fold. In other words, weaker base pairs must be used in lower concentrations to achieve effective switching. As the ΔpK_aH increases the effective range of concentrations for switching decreases. On the other hand, with two bases of the same pK_aH we can see that the accessible concentration range for effective switching is quite large (approx. 0.5 mM to 1.0 M for base Y pK_aH = 9) as was predicted for single base systems. For every increase in ΔpK_aH by 1 the range for effective switching decreases by a factor of ∼10. Once ΔpK_aH ≃ 3 is reached, the effective range is predicted to shrink to a single concentration. At ΔpK_aH > 3, there are no concentrations at which the criteria are satisfied. Thus, CO₂-switching of two bases of very different basicities is not possible.

Fig. 3 The minimum and maximum effective concentrations to achieve <10% protonation under air and >90% protonation under CO₂ with the basicity pK_X of the weaker base being allowed to vary but the basicity pK_Y of the stronger base remaining fixed at = (A) 8.0 (B) 9.0 (C) 10 and (D) 11.

These predictions show that increasing the ΔpK_aH of two base systems in water will have little effect on the minimum concentration to achieve <10% protonation under air while having a significant effect on the maximum allowable concentration for >90% protonation under CO₂. The minimum concentration changes very little with ΔpK_aH due to the stronger base always deprotonating last, negating any influence of the weaker base. At higher concentrations of base under CO₂, the stronger base raises the pH to a point near or above the pK_aH of the weaker base preventing it from achieving the >90% protonation requirement. As the ΔpK_aH between the two bases increases this effect becomes more pronounced to where at ΔpK_aH > 3 the allowable range of concentrations for the two bases has disappeared.

2.3. Scenario 2: two base systems with different concentrations of bases X and Y: [X]₀ < [Y]₀ and [X]₀ > [Y]₀

All concentrations referenced in the following text and graphs are those of the stronger base Y. In the previous scenario where both bases had the same concentration, this distinction was not necessary.

We first investigated what effect increasing the amount of weaker base (X) relative to the stronger base had on the minimum and maximum concentrations for effective switching. In these scenarios the pK_aH of base Y in the two base system was set to 10 and the ΔpK_aH was 0, 0.3, 1, 2 and 3 units. Increasing the amount of weak base (X) relative to strong base (Y) has a significant impact on both the minimum and maximum concentration for effective switching. With every 10-fold increase in the concentration of X relative to Y, the maximum [Y]₀ for >90% protonation under CO₂ decreases by a factor of 10 (red line in Fig. 4).

Fig. 4 The minimum and maximum effective concentrations to achieve <10% protonation under air and >90% protonation under CO₂ the basicity pK_X of the weaker base being allowed to vary but the basicity pK_Y of the stronger base remaining fixed at = 10. The [X]₀ was increased to observe the changes in the acceptable concentration ranges. [Y]₀:[X]₀ = (A) 1 : 1, (B) 1 : 10, (C) 1 : 100, and (D) 1 : 1000.

The minimum concentration also decreases with every 10-fold increase in X relative to Y (Fig. 5). This relationship is far less linear than the observed effect on maximum concentration. Once again, this effect can be attributed to the final pH of the two-base solution. As the concentration of both bases in solution increases so too does the pH. As the pH rises closer to the pK_aH of the weaker base the protonation of that base decreases and it will fall below the >90% protonation requirement.

Fig. 5 The minimum and maximum effective concentrations to achieve <10% protonation under air and >90% protonation under CO₂ with the basicity pK_X of the weaker base being allowed to vary but the basicity pK_Y of the stronger base remaining fixed at 10. The ratio of [Y]₀ : [X]₀ was increased to observe the changes in the acceptable concentration ranges. (A) 1 : 1, (B) 10 : 1, (C) 100 : 1, and (D) 1000 : 1. Strong base Y, being simultaneously stronger and at higher concentrations than X, determines the acceptable concentration range.

As shown in Fig. 5, increasing the ratio of strong to weak base has little effect on the acceptable range of concentrations. Increasing the [Y] : [X] ratio from 1 : 1 to 10 : 1 slightly lowers the maximum and minimum concentrations, and further increases in the ratio have no significant effect.

3. Experimental confirmation of predictive model

To test the validity of these predictions, 12 discrete combinations of ΔpK_aH and [Y]₀ : [X]₀ mole ratio were tested experimentally (Table 1). Solutions of two bases in water were prepared for each of the 12 combinations, in triplicate, and tested under air and under CO₂ at 0.1 MPa. Tertiary amine small molecules were chosen as the bases for use in this study as they can only form bicarbonate salts with CO₂ in water, not carbamate salts.

Table 1 Combinations of different ΔpK_aH and concentrations explored in a two-base system

Concentration	pKaH difference between amines
Equal	0.5	1	2	3
10× excess stronger base	0.5	1	2	3
10× excess weaker base	0.5	1	2	3

---

The amines chosen for this study (Table 2) were selected for their solubility in water in both their neutral and bicarbonate forms. Under both air and CO₂ these solutions will remain monophasic, eliminating complications due to phase separation of the neutral organic base.

Table 2 Amines and their reported pK_aH used in the preparation of the 2-base solutions

Amine	Structure	Reported pKaH
4-Methylmorphine (MM)		7.38^11
Triethanolamine (TEA)		7.85^12
2-(Dimethylamino)ethanol (DMAE)		9.31^13
3-Diethylamino-1-propanol (DEAP)		10.39^14

---

Each combination was analyzed under air and CO₂ by ¹H NMR spectroscopy to determine the % protonation of each amine in the solution. To determine % protonation, the chemical shift (ppm) of the protons alpha to the nitrogen was measured. This value was compared to calibration spectra of the same amine with 0 and 100% protonation. These calibration values were determined by adding the amine to either a 1 M KOH or HCl solution. For a given amine pair, the chemical shifts of key protons in both amines were observed and then compared against the values obtained in HCl and KOH solutions.

The % protonation of an amine under air and under CO₂ is expressed as eqn (9), where ppm_obs is the chemical shift observed under either air or CO₂.

3.1. Equal concentration results

To isolate the effect of ΔpK_aH on % protonation, solutions were prepared with equal concentrations of the stronger and weaker bases. The pH and % protonation were first determined under air; both amines were weighed into the same vial and dissolved into Millipore® water. After the dissolution of the amines, the pH of the samples was immediately analyzed in triplicate. This was done to minimize the effects of atmospheric CO₂ interacting with the sample. The measured pH values for each ΔpK_aH pair agree with the predictive model, indicating some preliminary validity to the model (Table 3).

Table 3 Predicted and measured pH and % protonation of solutions with 0.1 M concentrations of stronger and weaker base under air and CO₂

ΔpKaH	Amines in solution	Under air		Under CO2
		pH^a^c	% protonation^b^c	pH^a^c	% protonation^b^c
a Measured at 20 °C, δ ± 0.1 pH unit. b Measured at 26 °C in a Bruker NEO 500 MHz NMR instrument, δ ± 1%. c Data in brackets are the observed values.
0.47	MM	10.5 (10.6)	0 (0)	7.0 (7.0)	71 (72)
	TEA		0 (4)		88 (89)
1.08	DMAE	11.7 (11.8)	1 (3)	7.1 (6.8)	99 (99)
	DEAP		5 (4)		100 (100)
1.93	MM	11.2 (11.3)	0 (0)	7.0 (6.9)	71 (70)
	DMAE		1 (4)		100 (100)
3.01	MM	11.7 (11.7)	0 (0)	7.0 (6.9)	71 (70)
	DEAP		5 (4)		100 (100)

---

Using the pH of an aqueous solution containing 2 different amines is insufficient to confirm the model's predictive ability of an individual amine's contribution. Analysis by ¹H NMR spectroscopy was used to compare the predicted % protonation to the experimental % protonation of each amine in solution (90% H₂O, 10% D₂O).

Under air, it is predicted that all the ΔpK_aH combinations would be mostly deprotonated, <10%. The ¹H NMR analysis confirmed that all the amines did not exceed 10% protonation under air (Table 3). The higher pK_aH amines were more protonated than the lower pK_aH amines, as expected. At low ΔpK_aH, the lower pK_aH amine does become slightly protonated but after a difference of about 2 units, the lower pK_aH amine remains completely deprotonated. This trend agrees with the model's prediction; a difference in pK_aH of 2 or more units will lead to a lower % protonation to the less basic amine when at the same concentration.

Upon completion of the analysis under air, the four samples were sparged with CO₂ gas to saturate the solutions with CO₂. The rate-limiting step for the dissolution of CO₂ is the mass transfer of CO₂ into the water, so the samples were sparged for 4 h to ensure saturation was achieved. While a glass fritted sparging tube would have a better mass transfer of gas into solution, a stainless steel needle was used instead because the sample could be nearly completely sealed with only a small gauge needle for venting. Slow sparging by this method helps to prevent significant water loss.

After 4 h of sparging with CO₂, the pH and % protonation of the solutions were determined. The predicted values of the pH were around 7 which was observed for 3 out of the 4 solutions (Table 3). The sample(s) with ΔpK_aH of 1.08 was 0.3 pH units lower than predicted but this lower pH had no significant influence on the % protonation as both bases had already approached 100% protonation by the predicted pH. Neutralizing a solution to exactly pH 7 with no buffer can be experimentally challenging. The concentrations of [H₃O⁺] and [⁻OH] are tiny, so any slight change in conditions will measurably change the pH.

The data obtained from the experimental pH and % protonation under air and CO₂ analysis using equal concentrations of amines match the predictions, within reasonable experimental error. These experiments also prove that it is certainly possible to switch two amines with significantly different basicities at the same time using CO₂ as the trigger. Under air, criterion #1 was met as all the amines remained <10% protonated. The weakest amine, MM struggled to reach >90% protonation simply because of its low pK_aH but the other 3 amines all achieved criterion #2 which >90% protonation under CO₂ in the presence of another amine.

3.2. Results with solutions containing an excess of the stronger base

With the effects of pK_aH difference established at equal concentrations, four new solutions were prepared with a 10 times excess of stronger base to observe how changing the pK_aH and concentration of stronger base affects each solution's pH and % protonation values. The solutions had a concentration of 0.1 M of stronger amine and 0.01 M of weaker amine and were prepared using the same method as the equal-concentration solutions. The pH of each solution was measured in triplicate immediately after preparation. The predicted and measured pH values for each solution were identical, which indicated that the model was accurate at predicting the pH these solutions under air (Table 4).

Table 4 Predicted and measured pH and % protonation of solutions with a 10 : 1 ratio of stronger to weaker base under air and CO₂

ΔpKaH	Amines in solution	Under air		Under CO2
		pH^a^c	% protonation^b^c	pH^a^c	% protonation^b^c
a Measured at 20 °C, ±0.1 unit. b Measured at 26 °C in a Bruker NEO 500 MHz NMR instrument, ±1%. c Data in brackets is the observed value.
0.47	MM	10.4 (10.4)	0 (0)	6.8 (6.7)	80 (79)
	TEA		0 (3)		92 (93)
1.08	DMAE	11.7 (11.7)	0 (2)	6.9 (6.8)	100 (99)
	DEAP		5 (4)		100 (99)
1.93	MM	11.2 (11.2)	0 (0)	6.8 (6.8)	78 (77)
	DMAE		1 (3)		100 (100)
3.01	MM	11.7 (11.7)	0 (0)	6.8 (6.8)	78 (79)
	DEAP		5 (4)		100 (100)

---

Under air, with 10 times excess of stronger amine, both amines were predicted to be mostly deprotonated in all ΔpK_aH cases. The ¹H NMR analysis of each solution confirmed that all solutions were below the 10% protonation cut-off; in some cases, the weaker amine was completely deprotonated as predicted (Table 4). The stronger amine in a 10 times excess dominates the solution, hindering the weaker amine's ability to become measurably protonated in some cases. The 0.1 M concentration of the stronger amine remained unchanged from the equal concentration testing and produced % protonation values similar to those samples. The experimental data matches the exact trends observed in the predictive model; an excess of the stronger amine produces a solution with an almost completely deprotonated weaker amine and mostly deprotonated stronger amine.

The 4 samples were sparged then with CO₂ for 4 h using the previously established method. The pH measurements of the 10 times excess stronger base samples showed similar results to the equal concentration samples. The observed pH of each sample was within 0.1 units of the predicted values. ¹H NMR spectra of the CO₂ sparged samples confirmed that the experimental % protonation was similar to the predicted % protonation.

The model consistently estimates the correct pH and % protonation even when the concentration of stronger amine is 10 times greater than the weaker amine.

3.3. Results with solutions containing an excess of the weaker base

The model demonstrated excellent predictive accuracy with a 10 times excess of stronger amine, so the opposite scenario was explored with a 10 times excess of the weaker amine to observe if the model could estimate this correctly. The 4 samples were prepared with a concentration of 0.1 M of weaker amine and 0.01 M of stronger amine using the established method. The pH of each sample was analyzed under air in triplicate and compared against the predicted value (Table 5). The observed pH again agreed with the predicted values.

Table 5 Predicted and measured pH and % protonation of solutions with a 1 : 10 ratio of stronger to weaker base under air and CO₂

ΔpKaH	Amines in solution	Under air		Under CO2
		pH^a^c	% protonation^b^c	pH^a^c	% protonation^b^c
a Measured at 20 °C, ±0.1 unit. b Measured at 26 °C in a Bruker NEO 500 MHz NMR instrument, ±1%. c Data in brackets is the observed value.
0.47	MM	10.3 (10.3)	0 (0)	6.8 (6.7)	81 (83)
	TEA		0 (1)		93 (92)
1.08	DMAE	11.3 (11.4)	1 (1)	6.9 (6.7)	100 (99)
	DEAP		11 (8)		100 (100)
1.93	MM	10.7 (10.7)	0 (0)	6.8 (6.7)	81 (83)
	DMAE		4 (4)		100 (100)
3.01	MM	11.2 (11.1)	0 (1)	6.8 (6.8)	81 (82)
	DEAP		15 (16)		100 (100)

---

With a lower concentration of stronger amine, some were predicted to have a higher than 10% protonation in some cases. At low amine concentrations, the amine's ability to become protonated increases, depending on its pK_aH; in the 10 times excess of stronger amine samples, the elevated pH caused by the stronger amine prevented the weaker base from being protonated. In these excess weaker amine cases, the more strongly basic amines take priority in becoming protonated as they are more basic. The low concentration, combined with the higher pK_aH leads to a >10% protonation under air (Table 5).

After the samples were sparged with CO₂ for 4 h, the pH and % protonation of each solution was determined. Each of the 4 solutions again matched the predicted values for both pH and % protonation with reasonable accuracy. The model consistently estimates the correct pH and % protonation when the concentration of stronger amine is 10 times lower compared to the weaker amine.

4. Conclusions

Combining the protonation equilibrium expressions of 2 different bases, a new predictive model has been generated to predict the protonation of 2 different bases under air and under CO₂ in water. Using the predictive model as a guide, the simultaneous CO₂ switching of two different amines in aqueous solution was experimentally determined to be possible, but with limitations. The ΔpK_aH of the 2 bases can be no larger than 3 units but even with a ΔpK_aH of 2 units the % protonation of the weaker amine struggles to reach >90% protonated under CO₂ even when in higher concentration. In cases where excess of the stronger amine is used, the % protonation of both amines will behave similarly to a solution that has equal concentrations of both the stronger and weaker bases; there is <10% protonation under air but slightly higher % protonation of the weaker amine under CO₂. An excess of weaker base leads to a slightly higher % protonation of stronger base under air but does not lead to increased % protonation of the weaker amine when under CO₂.

The model was consistent at predicting the pH and % protonation under air and under CO₂ at equal and unequal concentrations of the two bases. The experimental data obtained at equal and unequal concentrations of each base proved the trends predicted by the model. This model provides a new method for predicting the behavior of a two-base system at any concentration of each base which will be beneficial to the design of more complex CO₂-switchable systems in the future.

Author contributions

M. Sanger: methodology, formal analysis, investigation, writing – original draft, writing – review & editing, visualization. D. Barker: methodology, validation, investigation, writing – original draft, writing – review & editing. P. G. Jessop: conceptualization, formal analysis, resources, writing – review & editing, supervision, project administration, funding acquisition.

Conflicts of interest

One of the authors (PGJ) is an inventor but not owner of several patents or patent applications that involve CO₂-switchable materials.

Acknowledgements

The authors gratefully acknowledge funding from the Natural Sciences and Engineering Research Council of Canada (NSERC, grant RGPIN-2023-05700). PGJ also thanks the Canada Research Chairs Program for support.

Notes and references

1. A. K. Alshamrani, J. R. Vanderveen and P. G. Jessop, A guide to the selection of switchable functional groups for CO₂-switchable compounds, Phys. Chem. Chem. Phys., 2016, 18, 19276–19288.
2. A. Darabi, P. G. Jessop and M. F. Cunningham, CO₂-responsive polymeric materials: Synthesis, self-assembly, and functional applications, Chem. Soc. Rev., 2016, 45, 4391–4436.
3. P. G. Jessop, S. M. Mercer and D. J. Heldebrant, CO₂-triggered switchable solvents, surfactants, and other materials, Energy Environ. Sci., 2012, 5, 7240–7253,  10.1039/c2ee02912j.
4. P. G. Jessop and M. F. Cunningham, CO₂-switchable Materials: Solvents, Surfactants, Solutes and Solids, Royal Society of Chemistry, Cambridge, 2020.
5. P. Papaphilippou, M. Christodoulou, O.-M. Marinica, A. Taculescu, L. Vekas, K. Chrissafis and T. Krasia-Christoforou, Multiresponsive Polymer Conetworks Capable of Responding to Changes in pH, Temperature, and Magnetic Field: Synthesis, Characterization, and Evaluation of Their Ability for Controlled Uptake and Release of Solutes, ACS Appl. Mater. Interfaces, 2012, 4, 2139–2147,  DOI:10.1021/am300144w.
6. K. Wang, S. Chen and W. Zhang, A New Family of Thermo-, pH-, and CO₂-Responsive Homopolymers of Poly[Oligo(ethylene glycol) (N-dialkylamino) methacrylate]s, Macromolecules, 2017, 50, 4686–4698,  DOI:10.1021/acs.macromol.7b00763.
7. H. Liu, S. Chen, H. Cui, J. Hu, H. Cai and W. Deng, Fabrication of triple responsive polymer brushes and their catalytic performance after loading palladium, RSC Adv., 2015, 5, 72444–72452,  10.1039/c5ra13245b.
8. M. Ramezani, S. N. Ellis, A. Riabtseva, M. F. Cunningham and P. G. Jessop, CO₂-Responsive Low Molecular Weight Polymer with High Osmotic Pressure as a Draw Solute for Forward Osmosis, ACS Omega, 2023, 8, 49259–49269,  DOI:10.1021/acsomega.3c07644.
9. X. Yan, Q. Chen, Z. Huo, N. Zhang and M. Ma, Programmable Multistimuli-Responsive and Multimodal Polymer Actuator Based on a Designed Energy Transduction Network, ACS Appl. Mater. Interfaces, 2022, 14, 13768–13777.
10. A. Stefansson, P. Benezeth and J. Schott, Carbonic acid ionization and the stability of sodium bicarbonate and carbonate ion pairs to 200 degrees C – A potentiometric and spectrophotometric study, Geochim. Cosmochim. Acta, 2013, 120, 600–611,  DOI:10.1016/j.gca.2013.04.023.
11. D. Evans and D. H. Ripin, Pka Values Compilation, 2022. https://organicchemistrydata.org/hansreich/resources/pka/ (accessed July 10th, 2023).
12. D. Xiong, Z. Li, H. Wang and J. Wang, Selective separation of aliphatic and aromatic amines with CO₂-switchable ionic liquids aqueous two-phase systems, Green Chem., 2013, 15, 1941–1948,  10.1039/c3gc40411k.
13. N. F. Hall and M. R. Sprinkle, Relations between the structure and strength of certain organic bases in aqueous solution, J. Am. Chem. Soc., 1932, 54, 3469–3485.
14. J. R. Vanderveen, J. Durelle and P. G. Jessop, Design and evaluation of switchable-hydrophilicity solvents, Green Chem., 2014, 16(3), 1187–1197,  10.1039/C3GC42164C.

---

Footnote

† Electronic supplementary information (ESI) available: (a) A spreadsheet for pH and % protonation predictions. (b) A document including derivations, graphs, example NMR spectra, example calculations, and experimental materials and methods. See DOI: https://doi.org/10.1039/d4cp00392f

---