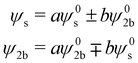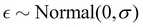Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The strength of the OH-bend/OH-stretch Fermi resonance in small water clusters†
Nils O. B.
Lüttschwager

Georg-August-Universität Göttingen, Institut für Physikalische Chemie, Tammannstraße 6, 37077 Göttingen, Germany. E-mail: nluetts@gwdg.de
First published on 15th March 2024
Abstract
A novel Raman jet-spectrometer is used to study the Fermi resonance between the OH bending overtone and OH stretching fundamental in small cyclic water clusters (H2O)n with n = 3, 4, 5. The new setup features a recirculating vacuum system which reduces the gas consumption by 2 to 3 orders of magnitude and enables long-term measurements of very weak Raman signals. Raman spectra measured from highly diluted expansions with unprecedented signal-to-noise ratio are presented and cluster-specific intensity ratios and effective coupling constants are derived using Markov-Chain Monte-Carlo methods, yielding a high probability for an almost “perfect” resonance for the tetramer and pentamer, i.e. a close frequency match of bend overtone and stretch fundamental with intensity ratios close to 1, but a larger coupling constant for the trimer, with best estimates close to W5 ≲ 50 cm−1 < W4 ≲ 60 cm−1 < W3 ≈ 65 cm−1.
1 Introduction
Water is arguably the central substance for life on earth and captures our scientific curiosity like few other molecules. To no surprise, water was studied extensively in the field of spectroscopy1–3 and quantum chemistry, seeking an ever more accurate description of its energy states and properties.4–8 The seemingly simple system H2O exhibits a rich vibrational spectrum where anharmonic effects play an important role, e.g. in form of various Darling–Dennison resonances9,10 or the Fermi resonance11 of the ν2 (OH bending) overtone and the ν1 (symmetric OH stretching) fundamental.12 Including such resonances is important to achieve good agreement with experiment when modeling spectra of liquid water13,14 or water clusters,15 and to correctly describe the energy transfer in liquid water,16 which is another interesting property of this substance for its functioning as reaction medium in biochemistry.A good number of experimental and theoretical works have been published that quantify the strength of the OH-bend/OH-stretch Fermi resonance for water under various conditions. For liquid water10,17–19 and water ice,20–22 reported coupling constants fall mainly into the range 50 to 100 cm−1, while the coupling constant for the isolated water molecule is smaller, with values mostly reported close to 30 cm−1 or below.12,13,23–25 Johnson and coworkers26,27 reported spectroscopic coupling constants of 30 ± 5 and 33 cm−1 for water in Br−·H2O and Cl−·H2O·(CCl4)n complexes, respectively, and Tabor et al. reported a value‡ of 64 cm−1 to best explain spectra of Bz⋯(H2O)4 complexes.28
This work explores this Fermi resonance in the transition region between isolated molecules and the condensed phase, by investigating small water clusters seeded in supersonic jet-expansions. Water clusters have previously been investigated largely on the basis of IR spectroscopy,29–36 showing that cyclic clusters dominate at low temperatures, in agreement with quantum chemical calculations, which found cyclic global minimum structures until 6 monomer units37 (from the hexamer onwards, 3D network structures are favored). Furthermore, composite MP2/CCSD(T) harmonic frequencies,38,39 anharmonic VSCF/VCI bend fundamental frequencies,40 and IR absorption band strengths40–42 have been reported and aid the interpretation of IR spectra.
The literature on experimental and theoretical Raman spectra of water clusters is more sparse. An early study based on coherent anti-Stokes Raman scattering (CARS) was published by Wuelfert et al.43 Otto et al. were the first to report spontaneous Raman scattering spectra of water clusters in supersonic jet expansions.44 More recently, Mohaček-Grošev et al. published the first Raman spectra of matrix-isolated water clusters.45 On the theory side, the (to our knowledge) most recent Raman activities for water clusters were published by Cybulski and Sadlej,46 calculated using B3LYP density functional theory and a basis set with an increased number of polarization functions (d-aug-cc-pVDZ). They found that for the dimer and cyclic clusters up to the cyclic hexamer, the lowest frequency OH stretching vibration should dominate the Raman spectrum by far, with a Raman activity that is proportional to the size of the cluster to a good approximation.
Otto et al. established a band assignment based on several experimental observables and compared Raman to complementary IR spectra31 with the goal to deduce the intermolecular coupling among OH stretching oscillators (exciton coupling). The lowest frequency symmetric OH stretching vibrations, where all monomer oscillators move in-phase (all-in-phase or concerted stretching vibrations), were found to dominate the Raman spectra, in agreement with the calculated Raman activities from Cybulski and Sadlej, with little or no Raman intensity for bands showing up in IR spectra. Otto et al. also discussed the importance of the Fermi resonance which is quite noticeable in Raman spectra, but has only a minor (if any) effect on IR spectra. They ascribed the relatively strong overtone band that they observed at 3214 cm−1 mainly to the tetramer and pentamer, where a larger ring size increasingly favors a strong overtone band, because the frequency difference of the OH bending overtones and concerted OH stretching fundamental decreases. For the pentamer, they gave a qualitative estimate of the Fermi coupling constant of 20 to 50 cm−1.
This work presents a series of Raman jet spectra that were measured with a new jet-spectrometer that uses gas recirculation36 to enable long-time measurements with drastically reduced gas consumption. The new setup allows to measure spectra at very high dilution but still with sufficient signal-to-noise ratio, and to repeat measurements under varying conditions without much added cost in consumables. The central measurement quantities are the band integrals§ of the weak OH bend overtone band and OH stretch fundamental bands. Through high dilution, contributions from the tetramer and larger clusters are largely suppressed, and it is shown that under the given measurement conditions, the trimer also contributes significant intensity to the overtone band. A simple Fermi resonance model that assumes mixing of only one overtone state with one fundamental state is applied and yields a larger effective coupling constant in case of the trimer compared to the tetramer and pentamer. Cluster-specific overtone to fundamental band intensity ratios and coupling constants are derived from two evaluation methods that both employ Monte-Carlo sampling to account for measurement uncertainties in band integrals and positions. The experimental spectra¶ and derived intensity ratios are valuable benchmark data for anharmonic quantum chemical predictions and will, hopefully, trigger further interest in the accurate prediction of the Raman spectra of small water clusters, where so far little is available beyond the work from Cybulski and Sadlej.
The article is structured as follows: Section 2 gives a detailed presentation of the new Raman setup and background information on data processing. It also introduces the simple Fermi resonance model that was used to derive effective coupling constants from the observed band integrals and distances. Section 3 presents the spectra and derived intensity ratios and coupling constants. The results are discussed in Section 4, in particular with regard to the validity of the intensity ratio/coupling constant retrieval methods and the limitations of the two-state Fermi resonance model. It is also shown that the model is able to produce a qualitatively correct spectrum from harmonic predictions of vibrational wavenumbers and Raman activities. The work is summarized and concluding remarks are made in Section 5.
With this publication, we made an effort to adhere to Open Science best practices: the full source code of the data evaluation is made available in the ESI,† mainly in the form of commented Jupyter notebooks,47 which were also exported to the PDF format for the readers convenience. To ensure reproducibility and accessibility of the research code, development and evaluation were done using a dedicated Docker image. The defining “Dockerfile”48 of this image is available from the ESI† as well. Using this Docker image is the easiest way to run the code. There is one regular supplementary document which we refer to as the “main supplement”. The notebooks will be referenced throughout this work via the token NB plus the notebook number and, optionally, the number of a particular section. For example, NB/1/4 is a reference to the notebook 1_cluster-integrals.ipynb, Section 4 Run Integration.
2 Methods
2.1 Setup and Raman measurement procedure
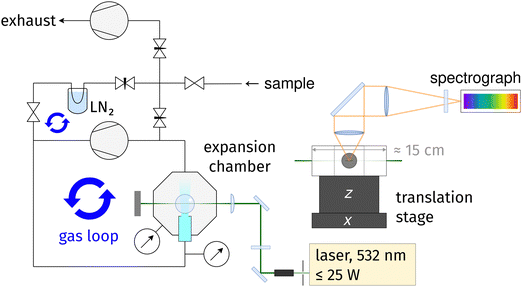
The new setup, called cookie-jet,|| is the direct predecessor of the curry-jet,44 a linear Raman jet-spectrometer that has served in spectroscopic investigations of conformational and clustering preferences of small molecules for well over a decade.49–51A schematic drawing of the cookie-jet setup is shown in Fig. 1. Raman excitation is provided by a 532 nm diode-pumped solid state laser with a maximum of 25 W optical output power (Spectra Physics, Millenia eV). The laser beam is expanded from about 2 mm to about 6 mm diameter using a beam expander (Edmund Optics, Vega Nd:YAG Laser Line Beam Expander). This helps two-fold: the irradiance on the subsequent optics is smaller, decreasing thermal stress, and the beam may be focused more sharply on the gas sample, leading to more light entering the spectrograph for the same slit width setting. A λ/2 wave plate is used to rotate the polarization plane of the laser beam such that the intensity of the nitrogen Q-branch at ∼2330 cm−1 is at a maximum.** An f = 15 cm plano-convex lens (Edmund Optics, TECHSPEC laser grade PCX lens) is used to focus the laser beam on the gas sample inside the vacuum chamber. All laser optics, including the 1.5 inch flat windows of the vacuum chamber, use specific 532 nm coatings with low reflectivity ≤0.25% or ≤0.1%. Scattered light is collected at a 90° angle and collimated with an f = 8 cm, ∅ = 50 mm achromatic lens. An f = 50 cm, ∅ = 50 mm achromatic lens focuses the collimated beam onto the 100 μm slit of an f = 750 mm spectrograph (HRS 750, Teledyne Princeton Instruments) equipped with a back-illuminated, liquid nitrogen-cooled CCD camera (PyLoN 400B, Teledyne Princeton Instruments, about 95% quantum efficiency in the spectral region investigated in this work). An OD 6 Raman-edge filter in front of the slit is used to suppress Rayleigh scattering by six orders of magnitude. The combination of laser, slit, spectrograph and CCD gives an approximate resolution of 2 cm−1 for the 1312 g mm−1 grating (see below). Data acquisition and control of spectrograph and CCD Camera is provided by the software LightField version 6.15.2 (Teledyne Princeton Instruments).
The vacuum chamber and nozzle are home-build by the workshop of the faculty of chemistry at the Göttingen university. 10 mbar and 1000 mbar pressure sensors (Baratron, MKS Instruments) are used to measure the pressure before (stagnation pressure p0 at the nozzle input) and after the expansion (background pressure pb inside the vacuum chamber). Gas circulation is provided by a dry-compressing, multi-stage roots pump with 55 m3 h−1 pumping speed (Leybold, Ecodry 65). With the employed 4 mm × 0.15 mm slit nozzle, the pumping speed of the roots pump is enough to provide a pressure gradient of two orders of magnitude: equilibrium pressure readings are p0 ≈ 500 mbar and pb ≈ 5 mbar for neon and p0 ≈ 600 mbar and pb ≈ 11 mbar for helium circulation. The primary gas loop is connected to a vacuum manifold that connects to a sample flask and exhaust pump. The manifold is connected up- and downstream of the circulation pump, forming a secondary gas loop that includes a cooling trap that can be used to remove substance from the carrier gas. The vacuum chamber is placed on motorized translation stages that provide about 1 cm travel in z-direction (Standa, 8MVT120-12-4247-MEn1) and several centimeter in x-direction (home-build linear stage with stepper motor by Physik-Instrumente GmbH) with micrometer accuracy. By moving the vacuum chamber (including the nozzle) while keeping the laser in a fixed position, gas expansions can be scanned in axial and lateral direction.
Gas samples were prepared by first pumping a few ml of water in a round flask (demineralized from in-house supply or from a Milli-Q model Advantage A10 water purifier, specified with 18 MΩ cm−1 specific resistance at 25 °C and <5 ppb organic carbon) for several minutes and then letting water evaporate into the vacuum system and dilute with the carrier gases helium (99.994%), neon or neon/argon mixtures (both 99.999%). The water monomer Q-branch at 3656 cm−1 was monitored to control the water amount. After switching on the circulation pump, the resulting expansion was probed mostly 2 mm downstream the nozzle. Raman spectra were recorded using a 1312 g mm−1 holographic grating or a 500 g mm−1 ruled grating that provided a better signal to noise ratio and a flatter baseline in the region of the overtone, at the expense of spectral resolution. Typically, the CCD was exposed for a duration of 5 to 15 minutes per scan (individual exposure) and up to several hundreds of such scans were cleaned from cosmic ray signals and averaged. For baseline correction, spectra of pure carrier gas (and in part CCD bias) were measured and subtracted from water spectra (NB/0). The amount of water vapor that was filled into the vacuum system was decreased successively, to suppress formation of larger clusters as much as possible. Table S1 (ESI†) in the main supplement lists the measurement conditions.
To demonstrate the benefits of gas-recycling, we estimate our savings in carrier gas in the following (the carrier gas is the only costly consumable in this work, but if an expensive substance would be investigated, similar considerations would apply). We estimate a gas consumption on the order of 10 L per measurement, used for flushing (cleaning) and filling the vacuum system for subsequent measurements. Then, with 10 helium and 6 neon measurements, we consume roughly 100 L of helium and 60 L of neon. To compare this against a conventional non-recycling approach, we estimate the volume flow through the nozzle during a measurement from the molar mass of the carrier gas, nozzle area, stagnation pressure and gas temperature prior to expansion (see main supplement, Section 1, ESI†). We end up with a mean volume flow of about 3 standard liters per minute for the neon measurements and a volume flow of about 12 standard liters per minute for the helium measurements (with standard we mean the volume at T = 293 K and p = 1.0 bar). With overall 87 hours of helium measurements and 45 hours of neon measurements, an equivalent Raman setup without gas recycling would thus have consumed about 12 L min−1 × 60 min h−1 × 87 h ≈ 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 L of helium (or about 6 gas cylinders with 50 L and 200 bar each) and 3 L min−1 × 60 min h−1 × 45 h ≈ 8000 L of neon (a bit less than one gas cylinder), i.e. the saving in carrier gas amounts to two to three orders of magnitude.
000 L of helium (or about 6 gas cylinders with 50 L and 200 bar each) and 3 L min−1 × 60 min h−1 × 45 h ≈ 8000 L of neon (a bit less than one gas cylinder), i.e. the saving in carrier gas amounts to two to three orders of magnitude.
2.2 Data processing
Raw spectra are retrieved as wavelength versus ADC counts datasets and require cosmic spike removal, background correction, Raman shift calculation, and counts to photoelectrons conversion data processing steps. After calculation of the Raman shift, the calibration of the wavenumber axis is corrected by shifting the spectra such that the ro-vibrational lines of the monomer bending overtone agree with published line positions.4,52 To yield a proportionality of Raman band integrals to transition moments, the dependence of the Raman scattering cross section on the frequency is also removed by scaling with a frequency-dependent factor. Further details are given in the main supplement, Section 2 (ESI†), and NB/0.Band integrals were retrieved from the processed spectra in units of (corrected, i.e. scaled) photoelectrons per second by numeric integration of the bands using the software library NoisySignalIntegration.jl (NSI).53 NSI uses Monte-Carlo sampling to estimate the uncertainty of band integrals due to noise, baseline and uncertain placement of integration bounds. One of the main inputs to NSI are uncertain integration bounds which are expressed using probability distributions. The bounds chosen throughout this work are depicted in the supplement (NB/1/3). The polarization dependent sensitivity and vignetting of the spectrograph was also included in the uncertainty estimation for band integrals. Ro-vibrational lines of the water monomer were fitted with Gaussian curves to derive the overall monomer overtone band integral and to remove ro-vibrational lines overlapping with the overtone band at 3212 cm−1 (NB/0/21). Since only relative intensities within one spectrum are relevant, band integrals were scaled to the sum of the best estimates (means) of the OH stretch fundamental bands. This facilitates comparability among the different spectra and yields better numeric stability when deriving cluster-specific overtone to fundamental intensity ratios.
2.3 Determination of intensity ratios & coupling constants
A Fermi resonance is associated with the redistribution of spectral intensity, commonly described as an overtone or combination tone “stealing” intensity from a fundamental vibrational state, and the “repulsion” (frequency shift) of the involved states. Using first order perturbation theory, the magnitude of these effects may be estimated by assuming harmonic vibrational states which are perturbed by anharmonic terms in the potential energy, leading to a coupling or mixing of the involved states.In this work we use a simple two-state/dark-state approximation to describe the Fermi resonance observed in the spectra of water clusters, meaning we assume that for each cluster only a single OH bending overtone is in resonance with a single OH stretch fundamental, namely the modes where all bend- or stretch-oscillators move in phase, and that the overtone transition would, in the absence of Fermi resonance, not exhibit Raman intensity on its own (that the unperturbed overtone state is a “dark state”). Using these simplifications, we derive a single, effective coupling constant as a measure of the strength of the Fermi resonance for the different cluster sizes. In the following, “coupling constant” always has to be understood as meaning an “effective” coupling constant. We note that this reduction to a single parameter in a normal mode picture is more useful for the smaller, near-symmetric cyclic structures investigated in this work, because all OH stretch oscillators are similar, but less useful for larger and less symmetric structures (which are favored from the hexamer onwards) where individual OH stretch oscillators are more heterogeneous and a description of the bend/stretch couplings in the local mode basis would be more informative. The impact that our simplifications may have on the comparability of the results to other studies is discussed in Section 4.4.
To model a two-state Fermi resonance, we start from the secular determinant with unperturbed energies E2b and Es (bending overtone and stretching fundamental state) and the coupling constant W:
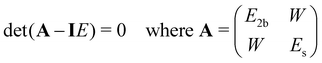 | (1) |
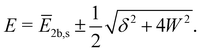 | (2) |
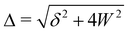 | (3) |
where the upper operator of ± and
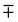 applies if W is positive and the lower operator if W is negative. The coefficients a and b are derived from the eigenvectors of A and may be expressed as
applies if W is positive and the lower operator if W is negative. The coefficients a and b are derived from the eigenvectors of A and may be expressed as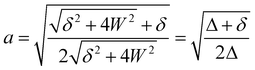 | (4) |
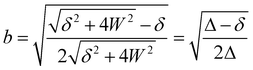 | (5) |
Thus, the coupling constant may be thought of as a measure of the “strength” of the Fermi resonance, a measure of how much the states repel each other and how much intensity is transferred, as it dictates how much the involved states mix. If W ≫ δ or δ ≈ 0, a and b approach the value 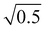 .
.
Using these equations and assuming that the transition moment for a transition from the ground state into the unperturbed overtone state 2b is negligible, the intensity ratio††R of the band of the overtone to the band of the fundamental vibration can be related to the coupling constant via the band distance Δ in a simple way:
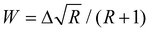 | (6) |
To derive Δ, band centers and their uncertainties were determined from the spectrum with the highest cluster concentration where the highest signal-to-noise ratio is available (labeled “NeAr/400/2.5/hr”, see below). Peaks in the Raman bands were taken as band centers while triangular probability distributions, roughly following the band shape, were used to model their uncertainties (see NB/3/4).
For the water monomer, ro-vibrational lines of the overtone and the vibrational band of the fundamental can be separated from their spectral surroundings, so that their integration and the subsequent determination of the intensity ratio R is not complicated by the need to resolve several contributors. It is thus a good test case and was included in the analysis. In case of water clusters, the overtone bands of clusters of several sizes overlap (discussed in Section 4.1), so band integrals for the different cluster sizes are not readily available. Two different evaluation strategies were followed to overcome this problem:
• Guessing sets of coupling constants {W2, W3, W4, W5}, calculating the implied intensity ratios, and comparing the predicted overtone band integral to the measured band integral to derive a best guess of coupling constants (termed “brute-force sampling” in the following).
• Using MCMC sampling (Bayesian inference) to derive what intensity ratios Rn (where n denotes the cluster size) fit the spectra best and calculating coupling constants from the inferred intensity ratios (“MCMC sampling”).
Brute-force sampling was the first evaluation approach used to derive coupling constants, but it has a few shortcomings compared to MCMC sampling and was thus eventually replaced by the latter. Brute-force sampling and its results (similar to results from MCMC sampling) are presented in the main supplement, Section 4, ESI.† The MCMC sampling approach will be presented in the following.
2.4 Bayesian regression (MCMC sampling)
The Bayesian model was set up using the R software-package brms54 which in turn uses the probabilistic programming language STAN55 as a backend to perform MCMC sampling. The model was setup such that the brms package would take into account the uncertainties in the measured band integrals plus (optionally) intrinsic scattering.56 The overtone area was modeled as the sum of fundamental band integrals Atruef,n multiplied by the particular intensity ratio Rn for each cluster of size n: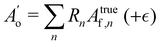 | (7) |
| Rn ∼ Uniform(0,1) | (8) |
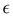 drawn from a normal distribution with zero mean and standard deviation σ
drawn from a normal distribution with zero mean and standard deviation σwhere σ is inferred from the data. Note that the exact implementation by brms differs from this simplified description, but the effect is equivalent. Intrinsic scatter accounts for deviations from the linear model that are larger than what one would expect based on the scatter of the fitted data alone (deviations that cannot be explained reasonably by the uncertainty in the fitted data points). For example, such deviations could stem from the non-uniform expansion temperature across the different spectra. A large inferred value for σ would indicate a poor fit. Intrinsic scatter is further discussed in Section 4.3.
Estimates of intensity ratios were derived by drawing 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samples using the No-U-Turn sampler (NUTS)57 as implemented in STAN. In a post-processing step, band separations were calculated from positions drawn from triangular distributions (NB/3/4) and coupling constants for each cluster were calculated from the inferred intensity ratios and eqn (6). Further details on the Bayesian model, the exact formulation of the model in brms, and the resulting STAN code is included in the supplement (NB/4).
000 samples using the No-U-Turn sampler (NUTS)57 as implemented in STAN. In a post-processing step, band separations were calculated from positions drawn from triangular distributions (NB/3/4) and coupling constants for each cluster were calculated from the inferred intensity ratios and eqn (6). Further details on the Bayesian model, the exact formulation of the model in brms, and the resulting STAN code is included in the supplement (NB/4).
3 Results
A selection of the recorded spectra measured with the 1312 g mm−1 grating is shown in Fig. 2, spectra measured at lower resolution with the 500 g mm−1 grating are shown in the main supplement, Fig. S1 (ESI†). Spectra labels indicate measurement conditions as follows: carrier gas/stagnation pressure in mbar/nozzle distance in mm/hr or lr for high or low resolution. A letter is appended to the nozzle distance if several measurement series with the same expansion conditions are present. For example, the spectrum labeled “He/600/2a/lr” was the first (a) low resolution (lr) measurement using helium as carrier gas, a nozzle pressure of 600 mbar, and a nozzle distance of 2 mm. In the measurement series “He/600/2b/lr” and “He/600/2c/lr” the amount of water vapor was unstable and several gas samples were measured, so individual scans were categorized by their peak signal at 3656 cm−1 (monomer symmetric stretch Q-branch) and combined to high concentration (suffix _h), medium concentration (_m), and low concentration (_l) spectra (NB/0/17 and NB/0/20). The spectra are ordered such that the relative cluster amount in the expansions decreases from top to bottom. Note that the same color code is used for these spectra throughout this work, including the supplement.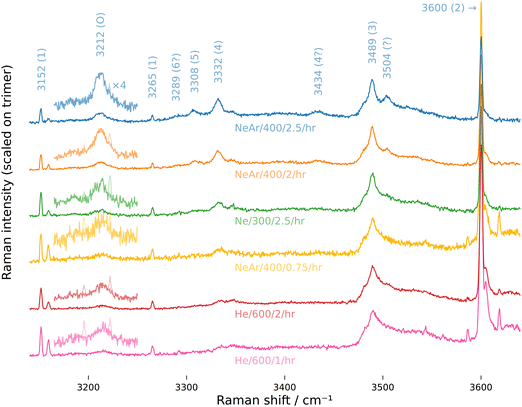 | ||
| Fig. 2 Raman jet spectra of water clusters measured under varying conditions using the 1312 g mm−1 grating (low resolutions spectra are shown in Fig. S1 (ESI†) in the main supplement). The labeling scheme is carrier gas/stagnation pressure in mbar/nozzle distance in mm/hr for high resolution, see first paragraph of Section 3. Table S1 (ESI†) in the main supplement lists further measurement conditions. For better visibility, the overtone band is magnified by a factor 4. Ro-vibrational lines of the water monomer that overlap with the overtone band were removed by fitting Gaussian peak functions and are drawn with fainter colors. | ||
The assignments of the most prominent spectral features are listed in Table 1: the broad trimer band with its peak at 3489 cm−1, tetramer band at 3332 cm−1, pentamer band at 3308 cm−1, overtone band at 3212 cm−1 and two smaller bands at 3504 cm−1 and 3434 cm−1 stemming from clusters larger than the trimer, based on how they scale with the water vapor concentration.44 Furthermore, sharp lines from monomer ro-vibrational transitions show up close to the overtone band and the dimer band at 3600 cm−1.52 Intensity ratios and coupling constants derived for the monomer are compiled in Table 2. Relative band integrals for clusters are compiled in Table 3. Fig. 5 shows a plot of the posterior distributions for the intensity ratios Rn for the clusters, derived through MCMC sampling. Posterior distributions of coupling constants calculated from these intensity ratios viaeqn (6) are shown in the same figure. Statistics for the posterior distributions are compiled in Table 4.
| Raman shift/cm−1 | Cluster size | Assignment | Ref./cm−1 |
|---|---|---|---|
| a Tennyson et al.4 b Avila et al.52 c Otto et al.44 | |||
| 3152 | 1 | 2ν2(000 ← 000) | 3151.630a |
| 3159 | 1 | 2ν2(111 ← 111) | 3158.956b |
| 3196 | 1 | 2ν2(212 ← 110) | 3195.546a |
| 3222 | 1 | 2ν2(202 ← 000) | 3221.961a |
| 3265 | 1 | 2ν2(303 ← 101) | 3265.448a |
| 3587 | 1 | ν 1(000 ← 202) | 3586.962b |
| 3619 | 1 | ν 1(110 ← 212) | 3618.995b |
| 3212 | 2…5 | Bending overtone | 3214c |
| 3289 | 6? | Concerted stretch | |
| 3308 | 5 | Concerted stretch | 3310c |
| 3332 | 4 | Concerted stretch | 3334c |
| 3434 | 4? | Out-of-phase stretch? | 3438c |
| 3489 | 3 | Concerted stretch | 3491c |
| 3504 | ≫3 | Stretch | 3506c |
| 3600 | 2 | Stretch | 3602c |
| 3656 | 1 | ν 1 | 3657c |
| Label | R 3152/3159 | R 1 | W/cm−1 |
|---|---|---|---|
| High resolution measurements (1312 g mm−1 grating) | |||
| He/600/1/hr | 1.9 (0.4) | 0.29 (0.03) | 27 (1) |
| He/600/2/hr | 3.1 (0.7) | 0.30 (0.03) | 28 (1) |
| Ne/200/2/hr | 2.9 (0.7) | 0.31 (0.03) | 28 (1) |
| Ne/300/2.5/hr | 5.0 (1.0) | 0.32 (0.03) | 28 (1) |
| NeAr/400/0.75/hr | 1.9 (0.5) | 0.28 (0.03) | 27 (1) |
| NeAr/400/1/hr | 2.5 (0.7) | 0.28 (0.03) | 26 (1) |
| NeAr/400/2/hr | 3.5 (0.9) | 0.32 (0.03) | 28 (1) |
| NeAr/400/2.5/hr | 4.6 (2.0) | 0.33 (0.04) | 29 (2) |
| Mean high resolution | 27.6 (0.5) | ||
| Low resolution measurements (500 g mm−1 grating) | |||
| He/600/1/lr | 2.0 (0.4) | 0.35 (0.03) | 30 (1) |
| He/600/1.5/lr | 2.6 (0.5) | 0.39 (0.03) | 31 (1) |
| He/600/2a/lr | 3.3 (0.9) | 0.36 (0.04) | 30 (2) |
| He/600/2b/lr_l | 4.4 (1.0) | 0.38 (0.05) | 31 (2) |
| He/600/2b/lr_m | 3.3 (0.6) | 0.40 (0.03) | 32 (1) |
| He/600/2b/lr_h | 3.4 (0.6) | 0.37 (0.02) | 30.7 (0.9) |
| He/600/2c/lr_l | 3.9 (0.9) | 0.37 (0.02) | 31 (1) |
| He/600/2c/lr_h | 4.1 (1.0) | 0.40 (0.03) | 32 (1) |
| Mean low resolution | 30.8 (0.5) | ||
| Label | Conv. | Dimer | Trimer | Tetramer | Pentamer | Overtone |
|---|---|---|---|---|---|---|
| a For the weak pentamer band measured at low concentration, integration yielded small negative band area samples, which were set to 0. | ||||||
| He/600/1/hr | 39.6 | 43.8 (0.4) | 55.6 (1.6) | 0.5 (0.2) | 0.1 (0.2) | 3.8 (1.0) |
| He/600/2/hr | 19.9 | 35.9 (0.3) | 62.9 (1.4) | 0.9 (0.2) | 0.4 (0.2) | 4.3 (0.8) |
| Ne/200/2/hr | 7.0 | 39.5 (0.7) | 58.0 (3.1) | 2.4 (0.5) | 0.1 (0.3) | 4.9 (2.0) |
| Ne/300/2.5/hr | 9.7 | 30.3 (0.5) | 65.8 (2.3) | 3.0 (0.4) | 0.9 (0.4) | 6.2 (1.5) |
| NeAr/400/0.75/hr | 22.1 | 49.2 (0.7) | 48.6 (3.5) | 1.7 (0.5) | 0.5 (0.5) | 5.8 (2.2) |
| NeAr/400/1/hr | 23.0 | 39.6 (0.8) | 57.9 (3.5) | 2.5 (0.6) | 0.0 (0.2)a | 6.1 (2.2) |
| NeAr/400/2/hr | 16.6 | 27.9 (0.4) | 65.3 (1.9) | 5.2 (0.4) | 1.7 (0.3) | 8.9 (1.3) |
| NeAr/400/2.5/hr | 14.3 | 20.2 (0.5) | 71.2 (2.3) | 6.3 (0.5) | 2.3 (0.4) | 10.5 (1.5) |
| He/600/1/lr | 52.4 | 42.3 (0.2) | 57.0 (0.7) | 0.5 (0.1) | 0.2 (0.2) | 5.4 (0.6) |
| He/600/1.5/lr | 39.8 | 35.5 (0.3) | 63.5 (1.0) | 0.7 (0.2) | 0.3 (0.2) | 5.5 (0.7) |
| He/600/2a/lr | 27.0 | 32.6 (0.3) | 65.8 (0.8) | 1.1 (0.2) | 0.4 (0.2) | 5.8 (0.6) |
| He/600/2b/lr_l | 10.2 | 44.0 (0.5) | 54.9 (2.1) | 0.7 (0.4) | 0.3 (0.4) | 3.7 (1.4) |
| He/600/2b/lr_m | 15.1 | 41.5 (0.3) | 58.0 (1.0) | 0.4 (0.2) | 0.2 (0.2) | 3.3 (0.7) |
| He/600/2b/lr_h | 20.0 | 38.2 (0.2) | 60.8 (0.5) | 0.7 (0.1) | 0.3 (0.1) | 4.2 (0.4) |
| He/600/2c/lr_l | 3.8 | 65.4 (0.6) | 33.6 (2.4) | 0.8 (0.4) | 0.2 (0.4) | 2.2 (1.5) |
| He/600/2c/lr_h | 6.8 | 56.5 (0.5) | 43.0 (1.6) | 0.5 (0.3) | 0.0 (0.0)a | 2.6 (1.0) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = mean, s = standard deviation. Density plots see Fig. 5
= mean, s = standard deviation. Density plots see Fig. 5
| Quantity | Percentile | ||||
|---|---|---|---|---|---|
| 2.5 | 50 | 97.5 |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
|
s | |
| (With intrinsic scatter) | |||||
| R 2/% | 0.03 | 0.76 | 3.24 | 0.98 | 0.86 |
| R 3/% | 3.9 | 5.8 | 7.1 | 5.7 | 0.8 |
| R 4/% | 43 | 76 | 98 | 75 | 15 |
| R 5/% | 4 | 58 | 98 | 56 | 28 |
| σ/% | 0.37 | 0.68 | 1.24 | 0.71 | 0.22 |
| W 2/cm−1 | 7 | 34 | 69 | 35 | 16 |
| W 3/cm−1 | 54 | 65 | 75 | 65 | 5 |
| W 4/cm−1 | 52 | 59 | 65 | 59 | 3 |
| W 5/cm−1 | 18 | 45 | 52 | 43 | 8 |
| (Without intrinsic scatter) | |||||
| R 2/% | 0.02 | 0.47 | 1.85 | 0.60 | 0.50 |
| R 3/% | 5.0 | 6.1 | 6.7 | 6.0 | 0.4 |
| R 4/% | 51 | 76 | 98 | 76 | 13 |
| R 5/% | 4 | 60 | 98 | 57 | 28 |
| W 2/cm−1 | 5 | 27 | 53 | 27 | 13 |
| W 3/cm−1 | 59 | 67 | 74 | 67 | 4 |
| W 4/cm−1 | 53 | 59 | 65 | 59 | 3 |
| W 5/cm−1 | 18 | 45 | 52 | 43 | 8 |
4 Discussion
4.1 Assignments
The appearance of the spectra of small water cluster is largely determined by hydrogen bond cooperativity, i.e. the strengthening of hydrogen bonds that takes place if several such bonds are chained.58,59 Firstly, cooperativity leads to cyclic clusters being favored over open chains or networks for small cluster size until 6 monomer units37 (from the hexamer onwards, 3D structures dominate)60 and these cyclic clusters dominate jet spectra at low temperatures. Secondly, with larger ring size, cooperativity increasingly softens OH stretch oscillators that form a hydrogen bond, which yields a sharp drop of the stretching frequency up to several hundred cm−1 and a band progression in Raman jet spectra where larger cyclic clusters are found at smaller Raman shifts.39,46 The binding energy per water molecule drops with increasing cluster size42,60 and with it the down-shift of bound OH stretching vibrations relative to the next smaller cluster. Besides these qualitative trends of vibrational frequencies, the relative intensities of the bands and their dependence on expansion conditions is more evidence that supports band assignments: in general, the effective temperature in supersonic expansions decreases with the atomic weight of the carrier gas (THe > TNe > TNe+Ar) and increasing nozzle distance which both facilitate cluster formation. The same is true for a higher stagnation pressure and larger water concentration. With this in mind, the jet spectra depicted in Fig. 2 and Fig. S1 (ESI†) show the anticipated behavior, namely the increase in cluster amount when switching from He to Ne(+10% Ar) as carrier gas, the increase in cluster amount when increasing the stagnation pressure (Ne measurements with 200 and 300 mbar stagnation pressure, the former not shown), and the increase in cluster amount when measuring further downstream the nozzle (He measurements with 1 mm and 2 mm nozzle distance and Ne + Ar measurements at 0.75 mm, 2 mm, and 2.5 mm nozzle distance).With these general clues and the dependence of spectra on expansion conditions, a sound assignment is possible and has already been established by Otto et al.44 for most of the Raman bands observed in Fig. 2. One may add that the proposed assignment qualitatively agrees with harmonic coupled-cluster predictions of relative red shifts reported by Howard et al.39 which yield that the distance between the dimer to the trimer band should be 124 cm−1, between trimer and tetramer 155 cm−1, and between tetramer and pentamer 31 cm−1, while the experiment yields 111, 157, and 24 cm−1 with the given assignment, respectively. For the band at 3434 cm−1, Otto et al. tentatively assigned a tetramer OH stretch, which agrees well with a spectral simulation that we prepared based on published calculated frequencies38,39,46 and Raman activities46 (Fig. 4, discussed below). The band at 3504 cm−1 was assigned by Otto et al. loosely to clusters much larger than the trimer. Likewise, we could not find a specific assignment. According to the data published by Cybulski and Sadlej, a C2 symmetric pentamer would have a strong Raman band at about that position, judging from its relative shift to the trimer,46 while exploratory calculations for this present work found that a tetramer with an additional water molecule attached to one of its corners would yield a strong Raman band at this position. It is plausible that such clusters where one additional water molecule attaches to a stable ring are kinetically favored and thus observable in supersonic expansions, but at this point this is merely speculation and the assignment of this band remains elusive. Note that for the measurements NeAr/400/2(.5)/hr where this band showed up, its area was subtracted from the trimer band integral.
Another speculative assignment is the in-phase OH symmetric stretch of the cyclic hexamer at 3289 cm−1, which is visible as a weak band only if we zoom in on the overtone, pentamer, and tetramer bands and apply a mild smoothing filter (Fig. 3, NeAr/400/2.5/hr). As mentioned earlier, the cyclic isomer is not the energy minimum anymore for the hexamer, but calculations of its relative population for varying temperature find that it competes with the most stable prism isomer at room temperature (and is even the most abundant isomer at even higher temperatures).60 It is not uncommon that higher energy structures are kinetically trapped during rapid cooling in supersonic expansions, so it may be that the weak signal on the low-frequency side of the pentamer band in the spectrum NeAr/400/2.5/hr is indeed cyclic hexamer that was frozen out during jet-cooling.
 | ||
| Fig. 3 High resolution Raman spectra, zoomed in on tetramer, pentamer and overtone band. Ro-vibrational lines of the monomer were removed from the overtone band and a moving average filter weighted by a Gaussian window (σ = 1.5 cm−1) was applied. The same color code as in Fig. 2 applies. | ||
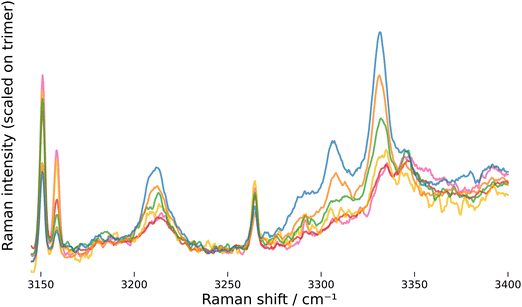
The assignment of “the” overtone band at 3212 cm−1 to clusters of various size, on which the analysis of the OH bend/stretch Fermi resonance is based, needs to be discussed in particular. A first argument in favor of this assignment can be made based on the experimental observation that this band does not scale like any of the individual OH stretch clusters bands with varying expansion conditions, which rules out an assignment to a specific cluster size (this is also apparent when band integral ratios are plotted, NB/1/7). A further argument is based on the development of the OH bend vibration, which becomes increasingly stiffer and shifts upwards with cluster size.39,46 Along with the down-shift of the OH stretching vibration described in the initial paragraph of this section, this leads to a convergence of the bend overtone and stretch fundamental frequencies with increasing cluster size and the conditions for a strong Fermi resonance become better (the unperturbed band distance δ in eqn (5) gets smaller). The repulsion of the two states due to Fermi resonance counteracts both, the up-shift of the bend state and the down-shift of the stretch state, and the bend overtone transitions of the different clusters end up with similar energies. Qualitatively, this argument can be demonstrated using quantum-chemical harmonic frequency and Raman activity predictions. In Fig. 4, simulated spectra based on calculations published by Cybulski and Sadlej46 (A, B) and Howard et al.38,39 (C, D) are compared against the high-resolution spectrum with the highest cluster amount. Since no Raman activities are available for the data from Howard et al., the Raman activities from Cybulski and Sadlej were used there as well. The left side (A, C) shows simulations with all coupling constants set to zero, i.e. no Fermi resonance, and the right side with the coupling constants set to values close to the most probable values found from MCMC sampling. States taking part in the Fermi resonance are marked with a square (bending overtones) or circle (stretching fundamentals). Details on the simulation are provided in the supplement, NB/5.
 | ||
| Fig. 4 Stick spectra simulated from quantum-chemical predictions published by Cybulski and Sadlej46 (A, B) and Howard et al. (C, D).38,39 Spectra on the left side are simulated with all coupling constants set to zero, spectra on the right side are simulated using the coupling constants W2 = 30 cm−1 for the dimer (blue), W3 = 65 cm−1 for the trimer (red), W4 = 60 cm−1 for the tetramer (green) and W5 = 48 cm−1 for the pentamer (magenta; this color code for cluster size is used throughout, also in the supplement and notebooks). To perform a basic correction of harmonic wavenumbers, unperturbed wavenumbers are derived by scaling stretch wavenumbers by 0.972 (A, B) or 0.957 (C, D) and calculating bend overtone wavenumber using a diagonal anharmonicity constant of −19 cm−1 (see NB/5 for details). To compare against the experiment, the spectrum “NeAr/400/2.5/hr” is shown and intensities are scaled to approximately match the composition of the experimental spectrum. The OH stretch fundamental of the trimer is cut-off at about two thirds to allow better visibility of the weaker vibrations. | ||
The simulations show what was described above: without the Fermi resonance, the overtone bands are spread over a spectral window of about 100 cm−1, clearly beyond the width of the experimental overtone band, but if we allow for a Fermi resonance with the coupling constants found from MCMC sampling, they all converge at a position close to the overtone band. The simulations also reveal another interesting issue: for the pentamer, the unperturbed stretch fundamental has a lower wavenumber than the unperturbed bend overtone (A and C in Fig. 4), meaning that in the simulation a state with more fundamental than overtone character contributes to the “overtone” band. This is important in so far as limiting the intensity ratio to the range [0, 1] when performing MCMC sampling (eqn (8)) would not be valid for the pentamer, if the simulation would capture the true physics here. We will come back to this issue below.
The zoomed and smoothed spectra in Fig. 3 and the magnified segments in Fig. 2 and Fig. S1 (ESI†) reveal that the overtone band has a bimodal structure with a weaker low-frequency component. The simulated stick spectra suggest that the lower-frequency component may stem mainly from the dimer and trimer. Recently published anharmonic frequency calculations for the dimer find in fact several transitions that fall in the range of the overtone band.8 Clearly, a further decomposition of the band would be desirable, but with our simple numeric integration, this is not possible. The same is true for the broad trimer band, where the simulation suggests that the two other symmetric OH stretch modes may contribute about 20% to the overall band intensity. Thus, we clearly have to view the derived coupling constants as effective values, tied to the applied simplifications. However, even this relatively simple model brings harmonic predictions qualitatively quite close to the observed spectrum, as the simulations show.
4.2 Monomer coupling constant
The determination of the Fermi resonance coupling constants for water clusters is complicated by the overlap of the overtone bands, but for the water monomer the overtone presents itself as clearly separated, sharp ro-vibrational lines. Therefore, a straightforward analysis for the monomer is possible. Also, other than for clusters, only a single overtone can be responsible for the observed Raman ro-vibrational lines and their assignment is well established.4,52 The monomer is thus a valuable test case to assess the retrieval of coupling constants from the presented spectra under simplified conditions. We acknowledge that a more accurate line-by-line analysis might be possible here, but choose to stick with the simpler analysis that is analogous to what we do for the clusters, namely summing over all lines and using a single overtone position to derive a single, effective coupling constant.The derived monomer coupling constants (Table 2) are in agreement with values reported in the literature, which are mostly close to or below 30 cm−1.12,13,23–25 From the intensity ratio of the lines at 3152 cm−1 and 3159 cm−1 (second column in Table 2) one can deduce that there is some notable variability of the temperature for the varying expansion conditions,‡‡ but it does not seem to have a strong effect on the derived coupling constants. For low-resolution spectra, a linear fit of a plot of the coupling constant versus the R3152/3159 line integral ratio yields no significant slope, while for high-resolution spectra a significant slope of (0.6 ± 0.2) cm−1 per one unit change of R3152/3159 is found (NB/2/5). This slope translates into a maximum change of 7% of the coupling constant in case of the high-resolution spectra.§§
The choice of grating also has a significant impact on the results. We suspect that this has to do with the effects of vignetting and polarization-dependent sensitivities of the gratings not being entirely removed by our correction efforts. For a discussion of these corrections, see the main supplement, Section 3, ESI.† Still, with W ≈ 30 cm−1, we yield a coupling constant compatible with values reported in the literature and view this test case for the recovery of coupling constants as a success.
When comparing this result for the monomer to coupling constants of cyclic clusters, one should be aware of an important difference between the relevant monomer and cluster vibrational normal modes: in the monomer, the coupling of the symmetric OH stretch vibration with the bend overtone involves two equivalent OH stretch oscillators, in the cyclic clusters, on the other hand, the hydrogen-bonded OH stretch oscillators have a considerable lower frequency than the free OH stretch oscillators, and it is largely the former bonded oscillators that vibrate in the lowest frequency, concerted stretching normal modes, which in turn couple most strongly with the bend overtone. Therefore, for the momoner, two OH stretch oscillators per water molecule vibrate in the normal mode relevant for the Fermi resonance, while in the corresponding normal modes of the cyclic clusters, it is only a single stretch oscillator per water molecule, which puts the normal mode-based coupling constants of the monomer and cyclic clusters on a somewhat unequal footing.
4.3 Clusters: coupling constants and intensity ratios
The coupling constants derived for the clusters, listed in Table 4 and depicted in Fig. 5, agree with the general finding that the coupling constant of the OH bend/OH stretch Fermi resonance is larger in the condensed phase than for the isolated monomer. Our tetramer value is close to the coupling constant found by Tabor et al. to best explain the spectrum of Bz⋯(H2O)4 measured with an UV-IR spectroscopic approach, namely 64 cm−1 (reported as 45 cm−1 in the local mode basis). Our pentamer value is compatible with the range given by Otto et al., which they estimated to be between 20 and 50 cm−1. We note the systematic trend of our effective coupling constants with regard to cluster size, W3 > W4 > W5, for which we find a probability of 84% from the posteriors of the fit including intrinsic scatter (NB/4/4.4). Further studying this trend, which may be rooted in the systematic development of ring tension with increasing size of the cyclic clusters, would be a good target for quantum-chemical investigations.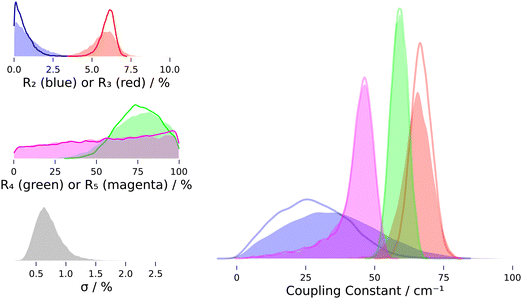 | ||
| Fig. 5 Probability density plots showing posterior distributions from MCMC sampling with (filled) and without (empty) inclusion of intrinsic scatter. The colors denote cluster size: blue – dimer, red – trimer, green – tetramer, magenta – pentamer. R = ratio of bend overtone band integral to stretch fundamental band integral (“intensity ratio”), σ = intrinsic scatter (relative to sum of fundamental band integrals). Statistics see Table 4. Note that density plots are smoothed by kernel density estimation, which leads to an artificial drop of probability density at the limiting values of Rn = 0 and Rn = 1. | ||
With regard to the intensity contributions to the overtone band, we find that the trimer almost always dominates under the given measurement conditions (NB/4.3), while the earlier study by Otto et al. concluded that the tetramer and pentamer most strongly contribute to the overtone band at higher cluster concentration.44 In spectra from this work, the trimer contribution is mostly >50%, except for the two measurements NeAr/400/2/hr and NeAr/400/2.5/h, where the tetramer also contributes substantially, about 40 to 50%. These are also the only spectra where we find the pentamer to contribute more notably, but its contribution is always inferred to be less than ∼20%. The dimer's contribution is most probably negligible in all spectra, with 0% contribution always having the highest probability.
Analog to the contribution to the overtone band, the dimer's intensity ratio is inferred to be negligible, with the posterior peaking¶¶ at R2 = 0 and most of the probability density being limited to R2 < 0.02. For the trimer, the 95% credible interval inferred for R3 is [0.04, 0.07] (allowing for intrinsic scatter). However, as stated in the last paragraph of Section 4.1, about 20% of the trimer's fundamental band may stem from its other two symmetric stretch fundamentals (see Fig. 4), a contributions which we cannot separate out with our numeric integration approach. Assuming a 20% smaller band integral for the concerted OH stretch translates into the intensity ratio R3 and effective coupling constant W3 being larger by about 25% and 6 cm−1, respectively. For the tetramer and especially the pentamer, the band integrals are much smaller than for the dimer and trimer, with relative uncertainties often in the range of 10% or more, so what can be learned about their intensity ratios is somewhat limited. In fact, for the pentamer, the posterior distribution of the intensity ratio R5 hardly departs from the uniform prior at all, as can be seen in Fig. 5. The fact that the posterior distribution of the coupling constant W5 still peaks close to the limiting value of half the band distance Δ/2 is mainly a property of the non-linear transformation from intensity ratio to coupling constant viaeqn (6). This can be seen most clearly when the prior distribution is transformed by this equation: the resulting distribution will peak close to Δ/2, even though the intensity ratio is uniformly distributed in the interval [0, 1]. For the tetramer the situation is better, since the posterior distribution of R4 is clearly lopsided with probability density mainly in the range ≥0.43, so 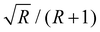 falls in the range [0.46, 0.5] and assuming a coupling constant close to the limiting value is more rooted in the data than in the model.
falls in the range [0.46, 0.5] and assuming a coupling constant close to the limiting value is more rooted in the data than in the model.
Having discussed the actual values inferred from MCMC sampling, we now want to focus on the reliability of our data evaluation approach. We performed a series of tests to investigate how robust the results are with regard to changes in the input parameters of MCMC sampling, most notably the in- and exclusion of intrinsic scatter that we included in the tables and figures reported in the main paper, but also sensitivity towards changes in prior distributions and changes in the input dataset, i.e. sensitivity towards leaving out individual spectra, where the concrete results can be found in the supplement. To investigate how accurately intensity ratios and coupling constants may be inferred from spectra in principle, we tested the MCMC approach using simulated spectra.
Variation of the trimer's coupling constant put into the simulation showed that its recovery was reliable, with errors <7% for W3 = 30 and 100 cm−1. For the tetramer, setting the input coupling constant from 60 to 45 cm−1 led to a notable shift of posterior probability density for R4 from the range [0.66, 0.99] to the range [0.1, 0.7], but the retrieved coupling constant was 52 cm−1 with a relative error of 15%. For 30 cm−1 or 0 cm−1 as input coupling constants, the posterior range for R4 dropped further to [0.0, 0.5], but the recovered coupling constant was severely overestimated with (45 ± 10) cm−1 and (41 ± 11) cm−1, respectively, due to the non-linearity of eqn (6) as discussed above. We can thus conclude that inference of small coupling constants is not possible with the given spread of the intensity ratio, but the simulations still confirm a coupling constant close to half the band distance for the tetramer, for if the coupling constant would be much smaller, we should have inferred a smaller intensity ratio with more probability density in the region R4 < 0.5.
For the pentamer we find that decreasing the coupling constant from 48 cm−1 (which is already the maximum value allowed in a two-state approximation for the given band distance) mostly leads to the posterior distribution of R5 departing from its prior uniform distribution even less. This is true even if W5 is unchanged but W4 is lowered, since both parameters are notably correlated. The fact that the posterior distribution from the fit of experimental data is lopsided towards larger values is then, as for the tetramer, the only hint from the experiment that makes a coupling constant close to the limiting value more likely. However, additional support for W5 ≈ Δ5/2 comes from the development of calculated vibrational frequencies39,46 where the distance between bend overtone and stretch fundamental states decreases with increasing cluster size.
In the last part of this discussion we want to address further possible contributions to the overtone band, which could compromise the validity of our results. As in every non-selective spectroscopy, such spectral impurities may not be excluded entirely, but we note that significant occasional impurities in individual spectra would show up as outliers in inferred “true” overtone band*** or fundamental band integrals, which we did not observe (the respective posterior distributions are shifted from the prior distributions by less than one standard deviation, NB/4/4.5). Also, as stated above, the comparatively small magnitude of intrinsic scatter shows that the data largely conforms with the linear model, and no significant outlier is present. A systematic impurity, at least in spectra measured at higher water concentration, may be the hexamer, which is known to contribute to the spectral region close to 3200 cm−1 in IR spectra.13,29,61 Other than for the smaller clusters, potential hexamer bands should stem primarily from non-cyclic isomers, the so-called prism and cage isomers, which are more stable than the cyclic isomer.60 For these non-cyclic hexamer variants, however, we think a significant contribution to the overtone band is rather unlikely, given that their OH stretch vibrations are about 3 times less Raman active than the concerted stretch in the cyclic pentamer46 and that the contribution from the latter is only a small fraction of the overtone band integral (Table 3 and NB/4.3). If contributions from these less symmetric hexamer isomers could be identified and quantified, a local mode-based analysis would be more informative than our two-state and normal mode-based analysis, as explained in Section 2.3, given that enough information could be extracted from Raman (and perhaps complementary IR) spectra.
The suspected cyclic hexamer band at 3289 cm−1 is much weaker than the pentamer band at 3308 cm−1, but a potential contribution of the cyclic hexamer to the overtone band could still be non-negligible if the respective contributing state(s) would have more fundamental than overtone character. If the cyclic hexamer does in fact contribute to the overtone band significantly at higher water concentration, we expect the effect to be limited to quantities inferred for the pentamer and perhaps the tetramer, which would then be overestimated. However, the hexamer assignment at 3289 cm−1 is put into question by the fact that complementary IR spectra from slit expansions are missing a hexamer band, even if the pentamer band is of comparable strength as the trimer and tetramer bands.31
4.4 Comparability to theory
As stated in Section 2.3, we derived coupling constants as effective values that would apply if only a single fundamental state would couple with a single overtone state, and if that overtone state would not contribute to the overall intensity of the observed transitions. In reality, the situation may be significantly more complex with increasing ring size, since each monomer unit contributes one more bending overtone state and several combination states, with potential anharmonic couplings among each other and the OH stretch fundamentals. Theoretical predictions may reveal such complex couplings and an effective coupling would have to be calculated and held against the results from this work in this case. At that point, it may be more convenient to compare to intensity ratios, which are not tied to a particular model of the Fermi resonance.From the experimental point of view, a more complex coupling cannot be ruled out. However, a Fermi resonance involving more than two states could potentially lead to a more complex band pattern, and the only experimental evidence for this, the apparent structure of the overtone band, scales non-uniformly with different expansion conditions (see Fig. 3) and thus is at least partially due to overlap from different cluster contributions. How structured the overtone band is for each individual cluster cannot be determined in this non size-selective experiment. We can only constrain that if the coupling is more complex, it has to yield a pattern where contributing states are close enough so that a single Raman band results at the resolution of our experiment. A further constraint on the complexity of the Fermi resonance comes from linear IR spectra of water clusters.31,33,36,44 In Raman jet spectra, the overtone band is comparable in intensity to the tetramer and pentamer OH stretch fundamental bands, in IR jet spectra, however, the analogous potential overtone band at ∼3228 cm−1 is much weaker than tetramer and pentamer stretch fundamental bands. If the state(s) responsible for the Raman overtone band would also couple substantially with the IR active stretch modes, we would expect a prominent overtone band in IR spectra as well. Overall, with regard to the complexity of the resonance, we conclude that a two-state model is sufficient to explain the spectra, but acknowledge that our coupling constants are effective values and a comparison to theory has to take this limitation into account.
Other than the significant contribution of more than two states to the Fermi resonance, the intensity of the unperturbed overtone, which we assumed to be negligible, may be of interest.62 If we denote the intensity ratio of the unperturbed states with R0, we can express the intensity of the perturbed states as follows:
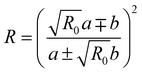 | (9) |
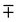 in the numerator applies if the coupling constant is positive and the lower operation if it is negative. In the absence of overtone intensity, R0 = 0 and eqn (9) becomes b2/a2. As can be seen from eqn (9), the common notion that the perturbing state “steals” intensity from the fundamental is not necessarily true if the coupling constant is negative and R0 is not negligible, and it may lead to surprising intensity ratios and “negative” Fermi resonances.62,63 Since R0 determines the mixing of states via its square root, even small intensity contributions from an overtone or combination tone can have a significant effect. However, quantum-chemical predictions of Raman intensities for the water monomer based on variational calculations find intensity ratios which fall in the range 10−3 to 10−4.64 If we use this range as an upper bound (we suspect some fundamental character of the state associated with the reported intensity due to the variational approach), we find that to yield the experimental band distances and intensity ratios, such an unperturbed intensity ratio would require a change of the coupling constant in the range from 12 to 4 cm−1 for the dimer, 8 to 3 cm−1 for the trimer and less than 2 cm−1 for the tetramer and pentamer (NB/6), which is within the 95% credible intervals of our posteriors. Still, intensity intrinsic to the unperturbed overtone could remove the difference in W3 and W4 that is found when no overtone intensity is assumed.
in the numerator applies if the coupling constant is positive and the lower operation if it is negative. In the absence of overtone intensity, R0 = 0 and eqn (9) becomes b2/a2. As can be seen from eqn (9), the common notion that the perturbing state “steals” intensity from the fundamental is not necessarily true if the coupling constant is negative and R0 is not negligible, and it may lead to surprising intensity ratios and “negative” Fermi resonances.62,63 Since R0 determines the mixing of states via its square root, even small intensity contributions from an overtone or combination tone can have a significant effect. However, quantum-chemical predictions of Raman intensities for the water monomer based on variational calculations find intensity ratios which fall in the range 10−3 to 10−4.64 If we use this range as an upper bound (we suspect some fundamental character of the state associated with the reported intensity due to the variational approach), we find that to yield the experimental band distances and intensity ratios, such an unperturbed intensity ratio would require a change of the coupling constant in the range from 12 to 4 cm−1 for the dimer, 8 to 3 cm−1 for the trimer and less than 2 cm−1 for the tetramer and pentamer (NB/6), which is within the 95% credible intervals of our posteriors. Still, intensity intrinsic to the unperturbed overtone could remove the difference in W3 and W4 that is found when no overtone intensity is assumed.
Another issue that should be considered when comparing against theory is the residual thermal excitation of the clusters in jet-expansions, which is in general non-uniform among their different degrees of freedom. We note that the ro-vibrational lines from the monomer show a clear effect of different carrier gases and nozzle pressure on the effective rotational temperature, but this did not have a strong effect on the determined monomer coupling constants (see Section 4.2). Vibrational degrees of freedom are less well cooled in jet-expansions,65,66 so we can expect the effective vibrational temperature to be closer to room temperature. For the monomer, thermal excitation of vibrational states is negligible even at room temperature, but for clusters, there may be some residual thermal excitation of their soft intermolecular modes3 even under jet-cooled conditions. Hot transitions originating from these excited intermolecular vibrational states may thus have a non-negligible effect on the cluster spectra. A heatable nozzle that we plan to use in future measurements will hopefully provide some additional information on the contribution of hot bands.
5 Conclusions and outlook
A novel, gas-recycling jet-spectrometer allowed us to measure Raman spectra of small water clusters with much longer exposure times than what would have been affordable with a conventional, non-recycling jet-spectrometer (Fig. 2, 3 and Fig. S1 in the main supplement, ESI†). With substantially improved signal-to-noise ratio for highly diluted measurements compared to spectra reported previously,44 we were able to quantitatively measure the intensity of the bending overtone band at 3212 cm−1 relative to the most Raman intense stretching fundamental bands of the dimer and cyclic trimer to cyclic pentamer (Table 3), and to resolve contributions to the overtone band by cluster size by applying Markov-Chain Monte-Carlo sampling (Table 4 and Fig. 5). The intensity ratio for the different clusters is connected to the Fermi resonance of bending overtone and stretching fundamental states and grants experimental insight into the anharmonicity of the potential energy surface of small water clusters. To our knowledge, this is the first systematic investigation of this Fermi resonance in small water clusters by Raman spectroscopic methods, which prove to be key here, since an analogous Fermi-enhanced band in IR spectra is missing. The results may be compared directly (Raman intensity ratios) or indirectly (effective coupling constants) against quantum chemical predictions that try to accurately model the vibrational dynamics of water clusters.Our more conservative MCMC sampling evaluation which includes intrinsic scatter56 yielded that the Raman intensity ratio is most likely negligible for the dimer with (1.0 ± 0.9)%, is a few percent for the trimer with (5.7 ± 0.8)%, and is likely above 50% for the tetramer and pentamer, hinting at a “perfect” Fermi resonance for these larger clusters. The trend towards a stronger resonance with larger ring size may be explained by the simultaneous increase of bending overtone and decrease of symmetric stretching fundamental frequencies for the normal modes where all oscillators move in phase, pushing these states towards each other in an unperturbed picture. The results for the tetramer and pentamer are tied to the assumption that the intensity ratio must fall into the range 0 to 1, which follows from a simple two-state/dark-state Fermi resonance model when the frequency of the unperturbed stretch fundamental is larger than the frequency of the unperturbed bend overtone. The same Fermi model yields effective coupling constants of (35 ± 16) cm−1 for the dimer, (65 ± 5) cm−1 for the trimer, and close to half the band distance, (59 ± 3) cm−1 and (43 ± 8) cm−1, for the tetramer and pentamer, respectively (Table 4). Simulations have shown that smaller coupling constants for the tetramer and pentamer would be missed by the posterior distributions of effective coupling constants, but still be detectable through their impact on inferred intensity ratios. We summarize the results on effective coupling constants as W5 ≲ 50 cm−1 < W4 ≲ 60 cm−1 < W3 ≈ 65 cm−1, which seems reasonable even if the restriction of the intensity ratio to the range [0, 1] is lifted. The results compare favorably with coupling constants reported in the literature, which are mostly ≤30 cm−1 for the water monomer12,13,23–25 (our estimate is close to 30 cm−1, Section 4.2) and ≥50 cm−1 for water in aggregates or the condensed phase.10,17–22,28
The results hint at a trend towards a larger effective coupling constant for the smaller and more strained cyclic trimer and tetramer compared to the pentamer. The accurate anharmonic modeling of Raman spectra and investigation of trends with regard to ring size is a next logical step in the investigation of small water clusters, and we hope that this work can motivate such research in the quantum chemical community. On the experimental side, measuring with a heated nozzle will allow us to investigate temperature effects and at the same time suppress larger cluster formation when measuring at higher concentration,44 enabling measurements with higher signal-to-noise ratio and potentially higher resolution. New jet measurements of D2O with its slightly narrower bands44 will also help us to learn more about the bend/stretch Fermi resonance in small water clusters, and to sharpen our understanding of a molecule that, despite its simple structure, keeps researchers busy even after decades of investigation and perpetual progress in experiment and theory.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
I thank Prof. Martin Suhm for motivating this work and for his invaluable support and discussions, and the Institute of Physical Chemistry for generous funding of the cookie-jet setup. The developments have furthermore profited from the benchmarking spirit and efforts in the research training group GRK 2455 which is funded by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 389479699. This work would not have been possible without countless contributors to free and open source software, in particular from the Python, Julia, and R community.References
- P. F. Bernath, Phys. Chem. Chem. Phys., 2002, 4, 1501–1509 RSC.
- F. Perakis, L. De Marco, A. Shalit, F. Tang, Z. R. Kann, T. D. Kühne, R. Torre, M. Bonn and Y. Nagata, Chem. Rev., 2016, 116, 7590–7607 CrossRef CAS PubMed.
- E. Vogt and H. G. Kjaergaard, Annu. Rev. Phys. Chem., 2022, 73, 209–231 CrossRef CAS PubMed.
- J. Tennyson, N. F. Zobov, R. Williamson, O. L. Polyansky and P. F. Bernath, J. Phys. Chem. Ref. Data, 2001, 30, 735–831 CrossRef CAS.
- O. L. Polyansky, A. G. Császár, S. V. Shirin, N. F. Zobov, P. Barletta, J. Tennyson, D. W. Schwenke and P. J. Knowles, Science, 2003, 299, 539–542 CrossRef CAS PubMed.
- L. Lodi, J. Tennyson and O. L. Polyansky, J. Chem. Phys., 2011, 135, 034113 CrossRef PubMed.
- Q. Yu, C. Qu, P. L. Houston, R. Conte, A. Nandi and J. M. Bowman, J. Phys. Chem. Lett., 2022, 13, 5068–5074 CrossRef CAS PubMed.
- X.-G. Wang and T. Carrington, J. Chem. Phys., 2023, 158, 084107 CrossRef CAS PubMed.
- B. T. Darling and D. M. Dennison, Phys. Rev., 1940, 57, 128–139 CrossRef CAS.
- I. V. Plastinin, S. A. Burikov, S. A. Dolenko and T. A. Dolenko, J. Raman Spectrosc., 2017, 48, 1235–1242 CrossRef CAS.
- E. Fermi, Zeitschrift für Physik, 1931, 71, 250–259 CrossRef CAS.
- D. F. Smith Jr. and J. Overend, Spectrochim. Acta, Part A, 1972, 28, 471–483 CrossRef.
- A. A. Kananenka and J. L. Skinner, J. Chem. Phys., 2018, 148, 244107 CrossRef PubMed.
- S. M. Matt and D. Ben-Amotz, J. Phys. Chem. B, 2018, 122, 5375–5380 CrossRef CAS PubMed.
- Y. Wang and J. M. Bowman, J. Phys. Chem. Lett., 2013, 4, 1104–1108 CrossRef CAS PubMed.
- J. Lindner, P. Vöhringer, M. S. Pshenichnikov, D. Cringus, D. A. Wiersma and M. Mostovoy, Chem. Phys. Lett., 2006, 421, 329–333 CrossRef CAS.
- V. Zhelyaskov, G. Georgiev and Z. Nickolov, J. Raman Spectrosc., 1988, 19, 405–412 CrossRef.
- A. Sokołowska, J. Raman Spectrosc., 1989, 20, 779–783 CrossRef.
- S. A. Burikov, T. A. Dolenko and D. M. Karpov, Opt. Spectrosc., 2010, 109, 272–278 CrossRef CAS.
- M. G. Sceats, M. Stavola and S. A. Rice, J. Chem. Phys., 1979, 71, 983–990 CrossRef CAS.
- M. S. Bergren and S. A. Rice, J. Chem. Phys., 1982, 77, 583–602 CrossRef CAS.
- K. Aoki, H. Yamawaki and M. Sakashita, Science, 1995, 268, 1322–1324 CrossRef CAS PubMed.
- J. E. Baggott, Mol. Phys., 1988, 65, 739–749 CrossRef CAS.
- A. B. McCoy and E. L. Silbert III, J. Chem. Phys., 1990, 92, 1893–1901 CrossRef CAS.
- H. G. Kjaergaard, B. R. Henry, H. Wei, S. Lefebvre, T. Carrington, O. Sonnich Mortensen and M. L. Sage, J. Chem. Phys., 1994, 100, 6228–6239 CrossRef CAS.
- P. Ayotte, G. H. Weddle, J. Kim and M. A. Johnson, J. Am. Chem. Soc., 1998, 120, 12361–12362 CrossRef CAS.
- W. H. Robertson, G. H. Weddle, J. A. Kelley and M. A. Johnson, J. Phys. Chem. A, 2002, 106, 1205–1209 CrossRef CAS.
- D. P. Tabor, R. Kusaka, P. S. Walsh, T. S. Zwier and E. L. Sibert III, J. Phys. Chem. A, 2015, 119, 9917–9930 CrossRef CAS PubMed.
- J. B. Paul, C. P. Collier, R. J. Saykally, J. J. Scherer and A. O'Keefe, J. Phys. Chem. A, 1997, 101, 5211–5214 CrossRef CAS.
- F. N. Keutsch and R. J. Saykally, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10533–10540 CrossRef CAS PubMed.
- D. Nesbitt, T. Häber and M. A. Suhm, Faraday Discuss., 2001, 118, 305–309 Search PubMed.
- K. Ohno, M. Okimura, N. Akai and Y. Katsumoto, Phys. Chem. Chem. Phys., 2005, 7, 3005–3014 RSC.
- A. Moudens, R. Georges, M. Goubet, J. Makarewicz, S. E. Lokshtanov and A. A. Vigasin, J. Chem. Phys., 2009, 131, 204312 CrossRef CAS PubMed.
- B. Tremblay, B. Madebène, M. E. Alikhani and J. P. Perchard, Chem. Phys., 2010, 378, 27–36 CrossRef CAS.
- J. Ceponkus, A. Engdahl, P. Uvdal and B. Nelander, Chem. Phys. Lett., 2013, 581, 1–9 CrossRef CAS.
- H. C. Gottschalk, T. L. Fischer, V. Meyer, R. Hildebrandt, U. Schmitt and M. A. Suhm, Instruments, 2021, 5, 12 CrossRef CAS.
- B. Temelso, K. A. Archer and G. C. Shields, J. Phys. Chem. A, 2011, 115, 12034–12046 CrossRef CAS PubMed.
- J. C. Howard, J. L. Gray, A. J. Hardwick, L. T. Nguyen and G. S. Tschumper, J. Chem. Theory Comput., 2014, 10, 5426–5435 CrossRef CAS PubMed.
- J. C. Howard and G. S. Tschumper, J. Chem. Theory Comput., 2015, 11, 2126–2136 CrossRef CAS PubMed.
- Y. Wang and J. M. Bowman, Phys. Chem. Chem. Phys., 2016, 18, 24057–24062 RSC.
- D. Bégué, I. Baraille, P. A. Garrain, A. Dargelos and T. Tassaing, J. Chem. Phys., 2010, 133, 034102 CrossRef PubMed.
- H. M. Lee, S. B. Suh, J. Y. Lee, P. Tarakeshwar and K. S. Kim, J. Chem. Phys., 2000, 112, 9759–9772 CrossRef CAS.
- S. Wuelfert, D. Herren and S. Leutwyler, J. Chem. Phys., 1987, 86, 3751–3753 CrossRef CAS.
- K. E. Otto, Z. Xue, P. Zielke and M. A. Suhm, Phys. Chem. Chem. Phys., 2014, 16, 9849–9858 RSC.
- V. Mohaček-Grošev, K. Furić and V. Vujnović, Spectrochim. Acta, Part A, 2022, 269, 120770 CrossRef PubMed.
- H. Cybulski and J. Sadlej, Chem. Phys., 2007, 342, 163–172 CrossRef CAS.
- A. Rule, A. Birmingham, C. Zuniga, I. Altintas, S.-C. Huang, R. Knight, N. Moshiri, M. H. Nguyen, S. B. Rosenthal, F. Pérez and P. W. Rose, PLoS Comput. Biol., 2019, 15, e1007007 CrossRef CAS PubMed.
- D. Nüst, V. Sochat, B. Marwick, S. J. Eglen, T. Head, T. Hirst and B. D. Evans, PLOS Comput. Biol., 2020, 16, e1008316 CrossRef PubMed.
- T. Scharge, T. N. Wassermann and M. A. Suhm, Zeitschrift für Physikalische Chemie, 2008, 222, 1407–1452 CrossRef CAS.
- N. O. B. Lüttschwager, T. N. Wassermann, R. A. Mata and M. A. Suhm, Angew. Chem., Int. Ed., 2013, 52, 463–466 CrossRef PubMed.
- M. Gawrilow and M. A. Suhm, Molecules, 2021, 26, 4523 CrossRef CAS PubMed.
- G. Avila, J. M. Fernández, G. Tejeda and S. Montero, J. Mol. Spectrosc., 2004, 228, 38–65 CrossRef CAS.
- N. O. B. Lüttschwager, J. Open Source Software, 2021, 6, 3526 CrossRef.
- P.-C. Bürkner, J. Stat. Softw., 2017, 80, 1–28 Search PubMed.
- B. Carpenter, A. Gelman, M. D. Hoffman, D. Lee, B. Goodrich, M. Betancourt, M. A. Brubaker, J. Guo, P. Li and A. Riddell, J. Stat. Softw., 2017, 76, 1 Search PubMed.
- B. C. Kelly, Astrophys. J., 2007, 665, 1489–1506 CrossRef.
- M. D. Hoffman and A. Gelman, J. Mach. Learn. Res., 2014, 15, 1593–1623 Search PubMed.
- A. Karpfen, Advances in Chemical Physics, John Wiley & Sons, Ltd, 2002, vol. 123, pp. 469–510 Search PubMed.
- M. A. Suhm, in Advances in Chemical Physics, ed. S. A. Rice, Wiley, 1st edn, 2009, vol. 142, pp. 1–57 Search PubMed.
- A. Malloum, J. J. Fifen, Z. Dhaouadi, S. G. N. Engo and J. Conradie, New J. Chem., 2019, 43, 13020–13037 RSC.
- S. Hirabayashi and K. M. T. Yamada, Chem. Phys. Lett., 2007, 435, 74–78 CrossRef CAS.
- R. N. Dixon, J. Chem. Phys., 1959, 31, 258–260 CrossRef CAS.
- I. R. Hill and I. W. Levin, J. Chem. Phys., 1979, 70, 842–851 CrossRef CAS.
- P. Seidler, J. Kongsted and O. Christiansen, J. Phys. Chem. A, 2007, 111, 11205–11213 CrossRef CAS PubMed.
- A. Amrein, M. Quack and U. Schmitt, J. Phys. Chem., 1988, 92, 5455–5466 CrossRef CAS.
- M. Louviot, N. Suas-David, V. Boudon, R. Georges, M. Rey and S. Kassi, J. Chem. Phys., 2015, 142, 214305 CrossRef CAS PubMed.
- E. L. Sibert III, J. T. Hynes and W. P. Reinhardt, J. Phys. Chem., 1983, 87, 2032–2037 CrossRef.
- N. O. B. Lüttschwager, Linear Raman Spectra of Small Water Clusters in Jet-Expansions, 2024 DOI:10.25625/IU7W3J.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06255d |
‡ Note that comparison of these Fermi coupling constants is complicated by the choice of coordinates, e.g. local modes versus normal modes or curvilinear versus rectilinear coordinates.67 Here, some of the quoted coupling constants were translated from local mode to normal mode representation by multiplying with 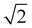 .13,23 The value stated in the paper by Tabor et al. is 45 cm−1, for the local mode basis. .13,23 The value stated in the paper by Tabor et al. is 45 cm−1, for the local mode basis. |
| § We sometimes use the term “area” interchangeably. |
| ¶ All Raman spectra presented in this work are available from the data repository GRO.data (https://data.goettingen-research-online.de/)68 and ESI.† |
| || For compact, cost-effective Raman workstation for molecular jet-spectroscopy. |
| ** Nitrogen is used for optical alignment and signal optimization. |
| †† Note that a (relative) intensity that we derive from a spectrum is always related to a band or line area (integral), never a peak height. |
| ‡‡ Several ro-vibrational transitions contribute to these lines, so a unique assignment and temperature analysis is not possible, but the line at 3152 cm−1 is the one with the lowest lower state energy contributors,4,52 thus its intensity should increase compared to 3159 cm−1 when the rotational temperature drops. |
| §§ R3152/3159 changes by at most 3.1 and the smallest coupling constant is 26 cm−1, thus 0.6 cm−1 × 3.1/26 cm−1 ≈ 0.07. |
| ¶¶ Note that the plots in Fig. 5 are smoothed by kernel density estimation, which leads to an artificial drop of probability density at the limiting values of Rn = 0 and Rn = 1. |
| |||| We calculate the error from the difference of the coupling constant's posterior mean and input coupling constant. |
| *** When intrinsic scatter is included in the fitting model, the true overtone band integral becomes another parameter that is inferred from the data. |
| This journal is © the Owner Societies 2024 |