Open Access Article
Open Access ArticleStrain-induced topological phase transition in ferromagnetic Janus monolayer MnSbBiS2Te2†
Romakanta
Bhattarai
 ,
Peter
Minch
,
Peter
Minch
 ,
Yunfan
Liang
,
Shengbai
Zhang
and
Trevor David
Rhone
*
,
Yunfan
Liang
,
Shengbai
Zhang
and
Trevor David
Rhone
*
Department of Physics, Applied Physics, and Astronomy, Rensselaer Polytechnic Institute, Troy, NY 12180, USA. E-mail: rhonet@rpi.edu
First published on 14th March 2024
Abstract
We investigate a strain-induced topological phase transition in the ferromagnetic Janus monolayer MnSbBiS2Te2 using first-principles calculations. The electronic, magnetic, and topological properties are studied under biaxial strain within the range of −8 to +8%. The ground state of monolayer MnSbBiS2Te2 is metallic with an out-of-plane magnetic easy axis. A band gap is opened when a compressive strain between −4% and −7% is applied. We observe a topological phase transition at a biaxial strain of −5%, where the material becomes a Chern insulator exhibiting a quantum anomalous hall (QAH) effect. We find that biaxial strain and spin–orbit coupling (SOC) are responsible for the topological phase transition in MnSbBiS2Te2. In addition, we find that biaxial strain can alter the direction of the magnetic easy axis of MnSbBiS2Te2. The Curie temperature is calculated using the Heisenberg model and is found to be 24 K. This study could pave the way to the design of topological materials with potential applications in spintronics, quantum computing, and dissipationless electronics.
Introduction
Two-dimensional (2D) magnetic Janus materials are a special class of materials that lack inversion symmetry. Because of their unique crystal structure and strong spin–orbit coupling, they possess many intriguing features, such as Rashba splitting,1–4 large vertical piezoelectricity,5–7 a tunable band gap,8,9 and a large Dzyaloshinskii–Moriya interaction (DMI).10,11 Therefore, 2D Janus materials have received a great deal of attention in nanoscience and nanotechnology in recent years. To date, several magnetic Janus materials have been discovered experimentally or predicted theoretically. For example, He et al. predicted that the Cr-based functionalized Janus MXene monolayers Cr2CXX′ (X, X′ = H, F, Cl, Br, OH) can have a Néel temperature of up to 400 K.12 Similarly, Akgenc et al. predicted a large Curie temperature of 1120 K in the monolayer CrScC, a Cr-based Janus MXene, suggesting a promising candidate for future spintronic applications.13 Jiao et al. proposed new 2D Janus Cr2O2XY (X = Cl, Y = Br/I) monolayers and investigated a phase transition from ferromagnetic to antiferromagnetic state with the strain, proposing Cr2O2XY as potential materials for the spintronic applications.14 In addition, Zhang et al. predicted a highly stable room-temperature ferromagnetic Janus VSSe monolayer with a large valley polarization, having potential applications in valleytronics V(S, Se)2.15 The study of these materials with unprecedented properties may provide some useful information for designing functional quantum devices. For example, MoSSe, and WSSe can be used in chemical sensing devices,16 hydrogen evolution reaction,17 and photocatalytic water splitting.18 Similarly, Janus graphene has potential applications in surface functionalization, field-effect transistors, Li-ion batteries, and actuators.19The search for the non-trivial topological features in 2D magnets started in 2019 after experiments identified MnBi2Te4 (MBT) to be the first antiferromagnetic topological insulator,20,21 which was already predicted theoretically by Otrokov et al. in 2017.22 Since then MBT has been the major focus of research on 2D materials. In addition, several exotic physical properties of MBT have also been investigated. For example, Lee et al. observed that MBT exhibits an intrinsic anomalous Hall effect arising from the noncollinear spin texture in the presence of the magnetic field.23 Zhang et al. predicted the axion insulating phase in the MBT with the quantized magnetocaloric effect.24 It was later verified by Liu et al. in 2020.25 Deng et al. and Liu et al. also observed that the Chern insulating phase exists in the few-layer MBT26,27 Moreover, Li et al. predicted several MBT-family materials that have a rich set of magnetic and topological properties such as topological insulators, Chern insulators, and Weyl semimetals28 In addition, the topological features were also observed in other members of the MBT-family, such as MnSb2Te4, MnBi2Se4, and MnSb2Se4.29,30 Further to this, several MBT-based heterostructures have also been investigated including (MnBi2Te4)m(Bi2Te3)n,31–33 and MBT/h-BN34 that exhibit non-trivial topological orders. Materials within the MBT family share the same crystal structure as MBT but with chemical substitutions at the lattice sites.
A monolayer of MBT was first experimentally realized in 2020.26 Calculations show that MBT is ferromagnetic with an HSE band gap of 0.7 eV.28 Since MBT is centrosymmetric, it lacks many intriguing physical phenomena, such as piezoelectricity, due to its inversion symmetry. Consequently, many efforts have been made to investigate materials within the MBT family that have small band gaps (required for topological behavior) and large piezoelectric responses. For example, Guo et al. theoretically predicted large intrinsic piezoelectricity in the Janus MnSbBiTe4 monolayer.7 Jiang et al. investigated the topological spin-textures in the 2D Janus MnBi2(Se, Te)435 Recently, Wu et al. found that the MnSbBiSe2Te2 Janus monolayer—isostructural to MBT—undergoes a phase transition from a trivial insulator to a topological insulator at −2% strain.11 Similarly, the Janus VSiGeN4 monolayer was shown to exhibit a trivial semiconductor–metal-QAH insulator transition with the strain.36 This method of strain engineering has also been applied to bilayers, heterostructures, and bulk materials.37–42 In addition, an external electric field has also been used to tune the properties of MBT-type materials. Cui et al. predicted that the electric control of the topological magnetic phase can be observed in the Janus magnetic MnBi2Se2Te2/In2Se3 heterostructure.43 You et al. investigated the electric field-induced topological phase transition in the family of monolayer MBT.44 These materials have potential applications in quantum computing, dissipationless electronics, spintronics,45 and photoelectric nanodevices.46
Recently, a data-driven approach that combines DFT calculations and machine learning was used to predict the properties of several monolayer vdW materials that are isostructural to MBT.47 The study highlighted several candidate Janus and non-Janus MBT-type materials that could exhibit topological order. While 2D Janus materials have been at the forefront of the current research, there are only a handful of MBT-type Janus materials that have been investigated systematically till now, such as MnSbBiTe4,7 MnSbBiSe2Te211 and MnBi2(S, Se)2Te2.35 In addition, the behavior of MBT-type materials that exhibit itinerant ferromagnetism in the monolayer hasn't been reported to date. These materials have applications in spintronic devices.28 This demands a systematic investigation of novel 2D Janus phases in the MBT family that may be useful to provide a deep insight into the behaviors of MBT-type materials. It may also provide avenues for future potential applications in quantum computing, dissipationless electronics, and spintronics. Inspired by this and guided by previous studies, we investigate MnSbBiS2Te2 a novel Janus ferromagnetic monolayer isostructural to MBT using first-principles calculations. We examine the chemical stability of this phase by calculating the formation energy, the phonon spectra, and ab initio molecular dynamics (AIMD) simulations. The calculations show that monolayer MnSbBiS2Te2 is ferromagnetic with zero band gap and an out-of-plane magnetization direction. The Curie temperature is found to be 24 K, which is comparable to that of other MBT-type materials. We apply a biaxial strain to the MnSbBiS2Te2 monolayer and investigate changes in the electronic, magnetic, and topological properties within the strain range of −8% to +8%. A band gap appears with a compressive strain between −4% and −7%. We observe a topological phase transition when the biaxial strain reaches −5%. In addition, we find that we can control the magnetic easy axis of MnSbBiS2Te2 by applying strain. Investigating the impact of strain on monolayer MnSbBiS2Te2 will help to further explore the electronic, magnetic, and topological degrees of freedom of MBT-type materials.
Methods
We perform density functional theory (DFT) calculations using the VASP package.48 A projector-augmented-wave (PAW)49 potential along with the exchange–correlation functional described by the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) is used for the calculations.50 To consider the localized states of Mn-3d electrons, we employ a DFT+U method with an effective Hubbard parameter of 4 eV.51 This value is taken from the literature.28,46,47,52 A plane wave basis set with an energy cutoff of 500 eV is used for the expansion of the wave function. Spin polarization and the spin–orbit interaction are considered in the calculations. A convergence criterion of 10−8 eV is set between any two successive electronic steps. The structures are allowed to relax fully until the force between any two ionic steps is less than 10−4 eV Å−1. A gamma-centered k-point mesh of 15 × 15 × 1 is used for the integration of the Brillouin zone. To avoid an interaction between vdW layers caused by the periodic boundary condition, a sufficiently large vacuum space of 45 Å is used along the z-axis. The calculations of topological invariants are performed using the Z2Pack code.53 The Curie temperature is calculated using Monte Carlo (MC) simulations based on the 2D Heisenberg model implemented in the Mcsolver package.54 The crystal orbital Hamilton population (COHP) analysis is performed using the LOBSTER package.55Results and discussion
The crystal structure of the MnSbBiS2Te2 Janus monolayer is shown in Fig. 1. It consists of 7 atoms in a unit cell that are arranged in a septuple layer in the following order: Te–Sb–Te–Mn–S–Bi–S. The Mn atoms are sandwiched between layers of SbTe2 and BiS2.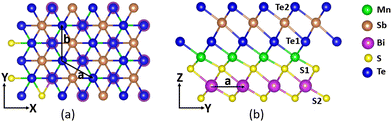 | ||
| Fig. 1 Crystal structure of monolayer MnSbBiS2Te2 (a) top view, and (b) side view. The lattice vectors are shown using solid black arrows. | ||
This structure is constructed from MBT by replacing Bi with Sb in the upper half and Te with S in the lower half of the MBT structure. MnSbBiS2Te2 possesses the same hexagonal lattice as MBT with the optimized lattice constant a = b = 4.13 Å, which is ≈ 5.7% lower than that of MBT (a = b = 4.38 Å). MnSbBiS2Te2 lacks inversion symmetry because of the asymmetric configurations of the atoms. To find the ground state of monolayer MnSbBiS2Te2, we consider a 2 × 1 × 1 supercell and perform calculations of ferromagnetic (FM) and antiferromagnetic (AFM) spin configurations. We find that the ground state of MnSbBiS2Te2 is ferromagnetic with an energy difference of 15.16 meV between FM and AFM states. Calculations show that the magnetic moment of monolayer MnSbBiS2Te2 is 5μB per unit cell.
We also calculate the magnetic anisotropy energy (MAE), which is the difference in energy between the in-plane (100) and out-of-plane (001) spin orientation of magnetic atoms (Mn) as given by the formula:
| MAE = E|| − E⊥ | (1) |
We investigate the chemical stability of monolayer MnSbBiS2Te2 by using three different methods. First, we calculate the formation energy, which is −1.063 eV per unit cell. We use formation energy as a proxy for chemical stability. Next, we perform the phonon dispersion calculations for a more robust check of chemical stability. We use a 4 × 4 × 1 supercell containing 112 atoms using the finite displacement method implemented in the Phonopy package.57 No imaginary phonon frequencies (that would indicate soft phonon modes) are seen in the phonon dispersion spectrum, thus implying its dynamical stability. The chemical stability is further tested by performing ab initio molecular dynamics (AIMD) simulations at 500 K for 30 ps with a time step of 2 fs. The total energy fluctuates without a sudden drop in the energy profile during the entire simulation period. These results provide evidence that monolayer MnSbBiS2Te2 is chemically stable. See ESI† for details.
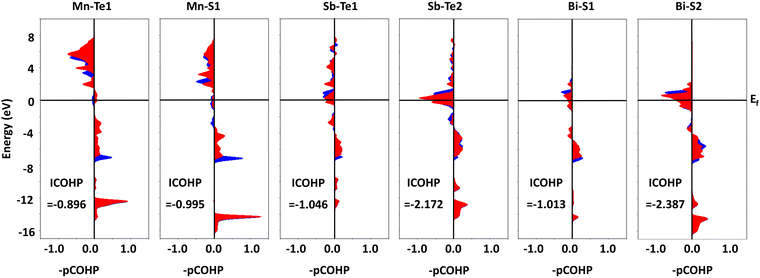
To understand the bonding and antibonding states in monolayer MnSbBiS2Te2, we perform the COHP analysis of monolayer MnSbBiS2Te2 using the LOBSTER package.55 The corresponding COHP plots are shown in Fig. 2. The positive (negative) values of –pCOHP represent the bonding (anti-bonding) orbitals. Fig. 1 shows that the valence band mainly consists of bonding orbitals for both spin-up and spin-down components. Also, the anti-bonding orbitals are found mostly near or above the Fermi level that constitutes the conduction band. The strength of interactions can be measured by doing the integral of the COHP (ICOHP). The negative values of ICOHP in all the COHP plots indicate the strong bonding nature among the constituting elements in the monolayer MnSbBiS2Te2.
To get further deeper into the electronic properties, we perform the Bader charge analysis of the monolayer MnSbBiS2Te2.58 We find that the elements occupying the X sites (i.e. S and Te) get the electronic charge transferred from the Mn, Sb, and Bi atoms. The Mn atom loses a charge of 1.109e, where ‘e’ is the charge of an electron, and its value is 1.67 × 10−19 C. This charge is transferred to the Te (0.461e) and S (0.648e) atoms that are bonded to the Mn atoms (i.e. Te1 and S1 respectively). Similarly, the Sb atom loses a charge of 0.594e, which is shared between two Te atoms (Te1 in the bulk and Te2 on the surface) as 0.259e and 0.335e respectively. Similarly, the Bi loses a charge of 1.244e and is shared by two S atoms (S1 in the bulk and S2 on the surface) as 0.468e and 0.776e, respectively. Thus, the Te atom on the surface gets a total charge of 0.335e, while that in the bulk gets 0.720e. Similarly, the S atom on the surface gets a total charge of 0.776e, while that in the bulk gets 1.116e. This mechanism implies that the elements occupying the X-sites in the MnSbBiS2Te2 are more electronegative than those of the A, and B sites.
We plot the total density of states and projected density of states of the monolayer MnSbBiS2Te2 using the DFT+U and hybrid-DFT (i.e. HSE06) methods59,60 by considering the spin–orbit interactions as shown in Fig. 3. We find that the DOS plots from both methods are similar and confirm the metallic character of the monolayer MnSbBiS2Te2. This validates the results of the DFT+U method. In Fig. 3(a), we find that Mn has a major contribution to both the valence band (VB) and conduction band (CB) but is far from the Fermi level (Ef). When talking about the contribution near Ef, we find that Bi and S contribute mainly to the CB, while Te contributes to the VB. The contribution of the Sb atom near Ef is very small although its contribution is significant to both the VB and CB far from Ef. A similar behavior is observed in Fig. 3(b). This also resembles the element-decomposed band structure in Fig. 6(a).
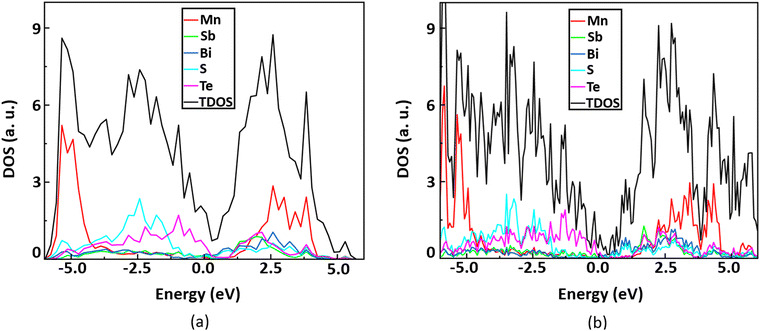 | ||
| Fig. 3 The total density of states and the projected density of states of the monolayer MnSbBiS2Te2 using (a) DFT+U, and (b) HSE method. The Fermi level is set to 0 eV. | ||
In the monolayer MnSbBiS2Te2, only the elements occupying A sites, namely Mn, are magnetic while all other elements are non-magnetic. However, the non-magnetic atoms still have very small but non-zero local magnetic moments arising from the indirect exchange and super–exchange interactions with the magnetic Mn atoms. Although they have a negligible contribution to the overall magnetic moment, the selection of these elements still affects the magnetic ordering of the material.47,61 Also, the unpaired spin-up electrons present in extremely localized 3d orbitals in the Mn atom are responsible for this magnetic behavior and the resulting magnetic dipole moment. In the monolayer MnSbBiS2Te2, Mn atom loses two 4s electrons, so it has a valency of +2. In addition, there is one 3d electron filling up each spin-up Mn-d sub-orbital, and there are 5 such sub-orbitals in Mn. Hence, the total number of spin-up electrons will be 5, and the local magnetic moment of Mn is 5μB.
Next, we calculate the Curie temperature (TC) of the MnSbBiS2Te2 monolayer using Monte Carlo simulations based on the Heisenberg model. The effect of localized 3d-orbitals of Mn atoms is taken into account by considering the following spin Hamiltonian:
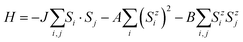 | (2) |
We consider the first, second, and third nearest neighbor exchange interactions while calculating the magnetic exchange parameters. The calculated values of J1, J2, and J3 are 1.994, −0.092, and −0.035 meV respectively. We find that J2 and J3 have very small values as compared to J1. Also, the negative signs in J2 and J3 imply that the second and third nearest neighbors always favor the AFM configurations. However, because of their much weaker strength as compared to J1, they are dominated by J1, which always favors the FM coupling. Hence, the preferred configuration of monolayer MnSbBiS2Te2 is FM. The dominating nature of J1 favoring FM state is also found in other members of the MBT-type materials such as MnBi2Te4, MnSbBiTe4, and MnSbBiSe2Te2 monolayers.7,11,44 Other methods also exist to model the magnetic structure of the materials using the Heisenberg Hamiltonian.66
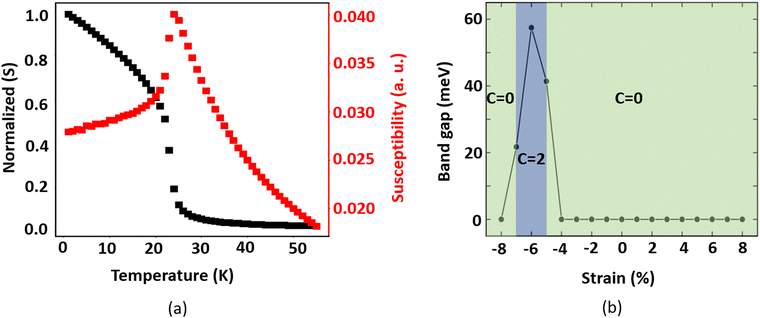
Since the total magnetic moment of monolayer MnSbBiS2Te2 is 5μB per unit cell, we consider S = 5/2 for the Mn atoms. The calculated value of A is 287 μeV per Mn atom. It should be noted that the normalized value of |S| is used when calculating the magnetic exchange parameters. We use the Wolff algorithm along with a supercell of size 50 × 50 × 1 and a temperature range of 1 to 55 K in the MC simulations. A plot of the magnetic moment and the magnetic susceptibility as a function of simulation temperature is shown in Fig. 4(a). The Curie temperature corresponds to the state where the magnetic susceptibility has its peak value. The predicted TC is found to be 24 K, which is larger than that of MnBi2Te4, MnSbBiTe4, MnSbBiSe2Te2, and MnBi2Se2Te2 monolayers.7,11 It is smaller than that of monolayer MnBi2S2Te2.44
It is well-known that the Heisenberg model is valid for materials with localized magnetic ordering. However, although monolayer MnSbBiS2Te2 is a ferromagnetic metal, the local magnetic moment of the Mn atom is very large (i.e. 5μB). This suggests that the Stoner model might be suitable for analyzing the magnetic properties of monolayer MnSbBiS2Te2. Thus, to justify the applicability of the Heisenberg model, we calculate the Stoner excitation energy (〈εk〉)67 and find it to be 0.92 eV. Since this value is much larger than TC of MnSbBiS2Te2 which is 24 K (≈ 2.07 meV), the ratio of the thermal energy of the FM transition (i.e. TC) to 〈εk〉 is very small. Thus, the effect of Stoner excitation won't be strong near the FM phase transition. So, we expect that the Heisenberg model should work just as a low-energy approximation for MnSbBiS2Te2. Notably, we expect this approximation to break down as the temperature increases beyond the FM transition and the Stoner excitation becomes relevant to the system. The Heisenberg model has been applied to many other famous 2D ferromagnetic metals including Fe3GeTe267,68 and MnSe2.69
We also calculate the TC using the analytical formula proposed by Torelli et al.70 and compare it with the result obtained from the MC simulations. Using the analytical formula, we find the TC to be 34.5 K, which is 10.5 K larger than the TC obtained from the MC simulations. It is apparent that the closed-form formula overestimates the TC of monolayer MnSbBiS2Te2. However, the above analytical formula can be a good source for getting a rough estimate of the TC for the magnetic materials.
We investigate the electronic, magnetic, and topological properties of monolayer MnSbBiS2Te2 under biaxial strain. The strain is defined as 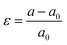 , where a and a0 are the lattice constants of strained and unstrained structures respectively. A positive (negative) value of ε indicates a tensile (compressive) strain. We also analyze the effect of biaxial strain on the magnetic easy axis of the monolayer MnSbBiS2Te2. In the range between −8% and +8% strain, we find that the monolayer MnSbBiS2Te2 prefers in-plane spin orientation from −3% to −4%. In all other cases, it prefers the out-of-plane spin orientation. See ESI† for details.
, where a and a0 are the lattice constants of strained and unstrained structures respectively. A positive (negative) value of ε indicates a tensile (compressive) strain. We also analyze the effect of biaxial strain on the magnetic easy axis of the monolayer MnSbBiS2Te2. In the range between −8% and +8% strain, we find that the monolayer MnSbBiS2Te2 prefers in-plane spin orientation from −3% to −4%. In all other cases, it prefers the out-of-plane spin orientation. See ESI† for details.
The strain dependence on the electronic band gap of monolayer MnSbBiS2Te2 is also investigated (see Fig. 4(b)). MnSbBiS2Te2 is metallic at 0% strain, but becomes an insulator when the compressive strain reaches −5%. At −5% strain, a gap is opened near the Γ point with a value of 41.39 meV, which changes to 57.5 meV at −6%, and 21.7 meV at −7% strain. If the strain is increased further, the metallic phase returns. As mentioned above, MnSbBiS2Te2 prefers an in-plane easy axis with no band gap at −4%. However, we find a small band gap (22.7 meV) when the magnetization axis is artificially switched to the out-of-plane (M || Z) direction. The previous reports show that the artificial switching of the magnetization axis in 2D magnets is feasible by applying a large external magnetic field.71,72 Meanwhile, tensile strain does not open a band gap in monolayer MnSbBiS2Te2. See ESI† for details.
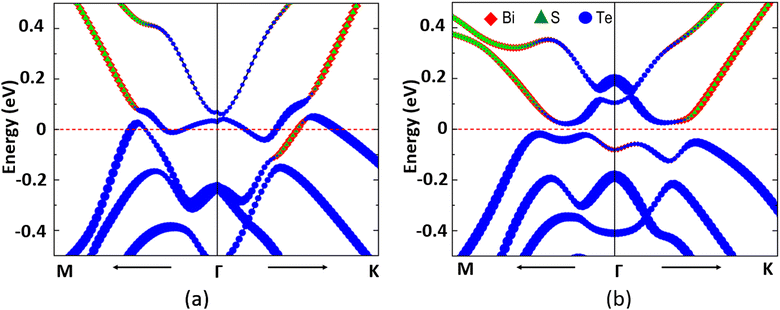
The band structure of monolayer MnSbBiS2Te2 at −5% strain is shown in Fig. 5. Fig. 5(a) shows the band structure with the SOC excluded from calculations. In the case of no SOC, the band gap is 0.18 eV. When SOC is turned on, the band gap is reduced to 41.39 meV (see Fig. 5(b)). The elemental-decomposed band structure is calculated and displayed in Fig. 6. The band inversion is not observed where the SOC is turned off. However, we see a clear band inversion near the Fermi level when the SOC is turned on (Fig. 6(b)). Thus the SOC-induced band inversion in strained MnSbBiS2Te2 indicates a possible topological phase transition. Several studies have shown that SOC plays a vital role in non-trivial topology because of the fact that SOC-induced band inversion is important for determining the existence of topological phases in the materials.11,28,44,52,73,74
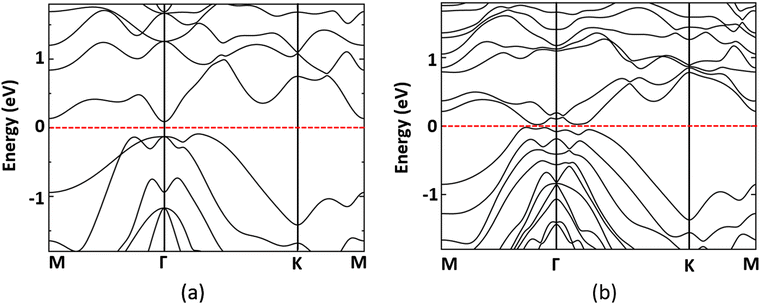 | ||
| Fig. 5 Electronic band structure of the MnSbBiS2Te2 Janus monolayer at −5% strain (a) without SOC, and (b) with SOC. | ||
The changes in the band gap can be explained by plotting the band structure at different values of strain along the high-symmetry path of the Brillouin zone. The band structure of the unstrained monolayer features a small overlap of the valence band (VB) and conduction band (CB) near the Fermi level. The overlap between VB and CB decreases with increasing compressive strain, then vanishes at −5%; followed by a band gap of 41.39 meV emerging near the Γ point. This gap changes to 57.5 meV at −6% and 21.7 meV at −7% strain. If the compressive strain is further applied, the material changes back to the metallic state. To confirm the metallic phase, we plot the band structure at −8% strain, which shows that the monolayer MnSbBiS2Te2 is indeed metallic at a biaxial strain of −8%. The band gap is not observed when the strain is applied in the positive direction. See ESI† for details.
To get a deeper insight into the origin of the band gap and the topological phase transition in monolayer MnSbBiS2Te2, we calculate the charge densities at the highest occupied energy band in the VB and lowest unoccupied energy band in the CB at different values of biaxial strain and follow their changes with the strain (see ESI†). The continuous change of the atomic orbitals with applied strain is observed in Te, Bi, and S atoms for both compressive and tensile strain. Interestingly, no change is observed in the 3d orbitals of Mn atoms throughout the strain range. This behavior is consistent with the elemental-decomposed band structure in Fig. 6. See ESI† for details.
The element-decomposed electronic band structure of unstrained monolayer MnSbBiS2Te2 is shown in Fig. 6(a). The 5s and 5p orbitals of the Te atoms contribute to the valence bands near the Fermi level while those of the conduction bands are from the joint contributions of the 3p orbitals of S and 6p orbitals of Bi atoms. The band crossings at two different points near the Fermi level indicate the possible topological states in monolayer MnSbBiS2Te2. When the applied strain reaches −5% (Fig. 6(b)), the overlapping regions on both sides of the Γ point disappear and a clear separation of VB and CB is observed. This results in an indirect band gap of 41.39 meV. We find that the biaxial strain not only changes the lattice parameters and the relative positions of ions in the crystal structure but also contributes to the change of atomic orbitals near the Fermi level. This potentially leads to the opening or closing of the energy gap at different values of strain in addition to SOC-induced band inversion. Hence, strain in the presence of SOC facilitates a topological phase transition.
We observe a band inversion of s and p orbitals of S and Bi atoms (CB → VB), and Te atoms (VB → CB) in the band structure in Fig. 6(b). This indicates a possible topological phase transition in the material at −5% strain (Fig. 4(b)). To confirm this transition, we perform calculations to determine the topological invariant (i.e. Chern number) using the Z2Pack package. From the calculations, we find a Chern number (C) = 2, thus confirming a Chern insulator state that exhibits the quantum anomalous hall (QAH) effect. This implies that the Hall conductivity is quantized at 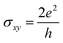 . Thus there exist two topologically protected chiral edge states that are capable of carrying a dissipationless current. We find that the QAH insulating phase remains unchanged with C = 2 until the applied strain reaches −8%. At −8% strain, the material goes back to the trivial metallic phase as shown in Fig. 4(b). We also investigate the Chern insulating phases where the magnetization directions are artificially switched between in-plane and out-of-plane. Interestingly, no QAH state is found when the spin magnetization is changed to an in-plane, which is different from the MnSbBiSe2Te2 monolayer.11 Our calculations suggest that the trivial insulating phase does not exist in the MnSbBiS2Te2 monolayer.
. Thus there exist two topologically protected chiral edge states that are capable of carrying a dissipationless current. We find that the QAH insulating phase remains unchanged with C = 2 until the applied strain reaches −8%. At −8% strain, the material goes back to the trivial metallic phase as shown in Fig. 4(b). We also investigate the Chern insulating phases where the magnetization directions are artificially switched between in-plane and out-of-plane. Interestingly, no QAH state is found when the spin magnetization is changed to an in-plane, which is different from the MnSbBiSe2Te2 monolayer.11 Our calculations suggest that the trivial insulating phase does not exist in the MnSbBiS2Te2 monolayer.
Now we investigate the effect of the Hubbard U parameter on the electronic and magnetic properties of monolayer MnSbBiS2Te2. When dealing with materials that contain strongly correlated electrons, such as transition metals, and rare-earth elements, it is extremely important to make sure that the electron correlations among all the localized d- and f-orbitals are properly addressed in the calculations. Otherwise, there will be convergence issues. i.e. the structures may not converge or converge to an incorrect configuration. The DFT+U method solves this issue by adding the Coulomb interaction via the Hubbard U parameter; thereby overcoming a main drawback of the standard DFT method. While the DFT+U method is widely used to accurately characterize such materials, it is important to note that it still has its own set of limitations. For example, the choice of the Hubbard U parameter requires careful consideration. Although the value of U is taken from the literature, we validate our results by considering different U values. We perform calculations of electronic and magnetic properties of the monolayer MnSbBiS2Te2 using the DFT, DFT+U with varying U values (U = 2, 3, 4, 5 eV), and the HSE methods and compare the results. We find that the standard DFT method with zero U value results in monolayer MnSbBiS2Te2 relaxing to the wrong magnetic configuration (i.e. AFM). To further verify this, we repeat the same calculations for the monolayer MBT, which is a well-known ferromagnetic material.20,28 We find that the MBT also converges to the AFM configuration, which is incorrect. This confirms that the results of the standard DFT alone (i.e. without U) are not reliable for predicting the properties of the MBT-type materials. The results of DFT+U (U = 2, 3, 4, 5 eV), and HSE methods are summarized in Table 1.
| Method | ΔE (meV) | MAE (μeV) | Easy axis (IP/OOP) | J 1 (meV) | J 2 (meV) | J 3 (meV) | Band gap at 0% (meV) | Band gap at −5% (meV) |
|---|---|---|---|---|---|---|---|---|
| DFT+2 eV | 10.118 | 317 | OOP | 1.468 | −0.188 | −0.122 | 0 | 61.934 |
| DFT+3 eV | 13.442 | 296 | OOP | 1.821 | −0.130 | −0.069 | 0 | 50.040 |
| DFT+4 eV | 15.156 | 287 | OOP | 1.994 | −.092 | −0.035 | 0 | 40.650 |
| DFT+5 eV | 15.905 | 233 | OOP | 2.056 | −0.066 | −0.012 | 0 | 34.212 |
| HSE | − | − | − | − | − | − | 0 | 46.141 |
Where ΔE is the energy difference between AFM and FM configurations (i.e. ΔE = EAFM − EFM). Table 1 shows that ΔE is positive and it increases with the Hubbard U parameter showing that MnSbBiS2Te2 always prefers FM ground state in the considered U range. The larger values of ΔE depict the enhanced magnetic coupling in MnSbBiS2Te2. Although the MAE decreases with an increase in U value, the easy axis of MnSbBiS2Te2 always remains the same (i.e. OOP) regardless of the U values. As the Hubbard U parameter increases, the strength of J1 increases while J2 and J3 decreases. The nature of FM and AFM exchange couplings remains the same in the considered U range. Thus, by incorporating the U parameter in the calculation, we are able to achieve the correct magnetic configuration of monolayer MnSbBiS2Te2. In addition, all the methods, including HSE, show the metallic character of monolayer MnSbBiS2Te2 at 0% strain (unstretched case), whereas at −5% strain, the gap changes with U values almost negligibly. This is because the atomic orbitals of Bi, S, and Te are mainly responsible for determining the band gap of MnSbBiS2Te2 as shown in the element decomposed band structures in Fig. 6. The d-orbitals of Mn, where the electron correlation effect is applied, are far away from the Fermi level. Hence, they have very little influence in determining the band gap. The band gap at U = 4 eV is close to the result from the HSE calculation, which validates our results.
While it is challenging to experimentally achieve the large compressive strains we predict are required for a phase transition, our results are still useful for understanding the topological properties of MBT-type materials. We expect that our study will create the impetus to search for other magnetic 2D materials that exhibit topological features without applying strain or materials that can undergo topological phase transitions at lower strain. Further to this, our work will also encourage future experimental investigations of these types of materials. It will be interesting to investigate the bilayers, multilayers, and heterostructures of MnSbBiS2Te2. Materials exhibiting tunable topological features have potential applications in devices with dissipationless transport, topological quantum electronics, and spintronics.
Conclusions
In summary, we propose a novel phase of monolayer MnSbBiS2Te2 using first-principles calculations. We investigate the chemical stability of MnSbBiS2Te2 using formation energy calculations, phonon spectra calculations, and AIMD simulations. Calculations show that unstrained monolayer MnSbBiS2Te2 is ferromagnetic with a zero band gap and an out-of-plane magnetization direction. The calculated Curie temperature is 24 K. We show that applying a biaxial strain to monolayer MnSbBiS2Te2 alters its electronic, magnetic, and topological properties. A band gap emerges when a compressive strain between −4% and −7% is applied. We also observe a metal-insulator-metal transition with applied strain. The material becomes a Chern insulator with C = 2 exhibiting the QAH effect when it is compressed to −5%. Our study provides some important features of the 2D magnetic topological material belonging to the MBT family which may serve as a potential candidate for future applications in topological quantum computing, magnetic sensors, and spintronics. This study also creates new avenues for the strain engineering of topological phase transitions in novel 2D materials with long-range magnetic order.Author contributions
T. R. conceived the idea of the project and assisted in writing the manuscript. R. B. performed the calculations, conducted the data analysis, and wrote the manuscript. P. M., Y. L., and S. Z. assisted with the data analysis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work used the Extreme Science and Engineering Discovery Environment (XSEDE), supported by National Science Foundation grant number ACI-1548562. In addition, we used the resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357. This material is based upon work supported by the NSF CAREER award under grant number 2044842. The authors thank Allan H. MacDonald (University of Texas at Austin), Chao Lei (University of Texas at Austin), and Kin Fai Mak (Cornell University) for useful discussions.Notes and references
- Y. Cheng, Z. Zhu, M. Tahir and U. Schwingenschlögl, Europhys. Lett., 2013, 102, 57001 CrossRef.
- Y. Wang, W. Wei, H. Wang, N. Mao, F. Li, B. Huang and Y. Dai, J. Phys. Chem. Lett., 2019, 10, 7426–7432 CrossRef CAS PubMed.
- J. Liang, Q. Cui and H. Yang, Phys. Rev. B, 2020, 102, 220409 CrossRef CAS.
- Q.-F. Yao, J. Cai, W.-Y. Tong, S.-J. Gong, J.-Q. Wang, X. Wan, C.-G. Duan and J. Chu, Phys. Rev. B, 2017, 95, 165401 CrossRef.
- L. Dong, J. Lou and V. B. Shenoy, ACS Nano, 2017, 11, 8242–8248 CrossRef CAS PubMed.
- Y. Guo, S. Zhou, Y. Bai and J. Zhao, Appl. Phys. Lett., 2017, 110, 163102 CrossRef.
- S.-D. Guo and M.-X. Wang, Phys. Chem. Chem. Phys., 2021, 23, 22443–22450 RSC.
- W. Chen, X. Hou, X. Shi and H. Pan, ACS Appl. Mater. Interfaces, 2018, 10, 35289–35295 CrossRef CAS PubMed.
- A. Kandemir and H. Sahin, Phys. Rev. B, 2018, 97, 155410 CrossRef CAS.
- J. Liang, W. Wang, H. Du, A. Hallal, K. Garcia, M. Chshiev, A. Fert and H. Yang, Phys. Rev. B, 2020, 101, 184401 CrossRef CAS.
- Z. Wu, Y. Xue, Z. Shen and C. Song, Phys. Chem. Chem. Phys., 2023, 25, 96–105 RSC.
- J. He, P. Lyu, L. Sun, A. M. Garcia and P. Nachtigall, J. Mater. Chem. C, 2016, 4, 6500–6509 RSC.
- B. Akgenç, E. Vatansever and F. Ersan, Phys. Rev. Mater., 2021, 5, 083403 CrossRef.
- J. Jiao, N. Miao, Z. Li, Y. Gan, J. Zhou and Z. Sun, J. Phys. Chem. Lett., 2019, 10, 3922–3928 CrossRef CAS PubMed.
- C. Zhang, Y. Nie, S. Sanvito and A. Du, Nano Lett., 2019, 19, 1366–1370 CrossRef CAS PubMed.
- C. Jin, X. Tang, X. Tan, S. C. Smith, Y. Dai and L. Kou, J. Mater. Chem. A, 2019, 7, 1099–1106 RSC.
- D. Er, H. Ye, N. C. Frey, H. Kumar, J. Lou and V. B. Shenoy, Nano Lett., 2018, 18, 3943–3949 CrossRef CAS PubMed.
- L. Ju, M. Bie, X. Tang, J. Shang and L. Kou, ACS Appl. Mater. Interfaces, 2020, 12, 29335–29343 CAS.
- S.-W. Ng, N. Noor and Z. Zheng, NPG Asia Mater., 2018, 10, 217–237 CrossRef CAS.
- M. M. Otrokov, I. I. Klimovskikh, H. Bentmann, D. Estyunin, A. Zeugner, Z. S. Aliev, S. Gaß, A. Wolter, A. Koroleva and A. M. Shikin, et al. , Nature, 2019, 576, 416–422 CrossRef CAS PubMed.
- Y. Gong, J. Guo, J. Li, K. Zhu, M. Liao, X. Liu, Q. Zhang, L. Gu, L. Tang and X. Feng, et al. , Chin. Phys. Lett., 2019, 36, 076801 CrossRef CAS.
- M. M. Otrokov, T. V. Menshchikova, M. G. Vergniory, I. P. Rusinov, A. Y. Vyazovskaya, Y. M. Koroteev, G. Bihlmayer, A. Ernst, P. M. Echenique and A. Arnau, et al. , 2D Mater., 2017, 4, 025082 CrossRef.
- S. H. Lee, Y. Zhu, Y. Wang, L. Miao, T. Pillsbury, H. Yi, S. Kempinger, J. Hu, C. A. Heikes and P. Quarterman, et al. , Phys. Rev. Res., 2019, 1, 012011 CrossRef CAS.
- D. Zhang, M. Shi, T. Zhu, D. Xing, H. Zhang and J. Wang, Phys. Rev. Lett., 2019, 122, 206401 CrossRef CAS PubMed.
- C. Liu, Y. Wang, H. Li, Y. Wu, Y. Li, J. Li, K. He, Y. Xu, J. Zhang and Y. Wang, Nat. Mater., 2020, 19, 522–527 CrossRef CAS PubMed.
- Y. Deng, Y. Yu, M. Z. Shi, Z. Guo, Z. Xu, J. Wang, X. H. Chen and Y. Zhang, Science, 2020, 367, 895–900 CrossRef CAS PubMed.
- C. Liu, Y. Wang, M. Yang, J. Mao, H. Li, Y. Li, J. Li, H. Zhu, J. Wang and L. Li, et al. , Nat. Commun., 2021, 12, 4647 CrossRef CAS PubMed.
- J. Li, Y. Li, S. Du, Z. Wang, B.-L. Gu, S.-C. Zhang, K. He, W. Duan and Y. Xu, Sci. Adv., 2019, 5, eaaw5685 CrossRef CAS PubMed.
- T. Murakami, Y. Nambu, T. Koretsune, G. Xiangyu, T. Yamamoto, C. M. Brown and H. Kageyama, Phys. Rev. B, 2019, 100, 195103 CrossRef CAS PubMed.
- H. Zhang, W. Yang, Y. Wang and X. Xu, Phys. Rev. B, 2021, 103, 094433 CrossRef CAS.
- E. D. Rienks, S. Wimmer, J. Sánchez-Barriga, O. Caha, P. S. Mandal, J. Ržička, A. Ney, H. Steiner, V. V. Volobuev and H. Groiß, et al. , Nature, 2019, 576, 423–428 CrossRef CAS PubMed.
- J. Wu, F. Liu, M. Sasase, K. Ienaga, Y. Obata, R. Yukawa, K. Horiba, H. Kumigashira, S. Okuma and T. Inoshita, et al. , Sci. Adv., 2019, 5, eaax9989 CrossRef CAS PubMed.
- I. I. Klimovskikh, M. M. Otrokov, D. Estyunin, S. V. Eremeev, S. O. Filnov, A. Koroleva, E. Shevchenko, V. Voroshnin, A. G. Rybkin and I. P. Rusinov, et al. , npj Quantum Mater., 2020, 5, 54 CrossRef CAS.
- R. Gao, G. Qin, S. Qi, Z. Qiao and W. Ren, Phys. Rev. Mater., 2021, 5, 114201 CrossRef CAS.
- J. Jiang, X. Liu, R. Li and W. Mi, Appl. Phys. Lett., 2021, 119, 072401 CrossRef CAS.
- S.-D. Guo, W.-Q. Mu, J.-H. Wang, Y.-X. Yang, B. Wang and Y.-S. Ang, Phys. Rev. B, 2022, 106, 064416 CrossRef CAS.
- Z. Tajkov, D. Visontai, L. Oroszlány and J. Koltai, Nanoscale, 2019, 11, 12704–12711 RSC.
- M. Trama, V. Cataudella and C. A. Perroni, Phys. Rev. Res., 2021, 3, 043038 CrossRef CAS.
- G. Luo, X. Lv, L. Wen, Z. Li and Z. Dai, Front. Phys., 2022, 17, 23502 CrossRef.
- R. Juneja, R. Shinde and A. K. Singh, J. Phys. Chem. Lett., 2018, 9, 2202–2207 CrossRef CAS PubMed.
- T. Ideue, M. Hirayama, H. Taiko, T. Takahashi, M. Murase, T. Miyake, S. Murakami, T. Sasagawa and Y. Iwasa, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 25530–25534 CrossRef CAS PubMed.
- J. Mutch, W.-C. Chen, P. Went, T. Qian, I. Z. Wilson, A. Andreev, C.-C. Chen and J.-H. Chu, Sci. Adv., 2019, 5, eaav9771 CrossRef CAS PubMed.
- Q. Cui, Y. Zhu, J. Jiang, J. Liang, D. Yu, P. Cui and H. Yang, Phys. Rev. Res., 2021, 3, 043011 CrossRef CAS.
- J.-Y. You, X.-J. Dong, B. Gu and G. Su, Phys. Rev. B, 2021, 103, 104403 CrossRef CAS.
- X.-L. Qi and S.-C. Zhang, Rev. Mod. Phys., 2011, 83, 1057–1110 CrossRef CAS.
- Y. An, K. Wang, S. Gong, Y. Hou, C. Ma, M. Zhu, C. Zhao, T. Wang, S. Ma and H. Wang, et al. , npj Comput. Mater., 2021, 7, 45 CrossRef CAS.
- R. Bhattarai, P. Minch and T. D. Rhone, J. Mater. Chem. C, 2023, 11(17), 5601–5610 RSC.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- Z. Li, J. Li, K. He, X. Wan, W. Duan and Y. Xu, Phys. Rev. B, 2020, 102, 081107 CrossRef CAS.
- D. Gresch, G. Autes, O. V. Yazyev, M. Troyer, D. Vanderbilt, B. A. Bernevig and A. A. Soluyanov, Phys. Rev. B, 2017, 95, 075146 CrossRef.
- L. Liu, X. Ren, J. Xie, B. Cheng, W. Liu, T. An, H. Qin and J. Hu, Appl. Surf. Sci., 2019, 480, 300–307 CrossRef CAS.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, LOBSTER: A tool to extract chemical bonding from plane-wave based DFT, 2016 Search PubMed.
- F. Xue, Z. Wang, Y. Hou, L. Gu and R. Wu, Phys. Rev. B, 2020, 101, 184426 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd and G. E. Scuseria, J. Chem. Phys., 2004, 121, 1187–1192 CrossRef CAS PubMed.
- T. D. Rhone, W. Chen, S. Desai, S. B. Torrisi, D. T. Larson, A. Yacoby and E. Kaxiras, Sci. Rep., 2020, 10, 15795 CrossRef CAS PubMed.
- M. N. Gjerding, A. Taghizadeh, A. Rasmussen, S. Ali, F. Bertoldo, T. Deilmann, N. R. Knøsgaard, M. Kruse, A. H. Larsen and S. Manti, et al. , 2D Mater., 2021, 8, 044002 CrossRef CAS.
- Y. Li, Z. Jiang, J. Li, S. Xu and W. Duan, Phys. Rev. B, 2019, 100, 134438 CrossRef CAS.
- Q. Cui, Y. Zhu, J. Liang, P. Cui and H. Yang, Phys. Rev. B, 2023, 107, 064422 CrossRef CAS.
- B.-C. Gong, Y. Gao, X.-L. Qiu, N.-N. Zhao, K. Liu and Z.-Y. Lu, Phys. Rev. B, 2022, 106, 235153 CrossRef CAS.
- S. Tiwari, M. L. Van de Put, B. Soree and W. G. Vandenberghe, Phys. Rev. B, 2021, 103, 014432 CrossRef CAS.
- Z.-X. Shen, X. Bo, K. Cao, X. Wan and L. He, Phys. Rev. B, 2021, 103, 085102 CrossRef CAS.
- H. L. Zhuang, P. Kent and R. G. Hennig, Phys. Rev. B, 2016, 93, 134407 CrossRef.
- J.-J. Liao, Y.-Z. Nie, X.-G. Wang, Z.-Y. Luo, Q.-L. Xia, R. Xiong and G.-H. Guo, Phys. B, 2024, 675, 415642 CrossRef CAS.
- D. Torelli and T. Olsen, 2D Mater., 2018, 6, 015028 CrossRef.
- J. Li, C. Wang, Z. Zhang, B.-L. Gu, W. Duan and Y. Xu, Phys. Rev. B, 2019, 100, 121103 CrossRef CAS.
- Y. Deng, Y. Yu, Y. Song, J. Zhang, N. Z. Wang, Z. Sun, Y. Yi, Y. Z. Wu, S. Wu and J. Zhu, et al. , Nature, 2018, 563, 94–99 CrossRef CAS PubMed.
- P. Li, J. Yu, Y. Wang and W. Luo, Phys. Rev. B, 2021, 103, 155118 CrossRef CAS.
- C. Lin, M. Ochi, R. Noguchi, K. Kuroda, M. Sakoda, A. Nomura, M. Tsubota, P. Zhang, C. Bareille, K. Kurokawa, Y. Arai, K. Kawaguchi, H. Tanaka, K. Yaji, A. Harasawa, M. Hashimoto, D. Lu, S. Shin, R. Arita, S. Tanda and T. Kondo, Nat. Mater., 2021, 20, 1093–1099 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05578g |
| This journal is © the Owner Societies 2024 |