Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Control of excitation selectivity in pulse EPR on spin-correlated radical pairs with shaped pulses†
Daniele
Panariti
 a,
Sarah M.
Conron
b,
Jinyuan
Zhang
b,
Michael R.
Wasielewski
a,
Sarah M.
Conron
b,
Jinyuan
Zhang
b,
Michael R.
Wasielewski
 b,
Marilena
Di Valentin
b,
Marilena
Di Valentin
 a and
Claudia E.
Tait
a and
Claudia E.
Tait
 *c
*c
aDepartment of Chemical Sciences, University of Padova, 35131 Padova, Italy
bDepartment of Chemistry, Applied Physics Program, and Center for Molecular Quantum Transduction, Northwestern University, Evanston, Illinois 60208-3113, USA
cDepartment of Chemistry, University of Oxford, Oxford OX1 3QZ, UK. E-mail: claudia.tait@chem.ox.ac.uk
First published on 26th December 2023
Abstract
Spin-correlated radical pairs generated by photoinduced electron transfer are characterised by a distinctive spin polarisation and a unique behaviour in pulse electron paramagnetic resonance (EPR) spectroscopy. Under non-selective excitation, an out-of-phase echo signal modulated by the dipolar and exchange coupling interactions characterising the radical pair is observed and allows extraction of geometric information in the two-pulse out-of-phase electron spin echo envelope modulation (ESEEM) experiment. The investigation of the role of spin-correlated radical pairs in a variety of biological processes and in the fundamental mechanisms underlying device function in optoelectronics, as well as their potential use in quantum information science, relies on the ability to precisely address and manipulate the spins using microwave pulses. Here, we explore the use of shaped pulses for controlled narrowband selective and broadband non-selective excitation of spin-correlated radical pairs in two model donor–bridge–acceptor triads, characterised by different spectral widths, at X- and Q-band frequencies. We demonstrate selective excitation with close to rectangular excitation profiles using BURP (band-selective, uniform response, pure-phase) pulses and complete non-selective excitation of both spins of the radical pair using frequency-swept chirp pulses. The use of frequency-swept pulses in out-of-phase ESEEM experiments enables increased modulation depths and, combined with echo transient detection and Fourier transformation, correlation of the dipolar frequencies with the EPR spectrum and therefore the potential to extract additional information on the donor–acceptor pair geometry.
1 Introduction
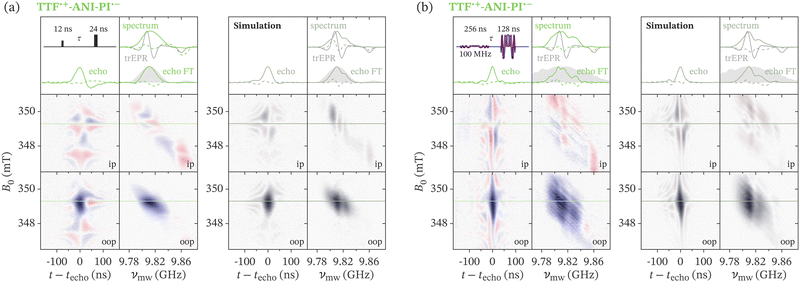
Photoexcitation of donor–acceptor systems is generally followed by electron transfer generating spin-correlated radical pairs (SCRPs) characterised by a unique spin polarisation as a result of the conservation of spin angular momentum. Spin-correlated radical pairs play a fundamental role in a wide variety of biological systems, including photosynthetic reaction centres,1,2 cryptochromes, and photolyases,3–5 and are at the basis of the photovoltaic process in organic solar cells.6–8 Their unique properties make spin-correlated radical pairs promising candidates for magnetic and electric field sensing in quantum information science.9–12The properties of spin-correlated radical pairs and their role in a variety of processes in biology and optoelectronics can be investigated by electron paramagnetic resonance (EPR) spectroscopy. Formation of a spin-correlated radical pair from a singlet state precursor leads to a distinctive spin polarisation pattern resulting from population of sublevels with singlet character.13 This initial state corresponds to the presence of longitudinal two-spin order and zero-quantum coherence, and leads to an unusual behaviour of spin-correlated radical pairs in pulse EPR experiments.14–18 The echo signal in a two-pulse experiment with non-selective excitation is characterised by an anomalous flip-angle dependence and a 90° phase shift compared to echoes typically observed for radicals in thermal equilibrium, and is therefore generally referred to as an out-of-phase echo.16–18 Theoretical calculations for weakly coupled spin-correlated radical pairs predict the maximum out-of-phase echo amplitude for a two-pulse sequence with flip angles of 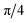 and π, compared to the typical
and π, compared to the typical  and π flip angles maximising the in-phase echo for Boltzmann-populated radicals or for selectively excited spin-correlated radical pairs.16,17 This predicted flip-angle dependence was first experimentally verified for the spin-correlated radical pair in photosystem I.19
and π flip angles maximising the in-phase echo for Boltzmann-populated radicals or for selectively excited spin-correlated radical pairs.16,17 This predicted flip-angle dependence was first experimentally verified for the spin-correlated radical pair in photosystem I.19
The intensity of the out-of-phase echo signal of spin-correlated radical pairs is modulated as a function of the inter-pulse delay due to electron spin–spin couplings. Measurement of this modulation in an out-of-phase electron spin echo envelope modulation (ESEEM) experiment (Fig. 1b) allows extraction of the exchange and dipolar interactions between the coupled radicals. The dipolar interaction can provide information on inter-spin distances and, in some cases, the overall geometry of the spin-correlated radical pair,18,20,21 allowing, for example, identification of donor and acceptor molecules and structural characterisation of spin-correlated radical pairs formed in biological systems.5,22,23 The exchange interaction additionally provides information on the electronic structure of the radical pair through its dependence on the extent of electronic overlap, J ∝ |VDA|2. Since the electronic coupling matrix element VDA determines the rate of electron transfer and charge recombination reactions, experimental measurements of the exchange coupling allow correlation of molecular structure with electron transfer and recombination efficiencies,24–28 enabling the design of optimised donor–acceptor systems for artificial photosynthesis and quantum sensing.11 The determination of spin–spin exchange and dipolar interactions using out-of-phase ESEEM has several advantages compared to alternative approaches in pulse dipolar EPR, in particular large signal intensities and modulation depths on account of the spin polarisation, and the absence of an intermolecular background contribution, but requires formation of the coupled radical pair in a spin-polarised spin-correlated state.20,21
The investigation of spin-correlated radical pairs in biological systems, optoelectronics and spintronics as well as their potential use as quantum sensors rely on the ability to precisely control the excitation selectivity of microwave pulses used for spin manipulations. The control of the pulse excitation profile is limited for rectangular pulses, but the pulse shaping capabilities of newer pulse EPR spectrometers now allow the use of arbitrarily amplitude- and/or phase-modulated pulses with tailored excitation bandwidths and profiles.29–31 Narrowband-selective amplitude-modulated pulses and broadband frequency-swept pulses originally designed for NMR spectroscopy have been successfully incorporated into EPR experiments, leading to increased sensitivity and enabling increased information content in FT-EPR correlated pulse experiments.29,32–39 Pulse shaping capabilities provide an opportunity to revisit excitation selectivity for pulse EPR experiments on spin-correlated radical pairs, in particular for the out-of-phase ESEEM experiment, where broadband excitation can facilitate extension of this experiment to higher frequencies and to a wider range of systems.
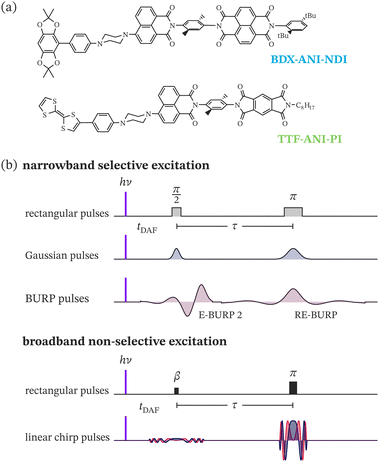
In this paper, we explore the use of narrowband-selective BURP (band-selective, uniform response, pure-phase)40 pulses and broadband frequency-swept pulses in EPR experiments on two different model donor–bridge–acceptor triads, BDX–ANI–NDI and TTF–ANI–PI,41,42 which form singlet-born spin-correlated radical pairs after photoexcitation. The donor radical cations, TTF˙+ and BDX˙+, are characterised by significant differences in g-anisotropy, leading to spin-correlated radical pair spectra with different spectral widths. We present a detailed analysis of the effect of rectangular and shaped pulses of varying excitation bandwidths on echo shapes and frequency-domain FT-EPR spectra, comparing experimental results with numerical simulations. We investigate the use of frequency-swept pulses in out-of-phase ESEEM experiments performed for the two triads with different spectral widths at both X- and Q-band, highlighting benefits and limitations of shaped pulses in this experiment.
2 Experimental methods
2.1 Sample preparation
The synthesis of BDX–ANI–NDI and TTF–ANI–PI has been reported previously.41,42 Samples for the EPR measurements were prepared by dissolving BDX–ANI–NDI and TTF–ANI–PI in toluene to an optical density of 0.4–0.6 at 416 nm (2 mm path length). The samples were flame-sealed in 2.9 mm o.d., 2.0 mm i.d. quartz EPR tubes after several freeze–pump–thaw cycles.2.2 EPR measurements
Transient and pulse EPR experiments were performed on a Bruker Elexsys E580 X/Q-band spectrometer equipped with a SpinJet 1.6 GSa s−1 arbitrary waveform generator (AWG). All measurements were performed at a temperature of 80 K using liquid nitrogen cooling with an Oxford Instruments CF935 cryostat and temperature-control system. X-band measurements (νmw = 9.8 GHz) were performed with a Bruker ER-4118X-MD5-W1 dielectric resonator and a 1 kW Applied Systems Engineering TWT amplifier. Q-band measurements (νmw = 34 GHz) were performed using a TE011 cylindrical cavity Q-band resonator with large sample access and optical window,43 built by the mechanical engineering workshop of the Physics department at the FU Berlin, and a 150 W TWT amplifier.Laser excitation at 416 nm (ca. 1 mJ incident on the optical window of the cryostat) was provided by an Opotek Opolette HE355 optoparametric oscillator (OPO) laser with tuneable wavelengths and a 20 Hz repetition rate. After the last laser turning mirror, the light was depolarized using an achromatic depolariser. A Stanford Research System digital delay generator (DG645) was used for synchronisation of the laser and EPR spectrometer.
Transient EPR experiments were performed by direct detection with the transient recorder (Video Amplifier III, 1 GHz bandwidth) without lock-in amplification using a microwave power of 0.4 mW for the X-band and 0.2 mW for the Q-band measurements. The laser background signal was removed by 2D baseline-correction determined based on low- and high-field off-resonance transients. The spectra were integrated over 0.8 μs starting at 0.2 μs after the laser flash.
Echo-detected field sweep and out-of-phase ESEEM experiments were performed with the pulse sequence laser flash – tDAF − tβ − τ − tπ − τ – echo (Fig. 1), where β refers to the flip angle of the first pulse, selected as described below. In this paper, we report τ as the delay between the centres of the two pulses. The delay between the laser flash and the start of the pulse sequence, tDAF, was set to 560 ns. Additional information on the dependence of the detected echo signal on the delay after photoexcitation is included in Section S4 in the ESI.† A two-step phase cycle on the first microwave pulse was used.
For non-selective excitation, linearly frequency-swept pulses with pulse edges smoothed by a quarter period of a sine over 10 ns33,44 were compared to short monochromatic rectangular pulses. Further details on the pulse parameters used for selective and non-selective excitation of BDX–ANI–NDI and TTF–ANI–PI are included in the text and figure captions. The chirp pulses were bandwidth-compensated following the procedure outlined in reference33 based on a resonator profile recorded through nutation experiments performed either on a similar sample containing a stable  radical signal or on the same sample using selective excitation (see Fig. S1 and Section S1.1 in the ESI† for details). To achieve refocusing without frequency dispersion in two-pulse echo experiments with linear chirp pulses, the length of the first pulse was set to twice the length of the refocusing pulse.29,34,45,46 The pulse amplitudes were optimised by detecting the echo signal as a function of the pulse amplitude programmed on the AWG and selecting the amplitude corresponding to the first maximum. For the amplitude-modulated selective pulses, the amplitude was additionally adjusted based on the calculated amplitude ratio for rectangular and shaped pulses.40 For measurements with non-selective pulses, the amplitude for each pulse was optimised independently, and the out-of-phase component of the echo was maximised (see Section S1.2 in the ESI† for details).
radical signal or on the same sample using selective excitation (see Fig. S1 and Section S1.1 in the ESI† for details). To achieve refocusing without frequency dispersion in two-pulse echo experiments with linear chirp pulses, the length of the first pulse was set to twice the length of the refocusing pulse.29,34,45,46 The pulse amplitudes were optimised by detecting the echo signal as a function of the pulse amplitude programmed on the AWG and selecting the amplitude corresponding to the first maximum. For the amplitude-modulated selective pulses, the amplitude was additionally adjusted based on the calculated amplitude ratio for rectangular and shaped pulses.40 For measurements with non-selective pulses, the amplitude for each pulse was optimised independently, and the out-of-phase component of the echo was maximised (see Section S1.2 in the ESI† for details).
All pulse experiments were performed as 2D experiments with acquisition of the full echo transients, which were then subsequently Fourier transformed. The detection phase was optimised based on the two-pulse echo recorded with selective pulses, taking the spin polarisation observed at the corresponding field position by transient EPR into account. Experiments with frequency-swept pulses required an additional phase correction prior to Fourier transform as a result of dynamic Bloch–Siegert shifts.29,47 The additional associated signal loss is inevitable in a two-pulse chirp sequence.29
Out-of-phase ESEEM traces were obtained by integration of the whole echo FT in the frequency domain, as for broadband excitation this resulted in improved and more reproducible results compared to echo integration in the time domain, where in some instances selection of the optimal integration window can be challenging. Deadtime reconstruction of the out-of-phase ESEEM traces was performed by fitting traces calculated according to the model function
S(τ,θ) = sin(ωeeτ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ ωee = d(3 θ ωee = d(3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1) − J θ − 1) − J | (1) |
In some measurements, a slow build-up of a dark signal, attributed to a stable radical state trapped at low temperatures, was observed over the course of the measurements and its contribution removed by subtraction of reference measurements performed with the pulse sequence preceding the laser flash.
2.3 Theory and simulations
Simulations of echo-detected field sweep and out-of-phase-ESEEM experiments were performed with a Matlab routine based on the EasySpin implementation of spidyan (EasySpin version 6.0).48–50The spin Hamiltonian for the two coupled spins was defined as
 | (2) |
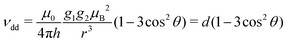 | (3) |
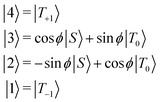 | (4) |
 | (5) |
Time-domain simulations of echo-detected field sweep and out-of-phase ESEEM experiments were carried out by propagation of the spin density matrix in Liouville space, explicitly considering evolution during monochromatic rectangular and frequency-swept pulses. The simulations included relaxation during the inter-pulse delays. The time propagation was carried out in a simulation frame offset by 0.5–1 GHz from the microwave frequency and the signals were subsequently downconverted.50 In order to account for line broadening resulting from unresolved hyperfine couplings and distributions of magnetic parameters, an anisotropic inhomogeneous broadening was taken into account through a loop over a range of resonance offsets combined with the powder averaging. To avoid artifacts from insufficient sampling while minimising computation time, the powder and offset averaging was performed using a Monte Carlo approach.
A more qualitative analysis of the effects of integrating frequency-swept pulses into the out-of-phase ESEEM experiment was performed using the product operator formalism in Mathematica51 following a previously reported approach.36,52 Details are reported in the discussion and in Section S6.1 in the ESI.†
The evolution of coherences during chirp pulses was calculated using the EasySpin implementation of spidyan50 following the approach previously described by Jeschke et al.46
DFT calculations were performed for the determination of the relative orientation of the g-frames of donor and acceptor radicals in the BDX–ANI–NDI and TTF–ANI–PI triads. Geometry optimisations of the donor and acceptor fragments, as well as the full triads, were performed in ORCA53 using the BP86 functional and the def2-SVP basis set, including a dispersion correction.54–57 Single-point calculations for the determination of the spin density distribution and g-values were performed for the optimised donor and acceptor radical fragments using the PBE0 functional and the EPR-III basis set for H, C, N and O and the IGLO-III basis set for S.58–61
3 Results and discussion
3.1 Transient EPR characterisation
The photoinduced spin-correlated radical pairs in the donor–bridge–acceptor triads BDX–ANI–NDI and TTF–ANI–PI were characterised in depth by transient EPR (trEPR) measurements performed at X- and Q-band. The spin system parameters were determined from a global fit of the spin-polarised spectra extracted at short times after laser excitation and shown in Fig. 2, including the results of the out-of-phase ESEEM experiments for the determination of the dipolar and exchange coupling parameters (vide infra). The relative orientations of the g-frames of the donor and acceptor radicals were determined from the results of DFT calculations and the calculated g-values were used as a starting point for the fitting procedure. The optimised spin system parameters leading to the simulations compared to the experimental results in Fig. 2 are reported in Section S2 in the ESI.† Simulations of the individual spectra of the donor and acceptor radicals constituting the spin-correlated radical pairs are also shown in Fig. 2. The EPR spectra of the BDX˙+–ANI–NDI˙− and TTF˙+–ANI–PI˙− triads differ significantly in spectral width on account of the large g-anisotropy of TTF˙+.62 The BDX˙+–ANI–NDI˙− spin-correlated radical pair is characterised by spectral widths of ca. 65 MHz and 100 MHz at X- and Q-band, respectively, while the corresponding spectral widths of the TTF˙+–ANI–PI˙− radical pair amount to ca. 95 MHz and 240 MHz.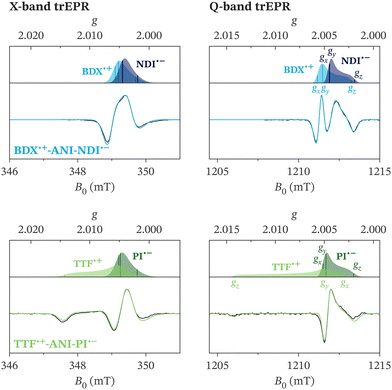 | ||
| Fig. 2 X- and Q-band transient EPR spectra recorded at 80 K averaged over 0.2–1.0 μs after photoexcitation at 416 nm. The experimental results (black) are compared to simulations shown in blue (BDX–ANI–NDI) or green (TTF–ANI–PI). The simulated spectra of the individual radicals and their principal g-values are also shown. The simulation parameters are reported in Section S2 in the ESI.† | ||
3.2 Excitation selectivity and the out-of-phase echo of SCRPs
The relatively narrow spectral width of BDX˙+–ANI–NDI˙− at X-band allows full, albeit non-uniform, excitation of the spectrum even with short rectangular pulses. Fig. 3a–c compares the in-phase and out-of-phase contributions of echo transients recorded for BDX˙+–ANI–NDI˙− as a function of magnetic field for rectangular pulses with varying length and therefore selectivity. For each two-pulse echo experiment, the in-phase (ip) and out-of-phase (oop) contributions to the echo transients are shown as a function of magnetic field on the left, and the corresponding echo Fourier transforms (FTs) are shown on the right. A selected echo transient is shown in the top left panel, and the corresponding Fourier transform is compared to the calculated pulse excitation profile in the top right panel. The echo-detected field sweep spectrum was constructed in the frequency domain as the sum of the individual echo Fourier transforms at different magnetic fields, following an approach first proposed by Bowman et al.63 for obtaining echo-detected spectra with increased spectral resolution and sensitivity compared to echo integration. The in-phase and out-of-phase contributions of the resulting echo-detected spectrum are compared to the EPR spectrum recorded using transient EPR on the top right.A two-pulse sequence with selective rectangular pulses (tπ/2 = 100 ns, tπ = 200 ns) results in an in-phase echo with a sign determined by the emissive-absorptive-emissive spin polarisation pattern of the BDX–ANI–NDI spin-correlated radical pair spectrum (Fig. 3a). The Fourier transform of the echo transient is in relatively close agreement with the calculated excitation profile of the 200 ns π-pulse. The echo-detected field sweep spectrum constructed in the frequency domain exhibits an in-phase contribution in close agreement with the trEPR spectrum, while the out-of-phase contribution is close to zero.
Non-selective excitation with a tπ/4 = 12 ns, tπ = 24 ns pulse sequence, on the other hand, results in an echo exclusively in the out-of-phase channel, with only the corresponding dispersive contribution in the in-phase channel (Fig. 3c). The out-of-phase echo in this case is maximised for a flip angle of the first pulse close to  , in agreement with the predicted behaviour for a singlet-born spin-correlated radical pair in the limit of weak coupling16,17 (see Section S1.2 in the ESI† for details). The out-of-phase echo is absorptive across the field range and the out-of-phase echo-detected spectrum approaches the shape of the absorptive Boltzmann-populated spectrum of the radical pair. The close agreement between the echo FT at a single field position and the full echo-detected spectrum indicates excitation of all spin packets contributing to the spectrum by the short non-selective pulses. The small remaining in-phase contribution to the spectrum still resembles the shape of the trEPR spectrum and the spectrum obtained with selective pulses, and would only be expected to approach zero for a truly uniform excitation of the whole radical pair spectrum.
, in agreement with the predicted behaviour for a singlet-born spin-correlated radical pair in the limit of weak coupling16,17 (see Section S1.2 in the ESI† for details). The out-of-phase echo is absorptive across the field range and the out-of-phase echo-detected spectrum approaches the shape of the absorptive Boltzmann-populated spectrum of the radical pair. The close agreement between the echo FT at a single field position and the full echo-detected spectrum indicates excitation of all spin packets contributing to the spectrum by the short non-selective pulses. The small remaining in-phase contribution to the spectrum still resembles the shape of the trEPR spectrum and the spectrum obtained with selective pulses, and would only be expected to approach zero for a truly uniform excitation of the whole radical pair spectrum.
The results obtained for a two-pulse sequence with intermediate pulse lengths of tπ/2 = 48 ns, tπ = 96 ns show contributions of both an out-of-phase and an in-phase echo, also reflected in the echo-detected spectrum, which now contains both an in-phase contribution resembling the spin-polarised trEPR spectrum as well as an out-of-phase fully absorptive contribution (Fig. 3b).
In contrast to BDX˙+–ANI–NDI˙−, the larger spectral width of the TTF˙+–ANI–PI˙− spectrum prevents full excitation with monochromatic rectangular pulses. The echo transients recorded with the tπ/4 = 12 ns, tπ = 24 ns pulse sequence and shown in Fig. 3d are characterised by an absorptive out-of-phase echo in the region of strong spectral overlap of the TTF˙+ and PI˙− signatures, but an emissive in-phase echo is still present at the field position corresponding to the TTF˙+gz value, with the corresponding dispersive pattern in the out-of-phase channel. This is also reflected in the echo-detected EPR spectrum constructed from the field-dependent echo FTs, which shows a clear emissive feature in the in-phase channel and no out-of-phase component at gz, while an absorptive out-of-phase feature dominates the spectrum at lower frequencies, with only a minor remaining in-phase contribution matching the shape of the trEPR spectrum.
Shaped pulses allow excitation bandwidths beyond those accessible with monochromatic rectangular pulses, as well as control over the shape of the excitation profile. Full excitation of the radical pair spectrum with broadband pulses maximises the out-of-phase echo, promising to improve sensitivity of the out-of-phase ESEEM experiment for the determination of spin–spin exchange and dipolar interactions in radical pairs and to enable experiments at higher frequencies and for spin-correlated radical pairs with larger spectral widths. More selective excitation compared to rectangular pulses and control over pulse excitation profiles, on the other hand, are advantageous for exploring the use of spin-correlated radical pairs for applications in quantum information science.11,12 In the rest of the paper, we therefore explore the use of narrowband selective and broadband non-selective shaped pulses for controlled excitation of spin-correlated radical pairs.
3.3 Narrowband selective excitation
The excitation profiles of rectangular pulses are sinc (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x/x) functions with oscillatory wings that result in non-negligible off-resonant excitation. Even though in practice distortion of the pulses in the excitation chain often leads to attenuation of the wings, significant improvements in selectivity can be achieved with Gaussian pulses.64,65 Selectivity can be improved further by designing amplitude-modulated pulses exhibiting close to rectangular excitation profiles, with uniform excitation across the selected bandwidth and sharp transition regions. Several different classes of narrowband selective amplitude-modulated pulses have been designed for NMR,66 with the BURP (Band-selective, Uniform Response, Pure-phase) class of pulses, based on finite Fourier series, generally exhibiting the sharpest transition regions. The inversion pulse of this class, I-BURP 2, has previously been to shown to perform well in EPR as a selective inversion pulse in Davies ENDOR.37
x/x) functions with oscillatory wings that result in non-negligible off-resonant excitation. Even though in practice distortion of the pulses in the excitation chain often leads to attenuation of the wings, significant improvements in selectivity can be achieved with Gaussian pulses.64,65 Selectivity can be improved further by designing amplitude-modulated pulses exhibiting close to rectangular excitation profiles, with uniform excitation across the selected bandwidth and sharp transition regions. Several different classes of narrowband selective amplitude-modulated pulses have been designed for NMR,66 with the BURP (Band-selective, Uniform Response, Pure-phase) class of pulses, based on finite Fourier series, generally exhibiting the sharpest transition regions. The inversion pulse of this class, I-BURP 2, has previously been to shown to perform well in EPR as a selective inversion pulse in Davies ENDOR.37
Two-pulse echo experiments performed on BDX˙+–ANI–NDI˙− as a function of magnetic field with selective rectangular, Gaussian and BURP pulses are compared in Fig. 4 and the corresponding results obtained for TTF˙+–ANI–PI˙− are reported in Fig. S5 in the ESI.† The experiments were performed for a constant centre-to-centre interpulse delay τ, and the length and full width at half maximum (FWHM) of the Gaussian pulses was selected to match the calculated width of the excitation profile of the corresponding rectangular pulses in a 100 ns–200 ns sequence. A comparison of the results obtained with selective rectangular and Gaussian pulses reveals an improved selectivity for the Gaussian pulses, with the calculated excitation profile matching the experimental result, while the experimental excitation profile of the rectangular pulse appears slightly broader than predicted, likely due to distortions of the sharp pulse edges in the excitation chain.‡
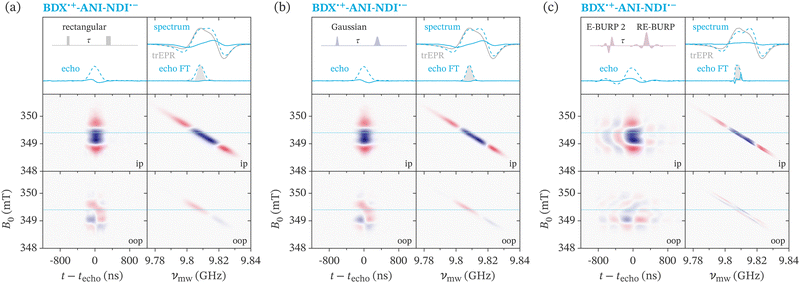 | ||
| Fig. 4 X-band echo-detected field sweep experiments with narrowband selective pulses on BDX˙+–ANI–NDI˙−. The echo transients were recorded as a function of magnetic field with two-pulse sequences consisting of rectangular 100 ns and 200 ns pulses (a), Gaussian 200 ns (tFWHM = 75 ns) and 400 ns (tFWHM = 150 ns) pulses (b), and a sequence consisting of an 800 ns E-BURP 2 and a 1600 ns RE-BURP pulse (c). The in- and out-of-phase echo transients and the corresponding Fourier transforms are shown as a function of magnetic field in the 2D plot (blue = positive signal/absorption, red = negative signal/emission). The in-phase (dashed line) and out-of-phase (solid line) contributions to the echo and echo FT extracted at the field position marked by the horizontal line (349.4 mT) are also shown and compared to the calculated excitation profile of the π pulse. The spectrum constructed from the sum of the echo FTs at the different magnetic field positions is compared to the trEPR spectrum. The corresponding results obtained for TTF–ANI–PI are shown in Fig. S5 in the ESI.† | ||
Further improvements in selectivity, enabling nearly uniform excitation within a narrow bandwidth and sharp edges of the excitation window, were achieved using the BURP-class of amplitude-modulated pulses. These pure-phase pulses are designed to excite magnetisation with a constant phase within the selected bandwidth.40 The results obtained with a two-pulse sequence based on the excitation pulse E-BURP 2 and the general rotation, refocusing π pulse RE-BURP40 are shown in Fig. 4c. The strongly oscillatory pattern of the echo signals already suggests a close to rectangular excitation profile, as confirmed by agreement of the echo FT with the profile calculated for the RE-BURP pulse. The reduced out-of-phase contribution to the echo-detected field sweep spectrum compared to that obtained with rectangular and Gaussian pulses, is likely also a consequence of the more selective excitation achieved with the BURP pulse sequence. The results of an additional experiment using the general rotation, universal  pulse U-BURP instead of the E-BURP 2 pulse specifically designed for excitation of magnetisation from the z-axis to the transverse plane are shown in Fig. S6 in the ESI.† The U-BURP pulse requires higher pulse amplitudes and is more sensitive to flip angle miscalibration§ and other experimental factors.40 While its performance in this type of pulse sequence was found to be inferior to that of the E-BURP 2 pulse, the excitation profile still exhibits sharp edges, demonstrating highly selective excitation.
pulse U-BURP instead of the E-BURP 2 pulse specifically designed for excitation of magnetisation from the z-axis to the transverse plane are shown in Fig. S6 in the ESI.† The U-BURP pulse requires higher pulse amplitudes and is more sensitive to flip angle miscalibration§ and other experimental factors.40 While its performance in this type of pulse sequence was found to be inferior to that of the E-BURP 2 pulse, the excitation profile still exhibits sharp edges, demonstrating highly selective excitation.
While BURP pulses allow more selective excitation, the long pulse lengths required for narrow effective bandwidths lead to relaxation becoming a concern, both in terms of reduced signal intensities as well as deviations from the desired excitation pattern caused by relaxation during the pulse. The phase memory time for BDX˙+–ANI–NDI˙− amounts to about 3.5 μs, and is therefore of the same order of magnitude as the 1.6 μs RE-BURP pulse used. The effect of relaxation during amplitude-modulated selective pulses was investigated extensively within the field of NMR,67–69 where it was shown that the BURP-class of pulses is more robust to relaxation compared to other types of amplitude-modulated pulses and that the pulse excitation patterns are generally more severely affected by longitudinal rather than transverse relaxation.69 For applications in EPR where T1 ≫ Tm, the main effect of relaxation will be a reduced signal intensity, while the effect of Tm on the selectivity of the excitation profile is likely to be minor. In systems where fast relaxation is a significant concern, modified BURP pulses designed taking relaxation during the pulse into account69 or different types of amplitude-modulated pulses that sacrifice frequency selectivity somewhat in order to achieve a lower time-bandwidth product66 can be considered.
Despite these significant improvements in selectivity, completely selective excitation of only one of the spins in the spin-correlated radical pair will only be possible in regions without spectral overlap, therefore selective amplitude-modulated pulses would have to be combined with the design of spin systems with reduced donor–acceptor spectral overlap.70
3.4 Non-selective excitation
Excitation bandwidths beyond those accessible through short monochromatic rectangular pulses can be achieved using frequency-swept pulses. By sweeping the frequency during the pulse, spin packets resonant within relatively wide bandwidths can be successively addressed and the pulse amplitude- and frequency-modulation functions can be designed to tailor the uniformity and selectivity of the excitation profile.71 Since different spin packets are excited and start acquiring phase at different times during the frequency sweep, refocusing of all spin packets to an echo in a two-pulse sequence requires a refocusing π pulse of half the length of the initial excitation pulse.45,46 The uniform excitation of both spins in EPR experiments on spin-correlated radical pairs is a requirement for the observation of an out-of-phase echo, and thus distance measurements using the out-of-phase ESEEM sequence. Therefore, we explored the use of chirp pulses with a linear frequency sweep and quarter-sine-apodised amplitude modulation functions in echo experiments on the spin-correlated radical pairs in BDX–ANI–NDI and TTF–ANI–PI.The results of two-pulse echo experiments performed with non-selective monochromatic rectangular pulses and with frequency-swept pulses on the BDX–ANI–NDI triad at X- and Q-band are shown in Fig. 5. The experimental results are compared to numerical simulations to verify agreement of the experimental performance of the different types of pulses with theoretical predictions. For the BDX–ANI–NDI triad characterised by a relatively narrow spectral width, at X-band, non-selective excitation is also achievable with short rectangular pulses, but chirp pulses allow a more uniform excitation, resulting in detection of an out-of-phase echo over a wider field range. At Q-band, rectangular pulses no longer have sufficient bandwidth to excite the whole spectrum of the BDX–ANI–NDI triad, resulting in the absence of an out-of-phase echo on the low-field edge of the spectrum and a contribution of an emissive in-phase echo, and correspondingly a clear in-phase contribution to the echo-detected EPR spectrum, while the out-of-phase contribution dominates at higher fields (lower frequencies) (see Fig. 5c). Improved non-selective excitation is achieved with chirp pulses, as demonstrated by the observation of an out-of-phase echo across the field range and a reduced spin-polarised in-phase contribution to the echo-detected EPR spectrum (Fig. 5d). The experimental field-dependent echo transients and corresponding FTs are in good agreement with numerical simulations both at X- and at Q-band, confirming the resonator-bandwidth compensated chirp pulses perform as desired.
The results of two-pulse echo experiments on TTF˙+–ANI–PI˙− with rectangular and chirp pulses at X-band are shown in Fig. 6 along with the corresponding simulations, and the corresponding Q-band data is shown in Fig. S10 in the ESI.† As noted earlier, the larger g-anisotropy of the TTF˙+ radical prevents full non-selective excitation of the spin-correlated radical pair on the TTF–ANI–PI triad with monochromatic rectangular pulses already at X-band, resulting in the observation of an out-of-phase echo only in the region of significant spectral overlap of TTF˙+ and PI˙− at the high-field end of the spectrum and a clear in-phase echo in the part of the spectrum corresponding to gz of TTF˙+. Excitation with chirp pulses leads to observation of the out-of-phase echo over a significantly wider field range at both X- and Q-band, and an almost negligible remaining in-phase echo on the low-field edge of the spectrum at X-band. The more drastic differences observed for this triad clearly illustrate improved non-selective excitation with frequency-swept pulses.
The absence of a perfect agreement between the in-phase echo-detected spectrum and the spin-polarised trEPR spectrum for selective excitation, or between the out-of-phase echo-detected spectrum and the expected fully absorptive spectrum of the coupled pair of radicals for non-selective excitation in experiments as well as simulations is likely a result of the pronounced flip-angle dependence of excitation in spin-correlated radical pairs.15 The optimal flip angle, which depends on the relative magnitudes of the resonance frequency difference between the two spins of the pair and the strength of the spin–spin coupling, varies across the spectrum, and a fixed pulse amplitude, calibrated at the maximum of the spectrum, can lead to sub-optimal excitation at other field positions. In the case of excitation with frequency-swept pulses, additional deviations may also arise due to interference effects72 discussed in more detail in the next section.
3.5 Out-of-phase ESEEM
The out-of-phase ESEEM experiment for the measurement of exchange and dipolar coupling between the electron spins in spin-correlated radical pairs relies on non-selective excitation and observation of an out-of-phase echo, and its sensitivity is determined by the amplitude of the out-of-phase echo. Therefore, we investigated the effects of improved broadband excitation with frequency-swept pulses in this experiment. The results of out-of-phase ESEEM experiments performed with monochromatic rectangular and frequency-swept pulses for BDX˙+–ANI–NDI˙− and TTF˙+–ANI–PI˙− at X- and Q-band are compared in Fig. 7. The figure shows the full out-of-phase echo transients recorded as a function of the inter-pulse delay τ and the corresponding Fourier transforms, compared to the trEPR spectrum and the calculated pulse excitation profiles, for experiments performed with the two different types of pulses. The τ values displayed in Fig. 7 correspond to the delay between the centres of the pulses. The out-of-phase ESEEM trace was obtained by integration of the whole echo FT signal in the frequency domain, as this was found to give more reliable results compared to echo integration in the time domain for echo shapes deviating from a Gaussian. Comparison of the integrated out-of-phase ESEEM traces in the bottom panels shows that, in all cases, we observe an increase in modulation depth for out-of-phase ESEEM with chirp pulses compared to rectangular pulses. At X-band, chirp out-of-phase ESEEM performed at the centre of the spectrum leads to an increase in modulation depth by factors of ca. 1.5 and 4 for BDX˙+–ANI–NDI˙− and TTF˙+–ANI–PI˙−, respectively (Fig. 7). For BDX–ANI–NDI, the central field position also corresponds to the maximum out-of-phase echo for rectangular pulses. For TTF˙+–ANI–PI˙−, the maximum out-of-phase echo is obtained at higher fields, and a comparison of the performance of rectangular and chirp pulses at the optimal field position for out-of-phase ESEEM with rectangular pulses still results in an enhancement factor of 1.5 (Fig. S15 in the ESI†). At Q-band, modulation depth enhancement factors of ca. 2 and 3, respectively, are observed at the centre of the spectrum for BDX˙+–ANI–NDI˙− and at the field position corresponding to the maximum signal for TTF˙+–ANI–PI˙−. The modulation depth for out-of-phase ESEEM with rectangular pulses on TTF˙+–ANI–PI˙− at Q-band is very low even at the field position corresponding to the maximum out-of-phase echo, and is clearly significantly enhanced for the broadband excitation possible with frequency-swept pulses. The increases in modulation depth correlate with the observation of increased out-of-phase echo contributions in the echo-detected field sweep spectra discussed in the previous section.In addition to the increase in modulation depth, a phase shift can also be observed, which is more pronounced for the TTF–ANI–PI triad and particularly large at Q-band. Comparison of out-of-phase ESEEM measurements with chirp pulses of different bandwidths and lengths for TTF˙+–ANI–PI˙− at X-band shows an increase in phase shift for pulses with larger bandwidths and increased pulse lengths (Fig. S15 in the ESI†). In order to determine the origin of the phase shift observed in the presence of chirp excitation, we considered the effects of sequential excitation of different spin packets during the chirp pulse in more detail, following the approaches previously used in the analysis of chirp effects in other pulse EPR experiments.29,35,36 In the two-pulse echo sequence with chirp pulses, the selection of pulse lengths with the ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 leads to refocusing of the frequency dispersion for the resonance offset, but not of the spin–spin coupling. Doll and Jeschke36 have analysed the frequency dispersion in a two-pulse chirp echo sequence for weakly coupled Boltzmann-populated nitroxides using the product operator formalism, and obtained modulation formulae including a phase shift and an additional modulation amplitude factor for the contribution of one of the spins, determined by an asymmetry in the evolution of the spins excited first or second during the first frequency-swept pulse. This approach is valid in the weak coupling limit, when both components of each doublet can be considered to be affected simultaneously.52 An equivalent analysis was performed for a spin-correlated radical pair, with an initial state of longitudinal two-spin order (σ0 = −S1,zS2,z), assuming the initial zero-quantum coherence has decayed during the delay tDAF between laser excitation and the start of the pulse sequence17 (see Section S4 in the ESI†). Consideration of a two-pulse echo experiment with ideal monochromatic pulses applied along x yields the familiar out-of-phase echo modulation
1 leads to refocusing of the frequency dispersion for the resonance offset, but not of the spin–spin coupling. Doll and Jeschke36 have analysed the frequency dispersion in a two-pulse chirp echo sequence for weakly coupled Boltzmann-populated nitroxides using the product operator formalism, and obtained modulation formulae including a phase shift and an additional modulation amplitude factor for the contribution of one of the spins, determined by an asymmetry in the evolution of the spins excited first or second during the first frequency-swept pulse. This approach is valid in the weak coupling limit, when both components of each doublet can be considered to be affected simultaneously.52 An equivalent analysis was performed for a spin-correlated radical pair, with an initial state of longitudinal two-spin order (σ0 = −S1,zS2,z), assuming the initial zero-quantum coherence has decayed during the delay tDAF between laser excitation and the start of the pulse sequence17 (see Section S4 in the ESI†). Consideration of a two-pulse echo experiment with ideal monochromatic pulses applied along x yields the familiar out-of-phase echo modulation
 | (6) |
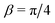 for the first pulse.17 For analysis of the chirp echo experiment, the frequency-swept pulse and subsequent delay can be split into sections of free evolution and time-delayed selective excitation of each spin of the pair36
for the first pulse.17 For analysis of the chirp echo experiment, the frequency-swept pulse and subsequent delay can be split into sections of free evolution and time-delayed selective excitation of each spin of the pair36 | (7) |
 is the inverse sweep rate of the linear chirp pulse and τ is defined as the delay between the centres of the two pulses as shown schematically in Fig. 8a. Defining δ1 = 2kΩ1 and δ12 = 2k(Ω2 − Ω1) (Fig. 8a),36 the modulation expression becomes
is the inverse sweep rate of the linear chirp pulse and τ is defined as the delay between the centres of the two pulses as shown schematically in Fig. 8a. Defining δ1 = 2kΩ1 and δ12 = 2k(Ω2 − Ω1) (Fig. 8a),36 the modulation expression becomes | (8) |
 | ||
Fig. 8 Effects of chirp pulse excitation in out-of-phase ESEEM: (a) schematic illustration of the out-of-phase ESEEM sequence with frequency-swept pulses with definition of the timings δ1, δ12 and τ and energy level diagram for a weakly coupled two-spin system with highlighted single-, zero- and double-quantum coherences. (b) Graphical illustration of the description of the out-of-phase ESEEM experiment within the product operator formalism for a pulse sequence with monochromatic rectangular pulses and with frequency-swept pulses, showing the asymmetry in evolution for the two spins of the coupled pair (see Section S6.1 in the ESI† for details). (c and d) Evaluation of chirp effects for BDX˙+–ANI–NDI˙− and TTF˙+–ANI–PI˙− with pulse sequences selected for out-of-phase ESEEM experiments at X- and Q-band. The probability distributions of the delays δ1, δ12 and  for the excitation pulses used in the experiments for the two triads at X- and Q-band are shown on top, the dashed line indicates for the excitation pulses used in the experiments for the two triads at X- and Q-band are shown on top, the dashed line indicates  . The evolution of the amplitudes of the single-, zero- and double-quantum coherences during the initial chirp pulse of the out-of-phase echo sequence averaged over all orientations is shown on the bottom, the dashed line indicates the coherence amplitudes after an ideal monochromatic . The evolution of the amplitudes of the single-, zero- and double-quantum coherences during the initial chirp pulse of the out-of-phase echo sequence averaged over all orientations is shown on the bottom, the dashed line indicates the coherence amplitudes after an ideal monochromatic  pulse (see Section S6.2 in the ESI† for details). pulse (see Section S6.2 in the ESI† for details). | ||
The distributions of the time delays δ1, δ12 and 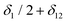 can be estimated from the spectra of the donor and acceptor radicals, the orientational correlation of the coupled spins, and the time-frequency relationship of the first chirp pulse, and are shown for the two different triads and the pulses chosen for the chirp out-of-phase ESEEM experiments at X- and Q-band in Fig. 8c and d. The distributions are affected by the length of the pulse through the time-frequency relationship of chirp pulses, with longer pulses required to cover a larger spectral bandwidth for a given microwave power leading to an increased likelihood of introducing distortions. The overall phase offset is determined by the difference between the mean of the
can be estimated from the spectra of the donor and acceptor radicals, the orientational correlation of the coupled spins, and the time-frequency relationship of the first chirp pulse, and are shown for the two different triads and the pulses chosen for the chirp out-of-phase ESEEM experiments at X- and Q-band in Fig. 8c and d. The distributions are affected by the length of the pulse through the time-frequency relationship of chirp pulses, with longer pulses required to cover a larger spectral bandwidth for a given microwave power leading to an increased likelihood of introducing distortions. The overall phase offset is determined by the difference between the mean of the  distribution and
distribution and  (indicated as a dashed line in the figure), and is in qualitative agreement with the phase shifts observed in the experimental chirp out-of-phase ESEEM traces, with a negligible phase shift for BDX˙+–ANI–NDI˙− at X-band, a slightly larger shift at Q-band and significantly increased phase shifts for TTF˙+–ANI–PI˙− at X- and Q-band, where a significant number of spin pairs are characterised by a large resonance offset due to the large gz value of TTF˙+.
(indicated as a dashed line in the figure), and is in qualitative agreement with the phase shifts observed in the experimental chirp out-of-phase ESEEM traces, with a negligible phase shift for BDX˙+–ANI–NDI˙− at X-band, a slightly larger shift at Q-band and significantly increased phase shifts for TTF˙+–ANI–PI˙− at X- and Q-band, where a significant number of spin pairs are characterised by a large resonance offset due to the large gz value of TTF˙+.
In addition to the dependence of the modulated sine terms on the delays δ1 and δ12, as evident from eqn (8), chirp excitation in out-of-phase ESEEM also leads to differences in the contribution of spins excited first or second to the final modulation, that can be traced back to interference resulting from sequential passage of transitions involving common levels.36,46 In order to gain increased insights into the degree of interference expected in our experiments, the evolution of single-, zero- and double-quantum coherences during the first chirp pulse of the out-of-phase ESEEM sequence was calculated, and Fig. 8c and d show the coherence amplitudes averaged over all orientations for the chirp pulses used in the experiments (see Fig. S13 and Section S6.2 in the ESI† for the contribution of selected orientations and the overall range of coherence amplitudes). In an out-of-phase ESEEM experiment with ideal monochromatic pulses, the initial longitudinal two-spin order is transformed into antiphase coherence, which ultimately evolves to the observable x magnetisation, as well as zero- and double-quantum coherence and residual two-spin order, (Fig. S12 in the ESI†), resulting in amplitudes of  for the single-, zero- and double-quantum coherences at the end of a pulse with flip angle
for the single-, zero- and double-quantum coherences at the end of a pulse with flip angle  .17 The calculated amplitudes of the single quantum coherences at the end of the chirp pulse only show negligible differences compared to those obtained with a monochromatic rectangular pulse for BDX˙+–ANI–NDI˙− at both X- and Q-band. This analysis also reveals that, for BDX˙+–ANI–NDI˙− at X-band, the assumption of simultaneous excitation of both components in each doublet made in the derivation of eqn (8) breaks down for most orientations (see Section S6.2 in the ESI†). Larger deviations and clear differences between coherence amplitudes |〈S+12〉|, |〈S+34〉| and |〈S+13〉|, |〈S+24〉| are observed for TTF˙+–ANI–PI˙−, in particular at Q-band. In this case, not only are the weights of the sine modulation terms for the two spins different, but the additional cosine modulation term in eqn (8) is also expected to contribute to the observed out-of-phase ESEEM modulation, affecting the overall phase shift. Inversion of the sweep direction of the chirp pulse leads to passage of transitions in the inverse order, therefore the δ1 and δ12 distributions and the coherence evolution will be different, potentially leading to differences in the resulting out-of-phase ESEEM trace. While we do observe differences in the τ-dependent echo Fourier transforms for upward and downward sweeps, we found the integrated out-of-phase ESEEM traces not to be significantly affected by the sweep direction of the chirp pulse (see Section S6.4 in the ESI† for details).
.17 The calculated amplitudes of the single quantum coherences at the end of the chirp pulse only show negligible differences compared to those obtained with a monochromatic rectangular pulse for BDX˙+–ANI–NDI˙− at both X- and Q-band. This analysis also reveals that, for BDX˙+–ANI–NDI˙− at X-band, the assumption of simultaneous excitation of both components in each doublet made in the derivation of eqn (8) breaks down for most orientations (see Section S6.2 in the ESI†). Larger deviations and clear differences between coherence amplitudes |〈S+12〉|, |〈S+34〉| and |〈S+13〉|, |〈S+24〉| are observed for TTF˙+–ANI–PI˙−, in particular at Q-band. In this case, not only are the weights of the sine modulation terms for the two spins different, but the additional cosine modulation term in eqn (8) is also expected to contribute to the observed out-of-phase ESEEM modulation, affecting the overall phase shift. Inversion of the sweep direction of the chirp pulse leads to passage of transitions in the inverse order, therefore the δ1 and δ12 distributions and the coherence evolution will be different, potentially leading to differences in the resulting out-of-phase ESEEM trace. While we do observe differences in the τ-dependent echo Fourier transforms for upward and downward sweeps, we found the integrated out-of-phase ESEEM traces not to be significantly affected by the sweep direction of the chirp pulse (see Section S6.4 in the ESI† for details).
In addition to this analysis that provides some insights into the expected consequences of replacing monochromatic rectangular pulses in the out-of-phase ESEEM experiment with frequency-swept pulses, we also performed numerical simulations of the out-of-phase ESEEM experiments with both types of pulses (see Fig. S14 in the ESI†). The results are in reasonable overall agreement with the experimental results and mirror the trends expected based on the considerations of the effect of sequential excitation during chirp pulses. Remaining discrepancies are attributed in part to experimental imperfections, including imperfect pulse amplitude selection and distortions of the pulses and recorded response by the resonator and excitation and detection chains. Additionally, the simulations did not take electron-nuclear hyperfine couplings into account and therefore do not include nuclear ESEEM effects that might contribute to the experimental results.
In summary, the experimental results suggest that the use of frequency-swept pulses in out-of-phase ESEEM can be beneficial in increasing the modulation depth and therefore improving the sensitivity of the experiment. For spin-correlated radical pairs with large resonance offsets between the coupled spins and for long pulses, chirp out-of-phase ESEEM results in a phase-shifted trace, which can complicate reconstruction of the initial part of the trace lost in the deadtime of the experiment. The modulation frequency is however not affected and will still allow interpretation of the out-of-phase ESEEM results for spin-correlated radical pairs with a well-defined interspin distance. For increased spectral and pulse bandwidths and long chirp pulses, destructive interference of coherences during the frequency sweeps will start to counteract any gains in modulation depth resulting from improved non-selective excitation of the coupled spin pair. The optimal chirp pulse bandwidth and pulse length to maximise the out-of-phase echo and therefore the sensitivity of the out-of-phase ESEEM experiment, while minimising interference effects that complicate the reliable extraction of distance information, will depend on the properties of the spin system and the experimental setup (resonator profile and available microwave power).
In addition to improved sensitivity, the use of chirp pulses in out-of-phase ESEEM has the additional benefit of enabling 2D EPR-correlated experiments that can provide information on the relative orientation of donor and acceptor radicals in addition to information on the strength of the dipolar and exchange coupling. This is illustrated for the BDX–ANI–NDI triad at Q-band in Fig. 9, showing the Fourier transform of the echo transients as a function of the interpulse delay τ as well as the two-dimensional Fourier transform correlating the antiphase Pake patterns with the EPR spectrum. Both clearly show the contribution of the dipolar frequency ν‖ at the high frequency end of the spectrum, corresponding to gx for both BDX˙+ and NDI˙−, while ν⊥ dominates at the low frequency end of the spectrum, corresponding to gz. This is consistent with the molecular structure of the triad and the orientation of the principal g-axes predicted by DFT calculations. Results of out-of-phase ESEEM experiments performed with monochromatic rectangular pulses at different field positions are shown in Fig. S17 in the ESI† for comparison and show that at least two separate experiments are required to cover the full spectral width of the BDX–ANI–NDI triad.
Determination of the relative orientation of donor and acceptor in spin-correlated radical pairs has generally relied on analysis of multifrequency transient EPR data, typically in combination with additional structural information, for example from high-resolution X-ray crystallography.73 For the radical pair in photosystem I, orientation-selective PELDOR and RIDME measurements have been used to demonstrate a reorientation of the acceptor compared to the X-ray structure under light illumination.74 To the best of our knowledge, this is the first report on the extraction of orientation information by out-of-phase ESEEM on disordered powder samples, as the requirement of non-selective excitation of both spins of the spin-correlated radical pair for the detection of the modulated out-of-phase echo generally restricts the possibilities of orientation-selective out-of-phase ESEEM measurements following the approach used for other pulse EPR experiments of performing separate experiments at different field positions. We have shown that out-of-phase ESEEM with echo transient detection followed by two-dimensional Fourier transform can be used to extract this information and that with the use of chirp pulses this can in principle be achieved in a single experiment with optimised sensitivity.
4 Conclusions
Spin-correlated radical pairs are spin systems with a unique set of properties arising from their formation by photoinduced charge separation from an excited singlet or triplet state precursor. The nature of the initial spin-polarised state has profound consequences for the behaviour of these spin systems in pulse EPR spectroscopy, leading to distinctly different responses for selective and non-selective excitation and enabling the extraction of information on the strength of the dipolar and exchange coupling using a simple two-pulse out-of-phase ESEEM experiment. In this paper, we have exploited the new opportunities provided by advanced pulse shaping capabilities to explore improved narrowband selective and broadband non-selective excitation for spin-correlated radical pairs on two model donor–bridge–acceptor systems, BDX˙+–ANI–NDI˙− and TTF˙+–ANI–PI˙−.Amplitude-modulated narrowband selective BURP pulses, originally designed for NMR, were shown to allow selective excitation with essentially rectangular excitation profiles. This class of pulses provides the limit of selective excitation and the best opportunity for selectively addressing individual spins in spin-correlated radical pairs, given a sufficient separation of the donor and acceptor radical spectra.
Non-selective uniform broadband excitation, addressing both partners of the radical pair and leading to the observation of an out-of-phase echo, was demonstrated with frequency-swept pulses with bandwidths matching the spectral width of the radical pair spectrum. The use of resonator bandwidth compensated chirp pulses was shown to enable detection of an out-of-phase echo across the whole spectrum for BDX˙+–ANI–NDI˙− at X- and Q-band and for TTF˙+–ANI–PI˙− at X-band. The improved non-selective excitation leads to increased out-of-phase echo contributions compared to experiments performed with monochromatic rectangular pulses and therefore increased sensitivity in chirp out-of-phase ESEEM experiments. Additionally, the larger excitation bandwidths accessible with shaped pulses facilitate out-of-phase ESEEM measurements at higher frequencies. The different nature of excitation with frequency-swept pulses, addressing different spin packets sequentially rather than simultaneously, has additional consequences for out-of-phase ESEEM traces recorded with chirp pulses that need to be considered in the selection of pulse bandwidths and lengths and in the analysis of the experimental results.
The improved broadband excitation with frequency-swept pulses was also shown to enable the determination of not only the dipolar and exchange coupling constants, but also orientational information in 2D FT-correlated out-of-phase ESEEM experiments performed with chirp pulses and echo transient detection. For BDX˙+–ANI–NDI˙− at Q-band, this experiment revealed distinct contributions of the parallel and perpendicular dipolar frequencies in different parts of the spectrum.
Overall, we have illustrated how the ability of precisely controlling excitation selectivity with shaped pulses can benefit pulse EPR experiments on spin-correlated radical pairs and highlighted important considerations for the use of these pulses in echo and out-of-phase ESEEM experiments. Improved control over excitation of spins in spin-correlated radical pairs provides advantages not only for the characterisation of spin-correlated radical pairs in biological systems and materials for optoelectronics and energy, but also for the potential use of spin-correlated radical pairs for quantum sensing.
Author contributions
CET designed the study. SMC, JZ and MRW designed and synthesised BDX–ANI–NDI and TTF–ANI–PI. DP and CET performed the experiments and simulations, and analysed and interpreted the results. DP and CET wrote the manuscript, all authors commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Prof. Christiane Timmel and Prof. Robert Bittl for helpful discussions. We are grateful to Dr Christian Teutloff and the mechanical engineering workshop in the Physics Department of the Freie Universität Berlin for the design optimisation and construction of the Q-band resonator. The authors would like to acknowledge the use of the University of Oxford Advanced Research Computing (ARC) facility in carrying out this work (https://dx.doi.org/10.5281/zenodo.22558). D. P. would like to acknowledge the European Union and the PON-R&I programme (CCI 2014IT16M2OP005 - Action IV.5, DOT1319897-2) for the financial support and the Fondazione Zegna for funding a research placement at the University of Oxford. M. D. V. is grateful to the Italian Ministry for University and Research (MUR) for funding of the PRIN Project (2022NMSFHN). This work was supported by the US National Science Foundation under Award # CHE-2154627 (synthesis of BDX–ANI–NDI and TTF–ANI–PI, M.R.W.). C. E. T. is thankful to the Royal Society for a University Research Fellowship (URF\R1\201071) and to Balliol College, Oxford, for an Early Career Fellowship.References
- P. J. Hore, D. A. Hunter, C. D. McKie and A. J. Hoff, Chem. Phys. Lett., 1987, 137, 495–500 CrossRef.
- R. Bittl and S. Weber, Biochim. Biophys. Acta, 2005, 1707, 117–126 CrossRef.
- S. Weber, T. Biskup, A. Okafuji, A. R. Marino, T. Berthold, G. Link, K. Hitomi, E. D. Getzoff, E. Schleicher and J. R. Norris, J. Phys. Chem. B, 2010, 114, 14745–14754 CrossRef PubMed.
- E. W. Evans, C. A. Dodson, K. Maeda, T. Biskup, C. J. Wedge and C. R. Timmel, Interface Focus, 2013, 3, 20130037 CrossRef PubMed.
- J. Xu, L. E. Jarocha, T. Zollitsch, M. Konowalczyk, K. B. Henbest, S. Richert, M. J. Golesworthy, J. Schmidt, V. Déjean, D. J. C. Sowood, M. Bassetto, J. Luo, J. R. Walton, J. Fleming, Y. Wei, T. L. Pitcher, G. Moise, M. Herrmann, H. Yin, H. Wu, R. Bartölke, S. J. Käsehagen, S. Horst, G. Dautaj, P. D. F. Murton, A. S. Gehrckens, Y. Chelliah, J. S. Takahashi, K.-W. Koch, S. Weber, I. A. Solov, C. Xie, S. R. Mackenzie, C. R. Timmel, H. Mouritsen and P. J. Hore, Nature, 2021, 594, 535–540 CrossRef PubMed.
- L. Pasimeni, M. Ruzzi, M. Prato, T. Da Ros, G. Barbarella and M. Zambianchi, Chem. Phys., 2001, 263, 83–94 CrossRef CAS.
- J. Behrends, A. Sperlich, A. Schnegg, T. Biskup, C. Teutloff, K. Lips, V. Dyakonov and R. Bittl, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125206 CrossRef.
- J. Niklas, S. Beaupré, M. Leclerc, T. Xu, L. Yu, A. Sperlich, V. Dyakonov and O. G. Poluektov, J. Phys. Chem. B, 2015, 119, 7407–7416 CrossRef CAS PubMed.
- K. Maeda, K. B. Henbest, F. Cintolesi, I. Kuprov, C. T. Rodgers, P. A. Liddell, D. Gust, C. R. Timmel and P. J. Hore, Nature, 2008, 453, 387–390 CrossRef CAS PubMed.
- C. Kerpal, S. Richert, J. G. Storey, S. Pillai, P. A. Liddell, D. Gust, S. R. Mackenzie, P. J. Hore and C. R. Timmel, Nat. Commun., 2019, 10, 3707 CrossRef PubMed.
- M. R. Wasielewski, M. D. E. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith, T. I. Goodson, M. L. Kirk, J. K. McCusker, J. P. Ogilvie, D. A. Shultz, S. Stoll and K. B. Whaley, Nat. Rev. Chem., 2020, 4, 490–504 CrossRef CAS PubMed.
- F. Xie, H. Mao, C. Lin, Y. Feng, J. F. Stoddart, R. M. Young and M. R. Wasielewski, J. Am. Chem. Soc., 2023, 145, 14922–14931 CrossRef CAS PubMed.
- P. J. Hore, in Advanced EPR – Applications in Biology and Biochemistry, ed. A. J. Hoff, Elsevier, 1989, ch. 12, pp. 405–440 Search PubMed.
- M. C. Thurnauer and J. R. Norris, Chem. Phys. Lett., 1980, 76, 557–561 CrossRef CAS.
- C. R. Timmel and P. J. Hore, Chem. Phys. Lett., 1994, 226, 144–150 CrossRef CAS.
- J. Tang, M. C. Thurnauer, A. Kubo, H. Hara and A. Kawamori, J. Chem. Phys., 1997, 106, 7471–7478 CrossRef CAS.
- C. R. Timmel, C. E. Fursman, A. J. Hoff and P. J. Hore, Chem. Phys., 1998, 226, 271–283 CrossRef CAS.
- R. Bittl and S. G. Zech, Biochim. Biophys. Acta, 2001, 1507, 194–211 CrossRef PubMed.
- H. Hara, J. Tang, A. Kawamori, S. Itoh and M. Iwaki, Appl. Magn. Reson., 1998, 14, 367–379 CrossRef.
- A. J. Hoff, P. Gast, S. A. Dzuba, C. R. Timmel, C. E. Fursman and P. J. Hore, Spectrochim. Acta, Part A, 1998, 54, 2283–2293 CrossRef.
- T. Al Said, S. Weber and E. Schleicher, Front. Mol. Biosci., 2022, 9, 890826 CrossRef PubMed.
- S. G. Zech, R. Bittl, A. T. Gardiner and W. Lubitz, Appl. Magn. Reson., 1997, 13, 517–529 CrossRef.
- D. Nohr, B. Paulus, R. Rodriguez, A. Okafuji, R. Bittl, E. Schleicher and S. Weber, Angew. Chem., Int. Ed., 2017, 56, 8550–8554 CrossRef PubMed.
- R. Calvo, E. C. Abresch, R. Bittl, G. Feher, W. Hofbauer, R. A. Isaacson, W. Lubitz, M. Y. Okamura and M. L. Paddock, J. Am. Chem. Soc., 2000, 122, 7327–7341 CrossRef CAS.
- E. A. Weiss, M. A. Ratner and M. R. Wasielewski, J. Phys. Chem. A, 2003, 107, 3639–3647 CrossRef.
- A. S. Lukas, P. J. Bushard, E. A. Weiss and M. R. Wasielewski, J. Am. Chem. Soc., 2003, 125, 3921–3930 CrossRef PubMed.
- M. Di Valentin, A. Bisol, G. Agostini, M. Fuhs, P. A. Liddell, A. L. Moore, T. A. Moore, D. Gust and D. Carbonera, J. Am. Chem. Soc., 2004, 126, 17074–17086 CrossRef PubMed.
- M. Di Valentin, A. Bisol, G. Agostini and D. Carbonera, J. Chem. Inf. Model., 2005, 45, 1580–1588 CrossRef PubMed.
- A. Doll and G. Jeschke, J. Magn. Reson., 2016, 280, 46–62 CrossRef PubMed.
- P. E. Spindler, P. Schöps, A. M. Bowen, B. Endeward and T. F. Prisner, eMagRes, 2016, 5, 1477–1492 Search PubMed.
- B. Endeward, M. Bretschneider, P. Trenkler and T. F. Prisner, Prog. Nucl. Magn. Reson. Spectrosc., 2023, 136–137, 61–82 CrossRef.
- P. E. Spindler, S. J. Glaser, T. E. Skinner and T. F. Prisner, Angew. Chem., Int. Ed., 2013, 52, 3425–3429 CrossRef.
- A. Doll, S. Pribitzer, R. Tschaggelar and G. Jeschke, J. Magn. Reson., 2013, 230, 27–39 CrossRef.
- P. Schöps, P. E. Spindler, A. Marko and T. F. Prisner, J. Magn. Reson., 2015, 250, 55–62 CrossRef.
- S. Pribitzer, T. F. Segawa, A. Doll and G. Jeschke, J. Magn. Reson., 2016, 272, 37–45 CrossRef PubMed.
- A. Doll and G. Jeschke, Phys. Chem. Chem. Phys., 2016, 18, 23111–23120 RSC.
- C. E. Tait and S. Stoll, J. Magn. Reson., 2017, 277, 36–44 CrossRef.
- N. Wili and G. Jeschke, J. Magn. Reson., 2018, 289, 26–34 CrossRef.
- C. J. Rogers, A. Bogdanov, M. Seal, M. E. Thornton, X. C. Su, L. S. Natrajan, D. Goldfarb and A. M. Bowen, J. Magn. Reson., 2023, 351, 1–9 CrossRef.
- H. Geen and R. Freeman, J. Magn. Reson., 1991, 93, 93–141 Search PubMed.
- R. Carmieli, Q. Mi, A. B. Ricks, E. M. Giacobbe, S. M. Mickley and M. R. Wasielewski, J. Am. Chem. Soc., 2009, 131, 8372–8373 CrossRef.
- M. T. Colvin, R. Carmieli, T. Miura, S. Richert, D. M. Gardner, A. L. Smeigh, S. M. Dyar, S. M. Conron, M. A. Ratner and M. R. Wasielewski, J. Phys. Chem. A, 2013, 117, 5314–5325 CrossRef.
- E. J. Reijerse, F. Lendzian, R. A. Isaacson and W. Lubitz, J. Magn. Reson., 2012, 214, 237–243 CrossRef.
- J.-M. Böhlen and G. Bodenhausen, J. Magn. Reson., 1993, 102, 293–301 CrossRef.
- J. M. Böhlen, M. Rey and G. Bodenhausen, J. Magn. Reson., 1989, 84, 191–197 Search PubMed.
- G. Jeschke, S. Pribitzer and A. Doll, J. Phys. Chem. B, 2015, 119, 13570–13582 CrossRef.
- F. Bloch and A. Siegert, Phys. Rev., 1940, 57, 522–527 CrossRef.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef PubMed.
- S. Stoll and R. D. Britt, Phys. Chem. Chem. Phys., 2009, 11, 6614–6625 RSC.
- S. Pribitzer, A. Doll and G. Jeschke, J. Magn. Reson., 2016, 263, 45–54 CrossRef.
- M. Brinksma, M. Ernst and B. Meier, NMR with Mathematica, 1998 Search PubMed.
- I. Burghardt, J.-M. Böhlen and G. Bodenhausen, J. Chem. Phys., 1990, 93, 7687–7697 CrossRef.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef PubMed.
- V. Barone, in Recent Advances in Density Functional Methods, ed. D. P. Chong, World Scientific Publ. Co., Singapore, 1995, ch. 8, vol. 1, pp. 287–334 Search PubMed.
- N. Rega, M. Cossi and V. Barone, J. Chem. Phys., 1996, 105, 11060–11067 CrossRef.
- S. Huzinaga, J. Chem. Phys., 1965, 42, 1293–1302 CrossRef.
- W. Kutzelnigg, U. Fleischer and M. Schindler, in NMR Basic Principles and Progress, ed. P. Diehl, E. Fluck, H. Günther, R. Kosfeld and J. Seelig, Springer, Heidelberg, 1990, vol. 23, p. 165 Search PubMed.
- J. N. Nelson, J. Zhang, J. Zhou, B. K. Rugg, M. D. Krzyaniak and M. R. Wasielewski, J. Chem. Phys., 2020, 152, 014503 CrossRef PubMed.
- M. K. Bowman, M. D. Krzyaniak, A. A. Cruce and R. T. Weber, J. Magn. Reson., 2013, 231, 117–125 CrossRef PubMed.
- T. Wacker and A. Schweiger, Chem. Phys. Lett., 1991, 186, 27–34 CrossRef.
- M. Teucher and E. Bordignon, J. Magn. Reson., 2018, 296, 103–111 CrossRef PubMed.
- R. Freeman, Chem. Rev., 1991, 91, 1397–1412 CrossRef.
- P. J. Hajduk, D. A. Horita and L. E. Lerner, J. Magn. Reson., Ser. A, 1993, 103, 40–52 CrossRef.
- D. A. Horita, P. J. Hajduk and L. E. Lerner, J. Magn. Reson., Ser. A, 1993, 103, 53–60 CrossRef.
- J. M. Nuzillard and R. Freeman, J. Magn. Reson., Ser. A, 1994, 107, 113–118 CrossRef CAS.
- H. Mao, G. J. Pažėra, R. M. Young, M. D. Krzyaniak and M. R. Wasielewski, J. Am. Chem. Soc., 2023, 145, 6585–6593 CrossRef CAS PubMed.
- M. Garwood and L. DelaBarre, J. Magn. Reson., 2001, 153, 155–177 CrossRef CAS.
- J. A. Ferretti and R. R. Ernst, J. Chem. Phys., 1976, 65, 4283–4293 CrossRef CAS.
- A. Van der Est, T. F. Prisner, R. Bittl, P. Fromme, W. Lubitz, K. Möbius and D. Stehlik, J. Phys. Chem. B, 1997, 101, 1437–1443 CrossRef CAS.
- A. Savitsky, A. A. Dubinskii, M. Flores, W. Lubitz and K. Möbius, J. Phys. Chem. B, 2007, 111, 6245–6262 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional details on experiments and simulations, additional experimental data, extended discussion of interference effects in out-of-phase ESEEM. See DOI: https://doi.org/10.1039/d3cp06009h |
| ‡ For the measurements reported in this paper, the rectangular pulses were also programmed on the AWG, more severe distortions were observed for pulses programmed using the SPFU channels, in particular for short pulse lengths (see Fig. S2 in the ESI†). |
| § Excitation with the designed, close to rectangular profile for BURP pulses relies strongly on the correct calibration of the pulse flip angle. The authors of ref. 40 recommend setting the pulse amplitudes of BURP pulses in relation to corresponding rectangular pulses. For the E-BURP 2 and RE-BURP pulses we have found close agreement between the predicted pulse amplitude and the one determined in amplitude sweep experiments. |
| This journal is © the Owner Societies 2024 |