Kinetic energy distributions of atomic ions from disintegration of argon containing nanoclusters in moderately intense nanosecond laser fields: Coulomb explosion or hydrodynamic expansion†
Steven
Tran
a,
Kim C.
Tran
a,
Axel
Saenz Rodriguez
b and
Wei
Kong
 *a
*a
aDepartment of Chemistry, Oregon State University, Corvallis, Oregon 97331, USA. E-mail: wei.kong@oregonstate.edu; Tel: +1 541-737-6714
bDepartment of Mathematics, Oregon State University, Corvallis, Oregon 97331, USA
First published on 26th February 2024
Abstract
We report kinetic energies (KE) of multiply charged atomic ions (MCAI) from interactions of moderately intense nanosecond lasers at 532 nm with argon containing clusters, including neat and doped clusters with a trace amount of trichlorobenzene. We develop a mathematical method to retrieve speed and thereby kinetic energy information from analyzing the time-of-flight profiles of the MCAI. This method should be generally applicable in detections of energetic charged particles with high velocities, a realm where velocity map imaging is inadequate. From this analysis, we discover that the KE of MCAI from doped clusters demonstrates a quadratic dependence on the charge of the atomic ions, while for neat clusters, the dependence is cubic. This result confirms the nature of the cluster disintegration process to be dominated by Coulomb explosion. This result bears more similarity to reports from extreme vacuum ultraviolet (EUV) fields with similar intensities, than to reports from near infrared (NIR) intense laser fields. However, the charge state distribution from our experiment is the opposite: we observe more higher charge state ions than reported in EUV fields, and our charge state distribution is actually similar to those reported in NIR fields. We also report a significant effect of the external electric field on the charge state distribution of the atomic ions: the presence of an electric field can significantly increase the charge from the atomic ions, as shown by a three-fold reduction in the average kinetic energy per charge. Although molecular dynamics simulations have been implemented for experiments in the EUV and NIR, our results allude to the need of a concerted effort in this regime of moderately intense nanosecond laser fields. The significant decrease in charge state distribution and the significant increase in KE from doped clusters, compared with neat clusters, is a telltale sign that the true interaction time between the laser field and the cluster may be substantially shorter than the duration of the laser, a welcome relief for molecular dynamics simulations.
1. Introduction
In the interactions between a ultrafast intense near infrared (NIR) laser or an extreme vacuum ultraviolet laser (EUV) with atomic or molecular clusters,1–3 two mechanisms are typically considered in the disintegration process of the nanoclusters: Coulomb explosion (CE) or hydrodynamic expansion (HE).4–7 The former is a result of the strong Coulomb force from highly charged atomic ions within the cluster, while the latter is driven by the highly energetic expanding electron cloud. Both CE and HE can occur simultaneously, although typically CE dominates in small clusters in intense NIR or EUV fields, while HE is more predominant in larger clusters forming quasi-neutral nanoplasmas in strong NIR fields.8 Earlier studies have suggested that if the kinetic energy (KE) distribution is linearly dependent on the charge of the atomic ions, the process is dominated by HE, because the characteristic speed of expansion is the plasma sound speed, which is directly proportional to the square root of the number of charges within the nanocluster.1,4,5,9 On the other hand, if the kinetic energy is quadratically dependent on the charge, the process is dominated by CE, since the surface energy of the charged cluster is proportional to the square of the charge on each atom.1,4,5,9However, experiments rarely report a strict quadratic relation between the KE and the charge state,7 and more detailed theoretical work proved that even in the case of CE, the quadratic relation is only partially obeyed.1–3 The work by Arbeiter and Fennel also pointed out that the KE distribution of ions is ambiguous in identification of the expansion mechanism.10 Instead, photoelectron spectroscopy is more indicative of the cluster disintegration mechanism.
Although the topic of CE or HE belongs to the realm of strong fields,1–3 more than a decade ago, Li's group has reported the observation of multiply charged atomic ions (MCAI) from moderately intense nanosecond laser fields,11 and the group termed the process Coulomb explosion without a detailed analysis of the kinetic energy distributions. More work by Vasta's group ensued,12,13 and average kinetic energies of both cations and electrons have been reported. Our group entered the foray and confirmed the observations of the pioneers,14–17 and we expanded the previous study by measuring the size of the clusters,18 by resolving an issue related to the space average effect in focused laser fields,19 and by reporting on the detailed dependence of the charge distribution on the laser intensity and cluster composition.14 Although we attempted to observe the kinetic energy distribution from photoelectrons using the velocity map imaging method, the image is circularly symmetric, and the radial intensity distribution demonstrates a monotonic decay peaked at zero kinetic energy. This result is insufficient for any conclusion on the cluster disintegration mechanism without a detailed simulation.1
In this work, we report a detailed analysis of the kinetic energy distributions of MCAI based on measurements from time-of-flight (TOF) mass spectrometry. Using mathematical tools and numerical simulation, we have been able to determine the KE distribution of each atomic charge state, and to derive the dependence of the average KE on the charge state. This method is simpler than the standard practices of using both electric and magnetic fields for simultaneous charge and kinetic energy resolution.7,20 An approximate quadratic relation between the KE and the atomic charge is observed, confirming the predominant surface CE process in the moderately intense nanosecond laser fields. The KE distribution from this study is similar to that in EUV fields of similar intensities, but the charge state distribution from our laser fields is much higher. In fact, our charge state distribution is similar to those observed in strong NIR fields. Addition of just a single organic molecule inside the Ar clusters significantly accelerates the atomic ions, in agreement with results from strong NIR fields.21,22 This result could be a clue that the interaction time between the cluster and the nanosecond laser may be much shorter than the laser duration. This possibility offers hope for simulating the process using molecular dynamics (MD): the time duration between ionization ignition23,24 and cluster disintegration may occur in less than 1 ns, hence the calculation may not take a prohibitively long time. We also present the impact of the external electric field on the observed atomic ions, showing that the field can significantly increase the charges of the MCAI. The presence of low energy electrons in the vicinity of the exploding cluster under a field free condition may play an important role in the cluster disintegration process.
2. Experimental setup and data processing methods
Our previous work has determined the size of the laser beam at the focal spot,19 and validated the scaling law in the size of the Ar clusters from our pulse valve.18 The current experiment is conducted using the same laser and the same vacuum system including the pulse valve, hence the information on the laser intensity and the cluster size of this work has been well documented. However, for some experiments reported below, an additional electrode upstream from the time-of-flight tube, i.e. the Retarder, was added, as shown in Fig. 1. The Extractor electrode has an aperture of 1 mm in diameter, hence only ions with velocities near parallel to the flight axis can pass through and reach the detector. On the other hand, all ions passing through the aperture can land on the effective area of the microchannel plate (MCP) and be detected. Similar to our previous work,14–17 the experiment is typically performed with active background subtraction: in one laser pulse, a background spectrum is taken when the pulse valve containing the Ar gas and molecular additives is off, and in the next pulse, a signal spectrum is taken when the pulse valve is on, and the difference between the signal and the background spectrum is used in this report as the net signal spectrum. This method can not only remove contributions from the residue gas in the chamber, but also assist with calibration of the mass spectrometer by relying on the assignment of the background mass spectrum.The vacuum in the ionization chamber is at 3 × 10−8 torr, and the focused laser beam at 532 nm from a Q-switched Nd:YAG laser with a spot size of 6.8 μm in diameter results in an intensity of 3.4 × 1012 W cm−2. The mass spectrum of the ionized residue gas contains singly charged atomic ions (SCAI) and molecular fragments, including H+, C+, CH+, etc., and the TOF of these ions are shown by the square symbols in Fig. 2. The assignment of the mass spectrum from the residue gas is used to calibrate the mass spectrometer, and to determine the parameters of the spectrometer, including the precise length of the flight tube and the position of ionization. The continuous line in Fig. 2 is the fitting result using the SCAI.
Fig. 3 shows the TOF spectrum obtained from neat Ar4800 at the laser intensity of 3.4 × 1012 W cm−2. The stagnation pressure of the pulse valve was 8 atm. The TOF profile of each MCAI is asymmetric, quite unlike the symmetric Gaussian profiles of the SCAI. We consider this an indication of the high kinetic energies of these ions. For mass assignment, we chose the peak position of each ion, and the red circles in Fig. 2 represent the charge assignment of the MCAI. The fact that all arrival times of the assigned MCAI fall on the straight line derived from the SCAI confirms the charge assignment of the MCAI, and the agreement also implies that the peak positions represent the flight times of MCAI with near-zero kinetic energies.
 | ||
| Fig. 3 Time-of-flight spectrum of neat clusters of Ar4800. The TOF profiles of each MCAI with +2 to +9 charges are fitted using eqn (1) (see text for details), and the composite from individual ions is shown as the red continuous line. Ions with charges above +9 are ignored. | ||
To obtain the kinetic energy distribution of the MCAI, we initially planned to use the velocity map imaging method. However, we observed that for Ar+, all ions landed at the center of the detector corresponding to zero kinetic energies, but for almost all MCAI, the whole detector lighted up, suggesting that the kinetic energies of these ions were too high for our detector. We therefore relied on the TOF profile to derive the KE distribution. For this purpose, the Kicker electrode was biased at 2000 V, the Extractor was grounded, and the Retarder was removed.
Derive kinetic energy distributions from TOF profiles
To extract the contribution of kinetic energy in the TOF profile, we first scaled and recentered all profiles of the MCAI (Fig. S1 in the ESI†), and observed that all profiles agree almost exactly on the right (longer time) side, and they also agree with the profile of Ar+ obtained from gaseous Ar. This implies that the falling edge on the right is determined by the response of the detector, independent of the atomic charge or KE of each ion. The small peak following each major mass peak is due to electrical ringing, because the same pattern with similar ratios and time separation are observed for all SCAI and MCAI, hence they are ignored from the fitting. In the calculation and simulation, we also ignored all ions with velocities opposite the flight axis, since based on our calculation and simulation, in the strong extraction field of 2 kV cm−1, it takes less than a few nanoseconds for ions flying in the opposite direction to return and fly toward the flight tube, negligible on the time scale of the total TOF of any ions. The TOF profiles of the forward and backward flying ions are therefore similar.An analytical expression of the TOF profile of each MCAI is necessary for mathematical manipulation. The Ar+ profile from the gaseous sample is well represented by a Gaussian function, hence we used two different functions to fit the TOF profile of the MCAI (the mass-to-charge ratio is denoted by the subscript m) represented by fm(t): the sum of the Gaussian function and a Generalized Logic function (Genlogistic):
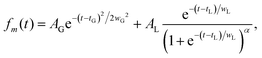 | (1) |
A detailed derivation and several method-validation procedures are presented in the ESI.† Although anisotropy in the velocity distributions of the MCAI has been reported from Coulomb explosion in intense femtosecond NIR laser fields,8 we do not observe any change in the mass spectrum when changing the polarization direction of the laser from parallel to perpendicular to the flight axis. Hence we assume an isotropic velocity distribution and only derive the speed and kinetic energy distribution from the TOF profiles. Each TOF profile fm(t) can be treated with a Jacobian factor  derived from the parameters of the TOF spectrometer to obtain the projected distribution Px(vx) along the flight axis (x):
derived from the parameters of the TOF spectrometer to obtain the projected distribution Px(vx) along the flight axis (x):
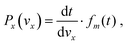 | (2) |
 , through:
, through: | (3) |
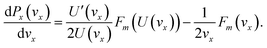 | (4) |
Using an iterative method and by setting a convergence precision in speed, Fm(v) and hence the kinetic energy distribution can be obtained.
We validated the above treatment using three different approaches, also detailed in the ESI.† In the first method, we created ions with a Gaussian kinetic energy distribution and used Monte Carlo processes from SIMION to obtain the TOF profile. In the second method, we used the same Gaussian kinetic energy distribution and generated ions using our own Python code to calculate the TOF profile using eqn (2) and (3). The TOF profiles from the two methods are essentially identical. The derived TOF profiles were then used to recalculate the kinetic energy distributions, which matched the original distribution. In the last approach, we used the derived kinetic energy distribution from the experimental TOF profile (Fig. 5) and recalculated the TOF profile, and the excellent agreement between the experimental and recalculated profiles further confirms the validity of our approach.
A caveat of this treatment is in the calculation of the average speed and kinetic energy: both calculations place a heavier weight on the faster ions, while the experimental data for faster ions are entangled in the TOF, particularly for the MCAI with charges from +5 to +9. Different fitting methods of the TOF profiles can result in different average values in speed and kinetic energy, and the Genlogistic fitting method represented by eqn (1) results in the lowest average speed and KE, hence we treat the values reported in this work as lower limits. Additionally, the kinetic energy of Ar+ from cluster disintegration is difficult to determine because of the large contribution of the detector's response in the TOF profile, and the resulting average kinetic energies vary from 1.3 to 2.8 eV, depending on the detailed fitting method of the TOF. Hence in the following discussion, the KE of Ar+ is only considered qualitatively.
This method is different from that used by Rupp et al.25 where the kinetic energy distribution was obtained from the TOF, the transmission function of the mass spectrometer, and an empirical linear relation between the flight time and kinetic energy of each MCAI established from SIMION simulations. The approximation in the method from Rupp et al. limits its application to high energy ions. Our method contains no approximation, and it requires no prior knowledge other than an assumption of isotropic spatial distributions. Nevertheless, the final kinetic energy distributions from our experiment under all conditions strongly resemble Maxwell distributions, with equivalent temperatures of each charge state on the order of several million Kelvins.
Two other methods have been used in the literature to determine average KE or KE distributions.4,8,22 The peak splitting method relies on the flight time difference between the forward and backward flying ions to derive the most probable KE of the MCAI.22 However, this method requires a clear identification of the peak from the backward flying ions, which in many cases could be difficult. For example, in our TOF spectrum, there is no obvious back peak to identify due to the strong extraction field, and the small peaks following each major peak are identified to be ringing effects of the detector. In addition, this method can only deduce the observed most probably KE, without any information on the KE distributions, being thermal, or bimodal, or exponential. A typical retardation experiment includes a retardation electrode placed in front of the MCP ion detector,4,8 different from our current setup where the retardation electrode is right next to the extractor. Ions are typically not accelerated in the ionization region; hence the resulting KE distribution contains limited to no information on the mass-to-charge ratio. Most importantly, the detection yields of both high (limited by the collection angle) and low (limited by the low transmission through the non-ideal vacuum) KE ions are low, resulting in low signal-to-noise ratios for reliable statistical analysis. When an acceleration voltage is applied in the ionization region thereby mass resolution is possible,26 the overlapping TOF profiles of MCAI still pose a challenge to the identification of the charge state, hence this retardation method is largely reserved to ions with large mass-to-charge ratios.
3. Results
Fig. 4 shows the KE distribution from neat Ar clusters containing 4800 Ar atoms derived using the above approach. The laser intensity is 3.4 × 1012 W cm−2, but the KE distribution is almost independent of the laser intensity: as long as MCAI can be observed, similar TOF spectra with similar TOF profiles for the MCAI can be observed, at least in the intensity range between 1011 W cm−2 and 1013 W cm−2. This result is in agreement with our previous report on the intensity effect on the yield of the MCAI:14,15 all MCAIs demonstrate similar dependence on the laser intensity within our experimental range, except for Ar+.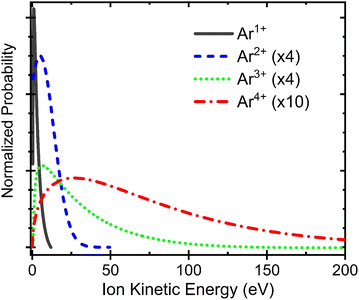 | ||
| Fig. 4 Kinetic energy distributions of Ar ions with +1 to +4 charges from neat clusters of Ar4800. The distributions of MCAI are scaled up to show their detailed features. | ||
Fig. 5 shows the KE distribution of Ar4+ from four different clusters: neat clusters containing 800 and 4800 Ar atoms, and similar clusters with a trace amount of trichlorobenzene (3ClB) . The doped clusters were generated by placing the sample 3ClB directly into the pulse valve at room temperature, with a vapor pressure 0.51 torr. No bimodal distribution is observed in the final speed and kinetic energy distributions, although the TOF profiles of Ar4+ contain two components in eqn (1). The Gaussian-function like peak observed in the TOF profile of each MCAI is therefore a result of the 100% transmission of near-zero kinetic energy ions in the presence of the small aperture on the Extractor electrode. The most probable and the average kinetic energies of the MCAIs are on the order of tens of eV from neat Ar clusters, but the distributions shift significantly to higher values, reaching nearly 1000 eV, with the addition of a trace amount of 3ClB.
 | ||
| Fig. 5 Kinetic energy distributions of Ar4+ from neat argon clusters of Ar800 and Ar4800 along with doped argon clusters of Ar8003ClB0.07 and Ar48003ClB0.02. | ||
Several major conclusions can be obtained from Fig. 5: the KE distribution shows negligible dependence on the cluster size, but it is extremely sensitive to the addition of 3ClB. The former is in general agreement with our previous reports:14–17 the TOF profiles of MCAI are similar and are only weakly dependent on the cluster size and laser intensity. This observation, however, is different from reports of strong laser fields, where larger clusters typically result in higher kinetic energies.1,4 We emphasize here that the negligible size effect observed in our studies is limited within the size range of our investigation, from hundreds to tens of thousands of Ar atoms. For clusters of much smaller sizes, the size effect should be much more dramatic as reported in the literature.27,28
In our previous work on the effect of organic dopants inside Ar clusters, we observed an increased overall ionization yield,14 but the charge state distribution of the MCAI shifts to lower states. In neat Ar clusters as shown in Fig. 3, the most intense charge state among the MCAI is +8, while for Ar8003ClB0.07, the most intense charge state is Ar4+, and the highest observable charge state is Ar8+. In Fig. 5, the addition of 1 molecule in a cluster containing 4800 Ar atoms, has a significant effect on the kinetic energy of Ar4+, extending the upper energy limit to nearly 1000 eV.
Fig. 6 shows the average kinetic energy 〈Ek〉m of each charge state m for different clusters calculated using:
 | (5) |
Effect of the extraction field on the KE distribution
To uncover the effect of the extraction field on the KE distribution, we performed a retardation experiment by biasing the Retardation electrode while setting the Kicker and Extractor to the same potential. In one experiment, both Kicker and Extractor were grounded, but the signal intensity was limited, hence in the next experiment, both electrodes were biased at 2 kV to increase the ion transmission through the TOF. The velocities of the cluster beam from the pulse valve are on the order of 500 m s−1, and it takes ∼1 μs for the cluster beam to migrate from the ionization region into the retardation region. This means that the cluster disintegration process, typically on the order of several picoseconds and no more than 1 ns, should have finished when the cluster passes the Extractor. As long as the bias voltages on both the Kicker and Extractor remain the same, cluster disintegration occurs under field-free conditions. Indeed the retardation results are the same under both settings of the bias voltages: 0 and 2 kV, although the results from 2 kV are of much higher signal-to-noise ratios. In the following discussion, for simplicity, we use the results obtained with a bias voltage of 2 kV on the Kicker and Extractor, and we refer to these results as “measured” in the following discussions.For comparison, we also simulated the experiment using the KE distributions obtained from Fig. 3 in an extraction field of 2 kV cm−1, and we refer to these results as “simulated” in the following discussions. In this simulation, we used the KE distributions presented in Fig. 4 and 5 and calculated the TOF profiles assuming both the Kicker and Extractor were biased at 2 kV when the bias voltage on the Retarder was changed from 2000 V to 3000 V.
The lack of fields in the ionization region prevents the detection of low KE ions even from the background, hence assignment of the TOF spectrum into mass-to-charge ratios is impossible. Each MCAI has a broad KE distribution, and the arrival times of the MCAI overlap into one broad peak, as shown in Fig. 7. Any detected ions with charge q must travel out of the laser excitation region on their own initial velocity, and to reach the detector, they also need to possess kinetic energies exceeding the potential energy difference between the retardation and the extraction electrode:
| Ek > qVR, | (6) |
 | ||
| Fig. 7 Effect of the retardation field on the ion yield obtained from Ar4800 under different extraction fields (labeled as “measured” at 0 kV cm−1 or “simulated” at 2 kV cm−1) and retardation field (labeled as 0 or 200 V). Without any acceleration field, there is no mass resolution of any ions. The red dot, red dash, and red shade are results obtained when both the Kicker and Extractor electrodes are biased at 2000 V, while varying the retardation voltage (see Fig. 1 for experimental setup). The blue line, shade, and triangles with error bars are calculated results based on the derived kinetic energy distribution from Fig. 4. The inset shows the total ion signal change with the retardation voltage. The vertical axis for the inset is normalized at 0 V retardation voltage for comparison. | ||
The profiles obtained under different extraction fields but without any retardation field (VR = 0 V) are similar (lines), although the profile obtained from an extraction field of 2 kV cm−1 is slightly broader (solid blue line), on both sides of the peak, than that from the field free conditions (dashed red line). More importantly, the centers of the peaks are within a few percent of the flight time, implying that the speed and therefore KE distributions of the MCAI are similar with and without the extraction field. Based on the calculation at 2 kV cm−1, the transmitted ions are mostly highly charged MCAI, with q = + 7 to +9, while contributions from lower charge state ions are largely negligible.
With increasing retardation potentials, ion counts on the longer time (right) side decrease, since these ions have a lower speed hence lower kinetic energy, and they are blocked by the retardation potential. At a retardation potential of 200 V (shaded areas), a dramatic difference between the two profiles obtained under the two extraction fields is observed. In an extraction field of 2 kV cm−1 (blue shade), a significant drop in ion intensity is observable, particularly on the right side corresponding to low speed ions. In the absence of the extraction field (red shade), the drop in the ion count is much less dramatic. If the KE distribution is similar under the two different extraction fields as observed with VR = 0 V, i.e. Ek remains the same, a likely explanation for the more favorable ion transmission in the absence of the extraction field (0 kV cm−1) is a lower charge state distribution, i.e., a lower q value in inequality (6). This result is thus similar to that in intense fields29 where Komar et al. argued that a weaker field allows the existence of high Rydberg state ions after electron recombination, leading to a lower net charge state distribution.
The overall ion yield as a function of the retardation potential is shown in the inset of Fig. 7. In the absence of any field in the cluster disintegration region (0 kV cm−1), 50% of the ions can pass through the retardation electrode with an effective retardation potential of 300 V, but in an extraction field of 2 kV cm−1, less than 50% of the ions can pass through an effective retardation potential of only 100 V. The average kinetic energy from all the MCAI based on the known kinetic energy distribution for each charge state derived in an extraction field of 2 kV cm−1 is calculated to be 470 eV. However, without resolving the charge state of the MCAI under field free conditions (0 kV cm−1), it is impossible to calculate the average kinetic energy. Instead, we can calculate the average kinetic energy per charge 〈Ek/q〉, by weighing the observed ion counts I(VR) with the retardation potential VR:
 | (7) |
The calculation shows that the external field at 2 kV cm−1 reduces the kinetic energy per charge by more than a factor of three: from 358 to 95 eV per charge. This change in 〈Ek/q〉 due to the extraction field should be largely attributed to the decreased charges on the MCAI under field free conditions.
The average charge in an extraction field of 2 kV cm−1 is +7.8 a.u. excluding the contribution of Ar+, which cannot reach the detector due to its low kinetic energies. Hence qualitatively, we can assess that in the absence of an extraction field, the average charge is reduced by a factor of three. We therefore can assert that even without the assistance of the external electric field, multiply charged atomic species are still produced, and that they are produced with substantial kinetic energies, in the moderately intense nanosecond laser field.
The effect of the external field can be qualitatively understood from the following arguments. The lack of any extraction field in the cluster disintegration region prevents low KE electrons from escaping the vicinity of the cluster upon outer ionization. The presence of these electrons may help neutralize the outgoing highly charged atomic ions from the exploding cluster. In the presence of an extraction field of 2 kV cm−1, all outer ionized electrons regardless of KE are removed from the cluster, which eliminates electron-cation recombination, resulting in a highly charged cluster. Alternatively, inner ionized electrons upon cluster expansion can recombine with the departing cations into high Rydberg states, and the electric field in the ionization region can field ionize the metastable atoms and ions, inducing a higher degree of ionization, by up to 90%.29,30
4. Discussion
Average kinetic energies of MCAI from moderately intense nanosecond laser fields have been reported in the literature,11,26,27,31–36 and the values from this work are in general agreement with these reports. However, our work represents the first time that kinetic energy distributions of each MCAI are derived, and it is also the first time that the average values are derived from an experimentally determined distribution, rather than from the observed double peaks related to the forward and backward traveling ions.A notable difference between the previous work of Li's and Vatsa's groups11,26,27,31–36 and our group is in the laser intensity: our intensity is generally two orders of magnitude higher than those reported by Li's and Vatsa's groups. However, the samples investigated by the two groups have much lower ionization energies, involving neat molecular clusters or molecular clusters embedded inside Ar clusters, hence fewer photons are needed for the first ionization event. We failed to observe any ions when the intensity is below 1011 W cm−2, and we attribute this higher intensity threshold to the higher ionization energy of Ar. Once the first ion is produced, the rest of the process should be largely similar in all moderately intense nanosecond laser fields.
The kinetic energy distributions from our experiment in nanosecond laser fields are orders of magnitude lower than those from strong NIR fields but are on par with those from EUV fields of similar intensties.4,28,37–39 According to Park et al.,8 at an intensity of 1014 W cm−2 and a wavelength of 500 nm, the average KE from similar clusters as ours is about 10 keV, although the report does not resolve any charge states. Interestingly, the average KE from EUV fields in the wavelength region between 52 and 90 nm, at similar or even higher laser intensities (1011–1014 W cm−2), are on the same order of magnitude as ours.4,28,38 One could argue that although the laser intensity of our nanosecond laser field is orders of magnitude lower, the laser pulse is also orders of magnitude longer. However, a longer laser duration does not necessarily mean a longer interaction time, since the cluster can disintegrate prior to the ending of the laser pulse. This possibility has been confirmed by studies using variable pulse durations in the NIR.1,40,41 In fact, an optimal laser pulse duration, on the order of 1 ps, was reported from several studies.40,41 If the interaction in the nanosecond laser field is only effective in sub-ns, the total pulse energy from our laser field should be similar to that of an intense NIR field with fs duration. The major difference in final kinetic energy suggests that the laser intensity rather than the pulse energy plays a more important role in determining the KE of the resulting MCAI.
The average charge from Fig. 3 is 4.6 a.u., significantly higher than that of Krikunova et al.42 obtained at similar laser intensities but at a much shorter wavelength (92 nm) from neat Xe clusters of similar size ranges. If we remove the significant contribution of Ar+, the average charge of the MCAI is increased to 7.8 a.u. This high large distribution from our experiment is very puzzling given that our photon energy is less than a quarter of that from the EUV pulse, and Ar has a much higher ionization threshold than Xe. Clearly the much longer laser pulse is more effective for ionization but not for accelerating the resulting MCAI. Interestingly, the average charge state from Park et al.8 is on par with our observation, although the laser intensity and the pulse duration differ by orders of magnitude in these two experiments. This situation implies that the mechanism of interaction in the moderately intense nanosecond laser field may be different from that in intense ultrafast NIR fields, and it is also different from that of ultrafast EUV fields.
The size of our clusters and the intensity of our laser field do not fit the typical conditions for Coulomb explosion. The Keldysh parameter of our laser field is nearly 9,43 hence initial ionization is in the regime of multiphoton ionization (MPI). The ponderomotive energy is less than 0.1 eV,1 and the effectiveness of inverse Bremsstrahlung heating is debatable,2,3,37,44 although recent experimental and theoretical work have both alluded to the effectiveness of the weak ponderomotive field.45–49 The clusters, even those with the smallest size from our study, contain tens to hundreds of layers of Ar. In the moderately intense laser field, with limited yield for MPI, and with limited ponderomotive energy, it is questionable if highly charged atomic ions can be formed inside the cluster, and yet the experiment demonstrates a remarkable predominance of Coulomb explosion and a high average charge from the resulting MCAI.
Borrowing the idea of CE in EUV and NIR fields,5,50,51 we hypothesize that the reason for the strong preference of CE in moderately intense nanosecond laser fields is the result of the accumulated high charge state ions on the surface of the cluster.16,17,52 Although MPI can occur at any spot inside the cluster, particularly for doped clusters, the positive charges are concentrated in the surface layers, resulting in CE. The Maxwellian distribution of the MCAI with equivalent temperatures of millions of Kelvin is insufficient evidence for HE.
The addition of an organic dopant inside an Ar cluster significantly accelerates the low charge state MCAI, but reduces the yield of high charge state MCAI. This could be related to the fact that the first ionization event, the rate-determining step in the cluster disintegration process, occurs at a much earlier time of the laser pulse due to the low ionization energies of the organic impurities. Electron avalanche24 occurs in an increasingly stronger laser field, allowing fast ionization and quick explosion of the cluster, short-changing the formation process of high charge state MCAI. The lower charge state distributions from doped clusters could well be a consequence of a shortened interaction time between the laser and the cluster. In this sense, although the laser pulse lasts for 10 ns, the interaction time between the laser and the cluster may be much shorter.24,53
Several mechanisms may contribute to the effectiveness of the moderately intense nanosecond laser fields in producing highly charged MCAI. The soft-core potential for the multi-electron atomic ions can significantly increase the efficiency of energy transfer from the laser field to the inner ionized electrons.46,48 The degree of ionization can be further assisted by the presence of excited states, and by the lowering of the ionization thresholds in the presence of the Coulomb fields from neighboring ions.45 Additionally, a unique process in clusters named interatomic coulomb decay (ICD) has proven more efficient than MPI in outer ionization of clusters when the excitation wavelength is in resonance with an atomic transition of the cluster atoms.54,55 In our previous publications, we called attention to the resonance of Ar3+ with an absorption cross section of 1 Å2 at 532 nm.16,17 Nanoplasmas can also form after an induction period, and resonant heating of the nanoplasma can be effective for electron acceleration and further impact ionization.56 However, without a detailed molecular dynamics calculation, it is difficult to assess the importance of each process in forming the observed MCAI. Fortunately, the possibility of a much shorter interaction time between the laser and the cluster offers a feasible path forward for a full MD simulation.
In one of our previous publications,15 we predicted that the KE distribution of Ar+ should be very different from those of MCAI, based on the dramatically different intensity dependence of the ion yields of Ar+ and MCAI. While the KE of MCAI is on the order of tens to hundreds of eV, the KE of Ar+ is less than 4 eV regardless of the fitting method for the TOF profiles. We also observe increased KE from clusters with 3ClB even for Ar+, in agreement with our previous observation.14 However, unimodular distributions are observed for both Ar+ and MCAI.
5. Conclusion
We report the kinetic energy distributions of multiply charged atomic ions from cluster disintegration in moderately intense nanosecond laser fields. Using a series of mathematical operations, the time-of-flight profiles of MCAI collected from an aperture limited mass spectrometer can be used to derive the speed and thereby kinetic energy distributions of the atomic ions, assuming isotropic velocity distributions. This method is validated using a series of independent simulations and calculations, and it should be universally applicable for measurements of fast charged particles, including cations, anions, and electrons.The kinetic energy distributions of MCAI from doped clusters are quadratically related to the charge of the atomic ions, similar to those from EUV fields, although an even higher order dependence is observed from neat clusters. The average energies are on the order of tens to hundreds of eV, again on par with those from EUV fields with similar field intensities but orders of magnitude lower than those from intense NIR fields. These observations allude to the mechanism of Coulomb explosion on the surface of the clusters, with limited contribution from hydrodynamic expansion. The charge state distribution from our work, however, is more similar to those from intense NIR fields, much higher than those from EUV fields. The moderately intense laser field relies on MPI for ionization ignition, and the ponderomotive energy is on the order of meV. Although several potential mechanisms of effective ionization exist in the cluster, a detailed calculation is needed to determine the relative significance of each mechanism. The addition of an organic dopant in the Ar clusters decreases the charge state distribution but significantly accelerates the MCAI. This result could be an indication that the rate determining step of cluster disintegration is the first ionization event inside the cluster, and that the time scale of disintegration may be far shorter than the ns duration of the laser field. This possibility is quite welcoming in considering the computational cost of modeling the process using molecular dynamics. We also discover a significant effect of the external electric field on the charge state distribution: the extraction field can increase the charge state distribution by three-fold.
Data availability statement
The data and software that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
Steven Tran and Kim C. Tran equally contributed to data curation, validation, and formal analysis. Axel Saenz Rodriguez developed the methodology for formal analysis. Wei Kong is responsible for funding acquisition, conceptualization, and writing.Conflicts of interest
The authors have no conflicts to disclose.Acknowledgements
This material is based upon work supported by the National Science Foundation under grant no. 1838522. We thank Dr Edward Ackad and Dr Nirmala Kandadai for their comments and suggestions regarding this work. Discussions with Dr Marcels Mudrich is deeply appreciated.References
- T. Fennel, K. H. Meiwes-Broer, J. Tiggesbaeumker, P. G. Reinhard, P. M. Dinh and E. Suraud, Rev. Mod. Phys., 2010, 82, 1793–1842 CrossRef.
- U. Saalmann, C. Siedschlag and J. M. Rost, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, R39–R77 CrossRef CAS.
- P. G. Reinhard and E. Suraud, Introduction to Cluster Dynamics, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2004 Search PubMed.
- H. Thomas, C. Bostedt, M. Hoener, E. Eremina, H. Wabnitz, T. Laarmann, E. Ploenjes, R. Treusch, A. R. B. de Castro and T. Moeller, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 134018 CrossRef.
- M. Hoener, C. Bostedt, H. Thomas, L. Landt, E. Eremina, H. Wabnitz, T. Laarmann, R. Treusch, A. R. B. de Castro and T. Moeller, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 181001 CrossRef.
- D. Mathur, Adv. Multi-Photon Processes Spectrosc., 2004, 16, 273–306 CAS.
- M. Lezius, S. Dobosz, D. Normand and M. Schmidt, Phys. Rev. Lett., 1998, 80, 261–264 CrossRef CAS.
- H. Park, A. Camacho Garibay, Z. Wang, T. Gorman, P. Agostini and L. F. DiMauro, Phys. Rev. Lett., 2022, 129, 203202 CrossRef CAS PubMed.
- I. Last, I. Schek and J. Jortner, J. Chem. Phys., 1997, 107, 6685–6692 CrossRef CAS.
- M. Arbeiter and T. Fennel, New J. Phys., 2011, 13, 053022 CrossRef.
- X. Kong, X. Luo, D. Niu and H. Li, Chem. Phys. Lett., 2004, 388, 139–143 CrossRef CAS.
- P. Badani, S. Das, P. Sharma and R. K. Vatsa, Mass Spectrom. Rev., 2017, 36, 188–212 CrossRef CAS PubMed.
- S. Das, P. M. Badani, P. Sharma and R. K. Vatsa, Curr. Sci., 2011, 100, 1008–1019 CAS.
- Y. Yao, J. Zhang and W. Kong, J. Chem. Phys., 2022, 157, 044307 CrossRef CAS PubMed.
- Y. Yao, J. Zhang, R. Pandey, D. Wu, W. Kong and L. Xue, J. Chem. Phys., 2021, 155, 144301 CrossRef CAS PubMed.
- J. Zhang, Y. Yao and W. Kong, J. Phys. Chem. Lett., 2020, 11, 1100–1105 CrossRef CAS PubMed.
- Y. Yao, J. Zhang, R. K. Pandey and W. Kong, J. Phys. Chem. Lett., 2020, 11, 9971–9974 CrossRef CAS PubMed.
- Y. Yao, J. Zhang, W. M. Freund, S. Tran and W. Kong, Chem. Phys. Lett., 2023, 813, 140312 CrossRef CAS.
- Y. Yao, W. M. Freund, J. Zhang and W. Kong, J. Chem. Phys., 2021, 155, 064202 CrossRef CAS PubMed.
- F. Treffert, Q. Ji, P. A. Seidl, A. Persaud, B. Ludewigt, J. J. Barnard, A. Friedman, D. P. Grote, E. P. Gilson, I. D. Kaganovich, A. Stepanov, M. Roth and T. Schenkel, Rev. Sci. Instrum., 2018, 89, 103302/103301 CrossRef PubMed.
- J. Jha, P. Sharma, V. Nataraju, R. K. Vatsa, D. Mathur and M. Krishnamurthy, Chem. Phys. Lett., 2006, 430, 26–31 CrossRef CAS.
- J. Purnell, E. M. Snyder, S. Wei and A. W. Castleman, Chem. Phys. Lett., 1994, 229, 333–339 CrossRef CAS.
- B. Schütte, M. Arbeiter, A. Mermillod-Blondin, M. J. J. Vrakking, A. Rouzee and T. Fennel, Phys. Rev. Lett., 2016, 116, 033001 CrossRef.
- C. Rose-Petruck, K. J. Schafer, K. R. Wilson and C. P. J. Barty, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 55, 1182–1190 CrossRef CAS.
- D. Rupp, L. Flückiger, M. Adolph, T. Gorkhover, M. Krikunova, J. P. Muller, M. Muller, T. Oelze, Y. Ovcharenko, B. Roben, M. Sauppe, S. Schorb, D. Wolter, T. Moller, L. Fluckiger, T. Gorkhover, S. Schorb, C. Bostedt, R. Mitzner, M. Wostmann, S. Roling, M. Harmand, R. Treusch, M. Arbeiter, T. Fennel, C. Bostedt and C. Bostedt, Phys. Rev. Lett., 2016, 117, 153401 CrossRef PubMed.
- S. Das, P. M. Badani, P. Sharma, R. K. Vatsa, D. Das, A. Majumder and A. K. Das, Rapid Commun. Mass Spectrom., 2011, 25, 1028–1036 CrossRef CAS PubMed.
- S. Das, P. M. Badani, P. Sharma and R. K. Vatsa, Chem. Phys. Lett., 2012, 552, 13–19 CrossRef CAS.
- H. Fukuzawa, X. J. Liu, G. Prumper, M. Okunishi, K. Shimada, K. Ueda, T. Harada, M. Toyoda, M. Yanagihara, M. Yamamoto, H. Iwayama, K. Nagaya, M. Yao, K. Motomura, N. Saito, A. Rudenko, J. Ullrich, L. Foucar, A. Czasch, R. Dorner, M. Nagasono, A. Higashiya, M. Yabashi, T. Ishikawa, H. Ohashi and H. Kimura, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 031201 CrossRef.
- D. Komar, L. Kazak, M. Almassarani, K. H. Meiwes-Broer and J. Tiggesbäumker, Phys. Rev. Lett., 2018, 120, 133207 CrossRef CAS PubMed.
- T. Fennel, L. Ramunno and T. Brabec, Phys. Rev. Lett., 2007, 99, 233401 CrossRef PubMed.
- P. M. Badani, S. Das, P. Sharma and R. K. Vatsa, Int. J. Mass Spectrom., 2014, 358, 36–42 CrossRef CAS.
- P. M. Badani, S. Das, V. R. Mundlapati, P. Sharma and R. K. Vatsa, AIP Adv., 2011, 1, 042164 CrossRef , 042113.
- S. Das, P. Sharma and R. K. Vatsa, J. Chem. Sci., 2009, 121, 965–972 CrossRef CAS.
- L. Wen, H. Li, X. Luo, D. Niu, X. Xiao, B. Wang, F. Liang, K. Hou and S. Shao, Chem. Phys., 2006, 322, 360–365 CrossRef CAS.
- P. Sharma, R. K. Vatsa, S. K. Kulshreshtha, J. Jha, D. Mathur and M. Krishnamurthy, J. Chem. Phys., 2006, 125, 034304 CrossRef CAS PubMed.
- X. Luo, D. Niu, X. Kong, L. Wen, F. Liang, K. Pei, B. Wang and H. Li, Chem. Phys., 2005, 310, 17–24 CrossRef CAS.
- M. Arbeiter and T. Fennel, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 013201 CrossRef.
- H. Iwayama, A. Sugishima, K. Nagaya, M. Yao, H. Fukuzawa, K. Motomura, X. J. Liu, A. Yamada, C. Wang, K. Ueda, N. Saito, M. Nagasono, K. Tono, M. Yabashi, T. Ishikawa, H. Ohashi, H. Kimura and T. Togashi, J. Phys. B., 2010, 43, 161001 CrossRef.
- T. Ditmire, E. Springate, J. W. G. Tisch, Y. L. Shao, M. B. Mason, N. Hay, J. P. Marangos and M. H. R. Hutchinson, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57, 369–382 CrossRef CAS.
- Y. Fukuda, K. Yamakawa, Y. Akahane, M. Aoyama, N. Inoue, H. Ueda and Y. Kishimoto, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 67, 061201 CrossRef.
- M. Schumacher, S. Teuber, L. Koller, J. Kohn, J. Tiggesbaumker and K. H. Meiwes-Broer, Eur. Phys. J. D, 1999, 9, 411–414 CrossRef CAS.
- M. Krikunova, M. Adolph, T. Gorkhover, D. Rupp, S. Schorb, C. Bostedt, S. Roling, B. Siemer, R. Mitzner, H. Zacharias and T. Moeller, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 105101 CrossRef.
- L. V. Keldysh, Zh. Eksp. Teor. Fiz., 1964, 47, 1945–1957 CAS.
- V. P. Krainov and M. B. Smirnov, Phys. Rep., 2002, 370, 237–331 CrossRef CAS.
- R. Pandit, N. Bigaouette, V. R. Becker, J. Thurston, K. Barrington, E. Ackad and L. Ramunno, Phys. Rev. A, 2019, 100, 063402 CrossRef CAS.
- Z. B. Walters, R. Santra and C. H. Greene, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 043204 CrossRef.
- C. Siedschlag and J.-M. Rost, Phys. Rev. Lett., 2004, 93, 043402 CrossRef PubMed.
- R. Santra and C. H. Greene, Phys. Rev. Lett., 2003, 91, 233401 CrossRef PubMed.
- H. Wabnitz, L. Bittner, A. R. B. de Castro, R. Doehrmann, P. Guertler, T. Laarmann, W. Laasch, J. Schulz, A. Swiderski, K. von Haeften, T. Moeller, B. Faatz, A. Fateev, J. Feldhaus, C. Gerth, U. Hahn, E. Saldin, E. Schneidmiller, K. Sytchev, K. Tiedtke, R. Treusch and M. Yurkov, Nature, 2002, 420, 482–485 CrossRef CAS PubMed.
- C. A. Saladrigas, A. J. Feinberg, M. P. Ziemkiewicz, C. Bacellar, M. Bucher, C. Bernando, S. Carron, A. S. Chatterley, F.-J. Decker, K. R. Ferguson, L. Gomez, T. Gorkhover, N. A. Helvy, C. F. Jones, J. J. Kwok, A. Lutman, D. Rupp, R. M. P. Tanyag, T. Möller, D. M. Neumark, C. Bostedt, A. F. Vilesov and O. Gessner, Eur. Phys. J.: Spec. Top., 2021, 230, 4011–4023 CAS.
- T. Gorkhover, S. Schorb, R. Coffee, M. Adolph, L. Foucar, D. Rupp, A. Aquila, J. D. Bozek, S. W. Epp, B. Erk, L. Gumprecht, L. Holmegaard, A. Hartmann, R. Hartmann, G. Hauser, P. Holl, A. Hömke, P. Johnsson, N. Kimmel, K.-U. Kühnel, M. Messerschmidt, C. Reich, A. Rouzée, B. Rudek, C. Schmidt, J. Schulz, H. Soltau, S. Stern, G. Weidenspointner, B. White, J. Küpper, L. Strüder, I. Schlichting, J. Ullrich, D. Rolles, A. Rudenko, T. Möller and C. Bostedt, Nat. Photonics, 2016, 10, 93–97 CrossRef CAS.
- B. Ziaja, H. Wabnitz, F. Wang, E. Weckert and T. Moller, Phys. Rev. Lett., 2009, 102, 205002 CrossRef CAS PubMed.
- F. Fehrer, P. G. Reinhard and E. Suraud, Appl. Phys. A: Mater. Sci. Process., 2006, 82, 145–150 CrossRef CAS.
- L. Ben Ltaief, K. Sishodia, S. Mandal, S. De, S. R. Krishnan, C. Medina, N. Pal, R. Richter, T. Fennel and M. Mudrich, Phys. Rev. Lett., 2023, 131, 023001 CrossRef CAS PubMed.
- A. I. Kuleff, K. Gokhberg, S. Kopelke and L. S. Cederbaum, Phys. Rev. Lett., 2010, 105, 043004 CrossRef PubMed.
- R. Singh, V. K. Tripathi, R. K. Vatsa and D. Das, Phys. Plasmas, 2017, 24, 082111 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: The mathematical relations between the KE distribution and the TOF profile are derived in detail, with illustrations of the different validation methods. Detailed comparison between the experimental and fitted TOF profiles of the MCAI is also shown. See DOI: https://doi.org/10.1039/d3cp05894h |
| This journal is © the Owner Societies 2024 |



