Intrinsic edge states and strain-tunable spin textures in the Janus 1T-VTeCl monolayer

Abstract

Using first-principles calculations and micro-magnetic simulations, we investigate the electronic structures, the effect of biaxial strain on the topological characteristics, magnetic anisotropy energy (MAE), Dzyaloshinskii–Moriya interaction (DMI) and spin textures in the Janus 1T phase VTeCl (1T-VTeCl) monolayer. Our results show that 1T-VTeCl has an intrinsic edge state, and a topological phase transition with a sizeable band gap is achieved by applying biaxial strain. Interestingly, the MAE can be switched from the in-plane to the off-plane with a compressive strain of −5%. Microscopically, the origin of MAE is mainly associated with the large spin–orbit coupling (SOC) from the heavy nonmagnetic Te atoms rather than that from the V atoms. Furthermore, the induced DMI (0.09 meV) can occur stabilizing magnetic merons without applying temperatures and magnetic fields. Then, the skyrmions, frustrated antiferromagnetism and vortex are induced after applying a suitable compressive strain. Our study provides compelling evidence that the 1T-VTeCl monolayer with topological properties holds great potential for application in spintronic devices, as well as information storage devices based on different magnetic phases achievable through strain engineering.

---

1 Introduction

Two-dimensional (2D) Janus ferromagnets whose inversion symmetry is broken as different anions occupy the top and bottom layers of transition metal atoms have captured increasing attention in research due to their distinctive properties and promising prospects in spintronics applications.^1–5 Owing to the spin–orbit coupling (SOC) effect and their inherent inversion asymmetry, the Janus magnets give rise to various fascinating qualities, such as the existence of inversion of energy bands, where the energy band gap appears in the protected edge state due to the presence of special topologies or topological invariants at the boundary. Then, the occurrence of the Dzyaloshinskii–Moriya interaction (DMI) induced by SOC and structural inversion asymmetry, which plays a crucial role in stabilizing the topologically protected spin textures that have potential applications in data storage and processing such as skyrmions, merons, bimerons and so on. Unlike skyrmions, an isolated meron is not stable, thus it prefers to exist in the form of groups or bimerons.

Recently, MnBi₂Te₄⁶ has gained significant attention as a topological insulator due to its rich magnetic topological states. It is important to note that the MnBi₂Te₄ monolayer behaves as a trivial insulator, and it is only in the odd layers of MnBi₂Te₄ where the quantum anomalous hall (QAH) effect is observed. In contrast, the VGa₂Te₄⁷ monolayer could turn to a Chern insulator by changing the orientation direction of spins. In addition, the unique quantum anomalous Hall effect observed in the antiferromagnetic MoO monolayer⁸ and hexagonal metal oxide lattices⁹ has significantly enhanced our comprehension of topological materials. Meanwhile, the advent of intrinsic magnets such as VSe₂,¹⁰ CrI₃,¹¹ Cr₂Ge₂Te₆,¹² MnSe₂¹³ and Fe₃GeTe₂¹⁴ opens up appealing avenues for the observation of chiral magnetic textures. The half-metallic character is still maintained and the magnetic anisotropy energy (MAE) is sizably enhanced upon applying a biaxial strain on FeClI and FeBrI monolayers.¹ Furthermore, the Janus MoSSe¹⁵ exhibits Rashba-type spin splitting near the point G owing to its inherent vertical dipole. Transition metal dichalcogenides such as VXY (X = Cl, Br, and I; Y = Se and Te) usually have a large range of applications due to their ferromagnetic semiconductor characteristics with large spin polarizations and high Curie temperatures.^16–18 Then, the 2H Janus VTeCl monolayer has been studied showing that it has a larger Berry curvature and a larger Rashba parameter.¹⁹ Generally, the strain has a great effect on the magnetic exchange interactions and the spin textures in 2D magnets. The ferromagnetic MnSbBiSe₂Te₂ monolayer achieves the coexistent phase of a nontrivial topological phase and skyrmions upon applying a biaxial strain.²⁰ The tensile strained FeGe films host a skyrmion phase above room temperature.²¹ Nevertheless, the physical mechanisms of strain governing the electronic structure and magnetic properties of the Janus magnetic 1T-VXY monolayer, including edge states and strain-tunable spin textures, remain unclear.

Inspired by the above studies, we propose a 2D Janus ferromagnet 1T-VTeCl, which is expected to exhibit a nontrivial topological phase intrinsically and strain-tunable spin textures. In this work, we investigate its band structures, topological characteristics and spin textures. The results show that the intrinsic 1T-VTeCl monolayer has a topological non-trivial edge state, which can be tuned to an ordinary insulator with a sizable bandgap upon applying a tensile strain. The magnetic ground state translates into an antiferromagnetic ordering from the ferromagnetic ordering upon applying a larger compressive strain. In addition, we find that the Heisenberg exchange interactions, DMI and MAE are sensitive to biaxial strain, resulting in various strain-tunable spin textures such as bimerons and skyrmions, frustrated antiferromagnetism and antiferromagnetic vortex. According to our findings, the nontrivial topological properties and various spin textures of 1T-VTeCl provide greater possibilities for its application in spintronic devices.

2 Computational details

The first-principles calculations based on density functional theory (DFT) were performed using the Vienna ab initio simulation package (VASP)²² with the projector augmented wave (PAW) method.²³ A Perdew–Burke–Ernzerhof (PBE) type generalized gradient approximation (GGA)²⁴ is chosen to approximate the exchange–correlation effects. In order to better describe the on-site Coulomb interaction for 3 d electrons of V atoms, the GGA+U method²⁵ is implemented with an effective Hubbard U of 2 eV. The cut off energy for plane-wave expansions was set to 400 eV. The primitive cell is fully relaxed with a high convergence standard of energy and force less than 10⁻⁷ eV and 0.001 eV Å⁻¹, respectively. The whole Brillouin zone was sampled with a Monkhorst Pack k-point grid of 6 × 6 × 1 and SOC was included in non-self-consistent calculations of band structures. To further explore the topological properties, we establish a tight-binding (TB) model by using the maximally localized Wannier functions (MLWFs)²⁶ implemented in the Wannier90 package.²⁷ The surface states are calculated using the Wannier-Tools package²⁷ with iterative Greens function methods.²⁸ The micromagnetic simulations are performed using the Spirit package²⁹ with the Landau–Lifshitz–Gilbert (LLG) equation,^30,31 to explore the spin textures of VTeCl. A supercell containing 14 400 atoms is chosen in the simulations with periodic boundary conditions.

To explore the electronic and magnetic properties of the Janus 1T-VTeCl monolayer, we use the following spin Hamiltonian:

where J₁, J₂ and J₃ are the Heisenberg exchange coefficients between the nearest-neighbor (NN), second NN, and third NN of the magnetic V atom, respectively, and d⃑_ij is the DMI vectors between spin S⃑_i and S⃑_j. K represents the single-ion anisotropy and S_i^z is the z component of S⃑_i. The magnetic moment of the V atom and external magnetic field are represented by μ_V and B, respectively. Here, the sign convention is that J < 0 favors ferromagnetic (FM) coupling while J > 0 represents the antiferromagnetic (AFM) coupling, K > 0 refers to the out-of-plane easy axis while K < 0 refers to the in-of-plane easy axis, and the modulus length of the DMI vector d_ij > 0 (d_ij < 0), which is inherently associated with the chirality of the DMI, represents the clockwise (CW) or anti-clockwise (ACW) spin configurations, respectively. All necessary magnetic parameters were acquired by first principles calculations using the total energy difference approach.^32–34

3 Results and discussion

Fig. 1(a) illustrates the crystal structure of the Janus 1T-VTeCl monolayer, which is derived from the prototype 1T-VSe₂.³⁵ The side and top views of the Janus VTeCl monolayer with the red, gold, and green balls representing V, Te, and Cl, respectively. The V atoms with a point group form a hexagonal close-packed (HCP) lattice and are sandwiched by two nonmagnetic atomic planes consisting of Te and Cl atoms. This special Janus structure makes the VTeCl monolayer possess an intrinsic spatial inversion asymmetry along the z direction. The solid lines in Fig. 1(a) show the unit cell of VTeCl with the optimized lattice parameters of a = b = 3.855 Å. In addition, 1T-VTeCl is the ground state and has the lattice dynamical and thermodynamic stability with or without strain effects (see Fig. S6 and the Fig. S9 of the ESI†).

Fig. 1 (a) Top and side views of a ball-stick structure. The red, golden and green balls represent V, Te, and Cl atoms, respectively. (b) Band structures of the VTeCl monolayer. The inset of (b) demonstrates the energy bands near the Fermi energy level and the Brillouin zone of Janus VTeCl with the reciprocal lattice vectors b₁, b₂ and points of high symmetry. (c) The edge states near the G points of the semi-infinite (100) surface. (d) The band gap of the janus VTeCl monolayer as a function of biaxial strain.

Unlike conventional insulators, topological insulators have the property of having non-trivial topological edge states at their boundaries. In this regard, SOC effects play an important role in the formation of topological insulators. The 1T-VTeCl monolayer is an ordinary insulator if the SOC effect is not considered (see Fig. S1 of the ESI†). However, as depicted in Fig. 1(b) considering the SOC, the two energy-concatenated spin-down valence bands near the Fermi energy level are cleaved at the high symmetry point G, resulting in the overlap of one of the spin-down valence bands and the other spin-up conduction band near the Fermi energy level, thus giving rise to the energy band inversion (see the inset of Fig. 1b) that can be regarded as one of the common features in topological insulators. In addition, another key criterion in a topological insulator is the topological invariant Z₂ or the existence of the topological edge state. The more reliable HSE06 function is employed to calculate the band structure as it tends to provide a more accurate estimation of the band gap for insulators when compared to the PBE function. Furthermore, we carefully consider the influence of different U values on the band gap and the topological state of 1T-VTeCl (see Fig. S7 and S8, ESI†). As shown in Fig. 1(c), we further calculate the edge states of the semi-infinite VTeCl thin film along the projected M′–G–M high-symmetry path, and find that a chiral edge state traverses across the bulk gap and the Fermi level, which connects the valence and conduction bands. Then, the Z₂ topological invariant is also calculated by tracing the evolution of Wannier charge centers (WCCs) to ensure the existence of nontrivial topological properties with Z₂ = 1 (see Fig. S2 of the ESI†). These features, together with the energy band flip, result in topological insulators with stable surface states and topologically protected electron transport properties. These interesting results are consistent with the recent studies.^6,36

As we know, the bandgap of 1T-VTeCl is particularly sensitive to strain, which can be written as: , where μ is the constant of strain, a and a₀ represent the lattice constants with and without strain, respectively. In Fig. 1(d), we observe that strain, particularly tensile strain, has a significant impact on modulating the bandgap of 1T-VTeCl. Within the biaxial strain ranging from −5% to 6%, the gradient blue, middle and gradient red regions represent topological metal (TMeta), topological semiconductor (TSemi) and ordinary semiconductor (OSemi), respectively. The topological nature of 1T-VTeCl is preserved under a small compressive strain (0–2%). As the compressive strain increases, the VTeCl monolayer undergoes a transition from a topological semiconductor to a topological metal. Conversely, as the tensile strain gradually increases, the band gap significantly expands up to 0.27 eV under a strain of 6% (see Fig. S3 of the ESI†). A similar phenomenon of topological phase transition by applying appropriate pressure in MnBi₂Te₄-family materials has also been reported.³⁷

In order to reveal the fundamental physical mechanisms and the behaviors of 1T-VTeCl, we firstly carry out the exploration of the magnetic ground state by comparing the energies of four spin configurations (FM, AFM1, AFM2 and AFM3, as shown in Fig. S4, ESI†) within the strain from −5% to 6%. The energy changes of the four magnetic states relative to ferromagnetism are shown in Fig. 2(a), in which the magnetic ground state is FM ordering when the strain is applied from −3% to 6%. Interestingly, a phase transition from FM to AFM occurs under a strain of −4% with the energy of the AFM2 configuration being the lowest. Microscopically, the spin exchange interaction between atoms/electrons is the core of long-range magnetic order, and the parallel/anti-parallel arrangement between local magnetic moments can make the material exhibit long-range FM or AFM. Based on the Hamiltonian (eqn (1)) of the spin Heisenberg model, we study the Heisenberg exchange interactions, in which a negative (positive) value corresponds to FM (AFM) coupling. As shown in Fig. 2(b), when applying a strain ranging from −5% to 6%, it is worth noting that J₂ remains negative and J₃ remains positive. However, J₁ retains the FM ordering and it decreases from the tensile strain to the compressive strain of −4%, and the values of J₁ change from negative to positive, which is consistent with the results of FM to AFM coupling as mentioned in Fig. 2(a). We further explore the physical origin of the transitions of J₁ using direct exchange and superexchange interaction theory. As depicted in the bottom of Fig. 2(e), J₁ can be expressed as J₁ = J_d + J_s, where J_s represents the sum of super-exchange interactions of the paths V–Cl–V and V–Te–V, and J_d represents the direct exchange interactions of the paths V–V. Based on the Goodenough–Kanamori–Anderson rule,^38–40 the dominant FM coupling mechanism is the e₁(d_x²–d_y²,d_xy)–(p_x/p_y)–e₁(d_x²–d_y²,d_xy) super-exchange FM coupling (J_s < 0) mechanism at nearly 90°,⁴¹ whereas this mechanism also allows electron (e₁–e₁) hopping between two V atoms which leads to the direct exchange interaction J_d that is AFM (J_d > 0) as shown in Fig. 2(f). To find out the relationship between the structural parameters and the exchange coupling, as depicted in Fig. 2(c) and (d), we analyze the variation of the V–V, V–Te, and V–Cl bond lengths, as well as the V–Cl–V and V–Te–V bond angles under the strain from −5% to 6%. When VTeCl is subjected to stretching, the distance of the V–V bond increases, thereby diminishing the AFM direct exchange interaction of the V atom. Simultaneously, the distance of the V–Te/Cl atom remains fairly stable, but the angle of V–Cl–V or V–Te–V gradually expands, leading to an incremental rise of the FM super-exchange interaction. Conversely, when VTeCl undergoes a compressed strain, the V–V bond length decreases, suggesting that the shrunken V–V distance intensifies the AFM direct exchange interaction. Meanwhile, the distance between V and Te/Cl atoms alters minimally, while the angle of V–Cl–V or V–Te–V diminishes progressively, causing a gradual attenuation of FM super-exchange interactions. In the arena of these competing exchange interactions, a phase transition emerges at a −4% strain threshold, shifting from the dominance of FM coupling via super-exchange to AFM coupling governed by direct interactions. A similar phenomenon has been observed in other magnets, such as CrSBr,⁴² CrI₃^43,44 and MnO₂.⁴⁵

Fig. 2 (a) Energies of the four spin configurations. (b) Heisenberg exchange coefficients (J₁, J₂, J₃). (c) Bond lengths of V–V,V–Te,V–Cl as a function of biaxial strain and (d) bond angles of V–Cl–V and V–Te–V. (e) Direct exchange as a hopping between the V–V orbitals and the superexchange interaction characterized hopping between V through the Te atom. (f) The direct interaction between two e₁ (d_x²–d_y², d_xy) orbitals and superexchange interaction in VTeCl via the e₁(d_x²–d_y², d_xy)–(p_x/p_y)–e₁(d_x²–d_y²,d_xy) orbitals.

After studying the topological non-trival edge state and Heisenberg exchange coefficients, here we come to the MAE of the 1T-VTeCl monolayer. The MAE is a crucial parameter for 2D magnets, and determines their low-temperature magnetic orientation in relation to the lattice structure and the thermal stability of spintronic devices. The magnetic shape anisotropy energy (MSA) of 1T-VTeCl is negligible in comparison to its magnetocrystalline anisotropy energy (MCA), thus making MCA the primary focus for MAE in our discussion. According to the Mermin–Wagner theorem,⁴⁶ a non-zero value of MAE is the prerequisite for a finite Curie temperature (T_c) in 2D magnets. The MAE is defined as MAE = E_z − E_x, where E_z (E_x) is the total energy when the magnetic moments are along the z (x) direction. The angular dependence of the MAE is illustrated in Fig. 3(a), which clearly shows that the MAE is isotropic in the XY plane, while its magnitude is strongly influenced by the magnetization direction in the XZ plane. Specifically, 1T-VTeCl exhibits an easy plane magnetization with no significant energy barrier for spin rotation in the XY plane. Consequently, the calculated MAE of the intrinsic 1T-VTeCl is −1.01 meV per unit cell (u.c.), indicating that the intrinsic 1T-VTeCl possesses an in-plane easy magnetic direction. As shown in Fig. 3(b), the MAE changes parabolically and reaches an in-plane maximum (−1.10 meV) at a strain of −3%. Moreover, the switching of MAE from in-plane to out-of-plane is observed when the compressive strain is −5%, suggesting that the easy axis is flipped vertically and the magnetization direction can be easily modulated by biaxial stain.

Fig. 3 (a) Angular dependence of magnetic anisotropy energy (MAE) under 0% strain with the direction of magnetization lying on the XY plane and XZ plane. (b) Tendency of MAE of the VTeCl monolayer under different biaxial strains. (c) Element-resolved MAEs of VTeCl as a function of biaxial strain. Orbital-resolved MAEs with a strain of (d) 0% and (e) −5%. (f) DMI components as a function of strain for the VTeCl monolayer.

To identify the microscopic origin of the MAE change under different strains, we calculate the SOC energy difference (ΔE_soc) associated with different atoms in 1T-VTeCl. As depicted in Fig. 3(c), the results reveal that the primary contribution to the MAE arises from the heavy Te atoms, which is similar to that reported in the previous works.^34,47 Furthermore, we further analyze the orbital-resolved ΔE_soc of the p orbitals of Te atoms to identify the main orbital contribution to the MAE. As we can see in Fig. 3(d) with a strain of 0%, both the hybridization of (p_x, p_y) exhibit negative (−1.16 meV) contributions to the MAE. However, as shown in Fig. 3(e) with a compressive strain of −5%, the hybridization of (p_y, p_x) gives rise to a substantial postive value (0.06 meV), which suggests that the in-plane magnetic anisotropy (IMA) of the VTeCl monolayer decreases, with more preference to out-plane magnetic anisotropy (OMA) under a compressive strain.

Not only the Heisenberg exchange interaction and the MAE affect the magnetic characteristics of 2D ferromagnets, but also the Dzyaloshinskii–Moriya interaction (DMI) plays a vital role in the formation and stability of different spin textures. Therefore, considering the inherent spatial inversion asymmetry of 1T-VTeCl, we use the chirality-dependent total energy difference method^32,48 to calculate the DMI as a function of biaxial strain. Both the in-plane and out-of-plane components of DMI vector d⃑_ij can be obtained using d = (E_CW − E_ACW)/12.⁴⁷ Generally, the strong DMI is mainly associated with the large ΔE_SOC located on the heavy nonmagnetic halogen Te atom, which is similar to what occurs in Co/Pt²⁷ and MnXY³⁴ systems. Owing to the strong role played by SOC of Te in the VTeCl monolayer, when a polarized electron transfers between V atoms via the intermediate Te atoms, the spin direction of the electron gets perturbed by the spin–orbital scattering, consequently causing a tilt in the local spins of adjacent V atoms, which can be explained using the Fert-Levy model.^32,49 As shown in Fig. 3(f), a small D_‖ (0.07 meV) is found in the unstrained VTeCl monolayer. It is unexpected that when applying a large compressive strain, D_‖ can be significantly enhanced up to 0.81 meV, which is more than ten times larger than that of unstrained VTeCl. However, when we apply a tensile strain, D_‖ declines first and then increases and undergoes chirality transition from CW to ACW under a strain of 3%.

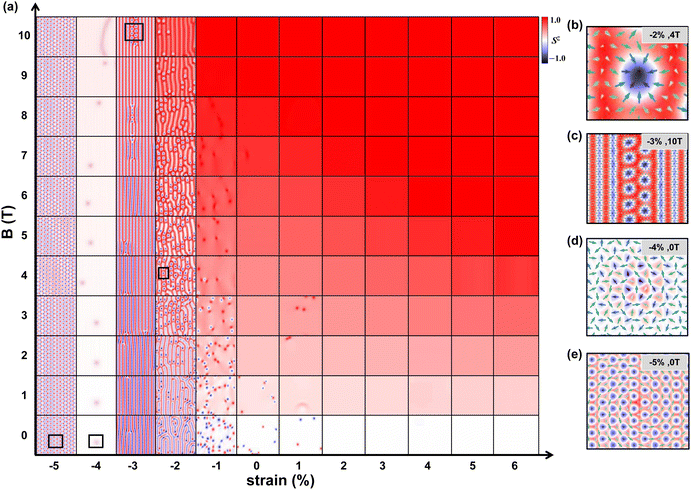
Next, using the magnetic interaction parameters obtained from first-principles calculations, we adopt the LLG equation to conduct micromagnetic simulations to explore the spin textures in our VTeCl monolayer. As illustrated in Fig. 4(a), due to the existence of DMI and easy-plane anisotropy, a lot of spontaneous merons appear without any external magnetic field at a temperature of 0 K, such as the vortex and antivortex states that are shown in the red line boxes 1 and 2, and the multiple meron state is shown in box 3. Nevertheless, it is essential to acknowledge that the magnetic field has been empirically demonstrated to exert a substantial influence on the chiral spin textures,⁵⁰ and the chiral merons may undergo ultimate annihilation in the presence of a strong magnetic field.⁴⁷ Then, with the introduction of a gradually increasing magnetic field, as depicted in Fig. 4(b), i.e. when an external magnetic field of 0.25 Tesla (T) is applied along the z direction, the magnetic moments of magnetic V atoms are redirected along the magnetic field direction, leading to a decrease in the count of isolated merons. As shown in the inset of Fig. 4(b), bimerons consist of two merons with opposite polarities, which make them more stable than the isolated merons.⁵¹ When an external magnetic field of 0.75 T is applied as shown in Fig. 4(c), the bimeron states disappear, giving way to the emergence of vortex and antivortex configurations, where the topological charge of the vortex differs by one minus sign from that of the vortex in box 2 of Fig. 4(a). Finally, as we further increase the magnetic field to 1.75 T, as depicted in Fig. 4(d), a chiral transition of the vortex takes place, resulting in the formation of skyrmion states, which are composed of a meron pair with the same charge but opposite vorticity. It is of significant note that magnetic fields have been shown to have a profound impact on the chiral spin textures in 2D magnets.^34,52,53

Fig. 4 (a) Spin texture of the intrinsic VTeCl monolayer without an external magnetic field at 0 K. Spin textures of the VTeCl monolayer with the magnetic fields along the z-direction being (b) 0.25 T, (c) 0.75 T, and (d) 1.75 T at 0 K.

In the subsequent investigation, we systematically examine the impact of strain on the spin textures of VTeCl. As depicted in Fig. 5(a), in the absence of applied strain or magnetic field, the spin textures of VTeCl exhibit meron states, as shown in Fig. 4(a). Upon the application of tensile strain, the DMI gradually diminishes, leading to a corresponding reduction in the simulated meron count. A reversal in the DMI chirality occurs under the continued growth of tensile strain, and the DMI gradually increases as mentioned above. Consequently, the simulation results for spin textures allude to an in-plane ferromagnetic state. This behavior arises from the gradual expansion of the lattice constant of VTeCl with increasing tensile strain, causing the magnitude of J₁ to surpass the growth rate of DMI, ultimately driving D_‖/J₁ toward zero and demonstrating ferromagnetic ordering. Furthermore, introducing a magnetic field along the z-axis induces a transition in the magnetic anisotropy energy (MAE) from in-plane to out-of-plane, transforming the material into an out-of-plane ferromagnet. Even under a slight compressive strain, the magnetic ground state remains ferromagnetic. However, with an augmented compressive strain, corresponding to the enhanced DMI, the emergence of domain walls becomes apparent. The application of a magnetic field induces the formation of skyrmions and a mixed state (comprising domain walls and skyrmions), as illustrated in Fig. 5(b) and (c). The typical range for the formation of skyrmions is a DMI/exchange coupling ratio of |D_‖/J| between 0.1 and 0.2. However, it should be noted that K can also significantly affect the formation and characters of the skyrmion phase. For a more precise theoretical design of the skyrmion phase, there exists a more accurate descriptor based on the three magnetic parameters of J, D and K.^54,55 Under −4% strain as shown in Fig. 5(d), the spin texture exhibits an in-plane easy axis-frustrated antiferromagnetic state.⁵⁶ Importantly, this characteristic persists when a magnetic field is applied, underscoring the robust resistance to frustrated interactions and resilience against external interference. Finally, under a larger compressive strain of −5%, as depicted in Fig. 5(e), a distinctive curly-type antiferromagnetic vortex⁵⁷ is observed. Thus, diverse spin textures are achieved through modulation via biaxial strain.

Fig. 5 (a) Evolutions of spin textures of the Janus VTeCl monolayer with strain and an external magnetic field. The schematic diagram of the (b) skyrmions, (c) domain walls and skyrmions (DW+SK), (d) in-plane easy axis frustrated antiferromagnetism and (e) curly-type antiferromagnetic vortex.

4 Conclusions

In summary, based on first-principles calculations and micro-magnetic simulations, we investigated a 2D Janus 1T-VTeCl monolayer and systematically investigated its topological properties, electronic structures, magnetism and spin textures. We found that the intrinsic 1T-VTeCl monolayer is a topological insulator with Z₂ = 1, and it undergoes a topological phase transition upon applying a biaxial strain. In particular, the magnetic ground state of VTeCl changes from FM to AFM and the MAE is switched between the in-plane and the off-plane under a compressive strain. Microscopically, the MAE is mainly associated with the strong SOC induced by Te atoms. When 3% tensile strain is applied, a chiral inversion of DMI occurs from CW to ACW. In addition, using micro-magnetic simulations, it was found that spontaneous magnetic merons accompanied by an in-plane vortex appear in the absence of an external magnetic field. Then, the chiral merons exist either as individual entities or in the form of groups or pairs (bimerons), and exhibit stability under a small magnetic field that ranges from 0 T to 1.75 T. Also, upon applying a strain and magnetic field, we obtain abundent spin textures for skyrmions, frustrated antiferromagnetism, and antiferromagnetic vortices at 0 K. Our work presents some interesting results for 2D Janus topological insulators, and it may provide useful guidelines for designing spintronic devices with intrinsic edge states and strain-tunable spin textures.

Author contributions

Zheng Chen: data curation (lead); formal analysis (lead); investigation (lead); methodology (equal); and writing – original draft (lead). Hongliang Hu: investigation (equal); methodology (equal); and writing – review and editing (equal). Dushuo Feng: investigation (equal); methodology (equal); and writing – review and editing (equal). Zhihao Guan: investigation (equal); methodology (equal); and writing – review and editing (equal). Tingting Zhong: investigation (equal); methodology (equal); and writing – review and editing (equal). Xiaoping Wu: investigation (equal); methodology (equal); and writing – review and editing (equal). Changsheng Song: conceptualization (lead); formal analysis (lead); funding acquisition (lead); project administration (lead); resources (lead); supervision (lead); writing – original draft (supporting); and writing – review and editing (lead).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 11804301), the Natural Science Foundation of Zhejiang Province (Grant No. LY21A040008), and the Fundamental Research Funds of Zhejiang Sci-Tech University (Grant No. 2021Q043-Y, LGYJY2021015).

References

1. R. Li, J. Jiang, X. Shi, W. Mi and H. Bai, ACS Appl. Mater. Interfaces, 2021, 13, 38897–38905.
2. J. Sampaio, V. Cros, S. Rohart, A. Thiaville and A. Fert, Nat. Nanotechnol., 2013, 8, 839–844.
3. S.-W. Ng, N. Noor and Z. Zheng, NPG Asia Mater., 2018, 10, 217–237.
4. H. Sun, S.-S. Li, W.-X. Ji and C.-W. Zhang, Phys. Rev. B, 2022, 105, 195112.
5. K. Jia, X.-J. Dong, S.-S. Li, W.-X. Ji and C.-W. Zhang, Nanoscale, 2023, 15, 8395–8405.
6. J. Li, Y. Li, S. Du, Z. Wang, B.-L. Gu, S.-C. Zhang, K. He, W. Duan and Y. Xu, Sci. Adv., 2019, 5, eaaw5685.
7. B.-C. Gong, Y. Gao, X.-L. Qiu, N.-N. Zhao, K. Liu and Z.-Y. Lu, Phys. Rev. B, 2022, 106, 235153.
8. B. Wu, Y.-l Song, W.-x Ji, P.-j Wang, S.-f Zhang and C.-w Zhang, Phys. Rev. B, 2023, 107, 214419.
9. S.-j Zhang, C.-w Zhang, S.-f Zhang, W.-x Ji, P. Li, P.-j Wang, S.-s Li and S.-s Yan, Phys. Rev. B, 2017, 96, 205433.
10. M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M. H. Phan and M. Batzill, Nat. Nanotechnol., 2018, 13, 289–293.
11. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden and W. Yao, Nature, 2017, 546, 270–273.
12. C. Song, W. Xiao, L. Li, Y. Lu, P. Jiang, C. Li, A. Chen and Z. Zhong, Phys. Rev. B, 2019, 99, 214435.
13. D. J. OHara, T. Zhu, A. H. Trout, A. S. Ahmed, Y. K. Luo, C. H. Lee, M. R. Brenner, S. Rajan, J. A. Gupta, D. W. McComb and R. K. Kawakami, Nano Lett., 2018, 18, 3125–3131.
14. Y. Deng, Y. Yu, Y. Song, J. Zhang, N. Z. Wang, Z. Sun, Y. Yi, Y. Z. Wu, S. Wu, J. Zhu, J. Wang, X. H. Chen and Y. Zhang, Nature, 2018, 563, 94–99.
15. A.-Y. Lu, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M.-Y. Chou, X. Zhang and L.-J. Li, Nat. Nanotechnol., 2017, 12, 744–749.
16. Z. Jiang, P. Wang, J. Xing, X. Jiang and J. Zhao, ACS Appl. Mater. Interfaces, 2018, 10, 39032–39039.
17. C. Wang, X. Zhou, L. Zhou, N.-H. Tong, Z.-Y. Lu and W. Ji, Sci. Bull., 2019, 64, 293–300.
18. R. Han, Z. Jiang and Y. Yan, J. Phys. Chem. C, 2020, 124, 7956–7964.
19. W. Liu, X. Li, C. Zhang and S. Yan, J. Semicond., 2022, 43, 042501.
20. Z. Wu, Y. Xue, Z. Shen and C. Song, Phys. Chem. Chem. Phys., 2023, 25, 96–105.
21. S. Budhathoki, A. Sapkota, K. M. Law, S. Ranjit, B. Nepal, B. D. Hoskins, A. S. Thind, A. Y. Borisevich, M. E. Jamer, T. J. Anderson, A. D. Koehler, K. D. Hobart, G. M. Stephen, D. Heiman, T. Mewes, R. Mishra, J. C. Gallagher and A. J. Hauser, Phys. Rev. B, 2020, 101, 220405.
22. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
23. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
24. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
25. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
26. N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Rev. Mod. Phys., 2012, 84, 1419–1475.
27. A. A. Mostofi, J. R. Yates, G. Pizzi, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2014, 185, 2309–2310.
28. Q. Wu, S. Zhang, H.-F. Song, M. Troyer and A. A. Soluyanov, Comput. Phys. Commun., 2018, 224, 405–416.
29. G. P. Müller, M. Hoffmann, C. Dißelkamp, D. Schürhoff, S. Mavros, M. Sallermann, N. S. Kiselev, H. Jónsson and S. Blügel, Phys. Rev. B, 2019, 99, 224414.
30. L. D. Landau and E. Lifshitz, Phys. Z. Sowjet., 1935, 8, 153.
31. T. L. Gilbert, IEEE Trans. Magn., 2004, 40, 3443–3449.
32. H. Yang, A. Thiaville, S. Rohart, A. Fert and M. Chshiev, Phys. Rev. Lett., 2015, 115, 267210.
33. H. Yang, G. Chen, A. A. C. Cotta, A. T. NDiaye, S. A. Nikolaev, E. A. Soares, W. A. A. Macedo, K. Liu, A. K. Schmid, A. Fert and M. Chshiev, Nat. Mater., 2018, 17, 605–609.
34. J. Liang, W. Wang, H. Du, A. Hallal, K. Garcia, M. Chshiev, A. Fert and H. Yang, Phys. Rev. B, 2020, 101, 184401.
35. A. M. Woolley and G. Wexler, J. Phys. C: Solid State Phys., 1977, 10, 2601.
36. Z. Li, J. Li, K. He, X. Wan, W. Duan and Y. Xu, Phys. Rev. B, 2020, 102, 081107.
37. P. Li, J. Yu, Y. Wang and W. Luo, Phys. Rev. B, 2021, 103, 155118.
38. J. B. Goodenough, Phys. Rev., 1955, 100, 564–573.
39. J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98.
40. P. W. Anderson, Phys. Rev., 1959, 115, 2–13.
41. M. A. Subramanian, A. P. Ramirez and W. J. Marshall, Phys. Rev. Lett., 1999, 82, 1558–1561.
42. K. Yang, G. Wang, L. Liu, D. Lu and H. Wu, Phys. Rev. B, 2021, 104, 144416.
43. B. Yang, X. Zhang, H. Yang, X. Han and Y. Yan, Appl. Phys. Lett., 2019, 114, 192405.
44. L. Webster and J.-A. Yan, Phys. Rev. B, 2018, 98, 144411.
45. M. Kan, J. Zhou, Q. Sun, Y. Kawazoe and P. Jena, J. Phys. Chem. Lett., 2013, 4, 3382–3386.
46. N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133–1136.
47. Q. Cui, J. Liang, Z. Shao, P. Cui and H. Yang, Phys. Rev. B, 2020, 102, 094425.
48. H. Yang, G. Chen, A. A. C. Cotta, A. T. NDiaye, S. A. Nikolaev, E. A. Soares, W. A. A. Macedo, K. Liu, A. K. Schmid, A. Fert and M. Chshiev, Nat. Mater., 2018, 17, 605–609.
49. A. Fert and P. M. Levy, Phys. Rev. Lett., 1980, 44, 1538–1541.
50. S. Seki, X. Z. Yu, S. Ishiwata and Y. Tokura, Science, 2012, 336, 198–201.
51. Z. Shen, Y. Xue, Z. Wu and C. Song, Phys. Chem. Chem. Phys., 2022, 24, 27612–27618.
52. S. Hayami, Phys. Rev. B, 2021, 103, 224418.
53. W. Du, K. Dou, Z. He, Y. Dai, B. Huang and Y. Ma, Nano Lett., 2022, 22, 3440–3446.
54. W. Du, K. Dou, Z. He, Y. Dai, B. Huang and Y. Ma, Nano Lett., 2022, 22, 3440–3446.
55. D. Feng, Z. Guan, X. Wu, Y. Wu and C. Song, arXiv, 2023, preprint, arXiv:2309.15679 DOI:10.48550/2309.15679.
56. C. L. Gao, W. Wulfhekel and J. Kirschner, Phys. Rev. Lett., 2008, 101, 267205.
57. R. Lopes, R. Silva, R. Silva, W. Moura-Melo and A. Pereira, Phys. Lett. A, 2020, 384, 126376.

---

Footnote

† Electronic supplementary information (ESI) available: Band structures of the intrinsic 1T-VTeCl monolayer without SOC, band structures of the 1T-VTeCl monolayer with different biaxial strains calculated using PBE+U, Wannier interpolated band structures of the intrinsic 1T-VTeCl monolayer, and the evolution of WCC along Ky in the intrinsic 1T-VTeCl monolayer. See DOI: https://doi.org/10.1039/d3cp05744e

---