Chemisorption of silicon tetrachloride on silicon nitride: a density functional theory study

Abstract

We studied the chemisorption of silicon tetrachloride (SiCl₄) on the NH₂/NH-terminated silicon nitride slab model using density functional theory (DFT) for atomic layer deposition (ALD) of silicon nitride. Initially, two reaction pathways were compared, forming HCl or NH₃⁺Cl⁻ as a byproduct. The NH₃⁺Cl⁻ complex formation was more exothermic than the HCl formation, with an activation energy of 0.26 eV. The –NH₂* reaction sites are restored by desorption of HCl from the NH₃⁺Cl⁻ complexes at elevated temperatures of 205 °C or higher. Next, three sequential ligand exchange reactions forming Si–N bonds were modeled and simulated. The reaction energies became progressively less exothermic as the reaction progressed, from −1.31 eV to −0.30 eV to 0.98 eV, due to the stretching of Si–N bonds and the distortion of the N–Si–N bond angles. Also, the activation energies for the second and third reactions were 2.17 eV and 1.55 eV, respectively, significantly higher than the 0.26 eV of the first reaction, mainly due to the additional dissociation of the N–H bond. The third Si–N bond formation is unfavorable due to the endothermic reaction and higher activation energy. Therefore, the chemisorbed species would be –SiCl₂* when the surface is exposed to SiCl₄.

---

Introduction

As the integration density of semiconductor devices continues to increase, advanced thin film deposition techniques such as atomic layer deposition (ALD) are being adopted in semiconductor manufacturing. ALD is an atomic layer-by-layer growth technique in which the substrate surface is alternately exposed to a precursor and a co-reactant. The self-limiting nature of ALD provides precise process control over material thickness, composition, and conformality in high aspect ratio (HAR) patterns. ALD of silicon nitride is used for various applications such as gate spacers¹ and diffusion barriers² in complementary metal-oxide-semiconductor (CMOS) devices and charge trapping³ and sacrificial layers³ in three-dimensional vertical NAND flash memory devices.

The ALD process of silicon nitride can be achieved by thermal ALD or plasma-enhanced ALD (PEALD). Although various types of silicon precursors, such as chlorosilanes,^4–6 aminosilanes,^7,8 silylamines,^9,10 cyclosilazanes,^11,12 and silanes,^4,13 have been investigated in PEALD, only chlorosilane-type silicon precursors have been studied in thermal ALD processes, such as silicon tetrachloride (SiCl₄),^14,15 dichlorosilane (DCS, SiH₂Cl₂),¹⁵ hexachlorodisilane (HCDS, Si₂Cl₆),¹⁶ and octachlorotrisilane (OCTS, Si₃Cl₈).¹⁷ Ammonia (NH₃)^14,15,17,18 or hydrazine (N₂H₄)^16,19 was used as the coreactant for thermal ALD.

The reaction mechanism of thermal silicon nitride ALD using SiCl₄ was investigated by in situ FTIR spectroscopy.¹⁴ SiCl₄ reacts with the –NH_x surface site to form –NSiCl_x with an HCl byproduct, and then NH₃ reacts with –NSiCl_x to restore –NH_x, resulting in the growth of silicon nitride film. Density functional theory (DFT) calculations were used to study the reaction mechanism of the ALD process of silicon nitride.^20–26 The surface reaction of bis(diethylamino)silane or bis(tert-butylamino)silane was studied on the β-Si₃N₄ (0001) slab model.²⁴ The surface reaction of SiCl₄, SiH₂Cl₂, Si₂Cl₆, or Si₃Cl₈ to form a Si–N bond was also studied on the NH/NH₂-terminated β-Si₃N₄ (0001) slab model.²⁵ Different silicon tetrahalides were compared by simulating the sequential ligand exchange reactions forming multiple Si–N bonds using the NH₂-terminated Si cluster model.²⁷

The above DFT studies assumed the formation of an HCl molecule as a reaction byproduct. However, Hartmann et al.²⁶ studied the surface reaction of SiH₂Cl₂ and suggested that the H from the –NH₂ could migrate to another –NH₂ site to form an NH₃⁺Cl⁻ complex instead of directly forming a gaseous HCl byproduct, resulting in a lower system energy. The formation of the NH₃⁺Cl⁻ complex has also been demonstrated by in situ FTIR and XPS analyses.²⁸ To date, no comparative study has been performed between the direct formation of an HCl molecule and the formation of an NH₃⁺Cl⁻ complex on the surface.

In this study, the chemisorption mechanism of a SiCl₄ molecule on a silicon nitride surface terminated with NH₂ and NH groups was investigated. SiCl₄ was chosen as the precursor to be investigated because it is the most basic chlorosilane molecule. First, the formation of the NH₃⁺Cl⁻ complex was compared to the formation of HCl. The desorption of HCl from the NH₃⁺Cl⁻ complex, resulting in the restoration of the original site, where the asterisk (*) indicates the surface species, was also studied. Finally, the sequential ligand exchange reactions forming Si–N bonds were modeled and simulated. The reaction and activation energies were obtained to suggest the end product of the chemisorption of SiCl₄.

Computational methods

The DFT calculations were performed with the DMol³ code in the Materials Studio 7.0 package^29,30 using the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional.³¹ The all-electron core treatment and the double numerical polarization (DNP) 4.4 basis set²⁹ with a global cutoff scheme at 4.6 Å were used for all calculations. The Brillouin zone integration was sampled within a 2 × 2 × 1 Monkhorst–Pack k-point mesh.³² Dispersion force corrections based on the Grimme's method (DFT-D2)³³ were considered to account for long-range van der Waals (vdW) interactions. The convergence tolerance, self-consistent field (SCF), and thermal smearing parameters were the same as in previous reports.^25,34 Transition state (TS) was located using the complete linear-quadratic synchronous transit (LST-QST) or QST method with root mean square (RMS) force gradient criteria of 0.002 Ha/Å.³⁵ The TS needed to meet the additional criterion of having only one imaginary vibration mode, which was determined by frequency calculation. Further details of the TS search have been reported elsewhere.³⁴

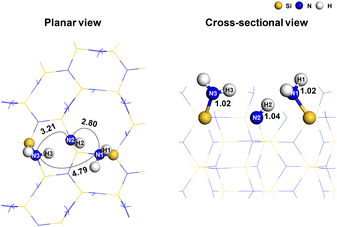
For this study, we chose the β-Si₃N₄ (001) surface that was fully passivated with and 12 NH*. This surface was also used in the previous reaction mechanism studies.^25,36,37 The surface had cell parameters of a = b = 15.320 Å. The slab model consisted of a four-layer (2 × 2) supercell with 184 atoms (48 silicon, 76 nitrogen, and 60 hydrogen atoms). The surface contained evenly distributed and –NH* sites, with a density of 5.89 per nm² each. The surface construction is described in detail in a previous work.³⁶Fig. 1 shows the atomistic structure of the surface before the surface reaction of SiCl₄. The N–H bonds that undergo subsequent ligand exchange reactions are labeled N1–H1, N2–H2, and N3–H3, respectively. The sites are more sterically exposed to the precursor molecules than the –NH* sites, so we assumed that the first reaction would occur at (N1–H1). We also assumed that the second and third reactions would occur at neighboring –NH* (N2–H2) and (N3–H3) sites adjacent to N1–H1. The distances between the sites were 2.80 Å, 3.21 Å and 4.79 Å. The N–H bond length was 1.02 Å for and 1.04 Å for –NH*. The lower half of the slab model was constrained, while the upper half was relaxed. A 20 Å-thick layer of vacuum was inserted between the adjacent slabs to prevent interactions.

Fig. 1 The atomistic structure of the and –NH* terminated silicon nitride surface with the reaction sites. In the planar view, the dotted lines represent the interatomic distances with corresponding values in Å. In the cross-sectional view, the N–H bond lengths are shown in Å.

Several states were considered for the interaction of the precursor molecules on the surface, namely the unbound reactant state (UR), the reactant state (R_n), and the product state (P_n). UR is the state in which the precursor does not interact with the surface, assuming it is at an infinite distance from the surface. R1 is the state where the precursor physisorbs on the surface. P1, P2, and P3 are the product states with first, second, and third Si–N bonds, respectively. R2 and R3 are the reactant states after removing a byproduct molecule to infinity from P1 and P2, respectively. TS1, TS2, and TS3 are the transition states between the reactant and product states. All the structures used in this work can be found as ESI† in XYZ file format. The adsorption energy (E_ads), reaction energy (ΔE_n), activation energy (E_An), and desorption energy (E_des,n) of the nth reaction (n = 1–3) are defined as follows:

E_ads = E_R − (E_surface + E_precursor) (1)

ΔE_n = E_Pn − E_Rn (2)

E_An = E_TSn − E_Rn (3)

E_des,n = (E_{Reacted surface} + E_byproduct) − E_Pn (4)

where E_Rn and E_Pn are the total system energies of the reactant and product states. E_TSn is the total energy of the transition state. E_surface, E_precursor, and E_byproduct are the energies of the surface only, a precursor molecule and a byproduct molecule, respectively. E_{Reacted surface} is the energy of the surfaces after the desorption of the byproduct molecules.

To study the desorption of the byproduct as a function of temperature, the free energies were determined by DFT using the following equation:

ΔG = ΔG° + RT ln p_byproduct (5)

where ΔG° is the standard free energy at 1 atm, R is the ideal gas constant (8.63 × 10⁻⁵ eV mol⁻¹ K⁻¹), T is the temperature in K, and p_byproduct is the partial pressure of the byproduct in atm. The partial pressure was assumed to be 1 Torr. ΔG° was estimated using the following equation:

ΔG° = (E_des,n + ΔZPE + ΔE_v(T) + ΔE_r(T) + ΔE_t(T) + RT) − TΔS(T) (6)

where ΔZPE, ΔE_v(T), ΔE_r(T), ΔE_t(T), and ΔS(T), represent the difference between R_n+1 and P_n states at temperature T (in K) in zero point energy, vibrational energy, rotational energy, translational energy, and entropy, respectively.

Results and discussion

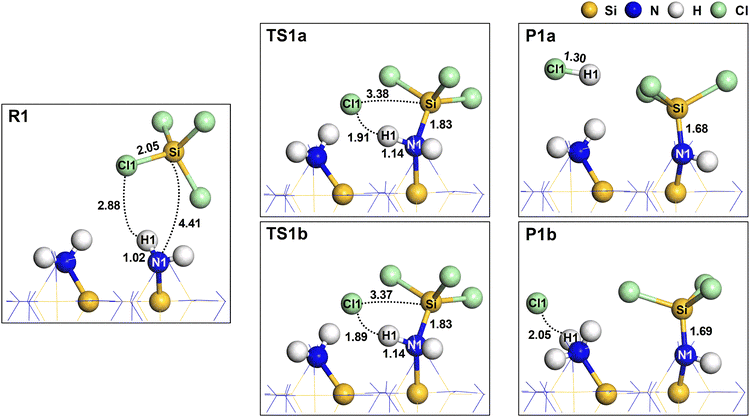
During the initial reaction of the silicon precursor with the β-Si₃N₄ (001) surface, the surface site is not only more sterically exposed but also more reactive than NH*, as discussed in the previous study.²⁵ Based on the electronegativity of Si (1.90) and Cl (3.16) atoms in SiCl₄ and N (3.04) and H (2.20) atoms of the surface site,³⁸ Si and Cl atoms are expected to interact with N and H atoms, respectively. Therefore, the two types of pathways, HCl byproduct formation (denoted as P1a) and NH₃⁺Cl⁻ complex formation (denoted as P1b), were modeled and simulated from the physisorption state (denoted as R1) as described in the following reaction equations:

Fig. 2 shows the reaction schemes from R1 to P1a or P1b, along with the corresponding reaction and activation energy values. Both pathways were exothermic. However, the formation of P1a was less exothermic (−0.73 eV) than that of P1b (−1.31 eV). The reaction energy of P1a was mainly due to the formation of Si–N (4.82 eV) and H–Cl (4.53 eV) bonds despite the dissociation of N–H (4.57 eV) and Si–Cl (4.57 eV) bonds. The bond dissociation energies (BDE) were estimated using gas-phase models, as summarized in Fig. S1 (ESI†). The reaction energy of P1b could not be explained solely by the formation of Si–N and N–H (3.40 eV) bonds and the dissociation of N–H and Si–Cl bonds alone. The ionic interaction between NH₃⁺ and Cl⁻ contributes to the reaction energy of P1b, making it more exothermic than P1a. Both P1a and P1b have similar activation energy values of 0.27 eV and 0.26 eV, respectively. The activation energy of 0.26 eV for P1b is similar to that of 0.3 eV reported for NH₃⁺Cl⁻ complex formation by DCS.²⁶P1b was found to be more favorable than P1a due to its greater exothemicity when SiCl₄ initially interacted with the silicon nitride surface.

Fig. 2 The reactions scheme from the reactant state R1 to the product states P1a and P1b. All energies are in eV.

Fig. 3 shows the changes in atomistic geometry during the initial reaction of SiCl₄. The other site shown in this figure is one of the neighboring sites to which the H atom will migrate in P1b, as shown in Fig. S2 (ESI†). In TS1a and TS1b, the Cl1 atom dissociated from SiCl₄, and the Si atom of SiCl₄ formed an elongated bond to the N1 atom with a distance of 1.83 Å. Additionally, the N1–H1 bond remained unbroken, resulting in a lower activation energy. The N1–H1 bond was elongated from 1.02 Å to 1.14 Å due to the overcoordination of the N1 atom. The strong interaction between the C11 and the surface H atoms also lowered the system energy. A similar transition state structure has also been reported.²⁷ In a previous work,²⁵ we obtained a transition state significantly different from TS1b. The Si–N1 bond was not formed, and H1 was dissociated from N1 to form the H1–Cl1 bond, resulting in a high activation energy of 4.49 eV.

Fig. 3 The atomistic structures for the reactant (R1), transition (TS1a and TS1b), and product (P1a and P1b) states. The dotted lines represent the interatomic distances with corresponding values in Å. The bond lengths are also shown in Å.

The Mulliken atomic charges³⁹ were calculated and are presented in Table 1. In R1, the Si and Cl atoms in SiCl₄ have charges of 1.257 e and −0.349 e, respectively. For the surface site, the N1 and H1 atoms have charges of −0.864 e and 0.232 e, respectively. In TS1a and TS1b, the atomic charge of Si and N1 atoms increased due to the formation of an elongated Si–N1 bond. In P1a and P1b, the stable Si–N1 bond formation slightly increased the atomic charges of Si and N1 atoms. The charges of H1 and Cl1 atoms in HCl were similar in P1a with values of 0.285 e and −0.290 e, respectively. However, in P1b, the charge of the Cl1 atom significantly increased to −0.710 e, indicating a strong ionic interaction between Cl and .

Table 1 The Mulliken atomic charges for the reactant (R1), transition (TS1a and TS1b), and product (P1a and P1b) states

Atom	Mulliken atomic charge (e)
	R1	TS1a	TS1b	P1a	P1b
Si	1.257	1.321	1.321	1.332	1.300
Cl	−0.349	−0.647	−0.647	−0.290	−0.710
N1	−0.864	−1.009	−1.009	−1.117	−1.134
H1	0.232	0.332	0.332	0.285	0.308

---

When HCl molecules were desorbed from the NH₃⁺Cl⁻ surface complex in P1b, the −NH₂ surface sites were restored, and the resulting surface became R2, the reactant state for the subsequent reaction. The energy required for the desorption of HCl molecules was calculated from eqn (4), and 1.29 eV was obtained. The free energy change due to the desorption of HCl molecules with temperature was also calculated from eqn (5), as shown in Fig. 4. A minimum temperature of 205 °C is required for HCl molecules to spontaneously desorb from the surface. Therefore, elevated temperature is a prerequisite for the recovery of the −NH₂* surface sites.

Fig. 4 The free energy change for the desorption of an HCl molecule from the NH₃⁺Cl⁻ surface site in P1b as a function of temperature.

Fig. 5 shows the comprehensive energy diagram for the surface reaction of SiCl₄ on the silicon nitride surface. Only the pathway associated with NH₃⁺Cl⁻ complex formation was considered. For the first ligand exchange reaction, only the P1b pathway in Fig. 2 is shown as P1 in Fig. 5. For the second and third reactions to form P2 and P3, the reactions of 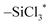with the N2–H2 site and with the N3–H3 site were assumed, as described in the following reaction equations:

Fig. 5 Energy diagram for the chemisorption of SiCl₄ on silicon nitride.

The reaction in eqn (9) was exothermic with an activation energy of 2.17 eV, while the reaction in eqn (10) was endothermic with an activation energy of 1.55 eV. The endothermic reaction and the higher activation energy indicate that the formation of P3 is not favorable. Therefore, the chemisorbed species would be when the surface is exposed to SiCl₄.

Fig. 6 shows the atomistic structures of the R2, TS2, and P2 states. The reaction energy was −0.30 eV, which is significantly less exothermic than P1 because the subsurface bonds were elongated in P2, as shown in Fig. S3 (ESI†). In addition, the reaction in eqn (9) had a higher activation energy of 2.17 eV than 0.26 eV in eqn (8). In TS2, the Si–Cl2 and N2–H2 bonds were dissociated, and an elongated Si–N2 bond with a length of 1.81 Å was formed. The higher activation energy to form P2 than P1 was mainly due to the additional dissociation of the N2–H2 bond. The Mulliken atomic charges for R2, TS2 and P2 states are presented in Table S1 (ESI†). The trend remains consistent with the change from R1 to P1b.

Fig. 6 The atomistic structures for the reactant (R2), transition (TS2), and product (P2) states of the second Si–N bond formation reaction. The dotted lines represent the interatomic distances with corresponding values displayed in Å. The bond lengths are also shown in Å.

Similar to the desorption of HCl from P1, the desorption of the HCl molecule from P2 was simulated. A desorption energy of 1.35 eV was obtained, similar to 1.29 eV for the P1 case. The free energy change due to the desorption of HCl was estimated as a function of temperature, as shown in Fig. 7. A minimum of 276 °C would be required to restore the −NH₂ site to form R3, the reactant state for the subsequent reaction.

Fig. 7 The free energy change for the desorption of an HCl molecule from the NH₃⁺Cl⁻ surface site in P2 as a function of the temperature.

Fig. 8 shows the atomistic structures of R3, TS3, and P3. The reaction was endothermic with a reaction energy of 0.98 eV, in contrast to the exothermicity of the previous reactions leading to P1 and P2. The endothermic nature of the reaction leading to P3 was mainly caused by the stretching of the Si–N1 and Si–N3 bonds, which were stretched to 1.79 Å in P3. In addition, the N–Si–N bond angles in P3 were significantly distorted from the tetrahedral structure. The N1–Si–N2 bond angle was reduced from 108.6° in R3 to 95.2° in P3. The angles of N1–Si–N3 and N2–Si–N3 were 146.8° and 97.0°, respectively. In TS3, the Si–Cl3 and N3–H3 bonds were dissociated, and elongated Si–N3 and H3–Cl3 bonds were formed with lengths of 1.87 Å and 1.48 Å, respectively. The lower activation energy for the formation of P3 than P2 was mainly due to the additional formation of the H3–Cl3 bond. The Mulliken atomic charges for R3, TS3, and P3 states are presented in Table S2 (ESI†). The trend remains consistent with the change from R1 to P1b.

Fig. 8 The atomistic structures for the reactant (R3), transition (TS3), and product (P3) states of the third Si–N bond formation reaction. The dotted lines represent the interatomic distances with corresponding values displayed in Å. The bond lengths are also shown in Å.

The present work shows that the NH₃⁺Cl⁻ complex formation is significant for the chemisorption of SiCl₄. Our calculation is consistent with previous findings on the chemisorption of DCS on the surface of silicon nitride, where NH₃⁺Cl⁻ complex formation has been reported.^26,28 The reaction sites are restored by desorption of HCl from the NH₃⁺Cl⁻ complexes at elevated temperatures. NH_x surface groups have been reported for various nitride surfaces, including titanium nitride,⁴⁰ and boron nitride.⁴¹ However, DFT studies on nitride surfaces have not considered the formation of NH₃⁺Cl⁻ but only HCl.^41,42 We hope that our work considering the NH₃⁺Cl⁻ complexes can be applied to the reaction mechanism studies of other nitride films using chloride precursors.

Conclusion

The chemisorption of SiCl₄ on the NH₂/NH-terminated silicon nitride surface was studied by DFT calculations using a slab model. The NH₃⁺Cl⁻ complex formation pathway was more exothermic than the HCl formation pathway, with a low activation energy of 0.26 eV. The reaction sites are restored by desorption of HCl from the NH₃⁺Cl⁻ complexes at elevated temperatures of 205 °C or higher. Three sequential ligand exchange reactions forming Si–N bonds on the silicon nitride surface were modeled and simulated. The reaction energies became progressively less exothermic as the reaction progressed due to the stretching of the Si–N bonds and the distortion of the N–Si–N bond angles in P2 and P3. Also, the activation energies for the second and third reactions were significantly higher than that of the first reaction, mainly due to the additional dissociation of the N–H bond. The endothermic reaction and the higher activation energy indicate that the species would be 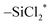when the surface is exposed to SiCl₄.

Author contributions

Tanzia Chowdhury: conceptualization, methodology, validation, formal analysis, investigation, writing – original draft, visualization. Khabib Khumaini: methodology, validation, formal analysis, investigation, writing – original draft, visualization. Romel Hidayat: methodology, validation, formal analysis, investigation, writing – review & editing. Hye-Lee Kim: methodology, validation, formal analysis, investigation, writing – review & editing. Won-Jun Lee: conceptualization, methodology, formal analysis, resources, writing – review & editing, supervision, project administration, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Technology Innovation Program (Public-private joint investment semiconductor R&D program (K-CHIPS) to foster high-quality human resources) (RS-2023-00232222) funded by the Ministry of Trade, Industry & Energy (MOTIE, Korea) (1415187363). This research was also supported by the Korea Basic Science Institute (National Research Facilities and Equipment Center) grant funded by the Ministry of Education (2022R1A6C101A774).

References

1. F. Koehler, D. H. Triyoso, I. Hussain, S. Mutas and H. Bernhardt, IOP Conf. Ser. Mater. Sci. Eng., 2012, 41, 012006.
2. H. Kim, H. Song, C. Shin, K. Kim, W. Jang, H. Kim, S. Shin and H. Jeon, J. Vac. Sci. Technol. A, 2017, 35, 01A101.
3. S. S. Kim, S. K. Yong, W. Kim, S. Kang, H. W. Park, K. J. Yoon, D. S. Sheen, S. Lee and C. S. Hwang, Adv. Mater., 2022, 35, 2200659.
4. R. A. Ovanesyan, E. A. Filatova, S. D. Elliott, D. M. Hausmann, D. C. Smith and S. Agarwal, J. Vac. Sci. Technol., A, 2019, 37, 060904.
5. R. A. Ovanesyan, D. M. Hausmann and S. Agarwal, ACS Appl. Mater. Interfaces, 2015, 7, 10806–10813.
6. S. Yokoyama, N. Ikeda, K. Kajikawa and Y. Nakashima, Appl. Surf. Sci., 1998, 130–132, 352–356.
7. H. C. M. Knoops, K. De Peuter and W. M. M. Kessels, Appl. Phys. Lett., 2015, 107, 014102.
8. N. Leick, J. M. M. Huijs, R. A. Ovanesyan, D. M. Hausmann and S. Agarwal, Plasma Process. Polym., 2019, 16, 1–7.
9. W. Jang, H. Jeon, C. Kang, H. Song, J. Park, H. Kim, H. Seo, M. Leskela and H. Jeon, Phys. Status Solidi A, 2014, 211, 2166–2171.
10. J.-M. Park, S. J. Jang, L. L. Yusup, W.-J. Lee and S.-I. Lee, ACS Appl. Mater. Interfaces, 2016, 8, 20865–20871.
11. J.-M. Park, S. J. Jang, S.-I. Lee and W.-J. Lee, ACS Appl. Mater. Interfaces, 2018, 10, 9155–9163.
12. H. Cho, N. Lee, H. Choi, H. Park, C. Jung, S. Song, H. Yuk, Y. Kim, J.-W. Kim, K. Kim, Y. Choi, S. Park, Y. Kwon and H. Jeon, Appl. Sci., 2019, 9, 3531.
13. X. Meng, Y.-C. Byun, H. S. Kim, J. S. Lee, A. T. Lucero, L. Cheng and J. Kim, Materials, 2016, 9, 1007.
14. J. W. Klaus, A. W. Ott, A. C. Dillon and S. M. George, Surf. Sci., 1998, 418, L14–L19.
15. W.-J. Lee, J.-H. Lee, C. O. Park, Y.-S. Lee, S.-J. Shin and S.-K. Rha, J. Korean Phys. Soc., 2004, 45, 1352–1355.
16. S. Morishita, S. Sugahara and M. Matsumura, Appl. Surf. Sci., 1997, 112, 198–204.
17. W.-J. Lee, U.-J. Kim, C.-H. Han, M.-H. Chun, S.-K. Rha and Y.-S. Lee, J. Korean Phys. Soc., 2005, 47, 598–602.
18. S. Riedel, J. Sundqvist and T. Gumprecht, Thin Solid Films, 2015, 577, 114–118.
19. M. Edmonds, K. Sardashti, S. Wolf, E. Chagarov, M. Clemons, T. Kent, J. H. Park, K. Tang, P. C. McIntyre, N. Yoshida, L. Dong, R. Holmes, D. Alvarez and A. C. Kummel, J. Chem. Phys., 2017, 146, 0–12.
20. D. Sibanda, S. T. Oyinbo and T. C. Jen, Nanotechnol. Rev., 2022, 11, 1332–1363.
21. Y. Widjaja and C. B. Musgrave, Phys. Rev. B, 2001, 64, 205303.
22. S. D. Elliott, G. Dey, Y. Maimaiti, H. Ablat, E. A. Filatova and G. N. Fomengia, Adv. Mater., 2016, 28, 5367–5380.
23. C. K. Ande, H. C. M. Knoops, K. De Peuter, M. Van Drunen, S. D. Elliott and W. M. M. Kessels, J. Phys. Chem. Lett., 2015, 6, 3610–3614.
24. L. Huang, B. Han, B. Han, A. Derecskei-Kovacs, M. Xiao, X. Lei, M. L. O’Neill, R. M. Pearlstein, H. Chandra and H. Cheng, Phys. Chem. Chem. Phys., 2014, 16, 18501–18512.
25. L. L. Yusup, J.-M. Park, T. R. Mayangsari, Y.-K. Kwon and W.-J. Lee, Appl. Surf. Sci., 2018, 432, 127–131.
26. G. Hartmann, P. L. G. Ventzek, T. Iwao, K. Ishibashi and G. S. Hwang, Phys. Chem. Chem. Phys., 2018, 20, 29152–29158.
27. N.-K. Yu, C. H. Moon, J. Park, H.-B.-R. Lee and B. Shong, Appl. Surf. Sci., 2021, 565, 150603.
28. T. Yang, E. S. Cheng, S. M. Johnson, T. Iwao, J. Zhao, J. G. Ekerdt, P. L. G. Ventzek and G. S. Hwang, Appl. Surf. Sci., 2023, 629, 157432.
29. B. Delley, J. Chem. Phys., 1990, 92, 508–517.
30. B. Delley, J. Chem. Phys., 2000, 113, 7756–7764.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
32. H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188.
33. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
34. K. Khumaini, R. Hidayat, T. R. Mayangsari, T. Chowdhury, H.-L. Kim, S.-I. Lee and W.-J. Lee, Appl. Surf. Sci., 2022, 585, 152750.
35. N. Govind, M. Petersen, G. Fitzgerald, D. King-Smith and J. Andzelm, Comput. Mater. Sci., 2003, 28, 250–258.
36. L. L. Yusup, J.-M. Park, Y. H. Noh, S. J. Kim, W.-J. Lee, S. Park and Y.-K. Kwon, RSC Adv., 2016, 6, 68515–68524.
37. T. Chowdhury, R. Hidayat, H.-L. Kim, T. R. Mayangsari, S. Cho, S. Park, J. Jung and W.-J. Lee, Appl. Surf. Sci., 2021, 554, 149481.
38. A. L. Allred, J. Inorg. Nucl. Chem., 1961, 17, 215–221.
39. R. S. Mulliken, J. Chem. Phys., 1955, 23, 2338–2342.
40. M. Q. Snyder, B. A. McCool, J. DiCarlo, C. P. Tripp and W. J. DeSisto, Thin Solid Films, 2006, 514, 97–102.
41. N. Uene, T. Mabuchi, M. Zaitsu, Y. Jin, S. Yasuhara and T. Tokumasu, Comput. Mater. Sci., 2023, 217, 111919.
42. J. Park, N. K. Yu, D. Jang, E. Jung, H. Noh, J. Moon, D. Kil and B. Shong, Coatings, 2020, 10, 712.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05799b

---