Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reactivity of quasi-free electrons toward N3− and its impact on H2 formation mechanism in water radiolysis
Denis
Dobrovolskii
 a,
Sergey A.
Denisov
a,
Sergey A.
Denisov
 a,
Howard E.
Sims
b and
Mehran
Mostafavi
a,
Howard E.
Sims
b and
Mehran
Mostafavi
 *a
*a
aInstitut de Chimie Physique, Université Paris-Saclay, CNRS, Bâtiment 349, Orsay, 91405, France. E-mail: mehran.mostafavi@universite-paris-saclay.fr
bCentral Laboratory, National Nuclear Laboratory, Sellafield, Seascale CA20 1PG, UK
First published on 18th March 2024
Abstract
Picosecond pulse radiolysis measurements were employed to assess the effectiveness of N3− in scavenging quasi-free electrons in aqueous solutions. The absorption spectra of hydrated electrons were recorded within a 100 ps timeframe across four distinct solutions with N3− concentrations of 0.5, 1, 2, and 5 M in water. The results revealed a concentration-dependent shift in the maximum absorption spectra of fully solvated electrons. Notably, at 5 M concentration, the maximum absorption occurred at 670 nm, in contrast to 715 nm observed for water. Intriguingly, the formation yield of hydrated electrons within the initial 5 ps electron pulse remained unaffected, showing that, even at a concentration of 5 M, N3− does not effectively scavenge quasi-free electrons. This is in disagreement with conclusions from stochastic models found in the literature. This observation has an important impact on understanding the mechanism of H2 formation in water radiolysis, which we discuss briefly here.
Introduction
The radiation chemistry of liquid water is of fundamental importance for various practical applications, particularly in the nuclear power industry, where radiolysis products cause corrosion and H2 evolution.1,2 Still, one century after observations of water radiolysis, the mechanism of radicals and molecular products of water radiolysis in a homogenous step, ca. 200 ns after energy deposition in water, are under debate.3–7 It is generally assumed that when exposed to ionizing radiation, water molecules undergo ionizations and excitations: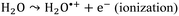 | (1) |
 | (2) |
After being generated by radiation, the excess electron undergoes a solvation process, quickly becoming fully solvated in water within 1 picosecond, having a broad absorption band, peaking at 715 nm.
The electron can be hydrated in less than 1 ps:
| e− → es− | (3) |
When the dose is low, the hydrated electron remains stable in pure water for up to 1 millisecond. Despite its stability, the solvated electron exhibits high reactivity, participating in various chemical reactions. In diluted aqueous solutions or pure water, where the electron primarily interacts with water molecules, it is denoted by the symbol eaq−. However, in solutions containing high concentrations of non-reactive metal cations like Na+, which can interact with the electron, the symbol es− represents the fully solvated electron.
In one picosecond, these processes result in a cascade of events leading to the formation of free radicals and molecular products along the track of the incident radiation. In pure water radiolysis, they essentially comprise the hydrated electron es−, H˙, ˙OH, H2, H2O2.2,8,9
Among these radiolysis products, one of the most interesting is molecular hydrogen, H2, largely due to its mechanism of formation, namely the nature of its precursor(s). Studies of a variety of scavenger systems at high concentrations4,5 in conjunction with computer simulations3,10 have suggested that the majority of the total H2 yield in 60Co-radiolysis involves reactions of short-lived, low-energy (“dry” or quasi-free) secondary electrons that have a kinetic energy during the sub-femtosecond physical stage. Four different mechanisms are considered to explain H2 production under water radiolys is of which 1–3 occur in less than 1 ps:
(1) The geminate recombination of the quasi-free electron with its short-lived H2O˙+ parent cation (or “hole”) due to their Coulomb attraction, which tends to draw them back together:11–15
| H2O˙+ + e− → H2O* | (4) |
| H2O* → H2 + O(1D) | (5) |
| H2O˙+ + H2O → H3O+ + ˙OH | (6) |
Since reaction (6) is ultrafast, reaction (4) can only involve the quasi-free electrons formed in the vicinity of the parent water cation and occurs in the first steps of their random walk, i.e., in times as short as a few femtoseconds.
(2) Decomposition of H2O* formed by direct excitation4,11,18–22
The excited state of water usually undergoes dissociation by forming ˙OH and ˙H radicals. However, another channel is considered for the dissociation process by forming H2 according to the following reaction:
| H2O* → H2 + ˙O | (7) |
(3) The “dissociative electron attachment” (or DEA) involves the resonant capture of a low-kinetic energy electron by a water molecule:23–27
| H2O + e− → H2O*− → H− + ˙OH | (8) |
| H− + H2O → H2 + OH− | (9) |
The reactions (8) and (9) are fast and occur in the fs range.
(4) The residual production of H2 through radiolysis is attributed to three specific radical–radical combination reactions involving the hydrated electron and H˙ atom.15,23,28–30 These reactions occur within the expanding tracks via diffusion during the nonhomogeneous chemical stage.
 | (10) |
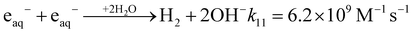 | (11) |
| 2H˙ → H2k12 = 4.6 × 109 M−1 s−1 | (12) |
Scavenging methods and simulations are used to evaluate each mechanism's contribution.
Azides, N3−, consisting of three nitrogen atoms arranged linearly, are known for their reactivity and have applications in various fields.31 The simplest azide is N3− anion, which is very soluble in water.32 N3− can undergo radiolysis when exposed to ionizing radiation in aqueous solution.33 It is well-known that azide reacts with OH˙ radical, forming the azide radical:34,35
| N3− + ˙OH → N3˙ | (13) |
The radical N3˙ is a less oxidizing species than OH˙ radical and is used as a one electron oxidizing radical.36,37 In contrast, the hydrated electron reaction with N3− is very slow, and the value of the rate constant of this reaction is estimated to be lower than 1.5 × 106 M−1 s−1.38,39 However, the reaction of N3− with H˙ atom is fast with a rate constant of k = 2.5 × 109 M−1 s−1:40
| N3− + H˙ → products | (14) |
The slow reaction with the hydrated electron and the fast reaction with the H˙ atom allows N3− as a selective scavenger to deduce information about the mechanism of H2 formation. Peled et al.39 showed that N3− reduces the yield of H2, G(H2), from 0.45 × 10−7 mol J−1 to 0.157 at 5 M N3− in neutral solutions and from 0.37 mol J−1 in 0.5 M solution to 0.21 mol J−1 at 4 M N3− in alkaline solutions. The hydrated electron reacts with azide very slowly, and the presence of 1 M N3− was found not to affect the solvated electron spectrum at 100 ns in their work.
In competition experiments between N3− and isopropyl alcohol, the rate constant kH+N3− = 2.7 × 109 M−l s−l was obtained.39 From the decrease of the yield of the hydrated electron by efficient electron scavengers, it was concluded that the reaction H˙ + eaq− → H2 + OH− contributes largely to the yield of H2 in spurs.
In order to fit these results using Monte Carlo track chemistry simulations, two groups33,41 concluded that “dry” secondary electrons, which serve as precursors to the “hydrated” electron (eaq−), must be effectively scavenged by N3− on the sub-picosecond timescale before hydration. This scavenging process was assumed to occur in the presence of a high concentration (>0.1–1 M) of azide ions (N3−) in water. Emphasis was placed on the intriguing observation that this is an uncommon result because of the low reactivity of N3− with eaq−. Typically, quasi-free electrons are found to be scavenged by solutes known to be reactive towards hydrated electrons.42 The authors did not discuss Peled's conclusions about the lack of reaction of prehydrated electrons.
The objective of the present study was to perform picosecond pulse radiolysis to observe directly if the dry electron (or quasi-free electron) reacts with N3−. The quasi-free electron is involved in two reactions (4) and (8) for H2 production in a short time. If the scavenging of a quasi-free electron occurs, that means: first, this is the first case where a hydrated electron does not react with a solute, but the quasi-free electron reacts very efficiently; second, the experiments of Peled et al. cannot be conclusive if N3− scavenges both quasi-free electron and H˙ atom. Therefore, the experimental result with picosecond pulse radiolysis greatly impacts the hydrogen production mechanism.
Experimental section
The formation and decay of the solvated electron were followed using the pulse radiolysis platform ELYSE – a laser-driven Cs2Te photo-cathode (260 nm) accelerator (Paris-Saclay University), which utilizes short 5 ps pulses of electrons to produce, and 100 fs broad supercontinuum (350–1400 nm), to examine transient species.43,44 The short electron pulses with a typical half-width of 5–7 ps, a charge of ca. 6 nC, and an energy of 7.8 MeV at a repetition rate of 5 Hz were utilized for experiments. The supercontinuum, generated by focusing a small part of the fundamental laser (780 nm) into a CaF2 (350–780 nm) crystal, is split 50/50: probe/reference paths. Both probe and reference paths are coupled into optical fibers, transmitted to a spectrometer, and dispersed onto a cooled CCD camera (Andor Newton 920) for UV-vis detection. All kinetics presented in this work are calculated by averaging 3 transient maps with 6 electron pulses at each time delay step.The formation yield of ehyd at just after the end of 5 ps electron pulse (G = 4.4 × 10−7 M J−1) correlates with the scavenging yield of a quasi-free electron. Less hydrated electron was formed if more quasi-free electrons were scavenged during the pulse.
Results and discussion
Four solutions of NaN3 with concentrations of 0.5, 1, 2, and 5 M, underwent investigation by observing hydrated electron kinetics within the 400 to 720 nm spectral range by pulse probe method (Fig. 1 top). A reference optical cell containing only water determined the dose per pulse for each sample. Fig. 1 illustrates each concentration's time-dependent absorption spectra acquired through pulse probe measurements. The absorption spectra of the solvated electron exhibiting temporal variations, i.e., blue-shift within the first 50 ps after of electron pulse, are particularly pronounced in the high-concentration azide solutions.Selected absorption spectra at different time intervals for each solution are presented in Fig. 1 to emphasize the observed shifts. The observed changes over time are attributed to the formation of a pair in the presence of a high concentration of Na+ and further solvation. At 5 M, the peak absorption shifts from 680 nm at the end of the electron pulse to 670 nm after 20 ps. Similar shifts are observed in 2 M but to a smaller extent. However, there is no detectable shift for the 0.1 M concentration, and the absorption band remains ca. 715 nm, the same as in water. The kinetics are reported for different samples at the absorption band maximum when an electron is fully solvated (Table 1), showing the solvated electron's stability during the first 100 ps. Except for the 0.1 M and 0.5 M solutions an increase in shorter wavelengths than 715 nm is observed just after the electron pulse. The shift of the absorption band of the solvated electron is very fast for a solution of 2 M N3−, which is why we treated only the case of 5 M N3− solution. Fig. 2 shows the dynamics of the solvation of electrons in 5 M azide solution by reporting the change of the maximum of the absorption band versus time. The data can be fitted with one exponential with a time constant of 16 ps. After 30 ps, the shape of the absorption spectra does not change and we can consider that the electron is fully solvated and paired with Na+.
| NaN3 concentration mol L−1 | ρ at 22 °C, g cm−3 ± 0.005 | λ max of the fully solvated electron ± 5 nm | Solvation time ps |
|---|---|---|---|
| 0 | 1 | 715 | <1 ps |
| 0.5 | 1 | 715 | <1 ps |
| 1 | 1.03 | 712 | A few ps |
| 2 | 1.06 | 708 | <10 ps |
| 5 | 1.18 | 670 | 16 ps |
 | ||
| Fig. 2 Change of the absorption band's maximum with time for the solution containing 5 M NaN3. The fit is a mono-exponential. | ||
The kinetics at the absorption band's maximum when the spectra stabilize are depicted in Fig. 2. The observed absorption is more intense for the concentrated solution. This effect is due to the density of the solution. The values of the density ρ and λmax are reported in Table 1.
Utilizing the dose per pulse (D) for each sample and the same extinction coefficient, ε(ehyd−), at the absorption band's maximum, λmax, the time-dependent yield of the solvated electron, Geaq−(t), in various samples is deduced from the following equation:45
| A(λ, t) = ε(eaq−)·c(t)·l = ε(eaq−)·D·Geaq−(t)·ρ·l | (15) |
Fig. 3 presents the time-dependent yield of the solvated electron for all solutions. The increase during the first 30 ps for 5 M solution is due to the absorption band shift. As shown, for all solutions 30 ps after the pulse, the yield is the same and equal to that of water. The results show clearly that even 5 M N3− cannot scavenge the quasi-free electron. This experimental result does not agree with recent water radiolysis simulations to explain the yield of H2. In fact, from our observations, it is clear that, there is no reaction between the precursor of the solvated electron and N3−.
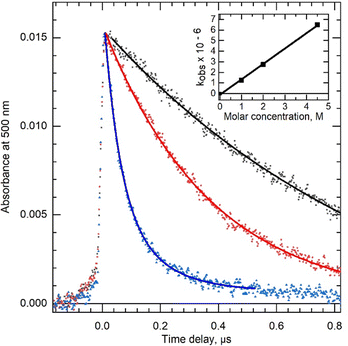
It is beyond the scope of this paper to discuss Peled's results on the yield of H2 further apart from to note that it must be concluded from their results that either H˙ is involved in the formation of a significant fraction of H2 (ca. 50%) or N3− is involved in some other mechanism apart from scavenging H˙ which suppresses H2. One possibility is hole scavenging, which is unlikely because high concentrations of Cl− do not affect the yield of H2.46 There is the possibility that N3− quenches excited states of water molecules, but this is unlikely to occur at the lower concentrations used in Peled's work. The use of very high concentrations such as 5 M azide, even if the purity of the reagent is high (such as 99% that we used), could, in Peled's experiment, have resulted in a fraction of solvated electrons being scavenged by impurities. However, he reported no change in yield at 100 ns. We performed pulse radiolysis in the microsecond range, and the decay of the solvated electron was observed for 1, 2, and 5 M azide solution. The decay is accelerated when the concentration of azide increases (Fig. 4). The observed rate constant is 1.4 × 106 M−1 s−1, which agrees with the previous value where only one concentration (1 M) was used for rate constant determination.39
This rate constant is low, and the solvated electron cannot be scavenged in the non-homogenous step. If e−aq does not react significantly with impurity, it can be concluded that reaction (11) is not involved in that component of H2 production, which was suppressed in the study, which agrees with Bartels15 conclusion based on yields in high-temperature water. Finally, the precise values for G(H2) at high concentrations of azide (>1 M) reported by Peled should be treated with caution because the calculated value depends on dosimetry in concentrated solutions. Peled chose to use the total dose corrected for solute, but if some of the H2 arises from reaction (5), then it might be expected that only the dose to the water fraction should be considered, and that would result in an increase in G(H2) in Peled's results which would suggest G(H2) in azide solutions decreases to a steady value with increasing azide concentration above 4 M.
It is important to note that contrary to the case of the scavengers used in previous works (such as SeO42−, MoO42−, Cr2O72−, NO2−, NO3−, Cd2+, Cu2+, and H2O2), which react very rapidly with the hydrated electron, the specific case of N3− is that its reaction with the hydrated electron is very slow. In general, stochastic models simulate the effects of prehydrated electron scavengers on H2 yield well, for example, with NO3−,41 typifying most of the species listed by Pastina et al.4 However, where the chemistry becomes more complex, for example, when Cu2+ is used, the model is less good and with no prehydrated electron scavenger, N3−, the model fails. In later work, Horne et al.11 required the quenching by NO3− of H2O* formed by direct excitation, which occurred at the same rate as the reaction of epre−. A problem for models is that there is no direct chemical evidence for the mechanisms, which ultimately involve the decomposition of excited states to form H2 at sub-picosecond timescales.
We can assume that the high concentration of Na+ does not affect the yield of H2,. H3O+ forms an ion pair with epre similar to Na+, which was included in a stochastic model for reactions of silver, and it was concluded that this ion pair reacted with Ag+ at the same rate as epre−.47
Finally, we note that in our previous measurements in the presence of silver ion, it was shown that within experimental error, the sum of the yields of a silver atom and that of hydrated electron rose only slightly with increasing silver concentration, showing that the quasi-free electron mainly solvates in water.47
Conclusions
It is concluded that the quasi-free electron does not react with N3− in agreement with the conclusions of Peled and in disagreement with assumptions used in stochastic models. In these concentrated solutions, the electron hydrates and rapidly forms an ion pair with Na+ resulting in a spectral shift as observed previously with H3O+.If the sole effect of N3− is to scavenge H˙, then the decrease in the yield of H2 measured by Peled must involve reactions of H˙ and rule out reaction (11), it can be concluded that if reactions (4) and (5) are important for the formation of part of the H2 yield, then only efficient quasi-free electron scavengers can suppress the H2 yield from this process.
Finally, because stochastic models require the reaction of quasi-free electrons with N3−, these models must be reassessed.
Conflicts of interest
There are no conflicts to declare.References
- G. Buxton, The Radiation Chemistry of Liquid Water, Charged Particle and Photon Interactions with Matter, CRC Press, 2003 Search PubMed.
- J. V. Belloni, M. Mostafavi, T. Douki and M. Spotheim-Maurizot, Radiation chemistry from basics to applications in material and life sciences, EDP Sciences, 2008 Search PubMed.
- H. A. Schwarz, Applications of the spur diffusion model to the radiation chemistry of aqueous solutions, J. Phys. Chem., 1969, 73(6), 1928–1937 CrossRef CAS.
- B. Pastina, J. A. LaVerne and S. M. Pimblott, Dependence of Molecular Hydrogen Formation in Water on Scavengers of the Precursor to the Hydrated Electron, J. Phys. Chem. A, 1999, 103(29), 5841–5846 CrossRef CAS.
- V. M. Byakov, The nature of the precursors of radiolytic molecular hydrogen in water, and the mechanism of positronium formation in liquids, Int. J. Radiat. Phys. Chem., 1976, 8(3), 283–288 CrossRef CAS.
- J. M. Wiesenfeld and E. P. Ippen, Dynamics of electron solvation in liquid water, Chem. Phys. Lett., 1980, 73(1), 47–50 CrossRef CAS.
- W. J. Chase and J. W. Hunt, Solvation time of the electron in polar liquids. Water and alcohols, J. Phys. Chem., 1975, 79(26), 2835–2845 CrossRef CAS.
- H. Morawetz, Radiation chemistry-principles and applications, Farhataziz and Michael A. J. Rodgers, Eds. VCH, New York and Germany, 1987, 641 pp. Price, J. Polym. Sci., Part C: Polym. Lett., 1987, 2512, 510 Search PubMed.
- J. Meesungnoen, S. Sanguanmith and J. P. Jay-Gerin, Yields of H2 and hydrated electrons in low-LET radiolysis of water determined by Monte Carlo track chemistry simulations using phenol/N2O aqueous solutions up to 350 °C, RSC Adv., 2015, 5(94), 76813–76824 RSC.
- W. G. Burns, H. E. Sims and J. A. B. Goodall, Radiation chemical diffusion kinetic calculations with prescribed and non-prescribed diffusion—I, Radiat. Phys. Chem., 1984, 23(1–2), 143–180 CrossRef CAS.
- G. P. Horne, S. M. Pimblott and J. A. LaVerne, Inhibition of Radiolytic Molecular Hydrogen Formation by Quenching of Excited State Water, J. Phys. Chem. B, 2017, 121(21), 5385–5390 CrossRef CAS PubMed.
- S. Sanguanmith, J. Meesungnoen, Y. Muroya and J. P. Jay-Gerin, Scavenging of “dry” electrons prior to hydration by azide ions: effect on the formation of H2 in the radiolysis of water by 60Co γ-rays and tritium β-electrons, Can. J. Chem., 2021, 99(11), 881–889 CrossRef CAS.
- R. L. Platzman, Subexcitation Electrons, Radiat. Res., 1955, 2(1), 1 CrossRef CAS PubMed.
- V. Cobut, J. P. Jay-Gerin, Y. Frongillo and J. P. Patau, On the dissociative electron attachment as a potential source of molecular hydrogen in irradiated liquid water, Radiat. Phys. Chem., 1996, 47(2), 247–250 CrossRef CAS.
- D. Janik, I. Janik and D. M. Bartels, Neutron and β/γ Radiolysis of Water up to Supercritical Conditions. 1. β/γ Yields for H2, H˙ Atom, and Hydrated Electron, J. Phys. Chem. A, 2007, 111(32), 7777–7786 CrossRef CAS PubMed.
- M. F. Lin, N. Singh, S. Liang, M. Mo, J. P. F. Nunes and K. Ledbetter, et al., Imaging the short-lived hydroxyl-hydronium pair in ionized liquid water, Science, 2021, 374(6563), 92–95 CrossRef CAS PubMed.
- Z. H. Loh, G. Doumy, C. Arnold, L. Kjellsson, S. H. Southworth and A. Al Haddad, et al., Observation of the fastest chemical processes in the radiolysis of water, Science, 2020, 367(6474), 179–182 CrossRef CAS PubMed.
- G. R. Sunaryo, Y. Katsumura, D. Hiroishi and K. Ishigure, Radiolysis of water at elevated temperatures—II. Irradiation with γ-rays and fast neutrons up to 250 °C, Radiat. Phys. Chem., 1995, 45(1), 131–139 CrossRef CAS.
- D. Swiatla-Wojcik and G. V. Buxton, Modeling of radiation spur processes in water at temperatures up to 300.degree, J. Phys. Chem., 1995, 99(29), 11464–11471 CrossRef CAS.
- W. G. Burns and W. R. Marsh, Radiation chemistry of high-temperature (300–410 °C) water. Part 1.—Reducing products from gamma radiolysis, J. Chem. Soc., Faraday Trans. 1, 1981, 77(1), 197 RSC.
- C. Lifshitz, Isotope Effects in X-ray-Irradiated Acidified H2O–D2O Solutions, Can. J. Chem., 1963, 41(9), 2175–2186 CrossRef CAS.
- S. Rose′n, A. Derkatch, J. Semaniak, A. Neau, A. Al-Khalili and A. Le Padellec, et al., Recombination of simple molecular ions studied in storage ring: dissociative recombination of H2O+, Faraday Discuss., 2000, 115, 295–302 RSC.
- M. Sterniczuk and D. M. Bartels, Source of Molecular Hydrogen in High-Temperature Water Radiolysis, J. Phys. Chem. A, 2016, 120(2), 200–209 CrossRef CAS PubMed.
- M. G. Curtis and I. C. Walker, Dissociative electron attachment in water and methanol (5–14 eV), J. Chem. Soc., Faraday Trans., 1992, 88(19), 2805–2810 RSC.
- C. E. Melton, Cross Sections and Interpretation of Dissociative Attachment Reactions Producing OH−, O−, and H− in H2O, J. Chem. Phys., 1972, 57(10), 4218–4225 CrossRef CAS.
- C. E. Melton and G. A. Neece, Rate constants and cross sections for the production of OH- from O- and H- in water, J. Am. Chem. Soc., 1971, 93(25), 6757–6759 CrossRef CAS.
- J. Ma, F. Wang and M. Mostafavi, Ultrafast Chemistry of Water Radical Cation, H2O˙+, in Aqueous Solutions, Molecules, 2018, 23(2), 244 CrossRef PubMed.
- G. A. Kimmel, T. M. Orlando, C. Vézina and L. Sanche, Low-energy electron-stimulated production of molecular hydrogen from amorphous water ice, J. Chem. Phys., 1994, 101(4), 3282–3286 CrossRef CAS.
- M. Faraggi, D. Zehavi and M. Anbar, Effect of thallous ions on the yields of hydrogen and hydrogen peroxide in radiolyzed aqueous solutions, Trans. Faraday Soc., 1971, 67, 2057 RSC.
- V. Cobut, J. P. Jay-Gerin, Y. Frongillo and J. P. Patau, On the dissociative electron attachment as a potential source of molecular hydrogen in irradiated liquid water, Radiat. Phys. Chem., 1996, 47(2), 247–250 CrossRef CAS.
- S. Bräse, C. Gil, K. Knepper and V. Zimmermann, Organic Azides: An Exploding Diversity of a Unique Class of Compounds, Angew. Chem., Int. Ed., 2005, 44(33), 5188–5240 CrossRef PubMed.
- K. Turnbull, B. Narsaiah, J. S. Yadav, T. Yakaiah and B. P. V. Lingaiah, Sodium Azide, Encyclopedia of Reagents for Organic Synthesis. Chichester, John Wiley & Sons, Ltd, UK, 2008 Search PubMed.
- S. Sanguanmith, J. Meesungnoen, Y. Muroya and J. P. Jay-Gerin, Scavenging of “dry” electrons prior to hydration by azide ions: effect on the formation of H2 in the radiolysis of water by 60Co γ-rays and tritium β-electrons, Can. J. Chem., 2021, 99(11), 881–889 CrossRef CAS.
- G. R. Dey, Nitrite formation in aerated aqueous azide solutions: A radiation chemical study, Res. Chem. Intermed., 2007, 33(7), 599–611 CrossRef CAS.
- A. T. Al-Kazwini, P. O’Neill, G. E. Adams, R. B. Cundall, G. Lang and A. Junino, Reactions of indolic radicals produced upon one-electron oxidation of 5,6-dihydroxyindole and its N(1)-methylated analogue, J. Chem. Soc., Perkin Trans. 2, 1991, 1941 RSC.
- S. Sanguanmith, J. Meesungnoen, C. R. Stuart, P. Causey and J. P. Jay-Gerin, Self-radiolysis of tritiated water. 4. The scavenging effect of azide ions (N3−) on the molecular hydrogen yield in the radiolysis of water by 60Co γ-rays and tritium β-particles at room temperature, RSC Adv., 2018, 8(5), 2449–2458 RSC.
- C. Lambert, T. G. Truscott, E. J. Land and P. A. Riley, Role of azide concentration in pulse radiolysis studies of oxidation: 3,4-dihydroxyphenylalanine, J. Chem. Soc., Faraday Trans., 1991, 87(18), 2939 RSC.
- B. Smaller, E. C. Avery and J. R. Remko, EPR Pulse Radiolysis Studies of the Hydrogen Atom in Aqueous Solution. I. Reactivity of the Hydrogen Atom, J. Chem. Phys., 1971, 55(5), 2414–2418 CrossRef CAS.
- E. Peled, U. Mirski and G. Czapski, Contribution of hydrogen atoms to GH2 in the radiation chemistry of aqueous solutions, J. Phys. Chem., 1971, 75(1), 31–35 CrossRef CAS.
- D. J. Deeble, B. J. Parsons and G. R. Alastair Johnson, Reactions of the hydrogen atom with azide, bromide and iodide ions in aqueous solution, Int. J. Radiat. Appl. Instrum., Part C, 1990, 36(3), 487–491 CAS.
- R. E. Harris and S. M. Pimblott, On 3H β-particle and 60Co γ irradiation of aqueous systems, Radiat. Res., 2002, 158(4), 493–504 CrossRef CAS PubMed.
- C. D. Jonah, J. R. Miller and M. S. Matheson, The reaction of the precursor of the hydrated electron with electron scavengers, J. Phys. Chem., 1977, 81(17), 1618–1622 CrossRef CAS.
- J. Belloni, H. Monard, F. Gobert, J. P. Larbre, A. Demarque and V. De Waele, et al., ELYSE - A picosecond electron accelerator for pulse radiolysis research, Nucl. Instrum. Methods Phys. Res., Sect. A, 2005, 527–539 CrossRef CAS.
- J. L. Marignier, V. de Waele, H. Monard, F. Gobert, J. P. Larbre and A. Demarque, et al., Time-resolved spectroscopy at the picosecond laser-triggered electron accelerator ELYSE, Radiat. Phys. Chem., 2006, 75(9), 1024–1033 CrossRef CAS.
- F. Wang, U. Schmidhammer, J. P. Larbre, Z. Zong, J. L. Marignier and M. Mostafavi, Time-dependent yield of the hydrated electron and the hydroxyl radical in D2O: a picosecond pulse radiolysis study, Phys. Chem. Chem. Phys., 2018, 20(23), 15671–15679 RSC.
- A. O. Allen, C. J. Hochanadel, J. A. Ghormley and T. W. Davis, Decomposition of Water and Aqueous Solutions under Mixed Fast Neutron and γ-Radiation, J. Phys. Chem., 1952, 56(5), 575–586 CrossRef.
- A. Balcerzyk, U. Schmidhammer, G. Horne, F. Wang, J. Ma and S. M. Pimblott, et al., Unexpected Ultrafast Silver Ion Reduction: Dynamics Driven by the Solvent Structure, J. Phys. Chem. B, 2015, 119(31), 10096–10101 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2024 |