Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Secondary nucleation in symmetric binary SALR mixtures
Jiazheng
Tan
 a and
Martin B.
Sweatman
*b
a and
Martin B.
Sweatman
*b
aSchool of Mechanical Engineering, Dongguan University of Technology, Dongguan 523808, China
bInstitute of Materials and Processes, School of Engineering, University of Edinburgh, Kings Buildings, Mayfield Road, Edinburgh, EH9 3FB, UK. E-mail: martin.sweatman@ed.ac.uk
First published on 22nd May 2024
Abstract
Monte Carlo simulation is used to study secondary nucleation, fissioning, or ‘reproduction’, of giant clusters in a symmetric binary model fluid with competing short-range (SA) and long-range (LR) interactions. Previous work [M. B. Sweatman, Mol. Phys., 116(15–16), 1945–1952] suggests that a pure SALR fluid can exhibit secondary nucleation if the solute concentration is slowly increased. We show this is also true for a binary symmetric SALR mixture where the cross-interactions can be tuned to generate clusters with three different kinds of structure; (i) independent clusters of each component, (ii) contact clusters of different components, and (iii) mixed clusters. In each case, the overall concentration of each component is identical. This binary model is an initial step towards using SALR fluids to model the intra-cellular space of biological cells that contain a wide range of membraneless organelles and the chemical ‘soup’ at the origin of life.
1 Introduction
Giant thermodynamically stable clusters occur in many chemical systems including micelles in surfactant systems1 and liquid-like droplets in complex coacervates and many polyelectrolyte solutions.2,3 Biological cells also contain a wide variety of giant, membraneless clusters, known as membraneless organelles,4,5 but it is not yet clear if these clusters are thermodynamically stable. Normally, it is thought they form through liquid–liquid phase separation (LLPS),6 but giant clusters are thermodynamically unstable if formed this way. Instead, the bulk liquid phase is stable. Therefore, we should expect a multitude of such large, finite-size clusters within biological cells to aggregate given sufficient time. Since this does not appear to happen, it seems that an unknown mechanism beyond LLPS stabilizes them.Giant, thermodynamically stable clusters can also form in SALR fluids, where particles interact via short-range attractive interactions (SA) and long-range repulsive interactions (LR).7–13 The SALR interaction has, therefore, been used to model some fluids where giant clusters are apparently stable, including membraneless organelles.14 Typically, the long-range repulsive part of the SALR interaction is modelled as a screened-coulomb interaction. Thus, giant SALR clusters are usually models of charged-stabilized clusters.
Since many biological molecules are charged in solution, it raises the possibility the SALR model could be a good model for many biological molecules and their condensates, including membraneless organelles. If this is the case, then the suggested mechanism (LLPS) for the formation of such condensates might not be accurate, since giant SALR clusters are not formed through liquid–liquid phase separation. Instead, the SALR phase diagram features a pseudo phase transition line known as the critical cluster concentration (CCC),8 analogous to the critical micelle concentration (CMC) of micelle-forming surfactants. However, more complex clustering behavior beyond the appearance of simple spherical clusters above the CCC has been revealed for a wide range of both pure and mixed SALR fluids14–18 and related to analogous behavior seen in real fluids. Normally, the SALR model interaction is taken to represent the effective interaction between solute particles mediated by a solvent (usually water) that is not explicitly represented in the model. That is, the solvent degrees-of-freedom are integrated-out.
Recently, Sweatman,19 using modified grand canonical Monte Carlo simulations and a novel kind of density functional theory for a pure SALR fluid, showed that giant SALR clusters can fission when the overall concentration of SALR particles is increased sufficiently slowly. This process might also be called secondary nucleation,20 or in the biological realm it might be called ‘reproduction’. On the other hand, when the SALR concentration is increased too rapidly, it was found that SALR clusters can grow along one axis into long ‘sausage’ shapes or primary nucleation of giant clusters can occur preferentially. Similar results should be obtained using Brownian dynamics simulations where the solute concentration is slowly increased.21,22 Whichever simulation method is used, since an increase in SALR particle concentration is equivalent to a decrease in implicit solvent concentration, Sweatman's19 findings also imply secondary nucleation of giant SALR clusters could occur through solvent evaporation.
Sweatman19 explained this behavior in terms of three competing rates; the rate of accumulation of SALR particles in the system, the rate at which particles diffuse through the solvent and the rate at which giant clusters can relax which is related to cluster viscosity. Provided particle diffusion and cluster relaxation are faster processes than particle accumulation, then the giant clusters should remain close to their equilibrium structures. However, if cluster size exceeds a geometric limit, further cluster growth occurs along one axis of a cluster in preference to primary nucleation of a new cluster. Eventually, as cluster size increases still further, a cluster instability threshold is encountered which results in clusters fissioning into two smaller spherical clusters. This instability is caused primarily by the competition between SA and LR interactions; above the size threshold, LR interactions dominate. Similar physics occurs in fissioning of atomic nuclei, except there the SA interactions are generated by the strong nuclear force.
An understanding of giant SALR cluster fissioning, i.e. secondary nucleation, could be especially important in biology. This is because recent research suggests the onset of many diseases, including some cancers and neurodegenerative diseases, is related to the rate of proliferation of specific biological condensates.23 In turn this rate could be sensitive to the mechanism by which such clusters are generated, i.e. primary versus secondary nucleation, since nucleation rates for these processes can differ by orders-of-magnitude. Therefore, treatment of some diseases, like cancers and neurodegenerative diseases, might be improved by a better understanding of nucleation in biological condensates. It follows that if giant SALR clusters are a good model of membraneless organelles, then a better understanding of primary versus secondary nucleation in giant SALR clusters might have implications for the treatment of many common diseases. In addition, cellular reproduction, which is essentially just secondary nucleation of large complex clusters, was obviously important in the initial development of life from non-living clusters since any species can only escape extinction through reproductive replacement. If the initial development of life involved membraneless organelles or other kinds of biological condensate, and if giant SALR clusters are good model of these aggregates as well, then a better understanding of the nucleation of giant SALR clusters could also be important in understanding the origin of life.
This work takes the initial work of Sweatman19 one step further. That is, we consider secondary nucleation of giant clusters in symmetric equimolar binary mixtures of SALR particles. We are interested in SALR mixtures because the cellular cytoplasm contains a wide range of biological molecules and membraneless organelles.4–6,23 Likewise, the chemical ‘soup’ leading to the development of life would have been highly mixed.24 Essentially, we view each type of cluster as a different kind of membraneless organelle or as a different species in models of early life. We choose symmetric equimolar SALR mixtures for simplicity and convenience. More complex mixtures that are more representative of real mixtures can be considered in future work.
The organization of this paper is as follows. In Section 2, computational details of the Monte Carlo simulations, as well as the model parameters, are given. Simulation results are presented and a discussion is provided in Section 3. A summary of this work is provided in Section 4.
2 Computational details
This work focuses on fluids consisting of equimolar symmetric binary mixtures of components A and B, with particles from both components interacting through short range attractive and long range repulsive (SALR) forces. Following Sweatman et al.,8,15 these SALR interactions are modelled by double-Yukawa potentials, extended here to the mixture case. Therefore, hard sphere interactions occur for r < 1, while for r > 1,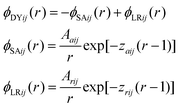 | (1) |
Using a modified kind of density functional theory, Sweatman et al.8 find that a cluster fluid occurs at low system concentrations in the pure SALR system with the following parameters; Aa ∈ [1.6,2.2], Ar = 0.5, za = 1, zr = 0.5 (note that reduced units are used throughout this work, so that energies are given in units of kBT, with kB being Boltzmann constant and T being the temperature, lengths are stated relative to the hard sphere diameter, d, and density is given in units of particles per d3). MC simulations confirm that choosing parameters within this range can lead to the formation of giant SALR clusters at equilibrium.8 Typically, such cluster states are highly metastable and therefore once equilibrium is achieved, no new cluster nucleation or evaporation events are observed in simulations within a reasonable time. Through investigation of a density functional theory model, Sweatman19 explained that this is because the free energy barrier for such events is too high, at least for the giant clusters we are interested in.
To ensure both components of our binary SALR fluid by themselves would also exhibit equilibrium clustering, the following interaction parameters are selected: AaAA = AaBB = 1.75, ArAA = ArBB = 0.5, zaAA = zaBB = zaAB = 1, and zrAA = zrBB = zrAB = 0.5. These parameters are identical to those used in earlier work that investigated giant SALR cluster formation in symmetric binary SALR mixtures.25 In that work, it was found that there are three general kinds of giant cluster scenario for these binary SALR fluids at equilibrium under equimolar conditions, which are determined by the choice of cross-interaction parameters. Choosing AaAB = 0.35, ArAB = 0.1 results in independent clusters of relatively pure A and pure B. Choosing AaAB = 0.55, ArAB = 0.1, on the other hand, results in relatively pure clusters of A and B that tend to touch. Finally, choosing AaAB = 1.4, ArAB = 0.3 results in larger mixed clusters. It is expected that these parameter selections cover the fundamental clustering behavior of interest to us.21
Since these giant SALR cluster states are highly metastable, they must be driven towards an instability to observe new cluster nucleation or evaporation events. Clearly, to observe nucleation events we should consider adding particles to the system. Sweatman previously achieved this using a modified grand canonical Monte Carlo (GCMC) approach to generate reproduction behavior in a pure SALR system.19 In this approach, (i) only small particle movements are allowed, i.e. no non-physical moves are performed; and (ii) grand canonical particle insertion attempts are allowed but particle deletion attempts are not. This asymmetry leads to a steady increase in particle concentration. Clearly, these simulations are not equilibrium simulations. This accords with our main interest which is to investigate the effect of the rate of accumulation of SALR particles on nucleation behavior. This situation, where the particle concentration increases steadily, could correspond to where, (i) proteins or other biomolecules, perhaps produced by a disease, are continually generated within a biological cell, or (ii) where water evaporates from a warm pond containing ‘primordial soup’.
Brownian dynamics simulation would be a natural choice for the simulation of solute systems. However, the Monte Carlo simulation method defined above is better suited to the hard particle interactions used here (1) and should produce similar outcomes to Brownian dynamics for suitably small step sizes.21,22 Therefore, in this paper, Sweatman's modified GCMC simulation method is used to also study the binary SALR mixture system.
Specifically, trial displacements have a maximum step size of 0.35 and the fictitious fugacity for particle insertions is set to 0.016 for both components. Also, one insertion attempt per 500 or 25 cycles is made for scenario 1 and scenario 2, while one insertion attempt per 1000 or 50 cycles is made for scenario 3 (a cycle consists of an attempt to move each particle). A cubic simulation box of side length 27 with periodic boundaries in each Cartesian direction and a long-ranged cut-off of half the box length is employed.
The initial configuration for scenarios 1 and 2 consists of 700 particles of each component, while the initial configuration for scenario 3 has 400 particles of each component. Thus, the particle concentrations used here are similar to those used in earlier work.25
Preliminary MC simulations begin with a random distribution of particles but without any trial insertions. These initial concentrations are chosen such that an initial pair of clusters will rapidly form for scenarios 1 and 2, or a single mixed cluster will spontaneously form for scenario 3, but no further clustering is observed with longer simulations. There is no selection bias for these initial states. We use the output configurations of these preliminary MC simulations as the input to our modified GCMC simulations, reported next.
3 Simulation results
Fig. 1, corresponding to scenario 1 (one insertion attempt per 500 cycles), shows the growth and reproduction of both blue and red clusters as the particle concentration slowly increases. Initially, as the clusters grow beyond a critical size, they both begin to grow along one axis. Further growth leads to an instability and secondary nucleation. The first reproduction event takes place just before 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles (blue cluster), followed by the second reproduction event at about 530
000 cycles (blue cluster), followed by the second reproduction event at about 530![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles (red cluster).
000 cycles (red cluster).
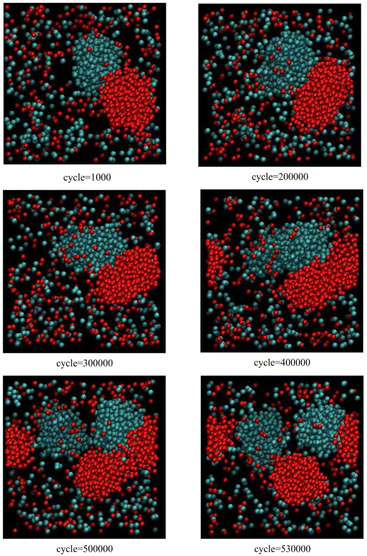 | ||
| Fig. 1 Snapshots from Monte Carlo simulations of binary SALR mixtures for scenario 1 corresponding to one insertion attempt per 500 cycles (see text). | ||
Fig. 2 also corresponds to scenario 1 but with one insertion attempt per 25 cycles. In this case, particle accumulation is faster than both particle diffusion and cluster relaxation. Now, both blue and red clusters keep growing along one axis without any secondary nucleation events, leading to elongated sausage-like shapes. In addition, primary nucleation events are observed for both components; the first occurs just before 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles (blue cluster), while the second occurs before 80
000 cycles (blue cluster), while the second occurs before 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles (red cluster).
000 cycles (red cluster).
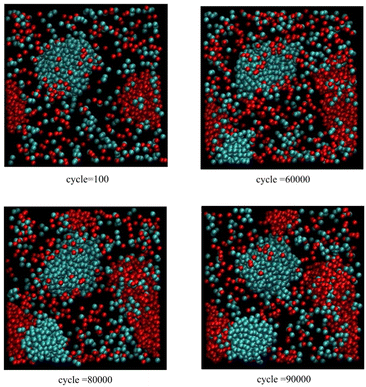 | ||
| Fig. 2 As for Fig. 1, except only one insertion attempt per 25 cycles. | ||
Fig. 3 corresponds to scenario 2, where clusters of relatively pure A and B touch, with one insertion attempt per 500 cycles. Initially, the fused red and blue clusters grow together. Subsequently, the blue cluster fissions before 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles with both blue daughter clusters still attached to the extended red cluster. Later, the red cluster also fissions before 670
000 cycles with both blue daughter clusters still attached to the extended red cluster. Later, the red cluster also fissions before 670![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles. The final configuration consists of two fused daughter clusters, each consisting of a pairs of red and blue daughter clusters in contact.
000 cycles. The final configuration consists of two fused daughter clusters, each consisting of a pairs of red and blue daughter clusters in contact.
 | ||
| Fig. 3 Snapshots from Monte Carlo simulations of binary SALR mixtures for scenario 2 corresponding to one insertion attempt per 500 cycles. | ||
Fig. 4 corresponds to scenario 2 with one insertion attempt per 25 cycles. This time, with this rapid rate of particle insertion, the original fused cluster grows continuously without any obvious fissioning events. However, a primary nucleation event occurs before 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles.
000 cycles.
 | ||
| Fig. 4 As for Fig. 3, except only one insertion attempt per 25 cycles. | ||
Fig. 5 corresponds to scenario 3, i.e. mixed clusters, with one insertion attempt per 1000 cycles. When the cluster grows beyond a size threshold at about 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, further growth occurs along one axis leading to formation of a non-spherical prolate cluster. The formation of a dumbbell or pinched shape can be observed at about 600
000 cycles, further growth occurs along one axis leading to formation of a non-spherical prolate cluster. The formation of a dumbbell or pinched shape can be observed at about 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles due to encountering an instability. Just before 800
000 cycles due to encountering an instability. Just before 800![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, the cluster fissions to create two daughter mixed clusters.
000 cycles, the cluster fissions to create two daughter mixed clusters.
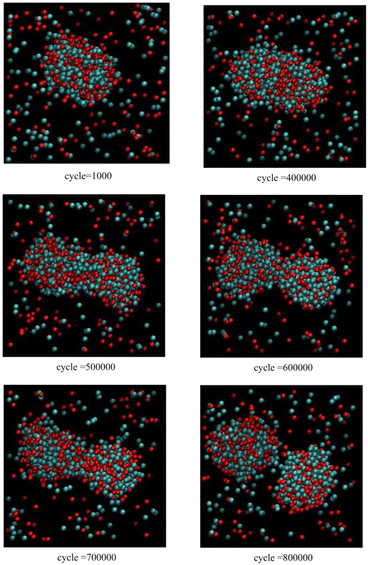 | ||
| Fig. 5 Snapshots from Monte Carlo simulations of binary SALR mixtures for scenario 3 corresponding to one insertion attempt per 1000 cycles. | ||
Fig. 6 corresponds to scenario 3, but now with one insertion attempt per 50 cycles. At this high rate of insertion, a new cluster forms via primary nucleation before 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles and continues to grow.
000 cycles and continues to grow.
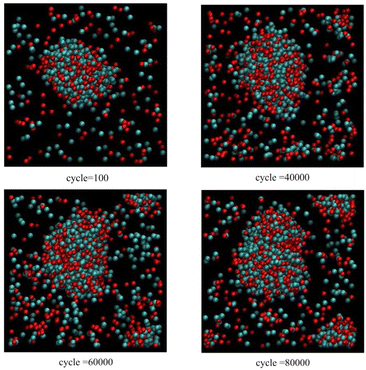 | ||
| Fig. 6 As for Fig. 5, except only one insertion attempt per 50 cycles. | ||
In general, we observe secondary nucleation, fissioning or ‘reproduction’, for all three scenarios when the insertion rate is sufficiently slow, as shown in Fig. 1, 3 and 5. However, when the insertion rate is fast (corresponding to the results in Fig. 2, 4 and 6), clusters do not have sufficient time to relax and undergo secondary nucleation and instead new cluster production typically occurs through primary nucleation in these SALR mixtures. This agrees with similar observations for the pure SALR fluid.19
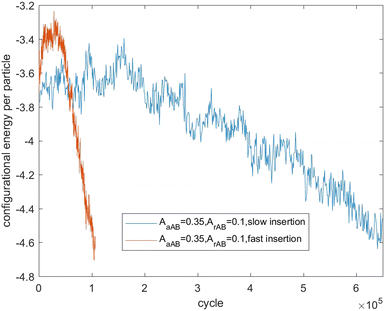
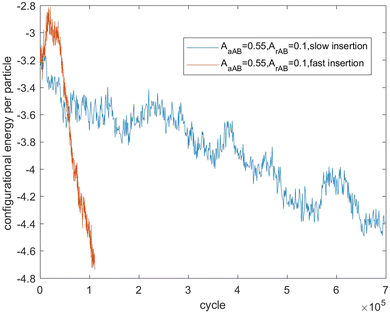
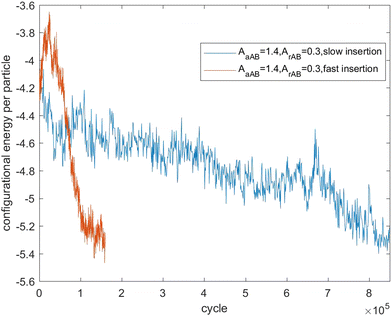
Fig. 7–9 present the evolution of the configurational energy per particle of scenarios 1, 2 and 3, where the blue plots refer to Fig. 1, 3 and 5 (secondary nucleation), and the red plots refer to Fig. 2, 4 and 6 (primary nucleation). A very important common feature of the red plots is that one can observe the formation of a large peak in configurational energy per particle relative to the blue plots. In contrast, all the blue plots tend to decrease gradually. As the starting point of the blue and red plots is identical, it can be concluded that these large energy peaks indicate a larger free energy barrier for primary nucleation compared with secondary nucleation, which agrees with the previous theoretical analysis for the pure SALR fluid.19
Also, in Fig. 10–12, the cluster size evolution of the above three scenarios is presented. Here we use the DBSCAN algorithm to calculate cluster size.26 This algorithm assigns particles to a cluster if they are virtually ‘bonded’ to at least n other particles, where a virtual bond is formed between particles that are separated by less than s. The DBSCAN algorithm should not be very sensitive to the choice of the parameters n and s provided sensible choices are made. Typically, it is sensible to choose n = D + 1, where D is the system dimensionality. This is because D + 1 points in D-dimensional space will generally describe a volume in that space. For s, a sensible choice is a distance similar to the interaction potential well width.
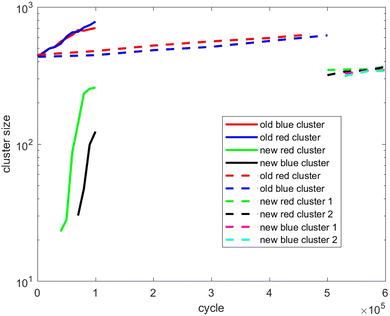 | ||
| Fig. 10 Evolution of the cluster size of scenario 1. The full lines refer to fast insertion and the dash lines refer to slow insertion. | ||
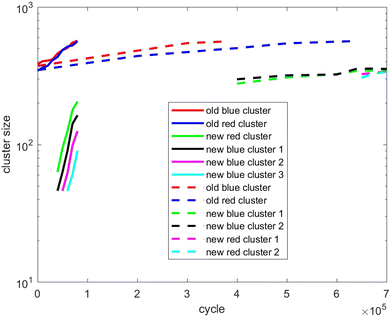 | ||
| Fig. 11 As for Fig. 10, except showing evolution of the cluster size of scenario 2. | ||
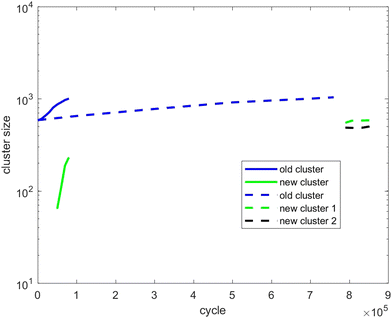 | ||
| Fig. 12 As for Fig. 10, except showing evolution of the cluster size of scenario 3. | ||
Therefore, we choose n = 4 and s = 1.5, which produces cluster sizes that agree well with visual inspection of the snapshots in Fig. 1–6. As there are rapid fluctuations in the population of tiny clusters that never exceed a critical nucleation size, we only consider clusters consisting of more than 10 particles.
Fig. 10 tracks the size of the giant clusters seen in Fig. 1 and 2 corresponding to scenario 1 with slow and fast insertion rates, respectively. We see that initially the cluster size for both clusters is around 450 particles, and for the slow insertion rate the clusters grow until an instability occurs at around 600 particles. Each parent cluster then divides into a pair of daughter clusters with around 300 particles each, as expected. In the case of fast insertion, the original clusters grow rapidly from their initial size of around 450 particles to around 700–800 particles by the end of the simulation without fissioning. New clusters are formed via primary nucleation, reaching sizes around 100–250 particles before the end of the simulation.
Fig. 11 tracks the size of the giant clusters seen in Fig. 3 and 4 corresponding to scenario 2 with slow and fast insertion rates, respectively. We see that initially the cluster size for both clusters is around 350–400 particles for the slow insertion rate and fissioning occurs once they reach around 600 particles. Each parent cluster divides into a pair of clusters with around 300 particles each, as expected. In the case of fast insertion, the original clusters grow rapidly from their initial size of around 350–400 particles to around 600 particles by the end of the simulation without fissioning. New clusters are formed via primary nucleation, reaching sizes between nearly 100 and 200 particles before the end of the simulation.
Fig. 12 tracks the size of the giant clusters seen in Fig. 5 and 6 corresponding to scenario 3 with slow and fast insertion rates, respectively. In this case, there is only one initial mixed cluster of nearly 600 particles. The cluster grows until fissioning at nearly 1000 particles into a pair of clusters with around 500 particles each, as expected. In the case of fast insertion, the original cluster grows rapidly to around 1000 particles by the end of the simulation without fissioning. A new cluster forms via primary nucleation, reaching over 200 particles before the end of the simulation.
4 Conclusions
Similar to the single SALR component system, it is demonstrated here that the clusters in an equimolar symmetric binary SALR mixture can also display secondary nucleation, i.e. fissioning or reproduction. Specifically, when the system concentration increases sufficiently slowly, clusters of this kind of SALR mixture can serve as nucleation centers to produce further clusters. This process seems to occur preferentially to primary nucleation regardless of the ‘scenario’, that is regardless of the cross-interaction strength and the kind of cluster in the system provided the particle concentration increases sufficiently slowly. Investigation of the configurational energy per particle suggests that secondary nucleation occurs in preference to primary nucleation because it has a lower free energy barrier, as predicted by earlier theoretical work.19On the other hand, with a faster insertion rate, the simulation results reveal primary nucleation is preferred. We suggest this is because local fluctuations in the particle concentration can be much larger and lead to the formation of nucleation centers.
As explained in the introduction, we are interested in giant cluster nucleation mechanisms mainly because it is thought they can have a profound effect on the onset of many diseases. Specifically, many diseases are thought to be mediated by cellular membraneless organelles or other biological condensates, and the rate of disease onset is thought to be determined by the proliferation rate of these biological aggregates. Therefore, it is possible that a better understanding of biological condensate nucleation pathways can lead to more effective treatments for many diseases. Since cells are typically crowded with many different kinds of biological molecule, organelle and other condensates, it is important to study the mixture case. Therefore, provided the SALR interaction is a good model for the biological molecules that form such condensates, the insights provided here might find use in future studies of disease.
Specifically, if the slow accumulation regime modelled here is typical within the cellular cytoplasm, and if the SALR interaction is a reasonable model of effective molecular interactions for biological molecules that form condensates within cells, then we can expect that secondary nucleation could also be the dominant production mode for such biological condensates. The reason for this seems to be that the nucleation barrier is much lower compared to primary nucleation. This was also the conclusion of earlier work with the pure SALR fluid.19 It follows that the reason for rapid onset of some diseases might be related to a low free energy barrier for secondary nucleation, compared to primary nucleation, in some biological condensates.
Regarding the origin of life, if the SALR model is reasonable for early biological molecules, then this work also suggests that the development of life might be related to a low free energy barrier for secondary nucleation, i.e. reproduction, relative to primary nucleation for the earliest life-like aggregates. This is perhaps a trivial observation, since it is obvious that no living species, however simple, can spontaneously nucleate through primary nucleation. Indeed, this might be considered a fundamental characteristic of life, which would tend to suggest that viruses, which procreate through primary nucleation, are not alive.
Author statement
All data required to reproduce this work is provided in the text. For the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) license to any Author Accepted Manuscript version arising from this submission.Conflicts of interest
There are no conflicts to declare.References
- S. P. Moulik, Micelles: self-organized surfactant assemblies, Curr. Sci., 1996, 368–376 CAS.
- C. E. Sing and S. L. Perry, Recent progress in the science of complex coacervation, Soft Matter, 2020, 16(12), 2885–2914 RSC.
- A. M. Rumyantsev, N. E. Jackson and J. J. De Pablo, Polyelectrolyte complex coacervates: Recent developments and new frontiers, Annu. Rev. Condens. Matter Phys., 2021, 12, 155–176 CrossRef.
- P. B. Sehgal, J. Westley and K. M. Lerea, et al., Biomolecular condensates in cell biology and virology: Phase-separated membraneless organelles (MLOs), Anal. Biochem., 2020, 597, 113691 CrossRef CAS PubMed.
- V. N. Uversky, Intrinsically disordered proteins in overcrowded milieu: Membrane-less organelles, phase separation, and intrinsic disorder, Curr. Opin. Struct. Biol., 2017, 44, 18–30 CrossRef CAS PubMed.
- I. A. Antifeeva, A. V. Fonin and A. S. Fefilova, et al., Liquid-liquid phase separation as an organizing principle of intracellular space: Overview of the evolution of the cell compartmentalization concept, Cell. Mol. Life Sci., 2022, 79(5), 251 CrossRef CAS PubMed.
- J. C. F. Toledano, F. Sciortino and E. Zaccarelli, Colloidal systems with competing interactions: from an arrested repulsive cluster phase to a gel, Soft Matter, 2009, 5(12), 2390–2398 RSC.
- M. B. Sweatman, R. Fartaria R and L. Lue, Cluster formation in fluids with competing short-range and long-range interactions, J. Chem. Phys., 2014, 140(12), 124508 CrossRef PubMed.
- F. Sciortino, S. Mossa and E. Zaccarelli, et al., Equilibrium cluster phases and low-density arrested disordered states: The role of short-range attraction and long-range repulsion, Phys. Rev. Lett., 2004, 93(5), 055701 CrossRef PubMed.
- A. Stradner, H. Sedgwick and F. Cardinaux, et al., Equilibrium cluster formation in concentrated protein solutions and colloids, Nature, 2004, 432(7016), 492–495 CrossRef CAS PubMed.
- P. D. Godfrin, R. Castañeda-Priego and Y. Liu, et al., Intermediate range order and structure in colloidal dispersions with competing interactions, J. Chem. Phys., 2013, 139, 15 CrossRef PubMed.
- J. A. Bollinger and T. M. Truskett, Fluids with competing interactions. I. Decoding the structure factor to detect and characterize self-limited clustering, J. Chem. Phys., 2016, 145(6), 064902 CrossRef.
- P. D. Godfrin, N. E. Valadez-Pérez and R. Castaneda-Priego, et al., Generalized phase behavior of cluster formation in colloidal dispersions with competing interactions, Soft Matter, 2014, 10(28), 5061–5071 RSC.
- M. B. Sweatman and R. Insall, Assembly of the actin catalyst WASP by giant SALR cluster formation, Adv. Theory Simul., 2019, 2(5), 1800203 CrossRef.
- O. Patsahan, A. Meyra and A. Ciach, Effect of a confining surface on a mixture with spontaneous inhomogeneities, J. Mol. Liq., 2022, 363, 119844 CrossRef CAS.
- G. Munaò, D. Costa and G. Malescio, et al., Competition between clustering and phase separation in binary mixtures containing SALR particles, Soft Matter, 2022, 18(34), 6453–6464 RSC.
- G. Munaò, S. Prestipino and J. M. Bomont, et al., Clustering in Mixtures of SALR Particles and Hard Spheres with Cross Attraction, J. Phys. Chem. B, 2022, 126(9), 2027–2039 CrossRef PubMed.
- O. Patsahan, A. Meyra and A. Ciach, Spontaneous pattern formation in monolayers of binary mixtures with competing interactions, Soft Matter, 2024, 20, 1410–1424 RSC.
- M. B. Sweatman, Giant SALR cluster reproduction, with implications for their chemical evolution, Mol. Phys., 2018, 116(15–16), 1945–1952 CrossRef CAS.
- S. Xu, Z. Hou and X. Chuai, et al., Overview of secondary nucleation: From fundamentals to application, Ind. Eng. Chem. Res., 2020, 59(41), 18335–18356 CrossRef CAS.
- E. Sanz and D. Marenduzzo, Dynamic Monte Carlo versus Brownian dynamics: A comparison for self-diffusion and crystallization in colloidal fluids, J. Chem. Phys., 2010, 132(19), 194102 CrossRef CAS PubMed.
- A. Cuetos and A. Patti, Equivalence of Brownian dynamics and dynamic Monte Carlo simulations in multicomponent colloidal suspensions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92(2), 022302 CrossRef PubMed.
- S. Spannl, M. Tereshchenko and G. J. Mastromarco, et al., Biomolecular condensates in neurodegeneration and cancer, Traffic, 2019, 20(12), 890–911 CrossRef CAS PubMed.
- P. Davies, The origin of life II: How did it begin?, Sci. Prog., 2001, 84(1), 17–29 CrossRef CAS PubMed.
- J. Tan, N. D. Afify and C. A. Ferreiro-Rangel, et al., Cluster formation in symmetric binary SALR mixtures, J. Chem. Phys., 2021, 154(7), 074504 CrossRef CAS PubMed.
- M. Hahsler, M. Piekenbrock and D. Doran, dbscan: Fast density-based clustering with R, J. Stat. Softw., 2019, 91, 1–30 Search PubMed.
| This journal is © the Owner Societies 2024 |